1

select

*

from

S

where

not exists(

select

P#

from

P

where

[WEIGHT]

=

17

and

not exists(

select

*

from

SPJ

where

SPJ

.

S#

=

S

.

S#

and

SPJ

.

P#

=

P

.

P#

)

)

select

*

from

S

where

not exists(

select

P#

from

P

where

[WEIGHT]

=

17

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

)

Komentarz do wykładu Lester MacCann (1)

A counting we will go

2

Komentarz do wykładu Lester MacCann (2)

A counting we will go

Zbędne złączenie z
tabelką P

3

Komentarz do wykładu Lester MacCann (3)

A counting we will go

select

*

from

S

where

not exists(

select

P#

from

P

where

[WEIGHT]

=

17

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

)

select

*

from

S

where

not exists(

select

P#

from

P

where

[WEIGHT]

=

17

except

select

P

.

P#

from

SPJ

,

P

where

SPJ

.

S#

=

S

.

S#

and

SPJ

.

P#

=

P

.

P#

and

P

.

[WEIGHT]

=

17

)

Teraz OK, jest to bo próba
ograniczenia rozmiaru 2go
operandu

4

Komentarz do wykładu Lester MacCann (4)

A counting we will go

Implementacja operatora except za pomocą left anti semi join

select

*

from

S

where

not exists(

select

*

from

P

left outer join

SPJ

on

SPJ

.

P#

=

P

.

P#

and

SPJ

.

S#

=

S

.

S#

where

SPJ

.

P#

is null and

[WEIGHT]

=

17

)

Dzielenie relacyjne z jednym zagnieżdżonym selektem! Duży postęp.

5

Komentarz do wykładu Lester MacCann (4a)

A counting we will go

W zwolnionym tempie:

select

*

from

P

left outer join

SPJ

on

SPJ

.

P#

=

P

.

P#

and

SPJ

.

S#

=

'S5'

where

P

.

[WEIGHT]

=

17

P#

PNAME

COLOR

WEIGHT

CITY

S#

P#

J#

QTY

P2

Bold

Green

17.00

Paris

S5

P2

J2

200

P2

Bold

Green

17.00

Paris

S5

P2

J4

100

P3

Screw

Blue

17.00

Rome

S5

P3

J4

200

select

*

from

P

left outer join

SPJ

on

SPJ

.

P#

=

P

.

P#

and

SPJ

.

S#

=

'S1'

where

P

.

[WEIGHT]

=

17

P#

PNAME

COLOR

WEIGHT

CITY

S#

P#

J#

QTY

P2

Bold

Green

17.00

Paris

NULL

NULL

NULL

NULL

P3

Screw

Blue

17.00

Rome

NULL

NULL

NULL

NULL

Jeżeli S należy do reszty z dzielenia to pojawia się NULL.

6

Komentarz do wykładu Lester MacCann (4b)

A counting we will go

select

*

from

Customers

where

not exists(

select

t2

.

ProductID

from

CEP t1

,

CEP t2

where

t1

.

CustomerID

=

Customers

.

CustomerID

and

t1

.

EmployeeID

=

t2

.

EmployeeID

and

not exists (

select

*

from

CEP t3

where

t3

.

CustomerID

=

Customers

.

CustomerID

and

t3

.

ProductID

=

t2

.

ProductID

and

t3

.

EmployeeID

=

t1

.

EmployeeID

)

)

Pierwsze rozwiązanie miało 6 selektów. (klienci którzy u obsługujących ich
pracowników kupują wszystko co ci pracownicy sprzedają)

Dotychczas: widok CEP oraz zastąpienie exists operatorem złączenia.

7

Komentarz do wykładu Lester MacCann (4c)

A counting we will go

select

*

from

Customers

where

not exists(

select

t2

.

ProductID

from

CEP t1

,

CEP t2

where

t1

.

CustomerID

=

Customers

.

CustomerID

and

t1

.

EmployeeID

=

t2

.

EmployeeID

except
select

t3

.

ProductID

from

CEP t3

where

t3

.

CustomerID

=

Customers

.

CustomerID

)

Krok 1szy zastąpienie podwójnej negacji sprawdzeniem zawierania się zbiorów.
i.e. A

⊆

B

⇔

|A-B|=0

W dalszym ciągu 2 klauzule select.

8

Komentarz do wykładu Lester MacCann (4d)

A counting we will go

select

*

from

Customers

where

not exists(

select

t2

.

ProductID

from

CEP t1

join

CEP t2

on

t1

.

CustomerID

=

Customers

.

CustomerID

and

t1

.

EmployeeID

=

t2

.

EmployeeID

left outer join

CEP t3

on

t3

.

ProductID

=

t2

.

ProductID

and

t3

.

CustomerID

=

Customers

.

CustomerID

where

t3

.

CustomerID

is NULL

)

Już tylko 2 klauzule select. Pamiętamy oryginalnie było 6.

Zadania:

•

wyeliminować ten ostatni operator exists za pomocą outer(anti)join

•

na serwerze aplikacji z wydajnym dostępem do tabel, zaimplementować
samodzielnie proceduralne znajdowanie przedmiotowego zbioru wynikowego.

9

select

*

from

Customers c

where

not exists

(

select

*

from

Employees e

where

exists

(

select

*

from

Orders o

where

o

.

EmployeeID

=

e

.

EmployeeID

and

o

.

CustomerID

=

c

.

CustomerID

)

and

exists (

select

*

from

Products

where

exists (

select

*

from

Orders o

,

[Order Details] od

where

o

.

OrderID

=

od

.

OrderID

and

o

.

EmployeeID

=

e

.

EmployeeID

and

od

.

ProductID

=

Products

.

ProductID

)

and

not exists(

select

*

from

Orders o

,

[Order Details] od

where

o

.

OrderID

=

od

.

OrderID

and

o

.

EmployeeID

=

e

.

EmployeeID

and

c

.

CustomerID

=

o

.

CustomerID

and

od

.

ProductID

=

Products

.

ProductID

)))

select

*

from

Customers

where

not exists(

select

t2

.

ProductID

from

CEP t1

join

CEP t2

on

t1

.

CustomerID

=

Customers

.

CustomerID

and

t1

.

EmployeeID

=

t2

.

EmployeeID

left outer join

CEP t3

on

t3

.

ProductID

=

t2

.

ProductID

and

t3

.

CustomerID

=

Customers

.

CustomerID

where

t3

.

CustomerID

is NULL)

Podwójna negacja, bez wyrażeń
tablicowych, dosłowne użycie
operatorów exists zamiast złączeń.
Tłumaczenie z „języka naturalnego”

Operator except w języku SQL – różnica zbiorów wierszy/ wyrażeń tablicowych

A – B

≡

select * from A

except

select * from B

Równoważna konstrukcja z użyciem exists:
select * from A

where not exists(

select * from B

where

A.a1=B.a1
…

A.an=B.an

)

10

Operator except w języku SQL – różnica zbiorów wierszy/ wyrażeń tablicowych

select OrderID from Orders

except

select EmployeeID from Employees

Bez sensu logicznie ale poprawne składniowo/operacyjnie:

Wymagania SQL dla argumentów operacji na zbiorach:

•

Równa liczba argumentów w wyrażeniach tablicowych

•

Wyrażenia „join compatible” tj. dające się porównać operatorem =

Wniosek: zawsze istnieje równoważ na konstrukcja z exists

exists jest starsze („bardziej standardowe”) niż except

na egzaminie prowadzący może zażądać rozwiązania
bez określonych konstrukcji

11

Dzielenie relacyjne w Wisconsin (1)

α÷β ≡ π

A-B

(

α

) –

π

A-B

(

π

A-B

(

α

)

× β

-

α

)

select A-B from

α

except
select A-B from

( select

α

.[A-B],

β

.B from

α

,

β

except

select * from

α

)

To samo z użyciem notacji SQL i wykorzystaniem operatora except:

Problemy: użyto except, gorsza sprawa – użyto from listen subquery

12

select A-B from

α

except
select A-B from

( select

α

.[A-B],

β

.B from

α

,

β

except

select * from

α

)

Dzielenie relacyjne w Wisconsin (2)

Transformacja automatyczna do exists:

select A-B from

α

where not exists

(

select * from

( select

α

.[A-B],

β

.B from

α

,

β

except

select * from

α

) t
where

t.[A-B]=

α

.[A-B]

)

13

select A-B from

α

where not exists

(

select * from

( select

α

.[A-B],

β

.B from

α

,

β

except

select * from

α

) t
where

t.[A-B]=

α

.[A-B]

)

Dzielenie relacyjne w Wisconsin (3)

select A-B from

α

where not exists

(

select * from

( select

α

1.[A-B],

β

.B from

α

1,

β

not exists

(

select * from

α α

2

where

α

2.[A-B]=

α

1.[A-B]

and

α

2.B =

β

.B

)

) t

where

t.[A-B]=

α

.[A-B]

)

14

select A-B from

α

where not exists

(

select * from

( select

α

1.[A-B],

β

.B from

α α

1,

β

where
not exists

(

select * from

α α

2

where

α

2.[A-B]=

α

1.[A-B]

and

α

2.B =

β

.B )

) t

where

t.[A-B]=

α

.[A-B]

)

Dzielenie relacyjne w Wisconsin (3)

select A-B from

α

where not exists

(

select

α

1.[A-B],

β

.B from

α α

1,

β

where

not exists

(

select * from

α α

2

where

α

2.[A-B]=

α

1.[A-B]

and

α

2.B =

β

.B

) and

α

1.[A-B]=

α

.[A-B]

)

Tzw. migracja predykatu (przeniesienie warunku do wyrażenia w klauzuli from)

15

Migracja predykatu (było na 1szym wykładzie)

select * from (select * from t) where

ϕ

(x)

Można zapisać jako:

select * from t where

ϕ

(x)

W ogólności

select * from (select * from t where

ϕ

1

(x)) where

ϕ

2

(x)

Jest równoważne

select * from t where

ϕ

1

(x) and

ϕ

2

(x)

W efekcie pokazaliśmy, że zapis y except i not exists są równoważne

16

17

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

from

P

select

COUNT

(*)

from

J

where

CITY

=

‘London'

Omówienie zdania 8 z zestawu lab6

Dwa komponenty rozwiązania

18

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

,

(

select

COUNT

(*)

from

J

where

CITY

=

'london'

)

[london jobs]

from

P

Omówienie zdania 8 z zestawu lab6

Dwa komponenty rozwiązania połączone w jedno query

19

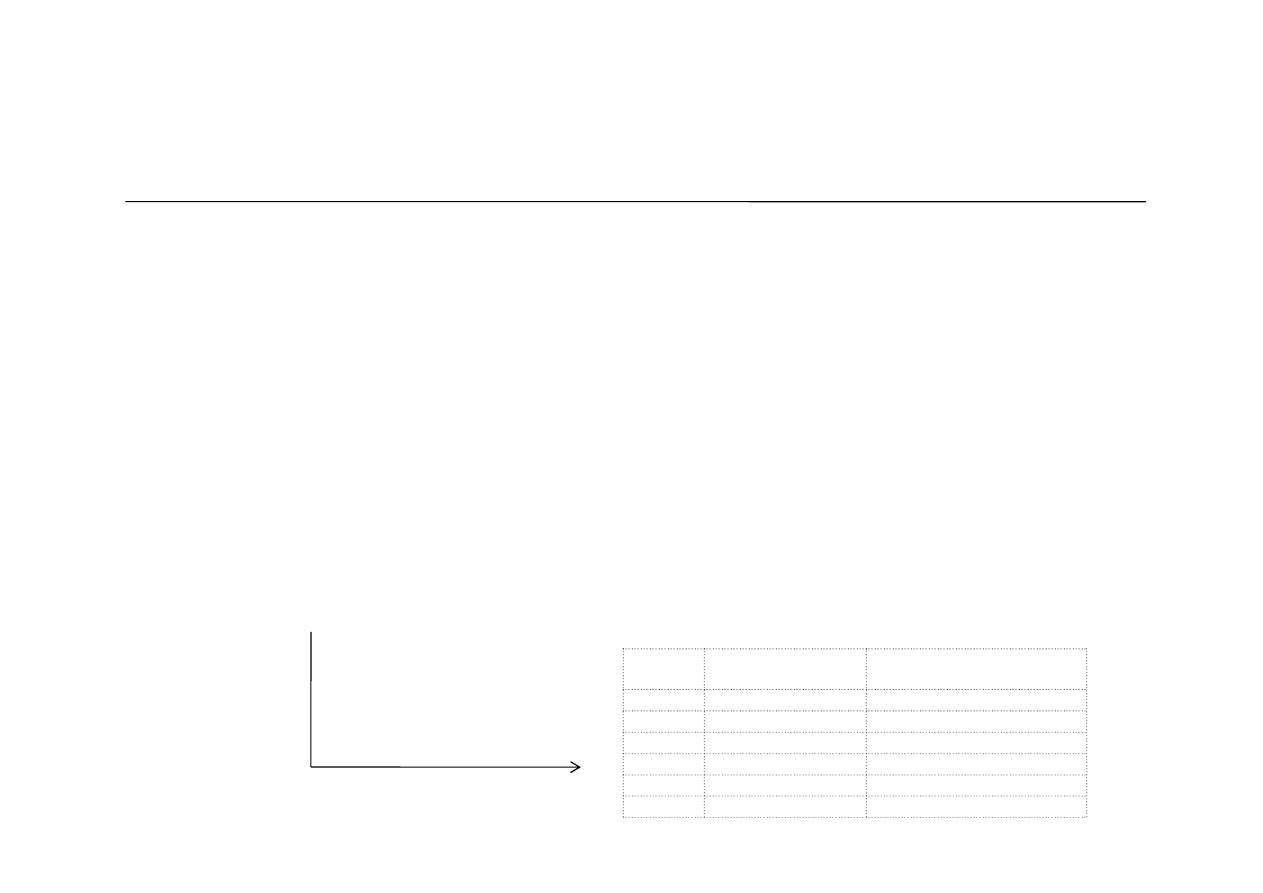
p#

London Jobs

consuming p#

london jobs

P1

0

2

P2

0

2

P3

2

2

P4

0

2

P5

2

2

P6

1

2

Omówienie zdania 8 z zestawu lab6

Jak formatować sprawozdania?

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

,

(

select

COUNT

(*)

from

J

where

CITY

=

'london'

)

[london jobs]

from

P

20

select

p#

from

(

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

,

(

select

COUNT

(*)

from

J

where

CITY

=

'london‘

)

[london jobs]

from

P

)

t

where

t

.

[london jobs]

=

t

.

[London Jobs consuming p#]

Omówienie zdania 8 z zestawu lab6

Łopatologicznie – from listen subquery i wybór wierszy

21

Omówienie zdania 8 z zestawu lab6

Łopatologicznie – from listen subquery i wybór wierszy (cd)

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

,

(

select

COUNT

(*)

from

J

where

CITY

=

'london'

)

[london jobs]

from

P

where

[London Jobs consuming p#]

=

[london jobs]

Nie wolno tak, mimo że logiczne:

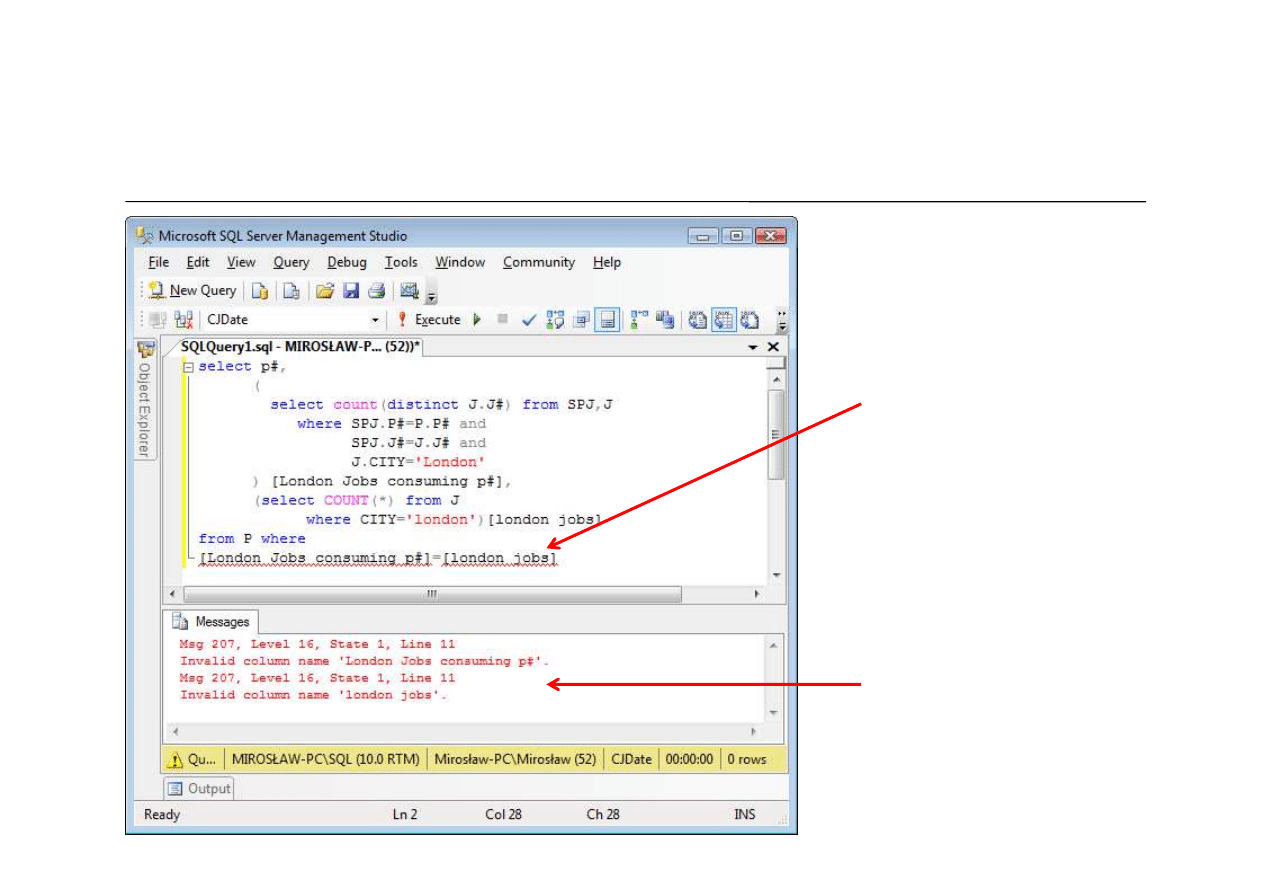
22

Omówienie zdania 8 z zestawu lab6

Łopatologicznie – from listen subquery i wybór wierszy (cd)

pola z klauzuli select

nie wolno

23

Omówienie zdania 8 z zestawu lab6

Łopatologicznie – from listen subquery i wybór wierszy (cd)

select

p#

from

P

where

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

) =
(

select

COUNT

(*)

from

J

where

CITY

=

'London'

)

select

p#

,

(

select

count

(

distinct

J

.

J#

)

from

SPJ

,

J

where

SPJ

.

P#

=

P

.

P#

and

SPJ

.

J#

=

J

.

J#

and

J

.

CITY

=

'London'

)

[London Jobs consuming p#]

,

(

select

COUNT

(*)

from

J

where

CITY

=

'london'

)

[london jobs]

from

P

where

[London Jobs consuming p#]

=

[london jobs]

Nie wolno:

Tak jest OK:

24

Podsumowanie tej części

Dzielenie relacyjne

Możliwe 2 rodzaje zadań:

•

względnie proste wtedy określona zostanie technika rozwiązania, ew. zostaną
nałożone pewne ograniczenia (e.g. nie używać except czy intersect)

•

bardziej złożone dzielenie relacyjne (lub zadania dające się sprowadzić do
dzielenia); wtedy swoboda w używaniu konstrukcji SQL

•

wykorzystanie CTE lub widoków w zadaniach dot. bazy northwind

•

wykorzystanie CTE lub widoków w zadaniach dot. bazy northwind i przekształcenie
wyniku do postaci korzystającej tylko tabelek bazowych

Dzielenie relacyjne - dokończenie

Dotychczas:

•

wykład wstępny poświecony SQL, proste przykłady

•

omówienie notacji opartych na podwójnej negacji i zliczaniu zbiorów wynikowych

•

Uogólnione dzielenie relacyjne (Todd, Date) – zadanie polegające na pokazaniu, że
dzielenie relacyjne jest szczególnym przypadkiem definicji uogólnionych

•

wykład dotyczący nauczania dzielenia relacyjnego Lester McCann: rachunek
relacyjny, operator różnicy zbiorów (except), podwójna negacja zliczanie i zwieranie
się zbiorów

Dalej:

•

Omówienie zadania 3 z zestawu laboratoryjnego 6

•

W sumie 6 różnych zapisów

•

Dokładne dzielenie relacyjne

•

Nowe zagadnienie - dokładne dzielenie relacyjne w wersji (Todd)

25

-- pary s,j: s# dostarcza wszystko co j# u

ż

ywa

-- ale niekoniecznie do j#

-- por. uogólnione dzielenie relacyjne w wersji Todd'a

select

J#

,

S#

from

J

,

S

where

not exists

(

select

*

from

SPJ

where

SPJ

.

J#

=

J

.

J#

and

not exists

(

select

*

from

SPJ SPJ1

where

SPJ1

.

P#

=

SPJ

.

P#

and

SPJ1

.

S#

=

S

.

S#

)

)

Podwójna negacja – kwantyfikator ogólny zastąpiony zanegowanym exists

26

27

-- pozostałe notacje (w sumie 3 z McCann + 2 warianty)

--z rachunku relacyjnego por. Lester McCann

-- uwaga: mo

ż

e by

ć

inna kolejno

ść

wierszy w zbiorze wynikowym!

select

J#

,

S#

from

S

,

J

except

select

J#

,

S#

from

(

select

S

.

S#

,

P#

,

J#

from

SPJ

,

S

except

select

SPJ1

.

S#

,

SPJ2

.

P#

,

SPJ2

.

J#

from

SPJ SPJ1

,

SPJ SPJ2

where

SPJ1

.

P#

=

SPJ2

.

P#

)

t

Rachunek relacyjny i użycie operatora except, dla dzielenia uogólnionego

Dostawcy dostarczają
Wszystkie wykorzystywane części

28

Zliczanie – 1sza postać

--zliczanie zbiorów wynikowych z grupowaniem

--notacja wg Lester McCann

select

J

.

J#

,

S

.

S#

from

J

,

S

,

SPJ

where

SPJ

.

J#

=

J

.

J#

group by

J

.

J#

,

S

.

S#

having

COUNT

(

distinct

P#

)=

(

select

COUNT

(

distinct

SPJ1

.

P#

)

from

SPJ SPJ1

,

SPJ SPJ2

where

SPJ1

.

P#

=

SPJ2

.

P#

and

SPJ1

.

S#

=

S

.

S#

and

SPJ2

.

J#

=

J

.

J#

)

29

--jeszcze raz wg McCann ale teraz odwrócenie zapyta

ń

:

--tj. głównego i podzapytania

select

SPJ1

.

J#

,

SPJ2

.

S#

from

SPJ SPJ1

,

SPJ SPJ2

where

SPJ1

.

P#

=

SPJ2

.

P#

group by

SPJ1

.

J#

,

SPJ2

.

S#

having

COUNT

(

distinct

SPJ1

.

P#

) =

(

select

COUNT

(

distinct

P#

)

from

SPJ

where

SPJ

.

J#

=

SPJ1

.

J#

)

Zliczanie – cd.

30

--zliczanie zbior

ó

w wynikowych z grupowaniem

--notacja podana na moim wykładzie

--przy pewnych zało

ż

eniach (jakich?)

--równowa

ż

no

ść

skorelowanych zapyta

ń

i grupowania

select

J#

,

S#

from

J

,

S

where

(

select

COUNT

(

distinct

P#

)

from

SPJ

where

SPJ

.

J#

=

J

.

J#

)=

(

select

COUNT

(

distinct

SPJ1

.

P#

)

from

SPJ SPJ1

,

SPJ SPJ2

where

SPJ1

.

P#

=

SPJ2

.

P#

and

SPJ1

.

S#

=

S

.

S#

and

SPJ2

.

J#

=

J

.

J#

)

Zliczanie – wersja z wykładu

31

--zawieranie si

ę

zbiorów (McCann)

--chyba najprostsza notacja

-- po wyrzuceniu except dostaje si

ę

rozwi

ą

zanie

-- z podwójn

ą

negacj

ą

--(por. moje uzupełnienie do wykładu McCann'a)

select

J#

,

S#

from

J

,

S

where

not exists

(

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

)

Zawieranie się zbiorów – tj. mniejszy odjąć większy równy pustemu

32

Zadanie 6.3a – do następnego sprawozdania

1) Zapytanie zmodyfikowane, pary s# i j# takie że s# dostarcza do j# wszystko co j#

używa

2) Dokładne dzielenie relacyjne : s# dostarcza dokładnie to co J# używa ( w omawianych

przykładach mógł dostarczać więcej części.

3) Jako wariant zadania 2, dzielenie dokładne z zastrzeżeniem z p.1, tj. dostarcza

dokładnie to co j# używa i dostarcza to do j# (choć może też do innych odbiorców)

4) Ponieważ jest aż 6 notacji z poprzednich slajdów – można podać aż 3*6=18 zapytań

SQL tylko dot. wariantów jednego zadania:)

33

select

J#

,

S#

from

J

,

S

where

not exists

(

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

) and

not exists

(

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

except

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

)

Zadanie 6.3a – dokładne dzielenie, notacja z zawieraniem
Kiedy dwa zbiory są równe?

A

⊆

B czyli A-B=

∅

A

⊇

B czyli B-A=

∅

Skoro A

⊆

B oraz A

⊇

B więc A=B

A

B

34

Zadanie 6.3a c.d. – s# ma dostarczać do j# wszystko co j# używa

select

J#

,

S#

from

J

,

S

where

not exists

(

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

and

SPJ

.

J#

=

J

.

J#

)

Zbiór B nieco pomniejszony
bo dodatkowy warunek.

35

Zadanie 6.3a c.d. – s# ma dostarczać do j# tylko to wszystko co j# używa

Można to zrobić w prosty
„mechaniczny” sposób:

•

za punkt wyjścia przyjąć
poprzednie rozwiązanie

•

skorzystać z różnicy z
zamienionymi argumentami

select

J#

,

S#

from

J

,

S

where

not exists

(

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

except

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

and

SPJ

.

J#

=

J

.

J#

)

and

not exists

(

select

P#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

and

SPJ

.

J#

=

J

.

J#

except

select

P#

from

SPJ

where

SPJ

.

J#

=

J

.

J#

)

36

Zadanie 6.10 dostawcy dostarczający wszystkie części do wszystkich odbiorców

/*

zadanie 10

rozwi

ą

zanie wg. McCann

wyprowadzenie z rachunku relacyjnego

*/

select

S#

from

S

except

select

S#

from

(

--pewien zbiór w którym je

ż

eli S# dostarcza P# do to wszystkich

select

S#

,

P#

,

J

.

J#

from

SPJ

,

J

except

--zobaczmy co z niego zostanie

select

S#

,

P#

,

J#

from

SPJ

)

t

37

Zadanie 6.10 cd.

/*

zadanie 10 rozwi

ą

zanie z pustym podzbiorem

*/

select

S#

from

S

where

not exists

(

select

S#

,

P#

,

J

.

J#

from

SPJ

,

J

where

SPJ

.

S#

=

S

.

S#

except
select

S#

,

P#

,

J#

from

SPJ

where

SPJ

.

S#

=

S

.

S#

)

38

Zadanie 6.10 – zbiór wynikowy

•

Tylko s2 dostarcza p3 do wszystkich odbiorców (a dostarcza jeszcze inne części)

•

Zbiór wynikowy jest pusty

•

Zadanie: dodać do spj wiersze tak, żeby chociaż jeden dostawca spełniał warunek.

•

Ponieważ ma być zachowana zawartość posłużyć się transakcją:

begin transaction

-- ró

ż

ne polecenia insert delete update

rollback transaction

-- przywrócenie stanu sprzed begin transaction

39

begin transaction

insert into

SPJ

(

S#

,

P#

,

J#

,

QTY

)

select

S#

,

P#

,

J

.

J#

,

100

from

SPJ

,

J

where

S#

=

'S1'

and

not exists
(

select

*

from

SPJ SPJ1

where

SPJ1

.

S#

=

SPJ

.

S#

and

SPJ1

.

P#

=

SPJ

.

P#

and

SPJ1

.

J#

=

J

.

J#

)

-- wykona

ć

select z zadania 10

rollback transaction

-- jeszcze raz ten select

Zadanie 6.10 – zbiór wynikowy, cd.

40

select

S#

from

S

where

exists

(

select

*

from

P

where

not exists

(

select

*

from

J

where

not exists

(

select

*

from

SPJ SPJ1

where

SPJ1

.

J#

=

J

.

J#

and

SPJ1

.

P#

=

P

.

P#

and

SPJ1

.

S#

=

S

.

S#

)

)

)

Zadanie 6.9 – w książce 6.43 dostawcy dostarczający jakąś część do wszystkich

/*zadanie 9

rozwi

ą

zanie na negacjach

exists dostawcy dla których

istnieje cz

ęść

taka

ż

e nie istnieje projekt

do której

ten dostawca jej

nie dostarcza

por. Date 6.43

*/

41

/*

rozwi

ą

zanie w ksi

ąż

ce jest długie

teraz skrót,

korzystamy z techniki zast

ę

powania exists

*/

select distinct

S#

from

SPJ

where

not exists

(

select

*

from

J

where

not exists

(

select

*

from

SPJ SPJ1

where

SPJ1

.

P#

=

SPJ

.

P#

and

SPJ1

.

J#

=

J

.

J#

and

SPJ1

.

S#

=

SPJ

.

S#

)

)

Zadanie 6.9 cd.

42

Lab 6 Zadanie Northwind 3 (1)

select

EmployeeID

,

CustomerId

from

Customers

,

Employees e

where

not exists
(

select

*

from

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

where

o

.

CustomerID

=

Customers

.

CustomerID

and

not exists

(

select

*

from

[Order Details] od1

join

Orders o1

on

o1

.

OrderID

=

od1

.

OrderID

where

od1

.

ProductID

=

od

.

ProductID

and

e

.

EmployeeID

=

o1

.

EmployeeID

)

)

Podwójna negacja:

Zadania analogiczne do p.3 i 4 dla bazy CJDate znaleźć pary pracownik (Employee) klient (Customer) takie, że
pracownik obsługuje sprzedaż wszystkich produktów kupowanych przez klienta.
Sens: zarząd firmy może szukać desygnowanych przedstawicieli dla relacji z określonymi klientami

43

Lab 6 Northwind 3 (2)

Rachunek relacyjny :

select

EmployeeID

,

CustomerId

from

Customers

,

Employees

except

select

EmployeeID

,

CustomerId

from

(

select

e

.

EmployeeId

,

ProductID

,

CustomerID

from

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

cross join

Employees e

except

select

o1

.

EmployeeId

,

od

.

ProductID

,

o

.

CustomerID

from

[Order Details] od1

join

Orders o1

on

o1

.

OrderID

=

od1

.

OrderID

,

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

where

od1

.

ProductID

=

od

.

ProductID

)

t

44

•

Koniec dzielenia relacyjnego (jeszcze kilka plansz)

•

Pojawi się dopiero na egzaminie.

•

Pozostaje tylko do ułożenie pozostałych 3*5=15 notacji rozwiązań. (2 z tych
15 jeszcze będą)

•

Oczywiście można rozwiązać tylko wybrane przypadki. Przy dobrym
zrozumieniu rozwiązania podstawowego i pokazanych technik, czynność
mechaniczna.

•

Jeżeli wykona się ćwiczenie w laboratorium: pomoc prowadzącego + dot.
stopień

Koniec

45

Lab 6 Northwind 3 (przedostatni raz)

select

EmployeeID

,

CustomerId

from

Customers

,

Employees e

where

not exists

(

select

*

from

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

where

o

.

CustomerID

=

Customers

.

CustomerID

and

not exists

(

select

*

from

[Order Details] od1

join

Orders o1

on

o1

.

OrderID

=

od1

.

OrderID

where

od1

.

ProductID

=

od

.

ProductID

and

e

.

EmployeeID

=

o1

.

EmployeeID

and

Customers.CustomerId= o1.CustomerId

)

)

Modyfikacja zadania 6 Northwind 3 – ma dostarczać do zadanego klienta

Dodatkowy warunek

46

Lab 6 Northwind 3 (ostatni raz)

To samo za pomocą except – rachunek relacyjny

select

EmployeeID

,

CustomerId

from

Customers

,

Employees

except

select

EmployeeID

,

CustomerId

from

(

select

e

.

EmployeeId

,

ProductID

,

CustomerID

from

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

cross join

Employees e

except

select

o1

.

EmployeeId

,

od

.

ProductID

,

o

.

CustomerID

from

[Order Details] od1

join

Orders o1

on

o1

.

OrderID

=

od1

.

OrderID

,

[Order Details] od

join

Orders o

on

o

.

OrderID

=

od

.

OrderID

where

od1

.

ProductID

=

od

.

ProductID

)

t

(tutaj sprzedaje wszystko co Customer kupuje ale niekoniecznie jemu)

select

EmployeeID

,

CustomerID

from

Employees

,

Customers

except

select

EmployeeID

,

CustomerID

from

(

select

e

.

EmployeeID

,

CustomerID

,

ProductID

from

Orders o

join

[Order Details] od

on

o

.

OrderID

=

od

.

OrderID

cross join

Employees e

except

select

EmployeeID

,

CustomerID

,

ProductID

from

Orders o

join

[Order Details] od

on

o

.

OrderID

=

od

.

OrderID

)

t

(tutaj sprzedaje wszystko co Customer kupuje ale wła

ś

nie jemu)

Ciekawostka: dodatkowy warunek w podwójnej negacji a tutaj krótsze zapytanie

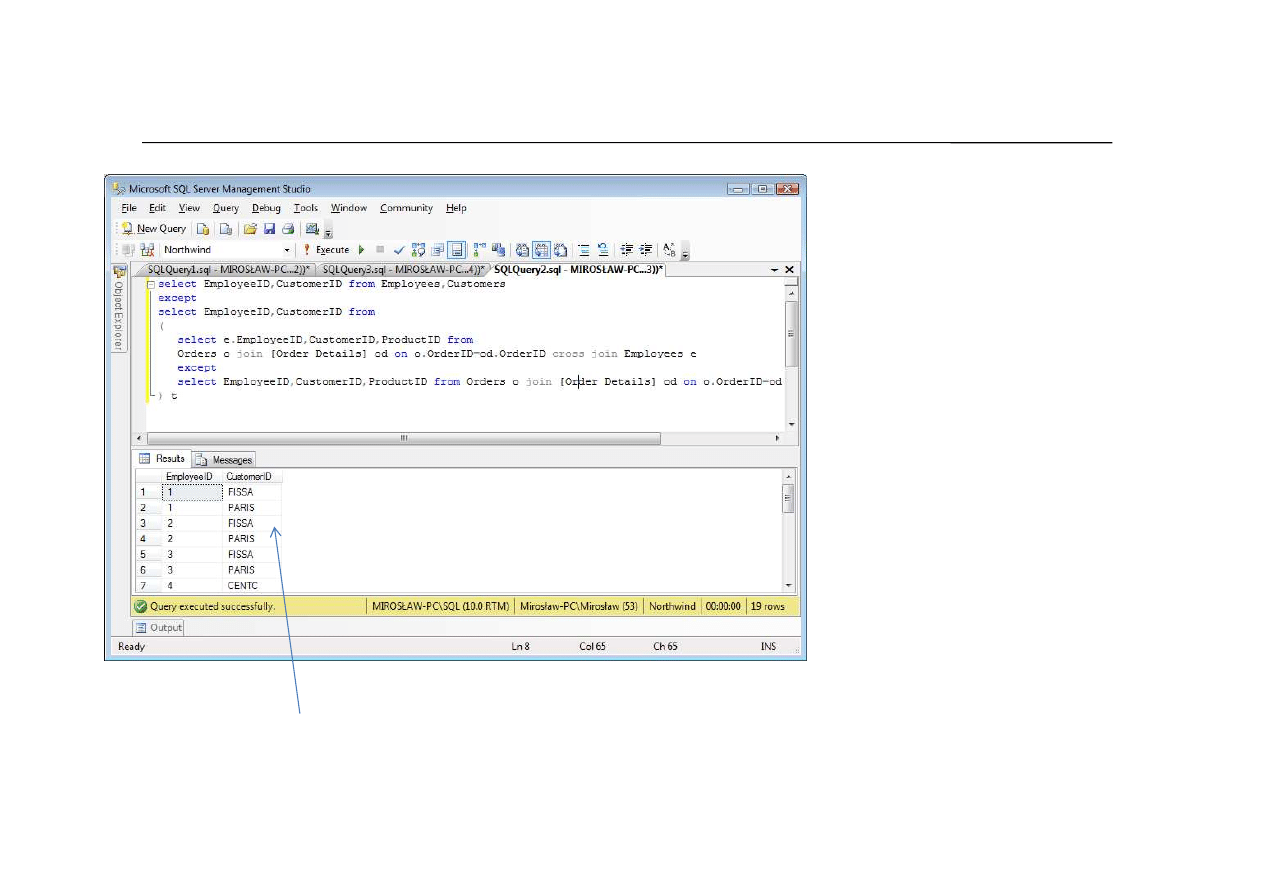
47

Temat pracy inżynierskiej (1)

•

Oprogramowanie edukacyjne.

•

Weryfikacja poprawności
zapytania SQL.

•

Sprawdzenie poprawności
poprzez porównanie zbiorów
wynikowych, warunek
konieczny, niewystarczający

•

Zapytania parametryzowane

Ten sam zbiór wynikowy

Parametryzowanie: zapytanie może być poprawne tylko dla określonych wartości parametrów

48

Temat pracy inżynierskiej (2)

Parametryzowanie: znaleźć dostawców którzy nie dostarczają P2

select

S#

from

S

where

S#

<>(

select distinct

S#

from

SPJ

where

P#

=

'P2'

)

Zadziała dla 1 elementowego zbioru dostawców, dlatego zadanie powinno brzmieć:
znaleźć dostawców którzy nie dostarczają określonej parametrem części

Trudniejsze:
Pytanie SQL jednak zawierają parametry jako stałe:
Program wykrywający te parametry i testujący dla różnych wartości.

Ogólne zasady dla dzielenia relacyjnego 1a

A/B= C

⇔

C= max {Z |Z

⊗

B

⊂

A}

Tj. r

∈

Z

⊗

C ⇒ r

∈

A

)

,

(

)

,

(

,

,

x

r

y

x

r

y

A

y

C

x

B

r

A

y

C

x

B

r

=

∃

¬

∃

¬

⇔

=

∃

∀

∈

∈

∈

∈

∈

∈

Podwójna negacja exists

Definicja, dla relacji A B wynikiem dzielenia jest taka relacja C że:

Reszta z dzielenia:

R=A-(A/B)

⊗

B ,

co jeśli R=

∅

?(zależność wielowartościowa)

49

50

Ogólne zasady dla dzielenia relacyjnego 1b

)

,

(

)

,

(

,

,

x

r

y

x

r

y

A

y

C

x

B

r

A

y

C

x

B

r

=

∃

¬

∃

¬

⇔

=

∃

∀

∈

∈

∈

∈

∈

∈

Podwójna negacja exists

A/B= C

⇔

C= max {Z |Z

⊗

B

⊂

A}

Analogia do dzielenia liczb:

A/B=C

⇔

C= max {Z |Z * B <A}

Mnożenie oraz zwykła relacja porządkująca zamiast iloczynu kartezjańskiego i relacji
zawierania

Ogólne zasady dla dzielenia relacyjnego 2

Zliczanie jako metoda sprawdzenia czy zbiory są równe.
Równa liczność jest warunkiem koniecznym ale niewystarczającym
Warunkiem wystarczającym jest ten sam lub silniejszy predykat (klauzula where)

A =B jeżeli
A={x|

ϕ

(x)},B={x|

φ

(x)} |A|=|B| oraz

ϕ

⇒

φ

. (na pewno jest |A|≤|B| )

Liczba wierszy spełniających predykat jest równa liczbie oczekiwanej.

Jeżeli podzbiór ma liczbę elementów równą nadzbiorowi to znaczy że jest mu równy.

51

Ogólne zasady dla dzielenia relacyjnego 3

Równość zbiorów

Przykład
Zadanie znaleźć pracowników którzy dostarczających te same produkty
Znaleźć pracowników dostarczających te same kategorie produktów.

Sprawdzanie równości zbiorów wynikowych:
1. A=B

⇔

(A

∪

B)- (A

∩

B) =0 (zapisać ten fakt przy użyciu SQL-owych działań na

zbiorach formułując odpowiednie zapytania zagnieżdżone)

2. Drugi sposób polega na tym żeby dwa razy skorzystać z podwójnej negacji w celu

sprawdzenia czy A sprzedaje wszystko co B (tj. czy A

⊂

B)oraz czy B sprzedaje

wszystko co A (B

⊂

A)

3. Wariant p2. korzystający ze zliczania zamiast z podwójnej negacji.

52

Ogólne zasady dla dzielenia relacyjnego 4

Uogólnienia dzielenia relacyjnego:
1) Definicja podstawowa E.F. Codd "A relational Model of large Shared Data Banks"
2) Uogólniona definicja Stephen Todd A{X,Y} i B{Y,Z} A/B zawiera takie wiersze X,Z że

{X,Y} występuje w A dla wszystkich {Y,Z} – prościej rozłożyć relację Y,Z na sumę
względem kolumny Z, wykonać dzielenie i z powrotem zsumować wynik. Gotowe
rozwiązanie zadań typu (kupują u niego wszystko co on sprzedaje)

3) Relacja uogólniona A divide B per AB , definicja (p. Date )

A.X where forall B exists AB {A.X=AB.X and B.Y=AB.Y}

4) Co to znaczy "uogólniona definicja"? ☺
4a) Pokazać że podstawowa definicja dzielenia relacyjnego jest szczególnym

przypadkiem definicji podanych w punktach 2 i 3.

53

54

Ogólne zasady dla dzielenia relacyjnego 4

chillout

2) Uogólniona definicja Stephen Todd A{X,Y} i B{Y,Z} A/B zawiera takie wiersze X,Z że {X,Y}

występuje w A dla wszystkich {Y,Z} – prościej rozłożyć relację Y,Z na sumę względem
kolumny Z, wykonać dzielenie i z powrotem zsumować wynik. Gotowe rozwiązanie
zadań typu (kupują u niego wszystko co on sprzedaje)

{X,Y} – X kupuje produkt Y // X=Customer Y=Product
{Y,Z} – Z sprzedaje Y

// Z=Employee

3) Relacja uogólniona A divide B per AB , definicja (p. Date )

A.X where forall B exists AB {A.X=AB.X and B.Y=AB.Y}

np. A=S B=P AB=SPJ

(AB

÷

B) A

55

Ogólne zasady dla dzielenia relacyjnego 4

Symbol Operatora złączenia

⊳⊲