1

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

1

Radiacyjna wymiana ciep

Radiacyjna wymiana ciep

ł

ł

a

a

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

2

Podstawy fizyczne

Podstawy fizyczne

2

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

3

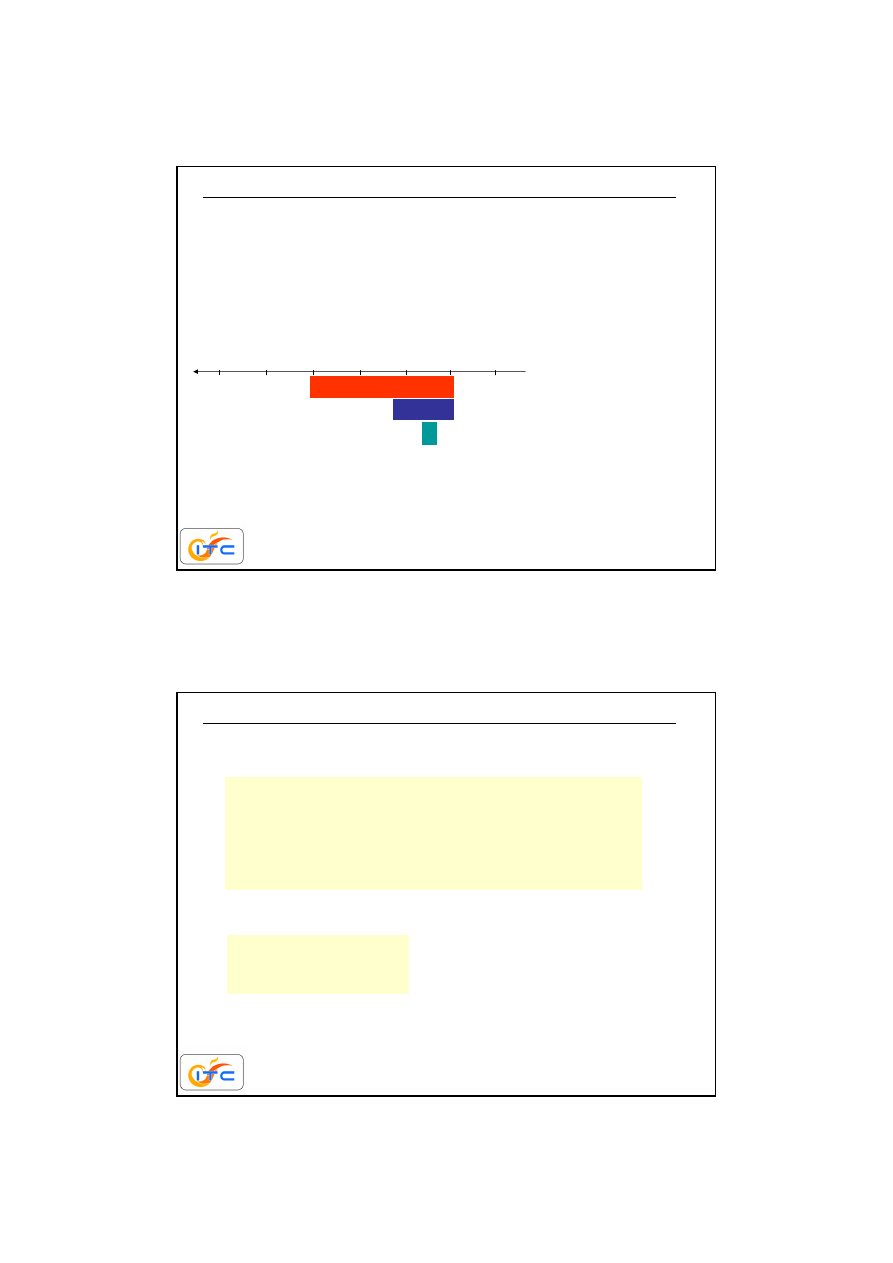
Promieniowanie

transmisja energii przez fale elektromagnetyczne

w pewnym zakresie widma

10

+4

długo

ść

fali

(

µ

m)

10

+3

10

+2

10

+1

10

0

10

-1

10

-2

Promieniowanie cieplne

~0.1-100

µ

m

promieniowanie słoneczne

~0.1-3

µ

m

zakres widzialny

~0.4-0.7

µ

m

λ

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

4

dlaczego promieniowanie jest wa

ż

ne

W podwy

ż

szonych temperaturach dominuj

ą

cy sposób

przekazywania ciepła
•promieniowanie w piecach przemysłowych ~90%
całkowitego strumienia energii
•komory spalania (turbina,spalanie wewn.) ~70%
•konwekcja swobodna temperatury pokojowe ~50%

Gazy rozrzedzone

•kosmos 100%
•techniki pró

ż

niowe ~90%

3

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

5

Ciała nieprzezroczyste

promieniowanie emitowane i pochłaniane w

przypowierzchniowej cienkiej (~1mm) warstwie materiału.

metale,

drewno, skała

MOTTO: Ciało o niezerowej temperaturze emituje
energi

ę

radiacyjn

ą

typy absorberów i emiterów promieniowania

Ciała półprzezroczyste

promieniowanie i pochłanianie w

całej obj

ę

to

ś

ci ciecze, kryształy szkło,

Ciała przezroczyste

nie uczestnicz

ą

w

radiacyjnej wymianie ciepła.

pró

ż

nia,

szkło

, gazy

Typ emitera (absorbera) mo

ż

e zale

ż

e

ć

od temperatury

(długo

ś

ci fali)

efekt szklarniowy

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

6

Podstawowe poj

ę

cia

Podstawowe poj

ę

cia

4

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

7

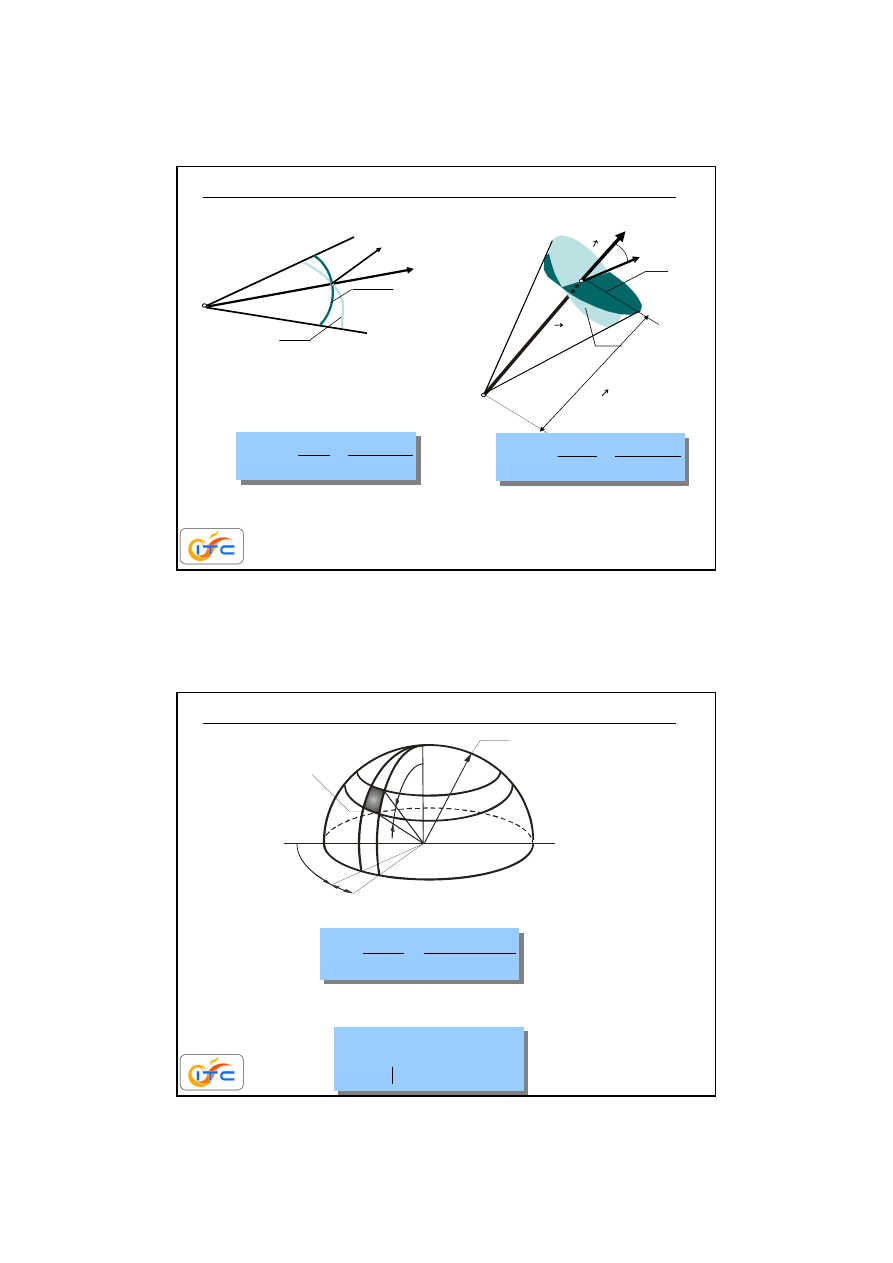
Kąt płaski

dL

dL

p

r

d

α(

p)

|

|

cos

d

|

|

d

)

(

d

p

r

p

r

p

r

r

r

L

L

φ

=

=

α

⊥

- ró

ż

niczkowa długo

ść

łuku

dL

-n

r

φ

r

⊥

kierunek
propagacji

kierunek
propagacji

p

r

d

Γ

⊥

d

Γ

-n

r

d

ω(

p)

φ

r

|r

p|

ω(

p

)

2

2

|

|

cos

d

|

|

d

)

(

d

p

r

p

r

p

r

r

r

r

φ

Γ

=

Γ

=

ω

⊥

- ró

ż

niczkowe pole powierzchni

d

ΓΓΓΓ

Kąt bryłowy

- ró

ż

niczkowa długo

ść

łuku

prostopadła do kierunku
propagacji

dL

⊥

⊥⊥

⊥

-

ró

ż

niczkowe pole powierzchni

prostopadłe do kierunku
propagacji

d

ΓΓΓΓ⊥⊥⊥⊥

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

8

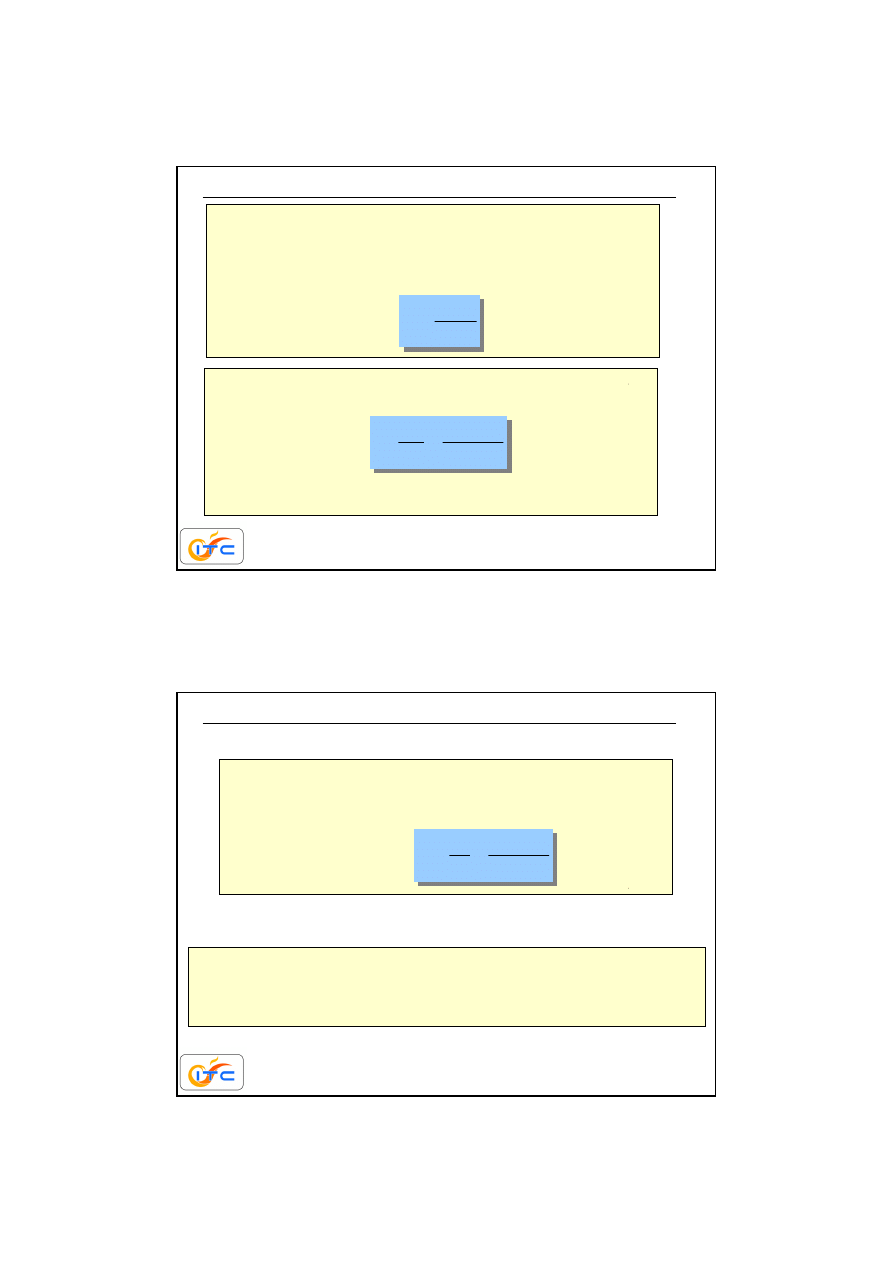
pole zacienionego krzywoliniowego prostok

ą

ta na jednostkowej

sferze jest równe ró

ż

niczkowemu k

ą

towi bryłowemu

2

2

1

d

d

sin

|

|

d

d

ϕ

⋅

Θ

ϕ

=

Γ

=

ω

p

r

r

r

k

ą

t bryłowy w obr

ę

bie półsfery=powierzchnia

jednostkowej półsfery

π

=

Θ

−

=

Θ

ϕ

−

=

ϕ

ϕ

Θ

=

ω

=

ω

∫

∫

∫

∫

∫

π

π

π

π

π

∩

2

1d

-

d

cos

d

sin

d

d

2

0

2

0

2

/

0

2

/

0

2

0

r

r

r =1

ϕ

sin

d

ϕ Θ

d

ϕ

θ

d

θ

5

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

9

strumie

ń

energii radiacyjnej (g

ę

sto

ść

strumienia energii

radiacyjnej)

miara energii przecinaj

ą

cej jednostkow

ą

prostopadł

ą

powierzchni

ę

w jednostkowym czasie

ω

∂

Γ

∂

∂

∂

=

ω

∂

∂

=

⊥

r

r

t

E

e

I

r

r

3

strumie

ń

energii radiacyjnej zawarty w jednostkowym

k

ą

cie bryłowym

⊥

Γ

∂

∂

∂

=

t

E

e

r

r

2

intensywno

ść

promieniowania

miara energii transportowanej w danym kierunku

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

10

spektralna intensywno

ść

promieniowania

strumie

ń

energii niesiony w obr

ę

bie k

ą

ta bryłowego przez fale o

danej długo

ś

ci

wielko

ś

ci spektralne – odniesione do danej długo

ś

ci fali

ω

∂

Γ

∂

∂

∂

=

λ

∂

∂

=

⊥

λ

r

t

E

I

I

r

3

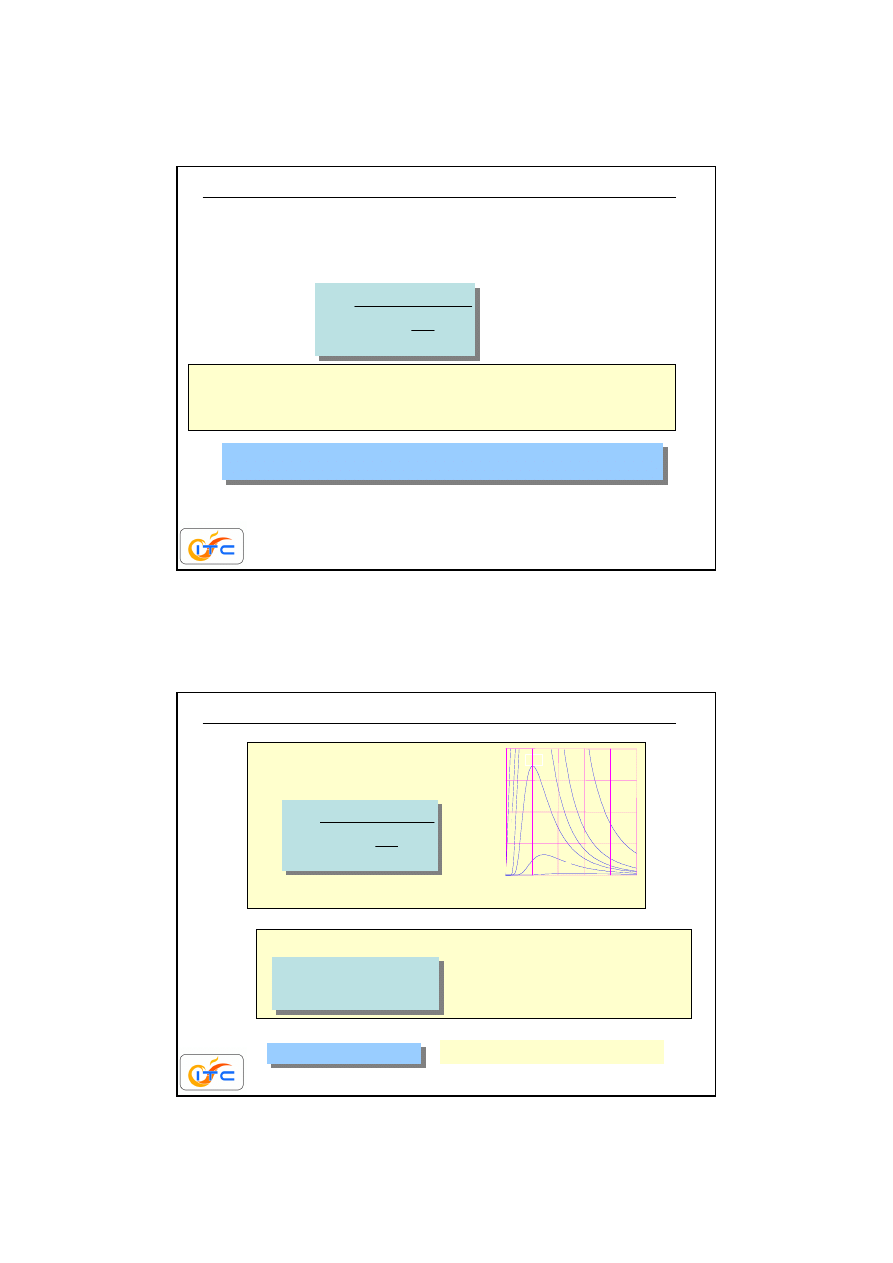
Ciało czarne-

spo

ś

ród wszystkich ciał o tej samej temperaturze ciało

czarne emituje (i absorbuje) najwi

ę

cej energii radiacyjnej. Cała energia

radiacyjna padaj

ą

ca na ciało czarne jest przez to ciało absorbowana.

Ciało czarne jest wa

ż

nym punktem odniesienia

.

6

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

11

Intesywno

ść

promieniowania opuszczaj

ą

cego ciało czarne nie zale

ż

y

od kierunku.

(Spektralna) intensywno

ść

promieniowania ciała

czarnego I

bl

jest stała

(izotropia promieniowania ciała czarnego).













−













λ

λ

=

λ

1

exp

2

5

1

T

C

C

I

b

Spektralna emisja ciała czarnego

Strumie

ń

energii radiacyjnej niesiony przez fale o danej długo

ś

ci,

emitowany przez jednostkow

ą

powierzchni

ę

ciała czarnego

składowa normalna intensywno

ś

ci promieniowania ciała

czarnego scałkowana po całym k

ą

cie bryłowym, do którego

emituje ciało czarne (półsferze)

wzór Plancka

λ

π

λ

π

π

λ

∩

λ

λ

π

=

Θ

=

ϕ

ϕ

ϕ

Θ

=

ω

ϕ

=

∫

∫

∫

∫

b

b

b

b

I

I

I

I

e

2

0

2

/

0

2

0

b

1/2d

d

cos

sin

d

d

cos

r

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

12

600K

1000K

1

8

0

0

K

6

00

0

K

80

60

40

20

2 4 6 8 10

długość fali

µ

m

sp

ek

tr

ra

ln

a

e

m

is

ja

c

a

ił

a

cz

ar

n

eg

o

G

W

/m

3

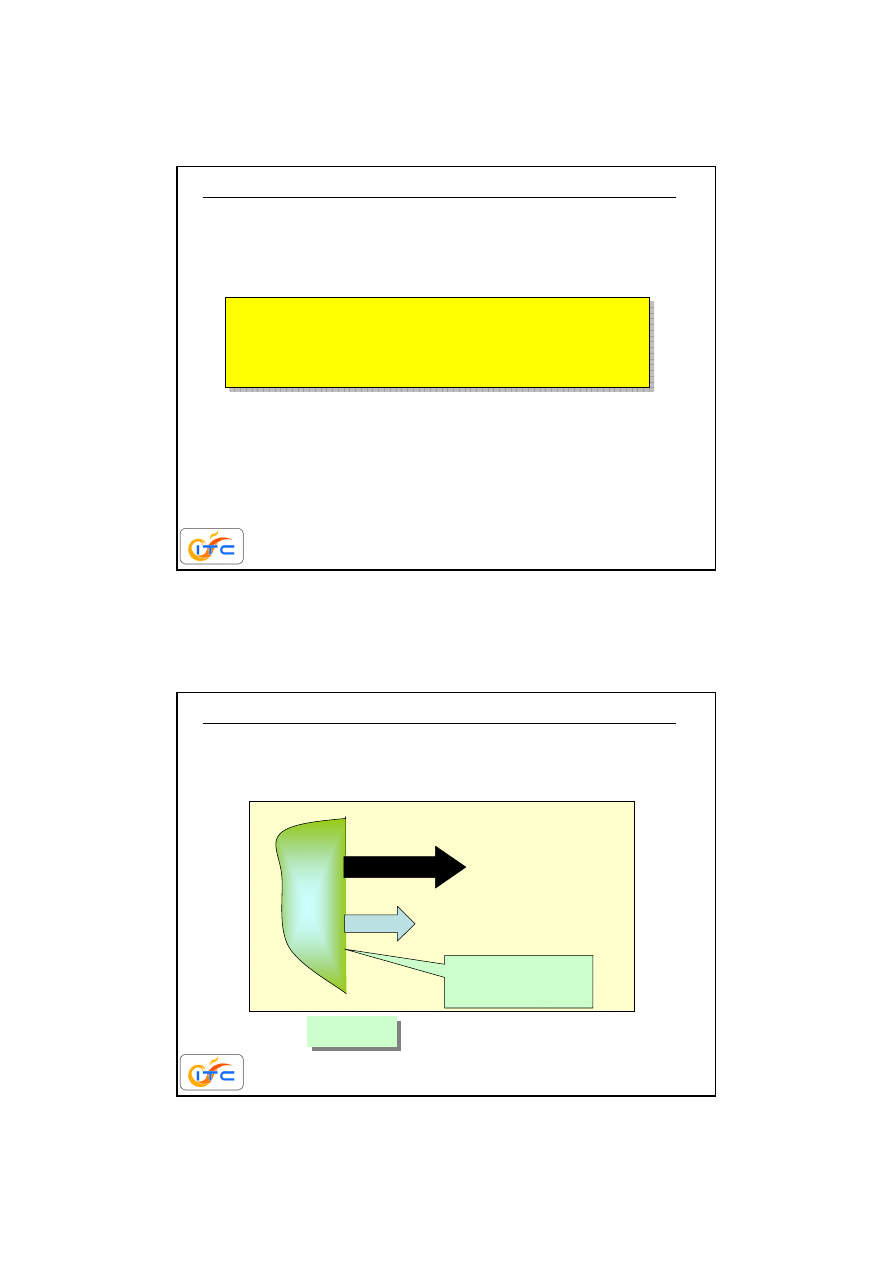
Funkcja Plancka













−













λ

λ

π

=

λ

1

exp

2

5

1

T

C

C

e

b

(całkowita) emisja ciała czarnego

∫

∞

λ

σ

=

π

=

λ

=

0

4

d

T

I

e

e

b

b

b

prawo Stefana
Boltzmanna

1400K

2

5

0

0

K

)

/(

10

667

.

5

4

2

8

K

m

W

⋅

⋅

=

σ

−

stała Stefana Boltzmanna

7

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

13

Promieniowanie powierzchni

nieprzezroczystych

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

14

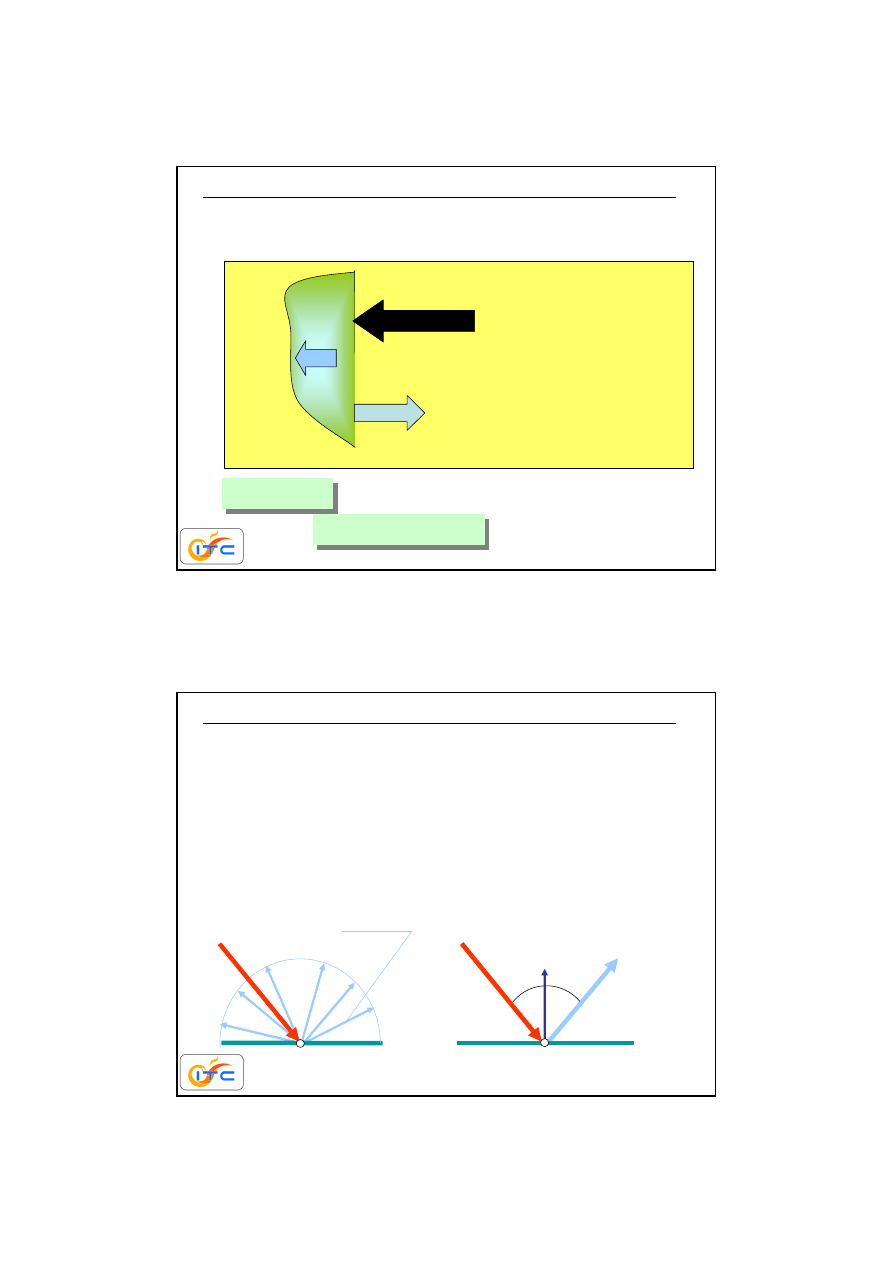
wła

ś

ciwo

ś

ci materiałowe rzeczywistych

powierzchni

e

b

–

emisja powierzchni czarnej=

emisja ciała czarnego

e

–

emisja rzeczywistej

powierzchni

ε =

ε =

ε =

ε =

e

/ / / /

e

b

ε =

ε =

ε =

ε =

e

/ / / /

e

b

powierzchnia

o temperaturze

T

emisyjno

ść

8

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

15

e

i

–

strumie

ń

dopływaj

ą

cej energii

radiacyjnej

e

r

–

strumie

ń

odbitej energii radiacyjnej

α =

α =

α =

α =

e

a

/e

i

=

ε

ε

ε

ε

α =

α =

α =

α =

e

a

/e

i

=

ε

ε

ε

ε

absorpcyjno

ść

=emisyjno

ść

Prawo Kirchhoffa

ρ =

ρ =

ρ =

ρ =

e

r

/e

i

====1111−−−−ε

ε

ε

ε

ρ =

ρ =

ρ =

ρ =

e

r

/e

i

====1111−−−−ε

ε

ε

ε

refleksyjno

ść

e

a

–

strumie

ń

zaabsorbowanej

energii radiacyjnej

wła

ś

ciwo

ś

ci materiałowe rzeczywistych

powierzchni

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

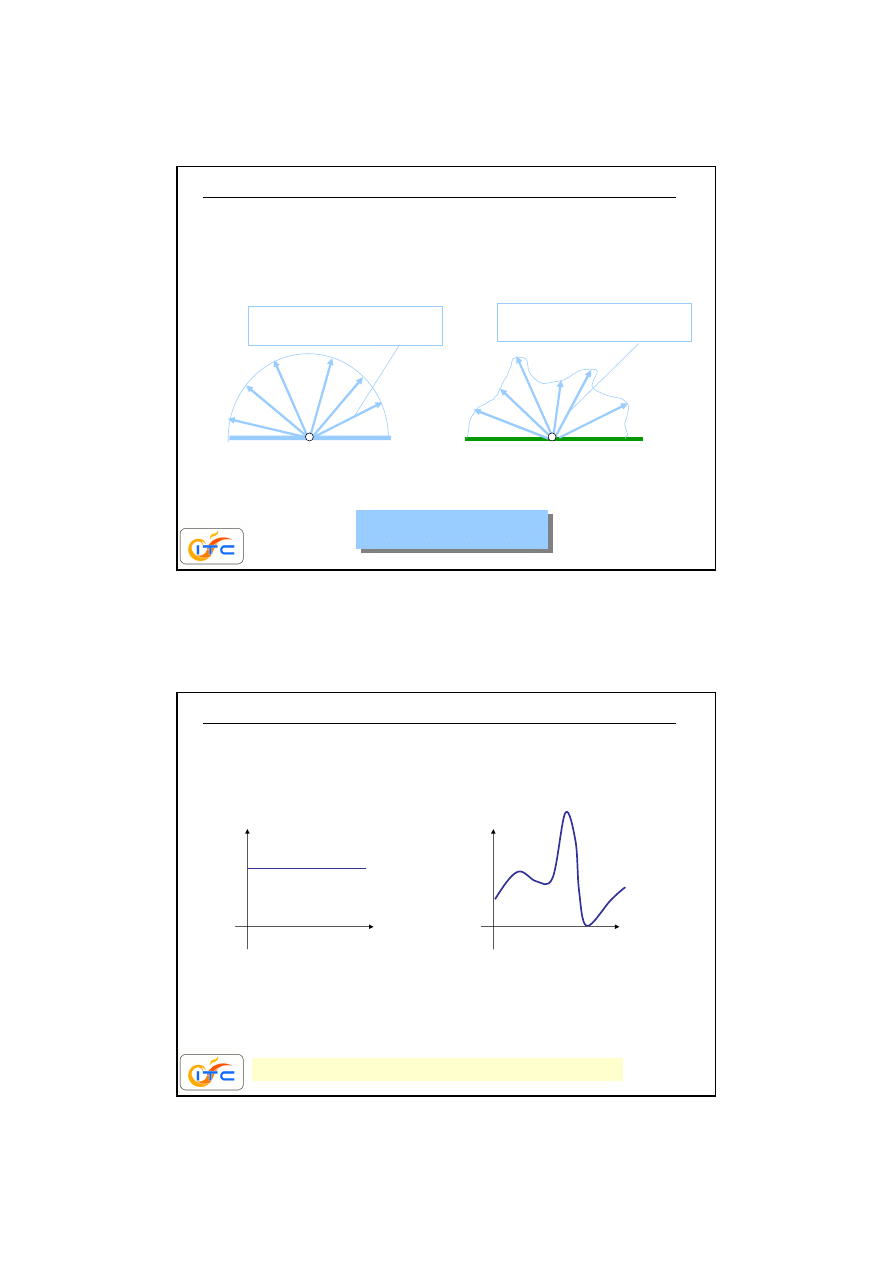
16

reflektor zwierciadlany

reflektor dyfuzyjny

intensywno

ść

odbitego

promieniowania nie zale

ż

y

od kierunku

intensywno

ść

odbitego

promieniowania

intensywno

ść

odbitego promieniowania

zale

ż

y od kierunku

(k

ą

t padania=k

ą

t odbicie)

φφφφ

φφφφ

odbicie promieniowania

intensywno

ść

promieniowania

padaj

ą

cego

I

in

intensywno

ść

promieniowania

padaj

ą

cego

intensywno

ść

promieniowania

odbitego

r

r

9

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

17

emiter niedyfuzyjny

emiter dyfuzyjny

intensywno

ść

promieniowania

emitowanego nie zale

ż

y od kierunku

intensywno

ść

emitowanego

promieniowania

emisja promieniowania

dyfuzyjny emiter i reflektor

– intensywno

ść

promieniowania

opuszczaj

ą

cego powierzchni

ę

nie zale

ż

y od kierunku

)

(

)

,

(

r

r

out

out

I

I

=

ω

r

intensywno

ść

promieniowania

emitowanego zale

ż

y od kierunku

intensywno

ść

emitowanego

promieniowania

r

r

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

18

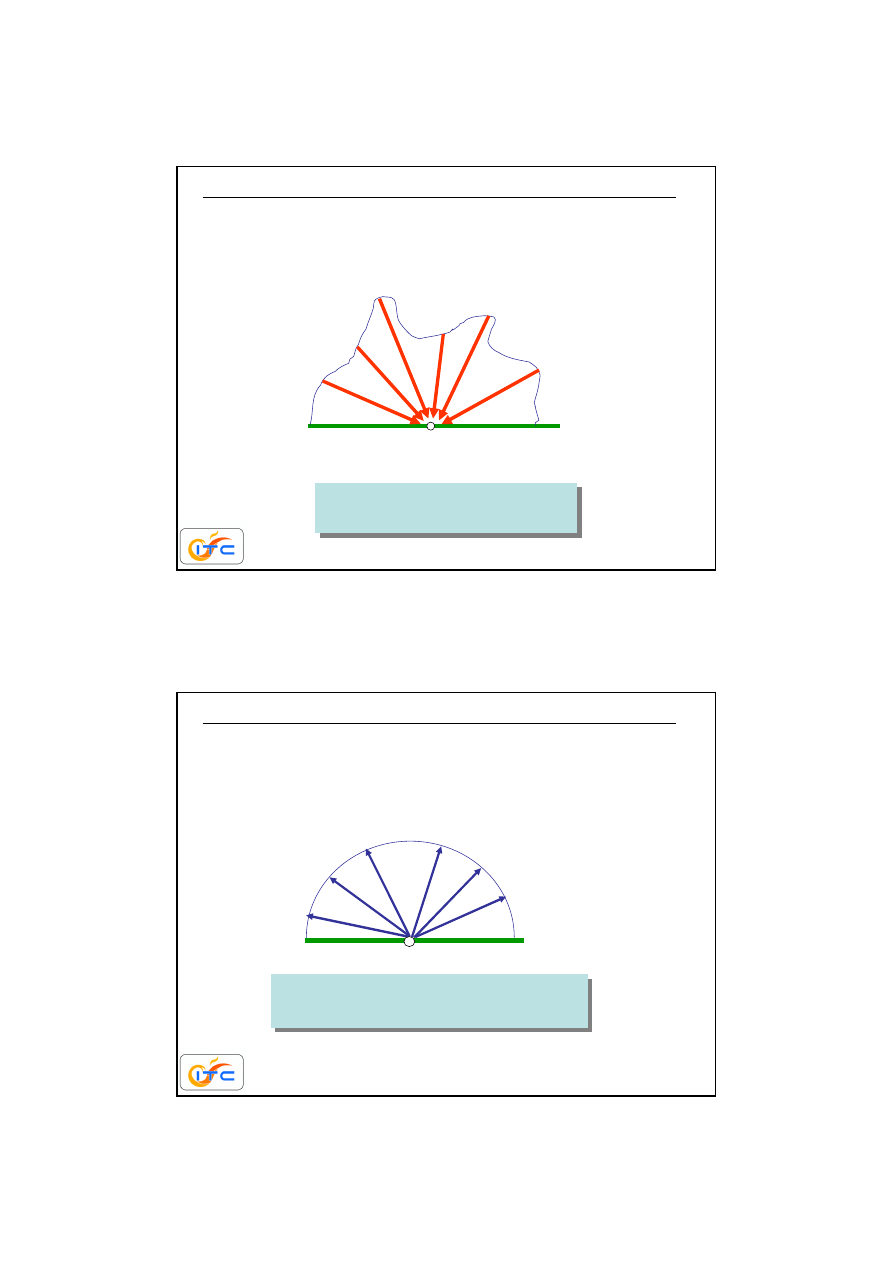
promieniowanie powierzchni

analiza dotyczy szarych i dyfuzyjnych powierzchni

wła

ś

ciwo

ś

ci mog

ą

zale

ż

e

ć

od kierunku i długo

ś

ci fali

• powierzchnia szara - wła

ś

ciwo

ś

ci nie zale

żą

od długo

ś

ci fali

• powierzchnia dyfuzyjna – wła

ś

ciwo

ś

ci nie zale

żą

od kierunku

λλλλ

ΙΙΙΙ

λλλλ

λλλλ

ΙΙΙΙ

λλλλ

ciało szare

ciało nieszare

intensywno

ść

promieniowania mo

ż

e zale

ż

e

ć

od długo

ś

ci fali

10

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

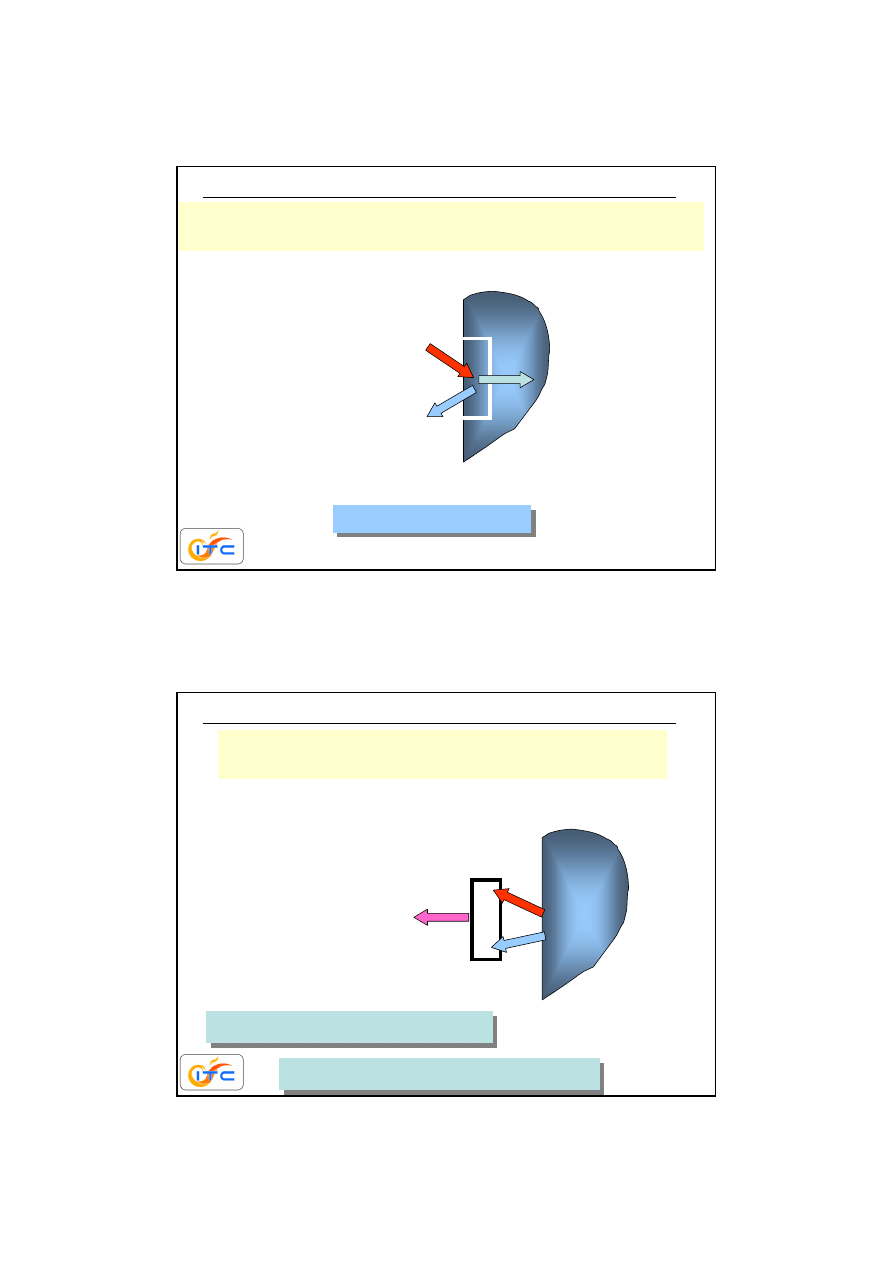
19

opromieniowanie

– całkowity strumie

ń

energii radiacyjnej

dopływaj

ą

cy do powierzchni

∫

π

ω

ϕ

ω

=

2

d

cos

)

,

(

)

(

r

r

r

in

I

g

r

r

silnie zale

ż

y od kierunku

)

,

(

ω

r

r

in

I

r

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

20

emisja własna

–strumie

ń

energii radiacyjnej

emitowanej przez powierzchni

ę

)

(

)

(

d

cos

)

(

)

(

)

(

2

r

r

r

r

r

b

r

b

e

I

e

ε

=

ω

ϕ

ε

=

∫

π

r

dla ciał dyfuzyjnych nie zale

ż

y od kierunku

r

11

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

21

wyemitowana emisja własna

zaabsorbowane opromieniowanie

)

(

)

(

r

r g

ε

( )

r

r

b

e

)

(

ε

q

r

(r)

radiacyjny
strumie

ń

ciepła

Radiacyjny strumie

ń

ciepła

strumie

ń

zaabsorbowanej przez

powierzchni

ę

energii radiacyjnej, netto

)

(

)

(

)

(

)

(

)

(

r

r

r

r

r

b

r

e

g

q

ε

−

ε

=

bilans pod skór

ą

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

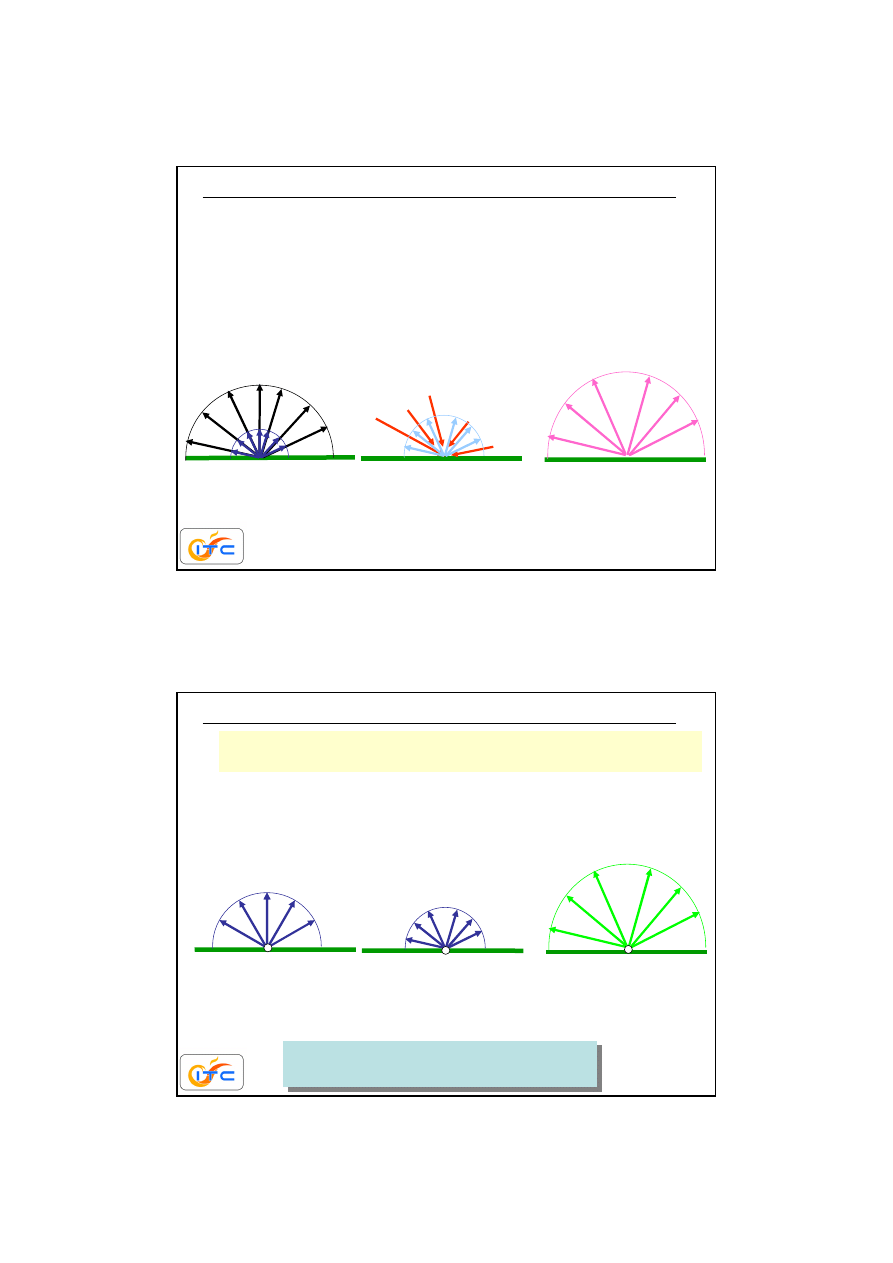
22

Jasno

ść

- całkowity strumie

ń

energii radiacyjnej

opuszczaj

ą

cy powierzchni

ę

jasno

ść

– suma promieniowania wyemitowanego i odbitego

)

(

)

(

)

(

)

(

)

(

r

r

r

r

r

b

g

e

b

=

ρ

+

ε

)

(

)

(

)]

(

1

[

)

(

)

(

r

r

r

r

r

b

g

e

b

=

ε

−

+

ε

ε

−

=

ρ

1

poniewa

ż

wyemitowana
emisja własna

opromieniowanie
odbite

)

(

)

(

r

r g

ρ

( )

r

r

b

e

)

(

ε

b(r)

jasno

ść

bilans nad skór

ą

12

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

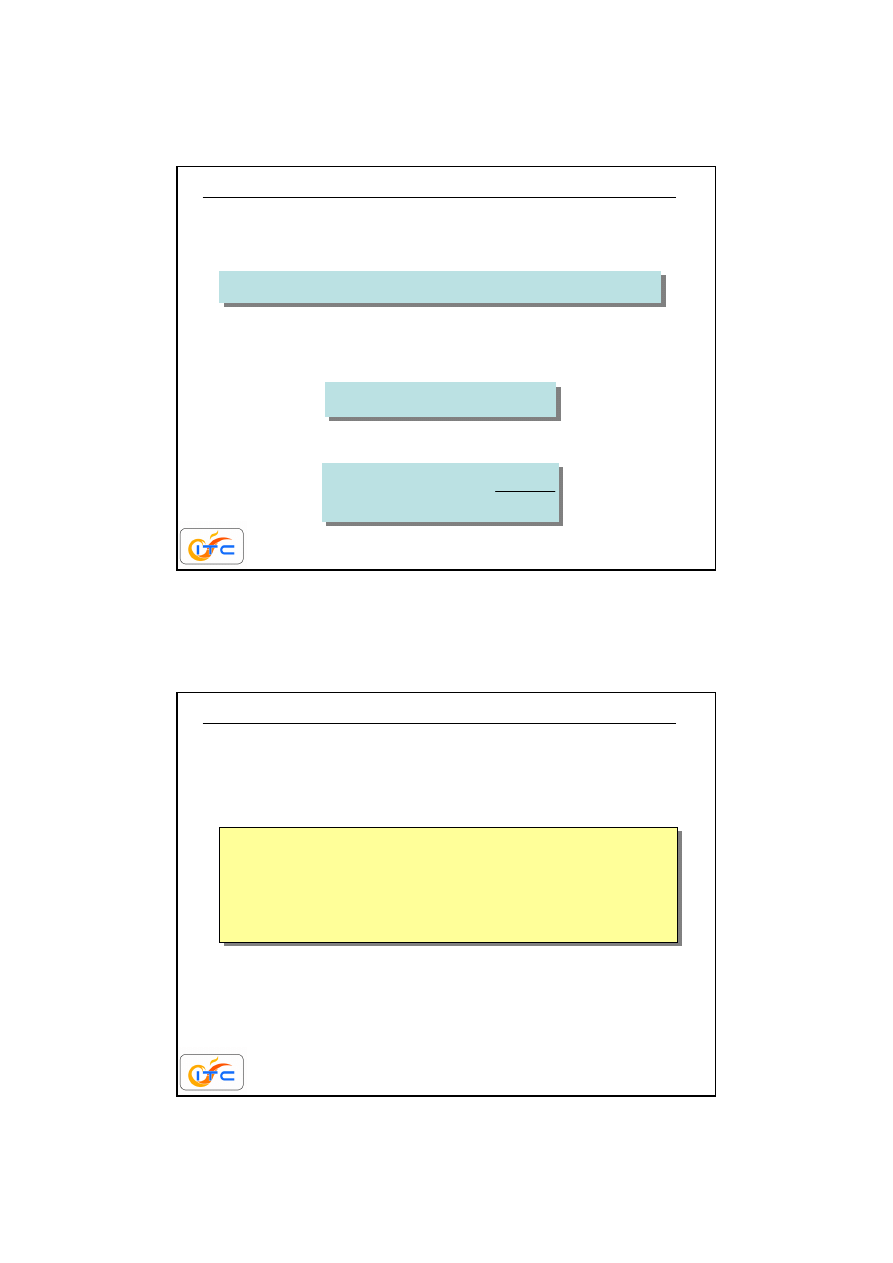
23

jasno

ść

– suma promieniowania wyemitowanego i odbitego

+

=

promieniowanie odbite

emisja

jasno

ść

jasno

ść

b(r)

promienie
padaj

ą

ce

g(r)

promienie
odbite

ρρρρ

(r)g(r)

e

b

(r)

emisja
ciała
czarnego

εεεε

(r)e

b

(r)

emisja
ciała
szarego

jaki charakter ma jasno

ść

: dyfuzyjny czy kierunkowy?

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

24

Zwi

ą

zek mi

ę

dzy jasno

ś

ci

ą

a intensywno

ś

ci

ą

promieniowania

opuszczaj

ą

cego powierzchni

ę

zało

ż

enie dyfuzyjnej emisji i dyfuzyjnego odbicia

powoduj

ą ż

e intensywno

ść

promieniowania opuszczaj

ą

cego

powierzchni

ę

nie zale

ż

y od k

ą

ta

+

=

( )

r

r

r

out

r

out

I

I

b

π

=

ω

ϕ

=

∫

π

2

d

cos

)

(

)

(

r

jasno

ść

jest całk

ą

po k

ą

cie bryłowym normalnej składowej (stałej)

intensywno

ś

ci promieniowania opuszczaj

ą

cego powierzchni

ę

promieniowanie odbite

emisja

jasno

ść

)

(r

out

I

r

r

r

13

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

25

jasno

ść

- suma promieniowania odbitego i emisji własnej

)

(

)]

(

1

[

)

(

)

(

)

(

)

(

)

(

)

(

)

(

r

r

r

r

r

r

r

r

r

g

e

g

e

b

b

b

ε

−

+

ε

=

ρ

+

ε

=

Radiacyjny strumie

ń

ciepła, ró

ż

nica mi

ę

dzy zaabsorbowanym

a wyemitowanym promieniowaniem

)

(

)

(

)

(

)

(

)

(

r

r

r

r

r

b

r

e

g

q

ε

−

ε

=

eliminuj

ą

c opromieniowanie otrzymuje si

ę

)

(

1

)

(

)]

(

)

(

[

)

(

r

r

r

r

r

ε

−

ε

−

=

b

r

e

b

q

Zwi

ą

zek mi

ę

dzy jasno

ś

ci

ą

a radiacyjnym strumieniem ciepła

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

26

Promieniowanie we wn

ę

kach

wypełnionych o

ś

rodkiem

przezroczystym

Promieniowanie we wn

ę

kach

wypełnionych o

ś

rodkiem

przezroczystym

14

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

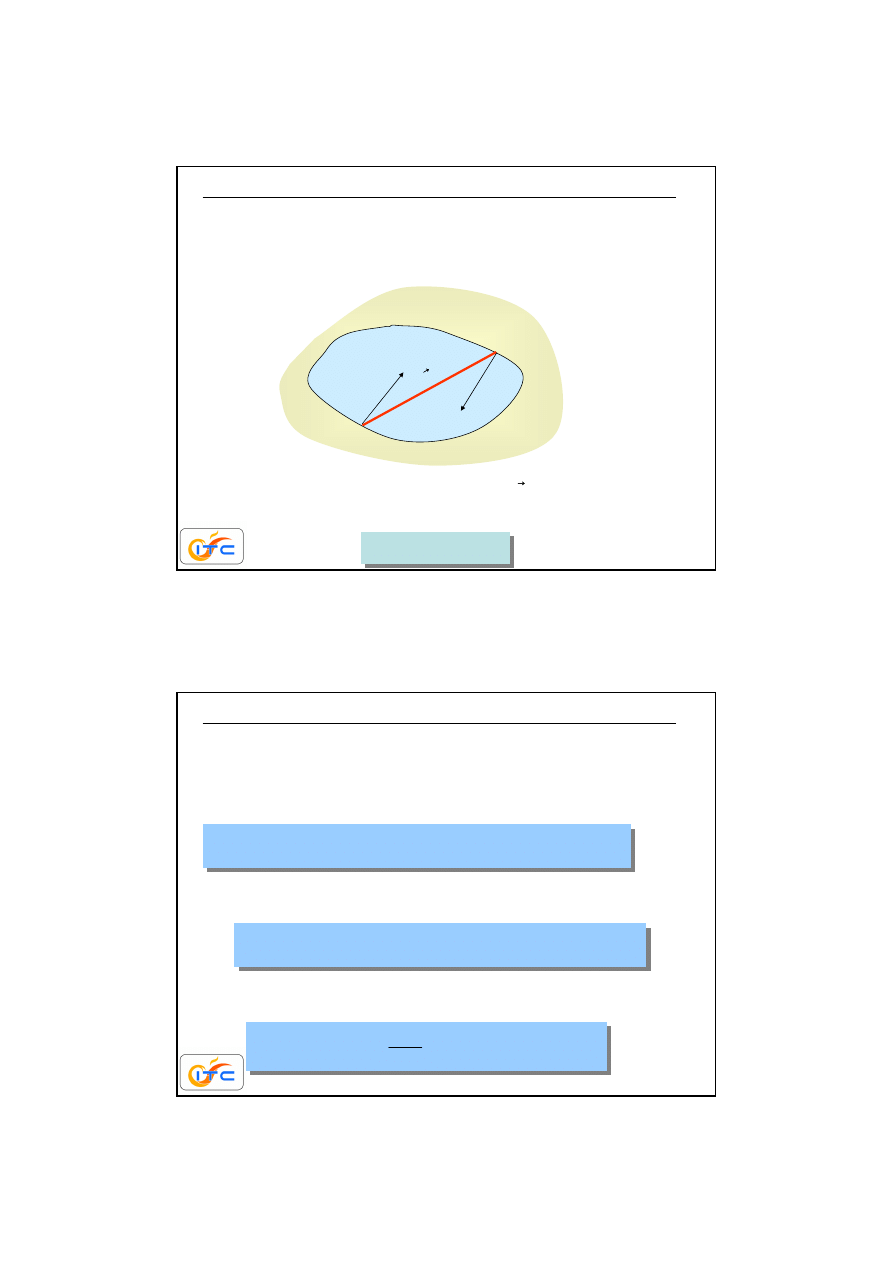
27

Medium nie wpływa na promieniowanie. Intensywno

ść

opuszczaj

ą

ca

punkt

r

nie zmienia si

ę

wzdłu

ż

drogi promienia

rp

.

W punkcie obserwacji

p

jest taka sama jak w punkcie

r

z którego promie

ń

wychodzi

ś

ciany

nieprz

ezrocz

yste

me

diu

m

pr

ze

zro

cz

ys

te

p

r

|rp

|

)

,

(

)

(

ω

=

r

p

r

in

out

I

I

Sformułowanie

• szare, dyfuzyjne

ś

ciany tworz

ą

zamkni

ę

t

ą

wn

ę

k

ę

•

ś

ciany s

ą

wykonane z nieprzezroczystego materiału (ciała stałego)

• medium wypełniaj

ą

ce wn

ę

k

ę

jest przezroczyste

φφφφ

r

φφφφ

p

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

28

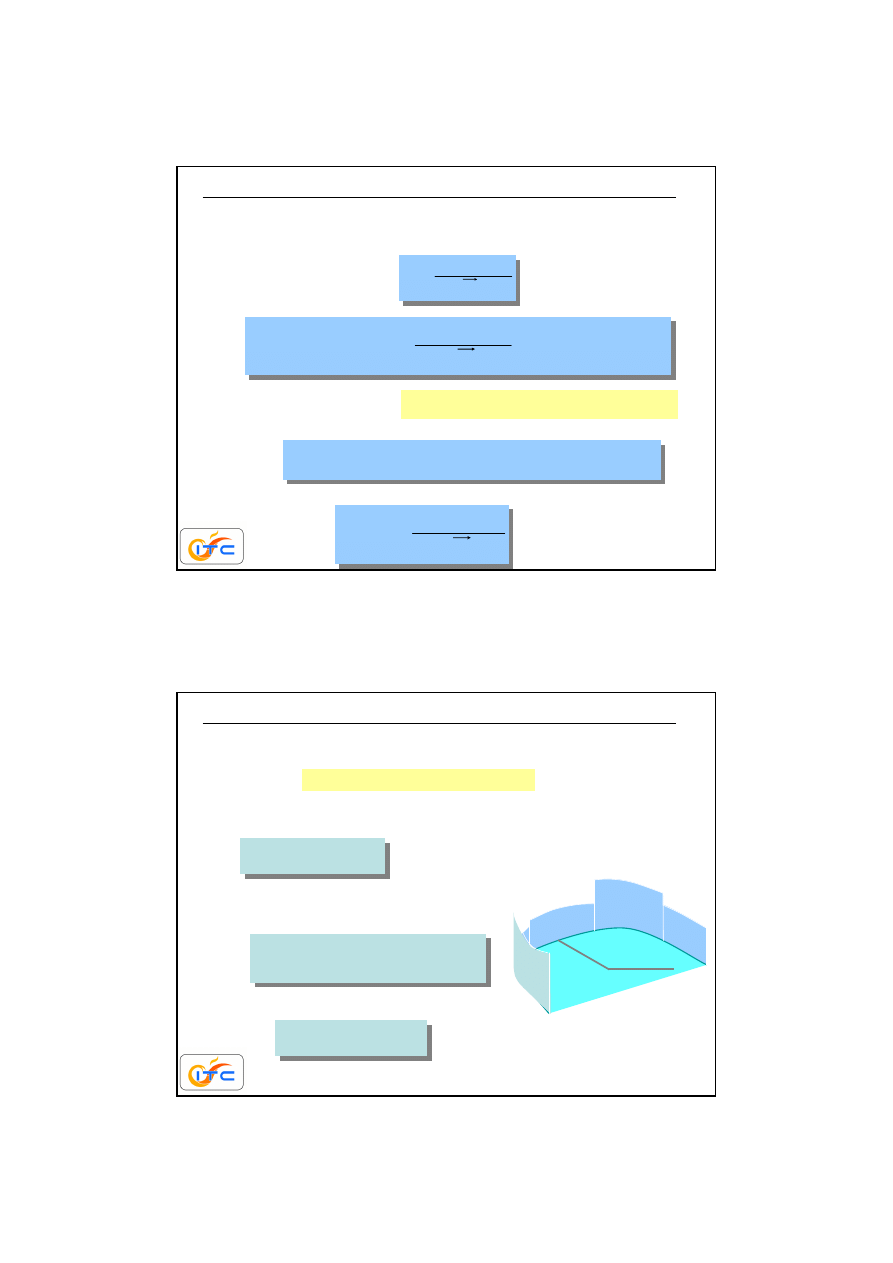
Poszukuje si

ę

zwi

ą

zku mi

ę

dzy

•jasno

ś

ci

ą

b

•emisj

ą

ciała czarnego

e

b

definicja jasno

ś

ci

)]

(

[

)

(

d

cos

)

,

(

)]

(

1

[

)

(

2

p

p

p

p

p

T

e

I

b

b

p

in

ε

+

ω

φ

ω

ε

−

=

∫

π

r

r

Intensywno

ść

w punkcie obserwacji

p

jest równa intensywno

ś

ci

opuszczaj

ą

cej punkt

r

(w kierunku punktu

p

).

)]

(

[

)

(

d

cos

)

(

)]

(

1

[

)

(

2

p

p

r

p

p

T

e

I

b

b

p

out

ε

+

ω

φ

ε

−

=

∫

π

r

)]

(

[

)

(

d

cos

)

(

)]

(

1

[

)

(

2

p

p

r

p

p

T

e

b

b

b

p

ε

+

ω

φ

π

ε

−

=

∫

π

r

Intensywno

ść

w punkcie

r

mo

ż

na wyrazi

ć

przez jasno

ść

w tym

samym punkcie

15

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

29

Wykorzystuj

ą

c definicj

ę

k

ą

ta bryłowego, całk

ę

po tym k

ą

cie

zast

ę

puje si

ę

całk

ą

po powierzchni

ś

cian tworz

ą

cych wn

ę

k

ę

równanie całkowe wi

ążą

ce :

e

b

emisj

ę

ciała czarnego i

b

jasno

ść

2

|

|

cos

cos

)

,

(

rp

p

r

π

φ

φ

=

r

p

K

j

ą

dro równania, zale

ż

y

tylko od geometrii

)]

(

[

)

(

)

(

d

|

|

cos

cos

)

(

)]

(

1

[

)

(

2

p

p

r

rp

r

p

p

T

e

b

b

b

p

r

ε

+

Γ

π

φ

φ

ε

−

=

∫

Γ

2

|

|

cos

)

(

d

d

rp

r

r

φ

Γ

=

ω

r

)]

(

[

)

(

)

(

)d

,

(

)

(

)]

(

1

[

)

(

p

p

r

p

r

r

p

p

T

e

K

b

b

b

ε

+

Γ

ε

−

=

∫

Γ

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

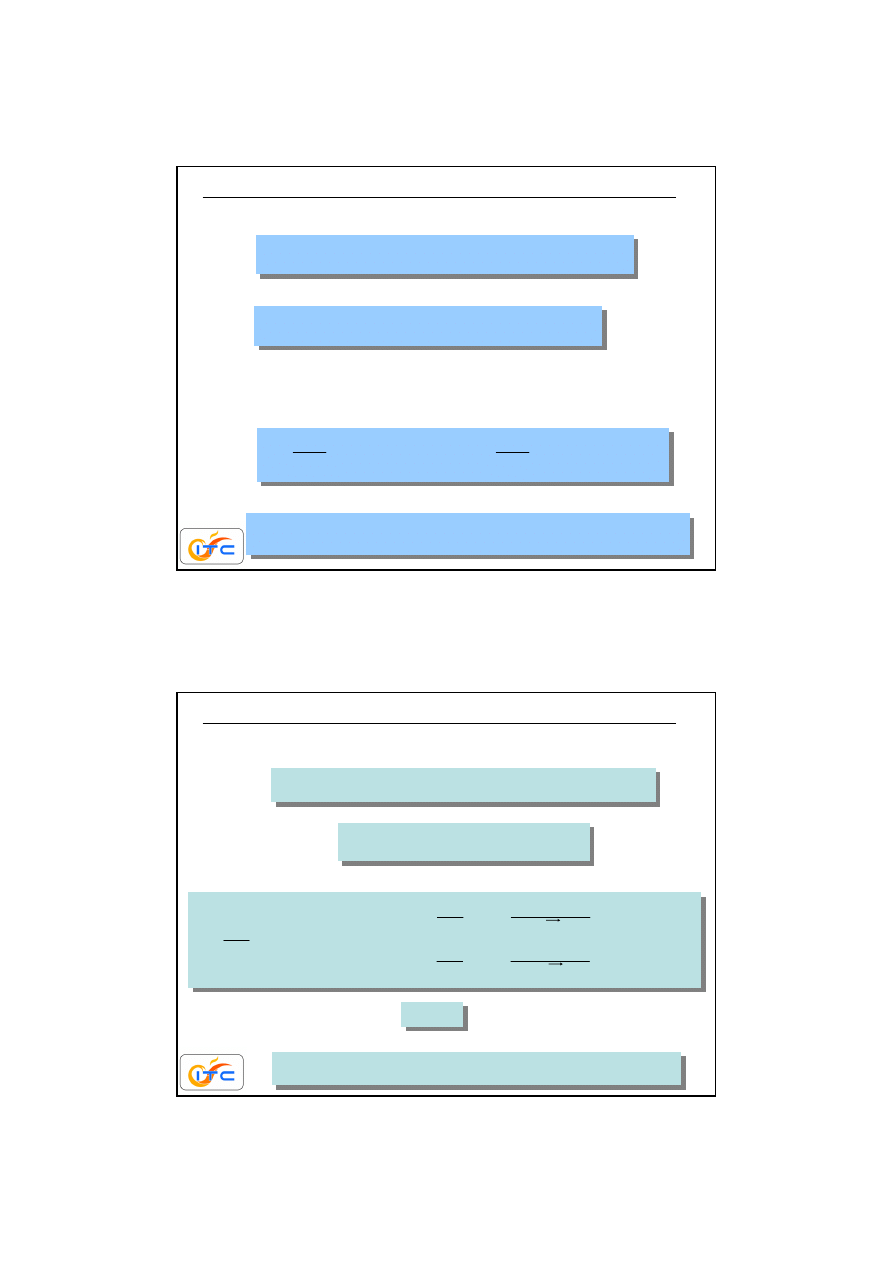
30

•podział brzegu na sko

ń

czon

ą

liczb

ę

N

elementów

∆Γ

∆Γ

∆Γ

∆Γ

i

•aproksymacja jasno

ś

ci i emisji ciała czarnego. Zamiast poszukiwa

ć

dokładnego rozkładu jasno

ś

ci i emisji ciała czarnego, szukamy

wielko

ś

ci

ś

rednich w elemencie

Uproszczenie

ś

rednia warto

ść

jasno

ś

ci w

i-

tym elemencie

N

i

(r)

funkcja okienkowa







∆Γ

−

elementach

h

pozostalyc

w

-

0

elemencie

tym

w

-

1

)

(

i

i

i

N r

e

b

aproksymowane analogicznie

brzeg

i

b

∑

=

≅

n

i

i

bi

b

N

e

e

1

)

(

)

(

r

r

∑

=

≅

n

i

i

i

N

b

b

1

)

(

)

(

r

r

1

−

i

b

i

b

1

+

i

b

funkcja schodkowa

16

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

31

wyj

ś

ciowe równanie

1

( )

[1

]

( , )d ( )

( )

i

n

j

i

j b

i

b

b

K

e

=

∆Γ

≈ − ε

Γ

− ε

∑

∫

p

r p

r

p

)]

(

[

)

(

)

(

)d

,

(

)

(

)]

(

1

[

)

(

p

p

r

p

r

r

p

p

T

e

K

b

b

b

ε

+

Γ

ε

−

=

∫

Γ

zakłada si

ę

stało

ść

emisyjno

ś

ci i jasno

ś

ci w elemencie

aby wprowadzi

ć ś

redni

ą

warto

ść

jasno

ś

ci i emisji ciała czarnego w

elemencie do którego nale

ż

y punkt

p

całkuje si

ę

obie strony po

elemencie

∆Γ

∆Γ

∆Γ

∆Γ

j

1

1

( )d ( );

( )d ( );

j

j

j

b j

b

j

j

b

b

e

e

∆Γ

∆Γ

=

Γ

=

Γ

∆Γ

∆Γ

∫

∫

p

p

p

p

po wprowadzeniu całek, wzór przyjmuje posta

ć

1

[1

]

( , )d ( )d ( )

j

i

n

j

j

j

i

j

j b j

i

b

b

K

e

=

∆Γ

∆Γ

∆Γ

= − ε

Γ

Γ

− ∆Γ ε

∑

∫ ∫

r p

r

p

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

32

równanie

0

)

(

d

)

(

d

)

,

(

]

1

[

1

=

∆Γ

ε

−

Γ

Γ

ε

−

−

∆Γ

∫ ∫

∑

∆Γ

∆Γ

=

j

bj

j

n

i

i

j

j

j

e

K

b

b

j

i

p

r

p

r

zapisuje si

ę

jako

ji

j

ji

ji

bj

j

j

j

j

F

e

b

)

1

(

}

{

}

{

;

}

{

ε

−

−

δ

=

ε

=

=

F

e

b

0

]

1

[

1

=

ε

−

ε

−

−

∑

=

bj

j

ji

n

i

i

j

j

e

F

b

b

gdzie

F

ji

współczynnik konfiguracji













Γ

Γ

φ

φ

∆Γ

Γ

Γ

π

φ

φ

∆Γ

=

Γ

Γ

∆Γ

=

∫ ∫

∫ ∫

∫ ∫

∆Γ

∆Γ

∆Γ

∆Γ

∆Γ

∆Γ

j

i

j

i

j

i

D

D

K

F

p

j

p

j

j

ji

2

)

(

d

)

(

d

|

|

2

cos

cos

1

3

)

(

d

)

(

d

|

|

cos

cos

1

)

(

d

)

(

d

)

,

(

1

r

2

r

p

r

rp

p

r

rp

p

r

p

r

w postaci macierzowej

e

Fb

=

gdzie elementy macierzy i wektorów zdefiniowane s

ą

jako

17

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

33

własno

ś

ci współczynników konfiguracji

zamkni

ę

to

ść

∫ ∫

∆Γ

∆Γ

Γ

Γ

π

φ

φ

=

∆Γ

=

∆Γ

j

i

p

ij

i

ji

j

F

F

)

(

d

)

(

d

|

|

cos

cos

2

r

p

r

rp

wzajemno

ść

0

=

ii

F

samoopromieniowanie

powierzchni płaskich i wypukłych

)

(

1

)

(

)]

(

)

(

[

)

(

r

r

r

r

r

ε

−

ε

−

=

b

r

e

b

q

dla układów izotermicznych nie ma przepływu
ciepła, czyli

q

r

j

=0

st

ą

d

b

j

=e

bj

∑

=

ε

−

+

ε

=

N

i

ji

bi

j

bj

j

j

b

F

e

e

e

1

)

1

(

∑

=

ε

−

+

ε

=

N

i

ji

i

j

bj

j

j

F

b

e

b

1

)

1

(

w układzie izotermicznym wszystkie emisje ciała czarnego s

ą

takie same

e

bj

=e

bj

∑

=

=

N

i

ji

F

1

1

∑

=

ε

−

+

ε

=

N

i

ji

j

j

F

1

)

1

(

1

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

34

wyznaczanie współczynników konfiguracji 1

je

ś

li układ składa si

ę

z

N

powierzchni jest

N

2

współczynników

1) zasada wzajemno

ś

ci generuje dodatkowych warunków

2) zasada zamkni

ę

to

ś

ci daje

N

dodatkowych warunków

3) je

ś

li nie ma powierzchni wkl

ę

słych – dodatkowo

N

warunków

Potrzeba co najwy

ż

ej

N(N-1)/2

współczynników (wszystkie elementy

s

ą

wkl

ę

słe) lub

N(N-3)/2

(nie ma ani jednego wkl

ę

słego elementu)

Dla układu trójpowierzchniowego o płaskich

ś

ciankach nie trzeba

ani jednego współczynnika konfiguracji. Dla pi

ę

ciopowierzchniowego

układu o płaskich elementach potrzeba pi

ęć

warto

ś

ci

F

ij

.

2

)

1

(

−

N

N

Brakuj

ą

ce współczynniki znale

źć

mo

ż

na

• w katalogach np.

http://www.me.utexas.edu/~howell/

• obliczy

ć

z definicji stosuj

ą

c kwadratury numeryczne (uwaga na

cienie i osobliwo

ść

funkcji podcałkowej)

• w 2D znale

źć

metod

ą

nitkow

ą

Hotella

18

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

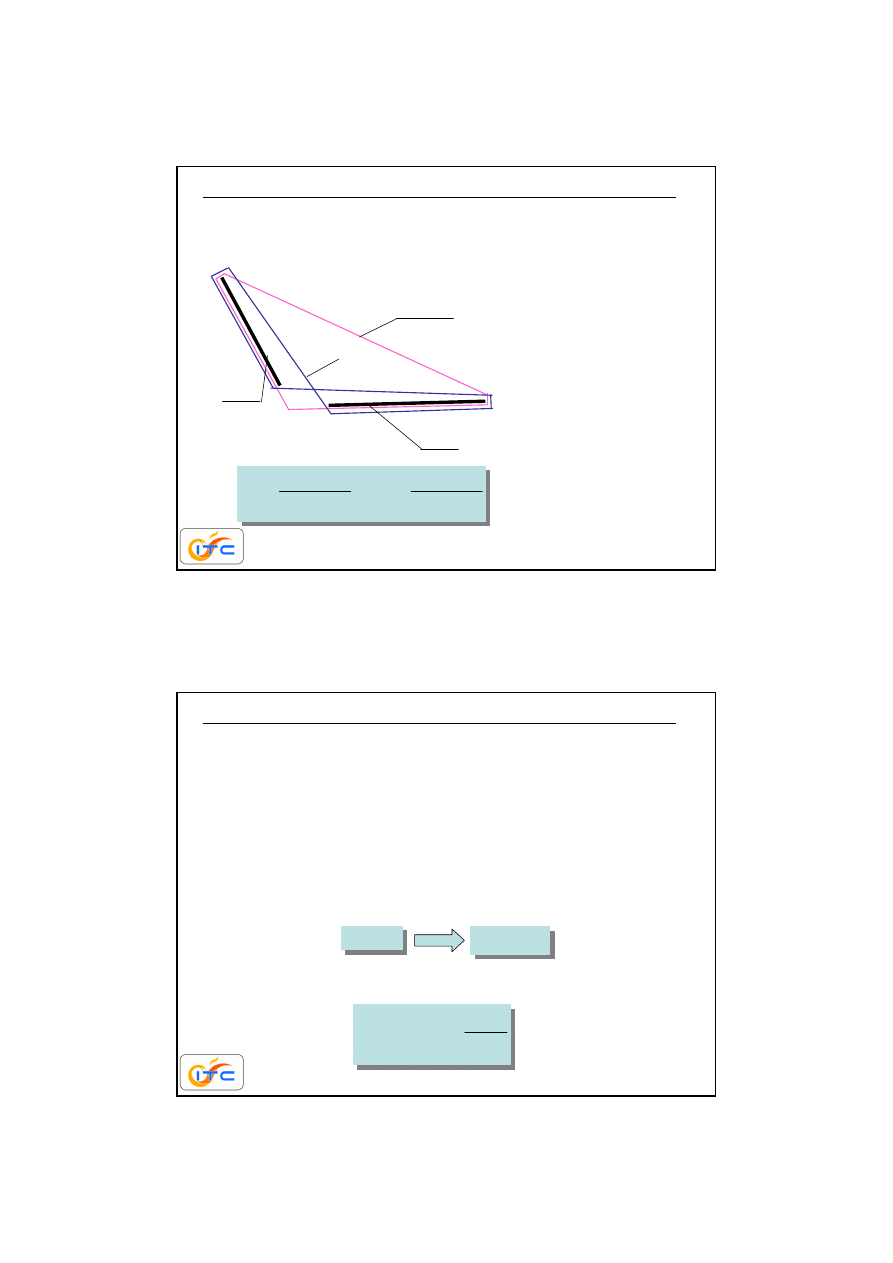
35

wyznaczanie współczynników konfiguracji 2

metoda nitkowa

L

sk

∆Γ

∆Γ

∆Γ

∆Γ

i

∆Γ

∆Γ

∆Γ

∆Γ

j

L

nsk

j

nsk

sk

ji

i

nsk

sk

ij

L

L

F

L

L

F

∆Γ

−

=

∆Γ

−

=

2

2

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

36

typowe zadanie promieniowania

dane

1.

geometria (podział numeryczny wn

ę

ki na elementy)

2.

emisyjno

ś

ci elementów

3.

temperatury elementów

szukane

1.

jasno

ś

ci elementów

2.

radiacyjne strumienie ciepła w ka

ż

dym elemencie

tok post

ę

powania

1.

znale

źć

wszystkie współczynniki konfiguracji

2.

rozwi

ą

za

ć

układ równa

ń

liniowych ze wzgl

ę

du na jasno

ś

ci

3. znale

źć

radiacyjne strumienie ciepła z równania

e

Fb

=

e

K

b

1

−

=

i

i

i

b

i

r

i

e

b

q

ε

−

ε

−

=

1

]

[

19

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

37

Wymiana ciepła mi

ę

dzy dwiema równoległymi płaszczyznami

εεεε

1

εεεε

2

ΤΤΤΤ

1

ΤΤΤΤ

2

12

`

21

F

F

=

0

;

0

22

11

=

=

F

F

1

;

1

22

21

12

11

=

+

=

+

F

F

F

F

0

0

;

1

;

1

22

11

21

12

=

=

=

=

F

F

F

F

samoopromieniowanie

wzajemno

ść

zamkni

ę

to

ść

wynikowe współczynniki konfiguracji

rozwi

ą

zanie

w jasno

ś

ciach

1

2

2

2

2

2

1

1

1

1

)

1

(

)

1

(

b

e

b

b

e

b

b

b

ε

−

+

ε

=

ε

−

+

ε

=

zdyskretyzowane równanie
promieniowania

)

1

)(

1

(

1

)

1

(

;

)

1

)(

1

(

1

)

1

(

2

1

1

1

2

2

2

2

2

1

2

2

1

1

1

1

ε

−

ε

−

−

ε

ε

−

+

ε

=

ε

−

ε

−

−

ε

ε

−

+

ε

=

b

b

b

b

e

e

b

e

e

b

rozwi

ą

zanie w radiacyjnych strumieniach ciepła

1

1

1

;

1

1

1

2

1

2

1

2

2

1

1

2

1

−

ε

+

ε

−

=

−

ε

+

ε

−

=

b

b

r

b

b

r

e

e

q

e

e

q

)

(

2

1

2

1

2

1

b

b

r

e

e

q

−

ε

=

−

−

)

1

/

1

/

1

/(

1

2

1

2

1

−

ε

+

ε

=

ε

−

gdzie

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

38

Radiacyjna wymiana ciepła w układzie dwupowierzchniowym,
zamkni

ę

tym (układ Christiansena)

εεεε

2

εεεε

1

ΤΤΤΤ

2

ΤΤΤΤ

1

Dwie izotermiczne powierzchnie tworz

ą

ce wn

ę

k

ę

. Powierzchnia nr 1

nie jest wkl

ę

sła.

εεεε

2

εεεε

1

ΤΤΤΤ

2

ΤΤΤΤ

1

12

1

21

2

F

F

∆Γ

=

∆Γ

0

11

=

F

1

;

1

22

21

12

11

=

+

=

+

F

F

F

F

2

1

22

11

2

1

21

12

/

1

0

;

/

;

1

∆Γ

∆Γ

−

=

=

∆Γ

∆Γ

=

=

F

F

F

F

samoopromieniowanie

wzajemno

ść

zamkni

ę

to

ść

wynikowe współczynniki konfiguracji

εεεε

2

εεεε

1

ΤΤΤΤ

2

ΤΤΤΤ

1

∆Γ

∆Γ

∆Γ

∆Γ

2

∆Γ

∆Γ

∆Γ

∆Γ

2

∆Γ

∆Γ

∆Γ

∆Γ

2

∆Γ

∆Γ

∆Γ

∆Γ

2

∆Γ

∆Γ

∆Γ

∆Γ

1

∆Γ

∆Γ

∆Γ

∆Γ

1

∆Γ

∆Γ

∆Γ

∆Γ

1

20

transport ciepła i masy

promieniowanie cieplne

©Ryszard A. Białecki

39

rozwi

ą

zanie w jasno

ś

ciach

)]

/

1

(

/

)[

1

(

)

1

(

1

1

2

2

1

1

2

2

2

2

2

1

1

1

1

∆Γ

∆Γ

−

+

∆Γ

∆Γ

ε

−

+

ε

=

ε

−

+

ε

=

b

b

e

b

b

e

b

b

b

zdyskretyzowane równanie promieniowania

)]

1

(

)

/

1

(

[

1

1

2

2

2

2

1

2

2

1

1

1

2

2

1

1

2

1

1

1

−

ε

∆Γ

ε

−

ε

∆Γ

∆Γ

−

−

ε

∆Γ

ε

ε

∆Γ

−

ε

∆Γ

−

ε

ε

∆Γ

=

b

b

e

e

b

]

)

1

(

[

1

2

2

2

2

1

1

1

2

2

1

1

2

1

1

2

∆Γ

ε

−

−

ε

∆Γ

ε

ε

∆Γ

−

ε

∆Γ

−

ε

ε

∆Γ

=

b

b

e

e

b

rozwi

ą

zanie w radiacyjnych strumieniach ciepła













−

ε

∆Γ

∆Γ

+

ε

−

=













−

ε

∆Γ

∆Γ

+

ε

−

=

1

1

1

;

1

1

1

2

2

1

1

2

1

2

2

2

1

1

1

2

1

b

b

r

b

b

r

e

e

q

e

e

q

)

(

2

1

2

1

2

1

b

b

r

e

e

q

−

ε

=

−

−













−

ε

∆Γ

∆Γ

+

ε

=

ε

−

1

1

1

1

2

2

1

1

2

1

gdzie