1

Program ćwiczeń rachunkowych z chemii nieorganicznej dla kierunku:

Technologia Żywności i Żywienie Człowieka

Rok akademicki 2012/2013

Semestr I

1. Pojęcia podstawowe z chemii.

Symbolika i nazewnictwo podstawowych związków chemicznych, stosowane jednostki.

Podstawowe prawa chemiczne (prawo stałości składu chemicznego, prawo stosunków

wielokrotnych). Wyznaczanie wzorów empirycznych (najprostszych) i rzeczywistych w oparciu

o skład procentowy związków chemicznych lub analizę chemiczną.

2. Stechiometria.

Podstawowe obliczenia oparte na równaniach reakcji. Reakcje z udziałem gazów. Prawa

gazowe.

3. Stężenia roztworów.

Sposoby wyrażania stężeń, stężenia procentowe, molowe, ułamki molowe. Metody przeliczania

stężeń. Rozcieńczanie, zatężanie i mieszanie roztworów.

4. Kolokwium sprawdzające I.

5. Roztwory elektrolitów

Iloczyn jonowy wody. pH i pOH. Dysocjacja elektrolitów mocnych i słabych, stała i stopień

dysocjacji. Siła jonowa roztworów, aktywność i współczynniki aktywności. Wyznaczanie pH

roztworów mocnych i słabych elektrolitów.

Hydroliza soli. Roztwory buforowe. Wyznaczanie pH roztworów buforowych i soli

hydrolizujących

.

6. Kolokwium sprawdzające II.

Literatura:

1. Z. Galus, Ćwiczenia rachunkowe z chemii analitycznej, PWN, 1996

2. R. Sołoniewicz, A. Korczyński, Obliczenia chemiczne, skrypt PŁ, 1993

3. A. Śliwa, Obliczenia chemiczne, PWN, 1980

4. H. Całus, Podstawy obliczeń chemicznych, WNT, 1983

2

Cyfry znaczące

Każda z wielkości mierzalnych, tj. wyznaczanych przy użyciu urządzeń pomiarowych

(masa, objętość itd.) jest obarczona błędem związanym z dokładnością wykonywanych pomiarów.

Przyjmuje się, że wielkości te są podawane w taki sposób, aby jedynie ostatnia cyfra wielkości była

niepewna. Np. jeżeli dokonuje się pomiaru masy na wadze z dokładnością 0,1 g masę 0,1869 g

podaje się także z dokładnością do miejsc dziesiętnych, czyli 0,2 g.

W obliczeniach dotyczących wielkości mierzalnych decydujące znaczenie mają cyfry znaczące.

- cyfry od 1 do 9 są zawsze cyframi znaczącymi;

- cyfra 0 JEST cyfrą znaczącą, gdy znajduje się w środku liczby (np. 606) oraz gdy stanowi o

dokładności wielkości mierzalnej np. 0,2000 (dokładność pomiaru do miejsc

dziesięciotysięcznych);

- cyfra 0 NIE JEST cyfrą znaczącą, gdy świadczy o rzędzie wielkości np. 0,005 (cyfrą znaczącą

jest tylko 5).

Zaokrąglanie do cyfr znaczących następuje podczas obliczeń z wykorzystaniem wielkości

mierzalnych

- ostatniej cyfry znaczącej nie zmienia się, jeśli następująca po niej cyfra jest mniejsza od 5;

- ostatnią cyfrę znaczącą podnosi o jednostkę, jeśli następująca po niej cyfra jest większa od 5;

- jeśli następująca po niej cyfrą jest 5, ostatnia cyfra znacząca (niepewna) powinna być cyfrą

parzystą

Wyznaczanie liczby cyfr znaczących w obliczeniach:

- suma dodawania wielkości mierzalnych ma taką samą dokładność, jak najmniej dokładny

składnik, niezależnie od liczby cyfr znaczących, np. suma 12,025 i 2,1 wynosi 14,1 a nie

14,125, podobnie dzieje się przy odejmowaniu. W obu działaniach liczby zaokrągla się do

wymaganego rzędu dokładności PRZED wykonaniem działania;

- wynik mnożenia ma tyle cyfr znaczących, co czynnik z ich najmniejszą liczbą, np. wynik

mnożenia 2,566 (4 cyfry znaczące) i 0,0021 (2 cyfry znaczące) wynosi 0,0054 (2 cyfry

znaczące), a nie 0,0053886; podobnie dzieje się w przypadku dzielenia.

W każdym obliczeniu, w którym następuje przeliczanie wielkości mierzalnych, wynik podaje się po

znaku „ = ”, niezależnie od wykonanych przybliżeń dokładności.

3

ARKUSZ 1 Kierunek Technologia Żywności i Żywienie Człowieka

Związek chemiczny - substancja złożona z dwóch lub więcej pierwiastków, która ma właściwości

zachowania stałego składu, tzn. nie zmienia składu procentowego poszczególnych
pierwiastków podczas częściowej zmiany stanu.

Wzory chemiczne związków:



Wzór empiryczny - wskazuje najprostszy z możliwych wzorów, który określa stechiometryczny
skład danego związku.



Wzór cząsteczkowy (rzeczywisty) - zgodny z prawidłową masą molową związku, podaje się
wtedy, gdy związek złożony jest z określonych cząsteczek, np. H

2

S

2

O

8

a nie HSO

4

.



We wzorach chemicznych na pierwszym miejscu umieszcza się zawsze składnik bardziej

elektrododatni, np. H

2

O a nie OH

2

.



W przypadku związków niemetali, umieszcza się najpierw symbole pierwiastka, który zajmuje
wcześniejszą pozycję w podanym wykazie:

R n , X e , K r , B , S i , C , S b , A s , P , N , H , T e , S e , S , A t , I , B r , C l , O , F .



W związkach łańcuchowych, które zawierają trzy lub więcej pierwiastków, kolejność zapisu
powinna być zgodna z rzeczywistym połączeniem w cząsteczce lub jonie, np. NCS

-

a nie CNS

-

.



Jeżeli z jednym atomem centralnym łączą się dwa lub więcej atomów różnych pierwiastków,
wówczas zapisuje się symbol atomu centralnego, a pozostałe pierwiastki zapisuje się w
kolejności alfabetycznej ich symboli, np. PBCl

2

(istnieją wyjątki od tej zasady, np. we wzorach

kwasów).

Wzór cząsteczkowy wyraża zarówno jakościowy, jak i ilościowy skład związku. Obliczenia
wykonywane przy pomocy wzorów chemicznych, jak i równań chemicznych, noszą nazwę obliczeń
stechiometrycznych i są oparte na następujących prawach:
 prawo zachowania masy – suma mas substancji reagujących nie ulega zmianie (suma mas

substratów jest równa sumie mas produktów reakcji)

 prawo stałych stosunków wagowych – związek chemiczny posiada stały skład ilościowy

wskutek przereagowania pierwiastków w stałych stosunkach wagowych.

 prawo stosunków wielokrotnych - jeżeli dwa pierwiastki tworzą kilka różnych związków

chemicznych, wówczas w związkach tych na tą samą ilość wagową jednego pierwiastka
przypadają ilości pierwiastka drugiego pozostające do siebie w stosunku niewielkich liczb
całkowitych.

 prawo stosunków objętościowych - w reakcji chemicznej objętości gazów wyjściowych i

produktów gazowych, odmierzone w jednakowych warunkach temperatury i ciśnienia,
pozostają do siebie w prostych stosunkach liczbowych.

4

PIERWIASTEK - substancja chemiczna, składająca się z atomów tylko jednego rodzaju i na które

można rozłożyć metodami chemicznymi dowolną substancję.

Izotopy - rodzaje atomów tego samego pierwiastka różniące się liczbą neutronów w jądrze.
Oznaczenie pierwiastka:

gdzie x - liczba masowa, podawana dla zaznaczenia izotopu, określa sumę protonów i neutronów

zawartych w jądrze;

y - liczba atomowa, dodatkowo dla zaznaczenia izotopu, określa liczbę protonów

wchodzących w skład jądra;

z - liczba łączących się atomów;
w - ładunek, zapisywany cyfrą arabską, po której podaje się znak ładunku,
a - stopień utlenienia pierwiastka (cyfra rzymska).

STOPIEŃ UTLENIENIA PIERWIASTKA – teoretyczny ładunek, który istniałby na atomie tego

pierwiastka, gdyby elektrony w każdym wiązaniu, które tworzy ten atom, należały do atomu
bardziej elektroujemnego. Stopień utlenienia zaznacza się cyfrą rzymską nad symbolem
pierwiastka.

Obliczanie stopnia utlenienia pierwiastka:



w stanie elementarnym atomom przypisuje się stopień utlenienia równy zeru.;
np.

Na

0

H

2

0



w prostych jonach, składających się z jednego atomu, stopień utlenienia równa się ładunkowi
jonu; np.

Al

3+

III

S

2-

-II



w związkach zawierających tlen stopień utlenienia atomu tlenu wynosi -II;

WYJĄTKI



w nadtlenkach np. H

2

O

2

-I;



w difluorku tlenu OF

2

II.



w związkach zawierających wodór stopień utlenienia atomu wodoru wynosi I;

WYJĄTKI



w wodorkach litowców i berylowców np. NaH

-I



suma stopni utlenienia pierwiastków wchodzących w skład związku wynosi zero dla cząsteczek

obojętnych lub równa się ładunkowi wypadkowemu dla jonów.
np. H

2

O

2 * I + ( - II ) = 0

OH

-

I + ( - II ) = -1

Obliczanie nie dotyczy:



w cząsteczce atomy pierwiastków łączą się między sobą;

np. FeS

2

( Fe II, S -II)

Fe

S

S



w cząsteczce stopnie utlenienia tego samego pierwiastka są różne;

np. Na

2

S

2

O

3

S

O

O

O

S

Na

Na

VI

-II



pierwiastki w związku wykazują jednakowe lub zbliżone elektroujemności.
np. NCl

3

.

a

w

z

x

y

E

5

Nazewnictwo związków chemicznych w systemie Stocka

1. Nazewnictwo tlenków
Po słowie tlenek i nazwie łączącego się z tlenem pierwiastka (rzeczownik w dopełniaczu)

podawany jest stopień utlenienia pierwiastka, pisany cyfrą rzymską w nawiasie.

np.

NO

tlenek azotu(II)

NO

2

tlenek azotu(IV)

FeO

tlenek żelaza(II)

Fe

2

O

3

tlenek żelaza(III)

2. Nazewnictwo wodorotlenków
Nazwy wodorotlenków tworzy się podając nazwę „wodorotlenek” oraz nazwę pierwiastka w
dopełniaczu liczby pojedynczej. Gdy istnieją dwa lub więcej wodorotlenki tego samego metalu, po
nazwie pierwiastka podaje się jego stopień utlenienia cyfrą rzymską w nawiasie.

np.

NaOH

wodorotlenek sodu

Fe(OH)

2

wodorotlenek żelaza(II)

Fe(OH)

3

wodorotlenek żelaza(III)

3. Nazewnictwo kwasów
Nazwy kwasów tlenowych tworzy się podając nazwę „kwas’ oraz nazwę atomu centralnego w
postaci przymiotnika z końcówką -OWY. Stopień utlenienia atomu centralnego zaznacza się cyfrą
rzymską w nawiasie tuż za nazwą kwasu.

np.

HClO

kwas chlorowy(I)

HClO

2

kwas chlorowy(III)

HClO

3

kwas chlorowy(V)

Nazwy kwasów beztlenowych tworzy się od nazwy anionu, zakończonej na -EK.

np.

H

2

S

siarczek wodoru (dopuszczalna nazwa kwas siarkowodorowy)

4. Nazewnictwo anionów
Nazwy anionów jednoatomowych tworzy się od nazwy pierwiastka z dodaniem końcówki -EK lub
–IK, np.

F

-

fluorek

Cl

-

chlorek

Br

-

bromek

I

-

jodek

S

2-

siarczek

Nazwy niektórych anionów wieloatomowych także posiadają końcówkę -EK.

np.

OH

-

wodorotlenek

CN

-

cyjanek

Nazwy anionów wieloatomowych tworzy się przez dodanie do rdzenia nazwy atomu centralnego
końcówki -AN i stopnia utlenienia atomu centralnego w anionie (cyfrą rzymską w nawiasie),

np.

NO

3

-

azotan(V)

SO

3

2-

siarczan(IV)

SO

4

2-

siarczan(VI)

MnO

4

-

manganian(VII)

CO

3

2-

węglan

SCN

-

tiocyjanian

[Fe(CN)

6

]

4-

heksacyjanożelazian(II)

[Fe(CN)

6

]

3-

heksacyjanożelazian(III)

5. Nazewnictwo soli



nazwy soli kwasów beztlenowych zapisuje się od nazwy anionu z końcówką -EK, następnie
nazwa pierwiastka (metalu) w dopełniaczu liczby pojedynczej, a tuż za nazwą podaje się stopień
utlenienia atomu metalu (cyfrą rzymską w nawiasie).

np.

FeCl

2

chlorek żelaza(II)

FeCl

3

chlorek żelaza(III)



nazwy soli kwasów tlenowych zapisuje się od nazwy anionu z końcówką -AN, stopnia utlenienia
atomu centralnego w anionie (cyfrą rzymską w nawiasie), następnie nazwa pierwiastka (metalu)
w dopełniaczu liczby pojedynczej, a tuż za nazwą podaje się stopień utlenienia atomu metalu
(cyfrą rzymską w nawiasie).

np.

BaSO

4

siarczan(VI) baru

Fe(NO

3

)

2

azotan(V) żelaza(II)

6

Zadania:

1. Analiza pewnego związku wykazała, że składa się on z 26,28 % C, 2,24 % H i 71,08 % O.

Podać jego wzór najprostszy.

2. Dolomit zawiera 30,35 % tlenku wapnia, 21,54 % tlenku magnezu i 47,76 % ditlenku węgla.

Podać uproszczony wzór tego minerału.

3. Ile kg siarczanu(VI) żelaza(II) można otrzymać z 336 kg metalicznego żelaza ?

4. Jak zmieni się zawartość procentowa miedzi, jeżeli próbkę mineralną o składzie CuSO

4

.

5H

2

O

poddamy dehydratacji ?

5. Pewien związek składa się z węgla (46,15 %) i azotu (53,85 %), a jego masa molowa wynosi

51,9 g/mol. Podać wzór rzeczywisty tego związku.

6. Pewien związek wodoru i fosforu zawiera 93,89 % fosforu, a jego masa molowa wynosi

65,97 g/mol. Podać jego wzór rzeczywisty.

7. Podać wzór rzeczywisty związku, którego masa molowa wynosi 395,68 g/mol, a zawiera on

75,74 % As i 24,26 % O.

8. Przez działanie kwasem solnym na 1 g tlenku ołowiu(II) otrzymano 1,246 g chlorku ołowiu(II).

Obliczyć masę molową ołowiu.

9. Przez wyprażenie 5,50 g zanieczyszczonego węglanu cynku otrzymano 1,0567 g ditlenku

węgla. Podać procentową zawartość węglanu cynku w próbce.

10. Stwierdzono, że z 1,3520 g rudy miedzi można otrzymać 86,9 mg tlenku miedzi(II). Podać

procentową zawartość miedzi w rudzie.

11. Uwodniony siarczan(VI) magnezu zawiera 51,17 % wody krystalizacyjnej. Obliczyć liczbę

cząsteczek wody przypadających na jedną cząsteczkę siarczanu(VI) magnezu.

12. W jednym z tlenków azotu o masie molowej 92 g/mol na każdy 1 g azotu przypada 2,2840 g

tlenu. Podać wzór tlenku.

13. W próbce związku o masie 22,32 g stwierdzono obecność 2,42 g Mg, 7,09 g Cl, a resztę stanowi

tlen. Podać wzór tego związku.

14. W wyniku spalania 1,15 g pewnego związku organicznego otrzymano 2,20 g ditlenku węgla i

1,35 g wody. Masa molowa związku wynosi 46 g/mol. Podać wzór rzeczywisty związku.

15. Związek chemiczny składa się z: 25,93 % K, 13,03 % Co, 61,04 % NO

2

. Podać wzór

empiryczny.

7

ARKUSZ 2.

Kierunek Technologia Żywności i Żywienie Człowieka

Obliczenia stechiometryczne - oparte na wzorach związków i znajomości mas atomowych,

pozwalają w oparciu o prawidłowo ułożone równanie reakcji na rozwiązanie wielu zagadnień:



obliczenie składu procentowego związku;



obliczenie ilości produktu z zadanej ilości substratu;



obliczenie niezbędnej ilości substratów dla otrzymania żądanej ilości produktu;



obliczenie ilości jednego substratu reagującej całkowicie z daną ilością innych substratów;



obliczenie ilości substancji nie przereagowanych, gdy jeden z substratów był użyty w nadmiarze.

Równanie reakcji chemicznej mówi nam o tym, w jakich stosunkach liczbowych reagują ze sobą

atomy i cząsteczki substancji. Jeżeli znamy ich masy molowe, możemy obliczyć również
stosunki masowe wszystkich reagentów.

Często reakcje nie przebiegają całkowicie i wówczas obliczenie wydajności reakcji opiera się na
porównaniu ilości rzeczywiście otrzymanego produktu z ilością, która powinna się wytworzyć
zgodnie z równaniem reakcji (przy 100 % wydajności).

Założenia gazu doskonałego:



cząsteczki gazu są tak małe, że można je uważać za punkty materialne;



pomiędzy cząsteczkami gazu nie występują siły wzajemnego przyciągania ani odpychania;



cząsteczki gazu poruszają się stale i bezładnie po torach prostoliniowych, zderzając się ze
sobą i ścianami naczynia, w którym się znajdują;



zderzenia cząsteczek są doskonale sprężyste;



średnia energia kinetyczna cząsteczek jest proporcjonalna do temperatury gazu wyrażonej w
kelwinach.

Prawo Avogadra - równe objętości różnych gazów w tej samej temperaturze i pod tym samym

ciśnieniem zawierają jednakową liczbę cząstek.

Objętość molowa gazu doskonałego w warunkach normalnych ( 0



C, 760 mm Hg) wynosi

V

mol

= 22,4 dm

3

/mol.

Prawo stosunków objętościowych (prawo Gay - Lussaca) - w reakcji chemicznej objętości gazów

wyjściowych i produktów gazowych, odmierzone w jednakowych warunkach temperatury
i ciśnienia, pozostają do siebie w prostych stosunkach liczbowych.

Równanie stanu gazu doskonałego:

pV = nRT

gdzie p - ciśnienie gazu [ Pa ];

V - objętość gazu [ m

3

];

n - liczba moli gazu [ mol ];
R - stała gazowa;
T - temperatura gazu [ K ].

Stała gazowa - określa pracę 1 mola gazu ogrzanego o 1 kelwin pod stałym ciśnieniem.

R = 8,314

J

mol



K

Równanie stanu gazu doskonałego dla 1 mola gazu nosi nazwę równania Clapeyrona:

pV = RT

8

Równanie stanu gazu rzeczywistego (równanie Van der Waalsa) dla 1 mola gazu





p

V

+

a

V

- b = RT

2







gdzie a, b - stałe dla danego rodzaju gazu.

Gęstość bezwzględna gazu doskonałego w warunkach normalnych wynosi:

mol

V

M

d



[g/dm

3

]

Gdy znamy gęstość względną gazu w stosunku do drugiego gazu o masie molowej M

Y

, to nieznaną

masę molową gazu M

X

obliczamy ze wzoru:

M

X

= D

X/Y

.

M

Y

gdzie

Y

X

Y

/

X

d

d

D



Jednostki ciśnienia



paskal [ Pa ] - jednostka ciśnienia w układzie SI

2

m

N

1

Pa

1





atmosfera techniczna [ at ]

1 at = 735,5 mm Hg



atmosfera fizyczna [ atm ]

1 atm = 760 mm Hg = 1,013

.

10

5

Pa



bar

1 bar = 10

5

Pa = 750 mm Hg



tor [ Tr ]

1 Tr = 1 mm Hg = 133,3 Pa

9

Zadania:

1. Dla określenia zawartości żelaza i glinu w roztworze wytrącono wodorotlenki tych metali i

przeprowadzono je w odpowiednie tlenki (Fe

2

O

3

i Al

2

O

3

). Ile gramów żelaza i glinu zawierał

roztwór, jeżeli otrzymano łącznie 1,25 g tlenków, a masa siarczku żelaza(III) jaką można
otrzymać z tego roztworu wynosi 0,72 g.

2. Do roztworu zawierającego 6,0 g zasady sodowej dodano roztwór zawierający 10,0 g kwasu

azotowego. Jakie substancje i w jakiej ilości, oprócz wody, są obecne w roztworze?

3. Ile gramów tlenku żelaza(III) można otrzymać wyprażając 10 g chlorku żelaza(III) z 5,0 %

zawartością zanieczyszczeń ?

4. Ile gramów tlenu otrzyma się przez rozkład termiczny 100 g manganianu(VII) potasu,

zachodzący z wydajnością 85 %, jeżeli rozkład zachodzi według równania:
4 KMnO

4



2 K

2

MnO

3

+ 2 MnO

2

+ 3O

2

5. Ile gramów wodoru otrzyma się rozpuszczając w kwasie 1,00 kg magnalu - stopu zawierającego

20 % glinu i 80 % magnezu? Jaka to objętość w warunkach normalnych?

6. Mieszanina węglanu wapnia i tlenku wapnia traci po wyprażeniu 12,55 % swojej masy.

Obliczyć skład procentowy mieszaniny.

7. Mieszaninę 100 g tlenku miedzi(II) i 225 g tlenku srebra(I) zredukowano do metali. Obliczyć

skład procentowy otrzymanego stopu.

8. Naważkę 100 g miedzi ogrzano ze 100 g siarki. Powstał siarczek miedzi(I). Jaka substancja

pozostała w nadmiarze?

9. Odważono 0,2774 g mieszaniny chlorku sodu i chlorku potasu, rozpuszczono w wodzie, a

następnie strącono chlorki azotanem(V) srebra, otrzymując 0,609 g chlorku srebra(I). Znaleźć
procentową zawartość obu chlorków w mieszaninie wyjściowej.

10. Pewna substancja organiczna zawiera 77,5 % węgla, 7,5 % wodoru i 15,0 % azotu.

Wyprowadzić wzór rzeczywisty tej substancji, jeśli gęstość jej par względem powietrza (M

śr

=

29 g/mol) wynosi 3,21.

11. Rozpuszczono w kwasie 6,00 g technicznego siarczku żelaza(II) zawierającego 5% domieszkę

metalicznego żelaza. Jaka będzie objętość wydzielonych gazów w warunkach normalnych? Jaki
jest skład procentowy mieszaniny gazowej (wyrażony w procentach objętościowych)?

12. Termiczny rozkład tlenku ołowiu(IV) zachodzi według równania: 3PbO

2



Pb

3

O

4

+ O

2

.

Obliczyć objętość wydzielonego tlenu w warunkach normalnych, jeśli rozkładowi uległo 180 g
tlenku. Jaką objętość zajmuje tlen w temperaturze 27



C i pod ciśnieniem 2034 hPa?

13. W celu otrzymania chlorowodoru sporządzono 1,00 g mieszaniny chloru i wodoru o łącznej

objętości 500 cm

3

(warunki normalne). Który z substratów użyto w nadmiarze i jaką otrzymano

masę chlorowodoru ?

10

ARKUSZ 3.

Kierunek Technologia Żywności i Żywienie Człowieka

Definicje stężeń.
1. Stężenie procentowe

a) wyrażone w procentach wagowych (% m/m), określa liczbę gramów rozpuszczonej

substancji zawartych w 100 g roztworu.

V

d

%

100

m

m

%

100

m

c

s

r

s

p











gdzie m

s

– masa substancji rozpuszczonej

m

r

– masa roztworu

V – objętość roztworu

d – gęstość roztworu

b) wyrażone w procentach objętościowych (% v/v), określa liczbę cm

3

substancji

rozpuszczonej w 100 cm

3

roztworu

c) wyrażone z procentach masowo-objętościowych (% m/v), określa liczbę gramów

substancji rozpuszczonej w 100 cm

3

roztworu.

2. Stężenie molowe określa liczbę moli substancji zawartych w 1 dm

3

roztworu.

V

M

m

V

n

c

s

m















3

dm

mol

gdzie n – liczba moli substancji rozpuszczonej

V – objętość roztworu

m

s

– masa substancji rozpuszczonej

M – masa molowa substancji rozpuszczonej

Stężenie molowe substancji AB może być zapisywane w sposób:

c(AB) = c

AB

= [AB]

3. Stężenie podane jako ułamek molowy wyraża stosunek liczby moli danego składnika do sumy

liczby moli wszystkich składników roztworu. Suma ułamków molowych wszystkich
składników roztworu równa się jedności.

m

2

1

i

i

i

n

...

n

n

n

n

n

x













4. Stężenie normalne określa liczbę gramorównoważników substancji zawartych w 1 dm

3

roztworu. Zgodnie z nową nomenklaturą stężenie normalne nie jest zalecane. Starsze
podręczniki zawierają jednak takie jednostki.

Gęstość roztworu











3

r

cm

g

V

m

d

1 g/dm

3

= 0,001 g/cm

3

1 g/cm

3

= 1000 g/dm

3

11

Zadania:

1. 5 cm

3

stężonego roztworu wodorotlenku potasu rozcieńczono wodą do objętości 250 cm

3

. Na

zobojętnienie 20,0 cm

3

tego roztworu zużyto 12,8 cm

3

roztworu kwasu solnego 0,25-

molowego. Jakie było stężenie molowe stężonego roztworu użytej zasady?

2. Do 200 cm

3

16,0 % roztworu wodorotlenku potasu o gęstości 1,150 g/cm

3

dodano 300 cm

3

roztworu wodorotlenku potasu o stężeniu 0,20 mol/dm

3

. Obliczyć stężenie molowe

otrzymanego roztworu.

3. Do 200 cm

3

20,0 % roztworu wodorotlenku potasu o gęstości 1,240 g/cm

3

dodano 300 cm

3

roztworu kwasu azotowego(V) 4,20 molowego. Obliczyć stężenie nieprzereagowanego
odczynnika.

4. Do 200 cm

3

roztworu wodorotlenku potasu 0,40 molowego (d = 1,02 g/cm

3

) dodano jeszcze

16,0 g stałej zasady. Obliczyć stężenie procentowe i molowe otrzymanego roztworu przy
założeniu, że objętość roztworu nie uległa zmianie.

5. Do 50,0 cm

3

roztworu chlorku baru o stężeniu 0,04 mol/dm

3

dodano 32 cm

3

2 % roztworu

kwasu siarkowego(VI) (d = 1,012 g/cm

3

). Podać, który odczynnik został użyty w nadmiarze.

Obliczyć stężenie nieprzereagowanego odczynnika i ile moli siarczanu(VI) baru powstało.

6. Do 54 g stałego wodorotlenku potasu dodano tyle wody, że otrzymano roztwór 20,0 %

(d = 1,186 g/cm

3

). Ile wody dodano, jaka była objętość roztworu i jego stężenie molowe?

7. Ile cm

3

10,0 % roztworu kwasu siarkowego(VI) (d = 1,070 g/cm

3

) zużyje się do całkowitego

zobojętnienia 16 g wodorotlenku sodu?

8. Ile cm

3

kwasu siarkowego(VI) 90 % (d = 1,814 g/cm

3

) i 36 % (d = 1,268 g/cm

3

) należy użyć,

aby otrzymać 2 dm

3

kwasu 65 % (d = 1,553 g/cm

3

).

9. Ile cm

3

wody należy dodać do 25 cm

3

27 % roztworu wodorotlenku potasu o gęstości

1,25 g/cm

3

aby otrzymać roztwór 0,20 molowy ?

10. Jak przygotować z 15,0 % roztworu węglanu sodu (d = 1,186 g/cm

3

) 5 dm

3

roztworu o

stężeniu 0,25 mol/dm

3

.

11. Jaką objętość 0,05 molowego roztworu wodorotlenku sodu należy dodać do 200 cm

3

0,12-molowego roztworu tej zasady aby otrzymać roztwór 0,10 molowy ?

12. Jaką objętość 25 % roztworu amoniaku o gęstości 0,910 g/cm

3

należy dodać do 500 cm

3

roztworu 0,20 molowego aby otrzymać roztwór o stężeniu 1,00 mol/dm

3

.

13. Na zobojętnienie 20 cm

3

roztworu kwasu siarkowego(VI) o stężeniu 0,15 mol/dm

3

zużyto

14,4 cm

3

roztworu wodorotlenku sodu. Ile gramów wodorotlenku sodu zawiera 1 dm

3

roztworu

wodorotlenku?

14. Obliczyć objętość 96 % roztworu kwasu siarkowego(VI) o gęstości 1,842 g/cm

3

potrzebną do

otrzymania 1,4 dm

3

roztworu o stężeniu 0,80 mol/dm

3

.

15. Zmieszano 120 g 80,0 % roztworu kwasu siarkowego(VI) (d = 1,727 g/cm

3

) z 500 cm

3

36 %

roztworu tego kwasu (d = 1,268 g/cm

3

). Jakie jest stężenie procentowe i molowe roztworu ?

12

ARKUSZ 4.

Kierunek Technologia Żywności i Żywienie Człowieka

Dysocjacja – rozpad cząsteczek na jony pod wpływem rozpuszczalnika; ulegają jej substancje o

budowie jonowej lub z wiązaniami spolaryzowanymi (dipole). Dysocjacja może być
całkowita (elektrolity mocne) lub częściowa (elektrolity słabe).

AB

A

+

+ B

-

Aktywność jonów – opisuje zjawisko oddziaływań elektrostatycznych jonów w roztworach

bardziej stężonych, ograniczających ruch jonów

f

c

a





gdzie a – aktywność jonu

c – stężenie molowe jonu

f – współczynnik aktywności jonu

Współczynnik aktywności jonu zależy od rodzaju jonu, jego ładunku, od stężenia i ładunku
innych jonów w roztworze.

Moc (siła) jonowa roztworu – miara oddziaływań międzyjonowych w roztworze





2

n

n

2

2

2

2

1

1

2

z

c

...

z

c

z

c

2

1

z

c

2

1























gdzie



- moc jonowa roztworu, [mol/dm

3

]

c – stężenie molowe jonu
z – ładunek jonu

Wartość współczynnika aktywności w roztworach rozcieńczonych jest równy 1, dla roztworów
bardziej stężonych f < 1, przy czym jego wartość liczbową wyznacza się eksperymentalnie lub ze
wzoru uproszczonego prawa granicznego Debye’a-Hückla:















1

z

0,5

f

log

2

gdzie z – ładunek jonu



- siła (moc) jonowa roztworu

Wzór ten stosuje się dla jonów jednowartościowych dla





0,05, dla jonów dwuwartościowych dla





0,014 i dla trójwartościowych przy





0,005. W przypadku roztworów bardziej stężonych

wartości współczynników aktywności obliczone przy użyciu powyższego wzoru są jedynie
przybliżone.

Stała dysocjacji (K) – opisuje równowagę pomiędzy jonami a cząsteczkami niezdysocjowanymi

]

AB

[

]

B

[

]

A

[

K









gdzie [A

+

], [B

-

] – stężenia jonów

[AB] – stężenie cząsteczek niezdysocjowanych

13

Stopień dysocjacji – stosunek liczby cząsteczek zdysocjowanych do ogólnej liczby cząsteczek

elektrolitu w roztworze; zależy od stężenia roztworu, temperatury, stałej dysocjacji i
obecności innych jonów w roztworze;

c

c







0 <





1 lub 0 % <





100 %

gdzie c



- stężenie cząsteczek zdysocjowanych

c – całkowite stężenie cząsteczek











1

c

K

2

lub dla





0,01 (10 %): K = c

.



2

Iloczyn jonowy wody – określa zależność pomiędzy jonami wodorowymi (hydroniowymi) i

wodorotlenowymi we wszystkich roztworach wodnych.

K

w

= K

.

[H

2

O] = [H

+

]

.

[OH

-

] = 10

-14

dla 25



C

lub pK

w

= pH + pOH = 14

gdzie pK

w

= - log K

w

pH = - log [H

+

]

pOH = - log [OH

-

]

pH – ujemny logarytm ze stężenia jonów wodorowych w roztworze

Wzór wyznaczający :

Sposób obliczania

pH roztworu mocnego kwasu

pH =

– log c

kw

(*)

pH roztworu mocnej zasady

pH = 14 + log c

zas

(**)

pH roztworu słabego kwasu

kw

kw

kw

c

K

c

]

H

[













kw

c

log

2

1

pK

2

1

pH

kw





pH roztworu słabej zasady

zas

zas

14

zas

14

c

K

10

c

10

]

H

[

















zas

c

log

2

1

pK

2

1

14

pH

zas







gdzie pK

kw

, pK

zas

– wartość ujemnego logarytmu ze stałej dysocjacji słabego kwasu/słabej zasady

c

kw,

c

zas

– stężenie molowe kwasu / zasady

* - dla kwasów jednoprotonowych HA

** - dla zasad jednowodorotlenowych BOH

14

Zadania:

1. Amoniak o objętości 305 dm

3

, mierzony w temperaturze 25



C i pod ciśnieniem 1 bara,

rozpuszczono w wodzie, a otrzymany roztwór wykazywał pH 11,5. Jaka była objętość
otrzymanego roztworu?

2. Do 100 cm

3

0,1-molowego roztworu kwasu octowego dodano 120 cm

3

0,08-molowego

roztworu wodorotlenku baru. Obliczyć pH roztworu końcowego.

3. Do 20 cm

3

roztworu kwasu siarkowego(VI) dodano 30 cm

3

roztworu wodorotlenku amonu o pH

= 10,87. Roztwór po reakcji wykazywał pH 4,00. Obliczyć stężenie wyjściowe roztworu kwasu
siarkowego(VI). K = 1,77

.

10

-5

.

4. Do 30 cm

3

roztworu wodorotlenku baru o pH 11,70 dodano 0,1-molowego roztworu kwasu

solnego tak, że pH po reakcji wynosiło 7,80. Jaką objętość roztworu kwasu solnego dodano?

5. Do 300 cm

3

0,01-molowego roztworu wodorotlenku sodu dodano 200 cm

3

0,015-molowego

roztworu kwasu siarkowego(VI). Obliczyć pH roztworu końcowego.

6. Do kolby miarowej wprowadzono 2 g 5 % roztworu kwasu octowego i rozcieńczono wodą do

objętości 2 dm

3

. Obliczyć pH otrzymanego roztworu oraz stopień dysocjacji kwasu.

7. Jak zmieni się pH 0,0125-molowego roztworu wodorotlenku sodu, jeżeli 5 cm

3

tego roztworu

zmieszamy z 495 cm

3

wody?

8. Jakie jest stężenie molowe jonów hydroksylowych w 5,1 % roztworu amoniaku o gęstości

0,97 g/cm

3

. ( K = 1,77

.

10

-5

)

9. Obliczyć stałą dysocjacji kwasu, którego 0,01-molowy roztwór wykazuje pH = 5,1.

10. Obliczyć współczynnik aktywności jonów cynku w 1 dm

3

0,005-molowego roztworu

siarczanu(VI) cynku, a następnie po dodaniu do tego roztworu 100 cm

3

0,1-molowego roztworu

kwasu siarkowego(VI).

11. Obliczyć wykładnik stężenia jonów wodorowych (pH) i wykładnik aktywności jonów

wodorowych (p

a

H) w 0,02-molowym i 0,002-molowym roztworze kwasu siarkowego(VI).

12. Po reakcji 2 cm

3

30 % roztworu kwasu siarkowego(VI) (d = 1,224 g/cm

3

) z 0,1 g cynku,

roztwór rozcieńczono do 1 dm

3

. Obliczyć pH otrzymanego roztworu.

13. Roztwór kwasu octowego o objętości 20 cm

3

rozcieńczono wodą do 1 dm

3

, a po rozcieńczeniu

pH wynosiło 3,50. Jakie było pierwotne stężenie kwasu?

14. Stopień dysocjacji 0,1-molowego roztworu kwasu octowego wynosi 1,35 %. Przy jakim

stężeniu roztworu tego kwasu stopień dysocjacji osiągnie wartość 95 % ?

15. Zmieszano 200 ml 0,05-molowego roztworu kwasu chlorowego(VII) i 300 ml 0,01-molowego

roztworu kwasu solnego. Do otrzymanego roztworu dodano 2 g wodorotlenku potasu. Jakie
było pH roztworu końcowego?

15

ARKUSZ 5.

Kierunek Technologia Żywności i Żywienie Człowieka

Hydroliza - reakcja związku chemicznego z wodą. W przypadku soli słabych elektrolitów,

hydroliza jest odwracalna i odwrotna do reakcji zobojętniania. Zgodnie z teorią
Brönsteda sole hydrolizujące są słabymi kwasami lub zasadami, które w reakcji z
wodą ulegają zobojętnieniu.

Hydrolizie ulegają sole słabych elektrolitów, tzn.:
- sole słabych kwasów i mocnych zasad









Na

COO

CH

COONa

CH

3

3

(dysocjacja)











OH

COOH

CH

O

H

COO

CH

3

2

3

odczyn zasadowy

- sole słabych zasad i mocnych kwasów









Cl

NH

Cl

NH

4

4

(dysocjacja)













H

O

H

NH

O

H

NH

2

3

2

4

odczyn kwaśny

- sole słabych kwasów i słabych zasad









4

3

4

3

NH

COO

CH

COONH

CH

(dysocjacja)











OH

COOH

CH

O

H

COO

CH

3

2

3













H

O

H

NH

O

H

NH

2

3

2

4

odczyn obojętny, słabo kwaśny lub słabo zasadowy, w zależności od wartości odpowiednich stałych

dysocjacji kwasu i zasady.

Wielkości charakteryzujące proces hydrolizy :
- stała hydrolizy K

h

(stała reakcji odwracalnej)

dys

w

K

K



h

K

gdzie K

w

- iloczyn jonowy wody

K

dys

- stała dysocjacji słabego kwasu lub słabej zasady

lub

zas

h

K

K





kw

w

K

K

jeżeli sól tworzą słaby kwas i słaba zasada

- stopień hydrolizy h ( 0



h



1 )

soli

czasteczek

liczba

calkowita

soli

czasteczek

wanych

zhydrolizo

liczba

h



=

c

c

h

 

h

-

1

c

c

h

c

h

K

h











; dla h



0,01 K

h

= c

.

h

2

c

K

h



h

gdzie K

h

- stała hydrolizy

c - stężenie soli [mol/dm

3

]

Wartość pH roztworów soli hydrolizujących oblicza się ze wzorów :
- dla soli słabych zasad jednowodorotlenowych, np. NH

4

Cl

 

zas

w

K

c

K

h

c

H











sól

zas

c

log

2

1

pK

2

1

7

pH







- dla soli słabych kwasów jednowodorowych, np. CH

3

COONa

 

c

K

K

h

c

K

H

kw

w

w











sól

kw

c

log

2

1

pK

2

1

7

pH







16

Bufory są to roztwory zawierające słaby kwas oraz jego sól z mocną zasadą lub słabą zasadę i

jej sól z mocnym kwasem, bądź roztwory wodorosoli kwasów wieloprotonowych. Bufory wykazują
stałość wykładnika pH podczas rozcieńczania wodą lub dodawania niewielkich ilości kwasów albo
zasad. Roztwór słabego kwasu i jego soli jest odporny na większe zmiany pH, bowiem mała ilość
jonów wodorowych dodana do roztworu powoduje, że większość jonów wodorowych jest wiązana
przez aniony, tworząc słaby kwas, zdysocjowany tylko w niewielkim stopniu i w rezultacie zmiana
stężenia jonów wodorowych w roztworze jest mała. Natomiast dodanie silnej zasady do roztworu
słabego kwasu powoduje zobojętnianie zasady i zmiany pH również są niewielkie aż do momentu,
kiedy większość kwasu zostanie zobojętniona.

Zakres wartości pH, w którym dana mieszanina buforowa wykazuje działanie buforujące,

zależy od wartości stałej dysocjacji i od stosunku stężeń składników mieszaniny buforowej.

Słaby kwas i jego sól



















sol

kw

kw

c

c

K

]

H

[

















sol

kw

kw

c

c

log

pK

pH

Słaba zasada i jej sól































zas

sól

zas

w

c

c

K

K

]

H

[



















sol

zas

zas

w

c

c

log

pK

pK

pH

Dana mieszanina buforowa wykazuje własności buforujące w zakresie od pH = pK

kw

- 1 do

pH = pK

kw

+ 1; działanie jej jest ograniczone, a skuteczność przeciwdziałania zmianom pH jest

określona pojemnością buforową. Liczba moli mocnej zasady, bądź mocnego kwasu, która musi
być dodana do 1dm

3

roztworu, aby spowodować zmianę pH o jedną jednostkę określa pojemność

buforową danego roztworu.

pH

Z











Z - ilość dodanej zasady (kwasu),



pH - przyrost pH.

W miarę dodawania mocnego kwasu lub zasady pojemność buforowa maleje osiągając w końcu
wartość zerową, gdy cała zawarta w buforze sól przejdzie w słaby kwas lub gdy słaby kwas
zostanie zastąpiony solą. Największą pojemność buforową mają roztwory, w których c

sol

= c

kw

, c

zas

= c

sol

i pH = pK

kw

lub pH = pK

zas

. Rozcieńczanie buforów nie zmienia pH, ale obniża



.

17

Zadania
1. 600 cm

3

roztworu zawiera 0,15 mola amoniaku i 0,12 mola chlorku amonu. Jak zmieni się pH,

jeżeli do roztworu dodano 400 cm

3

:

a) wody destylowanej,
b) roztworu azotanu(V) amonu o stężeniu 0,1 mol/dm

3

,

c) buforu otrzymanego przez zmieszanie 500 cm

3

roztworu amoniaku o stężeniu 0,12 mol/dm

3

z 500 cm

3

roztworu azotanu(V) amonu o stężeniu 0,15 mol/dm

3

.

Obliczyć zmianę pH w każdym z roztworów. ( K

zas

= 1,85

.

10

-5

)

2. Do 1 dm

3

roztworu zawierającego 0,1 mol kwasu octowego, 0,1 mol octanu sodu dodano

a) 10 cm

3

1 molowego roztworu kwasu solnego,

b) 750 cm

3

wody.

Jak zmieni się pH roztworu? ( K

kw

= 1,85

.

10

-5

)

3. Do 100 cm

3

roztworu kwasu octowego o stężeniu 0,5 mol/dm

3

dodano 4,63 g octanu sodu, a

następnie roztwór rozcieńczono wodą destylowaną do objętości 250 cm

3

. Obliczyć pH

otrzymanego roztworu. ( K

kw

= 1,85

.

10

-5

)

4. Do 200 cm

3

roztworu kwasu solnego o stężeniu 0,5 mol/dm

3

wprowadzono ilościowo 4,48 dm

3

gazowego amoniaku (objętość mierzono pod ciśnieniem 3 atm w temp. 20



C). Jakie jest pH

otrzymanego roztworu ? ( K

zas

= 1,8

.

10

-5

).

5. Do objętości 20,8 cm

3

0,11-molowego kwasu mrówkowego dodano 20 cm

3

0,1-molowego

wodorotlenku sodu. Obliczyć pH powstałego roztworu. ( K

kw

= 1,76

.

10

-4

)

6. Ile gramów octanu sodu należy rozpuścić w 0,5 dm

3

0,2 molowego roztworu kwasu octowego,

aby pH otrzymanego buforu różniło się dwie jednostki od pH roztworu kwasu octowego ?
( K

kw

= 1,85

.

10

-5

)

7. Jak zmieni się pH roztworu chlorku amonu o stężeniu 0,03-molowym, jeżeli do 100 cm

3

tego

roztworu dodano 400 cm

3

wody ? ( K

zas

= 1,8

.

10

-5

)

8. Jak zmieni się pH roztworu octanu potasu o stężeniu 0,05-molowym, jeżeli do 150 cm

3

tego

roztworu dodano 5 g tej soli ? ( K

kw

= 1,85

.

10

-5

)

9. Jak zmienił się stopień hydrolizy octanu potasu, jeżeli 50 cm

3

0,1-molowego roztworu

pierwotnego rozcieńczono wodą do objętości końcowej 250 cm

3

? ( K

kw

= 1,85

.

10

-5

)

10. Obliczyć pH 0,05-molowego roztworu węglanu sodu. ( pK

1

= 6,4; pK

2

= 10,3 )

11. Obliczyć pH w 0,75 % roztworze azotanu(V) amonu. ( K

zas

= 1,8

.

10

-5

; przyjąć d = 1 g/cm

3

)

12. Obliczyć stałą dysocjacji kwasu cyjanowodorowego, jeżeli w 0,05-molowym roztworze

cyjanku potasu stopień hydrolizy cząsteczek soli wynosi 0,053.

13. Roztwór zawiera 0,056 mola amoniaku i 0,1 mola chlorku amonu w 1 dm

3

. Obliczyć pH tego

roztworu przed i po dodaniu 0,02 mola wodorotlenku sodu lub 0,02 mola kwasu solnego.
K

zas

= 1,8

.

10

-5

14. W skład dwóch roztworów buforowych wchodzą sole NaH

2

PO

4

, i Na

2

HPO

4

:

a) roztwór zawiera 0,500 mola NaH

2

PO

4

i 0,310 mola Na

2

HPO

4

w 1dm

3

,

b) roztwór zawiera 0,100 mola NaH

2

PO

4

i 0,062 mola Na

2

HPO

4

w 1dm

3

.

Do roztworów dodano tyle wodorotlenku sodu, że stężenie molowe wodorotlenku w nich było
jednakowe i wynosiło 0,025 mol/dm

3

. Obliczyć zmianę pH dla każdego z nich. K

k2

= 6,62

.

10

-8

.

18

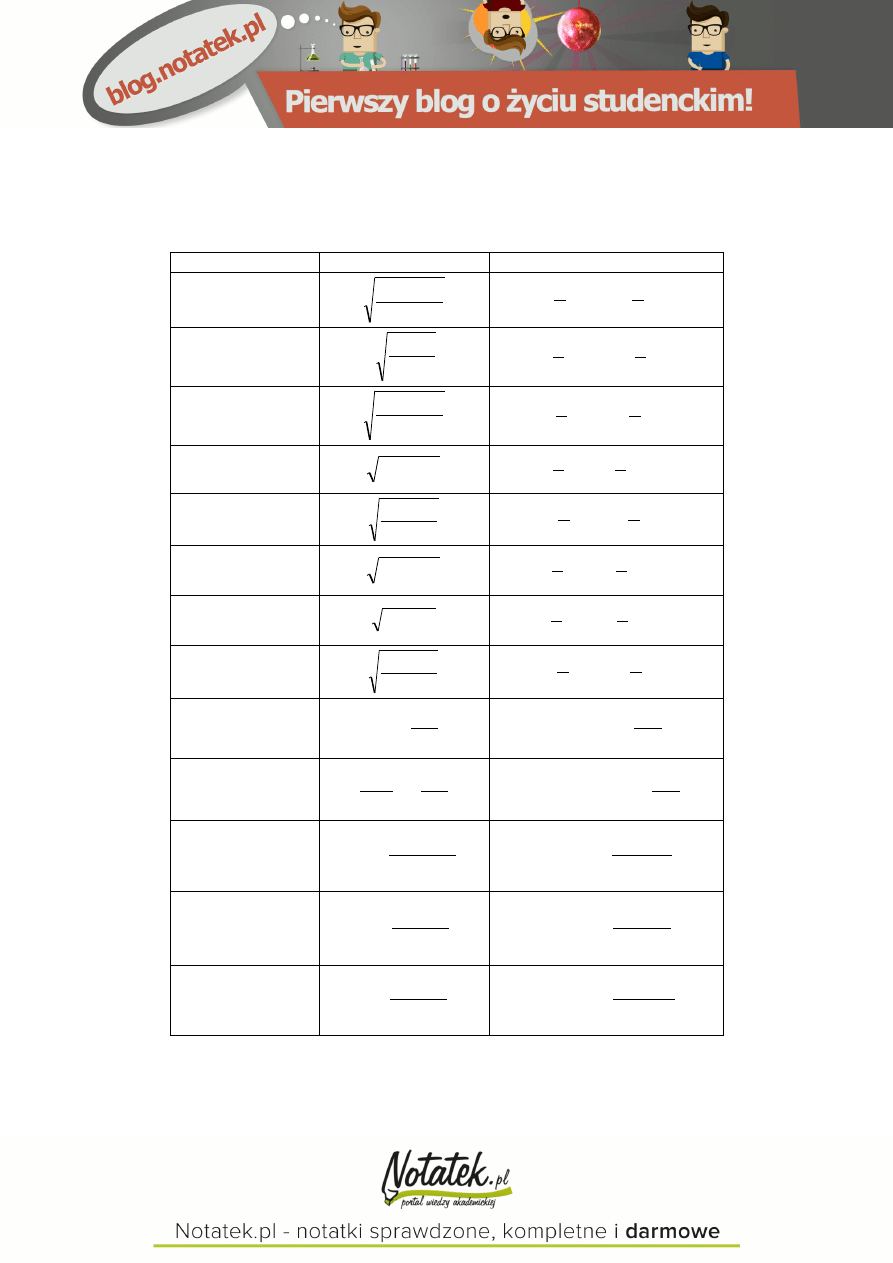
Wyznaczanie pH roztworów soli hydrolizujących i buforów

Roztwór zawiera:

[H

+

]

pH

CH

3

COONa

c

K

K

kw

w



c

log

2

1

pK

2

1

7

kw





NH

4

Cl

zas

w

K

c

K



c

log

2

1

pK

2

1

7

zas





CH

3

COONH

4

zas

kw

w

K

K

K



zas

kw

pK

2

1

pK

2

1

7





NaHCO

3

2

1

K

K



2

1

pK

2

1

pK

2

1



Na

2

CO

3

c

K

K

2

w



c

log

2

1

pK

2

1

7

2





NaH

2

PO

4

2

1

K

K



2

1

pK

2

1

pK

2

1



Na

2

HPO

4

3

2

K

K



3

2

pK

2

1

pK

2

1



Na

3

PO

4

c

K

K

3

w



c

log

2

1

pK

2

1

7

3





CH

3

COOH i

CH

3

COONa















sol

kw

kw

c

c

K















sol

kw

kw

c

c

log

pK

NH

3

.

H

2

O i NH

4

Cl



























zas

sól

zas

w

c

c

K

K

















sol

zas

zas

c

c

log

pK

14

Na

3

PO

4

i Na

2

HPO

4

















4

3

4

2

PO

Na

HPO

Na

3

c

c

K

















4

3

2

PO

Na

4

HPO

Na

3

c

c

log

pK

Na

2

HPO

4

i

NaH

2

PO

4

















4

2

4

2

HPO

Na

PO

NaH

2

c

c

K

















4

2

4

2

HPO

Na

PO

NaH

2

c

c

log

pK

NaH

2

PO

4

i H

3

PO

4

















4

2

4

3

PO

NaH

PO

H

1

c

c

K

















4

2

4

3

PO

NaH

PO

H

1

c

c

log

pK

19

Odpowiedzi do zadań.

Arkusz 1.

1) CHO

2

2) CaO

.

MgO

.

2CO

2

3) 913,9 kg

4) wzrośnie z 25,4% do 39,8%.

5) C

2

N

2

6) P

2

H

4

7) As

4

O

6

8) 207,6 g/mol.

9) 54,6%.

10) 5,13%.

11) 7

12) N

2

O

4

13) MgCl

2

O

8

14) C

2

H

6

O

15) K

3

Co(NO

2

)

6

Arkusz 2.

1) 0,39 g Fe, 0,36 g Al

2) 0,6 g HNO

3

i 12,8 g NaNO

3

.

3) 4,68 g

4) 12,9 g

5) 88,8 g, 994 dm

3

6) 28,5% CaCO

3

, 71,5% CaO

7) 27,6% Cu, 72,4% Ag

8) siarka

9) 50,6%NaCl, 49,4% KCl

10) C

6

H

7

N

11) 1,57 dm

3

, 7,6% H

2

, 92,4% H

2

S

12) 5,62 dm

3

, 3,06 dm

3

13) chlor, 0,6205 g HCl

Arkusz 3.

1) 8,0 mol/dm

3

.

2) 1,43 mol/dm

3

.

3) 0,76 mol/dm

3

HNO

3

4) 9,31%, 1,8 mol/dm

3

.

5) H

2

SO

4

, 0,056 mol/dm

3

, 0,002 mol

6) 216 cm

3

, 228 cm

3

, 4,23 mol/dm

3

.

7) 183 cm

3

.

8) 919,5 cm

3

, 1134 cm

3

.

9) 0,725 dm

3

.

10) 0,745 dm3 i uzupełnić wodą.

11) 0,08 dm

3

.

12) 0,073 dm

3

.

13) 16,7 g

14) 62,07 cm

3

.

15) 43,0%, 5,81 mol/dm

3

.

Arkusz 4

1) 21,6 dm

3

.

2) 12,62

3) 0,024 mol/dm

3

,

4) 1,5 cm

3

5) 2,22

6) pH = 3,9; 0,14

7) zmaleje o 2,00

8) 0,0053 mol/dm

3

,

9) 6,3 * 10

-9

10) 0,56; 0,44,

11) 1,49 – 1,40, 2,43 – 2,40

12) 1,92

13) 0,28 mol/dm

3

,

14) 1,0 * 10

-6

mol/dm

3

,

15) 12,66

Arkusz 5

1) a) bez zmian b) zmaleje o 0,12, c) zmaleje o 0,03

2) a) zmaleje o 0,08, b) bez zmian

3) 4,79

4) 9,92

5) 4,60

6) 7,77 g

7) wzrośnie o 0,35

8) wzrośnie o 0,44

9) wzrośnie 2,2 razy

10) 11,50

11) 5,14

12) 7,1 * 10

-11

13) 9,00, 9,23, 8,73

14) a)wzrośnie o 0,06 , b) wzrośnie o 0,27