Projekt nr 2 - metody obliczeniowe

METODA RAYLEIGHA-RITZA

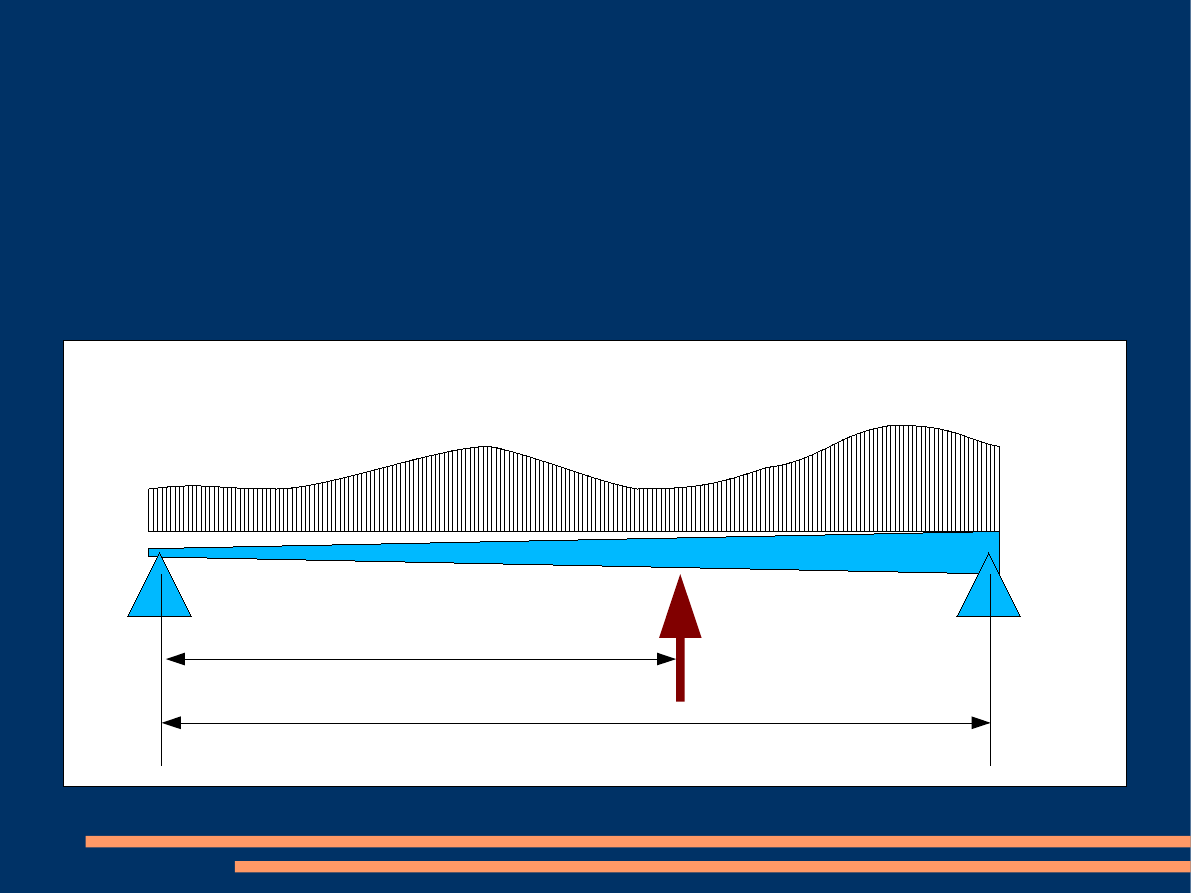
Belka wolnopodparta o zmiennym
przekroju, obciążona obciążeniem

ciągłym i siłą skupioną

L

L

a

q(x) = q

0

*f

1

(x)

J(x) = J

0

*f

2

(x)

P

Metoda Ritza – teoria
(przypomnienie)



p



u =

1
2

∫





T



d −

∫



u

T

f d -

∫

∂ 

u

T

t d ∂

●

Potencjał energii sprężystej

Przyjęte rozwiązanie



u  x≈ u

N



x=

∑

j=1

N

c

j



j



x 

0



x 

Funkcjonał belki

=

∫

0

L



EJ

2



d

2

u

dx

2



2

−

u⋅q



dx−Pu a

Przyjmujemy jako funkcje bazowe



i

=

sin



i⋅⋅x

L



,



0

=

0

Funkcja bazowa i jej druga
pochodna



i

=

sin



i⋅⋅x

L



d

2



i

dx

2

=−

i

2



2

L

2

sin



i⋅⋅x

L



Układ równań algebraicznych

0= =

 



c

1



c

1



 


c

2



c

2

⋯

 



c

N



c

N

=

=

∑

i =1

N



 



c

i



c

i



 



c

j

=

∑

j =1

N

A

ij

c

j

−

b

i

=

0

lub

 


c

j

=

∑

j=1

N

A

ij

c

j

=

b

i



i=1, , N 

Pochodna funkcjonału

∂ 

∂

c

i

=

∫

0

L



EJ  x

∂

∑

j=1

N

c

j

⋅

j

' ' 

∂

c

i

⋅

∑

j =1

N

c

j

⋅

j

' ' 



dx

−

∫

0

L



q x

∂

∑

j=1

N

c

j

⋅

j



∂

c

i



dx−P⋅

∂

∑

j =1

N

c

j

⋅

j



a

∂

c

i

=

0

i=1, , N

Układ równań algebraicznych

[

A

11

A

12

A

13

A

21

A

22

A

23

A

31

A

32

A

33

][

c

1

c

2

c

3

]

=

[

b

1

b

2

b

3

]

Dla trzech funkcji

Współczynniki układu równań

A

ij

=

∫

0

L

EJ  x 

d

2



i

dx

2

⋅

d

2



j

dx

2

dx

b

i

=

∫

0

L

q x⋅

i

dxP⋅

i



a 

A

ii

=

∫

0

L

EJ  x 



d

2



i

dx

2



2

dx

A

ij

=

0

ponieważ funkcja bazowa sinus jest funkcją

ortogonalną to iloczyn

ϕ

i

ϕ

j

= 0 dla i

ǂ j, to

Układ równań algebraicznych

[

A

11

0

0

0

A

22

0

0

0

A

33

][

c

1

c

2

c

3

]

=

[

b

1

b

2

b

3

]

Współczynniki równań

Po podstawieniu drugiej pochodnej z funkcji sinus

A

ii

=

i

4



4

L

4

EJ

0

∫

0

L

sin

2



i⋅



x

L



⋅

f

2



x dx

b

i

=

q

0

∫

0

L

sin



i⋅



x

L



⋅

f

1



x dx P⋅sin



i⋅



a

L



c

i

=

b

i

A

ii

Linia ugięcia i moment zginający

u  x=

∑

i =1

N

c

i

⋅

sin



i⋅⋅x

L



M  x 

EJ

=

d

2

u  x 

dx

2

=

∑

i=1

N

c

i

⋅

d

2



i

dx

2

=

−

i

2



2

L

2

∑

i=1

N

c

i

⋅

sin



i⋅⋅x

L



Matlab – zadania do wykonania

●

Definiuj stałe : E, J

0

, q

0

, P, L, a

●

Określ liczbę funkcji bazowych N

●

Ewentualnie (dyspozycja prowadzącego zajęcia)
zdefiniuj funkcje rozkładu zmienności obciążenia
f

1

(x) i zmienności sztywności f

2

(x)

●

Oblicz współczynniki równań A

ii

, b

i

●

Oblicz współczynniki rozkładu c

i

●

Narysuj linię ugięcia

Matlab

Do obliczenia całki skończonej użyj funkcji
quad(F,a,b), gdzie

F-obliczana funkcja, a,b-granice
całkowania
Funkcję F należy definiować w następujący sposób

Fi=@(x)sin(i*pi*x/L)
Fi2= @(x)sin(i*pi*x/L).^2
i wywoływać w sposób następujący:
quad(Fi,0,L) lub quad(Fi2,0,L)

Matlab – użycie pętli

Jeżeli chcemy wykonać powtarzające się działania
dla różnego indeksu

i

to używamy instrukcji pętli:

for i=1:N

Fi = @(x)......
Fi2 = @(x)......

A(i) = .........
b(i) = .........

c(i) = .........
u = u +c(i) * sin(.....)
end

plot(..., -u)

Rozszerzenia

●

Obliczyć i narysować wykres momentu zginającego

●

Obliczyć i narysować wykres siły poprzecznej

●

Uwzględnić zmienność sztywności belki i
obciążenia ciągłego

●

Rozszerzyć formułę obliczeń na wiele sił
skupionych

●

Obliczyć i narysować wykres momentu zginającego
i siły poprzecznej korzystając z operatorów
różnicowych