L2: 6.111 Spring 2006

1

Introductory Digital Systems Laboratory

L2: Combinational Logic Design

L2: Combinational Logic Design

(Construction and Boolean Algebra)

(Construction and Boolean Algebra)

Acknowledgements:

Materials in this lecture are courtesy of the following sources and are used with permission.

Prof. Randy Katz (Unified Microelectronics Corporation Distinguished Professor in Electrical

Engineering and Computer Science at the University of California, Berkeley) and Prof. Gaetano

Borriello (University of Washington Department of Computer Science & Engineering) from Chapter 2

of R. Katz, G. Borriello. Contemporary Logic Design. 2nd ed. Pentice-Hall/Pearson Education, 2005.

J. Rabaey, A. Chandrakasan, B. Nikolic. Digital Integrated Circuits: A Design Perspective.

Prentice Hall/Pearson, 2003.

L2: 6.111 Spring 2006

2

Introductory Digital Systems Laboratory

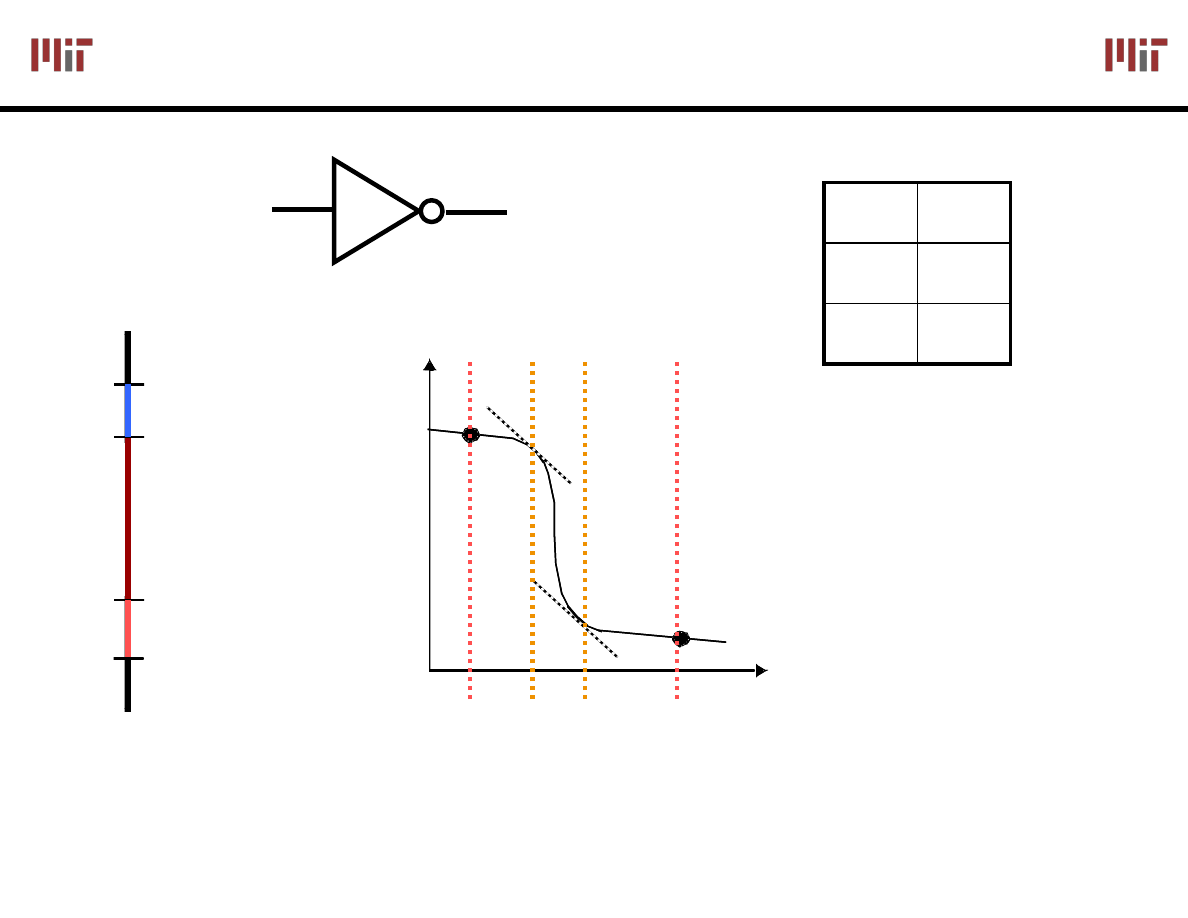
Review: Noise Margin

Review: Noise Margin

IN

OUT

IN

OUT

0

1

1

0

V(x)

V(y)

VOH

VOL

V

IH

V

IL

Slope = -1

Slope = -1

V

OL

VOH

"1"

"0"

V

OH

V

IH

V

IL

V

OL

Undefined

Region

ƒ

Large noise margins

protect against various noise sources

NM

L

= V

IL

-V

OL

NM

H

= V

OH

-V

IH

Truth Table

L2: 6.111 Spring 2006

3

Introductory Digital Systems Laboratory

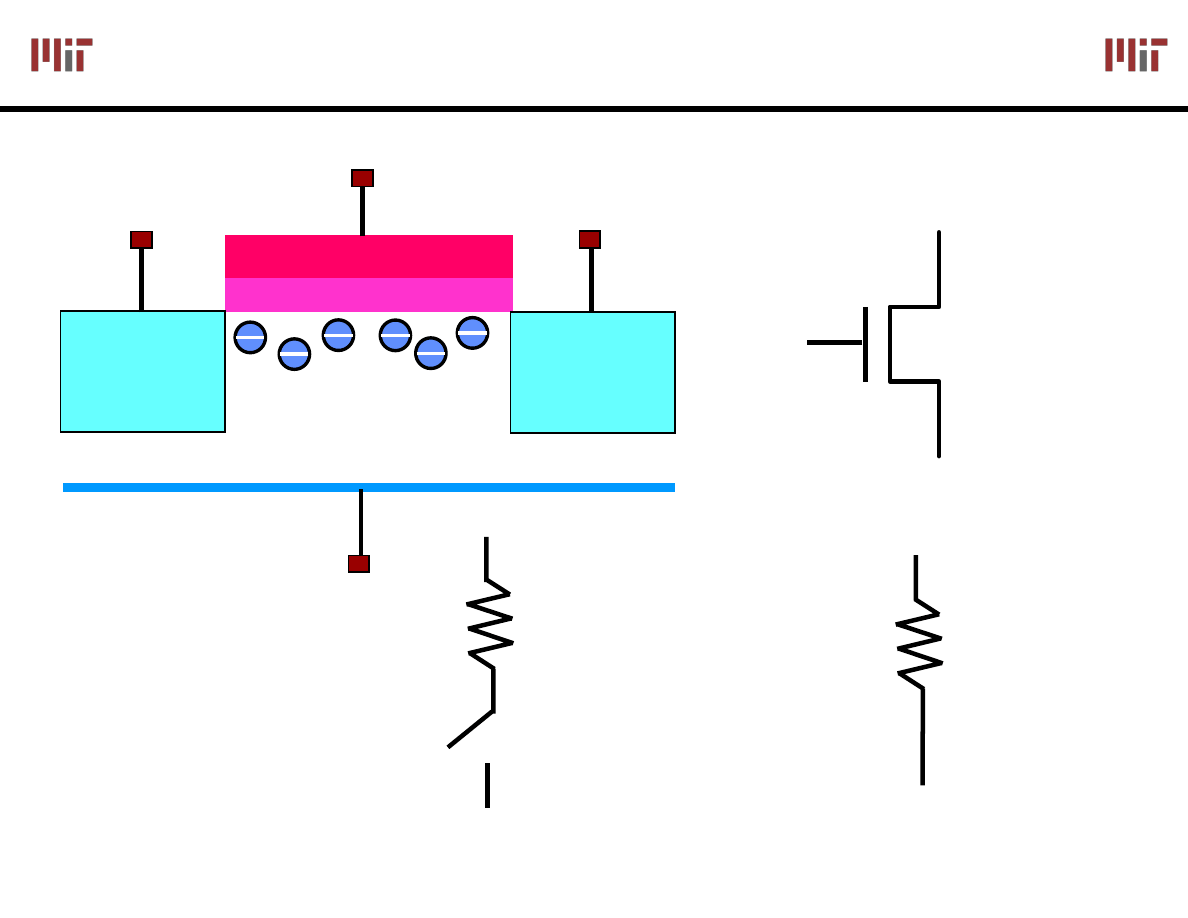
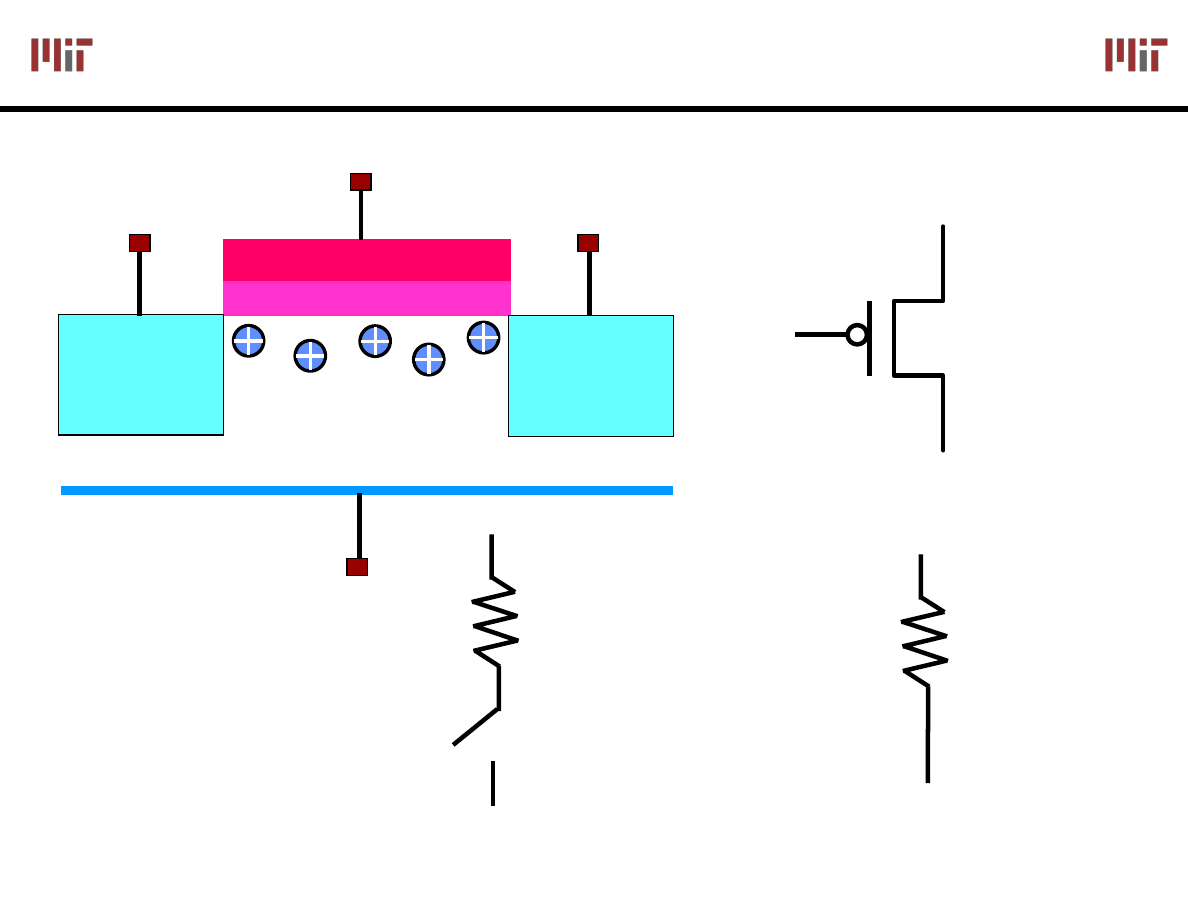
MOS Technology: The NMOS Switch

MOS Technology: The NMOS Switch

D

G

S

gate

N+

P-substrate

N+

drain

source

R

NMOS

Switch
Model

V

T

= 0.5V

V

GS

< V

T

OFF

R

NMOS

V

GS

> V

T

ON

V

s

NMOS ON when Switch Input is High

L2: 6.111 Spring 2006

4

Introductory Digital Systems Laboratory

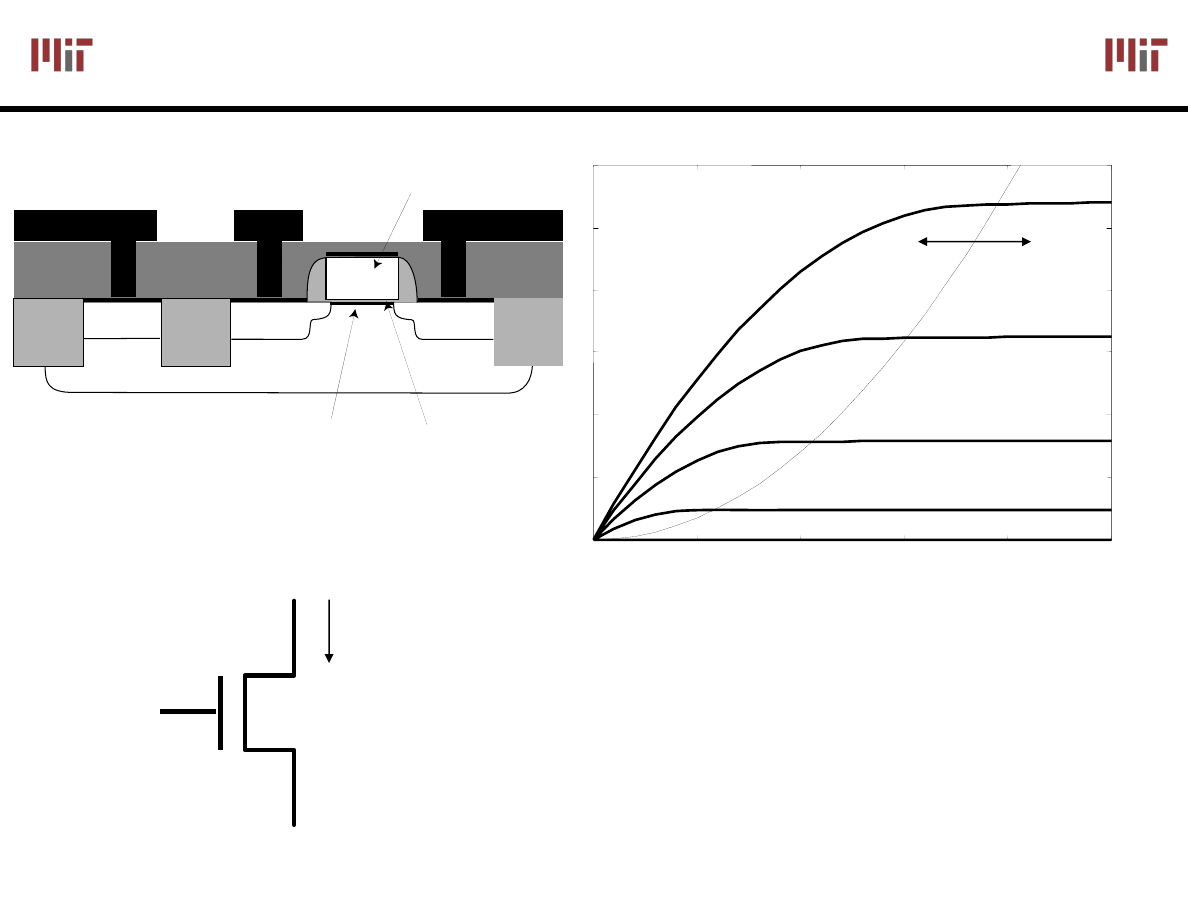
NMOS Device Characteristics

NMOS Device Characteristics

0

0.5

1

1.5

2

2.5

0

VGS= 1.0 V

V

DS

(V)

D

G

V

T

= 0.5V

I

D

¾ MOS is a very non-linear.

+

¾ Switch-resistor model

V

GS

sufficient for first order analysis.

-

1

2

3

4

5

6

D

(A)

VGS= 2.5 V

VGS= 2.0 V

VGS= 1.5 V

Resistive

Saturation

x 10

-4

I

S

polysilicon gate

body

source

drain

gate

p

p+

n+

n+

n+

inversion layer�

gate oxide

n

channel

L2: 6.111 Spring 2006

5

Introductory Digital Systems Laboratory

PMOS: The Complementary Switch

PMOS: The Complementary Switch

S

G

D

gate

P+

N-substrate

P+

drain

source

R

PMOS

Switch
Model

V

T

= -0.5V

V

GS

> V

T

OFF

R

PMOS

V

GS

< V

T

ON

PMOS ON when Switch Input is Low

V

DD

L2: 6.111 Spring 2006

6

Introductory Digital Systems Laboratory

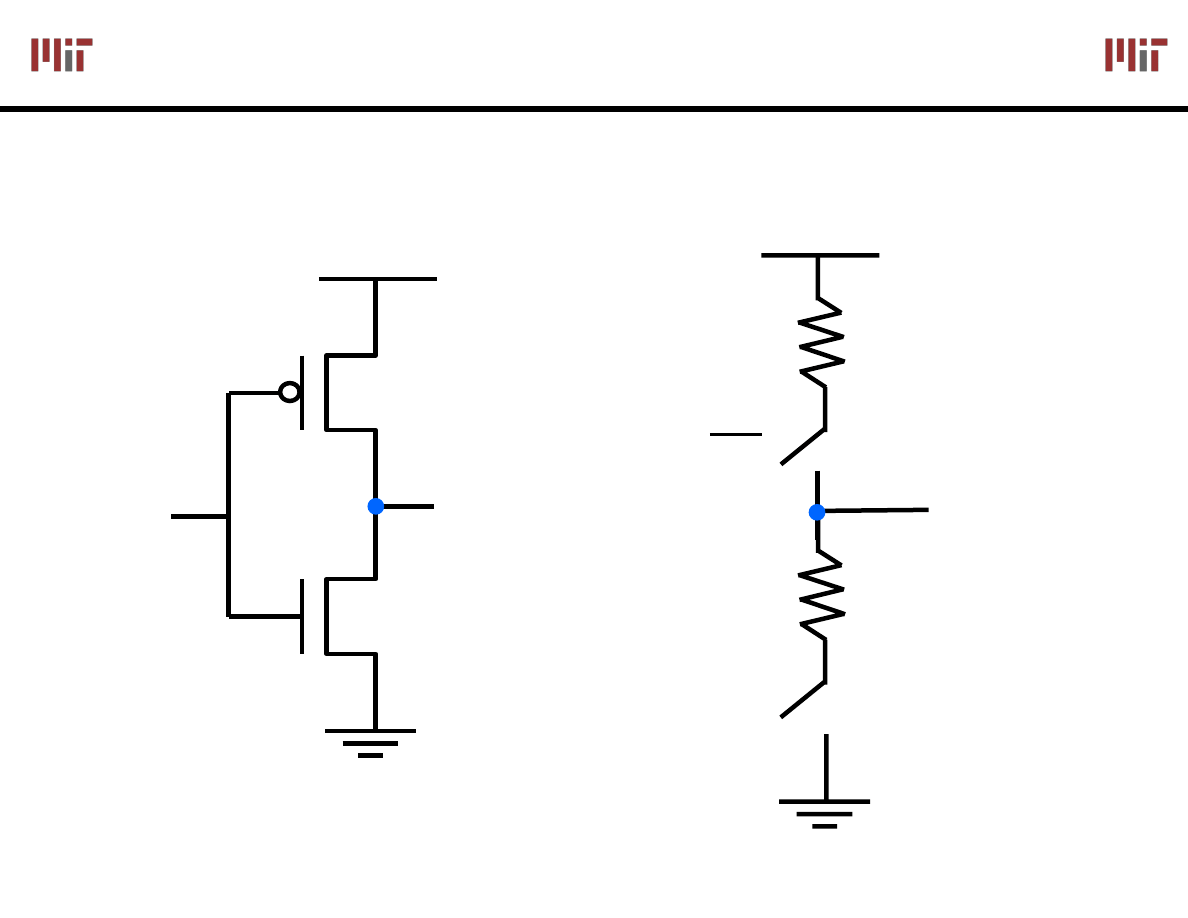
The CMOS Inverter

The CMOS Inverter

IN

OUT

V

DD

V

DD

OUT

R

PMOS

R

NMOS

IN

IN

Switch Model

S

G

G

D

D

S

Rail-to-rail Swing in CMOS

L2: 6.111 Spring 2006

7

Introductory Digital Systems Laboratory

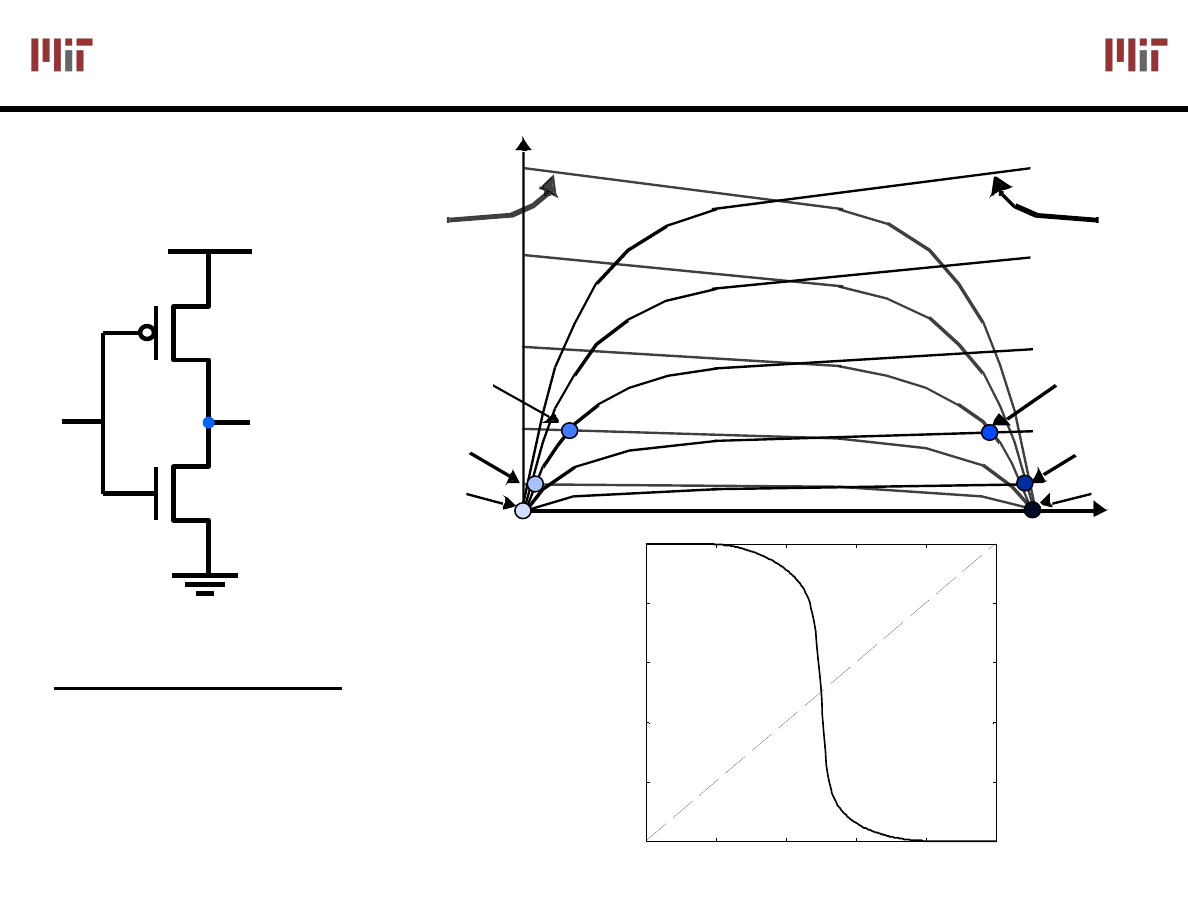
Inverter VTC: Load Line Analysis

Inverter VTC: Load Line Analysis

IN

OUT

V

DD

S

G

D

D

S

G

I

D n

V

out

V

in

= 2.5

V

in

= 2

V

in

= 1.5

V

in

= 0

V

in

= 0.5

V

in

= 1

NMOS

V

in

= 0

V

in

= 0.5

V

in

= 1

V

in

= 1.5

V

in

= 2

V

in

= 2.5

V

in

= 1

V

in

= 1.5

PMOS

0

0.5

1

1.5

2

2.5

0

0.5

1

1.5

2

2.5

V

in

(V)

V

out

(V

)

CMOS gates have:

ƒ

Rail-to-rail swing (0V to V

DD

)

ƒ

Large noise margins

ƒ

“zero” static power dissipation

L2: 6.111 Spring 2006

8

Introductory Digital Systems Laboratory

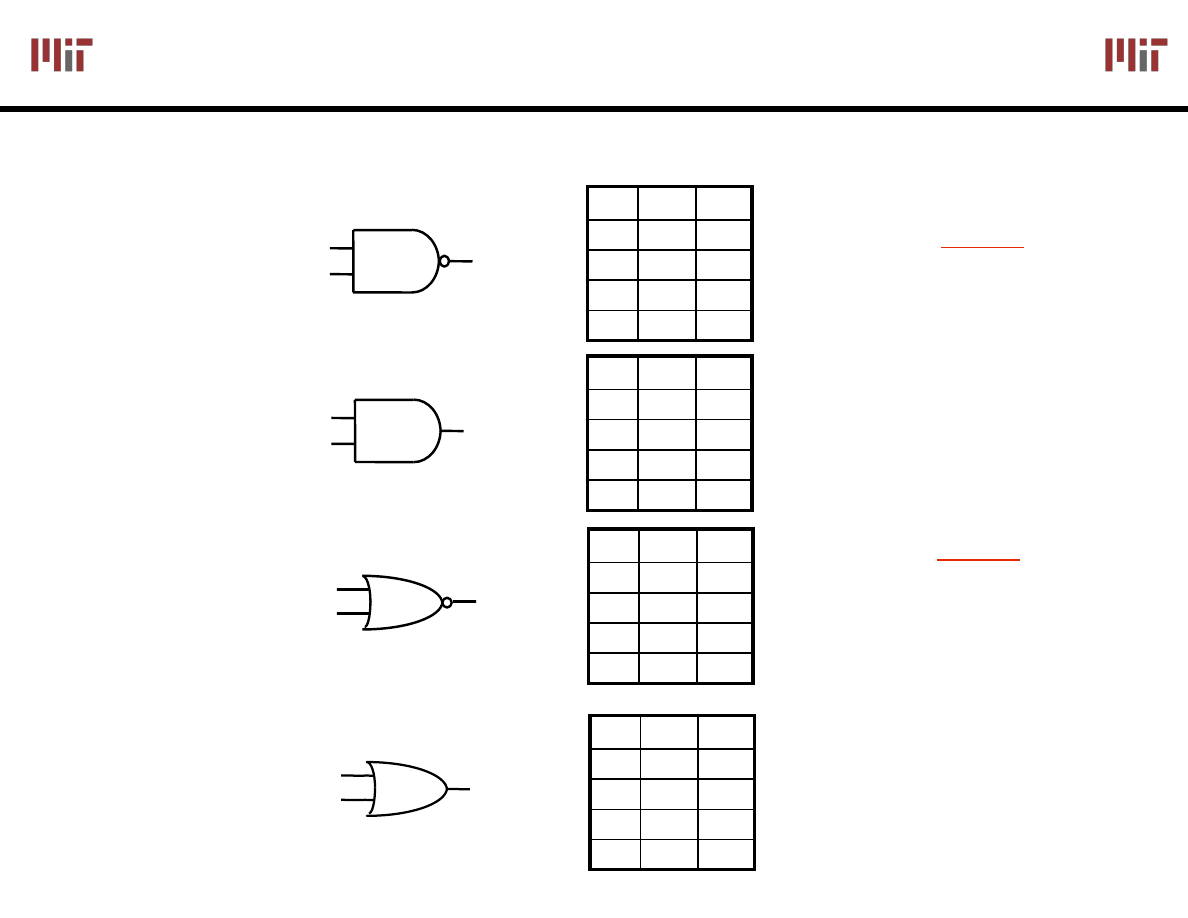
Possible Function of Two Inputs

Possible Function of Two Inputs

X
Y

F

X

Y

16 possible functions (F

0

–F

15

)

0

0 0

0

0

0

0

0

0

0

1

1

1

1

1

1

1

1

0

1 0

0

0

0

1

1

1

1

0

0

0

0

1

1

1

1

1

0 0

0

1

1

0

0

1

1

0

0

1

1

0

0

1

1

1

1 0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

X

Y

X

NOR

Y

NOT

(X

OR

Y)

X

NAND

Y

NOT

(X

AND

Y)

1

0

NOT

X

X

AND

Y

X

OR

Y

NOT

Y

X

XOR

Y

X = Y

There are 16 possible functions of 2 input variables:

In general, there are 2

(2^n)

functions of n inputs

L2: 6.111 Spring 2006

9

Introductory Digital Systems Laboratory

Common Logic Gates

Common Logic Gates

X

Y

Z

Z

X
Y

X

Y

Z

0

0

1

1

0

1

1

1

0

1

1

0

NAND

Gate

Symbol

Truth-Table

Expression

X

Y

Z

0

0

1

1

0

1

1

0

0

0

1

0

NOR

Z = X • Y

Z = X + Y

Z

X
Y

X

Y

Z

0

0

1

1

0

0

1

1

0

1

1

1

OR

Z = X + Y

X

Y

Z

X

Y

Z

0

0

1

1

0

0

1

0

0

0

1

1

AND

Z = X • Y

L2: 6.111 Spring 2006

10

Introductory Digital Systems Laboratory

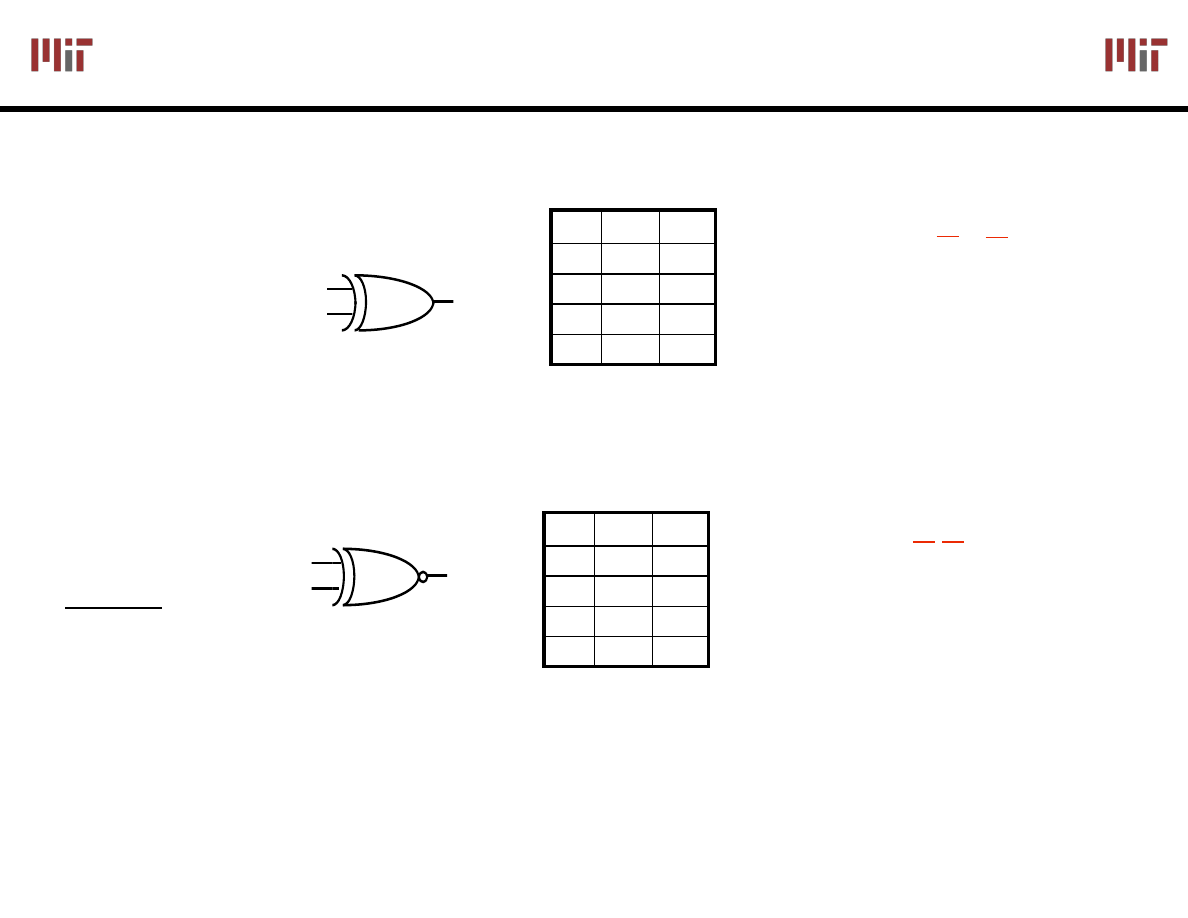
Exclusive (N)OR Gate

Exclusive (N)OR Gate

X

Y

Z

Z

X

Y

X

Y

Z

0

0

1

1

0

0

1

1

0

1

1

0

X

Y

Z

0

0

1

1

0

1

1

0

0

0

1

1

XOR

(X ⊕ Y)

XNOR

(X ⊕ Y)

Widely used in arithmetic structures such as adders and multipliers

Z = X Y + X Y

X or Y but not both

("inequality", "difference")

Z = X Y + X Y

X and Y the same

("equality")

L2: 6.111 Spring 2006

11

Introductory Digital Systems Laboratory

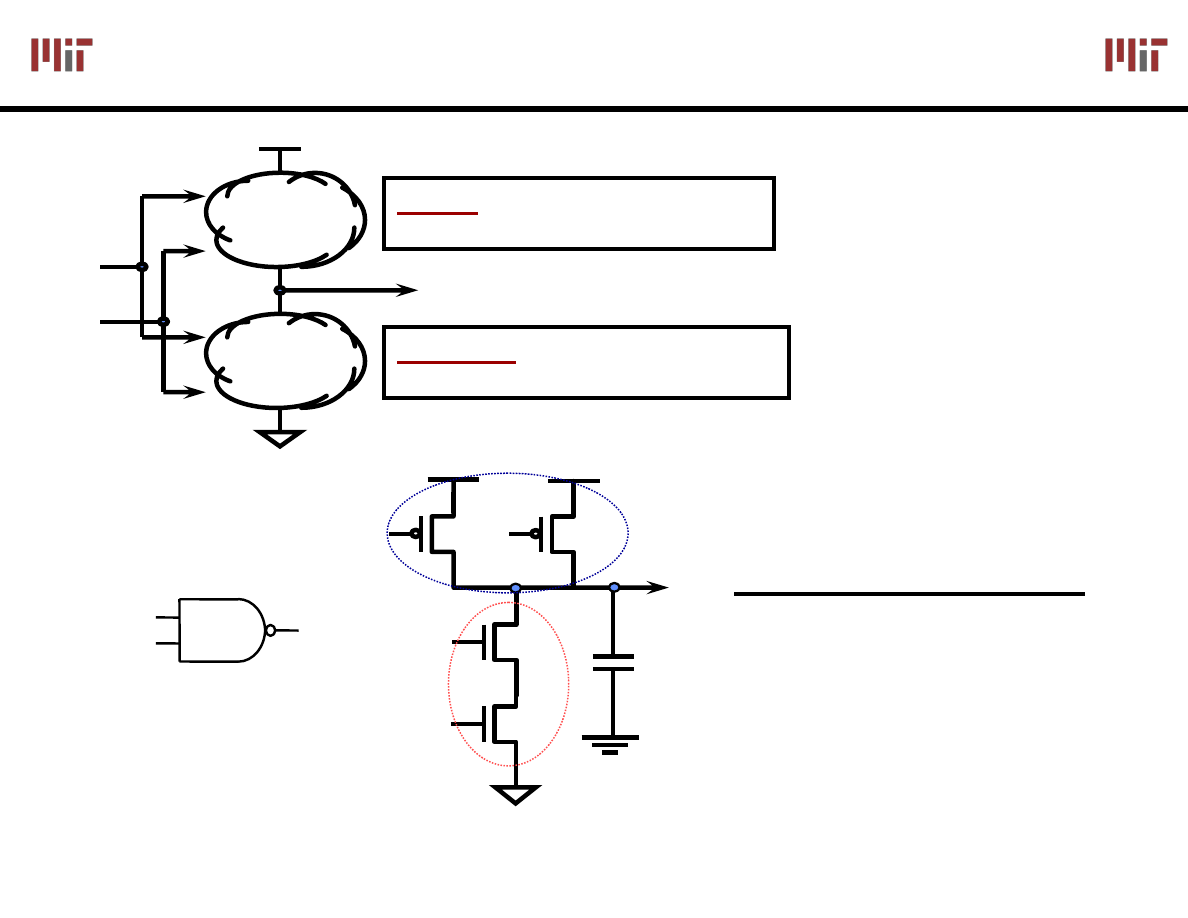
Generic CMOS Recipe

Generic CMOS Recipe

V

dd

A

1

F(A

1

,…,A

n

)

pullup

: make this connection

when we want F(A

1

,…,A

n

) = 1

pulldown

: make this connection

when we want F(A

1

,…,A

n

) = 0

A

n

...

...

...

A

B

A B PDN PUN O
0 0 0ff

0n

1

0 1 0ff

0n

1

1 0 0ff

0n

1

1 1

0n

0ff 0

B

A

C

L

PUN

PDN

How do you build a 2-input NOR Gate?

A

B

Note:

CMOS gates

result in inverting
functions!

(easier to build NAND
vs. AND)

O

L2: 6.111 Spring 2006

12

Introductory Digital Systems Laboratory

Theorems of Boolean Algebra (I)

Theorems of Boolean Algebra (I)

„

Elementary

1. X + 0 = X

1D. X • 1 = X

2. X + 1 = 1

2D. X • 0 = 0

3. X + X = X

3D. X • X = X

4. (X) = X

5. X + X = 1

5D. X • X = 0

„

Commutativity:

6. X + Y = Y + X

6D. X • Y = Y • X

„

Associativity:

7. (X + Y) + Z = X + (Y + Z)

7D. (X • Y) • Z = X • (Y • Z)

„

Distributivity:

8. X • (Y + Z) = (X • Y) + (X • Z)

8D. X + (Y • Z) = (X + Y) • (X + Z)

„

Uniting:

9. X • Y + X • Y = X

9D. (X + Y) • (X + Y) = X

„

Absorption:

10. X + X • Y = X

10D. X • (X + Y) = X

11. (X + Y) • Y = X • Y

11D. (X • Y) + Y = X + Y

L2: 6.111 Spring 2006

13

Introductory Digital Systems Laboratory

Theorems of Boolean Algebra (II)

Theorems of Boolean Algebra (II)

„

Factoring:

12. (X

•

Y) + (X • Z) =

12D. (X + Y) • (X + Z) =

X • (Y + Z)

X + (Y • Z)

„

Consensus:

13. (X • Y) + (Y • Z) + (X • Z) =

13D. (X + Y) • (Y + Z) • (X + Z) =

X • Y + X • Z

(X + Y) • (X + Z)

„

De Morgan's:

14.

(X + Y + ...) = X • Y • ...

14D.

(X • Y • ...) = X + Y + ...

„

Generalized De Morgan's:

15. f(X1,X2,...,Xn,0,1,+,•) = f(X1,X2,...,Xn,1,0,•,+)

„

Duality

†

Dual of a Boolean expression is derived by replacing • by +, + by •, 0

by 1, and 1 by 0, and leaving variables unchanged

†

f (X1,X2,...,Xn,0,1,+,•)

⇔ f(X1,X2,...,Xn,1,0,•,+)

L2: 6.111 Spring 2006

14

Introductory Digital Systems Laboratory

Simple Example: One Bit Adder

Simple Example: One Bit Adder

„

1-bit binary adder

†

inputs: A, B, Carry-in

†

outputs: Sum, Carry-out

A
B

Cin

Cout

S

A B

Cin S Cout

0

0

0

0

0

1

0

1

0

0

1

1

1

0

0

1

0

1

1

1

0

1

1

1

0

1

1

0

1

0

0

1

0

0

0

1

0

1

1

1

Sum-of-Products Canonical Form

S = A B Cin + A B Cin + A B Cin + A B Cin

Cout = A B Cin + A B Cin + A B Cin + A B Cin

„

Product term (or minterm)

†

ANDed product of literals – input combination for which output
is true

†

Each variable appears exactly once, in true or inverted form (but
not both)

L2: 6.111 Spring 2006

15

Introductory Digital Systems Laboratory

Simplify Boolean Expressions

Simplify Boolean Expressions

Cout

= A B Cin + A B Cin + A B Cin + A B Cin
= A B Cin +

A B Cin

+ A B Cin +

A B Cin

+ A B Cin +

A B Cin

= (A + A) B Cin + A (B + B) Cin + A B (Cin + Cin)
= B Cin + A Cin + A B
= (B + A) Cin + A B

S = A B Cin + A B Cin + A B Cin + A B Cin

=( A B + A B )Cin + (A B + A B) Cin

=(A ⊕ B) Cin + (A ⊕ B) Cin
= A ⊕ B ⊕ Cin

L2: 6.111 Spring 2006

16

Introductory Digital Systems Laboratory

Sum

Sum

-

-

of

of

-

-

Products & Product

Products & Product

-

-

of

of

-

-

Sum

Sum

short-hand notation form in terms of 3 variables

A

B

C

minterms

0

0

0

A B C

m0

0

0

1

A B C

m1

0

1

0

A B C

m2

0

1

1

A B C

m3

1

0

0

A B C

m4

1

0

1

A B C

m5

1

1

0

A B C

m6

1

1

1

A B C

m7

F in canonical form:

F(A, B, C) = Σm(1,3,5,6,7)

= m1 + m3 + m5 + m6 + m7

canonical form ≠ minimal form

F(A, B, C) = A B C + A B C + AB C + ABC + ABC

= (A B + A B + AB + AB)C + ABC

= ((A + A)(B + B))C + ABC

= C + ABC = ABC + C = AB + C

„

Product term

(or minterm): ANDed product of literals – input combination for which output is true

F =

+ A B C+ A B C + A B C + ABC

A B C

A

B

C

maxterms

0

0

0

A + B + C

M0

0

0

1

A + B + C M1

0

1

0

A + B + C

M2

0

1

1

A + B + C M3

1

0

0

A + B + C

M4

1

0

1

A + B+ C

M5

1

1

0

A + B +C

M6

1

1

1

A +B + C

M7

short-hand notation for maxterms of 3 variables

F in canonical form:

F(A, B, C) = ΠM(0,2,4)

= M0 • M2 • M4

= (A + B + C) (A + B + C) (A + B + C)

canonical form ≠ minimal form

F(A, B, C) = (A + B + C) (A + B + C) (A + B + C)

= (A + B + C) (A + B + C)

(A + B + C) (A + B + C)

= (A + C) (B + C)

„

Sum term

(or maxterm) - ORed sum of literals – input combination for which output is false

L2: 6.111 Spring 2006

17

Introductory Digital Systems Laboratory

Mapping Between Forms

Mapping Between Forms

1.

Minterm to Maxterm conversion:

rewrite minterm shorthand using maxterm shorthand
replace minterm indices with the indices not already used

E.g., F(A,B,C) =

Σm(3,4,5,6,7) = ΠM(0,1,2)

2.

Maxterm to Minterm conversion:

rewrite maxterm shorthand using minterm shorthand
replace maxterm indices with the indices not already used

E.g., F(A,B,C) =

ΠM(0,1,2) = Σm(3,4,5,6,7)

3.

Minterm expansion of F to Minterm expansion of F':

in minterm shorthand form, list the indices not already used in F

E.g., F(A,B,C) =

Σm(3,4,5,6,7) F'(A,B,C) = Σm(0,1,2)

=

ΠM(0,1,2) = ΠM(3,4,5,6,7)

4.

Minterm expansion of F to Maxterm expansion of F':

rewrite in Maxterm form, using the same indices as F

E.g., F(A,B,C) =

Σm(3,4,5,6,7) F'(A,B,C) = ΠM(3,4,5,6,7)

=

ΠM(0,1,2) = Σm(0,1,2)

L2: 6.111 Spring 2006

18

Introductory Digital Systems Laboratory

The Uniting Theorem

The Uniting Theorem

A

B

F

0

0

1

0

1

0

1

0

1

1

1

0

B has the same value in both on-set rows

– B remains

A has a different value in the two rows

– A is eliminated

F = A B +AB = (A +A)B = B

„

Key tool to simplification: A (B + B) = A

„

Essence of simplification of two-level logic

†

Find two element subsets of the ON-set where only one variable
changes its value – this single varying variable can be
eliminated and a single product term used to represent both
elements

L2: 6.111 Spring 2006

19

Introductory Digital Systems Laboratory

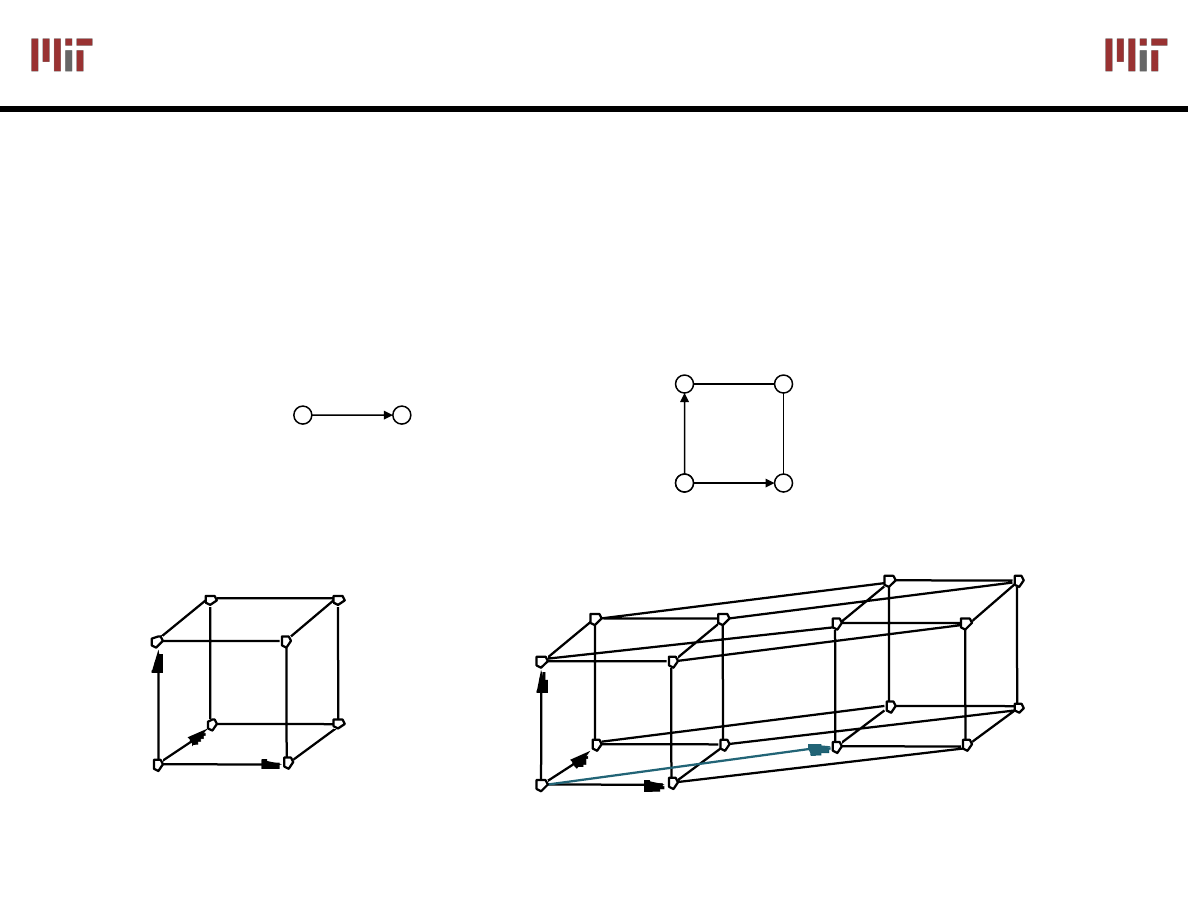
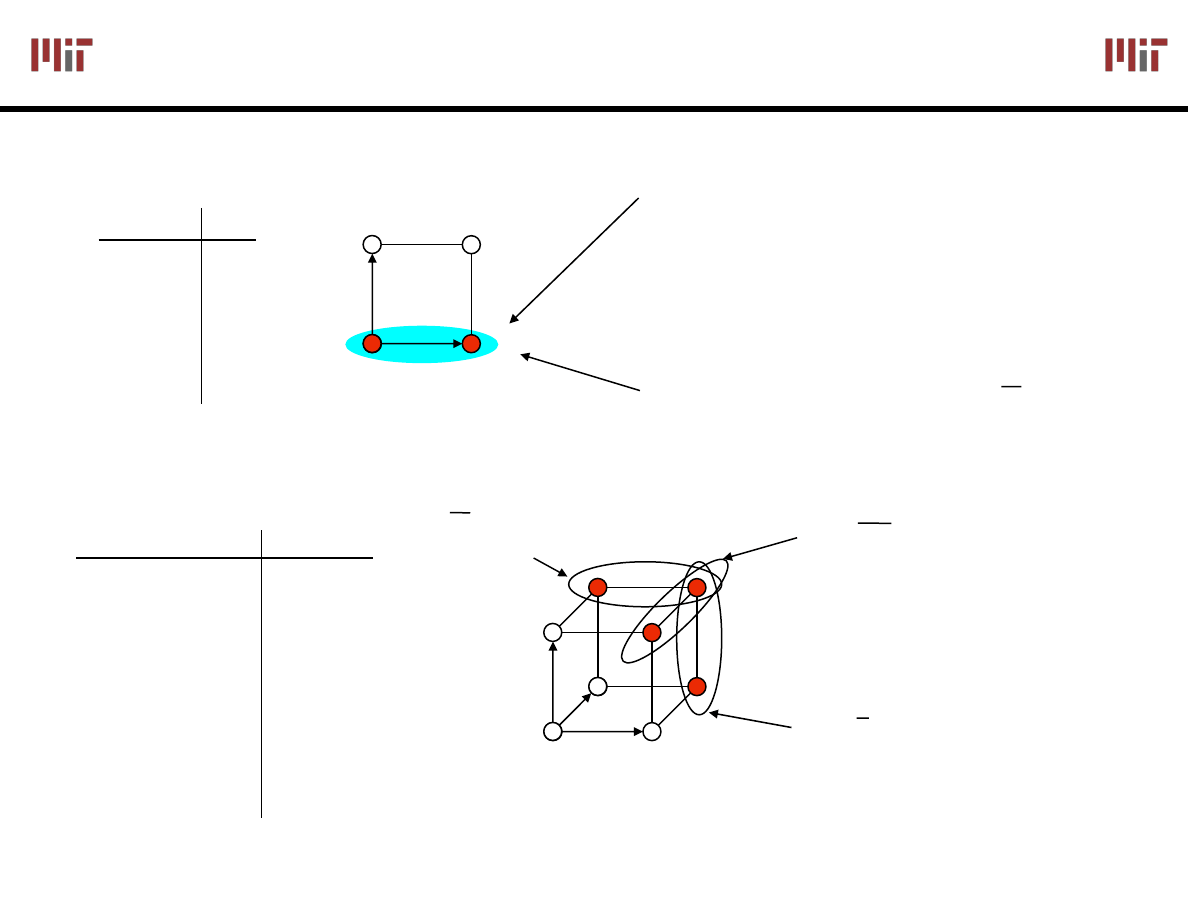
Boolean Cubes

Boolean Cubes

1-cube

X

0

1

„

Just another way to represent truth table

„

Visual technique for identifying when the uniting theorem
can be applied

„

n input variables = n-dimensional "cube"

2-cube

X

Y

11

00

01

10

WXYZ

0111

0011

0010

0000

0001

0110

1010

0101

0100

1000

1011

1001

1110

1111

1101

1100

Y

Z

W

X

3-cube

XYZ

X

011

010

000

001

111

110

100

101

Y

Z

4-cube

XY

L2: 6.111 Spring 2006

20

Introductory Digital Systems Laboratory

A

B

F

0

0

1

0

1

0

1

0

1

1

1

0

ON-set = solid nodes

OFF-set = empty nodes

Circled group of the on-set is called the

adjacency

plane. Each adjacency plane

corresponds to a product term.

A varies within face, B does not

this face represents the literal B

Mapping Truth Tables onto Boolean Cubes

Mapping Truth Tables onto Boolean Cubes

„

Uniting theorem

A

B

11

00

01

10

F

A B

Cin

Cout

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

1

Cout = BCin+AB+ACin

A(B+B)Cin

The on-set is completely covered by the combination (OR) of the subcubes of
lower dimensionality - note that “111” is covered three times

A

B C

000

111

101

(A+A)BCin

AB(Cin+Cin)

„

Three variable example: Binary full-adder carry-out logic

L2: 6.111 Spring 2006

21

Introductory Digital Systems Laboratory

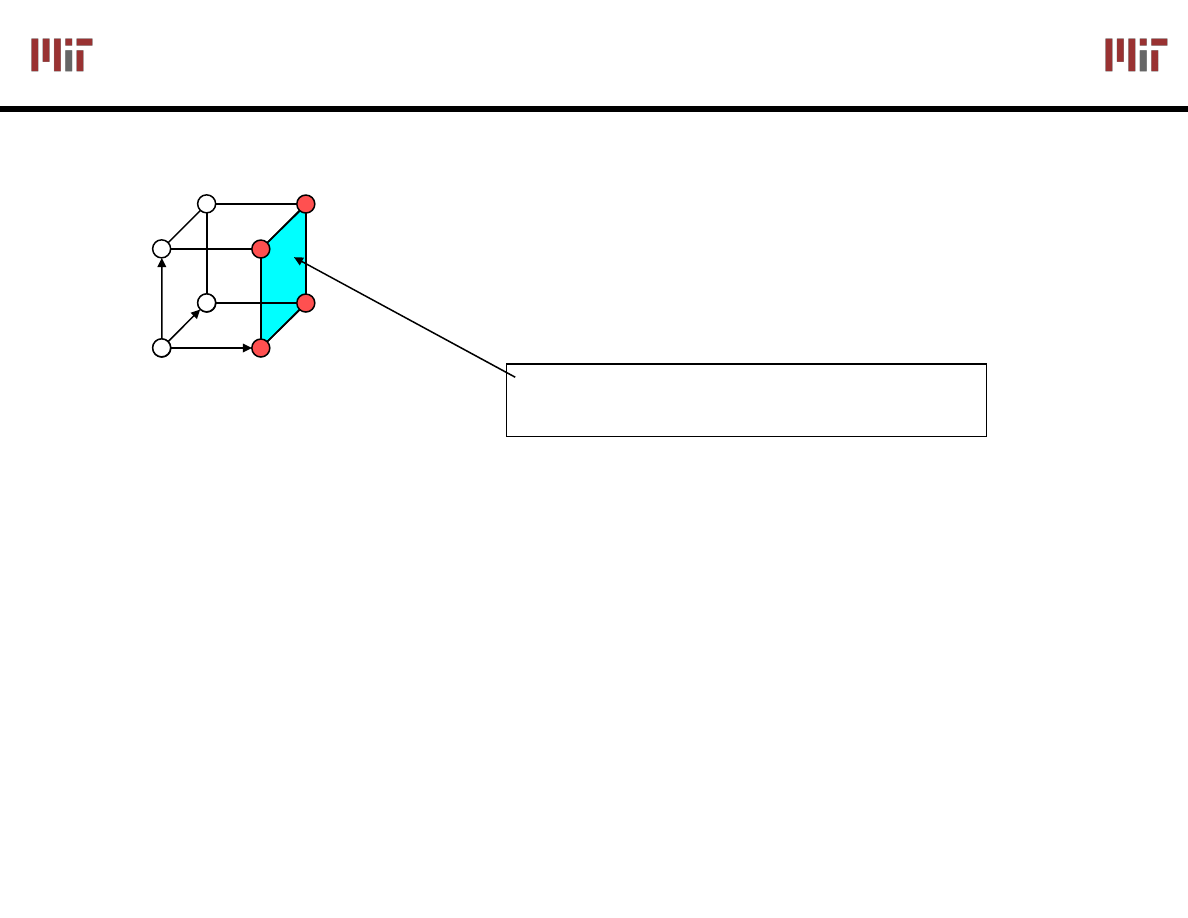
Higher Dimension Cubes

Higher Dimension Cubes

F(A,B,C) = Σm(4,5,6,7)
on-set forms a square

i.e., a cube of dimension 2 (2-D adjacency plane)

represents an expression in one variable

i.e., 3 dimensions – 2 dimensions

A is asserted (true) and unchanged

B and C vary

This subcube represents the literal A

A

B C

000

111

101

100

001

010

011

110

„

In a 3-cube (three variables):

†

0-cube, i.e., a single node, yields a term in 3 literals

†

1-cube, i.e., a line of two nodes, yields a term in 2 literals

†

2-cube, i.e., a plane of four nodes, yields a term in 1 literal

†

3-cube, i.e., a cube of eight nodes, yields a constant term "1"

„

In general,

†

m-subcube within an n-cube (m < n) yields a term with n – m
literals

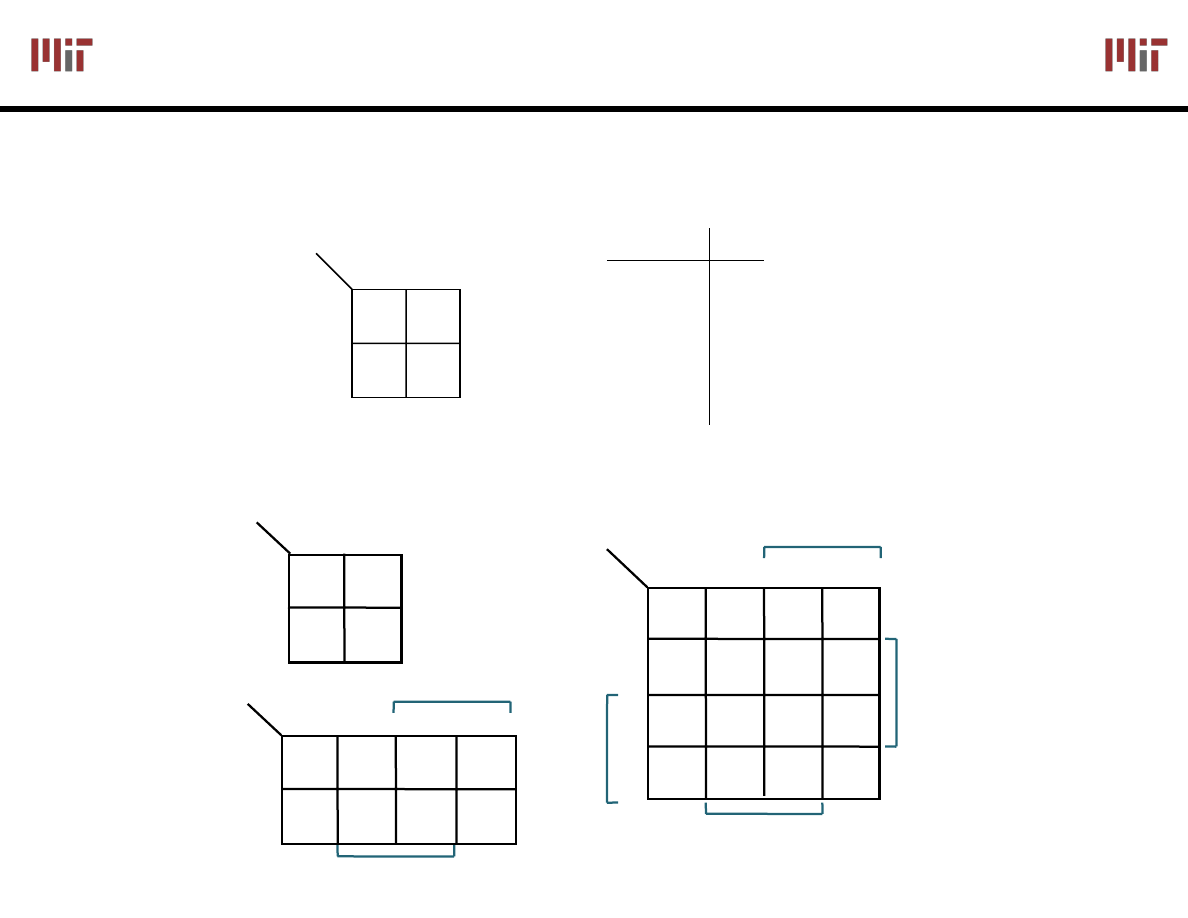
L2: 6.111 Spring 2006

22

Introductory Digital Systems Laboratory

Karnaugh

Karnaugh

Maps

Maps

A

B

F

0

0

1

0

1

0

1

0

1

1

1

0

„

Alternative to truth-tables to help visualize adjacencies

†

Guide to applying the uniting theorem - On-set elements with only one
variable changing value are adjacent unlike in a linear truth-table

0

2

1

3

0

1

A

B

0

1

1

0

0

1

„

Numbering scheme based on Gray–code

†

e.g., 00, 01, 11, 10 (only a single bit changes in code for adjacent map cells)

A

B

0 1

0

1

0

1

2

3

0

1

2

3

6

7

4

5

AB

C

0

1

3

2

4

5

7

6

12

13

15

14

8

9

11

10

A

B

AB

CD

A

00 01 11 10

0

1

00 01 11 10

00

01

11

10

C

B

D

2-variable

K-map

3-variable

K-map

4-variable

K-map

L2: 6.111 Spring 2006

23

Introductory Digital Systems Laboratory

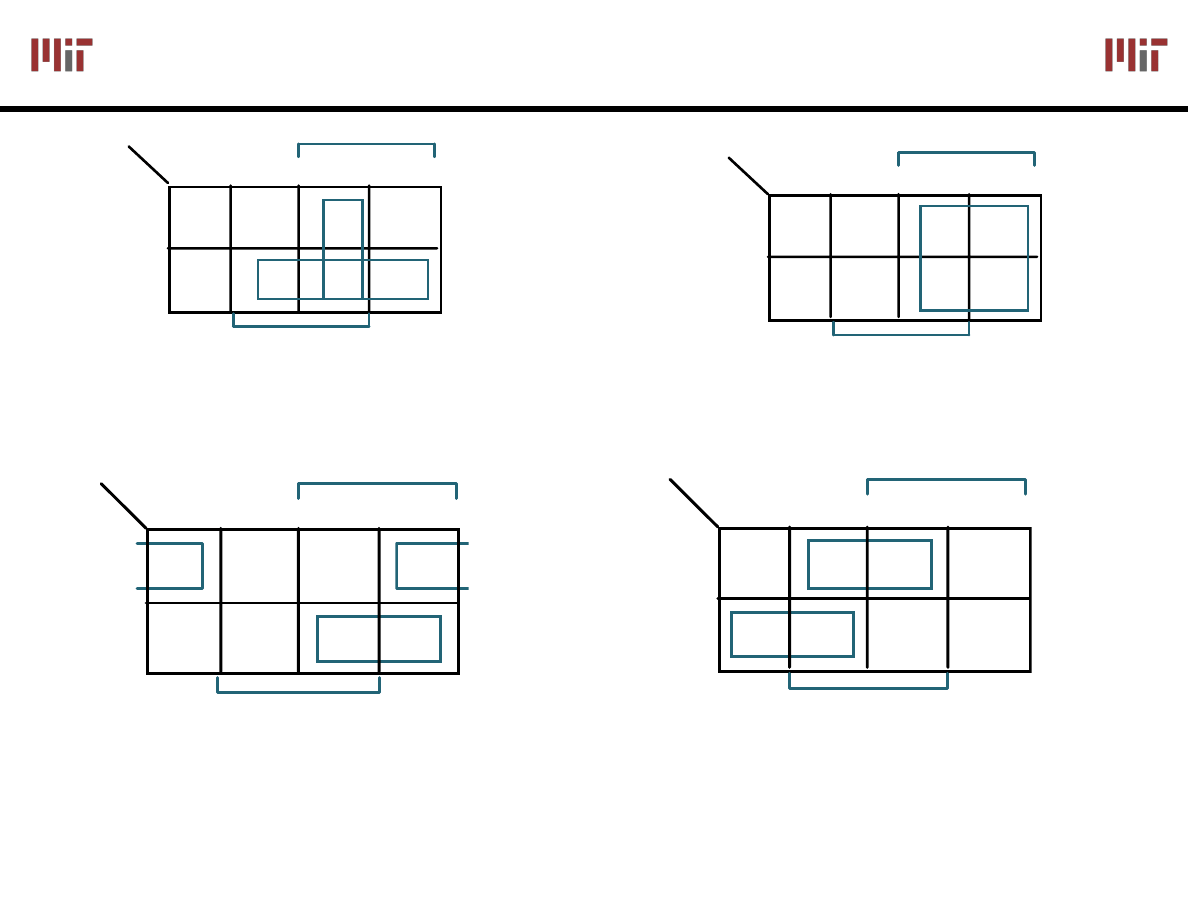
K

K

-

-

Map Examples

Map Examples

Cout =

F(A,B,C) =

A B

A

B

Cin

00 01 11 10

0

1

0

0

0

1

1

1

0

1

AB

C

A

00 01 11 10

0

1

0

0

0

0

1

1

1

1

B

F(A,B,C) =

Σm(0,4,5,7)

F =

00

C

AB

01 11 10

1

0

0

1

1

1

0

0

A

B

0

1

00

C

AB

01 11 10

0

1

1

0

0

0

1

1

A

B

0

1

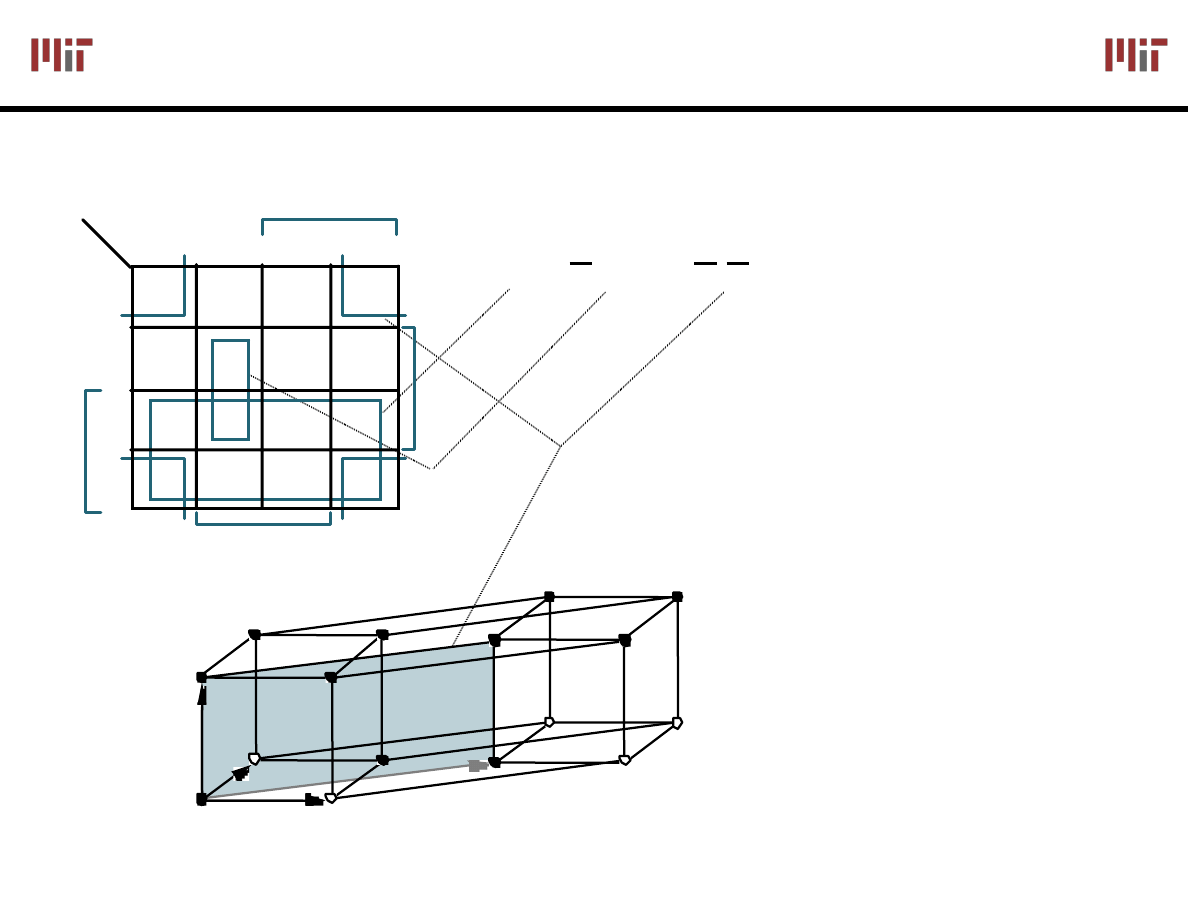
F' simply replace 1's with 0's and vice versa

F'(A,B,C) =

Σm(1,2,3,6)

F' =

L2: 6.111 Spring 2006

24

Introductory Digital Systems Laboratory

Four Variable

Four Variable

Karnaugh

Karnaugh

Map

Map

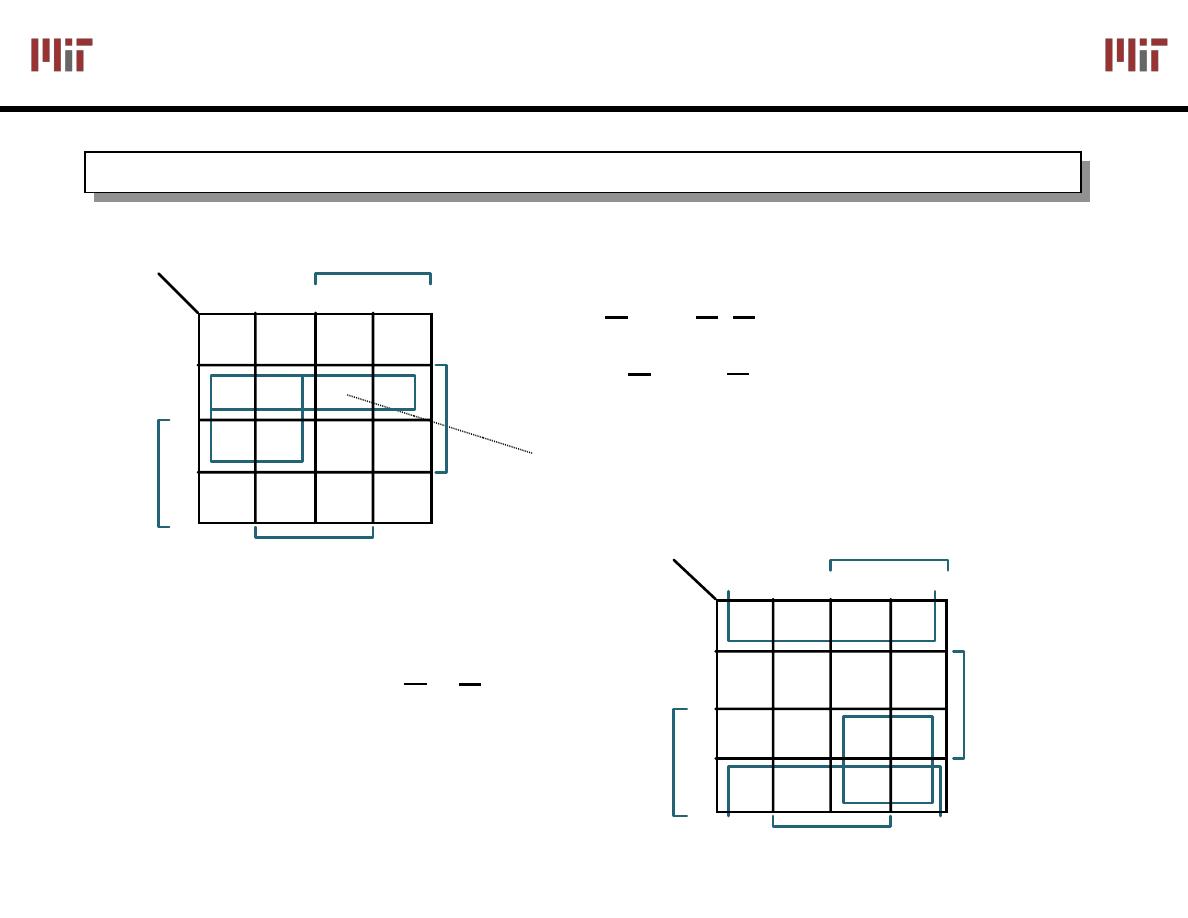
F(A,B,C,D) =

Σm(0,2,3,5,6,7,8,10,11,14,15)

F = C + A B D + B D

K-map Corner Adjacency

Illustrated in the 4-Cube

Find the smallest number

of the largest possible

subcubes that cover the

ON-set

AB

00 01 11 10

1 0 0 1

0 1 0 0

1 1 1 1

1 1 1 1

00

01

11

10

C

CD

A

D

B

0011

D

0010

0000

0111

0110

0001

C

A

B

0100

1000

1100

1101

1111

1110

1001

1011

1010

0101

L2: 6.111 Spring 2006

25

Introductory Digital Systems Laboratory

K

K

-

-

Map Example: Don

Map Example: Don

’

’

t Cares

t Cares

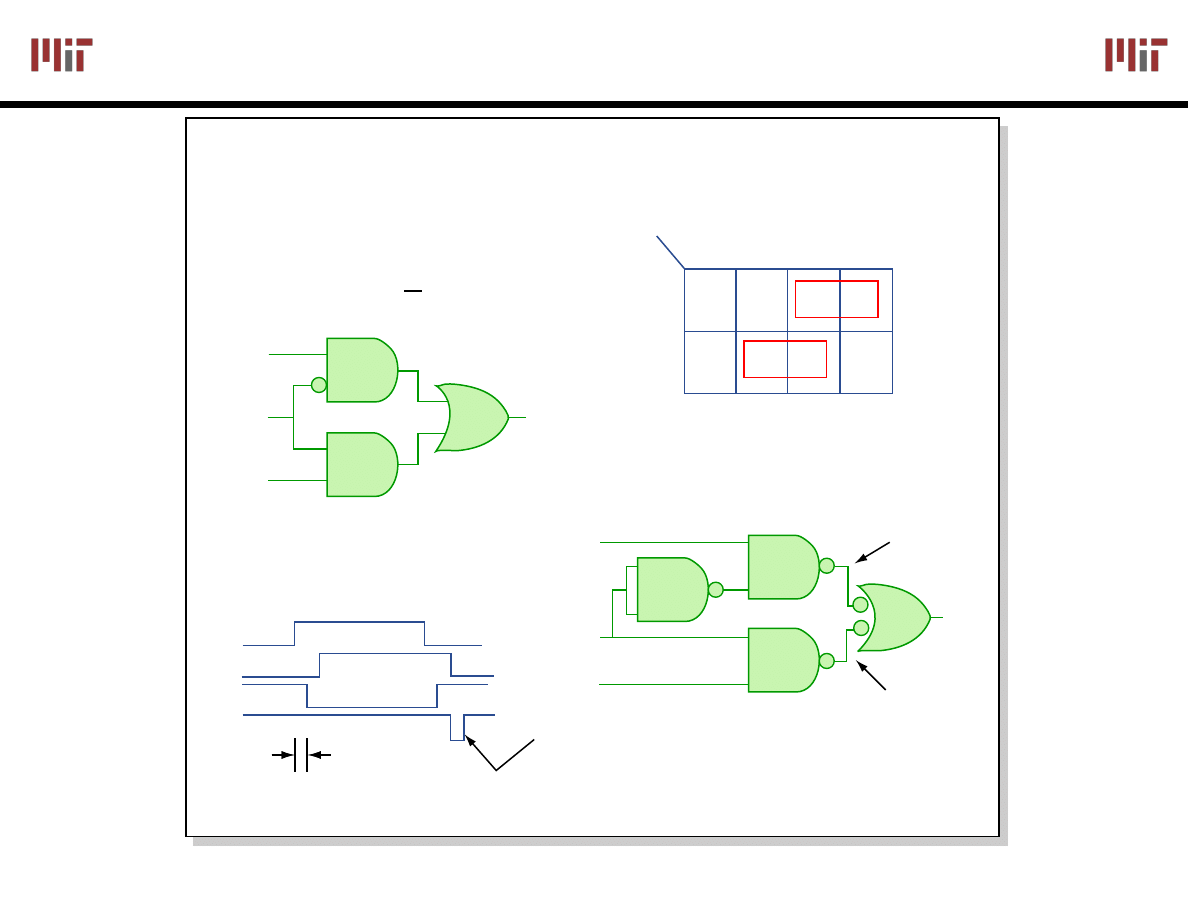
F(A,B,C,D) =

Σm(1,3,5,7,9) + Σd(6,12,13)

F = A D + B C D w/o don't cares

F = C D + A D w/ don't cares

Don't Cares can be treated as 1's or 0's if it is advantageous to do so

Don't Cares can be treated as 1's or 0's if it is advantageous to do so

By treating this DC as a "1", a 2-cube
can be formed rather than one 0-cube

AB

00 01 11 10

0 0 X 0

1 1 X 1

1 1 0 0

0 X 0 0

00

01

11

10

C

CD

A

D

B

AB

00 01 11 10

0 0 X 0

1 1 X 1

1 1 0 0

0 X 0 0

00

01

11

10

C

CD

A

D

B

In PoS form: F = D (A + C)

Equivalent answer as above,
but fewer literals

L2: 6.111 Spring 2006

26

Introductory Digital Systems Laboratory

Hazards

Hazards

Figure by MIT OpenCourseWare.

A

C

B

A = B = 1

C

1

2

F

Gate delay

Glitch

F

Static hazards: Consider this function:

Implemented with MSI gates:

'00

'00

'00

'00

A

C
B

F

2

1

C

AB

00 01 11 10

0 0

0

0

0

1

1

1

1

1

F = A * C + B * C

L2: 6.111 Spring 2006

27

Introductory Digital Systems Laboratory

Fixing Hazards

Fixing Hazards

ƒ

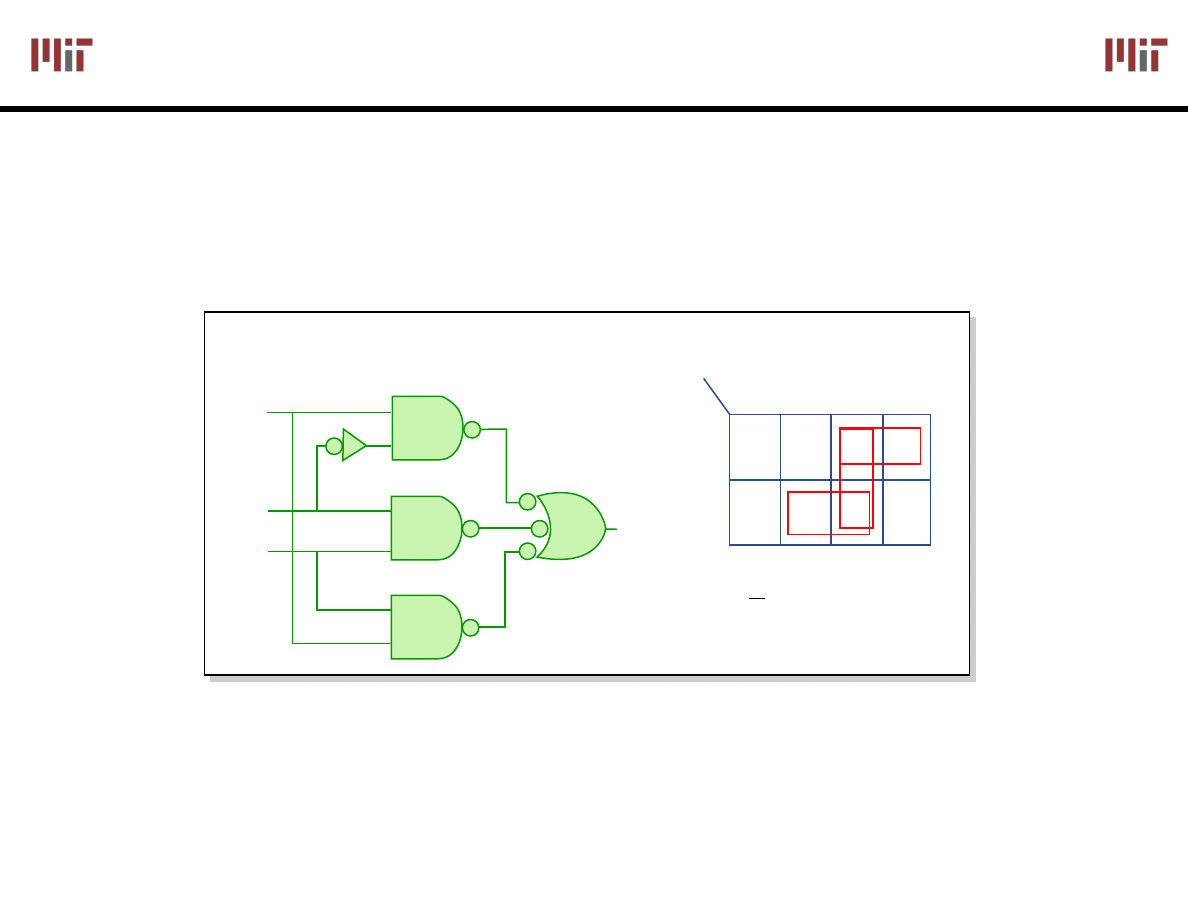
In general, it is difficult to avoid hazards – need a robust

design methodology to deal with hazards.

The glitch is the result of timing differences

in parallel data paths. It is associated with the

function jumping between groupings or product

terms on the K-map. To fix it, cover it up with

another grouping or product term!

Figure by MIT OpenCourseWare.

C

AB

00 01 11 10

0 0 0

0

0

1 1

1

1

1

A

C
B

F

F = A * C + B * C + A * B