MECHANIKA BUDOWLI  

 

Wykład 2:  

TWIERDZENIA O WZAJEMNOŚCI 

 

Prowadzący: dr inż. Wojciech Zielichowski-Haber 

 

Twierdzenie o wzajemności prac  

Plan wykładu 

1. Informacje wstępne 
2. Twierdzenie o wzajemności prac 
3. Twierdzenie o wzajemności przemieszczeń 
4. Twierdzenie o wzajemności reakcji 
5. Twierdzenie o wzajemności reakcji i przemieszczeń 

 

Twierdzenie o wzajemności prac  

Informacje wstępne 

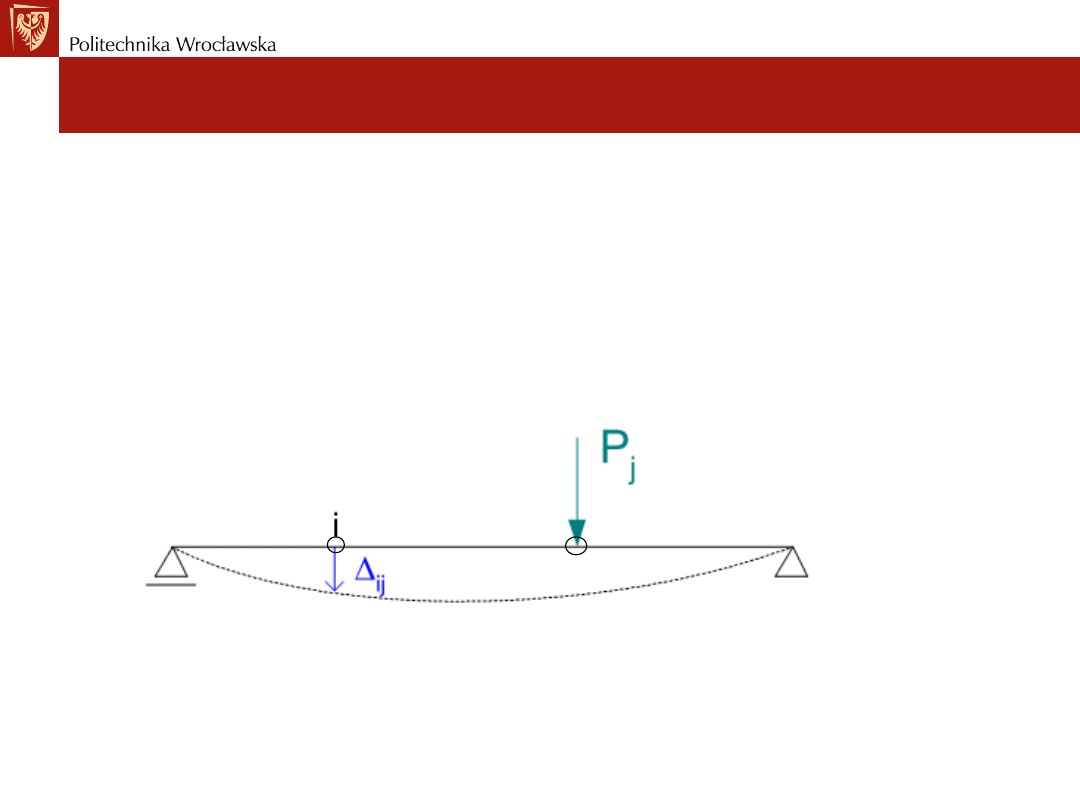
W zapisie przemieszczeń i reakcji używamy dwóch indeksów np. 
dla ∆

ij

 notacja jest następująca: 

  pierwszy indeks czyli i określa miejsce gdzie występuje dana 

wielkość (przemieszczenie lub reakcja),  

  drugi indeks czyli j oznacza przyczynę ją wywołującą 

(przemieszczenie lub reakcja). 

 
 
 
 

∆

ij

 oznacza przemieszczenie punktu i belki wywołane 

siłą P działającą w punkcie j belki. 

j 

Twierdzenie o wzajemności prac 

Informacje wstępne 

 Stosowane oznaczenia przemieszczeń i reakcji, które 

występują w poniższych wzorach i twierdzeniach.  

 

 

 

Twierdzenie o wzajemności prac 

Informacje wstępne 

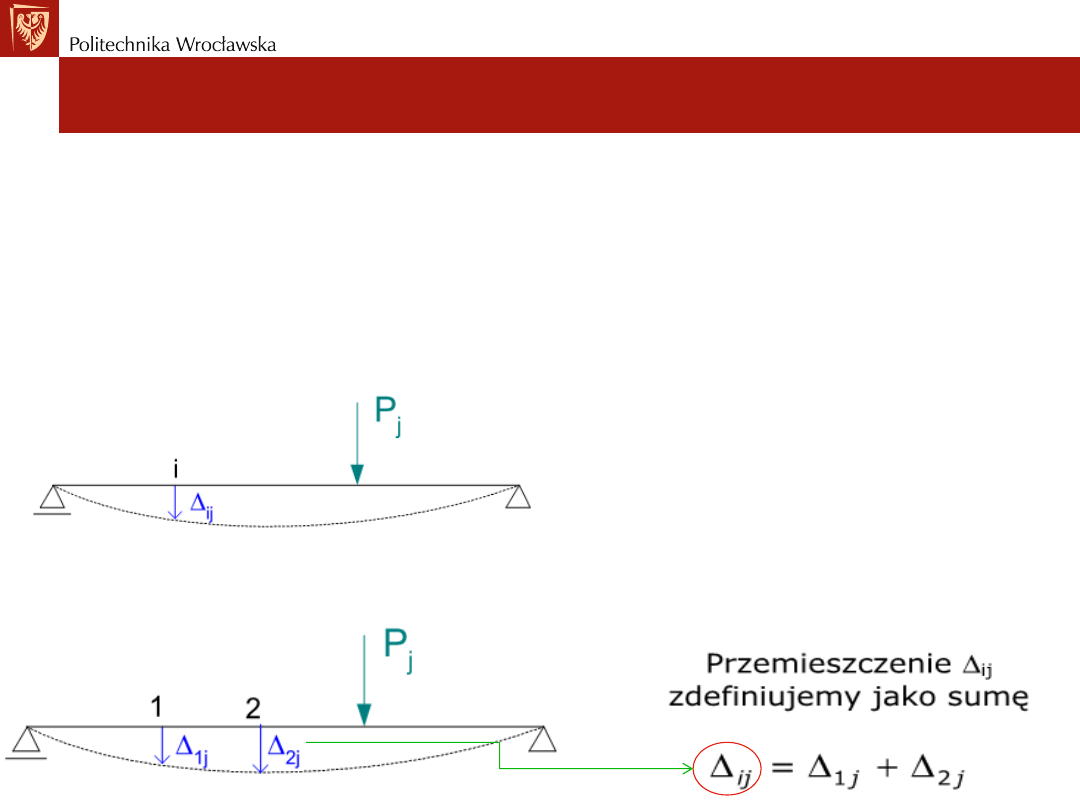
  Miejsce i kierunek i, w którym definiowane jest 

przemieszczenie lub reakcja może oznaczać konkretne 
miejsce  i  kierunek lub też 

sumę określonych  

przemieszczeń  i  reakcji.

   

Zilustrowano to poniżej: 

 

Twierdzenie o wzajemności prac.  

Informacje wstępne 

Zakładamy, że układy prętowe: 
 zbudowane są z materiału sprężystego spełniającego prawo 

Hooke'a tj. liniowa zależność pomiędzy naprężeniem, a 
odkształceniem, 
 
 
 
 

 warunki kinematyczne układu nie ulegają zmianie w trakcie 

obciążenia (układ Clapeyrona – liniowo sprężysty) 

 
 

 

Twierdzenie o wzajemności prac.  

Informacje wstępne 

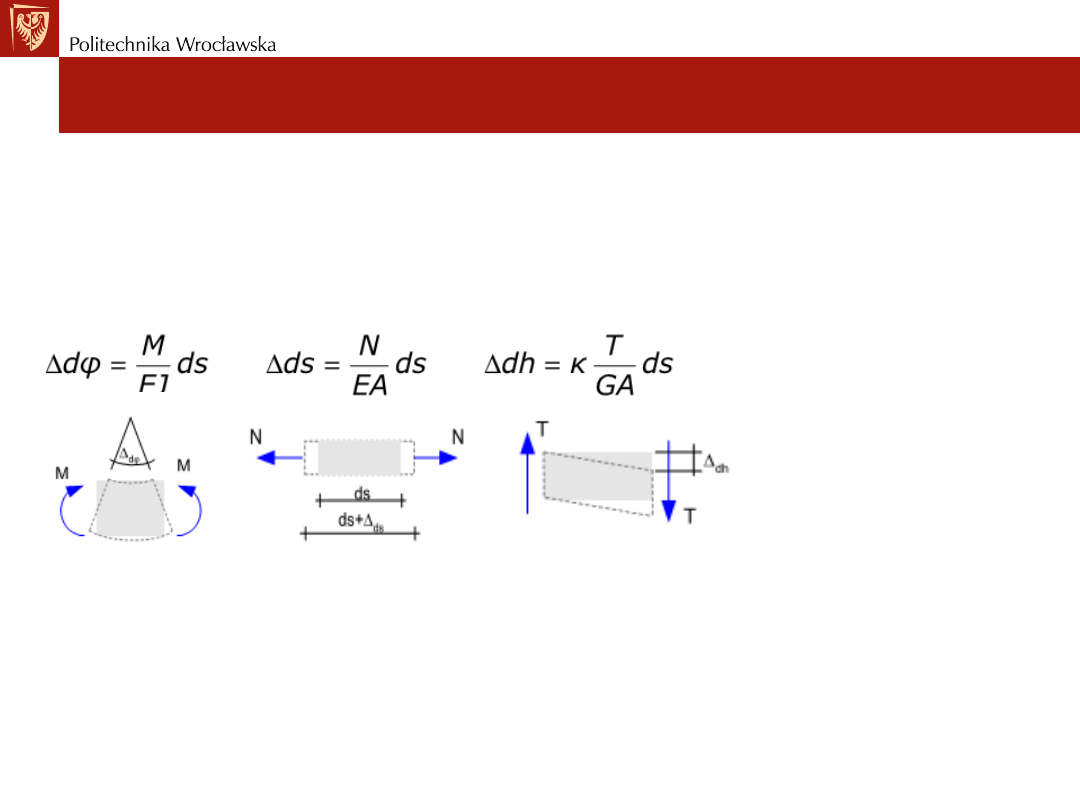
 Podobnie można określić pozostałe odkształcenia: 

• kątowe 

∆𝒅𝝋 wywołane momentem zginającym M, 

 

• podłużne 

∆𝒅𝒔 wywołane siłą podłużną N, 

• postaciowe 

∆𝒅h wywołane siłą tnącą T. 

 

 
 
 
 
gdzie potrzebne są następujące dane: 
 

E - moduł Young’a np. E = 205GPa dla stali, 

 

G - moduł Kirchoff’a G = [ E / 2(1+v) ] = 80 GPa dla stali 

 

v – współczynnik Poisson’a v = 0.3 dla stali, 

 

A - pole przekroju poprzecznego pręta,  

 

 

 

 

J - moment bezwładności przekroju pręta względem osi obojętnej.  

 
 

 

Twierdzenie o wzajemności prac 

Informacje wstępne 

 κ to współczynnik uwzględniający 

nierównomierności 

rozkładu naprężeń stycznych 

w przekroju belki  

(zależny od kształtu przekroju poprzecznego) 

 Wyznacza się ze wzoru: 

 
 
 

gdzie: 
S - moment statyczny odciętej części przekroju względem osi obojętnej, 
b – szerokość pręta (w ogólnym przypadku zmienna po wysokości). 

 Współczynnik κ dla różnych kształtów: 

 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

 Podstawowe  twierdzenie o  wzajemności  prac jest  tw. Bettiego       

(I tw. o wzajemności).   

• Rozpatrujemy dwa stany obciążeń działających  na układ  prętowy.            

Pierwszy  stan  oznaczamy indeksem "i" a drugi stan indeksem "j" 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

• Oznaczmy przez 

𝑃

𝑛𝑖

 oraz 

𝑅

𝑟𝑖

 siły i reakcje działające w układzie "i", 

a przez 

𝑀

𝑖

, 

𝑇

𝑖

, 

𝑁

𝑖

 oraz 

∆𝑑𝜑

𝑖

, 

∆𝑑ℎ

𝑖

 i 

∆𝑑𝑠

𝑖

 odpowiadające im siły 

przekrojowe i odkształcenia. Wielkościami 

∆

𝑛𝑗

 i 

∆

𝑟𝑗

 oznaczamy 

przemieszczenia w układzie „j” występujące w miejscu i kierunku 
siły oraz reakcje układu „i”.  

• Oznaczmy przez 

𝑃

𝑘𝑗

 oraz 

𝑅

𝑟𝑗

 siły i reakcje działające w układzie 

„j", a przez 

𝑀

𝑗

, 

𝑇

𝑗

, 

𝑁

𝑗

 oraz 

∆𝑑𝜑

𝑗

, 

∆𝑑ℎ

𝑗

 i 

∆𝑑𝑠

𝑗

 odpowiadające im siły 

przekrojowe i odkształcenia. Wielkościami 

∆

𝑘𝑖

 i 

∆

𝑟𝑖

 oznaczamy 

przemieszczenia w układzie „i” występujące w miejscu i kierunku 
siły oraz reakcje układu „j”.  

 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

• Traktując układ sił i przemieszczeń układu "i" jako obciążenie i 

przemieszczenie wirtualne dla układu "j" z zasady prac wirtualnych 

otrzymuje się: 

 
 
 
 
 
 

 
 

• Równanie pierwsze można traktować jako pracę wirtualnych obciążeń i  

sił przekrojowych układu  "i" na rzeczywistych  przemieszczeniach  i  

odkształceniach  układu  "j"  (II  zasada  prac  wirtualnych), natomiast 

równanie drugie traktujemy jako pracę rzeczywistych obciążeń i sił 

przekrojowych układu "j" na wirtualnych  przemieszczeniach  i  

odkształceniach  układu  "i"  (I  zasada  prac  wirtualnych). 

 

 
 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

• Biorąc pod uwagę zależności 

 
 
 
 
 

 

powyższe równania przyjmują postać: 
 
 
 
 
 
 
 
Zauważmy, że prawe strony w powyższych równaniach są sobie równe.  
  

 
 

 

 
 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

Stąd otrzymuje się tw. Bettiego o wzajemności prac  

(I tw. o wzajemności).   

 
 

Jeżeli    na    ustrój    sprężysty    działają    dwa    niezależne    od    siebie  
układy  obciążeń, spełniające  warunki  równowagi,  to  praca  obciążeń  
jednego    układu    wykonywana    na  przemieszczeniach    wywołanych  
drugim  układem  obciążeń  jest  równa pracy obciążeń drugiego układu 
wykonywanej  na  przemieszczeniach  wywołanych  pierwszym  układem 
obciążeń.  

 

 

 

Przykłady: 

 

 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności prac 

 

 

Twierdzenie o wzajemności prac. 

Twierdzenie o wzajemności przemieszczeń 

• Z  tw.  Bettiego  wynika drugie  twierdzenie o wzajemności.  

Zakłada się,  że  zarówno  w układzie "i" jak i "j" podpory nie 
ulegają przesunięciom, a więc  

∆

𝑟𝑖

= 0 i ∆

𝑟𝑗

= 0 (dla  wszystkich  r)  

i  w  obu układach występują tylko siły jednostkowe: 

𝑃

𝑛𝑖

= 1

𝑛𝑖

  i 

𝑃

𝑘𝑗

= 1

𝑘𝑗

.  

Wówczas  z  równania  otrzymuje się: 

 
 

Ponieważ  

 
 
 

Zgodnie z wcześniej przyjętymi oznaczeniami ma formę:  

 

 

 

 

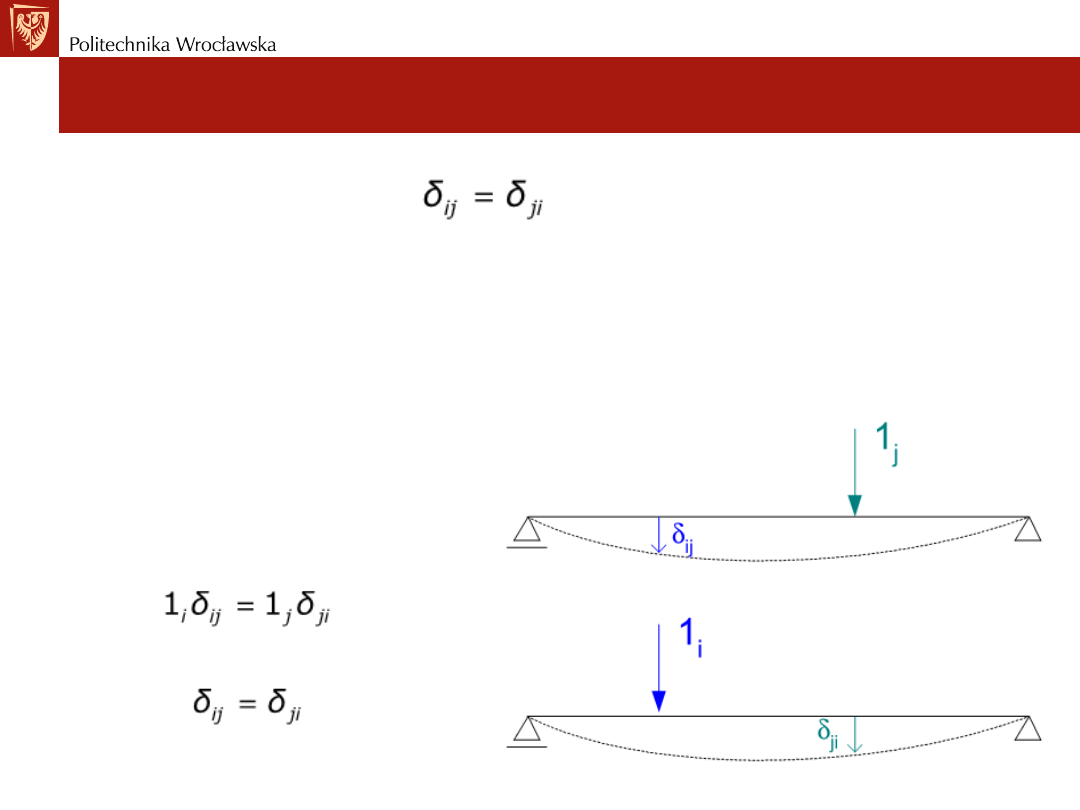
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności przemieszczeń 

Zależność:  
 
stanowi 

tw. Maxwella o wzajemności przemieszczeń: 

Przemieszczenie  w  miejscu  "i"  wywołane jednostkowym  
obciążeniem działającym w miejscu "j" jest równe przemieszczeniu 
w miejscu  "j" wywołanemu jednostkowym obciążeniem działąjącym 
w miejscu "i". 

 
Przykład nr1: 

 

 

 

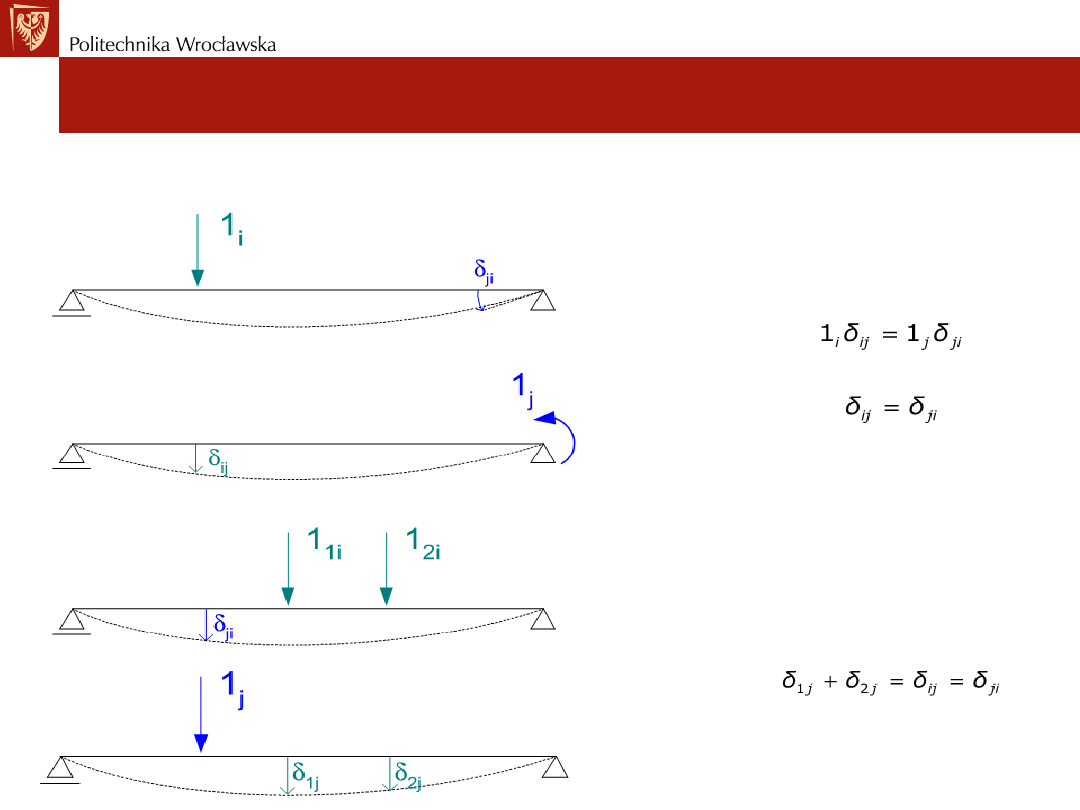
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności przemieszczeń 

Przykład nr2. 

 
 
 

 

Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji 

• Z  tw.  Bettiego  wynika trzecie  twierdzenie o wzajemności. 

Rozpatrzmy  sytuację,  gdy  w  obu  stanach  "i"  oraz  "j"  siły  
są  równe  zeru,  a  więc  

𝑃

𝑛𝑖

= 𝑃

𝑘𝑗

= 0  dla wszystkich n oraz 

k, natomiast w obu stanach obciążenie stanowią 
jednostkowe przemieszczenia podpór, a  więc 

∆

𝑟𝑖

= 1

𝑟𝑖

i 

∆

𝑟𝑗

= 1

𝑟𝑗

  przynajmniej dla niektórych r w każdym stanie.  

 

Z twierdzenie Bettiego  orzymuje się:  
 
 
 
Zgodnie z wcześniej przyjętymi oznaczeniami ma formę:  

 

 

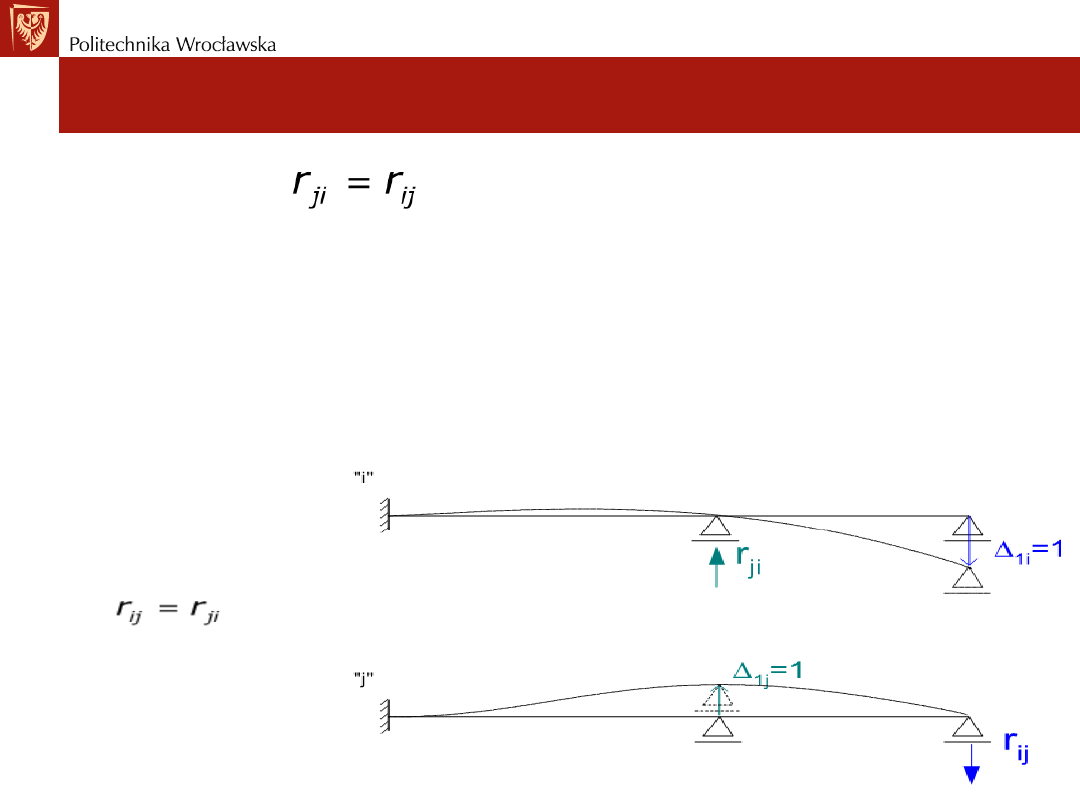
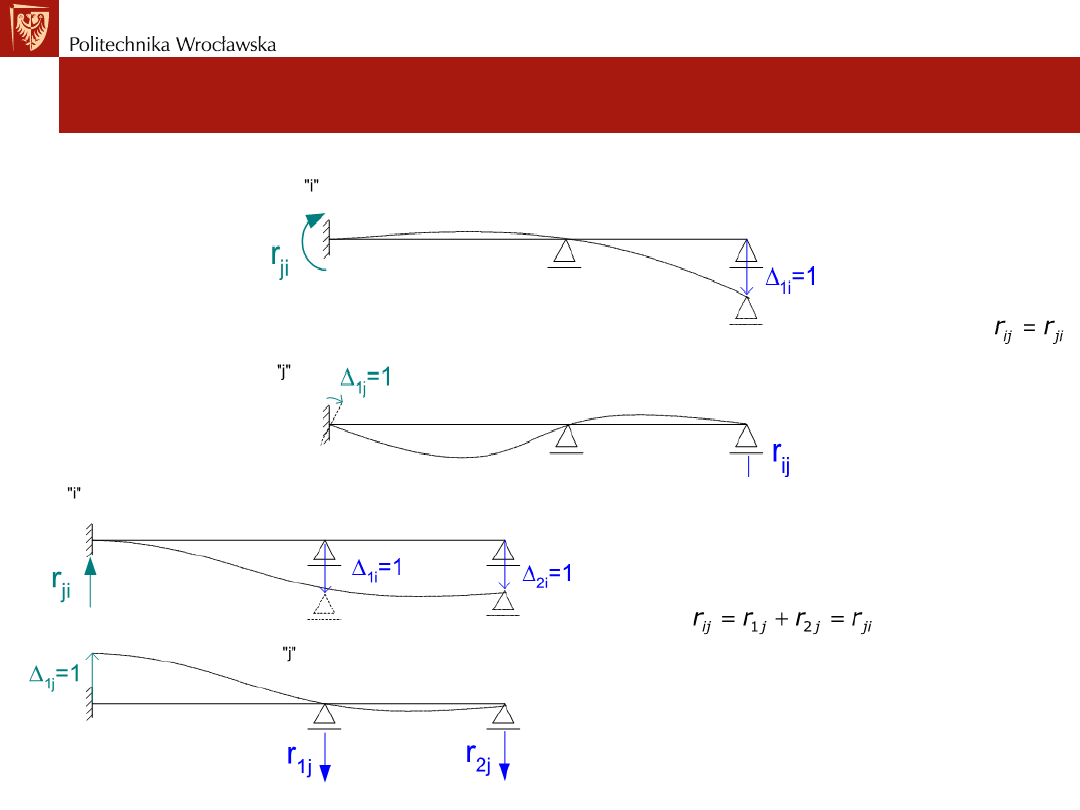
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji 

Zależność: 

 

stanowi 

tw. o wzajemności reakcji – tw. Rayleigha

. 

Reakcja  w  miejscu  i  na  kierunku  "i"  wywołana  jednostkowym  
przemieszczeniem zadanym w miejscu i na kierunku "j" jest równa 
reakcji w miejscu  i  na  kierunku  "j" wywołanej jednostkowym 
przemieszczeniem zadanym w miejscu i na kierunku "i"

. 

Przykład nr1: 
 

 
 

 

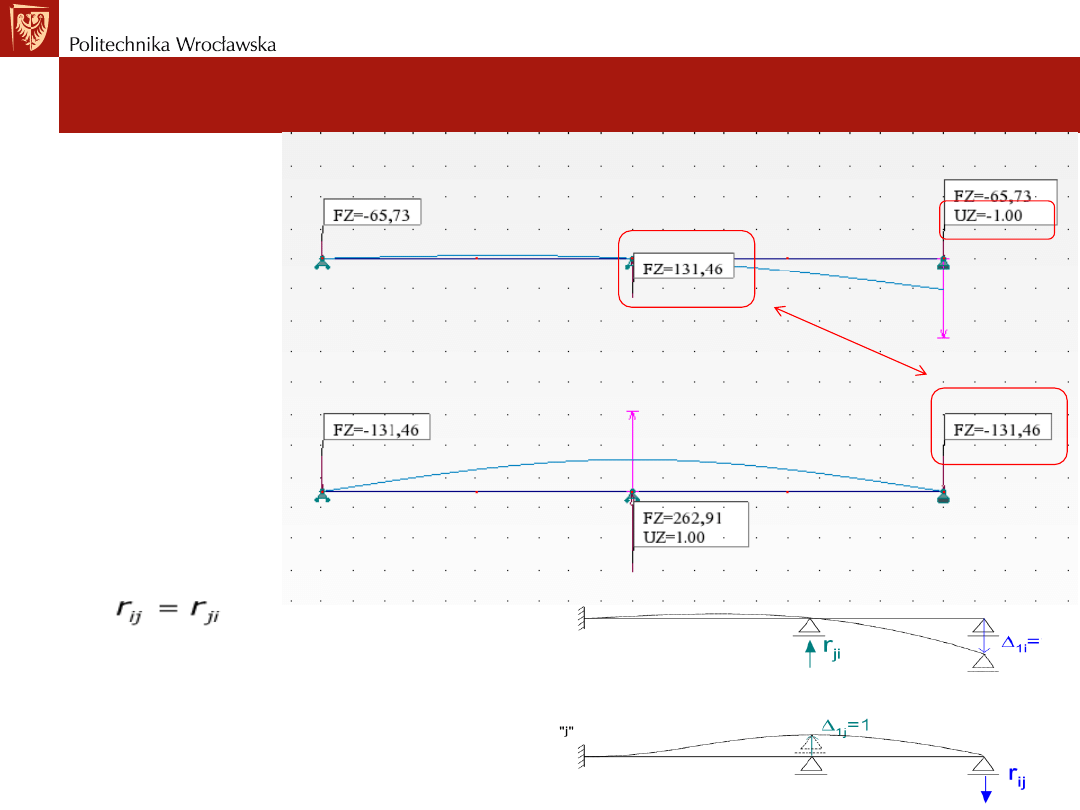
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji 

Przykład nr2: 
 

 
 

 

Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji 

Przykład nr3: 
 
 
 
 
 
Przykład nr4: 

 

 

 

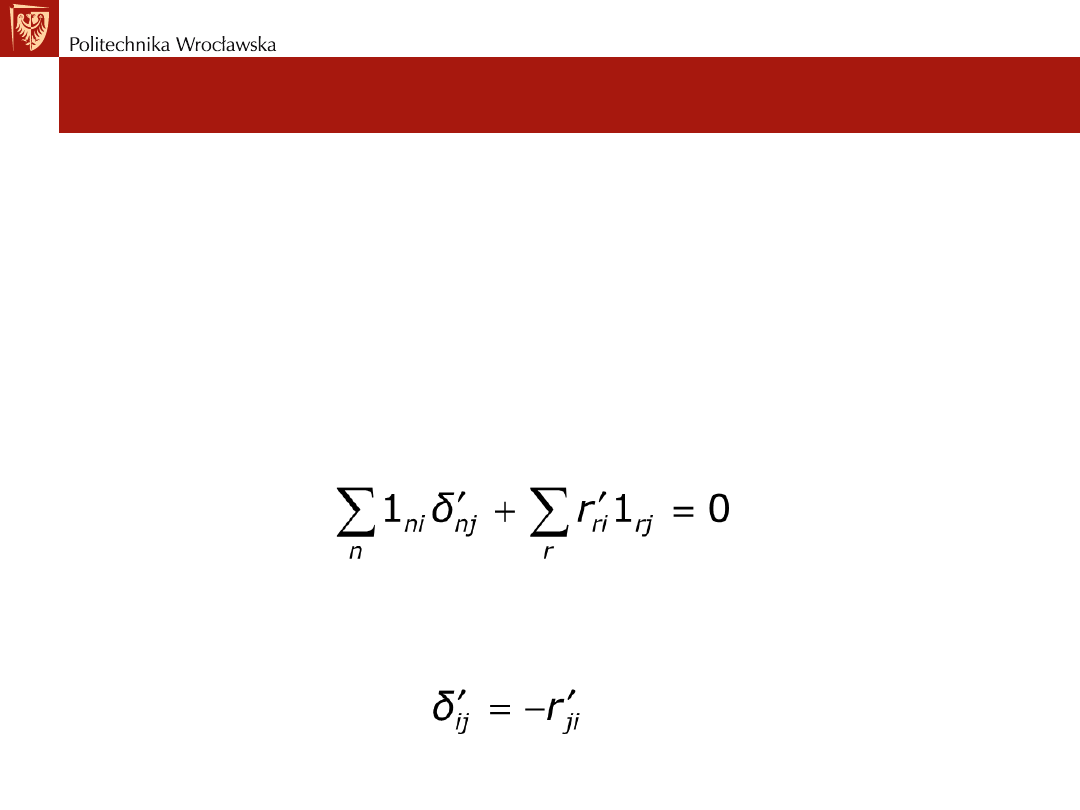
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji i przemieszczeń 

• Ostatnie  twierdzenie  o  wzajemności. W  stanie  i  obciążenie  

stanowią siły jednostkowe 

𝑃

𝑛𝑖

= 1

𝑛𝑖

,   (przynajmniej dla jednego 

n), a 

∆

𝑟𝑖

= 0 (dla wszystkich r), zaś w stanie j  obciążenie stanowią 

jednostkowe  przemieszczenia 

∆

𝑟𝑗

= 1 (przynajmniej dla jednego 

r), a wszystkie 

𝑃

𝑛𝑖

= 0.  

 

Z twierdzenie Bettiego otrzymuje się:   
 
 
 
Zgodnie z przyjętymi oznaczeniami zależność ma postać: 
 

 

 

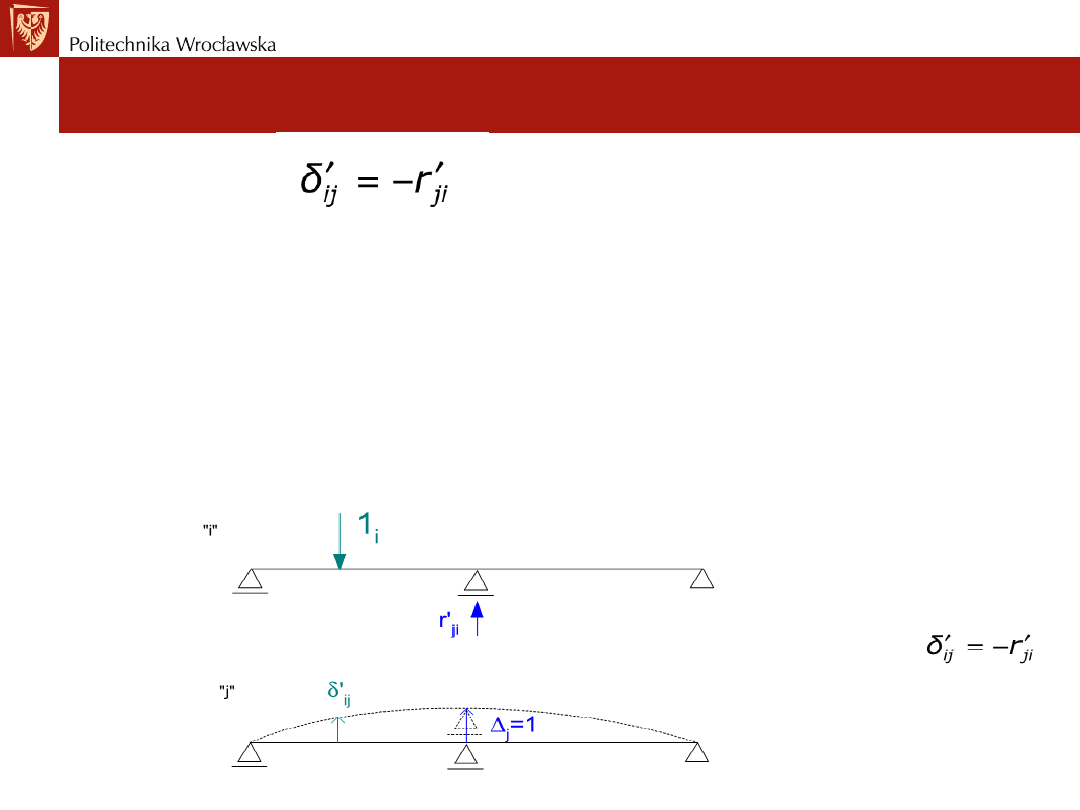
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji i przemieszczeń 

Zależność  
 
Stanowi twierdzenie o wzajemności przemieszczeń i reakcji. 
Przemieszczenie  w  miejscu  i  na  kierunku  "i"  wywołane  
jednostkowym przemieszczeniem zadanym w miejscu i na kierunku 
"j" jest równe  ze  znakiem przeciwnym reakcji w miejscu i na 
kierunku "j" wywołanej jednostkowymi  siłami działającymi w 
miejscu i na kierunku "i". 
Przykład 1:  

 

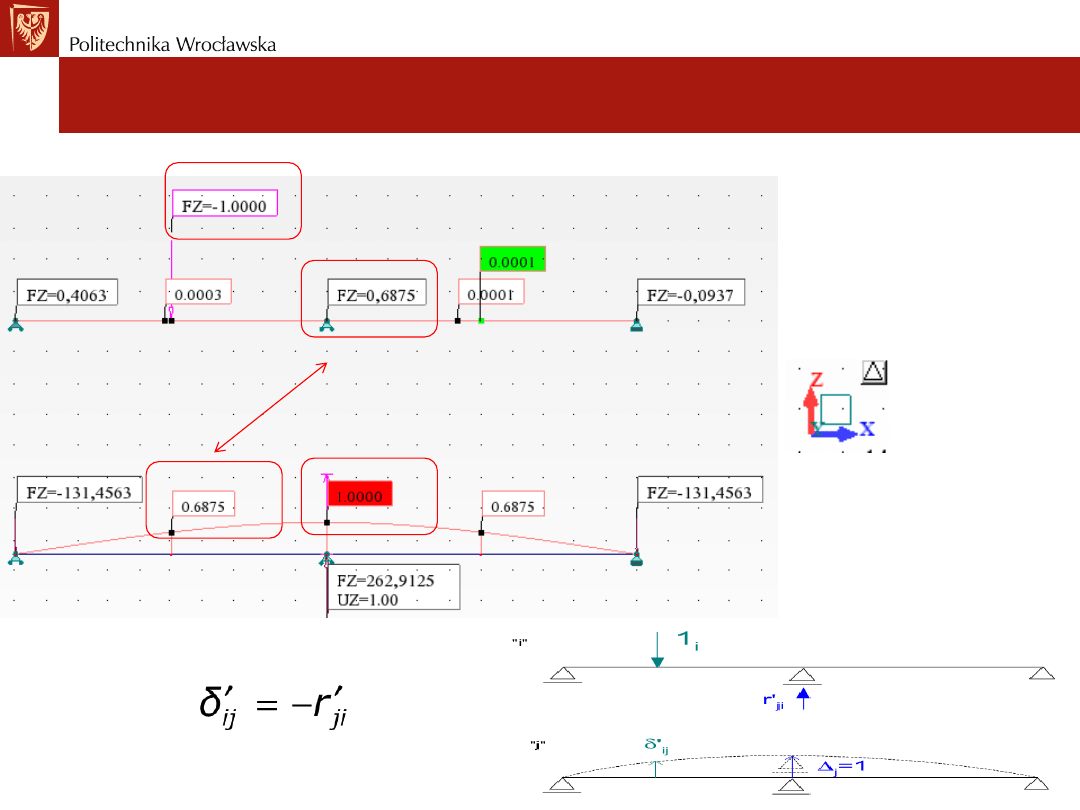
Twierdzenie o wzajemności prac.  

Twierdzenie o wzajemności reakcji i przemieszczeń 

Przykład 2: