MB W04 PWr

MECHANIKA BUDOWLI

Wykład 4:

USTROJE STATYCZNIE NIEWYZNACZALNE.

METODA SIŁ.

Prowadzący: dr inż. Wojciech Zielichowski-Haber

Ustroje statycznie niewyznaczalne. Metoda sił

Plan wykładu

1. Stopień statycznej niewyznaczalności
2. Sformułowanie metody sił dla belek i ram
3. Układ podstawowy i układ równań kanonicznych dla ustrojów

poddanym obciążeniom mechanicznym

4. Kontrola poprawności rozwiązania
5. Sformułowanie metody sił dla kratownic
6. Belki statycznie niewyznaczalne
7. Wyznaczanie przemieszczeń w układach statycznie

niewyznaczalnych od obciążeń mechanicznych

8. Układ podstawowy i układ równań kanonicznych dla ustrojów

poddanym obciążeniom nie mechanicznym

9. Wyznaczanie przemieszczeń w układach statycznie

niewyznaczalnych od obciążeń niemechanicznych

10. Przykłady
11. Podsumowanie

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

Właściwości płaskich układów prętowych:
• każdy płaski ustrój prętowy można podzielić na:

oddzielne tarcze i łączące je więzi,

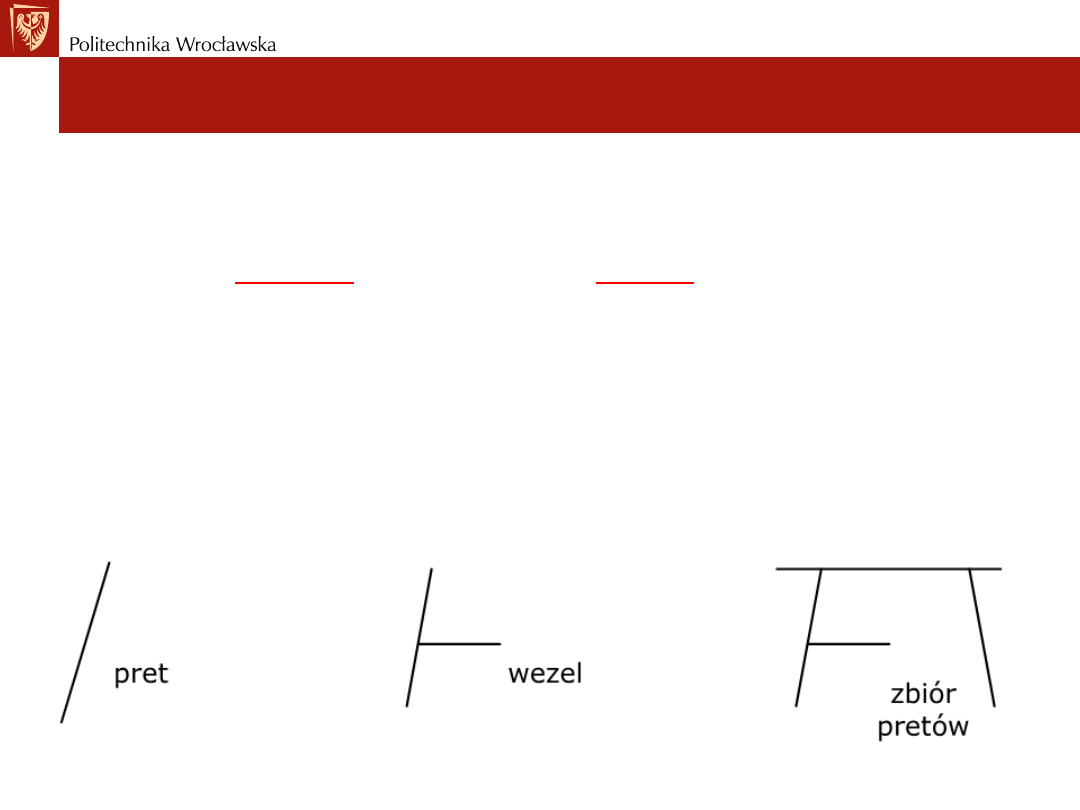
• za tarczę będziemy uważać:
a) wydzielony pręt
b) wydzielony węzeł
c) zbiór prętów połączonych węzłami sztywnymi tworzących formę

otwartą

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

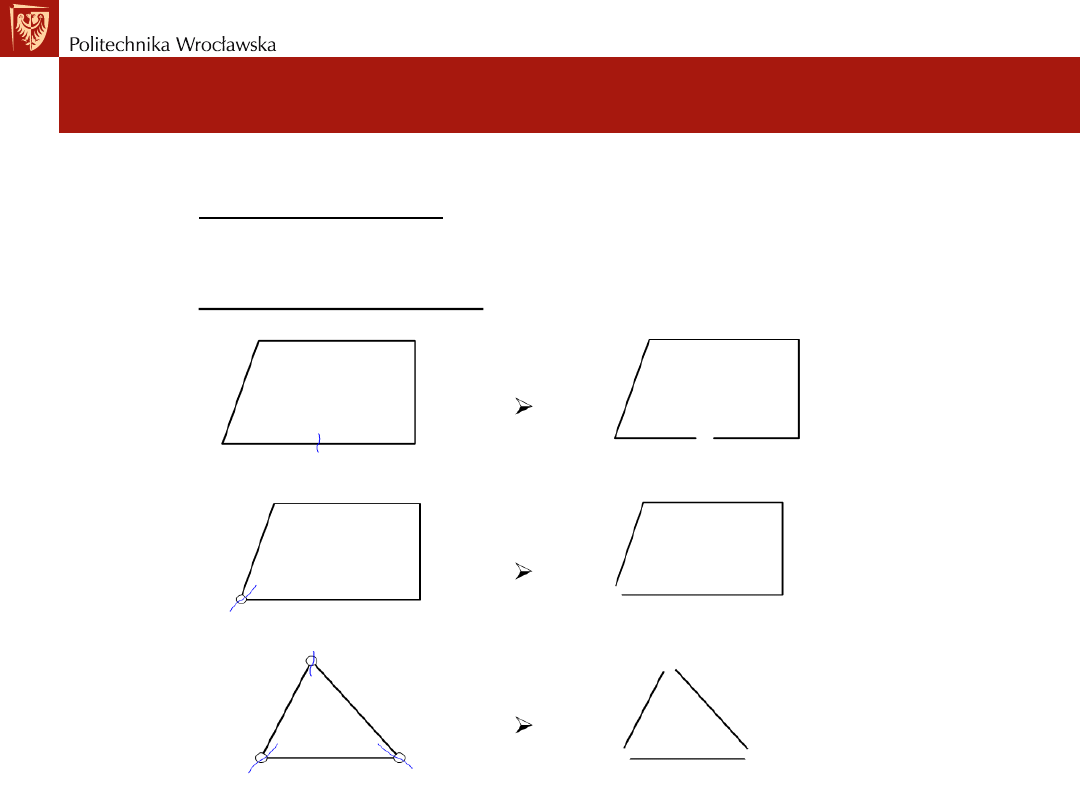
Stopień statycznej niewyznaczalności dla zbioru prętów
tworzących

formę otwartą

można wyznaczyć bezpośrednio,

Stopień statycznej niewyznaczalności dla zbioru prętów
tworzących

formę zamkniętą

określamy poprzez rozcięcie go jak

poniżej:

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

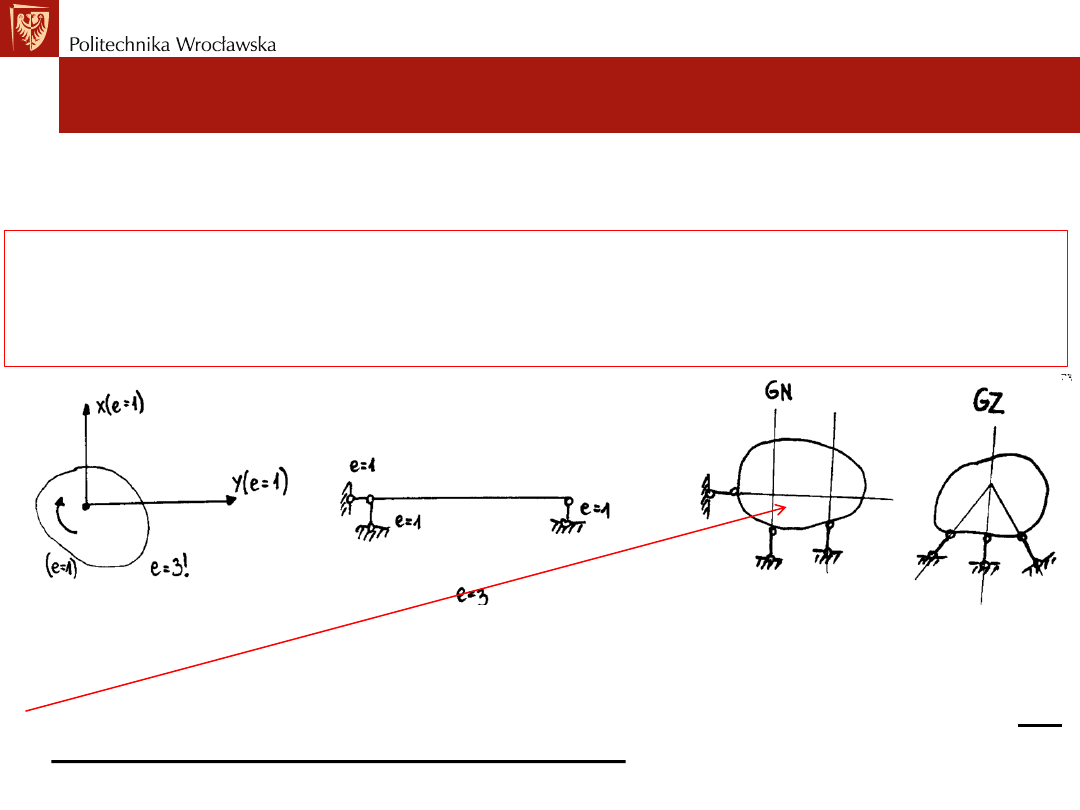
• Każda swobodna!!! tarcza sztywna ma trzy

(3!!!) stopnie

swobody

na płaszczyźnie.

Liczbą stopni swobody SS danego układu nazywamy liczbę
niezależnych parametrów niezbędnych do jednoznacznego
określenia możliwości jego ruchu w przestrzeni.

• Aby układ był geometrycznie niezmienny

(nie jest mechanizmem,

nie ma możliwości ruchu swobodnego), musi zostać unieruchomiony.

• Aby tarczę unieruchomić należy przyłożyć trzy (3) więzi elementarne nie

przecinające się w jednym punkcie na paszczyźnie, łączące daną
tarcze z częścią nieruchomą konstrukcji (fundament).

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

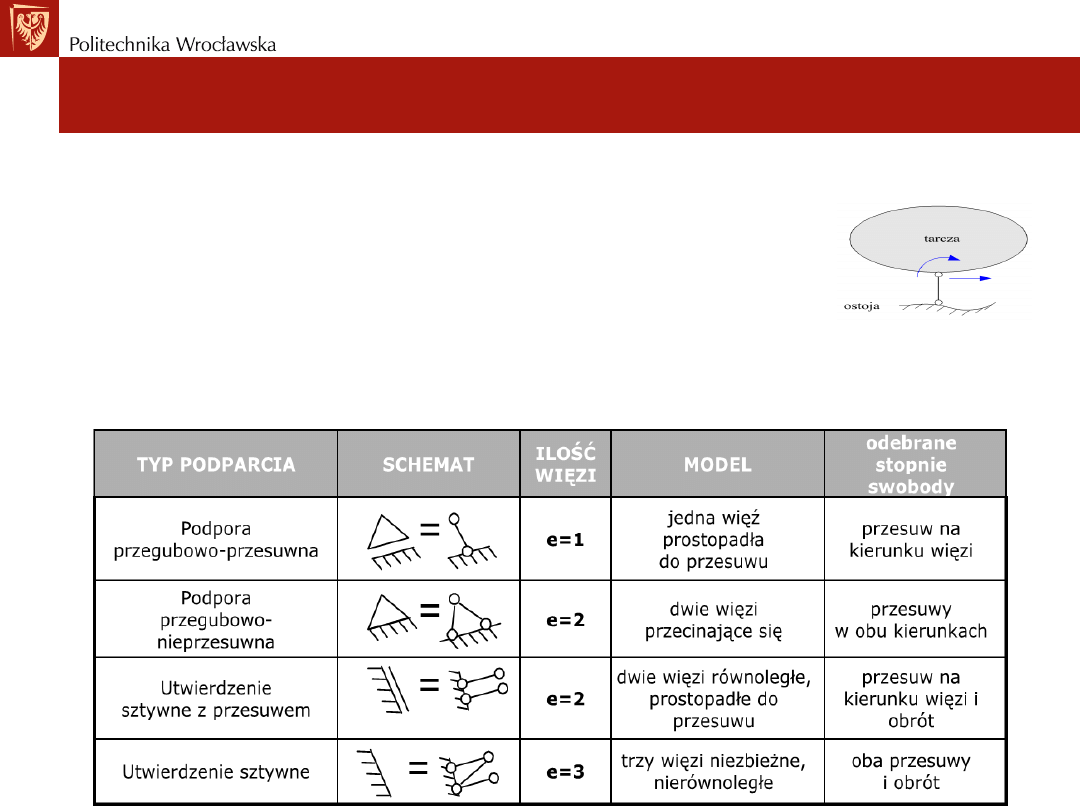
• Więź elementarną

stanowi nieściśliwy pręt przegubowo-przegubowy.

Odbiera ona tarczy

t jeden (1) stopień swobody

• Litera

e oznacza liczbę więzi elementarnych,

• Podstawowe podpory i odpowiadające im liczby więzi elementarnych

(łączące z fundamentem).

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

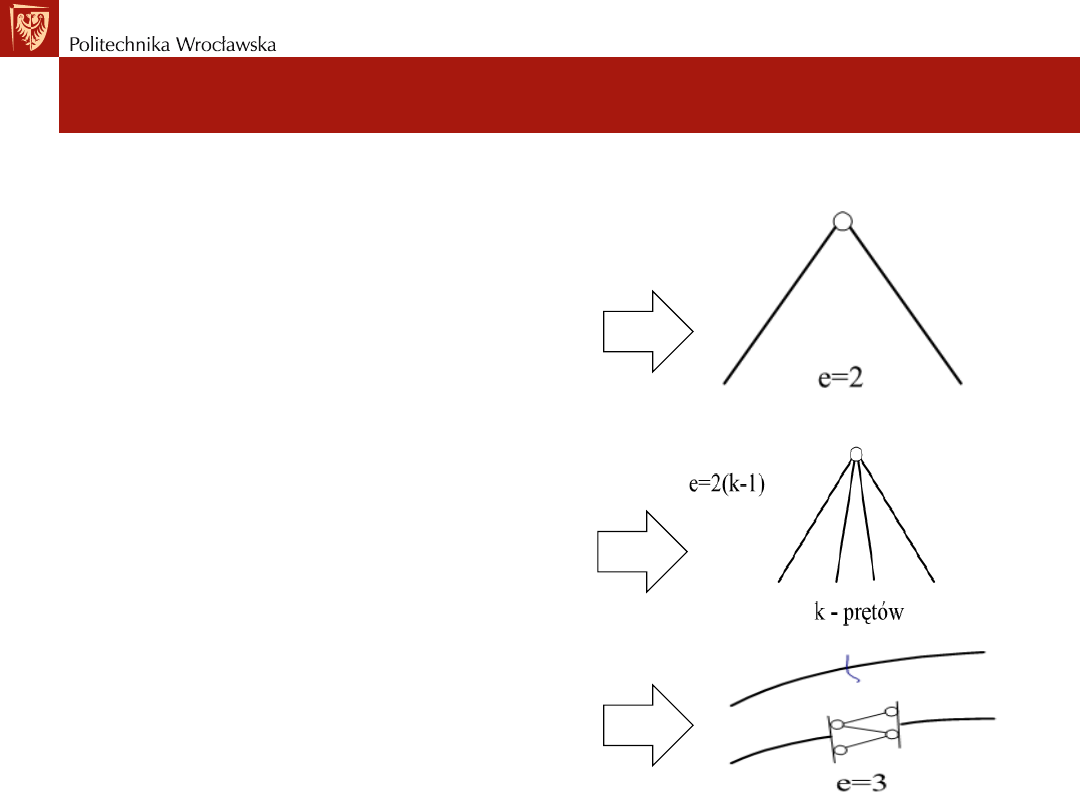
• Dwa pręty połączone przegubem -
unieruchomiony jeden z nich, drugi
traci dwa (2) stopnie swobody ->
Możliwy jest tylko jego obrót względem
unieruchomionego przegubu -> e=2,

• W przegubie połączonych jest k prętów –
unieruchomiony jednego z nich, każdy
pozostały traci dwa (2) stopnie
swobody -> e=2(k-1).

• Połączenie szytywne odbiera każdemu
połączeniu 3 stopnie swobody -> e=3

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

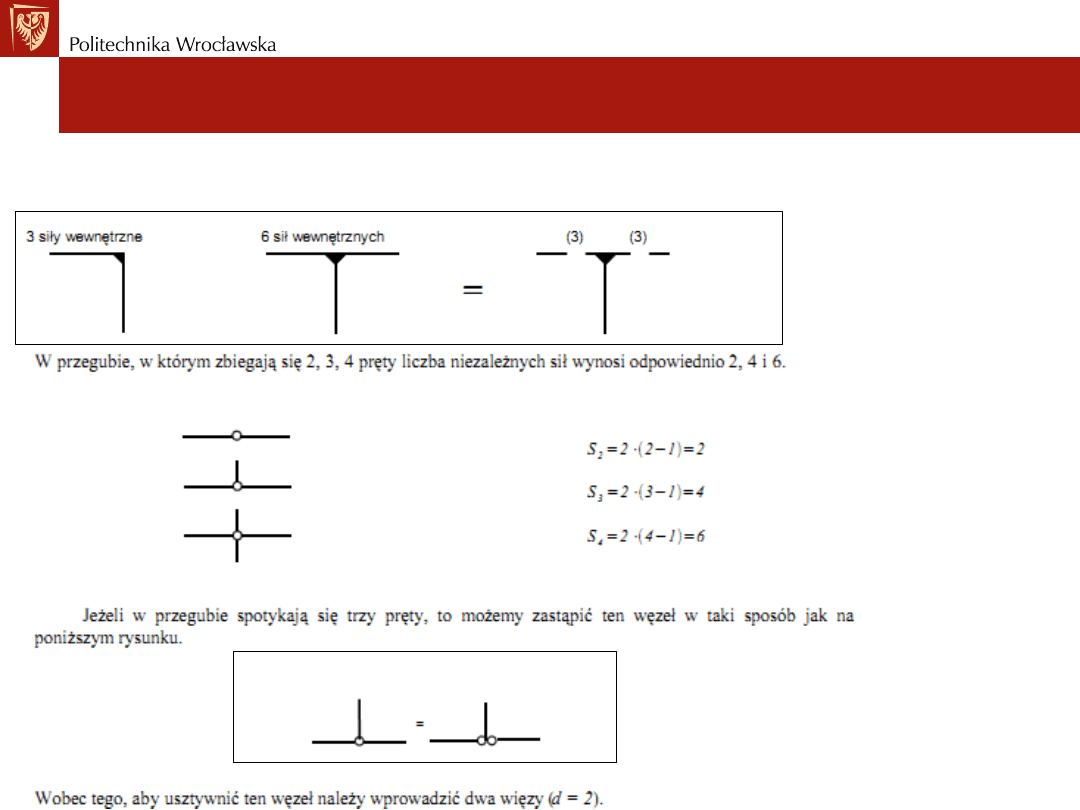
• W przypadku prętów sztywno zamocowanych liczbę sił niezależnych można

określić -> e=3(k-1)

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

• Warunek konieczny, aby ustrój był

statycznie wyznaczalny (SW)

(czyli

można go rozwiązać korzystając tylko z warunków równowagi) jest
spełnienie równości mającej charakter ilościowy:

e=3t

lub

e-3t=0

• Warunek ten jest konieczny, ale nie wystarczający. Dodatkowym

wymaganiem jest, aby ustrój był

geometrycznie niezmienny (GN).

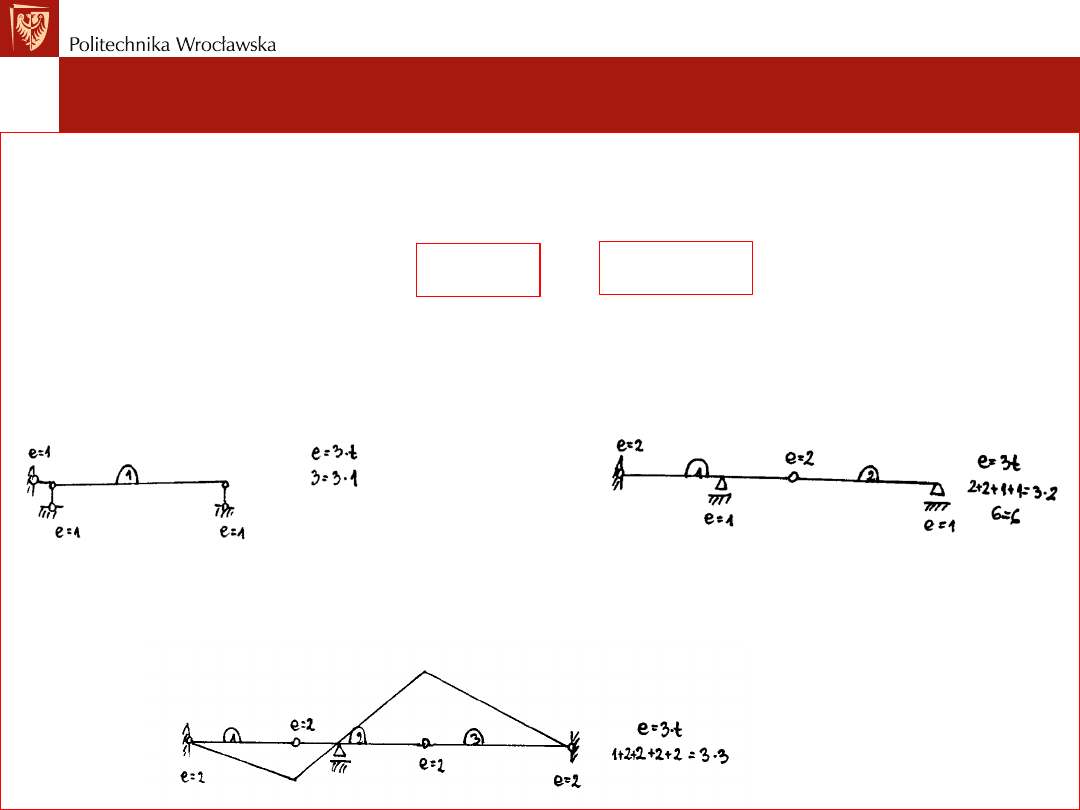
SW, GN

SW, GZ

– układ jest mechanizmem!!!

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

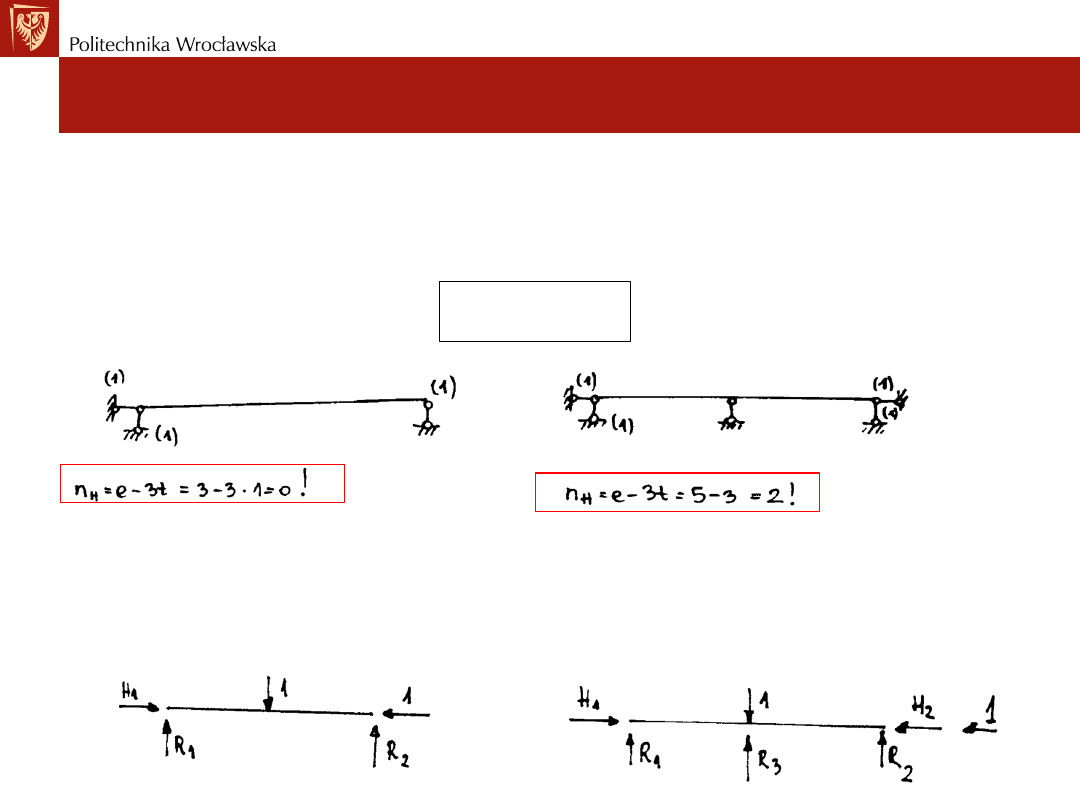
 Liczbę

więzi nadliczbowych nh

równą liczbie brakujących równań

równowagi, które należało by odrzucić aby układ był statycznie
wyznaczalny (SW) nazywamy stopniem statycznej niewyznaczalności
(SSN):

=e-3t>0

 Dla każdej tarczy t można ułożyć trzy równania równowagi (3t

niezależnych równań). Wielkościami nieznanymi są siły w więziach
elementarnych, a liczba niewiadomych sił wynosi e. W każdym węźle
występuje e nieznanych sił.

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

 Ustrój

statycznie niewyznaczalny (SN) lub hiperstatyczny o SSN nh to

ustrój

, który jest przesztywniony -> posiada więcej więzi e niż jest

potrzebne, aby układ był statycznie wyznaczalny (SW).

 Do rozwiązywania układów hiperstatycznych trzeba zbudować

dodatkowe

nh równań

, wynikających z warunku ciągłości konstrukcji (ograniczenia

przemieszczeń konstrukcji).

 SSN nh > 0 oznacza

, że układ ma więcej niewiadomych wielkości e niż

równań równowagi i układu nie da się rozwiązać przy zastosowaniu tylko
równań równowagi.

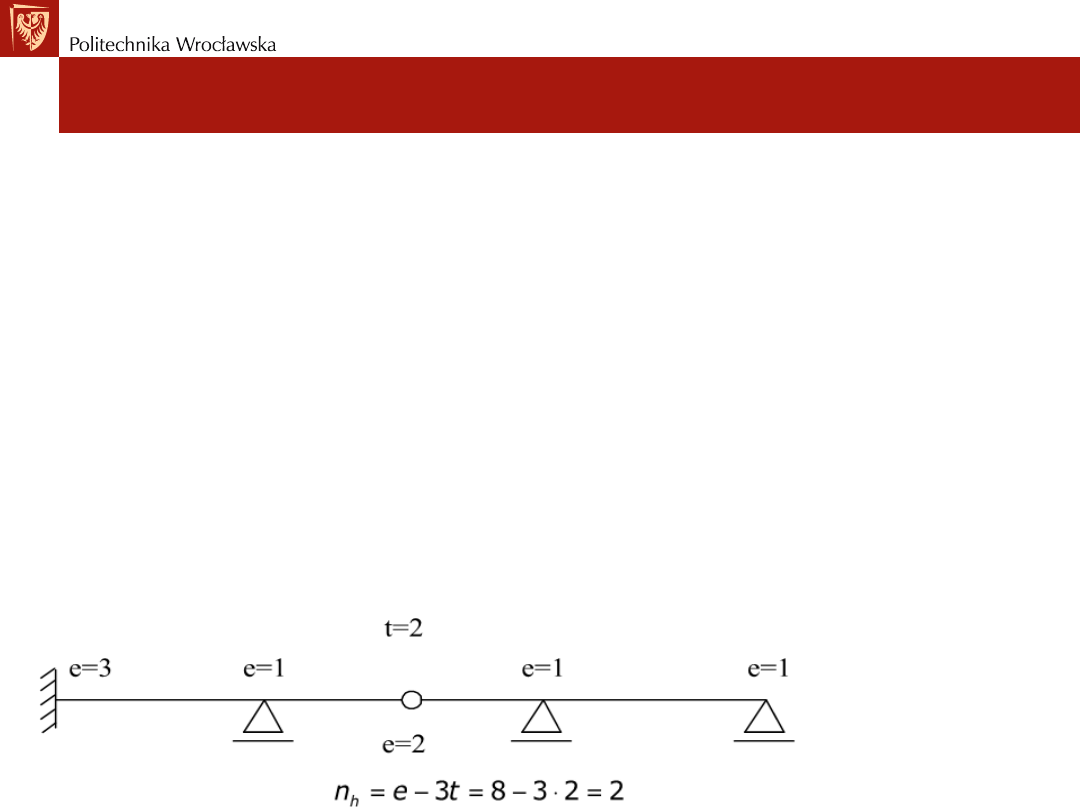
Przykład nr1: Określić SSN - nh dla belki

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

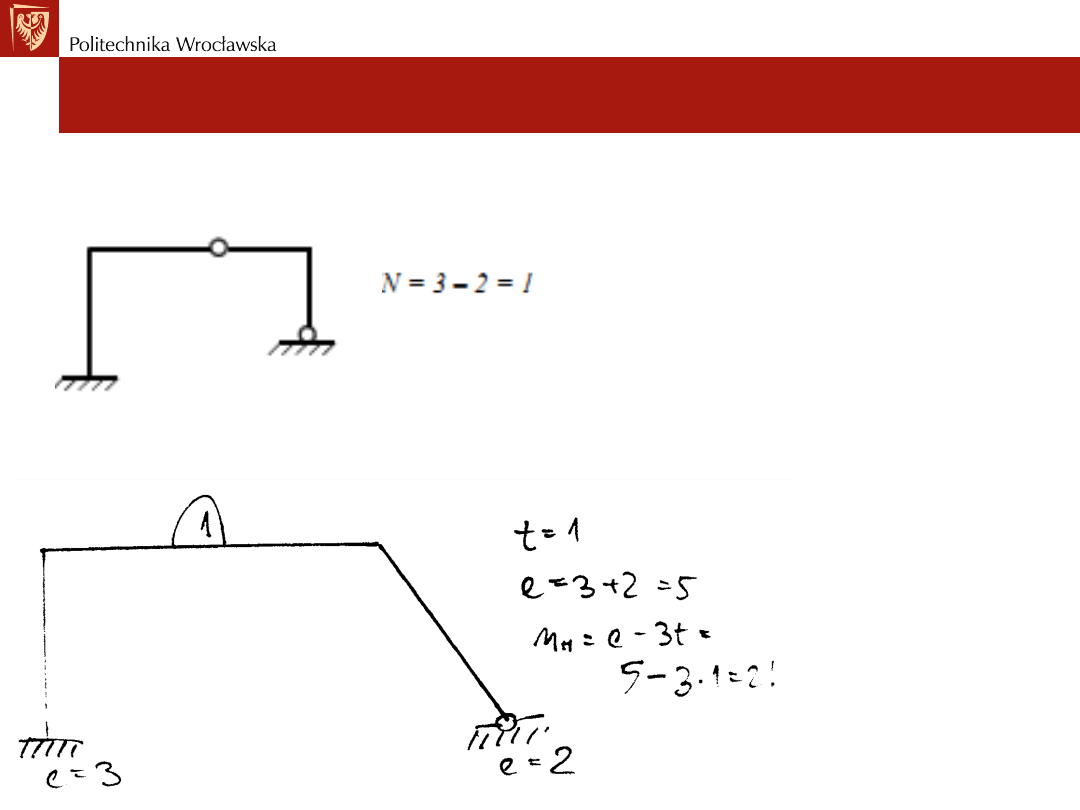
Przykład nr2: Określić SSN - nh dla ramy

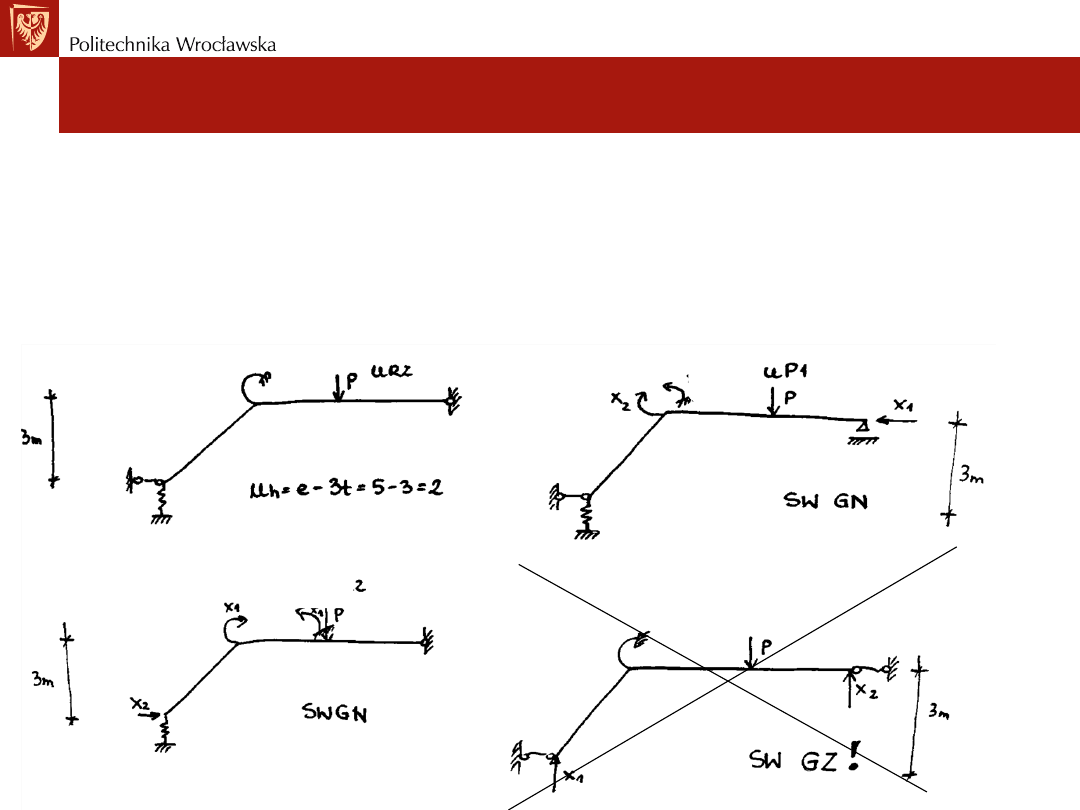
Przykład nr3: Określić SSN - nh dla ramy

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

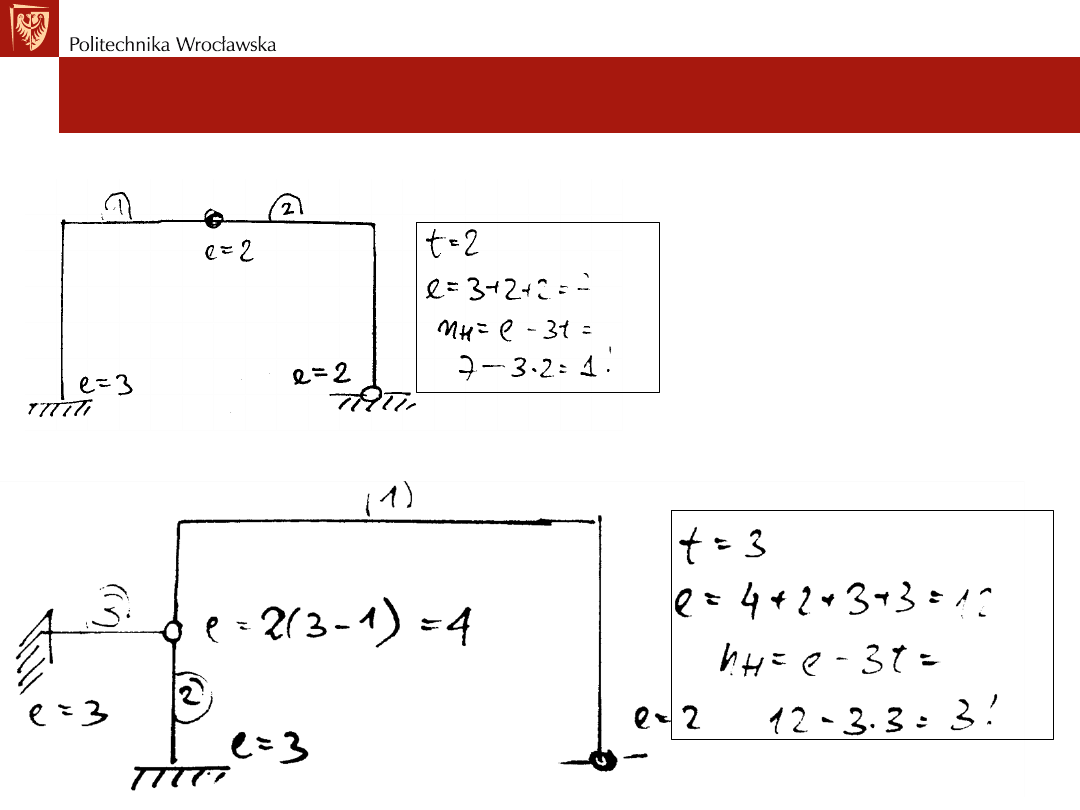
Przykład nr4: Określić SSN - nh dla ramy

Przykład nr5: Określić SSN - nh dla ramy

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

 SSN kratownicy płaskiej zależy od liczby węzłów, liczby prętów i liczby

więzi podporowych.

Stosujemy następujące oznaczenia:
p – liczba prętów kratownicy,
w- liczba węzłów,
r - liczba więzi elementarnych.

Stopień statycznej niewyznaczalności (SSN) kratownic wynosi:

 Suma p+r określa liczbę wielkości niewiadomych, gdyż nieznane są siły w

prętach i reakcje podporowe.

Ponieważ w każdym węźle mamy zbieżny układ sił stąd dla każdego węzła
możemy ułożyć dwa równania równowagi (trzecie spełnione jest
tożsamościowo).

Ustroje statycznie niewyznaczalne. Metoda sił

Stopień statycznej niewyznaczalności

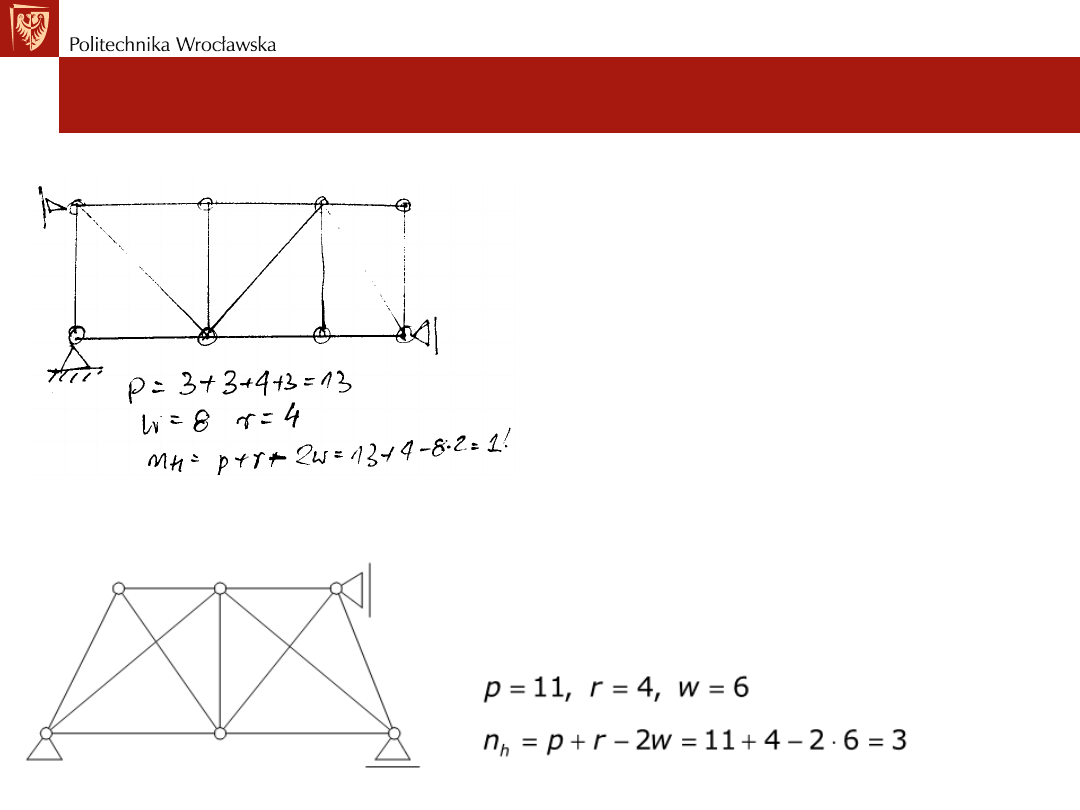
Przykład nr1: Określić SSN - nh dla kratownicy

Przykład nr2: Określić SSN - nh dla kratownicy

Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla belek i ram

 Algorytm postępowania w metodzie sił:

1) Sprawdzenie statycznej niewyznaczalności nh układu rozpatrywanego

rzeczywistego URZ, który jest statycznie niewyznaczalny SN i geomerycznie
niezmienny GN. Wyznaczenie liczby nadliczbowych więzi nh w układzie.

Układu SN nie da się rozwiązać (tj. wyznaczyć sił w więziach nadliczbowych) za
pomocą równań równowagi.

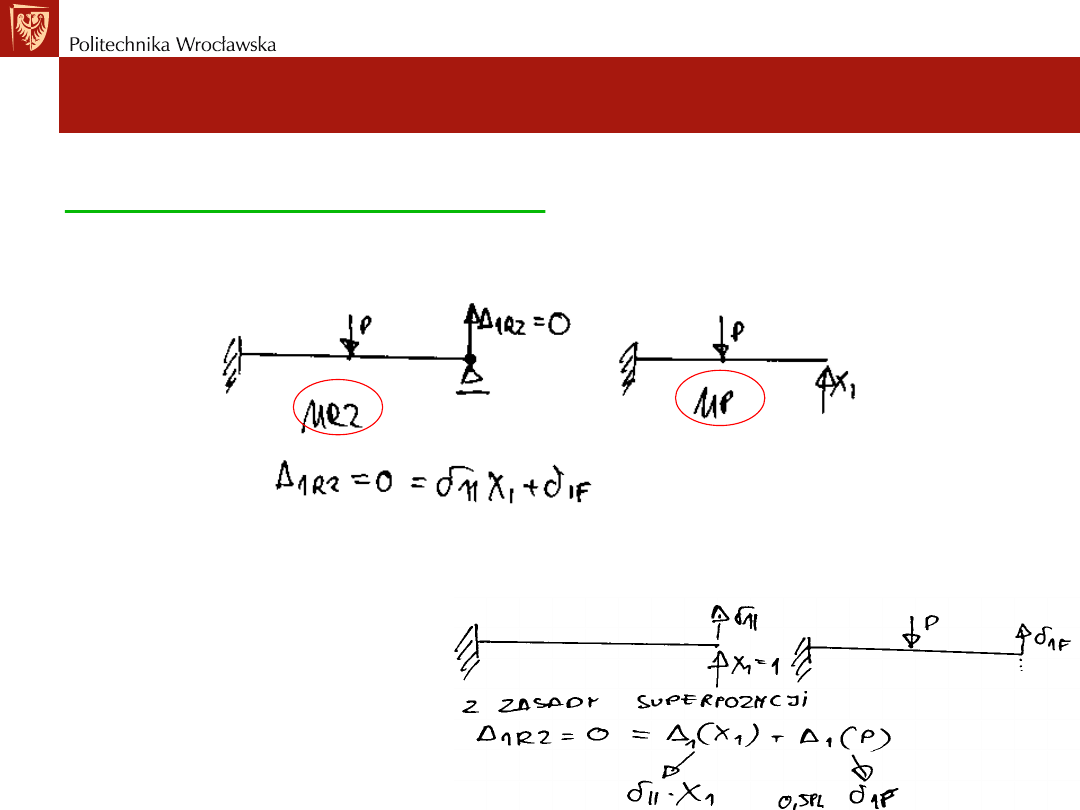
Algorytm postępowania w metodzie sił:

3) utworzenie układu podstawowego UP (który jest SW i GN)

poprzez wstawienie

w miejsce usuniętych więzi niewiadomych (szukanych) sił hiperstatycznych
(nadliczbowych), aby zachować kinematyczną i statyczną identyczność URZ z
nowym

UP,

4) określenie sumarycznych przemieszczeń po kierunkach działania niewiadomych sił

i zapisanie układu równań kanonicznych metody sił,

ponieważ w rzeczywistości
w miejscach usuniętych podpór
istniały więzy, które uniemożliwiały
przemieszczenia, przemieszczenia
w tych miejscach są równe zero.

Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla belek i ram

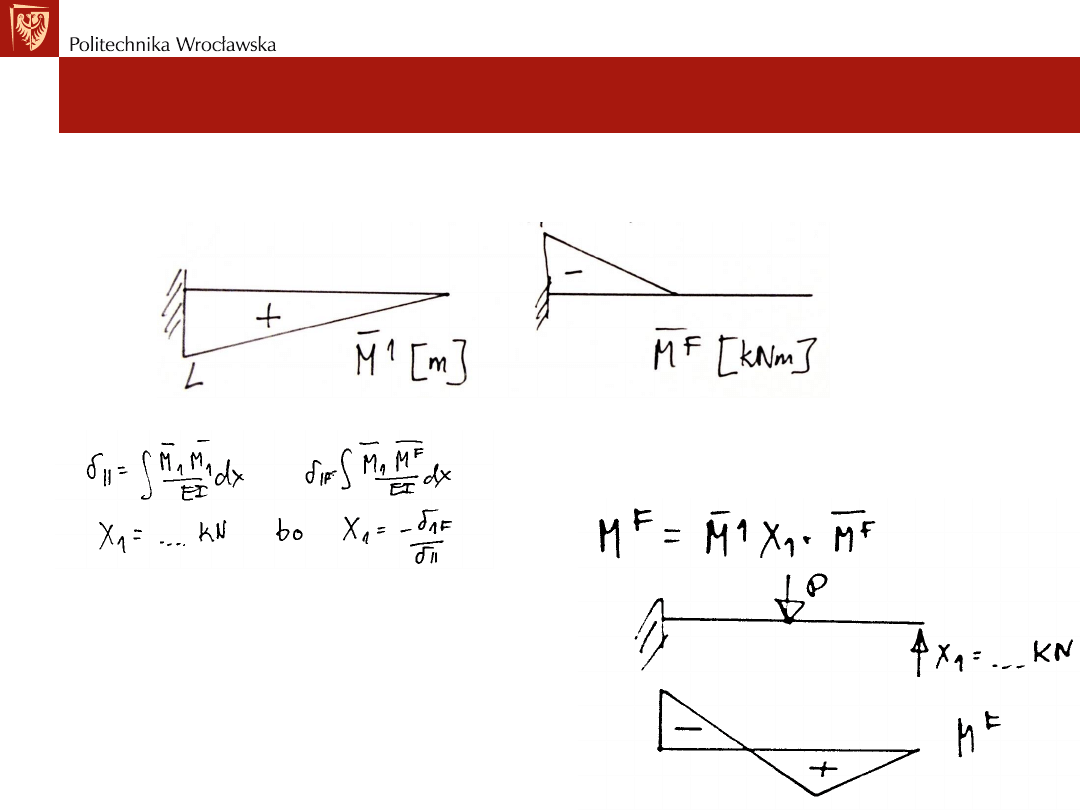
Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla belek i ram

Algorytm postępowania w metodzie sił:

6) wyznaczenie wielkości sił przekrojowych (momentów zginających) od

obciążenia jednostkowego X1=1 i obciążenia danego P w UP,

7) wyznaczenie wartości przemieszczeń i niewiadomej (szukanych) siły X1,

7) wyznaczenie sił wewnętrznych
w URZ (SN i GN) przy użyciu
wyznaczonej wartości sił X1 w UP (SW i GN).

Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla belek i ram.

 Idea rozwiązania metodą sił zadanego układu rzeczywistego URZ, który jest SN

i GN (geometrycznie niezmienny) sprowadza się do:

1. utworzenia układu podstawowego UP (SW i GN), który powstał z układu

rzeczywistego URZ (SN i GN) przez wprowadzenie w miejsce odrzuconej

więzów niewiadomej siły hiperstatycznych X1,

2. rozwiązania układu postawowego UP (układu SW) od obciążenia

hiperstatyczną siłą jednostkową X1 = 1 oraz od obciążenia zadanego P,

3. wyznaczeniu wartości niewiadomej siły hiperstatycznej X1 z równania

kanonicznego,

4. rozwiazaniu zadanego URZ (SN) poprzez rozwiązanie UP (SW) po

uwzględnieniu wartości wyznaczonej sił hiperstatycznej X1 i obciążenia

zadanego P.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Układ podstawowy UP jest układem SW oraz GN i spełnia również trzy

warunki identyczności z zadanym układem rzeczywistym URZ:

• geometryczna (zgodność wymiarów),
• kinematyczna (zgodność przemieszczeń – równania kanoniczne),
• statyczna (zgodność obciążeń).

UP 1

UP 2

UP 3

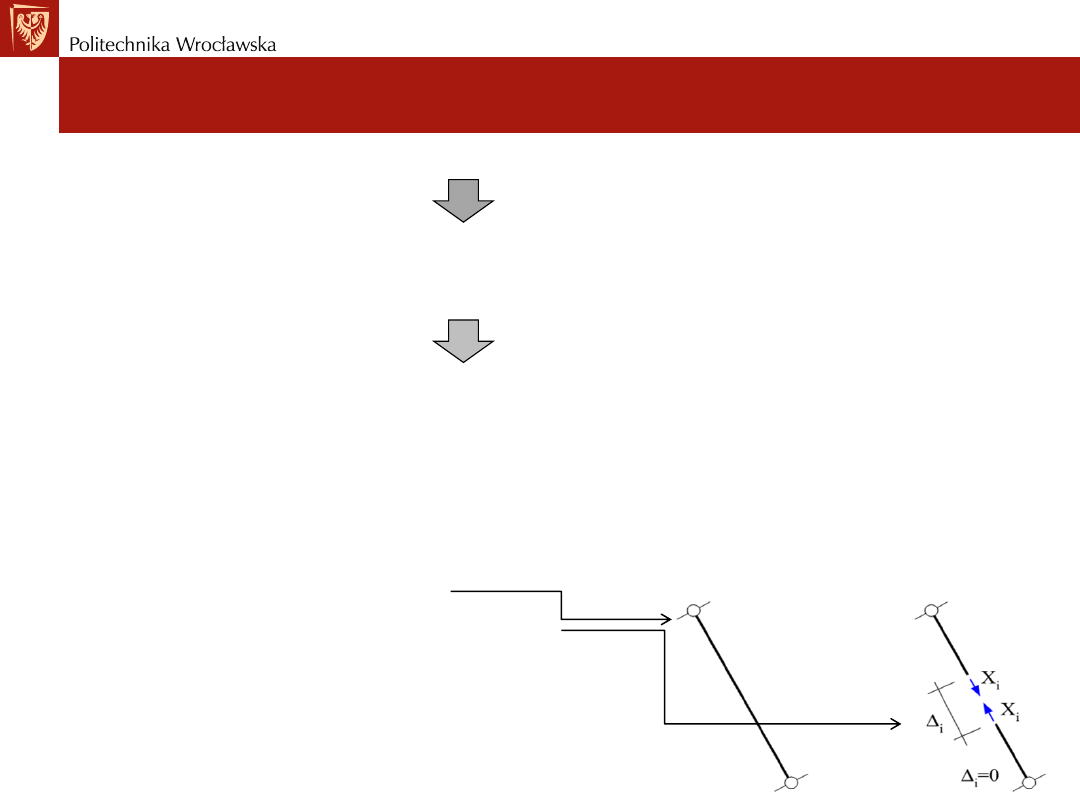
Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Jeżeli mamy układ prętowy URZ n-krotnie SN (n więzi nadliczbowych).

 Musimy wyznaczyć n sił hiperstatycznych X1,…, Xn w więziach

nadliczbowych, których nie uzyskuje się bezpośrednio z warunków
równowagi.

 Obok równań równowagi (3 równania) należy ułożyć dodatkowych n-

równań (w formie układu równań kanonicznych) z których wyznaczymy
wartości n-sił hiperstatycznych X1,…, Xn w więziach nadliczbowych.

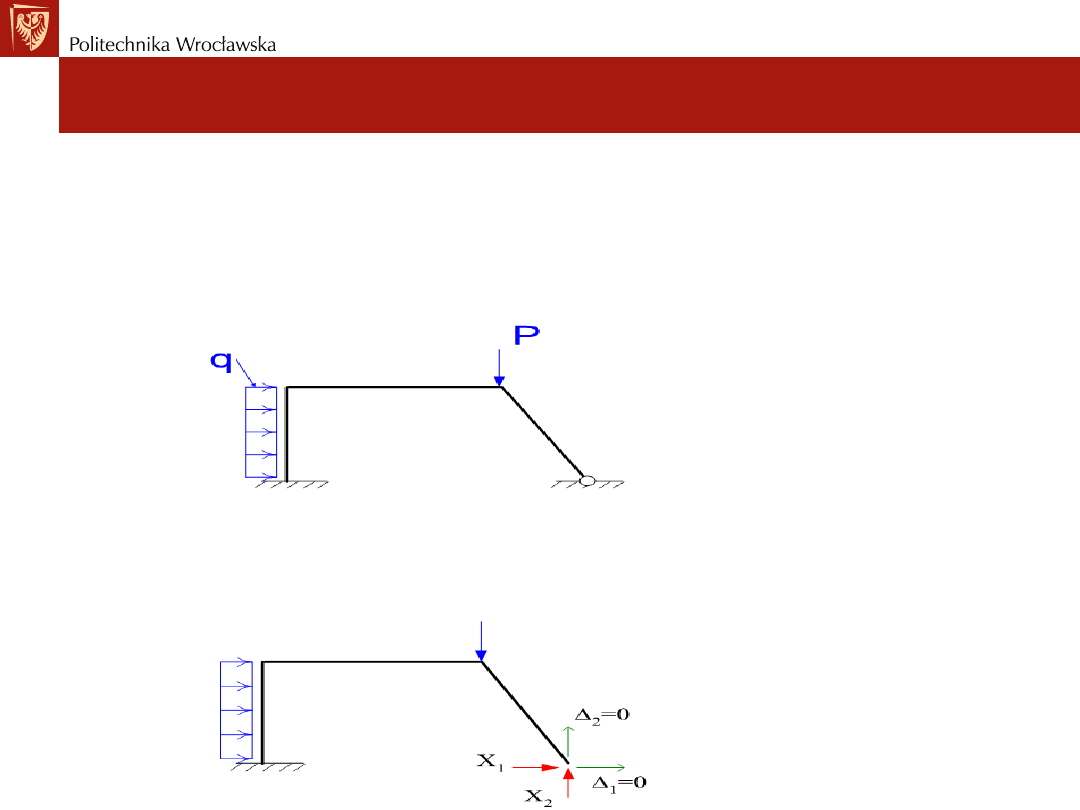
• Rozpatrzmy więź hiperstatyczną „i” którą przecinamy.

• W URZ więź jest nieprzecięta.
• W UP jest przęcięta i występuje siła Xi.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

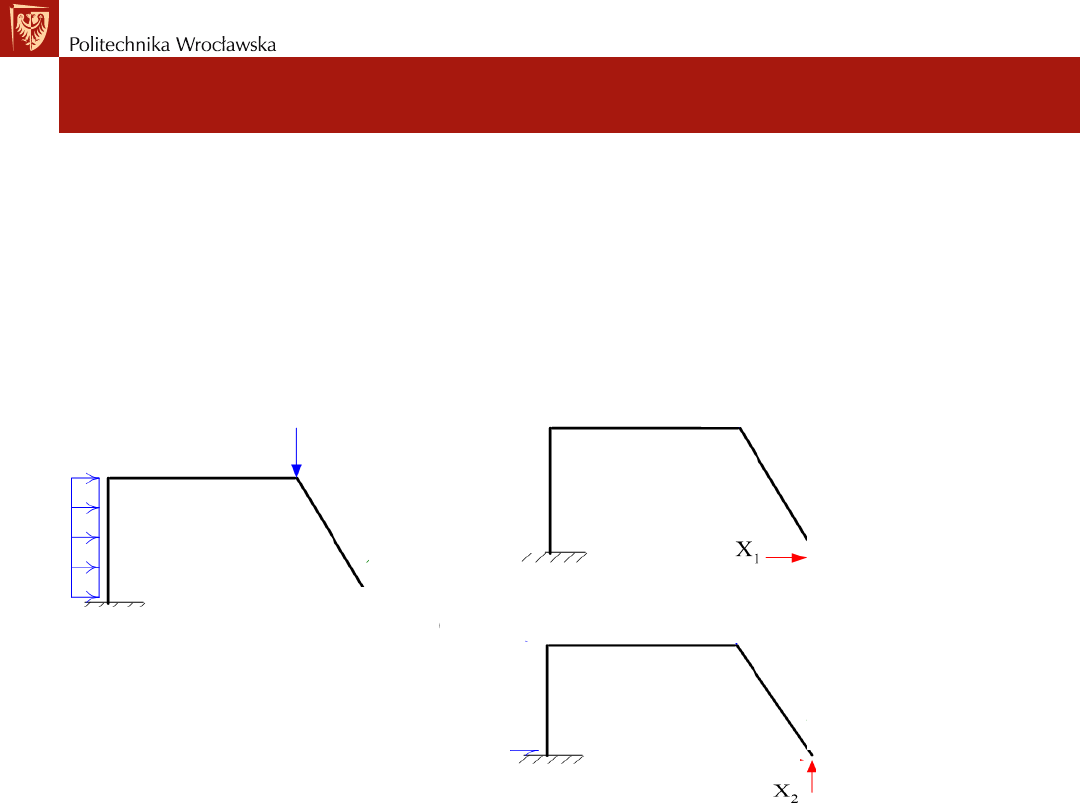
 W rzeczywistym układzie przecinamy n-więzi

(np. 2)

nadliczbowych i

w miejscu tych więzi przykładamy dodatkowe nieznane siły
hiperstatyczne w postaci X1,...,Xn

(np. X1 i X2)

. Układ z przeciętymi

więziami nadliczbowymi i przyłożonymi siłami X1,...,Xn

(np. X1 i X2)

ich miejsce to Układ Podstawowy Metody Sił.

 Otrzymujemy n-warunków na przemieszczenia w układzie

podstawowym ∆i=0 (i=1,2,...,n) (np. 2 warunki ∆1=0 i ∆2=0), które
prowadzą do liczby n (np. 2) dodatkowych równań:

URZ

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

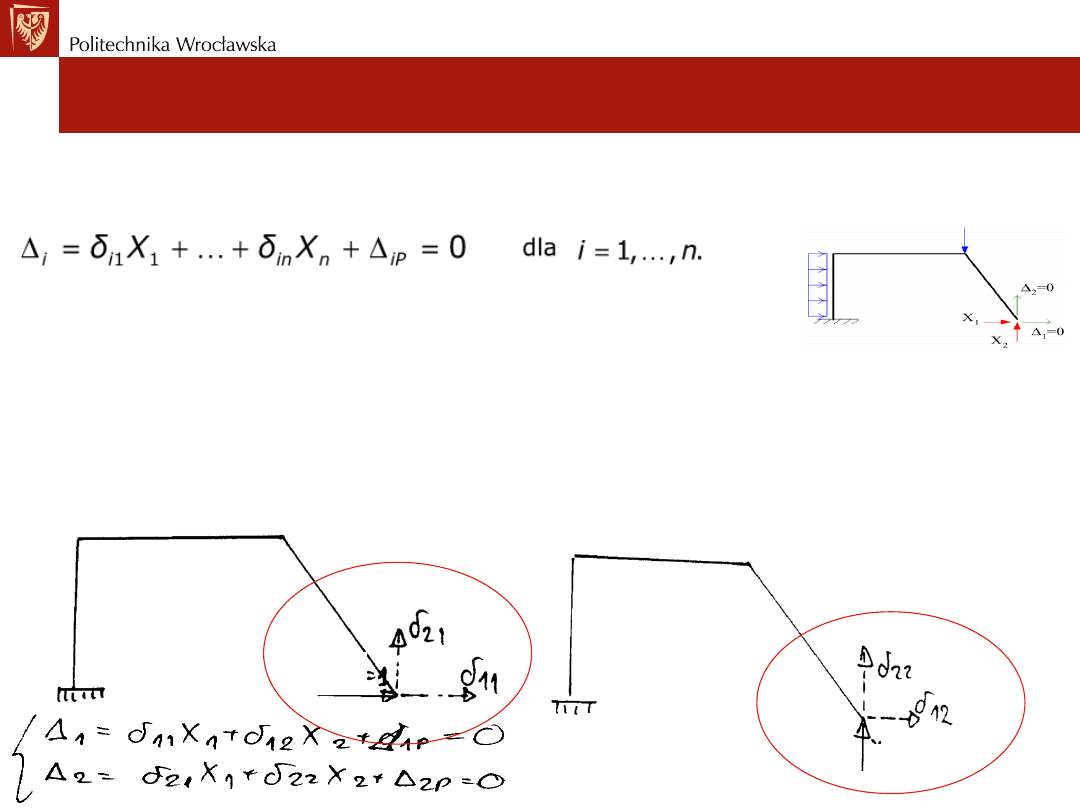
 Przemieszczenia ∆i (i=1,2,...,n) w miejscu przeciętych więzi

nadliczbowych, gdzie występuj wielkości hiperstatyczne Xi (i=1,2,...,n)
(np. X1 i X2) obliczamy w UP od wszystkich wpływów, a więc od
obciążenia zewnętrznego (typu P,q,M) oraz od wielkości hiperstatycznych
Xi (np. od X1 i od X2).

 Układy te tj. 1. od P,q,M, 2. od X1=1 i 3. od X2=1 traktujemy i

rozwiązujemy osobno.

UP od obc. danego PqM

UP od obc. X2=1

UP od obc. X1=1

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

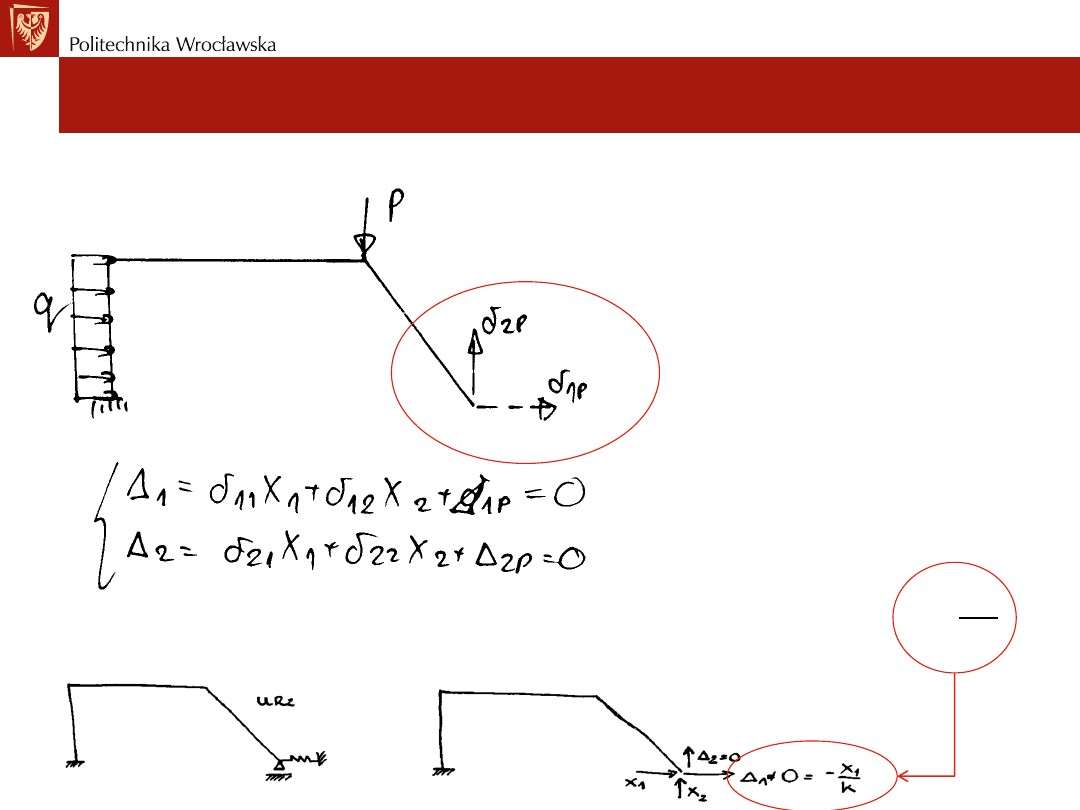
 Wyznaczamy przemieszczenie ∆i(i=1,2,...,n) (np. ∆1 i ∆2) w układzie

podstawowym jako sumę przemieszczeń od wszystkich wpływów w postaci:

gdzie przemieszczenie:
• ∆

to przemieszczenie od obciążenia zewnętrznego P,q,M

• δ

Xj to przemieszczenie od wielkości hiperstatycznych X

• δ

to przemieszczenie od wielkości hiperstatycznych X

=1.

Od wpływu X1=1 i X2=1 mamy następujące przemieszczenia:

X2=1

X1=1

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

Od wpływu P,q,M mamy następujące przemieszczenia:

 Gdy podparcie jest sprężyste o sztywności k, to

∆

𝑖

≠ 0 i wynosi ∆

𝑖

−𝑋

𝑖

𝑘

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Po rozpisaniu kanoniczny układ równań metody sił ma postać:

sens fizyczny poszczególnych wyrażeń:

przemieszczenie w miejscu i kierunku wielkości hiperstatycznej Xi wywołane

wielkością hiperstatyczną Xj=1 w UP;

przemieszczenie w miejscu i kierunku wielkości hiperstatycznej Xi wywołane

wielkością hiperstatyczną Xj w UP;

przemieszczenie w miejscu i kierunku wielkości hiperstatycznej Xi wywołane

obciążeniem zewnętrznym w UP;

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Ze wzorów na wyznaczanie przemieszczeń współczynniki w

kanonicznym układzie równań metody sił określone są wzorami:

• Kreseczka nad

𝑀

𝑖

𝑁

𝑖

𝑇

𝑖

(siły wewnętrzne) oraz 𝑆

𝑖

(siły w więziach

sprężystych) oznacza, że są one wyznaczone

w UP czyli SW

• W ramach i belkach wpływ T i N (siły tnące i osiowe) jest mały,

przyjmujemy EA=∞ oraz GA=∞ i dlatego pomijamy niektóre całki.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Wnioski i spostrzeżenia:
• Macierz podatności (współczynników) utworzona na podstawie

współczynników równań kanonicznych jest symetryczna,

• Równania kanoniczne są nieodłącznym składnikiem układu

podstawowego, gdyż zapewniają kinematyczną zgodność z układem
rzeczywistym,

• Z równań kanonicznych można obliczyć wartości niewiadomych sił

hiperstatycznych Xi.

 Po rozwiązaniu układu równań otrzymuje się nadliczbowe wielkości

hiperstatyczne X1, …., Xn, (np. X1 i X2) a następnie wyznacza się
rzeczywiste (w układzie SN) sił przekrojowe M, N, T oraz reakcje.

Można tego dokonać na dwa sposoby.

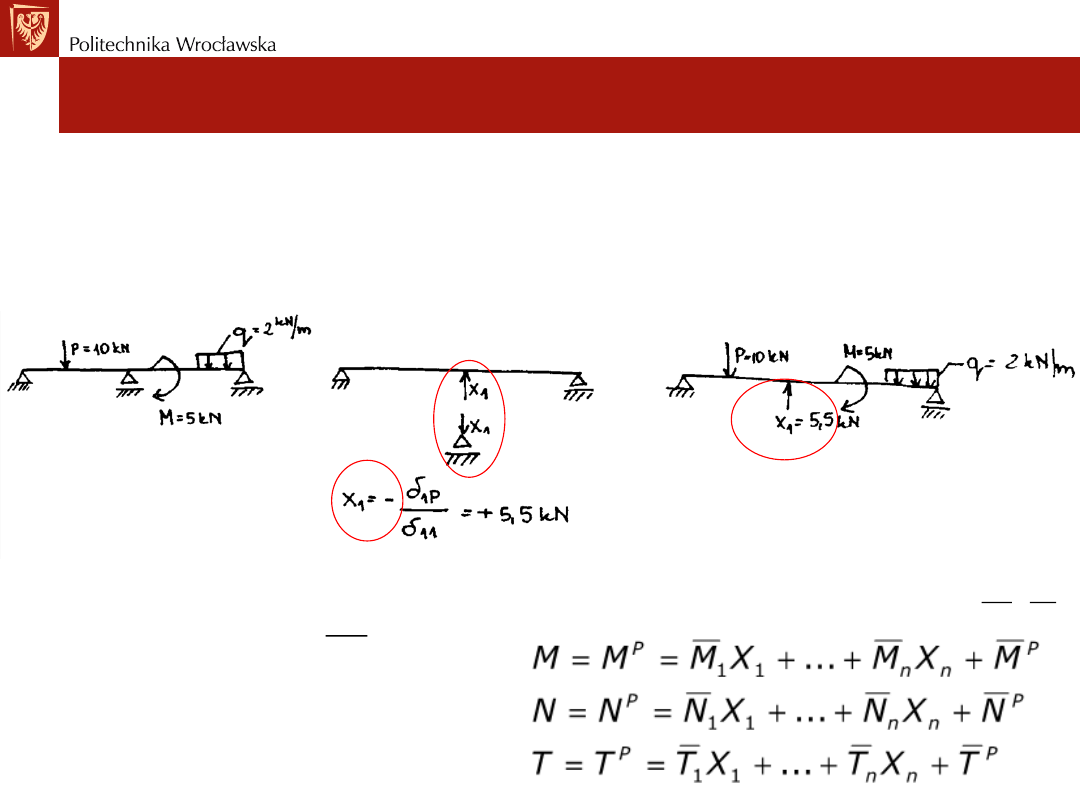
Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

1) W układzie podstawowym, który jest SW występuje znane obciążenie

zewnętrzne oraz obciążenie znanymi już siłami hiperstatycznymi X1,…, Xn.
Rozwiązujemy układ podstawowy UP (SW) obciążony obciążeniem
zewnętrznym i siłami hiperstatycznymi i jako rezultat otrzymujemy siły
przekrojowe M, N, T czyli siły przekrojowe w URZ (SN).

2) Drugi sposób wyznaczania sił przekrojowych polega na wykorzystaniu zasady

superpozycji. Wykorzystujemy już znane wykresy sił przekrojowych

𝑀

𝑖

𝑁

𝑖

𝑇

𝑖

(i=1,2,...,n) oraz

𝑀

𝑃

Rzędne rzeczywistych wykresów
sił przekrojowych

wyznaczamy

z następujących zależności:

Ustroje statycznie niewyznaczalne. Metoda sił

Kontrola poprawności rozwiązania

 Kontrola poprawności rozwiązania:
1. Sprawdzenie czy wszystkie obciążenia (reakcje) spełniają warunki

równowagi – sprawdzamy równowagę sił na prętach (równowaga sił
poziomych i pionowych) i w węzłach (równowaga momentów).

2. Sprawdzenie ciągłości konstrukcji w wybranych punktach – w miejscu

wielkości hiperstatycznych.

Ponieważ w układzie rzeczywistym SN (hiperstatycznym) więzi nadliczbowe
nie istnieją (nie są przecięte), przemieszczenia na kierunkach tych więźi
powinny być równe zero (∆

=0 dla i=1,2,…,n).

W przypadku obciążenia siłami przemieszczenie ∆

wynosi

gdzie M

i S

są momentami zginającymi i siłami w więziach sprężystych

występują w układzie rzeczywistym (SN) czyli te wyliczone oraz

𝑀

𝑖

𝑆

𝑠𝑖

są

momentami zginającymi i siłami w więziach sprężystych występujące w
układzie podstawowym (SW).

Ustroje statycznie niewyznaczalne. Metoda sił

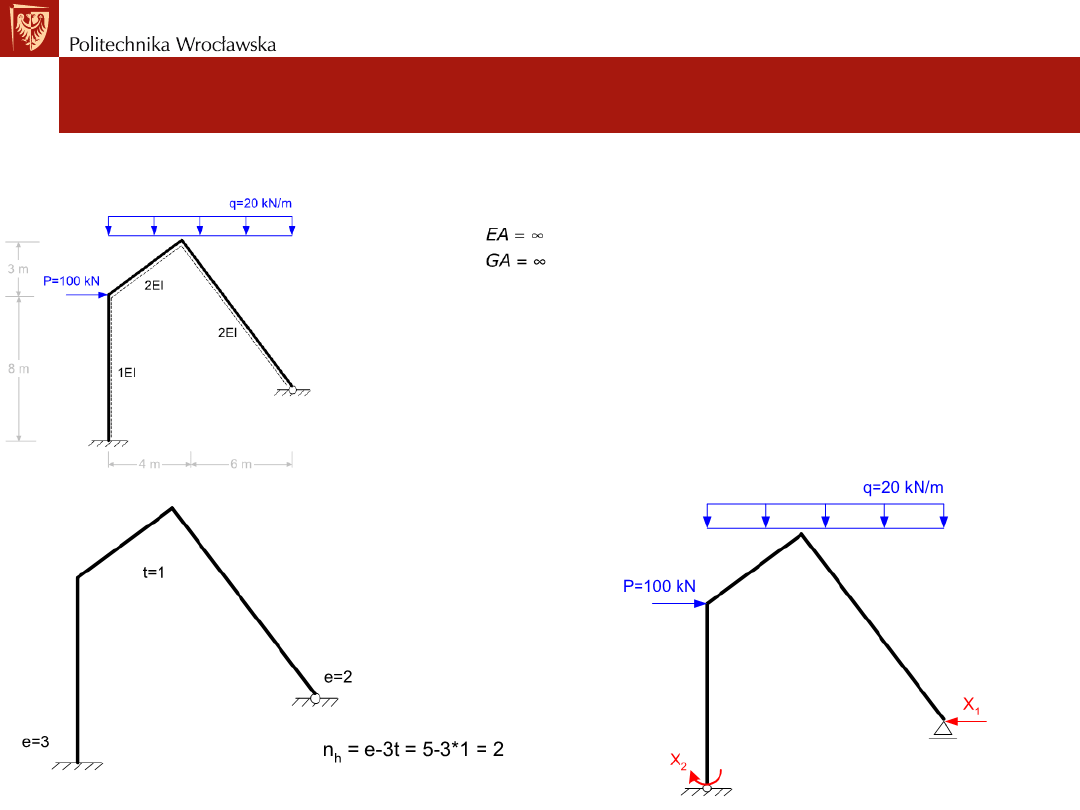
Układ podstawowy i układ równań kanonicznych

• Przykład nr1. Rozwiązanie ramy metodą sił

określenie SSN i dobranie UP

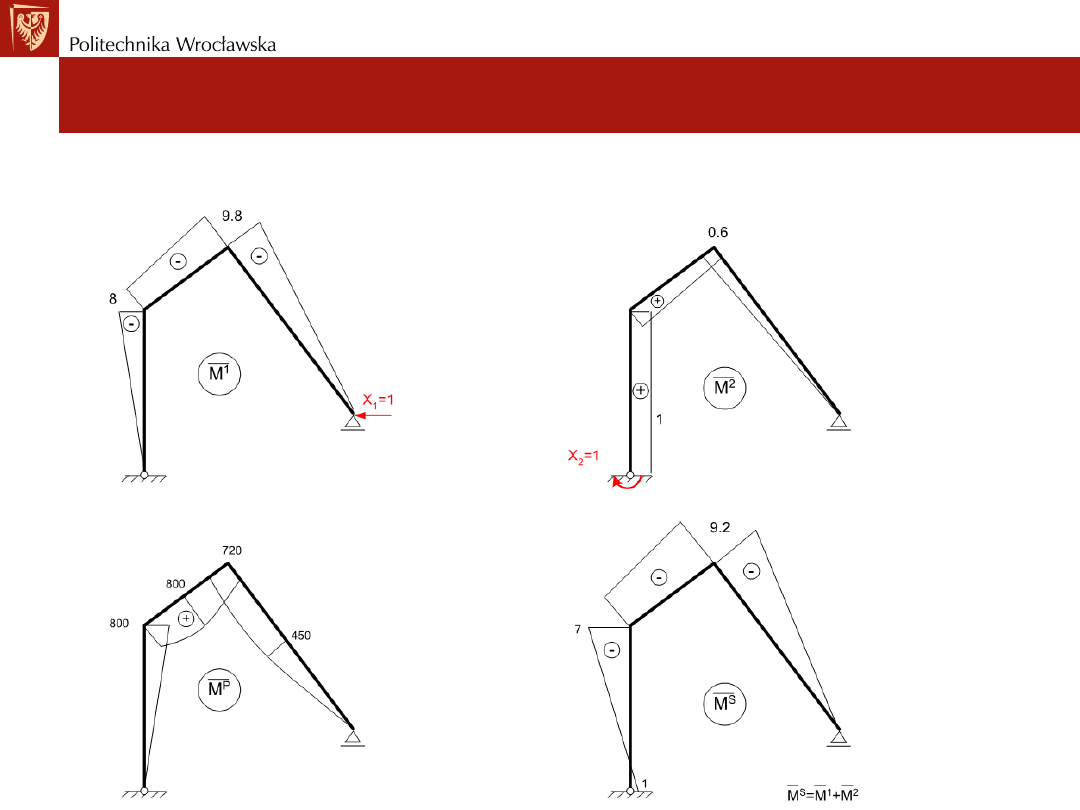
Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

• Wykresy momentów zginających w UP

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

• Obliczenia współczynników równań kanonicznych

• Układ kanoniczny metody sił i jego rozwiązanie

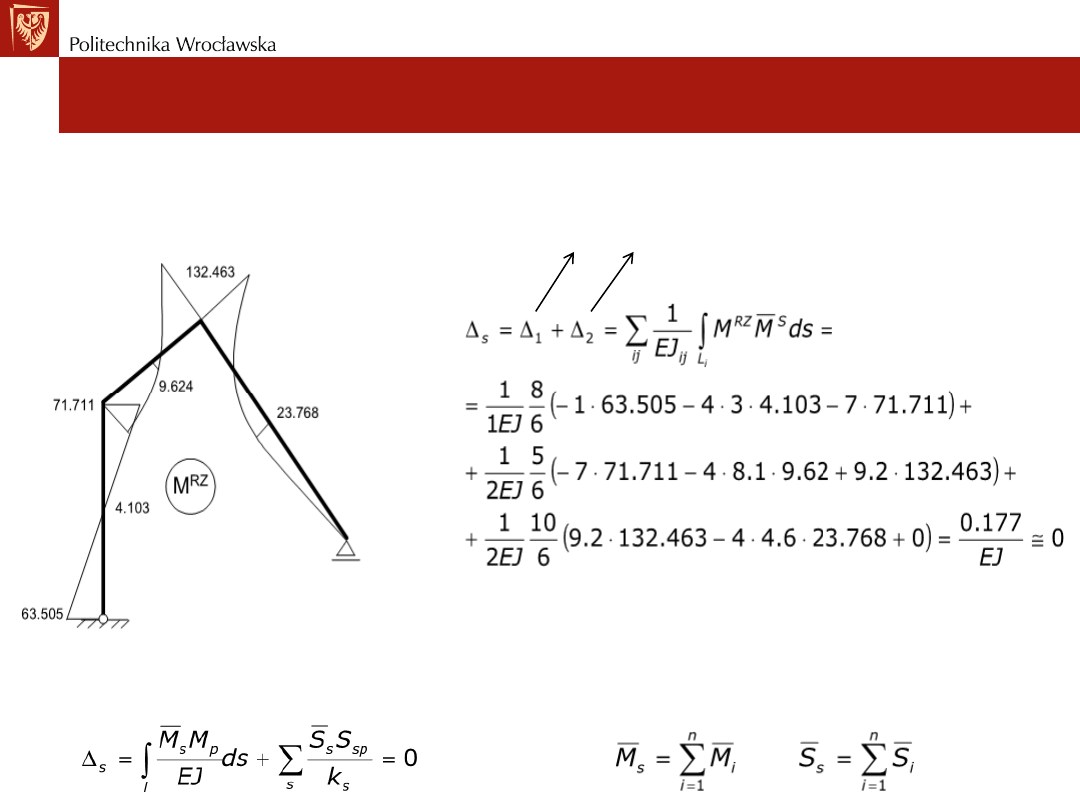
Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

• Wyznaczenie wykresu rzeczywistych momnetów zgnających oraz kontrola

ciągłości konstrukcji

Ponieważ ∆i=0 dla i=1,…,n stąd ∆s=∆1+…∆n=0 więc wykonujemy jedną
kontrolę sprawdzając:

gdzie

Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla kratownic

 Dla kratownic wzory w ramach Metody Sił ulegają modyfikacji:

Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla kratownic

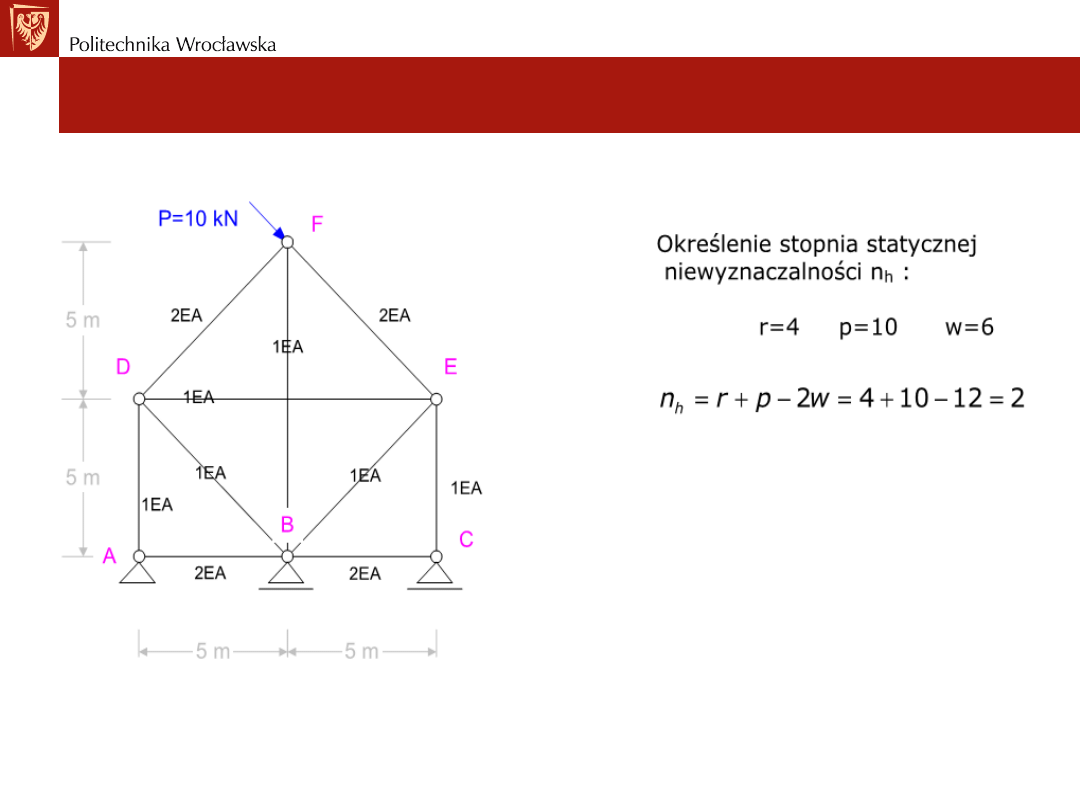
• Przykład: kratownice rozwiązać metodą sił

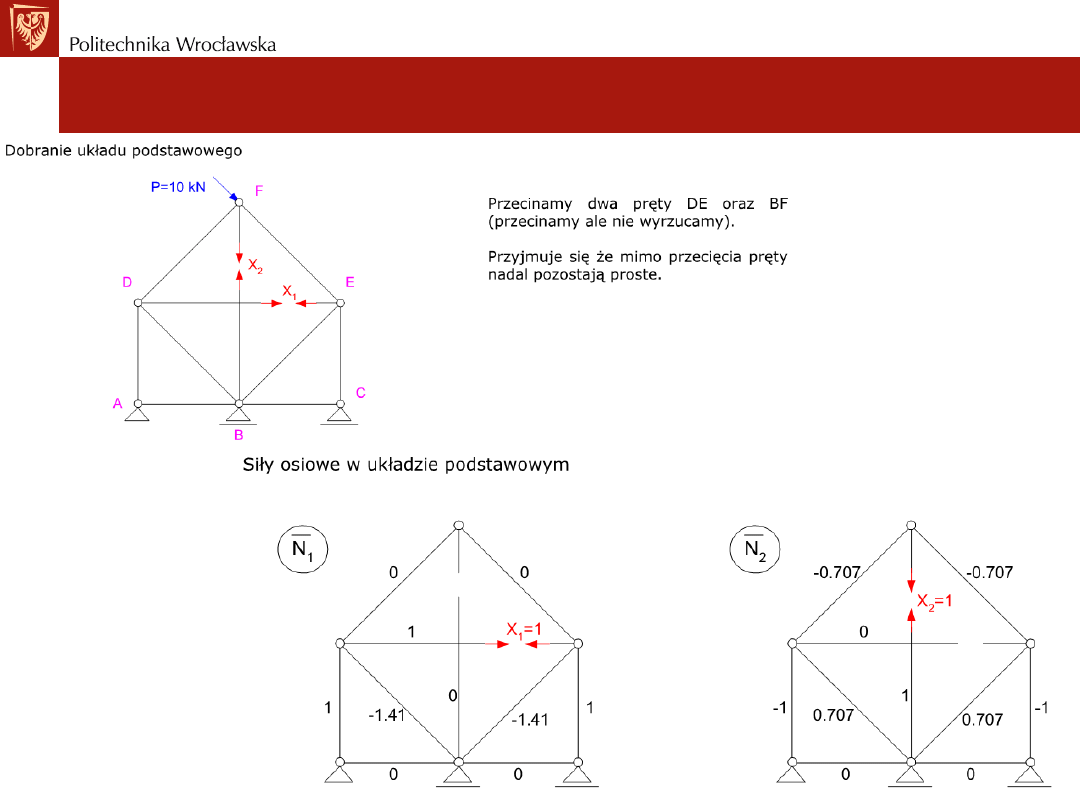
Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla kratownic

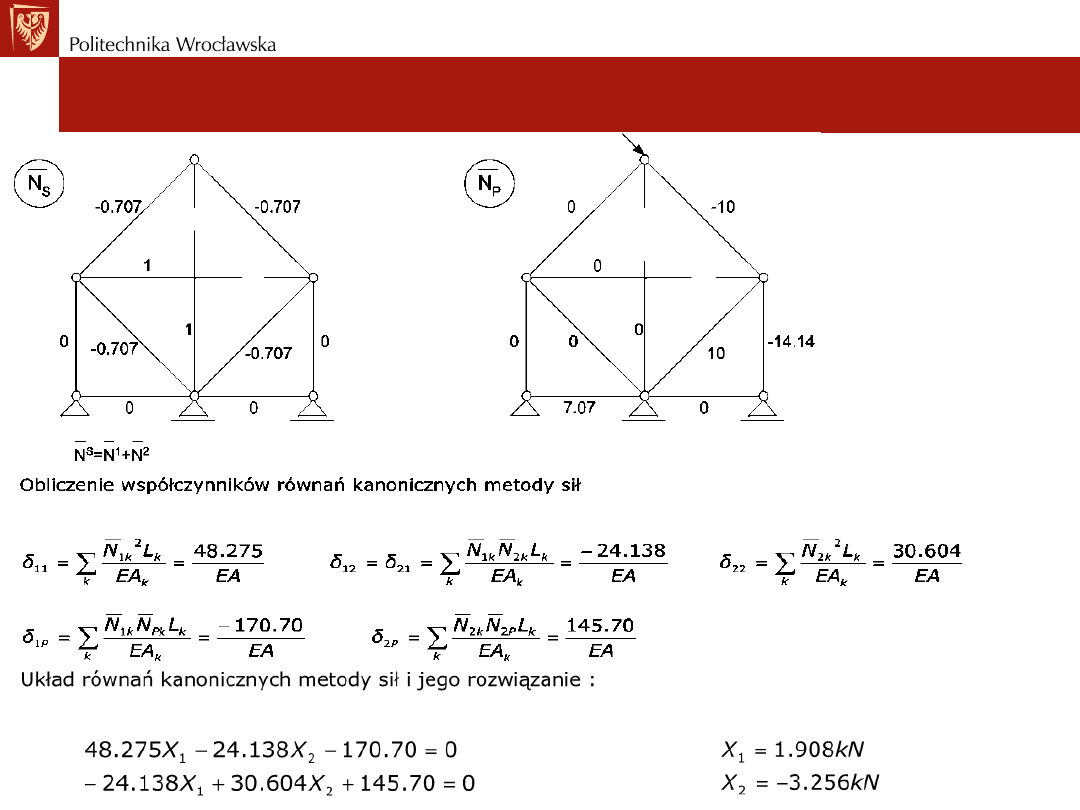
Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla kratownic

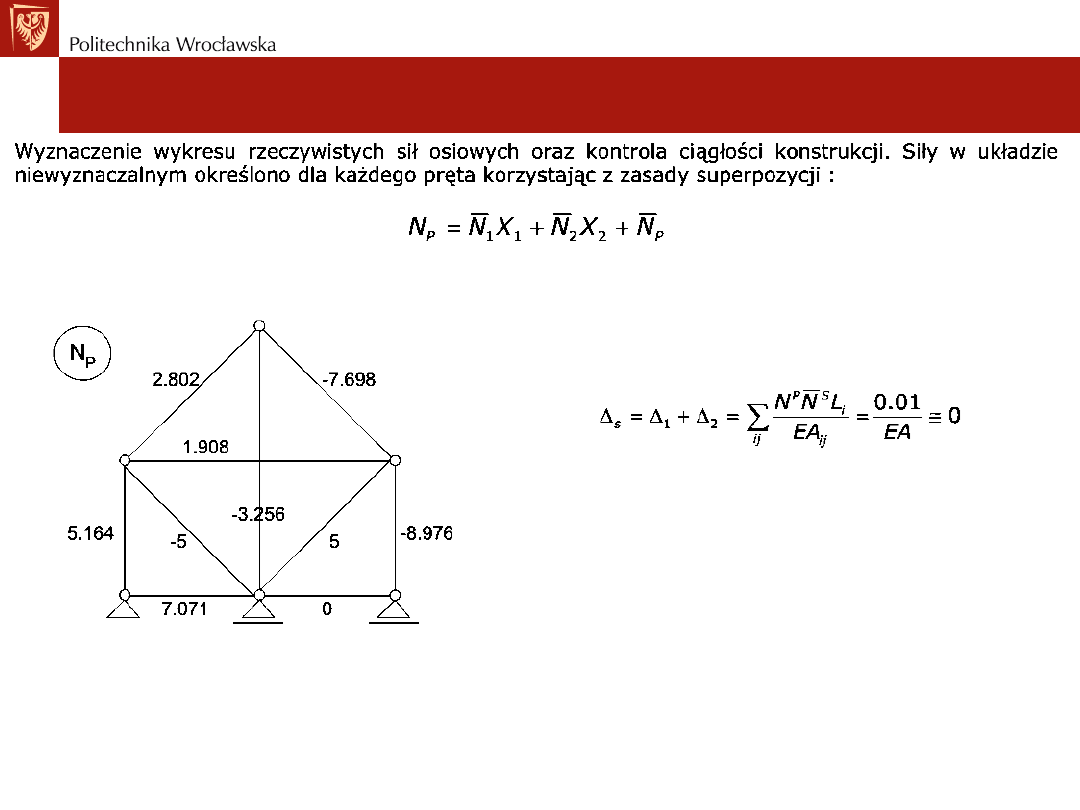
Ustroje statycznie niewyznaczalne. Metoda sił

Sformułowanie metody sił dla kratownic

Ustroje statycznie niewyznaczalne. Metoda sił

Belki statycznie niewyznaczalne

 W metodzie sił przyjęcie odpowiedniego schematu podstawowego

może znacznie uprościć obliczenia.

Jeżeli to możliwe staramy się tak dobrać układ podstawowy, aby jak
najwięcej współczynników równań kanonicznych była równa zeru.
Poniżej pokażemy przykład takiego schematu podstawowego dla
szczególnego przypadku – belki ciągłej.

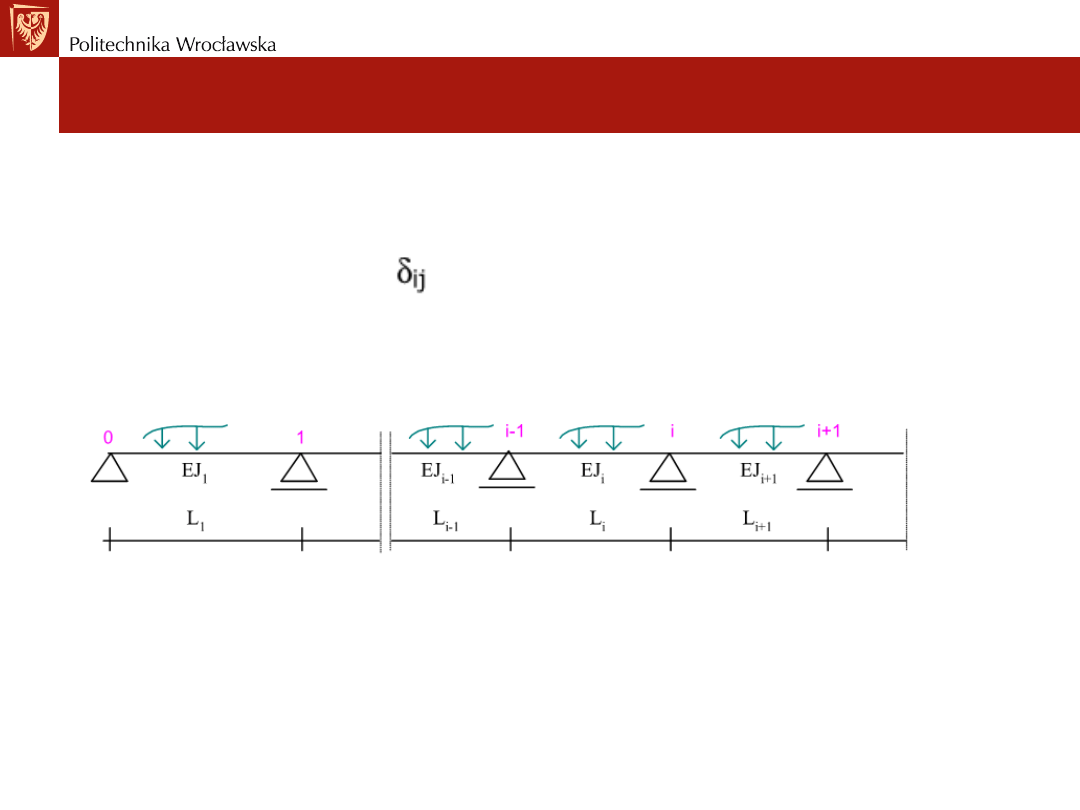
Rozwiązując metodą sił belki ciągłe – jako wielkości hiperstatyczne
wygodnie jest przyjąć momenty zginające nad podporami pośrednimi
(kolejno).

Ustroje statycznie niewyznaczalne. Metoda sił

Belki statycznie niewyznaczalne

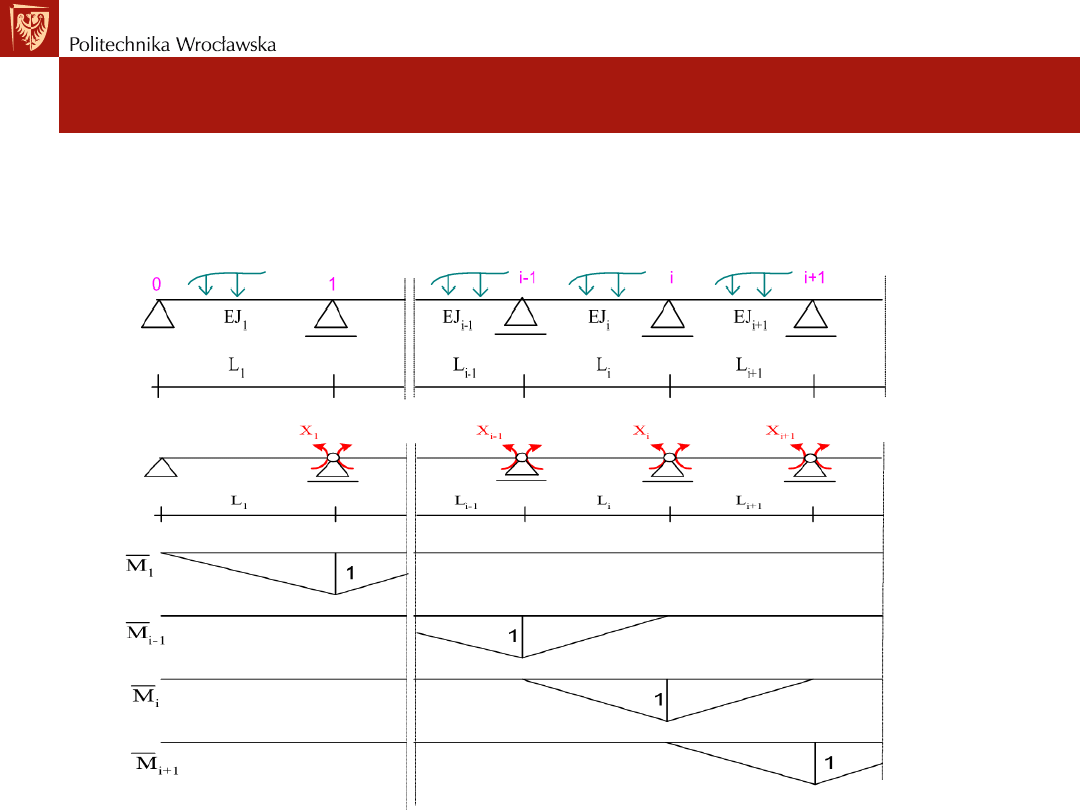
 Prowadzi to do układu równań, w którym w pojedynczym równaniu

występują najwyżej trzy niewiadome. Rozpatrzmy belkę ciągłą jak na
rysunku poniżej. Układ podstawowy metody sił

URZ

Ustroje statycznie niewyznaczalne. Metoda sił

Belki statycznie niewyznaczalne

• Odpowiednie współczynniki określone są przez następujące zależności:

• Pozostałe współczynniki sąrówne zero – co widać z wykresów. I-te

równanie kanoniczne metody sił ma postać:

Ustroje statycznie niewyznaczalne. Metoda sił

Belki statycznie niewyznaczalne

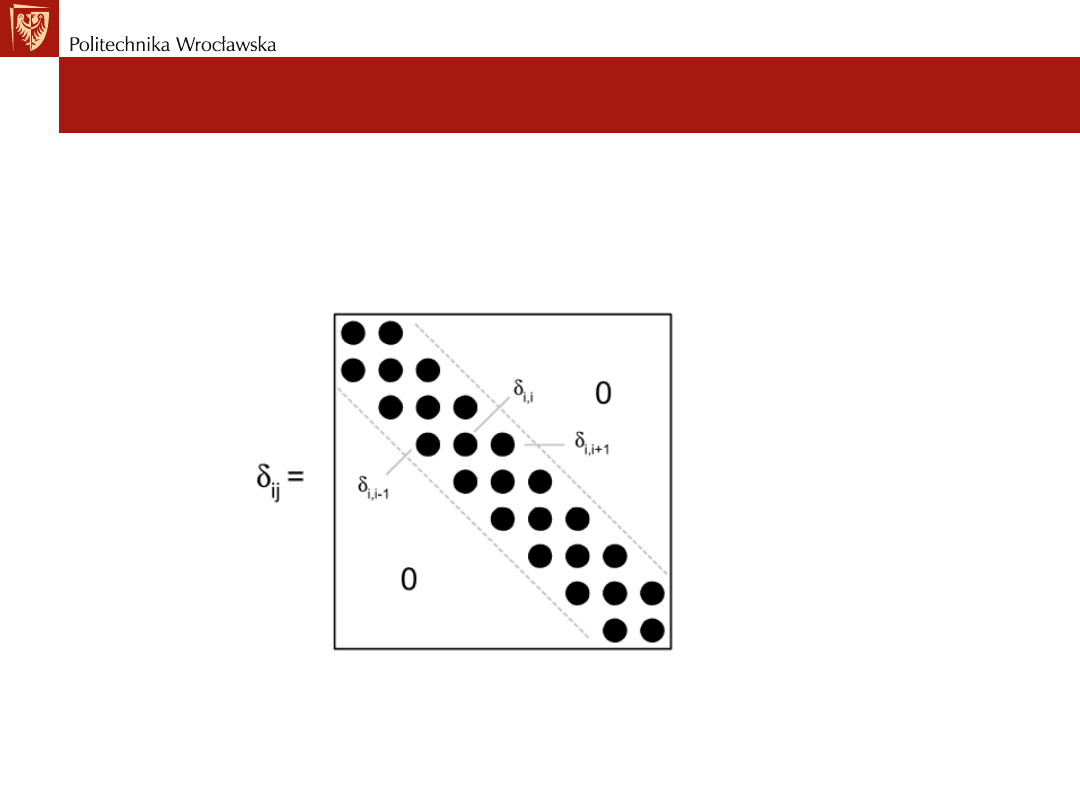
• Powyższe równanie jest często nazywane równaniem trzech

momentów. Jeżeli skrajne podpory są przegubowe to w pierwszym i
ostatnim równaniu występują tylko dwie niewiadome. Układ równń
ma charakter pasmowy, co pokazano na poniższym rysunku.

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

 Wzory do wyznaczania przemieszczeń od obciążeń mechanicznych są

ważne także dla układów SN.

Obciążenie jednostkowe jest obciążeniem wirtualnym, w przypadku układu
statycznie niewyznaczalnego może być ono

przyłożone do układu SW – na

przykład układu podstawowego – zamiast do układu SN!!!

Stan p oznacza obciążenie dane (rzeczywiste) przyłożone w tym przypadku

do układu SN:

Fakt ten nazywany bywa

twierdzeniem redukcyjnym.

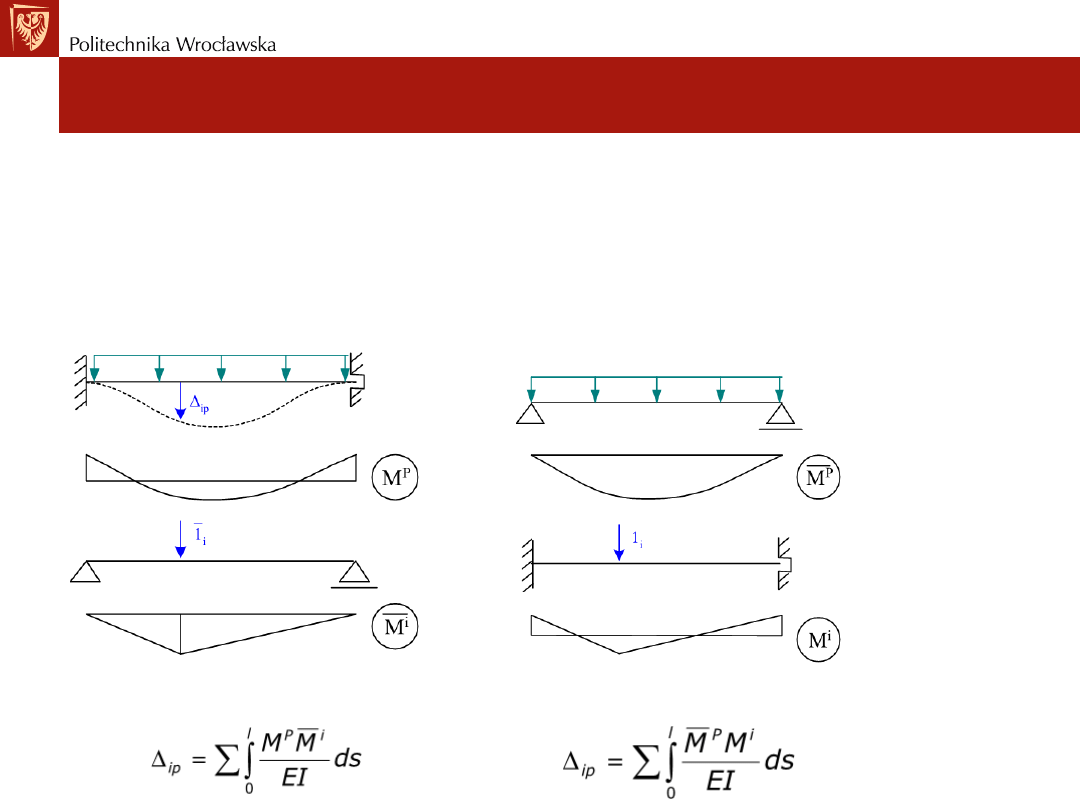
• Interpretację wersji twierdzenia redukcyjnego przedstawimy na

przykładzie belki sztywno zamocowanej na obu końcach.

• Wyznaczymy przemieszczenie pionowe w punkcie „i”. Skorzystamy z

dwóch wariantów twierdzenia redukcyjnego.

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

 Pierwsza i druga wersja twierdzenia redukcyjnego

• Interpretację wersji twierdzenia redukcyjnego przedstawimy na

przykładzie belki sztywno zamocowanej na obu końcach. Wyznaczymy
przemieszczenie pionowe w punkcie „i”. Skorzystamy z dwóch wariantów
twierdzenia redukcyjnego.

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

 Przemieszczenia w układach SN można określać z zależności podanych

poniżej:

 Podsumowanie

Można stwierdzić na podstawie twierdzeń redukcyjnych, że chcąc
wyznaczyć przemieszczenie w układzie statycznie niewyznaczalnym można
wyniki dla jednego ze schematów – dla obciążenia albo dla schematu
wirtualnego – uzyskać w układzie statycznie wyznaczalnym (na przykład w
układzie podstawowym

My będziemy posługiwać się schematem w którym wyznaczamy
siły wewnętrzne od obciążenia w URZ (SN), a siły wewnętrzne od
obciążenia na kierunku przemieszczenia w UP (SW).

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

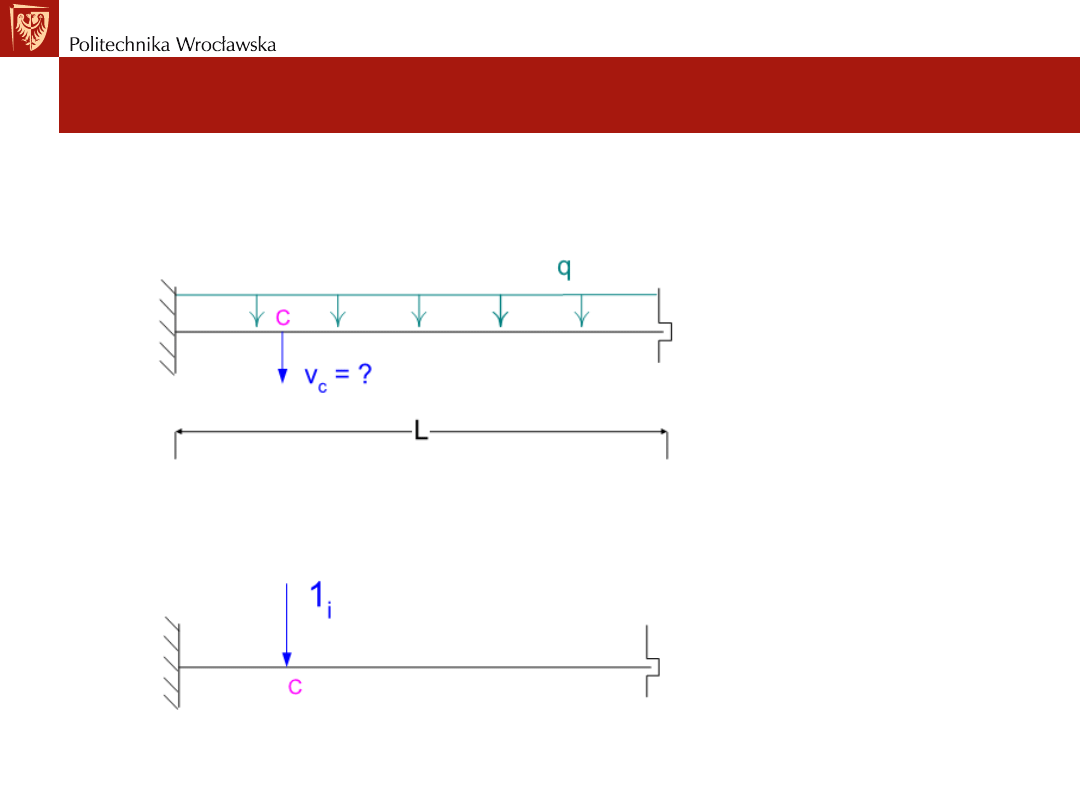
Problem wyznaczenia przemieszczenia w belce statycznie niewyznaczalnej.
Wyznaczamy przemieszczenie pionowe w punkcie „c” od obciążenia
równomiernie rozłożonego.

Aby wyznaczyć przemieszczenie w punkcie „c” przykładamy jednostkowe
obciążenie w tym punkcie.

URZ

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

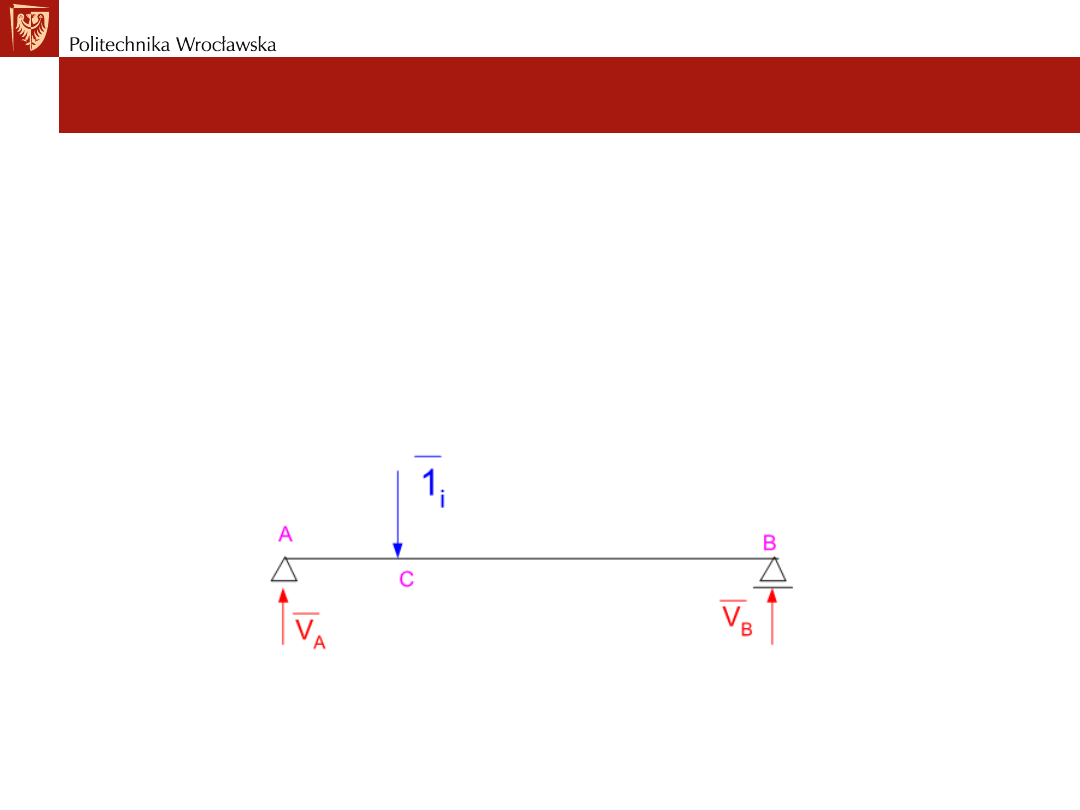
• Zachodzi potrzeba rozwiązania belki statycznie niewyznaczalnej od siły

jednostkowej. Jak wynika z II zasady prac wirtualnych – obciążenie
jednostkowe jest obciążeniem wirtualnym, a więc wystarczy aby spełniało
warunki równowagi.

• Wynika więc, że jako stan jednostkowy wystarczy przyjąć schemat

statyczny wyznaczalny – układ SW(w którym wszystkie wartości
zaznaczamy kreseczką).

• Możliwość przyjęcia stanu jednostkowego przedstawionego powyżej

zamiast przyjęcia schematu SN jest treścią twierdzenia redukcyjnego.

Ustroje statycznie niewyznaczalne. Metoda sił

Wyznaczanie przemieszczeń

 Schemat obliczenia przemieszczeń w układzie SN:
• Wyznaczenie sił wewnętrznych w układzie SN od zadanego obciążenia mech.

• Wyznaczenie sił wewnętrznych w układzie SW od obciążenia jednostkowego
na kierunku szukanego przemieszczenia

• Wyznaczenie przemieszczenia

Ustroje statycznie niewyznaczalne. Metoda sił

Podsumowanie

Ustroje statycznie niewyznaczalne. Metoda sił

Podsumowanie

Ustroje statycznie niewyznaczalne. Metoda sił

Podsumowanie

Ustroje statycznie niewyznaczalne. Metoda sił

Rozwiązanie MS od obciążenia temperaturą

 Ze wzorów na wyznaczanie przemieszczeń współczynniki w

kanonicznym układzie równań metody sił określone są wzorami:

• Kreseczka nad

𝑀

𝑖

𝑁

𝑖

𝑇

𝑖

oraz 𝑆

𝑖

oznacza, że są one wyznaczone w UP

czyli SW.

• W ramach i belkach wpływ T i N jest mały, przyjmujemy EA=∞ oraz

GA=∞, co powoduje pominięcie całek poszczególnych całek.

• Całki z iloczynu momentów zginających należy wyznaczyć za pomocą

wzorów

Simpsona

i Wereszczagina.

• Siła w podporze sprężystej jest równa co do wartości reakcji w tej wiezi

lecz

z przeciwnym znakiem np. Ss=-Vs

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

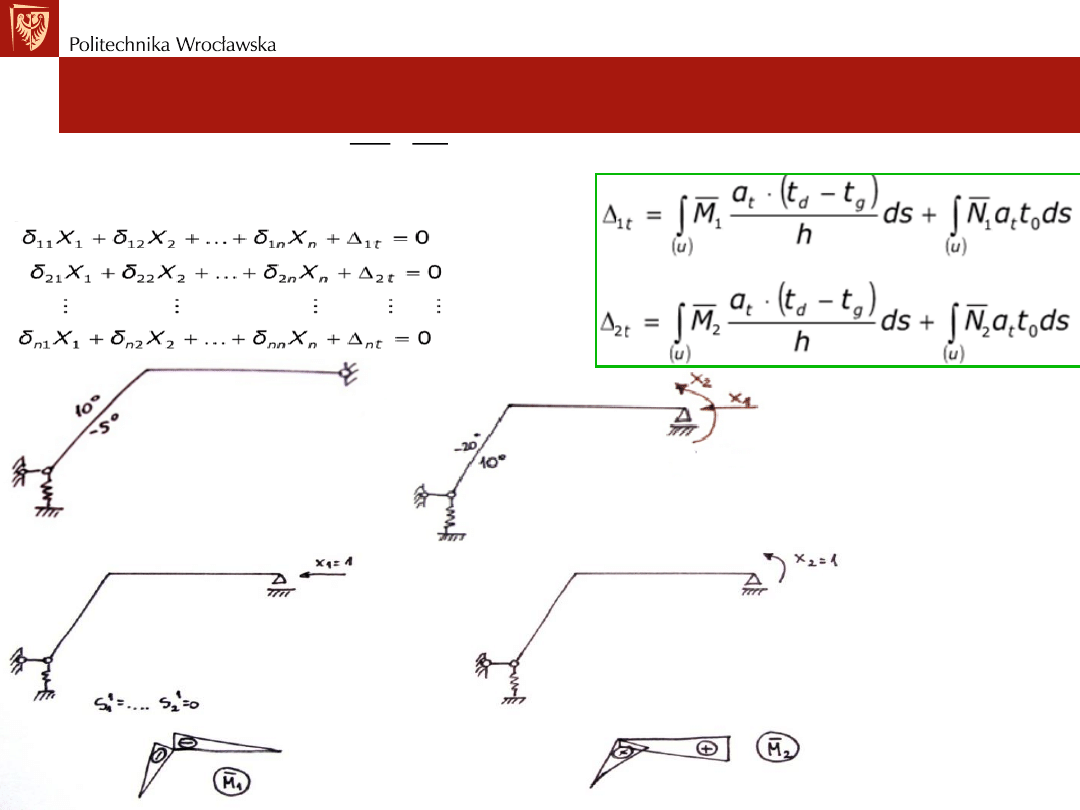
 Gdy obciążenie stanowi

zmiana temperatury

, wówczas w miejsce ∆

układzie równań podstawiamy ∆

określony wzorem:

gdzie:
oznacza odkształcenie sprężyny wywołane zmianą temperatury,
oznacza przemieszczenie w miejscu i kierunku wielkości hiperstatycznej

Xi=1 wywołane zmianą temperatury w układzie podstawowym.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

• Poszczególne całki

𝑴

𝒊

𝑵

𝒊

𝑻

𝒊

należy traktować jako pola

wykresów dla wszystkich prętów.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

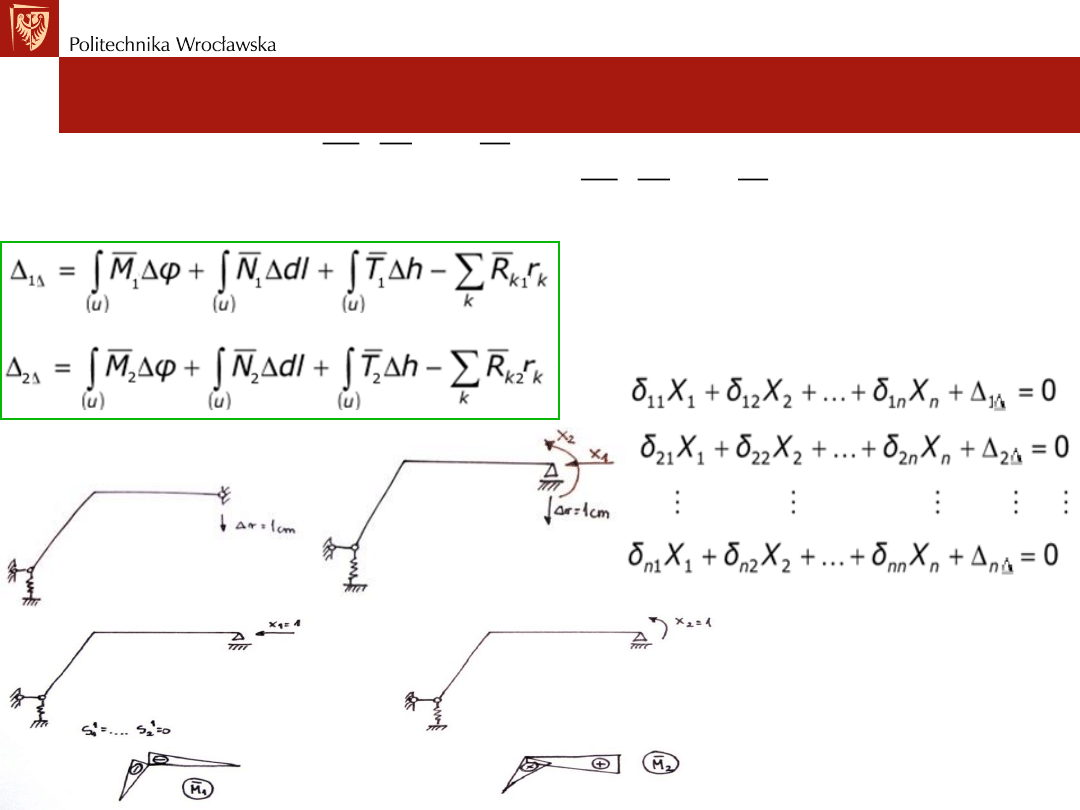
 Gdy obciążenie stanowią

osiadania (przemieszczenia) podpór r

oraz

imperfekcje ∆φ, ∆l, ∆h (błędy montażu),

wówczas w miejsce ∆

układzie równań podstawiamy ∆

i∆

określony wzorem:

gdzie:

oznacza przemieszczenie w miejscu i kierunku wielkości Xi w UP

wywołane błędami montażu i przemieszczeniem podpór w układzie
podstawowym,
oznacza przemieszczenie w URZ w miejscu wielkości hiperstatycznej Xi.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

• Poszczególne całki

𝑴

𝒊

𝑵

𝒊

𝑻

𝒊

,𝑹

𝒊

dla dyskretnych błędów montażu

można traktować jako sumy wartości

𝑴

𝒊

𝑵

𝒊

𝑻

𝒊

, 𝑹

𝒊

w miejscach

imperfekcji danego typu.

Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Wnioski:

•

Macierz podatności (współczynników) utworzona na podstawie współczynników równań
kanonicznych jest symetryczna,

•

Równania kanoniczne są nieodłącznym składnikiem układu podstawowego, gdyż zapewniają
kinematyczną zgodność z układem rzeczywistym,

•

Z równań kanonicznych można obliczyć wartości niewiadomych sił uogólnionych Xi.

 Przykład obliczeniowy

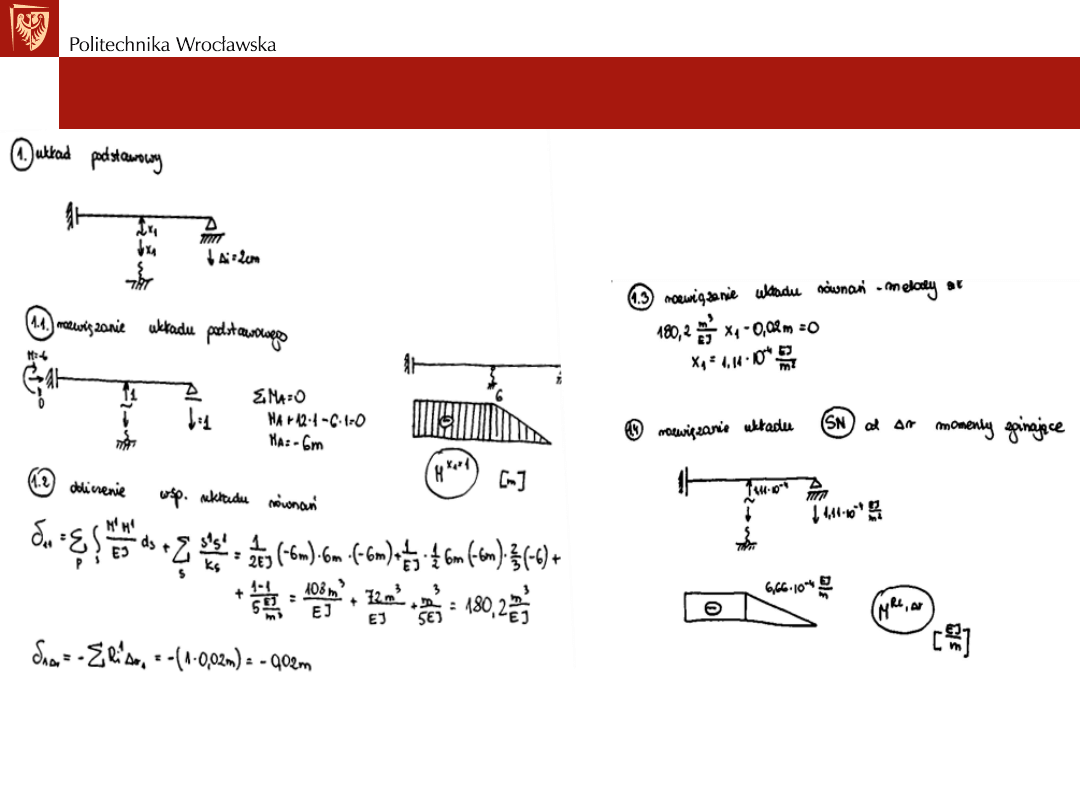
Ustroje statycznie niewyznaczalne. Metoda sił

Układ podstawowy i układ równań kanonicznych

 Po rozwiązaniu układu równań otrzymuje się nadliczbowe wielkości

hiperstatyczne X1, …., Xn, a następnie wyznacza się rzeczywiste (w układzie
SN) sił przekrojowe M, N, T oraz reakcje.

Ustroje statycznie niewyznaczalne. Metoda sił

Kontrola poprawności rozwiązania

 Kontrola poprawności rozwiązania dla obciążenia temperaturą
Odpowiednie siły przekrojowe w układzie rzeczywistym oznaczamy Mp=MT
oraz Ssp=SsT. Poprawne rozwiązanie od obciążenia temperaturą spełnia
równanie:

Ustroje statycznie niewyznaczalne. Metoda sił

Kontrola poprawności rozwiązania

 Kontrola poprawności rozwiązania dla obciążenia imperfekacjami i

osiadaniem podpór

Odpowiednie siły przekrojowe w układzie rzeczywistym oznaczamy Mp=M∆
oraz Ssp=Ss∆. Poprawne rozwiązanie od obciążenia imperfekcjami oraz
osiadaniem podpór: