MECHANIKA BUDOWLI

Wykład 3:

WYZNACZANIE PRZEMIESZCZEŃ.

UKŁADY STATYCZNIE WYZNACZALNE

Prowadzący: dr inż. Wojciech Zielichowski-Haber

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Plan wykładu

1. Rodzaje więzi sprężystych
2. Zasady prac wirtualnych dla więzi sprężystych
3. Wyznaczanie przemieszczeń wywołanych działaniem sił
4. Stany jednostkowe w wyznaczaniu przemieszczeń
5. Metody obliczenia całek
6. Wyznaczanie przemieszczeń wywołanych osiadaniem podpór
7. Wyznaczanie przemieszczeń wywołanych zmianą temperatury
8. Wyznaczanie przemieszczeń wywołanych imperfekcjami

geometrycznymi

9. Podsumowanie
10. Przykłady

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

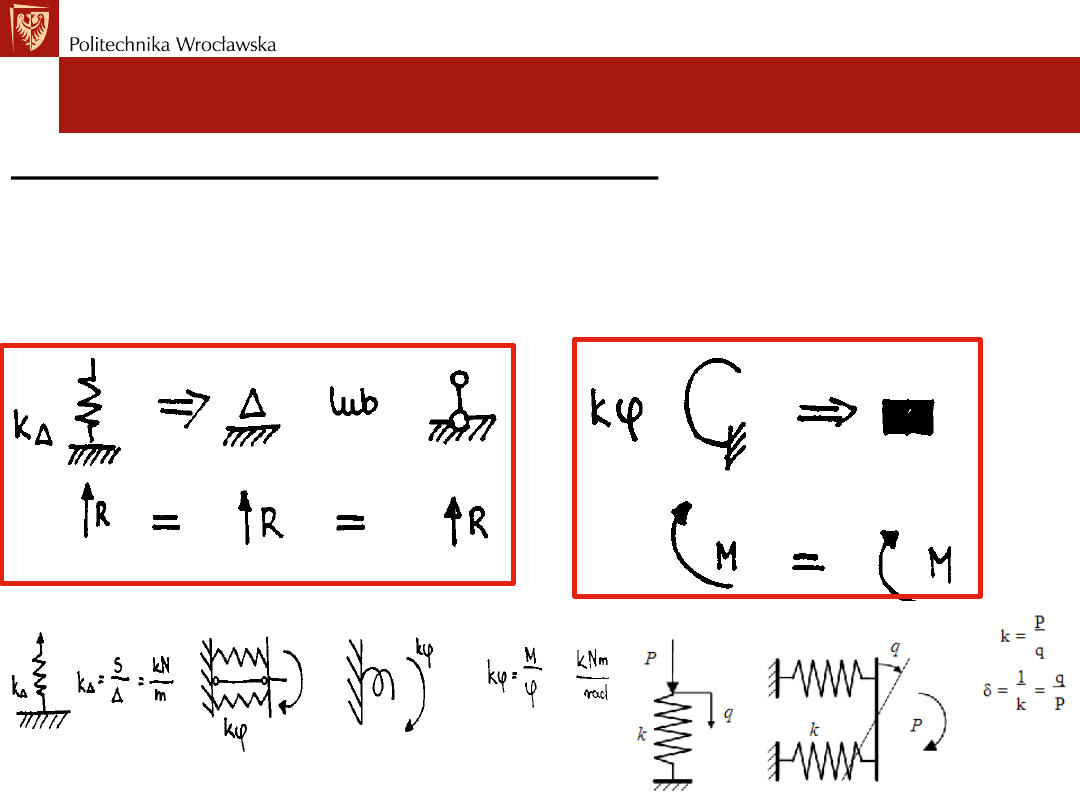
Rodzaje więzi sprężystych

Więzi sprężyste w schemacie statycznym:

• Każda więź sztywna ma swój odpowiednik sprężysty,
• Wartość reakcji oraz sił wewnętrznych w podporze sprężystej w układach

SW jest identyczna jak w podporze sztywnej, w układzie SN nie jest
identyczna.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

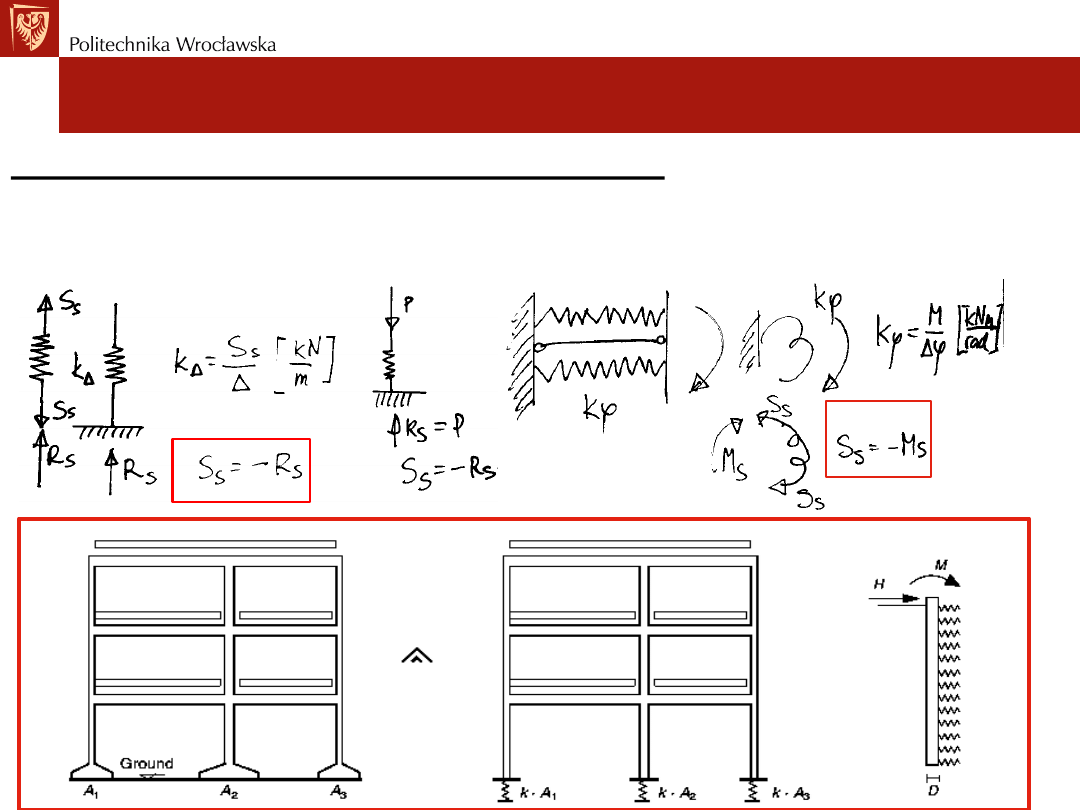
Rodzaje więzi sprężystych

Rozróżnia się dwa typy więzi sprężystych:

a) więzi translacyjne przenoszące tylko siły podłużne (pionowe i poziome),
b) więzi rotacyjne przenoszące tylko momenty zginające.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

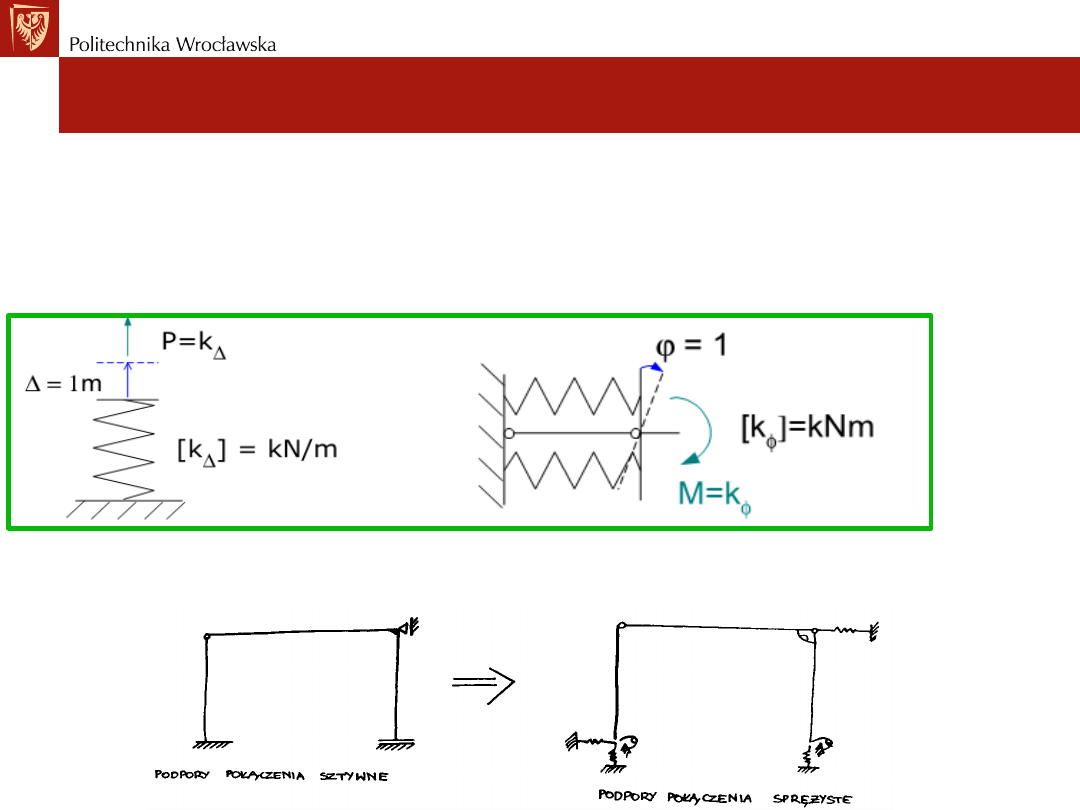
Rodzaje więzi sprężystych

Więzi sprężyste charakteryzuje jeden parametr - sztywność k.

• Sztywność

k

∆

lub

k

φ

jest równa sile (reakcji) / momentowi

zgniającemu, która powoduje jednostkowe odkształcenie więzi w
postaci translacji (wydłużenie, skrócenie) / rotacji (obrót).

• Więzi sztywne są szczególnym przypadkiem więzi sprężystych, gdzie

sztywność k = ∞ (jest nieskończona).

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

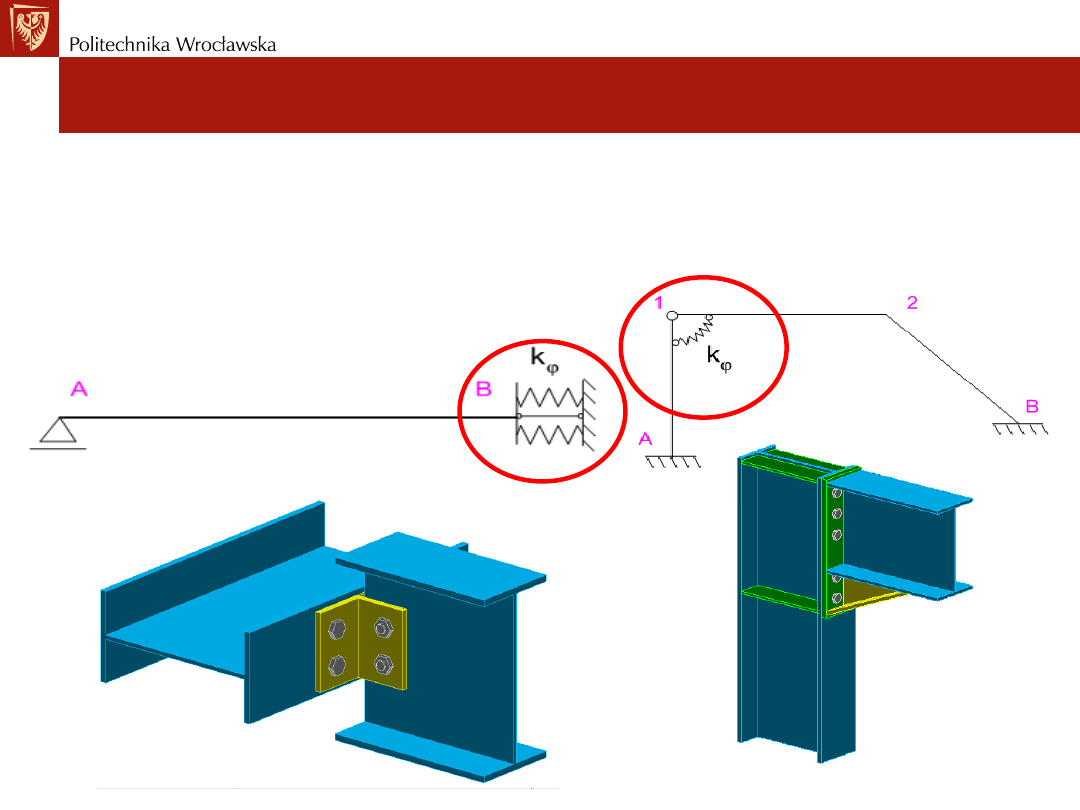
Rodzaje więzi sprężystych

Przykłady:

• Sztywność sprężystego zamocowania na obrót belki oraz

sprężystego węzła w ramie

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Rodzaje więzi sprężystych

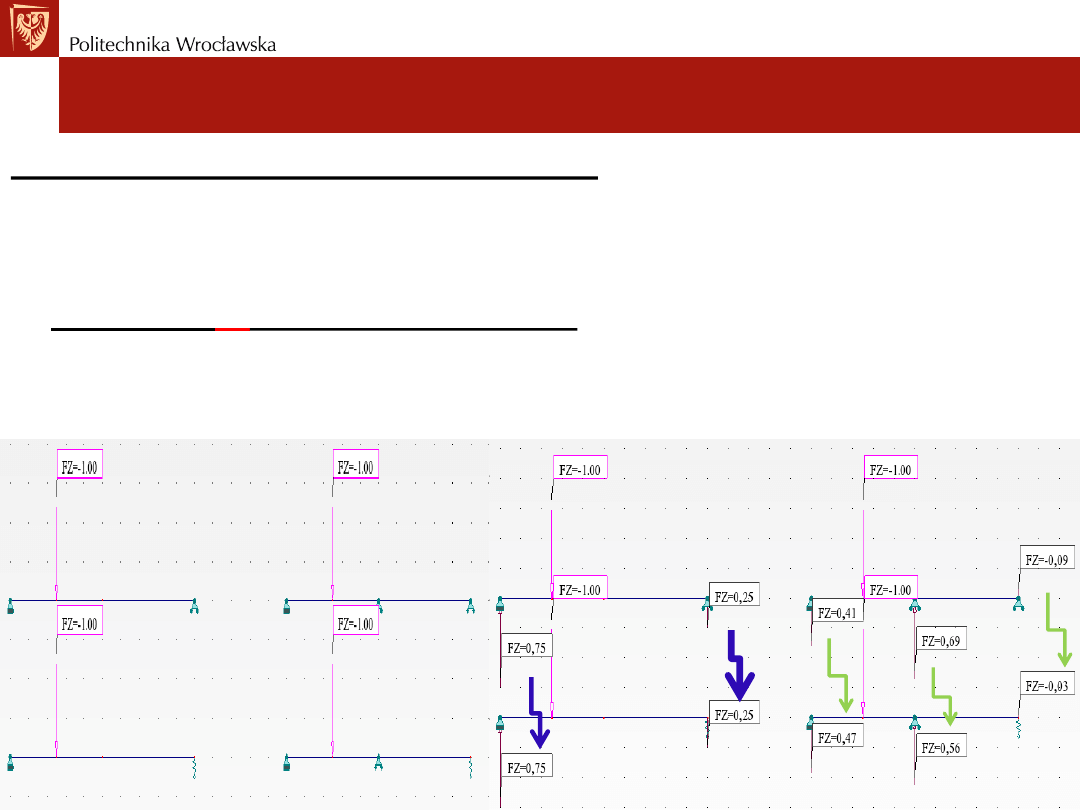
Więzi sprężyste w schemacie SW i SN:

 W układach

SW

wartość reakcji w danym schemacie statycznym z podporą

lub podporami sprężystymi i sztywnymi jest identyczna jak w tym samym
schemacie z podporami tylko sztywnymi.
W układach

SN

nie są one identyczne.

Dotyczy to również sił wewnętrznych M, N, V które zależą od działającego
obciążenia i powstałych reakcji.

SW

SN

SW

SN

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

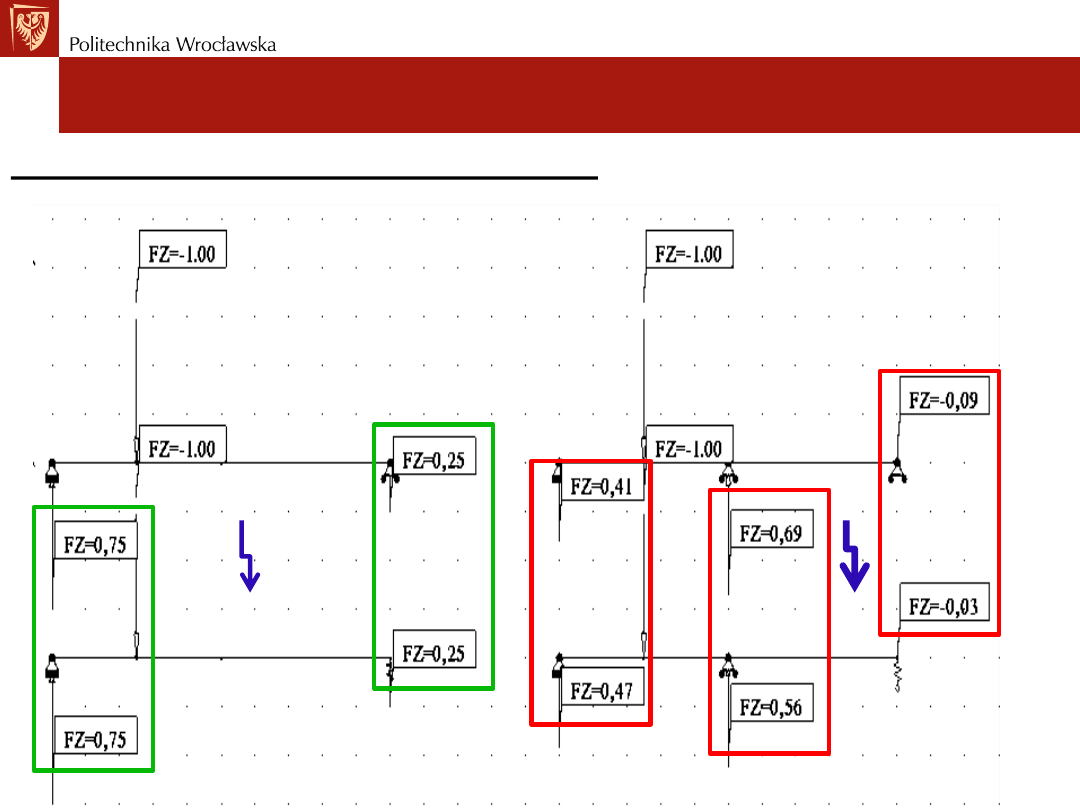
Rodzaje więzi sprężystych

Więzi sprężyste w schemacie SW i SN:

SW

SN

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

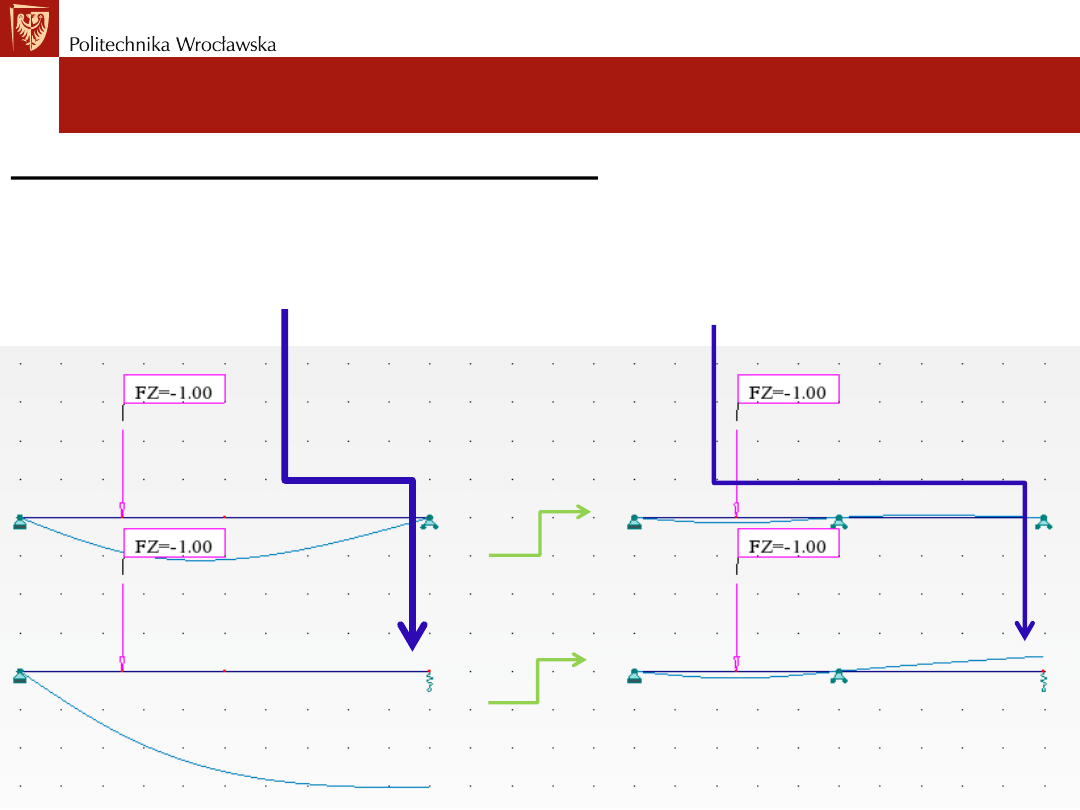
Rodzaje więzi sprężystych

Więzi sprężyste w schemacie SW i SN:

 W układach

SW

i

SN

przemieszczenia w danym schemacie statycznym na

podporach sprężystych są inne jak na podporach sztywnych. Podpory
sprężyste ściskają się (przem. w dół) lub też rozciągają (przem. w górę).

SW

SN

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

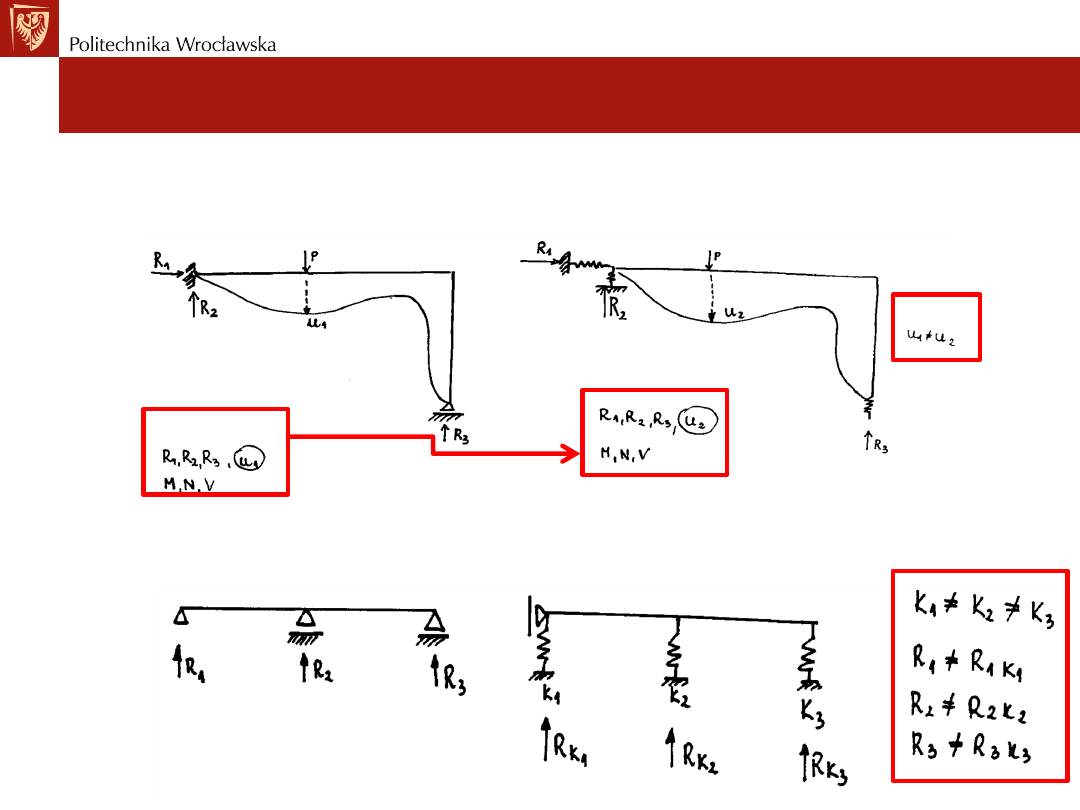
Rodzaje więzi sprężystych

• Reakcje, siły wew. i przemieszczenia dla podpór sztywnych i

sprężystych w układach SW

• Reakcje, siły wew. i przemieszczenia dla podpór sztywnych i

sprężystych w układach SN

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Zasady prac wirtualnych dla więzi sprężystych

Wartości całek występujących w sformułowaniach zasady prac wirtualnych
dla więzu sprężystych.
• Oznaczmy przez „i” stan wirtualny, a przez „j” stan rzeczywisty.

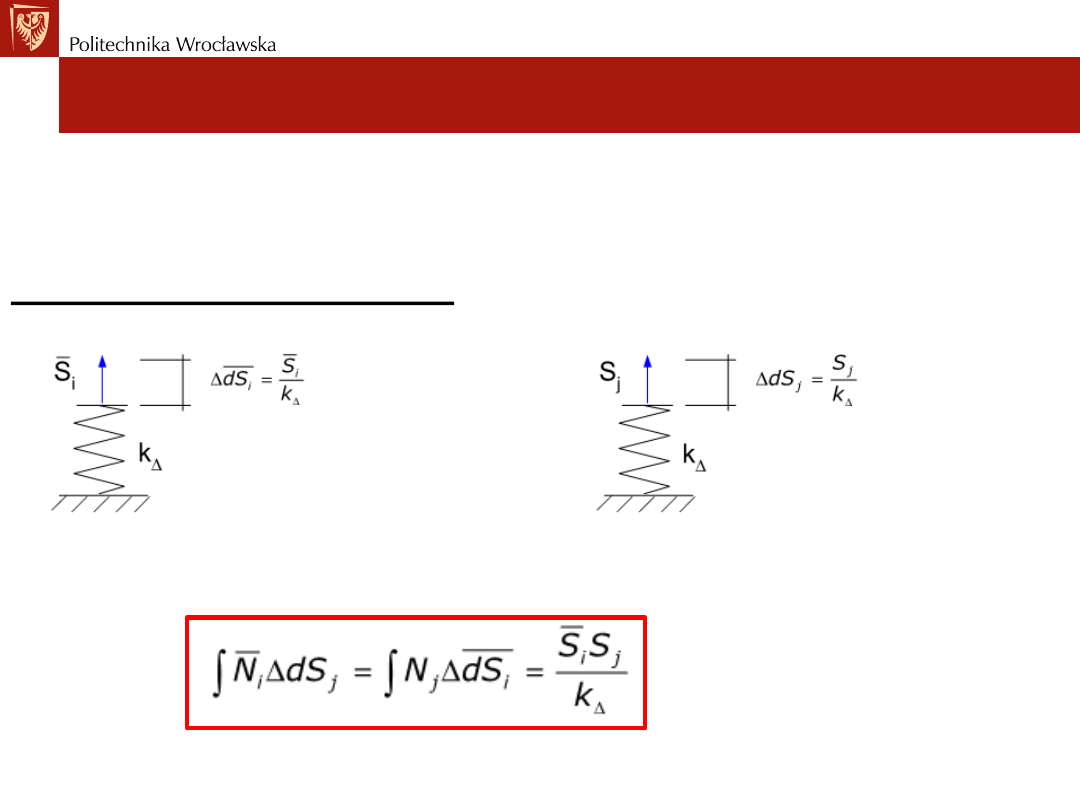
1. Dla więzi translacyjnej:

Mamy:

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Zasady prac wirtualnych dla więzi sprężystych

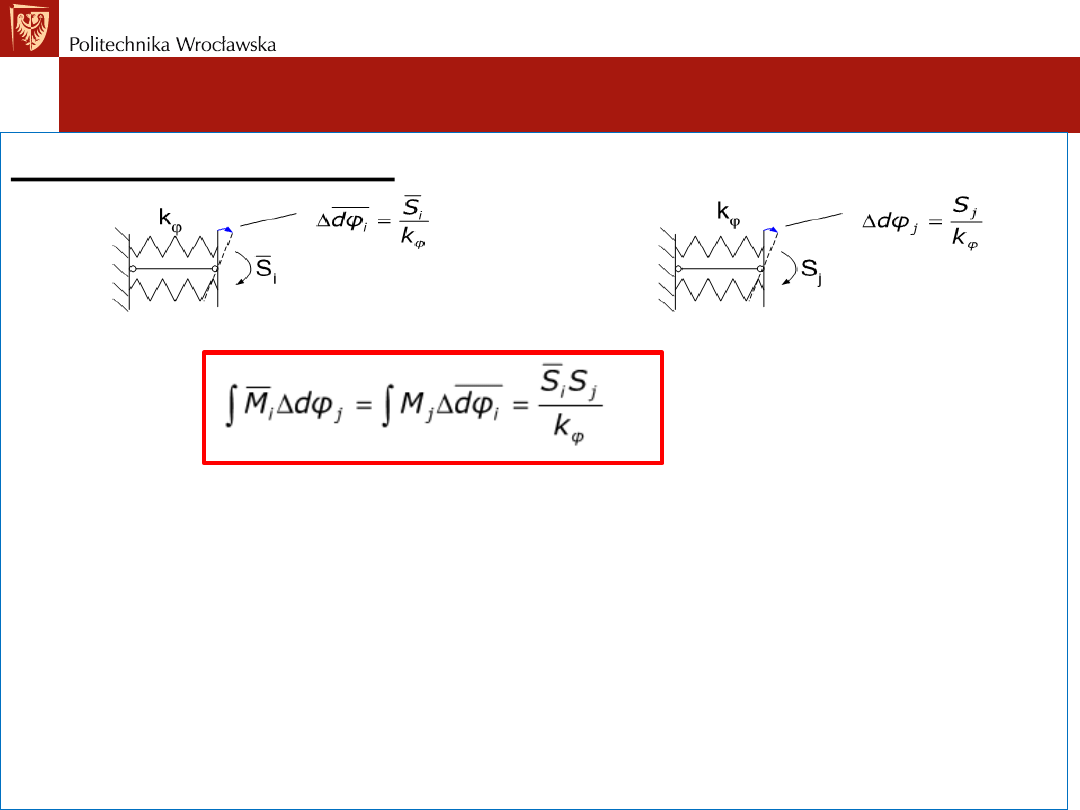
2. Dla więzi rotacyjnej



Mamy:

Stany „i” obciążenia i przemieszczeń traktujemy jako wirtualne, a
stany „j” jako rzeczywiste

.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

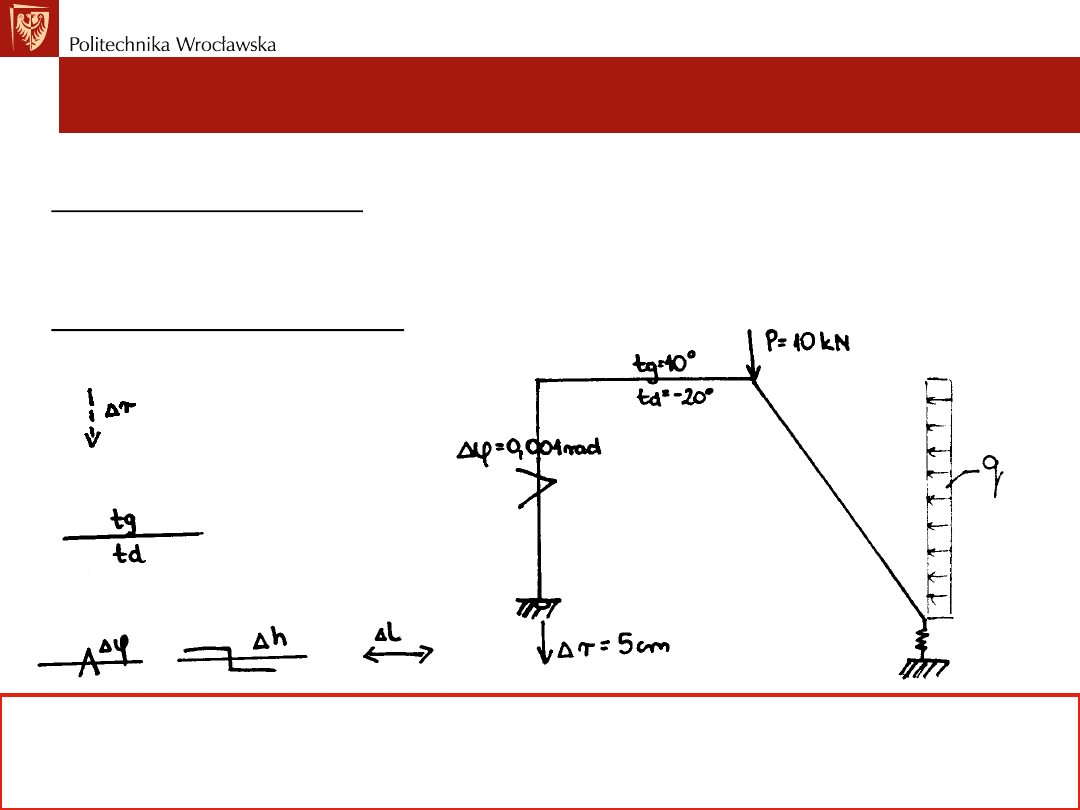
 Rozpatrujemy układ prętowy, na który działają obciążenia:

• mechaniczne w postaci
1. sił i momentów skupionych P [kN], M [kNm],
2. obciążeń i momentów równomiernie rozłożonych q [kN/m], m [kNm/m],
• niemechaniczne w postaci
1. przem. podpory [m],

2. wpływy termiczne [C],

3. błędy montażu [m].

Celem jest wyznaczenie przemieszczenia ∆

ip

w miejscu i na kierunku „i” od

przyłożonego obciążenia mechanicznego P i niemechanicznego ∆

i∆r

,

∆

iT

,

…etc.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

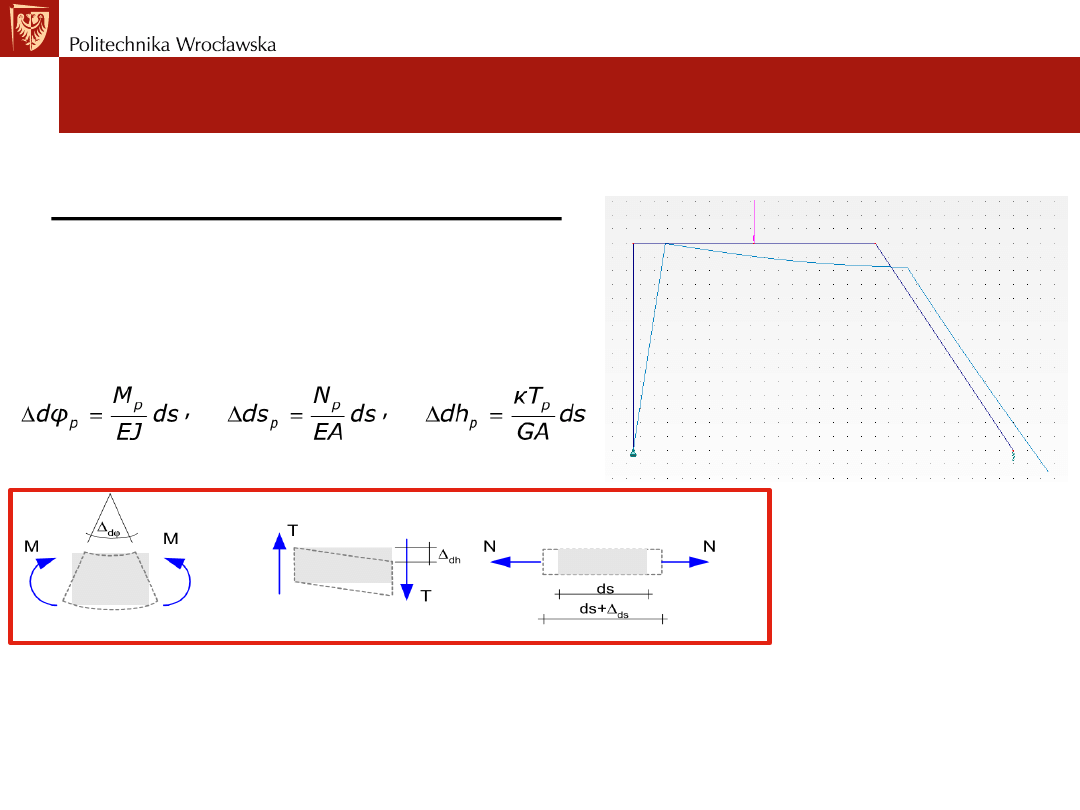
Wyznaczanie przemieszczeń

 Obciążenia wywołują siły przekrojowe

𝑀

𝑝

,

𝑁

𝑝

,

𝑇

𝑝

oraz

odkształcenia układu prętowego:

1. kątowe (obrót o kąt) ,
2. wzdłuż osi pręta (wydłużenie),
3. prostopadłe do osi (postaciowe).

 Obowiązuje:

1) Prawo Hooka 2) warunki kinematyczne układu nie ulegają zmianie w
trakcie trwania obciążenia - ukł. Clapeyrona

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

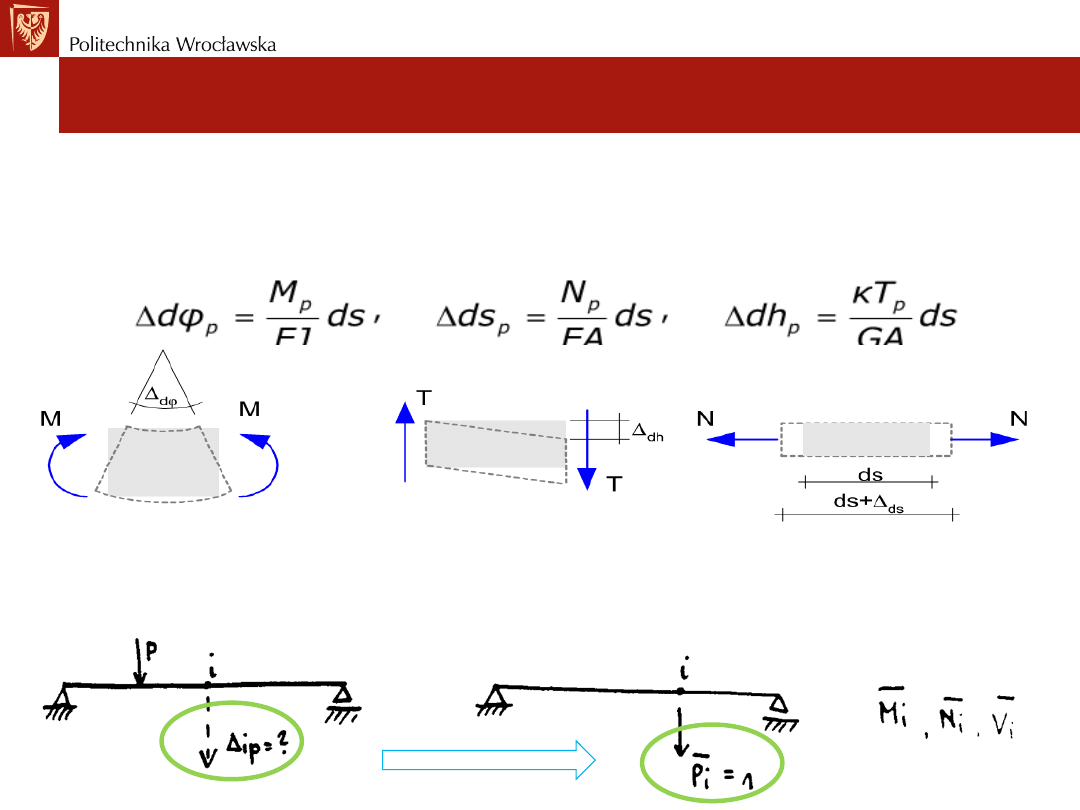
Zasady prac wirtualnych dla więzi sprężystych

 Pierwsza i druga zasada prac wirtualnych z uwzględnieniem więzi

sprężystych przedstawia się następująco:

 Zasada I:

 Zasada II

 We wzorach indeks „s” oznacza sumowanie po więziach sprężystych

(rotacyjnych i translacyjnych)

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

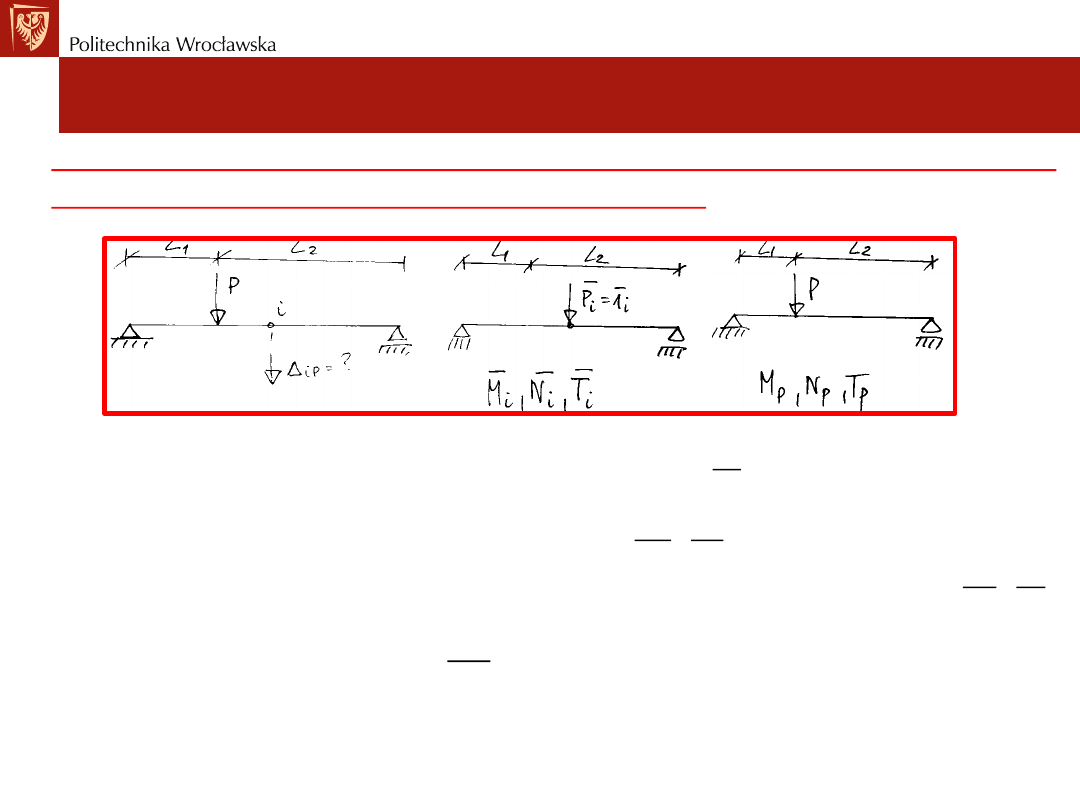
Wyznaczanie przemieszczeń

Rozpatrujemy układ prętowy, na który działają obciążenia
mechaniczne (w postaci P, q, M), które wywołują siły przekrojowe
𝑀

𝑝

,

𝑁

𝑝

,

𝑇

𝑝

oraz odkształcenia układu prętowego:

Celem jest wyznaczenie przemieszczenia ∆

ip

w miejscu i na

kierunku „i” od przyłożonego obciążenia mechnicznego P.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

 Wzór na wyznaczenie przemieszczenia

∆

𝒊𝒑

w miejscu i na kierunku „i” układu

prętowego od obciążenia mechanicznego (P, q, M):

1. Przykładamy jednostkowe obciążenie wirtualne

𝑷

𝒊

=

𝟏

𝒊

(tylko siła

jednostkowa) w miejscu i na kierunku „i” układu prętowego któremu
odpowiadają wirtualne siły przekrojowe

𝑴

𝒊

,

𝑵

𝒊

,

𝑻

𝒊

.

2. Praca wirtualna układu prętowego dla

𝑃

𝑖

=

1

𝑖

i sił przekrojowych

𝑀

𝑖

,

𝑁

𝑖

,

𝑇

𝑖

na rzeczywistych przemieszczeniach ∆

𝑖𝑝

oraz odkształceniach ∆𝑑𝜑

𝑝

,

∆𝑑𝑠

𝑝

i

∆𝑑ℎ

𝑝

, dla przyjętego

𝑃

𝑛𝑖

=

1

𝑖

oraz symbolu „j” zastąpionego

symbolem „p”. Z II zasady prac wirtualnych otrzymuje się wzór
Maxwella-Mohra na przemieszczenie

∆

𝒊𝒑

:

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

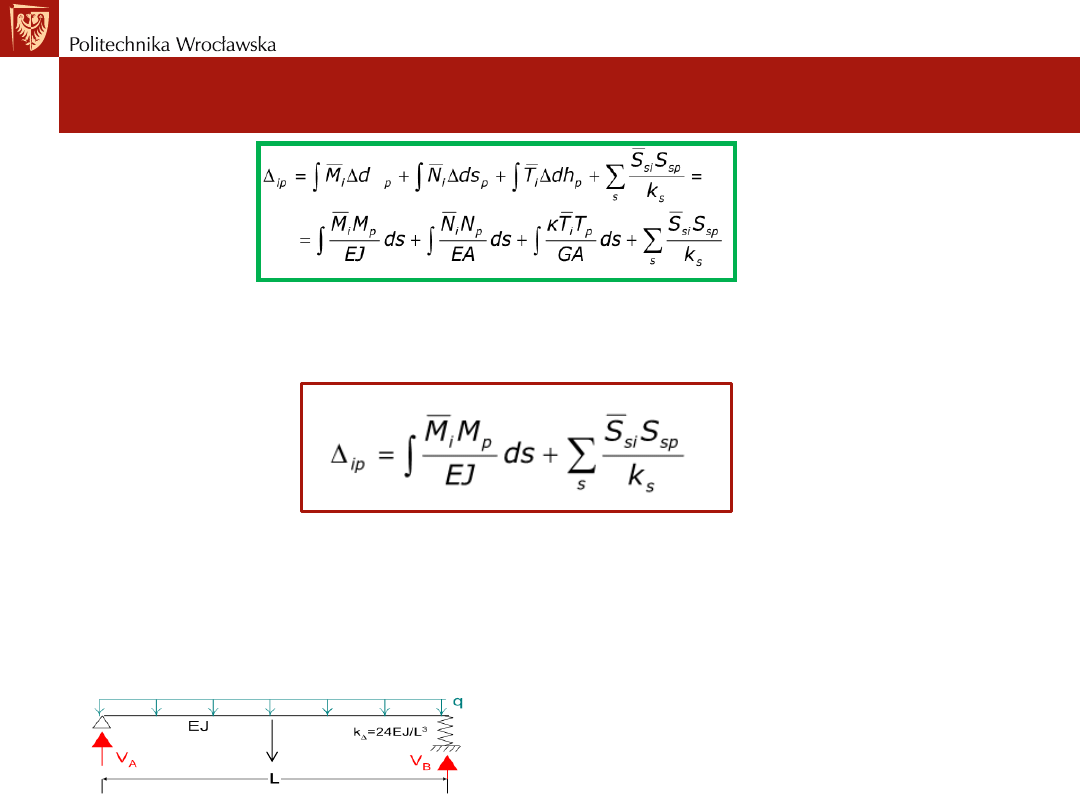
Wyznaczanie przemieszczeń

 Dla belek i ram wpływ sił osiowych i sił tnących na przemieszczenia

jest pomijalnie mały. Wzór na wyznaczanie przemieszczeń

∆

𝒊𝒑

ma

postać:

• Całki w powyższych wzorach dotyczą całego ustroju prętowego

(wszystkich prętów).

 Algorytm wyznaczania przemieszczenie

∆

𝑖𝑝

dla ustroju prętowego

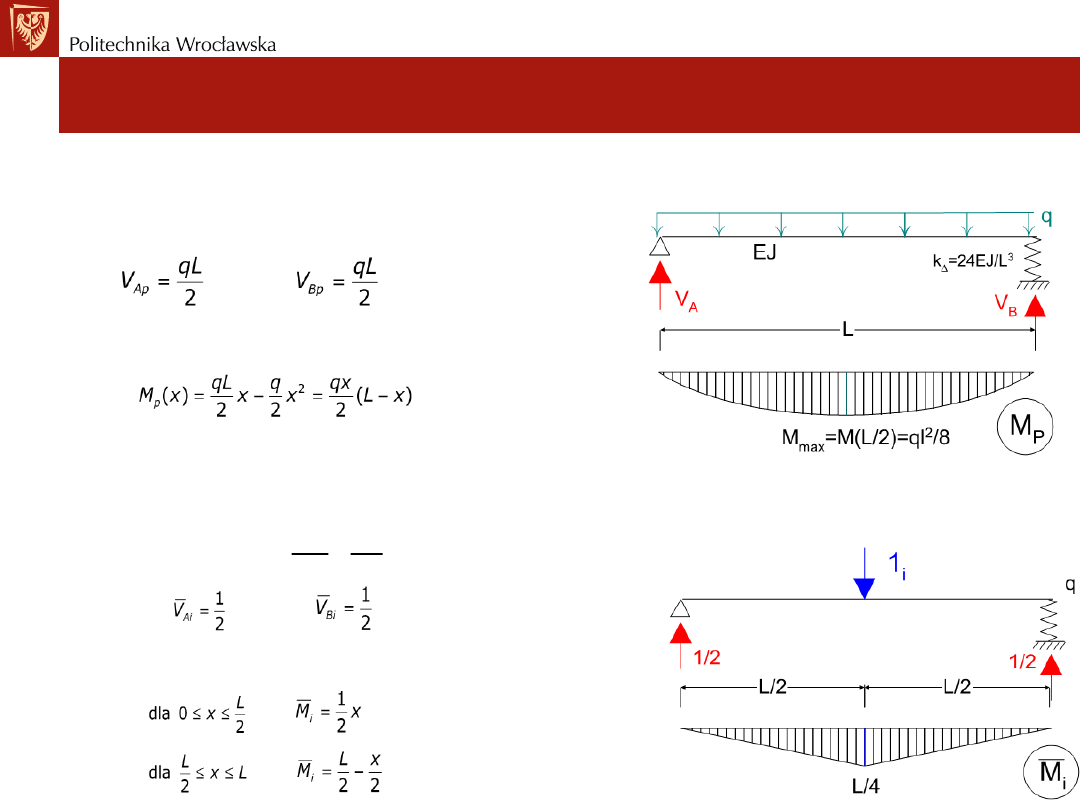
(rama, belka): Obliczenie przemieszczeń w środku belki

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

1) Wyznaczenie sił przekrojowych

𝑀

𝑝

(𝑁

𝑝

,

𝑇

𝑝

) i reakcji w więziach

sprężystych

𝑆

𝑝

od obciążenia danego,

2) Przyłożenie jednostkowego obciążenia wirtualnego

𝑃

𝑖

= 1

𝑖

w

miejscu i kierunku „i” oraz wyznaczeniu wirtualnych sił
przekrojowych

𝑀

𝑖

,

𝑁

𝑖

,

𝑉

𝑖

i reakcji 𝑅

𝑖

oraz w więziach sprężystych

𝑆

𝑖

,

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

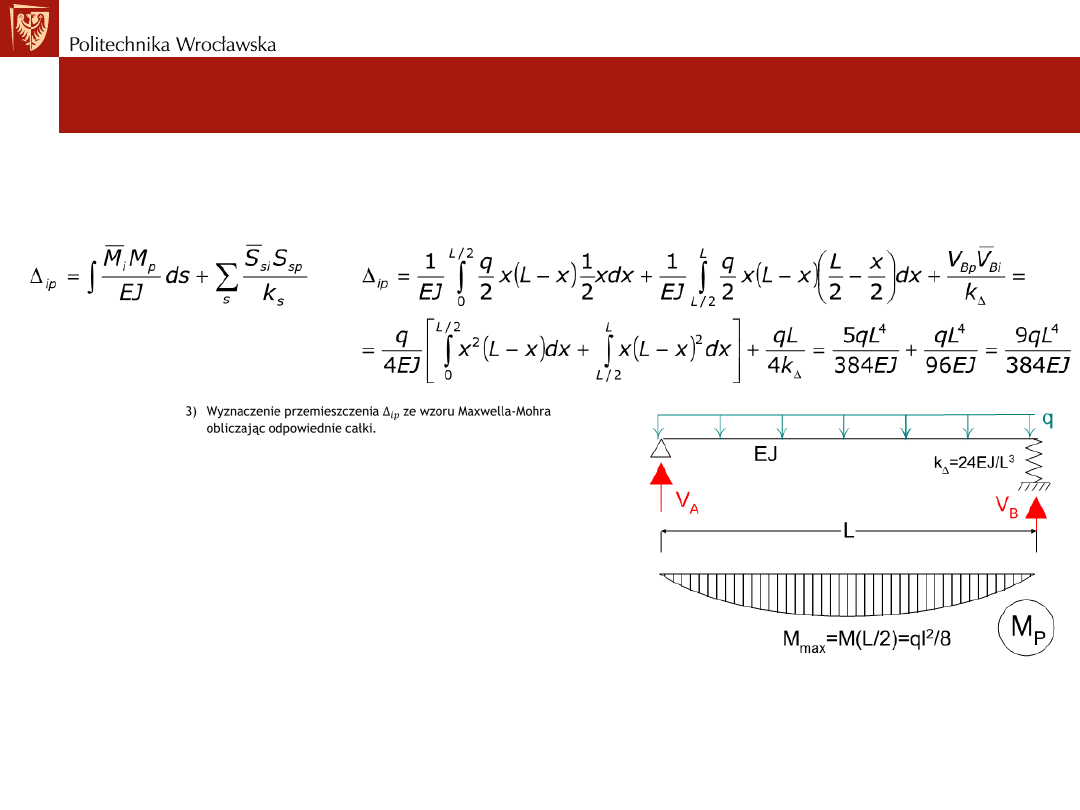
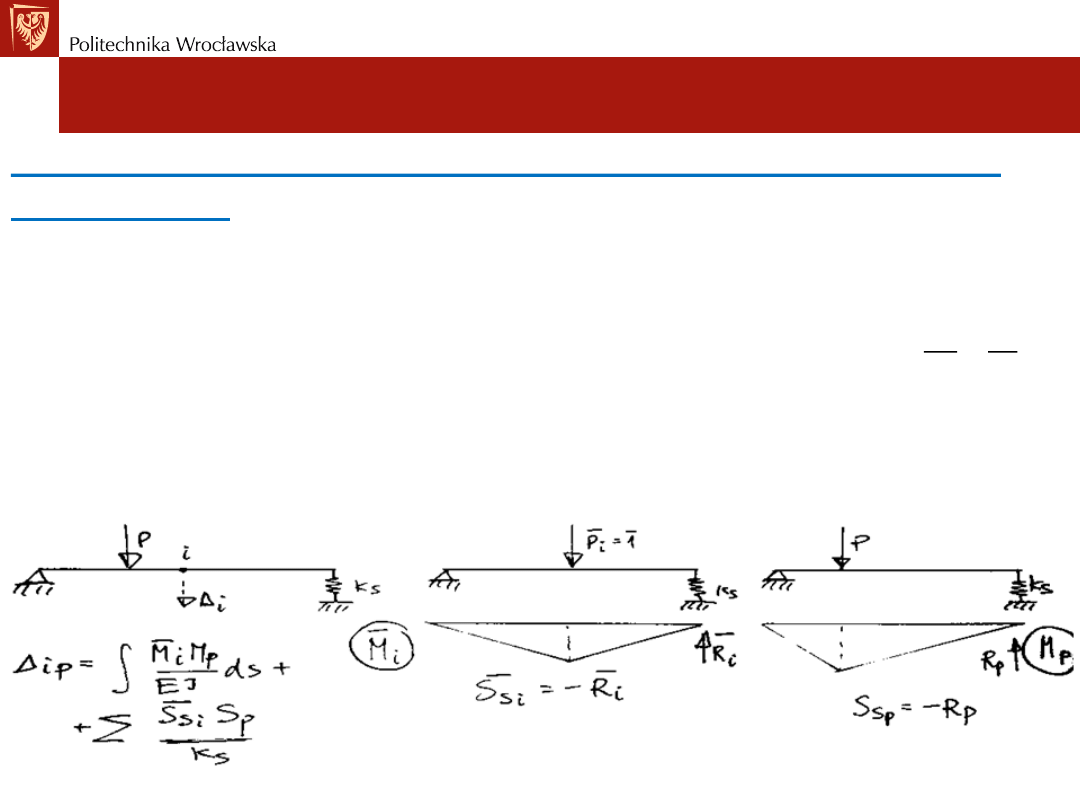
3) Wyznaczenie przemieszczenia

∆

𝑖𝑝

ze wzoru Maxwella-Mohra

obliczając odpowiednie całki.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

Algorytm wyznaczyć przemieszczenie

∆

𝒊𝒑

dla ustroju prętowego

(rama, belka):

1. Wyznaczenie sił przekrojowych

𝑀

𝑝

(𝑁

𝑝

,

𝑇

𝑝

) oraz reakcji

𝑅

𝑝

i

𝑆

𝑝

od

obciążenia danego

2. Przyłożenie jednostkowego obciążenia wirtualnego

𝑃

𝑖

= 1

𝑖

w miejscu i

kierunku „i” oraz wyznaczeniu wirtualnych sił przekrojowych

𝑀

𝑖

, (

𝑁

𝑖

,

𝑇

𝑖

)

oraz reakcji

𝑅

𝑖

i 𝑆

𝑖

,

3. Wyznaczenie przemieszczenia

∆

𝑖𝑃

na podstawie wzoru z zasady prac

wirtaulnych

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

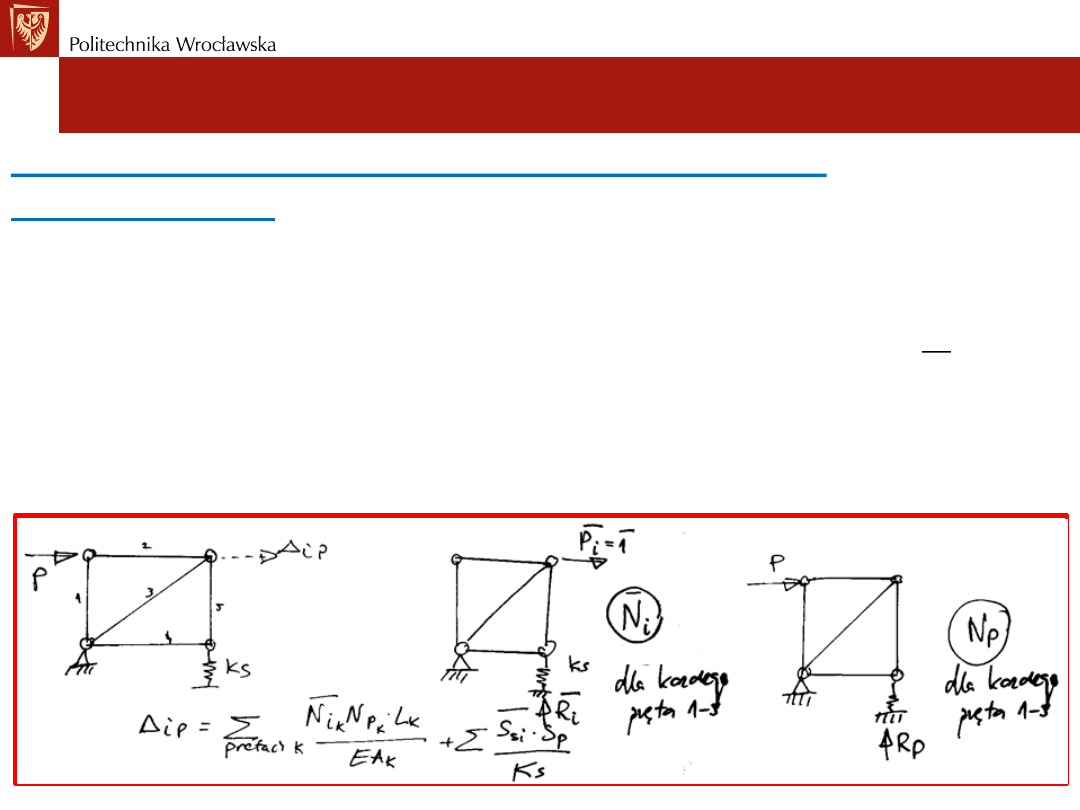
 W przypadku wyznaczania przemieszczenia w kratownicach wzór

ulega modyfikacji: występują tylko siły osiowe i są one stałe na

całej długości pręta. Stąd mamy :

- k określa numer każdego pręta,
- l

k

i (EA)

k

odpowiednio długość i sztywność osiową na

rozciąganie (ściskanie) każdego pręta k,
- 𝑁

𝑘𝑝

siły osiowe dla każdego pręta k i reakcje w więziach

sprężystych

𝑆

𝑠𝑝

od obciążenia danego,

-

𝑁

𝑘𝑖

siły osiowe dla każdego pręta k i reakcje w więziach

sprężystych

𝑆

𝑠𝑖

od jednostkowego obciążenia wirtualnego

𝑃

𝑖

=

1

𝑖

w miejscu i kierunku „i”.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

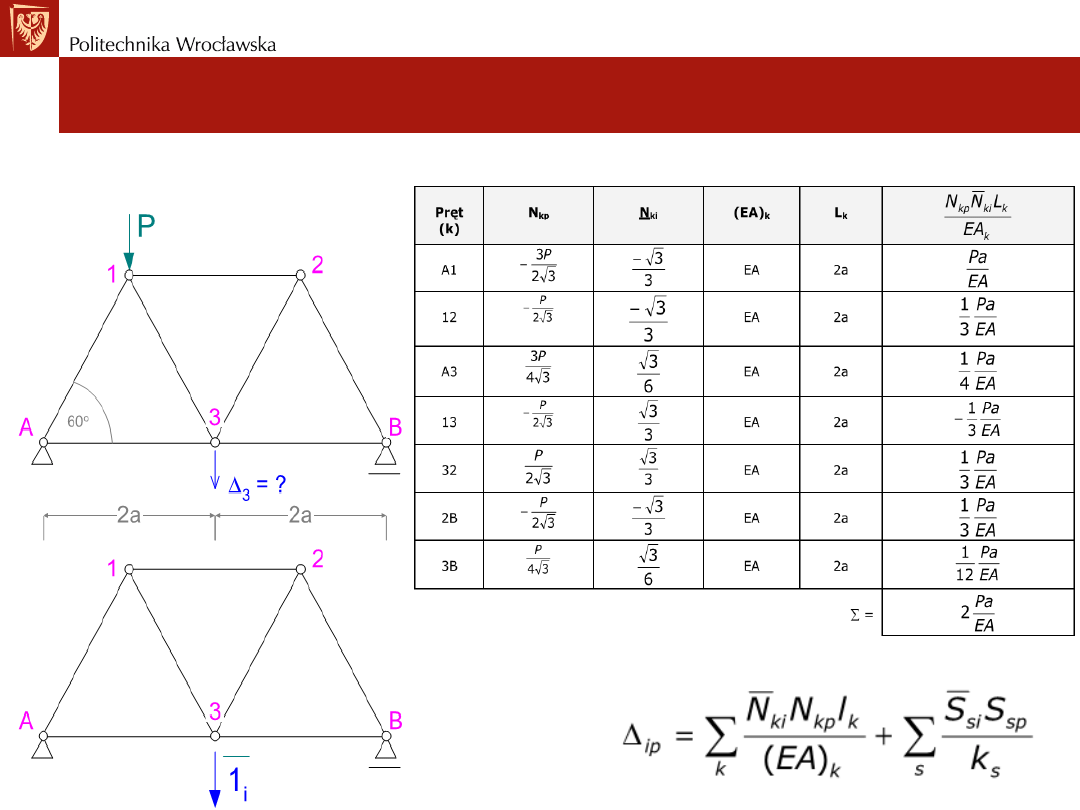
Wyznaczanie przemieszczeń

Algorytm wyznaczyć przemieszczenie

∆

𝒊𝒑

dla ustroju

kratownicowego:

1. Wyznaczenie sił przekrojowych

𝑁

𝑝

oraz reakcji 𝑅

𝑝

i

𝑆

𝑝

od obciążenia

danego,

2. Przyłożenie jednostkowego obciążenia wirtualnego

𝑃

𝑖

= 1

𝑖

w miejscu i

kierunku „i” oraz wyznaczeniu wirtualnych sił przekrojowych

𝑁

𝑖

oraz

reakcji

𝑅

𝑖

i 𝑆

𝑖

,

3. Wyznaczenie przemieszczenia

∆

𝑖𝑃

na podstawie wzoru z zasady prac

wirtualnych

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Wyznaczanie przemieszczeń

 Obliczenie przemieszczeń w środku kratownicy

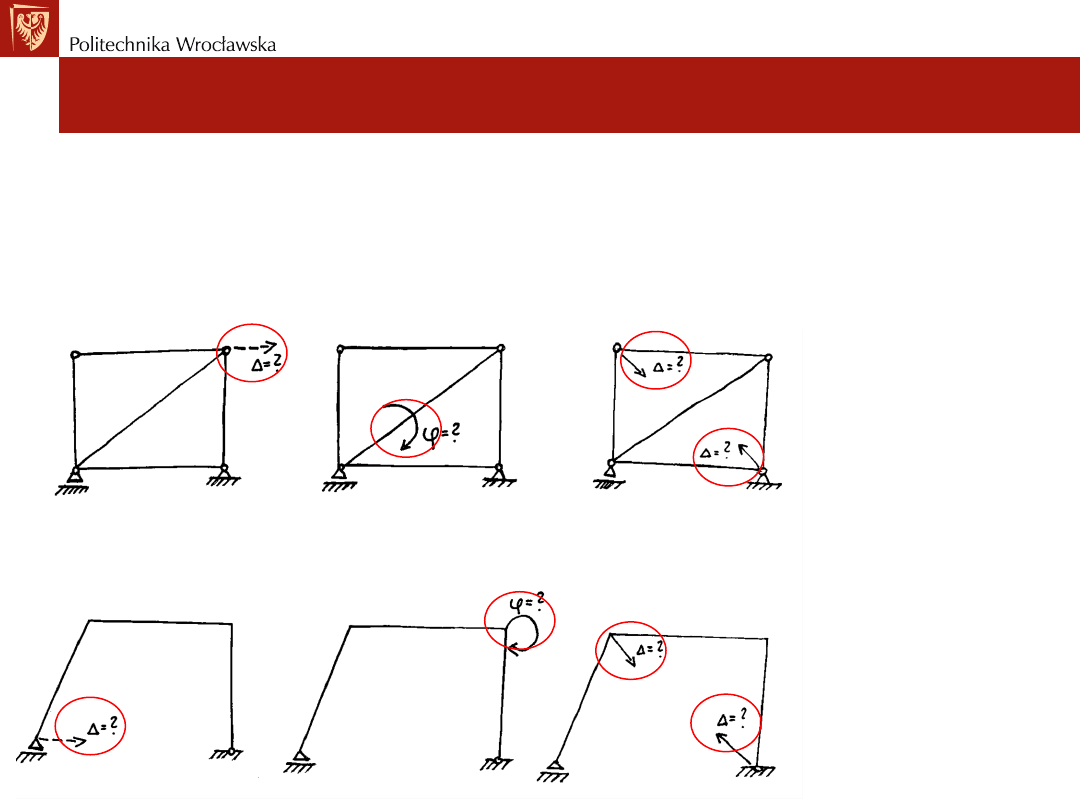
 Szukane przemieszczenia:

• przesunięcia poziome i pionowe,
• kąty obrotu prętów,
• zmiany odległości między węzłami, katą miedzy stycznymi.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Stany jednostkowe

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Stany jednostkowe

 Można rozpatrywać przemieszczenie w konkretnym miejscu i na

konkretnym kierunku, ale także jako sume przemieszczeń zgodnie ze
wzorem:

Jak wyznaczyć przemieszczenia?

Należy przyłożyć w miejscu i na kierunku poszukiwanego
przemieszczenia:

• jednostkową siłę

𝑷

𝒊

=

𝟏

𝒊

w przypadku szukanego przesunięcia, zmiany

odległości miedzy węzłami,

• jednostkowy moment zginający

𝑴

𝒊

=

𝟏

𝒊

w przypadku szukanego kąta

obrotu, zmiany kąta między stycznymi.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

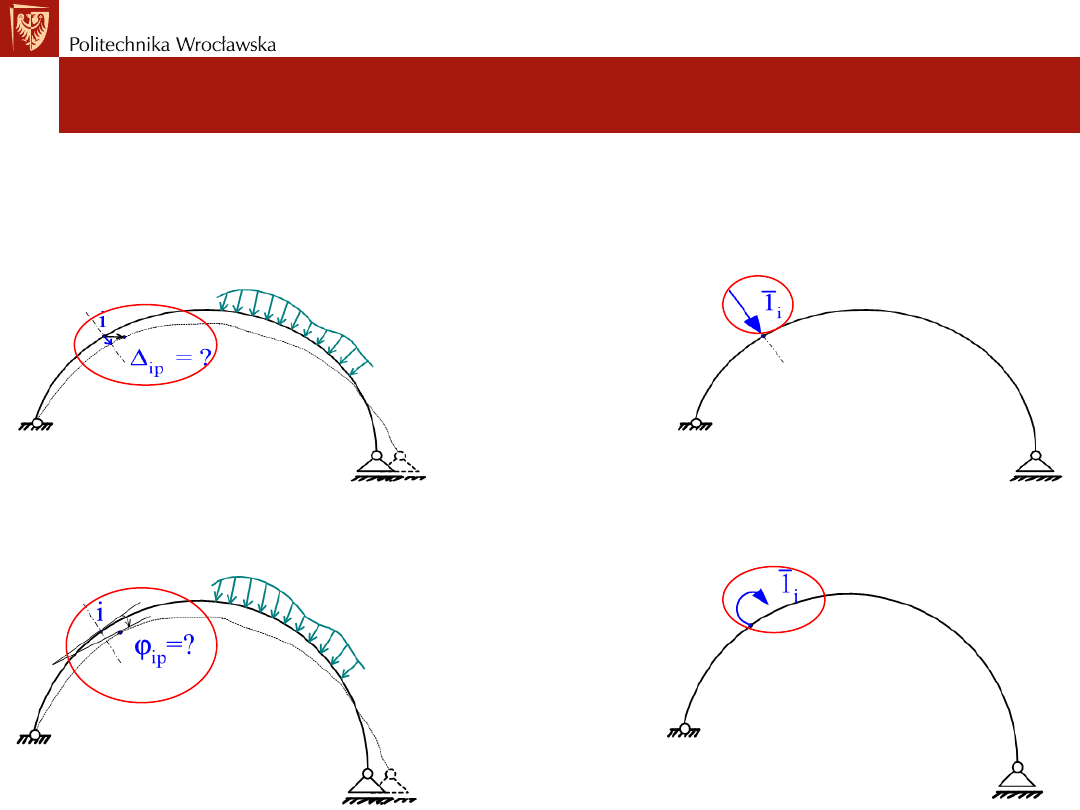
Stany jednostkowe

Stany jednostkowe dla konstrukcji ramowych jakie należy
przyjmować dla różnych szukanych typów przemieszczeń:
• przesunięcie punktu (węzła)

• kąt obrotu pręta

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

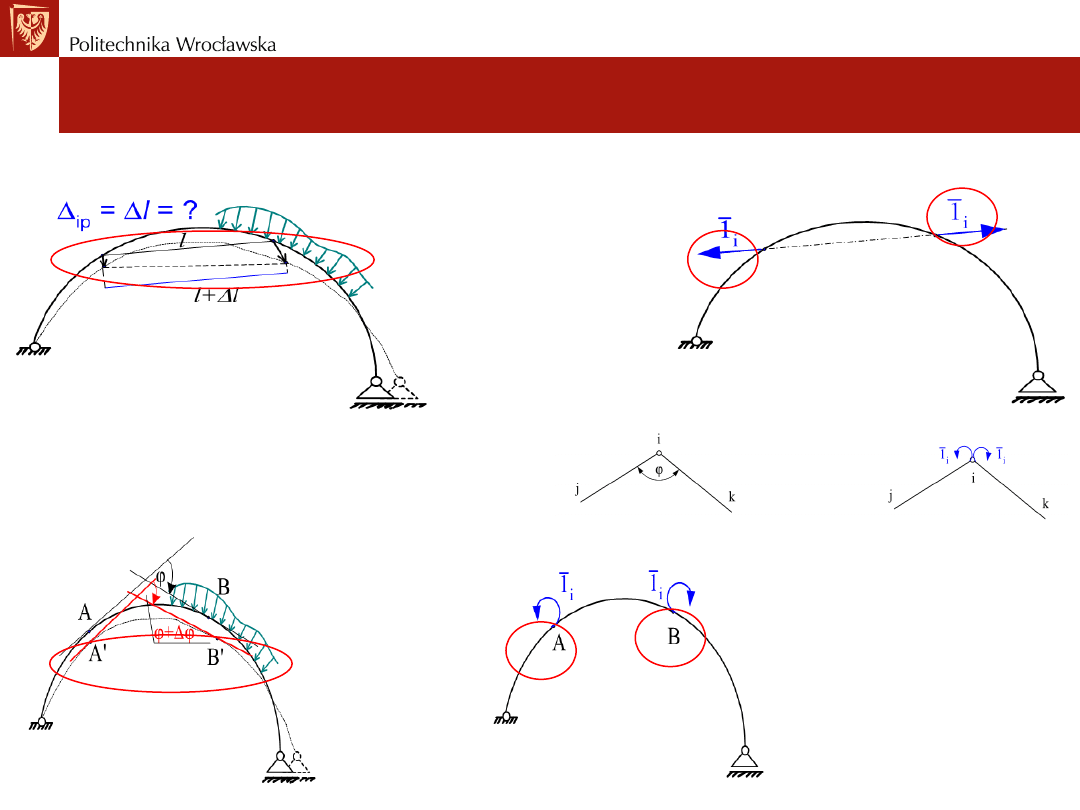
Stany jednostkowe

• zmiana odległości pomiedzy punktami

• zmiana kąta między stycznymi

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

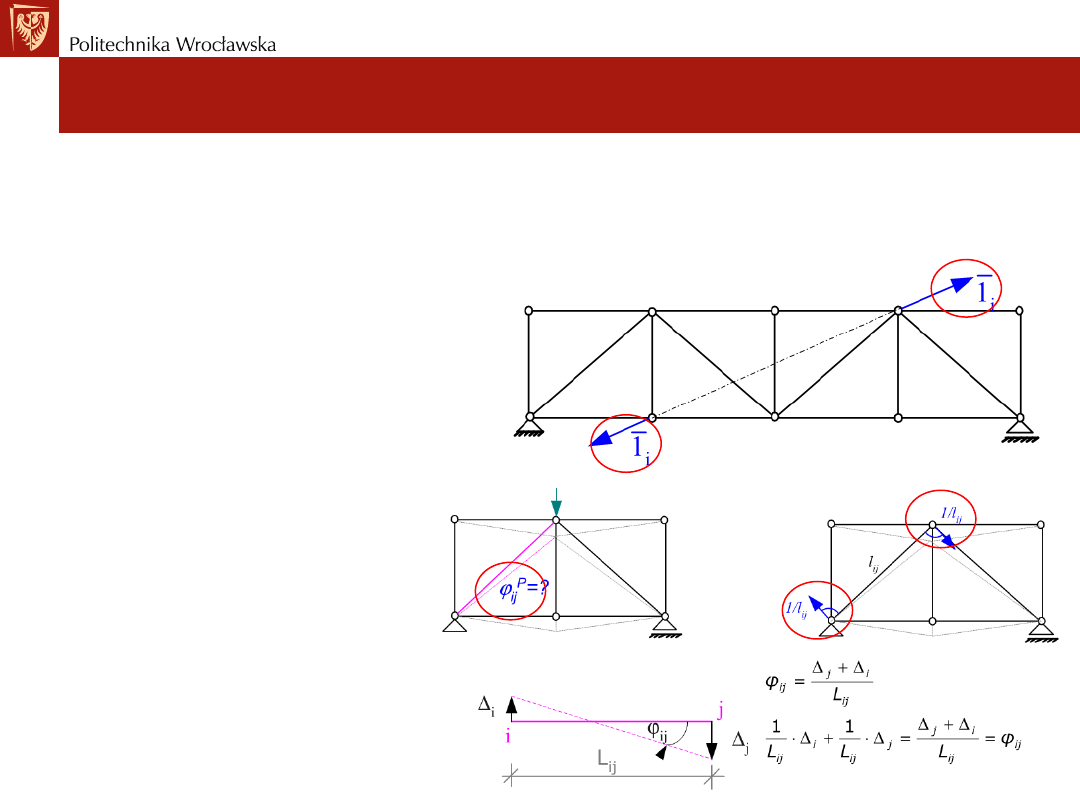
Stany jednostkowe

Stany jednostkowe dla konstrukcji kratownicowych jakie należy
przyjmować dla różnych szukanych typów przemieszczeń:

• Przesunięcie i zmiana odległości między prętami

• kąt obrotu pręta

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Metody obliczania całek

 Aby wyznaczyć szukane przemieszczenie należy wyznaczyć:

• wykresy sił przekrojowych od obciążeń mechanicznych

𝑀

𝑝

,

𝑁

𝑝

,

𝑇

𝑝

,

• wykresy sił przekrojowych od stanu jednostkowego

𝑀

𝑖

,

𝑁

𝑖

,

𝑇

𝑖

,

• oblczyć przemieszczenie jako odpowiednie całki iloczynu funkcji sił

wewnętrznych tj. wykresów sił wewnętrznych w postaci

 Poniżej podane są reguły, które pozwalają w łatwy sposób obliczać

całki występujące we wzorach określających przemieszczenie.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Metody obliczania całek

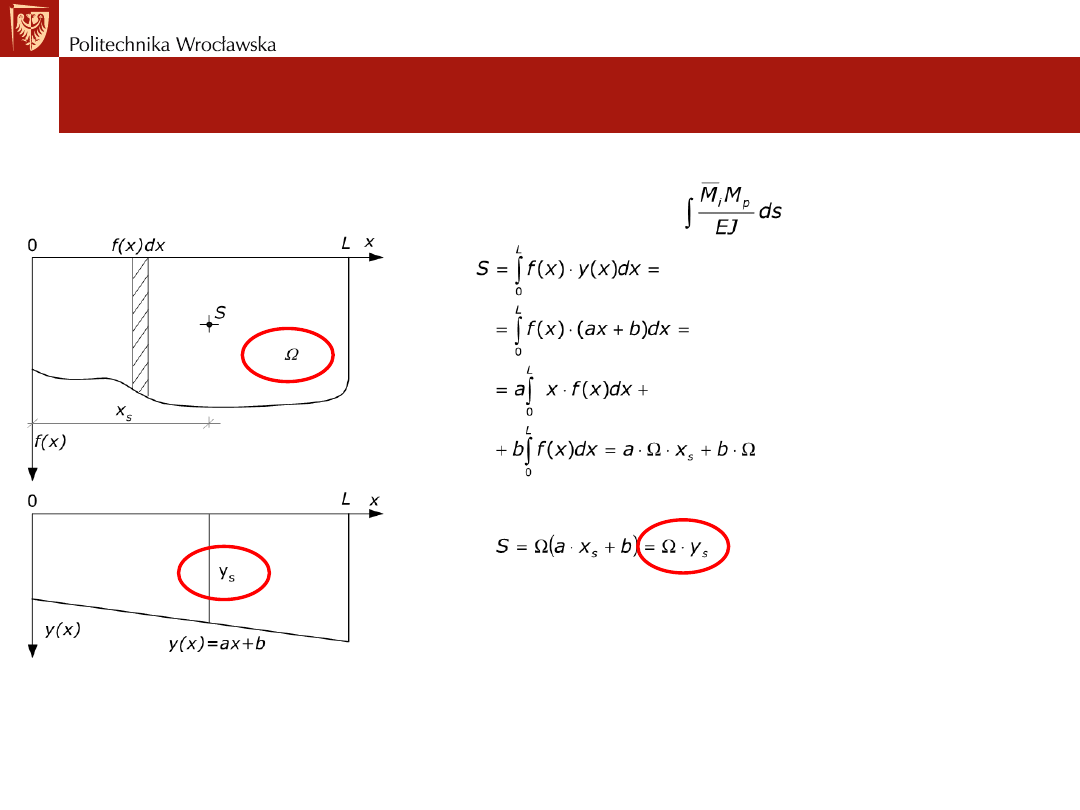
Wyznaczanie całki oznaczonej iloczynu dwóch funkcji f(x) i y(x)
jak np. iloczynu wykresów momentów w postaci

gdzie x

s

- położenie środka ciężkości pola wykresu f(x),

y

s

– rzędna funkcji y(x) w miejscu środka pola S,

Ω – pole pomiędzy osią x, a f(x).

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Metody obliczania całek

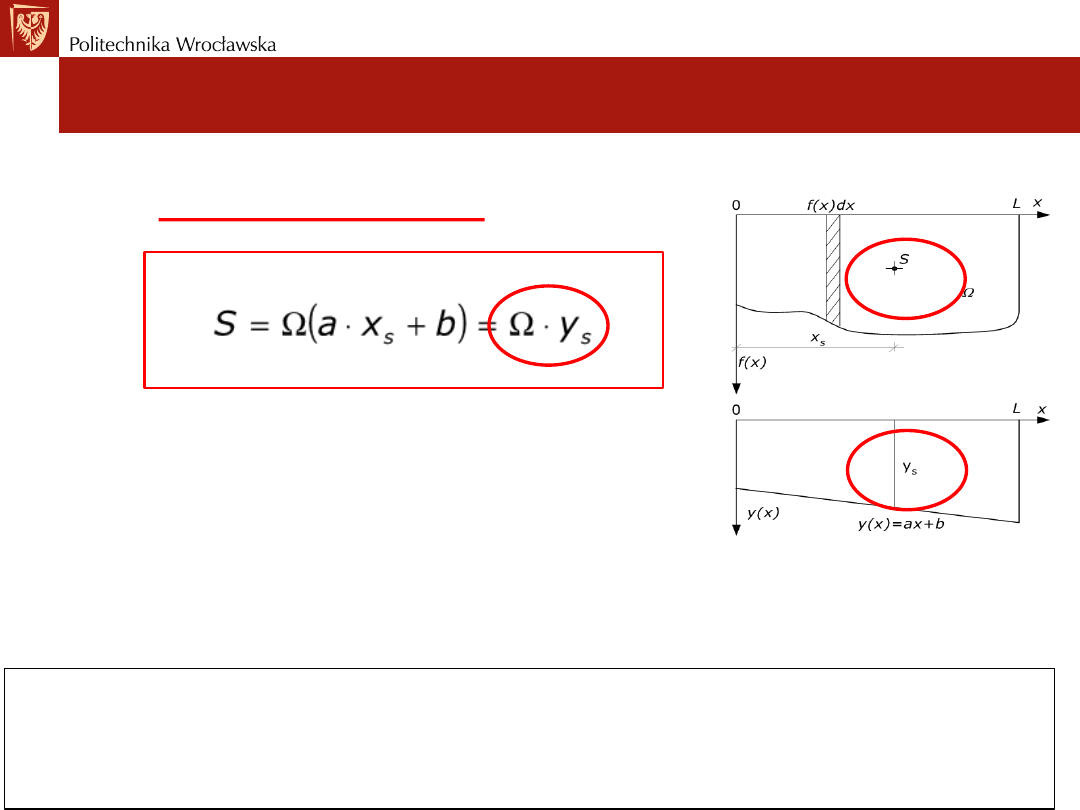
Wzór na obliczenie całki dwóch funkcji znany jest jako

wzór Wereszczagina.

Całkę obliczamy od 0 do L.
• Warunki dla stosowania wzoru Wereszczagina:
1) funkcja ciągła f(x) może być dowolna ale nieujemna,
2) funkcja y(x) musi być liniowa określona wzorem y(x)=ax+b.

Całka iloczynu funkcji dowolnej i funkcji liniowej równa się
iloczynowi pola Ω ograniczonego funkcją dowolną i rzędnej ys
funkcji liniowej pod środkiem ciężkości pola Ω.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Metody obliczania całek

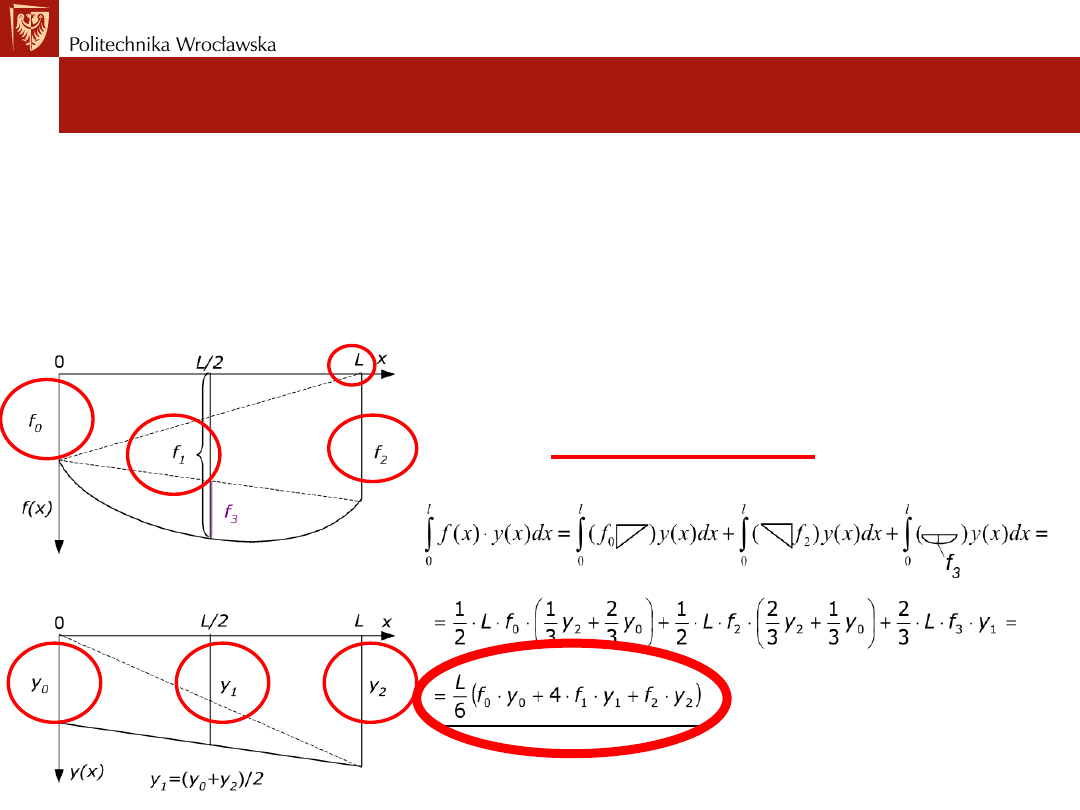
 Przypadek szczególny - funkcja f(x) jest parabolą.

Funkcje f(x) rozkłada się na sumę dwóch wykresów trójkątnych oraz
parabolę, której pole równa się 2/3 pola odpowiedniego f(x) prostokąta
przedstawimy to w sposób wykreślny i skorzystamy ze wzoru
Wereszczagina.

Wzór na obliczenie całki dwóch funkcji:

wzór Simpsona.

Wyznaczanie przemieszczeń. Układy statycznie wyznaczalne

Metody obliczania całek

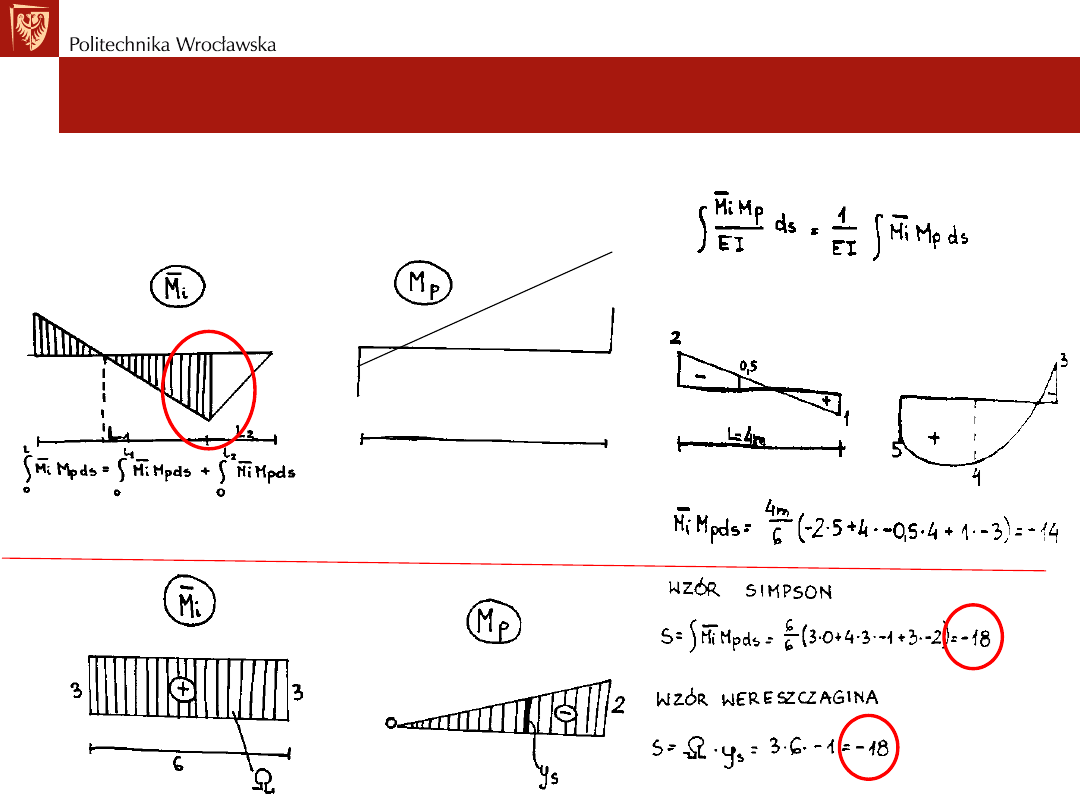
 Przykład nr1: dzielenie wykresów Przykład nr2.

Metoda Simpsona

w miejscu załamania lub skoku wykresu

 Przykład nr3

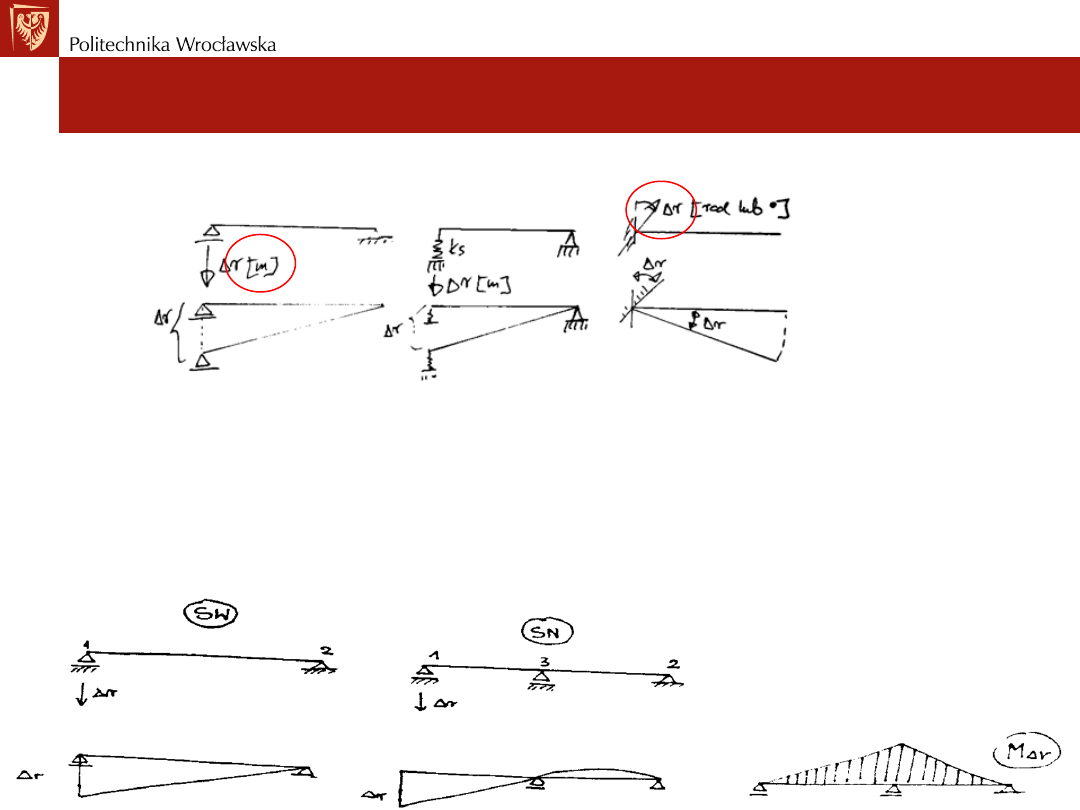
Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane wpływem podpór

 Zakładamy, że przynajmniej jedna podpora ulega przemieszczeniu.

Oznaczamy przez ∆r przemieszczenia podpór.

 Przemieszczenia podpór w układach:
• SW nie wywołuja sił przekrojowych i powodują przemieszczenie układu,
• SN wywołują siły przekrojowe

𝑀

∆

,

𝑁

∆

, 𝑉

∆

oraz siły w więziach

sprężystych

𝑆

∆

i powodują przemieszczenie układu.

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane wpływem podpór

 Przyjmijmy w miejscu i kierunku i szukanego przemieszczenia

jednostkowe obciążenie wirtualne

𝑃

𝑖

= 1

𝑖

, któremu odpowiadają

wirtualne reakcje

𝑅

𝑖

, siły w więziach sprężystych 𝑆

𝑠𝑖

oraz siły

przekrojowe

𝑀

𝑖

,

𝑁

𝑖

,

𝑇

𝑖

.

• Wykorzystując II zasadę pracy wirtualnej otrzymujemy zależność

dla szukanego przemieszczenia:

• Ponieważ dla układów SW przemieszczenie podpór nie wywołuje

sił przekrojowych i sił w więziach, a więc

𝑀

𝑖

=0,

𝑁

𝑖

=0,

𝑇

𝑖

=0 oraz

𝑆

𝑠𝑖

=0.

• Wzór na przemieszczenie od osiadania podpory jest w

postaci:

 Przykład:

• Dla kratownic obowiązuje wzór przyjmuje

• A dla układów SW obowiązuje wzór

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane wpływem podpór

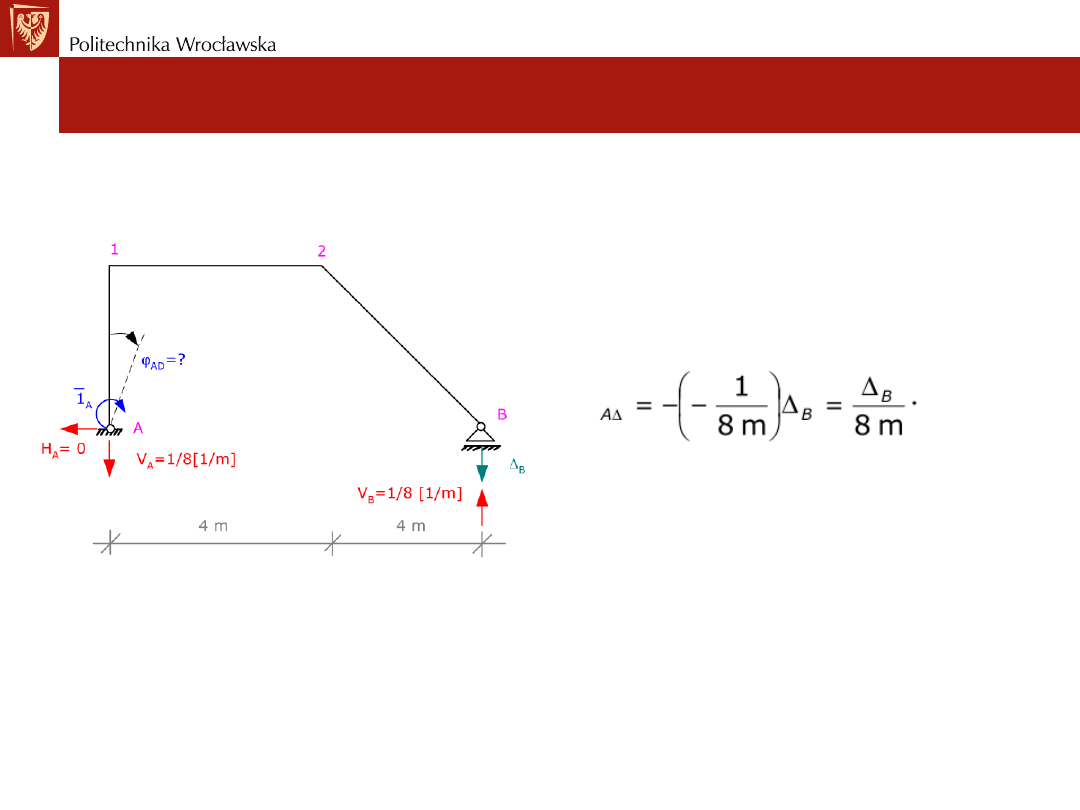
Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane wpływem podpór

• Przykład nr1:

Wyznaczyć kąt obrotu końca A preta A1 wywołany osiadaniem podpory B o ∆

B.

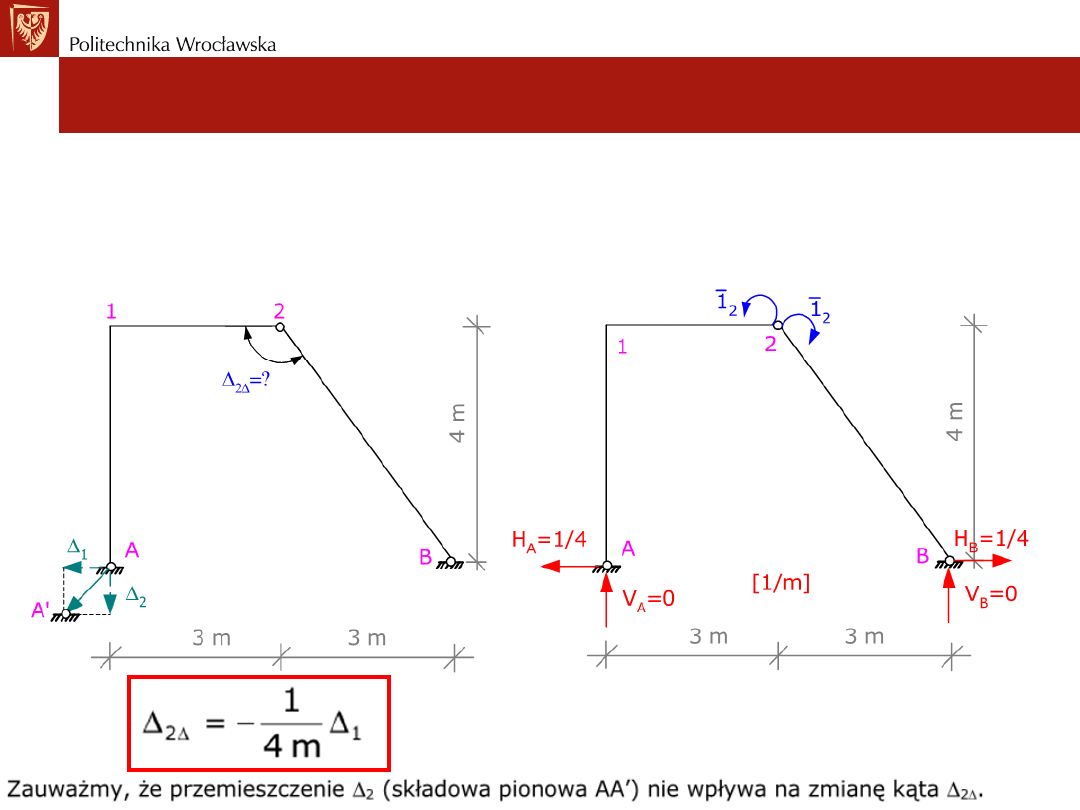
Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane wpływem podpór

• Przykład nr2:

Wyznaczyć zmianę kąta między końcem 2 pręta 12 i początkiem 2 pręta 2B
wywołane przemieszczeniem węzła A.

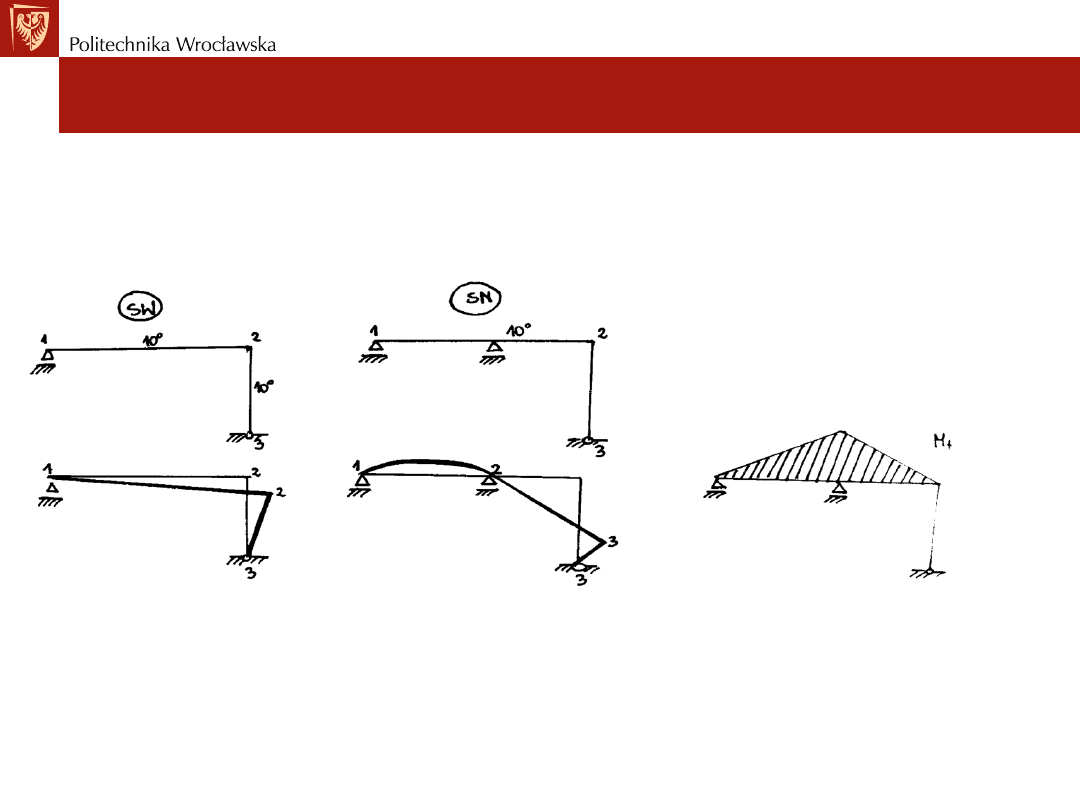
Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane temperaturą

• Zmiana temperatury powoduje odkształcenia podużne prętów

oraz w wyniku nierównomiernego rozkładu temperatury po
wysokości przekroju pręta odkształcenia kątowe.

Zmiana temperatury w układach:
• SW nie wywołuje sił przekrojowych -> powoduje

przemieszczenie układu,

• SN wywołuje siły przekrojowe

𝑴

𝒕

,

𝑵

𝒕

, 𝑽

𝒕

oraz siły w więziach

sprężystych

𝑺

𝒔𝒕

i powodują przemieszczenie układu.

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane temperaturą

• Zmiany temperatury mierzymy przeważnie względem

temperatury montażu konstrukcji.

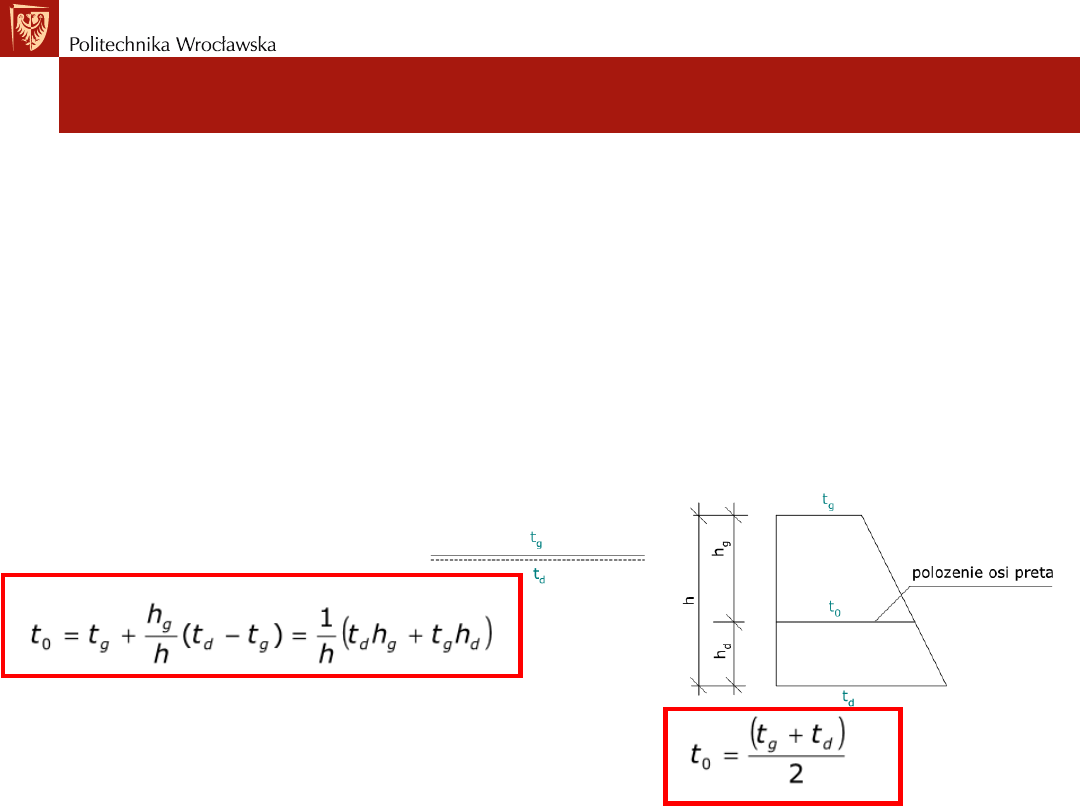
• Przy wyznaczaniu deformacji kątowej zakłada się, że rozkład

przyrostu temperatury po wysokości przekroju pręta jest liniowy. W
każdym pręcie układu zaznaczamy kreskami włókna dolne, jako
uprzywilejowane. Symbolami

𝒕

𝒈

,

𝒕

𝒅

, 𝒕

𝟎

oznaczono przyrost

temperatury w stosunku do temperatury montażu odpowiednio we
włóknach górnych, dolnych oraz w osi pręta.

• W przypadku pręta symetrycznego względem osi

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane temperaturą

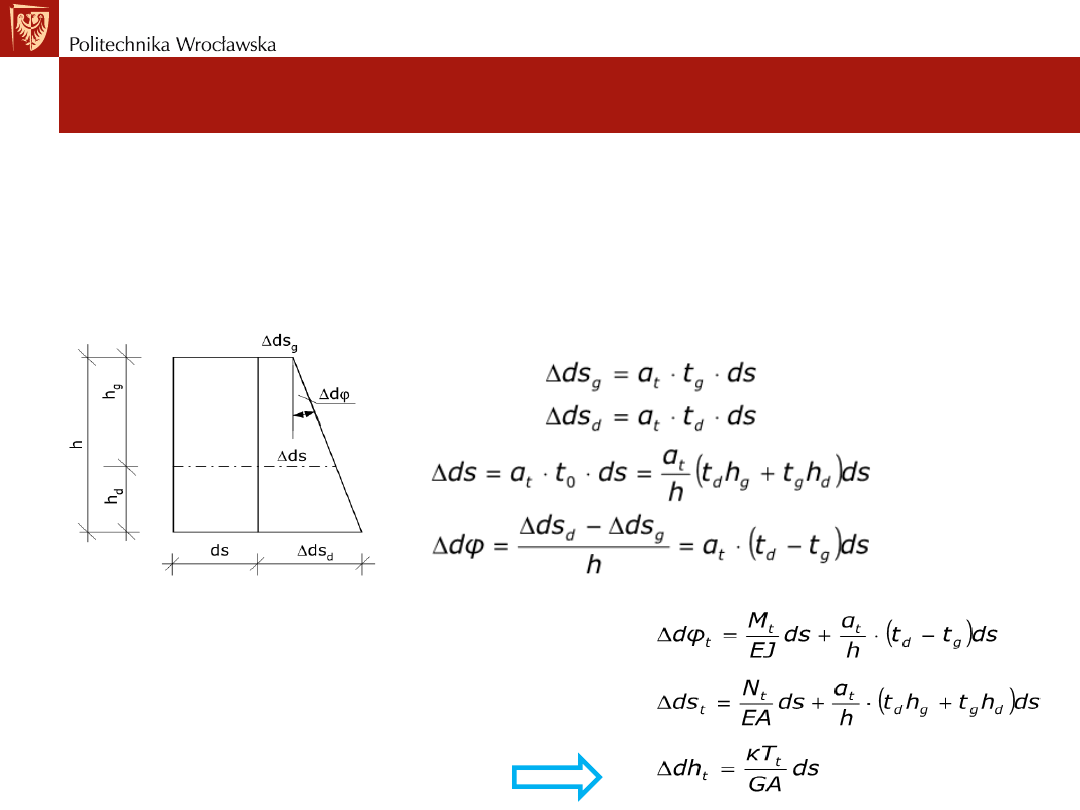
 Wyznaczamy odpowiednie odkształcenia wywołane zmianą

temperatury.

• Niech

𝜶

𝒊

oznacza współczynnik rozszerzalności termicznej.

Rozpatrzmy element pręta o długości ds.

• Zmiana temperatury powoduje

w układach SN dodatkowe siły
przekrojowe

𝑀

𝑡

,

𝑁

𝑡

, 𝑉

𝑡

oraz siły

w więziach sprężystych

𝑆

𝑡

.

Odkształcenia pręta wynoszą:

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane temperaturą

• Wzór na przemieszczenie w miejscu i kierunku “i” ma postać

• Dla układów SW wzór redukuje się do postaci

Całkę w tym przypadku całki traktujemy jako pola

𝑴

𝒊

i

𝑵

𝒊

.

• W przypadku kratownic otrzymujemy wzory:

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane temperaturą

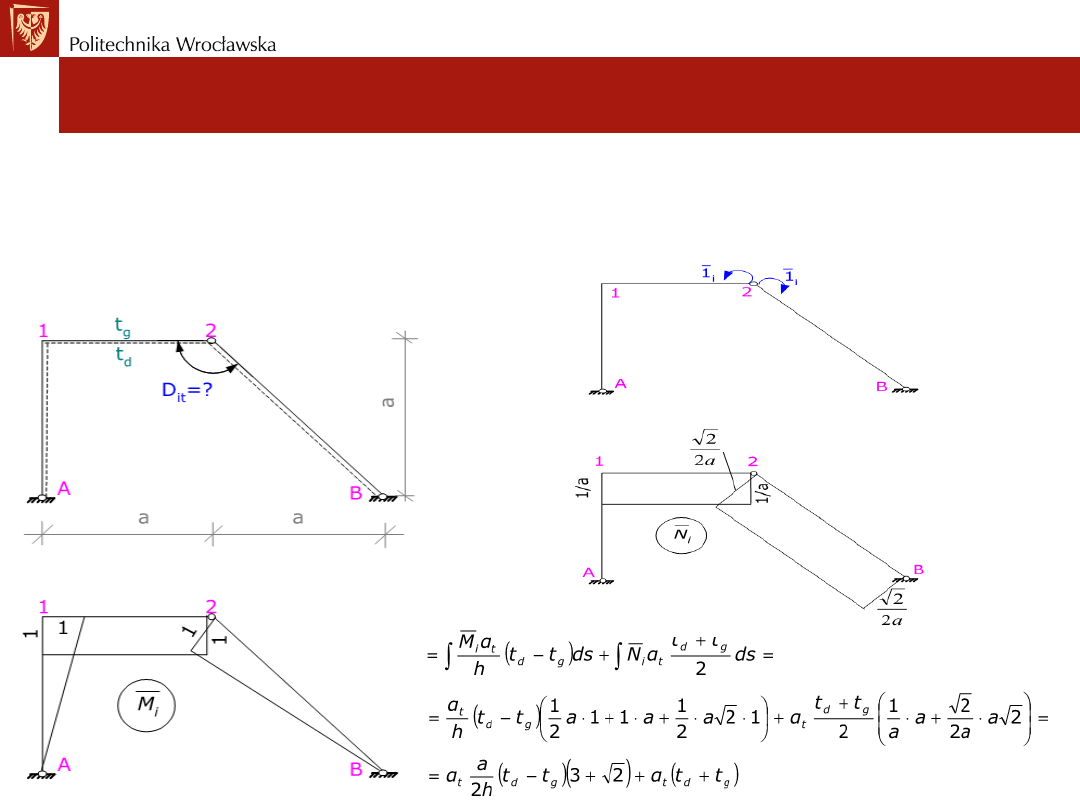
• Przykład nr2:

Wyznaczyć zmianę kąta między przekrojami 21 i 2B

wywołaną zmianą temperatury. Przekrój pręta jest symetryczny, a więc
hg=hd=h/2 dla wszystkich prętów. Zmiana temperatury jest jednakowa dla
wszystkich prętów (tg-td =const).

Wyznaczanie przemieszczeń w układach SW

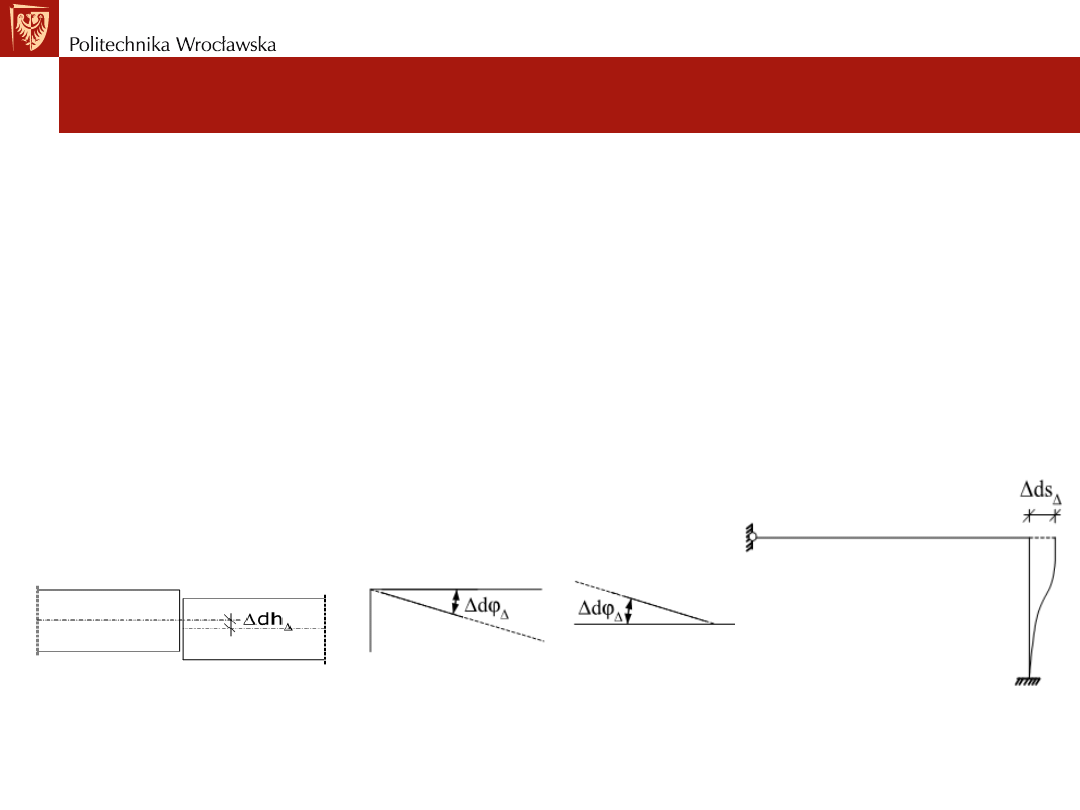
Przemieszczenia wywołane imperfekcjami

 Rozpatrujemy imperfekcje geometryczne (niedokładności, błędy

montażu) rzeczywistych konstrukcji.

 Rodzaje imperfekcji:

• typu ciągłego np. wygięcie całego pręta,
• typu dyskretnego np. występujące w ustalonych punktach.

Przykładowe i rozpatrywane błędy montażu:
 łączenie elementów pod niewłaściwym kątem,
 łączenie elementów niewspółosiowo,
 montaż elementów zbyt długich lub krótkich.

 Imperfekcje geometryczne mogą powodować odkształcenia podużne

i poprzeczne prętów oraz odkształcenia kątowe.

 Imperfekcja (błąd montażu) w układach:
• SW nie wywołuje sił przekrojowych -> powoduje przemieszczenie układu,
• SN wywołuje siły przekrojowe

𝑀

∆

,

𝑁

∆

, 𝑉

∆

oraz siły w więziach

sprężystych

𝑆

s∆

i powodują przemieszczenie układu.

 Imperfekcje w układach hiperstatycznych wywołują siły

przekrojowe

𝑀

∆

,

𝑇

∆

,

𝑁

∆

oraz siły

𝑆

∆

w więziach sprężystych. Wzór

na przemieszczenia ma postać:

 W układach SW gdy

𝑀

∆

= 0, 𝑇

∆

= 0, 𝑁

∆

= 0 oraz 𝑆

𝑠∆

= 0 wzór na

przemieszczenia ma postać:

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane imperfekcjami

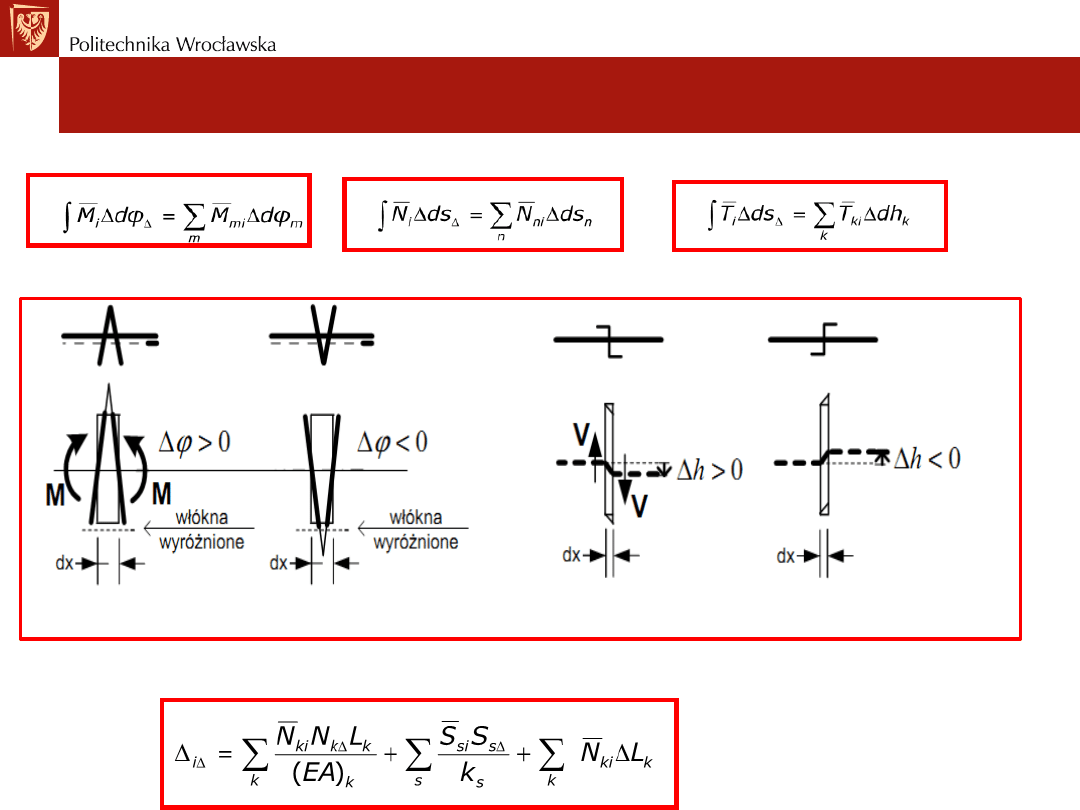
Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane imperfekcjami

• W układach SW odpowiednie całki przechodzą w sumy:

• Znakowanie błędów montażu

 W przypadku kratownic wzór na przemieszczenia ma postać:

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane imperfekcjami

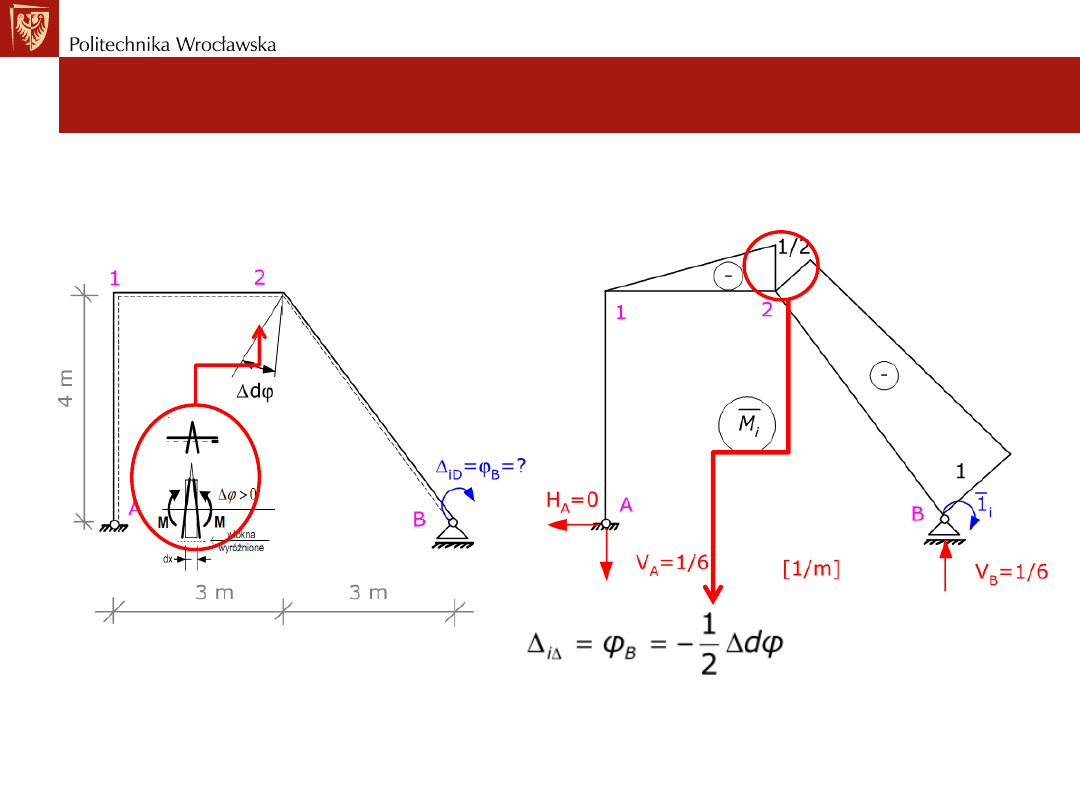
• Przykład nr1:

Wyznaczyć obrót przekroju B pręta B2 wywołany imperfekcją kątową w węźle 2.

Znak minus

ponieważ imperfekcja powoduje rozciąganie włókien dolnych

(błąd ze znakiem +), a momenty zginające powodują rozciąganie włókien
górnych (momenty zginające ze znakiem -).

Wyznaczanie przemieszczeń w układach SW

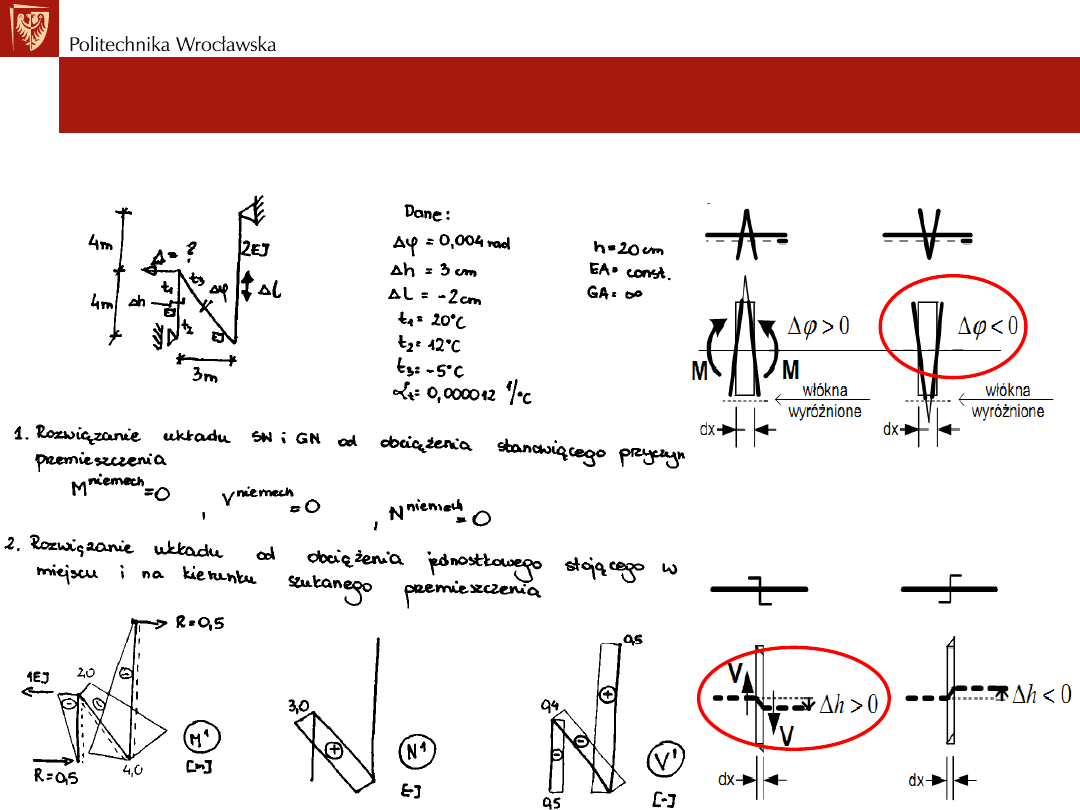
Przemieszczenia wywołane imperfekcjami

Przykład. Wyznaczyć przemieszczenie wywołane obciążeniem niemechanicznym

Wyznaczanie przemieszczeń w układach SW

Przemieszczenia wywołane imperfekcjami

 Przykład:

Wyznaczanie przemieszczeń w układach SW

Podsumowanie

Wyznaczanie przemieszczeń w układach SW

Podsumowanie

Wyznaczanie przemieszczeń w układach SW

Podsumowanie