CYFROWE PRZETWARZANIE SYGNAŁÓW
1
Ćwiczenie 1
Zadanie 1. (DSP02.PAAS)
Na
przykładzie spróbkowanego sygnału
( )
x t
e
t
t
( )
cos
=
β
ω
przeanalizować
jednoznaczność próbkowania. Uzasadnienia zilustrować wydrukami.
Zadanie 2. (DSP04.PAS DSP09.PAS)
Dysponując strukturą układu dyskretnego wyznaczyć transmitancję, równanie różnicowe,
reakcję impulsową, charakterystykę amplitudową i fazową dla podanego układu. Wykazać związek
pomiędzy badanymi charakterystykami.
Zadanie 3. (DSP17.PAW)
Zbadać wpływ okna na charakterystykę filtru nierekursywnego. Uzasadnienie zilustrować
wydrukami. Narysować strukturę układu na podstawie reakcji impulsowej.
Zadanie 4. (DSP21.PAS)
Wyznaczyć transmitancję filtru z rodziny Butterworth’a i Chebyshev’a dla zadanych
aproksymacji:
charakterystyka dolnoprzepustowa
charakterystyka górnoprzepustowa
charakterystyka środkowoprzepustowa
Narysować możliwe struktury filtru. Dołączyć wydruki charakterystyk amplitudowych.
Zadanie 1.
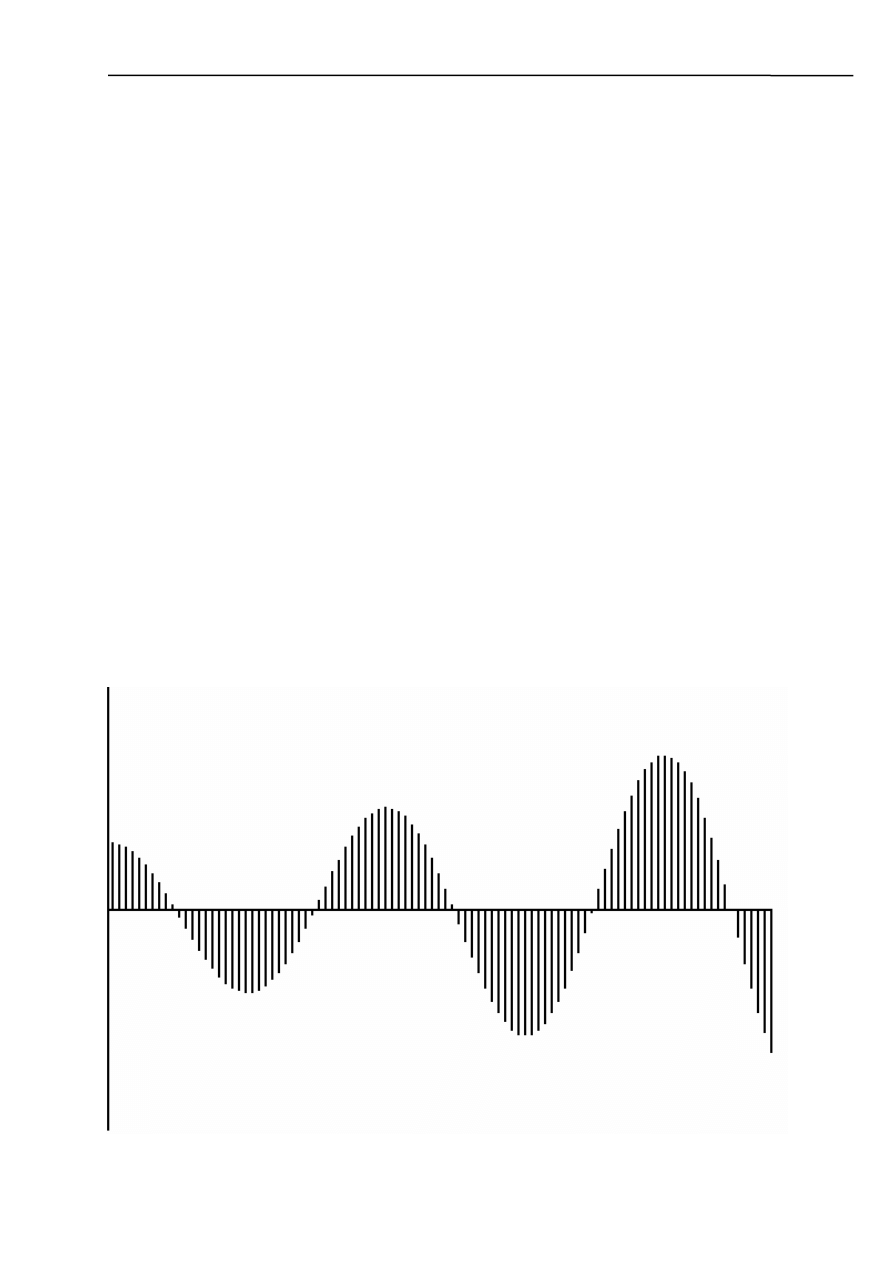
Program generuje sygnał spróbkowany zadany wzorem:
(
)
( )
x t
N
t
( )
exp
cos
=
⋅
⋅
β
ω
0
,
gdzie: N – ilość próbek.
a)
β=0,01; ω=19
Widać, że dla tak dobranych wartości poprawne odtworzenie sygnału nie sprawia żadnych problemów
(obrys sygnału spróbkowanego wiernie odtworzy nam funkcję wejściową).
CYFROWE PRZETWARZANIE SYGNAŁÓW
2
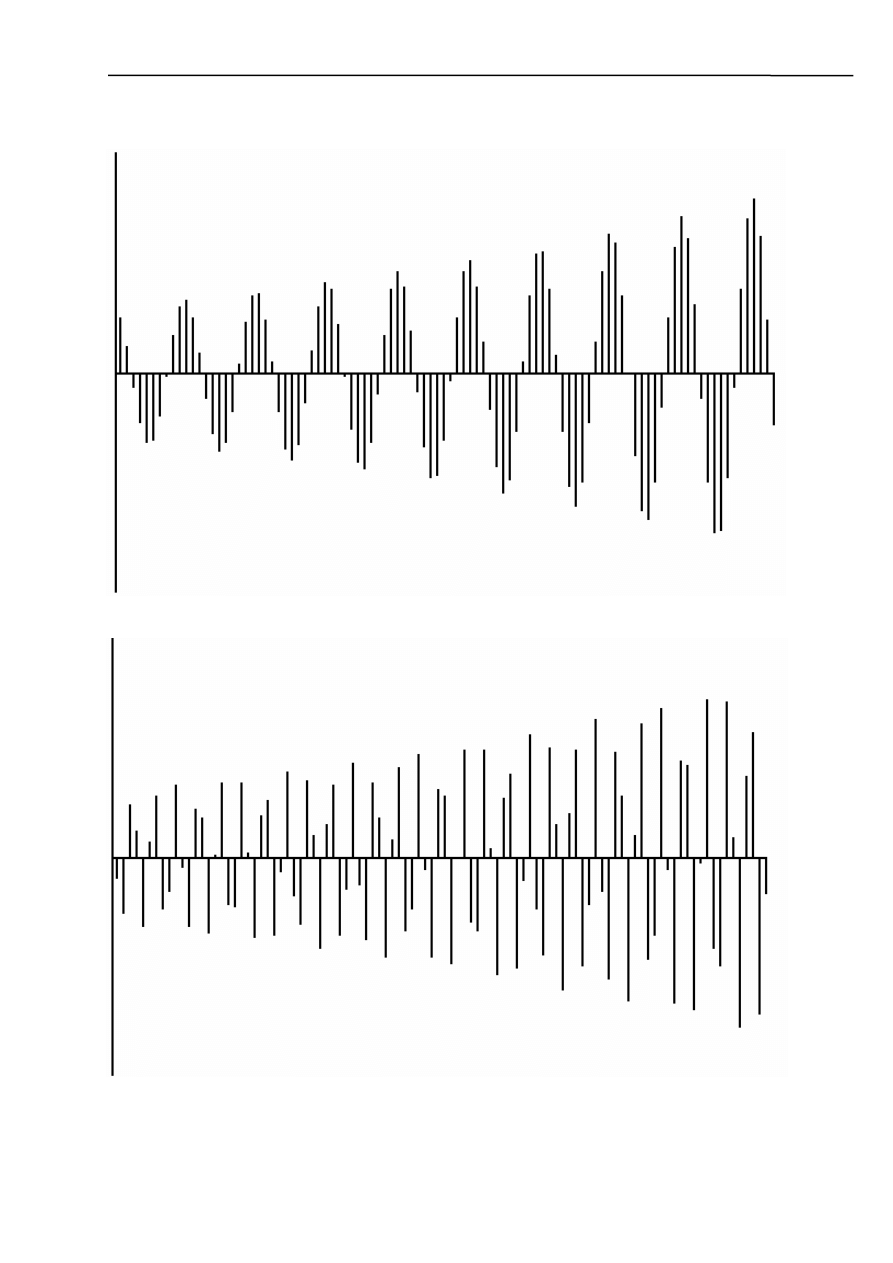
b)
β=0,01; ω=32
Dla takich wartości odtworzenie sygnału jest możliwe lecz nie jest już tak dokładne jak w podpunkcie
a.
c)
β=0,01; ω=27
Dla takiej wartości pulsacji odtworzenie przebiegu jest niemożliwe

CYFROWE PRZETWARZANIE SYGNAŁÓW
3
Przez próbkowanie rozumiemy pobieranie, w określonych odstępach czasu, rzędnych (próbek
wartości) funkcji w taki sposób, aby ciąg próbek umożliwiał jak najwierniejsze odtworzenie (czyli
interpolację) całego przebiegu funkcji.
Innymi słowy, ma miejsce dyskretyzacja argumentu funkcji:
t
nT n
n
N
=
∈
,
, a ciąg próbek
{x(nT)}
stanowi dyskretną reprezentację sygnału, w której zawiera się prawie cała informacja
przenoszona przez sygnał x(t). W analizie klasycznej zakłada się próbkowanie okresowe z odstępem
T
; stałą
f
T
p
=
1
nazywamy częstością próbkowania. Model sygnału jest ściśle deterministyczny.
Układ próbkowania idealnego ma dwa wejścia: sygnałowe i impulsowe (bramkowania punktowego).
Wybieranie wartości funkcji realizuje ciąg impulsów delta, który interpretujemy jako nośną
grzebieniową
. Modulacja iloczynowa impulsu o numerze n wartością sygnału x(nT)
wytwarza próbkę, której przypisujemy reprezentację dystrybucyjną:
( )
δ
T
t
( )
( ) (
)
x
nT
x nT
t
nT
p
=
−
δ
Wartość próbki x(nT) określa nie amplitudę, lecz intensywność (wagę ze znakiem) odnośnego
impulsu idealnego na wyjściu. Wobec tego sygnał spróbkowany zapisujemy jako:
x t
x nT
t
nT
x t
t
p
T
n
( )
( )(
)
( ) ( )
=
−
=
∑
= −∞
∞
δ
δ
czyli jako sygnał z modulacją bipolarną intensywności impulsów idealnych delta.
W celu odtworzenia oryginału z ciągu próbek należy wydzielić - w drodze idealnej filtracji
dolnopasmowej - część główną widma X
p
(
ω) położoną w otoczeniu początku układu. Jest to możliwe
tylko wówczas, gdy poszczególne segmenty widma nie zachodzą na siebie, czyli gdy:
( )
ω
π
ω
p
g
T
=
≥
2
2
Relacja ta jest podstawą twierdzenia o próbkowaniu Kotielnikowa-Shannona o następującej treści:
Przebieg ściśle dolnopasmowy o częstotliwości granicznej f
g
jest całkowicie określony przez swoje
próbki pobierane w odstępach nie większych niż
1
2
f
g
sekund.
Zadanie 2.
W zadaniu drugim skorzystaliśmy z programu prezentującego odpowiedź procesora LTI na
pobudzenie deltą Kroneckera. Po uruchomieniu programu należy podać trzy nierekursywne
współczynniki (przyjęliśmy następujące wartości tych współczynników: 1.3,-0.85,0 i 1,0,0),
które są podstawiane do wzoru:
[ ]
[
]
[
]
[
]
[ ]
[
]
[
]
y n
a y n
a y n
a y n
b x n
b x n
b x n
=
−
+
−
+
−
+
+
−
+
−
1
2
3
0
1
2
1
2
3
1
2
Wart
ości, które przyjęliśmy są wykorzystane przez drugi program, który umożliwia obliczenie modułu oraz
fazy transmitancji dla zadanego równania różnicowego.
Po uzyskaniu części rzeczywistej oraz urojonej transmitancji program oblicza moduł i fazę oraz
przedstawia wynik w postaci wykresu.
– równanie różnicowe
[ ]
[
]
[
]
[ ]
y n
y n
y n
x n
=
−
−
−
+
13
1
0 85
2
.
.
– transmitancja układu
( )
H z
z
z
=
−
+
−
−
1
1
1 3
0 85
1
2
.
.
CYFROWE PRZETWARZANIE SYGNAŁÓW
4
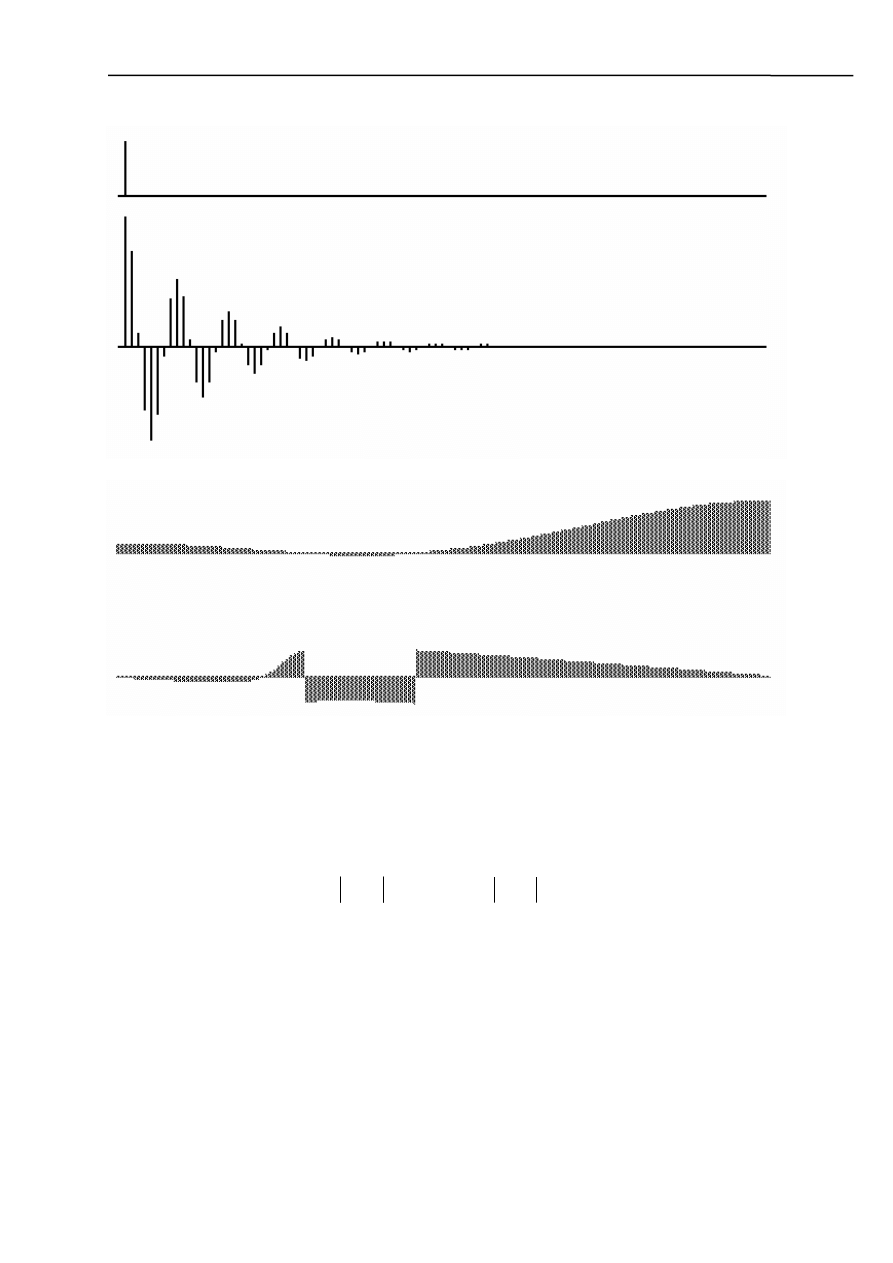
– reakcja impulsowa
– charakterystyki : modułu i fazy
Odpowiedź impulsowa jest funkcją czasu wyrażającą odpowiedź obwodu na sygnał wejściowy
o postaci impulsu jednostkowego, doprowadzonego w chwili t=0, tj. gdy x(t)=
δ(t). Funkcję
przenoszenia otrzymamy z zależności: H(
ω) = F{h(t)}
Krótko mówiąc, odpowiedź impulsowa obwodu i jego funkcja przenoszenia są parą transformat
Fouriera. Ogólnie funkcja przenoszenia H(
ω) jest zespoloną funkcją częstotliwości i jest zwykle
wyrażana w postaci:
( )
( )
( )
H
H
e
j
ω
ω
ω
=
Θ
, gdzie
( )
H
ω
– jest nazywane charakterystyką
amplitudową obwodu, a
– charakterystyką fazową. Charakterystyka amplitudowa jest parzystą
funkcją częstotliwości a charakterystyka fazowa - nieparzystą funkcją częstotliwości.
( )
Θ ω
CYFROWE PRZETWARZANIE SYGNAŁÓW
5
Zadanie 3.
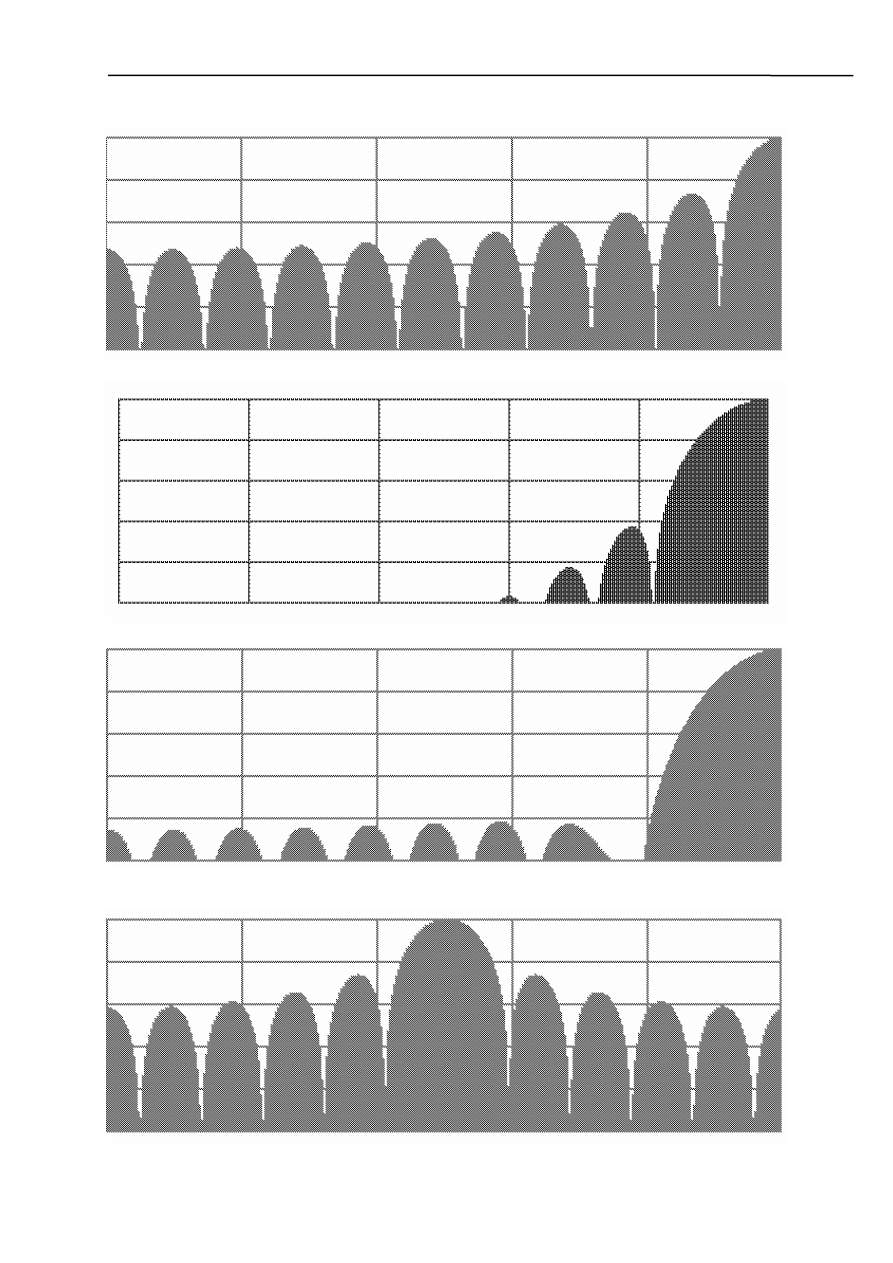
Program przedstawia nierekursywny filtr dolno-, górno- i środkowoprzepustowy umieszczony
w wybranym oknie (prostokątnym, van Hann’a oraz Hamminga).
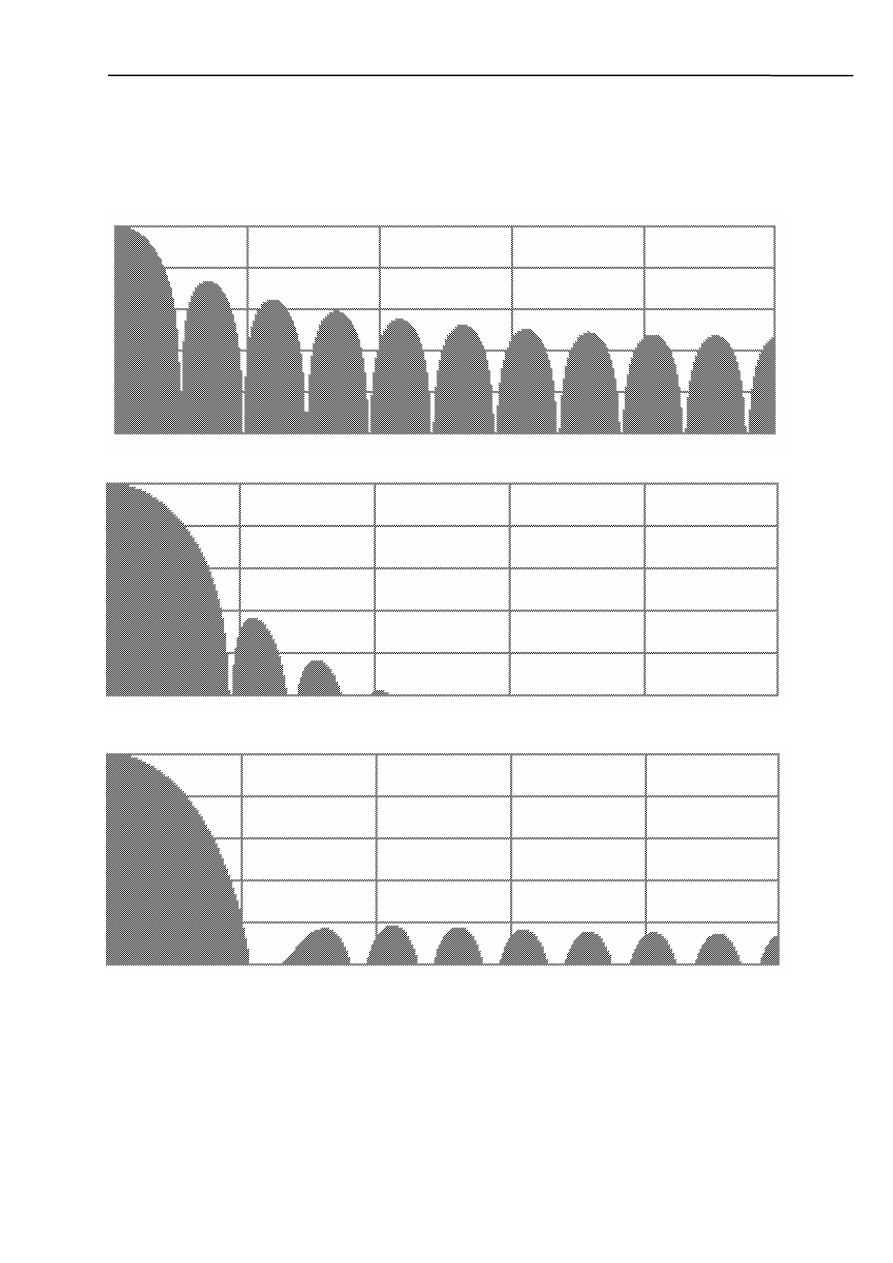
a) filtr dolnoprzepustowy
- okno prostokątne
- okno von Hann’a
- okno Hamminga
CYFROWE PRZETWARZANIE SYGNAŁÓW
6
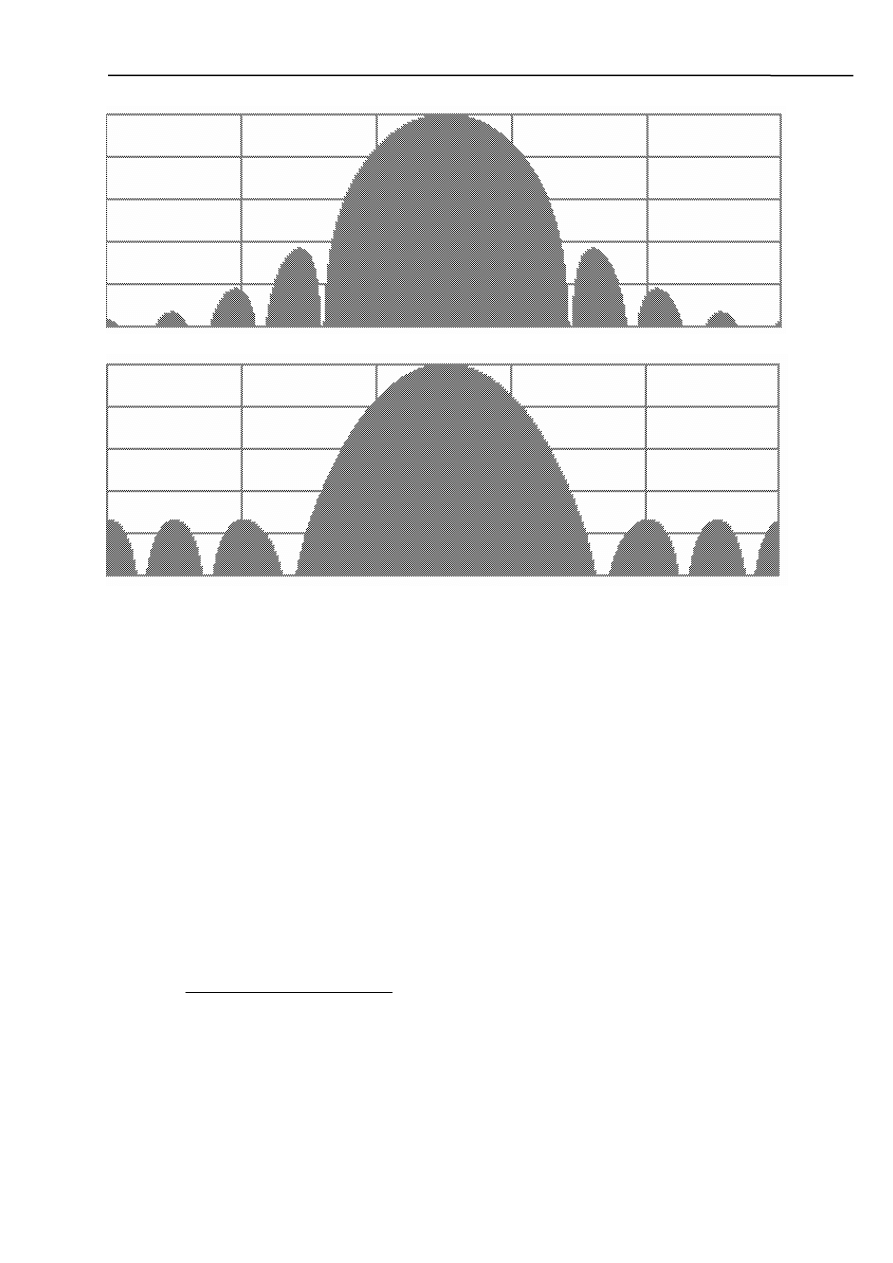
b) filtr górnoprzepustowy
- okno prostokątne
- okno von Hann’a
- okno Hamminga
c) filtr środkowoprzepustowy
- okno prostokątne
CYFROWE PRZETWARZANIE SYGNAŁÓW
7
- okno von Hann’a
- okno Hamminga
Stosowanie okien ma na celu wyeliminowanie efektu Gibbsa oraz zwiększenia tłumienia w
paśmie zaporowym.
Jak można się przekonać na podstawie powyższych charakterystyk nie wszystkie okna w jednakowy
sposób tłumią sygnał. Najgorszym oknem jest okno prostokątne, które słabo tłumi sygnał. Okno von
Hann’a zapewnia nam bardzo duże tłumienie lecz pierwsza harmoniczna nie jest dostatecznie
tłumiona. Okno Hamminga charakteryzuje się zaś tłumieniem wszystkich harmonicznych na
jednakowym poziomie lecz nie tłumi ich do końca tak jak jest to przy zastosowaniu okna van Hann’a.
Zadanie 4.
Celem tego zadania było wyznaczenie transmitancji filtru dla charakterystyk Butterworth’a i
Chebyshev’a. Do wykonania tego zadania przewidziany był program napisany w Pascalu. My
skorzystaliśmy z Matlaba, dlatego że oprócz przyjemniejszego shella niż ten z programu DSP21.PAS,
można było wyrysować charakterystyki amplitudowe. Wszystkie transmitancje są postaci:
H z
b
b z
b z
a z
a z
n
n
m
m
( )
...
...
=
+
+ +
+
+ +
−
−
−
−
0
1
1
1
1
1
Współczynniki podane są w kolejności rosnącej (a
1
, a
2
, ...,a
m
; b
0
, b
1
, ...,b
n
):
CYFROWE PRZETWARZANIE SYGNAŁÓW
8
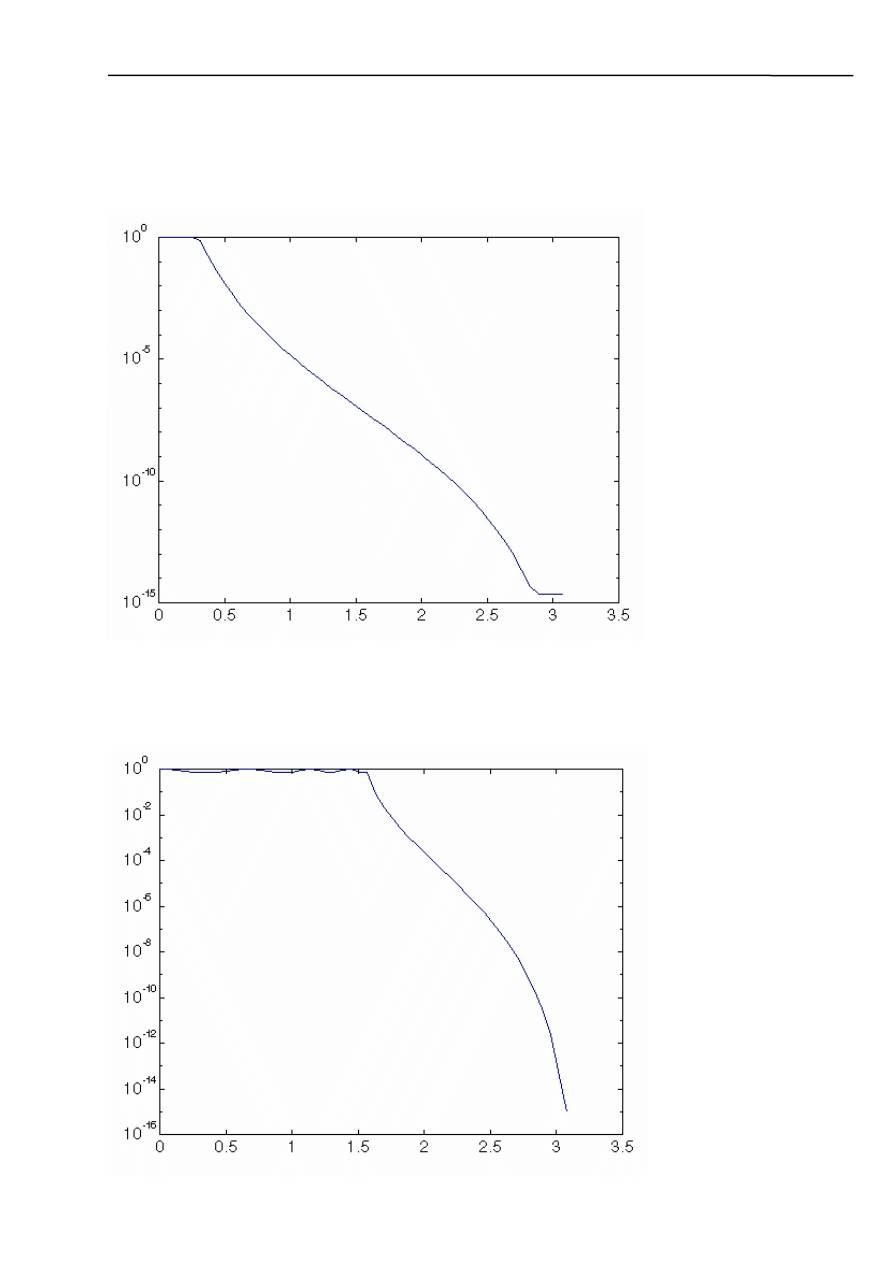
a) filtr dolnoprzepustowy
- charakterystyka Butterworth’a
A =
1.0000 -7.1914 23.1362 -43.6819 53.3153 -43.6086 23.8956 -8.4560 1.7531 -0.1622
B = 1.0e-005 *
0.0025 0.0227 0.0909 0.2122 0.3183 0.3183 0.2122 0.0909 0.0227 0.0025
- charakterystyka Chebyshev’a
A =
1.0000 -3.1658 6.8714 -10.4858 12.3930 -11.4549 8.2837 -4.5605 1.7674 -0.4120
B=
0.0005 0.0042 0.0166 0.0388 0.0582 0.0582 0.0388 0.0166 0.0042 0.0005
CYFROWE PRZETWARZANIE SYGNAŁÓW
9
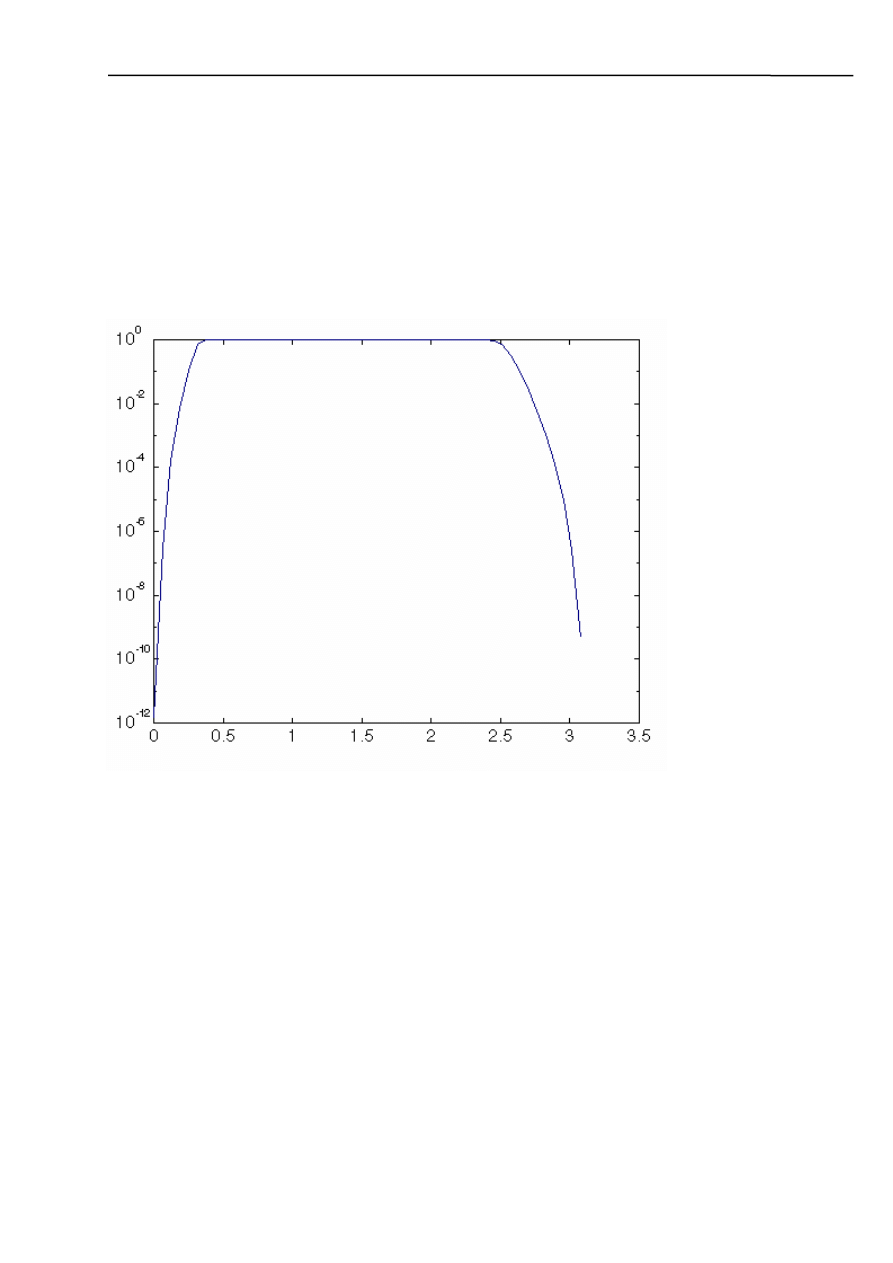
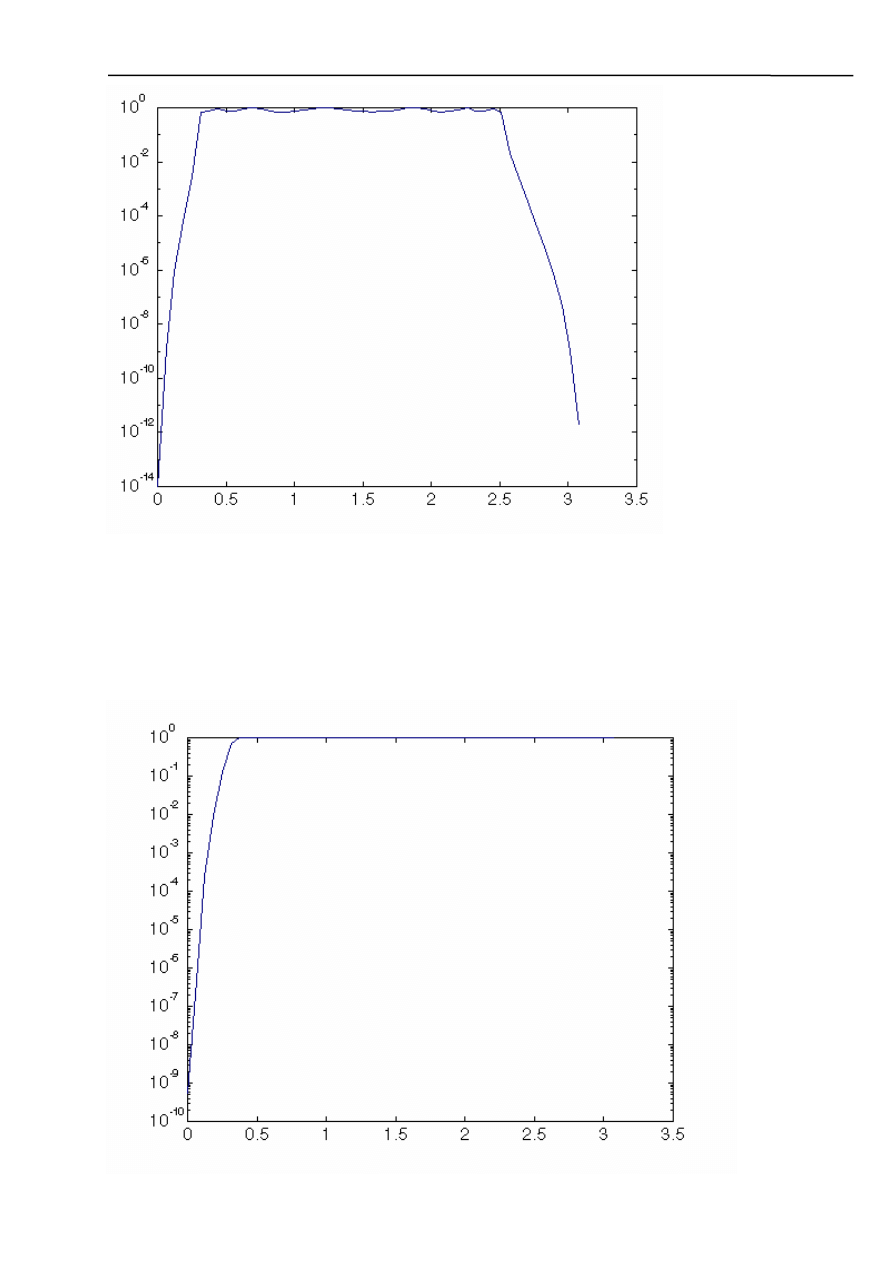
b) filtr środkowoprzepustowy
- charakterystyka Butterworth’a
a =
1.0000 -1.8654 -1.9397 4.4684 3.1799 -6.5624 -3.5077
6.0629 2.9970 -3.8629 -1.8519 1.6716 0.8132 -0.4764
-0.2381 0.0807 0.0418 -0.0062 -0.0033
b =
0.0576 0.0000 -0.5186 0.0000 2.0743 0.0000 -4.8401
0.0000 7.2602 0.0000 -7.2602 0.0000 4.8401 0.0000
-2.0743 0.0000 0.5186 0.0000 -0.0576
- charakterystyka Chebyshev’a
a=
1.0000 -2.6599 2.0782 -0.8633 3.4953 -6.2018 4.7226
-3.6444 5.3823 -5.9853 4.6851 -3.7982 3.7364 -3.2953
2.1253 -1.2255 1.1093 -0.8613 0.2894
b =
0.0131 0.0000 -0.1183 0.0000 0.4733 0.0000 -1.1044
0.0000 1.6566 0.0000 -1.6566 0.0000 1.1044 0.0000
-0.4733 0.0000 0.1183 0.0000 -0.0131
CYFROWE PRZETWARZANIE SYGNAŁÓW
10
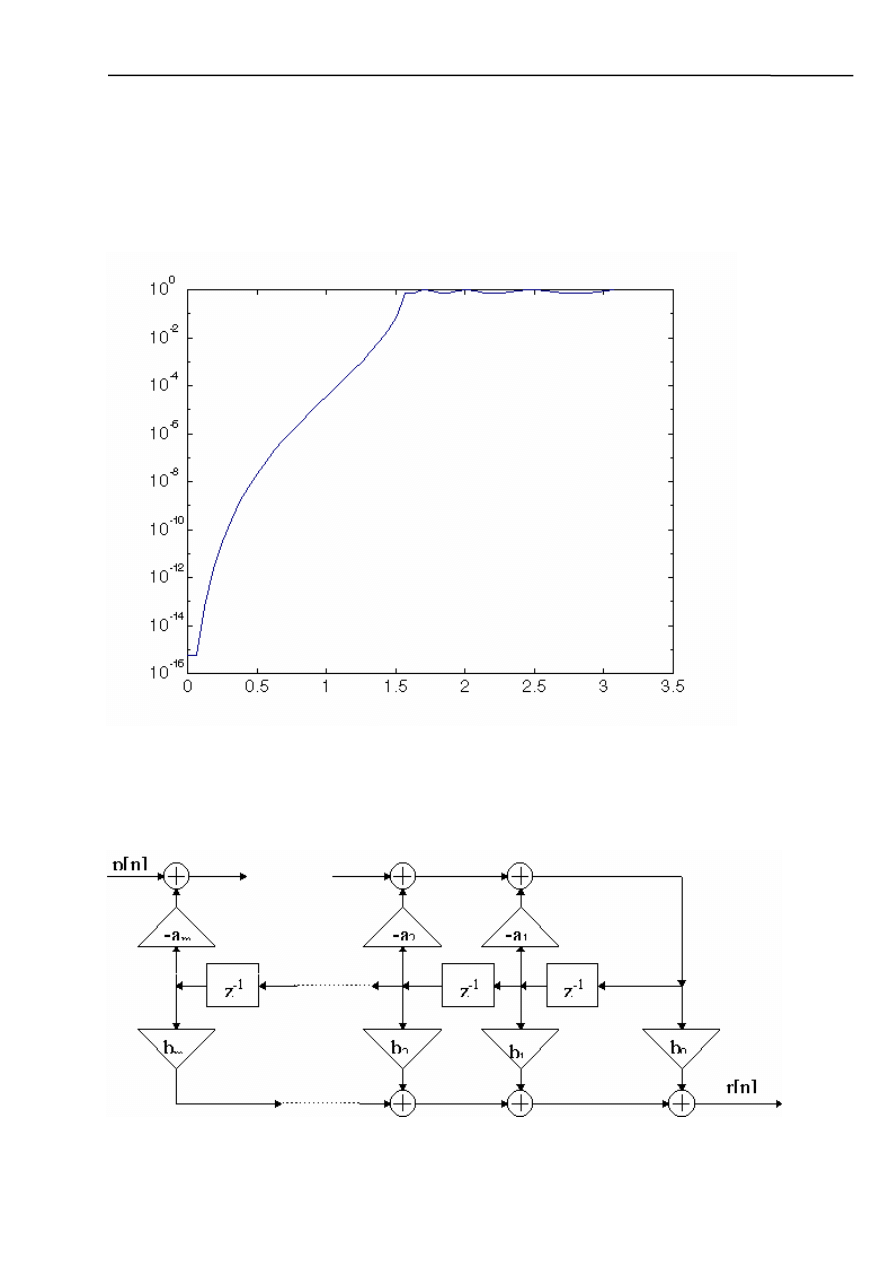
c) filtr górnoprzepustowy
- charakterystyka Butterworth’a
A =
1.0000 -7.1914 23.1362 -43.6819 53.3153 -43.6086 23.8956
-8.4560 1.7531 -0.1622
B =
0.4027 -3.6246 14.4985 -33.8297 50.7446 -50.7446 33.8297
-14.4985 3.6246 -0.4027
CYFROWE PRZETWARZANIE SYGNAŁÓW
11
- charakterystyka Chebyshev’a
a =
1.0000 3.1658 6.8714 10.4858 12.3930 11.4549 8.2837
4.5605 1.7674 0.4120
b =
0.0005 -0.0042 0.0166 -0.0388 0.0582 -0.0582 0.0388
-0.0166 0.0042 -0.0005
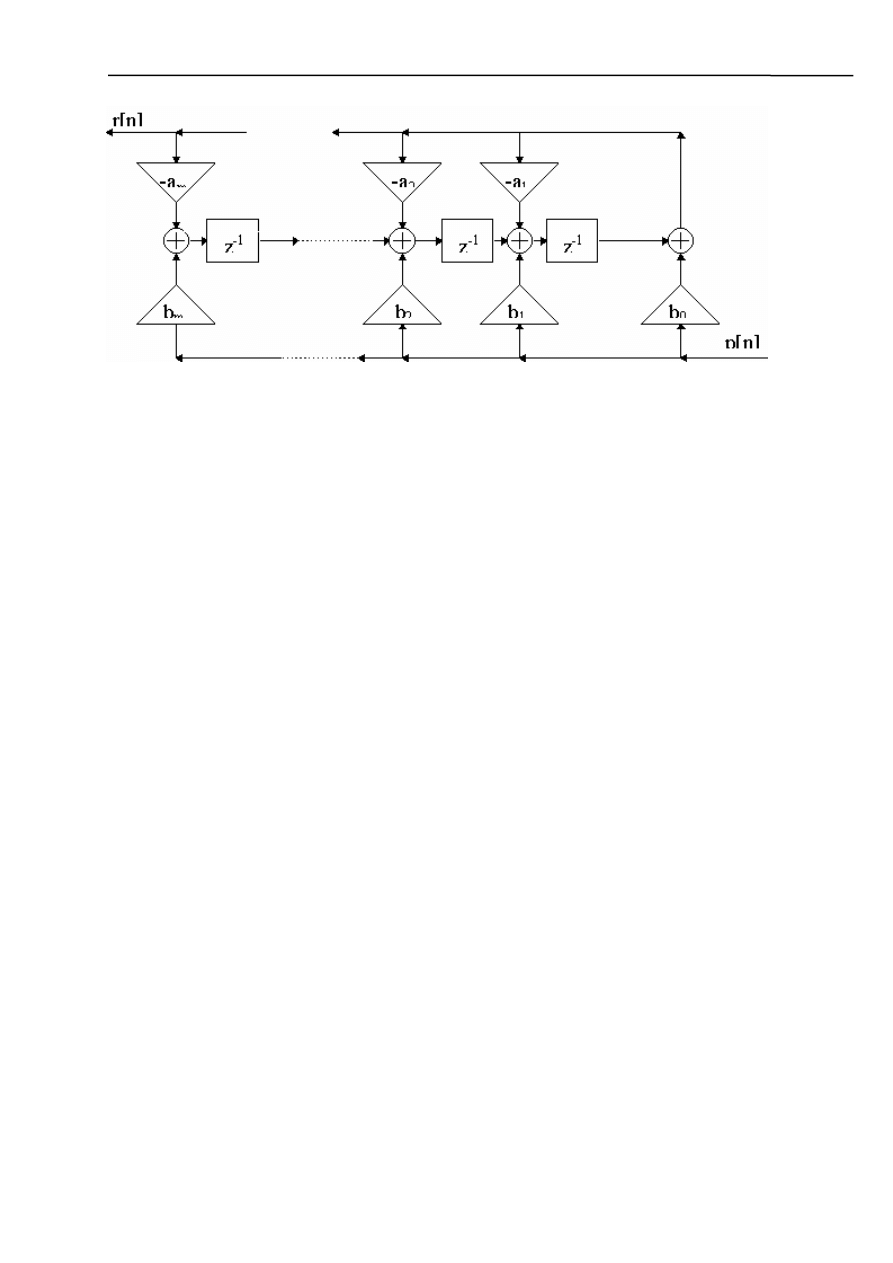
Poniżej zamieszczamy schematy blokowe podstawowych struktur zaprojektowanych filtrów. Należy
tylko podstawić odpowiednie wartości pod odpowiednie współczynniki, które zostały podane w
tabelach.
a) Struktura kontrolera
CYFROWE PRZETWARZANIE SYGNAŁÓW
12
b) struktura obserwera
Całość ćwiczenia miała na celu zapoznanie nas z podstawowymi wiadomościami dotyczącymi
cyfrowego przetwarzania sygnałów. W ćwiczeniu tym przypomnieliśmy sobie związki pomiędzy
poszczególnymi charakterystykami układów, prawa rządzące próbkowaniem sygnałów oraz metody
projektowania filtrów o zadanych gabarytach różnymi rodzajami aproksymacji.

CYFROWE PRZETWARZANIE SYGNAŁÓW
13
Ćwiczenie 2
Zadanie 1
Zbadać zależność szerokości widma amplitudowego i czasu trwania sygnałów.
Zadanie 2
Stworzyć programowy 8-bitowy przetwornik stałopozycyjny A/C. Dokonać próbkowania
dowolnego przebiegu wykorzystując pełną dynamikę przetwornika. Czy powstały błąd kwantyzacji
może być uważany za sygnał generowany przez niezależne źródło szumu?
Zadanie 3
Estymacja funkcji autokorelacji (porównać wynik teoretyczny z wynikami estymacji dla
ergodycznego sygnału sinusoidalnego).
Zadanie 4
Generowanie
sygnałów stacjonarnych o zadanym widmie mocy (przechodzenie widma przez
system liniowy, wybielanie sygnałów).
Zadanie 5
Wygenerować stacjonarny skorelowany przebieg x(t). Na podstawie fragmentu przebiegu
zbudować estymator postaci ax(t) wykorzystując zasadę ortogonalności. Sprawdzić błąd estymacji
całego x(t) i porównać z wynikami teoretycznymi.
Zadanie 1
Zawartość m-pliku:
echo on
%Badanie zależności szerokości widma
amplitudowego i czasu trwania sygnału.
%
echo off
n=10;
y=[ones([1 n]) zeros([1 1000-n])];
subplot(2,2,1);
plot(y);
pause
subplot(2,2,2);
plot(fftshift(abs(fft(y))))
pause
n=100;
y=[ones([1 n]) zeros([1 1000-n])];
subplot(2,2,3)
plot(y)
pause
subplot(2,2,4)
plot(fftshift(abs(fft(y))))
pause
clf;
n=300;
y=[ones([1 n]) zeros([1 1000-n])];
subplot(2,2,1)
plot(y)
pause
subplot(2,2,2)
plot(fftshift(abs(fft(y))))
pause
n=800;
y=[ones([1 n]) zeros([1 1000-n])];
subplot(2,2,3)
plot(y)
pause
subplot(2,2,4)
plot(fftshift(abs(fft(y))))
pause
clf
CYFROWE PRZETWARZANIE SYGNAŁÓW
14
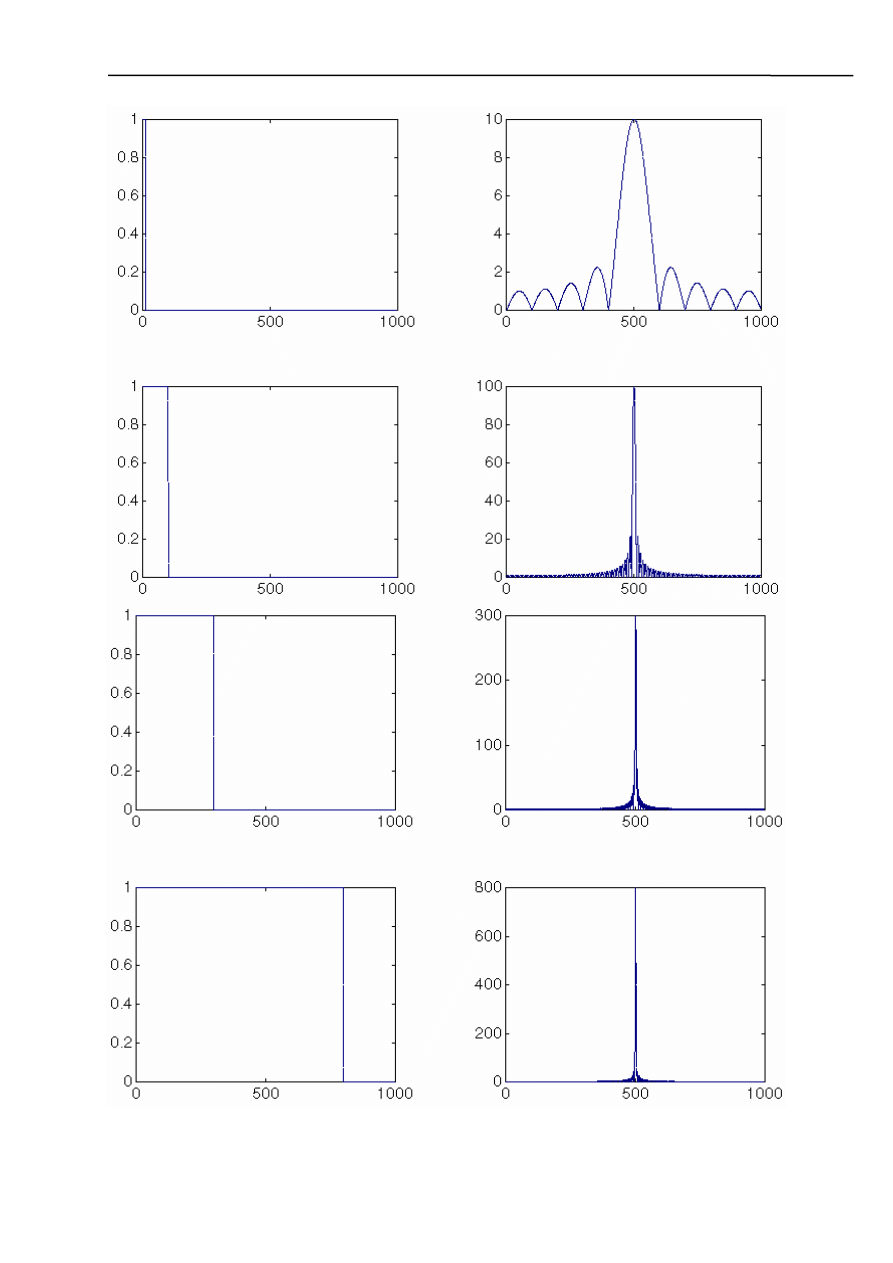
Sygnały o długościach 10, 100, 300, 800 i odpowiadające im widma.
Z twierdzenia o zmianie skali wynika, że szerokość widma amplitudowego jest odwrotnie
proporcjonalne do czasu trwania sygnału tzn. im krótszy jest sygnał energii tym szersze jest jego
CYFROWE PRZETWARZANIE SYGNAŁÓW
15
widmo. Jest to bardzo ciekawe zjawisko, wykorzystywane szczególnie w telekomunikacji, gdzie dąży
się do tego aby sygnał był jak najkrótszy, zaś jego widmo bardzo wąskie. Krótki czas trwania sygnału
pozwala na szybkie przesyłanie informacji, zaś wąskie pasmo przesyłania jest bardziej odporne na
zakłócenia.
Jak
widać z rozważań teoretycznych i przeprowadzonych pomiarów nie da się przesłać sygnału
krótkiego i zarazem o wąskim widmie. Pozostaje więc droga kompromisu: czy szybko przesłać sygnał,
czy też przesłać sygnał odporny na zakłócenia.
Zadanie 2
Zawartość m-pliku:
x=0:0.001:2*pi;
plot(x)
pause
y=(sin(x)*8);
subplot(3,1,1),plot(y)
pause
z=round(y);
subplot(3,1,2),plot(z)
pause
w=y-z;
subplot(3,1,3),plot(w)
pause
clf
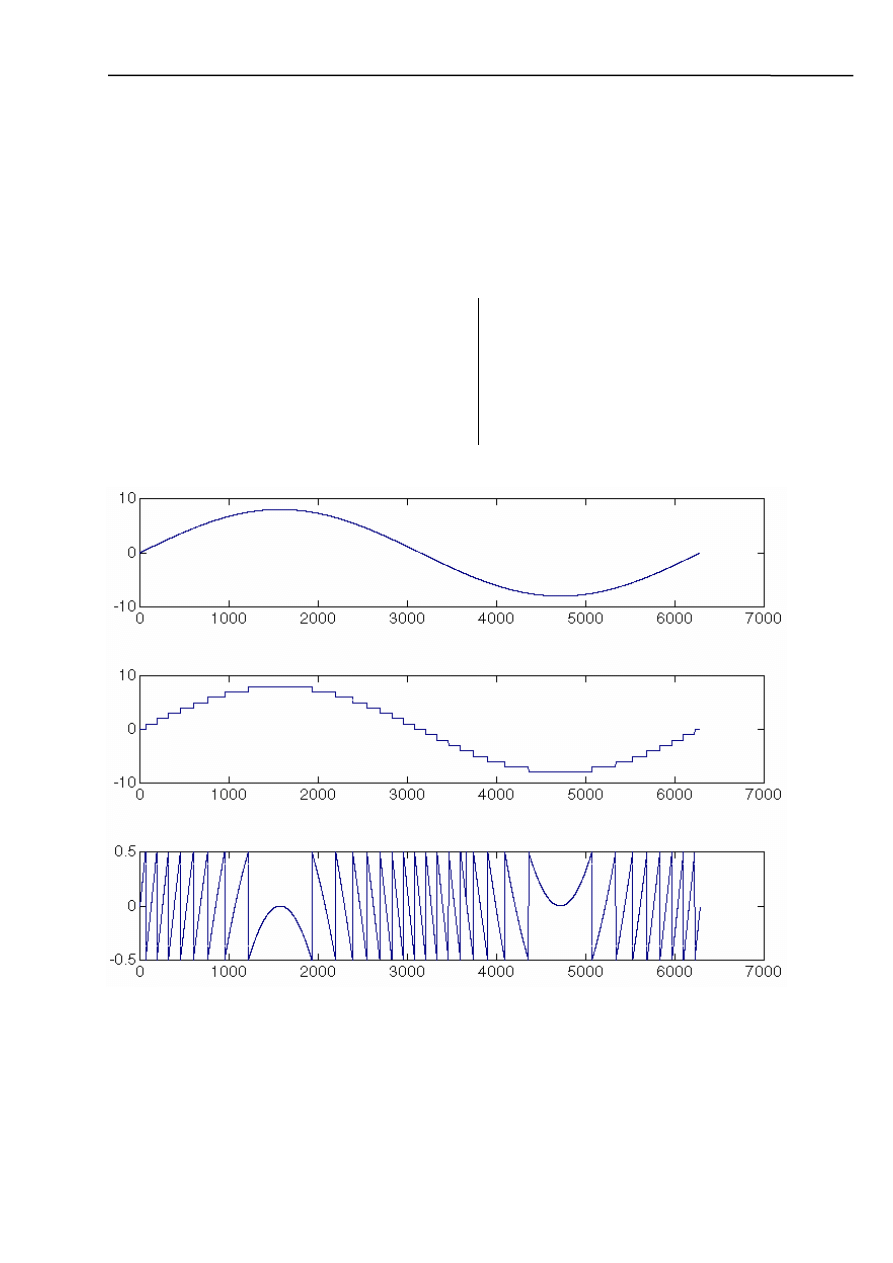
Sygnał wejściowy, skwantowany i błąd kwantyzacji.
Aby
błąd kwantyzacji mógł być uznany za niezależne źródło szumu, różnica między
sąsiednimi próbkami musi być znaczna w porównaniu z krokiem kwantowania (brak jest
jakichkolwiek korelacji zarówno między próbkami szumu kwantowania, jak i między szumem i
sygnałem).
CYFROWE PRZETWARZANIE SYGNAŁÓW
16
Zadanie 3
Zawartość m-pliku:
echo on
k=200;
n=200;
a=[1:0.1:100];
x=sin(a);
subplot(2,1,1);plot(x);
pause
r=zeros(1,200);
for i=1:k;
for j=1:n;
r(i)=r(i)+1/n*x(j)*x(j+i);
end
end
subplot(2,1,2);plot(r);
pause
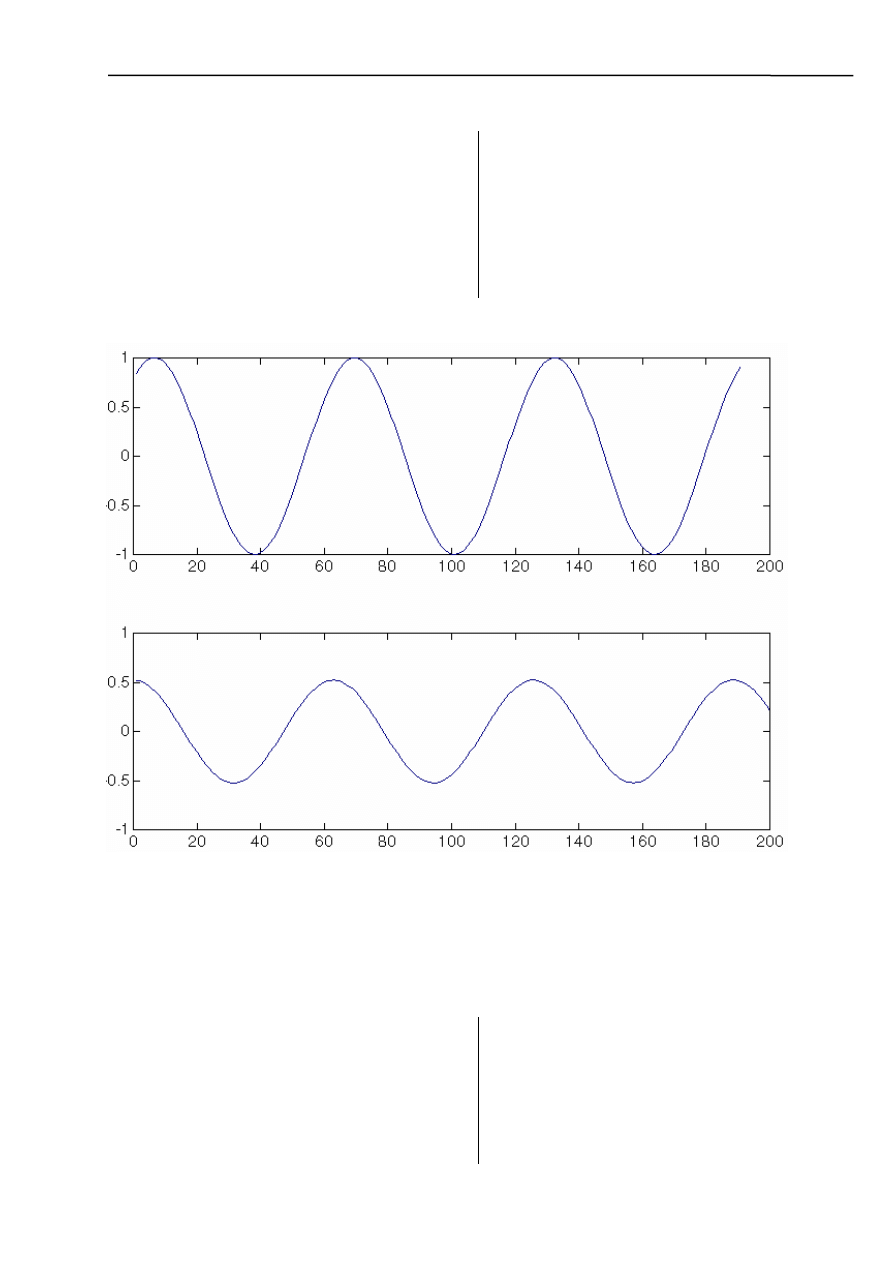
Wykres funkcji sinus i funkcji autokorelacji
Funkcja autokorelacji jest zgodna z wynikiem teoretycznym, to znaczy jest to funkcja
parzysta o tym samym okresie co funkcja sin(t).
Zadanie 4
m-plik:
[N,Wn]=buttord(0.1,0.3,1,80);
[B,A]=butter(N,Wn);
[h,w]=freqz(B,A,128);
subplot(2,2,1);plot(abs(h).^2);
pause;
x=rand([1 128]);
fx=fftshift(abs(fft(x)));
subplot(2,2,1);plot(fx);
pause;
yy=filter(B,A,x);
y=[yy zeros([1 128])];
subplot(2,2,2);plot(y);
pause;
n=128;
CYFROWE PRZETWARZANIE SYGNAŁÓW
17
k=128;
r=zeros(1,256);
for i=1:k;
for j=1:n;
r(i)=r(i)+1/n*y(j)*y(j+i);
end
end
subplot(2,2,3);plot(r);
pause
z=fftshift(abs(fft(r)));
subplot(2,2,4);plot(z);
pause;
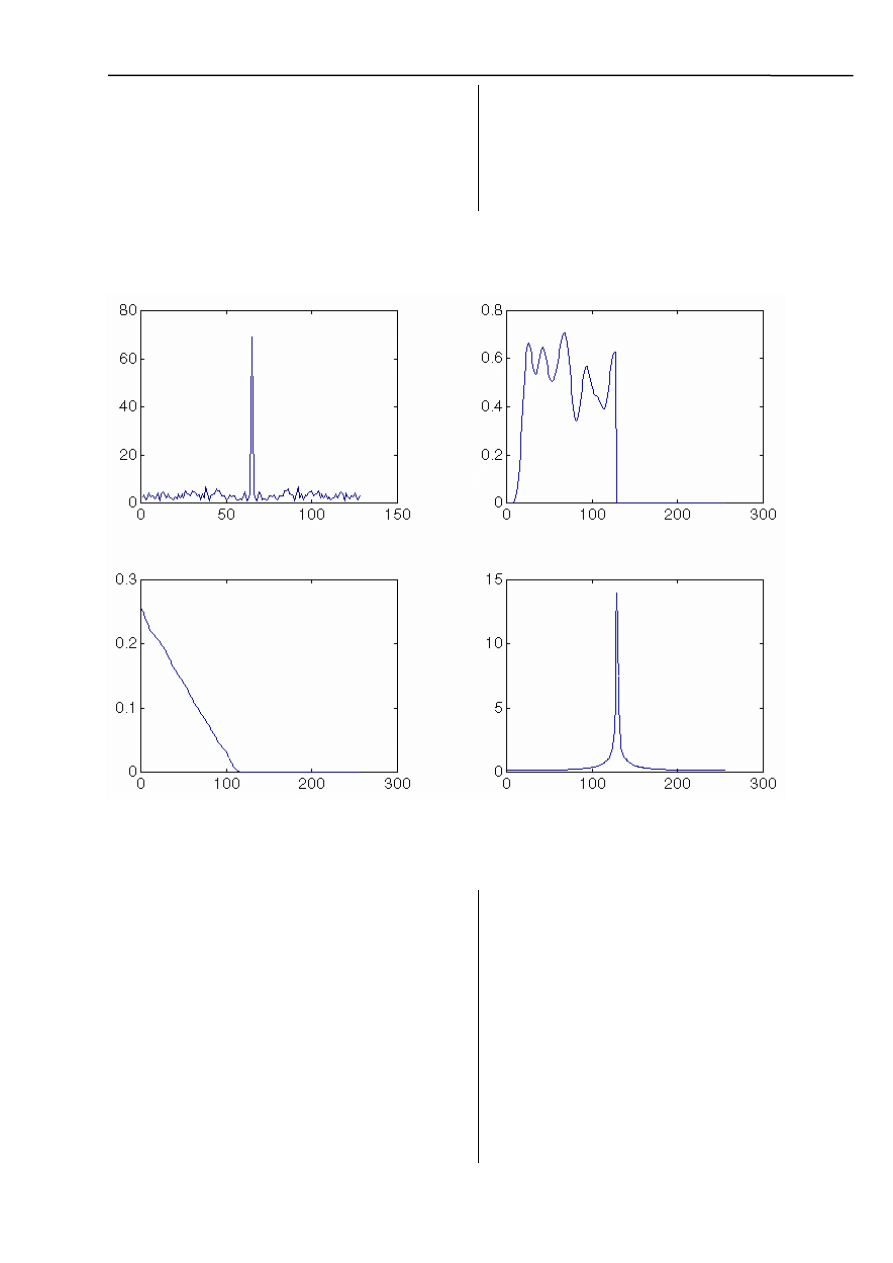
Wykresy przedstawiają: widmo, sygnał na wyjściu systemu liniowego, autokorelacja sygnału
wyjściowego, widmo gęstości mocy sygnału wyjściowego.
Zadanie 5
Zawartość m-pliku:
echo on
k=200;
n=200;
a=[0.1:0.1:20];
y=1/5*rand(size(a));
c=sin(a)+y;
x=[c zeros([1 200])];
subplot(2,2,1);plot(x);
pause
subplot(2,2,2);plot(fftshift(abs(fft(c))));
pause
r=zeros(1,200);
for i=1:k;
for j=1:n;
r(i)=r(i)+1/n*x(j)*x(j+i);
end
end
w=0;
for i=1:n
w=w+1/n*x(i)*x(i);
end
subplot(2,2,3);plot(r);
pause
for i=1:n
aa(i)=r(i)/w;
end
CYFROWE PRZETWARZANIE SYGNAŁÓW
18
p=aa.*c;
subplot(2,2,4);plot(p);
pause
clf
subplot(2,2,1);plot(fftshift(abs(fft(p))));
pause
for i=1:n
e(i)=w-aa(i).*r(i);
end
subplot(2,2,2);plot(e)
pause
clf
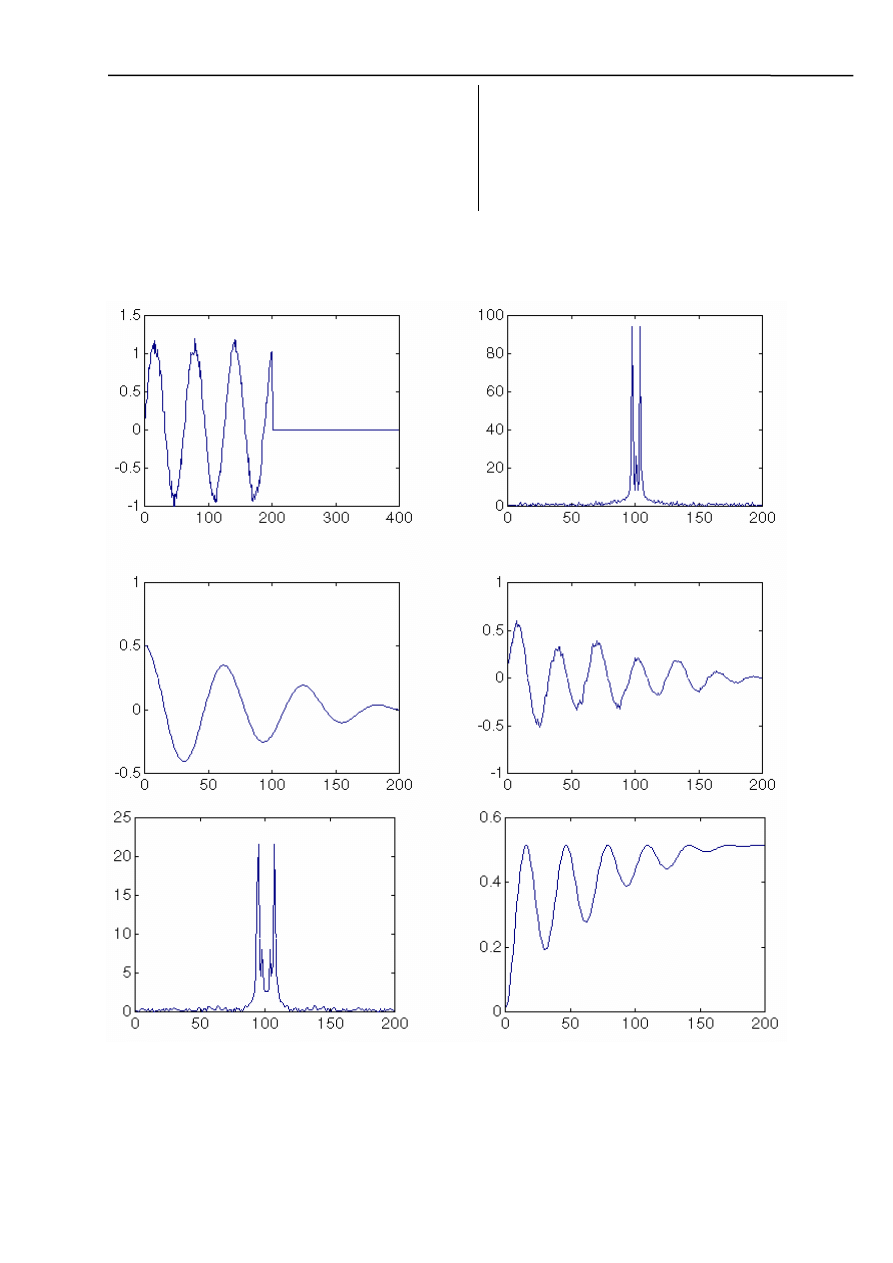
Charakterystyki przedstawiają: zaszumiony przebieg sinusoidalny, jego widmo, autokorelację,
przebieg prognozowany, jego widmo, błąd estymacji

CYFROWE PRZETWARZANIE SYGNAŁÓW
19
Ćwiczenie 3
Zadanie 1.
Zaprojektować następujące filtry cyfrowe aproksymujące tę samą charakterystykę idealną:
• Butterworth’a
• Chebyshev’a
• Bessel’a
• FIR
Zadanie 2.
Zbadać położenie biegunów, widmo transmitancji, opóźnienie grupowe zaprojektowanych
filtrów.
Zadanie 3.
Zbudować fourierowski filtr cyfrowy pracujący wg. schematu blokowego poniżej, realizujący
charakterystykę idealną założoną w zadaniu 1. Zbadać właściwości filtru.
Zadanie 4.
Zbadać zdolność stworzonych filtrów cyfrowych do filtracji przebiegów harmonicznych z
szumów.
Zadanie 1, 2.
Projekty filtrów cyfrowych (Butterworth’a, Chebyshev’a, Bessel’a oraz FIR), badanie
położenia biegunów, widma transmitancji, opóźnienie grupowe wykonaliśmy za pomocą pakietu
Matlab.
Poniżej zamieszczamy ich charakterystyki amplitudowe, fazowe, opóźnienia grupowego oraz
rozmieszczenie zer i biegunów.
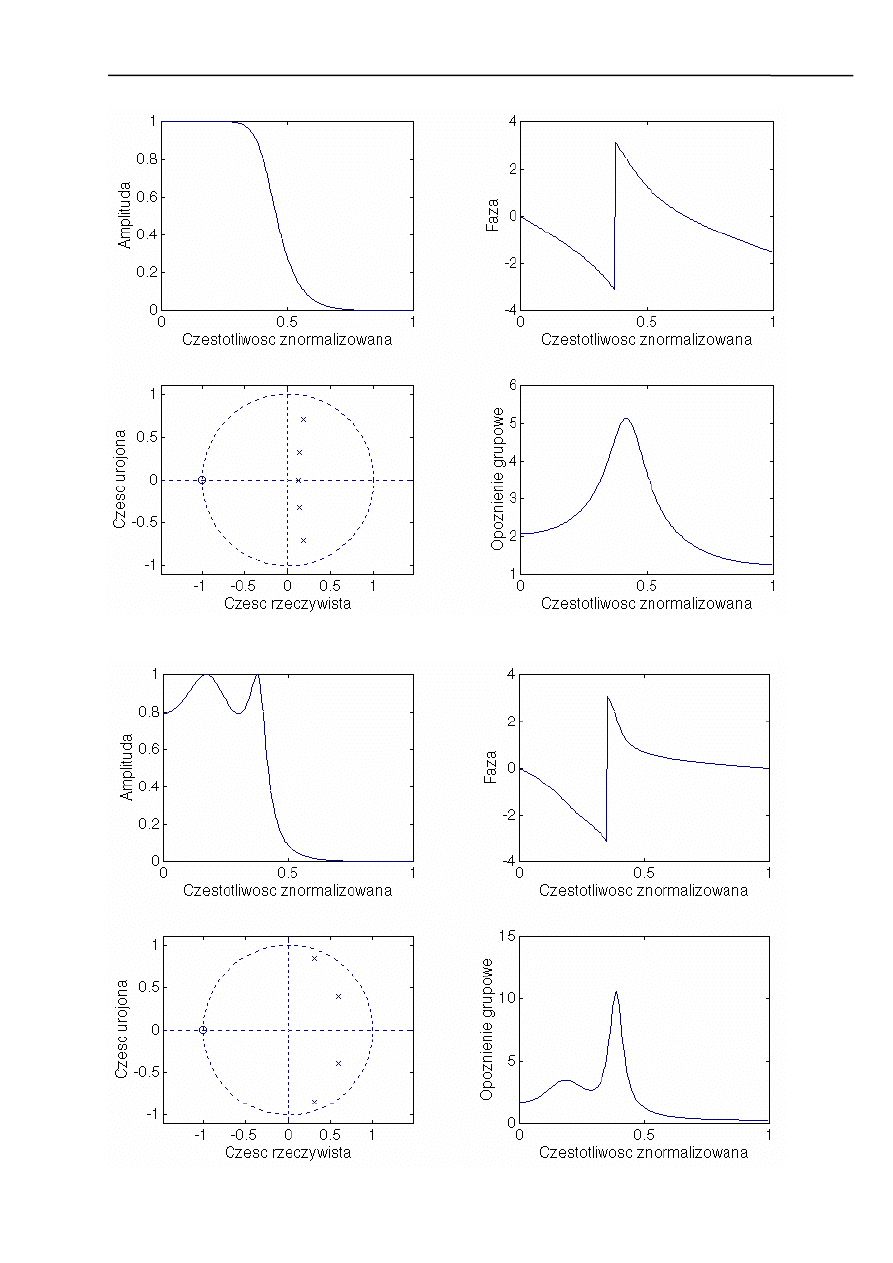
Poniższe charakterystyki przedstawiają kolejno:
• charakterystykę amplitudową;
• charakterystykę fazową;
• rozmieszczenie zer i biegunów;
• opóźnienie grupowe.
CYFROWE PRZETWARZANIE SYGNAŁÓW
20
Dla filtru Butterworth’a:
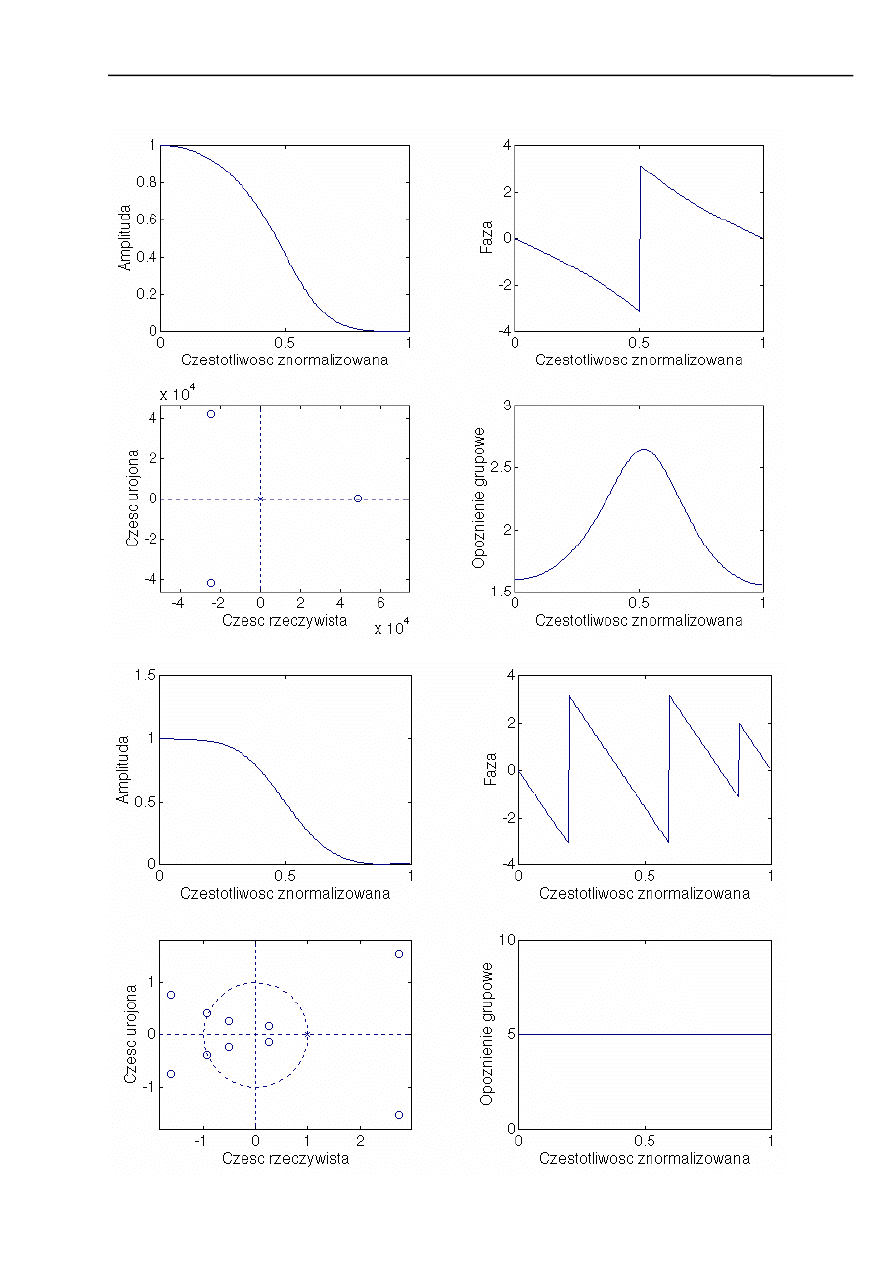
Dla filtru Chebyshev’a:
CYFROWE PRZETWARZANIE SYGNAŁÓW
21
Dla filtru Bessel’a:
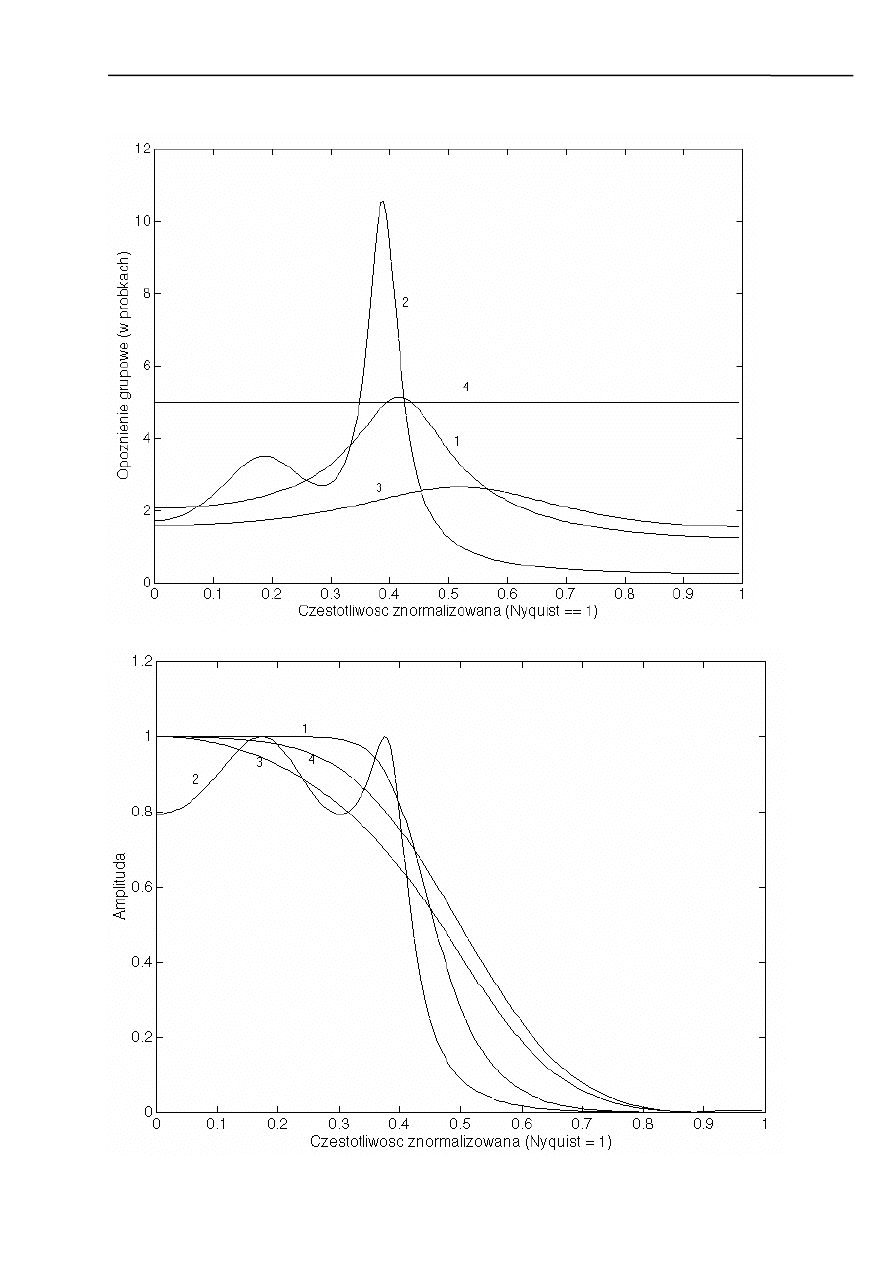
Dla filtru FIR:
CYFROWE PRZETWARZANIE SYGNAŁÓW
22
Opóźnienie grupowe zaprojektowanych filtrów:
Charakterystyki amplitudowe wszystkich filtrów.
CYFROWE PRZETWARZANIE SYGNAŁÓW
23
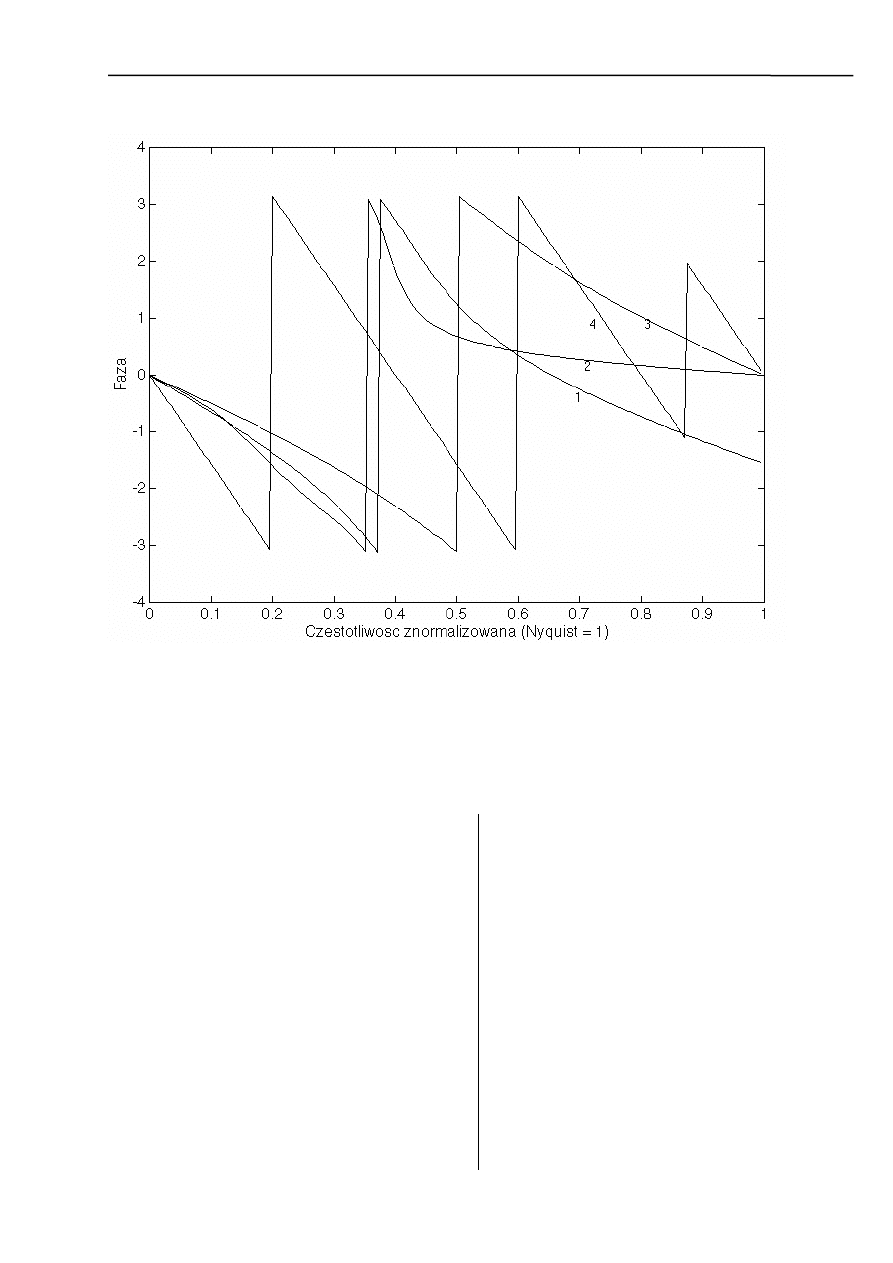
Charakterystyki fazowe:
gdzie:
1– dla filtru Butterworth’a
2– dla filtru Chebyshev’a
3– dla filtru Bessel’a
4– dla filtru FIR
Poniżej zostały dołączone wydruki m-plików:
1)
echo on
% Filtr Butterworth’a.
% Hbutt - punkty do charakterystyki
amplitudowej,
% Gdbutt - punkty do opóźnienia grupowego.
% Charakterystyka amplitudowa, zera i
bieguny, opóźnienie grupowe.
echo off
[N,Wn]=buttord(0.4,0.7,4,40);
[B,A]=butter(N,Wn);
[Hbutt,W]=freqz(B,A,200);
[Gdbutt,W] = grpdelay(B,A,200);
f=W/pi;
h1=abs(Hbutt);
p1=angle(Hbutt);
subplot(2,2,1);
plot(f,h1);
xlabel('Czestotliwosc znormalizowana')
ylabel('Amplituda')
subplot(2,2,2);
p1=angle(Hbutt);
plot(f,p1);
xlabel('Czestotliwosc znormalizowana')
ylabel('Faza')
subplot(2,2,3);
zplane(B,A);
subplot(2,2,4);
plot(f,Gdbutt);
xlabel('Czestotliwosc znormalizowana')
ylabel('Opoznienie grupowe')
echo on
pause
%

CYFROWE PRZETWARZANIE SYGNAŁÓW
24
% Filtr Chebyshev’a.
% Hczeb - punkty do charakterystyki
amplitudowej,
% Gdczeb - punkty do opóźnienia grupowego.
% Charakterystyka amplitudowa, zera i
bieguny, opóźnienie grupowe.
echo off
[N,Wn]=cheb1ord(0.4,0.7,4,40);
[B,A]=cheby1(N,2,Wn);
[Hczeb,W]=freqz(B,A,200);
[Gdczeb,W] = grpdelay(B,A,200);
f=W/pi;
h2=abs(Hczeb);
p2=angle(Hczeb);
subplot(2,2,1);
plot(f,h2);
xlabel('Czestotliwosc znormalizowana')
ylabel('Amplituda')
subplot(2,2,2);
p2=angle(Hczeb);
plot(f,p2);
xlabel('Czestotliwosc znormalizowana')
ylabel('Faza')
subplot(2,2,3);
zplane(B,A);
subplot(2,2,4);
plot(f,Gdczeb);
xlabel('Czestotliwosc znormalizowana')
ylabel('Opoznienie grupowe')
echo on
pause
%
% Filtr Bessel’a.
% Hbes - punkty do charakterystyki
amplitudowej,
% Gdbes - punkty do opóźnienia grupowego.
% Charakterystyka amplitudowa, zera i
bieguny, opóźnienie grupowe.
echo off
[B,A]=besself(4,0.4);
[NUMd,DENd]=bilinear(B,A,0.2); %
przekształcenie biliniowe dla Fs=0.1
[Hbes,W]=freqz(NUMd,DENd,200);
[Gdbes,W] = grpdelay(NUMd,DENd,200);
f=W/pi;
h3=abs(Hbes);
p3=angle(Hbes);
subplot(2,2,1);
plot(f,h3);
xlabel('Czestotliwosc znormalizowana')
ylabel('Amplituda')
subplot(2,2,2);
p3=angle(Hbes);
plot(f,p3);
xlabel('Czestotliwosc znormalizowana')
ylabel('Faza')
subplot(2,2,3);
zplane(B,A);
subplot(2,2,4);
plot(f,Gdbes);
xlabel('Czestotliwosc znormalizowana')
ylabel('Opoznienie grupowe')
echo on
pause
%
% Filtr FIR.
% Hfir - punkty do charakterystyki
amplitudowej,
% Gdfir - punkty do opóźnienia grupowego.
% Charakterystyka amplitudowa, zera i
bieguny, opóźnienie grupowe.
echo off
N=10;
A=1;
B = fir1(N,0.5);
[Hfir,w]=freqz(B,1,200);
[Gdfir,W] = grpdelay(B,A,200);
f=w/pi;
h4=abs(Hfir);
p4=angle(Hfir);
subplot(2,2,1);
plot(f,h4);
xlabel('Czestotliwosc znormalizowana')
ylabel('Amplituda')
subplot(2,2,2);
p4=angle(Hfir);
plot(f,p4);
xlabel('Czestotliwosc znormalizowana')
ylabel('Faza')
subplot(2,2,3);
zplane(B,A);
subplot(2,2,4);
plot(f,Gdfir);
xlabel('Czestotliwosc znormalizowana')
ylabel('Opoznienie grupowe')
pause
clf
echo on
% To już wszystko!
echo off
2)
echo on
% Wykresy zbiorowe filtrów.
CYFROWE PRZETWARZANIE SYGNAŁÓW
25
echo off
plot(f,h1,f,h2,f,h3,f,h4);
xlabel('Czestotliwosc znormalizowana (Nyquist
= 1)')
ylabel('Amplituda')
echo
% Charakterystyki amplitudowe
pause
echo off
plot(f,p1,f,p2,f,p3,f,p4);
xlabel('Czestotliwosc znormalizowana (Nyquist
= 1)')
ylabel('Faza')
echo on
%Charakterystyki fazowe
pause
echo off
plot(f,Gdbutt,f,Gdczeb,f,Gdbes,f,Gdfir);
xlabel('Czestotliwosc znormalizowana (Nyquist
== 1)')
ylabel('Opoznienie grupowe (w probkach)')
echo on
% Opóźnienie grupowe
pause
echo off
clf;
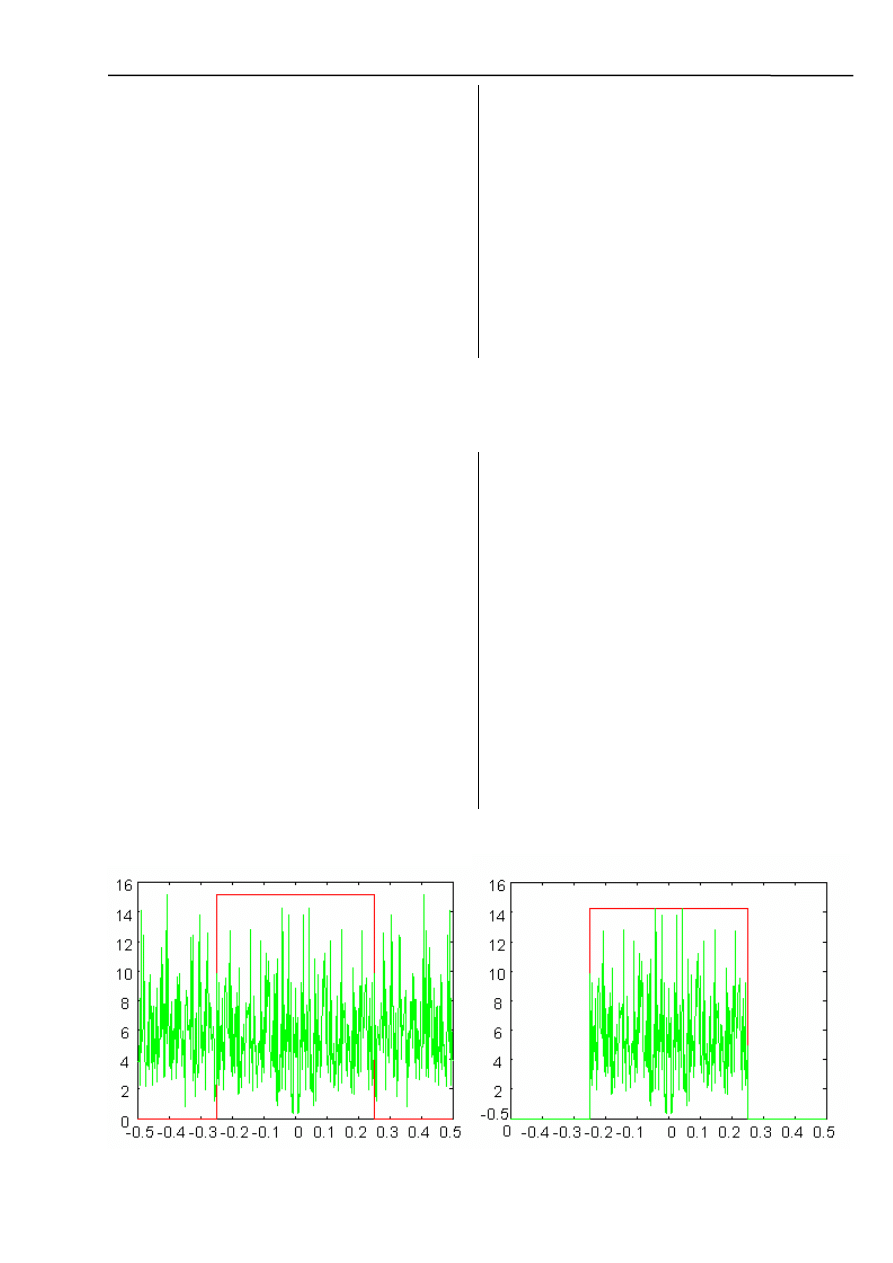
Zadanie 3.
Wydruk m-pliku:
t=[1:512];
%x=rand([1:512]);
x=0.1*sin(2*pi*t/8)+sin(2*pi*t/64);
plot(t,x)
pause
ny=512;
st=512;
d=[ones([1:512])]; %filtry
HP
d=[zeros([1:128]) ones([1:256])]; %filtry LP
%d=[ones([1:128]) zeros([1:256])];
[md,nd]=size(d);
%if nd<ny, nx=ny-nd, d=[d,ones([1:nx])]; end
if nd<ny, nx=ny-nd, d=[d,zeros([1:nx])]; end
%dls
st=256
pause
kr=512/st-1;
for i=0:kr,
y1((i*st+1):(i*st+st))=fft(x((i*st+1):(i*st+st)));,
z((i*st+1):(i*st+st))=y1((i*st+1):(i*st+st)).*d((i
*st+1):(i*st+st));,
q((i*st+1):(i*st+st))=ifft(z((i*st+1):(i*st+st)));,
pp((i*st+1):(i*st+st))=fft(q((i*st+1):(i*st+st)));,
p=abs(pp);
end
plot(t,q)
pause
wsp=max(p);
wspy1=max(abs(y1));
f=([1:ny]/ny-0.5);
plot(f,wspy1*d,f,abs(y1));
pause
plot(f,wsp*d,f,p);
pause
Widmo szumu i funkcja filtrująca, wygląd po filtracji (filtr środkowo przepustowy)
CYFROWE PRZETWARZANIE SYGNAŁÓW
26
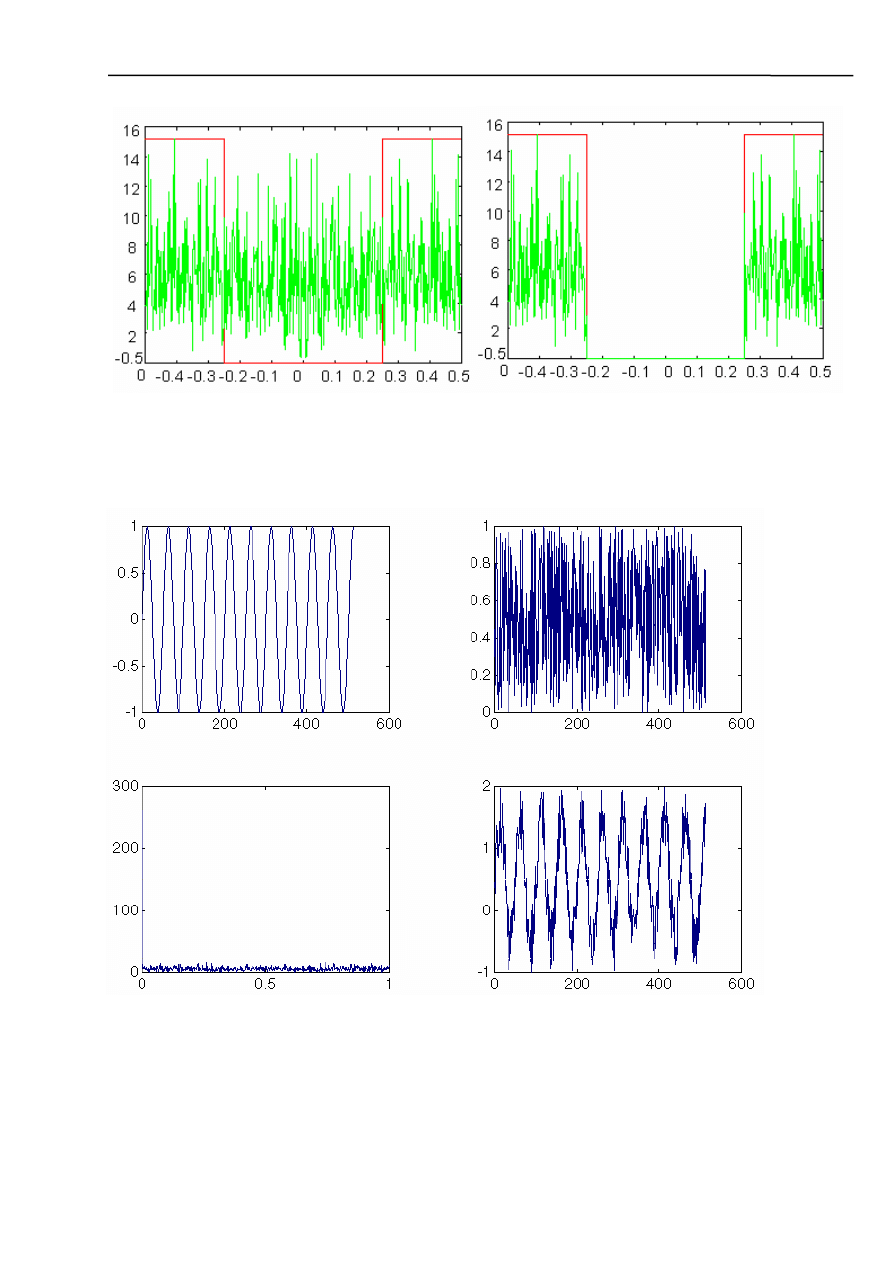
Widmo szumu i funkcja filtrująca, wygląd po filtracji (filtr środkowo zaporowy)
Zadanie 4.
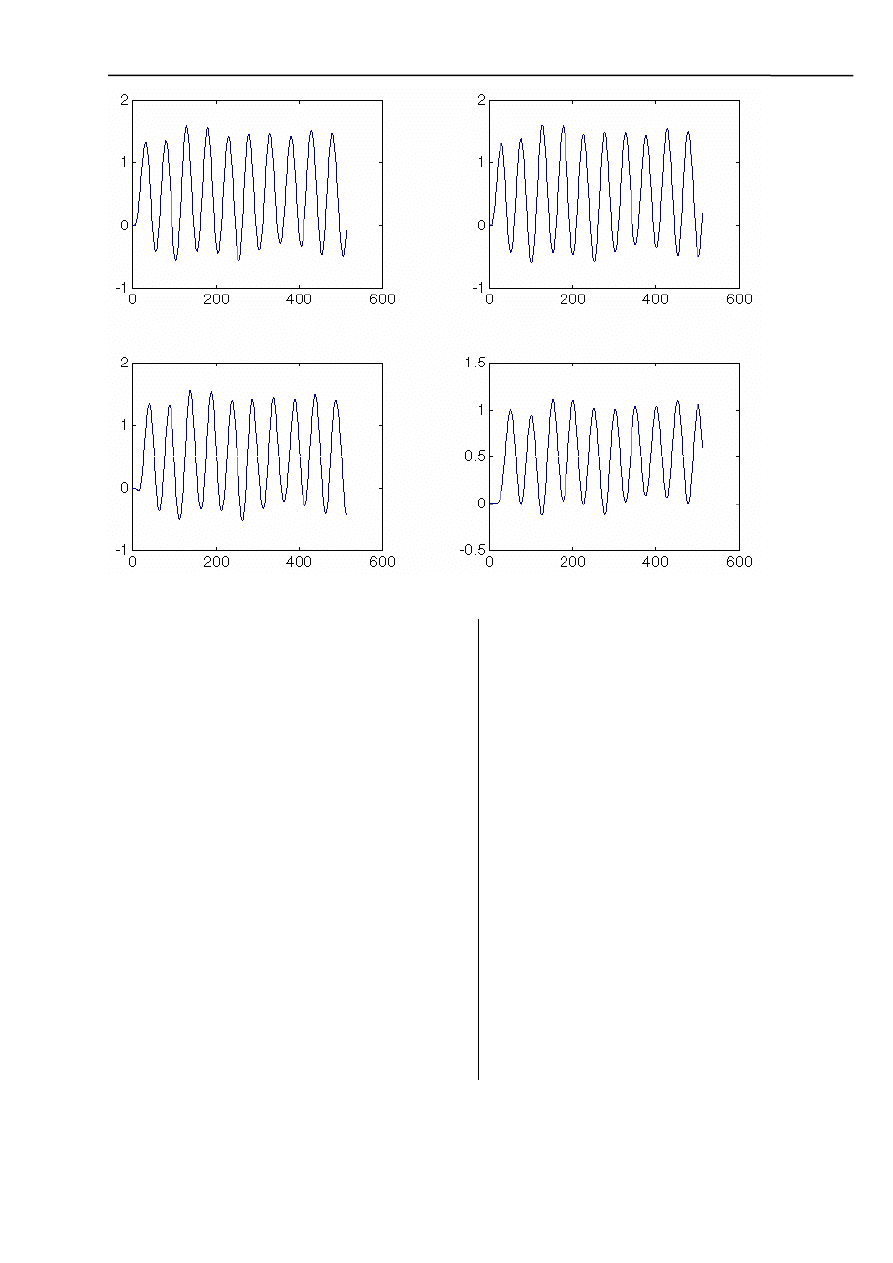
Wykresy przedstawiają: funkcję sinus, szum, widmo szumu, sinus plus szum, sygnały po filtracji
filtrem Butterworth’a, Chebyshev’a, Bessel’a, FIR.
CYFROWE PRZETWARZANIE SYGNAŁÓW
27
Wydruk z m-pliku:
[N,Wn]=buttord(0.05,0.1,2,20);
[B,A]=butter(N,Wn); %N=13
D=B;C=A;
[Hbutt,W]=freqz(B,A,512);
[N,Wn]=cheb1ord(0.05,0.1,2,20);
[B,A]=cheby1(N,0.5,Wn);
F=B;E=A;
[Hczeb,W]=freqz(B,A,512);
[B,A]=besself(10,0.1);
[NUMd,DENd]=bilinear(B,A,0.5);
[Hbes,W]=freqz(NUMd,DENd,512);
N=50;
A=1;
B = fir1(N,0.08);
[Hfir,W]=freqz(B,1,512);
Hbutt=abs(Hbutt);
Hczeb=abs(Hczeb);
Hbes=abs(Hbes);
Hfir=abs(Hfir);
f=W/pi;
t = 0:0.01:5.12;
x = sin(2*pi*2*t);
subplot(2,2,1);plot(x);
y = rand(size(t));
subplot(2,2,2);plot(y);
fy=fft(y);
subplot(2,2,3);plot(f,abs(fy(1:512)));
pause
z=x+y;
subplot(2,2,4);plot(z(1:512))
pause
clf;
Y=filter(D,C,z); %Butterworth
subplot(2,2,1);plot(Y)
pause
Y=filter(F,E,z); %Chebyschev
subplot(2,2,2);plot(Y)
Y=filter(B,A,z); %Bessel
subplot(2,2,3);plot(Y)
Y=filter(NUMd,DENd,z); %FIR
subplot(2,2,4);plot(Y)
pause
clf
Wszystkie stworzone przez nas filtry nadają się do filtracji przebiegów harmonicznych z szumu.
Jednak, który filtr zastosujemy zależy od konkretnego przypadku, potrzeby (wszystkie filtry mają
zalety jak i wady).
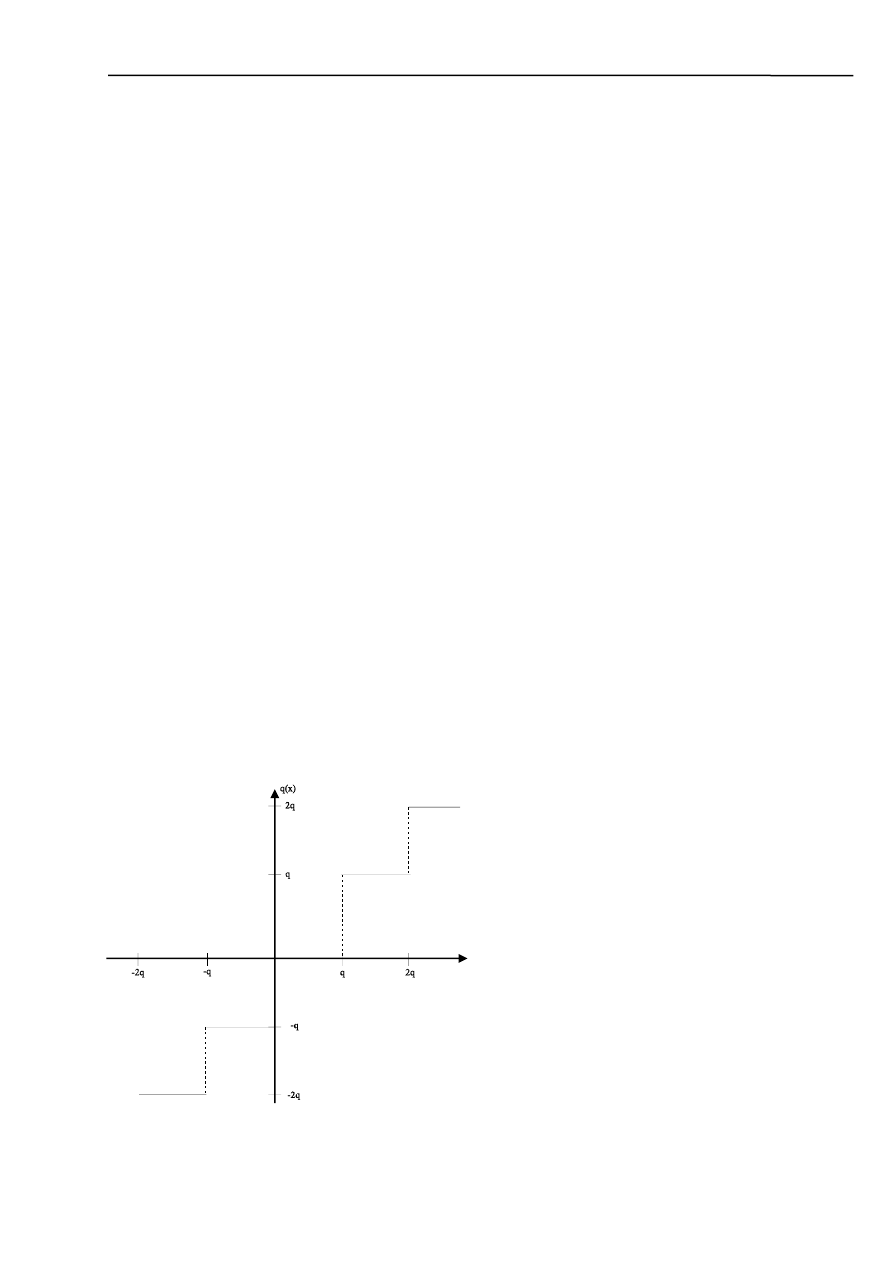
CYFROWE PRZETWARZANIE SYGNAŁÓW
28
Ćwiczenie TMS
Zadanie 1
Badanie przetwornika AC i CA. (CWI1.ASM)
Określić parametry:
a) częstotliwość próbkowania wykorzystując
-czas
opóźnienia próbek pomiędzy wejściem i wyjściem
-maksymalną częstotliwość wejściową
b) rodzaj zjawisk nieliniowych (arytmetyka, przepełnienie)
Wyniki zilustrować rysunkami.
Zadanie 2
Filtr Cyfrowy FIR. (CWI8.ASM)
Zaprojektować dowolny filtr cyfrowy FIR 21 rzędu. Utworzyć program realizujący zaprojektowany
filtr (wykorzystując CWI8.ASM). Zbadać funkcje transmitancji filtru, porównać przebiegi z wynikami
teoretycznymi.
Zadanie 3
Badanie
filtru
środkowo-przepustowego. (CWI5.HEX)
Celem ćwiczenia było uruchomienie oraz przebadanie eliptycznego filtru środkowo-przepustowego
5-go rzędu, którego pasmo zawiera się w granicach od 1.7 kHz do 2.3 kHZ.
Zadanie 1
Ćwiczenie to polegało na zapoznaniu się z możliwościami przetworników AC i CA oraz
określeniu właściwości takiego przetwornika.
Częstotliwość próbkowania określiliśmy na podstawie czasu opóźnienia próbek pomiędzy
wejściem i wyjściem oraz na podstawie maksymalnej częstotliwości wejściowej:
– czas opóźnienia próbek pomiędzy wejściem i wyjściem wynosił T=39
μs. Częstotliwość
próbkowania wynosi więc około f
p
=25kHz.
– maksymalna częstotliwość wejściowa przy której sygnał był poprawny wyniosła 12kHz. Wynika
stąd, że f
p
=24kHz.
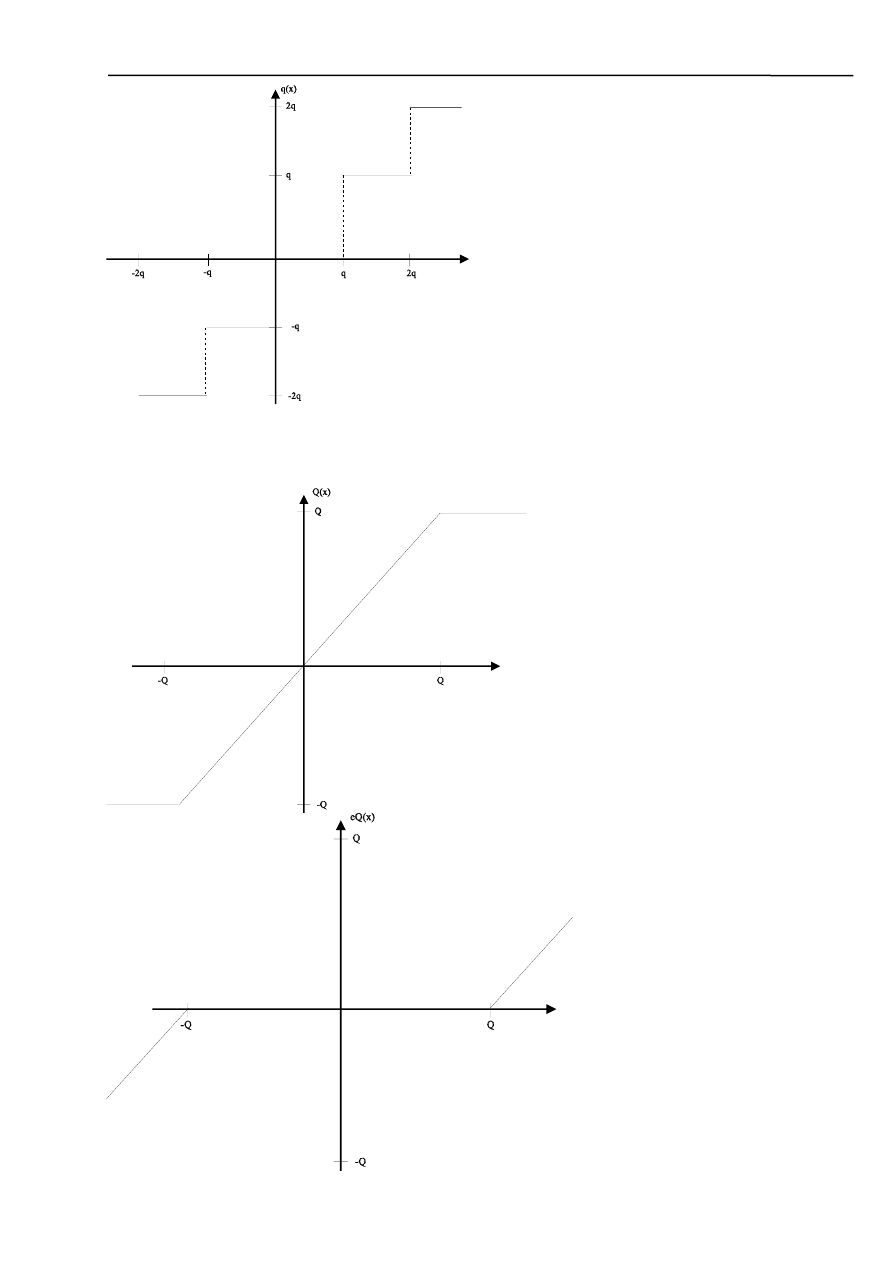
Po przebadaniu przetwornika stwierdziliśmy, że jest to kwantyzer z obcięciem (jest jeszcze
kwantyzacja z zaokrągleniem). Poniżej przedstawiamy charakterystykę przejściową oraz wykres
obrazujący błąd kwantyzacji.
CYFROWE PRZETWARZANIE SYGNAŁÓW
29
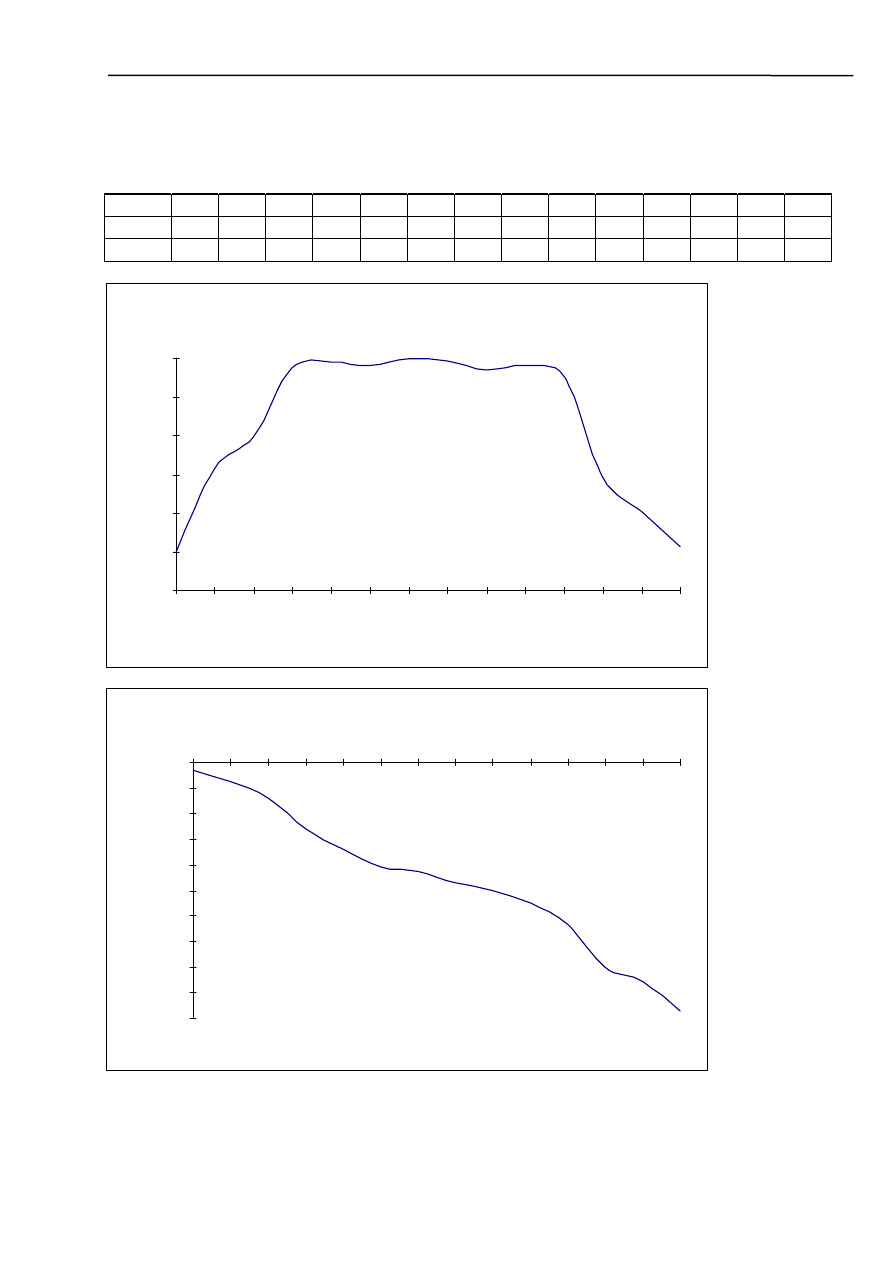
Z naszych spostrzeżeń wynika również, że mamy doczynienia z układem z nasyceniem, tzn. może
nastąpić przepełnienie i sygnał wyjściowy będzie utrzymywał się na stałym poziomie. Poniżej
zamieszczamy charakterystykę poziomów wyjściowych od wejściowych oraz charakterystykę błędów
kwantyzera spowodowanych nasycenim.
CYFROWE PRZETWARZANIE SYGNAŁÓW
30
Zadanie 2
Załadowaliśmy filtr cyfrowy środkowo-przepustowy, podaliśmy z generatora na wejście sygnał
sinusoidalny o amplitudzie 1,5V. Przy pomocy oscyloskopu zbadaliśmy charakterystykę amplitudową
i fazową filtru. Wyniki pomiarów zamieszczamy w tabeli poniżej.
f[kHz] 1,9 1,95 2 2,05 2,1 2,15
2,2 2,25
2,3 2,35 2,4 2,45 2,5 2,55
Up[V] 0,495 1,57 1,99 2,87 2,94
2,9 2,98 2,95 2,835 2,9 2,75 1,46 1,01 0,56
φ [deg] -32,1 -75 -140 -260 -340 -409 -428 -472 -503 -551 -635 -800 -860 -975
Charakterystyka amplitudowa
0
0,5
1
1,5
2
2,5
3
1,9
1,95
2
2,05
2,1
2,15
2,2
2,25
2,3
2,35
2,4
2,45
2,5
2,55
f [kHz]
Up [V]
Charakterystyka fazowa
-1000
-900
-800
-700
-600
-500
-400
-300
-200
-100
0
1,
9
1,
95
2
2,
05
2,
1
2,
15
2,
2
2,
25
2,
3
2,
35
2,
4
2,
45
2,
5
2,
55
f [kHz]
faza [
deg]
Z wykresu charakterystyki amplitudowej wynika, że jest to filtr o dużej selektywności (duże
nachylenie zboczy w paśmie przepustowym i małe zafalowania). Ponadto filtr ten wzmacnia sygnał
ponad dwukrotnie w paśmie przenoszenia. Jego charakterystyka fazowa jest jednostajnie opadająca o
bardzo dużym opóźnieniu fazowym.
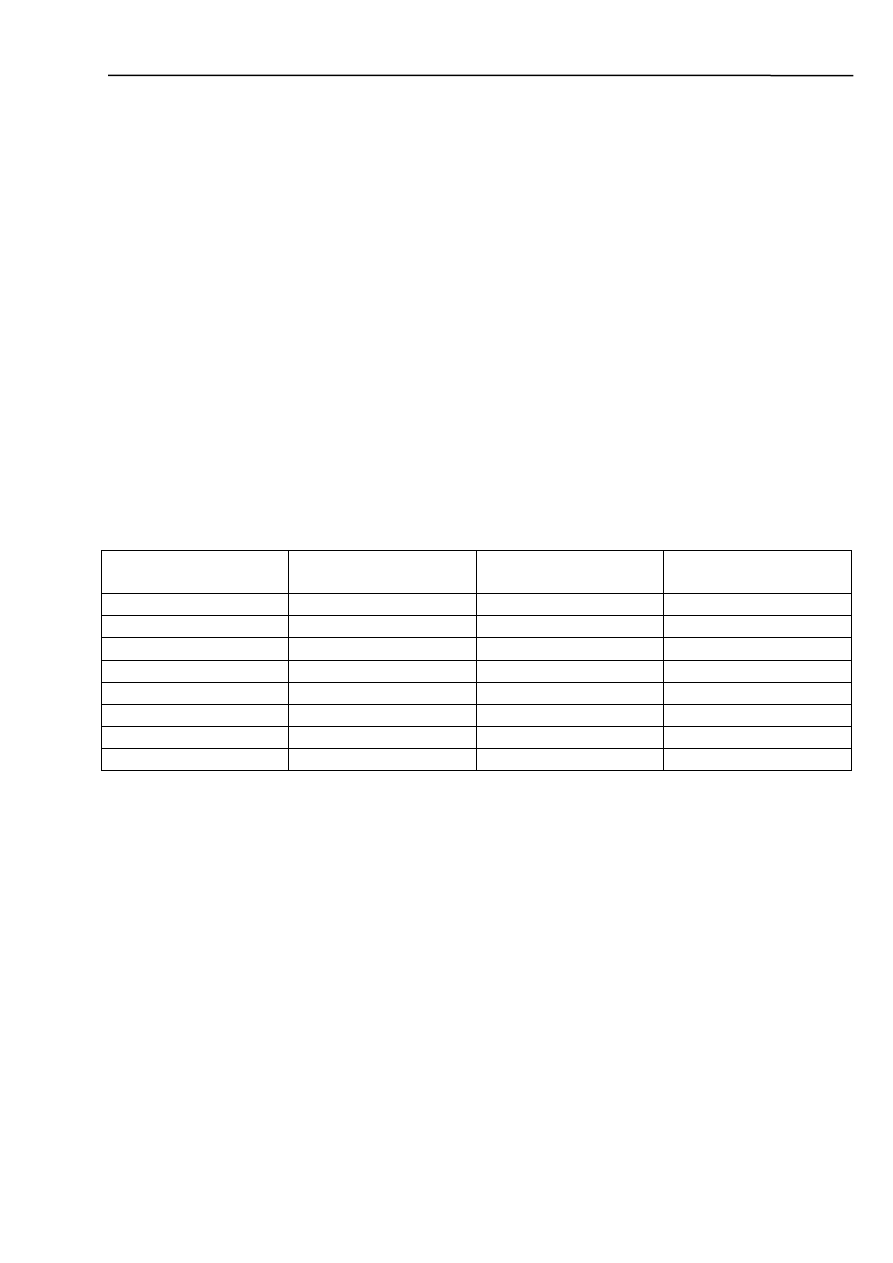
CYFROWE PRZETWARZANIE SYGNAŁÓW
31
Zadanie 3
Ćwiczenie było realizowane na procesorze sygnałowym TMS 320, który jest ukierunkowany na
cyfrowe przetwarzanie sygnałów i na zastosowanie telekomunikacyjne. Ponadto jest on stosowany do
przetwarzania sygnału mowy, w zagadnieniach analizy widmowej, korelacji, filtracji cyfrowej,
kodowaniu liniowo-predykcyjnym, a także w algorytmach cyfrowego przetwarzania sygnałów w
robotyce. TMS 320 jest nie tylko specjalizowanym układem do cyfrowego przetwarzania sygnałów,
ale także kostką mikrokomputerową ogólnego stosowania z bardzo szybką 32-bitową jednostką
arytmetyczno-logiczną i równoległym układem mnożącym 16x16 bitów.
Analizowany filtr został zrealizowany przez procesor DSP w zestawie doświadczalnym TMS320 C15
po załadowaniu do niego programu cwi5.hex. Do obsługi zestawu DSP wykorzystano program obsługi
DSP Loader.
W celu zbadania charakterystyk częstotliwościowych załadowano do układu DSP program realizujący
cyfrowy filtr dolnoprzepustowy oraz podano z generatora na wejście sygnał sinusoidalny o stałej
amplitudzie równej U = 0.5 [V].
Do pomiarów sygnałów wejściowych (z generatora) i wyjściowych (z procesora DSP) wykorzystano
funkcje: CURSOR AMPLITUDE, CURSOR I/TIME i CURSOR TIME znajdujące się w
oscyloskopie.
Wyniki pomiarów zestawiono w tabeli:
Częstotliwość
wejściowa [Hz]
Amplituda sygnału
wyjściowego [V]
Okres [s]
Opóźnienie [s]
100 0,925 8,83m 310µ
500 0,845 2m 320µ
1k 0,684 950µ 331µ
2k 0,324 503µ 325µ
3k 0,157
319,4µ
324µ
4k 0,12 250µ 76µ
5k 0,057 200µ 112µ
8k 0,01 125µ
125µ
CYFROWE PRZETWARZANIE SYGNAŁÓW
32
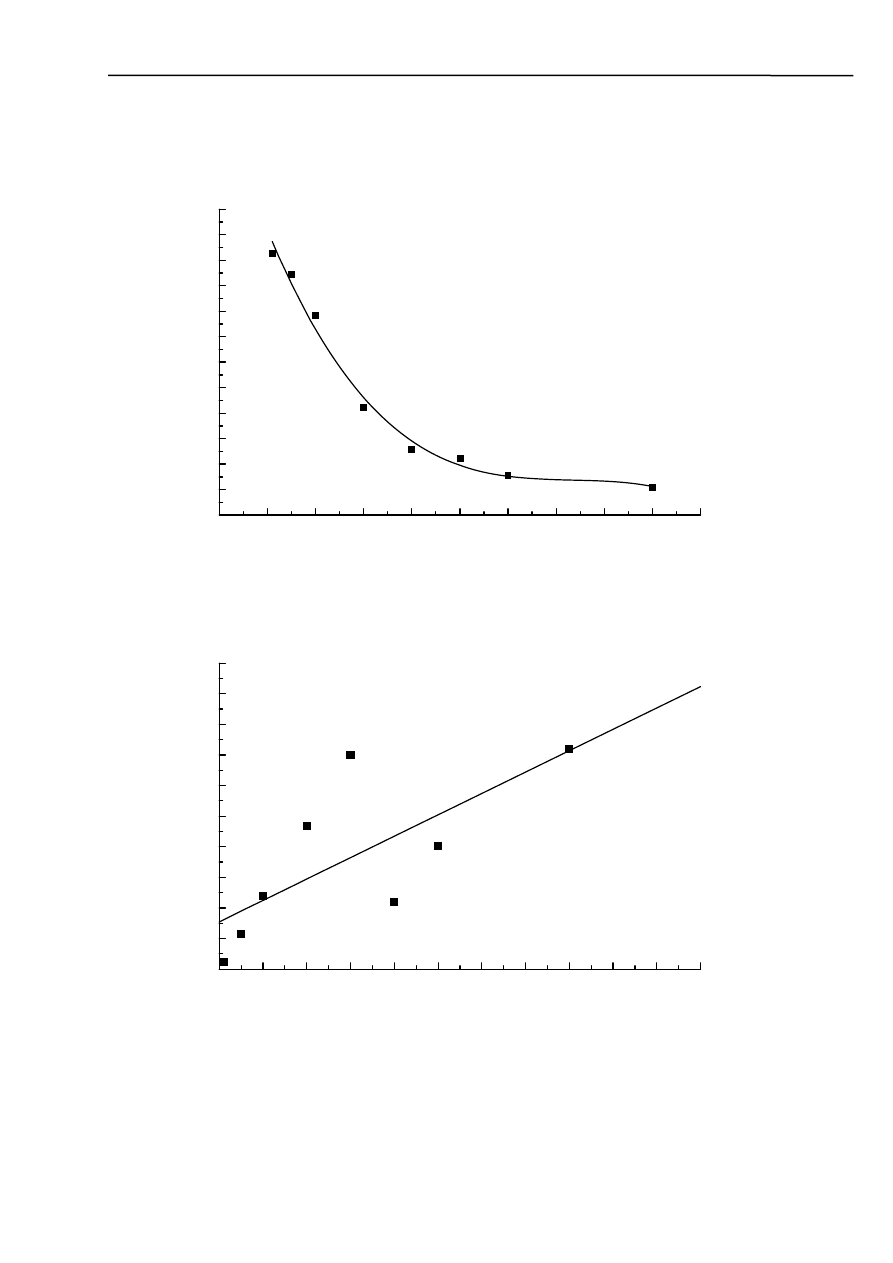
Na podstawie wyników pomiarów zestawionych w tabeli wykonano charakterystyki
częstotliwościowe:
• amplitudową
-1,0k
0,0
1,0k
2,0k
3,0k
4,0k
5,0k
6,0k
7,0k
8,0k
9,0k
-0,2
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
W
zm
oc
ni
eni
e [
V/
V]
Częstotliwość [Hz]
• fazową
0,0
1,0k
2,0k
3,0k
4,0k
5,0k
6,0k
7,0k
8,0k
9,0k
10,0k 11,0k
0,0
50,0
100,0
150,0
200,0
250,0
300,0
350,0
400,0
450,0
500,0
P
rz
es
uni
ęci
e f
az
ow
e [
o
]
Częstotliwość [Hz]

CYFROWE PRZETWARZANIE SYGNAŁÓW
33
Na podstawie pomiarów i wykreślonych charakterystyk możemy zauważyć, że badany układ jest
filtrem 5-go rzędu o nieco przesuniętym paśmie w stronę wyższych częstotliwości do 5 kHz. W
założeniach pasmo filtru powinno się zawierać w granicach 0 do 1 kHz, natomiast z pomiarów
wynika, iż pasmo przepustowe mieści się w przedziale 0 do 5 kHz. Wynika to z niedokładności
wykonanych pomiarów. Charakterystyka amplitudowa w paśmie zaporowym jest mało stroma. Filtr
wzmacnia sygnał wejściowy w przybliżeniu dwukrotnie. Charakterystyka fazowa została
aproksymowana liniowo i jest rosnący. W pasmie przepustowym opóźnienie fazowe wynosi od 75
° do
250
o
i rośnie ze wzrostem częstotliwości. Dla częstotliwości 1kHz wynosi ok. 117
o
.
Wyszukiwarka
Podobne podstrony:
1f Cyfrowe przetwarzanie sygnal Nieznany
Cyfrowe Przetwarzanie Sygnalow Nieznany
1f Cyfrowe przetwarzanie sygnal Nieznany
30 Cyfrowe przetwarzanie sygnałów
Cyfrowe Przetwarzanie Sygnałów Wykład cz1
1f Cyfrowe Przetwarzanie sygnałów
Cyfrowe przetwarzanie sygnałów fonicznych (CPSF) wykład 06 art
zad egz 2002-, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAM
Cyfrowe przetwarzanie sygnałów
zad egz 2001-, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAM
filtr-cyfrowy, Politechnika, IV sem, Cyfrowe Przetwarzanie Sygnałów i Obrazów
TS 15 Wrzesnia 2003r, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANI
falki, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAMIN 2
Wysylanie wiadomosci e mail Cyfrowe przetwarzanisygnalow Filtry, Cyfrowe przetwarzanisygnałów Filtry
1 Cyfrowe przetwarzanie sygnalow(CPS) Wprowadzenieid 9141 ppt
Cyfrowe Przetwarzanie Sygnałów Wykład cz1
Cyfrowe przetwarzanie sygnałów fonicznych (CPSF) wykład 06 art
więcej podobnych podstron