Cyfrowe

Cyfrowe

Przetwarzanie

Przetwarzanie

Sygnałów

Sygnałów

dla kierunku: Informatyka

specjalność: Przemysłowe Systemy Informatyczne

cześć 1

Wybrane zagadnienia z teorii sygnałów

Dyskretyzacja sygnału analogowego

Odtwarzanie i obliczanie parametrów sygnału na podstawie

próbek

Instytut Metrologii Elektrycznej

UNIWERSYTETU ZIELONOGÓRSKIEGO

dr hab. inż. Jerzy Bolikowski, prof. UZ

OGÓLNA CHARAKTERYSTYKA PRZEDMIOTU

CPS

1-2

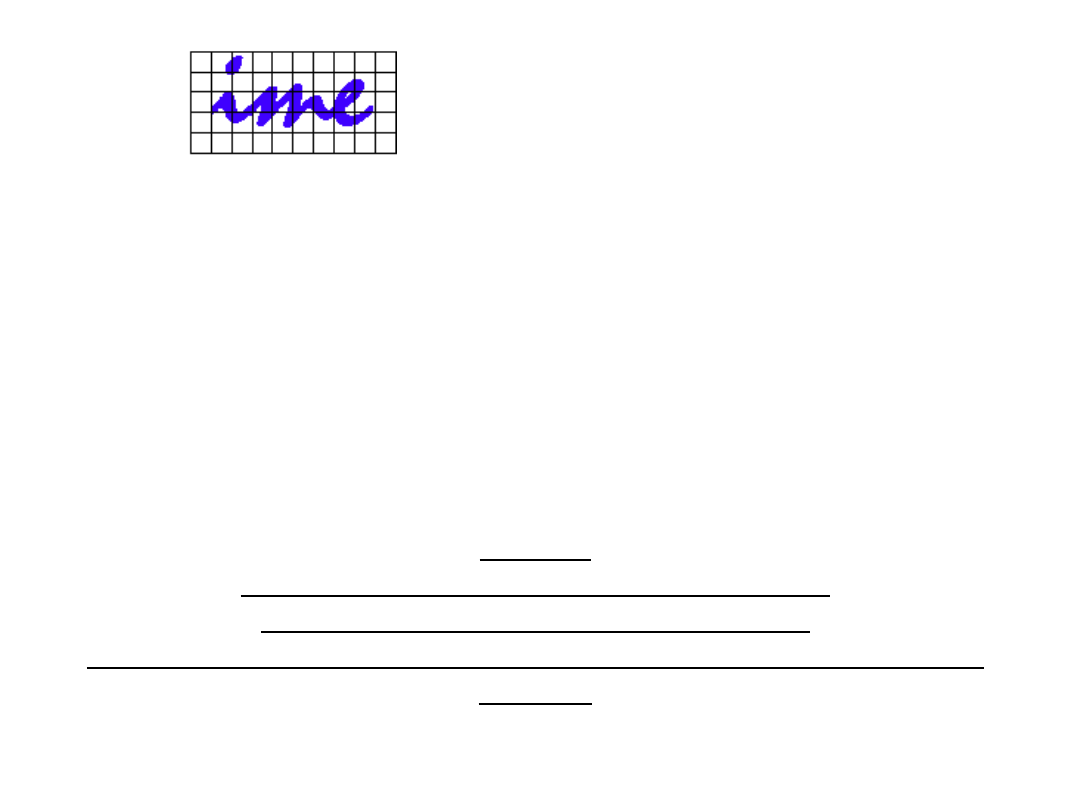
W otaczającym nas środowisku występuje wiele sygnałów fizycznych niosących informację na,
podstawie której podejmowane są różne decyzje. Organizm człowieka wyposażony jest w pięć kategorii
czujników: słuchu, dotyku, smaku, zapachu i wzroku. Czujniki te przetwarzają wielkości fizyczne w
sygnały elektryczne, które za pośrednictwem nerwów przesyłane są do „analogowego superkomputera”
jakim jest mózg. W większości przypadków decyzje podejmowane są samodzielnie przez człowieka.
Istnieją jednak sytuacje, w których niezbędne lub celowe jest wspomaganie człowieka przez urządzenia
elektroniczne, a przede wszystkim przez cyfrowy mikrokomputer. Aby komputer mógł przeprowadzić
odpowiednią analizę zawartej w sygnałach informacji (cyfrowe przetwarzanie sygnałów) do jego pamięci
muszą być wprowadzone liczby, które z wystarczającą dokładnością odwzorowują rzeczywiste sygnały.
Po przetworzeniu przez mikrokomputer rezultat obróbki ma postać sekwencji liczb. Praktyczne
wykorzystanie wyników cyfrowego przetwarzania sygnałów wymaga zazwyczaj przetworzenia ich w
postać analogową, a więc w sygnał elektryczny.

Operacje na sygnałach elektrycznych mogą
być

przeprowadzone

z

pominięciem

konwersji analogowo-cyfrowej a potem
cyfrowo-analogowej

przez

coraz

doskonalsze układy elektroniki analogowej
w

które

przemysł

półprzewodnikowy

zainwestował wielkie sumy pieniędzy.

Czym zatem uzasadnione jest coraz

powszechniejsze stosowanie

cyfrowego przetwarzania sygnałów?

W

ie

lk

o

śc

i

fi

zy

cz

n

e

czujniki

sygnały

elektryczne

przetwarzanie

analogowo-

cyfrowe

liczb

y

cyfrowe

przetwarzanie

sygnałów

przetwarzanie

cyfrowo-

analogowe

liczb

y

sygnały

elektryczne

LITERATURA PODSTAWOWA

•

Marven C., Evers G.: Zarys cyfrowego

przetwarzania sygnałów. WKiŁ. 1999.

•

Lyons R.G.: Wprowadzenie do cyfrowego

przetwarza-nia sygnałów. WKiŁ. 1999.

•

Szabatin J.: Podstawy teorii sygnałów. WKiŁ.

1982.

•

van de Plassche R.: Scalone przetworniki

analogo-wo-cyfrowe i cyfrowo-analogowe. WKiŁ.
1997.

•

Kulka Z., Libura A., Nadachowski M.:

Przetworniki analogowo-cyfrowe i cyfrowo-
analogowe. WKiŁ. 1987.

CPS

1-3

programowalność

możliwe jest skonstruowanie jednej konfiguracji sprzętowej, która przez zmianę
oprogramowania może służyć do realizacji różnych zadań cyfrowego przetwarzania
sygnałów. W technice analogowej do każdego zadania musi być zaprojektowany i
wykonany inny układ elektroniczny.

stabilność

algorytmy cyfrowego przetwarzania sygnałów (programy) są odporne na zmianę
warunków eksploatacji (temperatura, wilgotność, zakłócenia elektromagnetyczne,
procesy starzeniowe itp.). Dla poprawnej pracy układów analogowych wymagane jest
stosowanie często bardzo skomplikowanych metod i układów korygujących wpływ
czynników zewnętrznych.

powtarzalność

Programy realizujące algorytmy cyfrowego przetwarzania sygnałów działają identycznie
na różnych egzemplarzach tego samego urządzenia. Każdy układ analogowy, ze
względu na rozrzut parametrów tworzących go elementów, ma inne, mieszczące się w
pewnym zakresie, właściwości.

kompresja danych

Przy ograniczonej przepustowości kanałów transmisji zachodzi konieczność kompresji
danych. Przy wykorzystaniu cyfrowej transmisji danych istnieje możliwość bezstratnej
kompresji w przeciwieństwie do transmisji analogowej, gdzie kompresja danych
związana jest z utratą części informacji.

WŁAŚCIWOŚCI CYFROWEGO PRZETWARZANIA SYGNAŁÓW

CPS

1-4

SYGNAŁY I ICH KLASYFIKACJA

W rozumieniu teorii sygnałów,

sygnał

jest pojęciem abstrakcyjnym, modelem

matematycznym wyrażającym się określoną funkcją, przebiegiem stochastycznym lub
dystrybucją.

W technice

sygnał

definiowany jest jako funkcja czasowa dowolnej wielkości o

charakterze energetycznym, w którym można wyróżnić dwa elementy: nośnik i parametr
informacyjny.

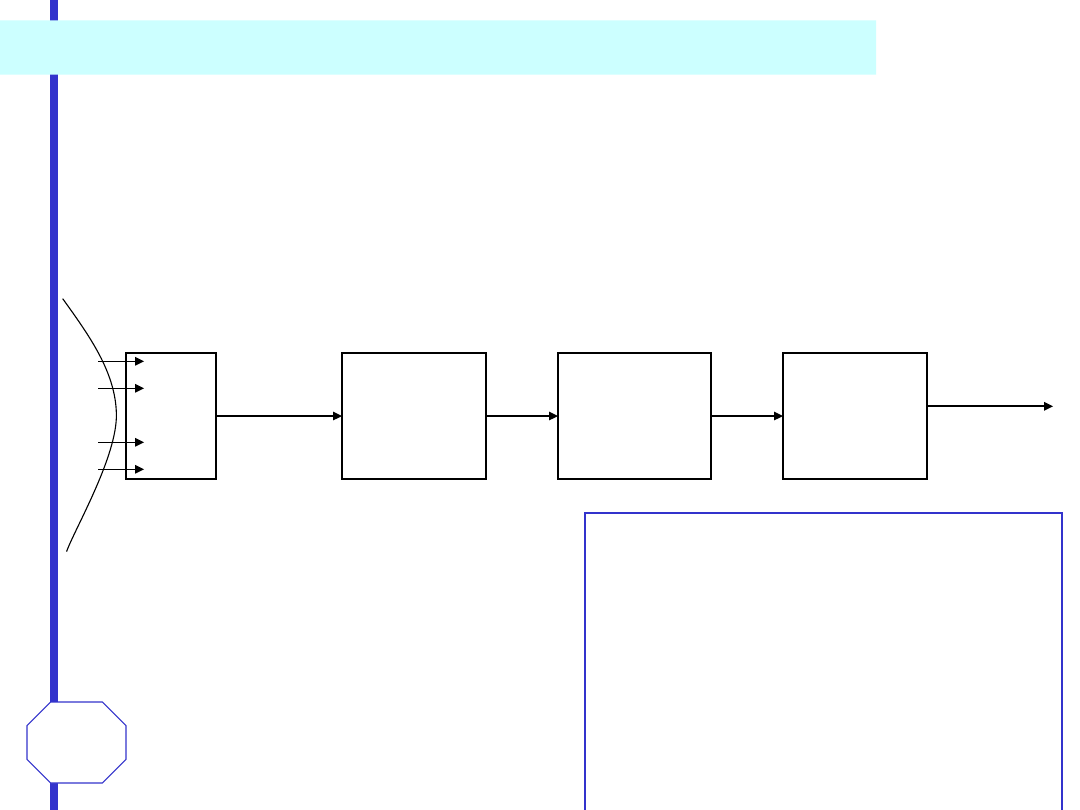
W teorii sygnałów stosowane są dwa, niezależne od siebie, sposoby podziału sygnałów. W
pierwszym sygnały dzieli się na deterministyczne i losowe; w drugim zaś rozróżnia się
sygnały: ciągłe i dyskretne.

sygnały deterministyczne

nieokresow

e

okresow

e

sinusoidalne
(harmoniczn

e)

niesinusoidalne

(poliharmoniczn

e)

niestacjonar

ne

sygnały losowe

stacjonarn

e

ergodyczne

nieergodyczne

Sygnałem ciągłym

w czasie jest

funkcja x(t), której dziedziną jest każdy
punkt pewnego przedziału osi czasu.

Sygnałem dyskretnym

w czasie jest

funkcja x[n], której dziedziną jest zbiór
liczb całkowitych.

Sygnałem deterministycznym

jest sygnał,

którego każda wartość jest jednoznacznie
określona za pomocą ścisłych zależności
matematycznych.

Sygnały opisane za pomocą procesu stochastycznego
nazywa się

sygnałami losowymi

, a konkretna funkcja

(sygnał) jest traktowana jedynie jako jedna z wielu
możliwych realizacji procesu stochastycznego.

Stacjonarnym

nazywany

jest

proces

stochastyczny,

którego

charakterystyki

statystyczne (wartość średnia, wartość średnia
kwadratowa, funkcja korelacji) nie są funkcjami
czasu.

Ergodycznym jest proces, którego dowolna
statystyczna charakterystyka, otrzymana ze
zbioru realizacji w dowolnej chwili, jest równa
podobnej charakterystyce otrzymanej z jednej
realizacji procesu obliczonej jako średnia w
dostatecznie długim czasie.

Na podstawie fundamentalnych praw lub w
rezultacie wielu obserwacji można opisać
dokładnie wartość syg-nału deterministycznego
w dowolnej chwili, również w przyszłości.

CPS

1-5

WYBRANE SYGNAŁY DETERMINISTYCZNE

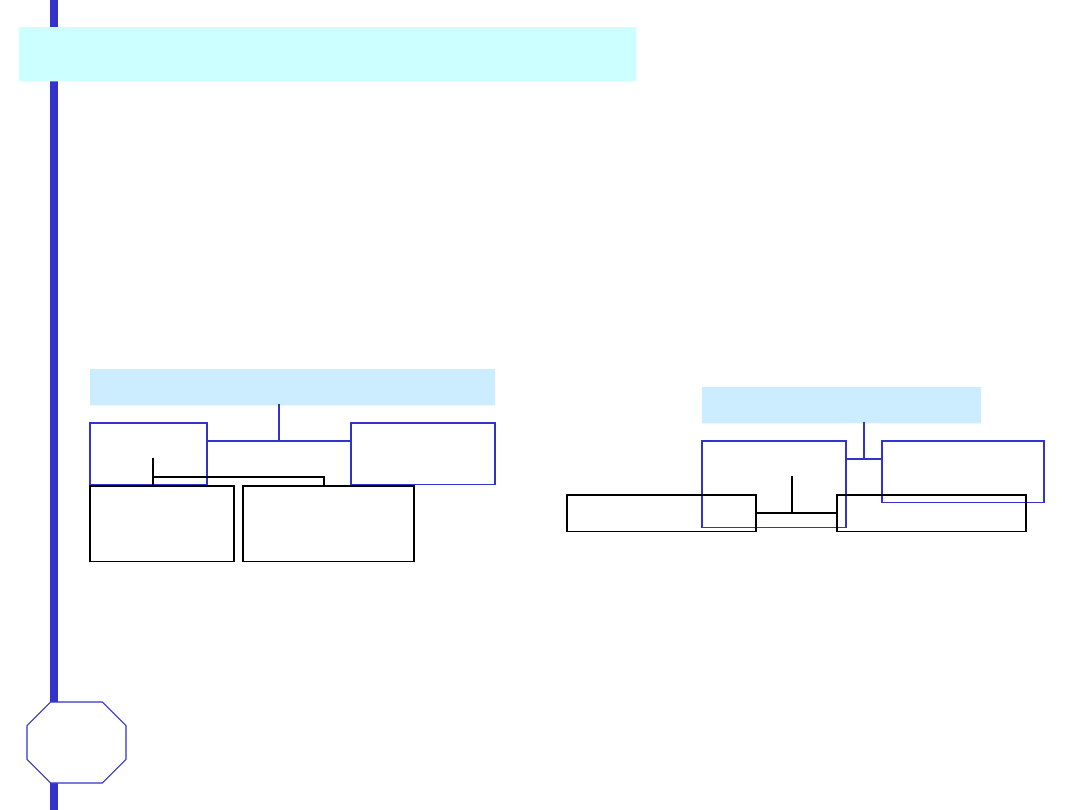
Impuls prostokątny (t)

x(t)

t

-1/2

1/2

0

1





























2

1

dla

1

2

1

dla

2

1

2

1

dla

0

t

t

t

t

t

x

)

(

)

(



x(t)

b

c

a

t











 



b

c

t

a

t

x



)

(

Sygnał Sa



















0

dla

1

0

dla

0

0

0

t

t

t

t

t

Sa

t

x







sin

)

(

0





0

3







0

3





0







CPS

1-6

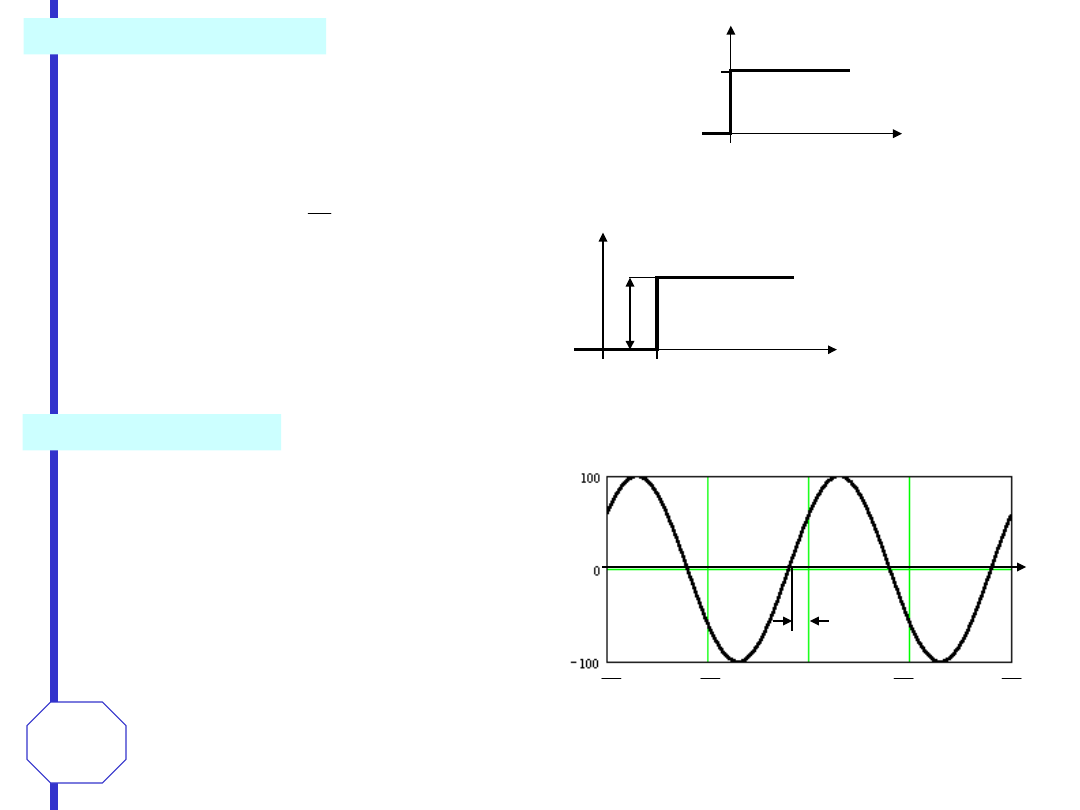
Skok jednostkowy - 1(t)






















0

dla

0

0

dla

2

1

0

dla

1

1

t

t

t

t

t

x

)

(

)

(

x(t)

t

1

Skok sygnału o dowolną wartość i w
dowolnym punkcie osi czasu można
zapisać jako:

)

(

)

(

0

1

t

t

A

t

x





x(t)

A

t

0

t

Sygnał sinusoidalny

)

,

(

)

sin(

)

(











t

t

X

t

x





0

t



0

0





0

2





0







0

2







CPS

1-7

WYBRANE SYGNAŁY STOCHASTYCZNE

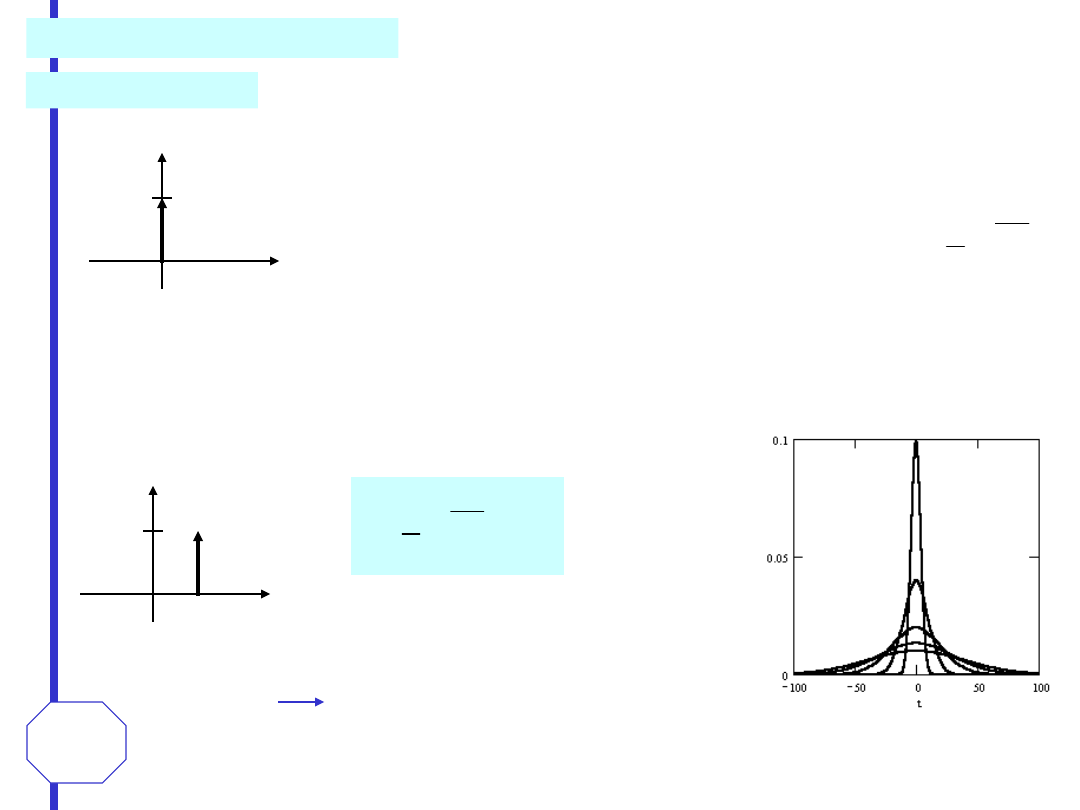
Sygnał harmoniczny stochastyczny

)

cos(

)

(

)

(













t

t

t

Konkretną realizacją sygnału

t jest sygnał harmoniczny deterministyczny

)

cos(

)

(









t

X

t

x

Zmienne losowe opisane odpowiednimi funkcjami gęstości prawdopodobieństwa

Szum śrutowy













i

i

t

k

t

)

(

)

(





Szum śrutowy jest przykładem sygnału z parametrem statystycznym;
jest ciągiem zmiennych losowych, których realizacje tworzą ciągi na osi
czasu, a k(t) jest sygnałem deterministycznym losowym. Można go traktować
jako sumę sygnałów impulsowych poprzesuwanych losowo względem siebie o
odcinki czasu . Szum śrutowy jest modelem matematycznym sygnałów
przypadkowych, których źródłem są zjawiska fizyczne związane z przepływem
prądu elektrycznego w elementach elektronicznych.

 

i



i



CPS

1-8

SYGNAŁY DYSTRYBUCYJNE

Delta Diraca - (t)

 

















0

t

dla

0

t

dla

0

t

(t)

0

t

1

Dystrybucja Diraca (delta Diraca) jest modelem matematycznym
sygnału impulsowego o nieskończenie krótkim czasie trwania i
nieskończenie dużej amplitudzie. Sygnał taki nie jest realizowalny
fizycznie, ale stanowi wygodny abstrakcyjny model sygnału
fizycznego, którego przebieg ma kształt bardzo wąskiego
impulsu.













1

dt

t)

(

(t-t

0

)

0

t

1

t

0

Ciągiem definiującym dystrybucję d(t) może
być na przykład ciąg funkcji gaussowskich o
postaci:

2

2

1











t

e

t





)

,

(

Wraz ze zbliżaniem się parametru  do zera funkcje gaussowskie

są coraz węższe, a jednocześnie rośnie ich wartość. W granicy
ciąg dąży do do wartości, która jest równa zeru dla t różnego od
zera i równa nieskończoności dla t = 0. Jednocześnie pole
ograniczone wykresem każdego elementu ciągu jest równe 1.
Zatem delta Diraca jest granicą ciągu funkcji gaussowskich

 

t

e

t

















2

2

1

0

lim

Jeżeli x(t) jest dowolnym sygnałem, to

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

0

0

0

0

t

t

t

x

t

t

t

x

t

x

t

t

x

















Właściwość
próbkowani
a

CPS

1-9

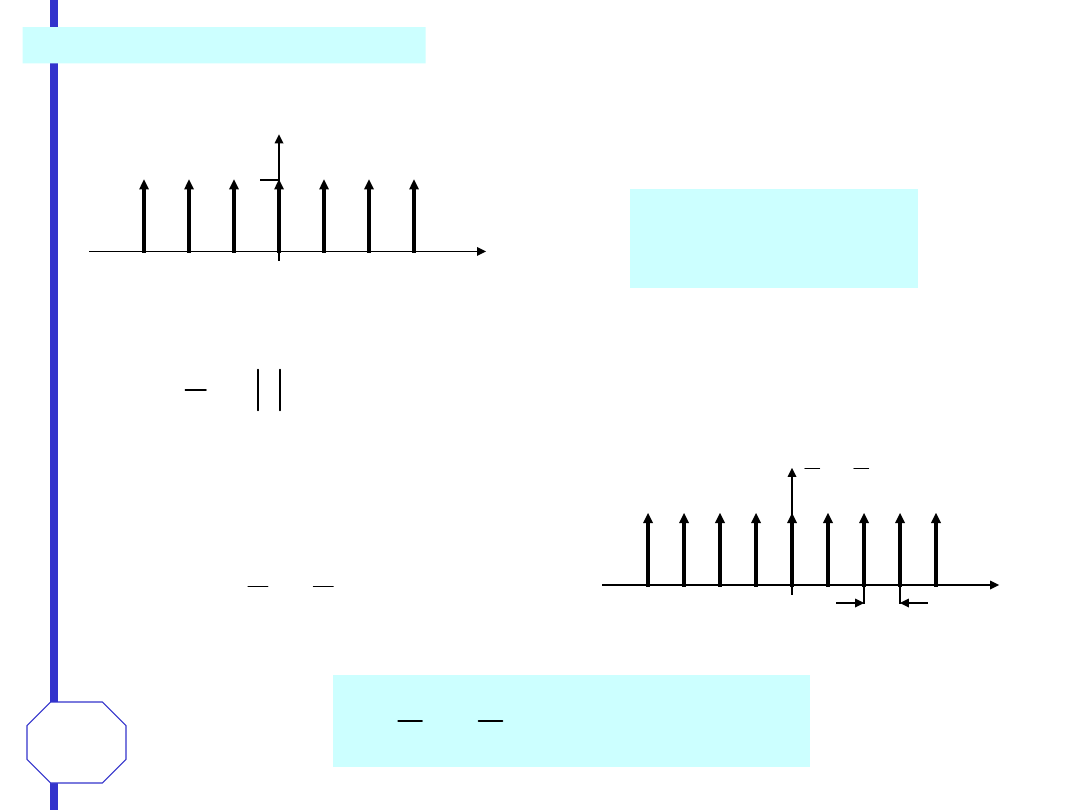
Dystrybucja grzebieniowa - III(t)

Dystrybucja grzebieniowa jest ciągiem okresowo
powtarzających się delt Diraca o jednostkowych
wysokościach

i

jednostkowym

okresie.

Zdefiniowana jest następującym wyrażeniem:













n

n

t

t

III

)

(

)

(















n

n

t

n

x

t

III

t

x

)

(

)

(

)

(

)

(



właściwość próbkowania













n

n

t

t

III

)

(

)

(









właściwość zmiany skali

t

T

)

(

T

t

III

T

1

t

0

1

2

-1

-2

-3

3

)

(t

III

1

Z właściwości zmiany skali wynika, że ciąg delt
Diraca jednakowo odległych od siebie o
dowolną odległość T i o jednostkowych
wysokościach można zapisać w postaci:

)

(

T

t

III

T

1

Wówczas operację próbkowania dowolnego sygnału w odstępach czasu T można zapisać następująco:













n

nT

t

nT

x

T

t

III

T

t

x

)

(

)

(

)

(

)

(



1

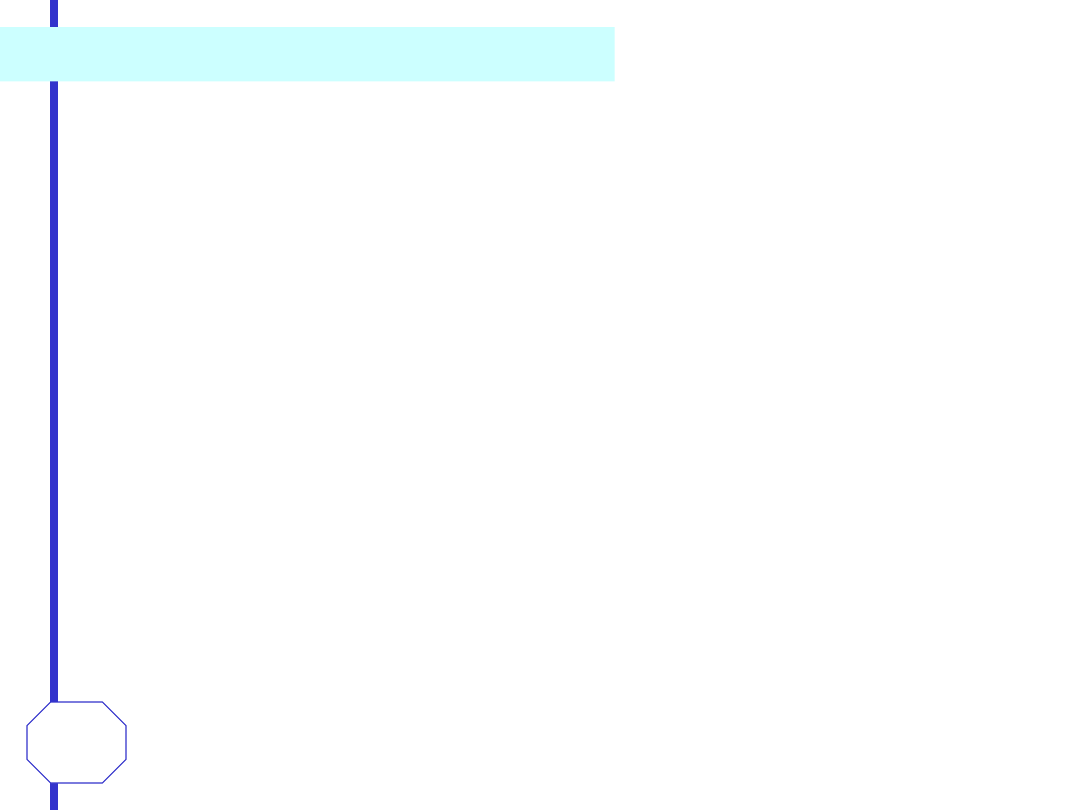
CPS

1-10

W teorii sygnałów pojęciu

sygnał

przyporządkowuje się odpowiednie modele

matematyczne. Wybór tych modeli jest w zasadzie arbitralny ale ze względów
praktycznych bierze się pod uwagę następujące aspekty:

•

Model powinien być możliwie ogólny, tak aby opisywał dostatecznie szeroką klasę

sygnałów fizycznych i abstrahował od jego natury fizycznej.

•

Model powinien zapewniać łatwość analizy matematycznej problemów generacji,

przetwarzania i przesyłania sygnałów.

Wszystkie sygnały fizyczne (istniejące w przyrodzie oraz generowane sztucznie przez
człowieka) trwają w czasie, mają na ogół bardzo skomplikowaną formę i nie dają się opisać
żadną funkcją elementarną. Bezpośrednie badanie analityczne takich sygnałów jest
niezwykle trudne, a czasami niemożliwe. Dobór odpowiedniej

analitycznej

reprezentacji sygnału

jest zagadnieniem kluczowym w analizie sygnałów.

Przedstawienie sygnału w postaci analitycznej powinno zapewnić uproszczenie obliczeń
przy badaniu właściwości sygnału i pomiarach jego parametrów oraz umożliwić głębszą
interpretację niektórych cech fizycznych.
Sygnały mogą być reprezentowane w

dziedzinie czasu

i w

dziedzinie częstotliwości

.

W zależności od celu analizy wybiera się jedną z tych dziedzin wykorzystując odpowiedni
aparat matematyczny.

METODY ANALIZY SYGNAŁÓW

Najczęściej stosowana jest

widmowa (dyskretna) reprezentacja sygnałów

(dziedzina częstotliwości). W przypadku sygnałów okresowych jest to
trygonometryczny lub zespolony

szereg Fouriera

,

a w przypadku sygnałów nieokresowych

całkowe przekształcenie (transformata) Fouriera.

W

dziedzinie czasu

sygnały opisuje się

średnią czasową rzędu

n

lub

funkcją korelacji

.

CPS

11

CPS

1-11

SZEREG FOURIERA - trygonometryczny

Z matematycznego punktu widzenia

zagadnienie dyskretnej reprezentacji

sygnału sprowadza się do aproksymacji

sygnału

x

szeregiem typu





n

i

i

i

x

1



x

i

-

ustalone funkcje



i



liczby rzeczywiste lub zespolone



Po ustaleniu funkcji aproksymującej wyznacza się liczby



i

tak, aby błąd aproksymacji

(według

ustalonego

kryterium)

był

najmniejszy.

Kryterium

tym

jest

błąd

średniokwadratowy. Można udowodnić, że błąd aproksymacji dąży do zera jeśli zastosuje
się zestaw zupełny funkcji ortogonalnych, a liczba wyrazów szeregu dąży do
nieskończoności. Jeśli do aproksymacji użyje się zestaw funkcji sinus i cosinus (najczęściej
stosowany), to dowolną funkcję okresową o okresie T

0

spełniającą warunki Dirichleta,

można przedstawić za pomocą nieskończonego szeregu, zwanego szeregiem Fouriera, o
równaniu

















1

0

0

0

2

1

n

n

n

t

n

b

t

n

a

a

t

x





sin

cos

)

(

dt

t

n

t

x

T

a

T

n





0

0

0

2



cos

)

(

dt

t

n

t

x

T

b

T

n





0

0

0

2



sin

)

(

0

0

2

T







trygonometryczny

szereg Fouriera

2

2

n

n

n

b

a

X



















n

n

n

a

b

arctg



widmo

amplitudowe

sygnału

widmo fazowe

sygnału

dt

t

t

x

T

a

T





0

0

0

1

)

(

ponieważ

)

cos(

sin

cos















X

b

a













1

0

0

2

1

n

n

n

t

n

X

a

t

x

)

cos(

)

(





gdzie:

SYGNAŁY W DZIEDZINIE CZĘSTOTLIWOŚCI

CPS

12

CPS

1-12

SZEREG FOURIERA - wykładniczy











n

t

jn

n

e

F

t

x

0



)

(

Uwzględniając zależności Eulera







sin

cos

j

e

j











sin

cos

j

e

j







otrzymuje się

można wykazać, że

)

(

)

(

n

n

n

n

n

n

jb

a

F

jb

a

F

a

F













2

1

2

1

0

0







0

0

0

0

1

T

t

jn

n

dt

e

t

f

T

F



)

(

zespolony szereg

Fouriera

zespolone widmo

Fouriera

oraz

n

n

n

n

n

n

n

n

n

n

F

b

a

A

F

F

j

b

F

F

a

2

2

2



















)

(

)

(

Przedstawienie funkcji okresowej za pomocą szeregu Fouriera jest równoważne
rozłożeniu funkcji okresowej na jej funkcje składowe. Częstotliwość f

0

= w

0

/2p

jest podstawową częstotliwością, a pozostałe harmonicznymi częstotliwości f

0

..

Dlatego analiza sygnału przy użyciu szeregu Fouriera nazywa się

analizą

harmoniczną

.

CPS

13

CPS

1-13

SZEREG FOURIERA -

Przykłady

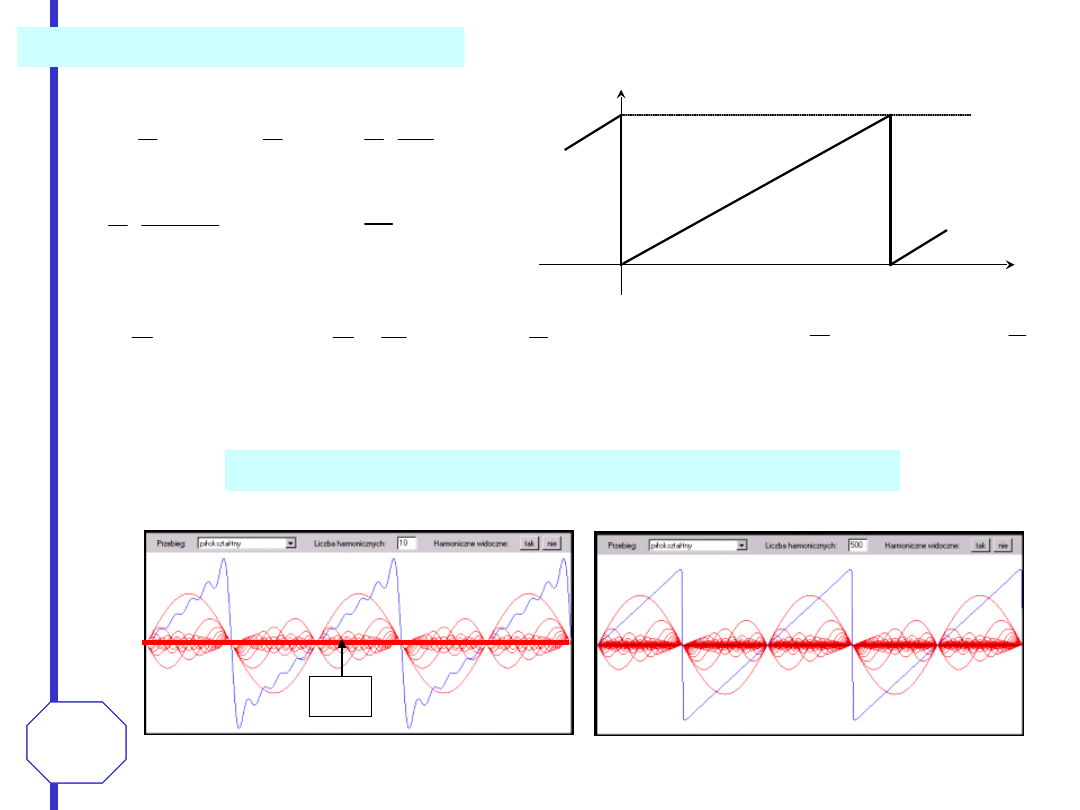
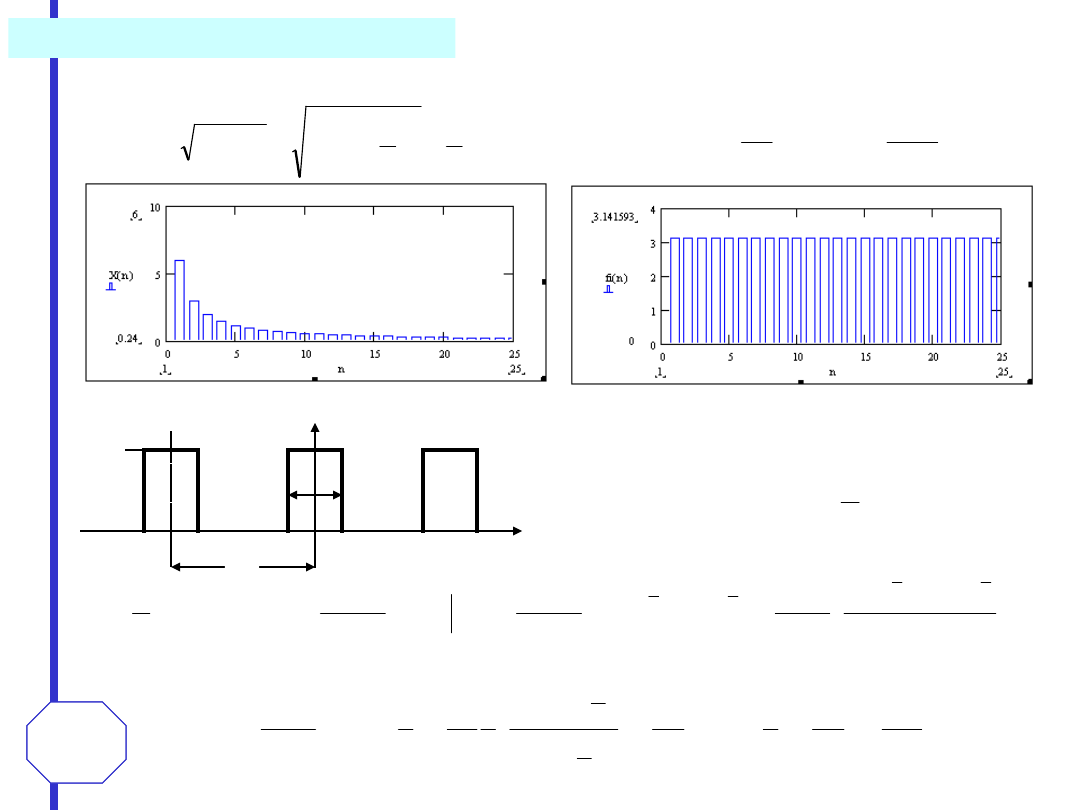
Stąd szereg Fouriera reprezentujący sygnał

x(t)=

3

t

(0<t<2

) ma postać:

Rozwinąć w szereg Fouriera sygnał: x(t)=3t
(0<t<2















6

0

2

2

3

1

2

3

1

3

1

2

2

2

0

2

2

0

0

0



















































)

(

)

(

t

tdt

dt

t

x

T

a

T



3

2

0



a

0

3

1

3

1

3

1

2

0

2

0

2

0

















































ktdt

k

kt

k

t

dx

kt

t

a

k

sin

sin

)

cos(

k

dt

kt

t

b

k

6

3

1

2

0









)

sin(





....

sin

.

sin

.

sin

sin

sin

t

t

t

t

t

y

5

2

1

4

5

1

3

2

2

3

6

3















k = 10

k = 500

źródło: http://skierka.zsh.konin.pl/andrzej/szeregf.html

a

0

/2

x(t)

t

y=3t



2

CPS

14

CPS

1-14

SZEREG FOURIERA -

Przykłady

widmo amplitudowe

k

k

b

a

n

X

n

n

6

6

0

2

2

2

2













 









)

(



































0

6

*

tg

tg

k

arc

a

b

arc

n

n

n

widmo fazowe

t

x(t)

T







A



















t

A

t

x )

(

Rozwinąć w wykładniczy szereg Fouriera sygnał okresowy:





























































































































T

n

Sa

T

A

n

Sa

T

A

n

n

A

n

T

n

A

j

e

e

T

n

A

e

e

T

jn

A

e

T

jn

A

dt

Ae

T

F

jn

jn

jn

jn

T

t

jn

t

jn

n





























































2

2

2

2

2

2

2

2

2

2

1

0

0

0

0

0

2

2

0

2

2

2

2

0

2

2

0

0

0

0

0

0

0

)

(

)

sin(

)

sin(

/

/

/

/

CPS

15

CPS

1-15

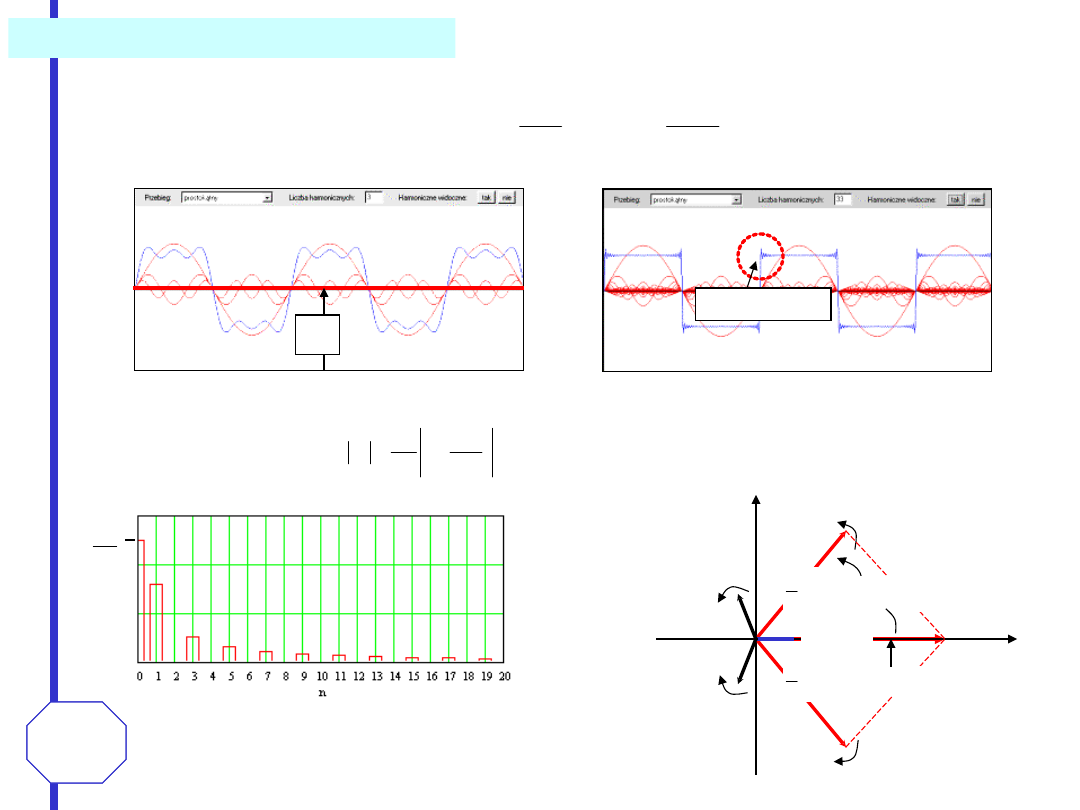
SZEREG FOURIERA -

Przykłady

































n

t

jn

n

t

jn

n

e

T

n

Sa

T

A

e

F

t

x

0

0









)

(

źródło: http://skierka.zsh.konin.pl/andrzej/szeregf.html

n = 3

n = 33

Efekt Gibbsa

F

0

0

0





1



1





1

7

1

7



Re

Im

1

X

2

1

1

X

2

1

)

t

cos(

X

1

1

1







t









1

1

widmo amplitudowe















T

n

Sa

T

A

F

n





T

A



Fazorowy model sygnału

fazor

- wektor obracający się na płaszczyźnie zespolonej

CPS

16

CPS

1-16

SZEREG KOTIELNIKOWA-SHANNONA

Dowolny sygnał x(t) o ograniczonym częstotliwością f

max

paśmie może być reprezentowany przez szereg

































n

m

n

m

nT

t

Sa

nT

x

nT

t

f

Sa

nT

x

t

x

)

(

)

(

)

(

2

)

(

)

(





współczynniki szeregu są wartościami sygnału x(t) w punktach nT

x(nT)

wartości sygnału w

dyskretnych chwilach

czasu

m

f

T

2

1



kolejne wyrazy szeregu

suma wyrazów szeregu

T

CPS

17

CPS

1-17

TRANSFORMACJA FOURIERA

Dyskretne widmo Fouriera istnieje dla sygnałów okresowych. Natomiast w praktycznych
zastosowaniach istnieje konieczność analizy sygnałów nieokresowych. Jeśli sygnał
nieokresowy potraktuje się jako sygnał periodyczny o okresie dążącym do nieskończoności,
to dyskretne widmo Fouriera takiego sygnału przechodzi w granicy w widmo ciągłe.



























0

0

2

1

2

n

d

T

d

T

T









)

(

)

(

)

(

)

(

)

(

)

(















j

X

F

d

e

j

X

t

x

t

x

F

dt

e

t

x

j

X

t

j

t

j

1

2

1





























Para transformat Fouriera

transformata prosta

zespolone widmo

sygnału

transformata odwrotna

)

(

Im

)

(

Re

)

(







j

X

j

j

X

j

X







 



2

2







j

j

j

X

Im(

)

Re(

)

(



















)

Re(

)

Im(

tg







j

j

arc

widmo amplitudowe

sygnału

widmo fazowe

sygnału

CPS

18

CPS

1-18

Sygnał zespolony jest abstrakcyjnym, nierealizowalnym fizycznie modelem sygnału.
Charakterystyki sygnału zespolonego określone są dla całej osi zmiennej



. Natomiast

interpretację fizyczna mają tylko ich prawe części dla

 

0

Widmo amplitudowe i widmo fazowe reprezentują strukturę częstotliwościową sygnału.
Reprezentacja ta ma dla sygnałów rzeczywistych wyraźny

sens fizyczny

. Dla



widmo

sygnału jest wielkością fizyczną w nie mniejszym stopniu niż sam sygnał. Można je
zmierzyć lub obejrzeć na ekranie analizatora widma. Na podstawie widma można w sposób
jednoznaczny odtworzyć sygnał. Widmo sygnału jest więc alternatywnym i równoważnym
sposobem przedstawienia sygnału. Pełna informacja o sygnale jest „zapisana” w jego
widmie. Wszelkie cechy sygnału w dziedzinie czasu mają swoje odzwierciedlenie w
dziedzinie częstotliwości. Operacje przeprowadzane na widmie sygnału oddziaływają na
przebieg i parametry sygnału w dziedzinie czasu.
Część mocy sygnału

P, która przypada na przyrost pulsacji  nazywana jest widmową

gęstością mocy

SENS FIZYCZNY WIDMA SYGNAŁU

















d

dP

P









lim

)

(

Widmo gęstości mocy jest rzeczywistą funkcją pulsacji



. Nie zawiera ono jednak żadnej

informacji o fazie sygnału. Informacja ta jest tracona przy obliczaniu wartości średniej, co
jest niezbędne dla wyznaczania mocy.
Widmo gęstości mocy jest rzeczywiste, zawsze dodatnie i parzyste.

Ponieważ przy obliczaniu gęstości widmowej mocy informacja o fazie jest tracona,
funkcja ta nie zawiera pełnej informacji o sygnale. Stąd obliczenie odwrotne nie jest
możliwe.

)

(

)

(













CPS

19

CPS

1-19

WYBRANE WŁAŚCIWOŚCI TRANSFORMACJI FOURIERA

)

(

)

(

)

(

)

(





bY

aX

t

by

t

ax





















a

X

a

at

x



1

)

(

0

0

t

j

e

X

t

t

x











)

(

)

(

liniowość

zmiana skali (podobieństwo)

Jeśli a>1, to skala czasu jest rozszerzana, sygnał jest „rozciągnięty” w czasie.
Rozszerzenie skali czasu powoduje zawężenie skali częstotliwości i jednocześnie zwiększa
się a-krotnie gęstość widmowa. Fizycznie oznacza to, że zmniejsza się szybkość zmian
sygnału, a widmo skupia się wokół małych częstotliwości, jego gęstość w tym zakresie
wzrasta.
Dla 0<a<1 sygnał jest „ściśnięty” w czasie, a efekty w dziedzinie częstotliwości są
przeciwne.

przesunięcie w dziedzinie czasu

Widmo amplitudowe sygnału przesuniętego nie ulega zmianie w stosunku do
widma amplitudowego sygnału nieprzesuniętego. Natomiast widmo fazowe
powiększa się o składnik (-

0

t). Jest to całkowicie zgodne z sensem fizycznym

przesunięcia sygnału na osi czasu. Struktura częstotliwościowa amplitud
poszczególnych harmonicznych sygnału nie zmienia się. Zmieniają się natomiast
fazy poszczególnych harmonicznych względem układu odniesienia.

0

t

j

e





Przesunięcie sygnału na osi czasu o t

0

odpowiada pomnożeniu widma przez czynnik zespolony .

CPS

20

CPS

1-20

)

(

)

(

0

0









 X

e

t

x

t

j

przesunięcie w dziedzinie częstotliwości (modulacja)

)

(

)

(

0

0









 X

e

t

x

t

j

)

(

)

(

0

0













X

e

t

x

t

j

Jeśli widmo sygnału przesuwa się w prawo o wartość 

0

>0, to sygnał należy pomnożyć

przez sygnał wykładniczy zespolony , czyli

t

j

e

0



Przesunięcie widma sygnału w lewo o wartość 

0

>0 odpowiada pomnożeniu sygnału

przez sygnał zespolony , a więc

t

j

e

0





Dodając stronami powyższe pary transformat otrzymuje się





)

(

)

(

cos

)

(

0

0

0

2

1



















X

X

t

t

x

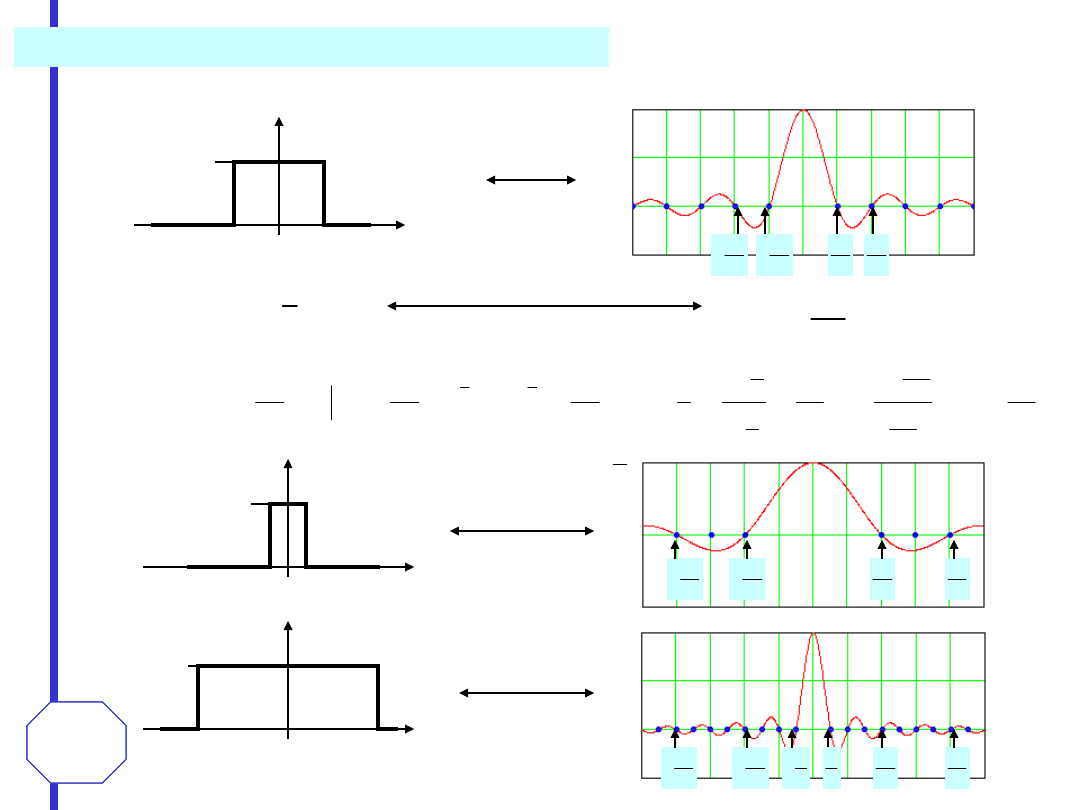
Z powyższej zależności wynika, że pomnożenie sygnału harmonicznego przez
sygnał

x(t)

powoduje rozszczepienie widma na dwie części przemieszczone w

prawo i w lewo o wartość 

0

. Operacja ta nazywana jest modulacją i

wykorzystywana jest w telekomunikacji do przesyłania sygnałów na dalsze
odległości. Sygnałem modulowanym jest sygnał harmoniczny (informacja zawarta
jest w jego częstotliwości), a sygnałem modulującym sygnał

x(t).

CPS

21

CPS

1-21

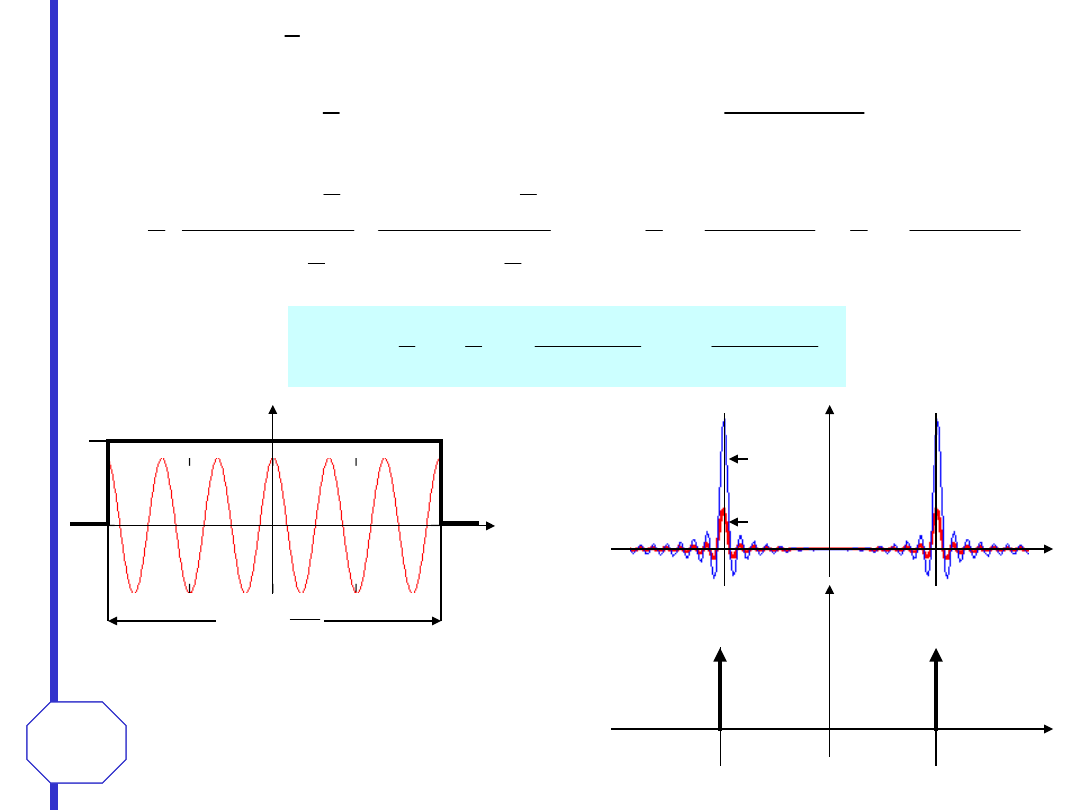
PRZYKŁADY PAR TRANSFORMAT FOURIERA

x(t)

t

-/4

/4

0

A

impuls prostokątny (funkcja bramkowa)























































2

2

2

2

2

2

2

2

2

2

2

2

2

2

2



















































Sa

A

A

A

j

j

A

e

e

j

A

e

j

A

dt

Ae

X

j

j

t

j

t

j

sin

sin

)

sin(

)

(

/

/

/

/

















t













2





Sa

A

x(t)

t

-



0

A

x(t)

t

-/2

/2

0

A





2





4





2







4





A

2



A



A

2





4







4





8





8











4





8











4







8



CPS

22

CPS

1-22



















































































































































2

2

2

2

2

2

2

2

2

2

0

0

0

0

0

0

2

2

2

2

0

0

0

0

)

(

)

(

lim

)

(

)

(

sin

)

(

)

(

sin

lim

lim

cos

lim

cos

/

/

/

/











































































Sa

Sa

dt

e

e

e

dt

e

t

t

t

F

t

j

t

j

t

j

t

j

















































2

2

2

0

0

0

)

(

)

(

cos





















Sa

Sa

t

t

1

0

0

12

6









 T

t

x(t)



















t

t

0

cos

funkcja

0





0





)

(



X

T

6





T

12





0





0





)

(



X







)

(







(t),



0

.

Zwiększanie szerokości impulsu prostokątnego
zwiększa koncentrację widma wokół pulsacji 

0

.

W granicy  funkcja Sa dąży do funkcji

impulsowej (t), co oznacza, że widmo funkcji

cosinus w przedziale nieograniczonym zawiera
funkcje impulsowe umieszczone w punktach 

0



0



0

CPS

23

CPS

1-23

SYGNAŁY W DZIEDZINIE CZASU

wartości średnie

Sygnał x(t) może być opisana średnią czasową rzędu

n

, nazywaną też momentem

zwykłym rzędu

n

:







T

T

n

n

dt

t

x

T

t

x

)

(

)

(

2

1

lub dla sygnałów nieokresowych:











T

T

n

T

n

dt

t

x

T

t

x

)

(

lim

)

(

2

1

Dla n=1 otrzymuje się średnią arytmetyczną, która może być interpretowana jako składowa o
zerowej częstotliwości - składowa stała sygnału lub współczynnik a

0

/2 szeregu Fouriera.

Dla n=2 - moment zwykły drugiego rzędu jest miarą mocy sygnału. Pierwiastek kwadratowy
tej wielkości jest wartością skuteczną sygnału:







T

T

sk

dt

t

x

T

X

)

(

2

2

1

funkcja korelacji

















T

T

T

xy

t

y

t

x

dt

t

y

t

x

T

R

)

(

)

(

)

(

)

(

)

(

lim







2

1

funkcja autokorelacji

















T

T

T

xx

t

x

t

x

dt

t

x

t

x

T

R

)

(

)

(

)

(

)

(

)

(

lim







2

1

CPS

24

CPS

2-24

CPS

24

CPS

2-24

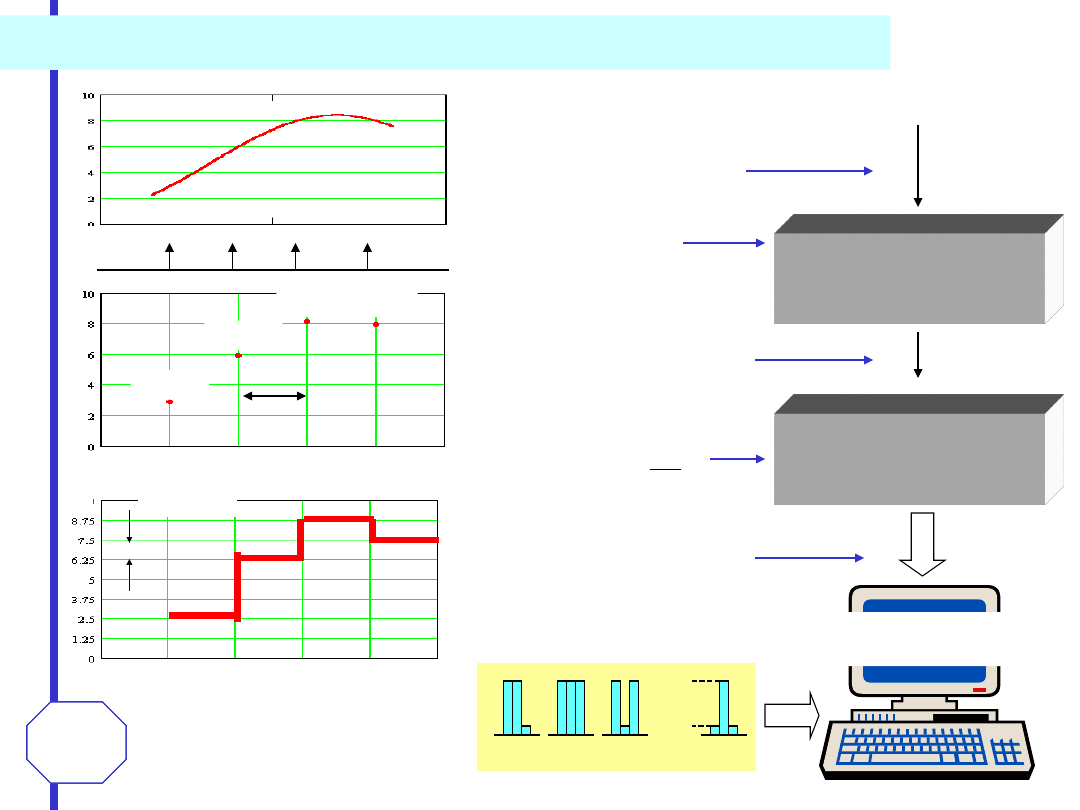
DYSKRETYZACJA SYGNAŁU ANALOGOWEGO

t

s

4t

s

3t

s

2t

s

2.901...

8.187...

5.982...

7.983...





















0

1

0





















1

0

1





















1

1

1





















0

1

1

Cyfrowe przetwarzanie

sygnału

L

H

 

1

x

 

4

x

 

3

x

 

2

x

sygnał cyfrowy w naturalnym

kodzie dwójkowym

Próbkowanie

kwantowani

e

Sygnał analogowy

x(t)

Sygnał o ciągłym

czasie i ciągłej

wartości

Sygnał o dyskretnym

czasie i ciągłej

wartości

Zakodowany
sygnał
o

dyskretnym

czasie
i

dyskretnej

wartości

Przetwornik

próbkująco-pamiętający

S/H

Przetwornik

analogowo-cyfrowy

A/C













1

0

)

(

)

(

)

(

N

n

s

nt

t

t

x

n

y



q=1.25V

7/8
6/8
5/8
4/8
3/8
2/8
1/8
0

V

10

U

FS



t

s















q

U

INT

liczba

we

kodowanie

CPS

25

CPS

2-25

CPS

25

CPS

2-25

CPS

25

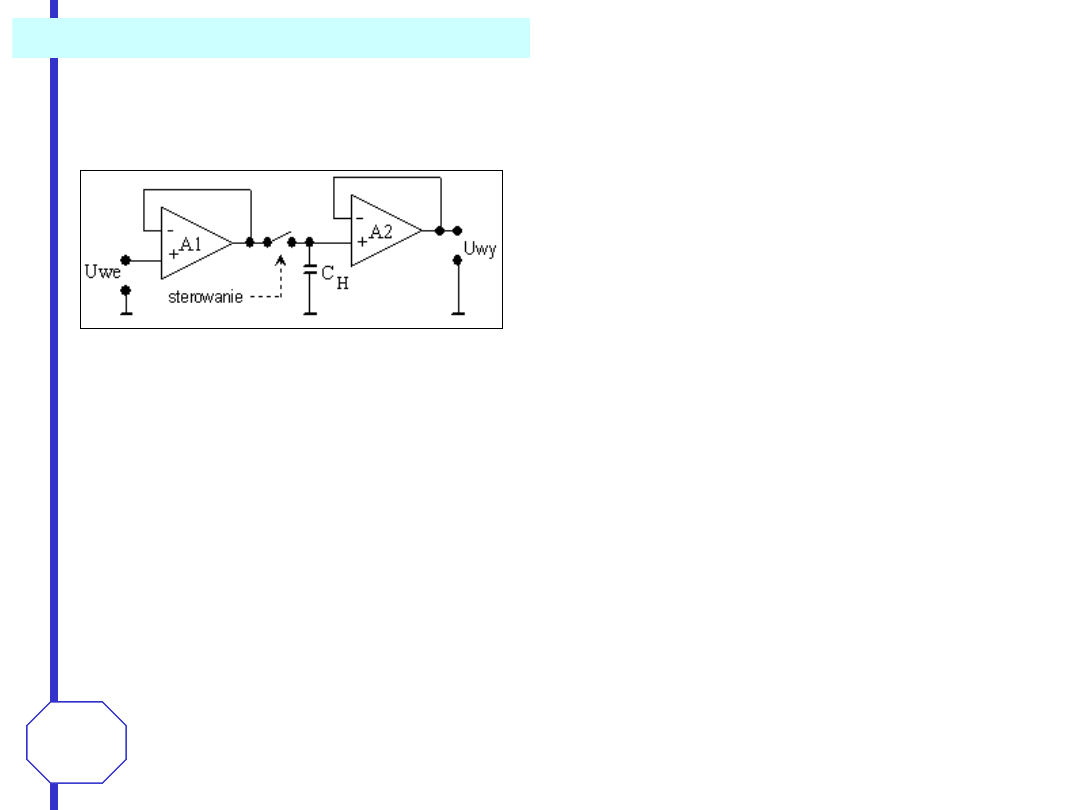
Przetwornik próbkująco-pamiętający

Przetwornik próbkująco-pamiętający (ang. sample-and-hold circuit - S/H) służy do pobrania
próbki napięcia w krótkim okresie (rzędu pojedynczych mikrosekund) i zapamiętania tej
próbki w czasie niezbędnym do przetworzenia jej przez przetwornik analogowo - cyfrowy.

Przetwornik S/H umożliwia zamianę ciągłej
funkcji U

we

(t) w ciąg impulsów U

wy

(t

n

) o

wartościach proporcjonalnych do wartości
napięcia wejściowego w chwilach t

n

.

Moment pobrania próbki określony jest
przez układ sterujący przełącznikiem.

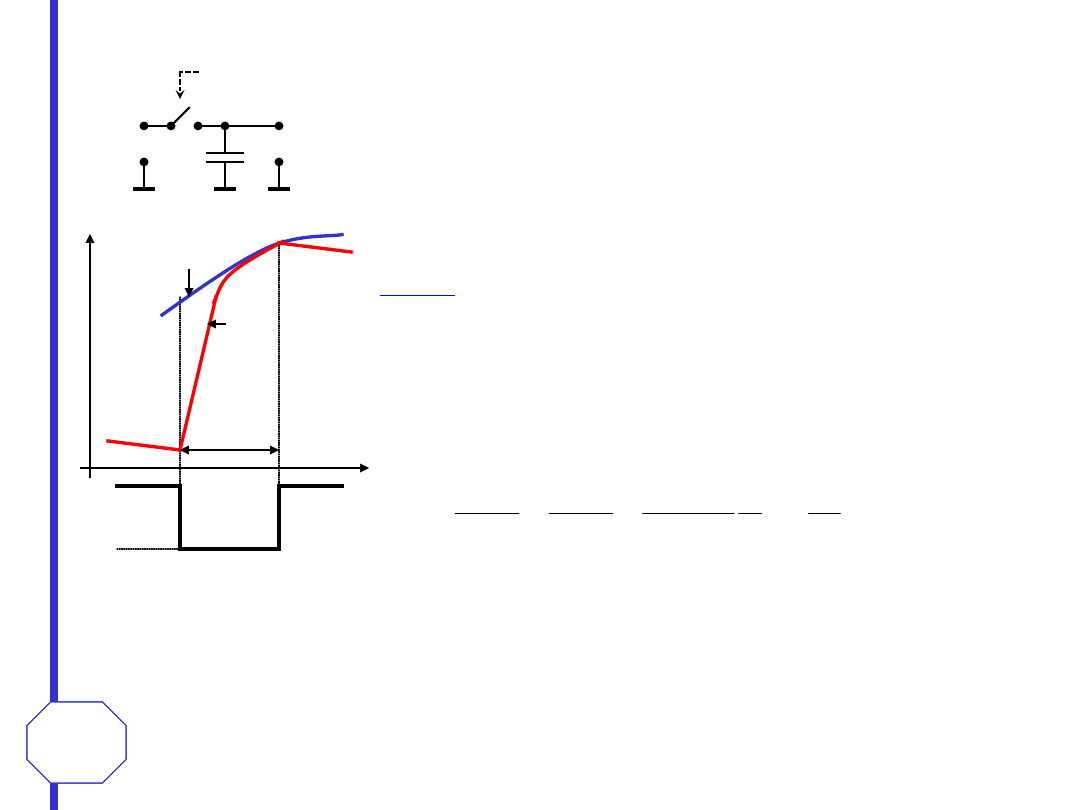
Po zamknięciu przełącznika kondensator pamiętający C

H

ładowany jest przez rezystancję

zamkniętego przełącznika do czasu aż napięcie na kondensatorze osiągnie, z
dopuszczalnym błędem, wartość napięcia wejściowego.
Ta faza pracy układu nazywana jest

próbkowaniem

a jej czas (

czas próbkowania t

S

) jest

równy czasowi trwania impulsu sterującego. Po zakończeniu fazy próbkowania
(przełącznik otwarty) napięcie na kondensatorze, nazywane

próbką napięcia

wejściowego

, jest dostępne na wyjściu układu przez czas zwany

czasem pamiętania t

H

..

Pomiędzy fazami próbkowania i pamiętania występują stany przejściowe.

Jeśli czas próbkowania jest krótszy od czasu pamiętania, to układ nazywany jest układem

próbkująco - pamiętającym

. W przeciwnym przypadku mamy do czynienia z układem

śledząco - pamiętającym T/H

(ang. track-and-hold circuit). Sumę czasów próbkowania i

pamiętania nazywa się

okresem próbkowania

, a jego odwrotność -

częstotliwościa

próbkowania

.

Czas, przez który musi być ładowany kondensator, aby otrzymać żądaną
dokładność próbki nazywany jest

czasem przyjęcia próbki

lub

czasem akwizycji

.

CPS

26

CPS

2-26

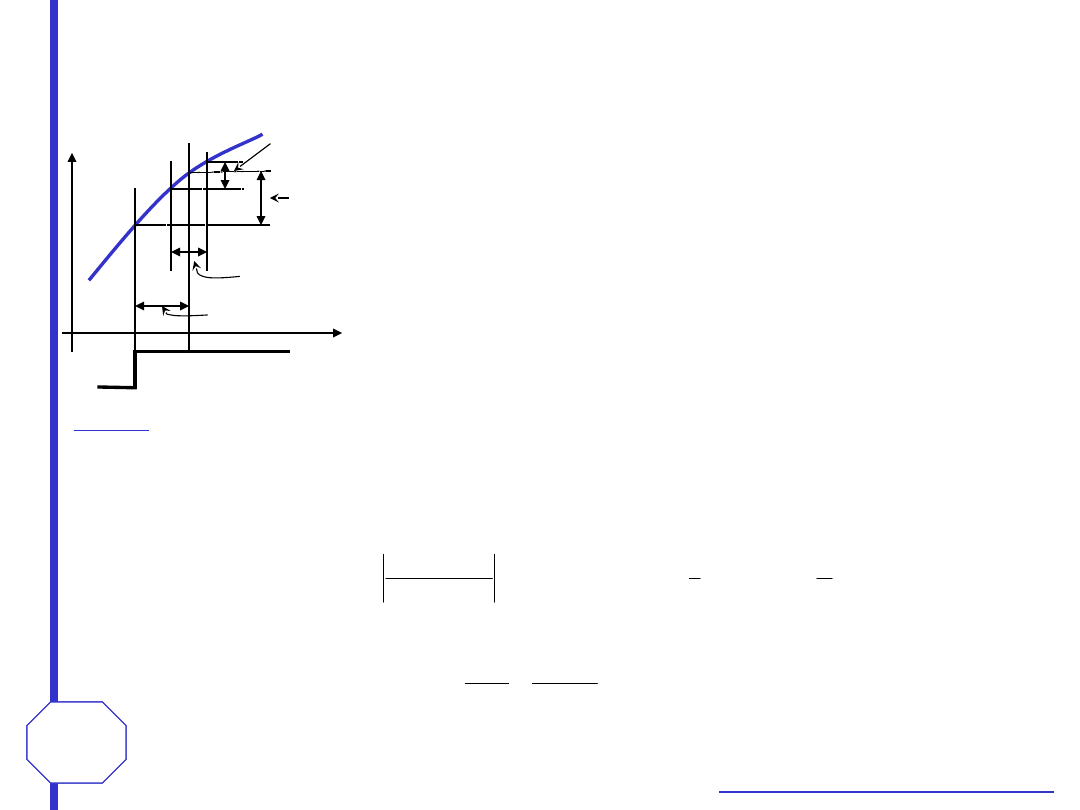
Trzy czynniki mają wpływ na czas przyjęcia próbki. Pierwszym
jest stała czasowa (r

zał

C

H

) wynikająca z rezystancji r

zał

przełącznika w stanie załączenia i pojemności kondensatora
pamiętającego. Drugim - maksymalny prąd wyjściowy I

0max

wzmacniacza A1. Trzecim - maksymalna szybkość zmian
napięcia S

U

na wyjściu tego wzmacniacza. Maksymalna

szybkość zmian napięcia na kondensatorze jest określona albo
przez szybkość ładowania kondensatora maksymalnym
prądem, albo przez maksymalną szybkość zmian napięcia na
wyjściu wzmacniacza, w zależności od tego, która z tych
wartości jest mniejsza.

we

U

H

C

H

C

U

sterowanie

Schemat zastępczy

Przykład

Należy obliczyć czas przyjęcia próbki o wartości 10 V z błędem  = 0.02%

dla układu S/H, w którym pojemność kondensatora pamiętającego C

H

= 5

nF, maksymalny prąd wyjściowy wzmacniacza I

0max

= 10 mA i

maksymalna szybkość zmian na wyjściu wzmacniacza wejściowego S

U

=

5V/ms. Sumaryczna rezystancja wyjściowa wzmacniacza i zamkniętego
przełącznika wynosi r

zał = 120 

Kondensator ładowany jest z szybkością:

s

V

s

V

C

I

dt

du

H

C

H



2

10

5

10

10

9

3

0















max

Szybkość ta nie przekracza maksymalnej szybkości zmian napięcia na wyjściu wzmacniacza,
a więc, w tym przypadku, maksymalna szybkość narastania napięcia na kondensatorze
ograniczona jest przez maksymalny prąd wyjściowy wzmacniacza. Takim prądem będzie
ładowany kondensator ze stałą szybkością 2V/s aż do momentu, kiedy suma napięć na

kondensatorze i sumarycznej rezystancji szeregowej osiągnie wartość 10V. Na
kondensatorze odłoży się w tym czasie napięcie:

t

U

H

S

czas

akwizycji

U

CH

U

we

sterowani

e

V

V

r

I

U

U

zal

we

C

H

8

8

120

10

10

10

3

0

.

max





















CPS

27

CPS

2-27

Stąd pierwszy składnik czasu akwizycji wynosi

s

t

aq



4

4

2

8

8

1

.

.

)

(





Od tego momentu ładowanie kondensatora przebiega wykładniczo ze stałą czasową

ns

F

C

r

H

zal

600

10

5

120

9



















Dopuszczalny bezwzględny błąd przyjęcia próbki wynosi

mV

V

U

U

we

we

2

10

100

02

0

100







.





Z takim błędem bezwzględnym musi ustalić się różnica (10 V - 8.8 V = 1.2 V). Błąd
względny dla tej wartości napięcia wynosi

0017

0

2

1

10

2

3

.

.

'











Czas niezbędny do naładowania kondensatora z takim błędem (drugi składnik czasu akwizycji) wynosi:

s

ns

t

aq







8

3

0017

0

600

2

.

)

.

ln(

)

ln(

'

)

(















Łączny czas przyjęcia próbki przez analizowany układ wynosi:

s

s

s

t

t

t

aq

aq

aq







2

8

8

3

4

4

2

1

.

.

.

)

(

)

(











W obliczeniach pominięto czas opóźnienia włączenia przełącznika, rzędu
kilkudziesięciu nano-sekund dla przełączników półprzewodnikowych.

Wynika stąd, że układ sterujący musi zamykać przełącznik na czas próbkowania nie krótszy niż t

s

= 8,2 s

koniec przykładu

CPS

28

CPS

2-28

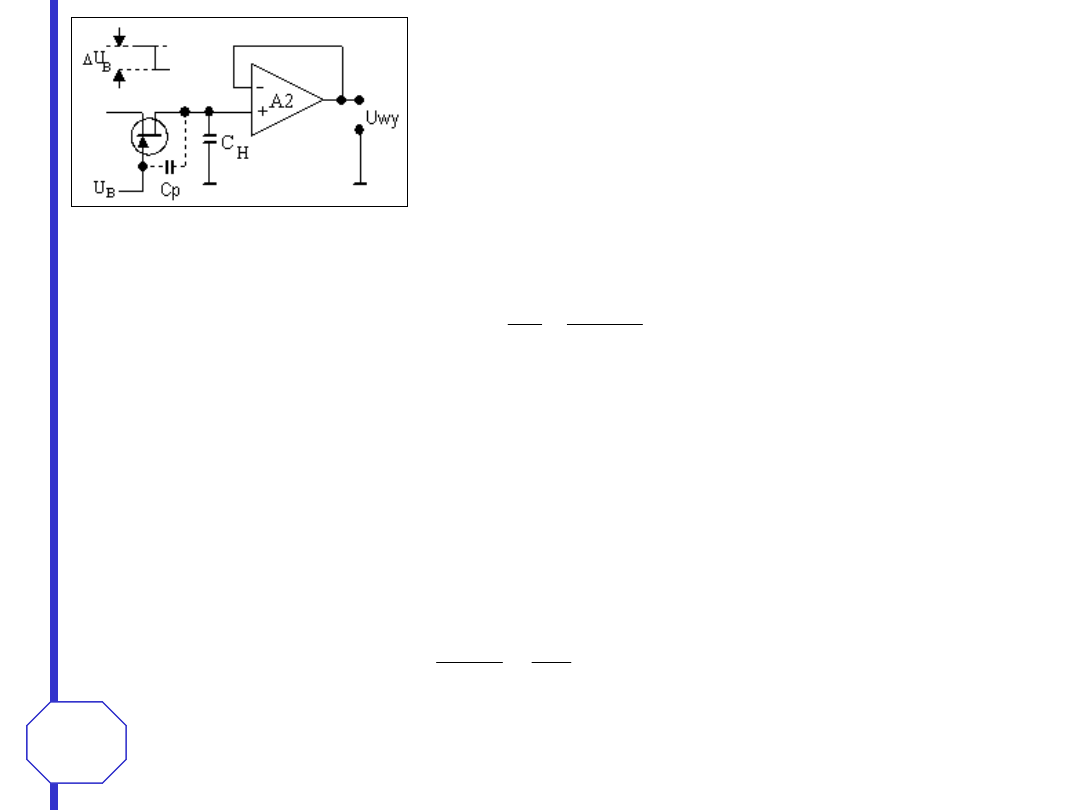
Czas przejścia od fazy próbkowania do fazy pamiętania jest różny od zera. Czas między
chwilą wystąpienia zmiany sygnału sterującego a chwilą pełnego rozwarcia przełącznika
jest określany jako

czas apertury

.

Czas ten może zmieniać się przypadkowo w pewnych
granicach zwanych

drżeniem fazy apertury

(ang. aperture

jitter).
Błąd spowodowany czasem apertury można korygować
przez właściwy dobór chwili zmiany sygnału sterującego.
Błąd wynikający z drżenia fazy apertury nie daje się
skorygować. Przejawia się on tym, że zapamiętana wartość
napięcia będzie się różnić od wartości chwilowej napięcia w
momencie zmiany sygnału sterującego. W pewnych
zastosowaniach wartość tego parametru może być
krytyczna.

Przykład
Mierzone jest napięcie sinusoidalne o wartości maksymalnej 10V i częstotliwości 3 kHz. Wymagane jest
aby błąd wynikający z drżenia fazy apertury był mniejszy od 0.01% wartości maksymalnej (U = 1 mV).

Obliczyć dopuszczalny czas drżenia fazy apertury układu S/H.

Maksymalna szybkość zmiany napięcia mierzonego (w chwili przejścia sinusoidy przez zero) wynosi

s

V

V

s

U

dt

t

U

d

S

t

188400

10

1

3000

2

0























max

max

max

sin

(

Czas, w którym napięcie zmieni się o 1 mV wynosi

ns

s

S

U

t

5

188400

10

1

3











max



Należy więc wybrać układ S/H o drżeniu fazy apertury mniejszym od 5 ns.
Wymaganie takie spełniają dobre scalone układy S/H.

koniec przykładu

czas apertury

drżenie

fazy

apertury

błąd

apertur

y

błąd drżenia

fazy apertury

t

U

H

S

CPS

29

CPS

2-29

CPS

29

CPS

2-29

CPS

29

CPS

2-29

CPS

29

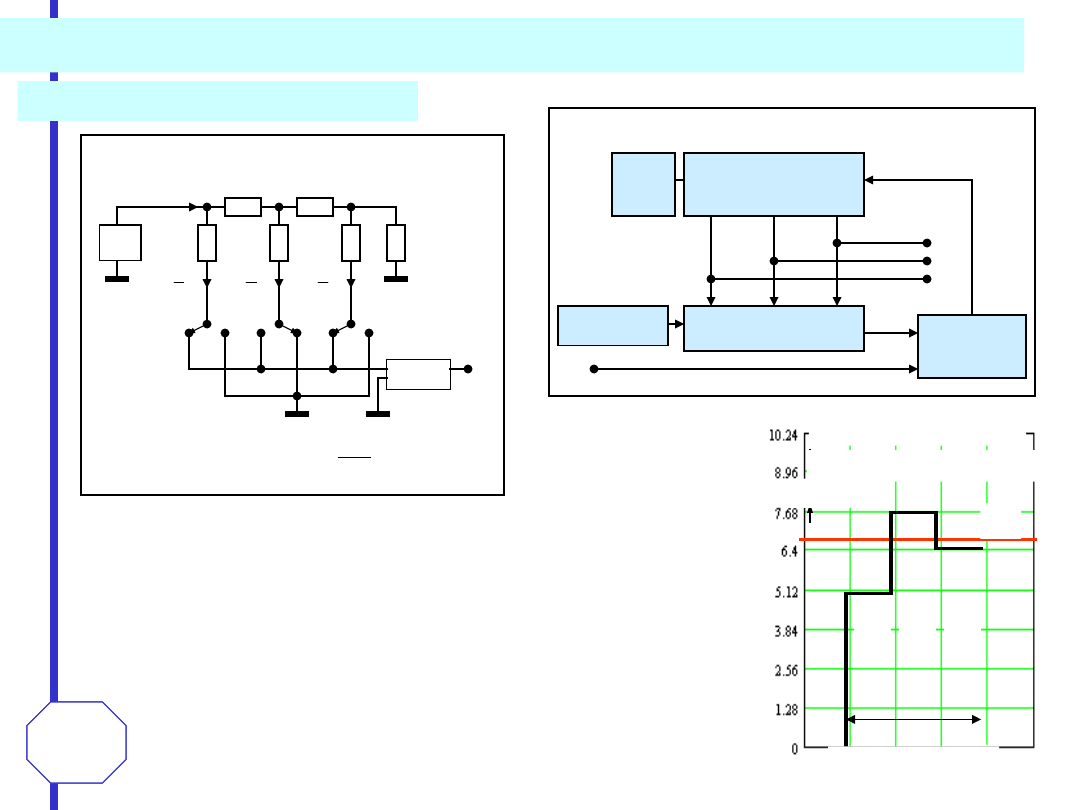
Przy rozłączaniu przełącznika może wystąpić zjawisko
polegające na zmianie ładunku zgromadzonego w
kondensatorze pamiętającym w wyniku oddziaływania
cyfrowego

układu

sterującego

na

kondensator

pamiętający. W chwili wyłączania przełącznika może
wystąpić przepływ ładunku między kondensatorem C

H

a

pasożytniczym kondensatorem C

p

między bramką a

drenem tranzystora.

S
H

Wartość tego ładunku jest równa: , gdzie DU

B

- zmiana napięcia bramki w

momencie wyłączania przełącznika. Na skutek odpływu ładunku q następuje zmiana
napięcia na kondensatorze pamiętającym

B

p

U

C

q





H

B

p

H

C

C

U

C

C

q

U

H









Zmiana ta nazywana jest

piedestałem

lub

błędem piedestału.

Przy przejściu od fazy próbkowania do fazy pamiętania występują krótkotrwałe oscylacje
tłumione napięcia pamiętanego. Czas trwania tych oscylacji, w zależności od rodzaju
układu S/H i wymaganej dokładności, wynosi od kilku nanosekund do kilku mikrosekund.
W katalogach zwykle podawana jest wartość tego czasu (

settling time

) dla różnych

rozdzielczości przetwornika a/c mierzącego zapamiętaną próbkę. Projektując sterowanie
układu należy przewidzieć opóźnienie impulsu inicjującego konwersję przetwornika a/c w
stosunku do zbocza inicjującego fazę pamiętania. Zapobiega to zakłóceniom pracy
przetwornika.

W fazie pamiętania najważniejszym parametrem jest

szybkość spadku napięcia na

kondensatorze pamiętającym

określona jako

Prąd upływowy

jest sumą algebraiczną czterech różnych składników mających

wpływ na jego wartość i polaryzację. W katalogach podawana jest wartość prądu
upływowego. Na tej podstawie można obliczyć szybkość zmian napięcia
pamiętanego.

H

L

C

C

I

dt

dU

H



gdzie I

L

- całkowity prąd upływowy.

CPS

30

CPS

2-30

WYBRANE PRZETWORNIKI ANALOGOWO-CYFROWE







N

k

K

R

K

wy

U

b

U

1

2

2R

R

2R

R

2R

2R

R

I

2

1

R

I

4

1

R

I

8

1

R

/

U

I

R

R



U

R

U

I 

1

0

1

1

0

0

U

wy

Przetwornik cyfrowo-analogowy (C/A)

przetwornik kompensacyjny

REJESTR SUKCESYWNEJ

APROKSYMACJI (SAR)

PRZETWORNIK

C/A

MSB

LSB

KOMPARATOR

ZEGAR

X

U

K

U

U

R

=U

FS

1

0

1

10,24 V

Kompensacyjny przetwornik A/C

1

0

1

q=1,28

U

x

czas

przetwarzan

ia

nominalny zakres U

FS

=q2

N

rzeczywisty zakres U

0

=q(2

N

-1)

Po ostatnim kroku napięcie kompensacyjne ma wartość równą z
dokładnością 1 LSB napięciu mierzonemu. Cyfrową reprezentacją
wartości napięcia mierzonego w kodzie binarnym jest stan
przerzutników.

Układ sterujący powoduje generowanie przez przetwornik C/A kolejno
napięć kompensacyjnych o wartościach U

R

/2, U

R

/4, ..., U

R

/2

N

, gdzie N jest

liczbą bitów przetwornika. W każdym kroku przetwarzania wartość
napięcia kompensacyjne-go jest porównywana z napięciem mierzonym.
Jeśli wartość tego napięcia po kolejnym k-tym kroku jest mniejsza od
napięcia mierzonego, to przerzutnik b

k

odpowiadający temu krokowi

pozostaje w stanie “1” i odpowiadająca mu część napięcia U

k

= U

R

/2

k

pozostaje włączona. Jeśli po kolejnym kroku napięcie kompensujące jest
większe od mierzonego (lub równe), to następuje skasowanie przerzutnika
(b

k

= 0) i odłączenie odpowiadającej temu krokowi składowej napięcia

kompensującego.

CPS

31

CPS

2-31

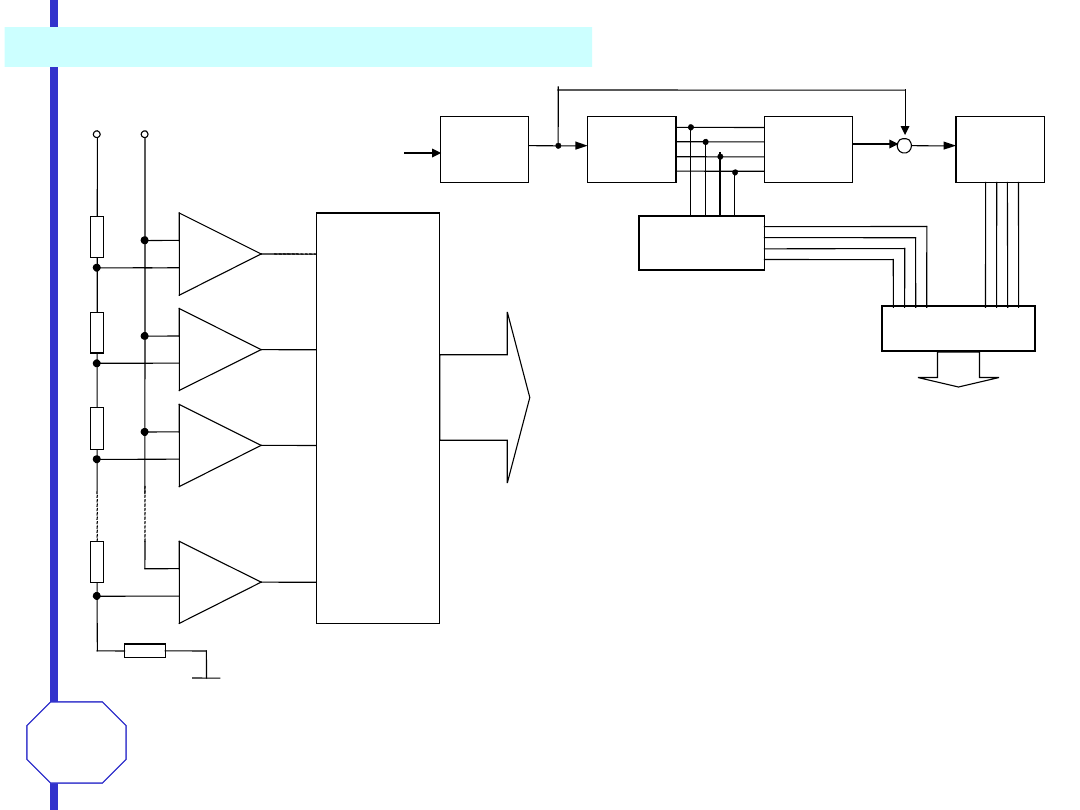
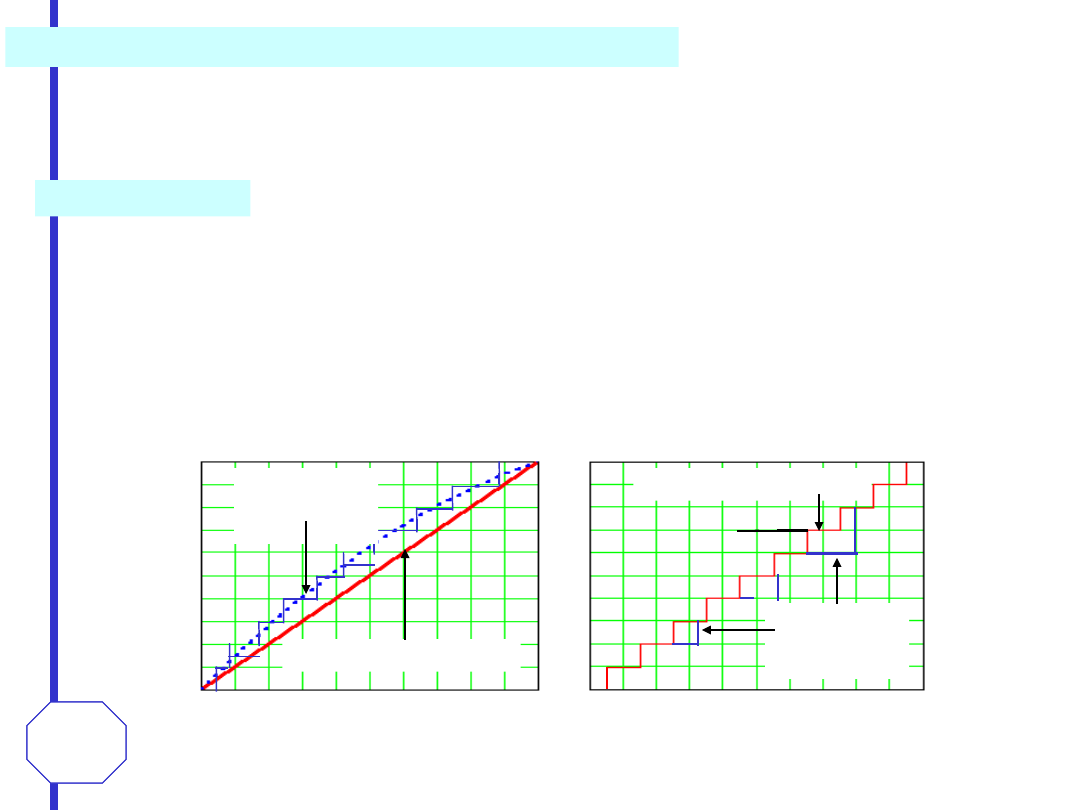
przetwornik natychmiastowy typu „flash”

W

ośmiobitowym

dwustopniowym

przetworniku typu „flash” po wykonaniu
kwantyzacji zgrubnej uzyskane 4-bitowe
słowo cyfrowe (bardziej znaczące bity)
jest przetwarzane na wartość analogową
w 4-bitowym przetworniku c/a. Ta wartość
jest

odejmowana

od

sygnału

wejściowego, a różnicę poddaje się
przetworzeniu a/c w drugim 4-bitowym
przetworniku „flash” dającym 4 mniej
znaczące bity wyniku przetwarzania.

-

+

-

+

-

+

-

+

R

R

R

R

R

U

WE

U

REF

r

Konwerte

r

kodów

Wyjście
cyfrowe

jednostopniowy

komparatory

Układ

S/H

„flash

”

4 bity

zgrubny

C/A

4 bity

Układ

zatrzaskowy

-

+

„flash

”

4 bity

dokładn

y

U

WE

rejestr

dwustopniowy

CPS

32

CPS

2-32

parametry przetworników analogowo-cyfrowych

Najważniejszymi parametrami przetworników analogowo-cyfrowych są te, które określają dokładność i
szybkość przetwarzania. Przetwornik analogowo-cyfrowy ma cechy układu cyfrowego jak i układu
analogowego. Z jego właściwościami jako układu cyfrowego związany jest błąd kwantyzacji określający
rozdzielczość przetwarzania, a z właściwościami analogowymi - błędy analogowe określające dokładność
względna i bezwzględną.

błąd analogowy

Błąd analogowy przetwornika a/c, tak jak każdego układu analogowego składa się z błędu zera, błędu
czułości (wzmocnienia) i błędu nieliniowości. Dwie pierwsze składowe błędu analogowego definiowane są
identycznie jak dla innych analogowych układów pomiarowych i wyrażane w wartościach względnych w
stosunku do nominalnego zakresu przetwarzania. Istotny dla użytkownika jest dodatkowy błąd
temperaturowy tych składowych. Dla temperatury odniesienia są zwykle skorygowane do pomijalnie
małej wartości.
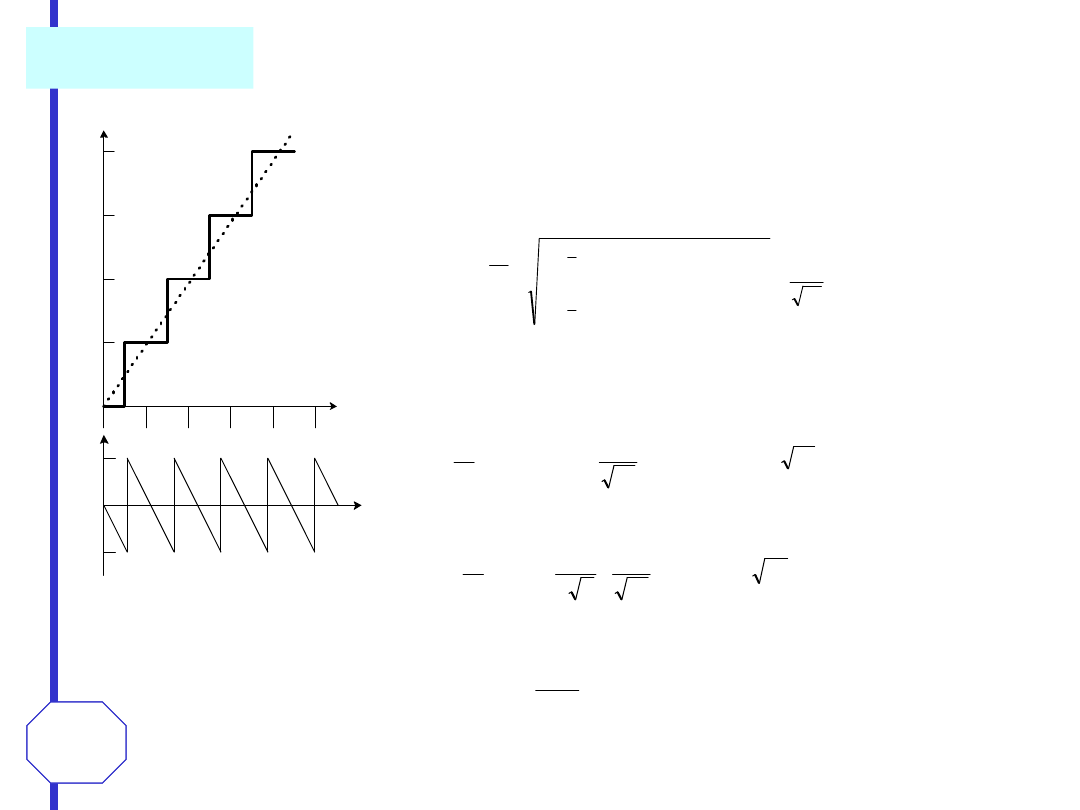
Błąd nieliniowości (tz.

nieliniowość całkowa

) określony jest jako maksymalne odchylenie rzeczywistej

charakterystyki przetwarzania (linia łącząca środki przedziałów zmian napięcia, przy których następuje
zmiana kodu) od charakterystyki idealnej. Zmiana wartości kodu w idealnym przetworniku następuje przy
zmianie napięcia o 1 LSB (1 kwant). W rzeczywistym przetworniku istnieją lokalne różnice w stosunku do 1
LSB (tzw.

nieliniowość różnicowa

). Jeśli błąd ten jest większy od 1 LSB, to pojawia się efekt gubienia kodu.

Wypadkową tych trzech składowych błędu jest

błąd podstawowy

określony jako maksymalna

różnica pomiędzy rzeczywistą charakterystyką przetwarzania a

charakterystyką idealną

(nominalną).

charakterystyka idealna

charakteryst

yka

rzeczywista

brakujący kod

charakteryst

yka

rzeczywista

charakterystyka idealna

nieliniowość całkowa

nieliniowość różniczkowa

CPS

33

CPS

2-33

Błąd cyfrowy -
błąd kwantyzacji

q

q

q

q

q

000

001

010

011

100

U

x

+½ q

-½ q

U

x

Zastąpienie rzeczywistych wartości U

x

odpowiednimi wartościami

dyskretnymi wprowadza

błąd kwantowania

zwany też ze względu na

przypadkowy charakter

szumem kwantowania

. Średnia wartość błędu

kwantyzacji w pełnym zakresie przetwarzania jest równa zeru, jeśli
charakterystyka przetwarzania jest przesunięta o wartość q/2 w stosunku
do początku układu współrzędnych.

Sygnał mierzony może przyjmować dowolną wartość pomiędzy dwoma
poziomami kwantowania z jednakowym prawdopodobieństwem (p=1/q).
Stąd błąd kwantowania może być określony na przykład przez odchylenie
standardowe (wartość skuteczną szumu kwantyzacji w woltach).

12

2

2

2

2

q

dU

U

p

U

U

q

q

U

q

U

x

x

x

x

xi

xi

i













)

(

)

(



Często przydatne jest określenie (w decybelach) stosunku wartości
skutecznej sygnału wejściowego (dla pełnego zakresu przetwarzania) do
szumu kwantyzacji (S/N). Zależy on od kształtu napięcia wejściowego.
W przypadku napięcia stałego unipolarnego

8

10

02

6

12

2

20

12

2

20

,

,

)

lg

(lg

)

/

lg(











N

q

q

N

S

N

N

Rozdzielczość

przetwornika analogowo-cyfrowego określa najmniejszą wartość sygnału wejściowego

rozróżnianą przez przetwornik. Może być wyrażona przez wartość napięcia wejściowego odpowiadającą
najmniej znaczącemu bitowi słowa wyjściowego (1 LSB).

N

FS

U

q

2



W przypadku napięcia sinusoidalnego o amplitudzie międzyszczytowej

q2

N

:

76

1

02

6

5

1

2

20

12

2

2

2

20

,

,

,

lg

)

/

lg(









N

q

q

N

S

N

N

Szybkość przetwarzania

określona jest przez czas niezbędny do przetworzenia w postać cyfrową

sygnału analogowego o wartości równej pełnemu zakresowi przetwarzania.

Częstotliwość

przetwarzania

jest w przybliżeniu równa odwrotności czasu przetwarzania.









s

s

s

s

s

s

nt

kf

f

nt

nt

m

f

m

nt

f

nt

f









































0

0

0

0

2

2

2

2

2











sin

sin

)

sin(

)

sin(

CPS

34

CPS

2-34

CPS

34

CPS

3-34

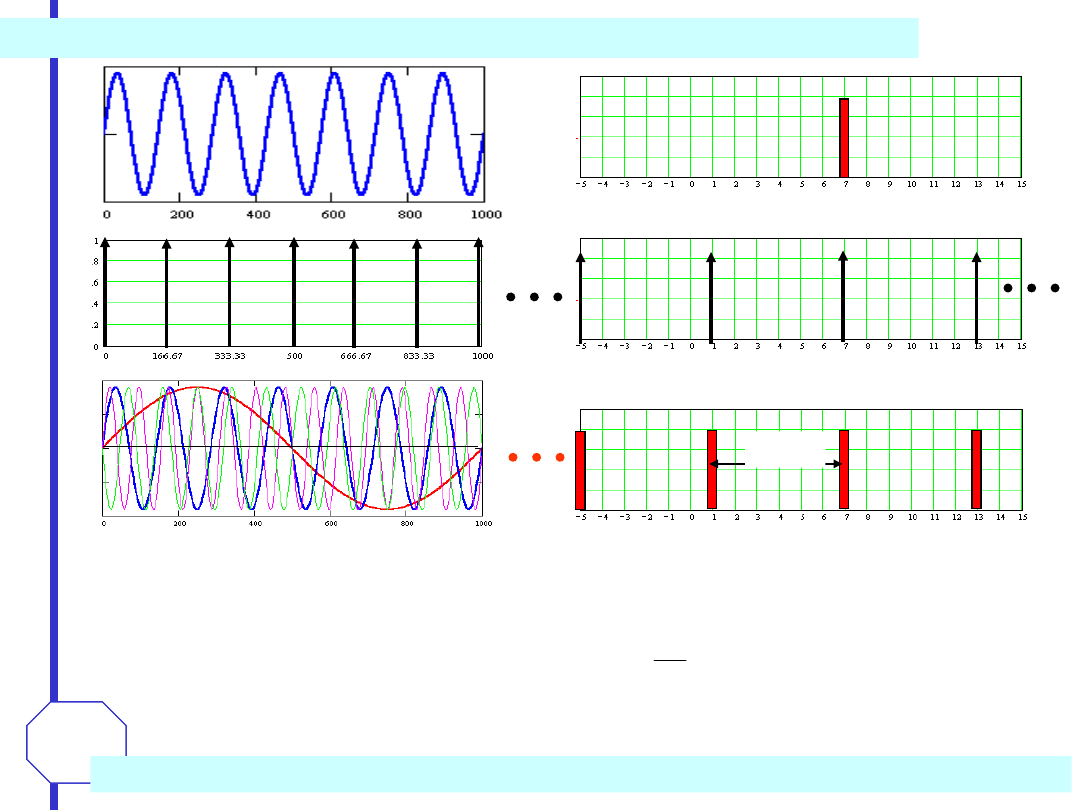
Przy próbkowaniu z częstotliwością f

s

nie można odróżnić spróbkowanych wartości sygnału sinusoidalnego o

częstotliwości f

0

Hz od spróbkowanych wartości sygnału sinusoidalnego o częstotliwości (f

0

+kf

s

) Hz.

niejednoznaczność sygnału dyskretnego w dziedzinie częstotliwości

Częstotliwość [kHz]

6 kHz

Po dyskretyzacji sygnału, jego widmo jest powielone. Okres pomiędzy powielonymi widmami
wynosi zawsze f

s

Sygnał okresowy ma widmo dyskretne. Sygnał dyskretny ma widmo okresowe.

Częstotliwość [kHz]

Częstotliwość [kHz]

[s]

f

0

=

7

k

H

z

[s]

f

s

=

6

k

H

z

[s]

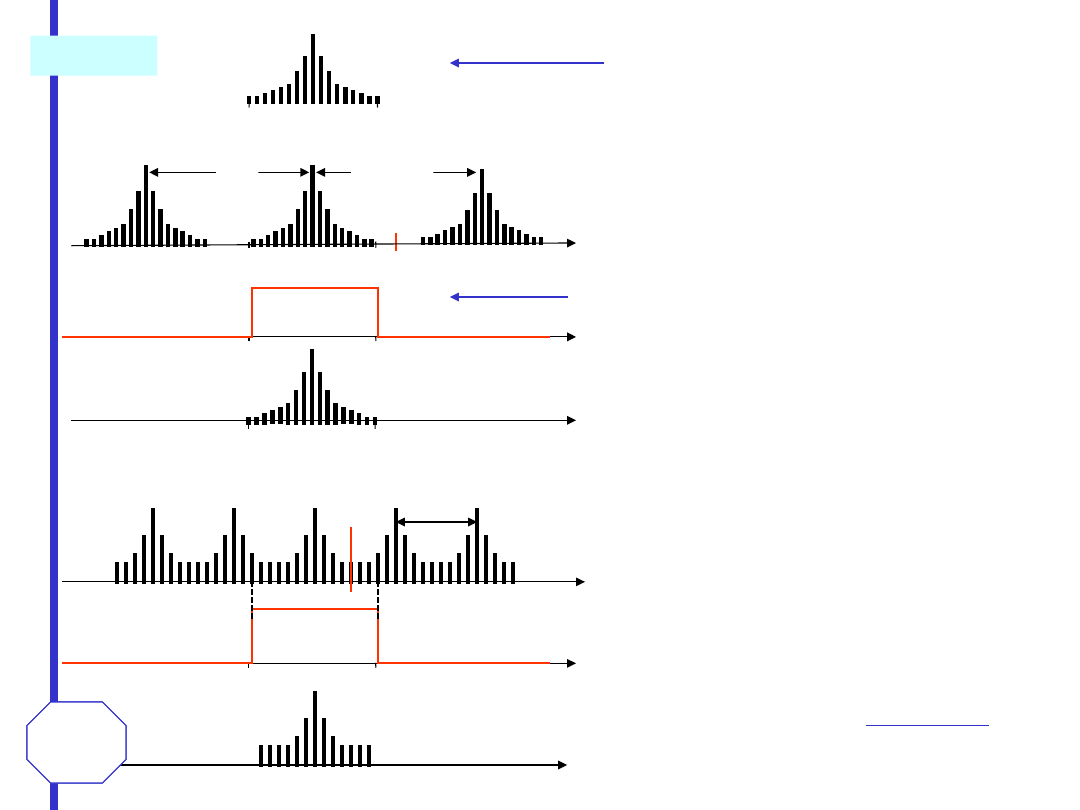
Widmo sygnału okresowego

poliharmonicznego

Po spróbkowaniu, każdy prążek widma jest

powielony okresowo z okresem f

s.

Odtworzenie sygnału oryginalnego wymaga

odfiltrowania powielonych segmentów widma

przez filtr dolnoprzepustowy.

f

g

-f

g

f

g

-f

g

f

f

g

-f

g

f

f

Charakterystyka idealnego filtru

dolnoprzepustowego o częstotliwości odcięcia f

g

.

Jeśli częstotliwość próbkowania jest co
najmniej dwa razy większa od częstotliwości
najwyższej

harmonicznej

w

sygnale

próbkowanym,

to

istnieje

możliwość

bezbłędnego odtworzenia sygnału przez
filtrację jego próbek.

f

f

g

-f

g

f

s

f

s

>2f

g

f

s

/2

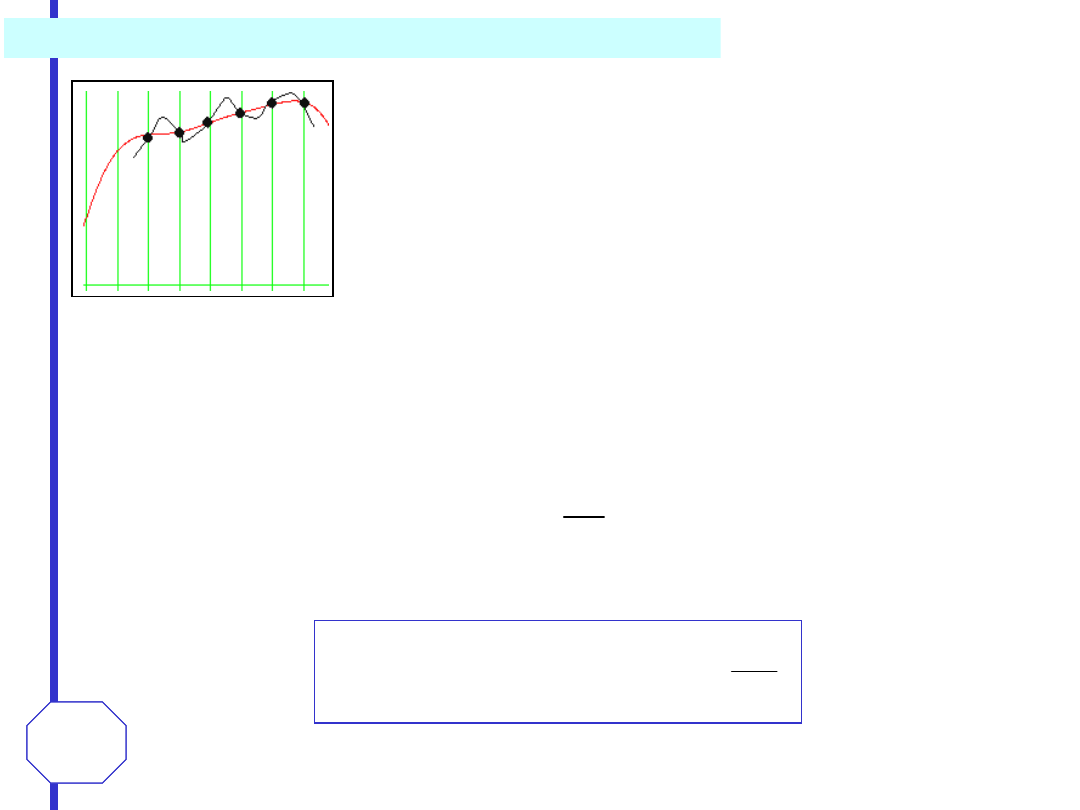
Jeśli częstotliwość próbkowania nie spełnia
powyższego warunku, niemożliwe jest wierne
odtworzenie widma sygnału oryginalnego
bez względu na dobór częstotliwości odcięcia
filtru. Fragmenty sąsiednich segmentów
widma zachodzą na siebie powodując ich
zniekształcenie. Zjawisko nakładania się
widm często nazywane jest

aliasingiem.

f

g

-f

g

f

f

f

s

/2

CPS

2-35

CPS

3-35

aliasing

f

s

<2f

g

CPS

2-36

CPS

3-36

Twierdzenie Kotielnikowa-Shannona o próbkowaniu

Jeśli sygnał nie może zmieniać się zbyt szybko, to na odcinki
sygnałów łączące dwie sąsiednie próbki są narzucone pewne
więzy. Na więzy te wpływają także wartości dalszych próbek. Im
próbki leżą bliżej siebie tym więzy te są silniejsze. Przy
wystarczająco bliskim położeniu więzy te mogą być tak silne, że
przez próbki można wykreślić sygnał tylko na jeden sposób. Tak
więc intuicyjnie można przyjąć, że przy ograniczonej szybkości
zmian sygnału (w sygnale nie ma harmonicznych powyżej
pewnego progu) i przy dostatecznie gęstym próbkowaniu istnieje
możliwość odtworzenia sygnału na podstawie jego próbek.

Twierdzenie o próbkowaniu

Niech x(t) będzie sygnałem, którego widmo X(

) spełnia warunek

m

X











dla

0

)

(

Sygnał x(t) jest równoważny zbiorowi swoich próbek odległych od siebie o stały przedział

m

T







to znaczy























m

T

n

nT

x

t

x





,

,

,

);

(

)

(



1

0

CPS

2-37

CPS

3-37

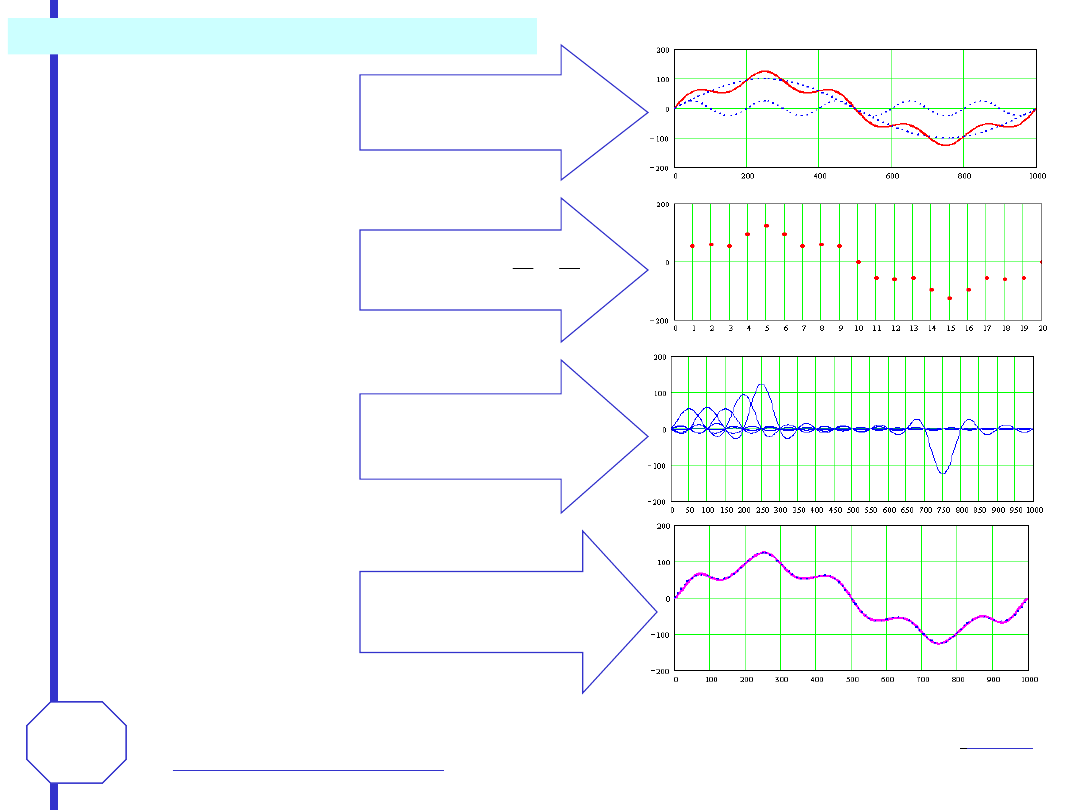
Dowód

Widmo sygnału poddane zostanie dwóm wzajemnie znoszącym się operacjom. Najpierw
operacji powielenia okresowego przez splecenie widma w dziedzinie częstotliwości z
dystrybucją grzebieniową. Powstaje w ten sposób widmo o okresie 2

m

równym odstępowi

między impulsami Diraca w dystrybucji grzebieniowej. Następnie widmo to poddawane jest
operacji idealnej filtracji poprzez pomnożenie go przez charakterystykę idealnego filtru
dolnoprzepustowego o pulsacji odcięcia 

m

.













































m

m

m

III

X

X

















2

2

2

1

)

(

)

(

Dokonując odwrotnego przekształcenia Fouriera obu stron powyższego równania otrzymuje

się

1

2

1

2















































n

m

m

m

m

t

Sa

nT

t

nT

x

t

Sa

T

t

III

T

t

x

t

Sa

T

t

III

t

x

t

x

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

















m

m

T













2

2

)

(

)

(

0

0

0

2















t

Sa

T

III

T

t

III

T









2

1

0

0





)

(

)

(

Uwzględniając właściwości splotu dystrybucji Diraca z dowolną funkcją

)

(

)

(

)

(

0

0

t

t

x

t

t

t

x











ostatecznie otrzymuje się

















n

m

nT

t

Sa

nT

x

t

x

)

(

)

(

)

(



Udowadnia to tezę twierdzenia o próbkowaniu.

Znajomość wartości próbek sygnału wystarcza do odtworzenia pozostałych wartości

sygnału.

CPS

2-38

CPS

3-38

CPS

2-38

CPS

3-38

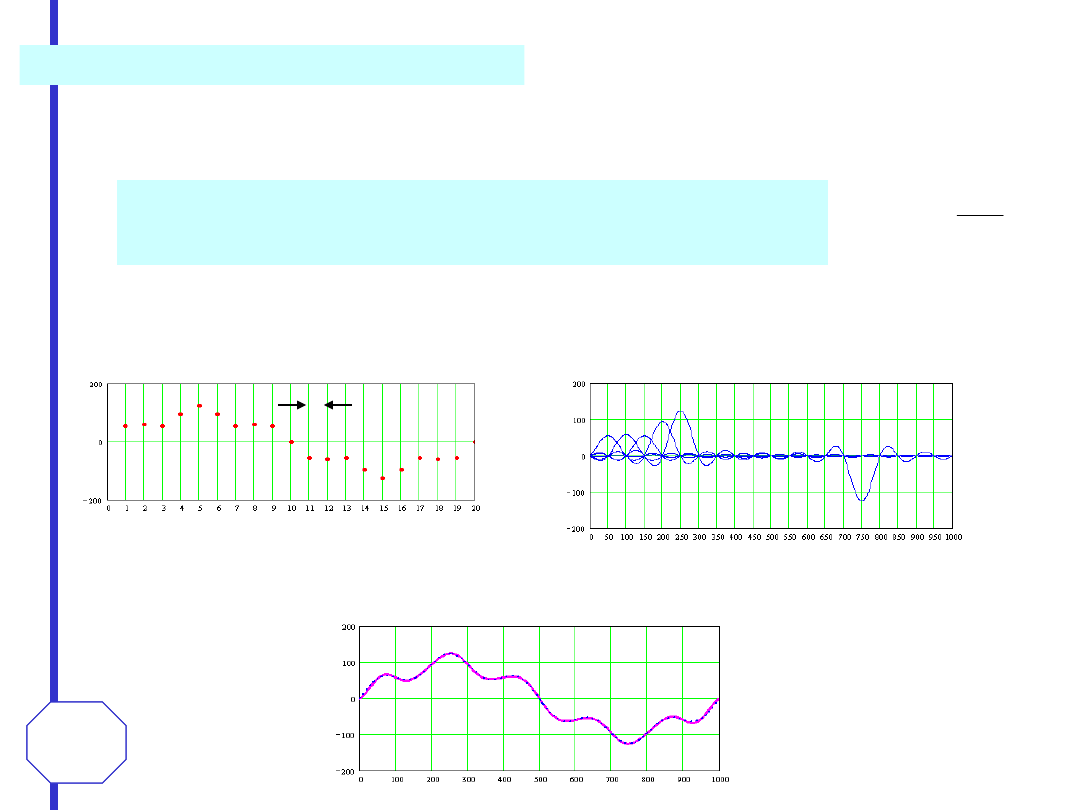
Odtwarzanie sygnału na podstawie próbek

 

t

x

 

 

p

p

p

T

t

III

T

1

t

x

nT

x





 









p

m

p

nT

t

Sa

nT

x







 

 



















N

1

p

m

p

nT

t

Sa

nT

x

t

x

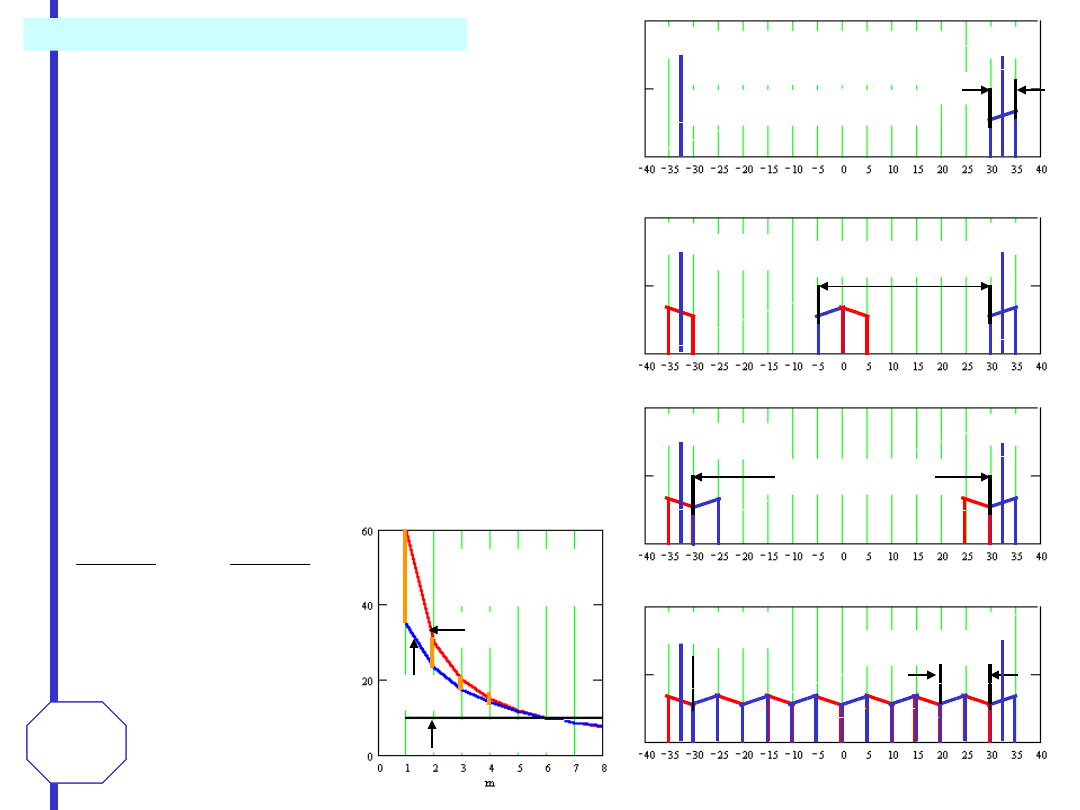
Na wyjściu filtru następuje sumowanie odpowiedzi na ciąg próbek reprezentujących sygnał
ciągły. Przy zachowaniu wymagań wynikających z twierdzenia Kotielnikowa-Shannona (

idealne

próbkowanie i idealna filtracja

) sygnał wyjściowy filtru jest identyczny z sygnałem wejściowym.

sygnał oryginalny

próbki sygnału oryginalnego

odpowiedź idealnego
filtru na kolejne próbki

sygnał odtworzony jako
suma odpowiedzi
idealnego filtru na
próbki sygnału

CPS

2-39

CPS

3-39

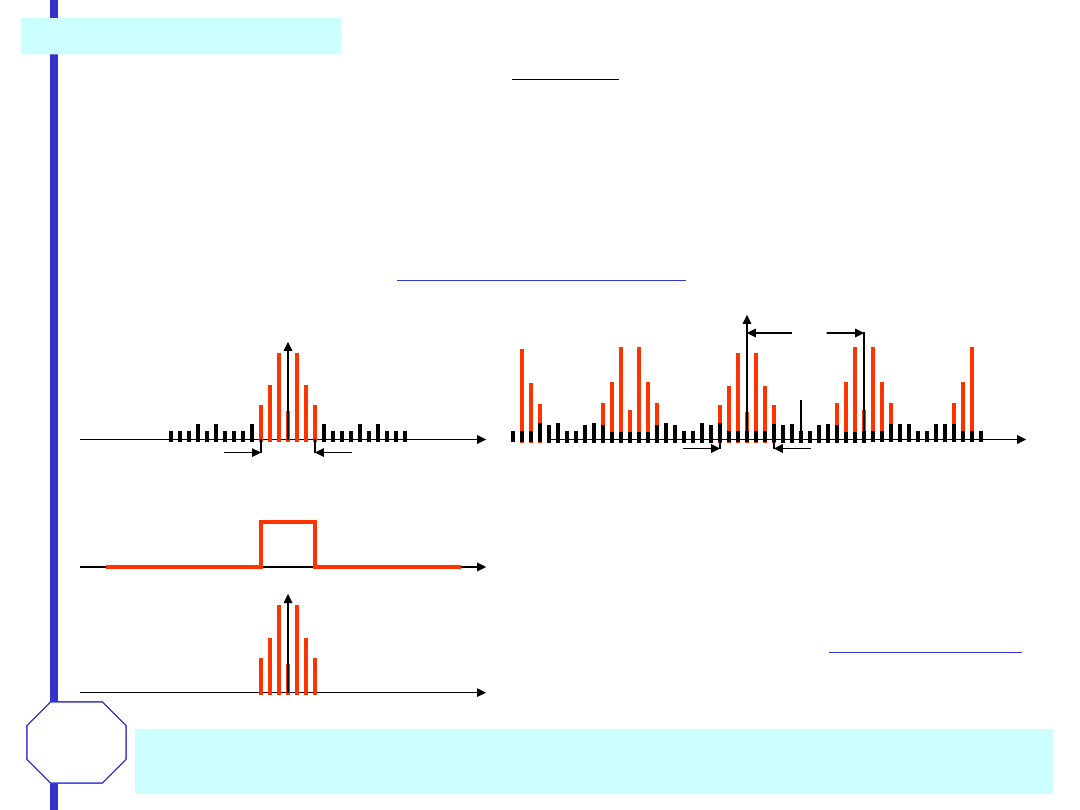
próbkowanie pasmowe - podpróbkowanie

Struktura częstotliwościowa powielonego widma
jest identyczna jak struktura częstotliwościowa
sygnału oryginalnego. Zmienione jest tylko
położenie widma na osi częstotliwości. Tak więc na
podstawie próbek pobieranych z częstotliwością
znacznie mniejszą od częstotliwości Nyquista
można wiernie odtworzyć informację zawartą w
sygnale

pasmowy

pod

warunkiem,

że

częstotliwość

„podpróbkowania”

spełnia

następujący warunek:

W praktyce występują sygnały, których widmo
jest skupione wokół pewnej częstotliwości
środkowej f

C.

i zajmuje pasmo B znacznie

mniejsze od od f

C.

Wykorzystując właściwość

okresowego powielenia widma sygnału po jego
spróbkowaniu, można odtworzyć sygnał pasmowy
bez

konieczności

próbkowania

go

z

częstotliwością spełniającą warunek Kotielnikowa-
Shannona.

1

2

2











m

B

f

f

m

B

f

C

S

C

gdzie m jest liczbą
naturalną taką, że

-f

C

f

C

częstotliwość [MHz]

f

SMIN

=f

SMAX

=2B

m=6

f

SMAX

=2f

C

-B=60MHz

-f

C

f

C

częstotliwość [MHz]

m=1

f

SMIN

=f

C

+B/2=35MHz

-f

C

f

C

częstotliwość [MHz]

m=1

B

f

S

2



f

C

= 32,5 MHz,

B = 5 MHz

2B = 10 MHz

f

SMIN

f

SMAX

C

zę

st

o

tl

iw

o

ść

[

M

H

z]

B

-f

C

f

C

częstotliwość [MHz]

Widmo sygnału pasmowego

przed próbowaniem

f

C

= 32,5 MHz, B = 5 MHz

CPS

2-40

CPS

3-40

Z twierdzenia Kotielnikowa-Shannona wynika teoretyczna możliwość przekazywania informacji zawartej
w sygnale ciągłym za pomocą jego próbek, przy założeniu, że sygnał ma ograniczone widmo (f

g

) i

próbkowany jest z częstotliwością f

s

nie mniejszą niż 2f

g.

Należy jednak zdawać sobie sprawę z różnicy

między teorią a fizyczną rzeczywistością. Istnieją trzy zasadnicze rozbieżności:

•

Sygnały rzeczywiste mają widmo nieograniczone (kryterium

Paleya-Wienera)

•

Impulsy Diraca są nierealizowalne w praktyce

•

Idealny filtr dolnoprzepustowy jest nierealizowalny w praktyce

próbkowanie rzeczywiste

Widmo każdego sygnału fizycznego ma charakter
malejący ze wzrostem częstotliwości i przyjmuje wartości
pomijalnie małe powyżej pewnej częstotliwości f

g.

różnej

dla różnych sygnałów. Ponadto, często znane jest pasmo,
w którym zawarta jest użyteczna informacja. W celu
uniknięcia aliasingu, sygnał ciągły przed próbkowanie
poddawany jest filtracji przez tzw.

filtr antyaliasingowy

o

arbitralnie ustalonej częstotliwości odcięcia f

g

. W wyniku

działania

filtru

na

układ

próbkująco-pamiętający

podawany jest sygnał, w którym praktycznie występują
tylko harmoniczne zawierające użyteczną informację.

filtr

antyaliasingowy

f

f

g

-
f

g

f

widmo sygnału

za filtrem

antyaliasingowy

m

-f

g

... f

g

pasmo, w

którym

przenoszona

jest informacja

f

f

g

-
f

g

przed próbkowaniem

f

f

g

-
f

g

f

s

f

s

/2

po próbkowaniu

Taki sygnał może być próbkowany z częstotliwością równą co najmniej 2f

g

bez

obawy, że nastąpi nakładanie się sąsiednich segmentów widma.

rzeczywiste widmo sygnału

CPS

2-41

CPS

3-41

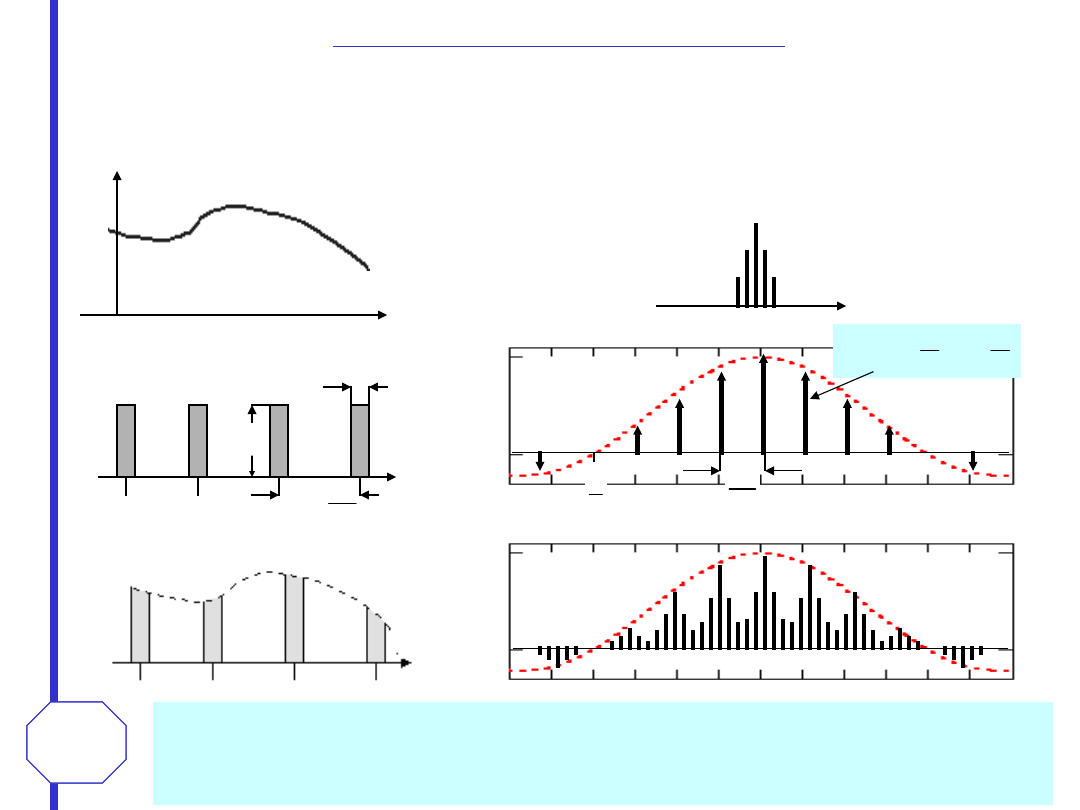
W praktycznej realizacji próbkowania, idealna dystrybucja grzebieniowa (niemożliwa do
zrealizowania) zastępowana jest prostokątną falą nośną (możliwą, w przybliżeniu, do
zrealizowania). W takim przypadku widmo sygnału próbkowanego splatane jest z widmem
fali prostokątnej. Widmem fali prostokątnej jest ciąg impulsów widmowych oddalonych o
1/t

s

, których obwiednią jest funkcja typu Sa.

t



g

s

f

2

1

t 

A

t

t

f

f

)

t

n

(

Sa

t

A

)

nf

(

X

s

s

s









f



1

s

t

1

Widmo sygnału spróbowanego falą prostokątną jest ciągiem oddalonych od siebie o 2f

g

segmentów widmowych, z których każdy jest tego samego kształtu co widmo sygnału
informacyjnego. Odtworzenie sygnału informacyjnego jest możliwe za pomocą filtru o
częstotliwości odcięcia równej f

g

.

Sygnał informacyjny

Widmo sygnału informacyjnego

rzeczywisty kształt impulsów próbkujących

CPS

2-42

CPS

3-42

Kolejne folie

w

przygotowaniu

CPS

2-43

CPS

3-43

CYFROWA ZMIANA SZYBKOŚCI PRÓBKOWANIA

Zmiana użytkowej częstotliwości próbkowania dokonywana na zbiorach liczb reprezentujących próbki
rzeczywistego sygnału. Stosowana jest wtedy, gdy częstotliwość fizycznego próbowania sygnału nie jest
odpowiednia (za duża lub za mała) dla realizacji konkretnego algorytmu cyfrowego przetwarzania
sygnałów.

decymacja -

zmniejszenie szybkości próbkowania o dowolny czynnik całkowity (D)

Wynik

decymacji

jest

identyczny

z

wynikiem

rzeczywistego prób-kowania
z częstotliwością f

NEW

.

Granica, do której można
prowadzić

decymację

wynika z twierdzenia o
próbkowaniu,

to

znaczy

f

NEW

>2B.

Zapewnia

to

uniknięcie aliasingu.

t

f

f

OLD

n

OLD

t

f

f

NEW

n

NEW

D

f

f

D

N

N

OLD

NEW

OLD

NEW





,

interpolacja -

zwiększenie szybkości próbkowania o dowolny czynnik całkowity (I)

Decymacja polega na odrzuceniu pewnej liczby ze zbioru próbek tak aby powstał nowy zbiór o liczbie
próbek D razy mniejszej.(D jest liczbą całkowitą). Dla N próbek ponumerowanych od p(0) do p(N-1) przy
decymacji o czynnik D pozostawiane są próbki p(Dn), gdzie n=0,1,2,3 itd.

Interpolacja o czynnik całkowity I polega na obliczeniu (I-1) nowych wartości
próbek równomiernie rozłożonych pomiędzy sąsiednimi próbkami
pochodzącymi z fizycznego procesu próbkowania. Cyfrowa filtracja (filtr
interpolacyjny) umożliwia obliczenia wartości próbek w dyskretnych
chwilach czasu.

Połączenie interpolacji z decymacją umożliwia przetworzenie zbioru rzeczywistych próbek sygnału
pobranych z częstotliwością f

OLD

w zbiór próbek tego samego sygnału odpowiadających

próbkowaniu z częstotliwością

OLD

NEW

OLD

NEW

If

f

IN

N





,

OLD

NEW

f

D

I

f



CPS

2-44

CPS

3-44