
Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Cyfrowe przetwarzanie sygnałów i obrazów
Grzegorz Pietrzak
Wydział Elektroniki Politechniki Wrocławskiej
09.11.2010

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Outline
1
2
3
4
Histogram i operacje na histogramie
5
Dyskretna transformacja Fouriera
6
7
8
9
Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
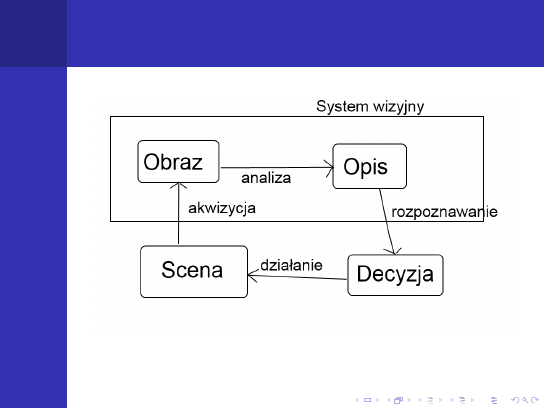
Petla sterowania
Rysunek:
P˛etla sterowania z wykorzystaniem systemu wizyjnego

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Definicja
Akwizycja - przetworzenie obrazu obiektu fizycznego (f(x,y)) do
postaci zbioru danych dyskretnych (obraz cyfrowy) nadaj ˛
acych
si ˛e do dalszego przetwarzania. Elementy procesu akwizycji:
O´swietlenie obrazu.
Formowanie obrazu (optyczne).
Detekcja obrazu.
Formowanie wyj´sciowego sygnału z urz ˛
adzenia (kamera,
skaner)
Obraz podczas tego procesu przyjmuje formy:
optyczna -> elektryczna -> cyfrowa

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Dyskretyzacja
Dyskretyzacja (próbkowanie, kwantyzacja w czasie) - proces
tworzenia sygnału dyskretnego, reprezentuj ˛
acego sygnał ci ˛
agły
za pomoc ˛
a ci ˛
agu warto´sci nazywanych próbkami
Dyskretyzacja idealna
f (v , w ) =
Z
RxR
f (x , y )δ(v − x , w − y )dxdy
(1)
Gdzie RxR - siatka, w której w ˛ezłach pobieramy próbki
Dyskretyzacja rzeczywista
f (v , w ) =
Z
RxR
f (x , y )γ(v − x , w − y )dxdy
(2)
Gdzie γ to funkcja próbkuj ˛
aca wynikaj ˛
aca z charakterystyki
urz ˛
adzenia

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Odtwarzanie sygnału ci ˛
agłego
Twierdzenie Kotielnikowa-Shannona: Sygnał ci ˛
agły mo˙ze by´c
ponownie wiernie odtworzony z sygnału dyskretnego, je´sli był
próbkowany z cz ˛estotliwo´sci ˛
a co najmniej dwa razy wi ˛eksz ˛
a od
granicznej cz ˛estotliwo´sci swego widma (tak zwany warunek
Nyquista).
Inaczej: Sygnał x(t) jest równowa˙zny zbiorowi swoich próbek
odległych od siebie o stały przedział T ≤
1
2f
m
ω
m
to taka cz ˛estotliwo´s´c, powy˙zej której widmo sygnału
próbkowanego zanika (X (ω) = 0 dla ω > ω
m
)
Jak wida´c, sygnał da si ˛e odpowiednio spróbowa´c tylko wtedy, gdy
jego widmo jest sko ´nczone.
Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
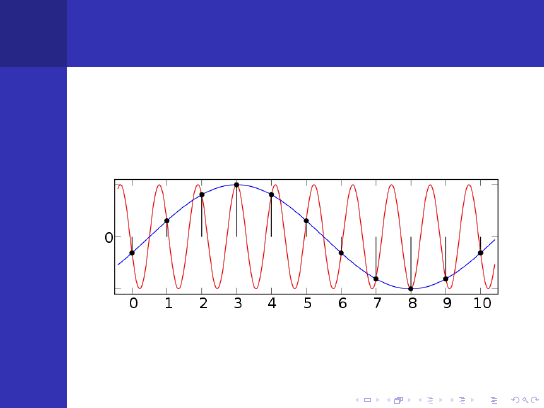
Aliasing
Powy˙zszy warunek nazywany jest warunkiem Nyquista
Je´sli nie jest spełniony, mo˙ze wyst ˛
api´c zjawisko
aliasingu -
pojawiania si ˛e w sygnale składowych o bł ˛ednych
cz ˛estotliwo´sciach.
Aby unikn ˛
a´c tego zjawiska zwi ˛eksza si ˛e cz ˛estotliwo´s´c
próbkowania lub ogranicza cz ˛estotliwo´s´c sygnału wej´sciowego za
pomoc ˛
a filtrów dolnoprzepustowych (o maksymalnie stromych
zboczach).

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Kwantyzacja
Kwantyzacja równomierna i nierównomierna
Miary jako´sci kwantyzatora:
´sredniokwadratowy bł ˛
ad kwantyzacji δ
2
q
=
∞
R
−∞
(
x − Q(x ))f (x )dx ,
gdzie Q(x ) jest kwantyzatorem
(´srednia) długo´s´c słowa kodowego - przy zadanym δ
2
q
R =
m
P
i=1
l
2
b
i
R
b
i
−
1
f (x )dx , l - długo´s´c słowa kodowego
odpowiadaj ˛
acego i-temu przedziałowi (i-tej warto´sci
rekonstrukcji)

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Typy transformacji obrazów
Typy transformacji obrazów
punktowe
lokalne
globalne

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Histogram
Histogram jest to takie przedstawienie empirycznego rozkładu
zmiennej, które dzieli warto´sci cechy na przedziały i
przyporz ˛
adkowuje ka˙zdemu z tych przedziałów liczb ˛e wyst ˛
apie ´n
(ew. g ˛esto´s´c prawdopodobie ´nstwa) warto´sci zmiennej w tym
przedziale.
Ogólnie histogram jest opisany wzorem H(z) =
R
χ
f
−
1
dxdy
Cechy Histogramu: ´srednia, dyspersja, asymetria, energia,
entropia

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Operacje na histogramie
H(z) - histogram, G(z) - histogram po transformacji T
v = T (z) - funkcja transformuj ˛
aca
0 ≤ z ≤ 1, 0 ≤ v ≤ 1
G(v ) = [H(z)
dz
dv
]
z=T
−
1
(
v )
Przykładowe operacje:
Rozci ˛
aganie histogramu
Normalizacja histogramu
Wyrównywanie histogramu (equalization)

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Dyskretna transformacja Fouriera
Dyskretna transformata Fouriera (DFT z ang. Discrete Fourier
Transform) jest transformat ˛
a Fouriera wyznaczon ˛
a dla sygnału
próbkowanego, a wi ˛ec dyskretnego.
DFT przekształca sko ´nczony
ci ˛
ag próbek sygnału (a
0
, a
1
, a
2
, . . . , a
N−1
)
, a
i
∈ R w ci ˛
ag
harmonicznych (A
0
, A
1
, A
2
, . . . , A
N−1
)
, A
i
∈ C zgodnie ze wzorem:
A
k
=
N−1
P
n=0
a
n
w
−
kn
N
, 0 6 k 6 N − 1, w
N
=
e
i
2π
N
Przekształcenie odwrotne: a
n
=
1
N
N−1
P
k =0
A
k
w
kn
N
, 0 6 n 6 N − 1

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Przypadek dwuwymiarowy
Dwuwymiarowe przekształcenie Fouriera w punkcie (m,n):
V (m, n) =
P
M−1
x =0
N−1
P
y =0
U(x , y )w
−
ny
N
w
−
mx
M
Przekształcenie odwrotne:
U(x , y ) =
1
NM
N−1
P
n=0
M−1
P
m=0
V (m, n)w
ny
N
w
mx
M

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
FFT
Obliczanie DFT wg tego wzoru ma zło˙zono´s´c obliczeniow ˛
a O(N
2
)
Istnieje algorytm SzybkiejTransformacjiFouriera, który pozwala na
obliczenie transformaty w czasie O(Nlog
2
N) Algorytmy (jak
algorytm Cooleya-Tukeya) obliczaj ˛
ace szybk ˛
a transformacj ˛e
Fouriera bazuj ˛
a na metodzie dziel i zwyci ˛e˙zaj rekurencyjnie
dziel ˛
ac transformat ˛e wielko´sci N = N
1
N
2
na transformaty
wielko´sci N
1
i N
2
z wykorzystaniem O(N) operacji mno˙zenia.
Najpopularniejsz ˛
a wersj ˛
a FFT jest FFT o podstawie 2. Jest to
bardzo efektywna operacja, jednak wektor próbek wej´sciowych
(spróbkowany sygnał) musi mie´c długo´s´c N = 2
k
, gdzie k to
pewna liczba naturalna. Wynik otrzymuje si ˛e na drodze
schematycznych przekształce ´n, opartych o tak zwane struktury
motylkowe.

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Zastosowania DFT w filtracji
Za pomoc ˛
a odpowiednich masek nało˙zonych na widmo sygnału i
transformacji odwrotnej mo˙zemy wyci ˛
a´c z obrazu pewne
składowe.
Filtry górno, dolno i pasmowo przepustowe pozwalaj ˛
a np. na
redukcj ˛e szumu czy wykrywanie kraw ˛edzi.

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Splot
Splot jest to sposób ł ˛
aczenia 2 sygnałów w celu utworzenia
trzeciego
Ma on t ˛e wła´sciwo´s´c, ˙ze d
f · g = b
f ∗
b
g i d
f ∗ g = b
f ·
b
g Wzór na splot
dyskretny w 2 wymiarach:
a[m, n] ∗ h[m, n] =
P
j
P
k
h[j, k ]a[m − j, n − k ]

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Filtry liniowe
Filtr Gaussa
g(i, j) =
2r
P
k =0
(
2r )!
(
2r −k )!k !
2r
P
l=0
(
2r )!
(
2r −l)!l!
f (i + r − k , j + r − l)
1
2
1
2
4
2
1
2
1
Filtr Laplace’a
g(i, j) = f (i − 1, j) + f (i + 1, j) + f (i, j − 1) + f (i, j + 1) − 4f (i, j)
0
1
0
1
−
4
1
0
1
0

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Filtry nieliniowe
Lokalne minimum
Lokalne maksimum
Filtr medianowy

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Rozplot
Algorytm rozplotu:
g
k +1
=
g
k
+ (
f − g
k
∗
h); g
0
=
f
Rozplot pozwala np na korekcj ˛e poruszonego obrazu, lub
niedokładnego zogniskowania obiektywu

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Progowanie
Progowanie jest globaln ˛
a metod ˛
a segmentacji
Progowanie podwójne
Progowanie zmienne (np. dla zacienionego obrazu)

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Operator gradientu
Gradient jest to kierunek zmian funkcji. Pozwala wykry´c
kraw ˛edzie przedmiotów widoczne na obrazie.
Operatory Robertsa - filtry lokalne realizuj ˛
ace składowe gradientu
0
0
0
0
1
−
1
0
0
0
0
0
0
0
1
0
0
−
1
0

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Laplasjan
Laplasjan dla obrazu 2D jest wyra˙zony wzorem:
∇
2
f =
∂
2
f
∂x
+
∂
2
f
∂y
Przykładowe maski realizuj ˛
ace operator Laplace’a:
0
−
1
0
−
1
4
−
1
0
−
1
0
1
16
1
4
1
4
−
20
4
1
4
1

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Inne metody wykrywania kraw ˛edzi
Maski wykrywaj ˛
ace konkretne wzorce (linie poziome,
pionowe, uko´sne, naro˙zniki)
Gradienty Sobela, Pewritta
Rozkład na kształty lokalne
Analiza obrazu w bazie F-C

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Detekcja i analiza ruchu
Problem polega na detekcji i analizie ruchu w sekwencji obrazów.
Najwi ˛eksze niedogodno´sci przy jego rozwi ˛
azywaniu:
zło˙zono´s´c obliczeniowa
nadmiar informacji
problem szczelinowy
zmienne o´swietlenie
zachodzenie obiektów na siebie
mały kontrast mi ˛edzy obiektami a tłem

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Pole ruchu
Pole ruchu (motion field) - rzut trójwymiarowych wektorów
ruchu na płaszczyznie obrazu; zawiera informacje o składowej
wektora ruchu równoległej do płaszczyzny obrazu; brak informacji
o składowej prostopadłej do płaszczyzny obrazu.
Przepływ optyczny (optical flow) pole wektorowe zawieraj ˛
ace
informacje umo˙zliwiaj ˛
ace przekształcenie jednego obrazu w drugi
przez przesuni ˛ecie obszarów z pierwszego obrazu w drugi; nie
jest jednoznacznie okre´slony.

Grzegorz
Pietrzak
Histogram i
operacje na
histogramie
Dyskretna
transformacja
Fouriera
Metody detekcji i ´sledzenia ruchu
ró˙znicowe umo˙zliwiaj ˛
ace detekcj ˛e i ´sledzenie ruchu dzi ˛eki
ró˙znicom pomi ˛edzy nast ˛epuj ˛
acymi klatkami,
korelacyjne przeszukuj ˛
ace obraz w poszukiwaniu
dopasowania regionów,
gradientowe opieraj ˛
ace si ˛e na wyznaczeniu pochodnych
czasowych i przestrzennych obrazu,
cz ˛estotliwo ´sciowe oparte na filtrach operuj ˛
acych w
dziedzinie cz ˛estotliwo´sci.
Document Outline
- Akwizycja obrazów i sygnaªów
- Dyskretyzacja i kwantyzacja
- Typy transformacji obrazów
- Histogram i operacje na histogramie
- Dyskretna transformacja Fouriera
- Filtry lokalne
- Progowanie
- Wykrywanie kraw¦dzi
- Analiza ruchu
Wyszukiwarka
Podobne podstrony:
1f Cyfrowe przetwarzanie sygnal Nieznany
1f Cyfrowe przetwarzanie sygnal Nieznany
30 Cyfrowe przetwarzanie sygnałów
Cyfrowe Przetwarzanie Sygnałów Wykład cz1
Cyfrowe przetwarzanie sygnałów fonicznych (CPSF) wykład 06 art
zad egz 2002-, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAM
Cyfrowe przetwarzanie sygnałów
Cyfrowe Przetwarzanie Sygnalow Nieznany
zad egz 2001-, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAM
Cyfrowe przetwarzanie sygnalow Nieznany (2)
filtr-cyfrowy, Politechnika, IV sem, Cyfrowe Przetwarzanie Sygnałów i Obrazów
TS 15 Wrzesnia 2003r, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANI
falki, Inżynieria Akustyczna, 4 semestr, CPS - Cyfrowe Przetwarzanie Sygnałów, ZADANIA EGZAMIN 2
Wysylanie wiadomosci e mail Cyfrowe przetwarzanisygnalow Filtry, Cyfrowe przetwarzanisygnałów Filtry
1 Cyfrowe przetwarzanie sygnalow(CPS) Wprowadzenieid 9141 ppt
Cyfrowe Przetwarzanie Sygnałów Wykład cz1
Cyfrowe przetwarzanie sygnałów fonicznych (CPSF) wykład 06 art
więcej podobnych podstron