1
7. Kinematyka i dynamika ruchu obrotowego bryły sztywnej
Ciało sztywne to ciało, które obraca się w taki sposób, że wszystkie jego części są związane ze sobą,
dzięki czemu kształt ciała nie ulega zmianie. Termin stała oś oznacza, że obrót zachodzi wokół osi,
której położenie nie zmienia się w czasie ruchu ciała. Oś obrotu jest to ciało sztywne o dowolnym
kształcie, obracające się wokół stałej osi.
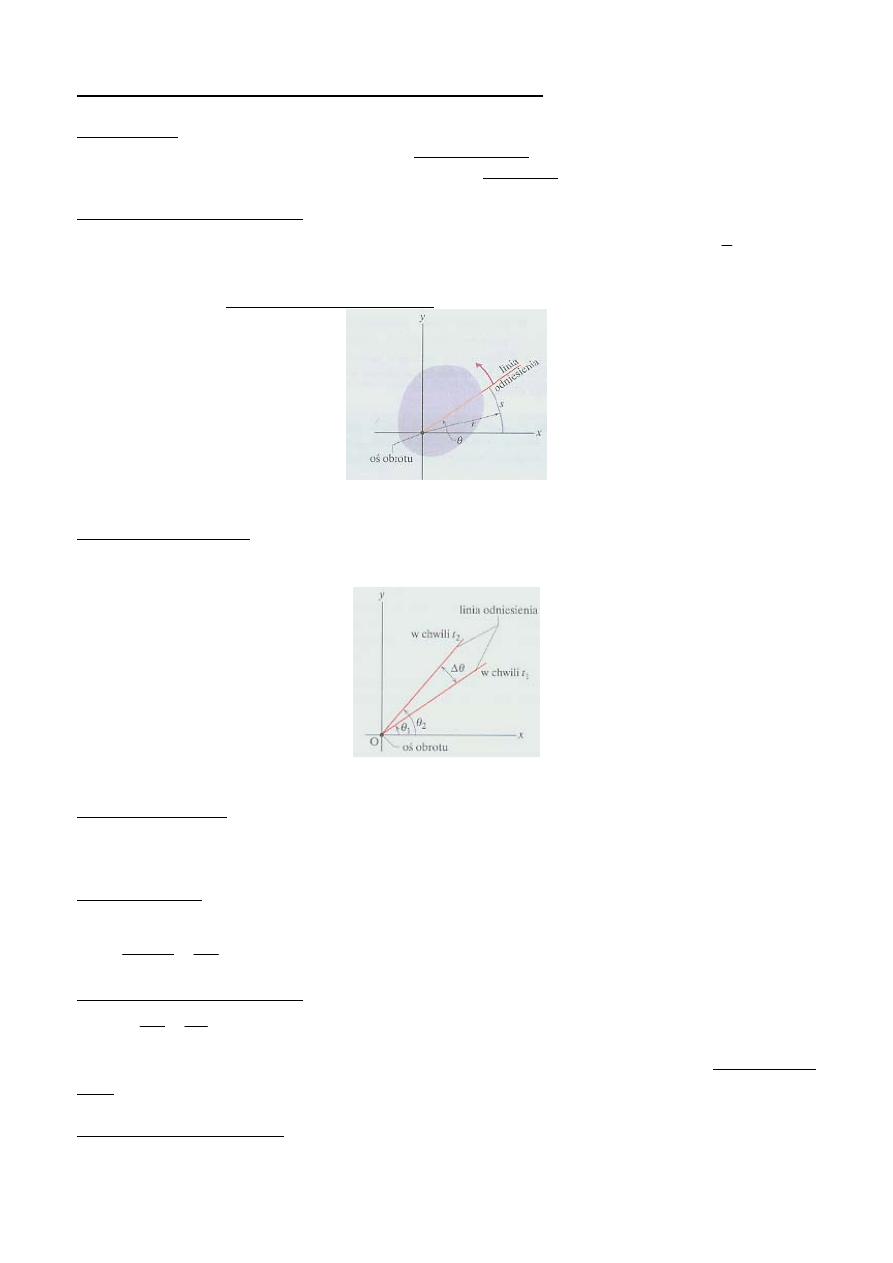
Położeniem kątowym ciała θ nazywamy kąt, jaki tworzy linia odniesienia z pewnym stałym
kierunkiem. Jeśli ten kąt jest wyrażony w mierze łukowej (tzn. w radianach), to:
r
s
=
θ
, gdzie s –
długość odpowiadająca kątowi θ łuku okręgu o promieniu r. Różne jednostki kąta wiążą się ze sobą w
następujący sposób: 1 pełny obrót = 360˚ = 2πrad
Rys.1. Przekrój płaszczyzną xy obracającego się ciała.
Przemieszczenie kątowe Jeśli ciało (Rys.1) obracające się wokół osi zmienia swoje położenie kątowe z
θ
1
na θ
2
, to doznaje ono przemieszczenia kątowego:
1
2
θ
θ
θ
−
=
Δ
Rys.2. Linia odniesienia ciała sztywnego.
Przesunięcie kątowe jest dodatnie, jeśli obrót zachodzi w kierunku przeciwnym do kierunku ruchu
wskazówek zegara, a jest ujemne, jeśli obrót zachodzi w kierunku zgodnym z kierunkiem ruchu
wskazówek zegara.
Prędkość kątowa Jeśli ciało doznaje przemieszczenia kątowego Δθ w przedziale czasu Δt, to jego
średnia prędkość kątowa
śr
ω
wynosi:
t
t
t
śr
Δ
Δ
=
−
−
=
θ
θ
θ
ω
1
2
1
2
, przy czym Δθ jest przemieszczeniem kątowym ciała w przedziale czasu Δt.
Prędkość kątowa ω (chwilowa) jest określana jako granica ilorazu , przy Δt dążącym do zera:
dt
d
t
t
θ
θ
ω
=
Δ
Δ
=
→
Δ
0
lim
.
Obie te wielkości
śr
ω
i ω są wektorami, których kierunek jest wyznaczony z reguły prawej
dłoni (palcami prawej ręki otaczamy oś obrotu tak, by końce palców wskazywały kierunek obrotu.
Odchylony kciuk wskazuje wówczas kierunek wektora prędkości kątowej).
Jednostką prędkości kątowej jest radian na sekundę (rad/s) i obrót na sekundę.
2
Prędkość kątowa obracającego się ciała sztywnego może być dodatnia lub ujemna w zależności od
tego, czy obrót zachodzi w kierunku przeciwnym do kierunku ruchu wskazówek zegara(wtedy jest
dodatnia), czy w kierunku zgodnym z kierunkiem ruchu wskazówek zegara (wtedy jest ujemna).
Przyspieszenie kątowe Jeśli prędkość kątowa ciała zmienia się z ω
1
na ω
2
w przedziale czasu Δt = t
2
-
t
1
, to średnie przyspieszenie kątowe
śr
α
obracającego się ciała wynosi:
t
t
t
śr
Δ
Δ
=
−
−
=
ω
ω
ω
α
1
2
1
2
przy czym Δω jest zmianą prędkości kątowej ciała w przedziale czasu Δt.
Przyspieszenie kątowe α (chwilowe) jest określone jako granica ilorazu, przy Δt dążącym do zera:
dt
d
t
t
ω
ω
α
=
Δ
Δ
=
→
Δ
0
lim
.
Jednostkami przyspieszenia kątowego są radian na sekundę kwadrat (rad/s
2
) i obrót na sekundę
kwadrat.
Ruch obrotowy ze stałym przyspieszeniem kątowym Przypadek, gdy ciało obraca się ze stałym
przyspieszeniem kątowym (α=const) jest ważnym przypadkiem szczególnym ruchu obrotowego.
Obowiązują w nim równania:
t
⋅
+
=
α
ω
ω
0
2
0
0
2
1
t
t
⋅
+
=
−
α
ω
θ
θ
)
(
2
0
2
0
2
θ
θ
α
ω
ω
−
+
=
t
)
(
2
1
0
0
ω
ω
θ
θ
+
=
−
2
0
2
1
t
t
⋅
−
⋅
=
−
α
ω
θ
θ
Związek zmiennych liniowych z kątowymi
Położenie
Punkt obracającego się ciała sztywnego, znajdujący się w odległości r od osi obrotu, porusza się po
okręgu o promieniu r. przy obrocie ciała o kąt θ zatacza on łuk o długości s równej:
r
s
⋅
=
θ
(miara łukowa)
Prędkość liniowa
→
v
punktu jest styczna do łuku, po którym porusza się punkt, a jej wartość v wynosi:
r
v
⋅
=
ω (miara łukowa)
Przyspieszenie liniowe
→
a
punktu ciała sztywnego ma składową styczną i radialną.
składowa styczna jest równa:
r
a
st
⋅
=
α
(miara łukowa), gdzie: α jest wartością przyspieszenia kątowego ciała.
składowa radialna przyspieszenia liniowego:
r
r
v
a
rad
2
2
ω
=
=
(miara łukowa)
Powoduje ona zmianę kierunku wektora prędkości liniowej
→
v
.
Okres ruchu
Jeśli punkt ciała porusza się ruchem jednostajnym po okręgu, to okres ruchu wynosi:
ω
π
π
2
2
=
⋅
=
v
r
T
(miara łukowa)
3
Energia kinetyczna ruchu obrotowego i moment bezwładności
Energia kinetyczna E
k
ciała sztywnego obracającego się wokół stałej osi jest równa:
2
2
1
ω
I
E
k
=
(miara łukowa)
gdzie: I jest momentem bezwładności ciała. Jest on zdefiniowany jako:
∑
=
2
i
i
r
m
I
dla układu oddzielnych cząstek oraz jako:
∫
=
dm
r
I
2
dla ciała o ciągłym rozkładzie masy. Wielkości r i r
i
są odległościami elementów ciała od
osi obrotu.
Jednostką momentu bezwładności
jest :[I] = [kg m
2
]
Im mniejszy jest moment bezwładności ciała, tym łatwiej wprawić je w ruch obrotowy.
Twierdzenie Steinera:
Podaje związek między momentem bezwładności I ciała względem dowolnej osi a jego momentem
bezwładności względem osi równoległej do danej i przechodzącej przez środek masy ciała:
2
mh
I
I
ŚM
+
=
gdzie: h – odległość tych osi.
Rys.4 Momenty bezwładności niektórych ciał.
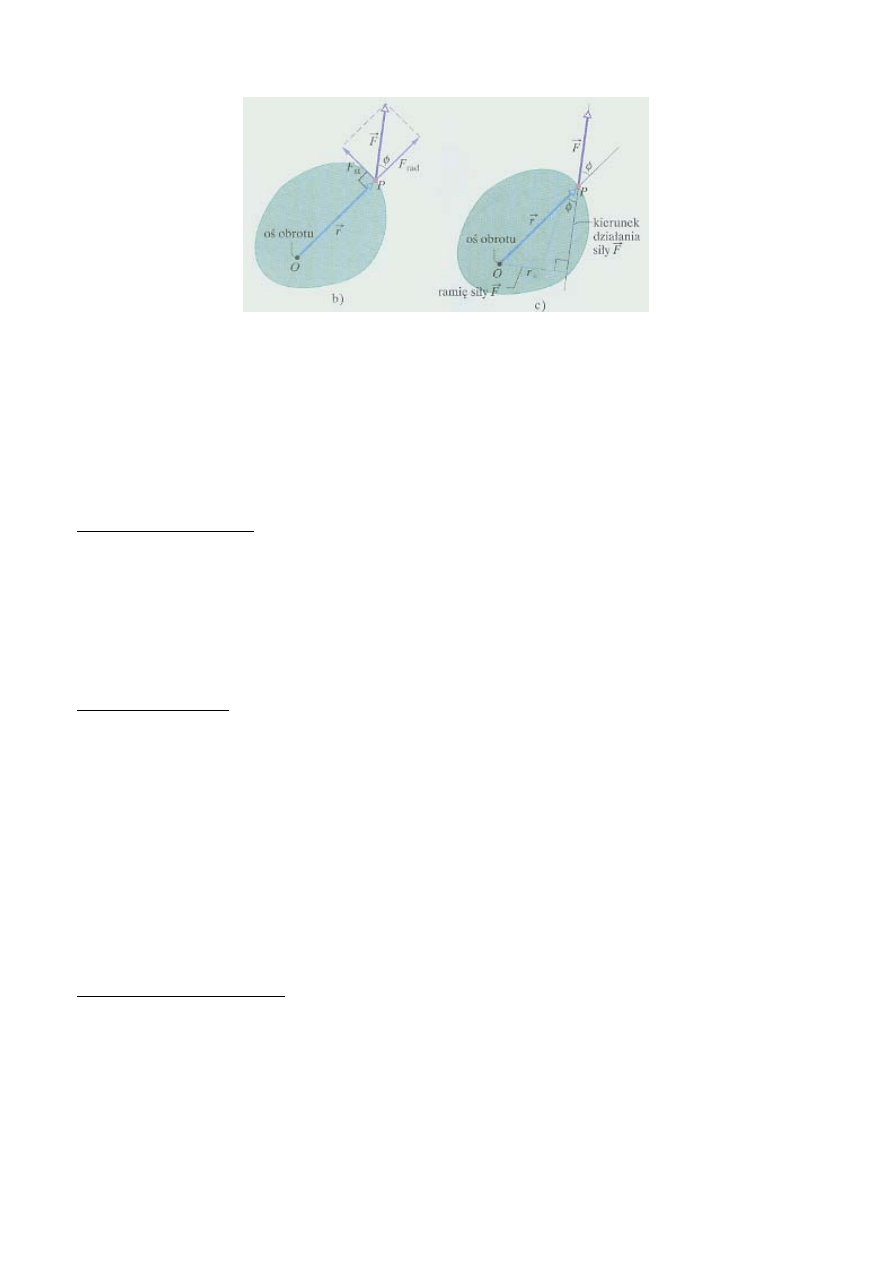
Moment siły
Moment siły jest to wielkość odpowiedzialna za obrót lub skręcenie ciała wokół pewnej osi obrotu,
gdy na to ciało działa siła
→
F
. Jeśli ta siła jest przyłożona w punkcie, którego położenie względem osi
jest dane przez wektor położenia
→
r
, to wartość momentu siły wynosi:
φ
sin
rF
F
r
rF
M
st
=
=
=
⊥
gdzie: F
st
jest składową
→
F , prostopadłą do
→
r ,
φ
- kątem między
→
F a
→
r , a
⊥
r
- odległością osi obrotu
od prostej, wzdłuż której leży wektor
→
F .
4
Kierunek tej prostej nazywamy kierunkiem działania siły
→
F , a
⊥
r
- ramieniem tej siły.
Ramieniem siły składowej F
st
jest r. jednostką momentu siły jest niuton razy metr: [M] = [Nm]
Jeśli obrót zachodzi w kierunku przeciwnym do kierunku ruchu wskazówek zegara, to moment siły
jest dodatni, a jeśli ciało obraca się w kierunku zgodnym z kierunkiem ruchu wskazówek zegara, to
moment siły jest ujemny. Dla momentów sił spełniona jest zasada superpozycji. Gdy na ciało działa
kilka momentów siły, wypadkowy moment siły, oznaczany jako M
wyp
, jest sumą poszczególnych
momentów siły.
Moment siły jako wektor
W trzech wymiarach moment siły
→
M jest wielkością wektorową, definiowaną względem
jakiegoś punktu odniesienia i jest równy:
→
→
→
×
=
F
r
M
gdzie:
→
F jest siłą przyłożoną do cząstki,
→
r - wektorem położenia cząstki względem punktu
odniesienia.
Moment pędu cząstki
Moment pędu
→
l cząstki o pędzie
→
p , masie m i prędkości liniowej
→
v jest wielkością
wektorową, definiowaną względem pewnego punktu odniesienia i jest równy:
)
(
→
→
→
→
→
×
=
×
=
v
r
m
p
r
l
Długość wektora
→
l wynosi:
mv
r
p
r
rmv
rp
rmv
l
⊥
⊥
⊥
⊥
=
=
=
=
=
φ
sin
gdzie:
φ
jest kątem między wektorami
→
r i
→
p ,
⊥
p
i
⊥
v
- składowymi
→
p i
→
v , prostopadłymi do
→
r ,
⊥
r
-
odległością punktu odniesienia od prostej, na której leży wektor
→
p . Kierunek wektora
→
l wyznaczamy
za pomocą reguły prawej dłoni dla iloczynu wektorowego.
Moment pędu układu cząstek
Moment pędu
→
L układu cząstek jest równy sumie wektorowej momentów pędu
poszczególnych cząstek układu:
∑
=
→
→
→
→
→
=
+
+
+
=
n
i
i
n
l
l
l
l
L
1
2
1
...
Szybkość, z jaką zmienia się ten moment pędu jest równa wypadkowemu zewnętrznemu momentowi
siły, jaki działa na układ(tzn. sumie wektorowej momentów siły, działających na cząstki układu, w
wyniku ich oddziaływania z cząstkami spoza układu):
5
dt
dL
M
wyp
→
→
=
Moment pędu ciała sztywnego
Składowa momentu pędu ciała sztywnego, obracającego się wokół stałej osi, równoległa do
osi obrotu, jest równa:
ω
I
L
=
Zachowanie momentu pędu
Moment pędu
→
L układu pozostaje stały, gdy wypadkowy zewnętrzny moment siły, działający
na układ, jest równy zeru:
const
L
=
→
lub
końo
pocz
L
L
→
→
=
Stwierdzenie to nazywamy zasadą zachowania momentu pędu.
Druga zasada dynamiki Newtona dla ruchu obrotowego
Odpowiednikiem drugiej zasady dynamiki Newtona, odnoszącym się do ruchu obrotowego
jest związek:
α
I
M
wyp
=
gdzie: M
wyp
jest wypadkowym momentem siły działającym na ciało sztywne, I – momentem
bezwładności ciała względem osi obrotu, α – przyspieszeniem kątowym ruchu obrotowego ciała
wokół tej osi.
dt
l
d
M
wyp
→
→
=
gdzie:
wyp
M
→
jest wypadkowym momentem siły, działającym na tę cząstkę, l – momentem pędu
cząstki.
Praca i energia kinetyczna ruchu obrotowego
Gdy moment siły wprawia ciało sztywne w ruch obrotowy wokół stałej osi, wykonuje on nad
ciałem pracę W. W związku z tym może zmieniać się energia kinetyczna, związana z ruchem
obrotowym ciała (
2
2
1
α
I
E
k
=
). Związek zmiany energii kinetycznej ΔE
k
ciała z pracą W, wykonaną
nad układem, ma postać:
W
I
I
E
E
E
pocz
końo
pocz
k
końo
k
k
=
−
=
−
=
Δ
2
2
_
_
2
1
ω
ω
,
gdzie: I – moment bezwładności ciała względem stałej osi,
pocz
ω
i
końo
ω
- prędkości kątowe ciała
przed wykonaniem pracy i po wykonaniu pracy nad układem.
Pracę można wyznaczyć z równania:
∫
=
końo
pocz
Md
W
θ
θ
θ
(praca – ruch obrotowy wokół stałej osi)
gdzie: M – moment siły, który wykonuje pracę W,
pocz
θ
i
końo
θ
- położenia kątowe ciała przed
wykonaniem pracy i po wykonaniu pracy nad układem. Gdy M jest stałe, wówczas:
)
(
pocz
końo
M
W
θ
θ
−
=
(praca – stały moment siły)
Szybkość, z jaką wykonywana jest praca, czyli moc, wynosi:
ω
M
dt
dW
P
=
=
(moc – ruch obrotowy wokół stałej osi)