
Usługi Ciesielskie - domy drewniane - domy szkieletowe - konstrukcje dachowe więźby
Spis treści
1. Opis techniczny ........................................................................................
2. Obliczenia statyczne .................................................................................
2.1.
Drewniana więźba dachowa ....................................................................
Obliczenia drewnianej więźby dachowej ................................................
Obliczenia krokwi ...................................................................................
Obliczenia płatwi ....................................................................................
Obliczenia słupka ....................................................................................
Obliczenia podwaliny ..............................................................................
2.2.
Słup .........................................................................................................
2.3. Stopa fundamentowa ...............................................................................
3
5
5
6
7
10
13
14
15
20

2
1. Opis techniczny
• Dane ogólne
: budynek magazynowy z poddaszem użytkowym, dwukondygnacyjny,
niepodpiwniczony. Na kondygnacji pierwszej i drugiej przewidziano powierzchnie
magazynowe,
•
Dane szczegółowe:
a) Elementy konstrukcji:
-
ławy żelbetowe monolityczne o wysokości 40 cm i szerokości 1 m nad ścianami
podłużnymi zewnętrznymi
-
ściany zewnętrzne osłonowe murowane z cegły pełnej klasy 10 o grubości 38 cm;
-
ściany działowe wykonane z cegły, grubości 10 cm;
-
ściana nośna klatki schodowej wykonana z cegły pełnej klasy 7,5 na zaprawie cementowo
wap
iennej, grubość 25 cm;
-
strop między piętrami nad kondygnacją I i II wylewany, żelbetowy oparty na żebrach
głównych i pośrednich, wykonany z betonu klasy B 30 i zbrojonych stalą A-III;
-
dach płatwiowo-kleszczowy nad poddaszem użytkowym (krokwie z drewna klasy C - 30,
pozostałe elementy z drewna klasy C - 30);
-
dach kryty dachówką cementową;
-
schody żelbetowe, płytowe z belkami spocznikowymi;
-
nadproża żelbetowe wylewane na mokro;
-
rampa żelbetowa wylewana;
-
wentylacja grawitacyjna w pomieszczeniach socjalnych i łazience; mechaniczna w
pomieszczeniach magazynowych;
-
izolacja termiczna ścian zewnętrznych nośnych: styropian i tynk na siatce.
b) Instalacje:
-
wodociągowa – zasilanie z sieci wodociągowej (ciepła woda z magistrali ciepłowniczej);
- kanalizacyjna – odprowadzanie
ścieków do kanalizacji miejskiej;
- gazowa – doprowadzanie przewodami z sieci miejskiej;
- elektryczna – podtynkowa;
- sygnalizacyjna;

3
- odgromowa – piorunochron z przewodów stalowych poprowadzonych od kalenicy do
gruntu.
c)
Dźwig towarowy MKE 3.10. – udźwig 2tony
d) Wy
posażenie pomieszczeń:
- zlewozmywaki z bateriami;
- muszla klozetowa;
- prysznic;
-
suszarka do rąk.
e)
Wykończenie:
-
wykończenie wnętrz – tynk cementowo-wapienny;
- pomieszczenia socjalne i klatka schodowa –
ściany malowane emulsją.
f)
Podłogi i posadzki:
- w pomieszczeniach magazynowych –
płytki Lastrico
- w pomieszczeniach socjalnych i kierowniczych – Gres
-
w łazienkach - terakota
g) Stolarka okienna i drzwiowa:
-
okna i drzwi wejściowe do budynku wykonane z PCV, szklone szkłem termoizolacyjnym
dwukomorowym;
- drzwi do magazynu rozsuwane wykonane ze stali;
-
drzwi do łazienki z kratką w dolnej części;
-
drzwi do pomieszczeń socjalnych – drewniane firmy STOLBUD.

4
2. Obliczenia statyczne
2.1. Drewniana więźba dachowa
OBCIĄŻENIA ŚNIEGIEM
Koluszki –
I strefa obciążenia charakterystycznego śniegiem gruntu, wobec tego
obciążenie charakterystyczne śniegiem wynosi Q
k
= 0,7 [kN/m
2
].
Współczynnik kształtu dachu „c” wylicza się ze wzoru:
30
)
60
(
2
,
1
l
c
−
=
, gdzie α = 40˚.
Współczynnik ten dla dachu krytego dachówką ceramiczną pod α = 40˚ równy jest:
c = 0,8
Obciążenie charakterystyczne śniegiem wylicza się z:
S
k
= Q
k
· c,
wynosi ono S
k
= 0,7·0,8 = 0,56 [kN/m
2
].
Ob
ciążenie obliczeniowe śniegiem wylicza się z: S = S
k
· γ
f
[kN/m
2
], gdzie γ
f
= 1,4
–
częściowy współczynnik bezpieczeństwa, i wynosi ono S = 0,784[kN/m
2
].
OBCIĄŻENIE WIATREM
Koluszki –
I strefa obciążenia charakterystycznego wiatrem, które liczymy z:
p
k
= q
k
· C
e
· c · β
według PN – 77/B – 02011
gdzie:
q
k
–
charakterystyczne ciśnienie prędkości wiatru, które przyjmuje się za
250 Pa = N/m
2
;
C
e
–
współczynniki ekspozycji; przyjęto teren B zabudowany przy wysokości istniejących
budynków powyżej 10 m; C
e
= 0
,8 według PN – 77/B – 02011;
c –
współczynnik aerodynamiczny – budowla zamknięta; wylicza się go ze wzoru:
c
p
= c
z
- c
w

5
Dla budowli zamkniętych c
w
= 0, a c
p
= c
z
c
z
= 0,015 · α – 0,2 = 0,4
, a więc c= 0,4
Budynek nie jest podatny na dynamiczne działanie wiatru, więc β = 1,8.
p
k
= 250 · 0,8 · 0,4 · 1,8 = 144 [N/m
2
]
Obliczeniowe obciążenie wiatrem:
p = p
k
· γ
f
= 144 · 1,3 = 187,2 [N/m
2
]
gdzie: γ
f
= 1,3
OBLICZENIA DREWNIANE
J WIĘŹBY DACHOWEJ
Założenia:
-
pokrycie blachą
- drewno klasy C-30
- wiatroizolacja – papa asfaltowa kryta pojedynczo;
- paroizolacja – folia;
-
obciążenie śniegiem – I strefa;
-
obciążenie wiatrem – I strefa;
- rozstaw krokwi – a = 0,84 m.
L1=3,7 [m]
L2=1,85 [m] L1+L2=(5,4+5,7)/2=5,55 [m]
L3=4,83[m] L3+L4=4,38+2,415=7,245[m]
l = 3,8
1
h = 1
H = 4,2
l = 1,9
2
l =
4,
64
3
l =
2,
32
4

6
L4=2,8[m]
Cos a=L2/L4 = L=5,55/cos40=7,245
L3=2/3*7,245=4,83 [m]
L4=1/3*7,245=2,415[m]
L1=cos40*L3=0,766*4,83=3,7[m]
L2=cos40*L4=0,766*2,415=1,85[m]
Obciążenia działające na 1 m
2
pochyłej powierzchni dachu:
-
obciążenie śniegiem S
k
= 560 [N/m
2
];
- obc
iążenia wiatrem p
k
= 144 [N/m
2
].
Zgodnie z PN-82/B-
02000 w pierwszym stanie granicznym użytkowania zastosowano
podstawową kombinację obciążeń:
F
0
= γ
f
· G
k
+ Ψ
0
· γ
f
· Q
ki
Ψ
0
= 1 dla śniegu; Ψ
0
= 0,9 dla wiatru
gdzie:
γ
f
–
współczynnik obciążenia (częściowy współczynnik bezpieczeństwa);
G
k
–
wartość charakterystyczna obciążenia stałego;
Ψ
0
–
współczynnik jednoczesności obciążeń zmiennych;
Q
ki
–
wartość charakterystyczna obciążenia zmiennego.
Tabela 1
.
Zestawienie obciążeń stałych
Rodzaj obciążenia
Warto
ść obciążenia [kN/m
2
]
pokrycie blachą z uwzględnieniem krokwi i łat deskowania
0,72
Wiatroizolacja (papa asfaltowa) 0,003*11kN/m3
0,0396
folia polietylenowa (paroizolacyjna)
0,00168
wełna mineralna gr.16cm 0,16*1,2kN/m3
0,2304
Płyta kartonowo gipsowa GKB gr. 1,5 cm 0,015*22kN/m3
0396
Razem
1,3877
Zestawienie obciążeń charakterystycznych na 1 m
2
pochyłej powierzchni dachu:
-
obciążenie wiatrem
0,144 · cosα = 0,1291
-
obciążenie śniegiem
0,560 N/m
2
· cosα
2
= 0,4601
F
k
= 1,3253=1325,3[N/m2]

7
OBLICZENIA KROKWI
Założenia:
- schemat statyczny krokwi: belka wolnopodparta –
podparcie stanowi murłat i płatew;
- rozstaw krokwi a = 0,84 m;
- klasa drewna C-30;
-
przyjęto do obliczenia przekrój krokwi 10×16 [cm].
Wytrzymałość charakterystyczna na zginanie Fmk=30[MPa]
Wytrzymałość obliczeniowa na zginanieFmd=0,9*30/1,3=20,8[Mpa]
Wytrzymałość charakterystyczna na ściskanie wzdłuż włókien Fc,o,k=23
Wytrzymałość
obliczeniowa
na
ściskanie
i
docisk
wzdłuż
włókien
Fc,o,d=0,9*23/1.3=15,9[MPa]
Wytrzymałość charakterystyczna na ściskanie w poprzek włókienFc,90,k=5,7[MPa]
Wytrzymałość obliczeniowa na ściskanie w poprzek włókien Fc,90,d=0,9*5,7/1,3=4[MPa]
Wytrzymałość charakterystyczna na ściskanie Fv,k=3[MPa]
Średni moduł sprężystości wzdłuż włókien Eo,mean=12000[MPa]
5%kwantyl m
odułu sprężystości wzdłuż włókien E0,05=8000[MPa]
Średni moduł sprężystości w poprzek włókien E90mean=400[MPa]
Średni moduł odkształcenia postaciowego Gmean=750[MPa]
Schemat statyczny:
Zestawienie obciążeń na 1 m krokwi:
-
obciążenie charakterystyczne
F
k
= 1,325,3*0,84=1113,25 [N/m]
-
obciążenie obliczeniowe
F
0
= 1652,2 · 0,84=1387,85 [N/m]
Maksymalny moment zginający:
4818
8
)
83
,
4
(
2
,
1652
8
)
(
2
2
3
max
=
⋅
=
=
l
q
M
[N·m]
Wskaźnik wytrzymałości:
0,5
4,64
2,32
M(q)
M
= q(l ) /8
max
3
2
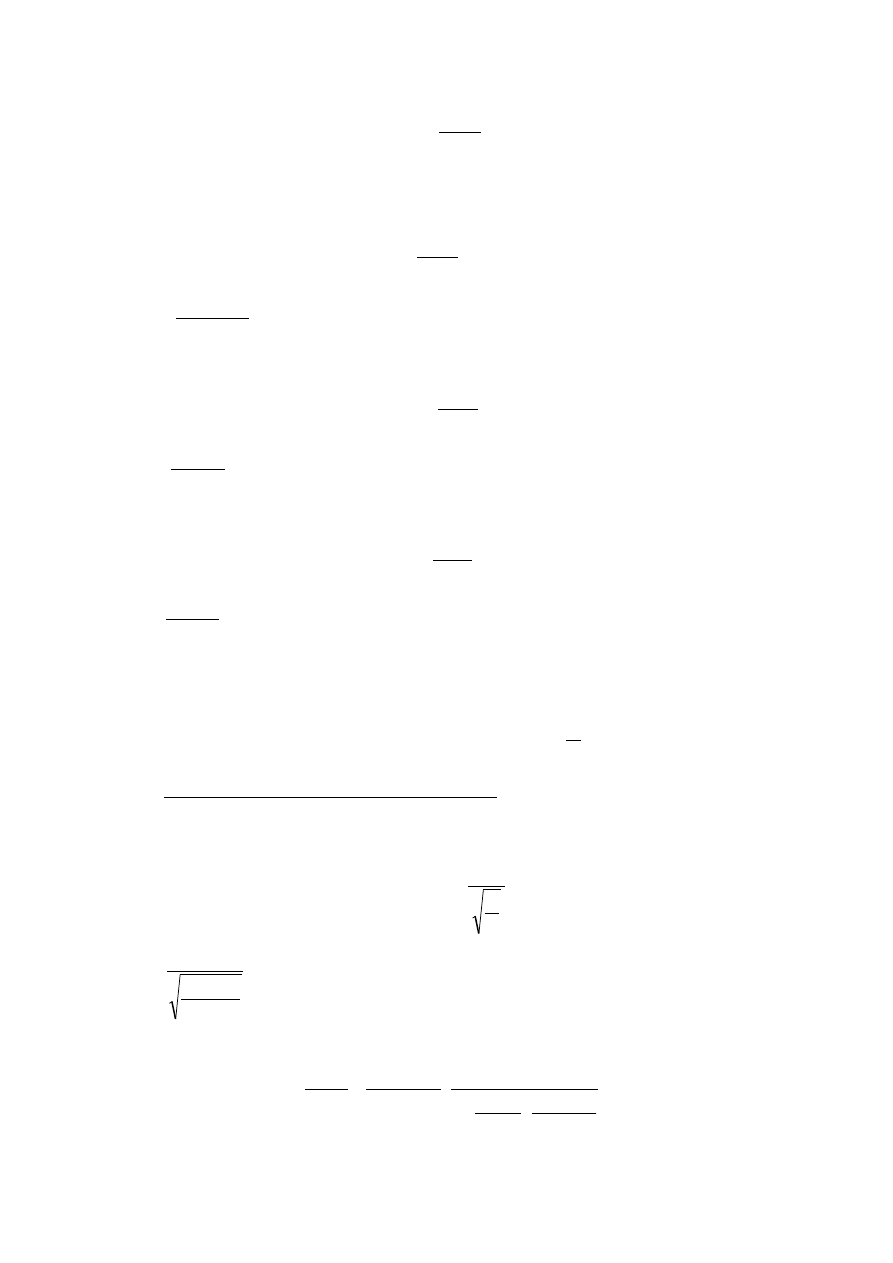
8
m
F
W
M
dm
x
⋅
≤
=
max
max
σ
gdzie: F
dm
= 2080N/cm
2
;
m = 1 –
współczynnik korekcyjny według PN-81/B-031250.01
m
R
M
W
dm
p
x
⋅
=
max
[cm
3
]
635
,
231
1
2080
100
4818
=
⋅
⋅
=
p
x
W
[cm
3
]
Przyjęto przekrój krokwi 10 × 16 cm, czyli A = 160 [cm
2
].
6
2
h
b
W
x
⋅
=
[cm
3
]
66
,
426
6
16
10
2
=
⋅
=
x
W
[cm
3
]
W
x
> W
x
p
426,66cm
3
>231,635 cm
3
Moment bezwładności przekroju:
12
3
h
b
I
x
⋅
=
[cm
4
]
33
,
3413
12
16
10
3
=
⋅
=
x
I
[cm
4
]
Sprawdzenie stanu granicznego nośności – sprawdzenie naprężeń w krokwi z
uwzględnieniem siły ściskającej N:
2
)
cos
sin
sin
(
3
0
0
l
a
S
g
N
⋅
⋅
⋅
⋅
+
⋅
=
α
α
α
[N]
5
,
2186
2
83
.
4
8
,
0
)
77
,
0
*
643
,
0
*
784
643
,
0
*
4
,
1156
(
=
⋅
⋅
⋅
+
=
N
[N]
Sprawdzenie smukłości:
A
I
l
µ
λ
⋅
=
3
0
15
573
,
104
160
33
,
3413
1
483
0
0
=
>
=
⋅
=
λ
λ
W związku z tym, że λ
0
jest większe od 15 nie można pominąć wpływu wyboczenia, stąd:
m
F
k
o
RFc
A
k
N
k
F
W
F
M
k
A
N
cod
E
w
dm
x
dc
w
⋅
≤
⋅
⋅
⋅
−
⋅
⋅
⋅
+
⋅
=
,
,
1
1
1
max
0
σ

9
gdzie:
m –
współczynnik korekcyjny = 1;
k
w
–
współczynnik wyboczeniowy wg PN-81/B-03150.02 = 0,33;
k
E
–
współczynnik wyboczeniowy Eulera
2
0
2
λ
⋅
⋅
Π
=
kc
k
E
R
E
k
47
,
0
573
,
104
23
12000
14
,
3
2
2
=
⋅
⋅
=
E
k
R
kc
–
wytrzymałość charakterystyczna na ściskanie = 20 MPa.
⋅
<
=
⋅
⋅
⋅
−
⋅
⋅
⋅
+
⋅
=
5
,
11
21
,
4
230
160
47
,
0
33
,
0
5
,
2186
1
1
2080
66
,
426
1150
79
,
281194
33
,
0
160
5
,
2186
0
σ
[MPa]
]
[
5
,
11
]
[
21
,
4
0
MPa
MPa
<
=
σ
Naprężenia obliczeniowe w krokwi nie przekraczają wytrzymałości obliczeniowej na
ściskania wzdłuż włókien.
Sprawdzenie stanu granicznego użytkowania – sprawdzenie strzałki ugięcia:
200
3
l
u
dop
=
[cm]
415
,
2
200
483 =
=
dop
u
[cm]
I
E
l
q
u
u
m
k
m
⋅
⋅
⋅
=
=
4
3
)
(
384
5
[cm]
5724
,
0
)
573
,
104
(
1200000
)
484
(
6024
,
10
384
5
2
4
=
⋅
⋅
⋅
=
=
m
u
u
[cm]
u=0,5724<udop=3,415[cm]
ostatecznie przyjęto krokiew 10x16
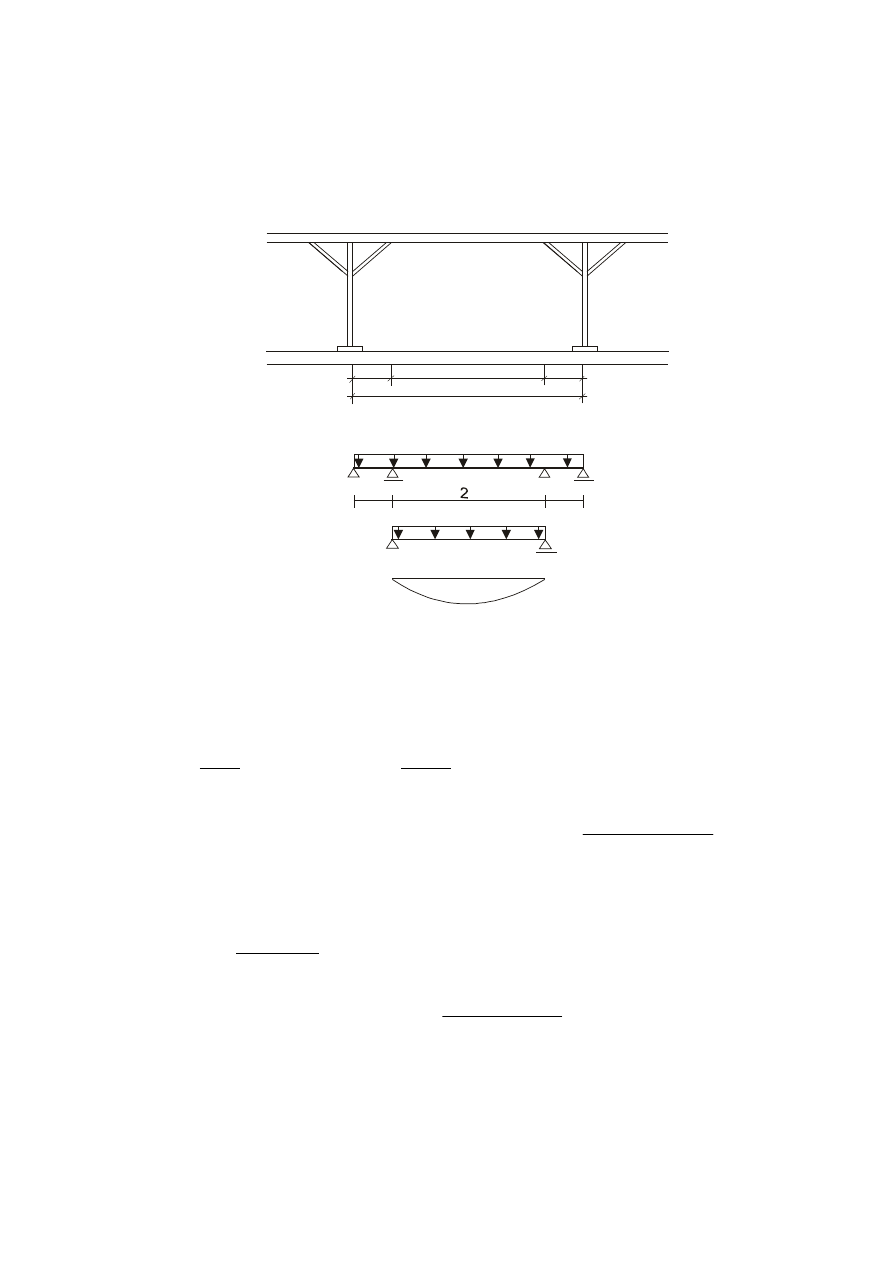
OBLICZENIE PŁATWI
Obliczeniową odległość płatwi stanowi odległość między słupkami, na których oparta
jest płatew. Do zmniejszenia rozpiętości i usztywnienia konstrukcji zastosowano miecze.
Założenia:
- oblic
zeniowa rozpiętość płatwi (rozstaw słupków), która wynosi 4 m;
-
obciążenie z pokrycia, przekazywane przez krokwie na płatwie przyjęto jako ciągłe;
- rozstaw krokwi a = 0,8 m;
10
-
zebranie obciążeń z dachu na płatew jest wygodniejsze, gdy przyjmuje się wymiar w
rzucie poziomym;
- klasa drewna C - 30;
-
przyjęto przekrój płatwi 12 × 22 cm
Schemat statystyczny do obliczeń:
Zebranie obciążeń:
Obciążenia charakterystyczne pionowe na 1 m płatwi:
•
śnieg + ciężar pokrycia
73
,
6116
)
85
,
1
7
,
3
5
,
0
(
)
77
,
0
4
,
1156
560
(
)
5
,
0
(
)
cos
(
2
1
=
+
⋅
⋅
+
=
+
⋅
+
l
l
g
S
k
k
α
[N/m]
F
k
= 6275,13[N/m]
Obciążenie obliczeniowe:
•
śnieg + ciężar pokrycia
073
,
7452
)
85
,
1
7
,
3
5
,
0
(
)
77
,
0
2
,
1
*
4
,
1156
4
,
1
560
(
=
+
⋅
⋅
+
⋅
[N/m]
•
ciężar własny płatwi
158,4· 1,1 = 174,24 [N/m]
F
o
= 7626,313
[N/m]
Składowe obciążenia charakterystycznego od parcia wiatrem:
8
,
532
)
85
,
1
7
,
3
5
,
0
(
144
)
5
,
0
(
2
1
=
+
⋅
=
+
=
l
l
p
W
k
vk
[N/m]
552
,
447
84
,
0
)
85
,
1
7
,
3
5
,
0
(
144
)
5
,
0
(
2
1
=
⋅
+
⋅
=
⋅
+
=
Η
α
tg
l
l
p
W
k
k
[N/m]
0,8
2
3,6
0,8
0,8
0,8
M(q)
M
= q(l ) /8
max
3
2

11
Składowe obciążenia obliczeniowego od parcia wiatrem:
64
,
692
)
85
,
1
7
,
3
5
,
0
(
2
,
187
)
5
,
0
(
2
1
=
+
⋅
=
+
=
l
l
p
W
o
vo
[N/m]
818
,
581
84
,
0
)
85
,
1
7
,
3
5
,
0
(
2
,
187
)
5
,
0
(
2
1
=
⋅
+
⋅
=
⋅
+
=
Η
α
tg
l
l
p
W
o
o
[N/m]
Momenty zginające:
65
,
5989
8
4
,
2
)
64
,
692
313
,
7626
(
8
)
(
2
2
6
=
⋅
+
=
⋅
+
=
l
W
q
M
vo
o
x
[N/m]
64
,
1163
8
4
818
,
581
8
2
2
5
=
⋅
=
⋅
=
l
W
M
ho
y
[N/m]
Wskaźnik wytrzymałości – można w przybliżeniu określić przyjmując stosunek
wskaźników wytrzymałości w dwóch kierunkach:
c = W
x
/W
y
= 1,8.
Po przeprowadzeniu wzoru na dwukierunkowe zginanie, otrzymujemy wzór na orientacyjną
wartość:
56
,
404
2080
64
,
1163
8
,
1
65
,
5989
=
⋅
+
=
⋅
+
=
dm
y
x
P
x
F
M
c
M
W
[cm
3
]
Dla przekroju 12 × 22 cm:
968
6
22
12
2
=
⋅
=
x
W
[cm
3
]
10648
12
22
12
3
=
⋅
=
x
I
[cm
3
]
528
6
22
12
2
=
⋅
=
y
W
[cm
3
]
3168
12
22
12
3
=
⋅
=
y
I
[cm
3
]
Wx>
664
,
388
=
p
x
W
Sprawdzenie stanu granicznego nośności – sprawdzenie naprężeń przy zginaniu
ukośnym:
Dla
4
≤
b
h
4
83
,
1
12
22
≤
=
m
F
W
M
W
M
dm
y
y
x
x
m
⋅
<
+
=
σ
]
[
39152
,
8
]
[
839152
528
116364
968
598965
MPa
MPa
m
=
=
+
=
σ
<20,8[MPa]
Sprawdzenie stanu granicznego użytkowania – sprawdzenie strzałki ugięcia:
Dla
20
6
<
h
l
20
91
,
10
22
240
<
=
93
,
6807
8
,
532
13
,
6275
=
+
=
+
=
vk
k
yk
W
F
g
[N/m]

12
]
)
(
2
,
19
1
[
384
5
2
6
4
6
l
h
I
E
l
g
u
x
omean
yk
y
⋅
+
⋅
⋅
⋅
⋅
⋅
=
[cm]
26734
,
0
]
[
734
,
26
]
)
240
22
(
2
,
19
1
[
10648
1200000
384
240
93
,
6807
5
2
4
=
=
⋅
+
⋅
⋅
⋅
⋅
⋅
=
m
u
y
[cm]
]
[
26734
,
0
]
[
2
,
1
cm
cm
u
ydop
>
=
Dla
20
>
b
l
20
33
,
33
12
400
>
=
g
xk
= W
hk
= 335,304 [N/m]
y
m
xk
x
I
E
l
g
u
⋅
⋅
⋅
⋅
=
384
5
4
5
[cm]
3924
,
0
]
[
24
,
39
3168
1200000
384
400
552
,
447
5
4
=
=
⋅
⋅
⋅
⋅
=
m
f
x
[cm]
]
[
3924
,
0
]
[
2
cm
cm
u
xdop
>
=
Wartość rzeczywista strzałki ugięcia:
2
,
1
475
,
0
26734
,
0
3924
,
0
2
2
2
2
<
=
+
=
+
=
x
y
u
u
u
[cm]
Ustalenie wartości dopuszczalnej strzałki ugięcia:
2
,
1
200
240
200
6
=
=
=
l
u
ydop
[cm]
2
200
400
200
5
=
=
=
l
u
xdop
[cm]
Ze względu na nie przekroczenie strzałki ugięcia i naprężeń przyjęto płatew o
wymiarach 12 × 22 cm.
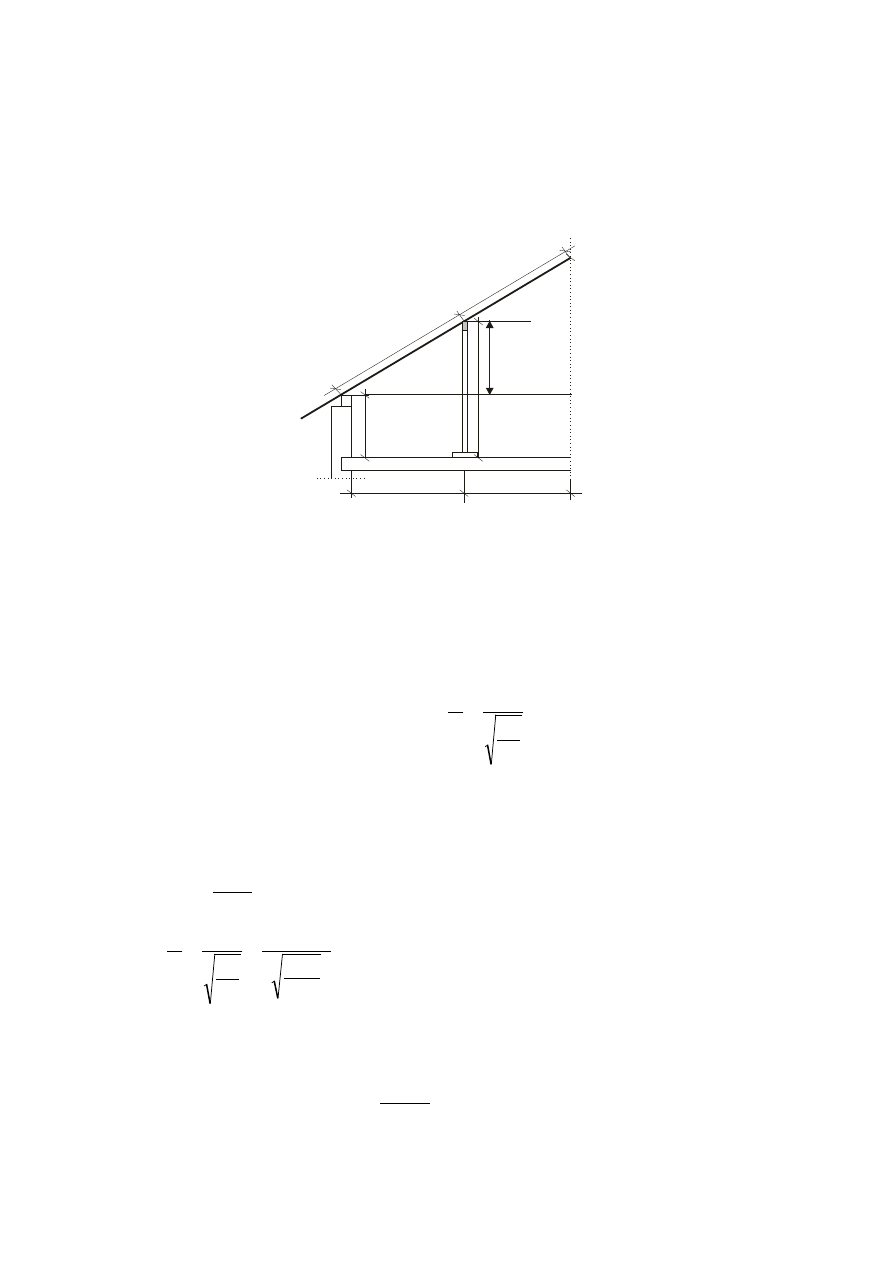
OBLICZENIE SŁUPKA
Założenia:
-
wysokość słupka H = 3,48 m;
- klasa drewna C - 30;
- fcod = 15,9 MPa = 1,59 kN/cm
2
–
wytrzymałość obliczeniowa na ściskanie wzdłuż
włókien;
13
- Fc,90,k = 5,7 MPa = 0,57 kN/cm
2
–
wytrzymałość obliczeniowa na ściskanie i docisk w
poprzek włókien;
-
przekrój słupka 12 × 12 cm.
Schemat obliczeniowy słupka
Obliczenie siły dociskowej:
-
siła dociskowa w słupku równa jest wartości reakcji płatwi:
5
)
(
l
W
F
S
vo
o
⋅
+
=
[N]
524
,
32832
4
)
818
,
581
313
,
7626
(
=
⋅
+
=
S
[N]
Obliczenie i sprawdzenie smukłości:
d
x
c
c
A
I
H
i
l
µ
λ
⋅
=
=
gdzie:
μ – współczynnik długości wyboczeniowej = 0,85
i –
promień bezwładności
A
d
– pole przekroju 12×12 = 144 cm
2
1728
12
3
=
⋅
=
h
b
I
x
[cm
4
]
4
,
85
144
1728
85
,
0
348
=
⋅
=
⋅
=
=
d
x
c
c
A
I
H
i
l
µ
λ
Dla λ
c
= 87 współczynnik wyboczenia wynosi k
w
= 0,3933
Warunek wytrzymałościowy:
d
o
Fc
kc
A
S
C
d
c
,
,
≤
⋅
=
[MPa]
l = 2,91
1
h = 1,1
H = 4,2
x = 3,1
0,24
0,12
l = 2,45
2
l =
4,
38
3
l =
3,
46
4

14
]
[
9
,
15
]
[
84625
,
5
39
,
0
144
524
,
32832
MPa
MPa
C
c
<
=
⋅
=
Warunek został spełniony, przyjęto słupek o wymiarach 12 × 12 cm.
OBLICZENIE PODWALINY
Sprawdzenie naprężeń na docisk w podwalinie:
m
F
k
A
F
G
dc
c
d
dc
⋅
⋅
<
=
90
90
m = 1 k
c
= 1
Siła nacisku F w miejscu oparcia słupka na podwalinie:
F = S + b · h · H · 6000 ·
γ
f
[N]
γ
f
= 1,1
F = 32832,524 + 0,12 · 0,12 · 3,84 · 6000 · 1,1=33197,478 [N]
Pole przekroju podwaliny:
A
d
= 12 · 12 = 144 cm
2
Naprężenie ze względu na docisk w podwaline:
]
[
4
]
[
3054
,
2
144
478
,
33197
90
MPa
MPa
G
dc
<
=
=
2.2. Słup
OBLICZENIE SŁUPA ŻELBETOWEGO (II KONDYGNACJA)
Założenia:
-
rozpiętość stropu: l
1
= 5,7 m; l
2
= 5,4 m;
-
rozpiętość podciągu 6,3 m;
- wysoko
ść kondygnacji (w świetle) wynosi: 3,3 m;
-
przekrój podciągów stropu 0,4 × 0,5 m;
-
przekrój żeber głównych 0,3 × 0,4 m,
Strop wylewany żelbetowy dwukierunkowo zbrojony.
-
przekrój słupa F
s
= 0,4 × 0,4 = 0,16 m
2
;
- powierzchnia rzutu poziomego
9
,
34
3
,
6
2
)
7
,
5
4
,
5
(
=
⋅
+
=
s
F
m
2
.
-
Wysokość słupa hsł=3,6-gpos-0,5+gpos=3,1[m]
Zestawienie obciążeń działających na słup II kondygnacji:
-
ciężar słupka
0,12 · 0,12 · 6,3 · 1,1 · 3,48= 0,347 kN
15
-
rzeczywisty nacisk słupka
33191,478 N = 33,197478 kN
Tabela 2
.
Zestawienie obci
ążeń działających na słup II kondygnacji
Rodzaj obciążenia
Obliczenia
Wynik [kN]
przenoszone przez słupki
0,5 · 4 · 33,197478 ·
66,39
posadzką – płytki lastriko gr.2 cm
0,76*1,2*34,9
31,38
gładzią cementową
21 · 0,02 · 1,3 · 34,9
19,05
płytą pilśniową
3 · 0,01 · 12 · 34,9
1,26
jastrychem cementowym
21 · 0,05 · 1,2 · 34,9
43,97
papą na lepiku
11 · 0,003· 1,2 · 34,9
1,38
ciężarem płyty stropowej
24 · 0,15 · 1,1 · 34,9
138,2
tynkiem cementowo-wapiennym
19 · 0,015 · 1,1 · 34,9
12,93
ciężarem żebra głównego
0,2·(0,3-0,15)·1,1·24·(5,55-0,3)
4,16
ciężarem podciągu
0,3 · (0,4-0,15) · 6,3 · 1,1 · 24
12,47
Technologiczne
7,5 · 1,2 · 34,9
314,1
ciężarem instalacji elektrycznej i wentylacyjnej
0,015 · 1,2 · 34,9
0,63
ciężarem słupa
tynkiem na slupie
0,3 · 0,3 · 24 · 1,1 · 3.1
4*3,1*0,3*19*1,3*0,015
7,4
1,38
Suma obciążeń
655,15
Razem: 655,15+33,197478=688,69[kN]
Wymiarowanie słupa żelbetowego:
Przyjęto słup wykonany z betonu klasy B30, zbrojony stalą klasy A-III.
Sprawdzenie nośności przekroju mimośrodowo-ściskanego (według PN-84/B-03264):
e
a
= 18,5 cm –
mimośród siły podłużnej z uwzględnieniem siły sprężającej względem środka
ciężkości zbrojenia rozciąganego;
e
ac
= 9 cm –
mimośród siły podłużnej N względem środka ciężkości zbrojenia ściskanego;
l
o
= 2,8 m –
długość obliczeniowa słupa;
b = 0,4 m –
szerokość przekroju słupa;
h = 0,4 m –
wysokość przekroju słupa;
m
b3
= 0,85 –
współczynnik korekcyjny do obliczeniowej wytrzymałości materiału;
ξ
gr
= 0,55 –
graniczna wartość względnej wysokości strefy ściskanej przekroju;
h
o
= h – a = 0,4 – 0,03 = 0,37 m –
wysokość obliczeniowa (użyteczna) przekroju słupa
żelbetowego;
F
a
= F
ac
= 1,51 cm
2
= 0,00151 m
2
–
pole przekroju zbrojenia ściskanego lub mniej
rozciąganego;
Pole przekroju zwiększamy o 20% ze względu na moment uderzenia wózkiem w słup:
Fa=Fac=0,00151+20%*0,00151=0,00181
Beton klasy B30.
R
b
= 17,1 MPa –
wytrzymałość obliczeniowa betonu na ściskanie dla konstrukcji
żelbetonowych;
16
R
ac
= 410 MPa –
wytrzymałość charakterystyczna dla stali zbrojeniowej klasy A-III;
R
a
= 350 MPa –
wytrzymałość obliczeniowa dla stali zbrojeniowej klasy A-III.
Obliczenie wysokości strefy ściskanej betonu x:
b
R
m
e
F
R
e
F
R
e
h
e
h
x
b
b
ac
ac
ac
a
a
a
a
o
a
o
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
+
−
+
−
=
3
2
5
,
0
)
(
[m]
37
,
0
3
,
0
1
,
17
85
,
0
5
,
0
09
,
0
00151
,
0
410
185
,
0
00181
,
0
350
)
185
,
0
27
,
0
(
185
,
0
27
,
0
2
=
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
+
−
+
−
=
x
[m]
x
gr
= 0,55 · 0,27 = 0,112 m < x = 0,37 m
x
gr
< x
Ponieważ graniczna wartość wysokości strefy ściskanej jest mniejsza od wartości
obliczeniowej musimy obliczyć ją jeszcze raz z uwzględnieniem odległości między prętami
zbrojenia c.
o
b
b
a
a
gr
a
h
b
R
m
F
R
e
c
⋅
⋅
⋅
⋅
⋅
−
⋅
=
3
1
2
ξ
[m]
37
,
0
27
,
0
3
,
0
1
,
17
85
,
0
00151
,
0
350
55
,
0
1
185
,
0
2
=
⋅
⋅
⋅
⋅
⋅
−
⋅
=
c
[m]
więc:
]
5
,
0
[
2
)
(
3
2
b
R
m
e
F
R
e
F
R
c
h
c
e
h
c
e
h
x
b
b
a
a
a
ac
ac
ac
o
a
o
a
o
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
−
−
+
−
−
=
[m]
]
[
074
,
0
]
27
,
0
3
,
0
1
,
17
85
,
0
185
,
0
00151
,
0
350
09
,
0
00151
,
0
410
37
,
0
[
27
,
0
2
)
37
,
0
185
,
0
27
,
0
(
37
,
0
185
,
0
27
,
0
2
m
x
x
=
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
−
−
+
−
−
=
274
,
0
27
,
0
074
,
0
=
=
=
o
h
x
ξ
toteż:
a
o
ac
ac
o
b
b
obl
e
a
h
F
R
x
h
x
b
R
m
N
)
(
)
2
(
3
−
⋅
⋅
+
−
⋅
⋅
⋅
⋅
=
[MN]
8235
,
2
185
,
0
)
03
,
0
27
,
0
(
00151
,
0
410
)
2
074
,
0
27
,
0
(
074
,
0
4
,
0
1
,
17
85
,
0
=
−
⋅
⋅
+
−
⋅
⋅
⋅
⋅
=
obl
N
[MN]
N
użytk
= 0,274 [MN]
N
użytkowe
= 0,274< N
obliczeniowe
= 2,8235
17
W tym przypadku obciążenie użytkowe słupa jest mniejsze od obciążenia obliczeniowego
słupa i element ten przyjmuje wymiary przekroju poprzecznego 0,3 × 0,3 m.
OBLICZENIE SŁUPA ŻELBETOWEGO (I KONDYGNACJA)
Założenia:
-
rozpiętość stropu: l
1
= 5,7 m,
l
2
= 5,4 m;
-
rozpiętość podciągu 6,3 m;
-
wysokość podciągu (w świetle) wynosi: 3,3 m;
- przekrój podc
iągów stropu 0,4 × 0,5 m;
-
przekrój żeber głównych 0,3 × 0, 4 m,
Strop wylewany żelbetowy dwukierunkowo zbrojony o grubosci 15 cm..
-
pole przekroju słupa F
s
= 0,4 × 0,4 = 0,16 m
2
;
- powierzchnia rzutu poziomego
9
,
34
3
,
6
2
)
7
,
5
4
,
5
(
=
⋅
+
=
s
F
m
2
;
Tabela 3
.
Zestawieni
e obciążeń działających na słup I kondygnacji
Rodzaj obciążenia
Obliczenia
Wynik [kN]
posadzką – plytki lastriko
0,76 · 1,2 · 34,9
31,38
gładzią cementową
21 · 0,02 · 1,3 · 34,9
19,05
płytą pilśniową
3 · 0,01 · 1,2 · 34,9
1,26
jastrychem cementowym
21 · 0,05 · 1,2 · 34,9
43,97
papą na lepiku
11 · 0,003 · 1,2 · 34,9
1,38
ciężarem płyty stropowej
24 · 0,15 · 1,1 · 34,9
138,2
tynkiem cementowo-wapiennym
19 · 0,015 · 1,3 · 34,9
12,93
ciężarem żebra głównego
0,3·(0,4-0,15)·1,1·24·(5,55-0,4)
10,2
ciężarem podciągu
0,4 · (0,5-0,15) · 6,3 · 1,1 · 24
23,28
technologiczne
10 · 1,2 34,9
418,8
ciężarem instalacji elektrycznej i wentylacyjnej
0,015 · 1,2 · 34,9
0,63
ciężarem słupa
0,4 · 0,4 · 24 · 1,1 · 3,1
13,09
obciążenie pojazdami (wózek widłowy)
tynkiem na slupie
9 · 3 · 1,05 · 1,2
4*3,1*0,3*19*1,3*0,015
34,02
1.38
ciężar II kondygnacji
0,5*4*33,197478
66,39
665,15
Suma obciążeń
1405,17
Przyjęto słup wykonany z betonu klasy B30, zbrojony stalą klasy A-III.
Sprawdzenie nośności przekroju mimośrodowo-ściskanego (według PN-84/B-03264):
e
a
= 18,5 cm –
mimośród siły podłużnej z uwzględnieniem siły sprężającej względem środka
ciężkości zbrojenia rozciąganego;
e
ac
= 9 cm –
mimośród siły podłużnej N względem środka ciężkości zbrojenia ściskanego;

18
l
o
= 2,85 m –
długość obliczeniowa słupa;
b = 0,4 m –
szerokość przekroju słupa;
h = 0,4 m –
wysokość przekroju słupa;
m
b3
= 0,85 –
współczynnik korekcyjny do obliczeniowej wytrzymałości materiału;
ξ
gr
= 0,55 –
graniczna wartość względnej wysokości strefy ściskanej przekroju;
h
o
= h – a = 0,4 – 0,03 = 0,37 m –
wysokość obliczeniowa (użyteczna) przekroju słupa
żelbetowego;
F
a
= F
ac
= 15,1 cm
2
= 0,00151 m
2
–
pole przekroju zbrojenia ściskanego lub mniej
rozciąganego;
Beton klasy B30.
R
b
= 17,1 MPa – wytrzym
ałość obliczeniowa betonu na ściskanie dla konstrukcji
żelbetonowych;
R
ac
= 410 MPa –
wytrzymałość charakterystyczna dla stali zbrojeniowej klasy A-III;
R
a
= 350 MPa –
wytrzymałość obliczeniowa dla stali zbrojeniowej klasy A-III.
Pole przekroju zwiększamy o 20% ze względu na moment uderzenia wózkiem w słup
Mu-
obciążenie wózkiem *0,58wysokości słupa
Mu- 34,02*0,5*3,1=52.731[kN]
Słup parteru wykonano podobnie jak slup I piętra z betonu klasy B30 zbrojonego stalą A-III.
Również i w tym przypadku zwiększono przekrój zbrojenia o 20% ze względu na moment
powstaly od uderzenia wozkiem widlowym w slup. Wymiary słupa są takie same jak słupa I
piętra w związku z tym ograniczono obliczenia do sprawdzenia nośności przekroju
mimosrodowego –
ściskanego.
8235
,
2
=
obl
N
[MN]
N
użytk
= 0,274 [MN]
N
użytkowe
= 0,274< N
obliczeniowe
= 2,8235
W tym przypadku obciążenie użytkowe słupa jest mniejsze od obciążenia obliczeniowego
słupa i element ten przyjmuje wymiary przekroju poprzecznego 0,4 × 0,4 m.
2.3. Stopa fundamentowa
19
ŻELBETOWA STOPA FUNDAMENTOWA
Stopa żelbetowa jest obciążona słupem o wymiarach poprzecznych 0,4 × 0,4 m
przenoszących obciążenie
1405,17
kN. Przyjęto klasę betonu B20 o wytrzymałości
obliczeniowej betonu na rozciąganie dla konstrukcji żelbetowych Fctd= 0,9 MPa oraz
zbrojenie stalą A-II o wytrzymałości obliczeniowej stali zbrojeniowej na rozciąganie i
ściskanie R
a
= 310 MPa. Głębokość posadowienia stopy D = 1,2 m. Założono stopę o
podstawie kwadratowej B × B. Jednostkowy obliczeniowy opór graniczny po
dłoża
q
f
= 300 kPa.
Zestawienie obciążeń działających na stopę:
Tabela 4
.
Zestawienie obciążeń działających na stopę
Rodzaj obciążenia
Obliczenia
Wynik [kN]
posadzką – plytki lastriko gr. 2 cm
0,76 · 1,2 · 3,84
3,5
gładzią cementową
21 · 0,02 · 1,3 · 3,84
20,96
szkłem piankowym
4 · 0,05 · 1,3 · 3,84
1,02
jastrychem cementowym
21 · 0,05 · 1,2 · 3,84
4,8
papą na lepiku
11 · 0,003 · 1,2 · 3,84
0,015
betonem
20 · 0,1 · 1,1 · 3,84
8,4
technologiczne
10 · 1,2 3,84
46,08
ubitym gruzem
12 · 0,05 · 1,2 · 3,84
2,64
obciążenie pojazdami (wózek widłowy)
9 · 3 · 1,05 · 1,2
34,02
Suma obciążeń
121,435
Q
s
= 1405,17 +
121,435
= 1526,605 [kN]
Moment zginający względem środka ciężkości:M=Qs*e
e=6,5cm
M=0,065*1526,605=99,23
Obliczenie obciążenia dopuszczalnego
qdop=m*qf
qdop=0,81*300=2.43 MPa
m=0,9*0,8=0,81-
wspołczynnik korekcyjny, który zniża opór graniczny podloża
qmax<gdop warunek spelniony
Ciężar obliczeniowy stopy i gruntu:
)
(
2
r
śr
r
D
B
G
γ
⋅
⋅
=
[kN]
2
2
4
,
27
83
,
22
2
,
1
B
B
G
r
⋅
=
⋅
⋅
=
[kN]
gdzie:
γ
śr
(r)
–
ciężar objętościowy: γ
śr
(r)
= γ
śr
(n)
· γ
f
= 20,75 · 1,1 = 22,83 [kN/m
3
]
γ
śr
(n)
= 20,75 [kN/m
3
]

20
γ
f
–
współczynnik obciążenia = 1,1 PN-82/B-02001
Fundament obciążony osiowo pionową siłą, do głębokości nośnej co najmniej dwukrotnej
szerokości fundamentu 2B, podłoże jednorodne.
f
r
s
rs
q
m
G
F
Q
q
⋅
≤
+
=
243
300
*
81
,
0
88
,
230
6
,
2
6
,
2
4
,
27
605
,
1526
2
2
=
≤
=
+
+
=
rs
q
Przyjęto bok stopy fundamentowej B =2,12. Pozostałe wymiary stopy: h
1
= 0,15 m,
s = 0,78 m, h = 0,5 m.
Ostatecznie przyjęto stopę fundamentową o boku B=2,12 cm
Sprawdzenie stopy na przebicie
Przyjeto otulinę zbrojenia c=5cm (pod stopą przyjęto warstwe betonu grubości 10cm)
wstępnie przyjęto pręty zbrojenia o średnicy 12 cm i odchyłkę grubości otuliny 1cm.
Warunek obliczeniowy
Qr-
sila nacisku slupa od obliczeniowej wartosci obciążen
L=B-
długosc boku
as1=as2=as –
równolegly do boku stopy bok przekroju słupa
Np.- sila powodujaca przebicie
Fctd-
obliczeniowa wytrzymalośc na rozciąganie dla konstrukcji żelbetowych
d-
wysokość użyteczna przekroju
Warunek obliczeniowy
D=h-c-o-0,50-dh=60-5-1,2-0,5*1,2-1=57,7 cm
Przyjęto d=57 cm
Up=4(as+d0=2(30+57,7)=350,8
Qr=Nr/B 1526,605/260=0,034
Fctd=0,87Mpa=0,087[kN/cm2]
Np=Nr-qr(as+2d)2<fctd*up*d
Np=1526,605-0,034*(30+2*57,7)2=1590,4<fctd*up*d
Np=1590,4<0,087*350,8*57,7=170,9
Warunek
zostal
spełniony

21
Usługi Ciesielskie - domy drewniane - domy szkieletowe - konstrukcje dachowe więźby
S
B
h
h
1
Document Outline
Wyszukiwarka
Podobne podstrony:
Projekt dachu opisówka, Więźba dachowa
projekt do wysłania, projekt dachu madlewski 01
KSPD projekt część opisowa
KSPD Projekt Część opisowa i rysunkowa
PROJEKT DACHU DLA BUDYNKU RODZINNEGO prezentacja
PROJEKT czesc opisowa
projekt dachu, kicek
Konstrukcje Drewniane i Murowe PROJEKT DACHU O KONSTRUKCJI DREWNIANEJ KRATOWEJ OPARTEJ NA ŚCIANACH
projekt czesc opisowa
Geologia semestr II projekt 1 część opisowa, Geologia projekt
projekt dachu (1), dom
projekt do wysłania, projekt dachu madlewski 01
Mathcad projekt dachu
projekt statystyka opisowa 2010 www przeklej pl
Projekt dachu
więcej podobnych podstron