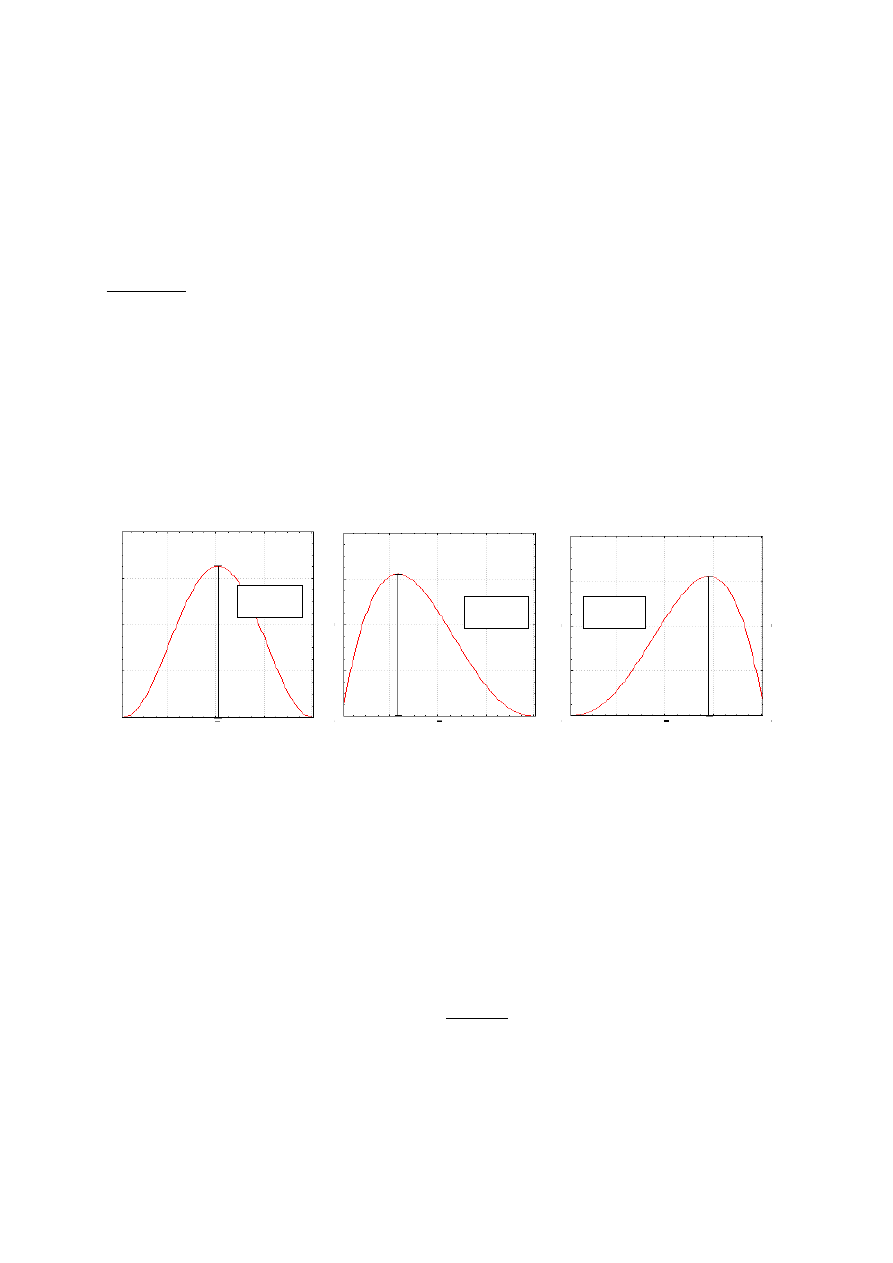
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Opis statystyczny struktury zbiorowości cz.2
Asymetria mówi do nas,
czy jest równo po obu stronach.
Asymetria
charakteryzuje równomierność (a raczej brak równomierności) rozproszenia danych wokół
przeciętnej.
Określenie tendencji centralnej i zmienności rozkładu analizowanej zmiennej nie
wyczerpuje opisu tegoż rozkładu. Czasem interesuje nas nie tylko wielkość rozproszenia lecz
również na ile rozproszenie danych wokół przeciętnej jest równomierne. Jedną z miar
asymetrii rozkładu jest współczynnik asymetrii A.
Gdy rozkład jest symetryczny współczynnik asymetrii A przyjmuje wartość zero (A=0).
Wartość dodatnia (A>0), wskazuje na asymetrię prawostronną. Wartość ujemna
współczynnika (A<0), na asymetrię lewostronną. Większa wartość bezwzględna
współczynnika odpowiada silniejszej asymetrii.
M=Me=Mo
Mo<Me<M
M<Me<Mo
Rozkład symetryczny
Rozkład prawostronnie
Rozkład lewostronnie
asymetryczny
asymetryczny
Rys.25. Rozkład symetryczny, prawostronnie asymetryczny i lewostronnie asymetryczny
W przypadku rozkładów umiarkowanie asymetrycznych jako przybliżoną miarę asymetrii można
przyjąć różnicę między średnią arytmetyczną M a modą Mo, nazywaną wskaźnikiem skośności: M –
Mo.
Rozkład jest symetryczny, gdy M – Mo = 0.
Rozkład jest prawostronnie asymetryczny, gdy M – Mo > 0.
Rozkład jest lewostronnie asymetryczny, gdy M – Mo < 0.
Bezwzględny współczynnik skośności określa kierunek asymetrii, ale nic nie mówi o jej sile.
Zarówno kierunek jak i siłę asymetrii wskazuje względny współczynnik skośności A
S
:
S
Mo
M
A
S
−
=
,
gdzie M – średnia arytmetyczna, Mo – moda, S – odchylenie standardowe. Im większa, co do
modułu, wartość współczynnika A
S
, tym bardziej asymetryczny jest rozkład.
A = 0
A>0
A<0
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Kwantyle rozkładu
Do opisu rozkładu wykorzystywane są też miary pozycyjne zwane kwantylami.
Kwantyle rozkładu to wartości zmiennej, które dzielą uporządkowaną według wartości zmiennej
zbiorowość w określonym stosunku liczbowym. Kwantylem rzędu q rozkładu zmiennej X w
N-elementowej zbiorowości jest taka wartość x
k
, że w uporządkowanej rosnąco ze względu na
zmienną X zbiorowości q*100% jednostek zajmuje pozycję nie dalszą niż x
k
, a pozostały procent
zbiorowości pozycję nie bliższą.
Najczęściej stosowane w opisie rozkładu kwantyle to:
kwantyl rzędu q=0,5 nazwany medianą; jest wartością zmiennej dzielącej uporządkowaną
zbiorowość na dwie równoliczne części;
kwantyle rzędu q=0,25; 0,50; 0,75, kwartyle;
trzy kwartyle dzielą uporządkowaną zbiorowość na
cztery równoliczne części;
kwantyle rzędu q=0,1; 0,2; ... 0,9, czyli decyle;
dziewięć decyli dzieli uporządkowaną zbiorowość
na dziesięć równolicznych części;
kwantyle rzędu q=0,01; 0,02; 0,50; ... 0,99, czyli centyle
lub percentyle; 99 centyli dzieli
uporządkowaną zbiorowość na 100 równolicznych części (stosowane są w przypadku opisu dużych
zbiorowości, N>100).
Za pomocą kwartyli konstruowane są miary kwantylowe opisu rozkładu zmiennej, zatem
przyjrzyjmy się im bliżej.
Kwartyl pierwszy
to jest miara,
co zbiorowość dzieli zaraz:
niższych jest wartości
ćwiartka,
wyższych będzie ze trzy
czwarte.
(Emilia Kozierkiewicz)
Kwartyl drugi
jak mediana dzieli szereg na
połówki i choć nazwa nie ta
sama wbij ją do swej ślicznej
główki.
(
Tomasz
Osyra
)
Kwartyl trzeci
dla twardzieli na te części
szereg dzieli: wyższych jest
wartości ćwiartka, niższych
będzie ze trzy czwarte.
(
Justyna
Kozierkiewicz
)
Q
1
- kwartyl pierwszy (dolny): dzieli uporządkowany zbiór danych w stosunku 1 : 4 tak,
że 25% danych zajmuje pozycję nie dalszą niż Q
1
a 75% danych pozycję nie bliższą; kwartyl
pierwszy jest kwantylem rzędu 0,25.
Q
2
- kwartyl drugi (mediana) dzieli uporządkowany zbiór danych w stosunku 1 : 2 tak, że
50% danych zajmuje pozycję nie dalszą niż Q
2
a 50% danych pozycję nie bliższą; mediana
jest kwantylem rzędu 0,5.
Q
3
- kwartyl trzeci (górny): dzieli uporządkowany zbiór danych w stosunku 3 : 4 tak, że
75% danych zajmuje pozycję nie dalszą niż Q
3
a 25% danych pozycję nie bliższą; kwartyl
trzeci jest kwantylem rzędu 0,75.
Miarą tendencji centralnej rozkładu określoną przy użyciu miar kwantylowych jest
mediana, czyli drugi kwartyl.
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Miarą rozproszenia rozkładu określoną przy użyciu miar kwantylowych jest różnica
1
3
Q
Q
−
nazywana rozstępem kwartylowym, gdzie: Q
3
- kwartyl trzeci (górny), Q
1
- kwartyl
pierwszy
Rozstęp kwartylowy określa zakres zmienności „środkowych” 50% danych zajmujących
w uporządkowanym ich zbiorze pozycje między pierwszym a trzecim kwartylem.
W praktyce stosowane jest też jako miara zmienności rozkładu odchylenie ćwiartkowe
(połówkowy rozstęp kwartylowy) Q:
2
1
3
Q
Q
Q
−
=
,
Względną miarę rozproszenia w opisie pozycyjnym określa współczynnik zmienności V
Q,
zdefiniowany jako stosunek odchylenia ćwiartkowego do mediany:
Me
Q
V
Q
=
,
gdzie Q - odchylenie ćwiartkowe, a Me - mediana.
Aby wyznaczyć pozycyjną miarę zmienności należy znaleźć wartość pierwszego i trzeciego
kwartyla.
118cm, 118cm, 119cm, 121cm, 123cm, 125cm, 126cm, 126cm, 126cm, 127cm, 130cm
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
x
10
x
11
Pierwszym kwartylem jest wartość
4
1
+
N
x
, czyli w naszym przykładzie x
3
, stąd Q
1
= 119cm. Trzeci
kwartyl to wartość
(
)
4
1
3
+
N
x
, czyli x
9
, stąd Q
3
= 126cm. Rozstęp kwartylowy wynosi Q
3
- Q
1
= 7cm, co
oznacza, że gdy pominiemy grupę 25% dzieci niższych i 25% dzieci wyższych to w pozostałej grupie
50% dzieci różnią się wzrostem nie więcej niż o 7cm.
Odchylenie ćwiartkowe równe jest:
cm
cm
cm
Q
Q
Q
5
,
3
2
119
126
2
1
3
=
−
=
−
=
,
a względne rozproszenie mierzone współczynnikiem
Me
Q
V
Q
=
028
,
0
125
5
,
3
=
=
Q
V
, co świadczy o dużej jednorodności zbioru danych.
Współczynnik asymetrii A
Q
zbudowany na miarach kwantylowych zdefiniowany jest
następująco:
(
) (
)
1
3
1
3
Q
Q
Q
Me
Me
Q
A
Q
−
−
−
−
=
,
lub w postaci równoważnej powyższej równości:
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Q
Me
Q
Q
A
Q
2
2
1
3
−
+
=
,
gdzie Q
1
i Q
3
to odpowiednio pierwszy i trzeci kwartyl, Me – mediana, Q – odchylenie
ćwiartkowe.
Większa, co do modułu, wartość współczynnika A
Q
wskazuje na silniejszą asymetrię
rozkładu. Współczynniki asymetrii są liczbami niemianowanymi.
Liczbowy opis rozkładu można uzupełnić wykresem pudełkowym (ramkowym). W
opisie z wykorzystaniem kwartyli wykres ten składa się z prostokąta o dowolnej szerokości,
którego wysokość wyznaczają pierwszy Q
1
i trzeci Q
3
kwartyl. Wewnątrz prostokąta
zaznaczana jest mediana. Prostokąt uzupełniają dwa odcinki (wąsy): jeden łączy bok
prostokąta na poziomie Q
1
z wartością minimalną zbioru danych, drugi zaś łączy Q
3
z
wartością maksymalną. Położenie mediany względem kwartyli pozwala ocenić symetrię
rozkładu; gdy odległość miedzy medianą a Q
1
jest większa niż między medianą a Q
3
, rozkład
jest lewostronnie asymetryczny, gdy jest odwrotnie otrzymany rozkład charakteryzuje się
asymetrią prawostronną.
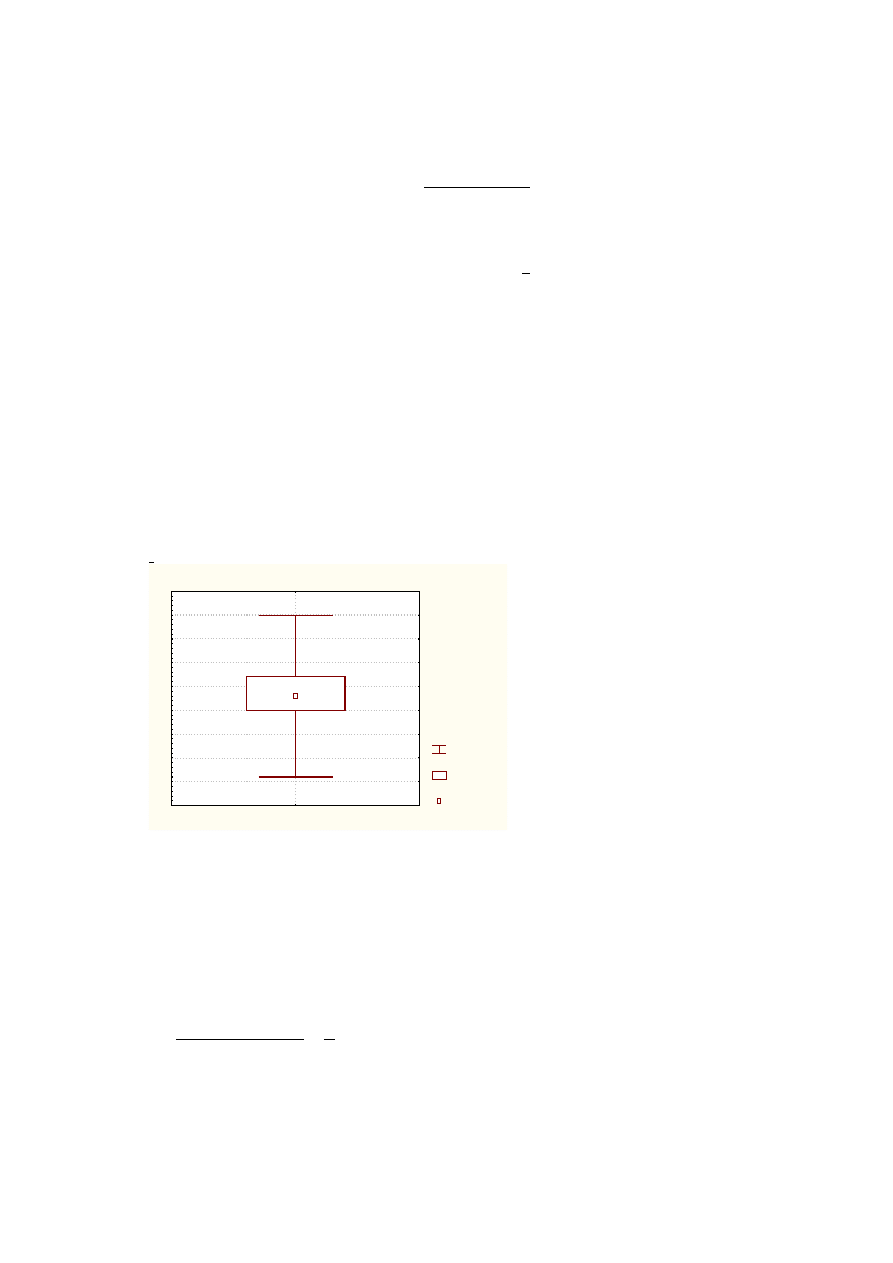
Wykres ramkowy charakterystyk pozycyjnych rozkładu zmiennej wzrost (tabela 3).
przedstawiony jest na rysunku 26.
Maks = 170 cm
Min = 136 cm
75% = 157 cm
25% = 150 cm
Mediana:
Med = 153 cm
Wykres ramkowy
130
135
140
145
150
155
160
165
170
175
Wzrost
Rys. 26. Wykres ramkowy (pudełkowy) obrazujący graficznie położenie mediany, kwartyli
oraz wartości minimalnej i maksymalnej zbioru danych
W legendzie obok wykresu podane są: wartość maksymalna x
max
= 170 cm, wartość
minimalna x
min
= 136 cm, kwartyl dolny Q
1
= 150 cm, kwartyl górny Q
3
= 157 cm, oraz
mediana Me = 153 cm. Położenie mediany (kwadracik wewnątrz prostokąta) względem
boków prostokąta na poziomie kwartyli wskazuje na słabą asymetrię prawostronną rozkładu.
Współczynnik asymetrii A
Q
jest równy w tym przypadku:
14
,
0
7
1
150
157
153
2
150
157
≈
=
−
⋅
−
+
=
Q
A
.
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Dwa zastosowania odchylenia standardowego
W zastosowaniach praktycznych odchylenie standardowe wykorzystywane jest do określania
obszaru wartości typowych dla danego rozkładu symetrycznego (w praktyce również rozkładu o
niewielkiej asymetrii) według zależności:
M – S < x
typ
< M + S
Obserwacje (dane) należące do tego obszaru, to wartości zmiennej typowe w badanej zbiorowości.
Jeżeli rozkład można uznać za rozkład normalny (w sensie zgodności badanego rozkładu
empirycznego z teoretycznym rozkładem normalnym wykazanej w procedurze weryfikacji
odpowiedniej hipotezy zgodności), poza obszarem typowym znajdzie się tylko około 32%
zbiorowości. Zatem typowe wartości analizowanej zmiennej to te, które zaobserwowano u ok. 68%
badanej zbiorowości.
Równie ważną rolę w praktyce statystycznej odgrywa mająca swe podstawy w nierówności
Czebyszewa tzw. reguła trzech sigm, w której odchylenie standardowe wykorzystuje się do
określenia obszaru wartości bardzo mało prawdopodobnych. Mówi ona o tym, że
prawdopodobieństwo zaobserwowania wartości zmiennej różniącej się o więcej niż trzy odchylenia
standardowe od średniej rozkładu tej zmiennej w populacji, wynosi mniej niż 0,001. Stosując tę
regułę możemy „wyłapać” takie dane, które pojawiły się w analizowanym zbiorze danych
przypadkowo.
Statystyka w badaniach. Opis statystyczny struktury danych. część 2
Urszula Augustyńska
Ćwiczenia i zadania
Zadanie 1.(T. Zimny, Metody statystyczne w badaniach i diagnostyce pedagogicznej. Wyd. Nauk.
Uniwersytetu Szczecińskiego, Szczecin 2007)
W oddziałach „a” i „b” IV klasy pewnej szkoły podstawowej przeprowadzono test zdolności
manualnych. Otrzymane rozkłady wyników testowych charakteryzują następujące miary:
Dolny
kwartyl
Mediana
Średnia
arytmetyczna
Odchylenie
standardowe
Oddział „a”
47 p
52 p
55 p
10 p
Oddział „b”
48 p
54 p
54 p
8 p
Na podstawie podanych charakterystyk rozkładów wyników testowych w oddziale „a” i oddziale „b”
określ prawdziwość stwierdzeń:
a) Połowa uczniów klasy IV oddziału „a” uzyskała nie więcej niż 52 punkty
Tak
Nie
b) Przeciętnie zdolności uczniów oddziału „a” są wyższe niż zdolności
uczniów oddziału „b”
Tak
Nie
c) W oddziale „a” jest kilku wyjątkowo zdolnych uczniów
Tak
Nie
d) W oddziale „b” 25% uczniów uzyskało nie więcej niż 48 punktów
Tak
Nie
e) Rozkład wyników testu zdolności w oddziale „a” jest symetryczny
Tak
Nie
f) Rozproszenie wyników testu jest większe w oddziale „a”
Tak
Nie
g) 75% uczniów oddziału „b” uzyskało wynik nie niższy niż 48 punktów
Tak
Nie
Wyniki typowe testu w oddziele „b” to wyniki od 46 punktów do . ........
Zadanie 2.
a) Jeżeli wzrost dziecka odpowiada 70 centylowi, to jaki procent dzieci jest od niego niewyższych?
b) Jeżeli masa ciała Jasia odpowiada 8 decylowi, to jaki procent dzieci ma masę ciała większą niż Jaś?
c) Jeżeli wzrost Jasia odpowiada 9 decylowi a masa ciała 30 centylowi to możemy się spodziewać, że
Jaś jest stosunkowo:
- niski i masywny
- wysoki i masywny
- niski i szczupły
- wysoki i szczupły
Zadanie 3
a) Ustal relację między miarami opisującymi ten sam rozkład (wstaw w miejsce kropek znak „<”, „>”
lub „=”):
Me ...... Q
1
Q
1
......... D
1
C
30
........ D
3
Q
1
....... C
30
b) Uzupełnij tak aby równość była prawdziwa w analizowanym rozkładzie (w miejsce kropek wpisz
odpowiedni numer centyla lub decyla):
Me = Q..... = D..... = C ......
Q
1
= C.....
C
30
= C.....