1

UKŁAD KASKADOWY NA STAŁ

Ą

MOC

Zasada regulacji pr

ę

dko

ś

ci k

ą

towej silników indukcyjnych w układach

kaskadowych polega na wprowadzeniu do ka

ż

dej fazy wirnika dodatkowej siły

elektromotorycznej E’d o cz

ę

stotliwo

ś

ci równej cz

ę

stotliwo

ś

ci po

ś

lizgu f2 =f1s. Przez

zmian

ę

modułu i fazy E’d w stosunku do siły elektromotorycznej E’20, indukowanej

w uzwojeniu wirnika, uzyskuje si

ę

zmian

ę

pr

ę

dko

ś

ci k

ą

towej i współczynnika mocy

silnika.

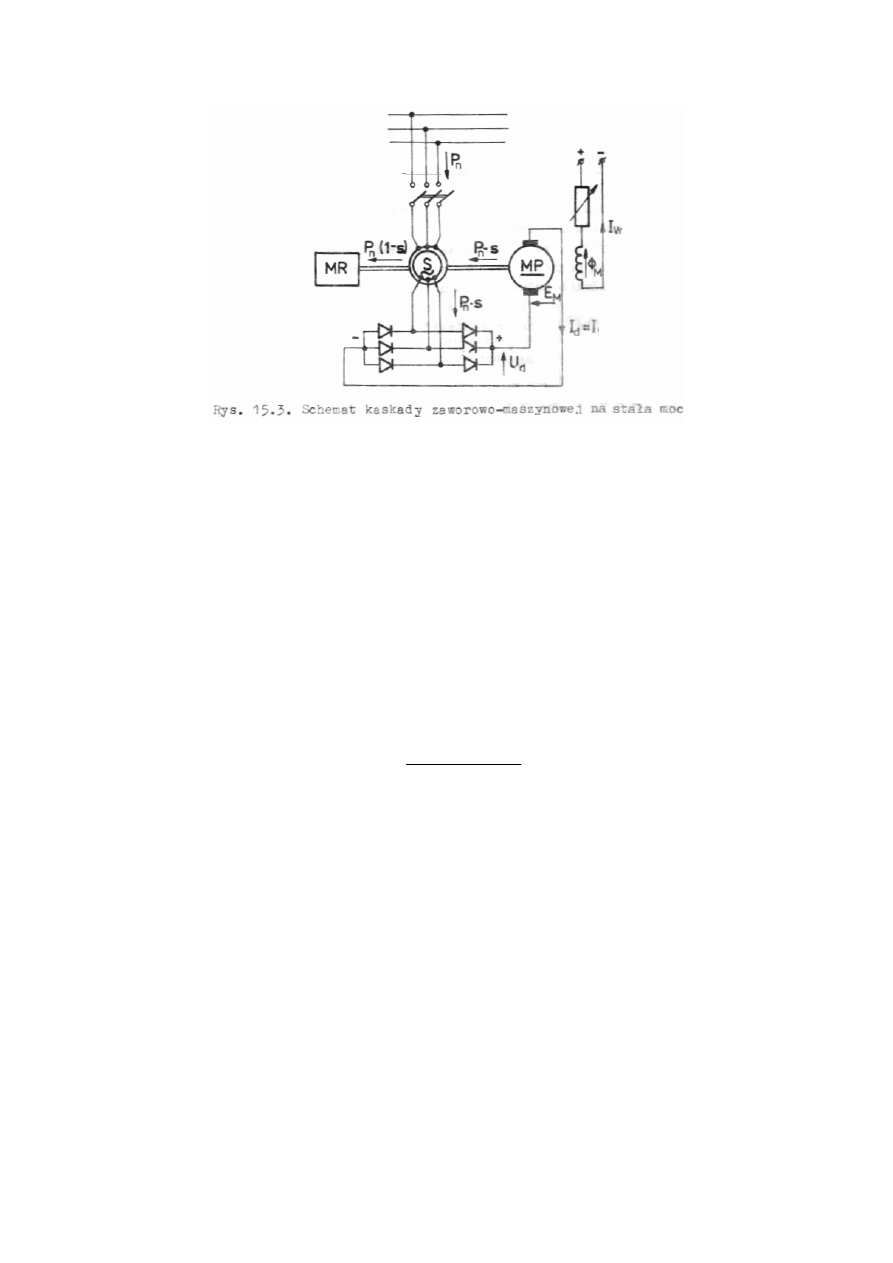
2

W układach kaskadowych na stał

ą

moc, moc pobrana z sieci przez silnik

indukcyjny zamieniona jest na moc mechaniczn

ą

s)

-

(1

P

P

n

=

oraz na tzw. moc

po

ś

lizgu w obwodzie wirnika

ns

P

. Moc po

ś

lizgu, po przetworzeniu w prostowniku

na moc pr

ą

du stałego, zasila silnik pr

ą

du stałego. Z kolei moc ta jest zamieniana na

moc mechaniczna i przekazywana na wał silnika indukcyjnego.

n

P

=

+

−

⋅

ns

n

P

s

P

)

1

(

Ś

redni

ą

warto

ść

pr

ą

du wyprostowanego I

d

okre

ś

la zale

ż

no

ść

:

Z

M

p

d

R

E

s

E

k

I

−

⋅

⋅

=

20

gdzie:

Z

R

– rezystancja zast

ę

pcza obwodu prostownika i twornika silnika pomocniczego,

20

E

– siła elektromotoryczna wirnika przy po

ś

lizgu s = 1,

mp

mp

k

p

/

sin

/

π

π

−

– stosunek napi

ę

cia wyprostowanego

0

d

U

przekształtnika mostkowego

w stanie jałowym do fazowego napi

ę

cia zasilania.

Przy zało

ż

eniu,

ż

e I

d

= 0 otrzymuje si

ę

zale

ż

no

ść

:

M

j

M

e

p

E

k

s

E

k

=

⋅

⋅

=

⋅

⋅

0

20

ϖ

φ

3

Po uwzgl

ę

dnieniu zale

ż

no

ś

ci na po

ś

lizg silnika indukcyjnego:

0

0

0

0

ϖ

ϖ

ϖ

j

s

−

=

otrzymuje

si

ę

zale

ż

no

ść

okre

ś

laj

ą

c

ą

charakterystyk

ę

regulacyjn

ą

układu

kaskadowego na stał

ą

moc:

0

20

20

0

0

ω

φ

ϖ

ϖ

⋅

⋅

+

⋅

⋅

=

M

e

p

p

j

k

E

k

E

k

gdzie:

oj

ω

– pr

ę

dko

ść

k

ą

towa idealnego biegu jałowego,

0

ω

– pr

ę

dko

ść

synchroniczna silnika.

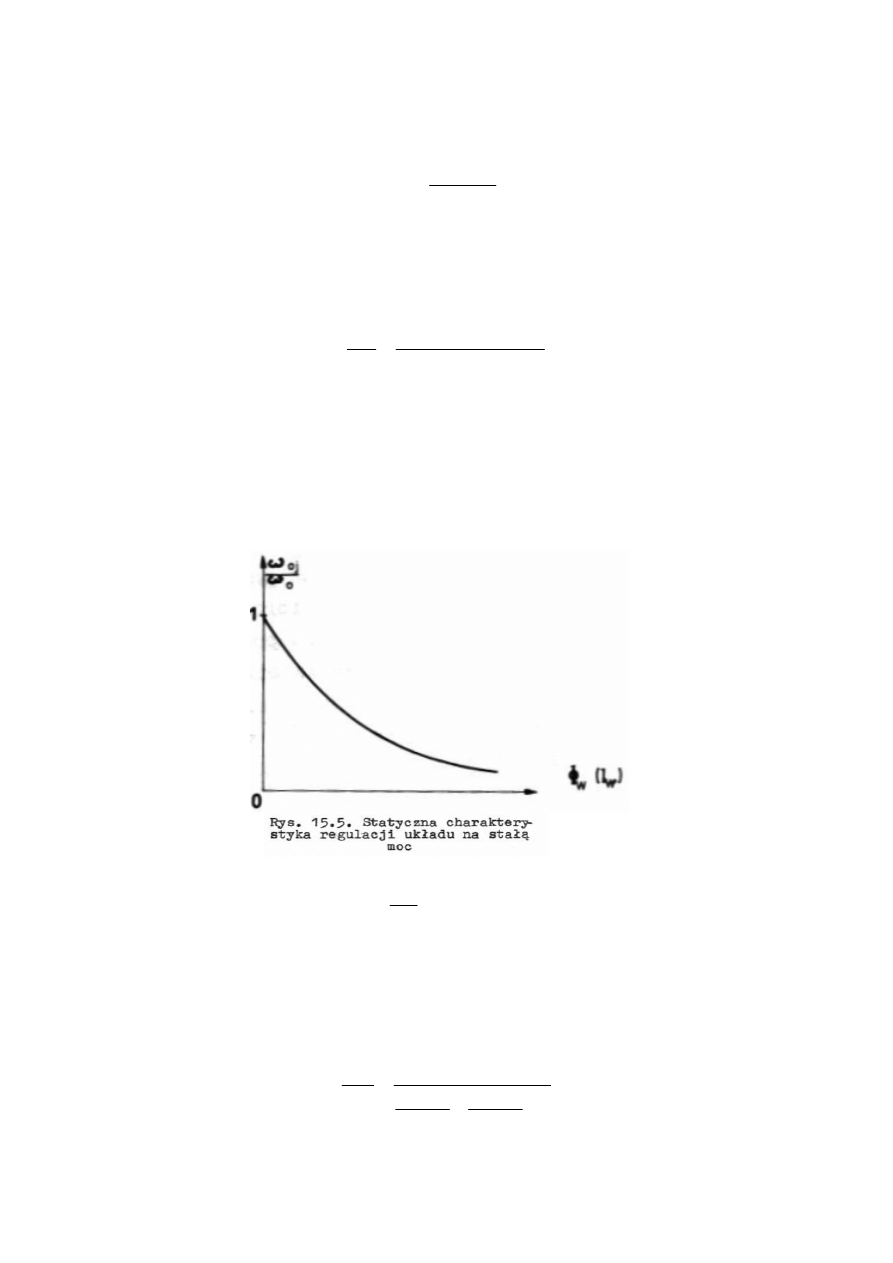
Z przebiegu charakterystyki

)

(

0

0

M

j

f

φ

ω

ω

=

wynika,

ż

e pr

ę

dko

ść

k

ą

towa zmienia

si

ę

hiperbolicznie w funkcji strumienia magnetycznego

M

φ

maszyny pomocniczej,

a wi

ę

c nie mo

ż

na doprowadzi

ć

silnika indukcyjnego do pr

ę

dko

ś

ci

0

=

ω

.

Moment obrotowy silnika indukcyjnego:

2

4

0

0

0

0

+

−

−

+

−

−

=

s

s

s

s

s

s

s

s

M

M

kk

kk

ek

ea

4

gdzie:

kk

s

– po

ś

lizg krytyczny w układzie kaskadowym,

ea

M

– moment obrotowy silnika indukcyjnego,

ek

M

– moment krytyczny silnika w układzie kaskadowym.

Całkowity moment elektromagnetyczny kaskady zaworowo-maszynowej, jako suma

momentu M

ea

silnika indukcyjnego i M

ep

silnika pomocniczego pr

ą

du stałego, wynosi:

)

1

(

λ

+

⋅

≡

+

=

ea

ep

ea

e

M

M

M

M

,

gdzie:

20

0

E

k

k

p

M

e

⋅

⋅

⋅

=

ω

φ

λ

.

Przy niewielkim zwi

ę

kszeniu zakresu regulacji, bardzo szybko zwi

ę

ksza si

ę

moc znamionowa silnika pomocniczego M

p

. Na skutek tego, w kaskadach zaworowo-

maszynowych na stał

ą

moc, praca układu odbywa si

ę

w zakresie po

ś

lizgów

idealnego biegu jałowego

5

,

0

0

≤

s

. Moment obrotowy silnika asynchronicznego

mo

ż

na wyznaczy

ć

z mocy po

ś

lizgu w obwodzie wyprostowanego pr

ą

du wirnika, czyli:

s

I

U

M

d

d

ea

⋅

⋅

=

0

ω

.

Moment krytyczny:

2

2

20

0

)

1

(

2

3

3

λ

π

ω

+

⋅

⋅

⋅

⋅

=

Z

ek

X

E

M

5

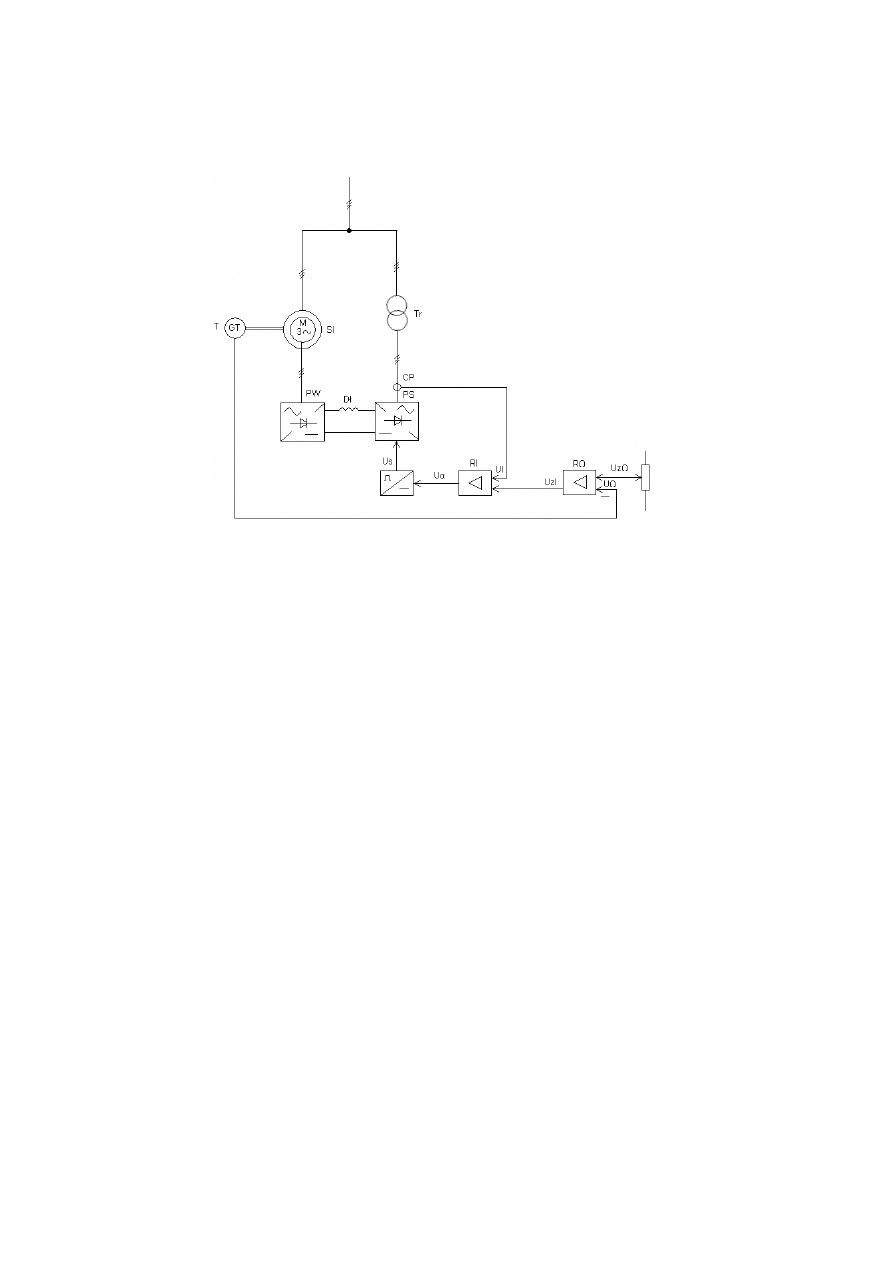
Przykładowy układ automatycznej regulacji pr

ę

dko

ś

ci i pr

ą

du w układzie

kaskadowym: