Eugeniusz Rosołowski, e-mail:
eugeniusz.rosolowski@pwr.wroc.pl
2.
OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE
CZASU
2.1.
Opis dynamiki systemu
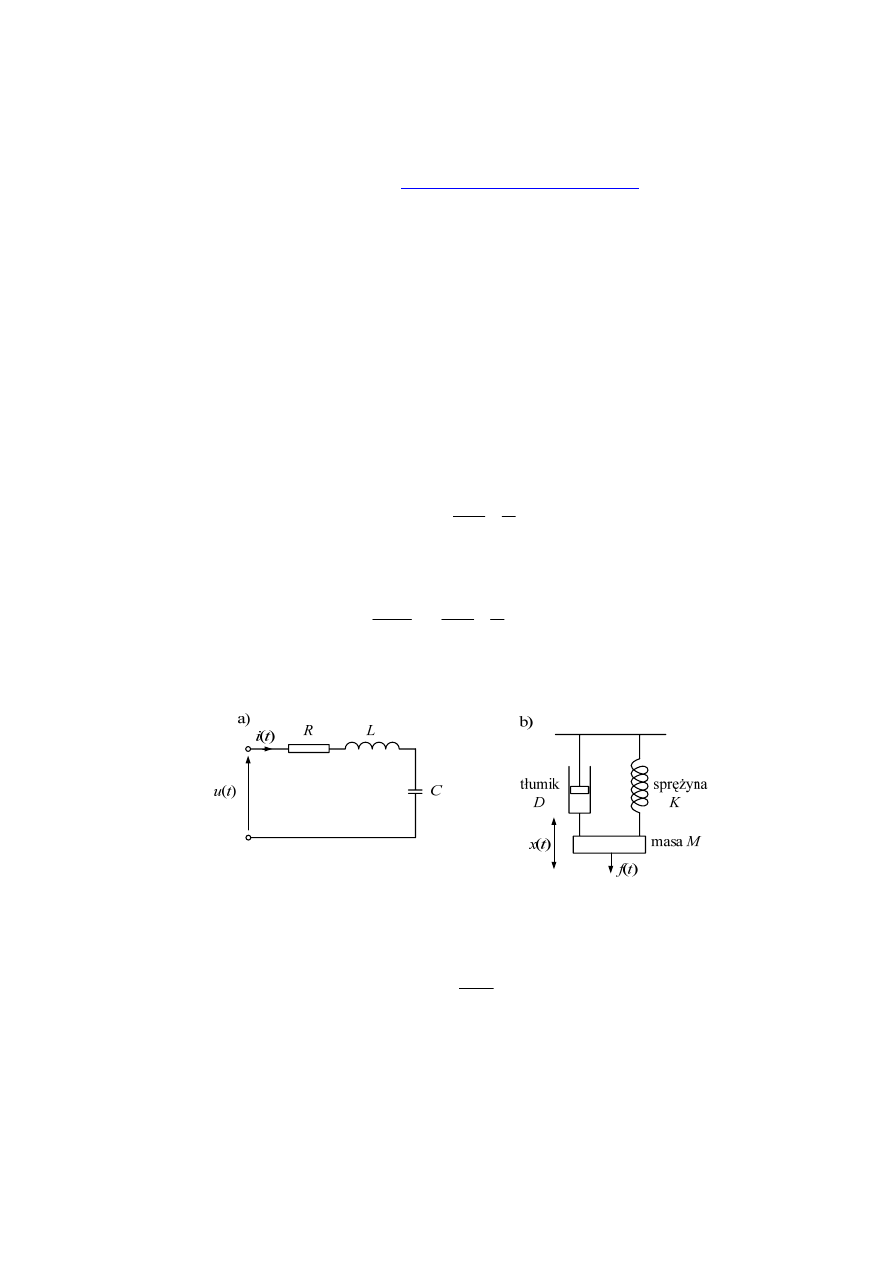
Rozważmy dwa układy fizyczne, których schematy są pokazane na rys. 2.1. Pierwszy
z nich (rys. 2.1a) przedstawia szeregowy obwód elektryczny RLC, który jest zasilany
napięciem u(t). Równanie napięciowe utworzonego oczka ma następującą postać:
∫
+
+
=
t
t
i
C
t
t
i
L
t
Ri
t
u
d
d
d
)
(
1
)
(
)
(
)
(
(2.1)
Po obustronnym zróżniczkowaniu, przy założeniu, że napięcie wymuszające jest
stałe: u(t) = U, otrzymujemy następujące równanie różniczkowe:
0
)
(
1
d
)
(
d
d
)
(
d
2
2
=
+
+
t
i
C
t
t
i
R
t
t
i
L
(2.2)
Jest to jednorodne równanie drugiego rzędu. Mówimy, że opisuje ono układ
drugiego rzędu.
Rys. 2.1. Przykłady układów dynamicznych; a – obwód elektryczny; b – układ mechaniczny
Podobne zależności otrzymamy dla układu mechanicznego (rys. 2.1b):
∫
+
+
=
t
t
v
K
t
t
v
M
t
Dv
t
f
d
d
d
)
(
)
(
)
(
)
(
(2.3)
2
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
gdzie: f(t) jest siłą wymuszającą zmianę położenia masy M; v(t) jest prędkością
zmiany położenia masy M; D jest współczynnikiem tłumienia; K – stała sprężyny.
Porównując zależności (2.1) i (2.3) łatwo zauważyć analogie pomiędzy
wielkościami elektrycznymi i mechanicznymi, na przykład:
napięcie elektryczne u(t) -
siła f(t),
prąd elektryczny i(t)
` - prędkość v(t)
i inne. Widać także, że różne co do charakteru zjawisk fizycznych systemy, mogą
mieć jednakowe dynamiczne modele matematyczne. To sprawia, że teoria systemów
jest dziedziną uniwersalną, gdyż jej język opisuje właściwości dynamiczne systemów
o bardzo różnym charakterze fizycznym.
Wracając do układu mechanicznego z rys. 2.1b, przy założeniu, że siła działająca
na ten układ jest stała: f(t) = F, równanie (2.3) przybiera następującą postać:
0
)
(
d
)
(
d
d
)
(
d
2
2
=
+
+
t
Kv
t
t
v
D
t
t
v
M
(2.4)
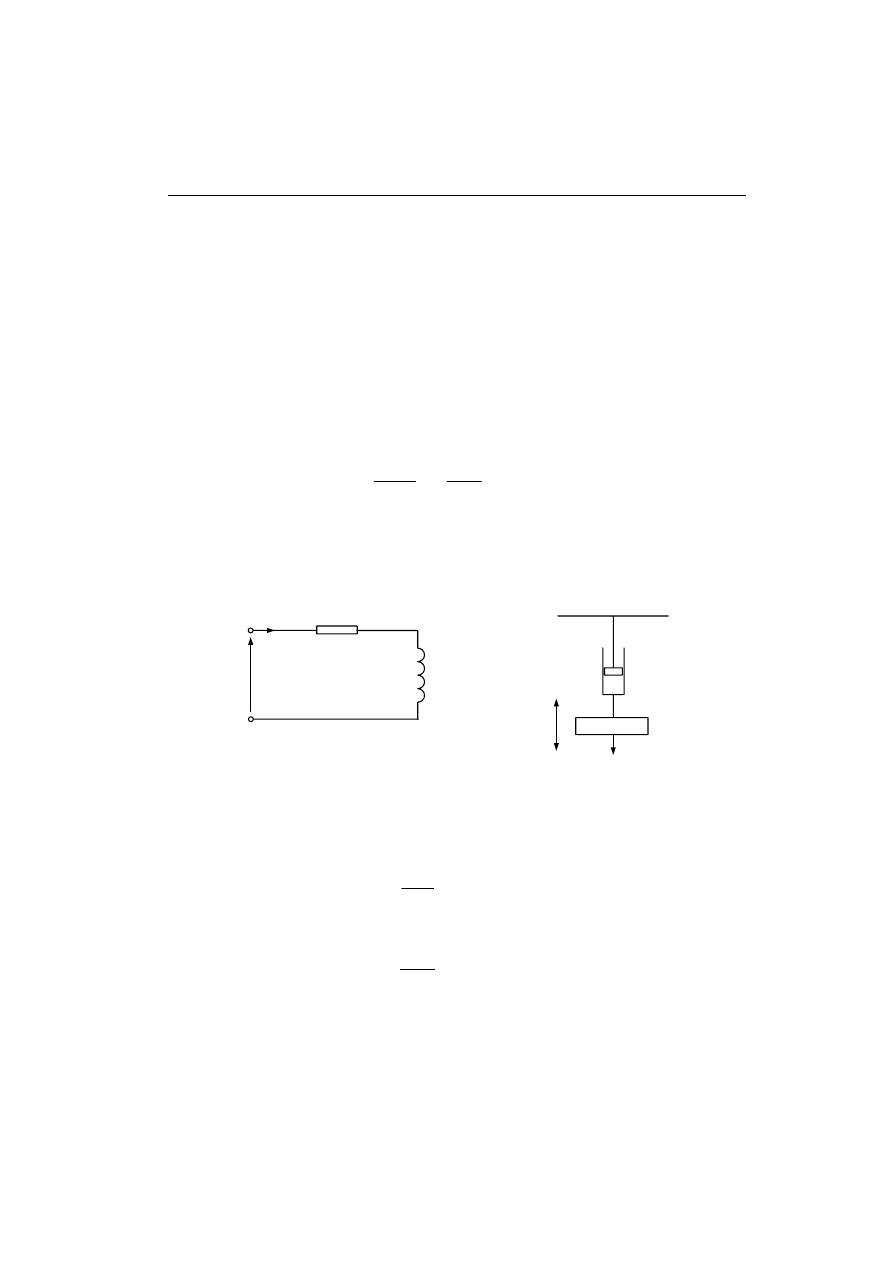
Jeśli w rozpatrywanych układach z rys. 2.1 pominąć kondensator w obwodzie
elektrycznym i sprężynę w układzie mechanicznym, to przyjmą one postać jak na rys.
2.2.
R
L
u(t)
i(t)
tłumik
masa M
x(t)
b)
a)
f(t)
D
Rys. 2.2. Przykłady układów dynamicznych pierwszego rzędu; a – obwód elektryczny;
b – układ mechaniczny
W tym przypadku równania dynamiki redukują się do postaci:
)
(
)
(
d
)
(
d
t
u
t
Ri
t
t
i
L
=
+
(2.5)
dla obwodu elektrycznego oraz:
)
(
)
(
d
)
(
d
t
f
t
Dv
t
t
v
M
=
+
(2.6)

2.1. Opis dynamiki systemu
3
dla układu mechanicznego. Są to równania różniczkowe pierwszego rzędu
niejednorodne (funkcja wymuszająca po prawej stronie równania jest różna od zera).
Związane z nimi układy są także nazywane układami pierwszego rzędu.
Z punktu widzenia automatyki (teorii sterowania) wygodnie jest opisywać
rozpatrywane powyżej układy za pomocą zależności wejście – wyjście. Na przykład,
jeśli w (2.5) w charakterze wejścia (wymuszenia) przyjmiemy napięcie u(t), to
wyjściem (odpowiedzią) będzie prąd: y(t) = i(t). Niech funkcja przetwarzania
(operator przetwarzania) takiego układu będzie oznaczona jako {g(t)}. Wówczas
rozpatrywany układ można określić za pomocą schematu jak na rys. 2.3.
Rys. 2.3. Schemat układu z jednym wejściem i jednym wyjściem
Użyte w tym zapisie nawiasy zewnętrzne służą do zasygnalizowania, że wyjście
nie jest bezpośrednio obliczane jako rezultat funkcji g(t) przy działaniu sygnału u(t).
Sposób użycia tego operatora przetwarzania będzie omówione w dalszej części
rozważań.
W systemach liniowych funkcja przetwarzania {g(u(t))} jest operatorem liniowym,
co oznacza, że zachodzi następująca relacja:
)
(
)
(
)
(
2
1
2
1
u
g
u
g
u
u
g
⋅
+
⋅
=
⋅
+
⋅
β
α
β
α
(2.7)
Jest to równoważne założeniu, że współczynniki w równaniu różniczkowym
opisującym dynamikę systemu nie zależą od zmiennych procesu oraz nie występują w
równaniu inne nieliniowe zależności względem tych zmiennych. Oto przykłady
równań systemów nieliniowych:
)
(
)
(
4
d
)
(
d
2
d
)
(
d
2
2
2
t
y
t
u
t
t
u
t
t
u
=
+
+
,
)
(
)
(
)
(
4
d
)
(
d
2
d
)
(
d
2
2
t
u
t
y
t
u
t
t
u
t
t
u
=
+
+
.
Liniowość parametrów systemu jest zawsze ograniczona do jakiegoś przedziału
zmian wielkości opisujących proces. Do określenia wartości parametru operatora
g(u(t)) w układzie z rys. 2.3 można posłużyć się przebiegiem funkcji określającej
zależność pomiędzy sygnałami na wejściu i na wyjściu rozpatrywanego bloku (rys.
2.4). W celu określenia przybliżonej liniowej zależności pomiędzy oboma sygnałami
w rejonie punktu u
0
można się posłużyć rozwinięciem nieliniowej funkcji g(u) w
szereg Taylora w pobliżu tego punktu:

4
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
(
)
...
!
2
d
)
(
d
!
1
d
)
(
d
)
(
)
(
2
0
2
2
0
0
0
0
+
−
+
−
+
=
=
=
=
u
u
u
u
g
u
u
u
u
g
u
g
u
g
y
u
u
u
u
(2.8)
0
d
)
(
d
u
u
u
u
g
=
Rys. 2.4. Charakterystyka elementu nieliniowego
Liniowe przybliżenie operatora g(u) sprowadza się ograniczeniu rozwinięcia (2.8)
do części liniowej związanej z dwoma pierwszymi wyrazami:
(
)
0
0
0
0
!
1
)
(
)
(
)
(
0
u
u
m
y
u
u
u
u
g
u
g
u
g
y
u
u
−
+
=
−
+
≈
=
=
d
d
(2.9)
gdzie
u
y
u
u
y
y
m
Δ
Δ
=
−
−
=
0
0
.
W przypadku systemu wielowejściowego operator przetwarzania jest zależny od
wielu zmiennych:
{
}
)
,...,
,
(
2
1
n
u
u
u
g
y
=
(2.10)
a liniowe przybliżenie wokół punktu określonego przez współrzędne (u
10
, u
20
, ..., u
n0
)
można wyznaczyć przez rozszerzenie rozwinięcia (2.8) na przypadek
wielowymiarowy:

2.1. Opis dynamiki systemu
5
(
)
(
)
(
)
0
20
2
2
10
1
1
0
20
10
2
1
0
20
2
10
1
...
)
,...,
,
(
)
,...,
,
(
n
n
u
u
n
u
u
u
u
n
n
u
u
u
g
u
u
u
g
u
u
u
g
u
u
u
g
u
u
u
g
y
n
n
−
+
+
−
+
−
+
≈
=
=
=
=
d
d
d
d
d
d
(2.11)
Technikę tą można stosować zarówno do systemów, jak również do ich
pojedynczych elementów.
Inną ważną cechą systemów jest zależność parametrów od czasu. Mówimy, że
system jest inwariantny względem czasu, jeśli operator przetwarzania z rys. 2.3
spełnia następującą zależność:
{
}
)
),
(
(
)
(
τ
τ
τ
−
−
=
−
t
t
u
g
t
y
, (2.12)
dla dowolnej wartości
τ
, co oznacza, że nie zmienia on swoich właściwości z czasem.
warunek ten można także sformułować następująco: jeśli y(t) jest odpowiedzią układu
na wymuszenie u(t), to dla wymuszenia: u(t-τ) odpowiedź powinna być określona
przez y(t-τ). Na przykład, układy opisane równaniami:
)
(
)
(
4
d
)
(
d
t
u
t
ty
t
t
y
=
+
,
( )
5
)
(
sin
d
)
(
d
=
+ t
y
at
t
t
y
,
przedstawiają układy, które są zależne od czasu.
Systemy liniowe inwariantne względem czasu (ang. Linear Time-Invariant – LTI)
stanowią podstawową klasę układów rozważanych w kontekście systemów
sterowania. Wynika to stąd, że większość praktycznie analizowanych systemów z
dużym przybliżeniem spełnia warunki liniowości i niezależności od czasu, a ponadto,
istnieją bardzo wygodne matematyczne narzędzia do analizy takich układów.
W podstawowej części niniejszego kursu będą prowadzone rozważania dotyczące
właśnie liniowych systemów niezależnych od czasu.
2.2. Modele
wymuszeń
Sygnały wejściowe w rozpatrywanych systemach mogą przyjmować różną formę w
zależności od tego, czy są one związane z rzeczywistymi procesami, czy też są
opisane analitycznymi funkcjami, spełniającymi rolę wymuszeń testowych. W celu
porównania właściwości różnych systemów (układów, elementów) wygodnie jest
stosować w charakterze wymuszeń pewne standardowe przebiegi.
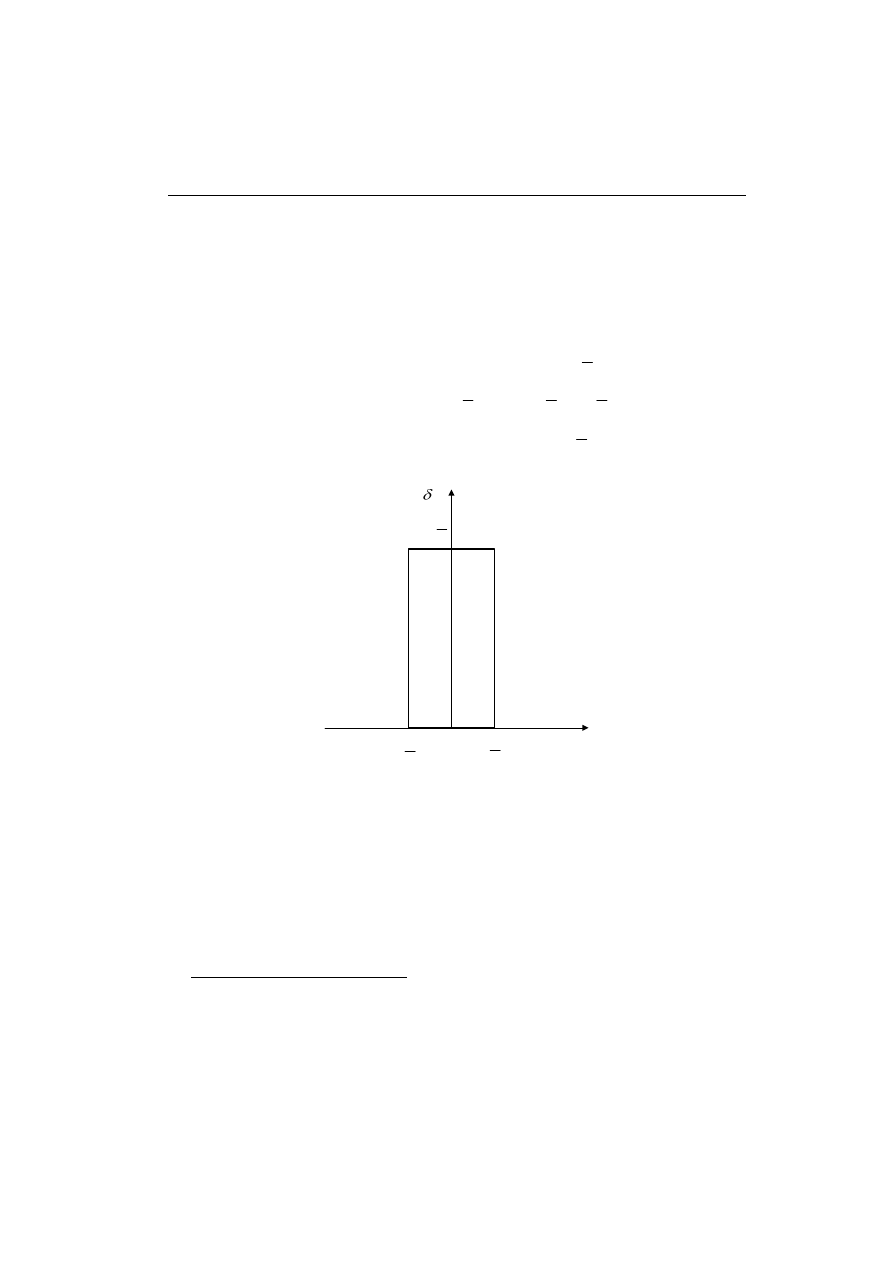
6
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
Najbardziej elementarnym sygnałem testowym stosowanym w teorii systemów jest
funkcja impulsowa δ(t) zwana też impulsem (deltą) Dirac’a
1
. Jej fizykalne znaczenie
wywodzi się z pomysłu skrócenia do zera czasu występowania jakiejś wielkości
fizycznej (masy, siły, napięcia elektrycznego itp.), której działanie jest normalnie
rozłożone w czasie. To intuicyjne podejście pozwala zdefiniować funkcję impulsową
(rys. 2.5):
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎨
⎧
>
<
<
−
−
<
=
=
→
→
2
dla
0
2
2
dla
1
2
dla
0
lim
)
,
(
lim
)
(
0
0
τ
τ
τ
τ
τ
τ
δ
δ
τ
τ
t
t
t
t
t
(2.13)
t
(t)
2
τ
2
τ
−
τ
1
Rys. 2.5. Model funkcji impulsowej
Bardziej funkcjonalna definicja funkcji impulsowej jest związana z jej
oddziaływaniem na każdą funkcję ciągłą w otoczeniu zera:
τ
τ
δ
τ
ϕ
ϕ
d
)
(
)
(
)
0
(
∫
+∞
∞
−
=
(2.14)
co prowadzi do ogólnego związku:
1
Paul Adrien Maurice Dirac (1902-1984), inżynier elektryk i fizyk, jeden z twórców
mechaniki kwantowej (nagroda Nobla z fizyki w 1933 roku).
2.2. Modele wymuszeń
7
τ
τ
δ
τ
ϕ
ϕ
d
)
(
)
(
)
(
0
0
∫
+∞
∞
−
−
=
t
t
(2.15)
Słuszna jest także następująca zależność:
)
(
1
d
)
,
0
(
d
)
(
2
/
2
/
t
t
t
=
=
∫
∫
+
−
+∞
∞
−
τ
τ
δ
δ
τ
τ
, (2.16)
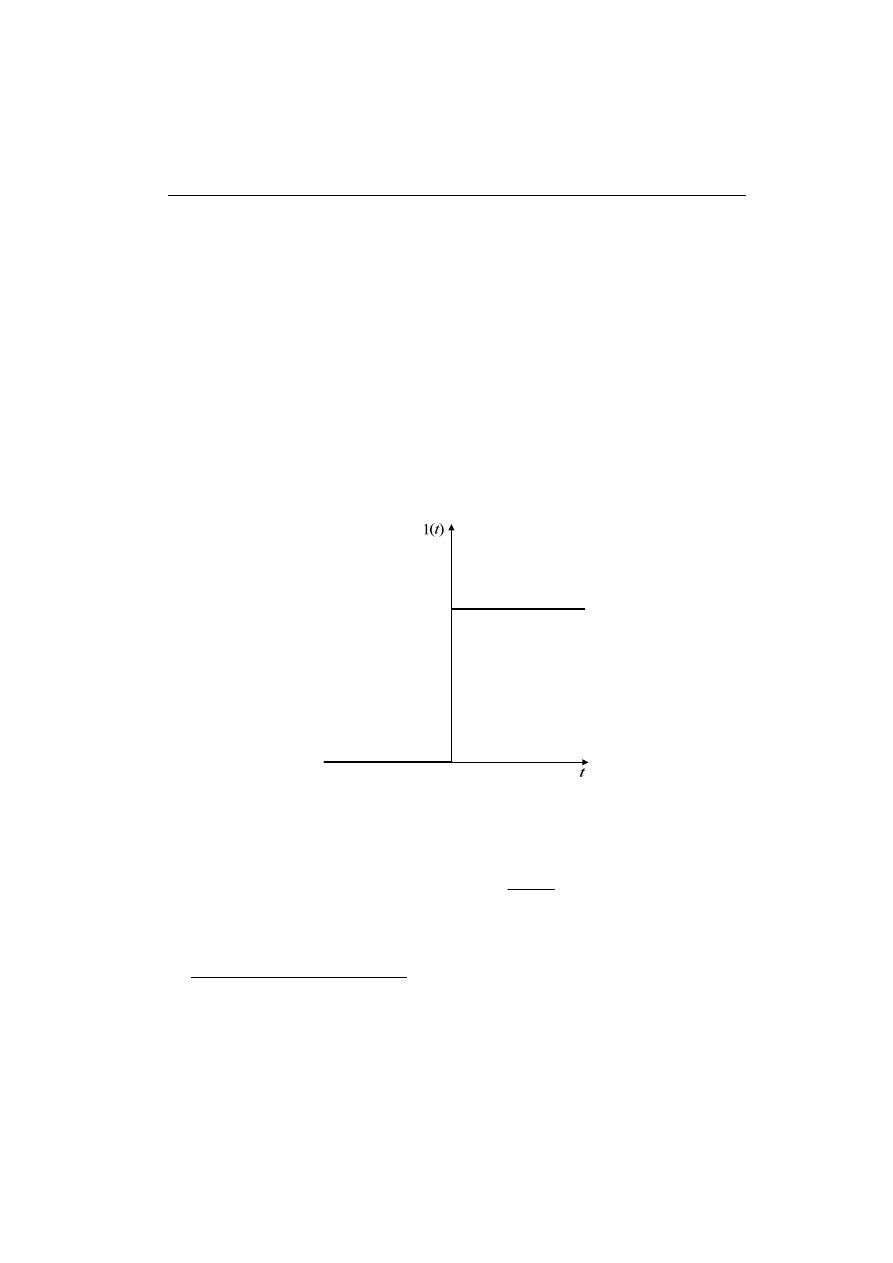
która bezpośrednio łączy się funkcją jednostkową 1(t):
⎩
⎨
⎧
>
<
=
0
dla
0
dla
t
t
t
1
0
)
(
1
(2.17)
Funkcja 1(t) jest nazywana skokiem jednostkowym lub funkcją Heaviside’a
2
. Jej
przebieg jest pokazany na rys. 2.6.
1
Rys. 2.6. Model funkcji skoku jednostkowego
Obie przedstawione funkcje łączą się za pomocą następującego związku:
t
t
t
t
d
)
,
(
1
d
lim
)
,
(
lim
)
(
0
0
τ
τ
δ
δ
τ
τ
→
→
=
=
(2.18)
Funkcja skoku jednostkowego jest wygodnym narzędziem do definicji innych
typowych wymuszeń:
2
Oliver Heaviside (1850-1925), angielski inżynier elektryk, matematyk, fizyk;
sformułował znaną postać równań telegrafistów.
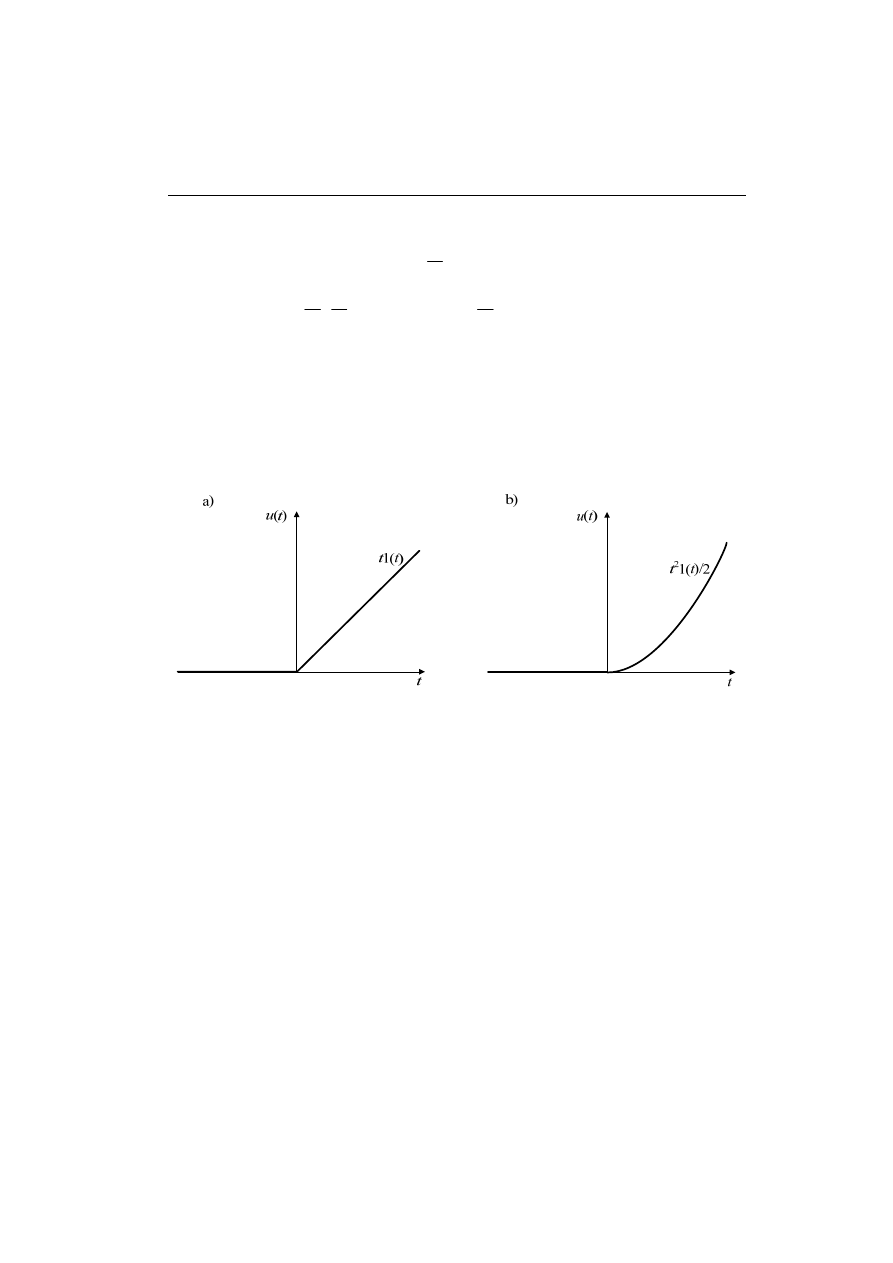
8
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
- skok prędkości:
)
(
1
)
(
t
t
t
u
=
- rys. 2.7a;
- skok przyśpieszenia:
)
(
1
2
)
(
2
t
t
t
u
=
- rys. 2.7b.
Zauważmy, że:
)
(
1
)
(
1
2
d
d
2
t
t
t
t
t
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
oraz:
( )
)
(
1
)
(
1
d
d
t
t
t
t
=
, co razem z (2.18) daje
szereg funkcji testujących, które pozostają w stosunku do siebie w zależności
różniczkowej.
Ponadto, w charakterze typowych wymuszeń stosowane są następujące funkcje:
- funkcja harmoniczna:
)
cos(
)
(
0
t
t
u
ω
=
lub w postaci zespolonej:
)
sin(
j
)
cos(
)
(
0
0
j
0
t
t
e
t
u
t
ω
ω
ω
+
=
=
;
- funkcja wykładnicza:
( )
...
2
/
)
(
2
2
1
0
+
+
+
=
t
a
t
a
a
t
u
Rys. 2.7. Przebiegi wymuszeń w postaci: a) skoku prędkości oraz b) skoku przyśpieszenia
2.3. Rozwiązywanie równań różniczkowych
2.3.1. Wprowadzenie
Rozpatrzmy system liniowy inwariantny względem czasu rzędu n. Załóżmy ponadto,
że jest to system z jednym wejściem i jednym wyjściem. Jego dynamika jest w
ogólnym przypadku opisana następującym równaniem różniczkowym:
)
(
)
(
)
(
)
(
...
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
t
f
t
y
a
t
y
a
t
y
a
t
y
a
t
y
n
n
n
=
+
+
+
+
+
−
−
(2.19)
przy czym, w ogólnym przypadku:
)
(
)
(
)
(
...
)
(
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
t
u
b
t
u
b
t
u
b
t
u
b
t
u
b
t
f
m
m
m
m
+
+
+
+
+
=
−
−
,
n
≥ m,

2.3. Rozwiązywanie równań różniczkowych 9
y(t), u(t) - sygnały, odpowiednio, na wyjściu i wejściu systemu (rys. 2.3),
k
k
k
t
t
y
t
y
d
d
)
(
)
(
)
(
=
,
a
k
, b
l
– stałe współczynniki (parametry systemu).
Warunkiem realizowalności systemu określonego równaniem (2.19) jest spełnienie
tzw. warunku przyczynowości, który wymaga, aby sygnał wyjściowy nie pojawił się
wcześniej niż sygnał wejściowy.
Równanie (2.19) jest znane jako równanie niejednorodne, którego rozwiązanie
można zapisać w postaci:
)
(
)
(
)
(
t
y
t
y
t
y
wym
sw
+
=
(2.20)
gdzie: )
(t
y
sw
oznacza odpowiedź swobodną, )
(t
y
wym
jest odpowiedzią wymuszoną.
Odpowiedź swobodna jest rozwiązaniem równania jednorodnego, w którym jest
zerowe wymuszenie:
0
)
(
)
(
)
(
...
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
=
+
+
+
+
+
−
−
t
y
a
t
y
a
t
y
a
t
y
a
t
y
n
n
n
(2.21)
Rozwiązanie tego równania ma następującą postać:
)
(
...
)
(
)
(
)
(
2
2
1
1
t
y
C
t
y
C
t
y
C
t
y
n
n
+
+
+
=
sw
(2.22)
gdzie: stałe C
1
, C
2
, ... C
n
zależą od warunków początkowych lub od warunków
granicznych, natomiast funkcje y
1
(t), y
2
(t),..., y
n
(t) zależą od pierwiastków
algebraicznego równania charakterystycznego o postaci:
0
...
0
1
2
2
1
1
=
+
+
+
+
+
−
−
a
r
a
r
a
r
a
r
n
n
n
(2.23)
Równanie (2.23) ma n pierwiastków, wśród których mogą być pojedyncze lub
wielokrotne pierwiastki rzeczywiste, czy też zespolone, przy czym, pierwiastki
zespolone tworzą pary wielkości sprzężonych. Stałe C
1
, C
2
, ... C
n
są
przyporządkowane do pierwiastków równania charakterystycznego zgodnie z
następującą zasadą:
– jeśli r
k
jest pojedynczym pierwiastkiem rzeczywistym, to:
t
r
k
k
e
t
y
=
)
(
;
– dla każdego l-krotnego pierwiastka rzeczywistego:
t
r
k
k
e
t
y
=
)
(
,
t
r
k
k
te
t
y
=
+
)
(
1
,
...,
t
r
l
l
k
k
e
t
t
y
1
1
)
(
−
−
+
=
;
– dla każdego pojedynczego pierwiastka zespolonego r
k
= a + jb:
bt
e
t
y
at
k
cos
)
(
=
,
bt
e
t
y
at
k
sin
)
(
1
=
+
;
– dla każdej l-krotnej pary pierwiastków zespolonych r
k
= a + jb:
bt
e
t
y
at
k
cos
)
(
=
,
bt
e
t
y
at
k
sin
)
(
1
=
+
,
bt
t
e
t
y
at
k
cos
)
(
2
=
+
,
bt
t
e
t
y
at
k
sin
)
(
3
=
+
,
...,
bt
t
e
t
y
l
at
l
k
cos
)
(
1
2
2
−
−
+
=
,
bt
t
e
t
y
l
at
l
k
sin
)
(
1
1
2
−
−
+
=
.

10
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
Przykład 2.1.
Określić odpowiedź swobodną (przejściową) dla równania jednorodnego:
0
2
3
2
3
=
−
−
y
t
y
t
y
d
d
d
d
Równanie charakterystyczne ma następującą postać:
0
2
3
3
=
−
− r
r
Można je przedstawić w postaci iloczynowej:
( ) (
)
0
2
1
2
=
−
+
r
r
,
skąd: r
1
= –1, r
2
= –1, r
3
= 2.
Zatem, swobodna odpowiedź systemu przybiera następującą formę:
(
)
t
t
e
C
e
t
C
C
t
y
2
3
2
1
)
(
+
+
=
−
sw
.
Stałe współczynniki w powyższym równaniu należy określić na podstawie warunków pełnego
rozwiązania równania niejednorodnego.
Postać odpowiedzi wymuszonej y
wym
(t) zależy od rodzaju funkcji wymuszającej
(prawa strona równania niejednorodnego). Może tu wystąpić duża różnorodność tych
funkcji. Dla najbardziej typowych obowiązują następujące zasady:
–
at
Ke
t
f
=
)
(
-
at
Ae
t
y
=
)
(
wym
, jeśli a nie jest pierwiastkiem równania
charakterystycznego;
at
l
e
At
t
y
=
)
(
wym
jeśli a jest l-krotnym pierwiastkiem
równania charakterystycznego;
–
t
K
t
f
ω
cos
)
(
=
lub
t
K
t
f
ω
sin
)
(
=
-
t
B
t
A
t
y
ω
ω
sin
cos
)
(
+
=
wym
;
–
k
Kt
t
f
=
)
(
, k > 0:
k
k
t
A
t
A
A
t
y
+
+
+
=
...
)
(
1
0
wym
- jeśli zero nie jest
pierwiastkiem równania charakterystycznego;
(
)
τ
τ
τ
d
0
wym
∫
+
+
+
=
t
t
k
k
A
A
A
t
y
...
)
(
1
0
- jeśli zero jest pierwiastkiem równania
charakterystycznego.
Wartości stałych współczynników w powyższych funkcjach można określić przez
ich podstawienie do oryginalnych równań niejednorodnych.
Przykład 2.2.
Określić odpowiedź wymuszoną (rozwiązanie szczegółowe), rozwiązanie
swobodne i rozwiązanie pełne następującego równania:
t
t
y
t
y
t
y
+
=
+
+
3
2
2
2
d
d
d
d
, przy warunkach początkowych: y(0) = 0, y
’
(0) =
20.
Wymuszenie jest funkcją wielomianową, więc zakładamy rozwiązanie szczegółowe o postaci:
3
3
2
2
1
0
)
(
t
A
t
A
t
A
A
t
y
+
+
+
=
wym
Po wstawieniu tej funkcji do wyjściowego równania otrzymamy:
(
)
t
t
t
A
A
t
A
t
A
A
t
A
t
A
t
A
A
+
=
+
+
+
+
+
+
+
+
3
3
2
2
3
2
1
3
3
2
2
1
0
12
4
3
2
2
2.3. Rozwiązywanie równań różniczkowych 11
Porządkując obie strony równania względem potęg zmiennej t otrzymamy:
(
) (
)
t
t
A
A
A
t
A
A
A
t
A
A
t
A
+
=
+
+
+
+
+
+
+
+
3
2
1
0
3
2
1
2
3
2
3
3
2
2
6
4
6
,
skąd uzyskujemy następujące warunki równości obu stron równania:
1
3
=
A
,
0
6
3
2
=
+ A
A
,
1
6
4
3
2
1
=
+
+
A
A
A
,
0
2
2
2
1
0
=
+
+
A
A
A
.
Ten układ czterech równań ma następujące rozwiązanie:
26
0
−
=
A
,
19
1
=
A
,
6
2
−
=
A
,
1
3
=
A
.
A zatem:
3
2
6
19
26
)
(
t
t
t
t
y
+
−
+
−
=
wym
.
W celu określenia rozwiązania swobodnego
)
(t
y
sw
należy określić pierwiastki równania
charakterystycznego:
( )
0
1
1
2
2
2
=
+
=
+
+
r
r
r
, a więc: r
1
= r
2
= –1.
Rozwiązanie swobodne ma zatem następującą postać:
(
)
t
e
t
C
C
t
y
−
+
=
2
1
)
(
sw
.
Pełne rozwiązanie równania niejednorodnego ma następującą postać (2.20):
)
(
)
(
)
(
t
y
t
y
t
y
wym
sw
+
=
=
t
t
te
C
e
C
−
−
+
2
1
–
3
2
6
19
26
t
t
t
+
−
+
.
W celu określenia współczynników C
1
, C
2
należy wykorzystać warunki początkowe. Są one
określone dla t = 0. Mamy stąd dwa równania:
=
)
0
(
y
(
t
t
te
C
e
C
−
−
+
2
1
–
3
2
6
19
26
t
t
t
+
−
+
)|
t = 0
= 0,
=
)
0
(
'
y
(
( )
t
t
e
t
C
e
C
−
−
−
+
−
1
2
1
+
2
3
12
19
t
t
+
−
)|
t = 0
= 20.
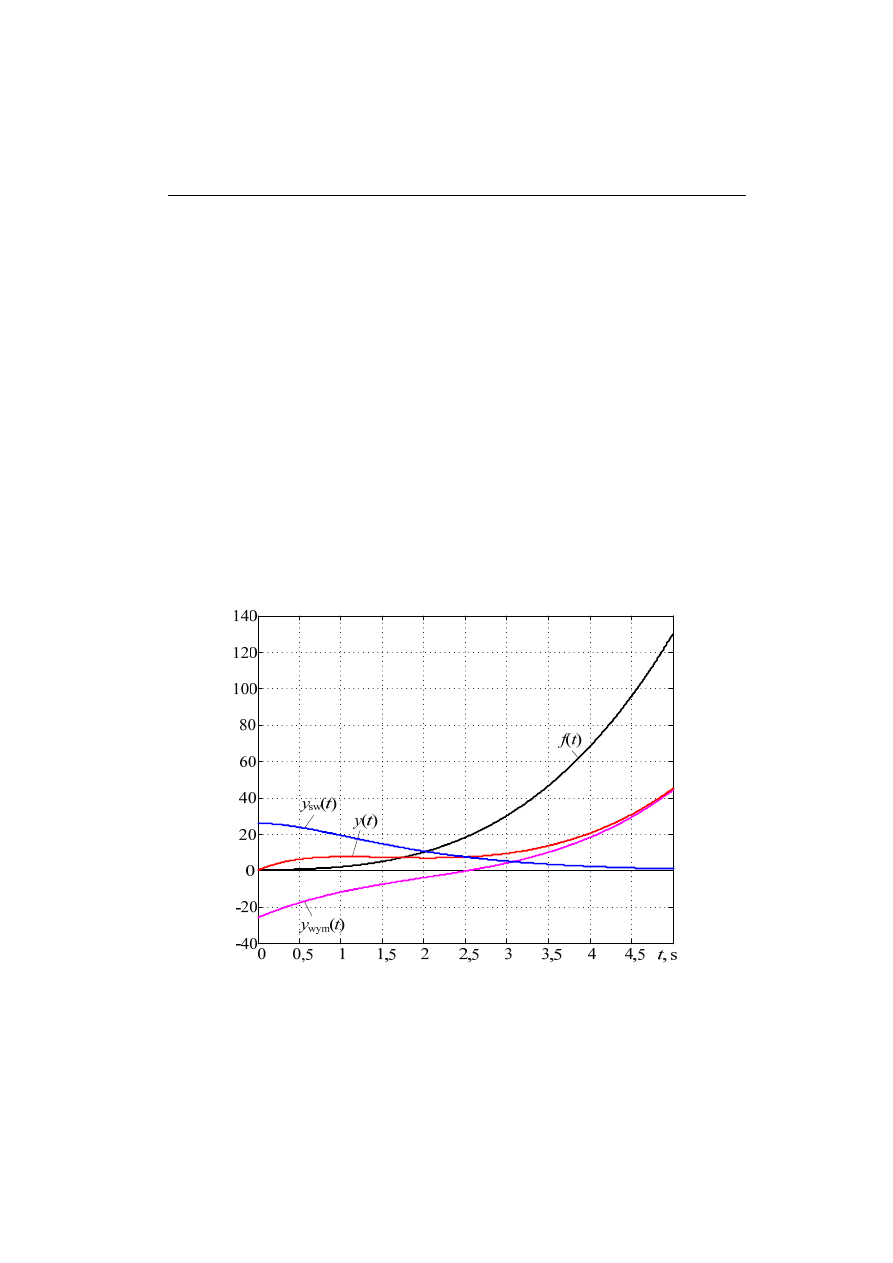
Rys. 2.8. Przebiegi funkcji składowych w równaniu różniczkowym

12
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
Z pierwszego równania otrzymujemy: C
1
= 26, zaś z drugiego: C
2
= 27.
Odpowiedź swobodna jest następująca:
(
)
t
e
t
t
y
−
+
=
27
26
)
(
sw
.
Ostatecznie, otrzymujemy następujące rozwiązanie:
=
)
(t
y
(
)
t
e
t
−
+ 27
26
–
3
2
6
19
26
t
t
t
+
−
+
.
Przebiegi poszczególnych funkcji składowych związanych z rozpatrywanym równaniem są
pokazane na rys. 2.8.
Widać, że składowa przejściowa y
sw
(t) z czasem zmierza do zera (układ jest stabilny),
przez co odpowiedź układu y(t) zbliża się do odpowiedzi wymuszonej y
wym
(t).
Uwagi końcowe
Na podstawie tego krótkiego przeglądu zagadnień związanych z rozwiązywaniem
równań różniczkowych opisujących dynamikę systemów liniowych inwariantnych
można sformułować następujące wnioski:
1. Odpowiedź systemu na wymuszenie w postaci sygnału wejściowego określonego
przez funkcję f(t) jest utworzona z dwóch części: składowej swobodnej - której
przebieg zależy od parametrów systemu i jego warunków początkowych oraz
składowej wymuszonej – której postać zależy od parametrów systemu i charakteru
wymuszenia.
2. Odpowiedź swobodna jest utworzona ze składników o postaci:
t
r
k
k
e
y
y
=
)
(
lub
bt
e
t
y
at
k
cos
)
(
=
z ewentualnym czynnikiem w postaci zmiennej t reprezentującej
czas (w odpowiedniej potędze), przy czym, stałe r
k
oraz a (jako składniki
rzeczywiste zespolonych liczb: a + jb) są odpowiednimi pierwiastkami równania
charakterystycznego. Można zauważyć, że jeśli pierwiastki rzeczywiste tego
równania są ujemne lub – w przypadku pierwiastków zespolonych – mają ujemne
części rzeczywiste, to powyższe składniki odpowiedzi z czasem zanikają do zera.
Dlatego też, odpowiedź swobodna jest także nazywana przejściową lub zanikającą.
Jeśli warunek ten nie jest spełniony, to (nawet przy braku wymuszenia) odpowiedź
z czasem narasta nieograniczenie. Taki system jest niestabilny. W przypadku
zerowych pierwiastków rzeczywistych (lub zespolonych z zerową częścią
rzeczywistą) mamy do czynienia z sytuacją graniczną (granica stabilności).
3. W przypadku stabilnego systemu, stan przejściowy (odpowiedź swobodna) z
czasem zanika i całkowita odpowiedź zależy wówczas tylko od parametrów
systemu i charakteru wymuszenia. System osiąga stan ustalony.

2.4.
Analiza systemów opisanych równaniami różniczkowymi
2.4.1. Wprowadzenie
W analizie systemów, których dynamika jest opisana za pomocą równań
różniczkowych ważną odgrywa stosowanie wymuszenia w postaci impulsu Diraca. W
ogólnym przypadku:
)
(
)
(
)
(
)
(
...
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
t
t
y
a
t
y
a
t
y
a
t
y
a
t
y
n
n
n
δ
=
+
+
+
+
+
−
−
(2.24)
Uzyskana w takim przypadku odpowiedź jest nazywana funkcją wagi g(t) = y(t):
)
(
)
(
)
(
)
(
...
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
t
t
g
a
t
g
a
t
g
a
t
g
a
t
g
n
n
n
δ
=
+
+
+
+
+
−
−
(2.25)
Funkcja wagi jest zatem odpowiedzią impulsową układu.
Rozwiązanie równania (2.25) wymaga ostrożnej analizy występujących tam
funkcji. Przede wszystkim, z warunku przyczynowości oraz liniowości układu
wynika, że funkcja wagi g(t) jest funkcją ciągłą w czasie dla wszystkich układów
opisanych równaniami różniczkowymi rzędu większego niż pierwszy. Stąd wynika,
że:
g(0) = g
0+
= 0,
(2.26)
gdyż g(t) = 0 dla t < 0, gdzie g
0+
oznacza granicę prawostronną (od strony dodatnich
wartości zmiennej t).
Całkując obustronnie (2.25) otrzymamy:
∫
∫
∫
∫
∫
−
−
−
−
−
−
−
=
+
+
+
+
2
/
2
/
2
/
2
/
0
2
/
2
/
'
1
2
/
2
/
)
1
(
1
2
/
2
/
)
(
d
)
(
d
)
(
d
)
(
...
d
)
(
d
)
(
τ
τ
τ
τ
τ
τ
τ
τ
τ
τ
δ
t
t
t
t
g
a
t
t
g
a
t
t
g
a
t
t
g
n
n
n
(2.27)
Wskazany przedział całkowania (τ → 0) jest uzasadniony ciągłością g(t) oraz tym, że
impuls
δ
(t) = 0 za wyjątkiem t = 0. Z prawej strony równania otrzymuje się wartość 1,
natomiast wszystkie składniki lewej strony są równe zero za wyjątkiem pierwszego z
nich:
)
1
(
0
)
1
(
0
)
1
(
0
2
/
2
/
)
1
(
)
1
(
2
/
2
/
)
(
d
)
(
d
d
)
(
−
+
−
−
−
+
−
−
−
−
=
−
=
=
∫
n
n
n
t
t
n
n
n
g
g
g
t
t
g
t
t
g
τ
τ
(2.28)
gdyż
0
)
1
(
0
=
−
−
n
g
.
Ostatecznie, rezultat całkowania (2.27) prowadzi do następującego związku:
1
)
1
(
0
=
−
+
n
g
(2.29)
14
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
Zależności (2.26) oraz (2.29) pozwalają określić odpowiedź impulsową (funkcję
wagi) układu na podstawie jego równania różniczkowego. Warto zauważyć, że
odpowiedź ta jest obliczana na podstawie równania jednorodnego z powyższymi
warunkami, gdyż funkcja wymuszająca f(t) =
δ
(t) ma zerową wartość za wyjątkiem
punktu t = 0.
Przykład 2.3.
Określić funkcję wagi układu z poprzedniego przykładu. Równanie
jednorodne ma następującą postać:
0
2
2
2
=
+
+
y
t
y
t
y
d
d
d
d
.
Miejscami zerowymi funkcji charakterystycznej są dwie jednakowe liczby:
r
1
= r
2
= –1.
Stan przejściowy jest zatem określony przez następującą funkcję:
(
)
t
e
t
C
C
t
y
−
+
=
2
1
)
(
sw
,
którą jest poszukiwana funkcja wagi: g(t) = y
sw
(t). Współczynniki tego równania można
wyznaczyć na podstawie podanych powyżej zależności:
(
)
0
)
0
(
0
2
1
=
+
=
=
−
t
t
e
t
C
C
g
,
(
)
1
)
1
(
)
0
(
0
2
1
'
=
−
+
−
=
=
−
t
t
e
t
C
C
g
.
A więc: C
1
= 0, C
2
= 1, co daje:
)
(
1
)
(
t
te
t
g
t
−
=
.
W przypadku równania różniczkowego pierwszego rzędu funkcja wagi g(t) nie jest
już funkcją ciągłą dla t = 0, natomiast przybiera ona wartość 1: g(0) = 1. Stąd też:
g(0) = g
0+
= 1
(2.30)
oraz:
1
)
0
(
0
1
=
=
=
t
rt
e
C
g
, a zatem:
1
1
=
C
.
Przykład 2.4.
Określić funkcję wagi układu, którego równanie różniczkowe jednorodne
ma następującą postać:
0
1 =
+ y
T
t
y
d
d
.
Funkcja charakterystyczna: r + 1/T = 0 ma rozwiązanie: r = –1/T. Rozwiązanie równania
jednorodnego ma zatem następującą postać:
T
t
rt
e
C
e
C
t
y
/
1
1
)
(
−
=
=
sw
.
Na podstawie powyższych rozważań C
1
= 1, więc odpowiedź impulsowa jest następująca:
)
(
1
)
(
)
(
/
t
e
t
y
t
g
T
t
−
=
=
sw
.
Warto zauważyć, że funkcja skoku jednostkowego w powyższym wyrażeniu ma na celu
zerowanie funkcji impulsowej dla czasu t
≤ 0.

2.4. Analiza systemów opisanych równaniami różniczkowymi 15
Znajomość funkcji wagi pozwala określić rozwiązanie równania różniczkowego
rozpatrywanego systemu dla dowolnego wymuszenia u(t), przy zerowych warunkach
początkowych:
)
(
)
(
)
(
)
(
)
(
t
g
t
u
t
g
u
t
y
⊗
=
−
=
∫
+∞
∞
−
τ
τ
τ
d
(2.31)
Powyższy związek jest nazywany splotem dwóch funkcji (sygnałów): u(t) oraz
g(t). Splot jest operacją przemienną, więc:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
t
u
t
g
t
u
g
t
g
u
t
g
t
u
⊗
=
−
=
−
=
⊗
∫
∫
+∞
∞
−
+∞
∞
−
τ
τ
τ
τ
τ
τ
d
d
(2.32)
Bardziej praktyczna operacja splotu zachodzi dla przypadku, gdy spełnione są
warunki: dla
0
<
t
,
0
)
(
=
t
u
oraz dla
(
)
0
<
−
τ
t
,
(
)
0
=
−
τ
t
g
. Wówczas:
∫
−
=
t
d
t
g
u
t
y
0
)
(
)
(
)
(
τ
τ
τ
(2.33)
Przykład 2.5.
Określić odpowiedź układu o funkcji wagi:
)
(
1
)
(
/
t
e
t
g
T
t
−
=
(patrz
przykład 2.4) na skok jednostkowy:
)
(
1
)
(
t
t
u
=
.
Podstawiając poszczególne funkcje do (2.33), otrzymamy:
)
(
1
1
)
(
1
1
)
(
1
)
(
0
0
)
(
1
t
e
T
t
e
Te
d
e
e
d
e
t
y
T
t
T
t
T
t
t
T
T
t
t
T
t
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
=
⋅
=
−
−
−
−
∫
∫
τ
τ
τ
τ
τ
Przykład 2.6.
W przykładzie 2.3 otrzymaliśmy następującą funkcję wagi:
)
(
1
)
(
t
te
t
g
t
−
=
analizowanego układu. Określić odpowiedź tego układu na
skok jednostkowy.
Odpowiedź na skok jednostkowy jest określona za pomocą całki:
∫
∫
∫
−
−
−
−
−
=
⋅
−
⋅
=
t
t
t
t
t
t
d
e
e
d
e
te
d
e
t
t
y
0
0
0
)
(
1
)
(
)
(
1
)
(
τ
τ
τ
τ
τ
τ
τ
τ
τ
.
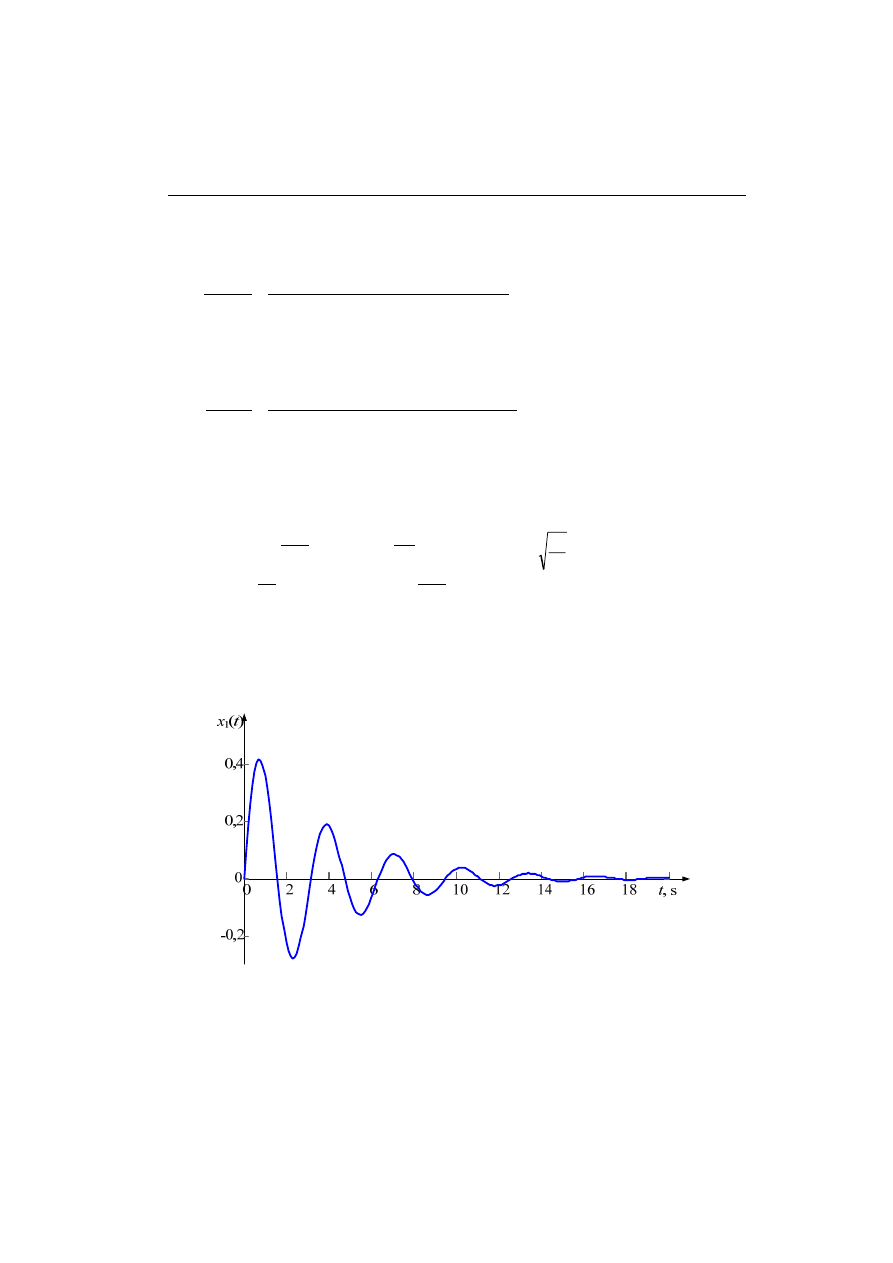
Stosując całkowanie przez części w odniesieniu do drugiej całki, po uproszczeniu otrzymamy:
t
e
t
t
y
−
+
−
=
)
1
(
1
)
(
1
.
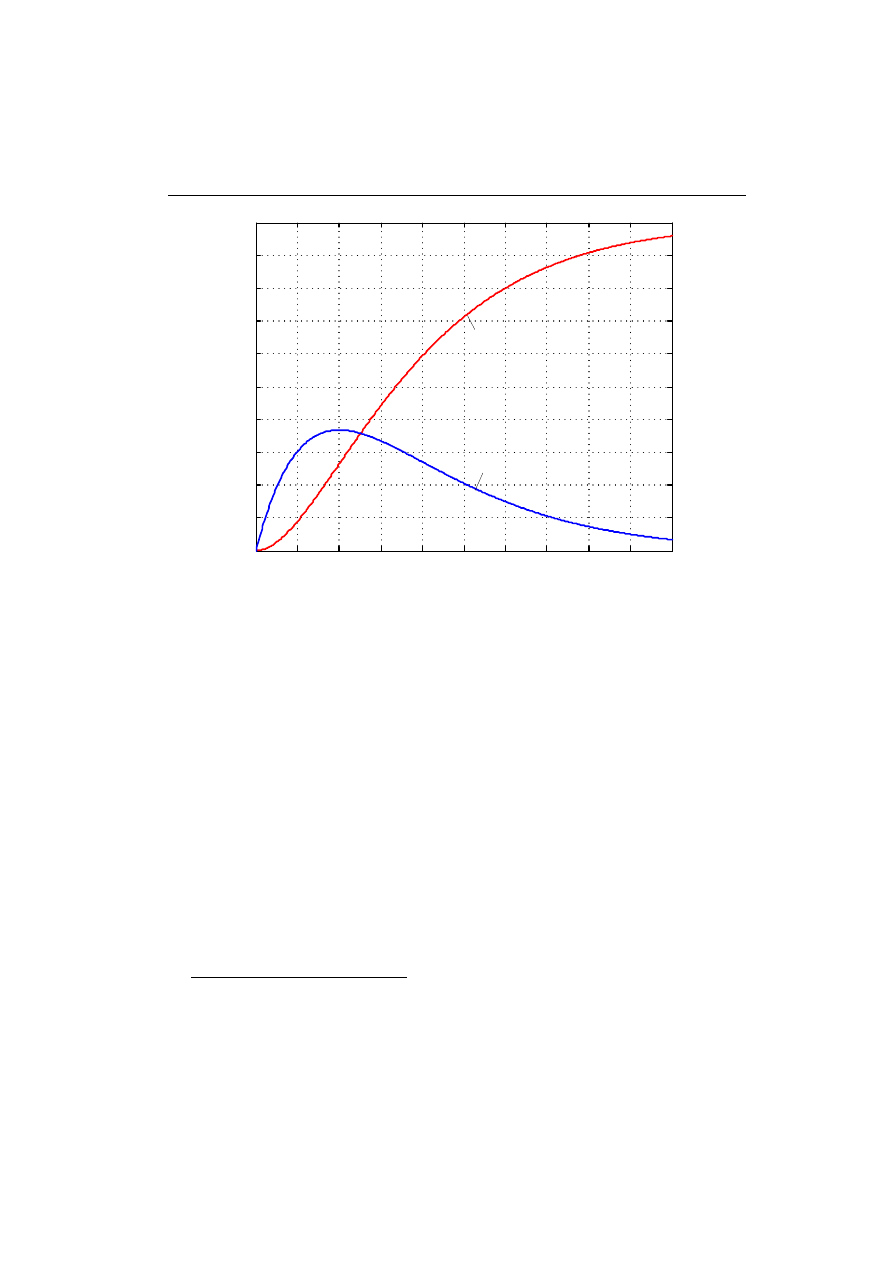
Przebiegi funkcji wagi: g(t) oraz odpowiedzi na skok jednostkowy: y
1
(t) dla rozważanego
systemu są pokazane na rys. 2.9.
16
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
t, s
y
1
(t)
g(t)
Rys. 2.9. Przebiegi funkcji wagi: g(t) oraz odpowiedzi na skok jednostkowy: y
1
(t)
Odpowiedź na dowolne wymuszenie u(t) można też wyznaczyć znając odpowiedź
układu na skok jednostkowy y
1
(t). Wyznacza to tzw. równanie Duhamel’a
3
:
∫
−
+
=
t
d
u
t
y
t
y
u
t
y
0
1
1
)
(
'
)
(
)
(
)
0
(
)
(
τ
τ
τ
(2.34)
Jest to bardzo użyteczny związek, gdyż z punktu widzenia funkcjonowania układu
i fizykalnej oceny jego właściwości dynamicznych najbardziej miarodajną jest
odpowiedź na skok jednostkowy y
1
(t).
2.4.2. Odpowiedź układu na wymuszenie harmoniczne
Zauważmy, że odpowiedź systemu na wymuszenie w postaci funkcji impulsowej lub
skoku jednostkowego z czasem zanika. Tę własność mają stabilne układy liniowe.
Domyślamy się, że jest to wynikiem zaniku zmian wymuszenia. Interesujące jest
zatem badanie odpowiedzi systemu przy wymuszeniu harmonicznym (sinusoidalnie
zmiennym). Wyjaśnia to następujący przykład.
3
Jean-Marie-Constant Duhamel (1797-1872), matematyk i fizyk francuski, prace na temat
transportu ciepła.
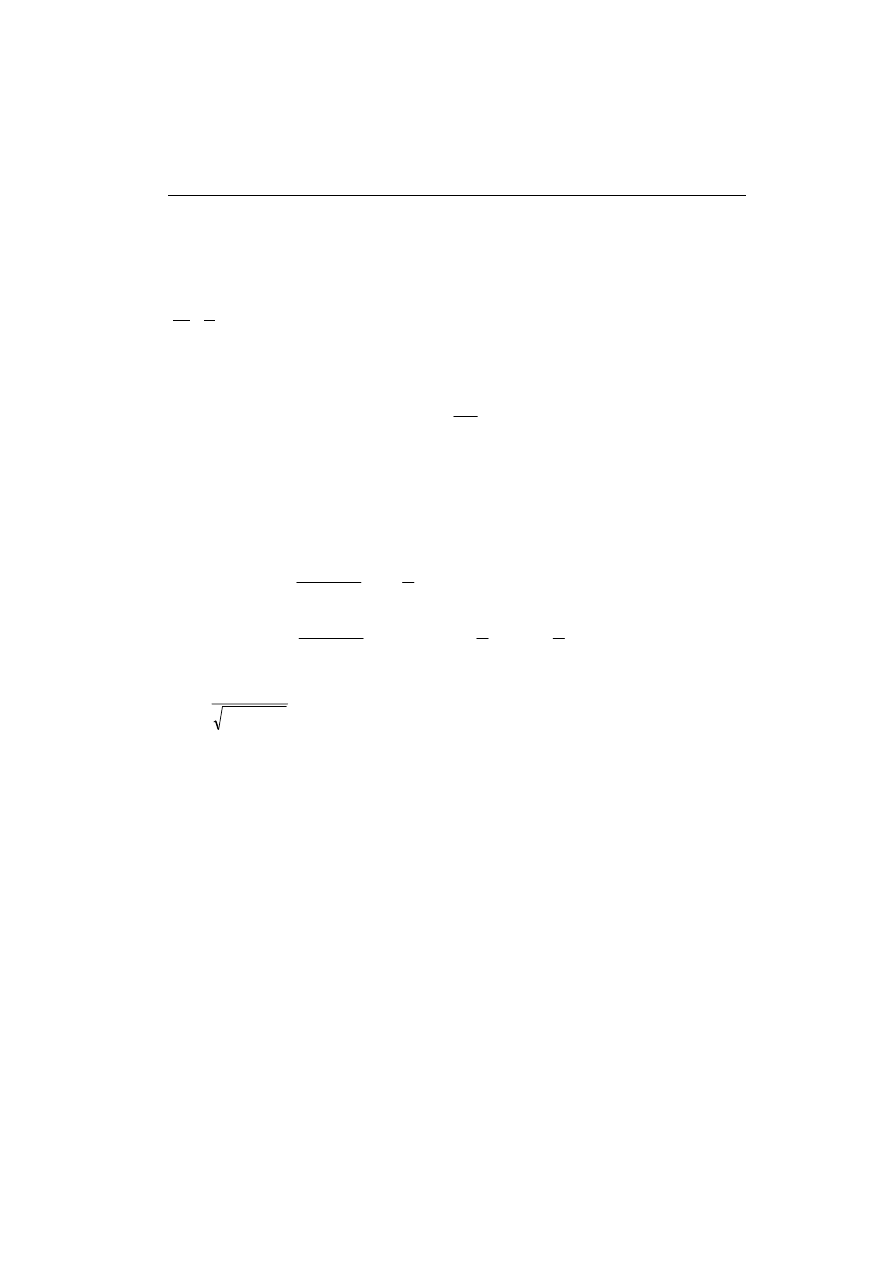
2.4. Analiza systemów opisanych równaniami różniczkowymi 17
Przykład 2.7.
Określić odpowiedź układu rozważanego w przykładzie 2.4 na sygnał o
postaci:
(
)
ϕ
ω
+
=
t
A
t
u
0
sin
)
(
.
Przypomnijmy, że w przykładzie 2.4 rozważany jest układ, którego jednorodne równanie
różniczkowe ma następującą postać:
0
1 =
+ y
T
t
y
d
d
.
W przykładzie 2.4 otrzymaliśmy następującą funkcję wagi:
)
(
1
)
(
/
t
e
t
g
T
t
−
=
tego układu.
Pozostaje zatem obliczenie całki (2.33) dla zadanego wymuszenia harmonicznego (przy
zerowych warunkach początkowych):
∫
−
=
t
d
t
g
u
t
y
0
)
(
)
(
)
(
τ
τ
τ
=
(
)
∫
−
−
⋅
+
t
T
t
d
e
A
0
)
(
0
sin
τ
ϕ
τ
ω
τ
=
(
)
∫
⋅
+
−
t
T
T
t
d
e
Ae
0
/
0
/
sin
τ
ϕ
τ
ω
τ
.
Ponieważ
(
)
( )
( )
ϕ
ω
ϕ
ω
ϕ
ω
sin
cos
cos
sin
sin
0
0
0
t
t
t
+
=
+
, więc:
( )
( )
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
⋅
=
∫
∫
−
t
T
t
T
T
t
d
e
n
d
e
Ae
t
y
0
/
0
0
/
0
/
cos
sin
sin
cos
)
(
τ
τ
ω
ϕ
τ
τ
ω
ϕ
τ
τ
.
Do obliczenia powyższych całek można skorzystać z metody całkowania przez części, co daje:
( )
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
⋅
∫
0
0
0
0
/
2
2
0
0
/
0
cos
sin
1
/
1
1
sin
ω
ω
ω
ω
ω
τ
τ
ω
τ
t
t
T
e
T
d
e
T
t
t
T
,
( )
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
⋅
∫
T
t
T
t
e
T
d
e
T
t
t
T
1
cos
1
sin
/
1
1
cos
0
0
0
/
2
2
0
0
/
0
ω
ω
ω
ω
τ
τ
ω
τ
.
Po wykonaniu niezbędnych przekształceń otrzymamy ostateczną odpowiedź:
(
)
(
)
(
)
δ
ϕ
δ
ϕ
ω
ω
−
−
−
+
+
=
−
sin
sin
/
1
)
(
/
0
2
2
0
T
t
e
t
T
A
t
y
,
gdzie:
(
)
)
/
1
/(
arctg
0
T
ω
δ =
.
Widać, że odpowiedź badanego systemu na wymuszenie sinusoidalne składa się z dwóch
części, z których pierwsza przedstawia funkcję harmoniczną o pulsacji równej pulsacji funkcji
wymuszającej, a druga przedstawia funkcję zanikającą wykładniczo do zera (y
sw
(t)).
Maksymalna początkowa amplituda składowej zanikającej występuje dla φ = δ ± π/2.
Na rys. 2.10 są pokazane przebiegi sygnału wymuszającego u(t), a także odpowiedzi y(t) i
odpowiedzi przejściowej y
sw
(t) dla następujących parametrów układu:
A = 10, T = 0,05,
ω
0
= 100
π,
ϕ = π/4.
Przebiegi odpowiedzi są przeskalowane sto razy.
Można zauważyć, że w przypadku układów liniowych inwariantnych odpowiedź
ustalona (składowa wymuszona odpowiedzi, po zaniku składowej przejściowej) przy
wymuszeniu harmonicznym jest również przebiegiem harmonicznym o tej samej
częstotliwości. Możliwa jest natomiast zmiana fazy oraz amplitudy sygnału
wyjściowego. Stopień zmiany amplitudy (wzmocnienie lub tłumienie) oraz fazy
18
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
sygnału wyjściowego zależy od zadanej częstotliwości sygnału wejściowego. Oba te
parametry: wzmocnienie oraz przesunięcie fazy wyznaczone dla pewnego zakresu
zmian częstotliwości tworzą, odpowiednio, charakterystykę amplitudową oraz
charakterystykę fazową badanego układu. Dostarczają one ważnych informacji o
właściwościach układu i będą przedmiotem analizy w dalszych rozważaniach.
Rys. 2.10. Przebiegi: wymuszenia harmonicznego oraz odpowiedzi układu
2.4.3. Odpowiedź szeregowo połączonych układów
Na podstawie (2.31), odpowiedz układu o funkcji impulsowej g
1
(t) na wymuszenie
u
1
(t) jest następująca:
)
(
)
(
)
(
)
(
)
(
1
1
1
1
1
1
1
t
u
t
g
t
u
g
t
y
⊗
=
−
=
∫
+∞
∞
−
τ
τ
τ
d
(2.35)
Jeśli wymuszenie u
1
(t) jest sygnałem wyjściowym z innego układu o funkcji
impulsowej g
0
(t) i wymuszeniu u
0
(t), to można napisać:
)
(
)
(
)
(
)
(
)
(
0
0
0
0
0
0
0
1
t
u
t
g
t
u
g
t
u
⊗
=
−
=
∫
+∞
∞
−
τ
τ
τ
d
(2.36)
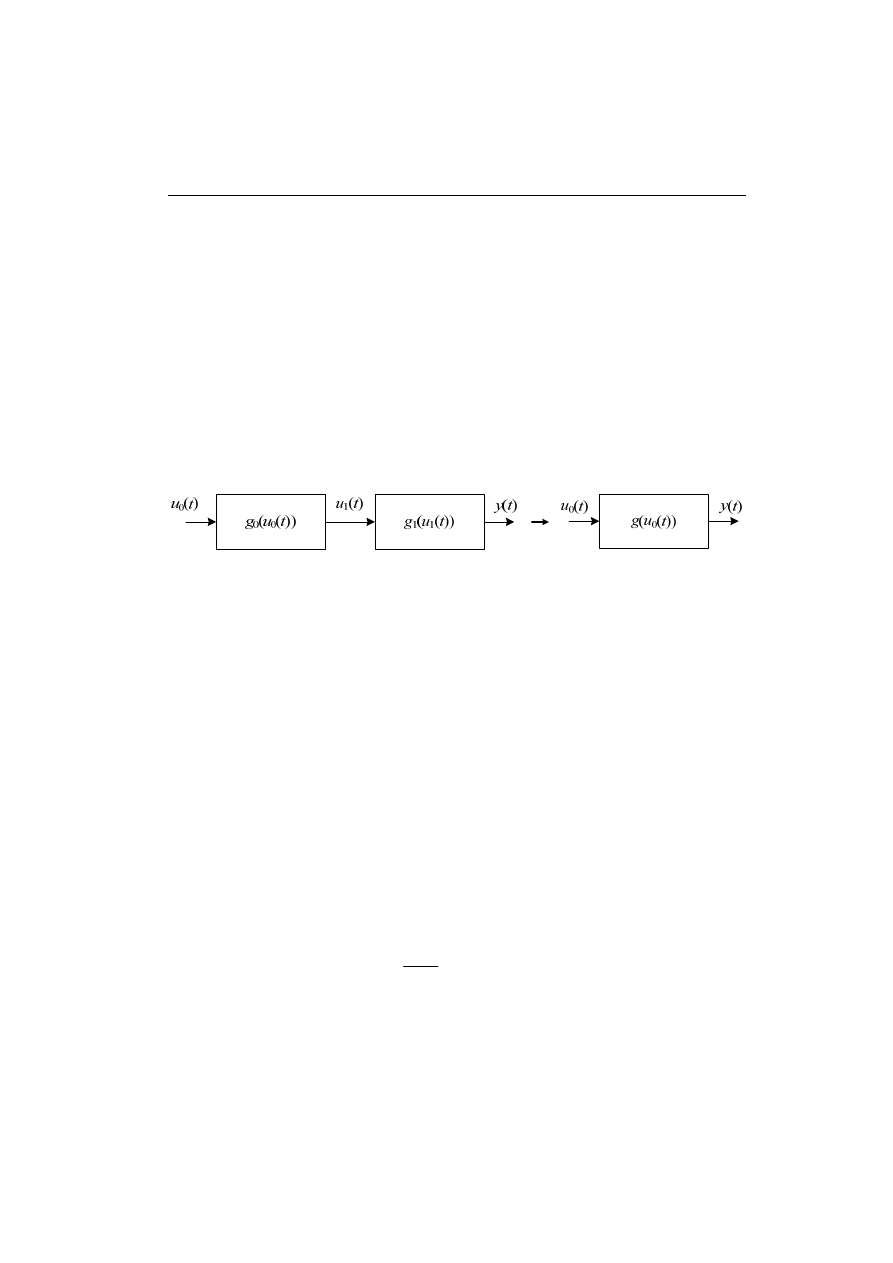
2.4. Analiza systemów opisanych równaniami różniczkowymi 19
Podstawiając (2.36) do (2.35), otrzymamy:
(
)
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
0
1
1
0
1
0
0
0
0
1
1
t
u
t
g
t
g
t
u
g
g
t
y
⊗
⊗
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
∫
∫
+∞
∞
−
+∞
∞
−
τ
τ
τ
τ
τ
τ
d
d
(2.37)
Powtarzając tę procedurę dla odwrotnej kolejności układów łatwo pokazać, że:
(
) (
)
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
0
1
0
0
1
0
0
1
t
u
t
g
t
g
t
g
t
u
t
g
t
u
t
g
t
g
⊗
⊗
=
⊗
⊗
=
⊗
⊗
(2.38)
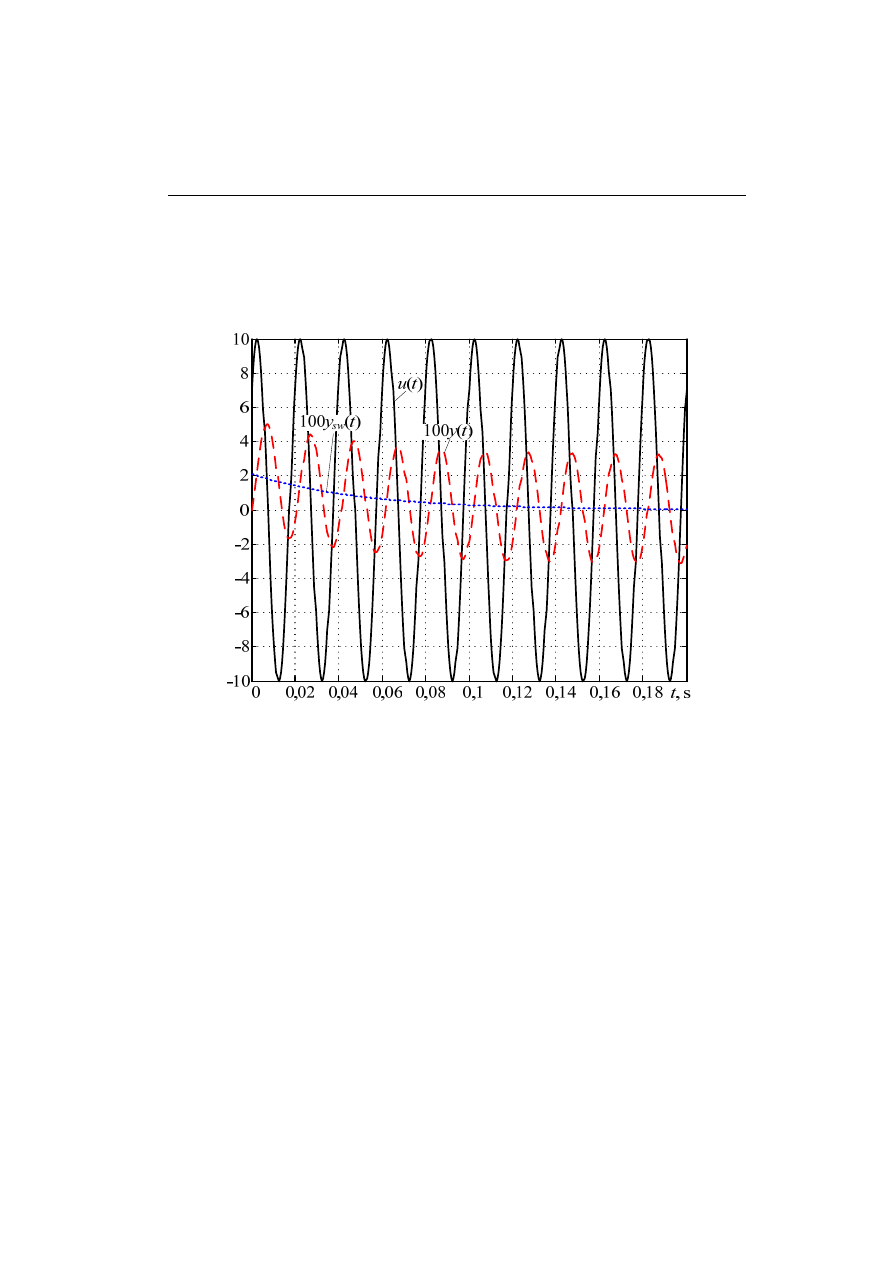
Widać stąd, że dla szeregowo połączonych układów o funkcjach impulsowych,
odpowiednio, g
0
(t) oraz g
1
(t), obowiązuje zależność (rys. 2.11):
)
(
)
(
)
(
1
0
t
g
t
g
t
g
⊗
=
(2.39)
gdzie g(t) jest funkcją impulsową ekwiwalentnego układu.
)
(
)
(
)
(
1
0
t
g
t
g
t
g
⊗
=
Rys. 2.11. Ekwiwalent szeregowo połączonych bloków
2.5.
Opis dynamiki systemu za pomocą równań stanu
2.5.1. Struktura
równań zmiennych stanu
W dotychczasowych rozważaniach zakładaliśmy, że sygnał wyjściowy dla danego
systemu o funkcji wagi g(t) może być określony za pomocą zależności splotowej
(2.31). W tym wyrażeniu zgubiona jest informacja o strukturze wewnętrznej systemu,
co można wykorzystać przy bardziej szczegółowej jego analizie. Ponadto, zapis
splotowy relacji wejście – wyjście komplikuje się dla systemów o większej liczbie
wejść i wyjść. W takim przypadku korzystnie jest stosować model systemu w postaci
równań stanu. Jego ideę można prześledzić na podstawie przykładu układu
mechanicznego, jaki był rozważany na początku tego rozdziału (rys. 2.1).
Siła f(t) przyłożona do masy M, zgodnie z (2.3) rozkłada się na trzy składniki:
)
(
)
(
)
(
)
(
t
f
t
f
t
f
t
f
S
M
D
+
+
=
(2.40)
gdzie:
)
(
)
(
t
Dv
t
f
D
=
,
t
t
v
M
t
f
M
d
)
(
d
)
(
=
,
∫
=
t
t
v
K
t
f
S
d
)
(
)
(
.
Różniczkując ostatni składnik otrzymamy równanie dynamiki sprężyny:

20
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
)
(
d
)
(
d
t
Kv
t
t
f
S
=
(2.41)
Podobnie, równanie dynamiki zawieszonej masy można przedstawić w
następującej postaci:
)
(
1
)
(
1
)
(
)
(
1
d
)
(
d
t
f
M
t
f
M
t
v
M
D
t
f
M
t
t
v
S
M
+
−
−
=
=
(2.42)
Siła związana z tłumikiem jest proporcjonalna do prędkości przemieszczania się
tłoka, jest więc wyrażona za pomocą zależności algebraicznej. Dynamika
rozważanego układu jest przedstawiona za pomocą dwóch powyższych równań, które
można zapisać w formie macierzowej:
)
(
1
0
)
(
)
(
1
0
d
)
(
d
d
)
(
d
t
f
M
t
v
t
f
M
D
M
K
t
t
v
t
t
f
S
S
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
(2.43)
W tym systemie wymuszeniem jest siła: u(t) = f(t), natomiast odpowiedzią -
prędkość: y(t) = v(t). Różniczkowane wielkości występujące po lewej stronie
powyższego równania: f
S
(t), v(t), są nazywane zmiennymi stanu. Ogólna postać tego
równania jest następująca:
Bu
Ax
x
+
=
&
(2.44)
Du
Cx
y
+
=
(2.45)
Pierwsze z tych równań jest nazywane równaniem stanu, a drugie – równaniem
wyjść
4
. Przy założeniu, że system ma b zmiennych wejściowych (wymuszeń), n
zmiennych stanu oraz m wyjść, macierze parametrów przyjmują następującą postać:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
L
M
M
M
M
L
L
2
1
2
22
21
1
12
11
A
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
nb
n
n
b
b
b
b
b
b
b
b
b
b
b
L
M
M
M
M
L
L
2
1
2
22
21
1
12
11
B
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
mn
m
m
n
n
c
c
c
c
c
c
c
c
c
L
M
M
M
M
L
L
2
1
2
22
21
1
12
11
C
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
mb
m
m
b
b
d
d
d
d
d
d
d
d
d
L
M
M
M
M
L
L
2
1
2
22
21
1
12
11
D
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
x
x
x
M
2
1
x
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
m
y
y
y
M
2
1
y
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
b
u
u
u
M
2
1
u
.
4
Niektórzy autorzy zapisują równanie wyjść z transponowaną macierzą C:
Du
x
C
y
+
=
T
.

2.5. Opis dynamiki systemu za pomocą równań stanu
21
W rozpatrywanym przykładzie mamy:
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
)
(
)
(
)
(
)
(
2
1
t
v
t
f
t
x
t
x
S
x
,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
M
D
M
K
a
a
a
a
1
0
22
21
12
11
A
,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
M
b
b
1
0
22
11
B
, )
(t
f
=
u
,
)
(
)
(
t
v
t
y
=
=
y
,
[
] [ ]
1
0
2
1
=
=
=
c
c
c
C
,
0
=
D
.
Jest to więc układ z jednym wejściem (b = 1), jednym wyjściem (m = 1) oraz dwoma
zmiennymi stanu (n = 2). Macierz A jest nazywana macierzą stanu lub macierzą
przejściową. Określa ona podstawowe dynamiczne właściwości systemu.
Można zauważyć, że w układach z jednym wejściem i jednym wyjściem liczba
zmiennych stanu jest wyznaczona przez rząd systemu. Równanie różniczkowe n-go
rzędu jest reprezentowane za pomocą n równań I rzędu. Dynamika systemu jest
reprezentowana za pomocą równania stanu. Znajomość aktualnych wartości
zmiennych stanu wraz z funkcjami określającymi wejścia pozwala jednoznacznie
określić przyszłe stany systemu.
Przejście pomiędzy opisem systemu za pomocą równania różniczkowego, a
równaniem stanu nie jest jednoznaczne. Ten sam system może być opisany różnymi
równaniami stanu. Zależy to od sposobu definicji zmiennych stanu, co można uzyskać
na drodze odpowiednich przekształceń początkowego równania różniczkowego lub
przyporządkowaniem odpowiedniej wielkości fizycznej do zmiennej stanu. Na
przykład, w analizowanym powyżej układzie mechanicznym zmienne stanu
reprezentują: siłę sprężyny f
S
(t) oraz prędkość zmian v(t). Ten wybór można zmienić,
jeśli założyć, że w miejsce prędkości v(t) chcemy śledzić zmianę położenia masy x(t).
Te zmienne pozostają w następującej relacji:
)
(
)
(
t
v
t
t
x
=
d
d
.
Podstawiając ten związek do składników (2.40), otrzymamy następujące równania
różniczkowe:
)
(
)
(
)
(
)
(
t
f
M
D
t
x
M
KD
t
f
M
D
t
t
f
D
D
+
−
−
=
d
d
(2.46)
)
(
1
)
(
)
(
t
f
D
t
v
t
t
x
D
=
=
d
d
(2.47)
Skąd otrzymujemy następujące równanie stanu:
)
(
0
)
(
)
(
0
1
)
(
)
(
t
f
M
D
t
x
t
f
D
M
KD
M
D
t
t
x
t
t
f
D
D
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
d
d
d
d
(2.48)
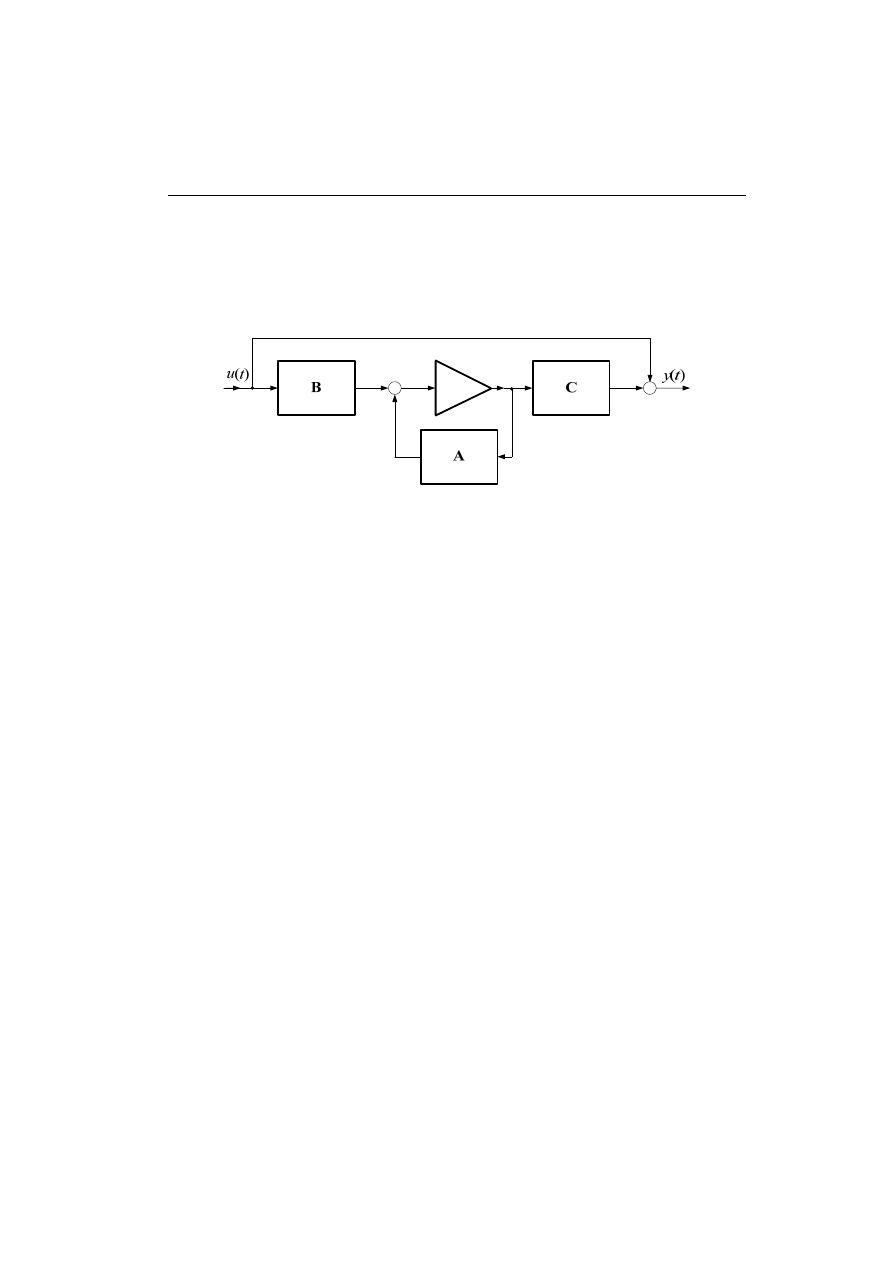
22
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
z równaniem wyjść: y = x(t). Tym razem zmiennymi stanu są: siła tłumienia f
D
(t) oraz
przesunięcie x(t).
Struktura zmiennych stanu dla systemu z jednym wejściem i jednym wyjściem jest
pokazana na rys. 2.12. Blok całkowania odwzorowuje proces rozwiązywania układu
równań różniczkowych opisujących dynamikę systemu.
)
(t
x&
)
(t
x
∫
Rys. 2.12. Struktura systemu zmiennych stanu
W przypadku układu z jednym wejściem i jednym wyjściem, schemat o strukturze
jak na rys. 2.12 jest ekwiwalentny schematowi z rys. 2.3, gdzie dynamika systemu jest
określona za pomocą równania różniczkowego n-tego rzędu. Rozmiar wektora stanu
x
(t) oraz kwadratowej macierzy stanu A zależy od rzędu ekwiwalentnego równania
różniczkowego.
2.5.2. Rozwiązywanie równań stanu
Rozpatrzmy jednorodne równanie stanu (2.44), w którym u = 0:
Ax
x
=
&
(2.49)
Dla przypadku jednowymiarowego (n = 1) otrzymujemy równanie: x
’
= ax, którego
rozwiązanie dla warunku początkowego x(0) ma następującą postać:
)
0
(
)
(
x
e
t
x
at
=
(2.50)
Jeśli warunek początkowy odnosi się do czasu t
0
: x(t
0
), to otrzymamy:
)
(
)
(
0
)
(
0
t
x
e
t
x
t
t
a
−
=
(2.51)
Rozwiązanie to można rozszerzyć na przypadek wielowymiarowy:
)
(
)
(
0
)
(
0
t
e
t
t
t
x
x
A
−
=
(2.52)
Funkcja wykładnicza o wykładniku w postaci kwadratowej macierzy At ma wymiar
macierzy A i może być przedstawiona w postaci szeregu potęgowego:

2.5. Opis dynamiki systemu za pomocą równań stanu
23
...
!
)
(
...
!
3
)
(
!
2
)
(
!
1
3
2
+
+
+
+
+
+
=
k
t
t
t
t
k
t
A
A
A
A
I
A
e
(2.53)
Macierz ta jest nazywana macierzą przenoszenia stanu
5
systemu (2.44) i dla wygody,
jest oznaczana następująco:
)
exp(
)
(
t
t
t
A
Φ
A
=
= e
(2.54)
Nazwa tej macierzy ma swoje uzasadnienie w zależności (2.52), z której widać, że
znajomość macierzy przenoszenia pozwala określić wartości wektora stanu dla
dowolnego czasu na podstawie jego wartości początkowej. Łatwo można sprawdzić,
że macierz przenoszenia ma następujące właściwości [D’Azzo]:
–
I
Φ
=
)
0
(
;
–
)
(t
Φ
jest macierzą nieosobliwą dla dowolnej ograniczonej wartości t;
–
)
(
)
(
1
t
t
−
=
−
Φ
Φ
;
–
)
(
)
(
)...
(
)
(
)
(
)
(
qt
t
t
t
t
t
q
Φ
Φ
Φ
Φ
Φ
Φ
=
=
, q – dodatnia liczba całkowita;
–
)
(
)
(
)
(
0
2
0
1
1
2
t
t
t
t
t
t
−
=
−
−
Φ
Φ
Φ
dla dowolnych wartości t
0
, t
1
, t
2
.
Rozwiązanie równania niejednorodnego (2.44) wymaga uwzględnienia
wymuszenia w postaci wektora u(t). Aby uzyskać odpowiednie zależności można
rozpatrzeć pochodną iloczynu następujących dwóch funkcji [D’Azzo]:
(
)
(
)
)
(
)
(
)
(
)
(
)
(
t
t
t
t
t
t
t
t
t
t
Ax
x
Ax
x
x
A
A
A
A
−
=
−
=
−
−
−
−
&
&
e
e
e
e
d
d
(2.55)
Na podstawie (2.44):
)
(
)
(
)
(
t
t
t
Bu
Ax
x
=
−
&
. Zatem:
(
)
)
(
)
(
t
t
t
t
t
Bu
x
A
A
−
−
= e
e
d
d
(2.56)
Całkując obustronnie powyższe równanie w granicach od t
0
do t otrzymamy:
(
)
∫
−
−
=
t
t
t
t
t
t
0
0
)
(
)
(
τ
τ
τ
d
e
e
Bu
x
A
A
, (2.57)
co prowadzi do następującej zależności:
∫
−
−
−
=
−
t
t
t
t
t
t
0
0
)
(
)
(
)
(
0
τ
τ
τ
d
e
e
e
Bu
x
x
A
A
A
(2.58)
Po wymnożeniu obu stron przez e
At
, ostatecznie otrzymamy:
5
Stosowane są także inne nazwy, jak macierz podstawowa (tranzycyjna) [Kaczorek]

24
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
∫
−
−
+
=
t
t
t
t
t
t
t
0
0
)
(
)
(
)
(
)
(
0
)
(
τ
τ
τ
d
e
e
Bu
x
x
A
A
(2.59)
lub, uwzględniając (2.54):
∫
−
+
−
=
t
t
t
t
t
t
t
0
d
)
(
)
(
)
(
)
(
)
(
0
0
τ
τ
τ
Bu
Φ
x
Φ
x
(2.60)
Obliczanie macierzy przenoszenia w powyższym równaniu zgodnie z (2.53) jest
niezwykle uciążliwe i dlatego stosuje się tu bardziej efektywne metody [Kaczorek,
Director]. Jedna z nich polega na stosowaniu wzoru Sylvestera [d’Azzo, Kacz.-
macierze]. Sprowadza się ona do następujących kroków:
Rozwiązując równanie charakterystyczne macierzy A:
[
]
0
...
det
0
1
1
1
=
+
+
+
+
=
−
−
−
a
a
a
n
n
n
λ
λ
λ
λ
I
A
(2.61)
określamy n jej wartości własnych
λ
1
,
λ
2
, ...,
λ
n
(ograniczymy rozważania do
przypadku, gdy macierz A ma jednokrotne wartości własne).
Określamy macierz przenoszenia ze wzoru Sylvestera:
∑
=
=
=
n
k
t
k
t
k
e
t
1
)
(
λ
Z
Φ
A
e
, (2.62)
przy czym:
∏
≠
=
−
−
=
n
k
i
i
i
k
i
k
1
λ
λ
λ
I
A
Z
, (2.63)
Przykład 2.8.
Określić odpowiedź układu rozważanego na str. 20, opisanego
równaniem (2.43), przy założeniu następujących parametrów systemu: K
= 4, D = 0,5, M = 1. W charakterze wymuszenia występuje skok
jednostkowy: f(t) = 1(t). Przyjąć zerowe warunki początkowe: x(0) = 0.
Po uwzględnieniu podanych parametrów i podstawieniu zmiennych: x
1
= fs oraz x
2
= v,
równanie (2.43) przyjmuje następującą postać:
)
(
)
(
)
(
1
1
0
)
(
)
(
5
,
0
1
4
0
)
(
)
(
2
1
2
1
t
t
t
t
x
t
x
t
t
x
t
t
x
Bu
Ax
+
=
⋅
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
d
d
d
d
Równanie charakterystyczne (2.61) macierzy A jest następujące:
0
4
5
,
0
5
,
0
1
4
0
det
2
=
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
λ
λ
λ
λ
,
2.5. Opis dynamiki systemu za pomocą równań stanu
25
Otrzymujemy stąd dwa pierwiastki:
λ
1,2
= –0,25
± j1,9843.
Macierze Z
1
i Z
2
należy obliczyć zgodnie z (2.63):
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
=
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
+
=
−
−
=
06299
,
0
5
,
0
25198
,
0
06299
,
0
5
,
0
)
(
)
(
5
,
0
1
4
2
1
2
1
j
j
j1,0079
j
j1,9843
0,25
j1,9843
0,25
j1,9843
0,25
j1,9843
0,25
-
-
-
-
λ
λ
λ
I
A
Z
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
+
−
−
⎥
⎦
⎤
⎢
⎣
⎡
+
+
−
−
−
=
−
−
=
06299
,
0
5
,
0
25198
,
0
06299
,
0
5
,
0
)
(
)
(
5
,
0
1
4
1
2
1
2
j
j
j1,0079
j
j1,9843
0,25
j1,9843
0,25
j1,9843
0,25
j1,9843
0,25
-
-
-
-
λ
λ
λ
I
A
Z
Macierz przenoszenia jest zatem równa:
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
+
=
+
=
+
=
−
−
−
t
t
t
t
t
t
t
t
t
t
t
t
t
0
0
0
0
0
0
0
0
0
0
25
,
0
9843
,
1
2
9843
,
1
1
25
,
0
2
1
sin
25
,
0
cos
sin
1
sin
4
sin
25
,
0
cos
)
(
2
1
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
λ
λ
e
e
e
e
e
e
j
j
Z
Z
Z
Z
Φ
,
9843
,
1
16
63
0
≈
=
ω
.
Odpowiedź układu na zadane wymuszenie można określić zgodnie z (2.60), przy czym:
⎥
⎦
⎤
⎢
⎣
⎡
=
1
0
B
, C = [0 1], D = 0.
Przebieg odpowiedzi: y(t) = x
1
(t) jest pokazany na rys. 2.13.
Rys. 2.13. Odpowiedź układu na skok jednostkowy

26
2. OPIS SYSTEMÓW LINIOWYCH W DZIEDZINIE CZASU
Przy danych parametrach układu i warunku początkowym, przebieg ten można łatwo otrzymać
w programie MATLAB pisząc dwie zaledwie komendy:
sys = ss(A,B,C,D);
lsim(sys,u,t);
gdzie u przedstawia wektor próbek sygnału wymuszającego określony na wektorze próbek
czasu t.
Zauważmy, że przebieg z rys. 2.13 przedstawia zmianę prędkości v(t) ruchu analizowanego
układu mechanicznego po wymuszeniu w postaci skoku jednostkowego działającego na ten
układ.
Zadania
2.1. Pokazać, że równanie:
)
(
)
(
4
)
(
2
)
(
2
2
t
u
t
y
t
t
y
t
t
y
=
+
+
d
d
d
d
2
nie spełnia warunku liniowości.
2.2. Określić sygnał wejściowy u(t) układu opisanego równaniem:
)
(
)
(
)
(
)
(
0
1
2
t
u
t
y
a
t
t
y
a
t
t
y
=
+
+
d
d
d
d
2
dla każdego z następujących sygnałów wyjściowych y(t):
(a) y(t) = t
2
,
(b) y(t) =
t
e
0
j
ω
, gdzie
ω
0
ma stałą wartość,
(c) y(t) = t
2
t
e
0
j
ω
.
2.3. Dla jakiej wartości pulsacji
ω
0
w zadaniu 2.2b funkcja wymuszająca u(t) = 0?
2.4. Załóżmy, że w układzie mechanicznym pokazanym na rys. 2.1b tłumienie jest niewielkie
i można przyjąć D = 0. Wówczas, przy sinusoidalnym wymuszeniu równanie (2.4)
przyjmie następującą postać:
t
A
t
Kv
t
t
v
M
ω
sin
)
(
)
(
2
=
+
d
d
2
Określić rozwiązanie tego równania przy zerowych warunkach początkowych: v(0) = 0,
v’(0) = 0.
2.5. Odpowiedź liniowego inwariantnego systemu na wymuszenie:
t
K
t
K
t
u
2
0
2
0
1
6
cos
)
(
+
−
=
ω
ω
ma postać:
y
(t) = K
1
cos
ω
0
t
+ K
2
t
3
, gdzie K
1
, K
2
– stałe. Jaka będzie odpowiedź układu na
wymuszenia:
(a)
t
t
u
0
cos
2
)
(
ω
=
,
(b)
3
)
(
−
= t
t
u
,
(c) jak wygląda równanie dynamiki systemu?

Zadania
27
2.6. Funkcja impulsowa liniowego układu inwariantnego jest następująca:
)
(
1
)
(
t
e
t
g
t
α
−
=
,
gdzie
α jest stałym współczynnikiem. Określić odpowiedź układu na następujące
wymuszenia:
(a)
)
(
)
(
t
t
u
δ
=
,
(b)
)
(
1
)
(
t
t
u
=
,
(c)
t
e
t
u
0
)
(
ω
j
=
,
ω
0
= const.
2.7. Obliczyć odpowiedź impulsową układu określonego następującym równaniem
różniczkowym:
(a)
)
(
)
(
2
)
(
t
u
t
y
t
t
y
=
−
d
d
,
(b)
)
(
)
(
)
(
t
u
t
y
t
t
y
=
+
d
d
,
(c)
)
(
)
(
2
t
u
t
t
y
=
d
d
2
,
(d)
)
(
)
(
29
d
)
(
d
10
d
)
(
d
2
2
t
u
t
y
t
t
y
t
t
y
=
+
−
.
2.8. Funkcja impulsowa liniowego układu inwariantnego jest następująca:
)
(
1
sin
)
(
0
t
e
t
g
t
α
ω
−
=
,
ω
0
,
α - stałe parametry. Określić odpowiedź układu na następujące
wymuszenia:
(a)
)
(
)
(
0
t
t
t
u
−
=
δ
, t
0
> 0,
(b)
)
cos(
)
(
0
t
t
u
ω
=
.
2.9. W przedstawionym obwodzie RL wymuszeniem jest napięcie u(t), a odpowiedzią – prąd
i(t). Napisać równanie różniczkowe określające dynamikę tego układu. Porównać
odpowiednie parametry równania z układem analizowanym w przykładzie 2.7.
R
L
u(t)
i(t)
2.10. Zapisać dynamikę układu RLC (2.2) za pomocą równań stanu. W charakterze zmiennych
stanu przyjąć: prąd i(t) oraz napięcie na kondensatorze u
C
(t) (rys. 2.1).
2.11. W przykładzie 2.7 jest analizowany układ mechaniczny w którym odpowiedź oznacza
prędkość przemieszczania się tego układu v(t). Powtórzyć tę analizę dla modelu
zmiennych stanu z równania (2.48), gdzie wyjście jest położeniem układu x(t). Przyjąć
dane jak w przykładzie 2.7.
Wyszukiwarka
Podobne podstrony:
opis systemu vendoHotel id 3370 Nieznany
Opis symboli lampek kontrolnych Nieznany
Planowanie systemow projekt 053 Nieznany
opis cwiczenia id 336864 Nieznany
48 USTAWA o systemie oceny zgo Nieznany (2)
opis systemu blueVendo Tour
opis techiczny id 337039 Nieznany
Kerberos opis systemu i instalacja w OS Linux
1 MSG i system GSid 8585 Nieznany (2)
Jak postawic system w 5 min prz Nieznany
1) Drgania w liniowych obwodach Nieznany
opis systemu topto v2 5 pl HSBSIRSSZ37UY4A4OA7HVYOHRVRREU7GXBRV6GQ
NAVTEX OPIS SYSTEMU
Opis systemu S12
Opis systemów operacyjnych-Linux, Informatyka -all, INFORMATYKA-all
mags1 ogolny opis systemu
17 Obsluga systemu finansowo ks Nieznany (2)
dobrucki,systemy operacyjne, op Nieznany
więcej podobnych podstron