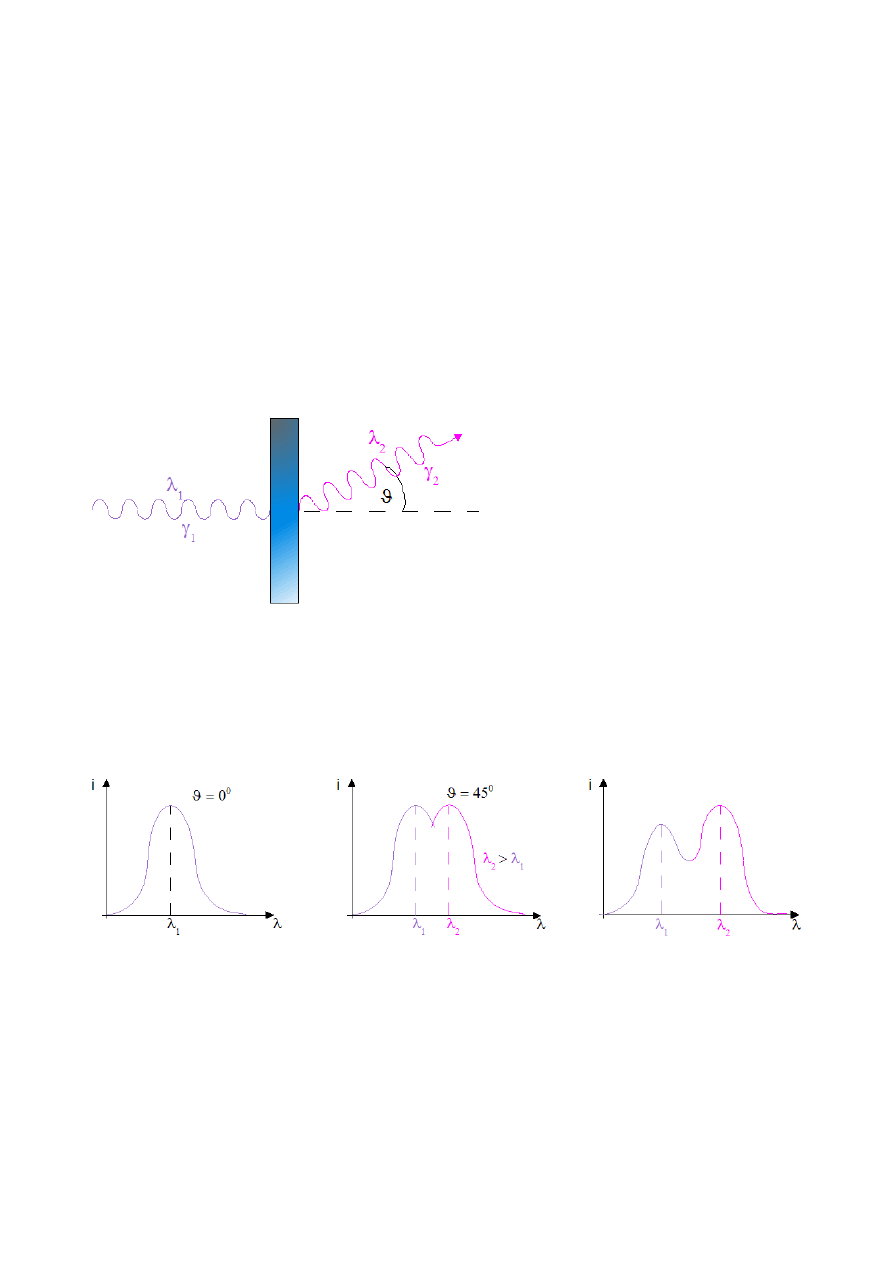
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

III.

EFEKT COMPTONA (1923)

Zjawisko zmiany długości fali promieniowania roentgenowskiego rozpraszanego na
swobodnych elektronach.

Zjawisko to stoi u podstaw mechaniki kwantowej.

III.1. EFEKT COMPTONA

Rys.III.1. Rozpraszanie kwantu

γ

na tarczy.

Compton badał rozpraszanie promieniowania roetgenowskiego na tarczy.

I – natężenie promieniowania roentgenowskiego po przejściu przez folię metalową

Rys.III.2. Zależność natężenia promieniowania Rtg po przejściu przez folię od długości fali promieniowania.

= 

2

−

1

= f



– nie zależy od długości fali
promieniowanie Rtg – jego energia 10000-100000eV

–

rozpraszanie ma miejsce na elektronach swobodnych (tzw. elektronach przewodzenia

– 1 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

lub walencyjnych)

Siły wiązań metalicznych – elektron swobodny odrywa się od atomu, tworzy gaz
elektronowy.

Równanie Comptona:

 = 1−cos

(III.1.1a)

 = 2  sin

2



2

(III.1.1b)

Λ – comptonowska długość fali

 =

h

m

0

c

= 0,0242 Å

(III.1.2)

E

= hf

Compton światło traktował jak strumień fotonów.

p

e

- pęd elektronu, który uzyskuje

po zderzeniu z fotonem

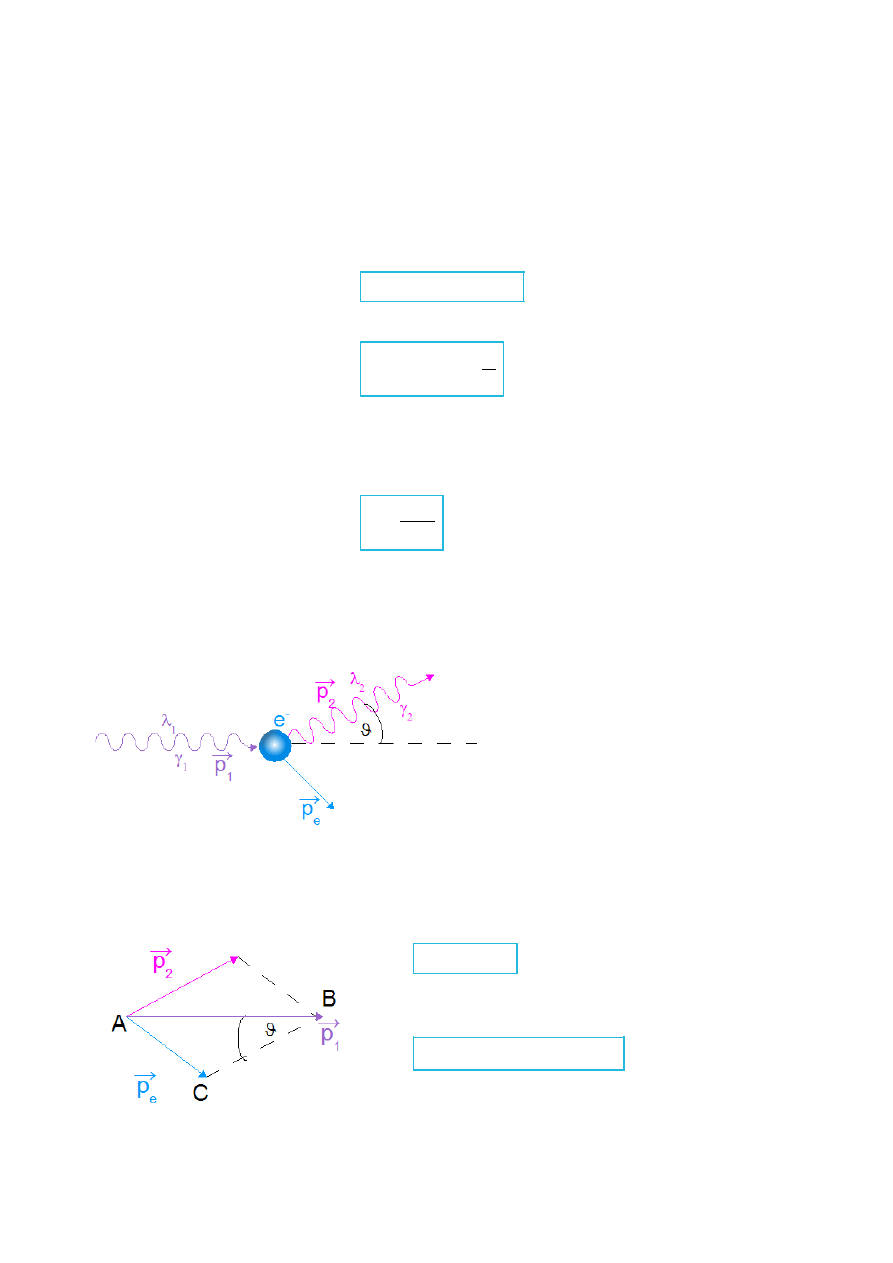
Rys.III.3. Zderzenie fotonu z elektronem. Po zderzeniu foton częściowo przekazuje swój pęd elektronowi.

–

prawo zachowania pędu:

p

1

= p

2

 p

e

(III.1.3)

z prawa cosinusów:

p

e

2

= p

1

2

 p

2

2

−2p

1

p

2

cos



(III.1.4)

Rys.III.4. Interpretacja wektorowa prawa zachowania pędu.

– 2 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

–

prawo zachowania energii:

E

2

= c

2

p

2

 m

0

c

2



2

(III.1.5)

dla fotonu:

m

0

= 0

(masa spoczynkowa)

z (III.1.5) wynika:

E = pc

(III.1.6)

p

1

c

m

0

c

2

= p

2

c





p

e

2

c

2

m

0

c

2



2

(III.1.7)

Wyprowadzimy równania Comptona z zależności (III.1.7):

p

1

m

0

c = p

2





p

e

2

m

0

2

c

2

(III.1.7a)

 p

1

− p

2

m

0

c



2

= p

e

2

m

0

2

c

2

(III.1.7b)

p

e

2

=

 p

1

− p

2

m

0

c



2

−m

0

2

c

2

(III.1.7c)

Z (III.1.4) i (III.1.7c) wynika:

 p

1

− p

2

m

0

c



2

−m

0

2

c

2

= p

1

2

 p

2

2

−2 p

1

p

2

cos



(III.1.8)

p

1

2

 p

2

2

−2 p

1

p

2

2 m

0

c

 p

1

− p

2

 = p

1

2

p

2

2

−2 p

1

p

2

cos



(III.1.8a)

p

1

p

2

1−cos=  p

1

− p

2

 m

0

c

(III.1.9)

Na podstawie postulatu Plancka:

p

1

=

E

1

c

=

hf

1

c

=

h



1

(III.1.10a)

p

2

=

h



2

(III.1.10b)

h

2



1



2

1−cos  = h



1



1

−

1



2



m

0

c

/⋅



1



2

h

2

(III.1.11)

– 3 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

1

−cos =

m

0

c

h



2

−

1

 /⋅

h

m

0

c

(III.1.12)

Otrzymaliśmy równanie (1b):



2

−

1

=

h

m

0

c

1−cos 

(III.1.13)



1

:

 = 0  =

h

m

0

c

= 0 <=> m

0

 ∞

Rozpraszanie na elektronach związanych.

Dualna natura światła – w różnych warunkach obserwujemy jego naturę:

–

falową (dyfrakcja, interferencja)

–

światło zachowuje się jak strumień cząstek.

Doświadczenie Comptona potwierdza fakt, że materia składa się z elektronów. Powstał
problem struktury atomu. Stwierdzono , że atomy składają się co najmniej z elektronów,
wykazano również jaki jest ładunek elektronu. Z drugiej strony wiedziano, że atom jest
elektrycznie obojętny, wynikało z tego, że muszą istnieć cząstki dodatnie wchodzące w
skład atomu.

III.2. KONCEPCJA BUDOWY ATOMU.

–

problem ładunku dodatniego (gdzie jest zlokalizowany, co go stanowi)

–

problem masy ( gdzie jest zlokalizowana i co stanowi masę atomu )

m

e

=

m

H

+

1836

– jest zbyt mały, by wytłumaczyć masę atomu

Model Thomsona

–

równomiernie naładowana sfera ładunkiem dodatnim z elektronami

r

~10

-10

m

q =

∣e∣⋅Z

– 4 –

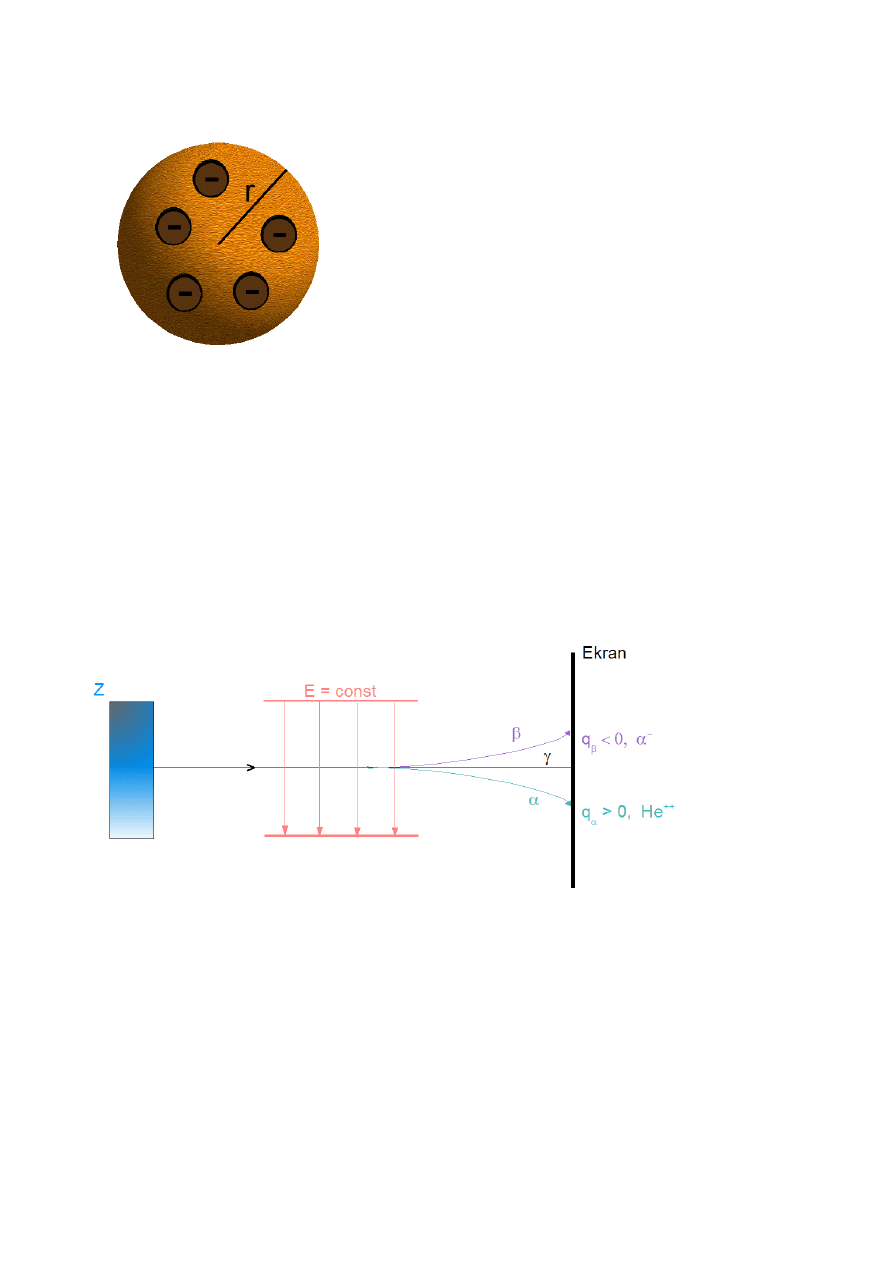
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

Rys.III.5. “Plum pudding model” (“ciasto z rodzynkami”) – model atomu Thomsona.

Weryfikacja modelu

Rutherford (1911) – poprzez swoje doświadczenie (rozpraszanie cząstek α) wykluczył
model Thomsona.

Cząstki α:
Becquerel odkrył, że rudy uranu wysyłają “tajemnicze” promieniowanie.

–

Składową naładowaną elektrycznie można zidentyfikować badając nań wpływ pola

E

lub

B

.

Rys.III.6. Wpływ pola elektrycznego na promieniowanie rudy uranu (Z)

γ

– emitowane zawsze gdy jądra atomowe są w stanie wzbudzonym

To samo można zrobić w polu magnetycznym



F

B

=q v×B



F

B

⊥v , B

.

Różnica jest taka, że odchylenie następuje w płaszczyźnie prostopadłej do kartki.

Rutherford badał prawdopodobieństwo rozproszenia cząstek α.

– 5 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

Ra - Rad
K - kolimator
D – detektor (ZnS)

Rys.III.7. Ilustracja graficzna doświadczenia Rutherforda.



max

e

=

q

~10

-4

rad

90

0

≤≤180

0

- cząstki rozproszone do tyłu

N

≥90

0



N

~10

-4

–

niemożliwe, żeby cząstka została rozproszona do tyłu, gdyby model Thomsona był
rzeczywisty, z tego wynika, że model atomu Rutherforda jest lepszym

–

koncepcja jądra atomowego – ulokowane w centralnej części atomu

–

masa atomu związana z ładunkiem dodatnim

Rutherford wyprowadził następującą formułę:

N

 d =



8

N

 t



zZe

2

1
2

Mv

2



2

sin



sin

4



2

d



(III.2.1)

Liczba cząstek α rozproszonych pod kątem



w kąt bryłowy

d



.

t – grubość tarczy
M – Masa cząstki α

=>

1
2

M v

2

=E

k

v – jej prędkość

– 6 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

ze

=q



, Ze

=q

Doświadczenie wykonywał stosując różne źródła cząstek α (dzięki czemu dysponował
cząstkami α o różnej energii kinetycznej) oraz tarcze o różnej grubości.
Eksperymentalnie stwierdził, że:

~t

~

1

E

k



Na podstawie otrzymanych wyników wyliczył ładunek jądra i stwierdził, że jest on równy
liczbie porządkowej w tablicy Mendelejewa.

Nierozwiązany problem: rozmiar jądra atomowego.

Rutherford oszacował rozmiar jądra atomowego:

R

=

D

2



1



1

sin 

2



D

=

zZe

2

1
2

Mv

2

D – odległość najbliższego zbliżenia (zderzenie centralne)
R jest równe D gdy cząstka jest rozproszona do tyłu (

=180

0

)

Dla

Cu

29

63

:

R

=

180

0

1,7

⋅10

-14

m

–

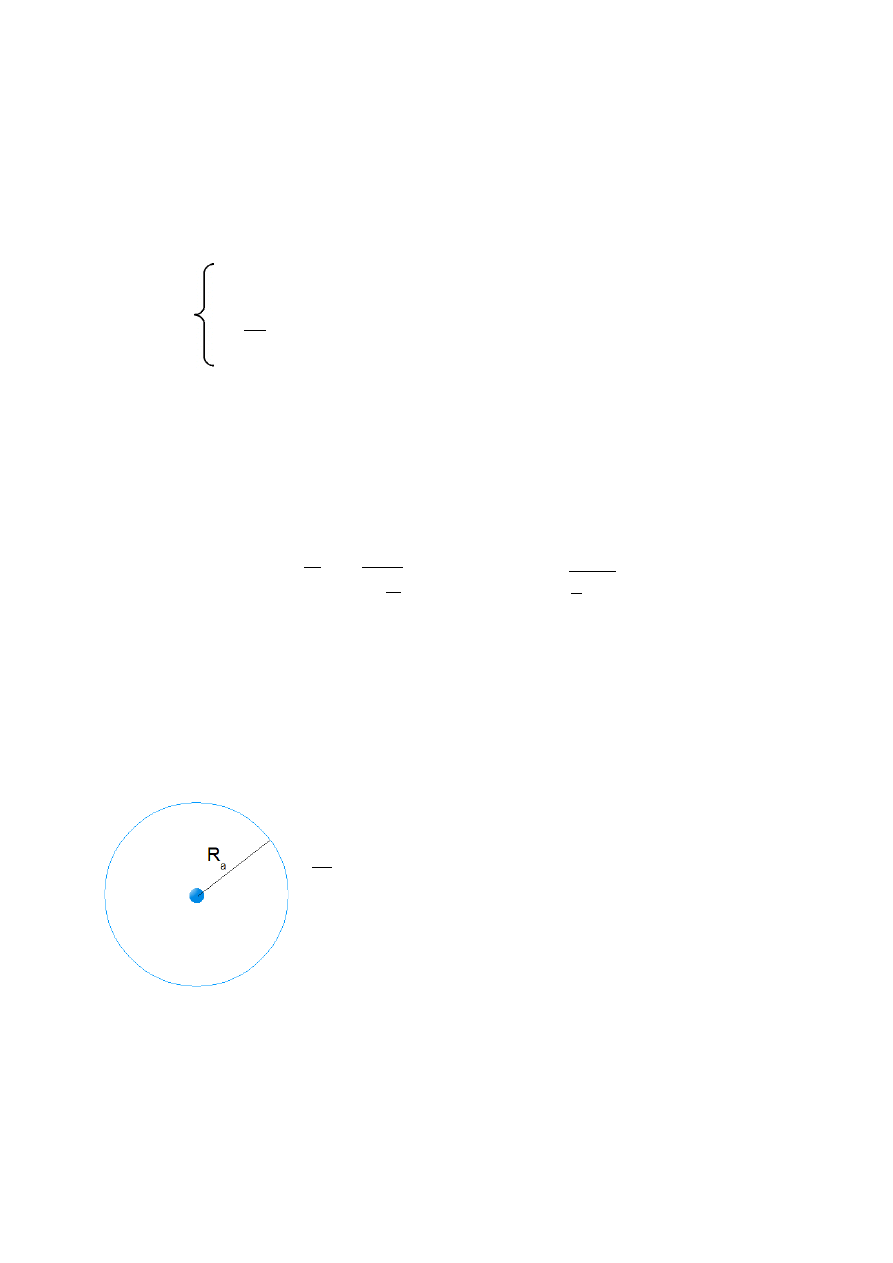
jądro atomu jest 10 tys. razy mniejsze od całego atomu.

R

a

R

=10

4

, R

a

– promień atomu, R – promień jądra

–

atom jest pusty (praktycznie cała materia skupiona jest w
jądrze)
analogia: pestka wiśni na środku stadionu piłkarskiego

Rys.III.8. Model atomu Rutherforda.

Problemem nie rozwiązanym przez Rutherforda była lokalizacja elektronów. Nie mogą być
one ulokowane w jądrze ani na jego powierzchni, bo atom byłby bardzo mały.
Przypuszczał, że elektrony mogą być rozmieszczone na orbitach.

– 7 –

N

 d =

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

Gdyby elektrony sie nie poruszały, to siła kulombowska przyciągnęłaby je do jądra,
natomiast gdy się poruszają, ładunek doznaje przyspieszenia, a więc traci energię,czyli
prędzej czy później spadałyby emitując promieniowanie o ciągłym widmie.
Mimo, iż Rutherford przypuszczał, że elektrony są na orbitach, nie rozwiązał problemu
stabilności atomu.

– 8 –