WYZNACZANIE OGNISKOWEJ SOCZEWKI

1

O5: WYZNACZANIE OGNISKOWEJ SOCZEWKI

Michał Dobrski, Piotr Słoma

Celem ćwiczenia jest wyznaczenie ogniskowych soczewek skupiających i rozpraszających

oraz układu soczewek przy użyciu wzoru soczewkowego, metody Bessela

i przy użyciu sferometru.

1.W

STĘP TEORETYCZNY

Soczewka jest to przedmiot wykonany z przezroczystego materiału (najczęściej szkła

lub tworzywa sztucznego) posiadający zdolność skupiania lub rozpraszania promieni światła.
Interesują nas cienkie soczewki sferyczne, czyli takie, których powierzchnie są wycinkami sfer
lub płaszczyznami. Określenie „soczewka cienka” oznacza, że grubość soczewki jest dużo
mniejsza od promieni sfer, które nadają jej kształt. Zakładamy także, że przedmioty, których
obraz daje soczewka cienka, są umieszczone w odległościach dużo większych niż jej grubość.
Przy takich założeniach słuszny jest zamieszczony poniżej, uproszczony opis.

Osią optyczną soczewki nazywamy prostą przechodzącą przez środki obu sfer

„wycinających” soczewkę. Jeśli jedna z powierzchni ograniczających soczewkę jest
płaszczyzną, to oś optyczna jest do niej prostopadła.

Korzystając z prawa załamania światła można wykazać, że wiązka promieni

równoległych do osi optycznej, leżących blisko niej (przyosiowych), po przejściu przez
soczewkę zostanie przekształcona na jeden z dwóch sposobów.

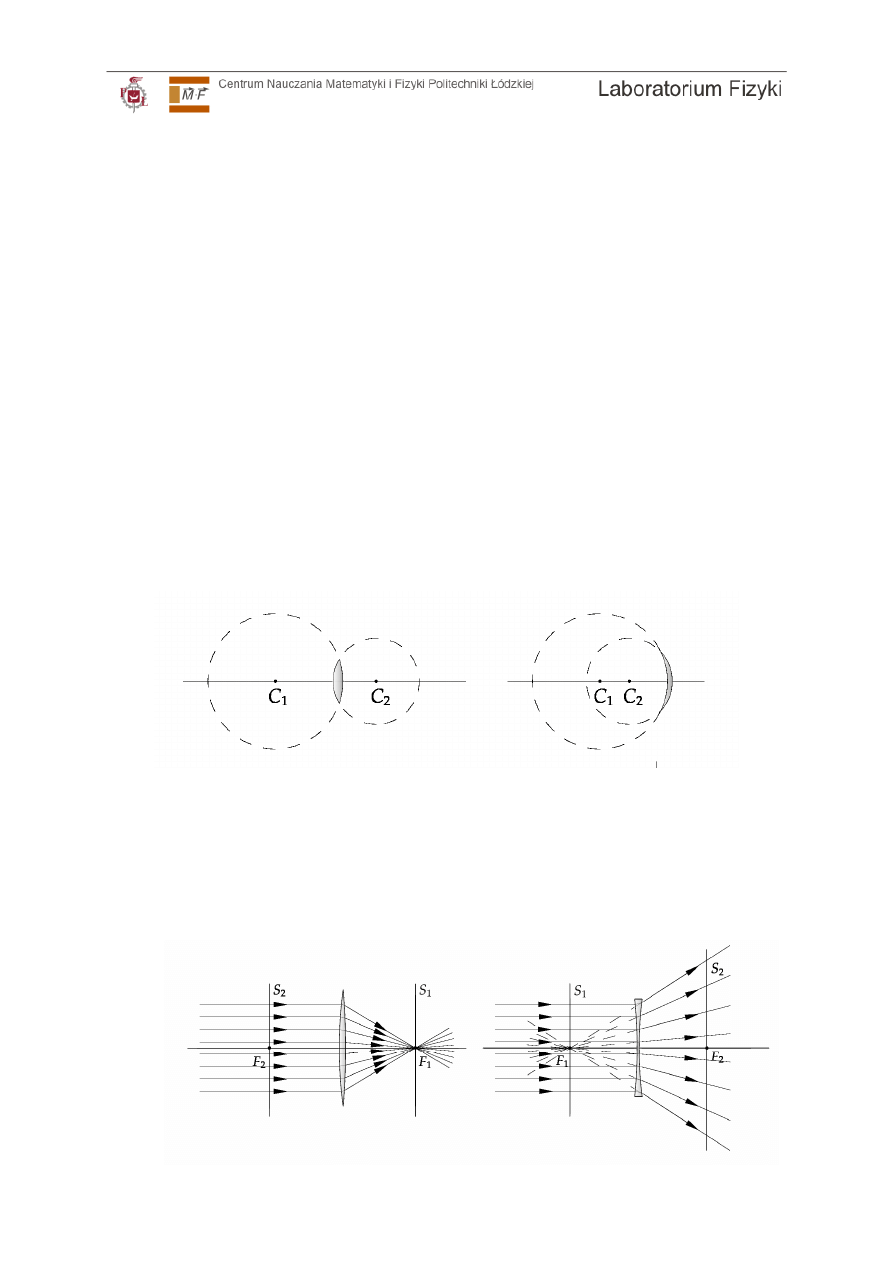
Ilustracja 1: Przykłady kształtów soczewek sferycznych. Na rysunku zaznaczono sfery i
płaszczyzny „wycinające” powierzchnie soczewek, środki tych sfer oraz położenie osi
optycznej.

Ilustracja 2: Promienie równoległe do osi optycznej wyznaczają położenie ogniska F

1

dla

soczewki skupiającej i rozpraszającej. Płaszczyzny ogniskowe oznaczono jako S

1

i S

2

.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

2

1.

Promienie przetną się w jednym punkcie (nazywanym ogniskiem rzeczywistym).

2.

Promienie rozproszą się, a w jednym punkcie (ognisku pozornym) przetną się ich

przedłużenia.

Te soczewki dla których zachodzi pierwszy wariant, nazywamy skupiającymi, a te dla których
obserwujemy drugą możliwość – rozpraszającymi. Ogniska leżą zawsze na osi optycznej, po
obu stronach soczewki. Mierzoną wzdłuż osi optycznej odległość ogniska od soczewki
określamy mianem ogniskowej. Wielkość tę oznaczamy literą f i przyjmujemy dodatnią dla
soczewek skupiających oraz ujemną dla rozpraszających. Odwrotność ogniskowej (D=1/f)
nosi nazwę zdolności skupiającej soczewki. Tradycyjną jednostką dla tej wielkości jest
dioptria (D=1/m). Płaszczyznę prostopadłą do osi optycznej i przechodzącą przez ognisko
nazywamy płaszczyzną ogniskową (rzeczywistą lub pozorną stosownie do rodzaju ogniska).

Ogniskową soczewki cienkiej można wyznaczyć ze wzoru

( )













+

−

=

2

1

1

1

1

1

r

r

n

f

(1)

gdzie n oznacza współczynnik załamania materiału soczewki względem otoczenia, a r

1

i r

2

są

promieniami sfer ograniczających soczewkę. Przyjmujemy, że promień sfery jest dodatni dla
powierzchni wypukłych i ujemny dla wklęsłych. Dla powierzchni płaskich uważamy, że jest
równy nieskończoności, a tym samym 1/r=0.

Promienie wychodzące z jednego punktu P (nieleżącego na rzeczywistej płaszczyźnie

ogniskowej) po przeniknięciu przez soczewkę są albo skupiane w jednym punkcie P' tworząc
obraz rzeczywisty punktu P, albo też ich przedłużenia po stronie punktu P przecinają się w
punkcie P' zwanym obrazem pozornym punktu P. Odległość x punktu P od soczewki oraz
odległość y obrazu P' od soczewki powiązane są następującym równaniem:

f

y

x

1

1

1

=

+

(2)

W powyższym wzorze wielkość y jest dodatnia dla obrazów rzeczywistych oraz ujemna dla
obrazów pozornych.

Soczewki skupiające mogą tworzyć zarówno obrazy rzeczywiste ( x>f ) jak i pozorne ( x<f ).
Soczewki rozpraszające utworzą w opisanej powyżej sytuacji wyłącznie obrazy pozorne.
Określając jako h odległość P od osi optycznej (wysokość przedmiotu) oraz jako h' odległość
P' od tejże osi (wysokość obrazu) można udowodnić następującą zależność:

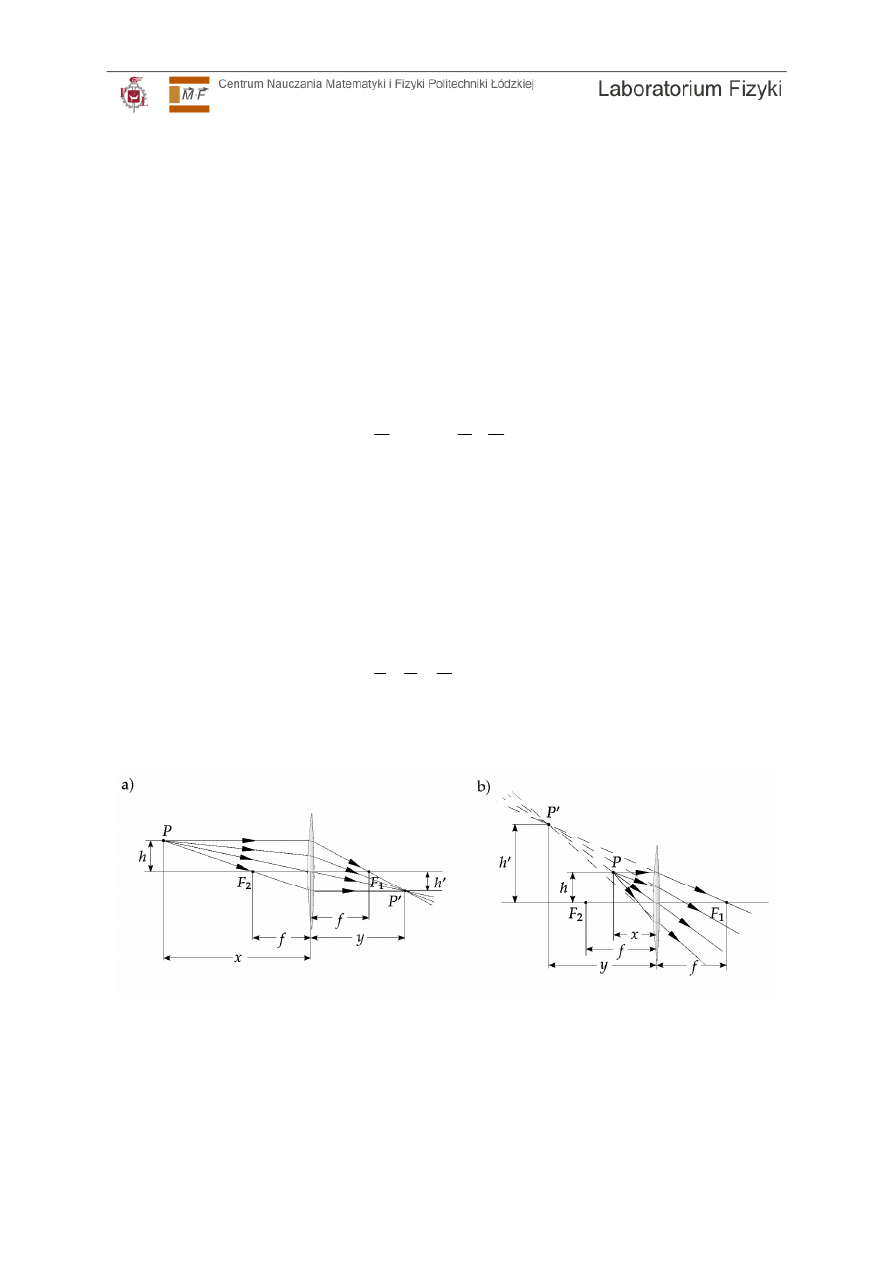
Ilustracja 3: Powstawanie obrazu w soczewce skupiającej. a) Odwrócony obraz rzeczywisty
(x>0, y>0, f>0, h>0, h'<0). b) Prosty (nieodwrócony) obraz pozorny (x>0, y<0, f>0, h>0, h'>0).

WYZNACZANIE OGNISKOWEJ SOCZEWKI

3

y

x

h

h

−

=

′

(3)

gdzie przyjmujemy h>0, natomiast h'>0 oznacza obrazy proste (nieodwrócone), zaś h'<0 –
odwrócone.

Na podstawie powyższych informacji można łatwo wskazać dwie proste metody

pomiaru ogniskowej soczewki. Pierwsza z nich polega na wyznaczeniu promieni sfer r

1

oraz

r

2

będących powierzchniami bocznymi soczewki. Służy do tego przyrząd zwany sferometrem,

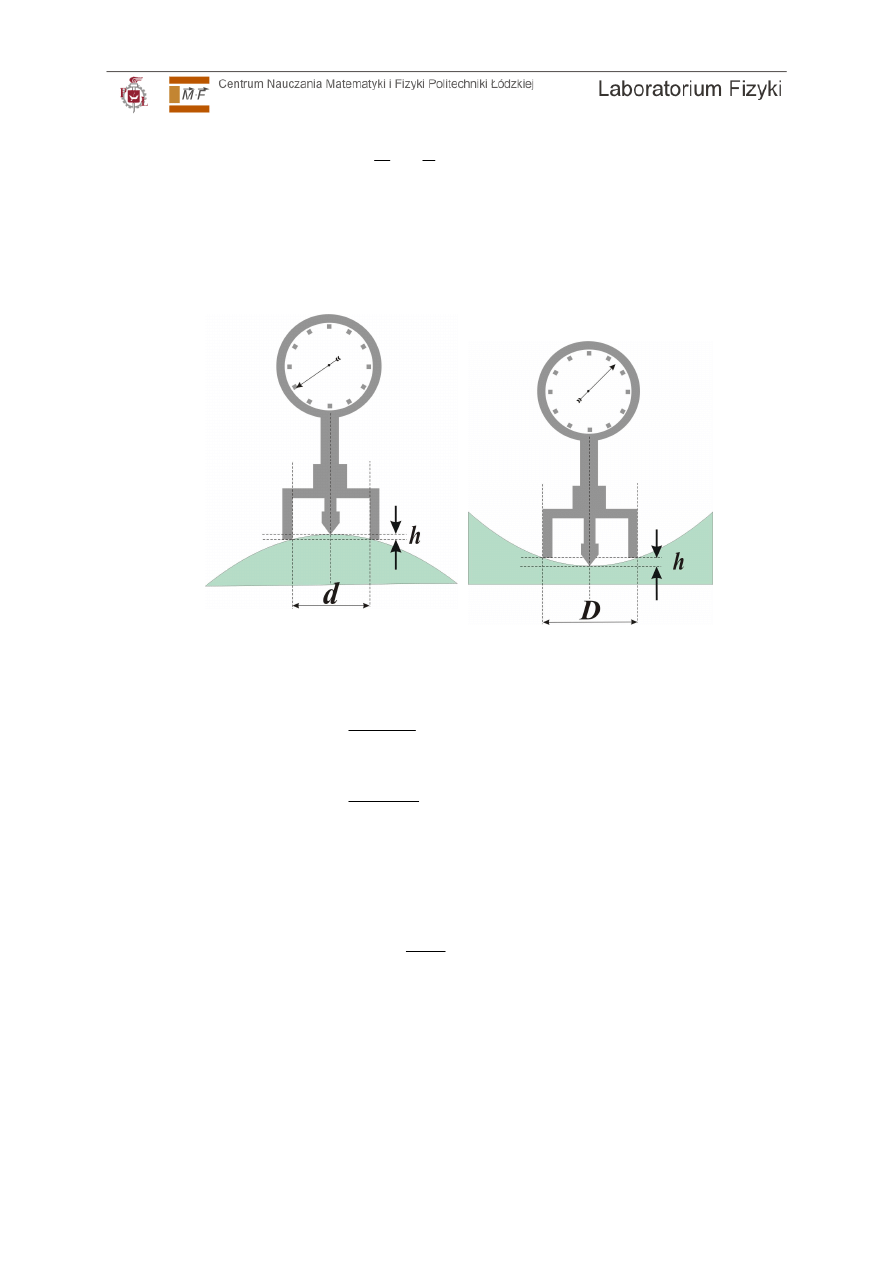
którego zasada działania została zobrazowana na ilustracji 4.

Ilustracja 4: Pomiar przy użyciu sferometru dla powierzchni wypukłej oraz wklęsłej.

Odczytując wskazanie sferometru h możemy obliczyć promienie krzywizn według
następujących wzorów:

h

h

d

r

8

4

2

2

+

=

dla powierzchni wypukłej,

(4a)

h

h

D

r

8

4

2

2

+

=

dla powierzchni wklęsłej.

(4b)

Znając dodatkowo współczynnik załamania n materiału, z którego wykonana jest dana
soczewka możemy obliczyć jej zdolność skupiającą ze wzoru (1).

Druga możliwość polega na wykonaniu pomiaru odległości x obiektu od soczewki

oraz odległości y obrazu rzeczywistego (uzyskanego na odpowiednio ustawionym ekranie) od
soczewki i wykorzystaniu wzoru (2) przekształconego do postaci

y

x

xy

f

+

=

(5)

Oba opisane sposoby posiadają istotne wady. Pierwszy wymaga znajomości

współczynnika załamania materiału soczewki. W drugim trudność stanowi pomiar wielkości x
oraz y. Okazuje się bowiem, że powinny być one mierzone od pewnego, charakterystycznego
dla każdej soczewki, punktu nazywanego środkiem optycznym soczewki. Bez precyzyjnej
znajomości parametrów geometrycznych soczewki nie jesteśmy w stanie dokładnie określić
jego położenia. W związku z tym, przy pomiarach musimy arbitralnie przyjąć jakiś punkt
(najczęściej stosunkowo niedokładnie wyznaczony geometryczny środek soczewki),
względem którego dokonujemy pomiarów odległości. Sytuacja ta rodzi ryzyko wystąpienia

WYZNACZANIE OGNISKOWEJ SOCZEWKI

4

błędu systematycznego, który istotnie obniża wiarygodność otrzymanych rezultatów. Co
więcej, im grubsza soczewka, tym mniejszy sens ma pojęcie środka optycznego. Można
bowiem pokazać, że uwzględniając grubość soczewki musimy wprowadzić dwa różne punkty,
jeden określający odniesienie dla odległości x, a drugi dla y. Fakt ten dodatkowo pogarsza
dokładność metody opartej na prostym pomiarze odległości między soczewką a obiektem i
jego obrazem.

Powyższe problemy rozwiązuje dla soczewek cienkich metoda Bessela. Zauważmy,

ż

e równanie (2) nie ulega zmianie po zamianie miejscami zmiennych x i y. Faktycznie, jeśli

umieścimy obiekt w odległości y, to wówczas obraz powstanie w odległości x. Jeśli przed
zmianą położenia powstawał obraz powiększony, to teraz otrzymamy obraz pomniejszony i
na odwrót. Nietrudno to spostrzec analizując wzór (3). Zdefiniujmy teraz wielkości b=y-x
oraz l=x+y. Zależność (5) możemy przekształcić do postaci

l

b

l

f

4

2

2

−

=

(6)

Zauważmy jednak, że l jest po prostu odległością między obiektem a ekranem, na którym
powstaje obraz. Natomiast b jest odległością między dwoma położeniami soczewki, dla
których na ekranie powstaje obraz obiektu. Zaobserwowanie obrazów rzeczywistych jest
możliwe tylko wtedy, gdy odległość między ekranem a obiektem jest wystarczająco duża.
Warunek ten ma postać l>4f i można go otrzymać poprzez analizę wzoru (6). Zwróćmy
uwagę, że dla soczewek cienkich (z dobrze określonym środkiem optycznym) pomiar l i b nie
wnosi ryzyka powstania opisanego wyżej błędu systematycznego.

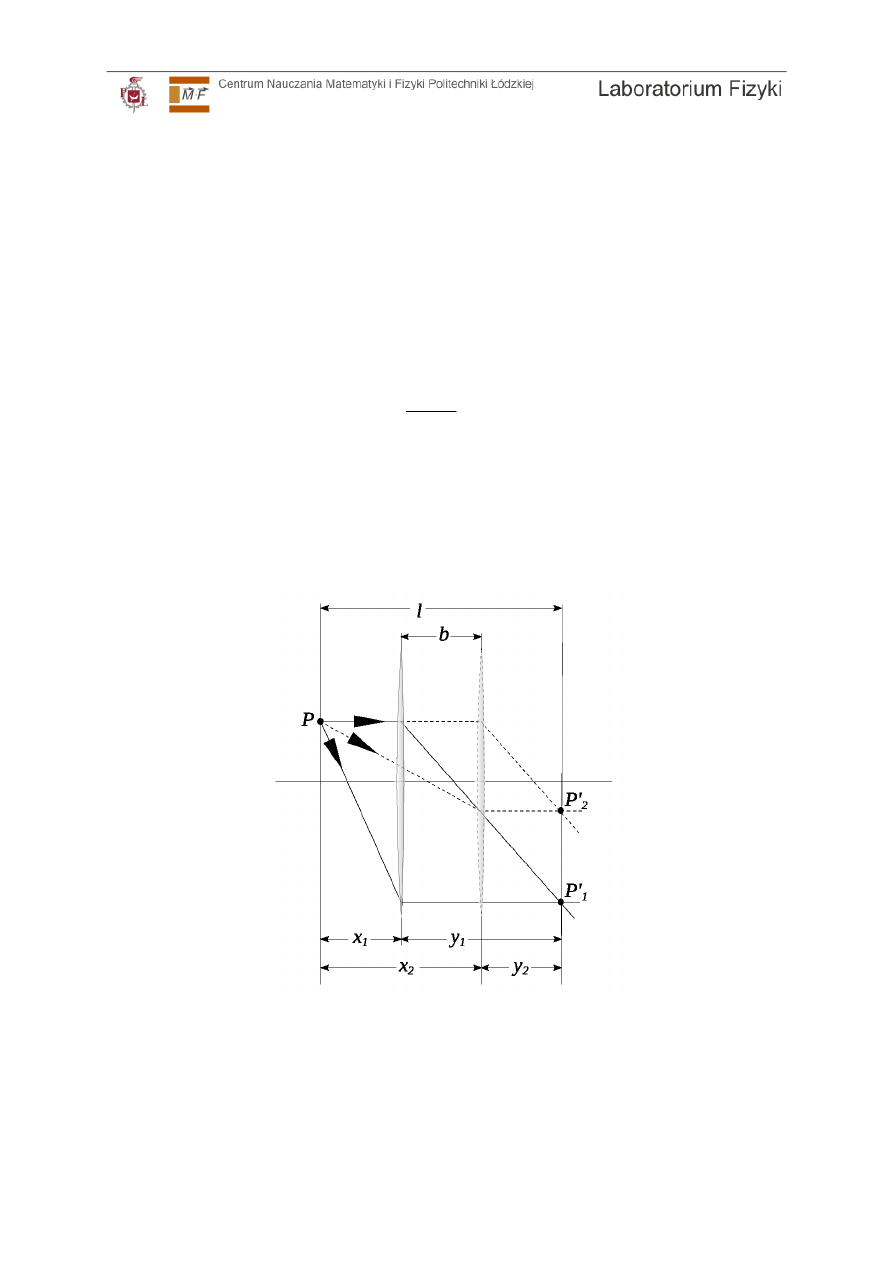
Ilustracja 5: Metoda Bessela. Soczewka ustawiona w odległości x

1

od P wytwarza

powiększony obraz P'

1

w odległości y

1

. Po odsunięciu soczewki na odległość x

2

=y

1

powstanie obraz pomniejszony leżący w odległości y

2

=x

1

. Odległość l między obiektem

a obrazem będzie w obu przypadkach taka sama.

Zarówno metoda Bessela jak i bezpośredni pomiar x i y możliwe są do

przeprowadzenia wyłącznie dla soczewek skupiających, gdyż wytwarzają one odpowiednie
obrazy rzeczywiste. Dla soczewek rozpraszających można postąpić w sposób następujący.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

5

Łącząc na jednej osi optycznej soczewkę rozpraszającą z soczewką skupiającą o znanej,
odpowiednio małej ogniskowej f

1

możemy wytworzyć układ, który będzie się zachowywał

jak soczewka skupiająca. Szczegółowa analiza prowadzi do wniosku, że ogniskowa f

u

układu

dwóch soczewek cienkich dana jest wzorem

2

1

2

1

1

1

1

f

f

m

f

f

f

u

−

+

=

(7)

gdzie m jest odległością między soczewkami. Rozwiązując powyższą zależność ze względu
na f

2

dostajemy

(

)

u

u

f

f

m

f

f

f

−

−

=

1

1

2

(8)

A zatem mierząc ogniskowe f

u

oraz f

1

możemy obliczyć poszukiwaną ogniskową f

2

soczewki

rozpraszającej.

2.

O

PIS ZESTAWU POMIAROWEGO

Ilustracja 4: Widok ogólny stanowiska pomiarowego do badania ogniskowych soczewek.

Zestaw składa się z ławy optycznej z podziałką milimetrową na której umieszczono:

•

oświetlacz z przedmiotem badanym („strzałka” lub inny dowolny kształt)

•

trzy koniki z możliwością montażu soczewek i ekranu

Ponadto w skład zestawu wchodzi sferometr wraz z płytką szklaną służącą do jego zerowania,
zasilacz 12V prądu przemiennego oraz dwie badane soczewki – skupiająca dwuwypukła i
rozpraszająca dwuwklęsła.

UWAGA!
Przed przystąpieniem do pomiarów należy zgłosić się do pracownika technicznego po

badane soczewki oraz sferometr z płytką szklaną. Po zakończonych pomiarach pobrane
przedmioty należy zwrócić pracownikowi technicznemu.

UWAGA!

Autorzy instrukcji zalecają wykonanie pomiaru ogniskowej wszystkimi trzema metodami.
Sposób zbierania pomiarów i opracowania wyników dostosowany jest do studentów nie po-
siadających umiejętności liczenia pochodnych – proponowany rachunek błędów oparty jest
o metodę Studenta. Jednakże pomiary zbierane w oparciu o instrukcję pozwalają policzyć
błędy również metodą różniczki zupełnej. Decyzję o sposobie przeprowadzenia pomiarów
jak i wyborze metody rachunku błędów podejmuje prowadzący w zależności od stopnia za-
awansowania „matematycznego” studentów wykonujących to doświadczenie.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

6

3.

P

RZEBIEG EKSPERYMENTU

A. Wyznaczenie ogniskowej na podstawie wzoru soczewkowego.

3.1.

Ustawić ekran na końcu ławy optycznej.

3.2.

Zamocować badaną soczewkę dwuwypukłą w wybranym koniku umieszczonym mie-
dzy oświetlaczem a ekranem – śrubę mocującą dokręcić z wyczuciem!

3.3.

Włączyć oświetlacz.

3.4.

Przesuwając konik z badaną soczewką wzdłuż ławy optycznej należy znaleźć na ekranie
ostry obraz przedmiotu – powiększony lub pomniejszony. Zanotować odległość x po-
między przedmiotem a soczewką i odległość y pomiędzy soczewką a ekranem.

Położenie soczewki wyznaczamy w oparciu o środek konika, czyli zakładamy, że środek

geometryczny soczewki jest dokładnie nad środkiem konika.

3.5.

Pomiary powtórzyć 10 razy.

3.6.

Oszacować błędy pomiarowe

∆∆∆∆

x i

∆∆∆∆

y przy wyznaczaniu odległości x i y:

•

przesuwając konik z soczewką w stronę oświetlacza należy ustalić odległość

∆∆∆∆

x

(

∆∆∆∆

y) o jaką możną przesunąć konik z soczewką, aby obraz na ekranie pozostał

ostry.

3.7.

W drugim koniku zamocować soczewkę dwuwklęsłą – śrubę mocującą dokręcić z
wyczuciem! i zbliżyć maksymalnie do konika z soczewką dwuwypukłą.

3.8.

Powtórzyć czynności pomiarowe z punktów od 3.4 do 3.6 dla tak powstałego układu
soczewek (koniki z soczewkami przesuwamy zawsze razem – koniki soczewek muszą
się zawsze ze sobą stykać w trakcie pomiarów).

3.9.

Zmierzyć i zanotować odległość m między środkami soczewek. Oszacować błąd pomia-
ru

∆∆∆∆

m.

3.10.

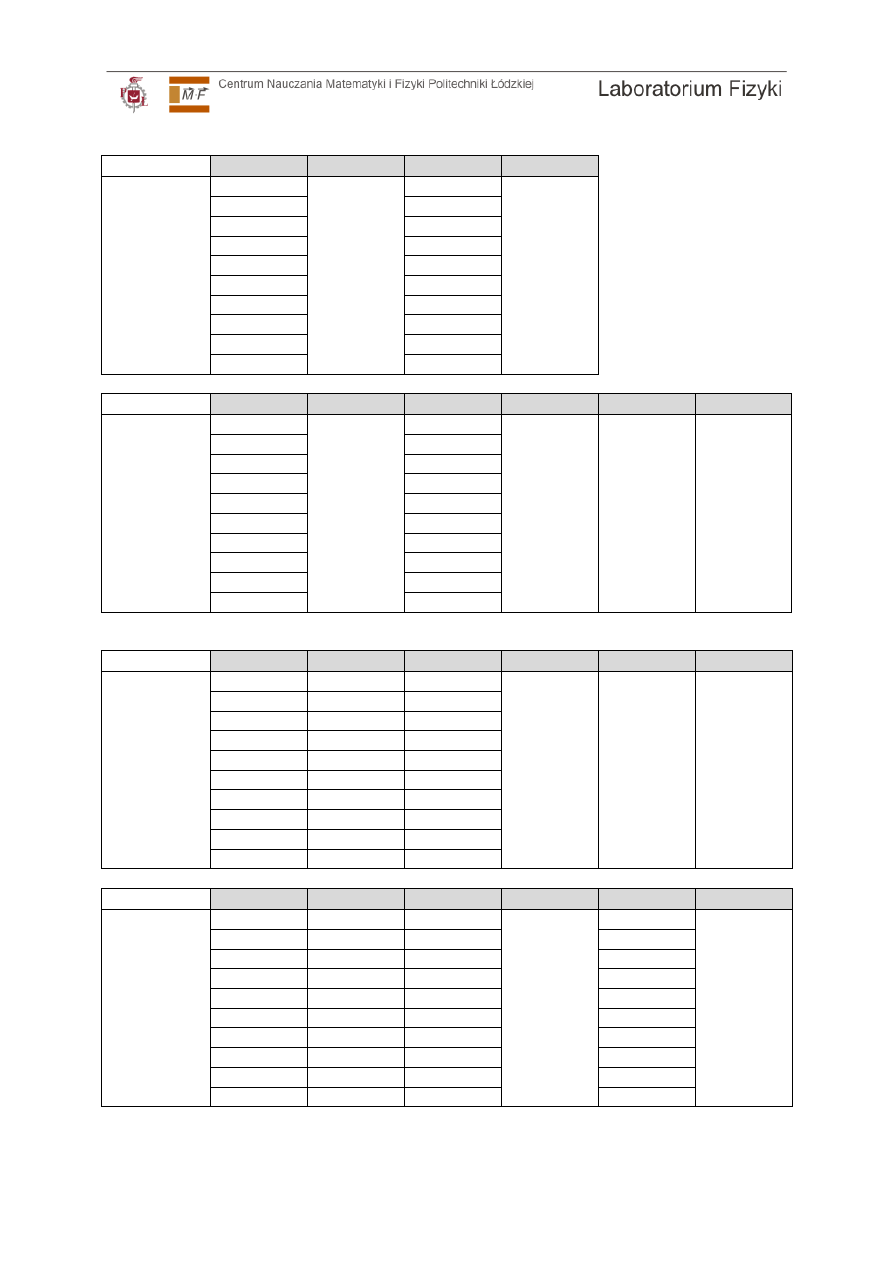
Wyniki pomiarów zanotować w tabeli – wzór tabeli do druku na końcu instrukcji.

B. Wyznaczenie ogniskowej metodą Bessela.

3.11.

Ustawić ekran na końcu ławy optycznej.

3.12.

Zamocować badaną soczewkę dwuwypukłą w wybranym koniku umieszczonym mie-
dzy oświetlaczem a ekranem – śrubę mocującą dokręcić z wyczuciem!

3.13.

Włączyć oświetlacz.

3.14.

Przesuwając konik z badaną soczewką dwuwypukłą wzdłuż ławy optycznej należy zna-
leźć na ekranie ostry obraz przedmiotu – powiększony i zanotować położenie soczewki
s

1

.

3.15.

Przesuwając konik z badaną soczewką dwuwypukłą wzdłuż ławy optycznej należy
znaleźć na ekranie ostry obraz przedmiotu – pomniejszony i zanotować położenie so-
czewki s

2

.

3.16.

Powtórzyć czynności z punktów 3.14 do 3.15 10 razy. Oszacować błąd wyznaczenia
położenia s

1

i s

2

.

3.17.

Zmierzyć i zanotować odległość l między przedmiotem a ekranem. Oszacować błąd
pomiaru

∆∆∆∆

l.

3.18.

W drugim koniku zamocować soczewkę dwuwklęsłą – śrubę mocującą dokręcić z
wyczuciem! i zbliżyć maksymalnie do konika z soczewką dwuwypukłą.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

7

3.19.

Powtórzyć czynności pomiarowe z punktów od 3.14 do 3.15 dla tak powstałego układu
soczewek (koniki z soczewkami przesuwamy zawsze razem – koniki soczewek muszą
się zawsze ze sobą stykać w trakcie pomiarów).

3.20.

Wyniki pomiarów zanotować w tabeli – wzór tabeli do druku na końcu instrukcji.

C. Wyznaczenie ogniskowej przy pomocy sferometru.

3.21.

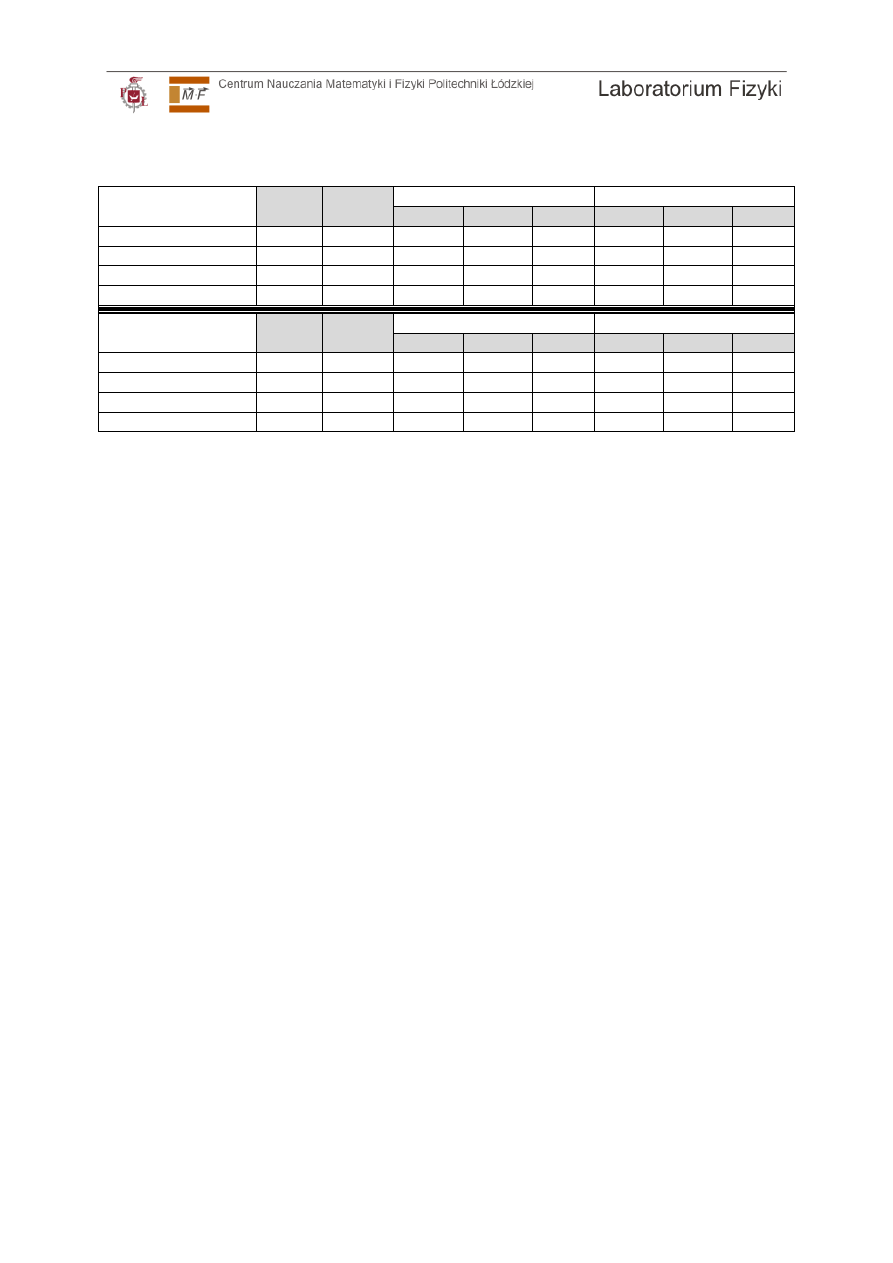
Przy pomocy suwmiarki zmierzyć trzykrotnie wewnętrzną średnicę podstawy sferome-
tru d. Pomiar powtórzyć trzykrotnie dla różnych średnic podstawy. Wyniki zanotować
w tabeli (wzór na końcu instrukcji). Analogiczny pomiar przeprowadzić dla średnicy
zewnętrznej podstawy sferometru D.

3.22.

Ustalić położenie zerowe sferometru h

0

, czyli ustawić sferometr na gładkiej płytce

szklanej i odczytać jego wskazanie.

3.23.

Ustawić sferometr na powierzchni badanej soczewki i odczytać jego wskazanie h

1

.

Różnica h=h

1

-h

0

jest wysokością czaszy, odciętej z danej powierzchni soczewki przez

podstawę sferometru. Pomiar powtórzyć trzykrotnie dla każdej ze stron soczewki. Jeśli
powierzchnia soczewki jest wklęsła to wartość h jest ujemna. Pomiary przeprowadzamy
dla badanych wcześniej soczewek. Wyniki pomiarów zapisać w odpowiedniej tabeli
(wzór na końcu instrukcji).

UWAGA!!! Pomiar wysokości czaszy można uprościć. Podczas ustalania położenia zerowego
sferometru można obrócić ruchomą tarczę sferometru tak, aby wskazówka pokazywała zero
na skali. Wtedy po przyłożeniu do powierzchni soczewki mamy od razu odczyt wielkości h.
Przy pomiarach należy zwrócić uwagę na małą tarczę pokazującą liczbę obrotów – dla du-
ż

ych wklęsłości bądź wypukłości wskazówka sferometru może wykonać więcej niż jeden pełny

obrót. Wskazania małej tarczy mogą mieć więc istotny wpływ na pomiar wysokości czaszy.

4.

O

PRACOWANIE WYNIKÓW

A. Wyznaczenie ogniskowej na podstawie wzoru soczewkowego.

4.1. Wyznacz ogniskową soczewki dwuwypukłej na podstawie wzoru (5) dla każdej z par

wielkości x i y.

4.2. Oblicz średnią wartość ogniskowej ( z 10 pomiarów), a następnie wyznacz jej błąd w

oparciu o metodę Studenta

.

4.3. Wynik zapisz w postaci

(

)

f

f

f

AS

∆

±

=

. Indeks

AS

oznacza ogniskową wyznaczoną na

podstawie wzoru soczewkowego dla soczewki skupiającej.

4.4. Analogiczne obliczenia wykonaj dla układu soczewek.

4.5.Wynik zapisz w postaci

(

)

f

f

f

AU

∆

±

=

. Indeks

AU

oznacza ogniskową wyznaczoną na

podstawie wzoru soczewkowego dla układu soczewek.

4.6.

Znając ogniskową soczewki skupiającej

AS

f

i ogniskową układu soczewek

AU

f

wyznacz

ogniskową soczewki dwuwklęsłej czyli rozpraszającej na podstawie wzoru (8).

WYZNACZANIE OGNISKOWEJ SOCZEWKI

8

4.7.Wynik zapisz w postaci

(

)

f

f

f

AR

∆

±

=

. Indeks

AR

oznacza ogniskową soczewki rozpra-

szającej. Błąd wartości ogniskowej soczewki rozpraszającej policz wykorzystując metodę róż-

niczki zupełnej na podstawie wzoru (8).

B. Wyznaczenie ogniskowej metodą Bessela.

4.8.

Wyznacz ogniskową soczewki dwuwypukłej na podstawie wzoru (6) dla każdej z wielkości b

i l.

4.9.Oblicz średnią wartość ogniskowej ( z 10 pomiarów), a następnie wyznacz jej błąd w

oparciu o metodę Studenta

.

4.10.

Wynik zapisz w postaci

(

)

f

f

f

BS

∆

±

=

. Indeks

BS

oznacza ogniskową wyznaczoną na

podstawie

metody Bessela dla soczewki skupiającej.

4.11.

Analogiczne obliczenia wykonaj dla układu soczewek.

4.12.

Wynik zapisz w postaci

(

)

f

f

f

BU

∆

±

=

. Indeks

BU

oznacza ogniskową wyznaczoną na

podstawie metody Bessela dla układu soczewek.

4.13.

Znając

ogniskową

soczewki

skupiającej

BS

f

i ogniskową układu soczewek

BU

f

wyznacz

ogniskową soczewki dwuwklęsłej czyli rozpraszającej na podstawie wzoru (8).

4.14.

Wynik zapisz w postaci

(

)

f

f

f

BR

∆

±

=

. Indeks

BR

oznacza ogniskową soczewki roz-

pra

s

zającej. Błąd wartości ogniskowej soczewki rozpraszającej policz wykorzystując metodę

różniczki zupełnej na podstawie wzoru (8).

C. Wyznaczenie ogniskowej przy pomocy sferometru.

4.15.

Wykorzystaj wzór (4a) i (4b) do policzenia promieni krzywizn powierzchni socze-

wek: dwuwypukłej i dwuwklęsłej.

4.16.

Na podstawie obliczonych promieni krzywizn obu stron każdej soczewki oblicz

ogniskową każdej z nich na podstawie wzoru (1). Przyjmij, że soczewki wykonane są ze

szkła o współczynniku załamania n=1,5.

4.17.

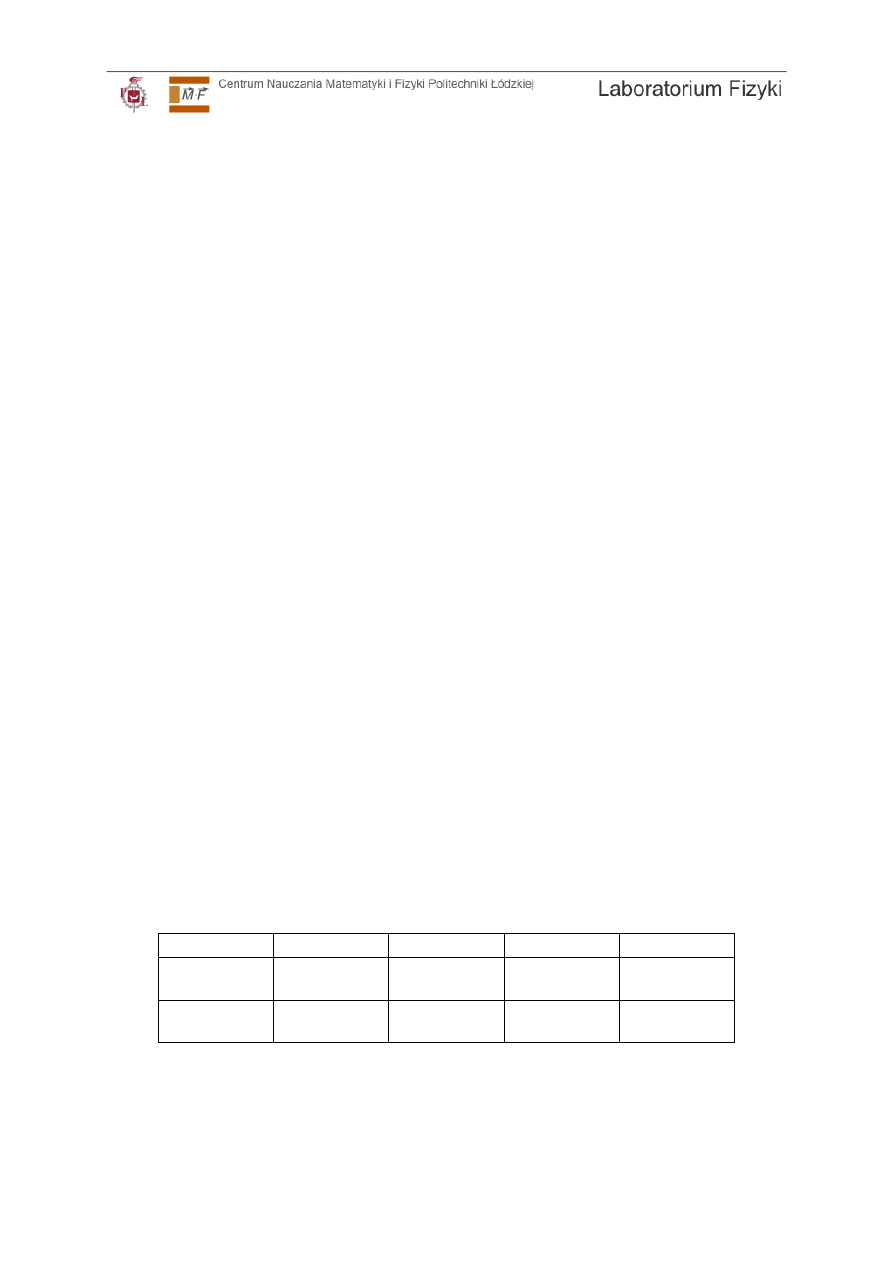
Wyniki zbierz w tabeli:

r

1

[m

]

r

2

[m

]

f [m]

oznaczenia

Soczewka

dwuwypukła

f

CS

Soczewka

dwuwklęsła

f

CR

4.18.

Mając ogniskową soczewki skupiającej f

CS

i rozpraszającej f

CR

oblicz ogniskową

układu tych soczewek f

CU

na podstawie wzoru (7) przyjmując m=0.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

9

4.19.

Zbierz w tabeli wyniki z części A, B i C. Porównaj otrzymane wyniki. Wyciągnij

wnioski.

f [m]

metoda

A

B

C

Soczewka

dwuwypukła

AS

f

=

BS

f

=

CS

f

=

Soczewka

dwuwklęsła

AR

f

=

BR

f

=

CR

f

=

Układ

soczewek

AU

f

=

BU

f

=

CU

f

=

5.

Z

AKRES MATERIAŁU

Prostoliniowy bieg światła, odbicie i załamanie światła, odwracalność biegu promienia,
soczewki, powstawanie obrazów w soczewkach, układy soczewek, wyznaczanie ogniskowej
soczewki, wady soczewek i sposoby ich redukcji.

L

ITERATURA

[1]

Wstęp do analizy matematycznej i wybranych zagadnień z fizyki, pod redakcją A.Justa,
Wydawnictwo PŁ, Łódź 2007.

[2]

Podstawy Fizyki, D.Halliday, R. Resnick i J. Walker. T.4, PWN 2007.

[3]

Optyka, A.Sojecki, WSiP, W-wa 1997.

WYZNACZANIE OGNISKOWEJ SOCZEWKI

10

A. Metoda wzoru soczewkowego

x [m]

∆∆∆∆

x [m]

y [m]

∆∆∆∆

y [m]

Soczewka
dwuwypukła

x [m]

∆∆∆∆

x [m]

y [m]

∆∆∆∆

y [m]

m[m]

∆∆∆∆

m [m]

Układ
soczewek

B. Wyznaczenie ogniskowej metodą Bessela

s

1

[m]

s

2

[m]

b=s

1

-s

2

[m]

∆∆∆∆

b [m]

l [m]

∆∆∆∆

l [m]

Soczewka
dwuwypukła

s

1

[m]

s

2

[m]

b=s

1

-s

2

[m]

∆∆∆∆

b [m]

l [m]

∆∆∆∆

l [m]

Układ
soczewek

WYZNACZANIE OGNISKOWEJ SOCZEWKI

11

C. Wyznaczenie ogniskowej przy pomocy sferometru.

Soczewka
dwuwypukła

d [m]

∆∆∆∆

d [m]

Powierzchnia 1

Powierzchnia 2

h

0

[m]

h

1

[m]

h[m]

h

0

[m]

h

1

[m]

h[m]

Pomiar 1

Pomiar 2

Pomiar 3

Wartość średnia

Soczewka
dwuwklęsła

D [m]

∆∆∆∆

D [m]

Powierzchnia 1

Powierzchnia 2

h

0

[m]

h

1

[m]

h[m]

h

0

[m]

h

1

[m]

h[m]

Pomiar 1

Pomiar 2

Pomiar 3

Wartość średnia