KONSTRUKCJE METALOWE II

dr inż. Jacek Tasarek

Politechnika Poznańska

Wydział Budownictwa i Inżynierii Środowiska

Instytut Konstrukcji Budowlanych

2

3

4

5

6

7

8

9

10

11

1.ELEMENTY ZGINANE - BELKI

Rozróżnia się kilka kryteriów podziału:

ze względu na schemat statyczny:

swobodnie podparte - najczęściej stosowane z uwagi na brak wpływu

temperatury i osiadania podpór, a także dogodny montaż. Niestety są

one mało ekonomiczne ze względu na duży przekrój, a więc masę w

porównaniu z belkami ciągłymi;

porównaniu z belkami ciągłymi;

ciągłe - mniejszy przekrój, a więc lżejsze, mają mniejsze ugięcia, są

jednak trudniejsze w montażu ze względu na pracochłonne styki

montażowe;

gerberowskie (przegubowe) – stosowane w płatwiach i mostownictwie;

łatwe w montażu o przekroju jak belki swobodnie podparte

12

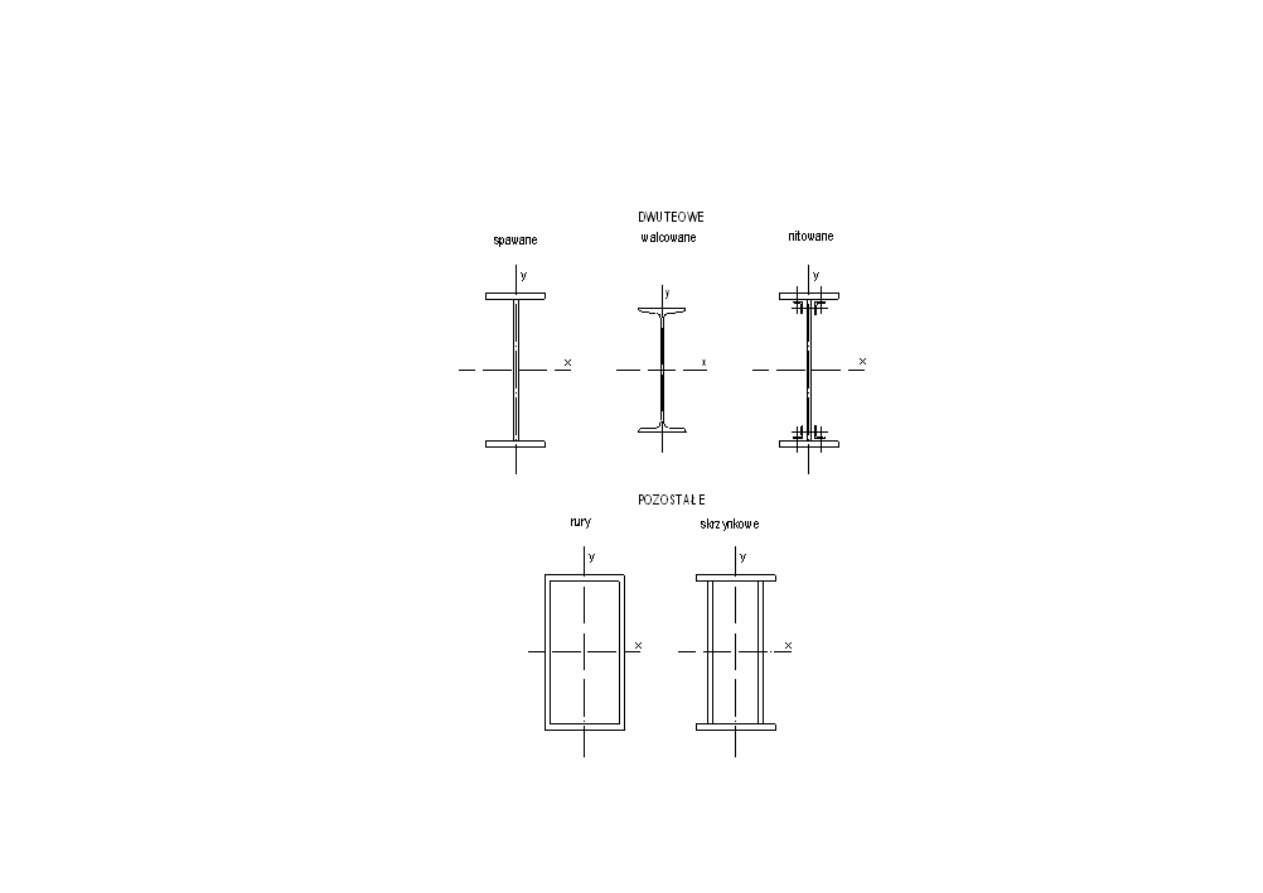
ze względu na przekrój poprzeczny

:

bisymetryczne

– środek ścinania pokrywa się ze środkiem ciężkości

13

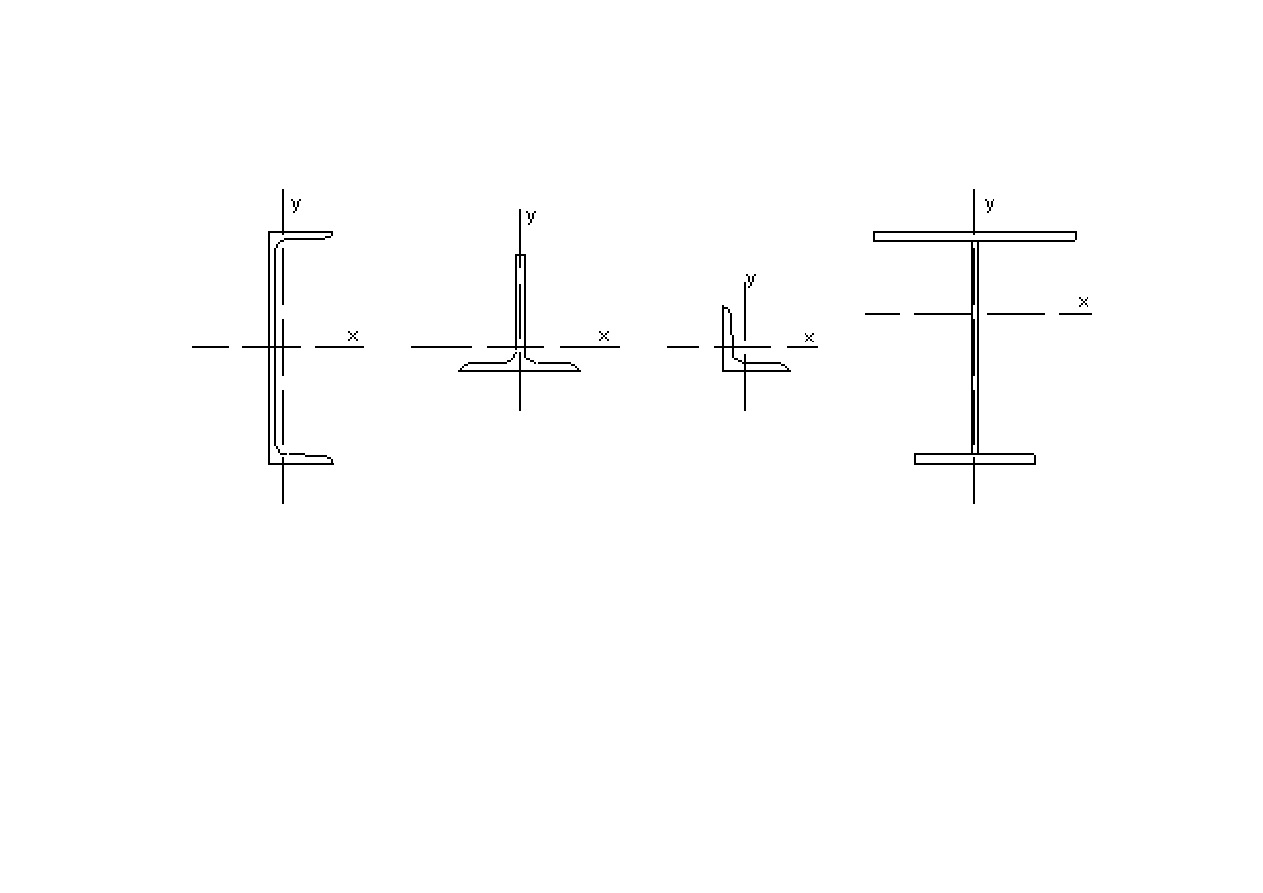
monosymetryczne środek ścinania nie pokrywa się ze środkiem
ciężkości- może wystąpić dodatkowe skręcanie od siły
poprzecznej

14

x

y

y

x

x

y

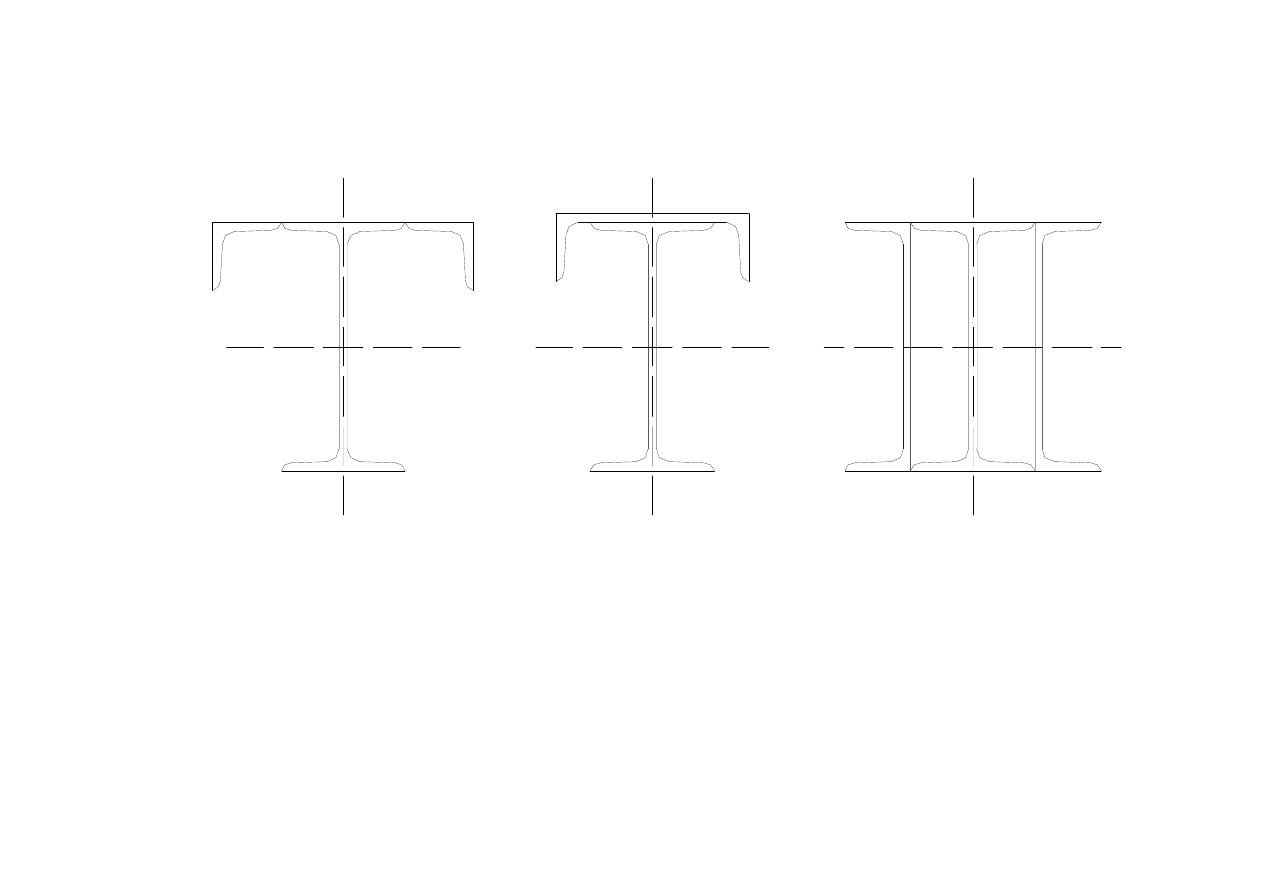
złożone

15

Specjalne

x

y

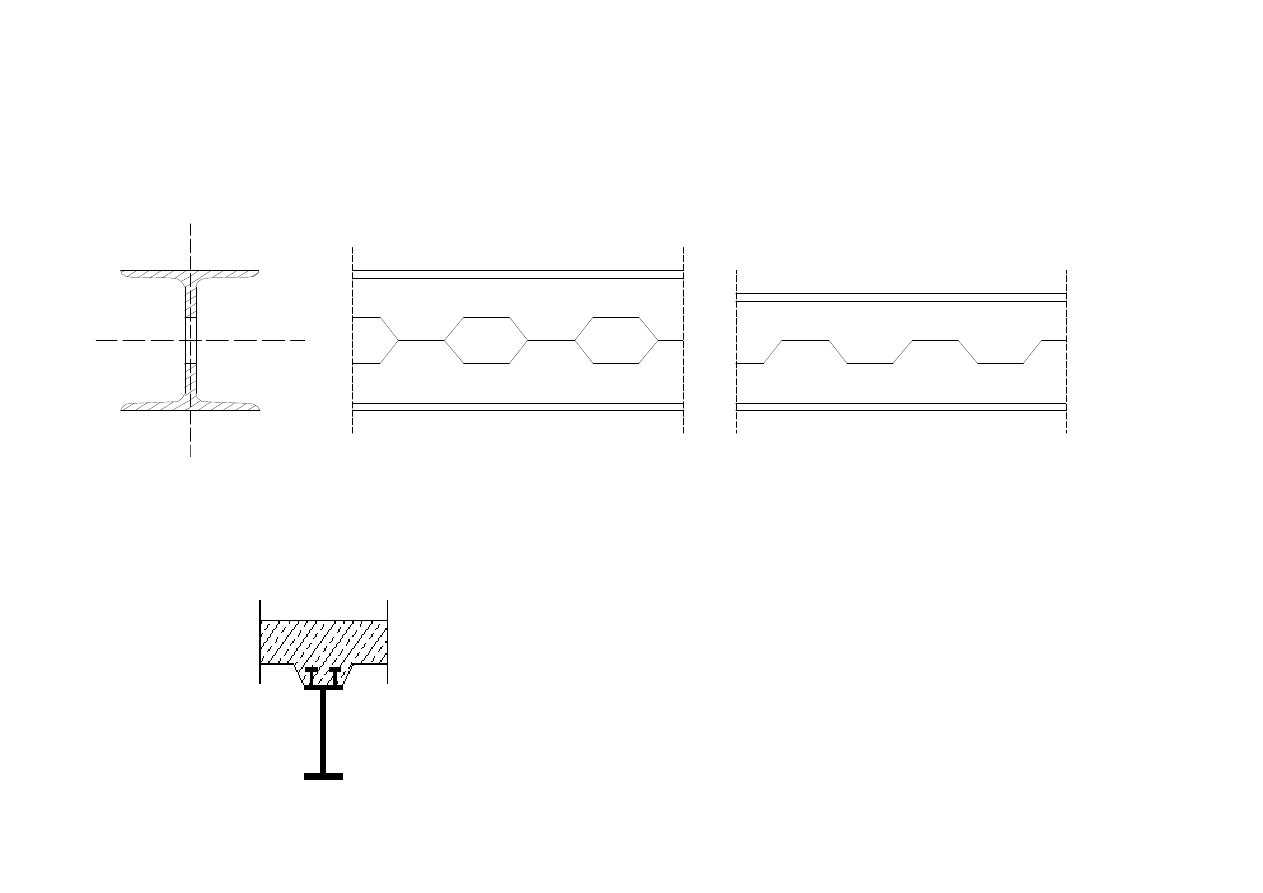
Belki ażurowe.

16

Belki zespolone stalowo żelbetowe

17

Belki z kształtowników zimnogiętych.

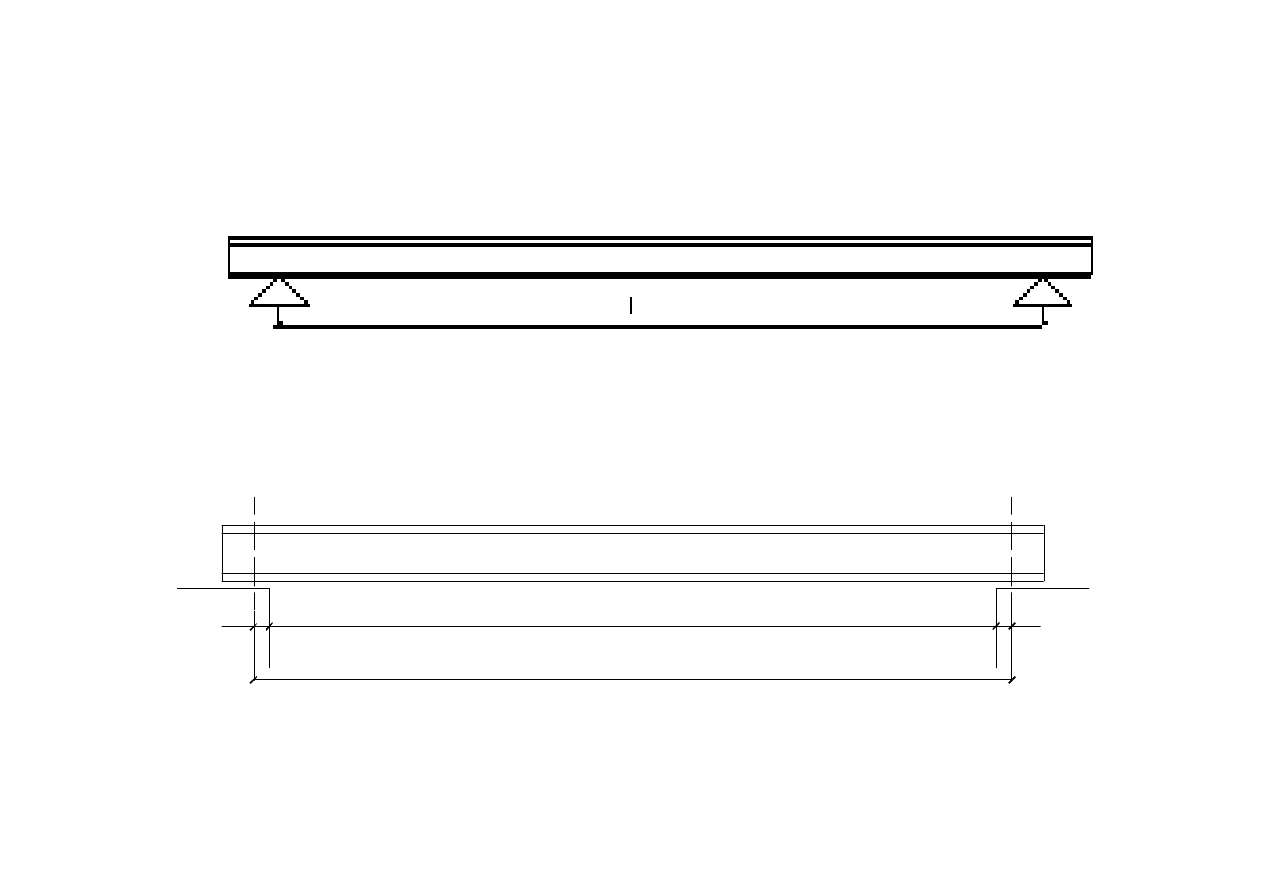
Rozpiętości obliczeniowe belek

Rozpiętość obliczeniowa belki opartej na łożyskach.

l

o

= l

2,5%·l

l

o

=l+2·0,025·l

l

2,5%·l

Rozpiętość obliczeniowa belek opartych na murze

18

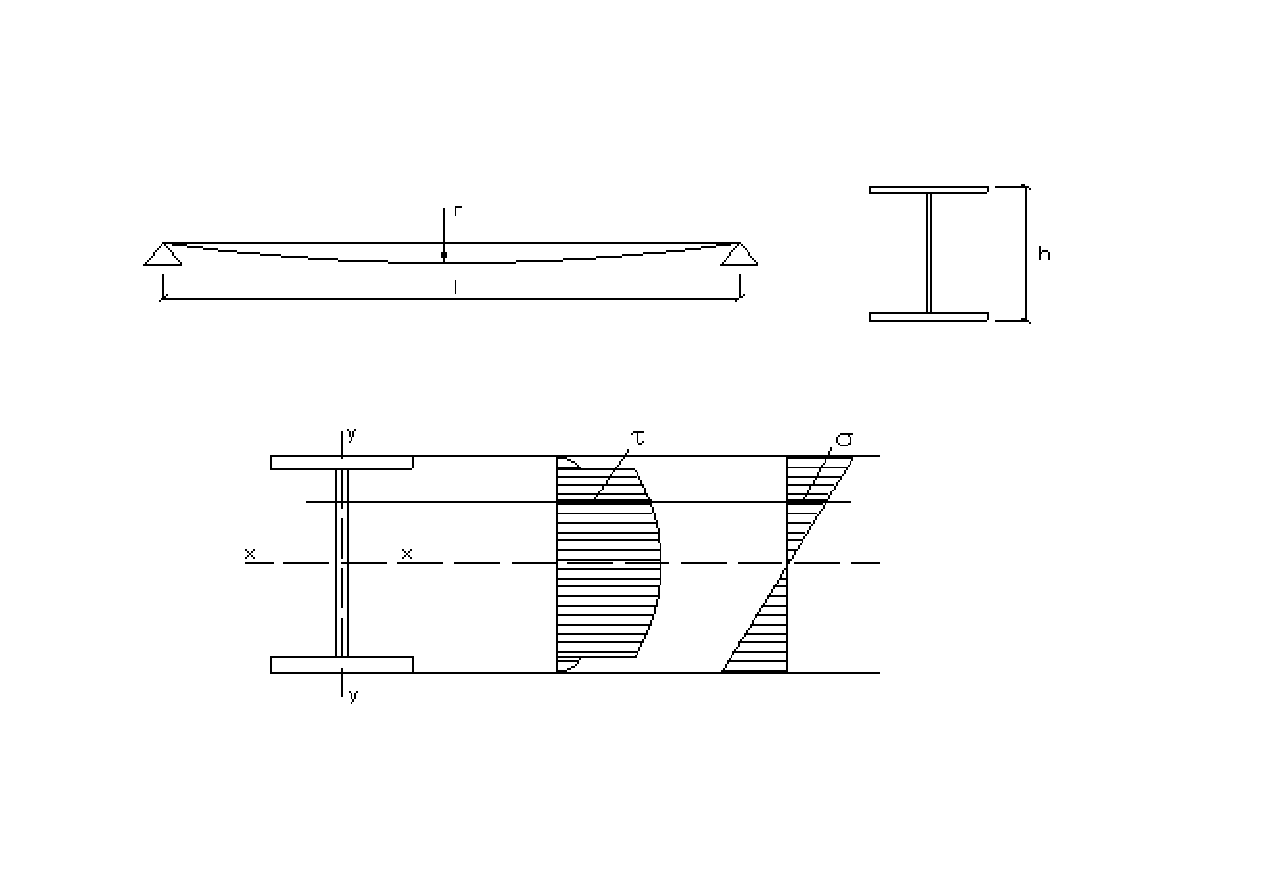
Zginanie belek w jednej płaszczyźnie.

Rozkład naprężeń w przekroju belki

zginanej

19

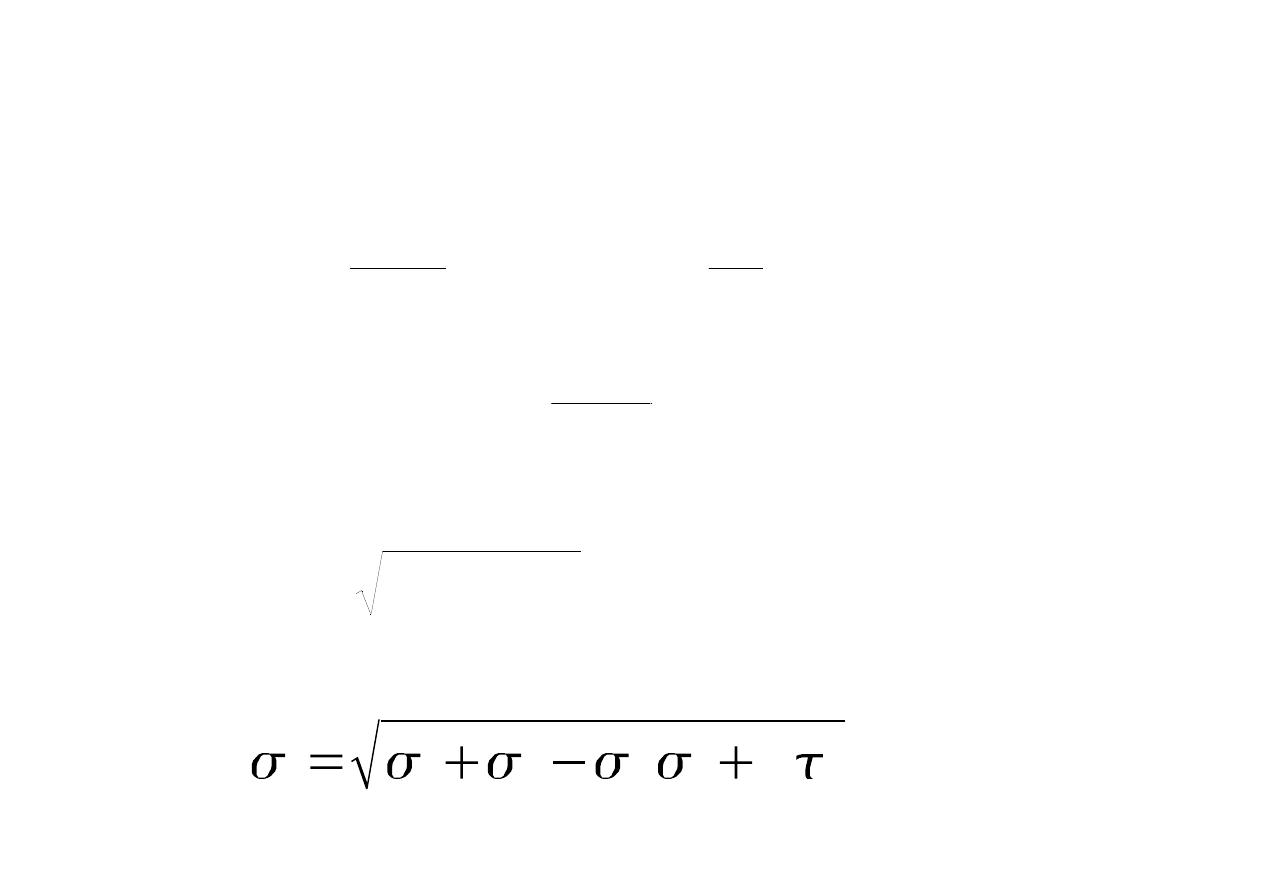
Naprężenia w przekroju

•

zginanie

x

I

y

M

⋅

=

σ

x

W

M

=

max

σ

•

ścinanie

t

I

S

Q

x

x

⋅

⋅

=

τ

t

I

x

⋅

•

zginanie ze ścinaniem dwuosiowy stan naprężeń :

2

2

3

τ

σ

σ

⋅

+

=

z

z

x

2

y

2

x

y

3

2

•

zginanie ze ścinaniem płaski stan naprężeń :

20

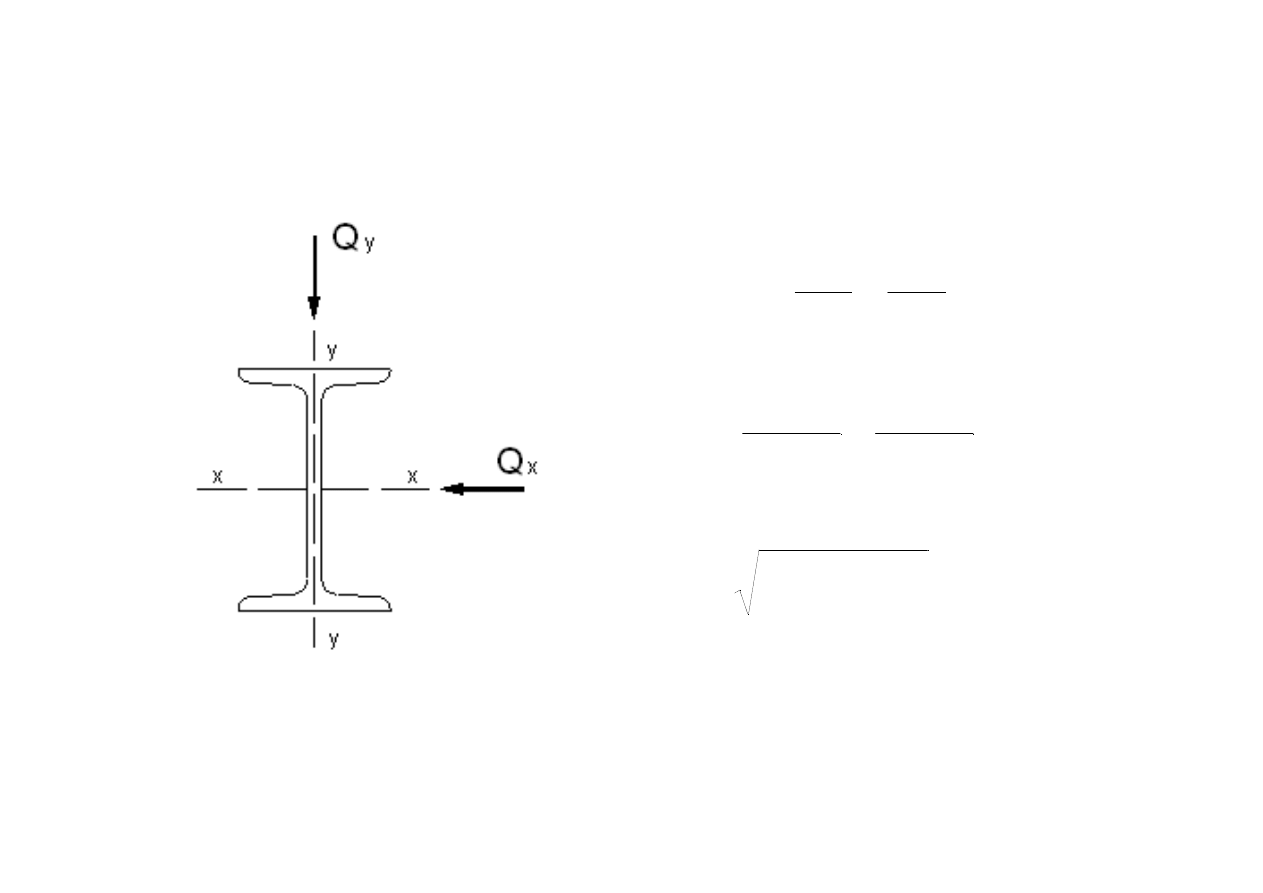
Zginanie belek w dwóch płaszczyznach – przekroje symetryczne.

obciążenie w osiach głównych

y

y

x

x

W

M

W

M

+

=

σ

y

x

x

y

b

I

S

Q

b

I

S

Q

⋅

⋅

+

⋅

⋅

=

τ

y

y

x

x

b

I

b

I

⋅

+

⋅

=

τ

2

2

3

τ

σ

σ

⋅

+

=

z

21

Ogólny warunek no

ś

no

ś

ci belki zginanej w jednej

płaszczy

ź

nie ma posta

ć

:

M

φ

L

M

R

≤ 1,0

gdzie:
M- maksymalny moment w prz

ęś

le belki okre

ś

lany

ze statyki,

22

ze statyki,

M

R

- no

ś

no

ść

belki na zginanie.

φ

L

- współczynnik niestateczno

ś

ci ogólnej przy

zginaniu ( zwichrzenie)

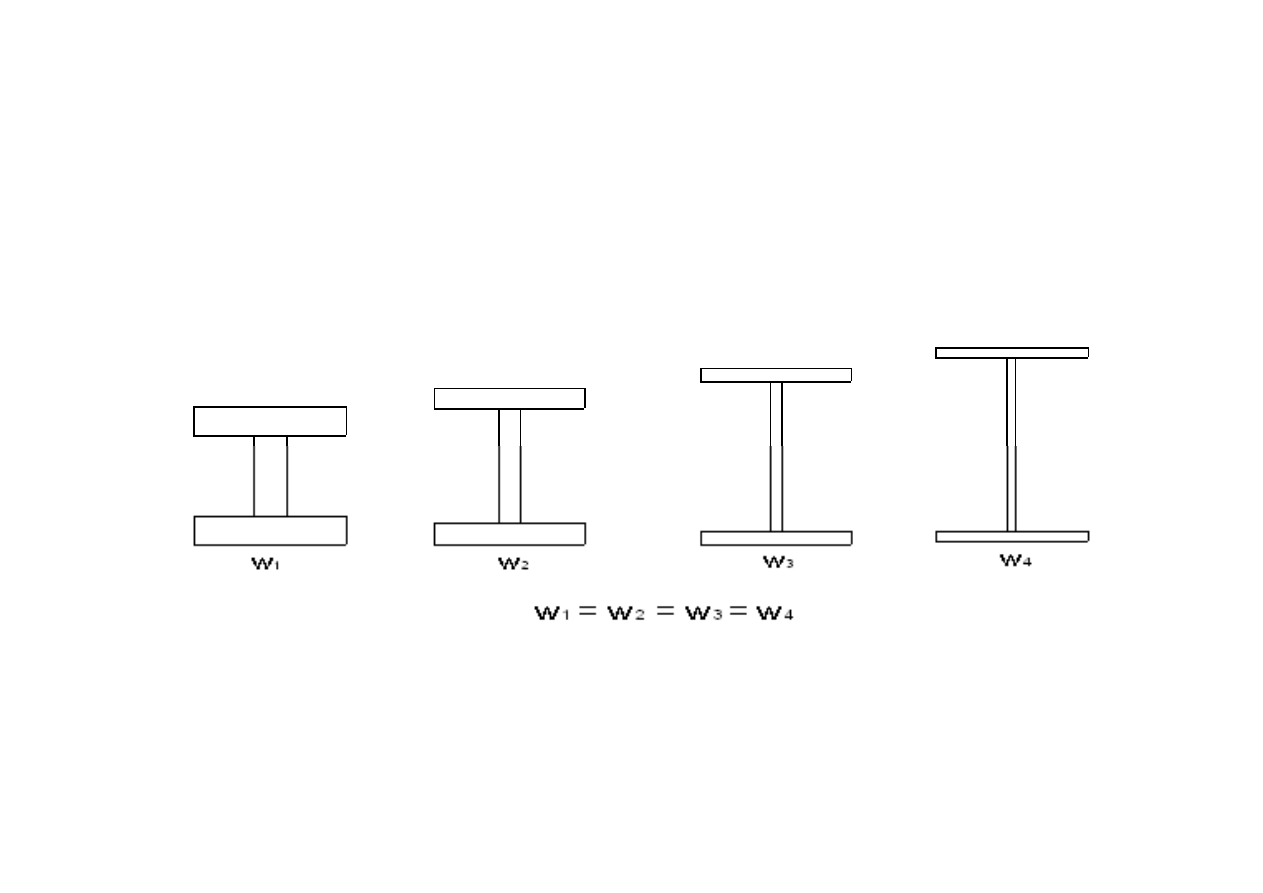
KLASYFIKACJA PRZEKROJÓW ELEMENTÓW

Ś

CISKANYCH

I ZGINANYCH.

Parametry geometryczne

przekroju a jego

nośność

.

Przekroje belek o ró

ż

nych proporcjach

ś

cianek i równym wska

ź

niku

wytrzymało

ś

ci W.

23

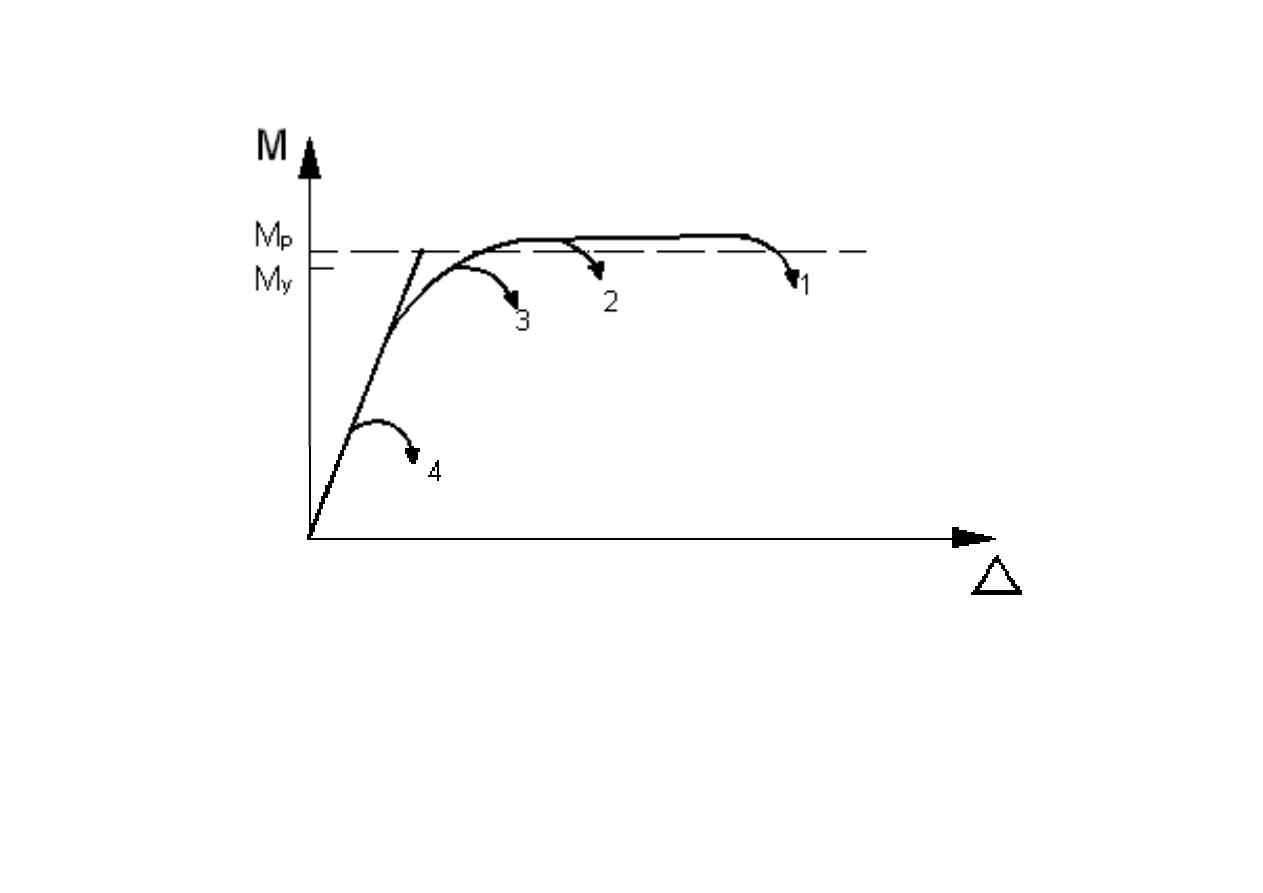
No

ś

no

ść

belki zginanej M wzgl

ę

dem ugi

ę

cia

∆

.

M

p

– no

ś

no

ść

w stanie plastycznym;

M

y

– no

ś

no

ść

w stanie spr

ęż

ystym;

∆

– strzałka ugi

ę

cia belki

24

KLASA 1 – przekroje mog

ą

osi

ą

gn

ąć

no

ś

no

ść

pełnego przegubu

plastycznego, istnieje mo

ż

liwo

ść

nieograniczonego obrotu;

KLASA 2 – przekroje mog

ą

osi

ą

gn

ąć

no

ś

no

ść

pełnego przegubu

plastycznego, jednak

ż

e obrót jest ograniczony niestateczno

ś

ci

ą

plastyczn

ą

;

KLASA 3 – no

ś

no

ść

przekroju ograniczona jest pocz

ą

tkiem

KLASA 3 – no

ś

no

ść

przekroju ograniczona jest pocz

ą

tkiem

uplastycznienia strefy

Ś

ciskanej,

σ

c

= f

d

KLASA 4 – no

ś

no

ść

przekroju ograniczona jest utrat

ą

stateczno

ść

lokalnej conajmniej jednej

ś

cianki przekroju znajduj

ą

cej si

ę

w strefie

ś

ciskanej,

σ

c

<f

d

;

25

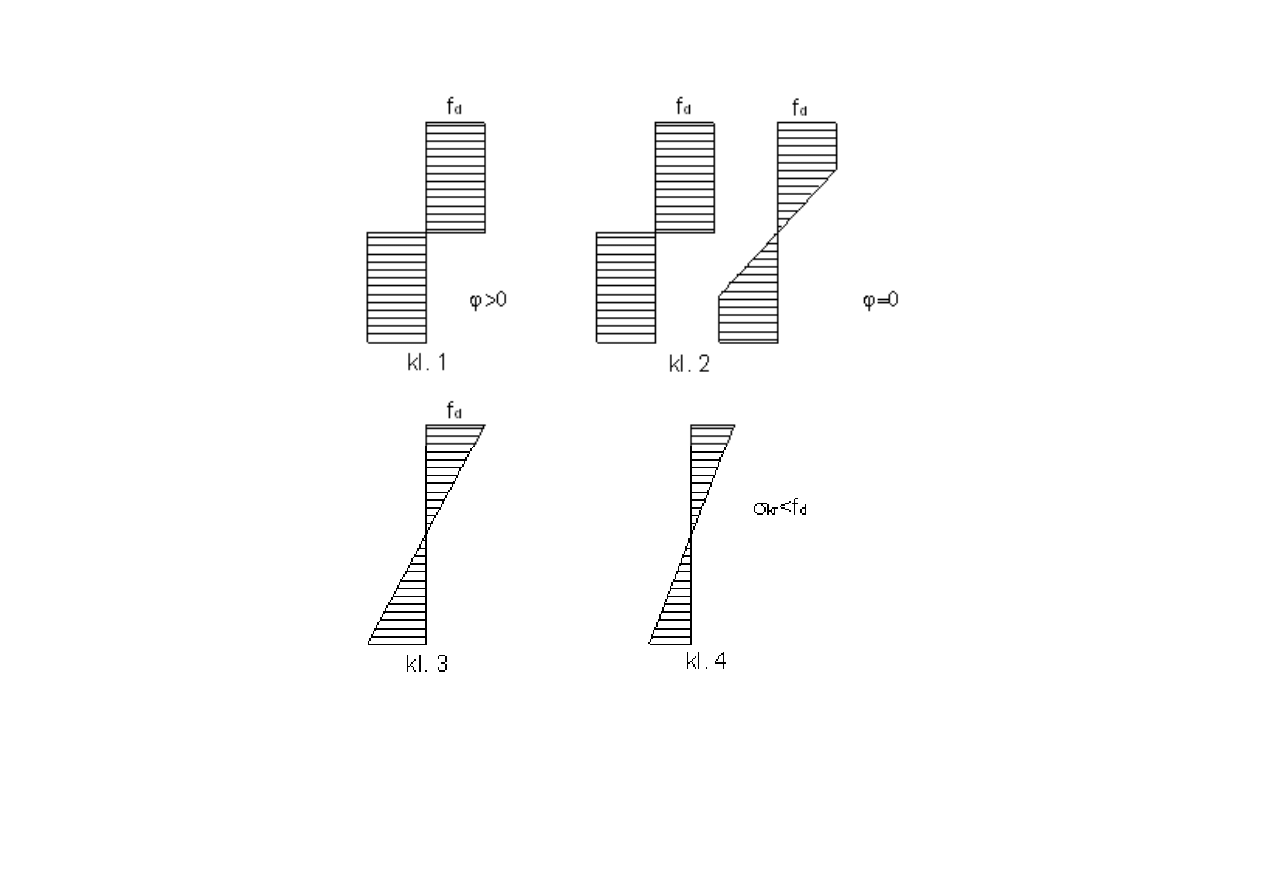
Wykresy napr

ęż

e

ń

normalnych

σ

w przekrojach belek w granicznym

stanie obci

ąż

enia momentem zginaj

ą

cym

.

26