1

15. Energia, pęd, kręt w ruchu ciała sztywnego.

Równoważność energii i pracy.

Twierdzenie Koeniga

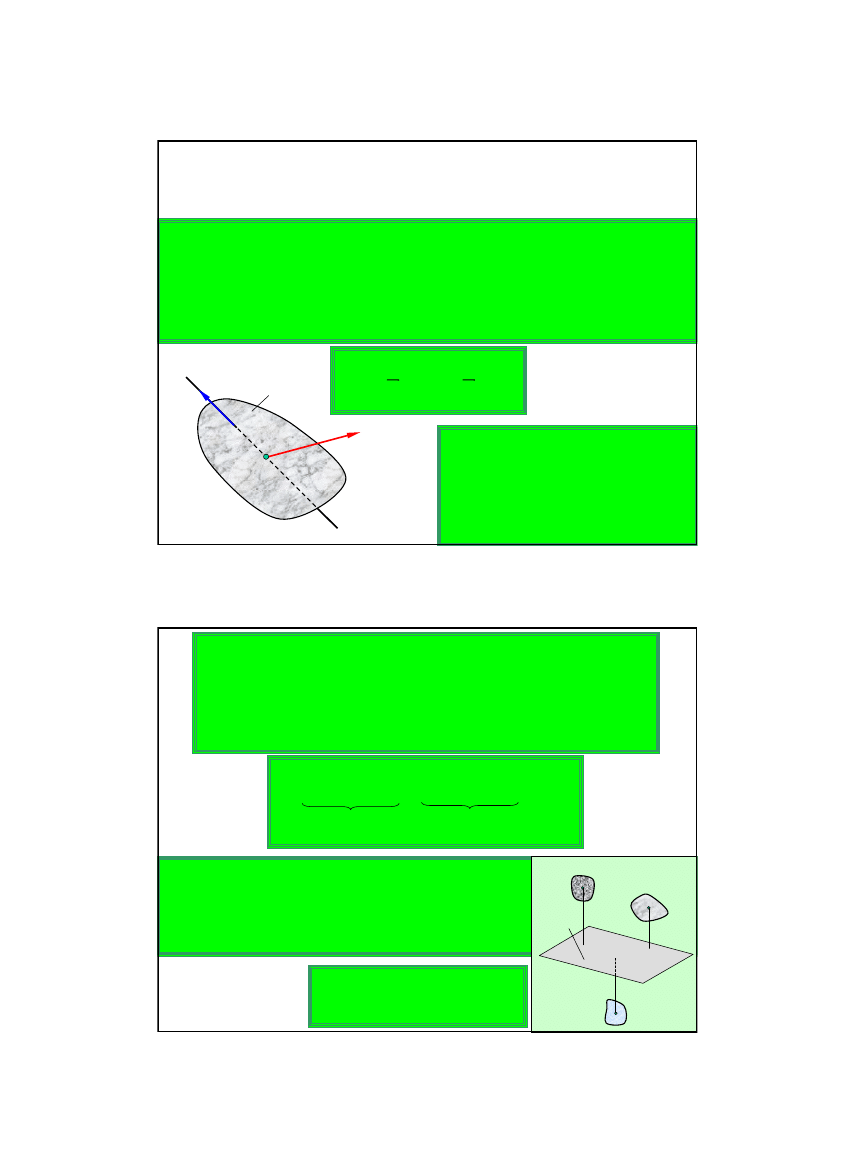
Energia kinetyczna

ciała sztywnego

równa jest sumie

energii kinetycznej ruchu postępowego z prędkością środka masy

i

energii ruchu obrotowego wokół osi przechodzącej przez środek

masy.

2

2

2

1

2

1

ω

υ

l

k

J

m

E

+

=

m

– masa ciała

J

l

– moment bezwładności

względem osi obrotu

Energia kinetyczna

układu ciał sztywnych

równa jest

sumie energii kinetycznych

poszczególnych ciał.

l

ω

ω

ω

ω

υ

υ

υ

υ

m

c

Przyrost energii mechanicznej

układu ciał sztywnych w skończonym przedziale czasu

równy jest

sumie prac sił zewnętrznych niepotencjalnych

działających układ.

( )

( )

(

)

( )

( )

(

)

( )

( )

1

2

2

,

1

1

1

2

2

m

m

p

k

p

k

E

E

W

E

E

E

E

=

+

−

+

Energia potencjalna układu znajdującego się w polu grawitacyjnym

równa jest

sumie iloczynów ciężarów poszczególnych ciał

i wzniesienia ich środków masy ponad dowolnie obrany poziom.

∑

∑

=

=

=

=

n

i

i

i

n

i

i

i

p

gh

m

h

Q

E

1

1

m

1

h

i

h

1

m

n

m

i

h

n

E

p

=0

2

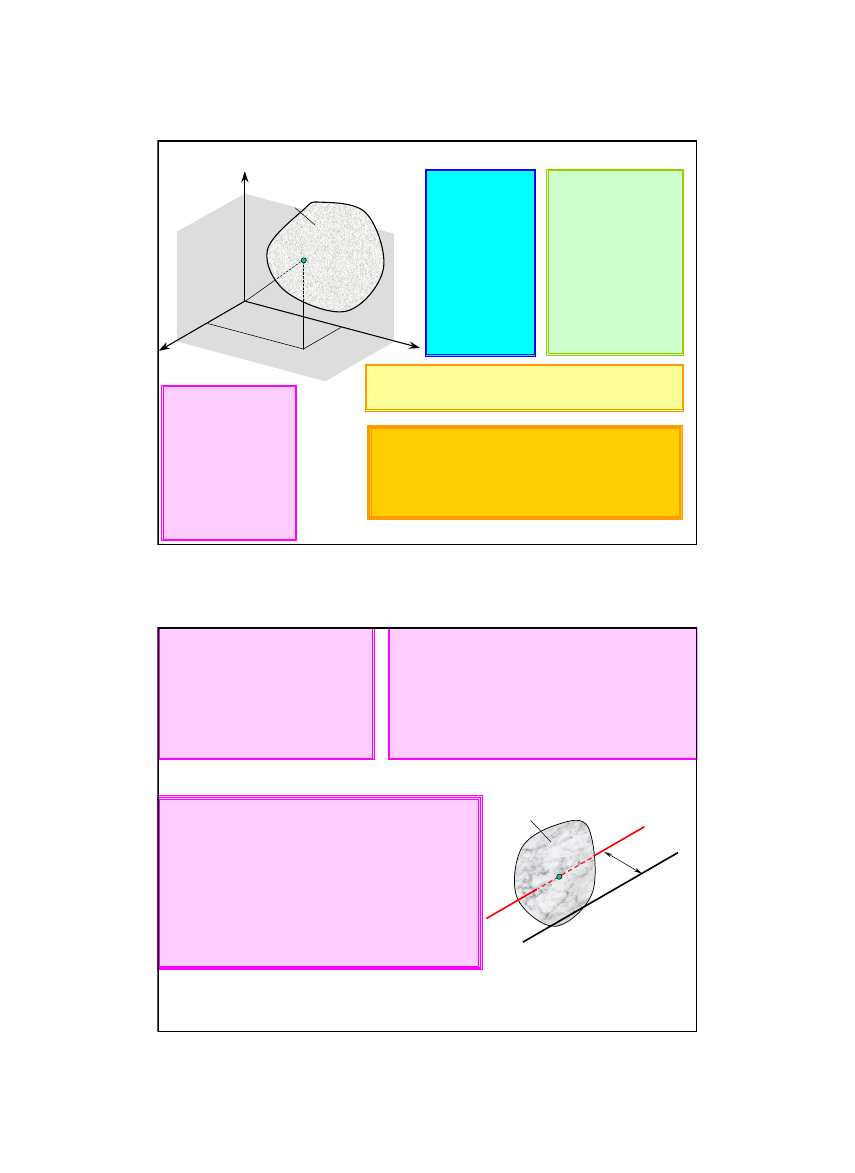
Momenty bezwładności

x

y

z

O

dm

m

y

x

z

r

π

1

π

2

π

3

względem
płaszczyzn

∫

∫

∫

=

=

=

m

m

m

dm

x

J

dm

y

J

dm

z

J

2

2

2

3

2

1

π

π

π

względem

osi

(

)

(

)

(

)

dm

y

x

J

dm

z

x

J

dm

z

y

J

m

z

m

y

m

x

∫

∫

∫

+

=

+

=

+

=

2

2

2

2

2

2

biegunowy

(

)

∫

∫

+

+

=

=

m

m

O

dm

z

y

x

dm

r

J

2

2

2

2

dewiacji

∫

∫

∫

=

=

=

=

=

=

m

xz

zx

m

zy

yz

m

yx

xy

zxdm

J

J

yzdm

J

J

xydm

J

J

[ ]





















−

−

−

−

−

−

=

z

zy

zx

yz

y

yx

xz

xy

x

J

J

J

J

J

J

J

J

J

J

macierz
momentów
bezwładności

Twierdzenie Steinera

Moment bezwładności ciała materialnego względem

dowolnej osi równy jest

sumie momentu bezwładności względem osi

równoległej przechodzącej przez środek masy

oraz

iloczynu masy ciała i kwadratu odległości między

tymi dwiema osiami.

J

l

=J

lc

+mh

2

3

2

3

1

2

1

π

π

π

π

π

π

J

J

J

J

J

J

J

J

J

z

y

x

+

=

+

=

+

=

moment bezwładności względem
osi równy jest sumie momentów
bezwładności względem
wzajemnie prostopadłych
płaszczyzn przecinających się
wzdłuż tej osi

biegunowy moment bezwładności
równy jest sumie momentów
bezwładności względem trzech
wzajemnie prostopadłych płaszczyzn
przecinających się w biegunie

1

2

3

π

π

π

J

J

J

J

O

+

+

=

c

lc

l

h

m

3

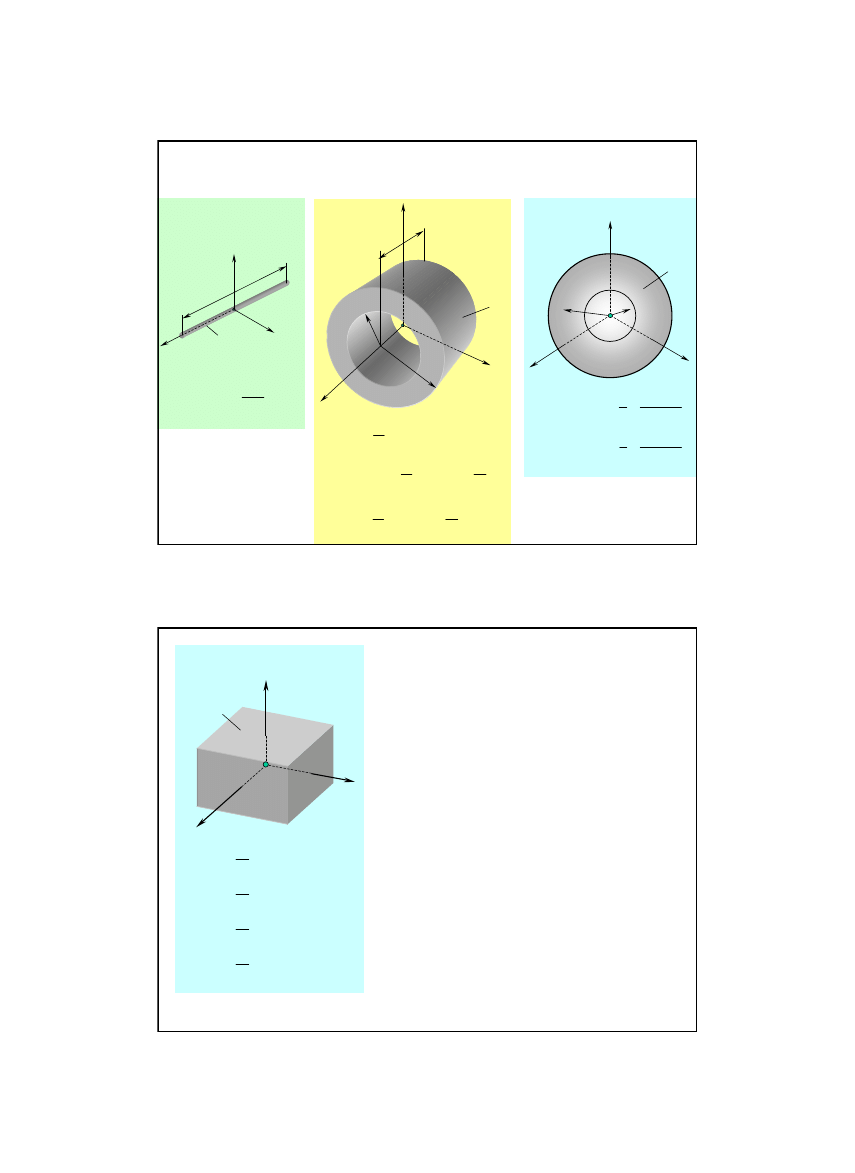
Momenty bezwładności wybranych brył jednorodnych

względem osi centralnych

c

x

y

z

l

m

cienki pręt

12

0

2

ml

J

J

J

z

y

x

=

=

=

z

y

x

c

r

R

l

m

cylinder

(

)















+

+

=















+

+

=

=

+

=

6

2

3

4

2

2

2

2

2

2

2

2

2

l

r

R

m

J

l

r

R

m

J

J

r

R

m

J

c

z

y

x

kula drążona

3

3

5

5

3

3

5

5

5

3

5

2

r

R

r

R

m

J

r

R

r

R

m

J

J

J

c

z

y

x

−

−

=

−

−

=

=

=

c

R

z

x

y

m

r

prostopadłościan

x

y

z

c

a

b

c

(

)

(

)

(

)

(

)

2

2

2

2

2

2

2

2

2

12

12

12

12

c

b

a

m

J

b

a

m

J

c

a

m

J

c

b

m

J

c

z

y

x

+

+

=

+

=

+

=

+

=

m

4

υ

υ

υ

υ

m

c

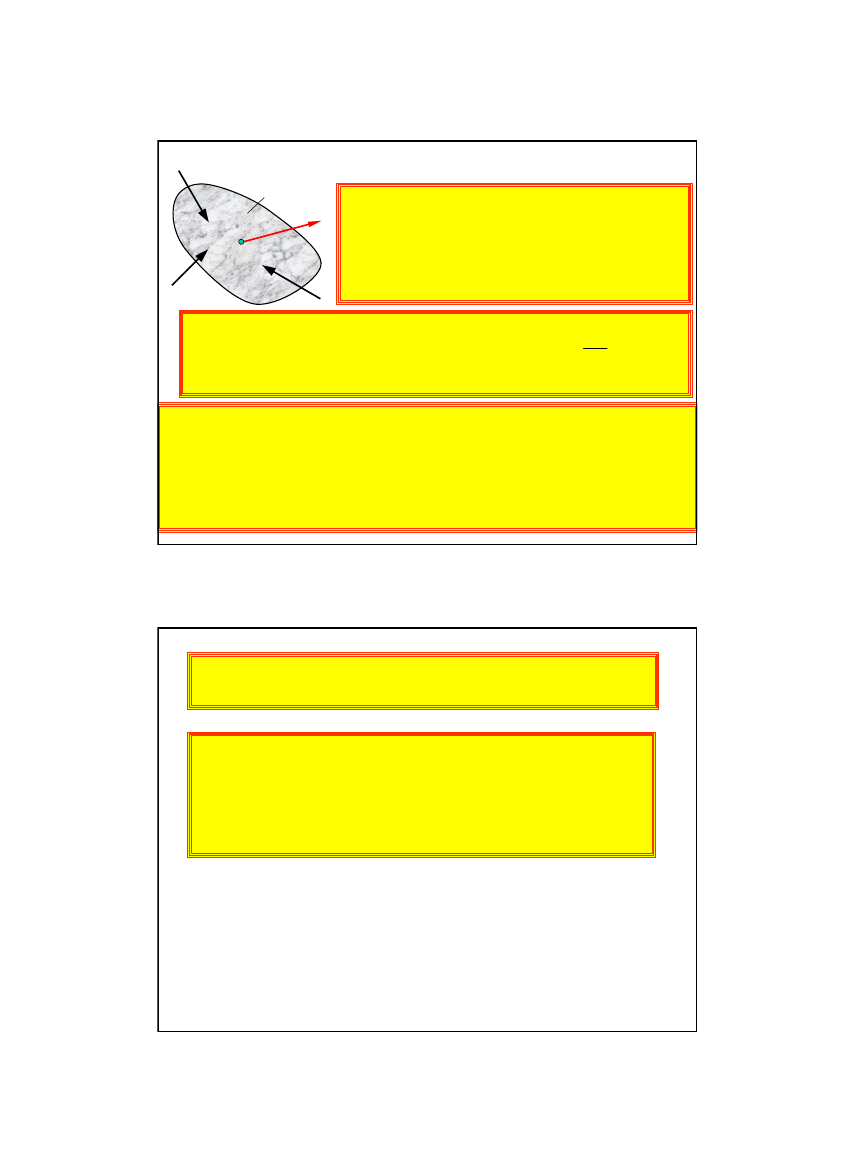
Pęd ciała sztywnego i układu ciał

Pęd ciała sztywnego równy jest iloczynowi

masy ciała

i prędkości jego środka masy

υ

r

r

m

p

=

Pochodna względem czasu pędu ciała sztywnego
równa jest sumie wszystkich sił zewnętrznych
działających na to ciało.

∑

=

=

n

i

i

F

dt

p

d

1

r

r

F

i

F

1

F

n

Przyrost pędu ciała sztywnego w skończonym przedziale czasu

równy jest sumie impulsów sił zewnętrznych działających na ciało.

(

)

∑ ∫

=

=

−

n

i

t

t

i

dt

F

m

1

1

2

2

1

r

r

r

υ

υ

Pęd układu ciał sztywnych równy jest iloczynowi

masy całkowitej układu i prędkości środka masy układu.

Twierdzenie o ruchu środka masy

Środek masy układu porusza się tak,

jakby w tym punkcie skupiona była cała masa układu

i jakby do tego punktu przyłożone były

wszystkie siły zewnętrzne.

5

c

m

l

ω

ω

ω

ω

Kręt ciała materialnego względem osi obrotu

równy jest iloczynowi

momentu bezwładności względem osi obrotu

i prędkości kątowej ciała.

ω

r

r

l

l

J

K

=

Kręt ciała sztywnego i układu ciał

x

y

z

m

c

ω

ω

ω

ω

[ ]





















=









































−

−

−

−

−

−

=

z

y

x

z

y

x

z

zy

zx

yz

y

yx

xz

xy

x

K

K

K

J

J

J

J

J

J

J

J

J

K

ω

ω

ω

Kręt ciała materialnego

względem środka masy

x

y

z

O

c

m

r

m

υ

υ

υ

υ

K

c

Kręt ciała materialnego względem

dowolnego bieguna O równy jest

sumie krętu względem środka

masy c oraz momentu względem

bieguna O wektora pędu

przyłożonego w środku masy

rozpatrywanego ciała.

υ

r

r

r

r

m

r

K

K

c

O

×

+

=

Pochodna względem czasu krętu układu

ciał materialnych względem środka masy

układu równa jest sumie momentów

wszystkich sił zewnętrznych względem

tegoż środka.

∑

=

=

n

i

ci

c

M

dt

K

d

1

r

r

6

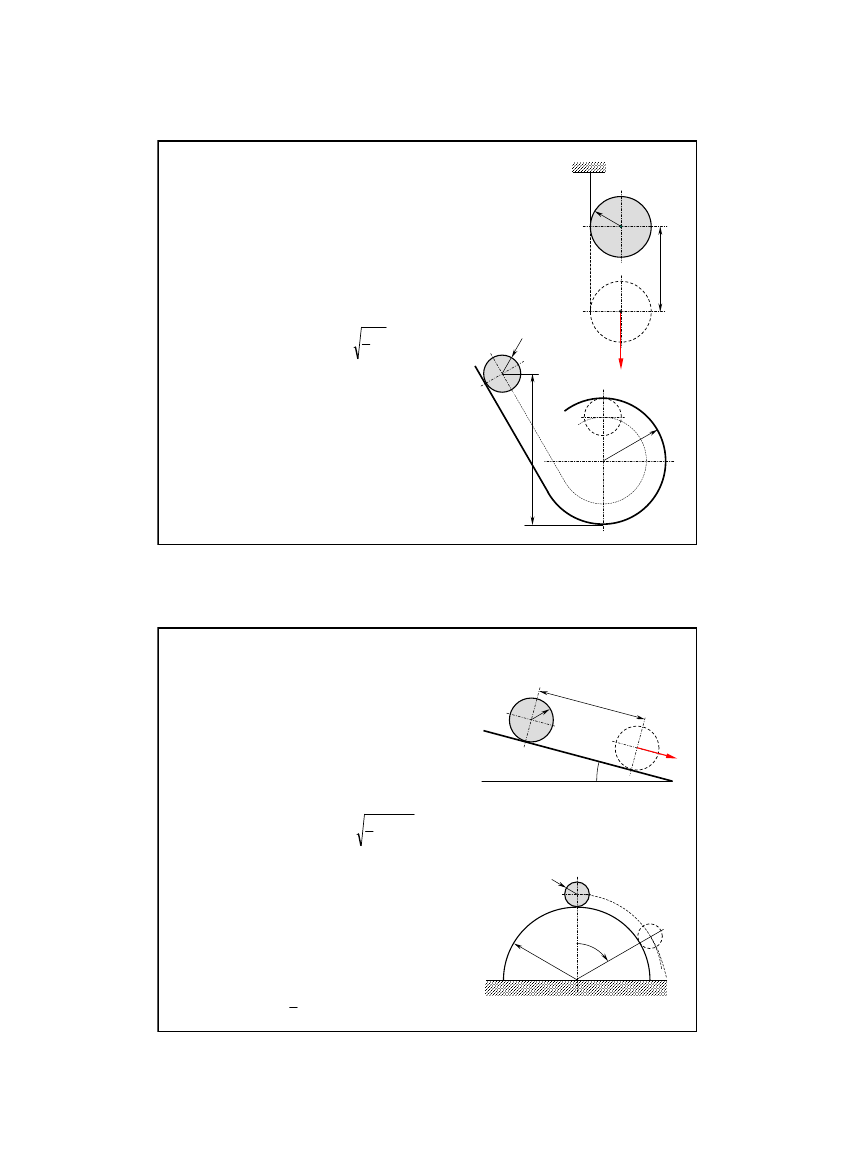
Zadanie 1/15
Jednorodny krążek o masie m i promieniu r
puszczono bez prędkości początkowej pozwalając mu
odwijać się z pionowo przebiegającej, nieważkiej nici.
Jaką prędkość υ uzyska środek O krążka po przebyciu
wysokość h?

h

r

m

υ

O

O

Zadanie 2/15
Z jakiej co najmniej wysokości h należy
puścić jednorodny wałek o masie m i
promieniu r aby, tocząc się bez poślizgu,
nie oderwał się w najwyższym punkcie
toru o promieniu R?

R

r

m

h

Odp.:

gh

3

4

=

υ

Zadanie 3/15
Jednorodny walec o masie m i
promieniu r, puszczony bez prędkości
początkowej, stacza się bez poślizgu po
równi nachylonej pod kątem α.
Jaką prędkość υ uzyska środek walca po
przebyciu drogi l?

α

r

m

l

υ

Zadanie 4/15
Z wierzchołka półwalca o promieniu R
stacza się bez poślizgu z pomijalnie małą
prędkością początkową jednorodny wałek
o masie m i promieniu r.
Przy jakim kącie α

0

wałek oderwie się od

półwalca?

R

r

m

α

0

Odp.:

o

2

.

55

7

4

arccos

0

≅

=

α

Odp.:

α

υ

sin

3

4

gl

=

7

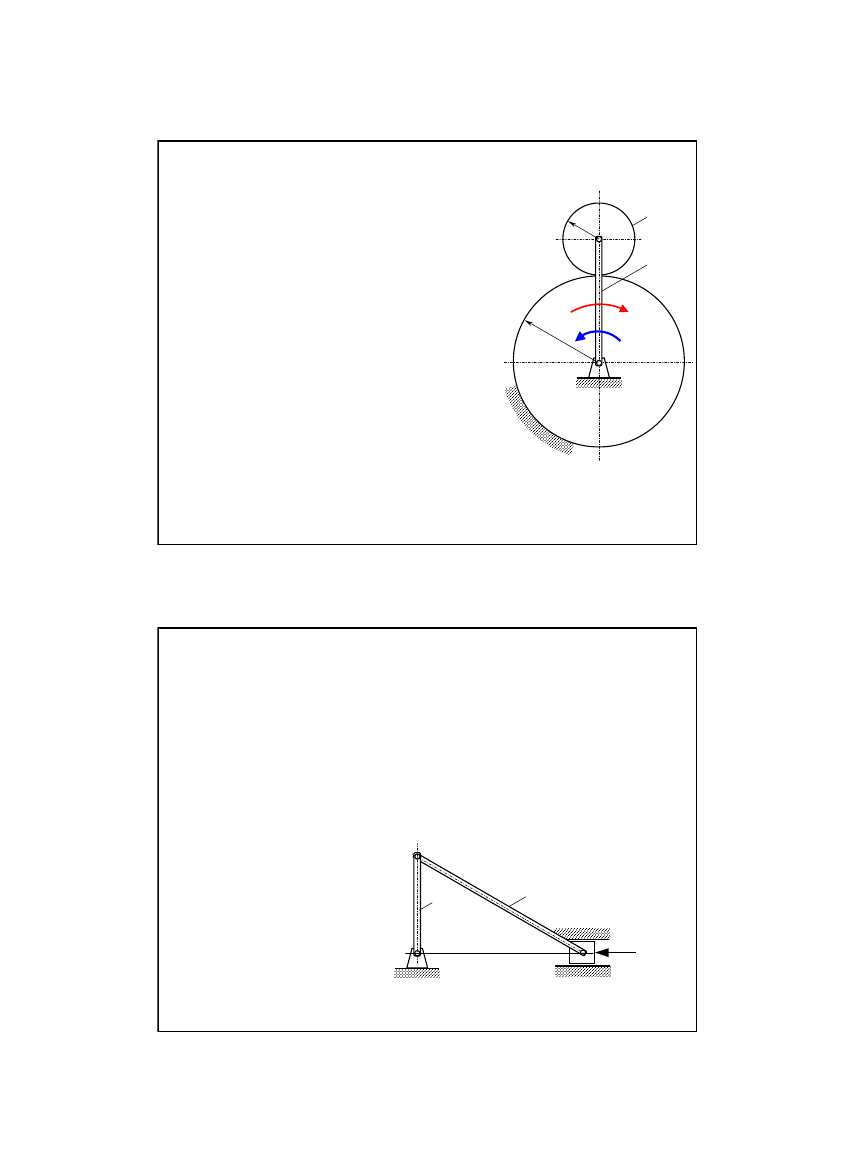
Zadanie 5/15
W położeniu mechanizmu pokazanym
na rysunku korba OA posiada prędkość
kątową ω.
Jaka będzie prędkość kątowa ω’ korby
w chwili, gdy punkt A zajmie najniższe
położenie, jeśli na korbę działa stały
moment hamujący M?
Jaka musi być wartość momentu M, aby
układ w tym położeniu pozostał
nieruchomy?
Korbę potraktować jako jednorodny
cienki pręt o masie m, zaś ruchome koło
jak jednorodny walec o masie m

1

i

promieniu r toczący się bez poślizgu po
nieruchomym kole o promieniu R.

R

r

A

O

ω

M

m

m

1

Zadanie 6/15
Mechanizm korbowy leżący w pionowej płaszczyźnie składa się z
korby OA o długości r i masie m

1

oraz korbowodu o długości l i

masie m

2

. W chwili, gdy punkt A zajmował najwyższe położenie

nadano mu pomijalnie małą prędkość skierowaną w prawo.
Obliczyć prędkość punktu A w chwili, gdy korba przyjmie poziome
położenie, jeśli na tłok B działa stała siła F=(m

1

+m

2

)g/4.

Masę tłoka zaniedbać. Korbę i korbowód potraktować jako
jednorodne, cienkie pręty.

B

F

O

A

r

l

m

1

m

2

8

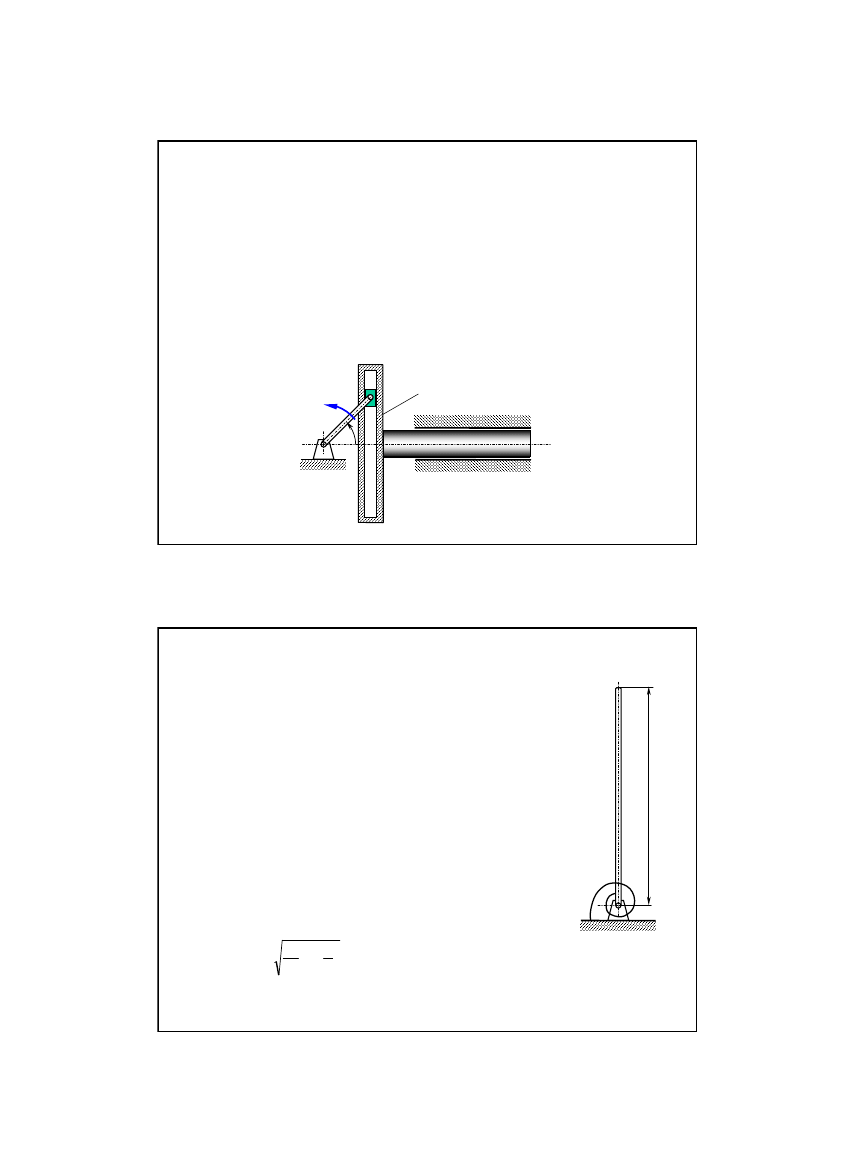
Zadanie 7/15
Na korbę OA mechanizmu korbowo-jarzmowego działa stały
moment obrotowy M. W chwili początkowej mechanizm znajdował
się w spoczynku w położeniu określonym przez kąt ϕ

0

.

Jaką prędkość korbową osiągnie korba po czasie jednego, pełnego
obrotu, jeśli jej długość wynosi r, moment bezwładności względem
osi obrotu J

0

, a masa jarzma równa jest m?

Przyjąć, że siła tarcia w prowadnicach jarzma jest stała i równa F.
Masę suwaka A pominąć.

O

A

ϕ

0

M

m

r

Zadanie 8/15
Jednorodny cienki pręt AB o długości 2a może
obracać się bez tarcia wokół poziomej osi A.
Do pręta zamocowana jest sprężyna spiralna o
takiej sztywności, że może utrzymać pręt
dokładnie w poziomym położeniu.
Z jaką prędkością kątową przejdzie pręt przez
położenie poziome, jeśli w początkowym
pionowym położeniu nadano mu pomijalnie
małą prędkość kątową, a sprężyna nie była
napięta?

A

B

2a

Odp.:













−

=

4

1

2

3

π

ω

a

g

9

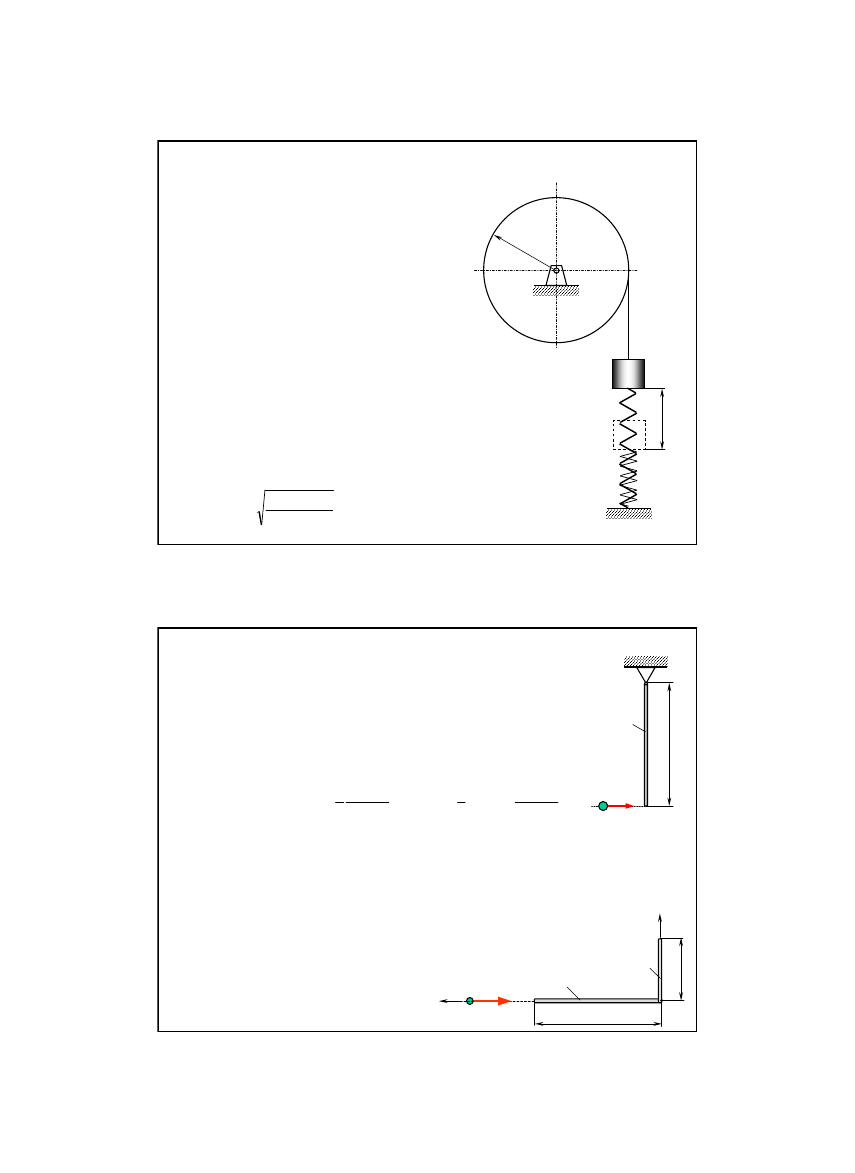
Zadanie 9/15
Na jednorodny cylinder o masie M i
promieniu R nawinięto nić, na końcu
której zawieszono masę m połączoną
z podłożem poprzez sprężynę o
sztywności c. Obracając cylinder
podniesiono masę m do położenia,
przy którym sprężyna została
rozciągnięta o długość s i puszczono
bez prędkości początkowej.
Obliczyć prędkość masy m w
położeniu, przy którym sprężyna nie
będzie napięta.
Masę nici i sprężyny pominąć.

R

M

m

s

c

Odp.:

m

M

cs

mgs

2

2

4

2

+

+

=

υ

Zadanie 10/15
Punkt o masie m uderza prostopadle z prędkością υ

0

w koniec B jednorodnego, cienkiego pręta AB o
masie M i długości l mogącego obracać się bez tarcia
wokół końca A i przykleja się do niego. Obliczyć
prędkość kątową ω pręta po uderzeniu oraz zmianę

∆

E

k

energii kinetycznej układu.

l

M

m

υ

υ

υ

υ

A

B

Odp.:













+

−

−

=

∆

+

=

m

M

m

m

E

m

M

m

l

k

3

3

1

2

1

3

3

2

υ

υ

ω

l

2

l

1

m

1

m

2

m

0

υ

0

x

y

Zadanie 11/15
Na gładkim stole spoczywają połączone ze sobą pod kątem prostym
jednorodne, cienkie pręty o masach i długościach odpowiednio:
m

1

=

1kg, l

1

=

1m oraz m

2

=

0.5kg, l

2

=0.5m.

W pierwszy w nich uderza z prędkością υ

0

=

1m/s punkt

materialny o masie m

0

=

1kg i przykleja się do jego końca.

Wyznaczyć ruch środka masy układu po zderzeniu oraz
zmianę

∆

E

k

energii kinetycznej układu.

Odp.: υ

x

=0, υ

y

=−0.4m/s, ω=0.107rad/s

∆

E

k

= −0.297J

10

O

r

2r

h

m

M

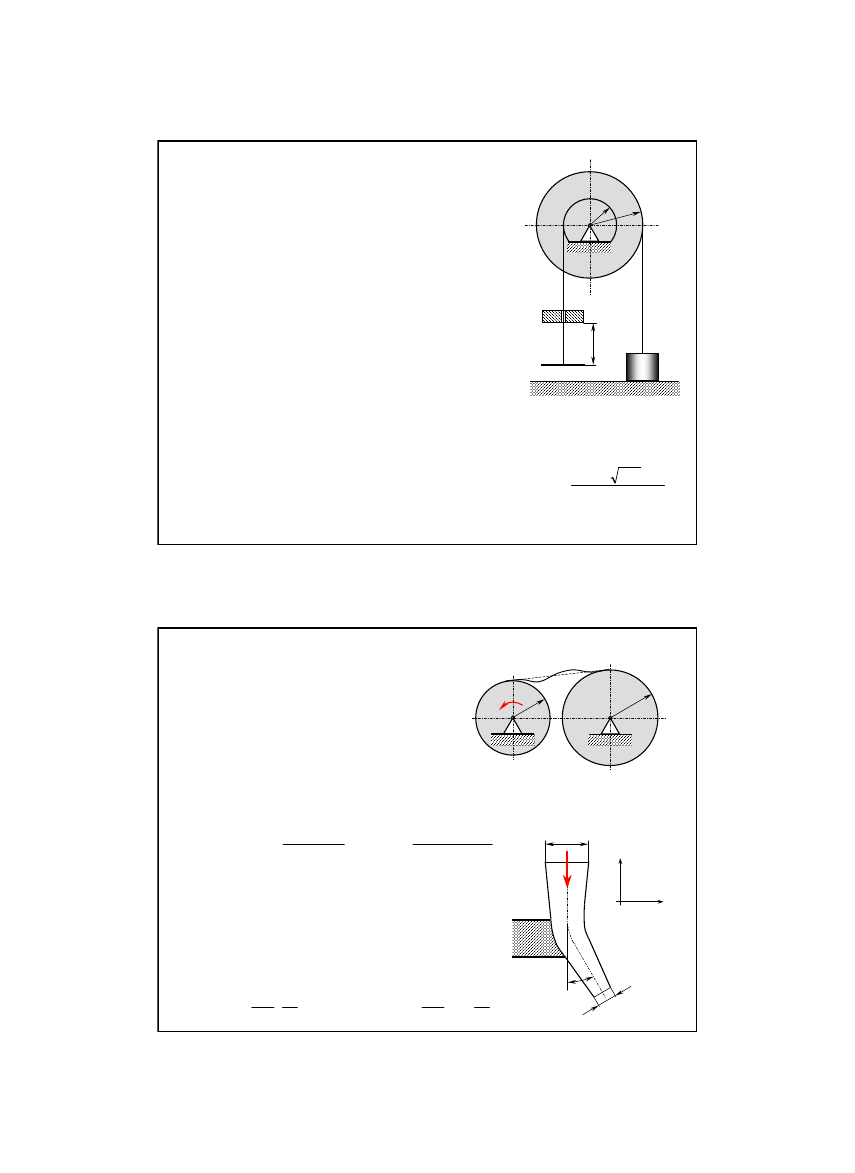
Zadanie 12/15
Układ składa się z bębna o promieniach r i 2r,
posiadającego względem osi obrotu moment
bezwładności J

0

oraz nawiniętych na nim

nieważkich, doskonale wiotkich linek, na
końcach których umocowano masę M oraz
nieważką szalkę. Jaką prędkość kątową ω
uzyska bęben, jeśli na szalkę spadnie z
wysokości h pierścień o masie m? Przed
opuszczeniem szalki układ był nieruchomy,
masa M spoczywała na podłożu a linka była
napięta.

Odp.:

2

2

0

4

2

Mr

mr

J

hg

mr

+

+

=

ω

r

2

r

1

m

1

m

2

ω

0

Zadanie 13/15
Na dwa jednorodne krążki o masach
i promieniach: m

1

, r

1

oraz m

2

, r

2

nawinięto nierozciągliwą, nieważką
linkę i poluzowano ją. Pierwszemu
krążkowi nadano prędkość kątową
ω

0

. Jakie prędkości kątowe ω

1

i ω

2

uzyskają krążki po szarpnięciu

linki oraz jaka będzie zmiana

∆

E

k

energii kinetycznej układu?

υ

1

d

1

d

2

α

x

y

Zadanie 14/15
Obliczyć reakcję kolana rury na podporę
jeśli dane są: prędkość wlotowa cieczy υ

1

,

ś

rednica wlotowa d

1

, średnica wylotowa d

2

,

gęstość cieczy ρ oraz kąt α.

Odp.:

(

)

2

2

2

1

1

2

1

1

0

2

2

2

1

1

1

1

0

1

r

r

m

r

m

r

m

r

m

r

m

r

m

+

=

+

=

ω

ω

ω

ω

Odp.:

2

1

2

2

1

2

1

2

1

2

2

1

2

1

cos

1

4

sin

4

υ

α

π

ρ

α

υ

π

ρ



























−

−

=













−

=

d

d

d

R

d

d

d

R

y

x

11

O

r

m

c

υ

ω

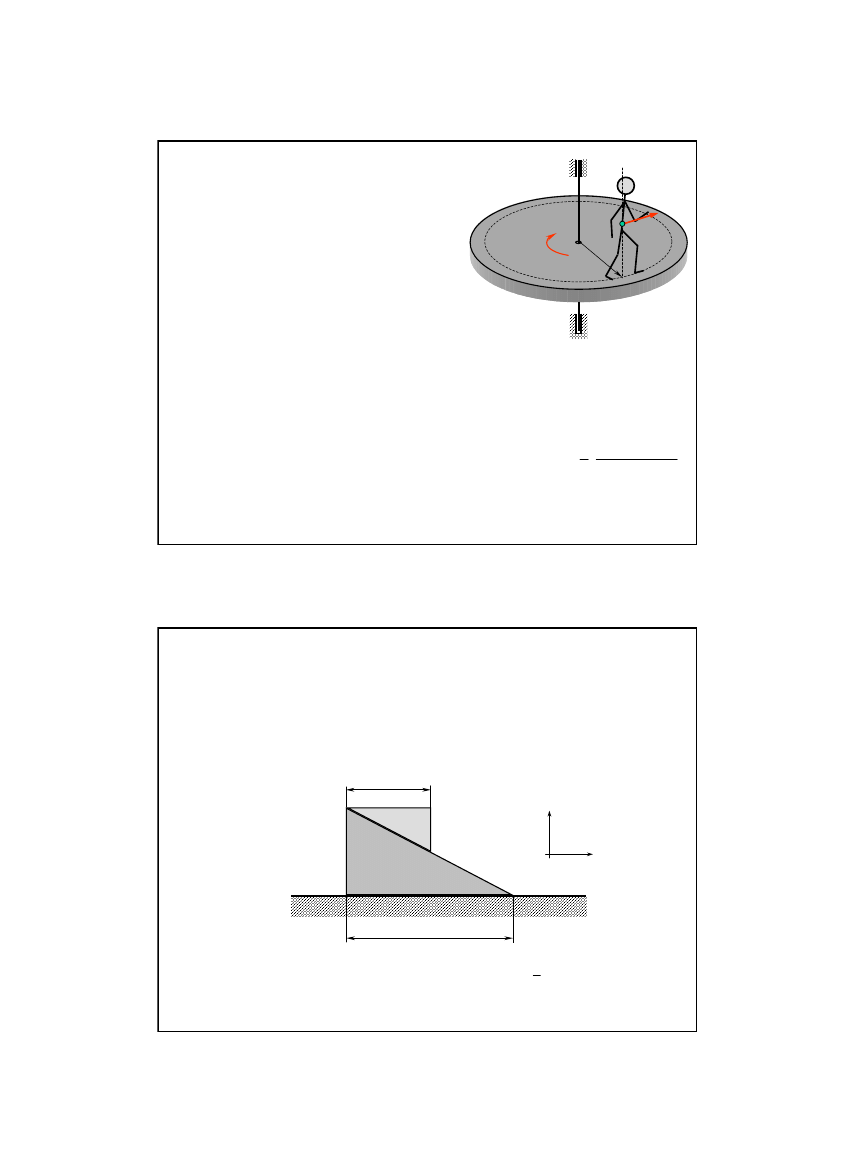
Zadanie 15/15
Na poziomo ustawionej, nieruchomej
tarczy mogącej obracać się bez tarcia
wokół pionowej osi stoi człowiek o
masie m

c

. Jaką prędkość kątową ω

uzyska tarcza jeśli człowiek zaczynie
iść wzdłuż okręgu o promieniu r z
prędkością υ względem tarczy?

Moment bezwładności tarczy względem osi obrotu równy jest J

0

,

zaś człowieka względem pionowej osi przechodzącej przez jego
ś

rodek ciężkości J

c

.

Odp.:

2

0

2

r

m

J

J

r

m

J

r

c

c

c

c

+

+

+

⋅

=

υ

ω

Zadanie 16/15
Na jednorodny klin o masie 4m i długości 2a, mogący ślizgać się
po gładkiej powierzchni, położono jak na rysunku klin o masie m
oraz długości a i puszczono bez prędkości początkowej. O ile
przesunie się klin dolny po zsunięciu się klina górnego?

2a

a

m

4m

x

y

Odp.:

a

x

5

1

=

∆

w lewo