1

7. Ruch punktu we współrzędnych

kartezjańskich

KINEMATYKA PUNKTU

Zadanie 1/7
Punkt porusza się w jednej płaszczyźnie.
Znaleźć:
1) równanie toru punktu,
2) położenie punktu w chwili początkowej,
3) prędkość i przyspieszenie punktu w charakterystycznych

punktach toru

jeśli równania ruchu punktu mają postać:

a)

0

,

0

cos

sin

2

>

>

=

=

k

b

kt

b

y

kt

a

x

b)

0

,

0

2

>

>

=

=

b

a

at

y

t

b

x

c)

kt

b

y

kt

a

x

sin

cos

=

=

d)

t

y

t

x

20

4

15

2

−

=

=

e)

0

,

0

sinh

cosh

>

>

=

=

b

a

kt

b

y

kt

a

x

f)

t

y

t

x

2

sin

5

1

2

cos

4

2

+

=

+

=

g)

0

,

0

sin

2

cos

>

>

=

=

b

a

kt

b

y

kt

a

x

2

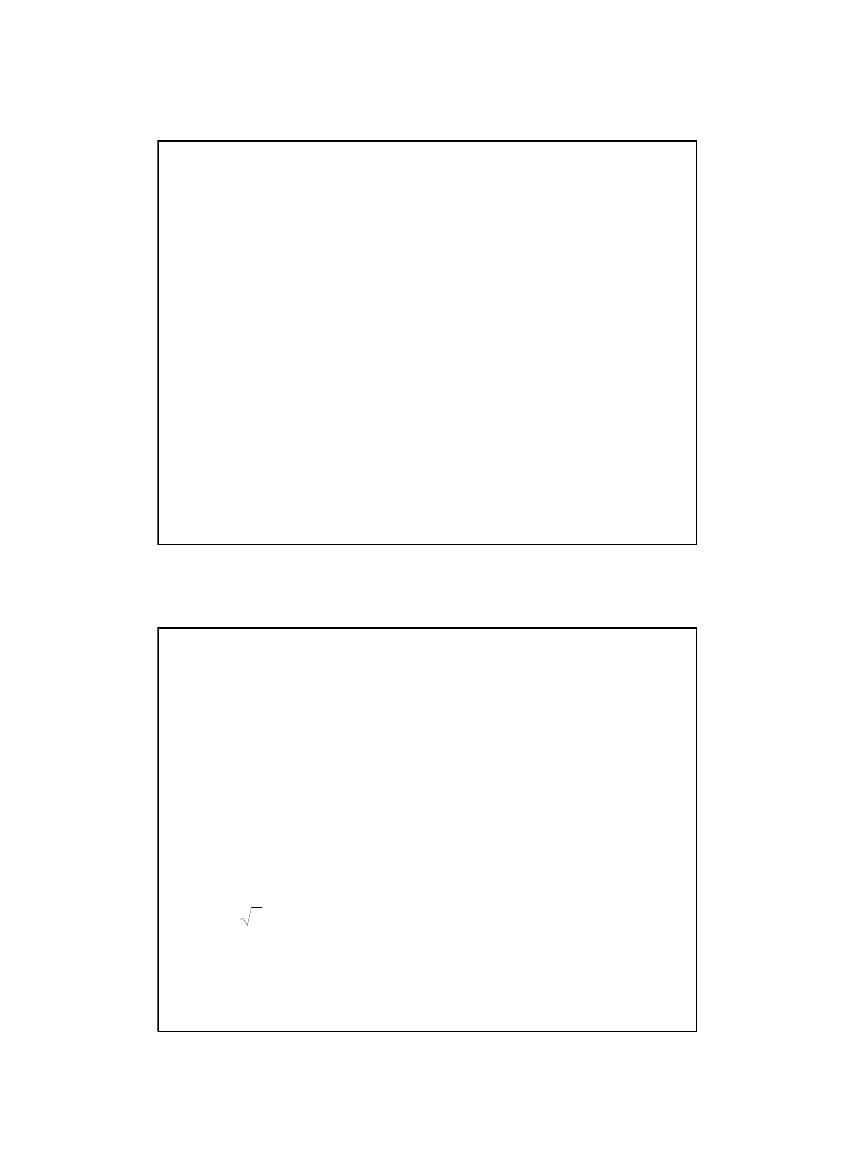
Zadanie 2/7

Ci

ęż

ar

C

przesuwany jest po pionowej prowadnicy za pomoc

ą

linki

przerzuconej przez niewielki kr

ąż

ek

A

odległy od prowadnicy o

wielko

ść

OA

=

a

.

u

a

A

O

C

x

Poda

ć

pr

ę

dko

ść

i przyspieszenie

ci

ęż

aru w zale

ż

no

ś

ci od odległo

ś

ci

OC

=

x

, je

ś

li swobodny koniec linki

ci

ą

gni

ę

ty jest ze stał

ą

pr

ę

dko

ś

ci

ą

u

.

3

2

2

2

2

x

a

u

x

a

x

x

u

x

C

C

−

=

+

−

=

&

&

&

Odp.:

Zadanie 3/7

Pr

ę

t

OA

obracaj

ą

c si

ę

wokół nieruchomego punktu

O

ze stał

ą

pr

ę

dko

ś

ci

ą

k

ą

tow

ą

ω

0

, wprawia w ruch mały pier

ś

cie

ń

P

, nasuni

ę

ty

na poziomo zamocowany drut

d

. Punkt

B

zamocowania drutu

znajduje si

ę

w odległo

ś

ci

b

od nieruchomego punktu

O

.

Znale

źć

pr

ę

dko

ść

i przyspieszenie pier

ś

cienia w funkcji odci

ę

tej

x

.

P

d

B

x

b

O

ω

0

(

)

(

)

2

2

2

2

0

2

2

0

2

x

b

x

b

x

x

b

b

x

+

=

+

=

ω

ω

&

&

&

Odp.:

3

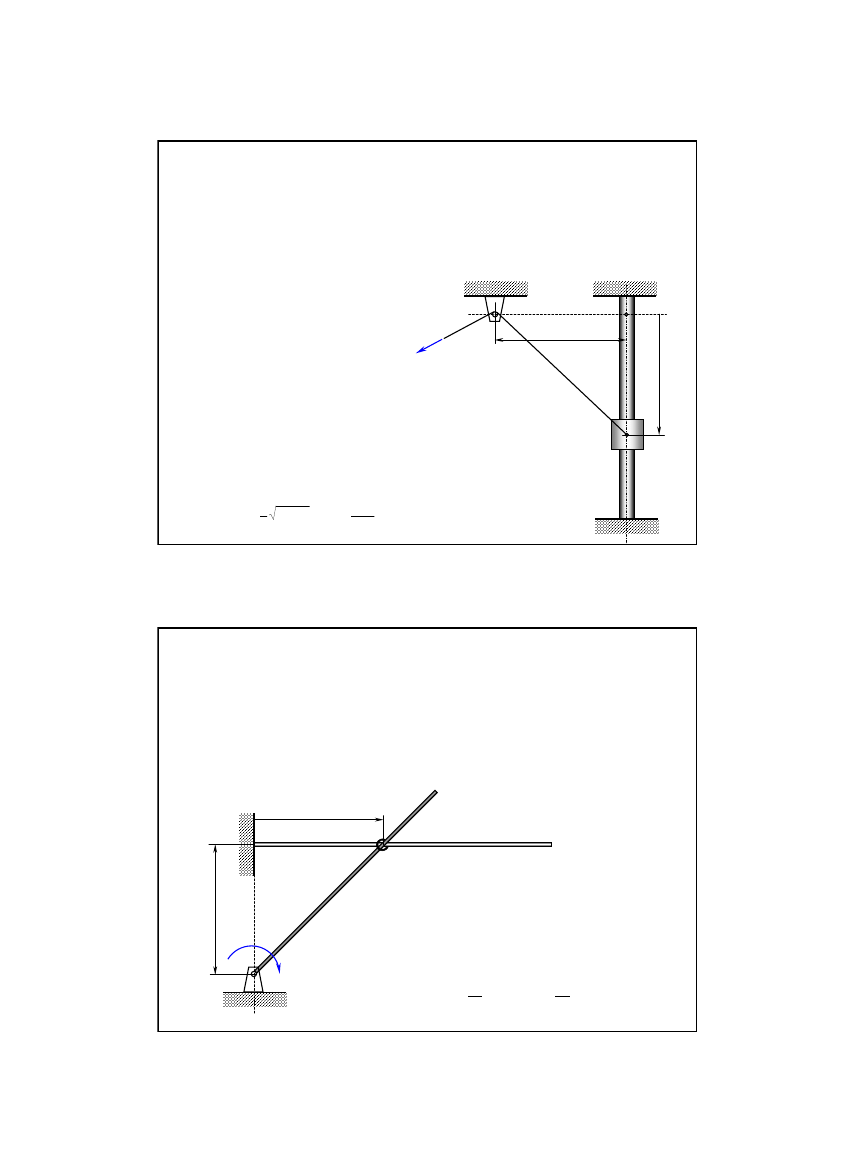
Zadanie 4/7

Suwak

A

zaopatrzony w pionowy pr

ę

t

AB

porusza si

ę

ze stał

ą

pr

ę

dko

ś

ci

ą

u

po prostej poziomej w ten sposób,

ż

e pr

ę

t styka si

ę

w

punkcie

M

z nieruchomym okr

ę

giem o promieniu

r

ustawionym w

płaszczy

ź

nie pionowej.

Wyznaczy

ć

pr

ę

dko

ść

i przyspieszenie
punktu

M

w funkcji

k

ą

ta

ϕ

. W chwili

t

=0

pr

ę

t zajmował

poło

ż

enie

A

0

B

0

.

r

A

0

B

0

M

ϕ

u

A

x

y

ϕ

ϕ

3

2

cos

0

r

u

y

utg

y

x

u

x

M

M

M

M

−

=

−

=

=

=

&

&

&

&

&

&

Odp.:

Zadanie 5/7

Pr

ę

t

AB

o długo

ś

ci

l

porusza si

ę

w ten sposób,

ż

e jego ko

ń

ce

ś

lizgaj

ą

si

ę

po dwóch wzajemnie prostopadłych prostych.

x

y

l

a

M

B

A

x

A

v

A

a

A

(

)

(

)

2

3

2

2

3

2

2

2

2

A

A

A

A

A

A

M

A

A

A

M

A

M

A

M

x

l

x

a

a

x

l

l

a

y

x

l

l

ax

y

l

a

l

a

x

l

a

l

x

−

−

+

⋅

−

=

−

−

=

−

=

−

=

ν

ν

ν

&

&

&

&

&

&

Odp.:

Wyznaczy

ć

pr

ę

dko

ść

i przyspieszenie

punktu

M

, znajduj

ą

cego si

ę

w odległo

ś

ci

a

od ko

ń

ca

A

, w zale

ż

no

ś

ci od poło

ż

enia

x

A

,

pr

ę

dko

ś

ci

v

A

i przyspieszenia

a

A

ko

ń

ca

A

.

4

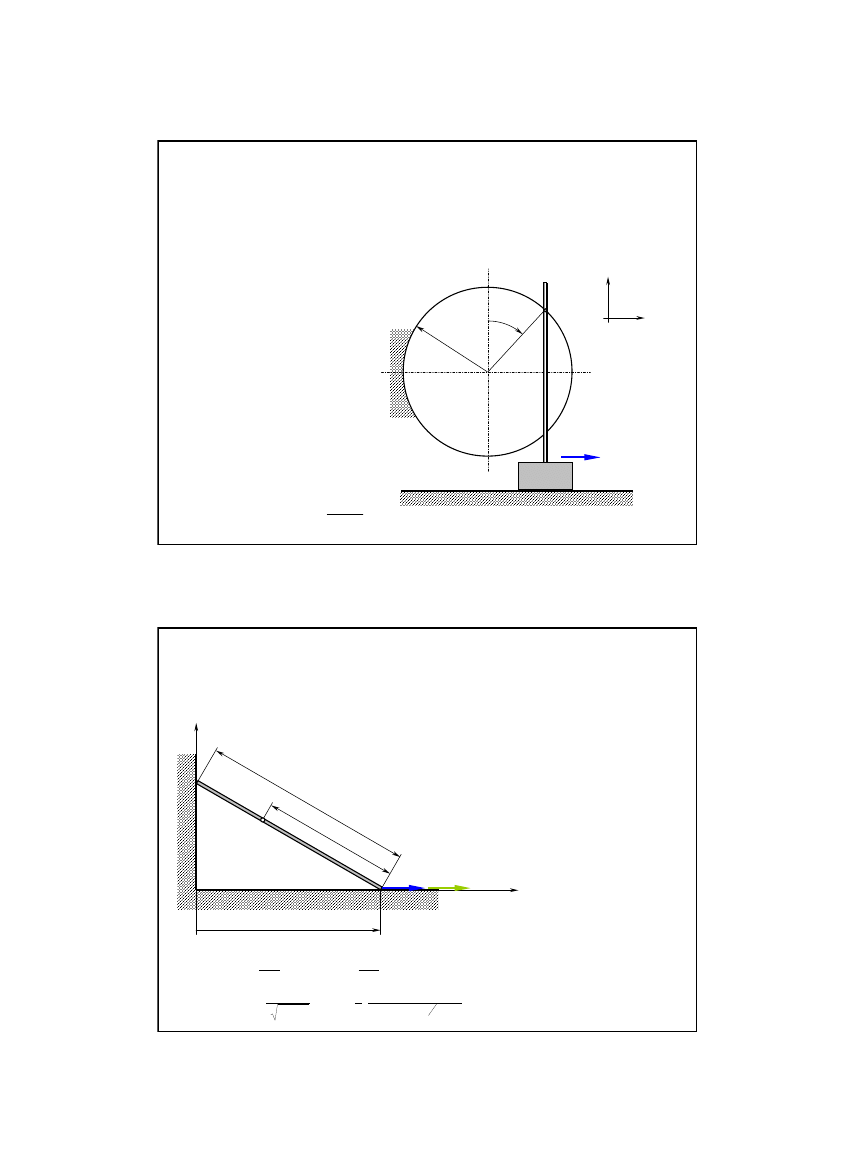
Zadanie 6/7

Krzywka w kształcie półkola o promieniu

r

porusza si

ę

ruchem

post

ę

powym ze stał

ą

pr

ę

dko

ś

ci

ą

v

0

.

Znale

źć

pr

ę

dko

ść

i przyspieszenie pr

ę

ta

opieraj

ą

cego si

ę

na krzywce za po

ś

rednictwem

rolki o promieniu

ρ

i swobodnie poruszaj

ą

cego

si

ę

w pionowej prowadnicy. W chwili

pocz

ą

tkowej pr

ę

t zajmował najwy

ż

sze poło

ż

enie.

ρ

r

v

0

x

(

)

( )

(

)

(

)

( )

[

]

2

3

2

0

2

2

2

0

2

0

2

2

0

t

r

r

x

t

r

t

x

ν

ρ

ρ

ν

ν

ρ

ν

−

+

+

=

−

+

=

&

&

&

Odp.:

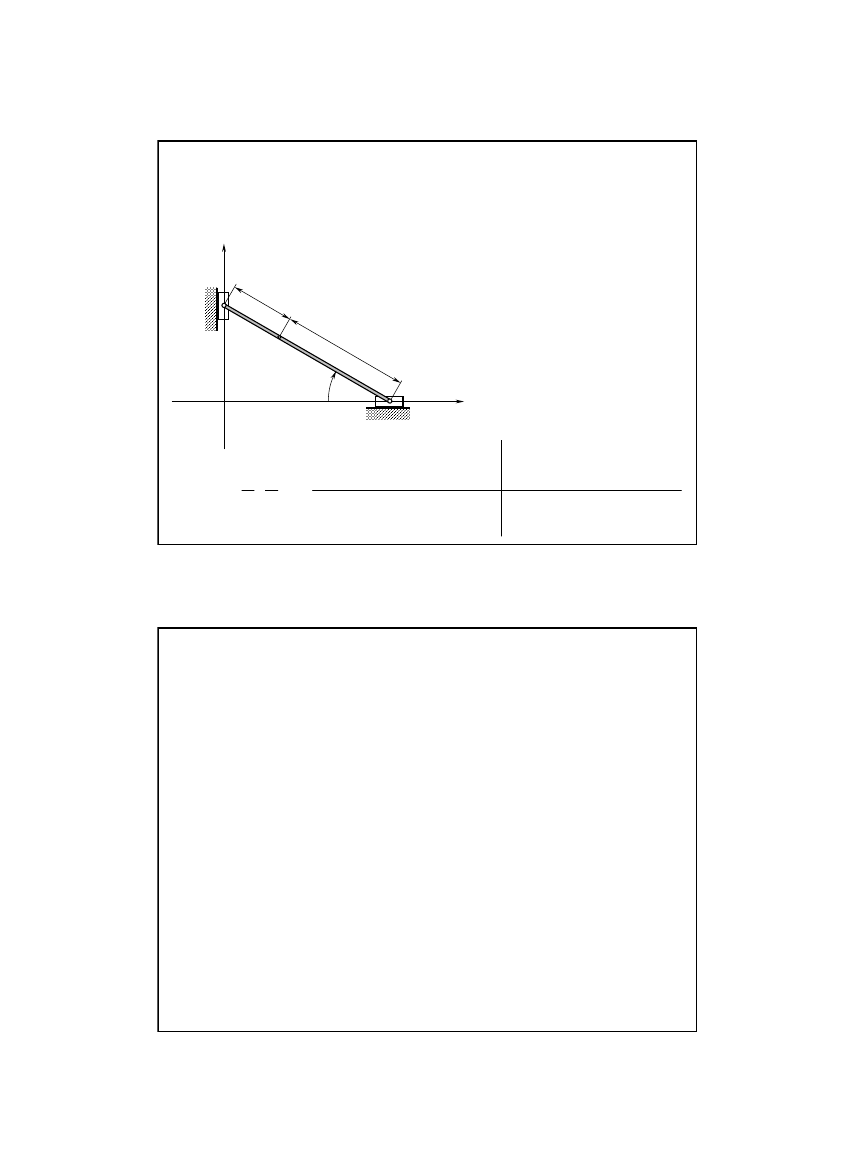
Zadanie 7/7

Kulka mo

ż

e przesuwa

ć

si

ę

w kanaliku w kształcie odcinka paraboli

o równaniu

x

=

y

2

/4. Równocze

ś

nie przesuwana jest za pomoc

ą

prowadnicy poruszaj

ą

cej si

ę

ze stał

ą

pr

ę

dko

ś

ci

ą

ν

0

.

Odp.:

Znale

źć

pr

ę

dko

ść

i przyspieszenie kulki w chwili, gdy zajmuje ona

poło

ż

enie okre

ś

lone przez współrz

ę

dn

ą

x

k

=4. W chwili pocz

ą

tkowej

kulka zajmowała poło

ż

enie okre

ś

lone współrz

ę

dn

ą

x

0

.

ν

0

y

x

x

0

3

2

0

0

0

2

0

x

y

x

y

x

x

ν

ν

ν

−

=

=

=

=

&

&

&

&

&

&

5

Zadanie 8/7

Ko

ń

ce linijki AB poruszaj

ą

si

ę

po dwóch wzajemnie prostopadłych

prostych

0x

i

0y

, przy czym k

ą

t

ϕ

=

ω

t

(

ω

=const).

Odp.:

Poda

ć

równanie toru ruchu

punktu

M

znajduj

ą

cego si

ę

w

odległo

ś

ciach

a

i

b

od ko

ń

ców

linijki oraz obliczy

ć

jego

pr

ę

dko

ść

i przyspieszenie w

chwilach, gdy znajdzie si

ę

on na

prostych

0x

oraz

0y

.

x

B

A

M

a

b

0

ϕ

y

1

2

2

2

2

=

+

b

y

a

x

0

0

0

2

=

=

=

−

=

=

=

M

M

M

M

M

M

y

b

y

y

a

x

x

a

x

&

&

&

&

&

&

ω

ω

2

0

0

0

ω

ω

b

y

y

b

y

x

a

x

x

M

M

M

M

M

M

−

=

=

=

=

−

=

=

&

&

&

&

&

&

0

0

0

2

=

−

=

=

=

=

−

=

M

M

M

M

M

M

y

b

y

y

a

x

x

a

x

&

&

&

&

&

&

ω

ω

2

0

0

0

ω

ω

b

y

y

b

y

x

a

x

x

M

M

M

M

M

M

=

=

−

=

=

=

=

&

&

&

&

&

&

Zadanie 9/7

Pocisk wystrzelono z pr

ę

dko

ś

ci

ą

pocz

ą

tkow

ą

ν

0

=700m/s pod k

ą

tem

α

1

=60

o

do poziomu. Po jakim czasie

∆

t

nale

ż

y wystrzeli

ć

drugi

pocisk pod k

ą

tem

α

2

=45

o

i z tak

ą

sam

ą

pr

ę

dko

ś

ci

ą

pocz

ą

tkow

ą

, aby

pociski zderzyły si

ę

w locie? Na jakiej wysoko

ś

ci

h

i w jakiej

odległo

ś

ci

l

od miejsca wystrzału nast

ą

pi zderzenie? Opór powietrza

pomin

ąć

, przyj

ąć

przyspieszenie ziemskie

g

=9.81m/s

2

.

Odp.:

∆

t

=104.5sek, h=9786m, l=36575m

Zadanie 10/7

Punkt zakre

ś

la figur

ę

Lissajous zgodnie z równaniami

Znale

źć

promie

ń

ρ

krzywizny toru w punkcie o współrz

ę

dnych

x

=0,

y

=0.

Odp.: ρ=∞

t

a

y

t

a

x

ω

ω

sin

2

sin

−

=

−

=

6

Zadanie 11/7

Punkt zakre

ś

la figur

ę

Lissajous zgodnie z równaniami

Znale

źć

pr

ę

dko

ść

i przyspieszenie punktu oraz promie

ń

ρ

A

krzywizny

toru w punkcie

A

okre

ś

lonym współrz

ę

dn

ą

x

A

=5.

kt

y

kt

x

cos

3

sin

5

=

=

5

81

0

9

5

0

2

=

=

=

−

=

=

A

A

A

A

A

y

k

y

k

x

x

ρ

&

&

&

&

&

&

Odp.:

Zadanie 12/7

Ruch punktu opisany jest równaniami

Znale

źć

równanie toru w postaci

y(x)

oraz pr

ę

dko

ść

i przyspieszenie

punktu w zale

ż

no

ś

ci od jego poło

ż

enia.

(

)

0

,

,

>

=

=

−

k

f

d

fe

y

de

x

kt

kt

Odp.:

y

k

y

ky

y

x

k

x

kx

x

x

fd

y

2

2

=

−

=

=

=

=

&

&

&

&

&

&

Zadanie 13/7

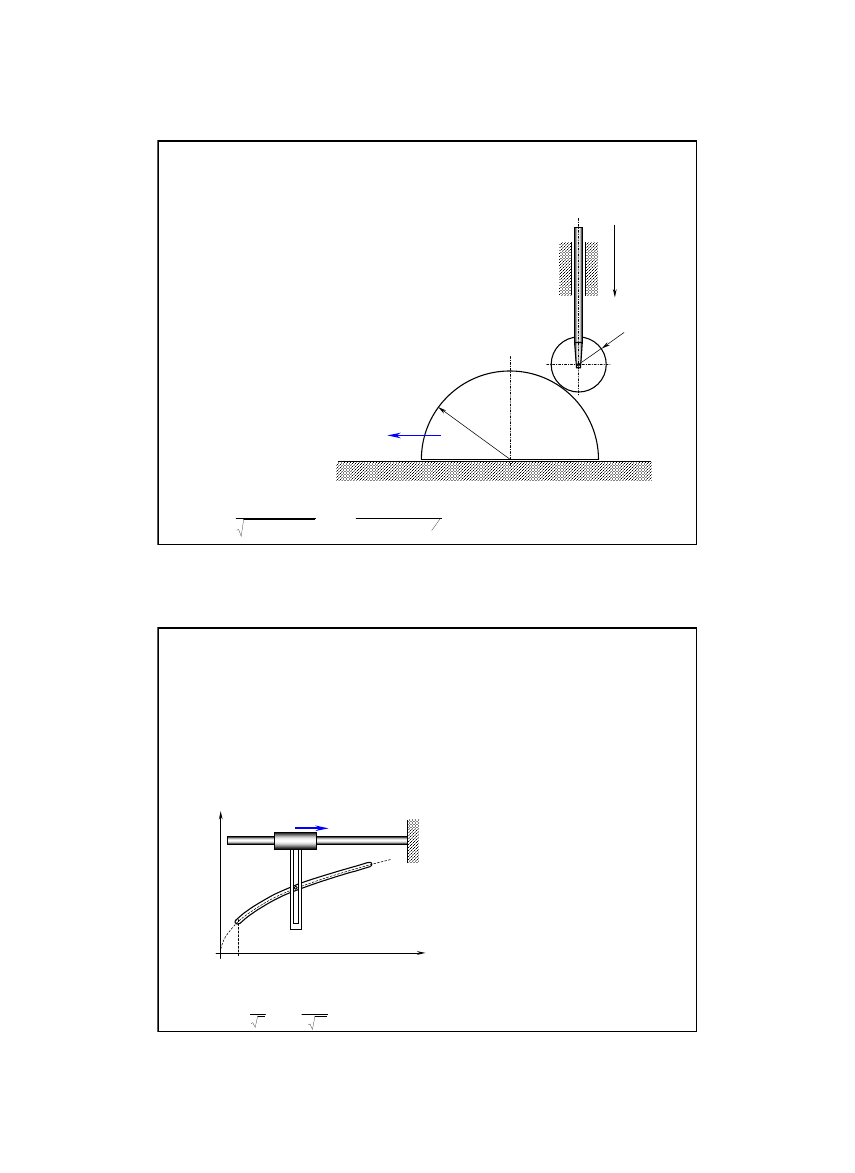
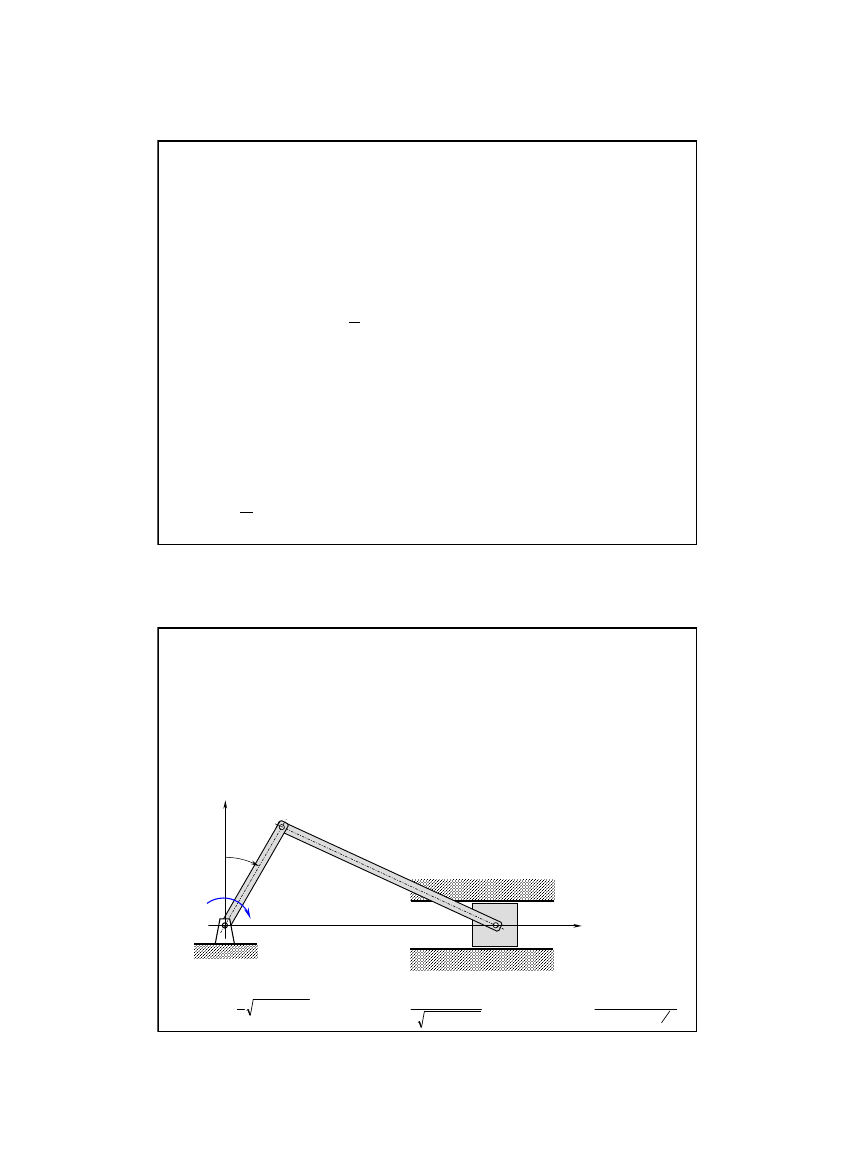
W mechanizmie korbowym przedstawionym na rysunku korba

OA

o długo

ś

ci

r

obraca si

ę

ze stał

ą

pr

ę

dko

ś

ci

ą

k

ą

tow

ą

ω

wokół

nieruchomego punktu

O

.

Wyznaczy

ć

poło

ż

enie, pr

ę

dko

ść

i przyspieszenie tłoka

B

w funkcji

poło

ż

enia korby okre

ś

lonego k

ą

tem

ϕ

. Stosunek długo

ś

ci korby do

długo

ś

ci

l

korbowodu

AB

wynosi

r

/

l

=

k

(0<k<1).

B

O

ω

ϕ

A

y

x

l

r

Odp.:

(

)

















−

−

+

−

=

















−

+

=













−

+

=

2

3

2

2

4

2

2

2

2

2

2

cos

1

cos

2

cos

sin

cos

1

2

2

sin

cos

cos

1

1

sin

ϕ

ϕ

ϕ

ϕ

ω

ϕ

ϕ

ϕ

ω

ϕ

ϕ

k

k

k

r

x

k

k

r

x

k

k

r

x

B

B

B

&

&

&