Cel ćwiczenia
Badanie rozkładu natężenia światła w obrazie dyfrakcyjnym pojedynczej szczeliny.
Zestaw doświadczalny
Gdzie:
1- podziałka milimetrowa
2- laser He-Ne o mocy wiązki 1.0 mW
3- szczelina
4- niewielki czarny ekran
5- fotoogniwo
6- śruba mikrometryczna
7- wzmacniacz
8- ekran multimetru digitalnego
Kolejność wykonywania czynności:
•
W uchwycie, który znajduje odległości ok.20cm od lasera umieścić była szczelinę o
szerokości 0,2 mm. Diafragma może się obracać wokół osi poziomej co umożliwia
ustawienie odpowiedniej szczeliny do pomiaru. Ramiona klamry uchwytu powinny się
znajdować na ramce diafragmy a nie na jej szkiełku
•
Ustawić mały ekran z fotoogniwem w odległości L (1010 mm ) od szczeliny.
•
Sprawdzić, czy płaszczyzna ekranu jest równoległa do płaszczyzny szczelin i
prostopadła do wiązki (osi) lasera. Skierować wiązkę lasera na szczelinę
,zaobserwować prążki dyfrakcyjne. Obraz jest bardzo wyraźny, jeśli geometria jest
ustawiona poprawnie. W razie konieczności skorygować.
•
Intensywność prążka dyfrakcyjnego jest rejestrowana za pośrednictwem fotoelementu
,przez mały otwór w ekranie zwany dalej "okiem" fotoelementu. Przesuw odbywa się
za pomocą pokrętła śruby mikrometrycznej.
•
Przekręcając pokrętło śruby w lewo przesunąć „oko” fotoelementu do pozycji
pierwszego minimum z lewej strony maksimum głównego.
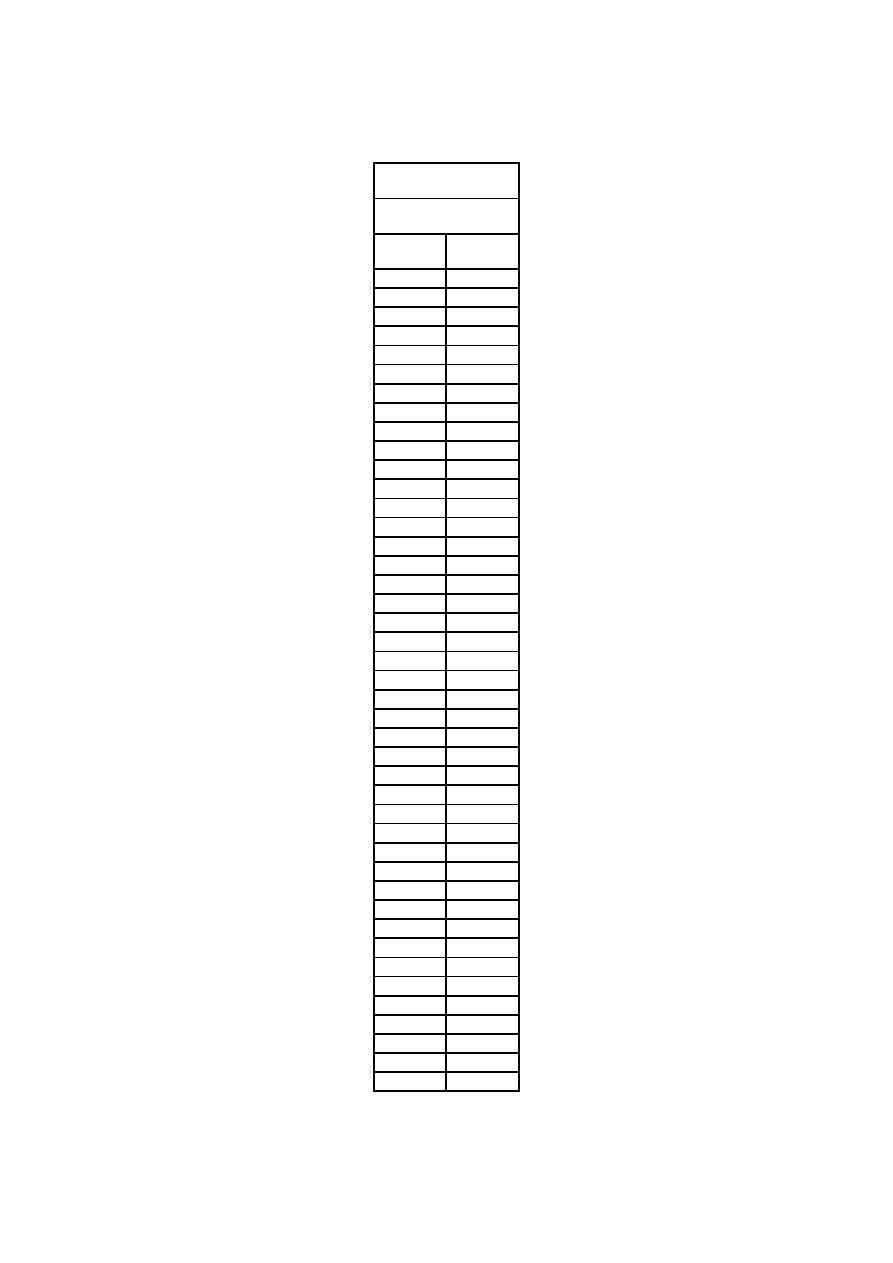
Tabela wyników:
d=0,2 mm
L=1010 [mm]
y[mm
U [V]
0
0,0713
0,5
0,0256
1
0,0164
1,5
0,0058
2
0,0618
2,5
0,2119
3
0,4035
3,5
0,6635
4
1,0235
4,5
1,4935
5
2,0435
5,5
2,7835
6
3,1835
6,5
3,5135
7
3,6135
7,5
3,6235
8
3,5835
8,5
3,3535
9
2,8735
9,5
2,4035
10
1,9435
10,5
1,4535
11
1,3235
11,5
0,7635
12
0,4735
12,5
0,2335
13
0,1035
13,5
0,0752
14
0,0037
14,5
0,0066
15
0,046
15,5
0,0726
16
0,09
16,5
0,0934
17
0,0817
17,5
0,0661
18
0,0392
18,5
0,0176
19
0,0054
19,5
0
20
0,0013
20,5
0,0084
21
0,0197
Minima i maksima odczytane z wykresu:
•
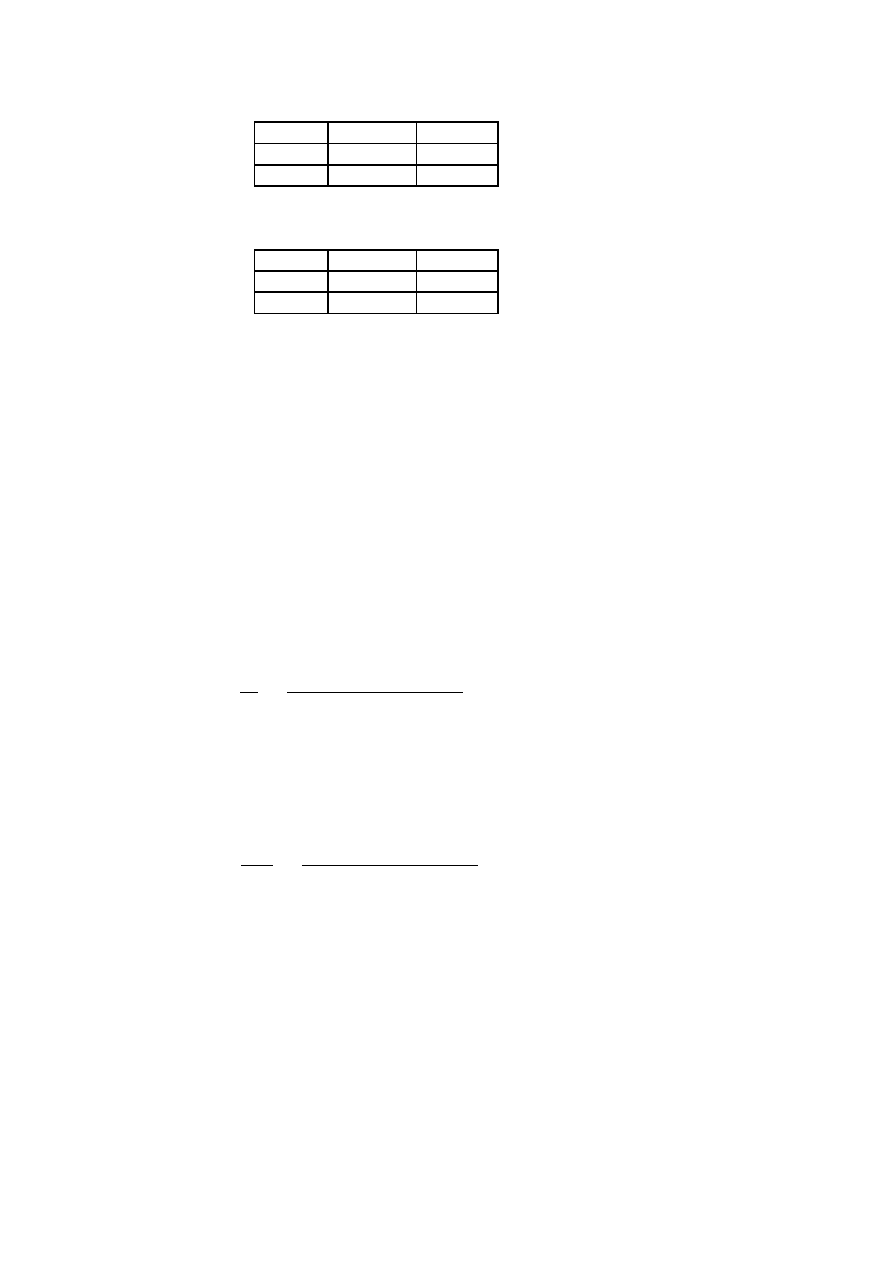
Minima
y[mm]
U [V]
1
14
0,0037
2
19,5
0
•
Maksima
y[mm]
U [V]
1
16,5
0,0394
2
21
0,0197
Opracowanie wyników
Gdzie:
λ = 0,0000006328 m
2a = (y
1
-y
0
)
L = 1010 mm
Obliczanie teoretyczne wartości kąta Θ dla minimów :
Dla rzędu I
0032
,
0
003164
,
0
0002
,
0
0000006328
,
0
sin
≈
=
=
=
m
m
d
λ
θ
Dla rzędu II
0063
,
0
006328
,
0
0002
,
0
0000012656
,
0
2
sin
≈
=
=
=
m
m
d
λ
θ
Obliczanie teoretyczna wartości kąta
θ
dla minimów:
Dla małych kątów wartości funkcji sinθ i tgθ są bardzo zbliżone do wartości kątów
wyrażonych w radianach.
Dla rzędu I
2a = 14mm – 7,5mm
2a = 6,5mm /: 2
a = 3,75mm
0037
,
0
003712871
,
0
1010
75
,
3
≈
=
=
=
mm
mm
L
a
tg
θ
Dla rzędu II
2a = 19,5mm – 7,5mm
2a = 12mm /:2
a = 6mm
0059
,
0
005940594
,
0
1010
6
≈
=
=
=
mm
mm
L
a
tg
θ
Obliczanie teoretyczne wartości kąta Θ dla maksimów:
Dla rzędu I
0047
,
0
004746
,
0
0002
,
0
0000006328
,
0
5
,
1
5
,
1
sin
≈
=
=
=
m
m
d
λ
θ
Dla rzędu II
0079
,
0
00791
,
0
0002
,
0
0000006328
,
0
5
,
2
5
,
2
sin
≈
=
=
=
m
m
d
λ
θ
Obliczanie eksperymentalnie wartości kąta θ dla maksimów:
Dla rzędu I
2a = 9mm /:2
a= 4,5mm
0045
,
0
004455
,
0
1010
5
,
4
≈
=
=
=
mm
mm
L
a
tg
θ
Dla rzędu II
2a = 13,5mm /: 2
a = 6,75mm
0067
,
0
006683
,
0
1010
75
,
6
≈
=
=
=
mm
mm
L
a
tg
θ
Obliczenie szerokości szczeliny z analizy prążków dyfrakcyjnych
przekształcając odpowiednio wzór:
θ
λ
λ
θ
λ
θ
sin
sin
sin
'
'
'
m
d
m
d
d
m
=
=
=
Obliczamy dla minimum rzędu I
mm
m
m
d
1964
,
0
000196406
,
0
00321782
,
0
0000006328
,
0
'
≈
=
=
Obliczamy błąd pojedynczego pomiaru przy określonej szerokości
szczeliny:
(
)
mm
mm
mm
a
a
L
L
d
d
0036
,
0
003591
,
0
013333
,
0
004950
,
0
196406
,
0
'
'
≈
=
=
+
=
∆
±
∆
=
∆
Gdzie:
ΔL = 5mm
Δa = 0,05mm
Ostateczny wynik:
d’ = ( 0,2 ± 0,4 10
-3
) mm
W nioski
:
Przy wykonywaniu wykresu zależności U=f(y) przeniosłyśmy oś poziomą o 73,5 mV
w górę, aby najmniejsze natężenie znalazło się w wartości zero, co spowodowało, że cały
wykres znajduje się w pierwszej ćwiartce układu współrzędnych.
Wartości natężenia były odczytywane podczas eksperymentu co 0,5mm dlatego
wykres jest wykonany w zakresie 0-21mm.
Wartości kątów θ otrzymane drogą eksperymentu są zbliżone do wartości tych kątów
wyznaczonych teoretycznie. Niewielkie różnice między nimi mogą wynikać z tego, że
pomiary natężenia były wykonywane co 0,5mm. Gdyby pomiary były dokonywane co
0,25mm różnice między katami byłyby mniejsze, gdyż ilość pomiarów wpływa na dokładność
wyników.
Obliczona szerokość szczeliny dla minimum I rzędu jest bliska szerokości
zastosowanej szczeliny, a niewielkie różnice mogą wynikać z zastosowania do obliczeń
kątów uzyskanych drogą eksperymentu.
