ANALIZA STATYCZNA

PŁYTY ŻELBETOWEJ

W SYSTEMIE ROBOT

Adam Wosatko

v. 0.1, marzec 2009

2

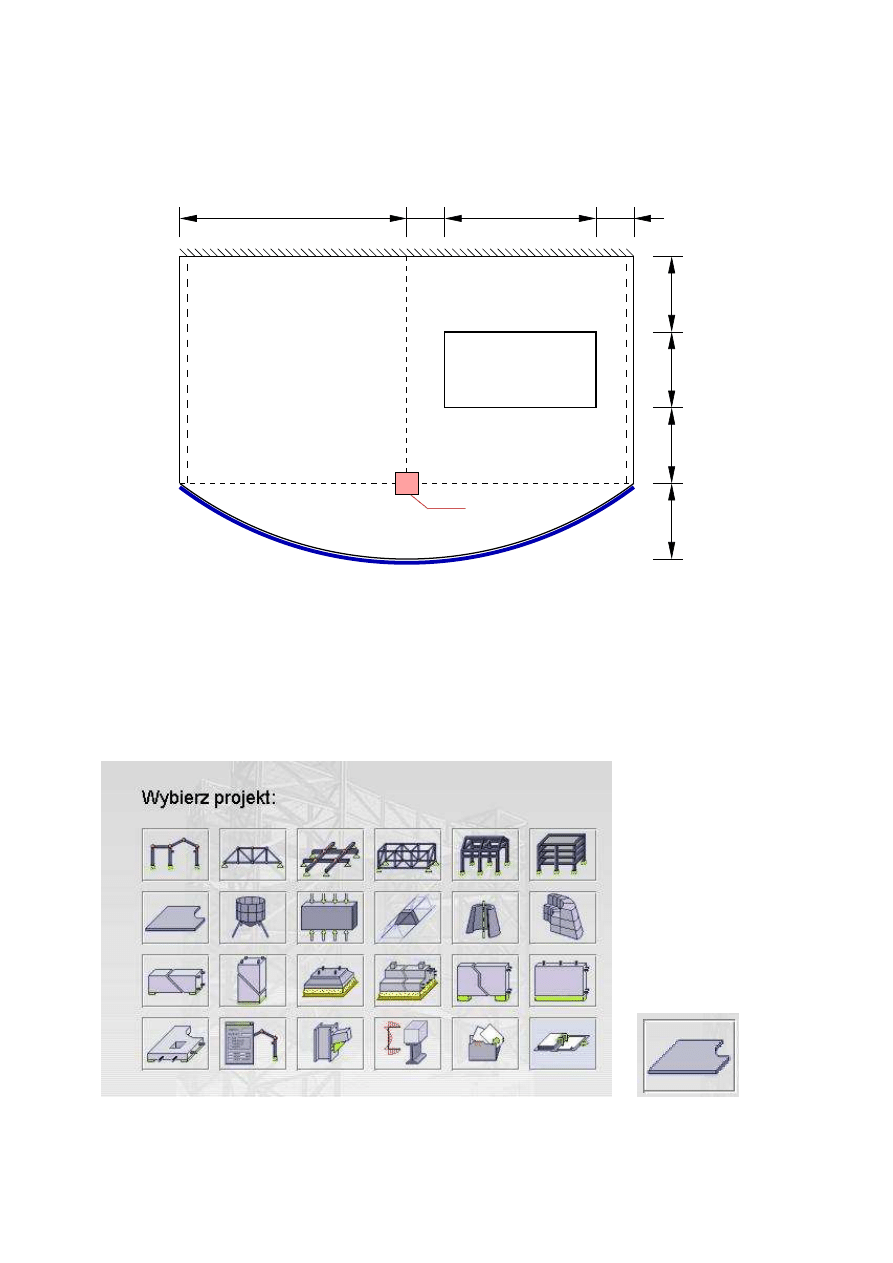
1. Definicja zadania

otwór

Beton B30

grubość: 20 cm

obciążenie równomierne:

stałe: 3 kPa, użytkowe: 2 kPa

obciążenie barierką: 1,5 kN/mb

6 m

4 m

1 m

1 m

2 m

2 m

2 m

2 m

słup

30 cm x 30 cm

śc

ia

n

a

25

cm

śc

ia

n

a

25

cm

ściana 20 cm

2. Typ zadania

Typ zadania. Spośród możliwych zadań (patrz rys. 1(a)) wybieramy statykę płyty
poprzez zaznaczenie ikony jak na rys. 1(b), która znajduje się w oknie (rys. 1(a)) w
drugim wierszu od góry i w pierwszej kolumnie od lewej.

(a) Startowe okno wyboru nowego zadania

(b) Płyta

Rys.1. Wybór typu zadania (konstrukcji)

3. DEFINICJA GEOMETRII

3

3. Definicja geometrii

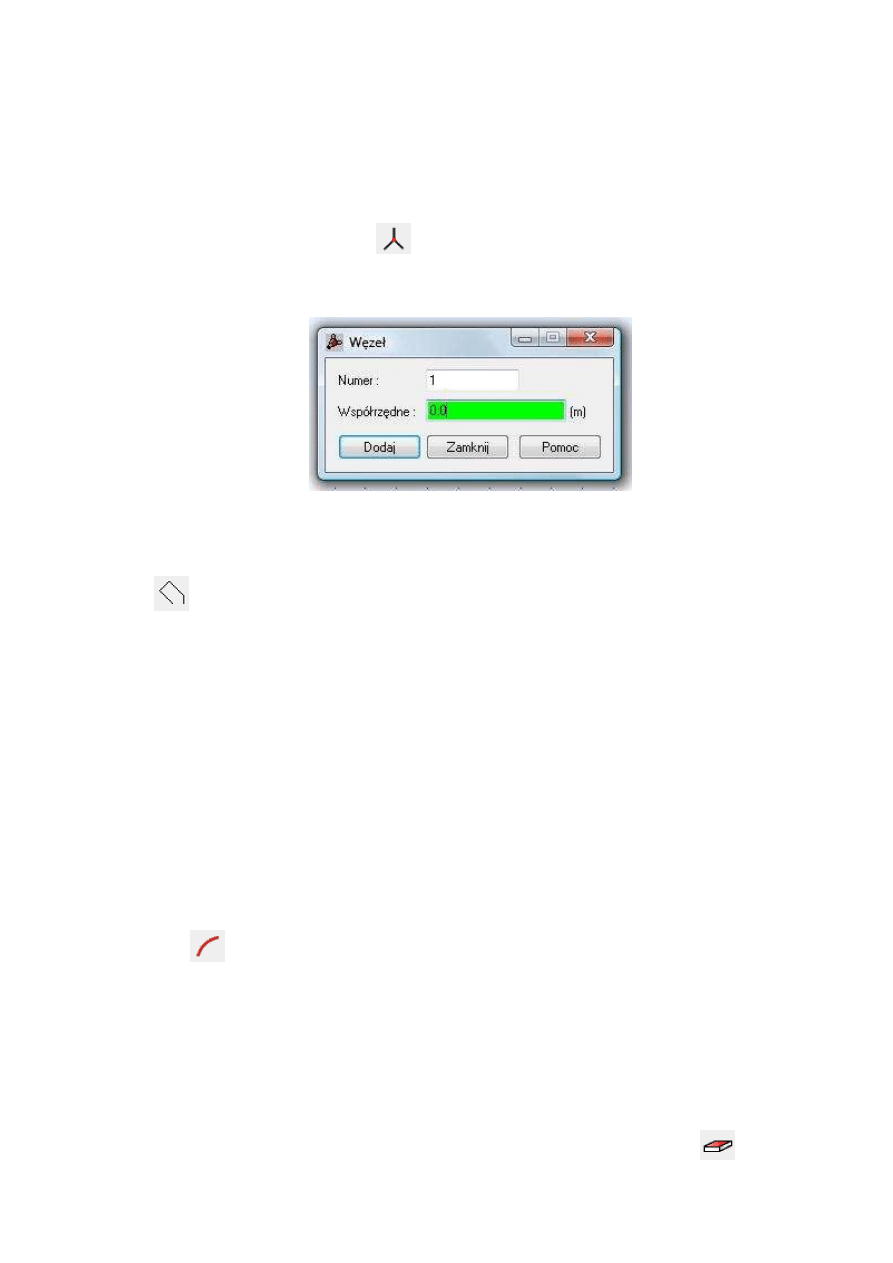
Definicja węzła dla podpory punktowej. Zadanie rozpoczynamy od wprowadzenia
węzła, któremu przypiszemy potem podporę punktową. W celu wprowadzenia współrzęd-

nych węzła wybieramy ikonkę

znajdującą się po prawej stronie ekranu. W oknie

jak na rys. 2 wpisujemy współrzędne 0;0, zatwierdzamy przyciskiem Dodaj i zamykamy
okno. Na ekranie pojawi się dość mało widoczna czerwona kropka.

Rys.2. Wprowadzanie węzła

Definicja konturów Kolejną czynnością będzie definicja konturów. Za pomocą ikon-

ki

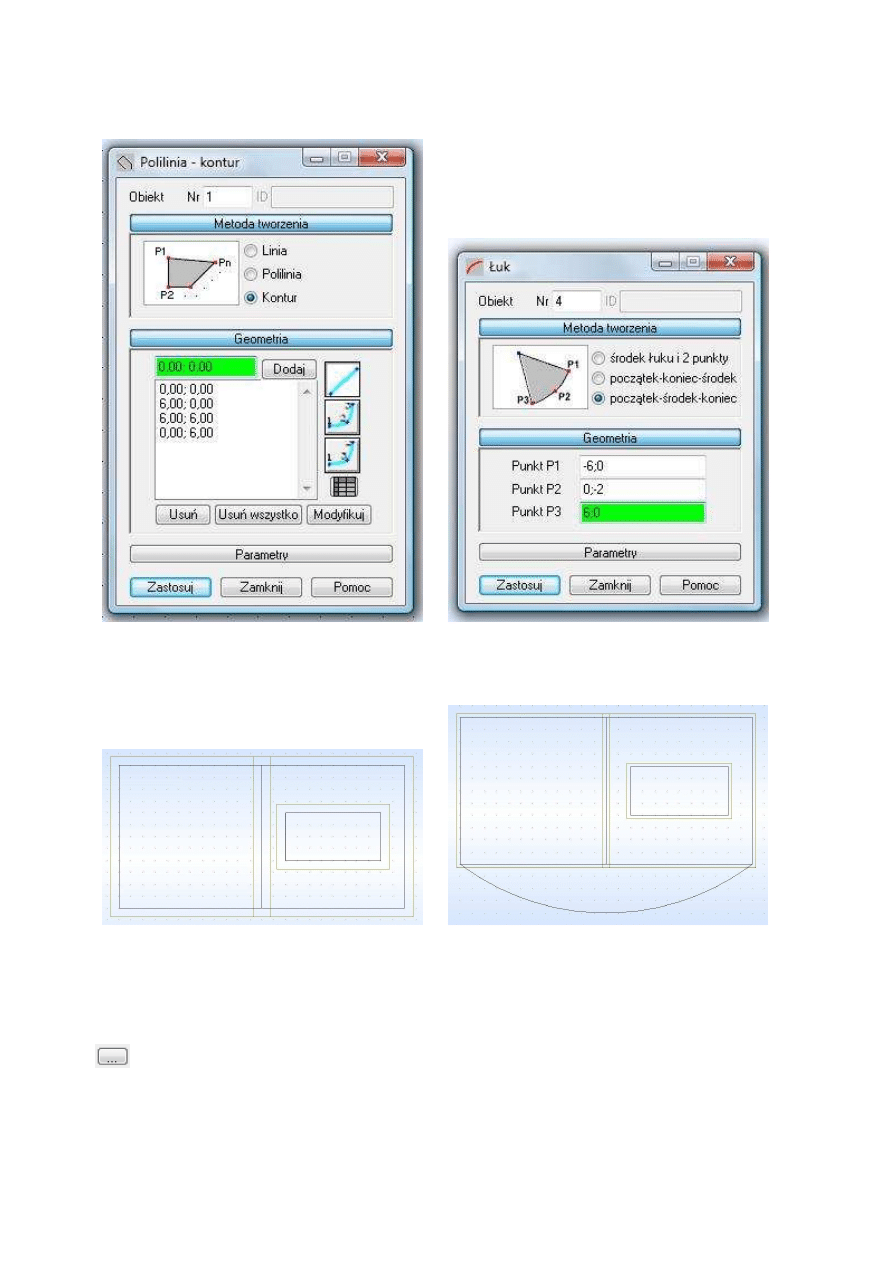
otwieramy okno jak na rys. 3(a). Nie zmieniamy metody tworzenia (Kontur)

i naciskamy na przycisk Geometria. Okno się powiększy i możemy teraz wprowadzać
współrzędne dla pierwszego konturu, za każdym razem potwierdzając przyciskiem Do-
daj. Współrzędne pierwszego konturu są następujące: 0;0, 6;0, 6;6, 0;6 i zamykamy
kontur poprzez wpisanie ponownie 0;0. Kontur powinien się utworzyć bez dodatkowego
zatwierdzania.

Geometrię konturów można też wprowadzić zaznaczając myszką naroża w przestrzeni

roboczej ekranu. Kolejne kontury mają współrzędne:

• 0;0, 0;6, -6;6, -6;0, 0;0

• 1;2, 5;2, 5;4, 1;4, 1;2

W efekcie otrzymujemy kontury zdefiniowane jak na rys. 4(a). Na koniec możemy powięk-
szyć widok.

Definicja łuku Łuk wprowadzamy zgodnie z oknem na rys. 3(b). Okno wywołujemy

ikonką

również znajdującą się po prawej stronie ekranu. Wybieramy początek-

środek-koniec jako metodę tworzenia i wpisujemy współrzędne punktów P1: -6;0, P2:
0;-2 i P3: 6;0. Zatwierdzamy przyciskiem Zastosuj i zamykamy okno. Teraz cała wpro-
dzona geometria powinna wyglądać tak, jak na rys.4(b).

4. Definicja paneli

Definicja materiału i grubości. W tym punkcie zaczniemy od przypisania danych

materiałowych do definiowanych za moment paneli. Klikamy na ikonkę

, po czym

4

(a) Definicja konturu

(b) Definicja łuku

Rys.3. Wprowadzanie współrzędnych dla konturu i łuku

(a) Zarys konturów

(b) Kontury + łuk

Rys.4. Zdefiniowana geometria

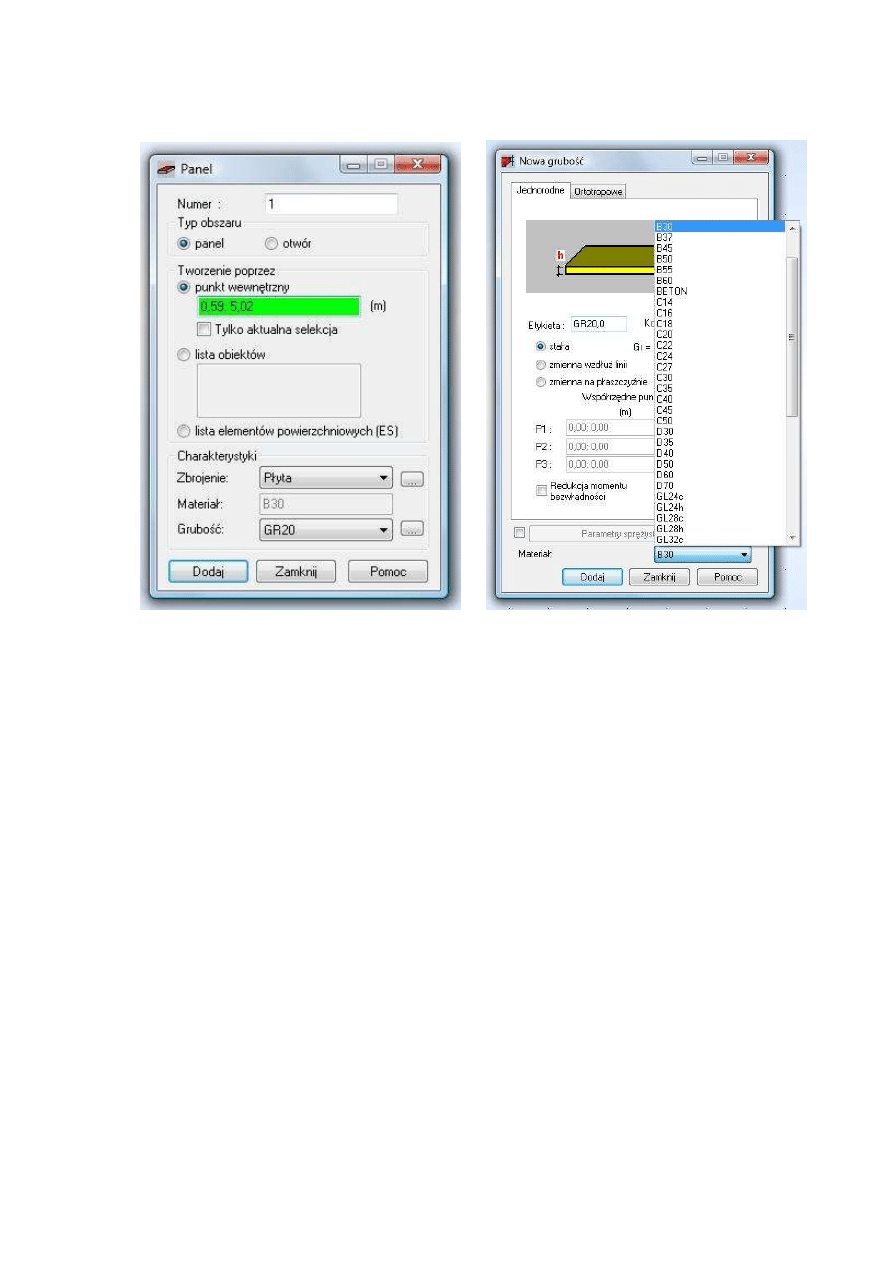
pojawia sie okno jak na rys. 5(a). Na wysokości opcji Grubość przyciskamy na ikonkę

.

W kolejnym oknie (rys. 5(b)) na dole rozwijamy listę i jako materiał wybieramy beton

B30. Poza tym wprowadzamy grubość Gr = 20 cm. Nazwa etykiety zostanie domyślnie
zapisana jako GR20,0. Zamykamy to okno, a w oknie z rys. 5(a) sprawdzamy jeszcze czy
wybrane są następujące charakterystyki:

4. DEFINICJA PANELI

5

(a) Panel

(b) Materiał

Rys.5. Panel – okna do definicji

• Zbrojenie: Płyta

• Materiał: B30 (ta opcja w tym oknie nie jest aktywna)

• Grubość: GR20,0 (nazwa etykiety!)

Przypisanie materiału do paneli. Teraz możemy przypisać dane materiałowe do
paneli. Dlatego w oknie z rys. 5(a) w ramce Tworzenie poprzez wybieramy punkt
wewnętrzny i zaznaczamy następujące obszary:

• kontur po lewej – wewnątrz

• kontury po prawej – pomiędzy wewnętrznym a zewnętrznym (nie zaznaczmy wnętrza

mniejszego konturu, ponieważ wówczas nie utworzy się otwór!)

• łuk na dole – dowolne miejsce powyżej tego łuku, a poniżej zadanych właśnie paneli

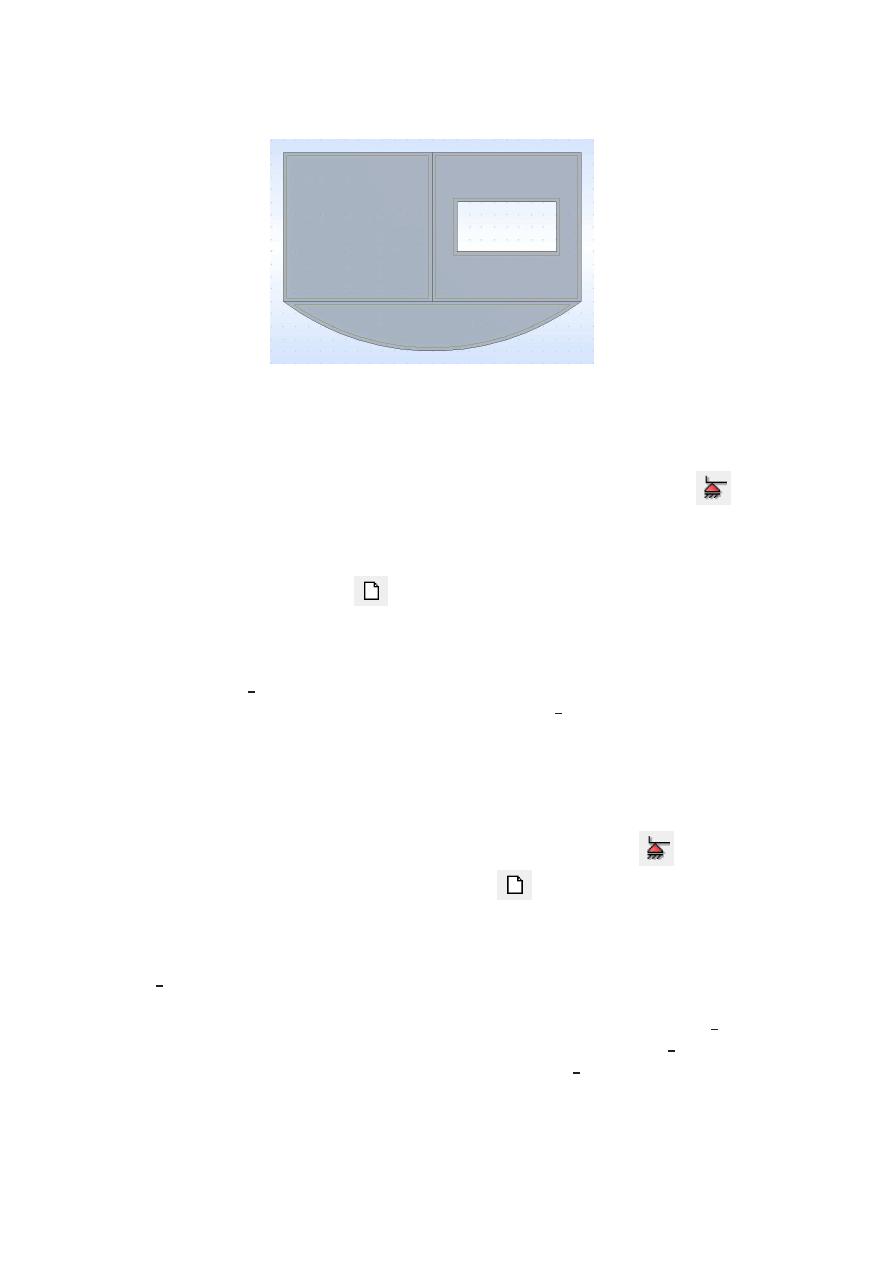
Na koniec zamykamy okno. Mamy zatem zdefiniowane dane geometryczne i materiałowe,
co potwierdza się na rys. 6.

6

Rys.6. Zdefiniowane panele

5. Definicja podpór i obciążeń

Definicja podpory punktowej. Po wybraniu (prawa strona ekranu) ikonki

poja-

wia się okno służące do definicji podpór. W celu zadania podpory w węźle, który wprowa-
dziliśmy na samym początku, najpierw określamy, że będzie to podpora węzłowa (zakładka
Węzłowe). Ponieważ interesującego nas typu nie ma w zestawie, należy go zdefiniować.

Na górze okna klikamy na ikonkę

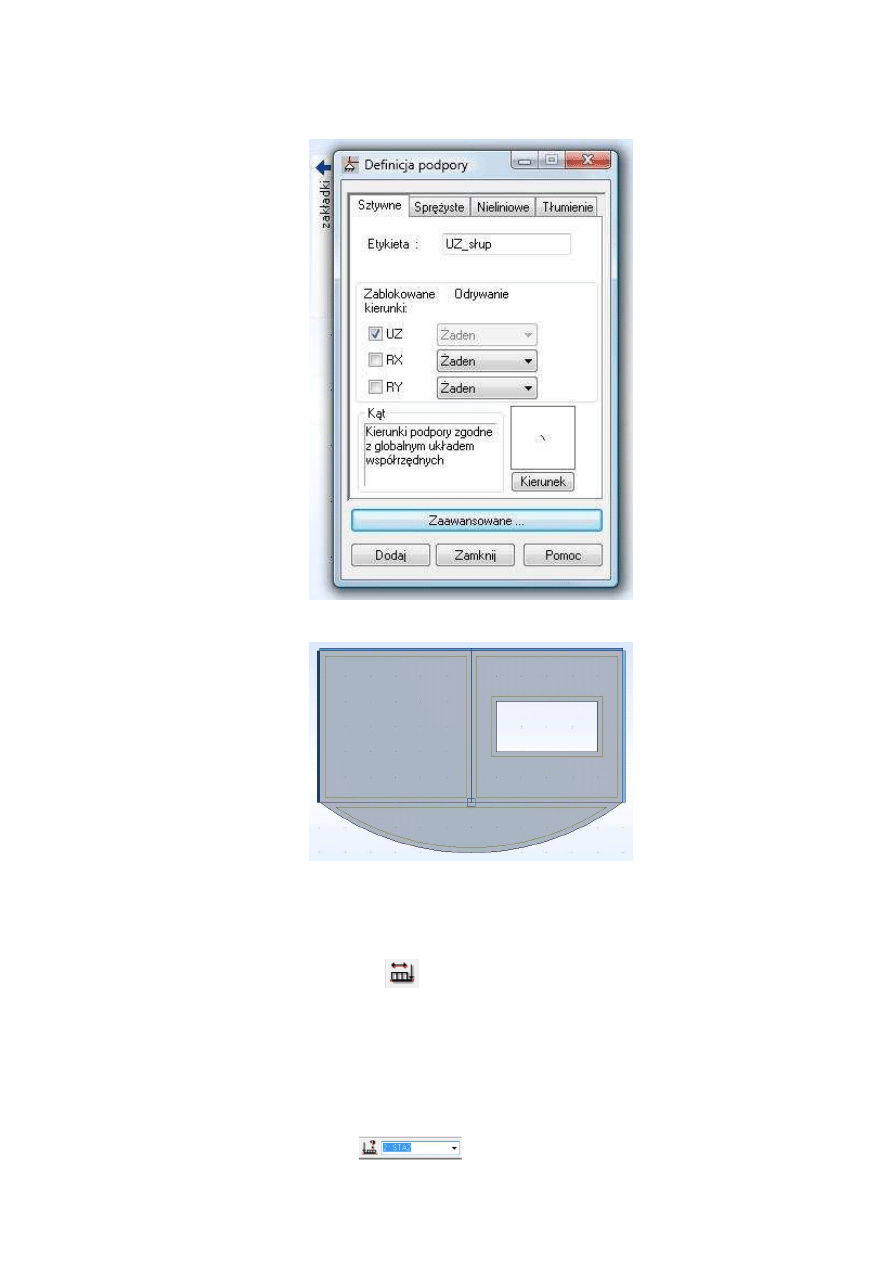
. W oknie jak na rys. 7, na zakładce Sztywne za-

znaczamy zablokowany kierunek UZ, a następnie przycisk Zaawansowane. W nowym
oknie (Definicja podpory - zaawansowane) wybieramy słup i prostokątny oraz
wpisujemy ten sam wymiar a = b = 30 cm. Zaznaczamy OK. Wpisujemy nazwę etykie-
ty podpory, np. UZ słup, zatwierdzamy Dodaj i Zamknij. Po zamknięciu okien (okno
Podpory jest nadal aktywne) wybieramy podporę typu UZ słup i przypisujemy tą pod-
porę do węzła, który został zadany na początku. Możemy to zrobić poprzez kliknięcie albo
wpisanie jego numeru.

Definicja podparcia liniowego krawędzi. Będziemy wykonywali sekwencję czynno-

ści podobnych do opisanych w poprzednim paragrafie. Poprzez ikonkę

, na zakładce

Liniowe ponownie definiujemy nowy typ podpory

. W oknie jak na rys. 7, na za-

kładce Sztywne zaznaczamy zablokowany kierunek UZ, a następnie przycisk Zaawan-
sowane. Teraz wybieramy opcje ściana oraz ceglana, wpisujemy wymiar b = 25 cm
i zaznaczamy OK. Wprowadzamy nazwę podpory, np. przykładową etykietą może być
Ściana cegła i zatwierdzamy Dodaj. Następnie zaznaczamy zablokowane UZ, RX i
RY. Po naciśnięciu na Zaawansowane interesuje nas ściana betonowa oraz wymiar b
= 20 cm. Zamykamy to okno poprzez OK. Nową etykietą może być np. Ściana beton.
Zatwierdzamy Dodaj i Zamknij. Następnie jako podpory typu Ściana cegła ozna-
czamy pionowe zewnętrzne krawędzie paneli, a jako Ściana beton – poziome proste
krawędzie (u góry paneli). Łatwiejszą od wprowadzania zgodnie z numeracją jest definicja
podpór liniowych poprzez zaznaczenie krawędzi myszką. Po wprowadzeniu warunków pod-
poarcia powinniśmy otrzymać widok zgodny z rys.8 W razie potrzeby zamykamy dostępne
okna.

5. DEFINICJA PODPÓR I OBCIĄŻEŃ

7

Rys.7. Wprowadzanie nowego typu podpory

Rys.8. Warunki podparcia

Definicja przypadków obciążeń. W celu definicji obciążeń lub ich kombinacji nale-
ży najpierw określić możliwe przypadki obciążeń. Okno służące do definicji przypadków

obciążeń można wywołać ikonką

. Po pojawieniu się okna naciskamy przycisk Nowy

i w ten sposób definiujemy ciężar własny. Kolejne 2 przypadki definiujemy podobnie –
zmieniamy tylko naturę obciążenia. Dla natury Stałe potwierdzamy przyciskiem Nowy
drugi przypadek obciążenia. Następnie zmieniamy naturę na Eksploatacyjne i ponow-
nie musimy potwierdzić (Nowy). Na koniec zamykamy okno.

Definicja stałego obciążenia. W celu definicji stałego obciążenia wybieramy ten przy-
padek poprzez pasek wyboru

na górze. Następnie klikamy na ikonę definiu-

8

jącą obciążenia

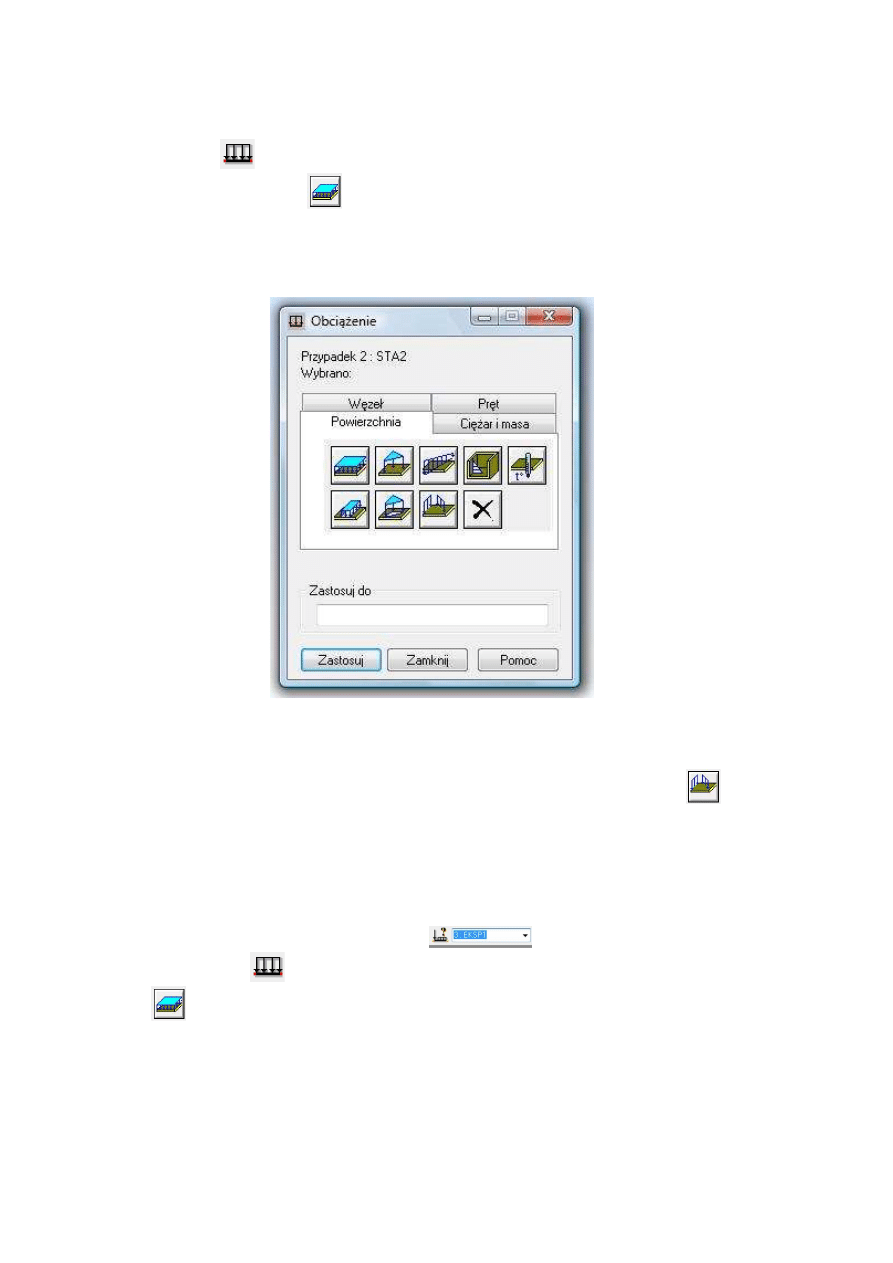
. Teraz pojawia się okno jak na rys. 9, gdzie wybieramy zakładkę

Powierchnia oraz ikonkę

dla obciążeń jednorodnych leżących na płycie. Wpisuje-

my na kierunku Z: -3 kPa, potwierdzamy przyciskiem Dodaj i Zamknij. Po zniknięciu
tego okna zaznaczamy myszką wszystkie panele. Trudniej wpisuje się ich numery w miej-
scu Zastosuj do.

Rys.9. Okno do definicji obciążeń

Jeszcze nie zmieniamy przypadku obciążenia. Na tej samej zakładce Powierzchnia

definiujemy teraz obciążenie dla barierką na krawędzi łuku. Za pomocą ikonki

wybie-

ramy typ obciążenia liniowego na krawędziach. Dla sił równomiernie rozłożonych zgodnie z
osią Z wpisujemy wartość -1,5 kN/m. Zatwierdzamy Dodaj oraz Zamknij. Zaznaczamy
teraz krawędź łuku i zamykamy okno.

Definicja obciążenia eksploatacyjnego. Przełączamy się na przypadek obciążenia
eksploatacyjnego za pomocą paska wyboru

na górze. Wybieramy ikonę de-

finiującą obciążenia

. W oknie jak na rys. 9 wybieramy zakładkę Powierchnia oraz

ikonkę

związaną z definicją obciążeń jednorodnych płyty. Wpisujemy na kierunku

Z: -2 kPa, zatwierdzamy Dodaj i Zamknij. Następnie zaznaczamy myszką wszystkie
panele. Zamykamy dostępne okna.

Kombinacje obciążeń (ręczne). Utworzymy jedną kombinację obciążeń. Poprzez wy-
bór z górnego menu Obciążenia → Kombinacje ręczne... otwieramy okno do definicji
przypadku kombinacji. Tam w razie potrzeby nadajemy nazwę kombinacji np. KOMB1

6. SIATKA ES, OBLICZENIA I PRZEGLĄD REZULTATÓW

9

oraz określamy typ kombinacji SGN. Pozostałe parametry są bez zmian. Zatwierdzamy
OK.

Teraz włącza się nowe okno, gdzie określamy jakie przypadki proste będą należeć

do kombinacji. Dla kombinacji KOMB1 wybieramy i dodajemy wszystkie 3 przypadki
proste. Pozostawiamy domyślne wartości częściowych współczynników bezpieczeństwa.
Mają one mieć wartości:

• ciężar własny, γ = 1.1

• stałe, γ = 1.1

• eksploatacyjne, γ = 1.3

Zatwierdzamy przyciskiem Zastosuj i zamykamy okno.

6. Siatka ES, obliczenia i przegląd rezultatów

Generacja siatki ES. Do generacji i modyfikacji siatki używamy paska narzędzi jak

na rys. 10. W celu jego wywołania używamy ikonki

z górnego menu.

Rys.10. Pasek narzędzi do generacji siatki ES

Siatkę stworzymy jednocześnie dla wszystkich paneli, dlatego uprzednio należy je za-

znaczyć (klawisze Ctrl+A). Po naciśnięciu na trzecią ikonkę z paska narzędzi (zob. rys. 10)
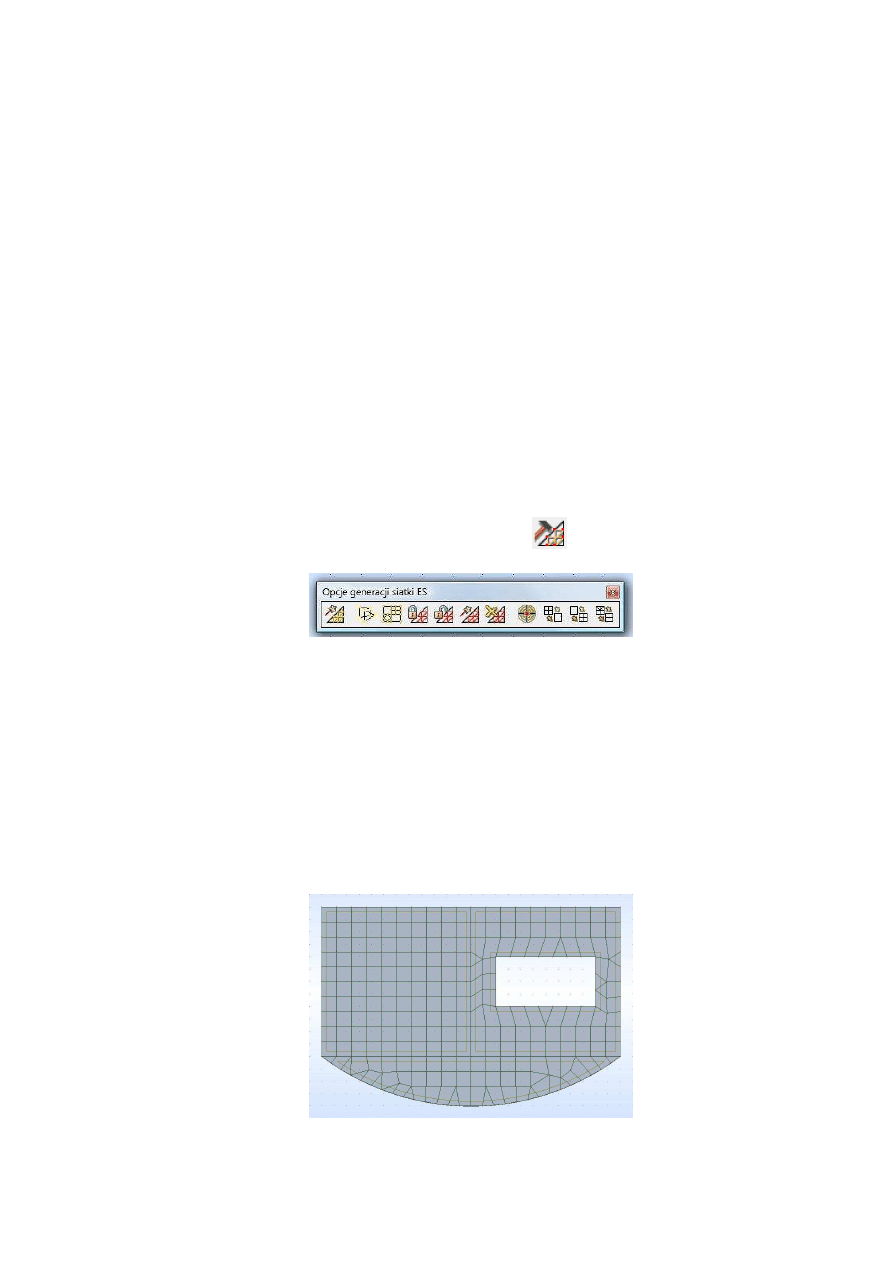
otwiera się okno do wyboru opcji siatkowania. Dla dopuszczalnych metod siatkowania wy-
bieramy Siatkowanie proste (Coons). Następnie w opcjach generacji siatki dokonuje-
my wyboru Rozmiar elementu i wpisujemy wartość oczka siatki 0,6 m. Zatwierdzamy
OK.

Pierwsza ikonka z paska narzędzi (rys. 10) służy do wykonania czynności wygenerowa-

nia siatki. Przykładowa wygenerowana siatka może mieć wygląd jak na rys. 11. Na koniec
możemy wyłączyć pasek narzędzi.

Rys.11. Przykładowa siatka ES dla obliczanego zadania

10

Wykonanie obliczeń. Obliczenia przeprowadzamy poprzez naciśnięcie ikonki

,

która znajduje się w górnym menu.

Podgląd wybranych rezultatów. Na liście rozwijalnej u góry wybieramy system okie-
nek Rezultaty to Rezultaty - mapy. W nowym układzie w okienku po prawej stronie
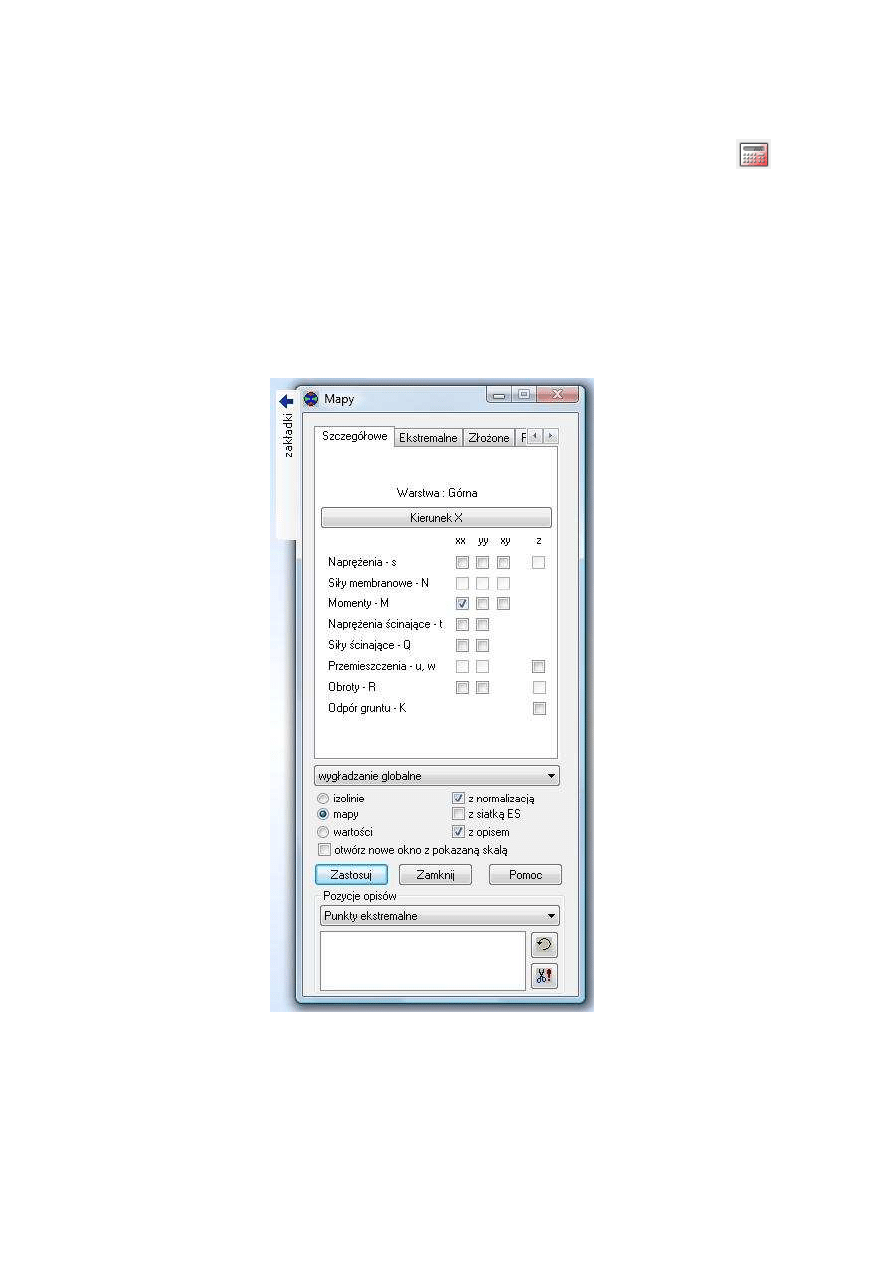
na zakładce Szczegółowe zaznaczamy przykładowo momenty Mxx, a następnie z opi-
sem i Punkty ekstremalne. Dodatkowo wprowadzamy globalne wygładzanie. Wów-
czas wybrane przez nas opcje powinny być zgodne z rys. 12, a w efekcie otrzymujemy
rozkład momentów jak na rys. 13(a).

Rys.12. Okno do wprowadzania opcji do wyświetlania map

W oknie z rys. 12 przechodzimy do zakładki Paramtery (tego nie ma na rysunku!),

a tam zaznaczamy Redukcja sił nad słupami i ścianami oraz zatwierdzamy Zasto-
suj. Następnie z powrotem przechodzimy do zakładki Szczegółowe, wybieramy opcje
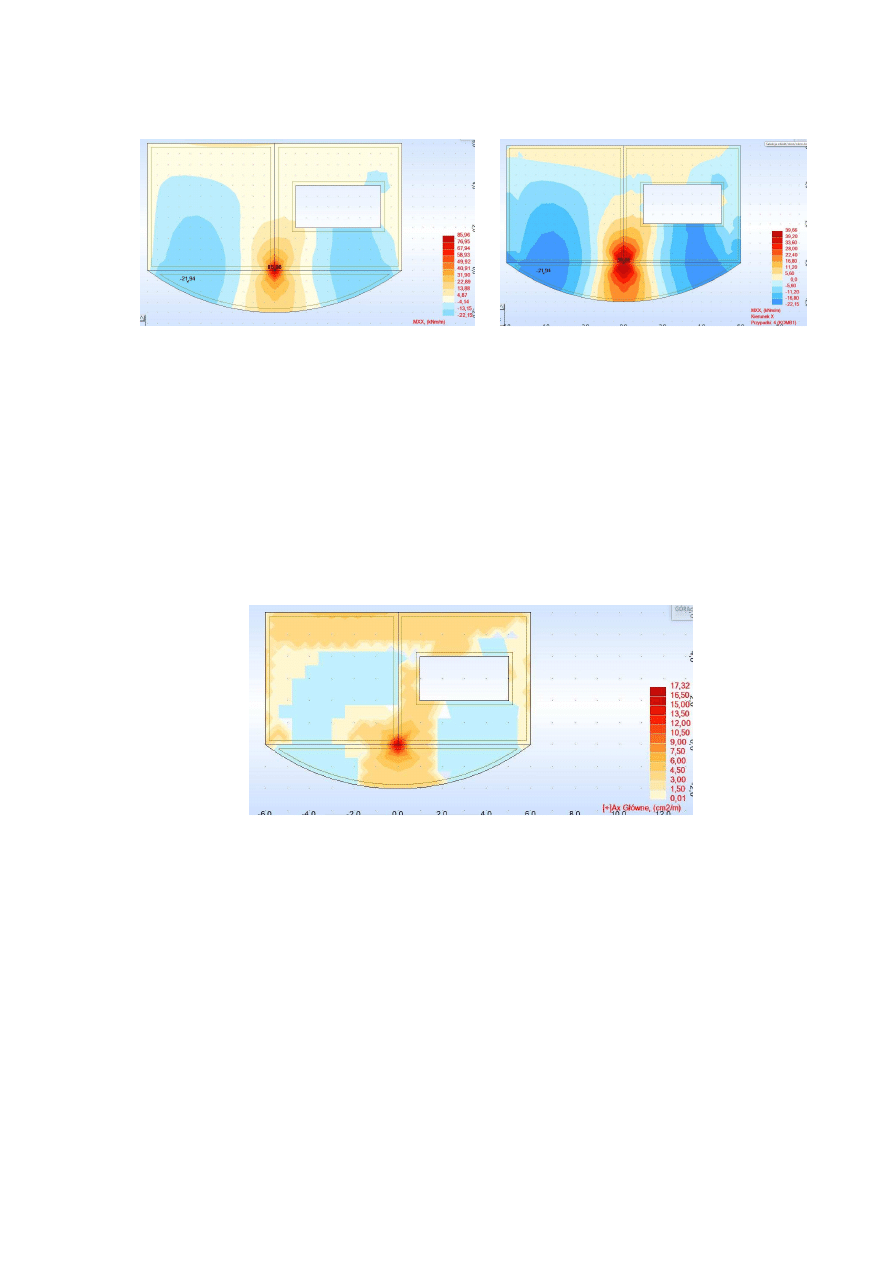
jak poprzednio i ponownie wyświetlamy rozkład momentów Mxx. Wartość maksymalna
powinna zostać zredukowana, jak to pokazano na rys. 13(b).

6. SIATKA ES, OBLICZENIA I PRZEGLĄD REZULTATÓW

11

(a) Bez redukcji sił

(b) Z redukcją sił

Rys.13. Rozkład momentów Mxx

Analiza zbrojenia. Na podstawie rezultatów otrzymanych z postprocessingu możemy
dalej analizować płytę, np. pod kątem zrojenia. W tym celu należy wybrać z górnego menu
Analiza → Wymiarowanie elementów żelbetowych → Wymiarowanie paneli

żelbetowych → Obliczenia. Następnie w wyświetlonym oknie naciskamy na Oblicz
i po obliczeniu zamykamy okno. Teraz można oglądać wstępne wyniki do wymiarowania,
np. Zbrojenie teoretyczne dla powierzchni AX[+] (por. rys. 14). Kontynuując mo-
żemy też wyświtlać wartości rzeczywiste powierzchni zbrojenia, albo proponowany przez
program układ zbrojenia.

Rys.14. Przykładowe zbrojenie teoretyczne AX[+]