Analiza stateczności ścianki

szczelnej z zastosowaniem

Metody Różnic Skończonych

Marek Cała, Jerzy Flisiak

Katedra Geomechaniki, Budownictwa i Geotechniki WGiG AGH

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

Do projektowania ścianek szczelnych wykorzystywane są najczęściej metody

stanów granicznych polegające na:

¾

wyznaczeniu metodą Coulomba sił parcia czynnego na część ścianki
powyżej dna wykopu i sił parcia biernego na część ścianki poniżej dna
wykopu oraz parcia wody,

¾

wyznaczeniu głębokości wbicia ścianki dla przyjętego sposobu jej
umocowania w gruncie (podparcie przegubowe lub utwierdzenie),

¾

obliczeniu momentów zginających i sił w elementach stabilizujących
metodami graficznymi lub analitycznymi (np. Bluma),

¾

wymiarowaniu elementów ścianki oraz elementów stabilizujących

¾ Stosowanie uproszczonych schematów może jednak prowadzić do

wyciągania błędnych wniosków.

¾ W stanach odbiegających od granicznych uzyskuje się zawyżone, w stosunku

do rzeczywistych, wartości sił odporu, prowadzące do zaniżenia wartości

momentów zginających i niewłaściwego zaprojektowania konstrukcji.

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

¾

Znaczne zwiększenie dokładności obliczeń oraz rezygnację z wielu
założeń upraszczających uzyskać można stosując do projektowania
konstrukcji oporowych numeryczne metody rozwiązywania zadań teorii
sprężystości i plastyczności.

¾

Stosowanie metod numerycznych do projektowania jest zgodne z
Eurokodem 7-1, gdzie zaliczane są one do jednej z czterech
podstawowych metod projektowania.

¾

Do analizy stateczności można zastosować metodę elementów
skończonych, czy też metodę różnic skończonych.

¾

W porównaniu do klasycznych metod obliczeniowych metody
numeryczne

posiadają jedno, bardzo istotne ograniczenie

. Mogą one

bowiem służyć tylko do analizy stateczności konstrukcji o z góry
określonych parametrach.

¾

Stosowanie ich jako jedyne narzędzie projektowe może nastręczać istotne
trudności. Nadają się one jednak świetnie do weryfikacji i korekty
wyników uzyskanych z klasycznych metod projektowych.

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Marek Cała – Katedra Geomechaniki, Budownictwa i Geotechniki

FLAC (Version 5.00)

LEGEND

1-May-05 19:38
step 96858
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

User-defined Groups

p_pylasty
pyl_piaszczysty
p_sredni

Grid plot

0

5E 0

Fixed Gridpoints

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X X-direction

Attached Gridpoints

interface id#'s

102

101

Net Applied Forces
max vector = 2.065E+04

0

5E 4

Beam plot

Cable plot

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

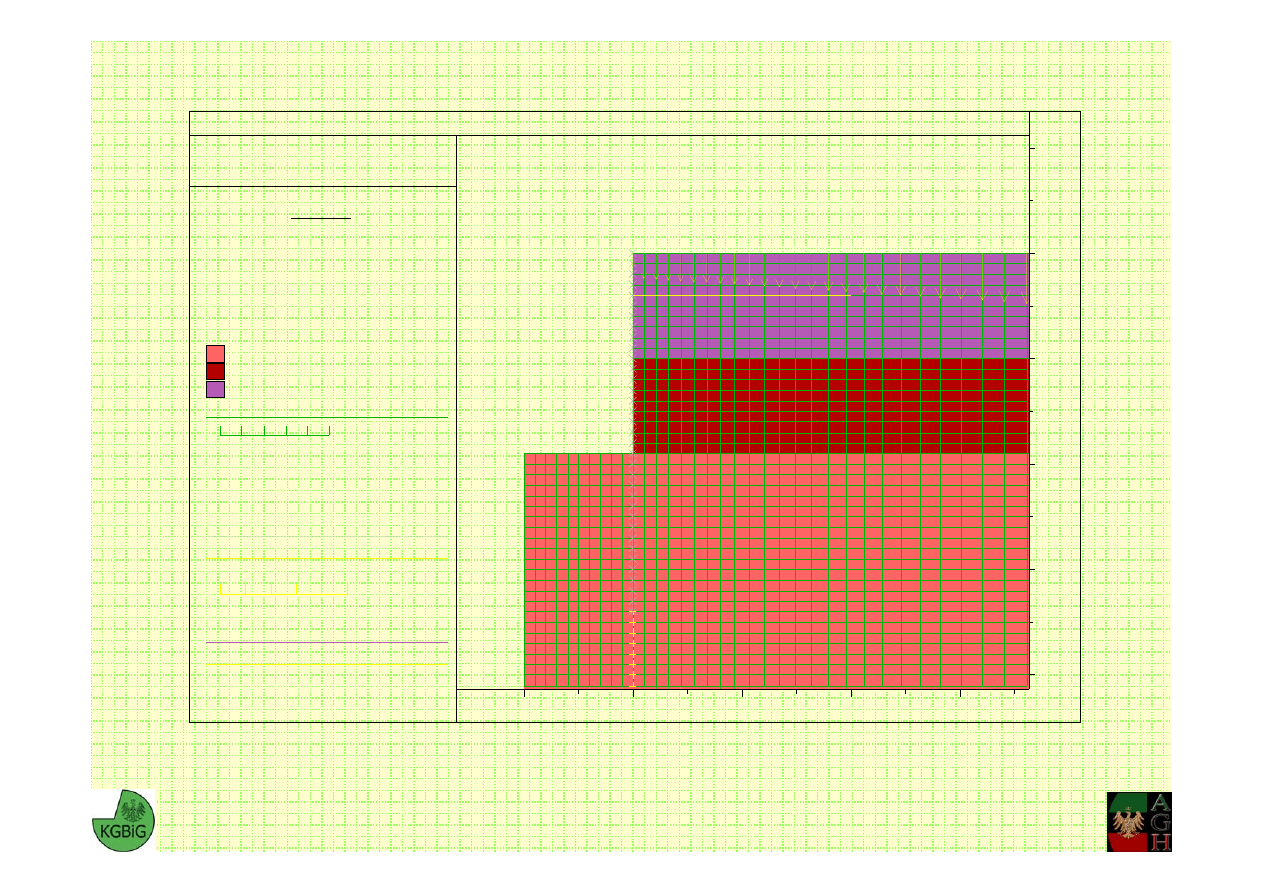
JOB TITLE : Geometria modelu

Marek Cala
Katedra Geomechaniki

19.62 kPa

Pył piaszczysty

Piasek średni

Piasek pylasty

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

¾ Na podstawie obliczeń z zastosowaniem metod klasycznych, w pracy

[11] stwierdza się, że dla zachowania stateczności wykopu należy
zastosować profile Larssena o wskaźniku wytrzymałości na zginanie
W

x

równym 2200 cm

3

o długości całkowitej równej 16.9 m (dla celów

obliczeń numerycznych przyjęto długość 17 m).

¾ Założono także, że ścianka musi być jednokrotnie kotwiona za pomocą

poziomych kotwi o nośności 183 kN, długości 10 m, budowanych z
krokiem 1.6 m w odległości 2.0 m od naziomu.

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

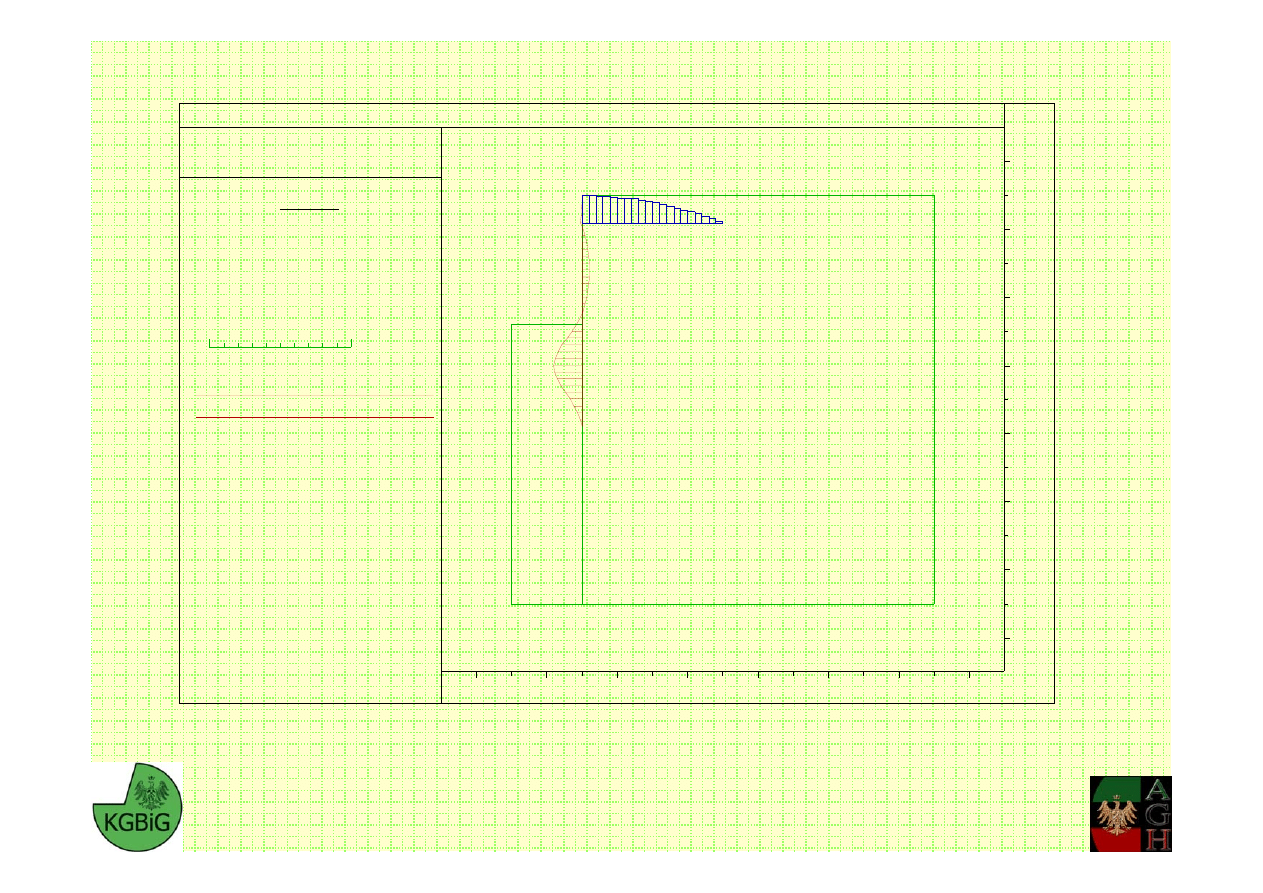
M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

M

gmax

= 515.1 kN →

σ = 234 MPa (!)

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

FLAC (Version 5.00)

LEGEND

1-May-05 19:38
step 96858
-5.000E+00 <x< 3.500E+01
-5.000E+00 <y< 3.500E+01

Boundary plot

0

1E 1

Beam Plot
Moment on
Structure Max. Value
# 1 (Beam ) -5.151E+05

Cable Plot
# 2 (Cable) -1.743E+05

-0.250

0.250

0.750

1.250

1.750

2.250

2.750

3.250

(*10^1)

-0.250

0.250

0.750

1.250

1.750

2.250

2.750

3.250

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

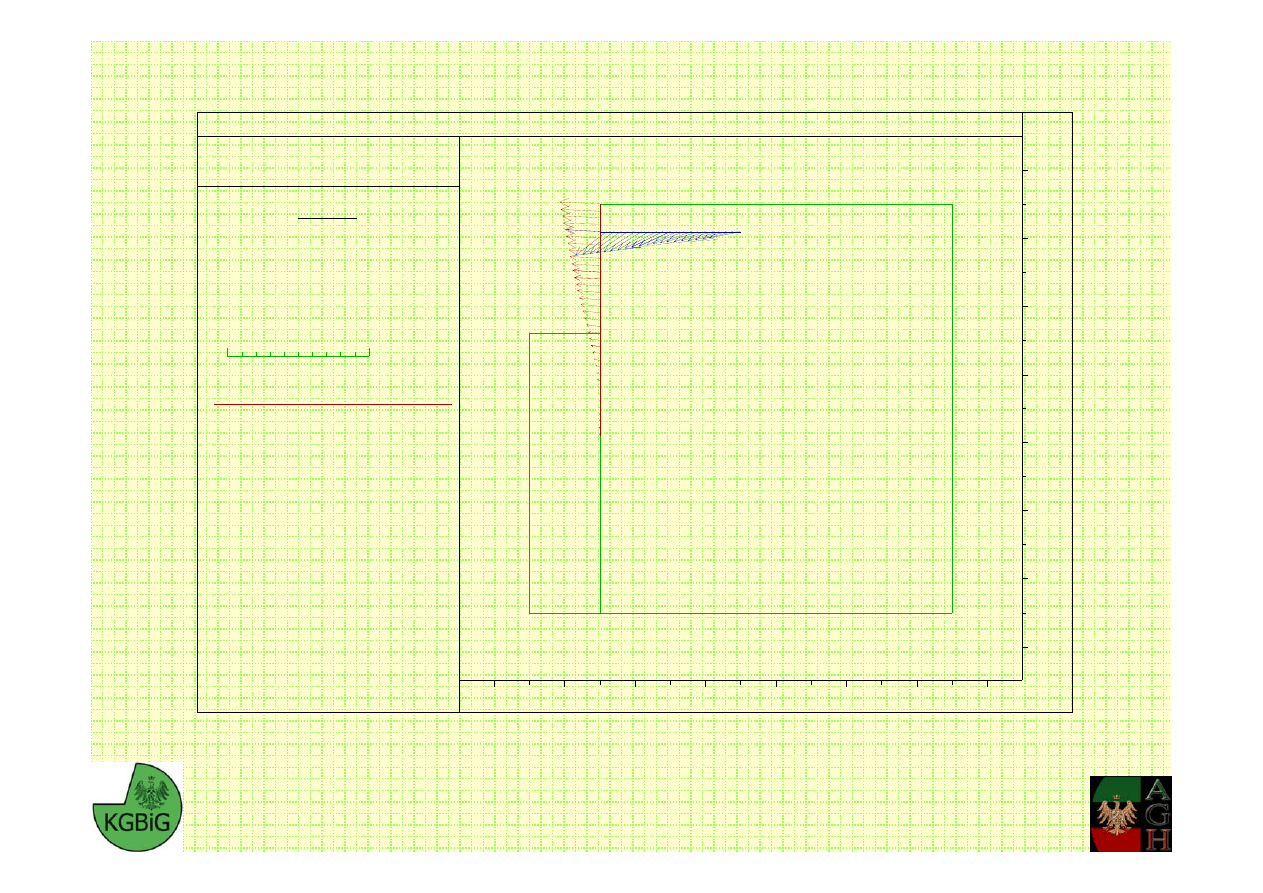
F

ax

= 174.3 kN →

ω = 95 %

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

-6x10

5

-4x10

5

-2x10

5

0x10

0

2x10

5

-5x10

5

-3x10

5

10

5

10

5

Moment gnący, Nm

18

16

14

12

10

8

6

4

2

0

G

łę

bok

o

ść

, m

Legenda

1m
2m
2.5m
3m
4m
5m
6m
7m
8m
9m
9.5m

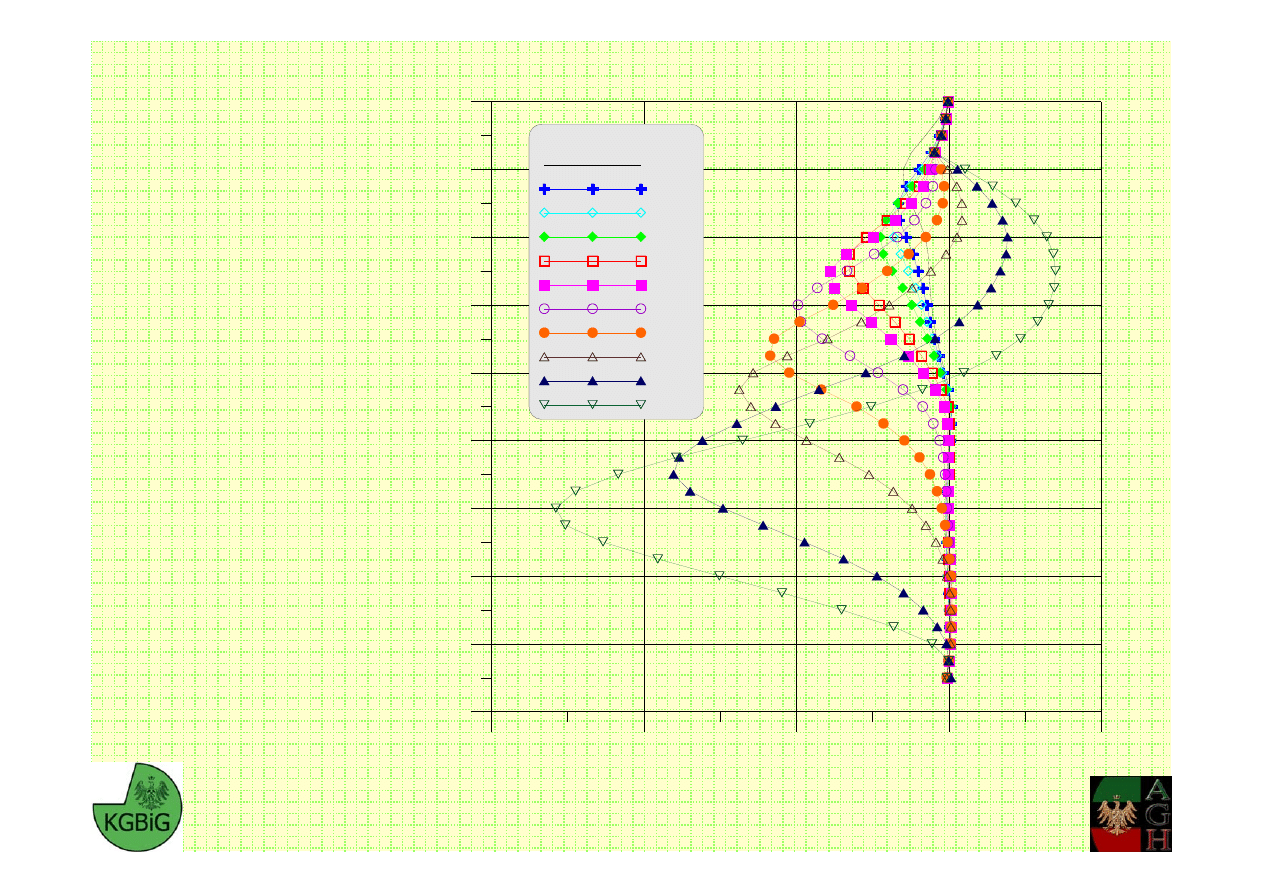
Rozkład momentów

gnących dla kolejnych

etapów pogłębiania

wykopu

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

FLAC (Version 5.00)

LEGEND

21-Sep-05 16:04
step 96858
-5.000E+00 <x< 3.500E+01
-5.000E+00 <y< 3.500E+01

Boundary plot

0

1E 1

Beam Plot
Structural Displacement
Max Value = 3.518E-01

Cable Plot
Structural Displacement
Max Value = 3.770E-01

-0.250

0.250

0.750

1.250

1.750

2.250

2.750

3.250

(*10^1)

-0.250

0.250

0.750

1.250

1.750

2.250

2.750

3.250

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

Przemieszczenia ścianki – 37.7 cm

Przemieszczenia kotwi – 35.2 cm

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

FLAC (Version 5.00)

LEGEND

1-May-05 21:02
step 134772
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

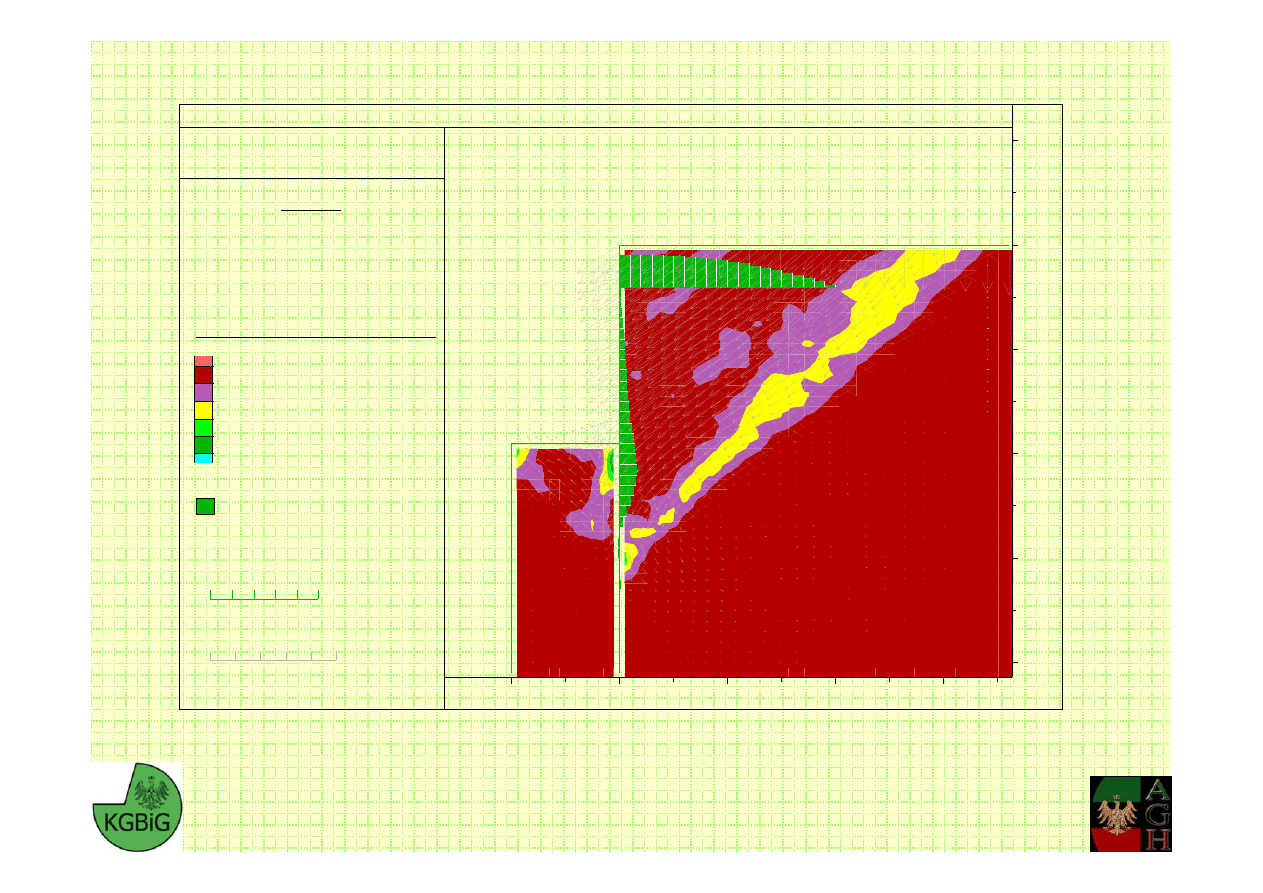
Factor of Safety 1.06

Max. shear strain-rate
0.00E+00
2.00E-08
4.00E-08
6.00E-08
8.00E-08
1.00E-07

Contour interval= 2.00E-08

Axial Force on

Structure Max. Value
# 1 (Beam ) 9.713E+04
# 2 (Cable) -1.830E+05
Boundary plot

0

5E 0

Cable plot

0

5E 4

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : Geometria modelu

Marek Cala
Katedra Geomechaniki

FS=1.06 (!)

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

FLAC (Version 5.00)

LEGEND

1-May-05 21:30
step 114543
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

User-defined Groups

p_pylasty
pyl_piaszczysty
p_sredni

Grid plot

0

5E 0

Fixed Gridpoints

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X X-direction

Attached Gridpoints

interface id#'s

102

101

Net Applied Forces
max vector = 2.065E+04

0

5E 4

Beam plot

Cable plot

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : Geometria modelu

Marek Cala
Katedra Geomechaniki

FLAC (Version 5.00)

LEGEND

1-May-05 21:59
step 130982
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

User-defined Groups

p_pylasty
pyl_piaszczysty
p_sredni

Grid plot

0

5E 0

Fixed Gridpoints

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X X-direction

Attached Gridpoints

interface id#'s

102

101

Net Applied Forces
max vector = 2.065E+04

0

5E 4

Beam plot

Cable plot

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

FLAC (Version 5.00)

LEGEND

1-May-05 21:59
step 130982
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

User-defined Groups

p_pylasty
pyl_piaszczysty
p_sredni

Grid plot

0

5E 0

Fixed Gridpoints

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X X-direction

Attached Gridpoints

interface id#'s

102

101

Net Applied Forces
max vector = 2.065E+04

0

5E 4

Beam plot

Cable plot

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

Nośność kotwi = 250 kN

FLAC (Version 5.00)

LEGEND

4-May-05 20:28
step 125115
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

User-defined Groups

p_pylasty
pyl_piaszczysty
p_sredni

Grid plot

0

5E 0

Fixed Gridpoints

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X X-direction

Attached Gridpoints

interface id#'s

102

101

Net Applied Forces
max vector = 2.065E+04

0

5E 4

Beam plot

Cable plot

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

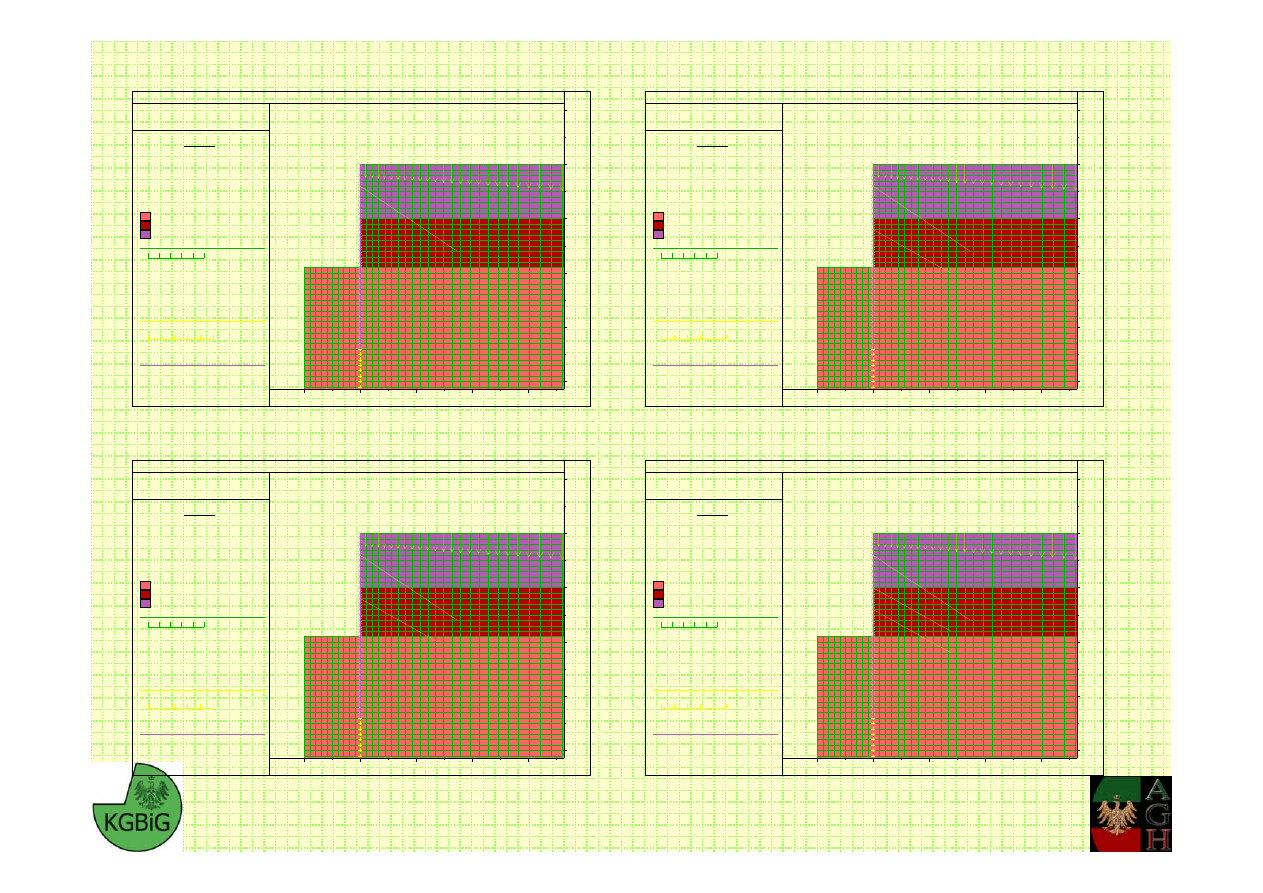
2

3

4

5

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

-6x10

5

-4x10

5

-2x10

5

0x10

0

2x10

5

-5x10

5

-3x10

5

10

5

10

5

Moment gnący, Nm

18

16

14

12

10

8

6

4

2

0

G

łę

bok

o

ść

, m

Legenda

wariant 1
wariant 2
wariant 3
wariant 4
wariant 5

σ, MPa

M

g

, kNm

Nr

112.2

246.8

5

126.2

277.7

4

119.4

262.6

3

246.1

541.4

2

234.1

515.1

1

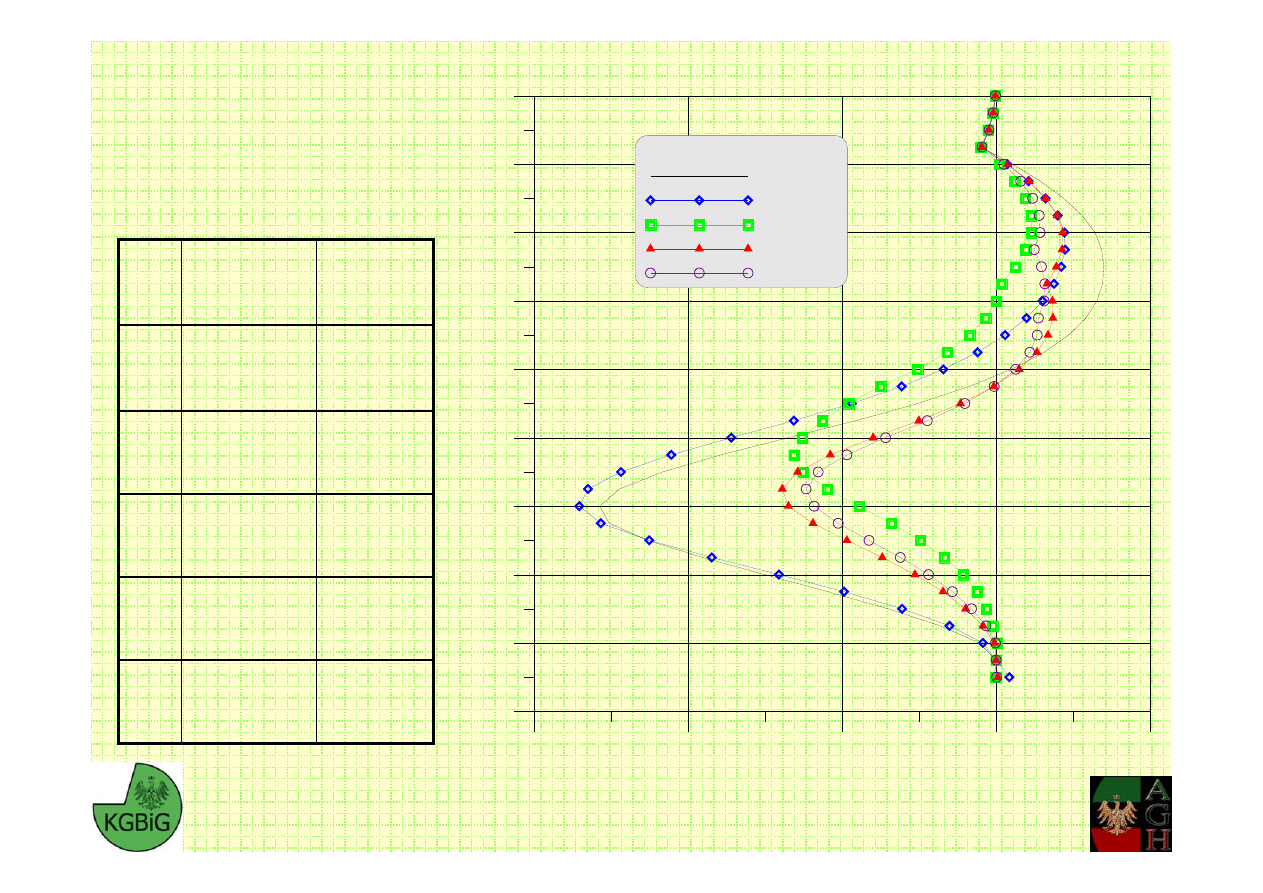
Rozkład momentów

gnących dla

poszczególnych

wariantów

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

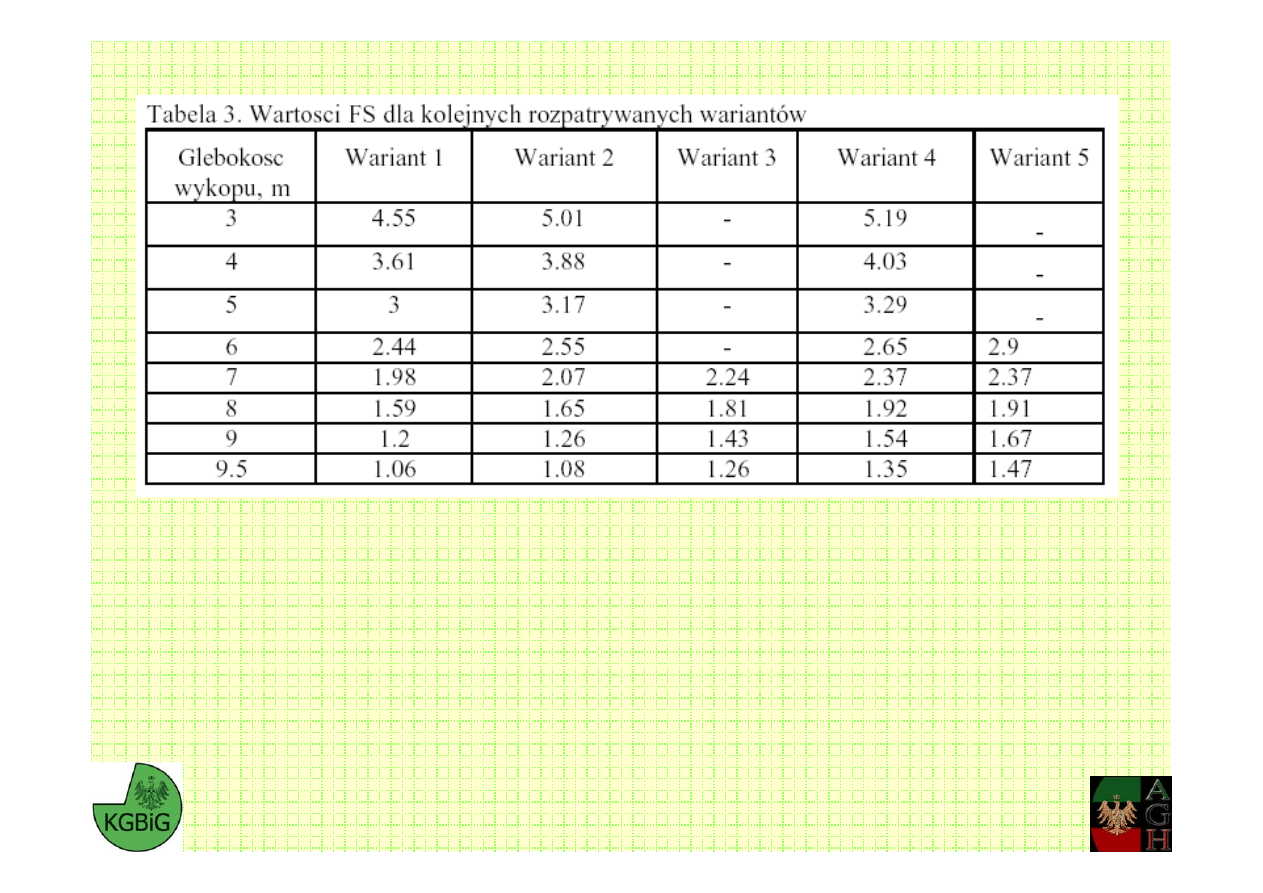
¾ Dla głębokości wykopu równej 9.5 m wskaźnik FS dla wariantu 3 osiąga

wartość 1.26.

¾ Zwiększenie nośności kotwi zaproponowane w wariancie 4 przyniosło

wzrost wartości FS o około 0.1 (docelowy FS=1.35).

¾ Zabudowa trzeciego rzędu kotwi (wariant 5) wywołuje dalszy wzrost

wartości FS, który, dla wykopu o głębokości 9.5 jest równy 1.47.

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

FLAC (Version 5.00)

LEGEND

4-May-05 20:28
step 125115
-4.948E+00 <x< 1.906E+01
9.495E+00 <y< 3.351E+01

Boundary plot

0

5E 0

Beam Plot
Structural Displacement
Max Value = 1.467E-01

Cable Plot
Structural Displacement
Max Value = 1.526E-01

1.000

1.400

1.800

2.200

2.600

3.000

(*10^1)

-0.200

0.200

0.600

1.000

1.400

1.800

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

Przemieszczenia ścianki – 14.67 cm

Przemieszczenia kotwi – 15.26 cm

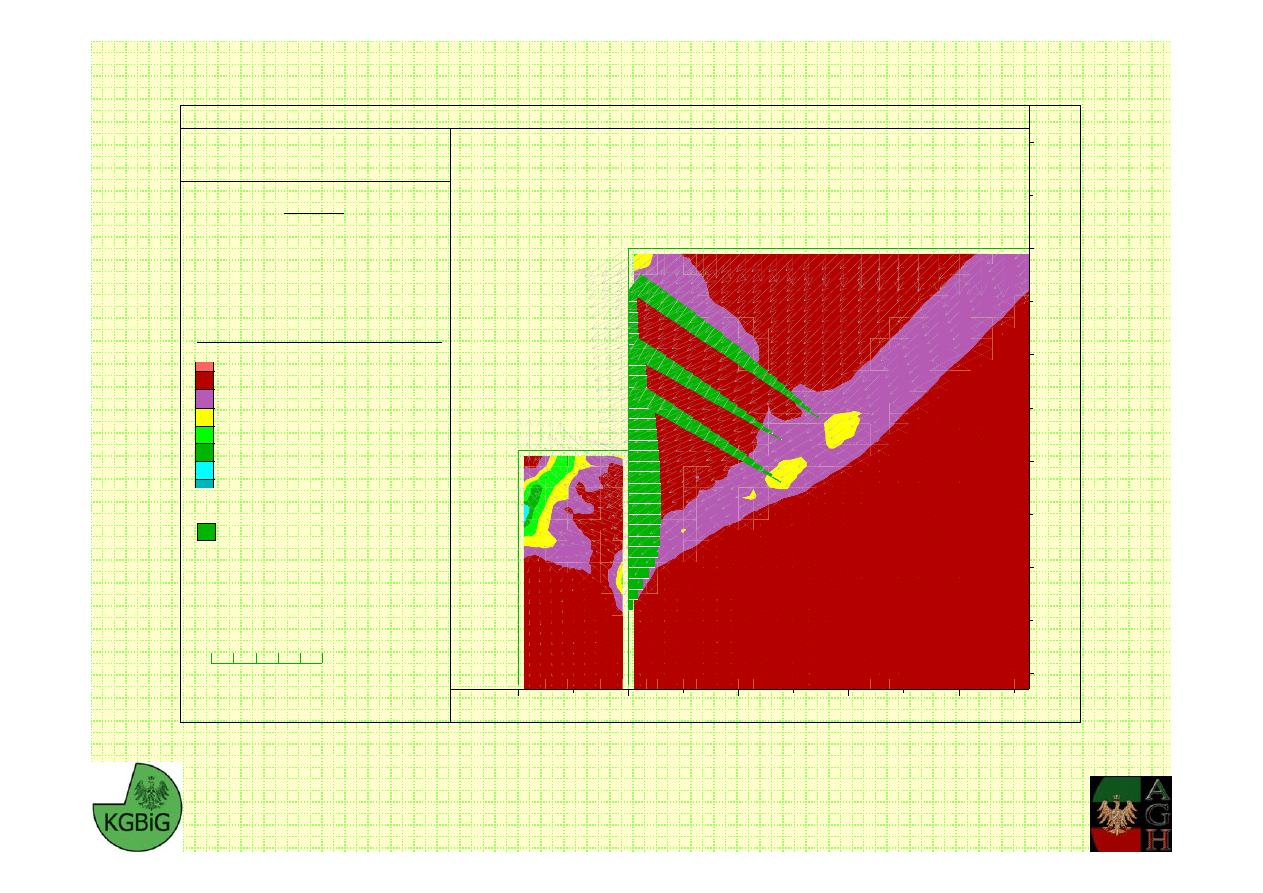
M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki

Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

FLAC (Version 5.00)

LEGEND

5-May-05 0:57
step 202131
-3.113E+00 <x< 2.320E+01
9.283E+00 <y< 3.559E+01

Factor of Safety 1.47

Max. shear strain-rate
0.00E+00
2.00E-08
4.00E-08
6.00E-08
8.00E-08
1.00E-07
1.20E-07

Contour interval= 2.00E-08

Axial Force on

Structure Max. Value
# 1 (Beam ) 3.913E+05
# 2 (Cable) -2.500E+05
# 3 (Cable) -2.306E+05
# 4 (Cable) -2.084E+05
Boundary plot

0

5E 0

1.000

1.500

2.000

2.500

3.000

3.500

(*10^1)

0.000

0.500

1.000

1.500

2.000

(*10^1)

JOB TITLE : .

Marek Cala
Katedra Geomechaniki

FS=1.47

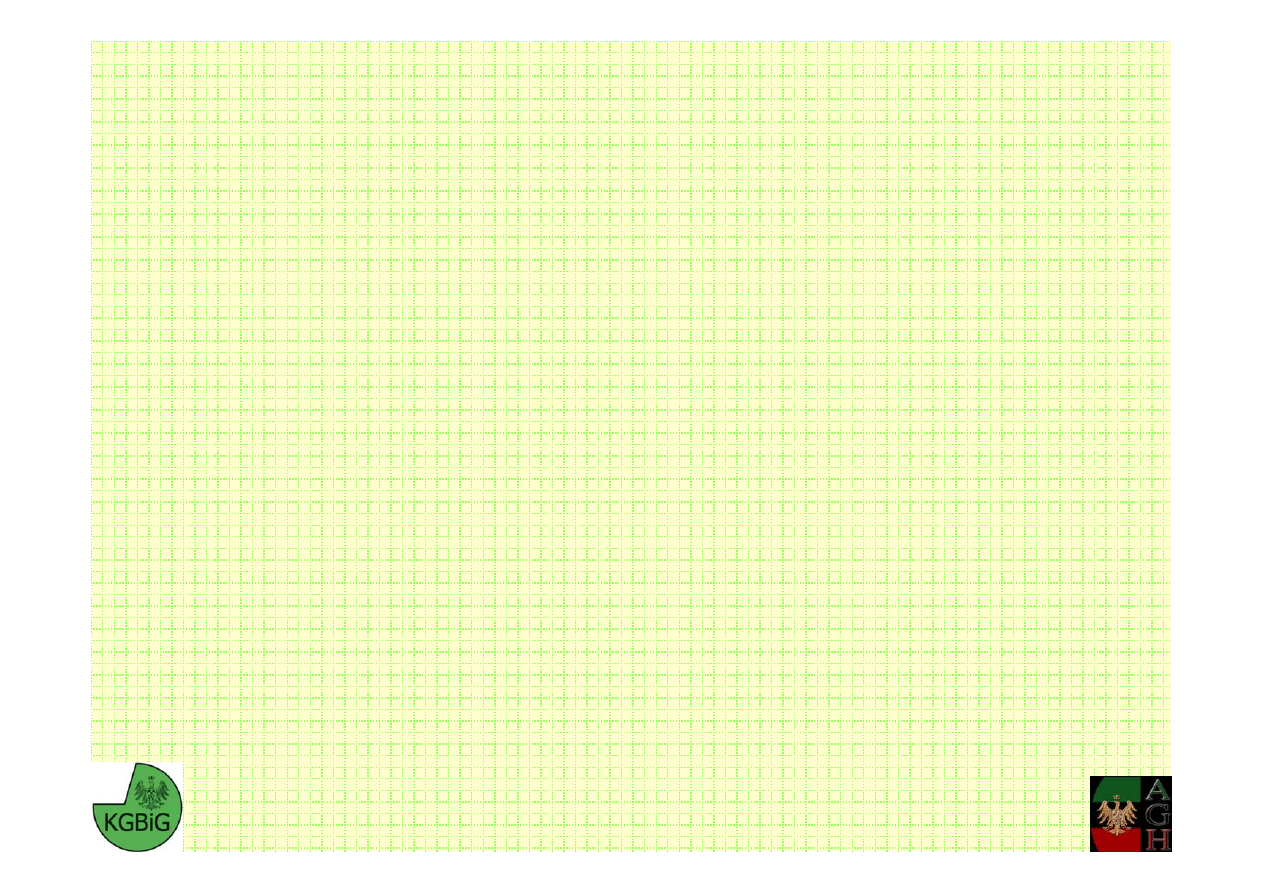
Analiza stateczności ścianki szczelnej z zastosowaniem Metody Różnic Skończonych

¾ Klasyczne metody obliczeniowe mogą prowadzić do popełnienia

znaczących błędów przy projektowaniu kotwionych ścianek
szczelnych.

¾ Nadają się one jednak świetnie do ustalenia wstępnych parametrów

konstrukcji kotwionej ścianki szczelnej (głębokość zabicia, profil
grodzicy, wymagana nośność kotwi). Parametry te mogą następnie być
dokładnie zweryfikowane i ewentualnie skorygowane poprzez
zastosowanie metod numerycznych.

¾ Pozwalają one na uniknięcie wielu uproszczeń, co w efekcie powoduje,

że analiza współpracy konstrukcji oporowej z gruntem jest bardziej
wiarygodna. Powinny być one stosowanie na znacznie szerszą skalę
jako narzędzie wspomagające projektowanie konstrukcji kotwionych
ścianek szczelnych.

Podsumowanie

M. Cała, J. Flisiak – Katedra Geomechaniki, Budownictwa i Geotechniki