Zastosowania metody symbolicznej
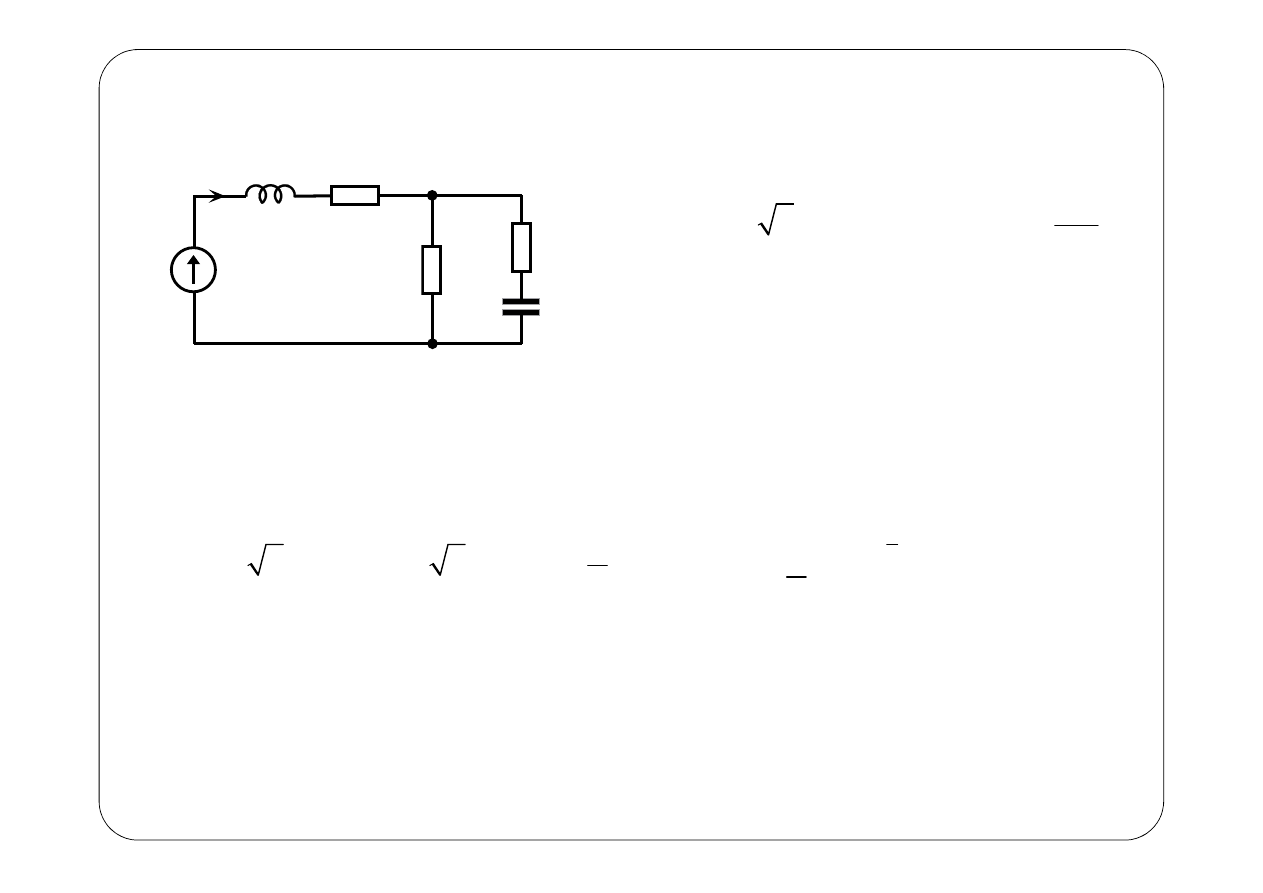
Przykład 1.
( )
e t
L
1
R
2
R
3
R
C
( )
i t
( )
6
0
0
1
2
3
rad
12 2 cos
V,
10
,
s
400Ω,
1kΩ,
500 Ω,
1mH,
2 nF.
e t
t
R
R
R
L
C
ω
ω
=
=
=
=
=
=
=
Wyznaczyć prąd (w stanie ustalonym)
( )
i t
Wyznaczyć prąd (w stanie ustalonym)
( )
i t
( )
( )
0
0
π
12 2 cos
12 2 sin
2
e t
t
t
ω
ω
=
=
+
π
j
2
12e
j12
E
=
=
⇌
E
L
1
R
2
R
3
R
C
I
Symboliczny schemat zastępczy:
Z
E
I
Z
=
gdzie
1
0
1
j
1
1
1
Z
R
L
R
R
ω
=
+
+
+
+
2
3
0
1
j
R
R
C
ω
+
Po podstawieniu danych liczbowych
(
)
3
3
1
1
400
j1000
0, 4
j
10
0,8
j0,8 10
1
1
2
1
1000
500
j500
1
j
Z
=
+
+
=
+ +
⋅
=
+
⋅
+
+
−
−
(
)
π
j
3
3
3
4
j12
10
7,5
j7,5 10
7,5 2 10 e
0,8
j0,8
I
−
−
−
=
⋅
=
+
⋅
=
⋅
+
( )
(
)
(
)
(
)
3
3
0
0
π
π
4
4
7,5 2 10
2 sin
15 10 sin
V.
i t
t
t
ω
ω
−
−
=
⋅
+
= ⋅
+
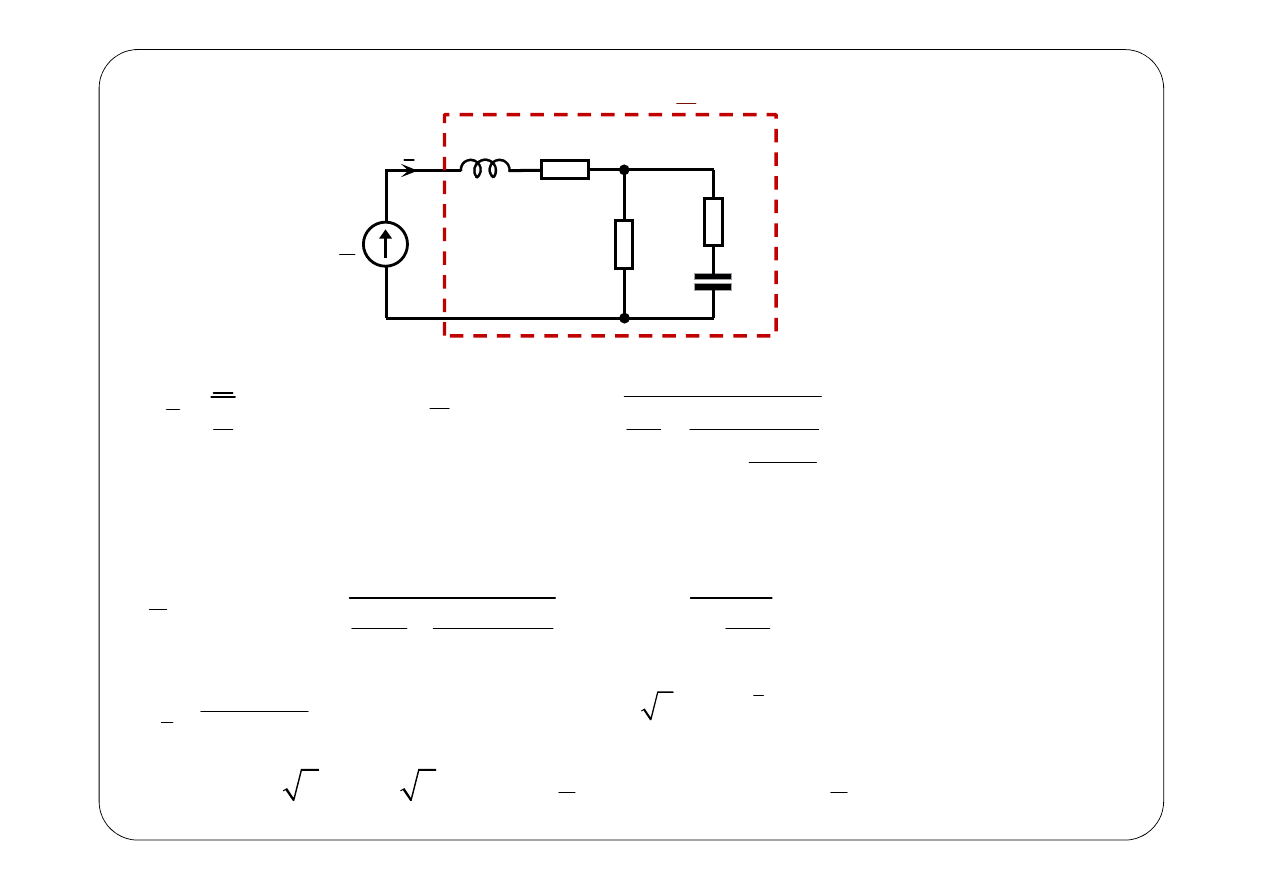
Przykład 2.
( )
z
i t
1
R
2
R
3
R
C
L
( )
u t
( )
(
)
3
4
z
0
0
1
2
3
π
4
rad
2 10 sin
A,
10
,
s
1kΩ,
2 kΩ,
2 kΩ,
0, 2 H,
50 nF.
i t
t
R
R
R
L
C
ω
ω
−
= ⋅
−
=
=
=
=
=
=
Wyznaczyć napięcie (w stanie ustalonym)
( )
u t
( )
( )
(
)
3
z
0
π
4
2 10 sin
i t
t
ω
−
= ⋅
−
π
3
3
j
4
z
2 10
2 10
π
π
e
cos
jsin
4
4
2
2
I
−
−
−
⋅
⋅
=
=
−
=
⇌
( )
3
3
2 10
2
2
j
1
j 10
2
2
2
−
−
⋅
=
−
= − ⋅
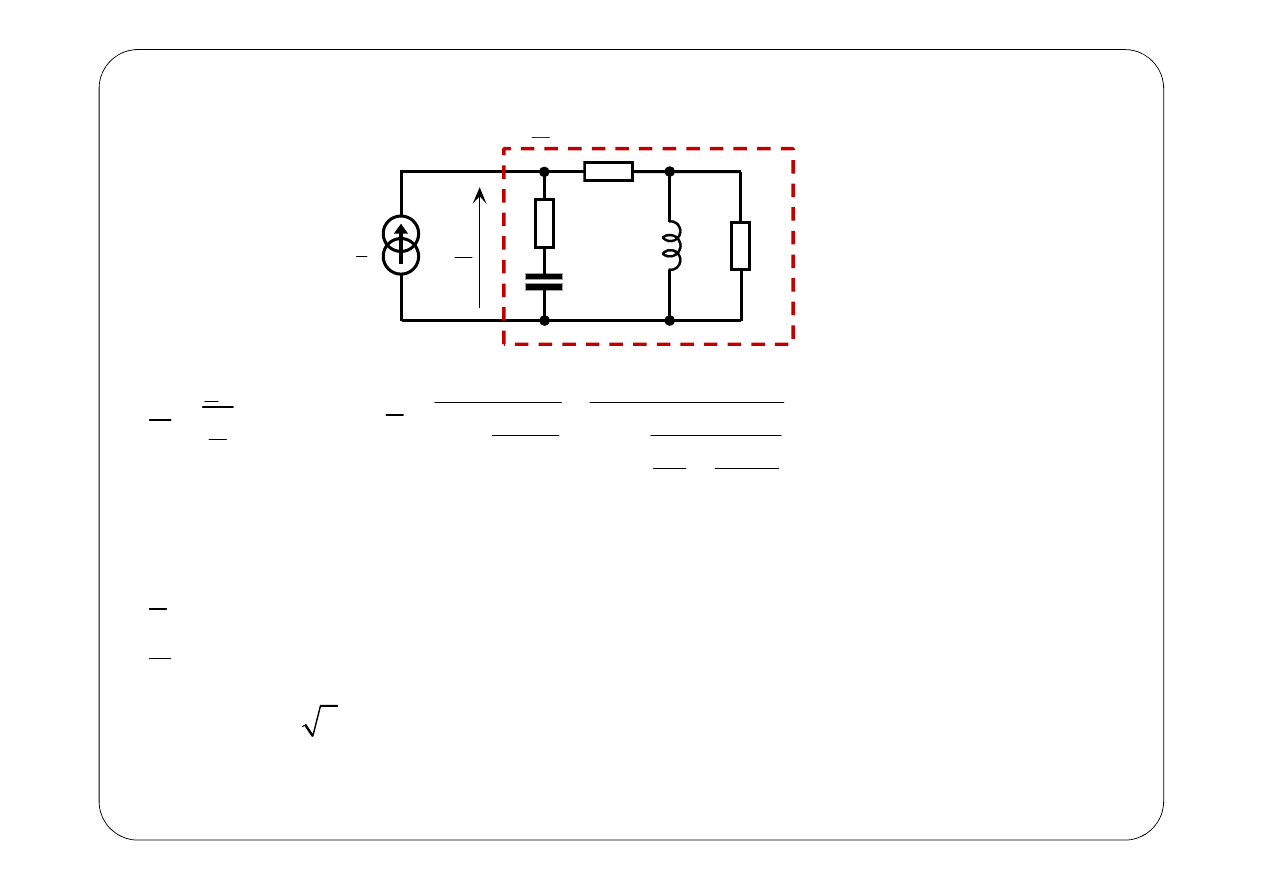
Z
I
1
R
2
R
3
R
C
L
U
Symboliczny schemat zastępczy:
z
,
I
U
Y
=
Y
1
2
1
1
gdzie
1
1
1
1
j
Y
R
R
C
ω
=
+
+
+
+
1
2
0
3
0
1
1
j
j
R
R
C
R
L
ω
ω
+
+
+
Po podstawieniu danych liczbowych
(
)
3
j1,326
0,5
j0,3 10 ,
0,5882
j2,353
2, 425e
,
Y
U
−
−
=
+
⋅
=
−
=
( )
(
)
0
2, 425 2 sin
1,326 V.
u t
t
ω
=
−
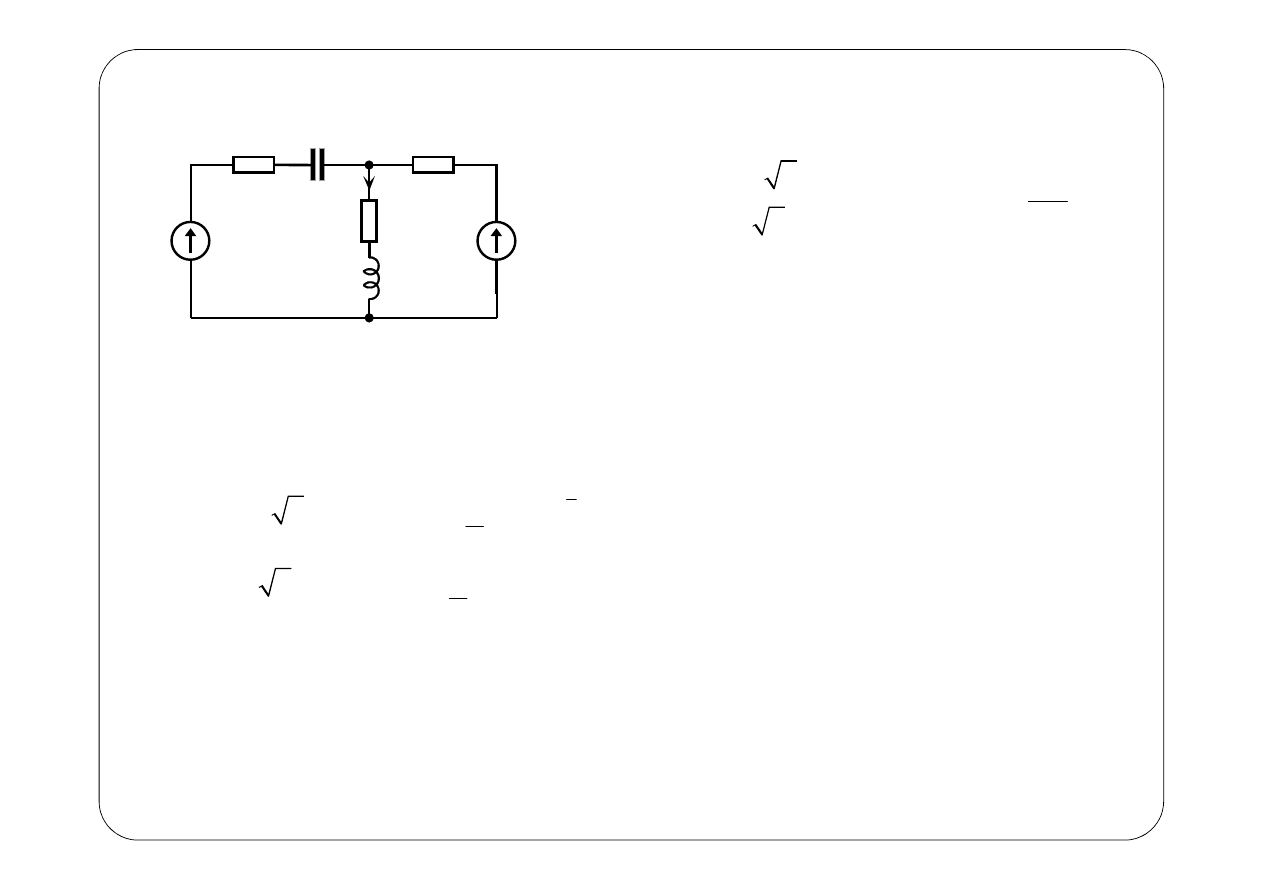
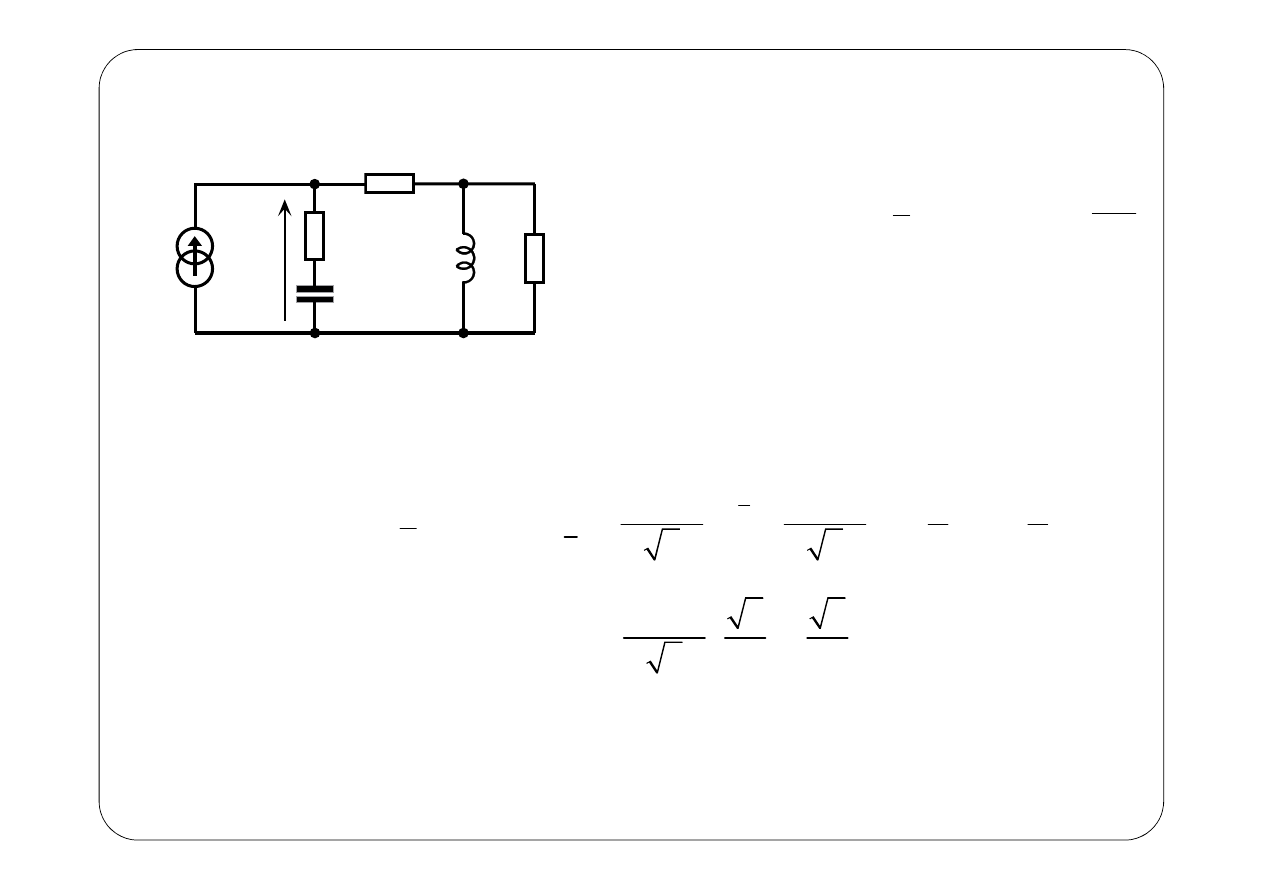
Przykład 3.
( )
i t
( )
2
e t
2
R
3
R
L
1
R
C
( )
1
e t
( )
( )
1
0
4
0
2
0
1
2
3
25 2 cos
V,
rad
10
,
s
5 2 sin
V,
1kΩ,
100 Ω,
100 Ω,
10 mH,
0,1µF.
e t
t
e t
t
R
R
R
L
C
ω
ω
ω
=
=
=
=
=
=
=
=
Wyznaczyć prąd (w stanie ustalonym)
( )
i t
( )
π
j
2
1
1
0
25 2 cos
25e
j 25
e t
t
E
ω
=
=
=
⇌
( )
j0
2
2
0
5 2 sin
5e
5
e t
t
E
ω
=
=
=
⇌
I
2
E
2
R
3
R
L
1
R
C
1
E
1
I
2
I
2
U
1
U
U
1
2
.
,
1
0
I
I
I
− − + =
1
a
b
Symboliczny schemat zastępczy:
(
)
1
1
1
1
1
,
1
1
I
U
E
U
R
R
ω
ω
=
=
−
+
+
Prawa Kirchhoffa
Prawo Ohma
1
1
1
1
a.
0,
E
U
U
U
E
U
−
+
+ =
⇒
=
−
2
2
2
2
0
b.
,
U
U
E
U
E
U
− −
+
=
⇒
=
−
(
)
1
1
0
0
2
2
2
2
2
3
0
1
1
j
j
1
1
,
1
.
j
R
R
C
C
I
U
E
U
R
R
I
U
R
L
ω
ω
ω
+
+
=
=
−
=
+
(
)
(
)
1
2
2
3
0
1
0
1
1
1
0
1
j
j
E
U
E
U
U
R
R
L
R
C
ω
ω
−
−
−
−
+
=
+
+
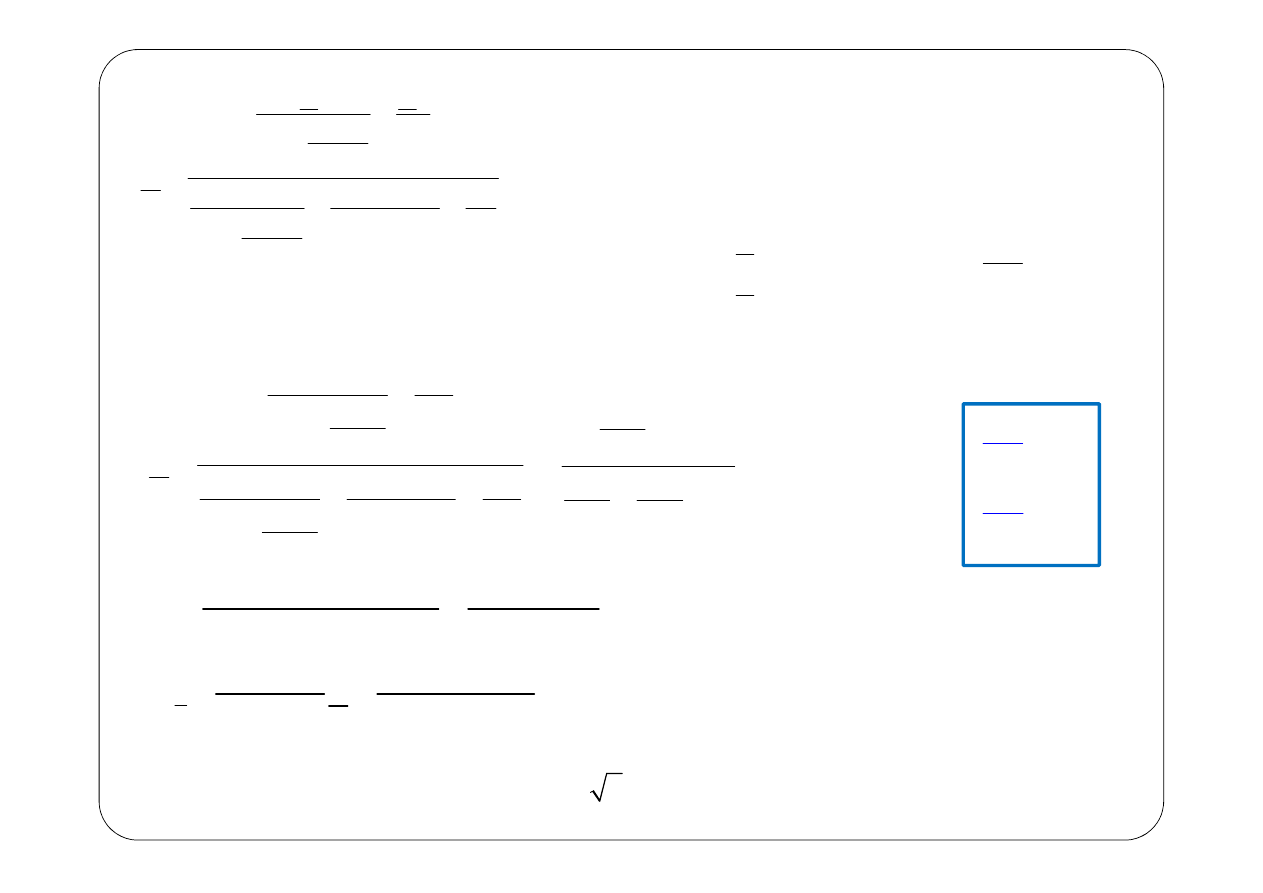
1
2
2
1
0
3
0
2
1
0
1
j
1
1
1
1
j
j
E
E
R
R
C
U
R
L
R
R
C
ω
ω
ω
+
+
=
+
+
+
+
Po podstawieniu danych liczbowych
1
4
0
2
1
2
3
j25 V,
rad
10
,
s
5 V,
1kΩ,
100Ω,
100Ω,
10 mH,
0,1µF.
E
E
R
R
R
L
C
ω
=
=
=
=
=
=
=
=
2
3
3
j25
5
1
10
10
j10
−
+
+
=
j25
50
1
j
+
−
2
1
j
= +
−
3
2
2
2
3
3
j10
1
1
1
1
10
j10
10
10
j10
U
−
−
=
+
+
+
+
1
j
1
10
10
1
j
1
j
−
=
=
+
+
−
+
37,5
j12,5
37,5
j12,5
2,015
j1,392
0,5
j0,5
5
j5+10
15,5
j4,5
+
+
=
=
=
+
+
+ −
−
(
)
3
3
0
1
2, 015
j1,392
17, 03
j3,119 10
j
100
j100
I
U
R
L
ω
−
+
=
=
=
−
⋅
+
+
3
j0,1811
17,32 10 e
−
−
=
⋅
( )
(
)
3
0
17,32 10
2 sin
0,1811 A.
i t
t
ω
−
=
⋅
−
1
j
1
j
2
1
j
1
j
= +
−
= −
+
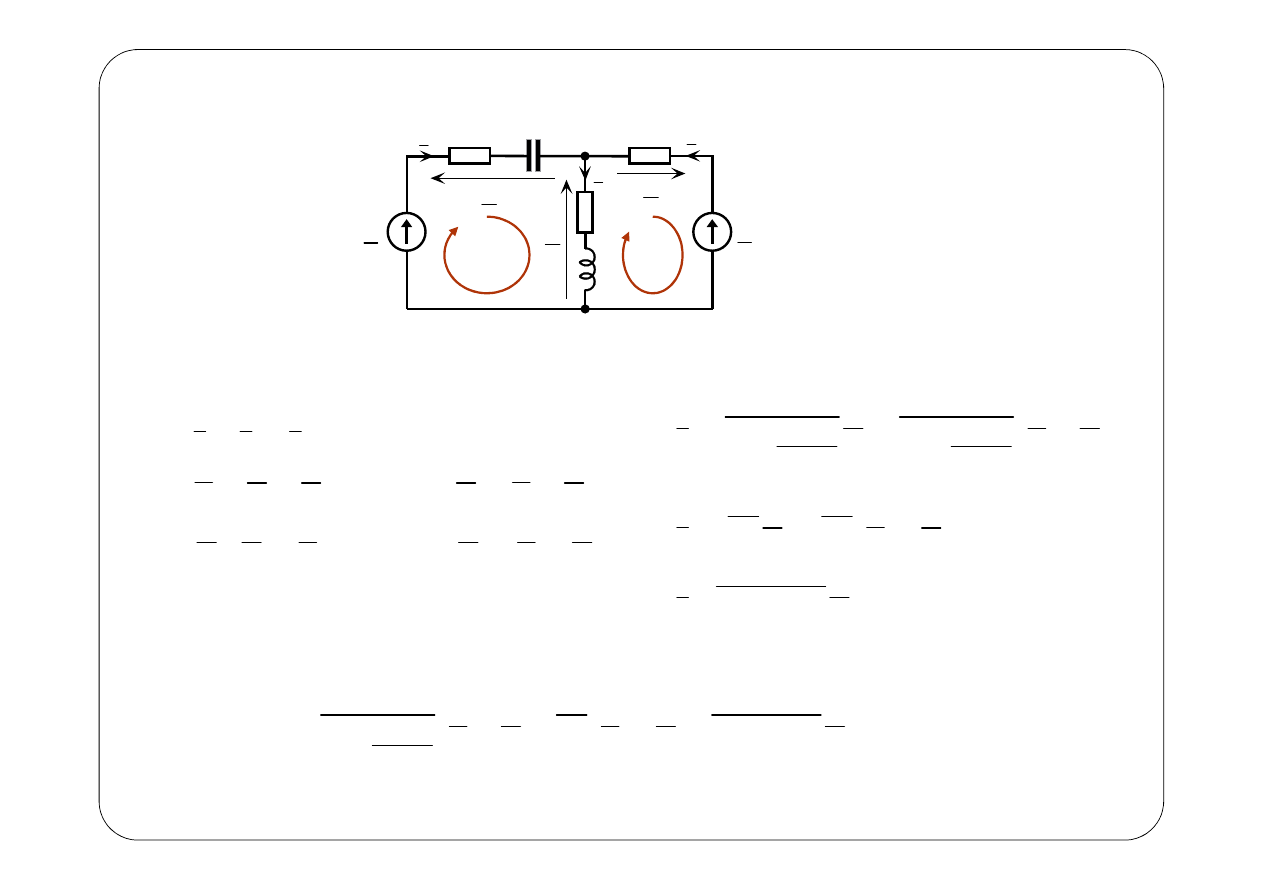
Przykład 4.
( )
e t
( )
z
i t
L
1
R
2
R
C
( )
i t
( )
(
)
( )
0
6
0
z
0
1
2
π
4
20sin
V,
rad
10
s
0,01 2 cos
A,
500Ω,
2, 2 kΩ,
0,8 mH,
1,5nF.
e t
t
i t
t
R
R
L
C
=
−
=
=
=
=
=
=
ω
ω
ω
Wyznaczyć prąd (w stanie ustalonym)
( )
i t
( )
(
)
( )
π
j
4
0
z
z
0
π
4
20
20sin
e
10
j10
2
0,01 2 cos
j0,01
e t
ω t
E
i t
ω t
I
−
=
−
=
= −
=
=
⇌
⇌
Symboliczny schemat zastępczy:
E
z
I
L
1
R
2
R
C
I
1
I
U
1
U
1
z
1
z
1
0,
0,
I
I
I
I
I
I
E
U
U
− + −
=
⇒
= +
− + +
=
(
)
1
0
1
z
1
0
0
2
2
1
,
1
1
j
1
1
,
1
1
j
j
U
I
R
L
U
I
I
I
C
C
R
R
=
+
=
=
+
+
+
ω
ω
ω
Prawa Kirchhoffa
Prawo Ohma
(
)
1
1
(
)
z
0
3
3
j0,6365
2
0
1
0
2
1
j
15,03
j11,11 10
18,69 10 e
1
1
1
1
1
j
j
I
E
C
R
I
C
R
L
R
−
−
−
−
+
=
=
−
⋅
=
⋅
+
+
+
ω
ω
ω
( )
(
)
3
0
18,69 10
2 sin
0,6365 A.
i t
t
−
=
⋅
−
ω
(
)
z
0
1
0
2
1
1
0
1
1
1
j
j
E
I
I
I
C
R
L
R
− +
+
+
=
+
+
ω
ω
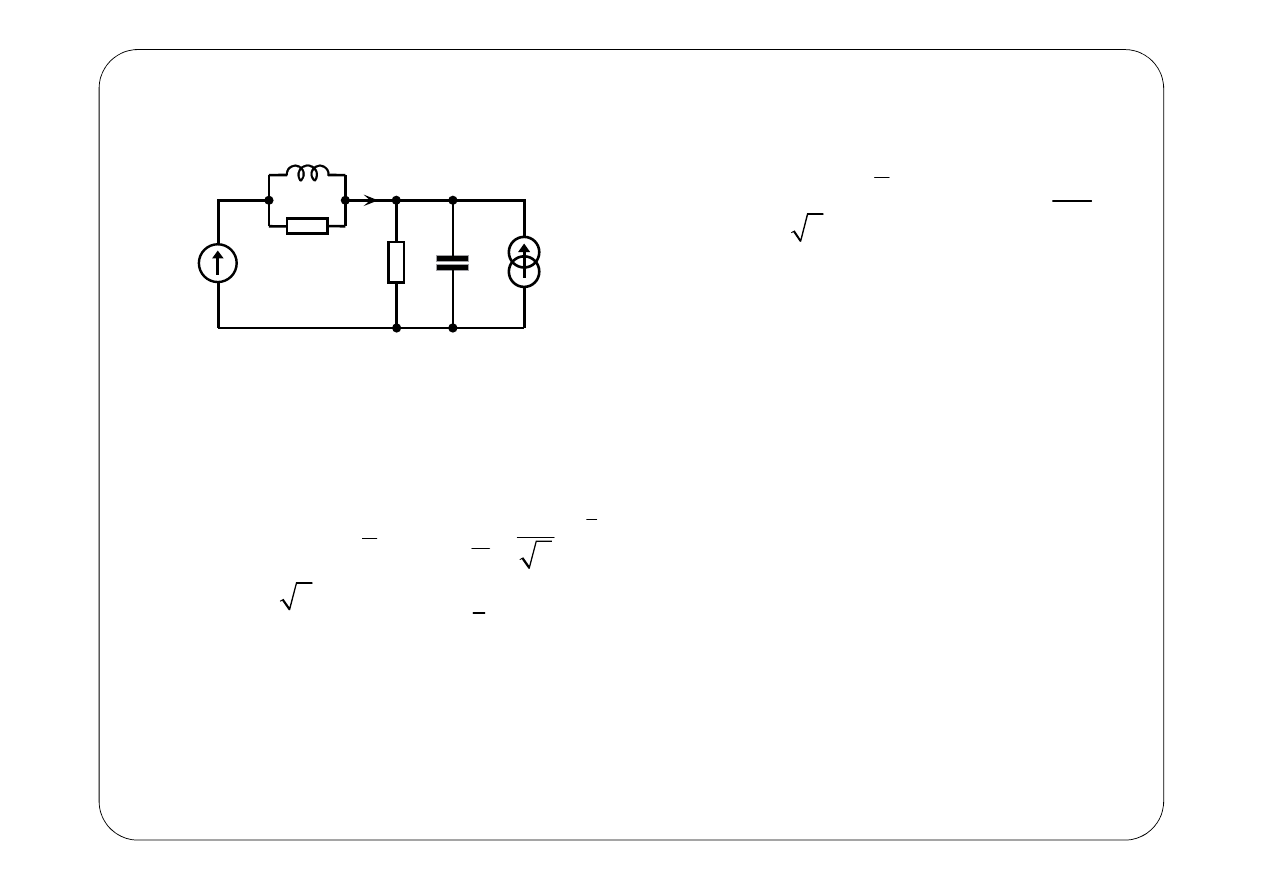
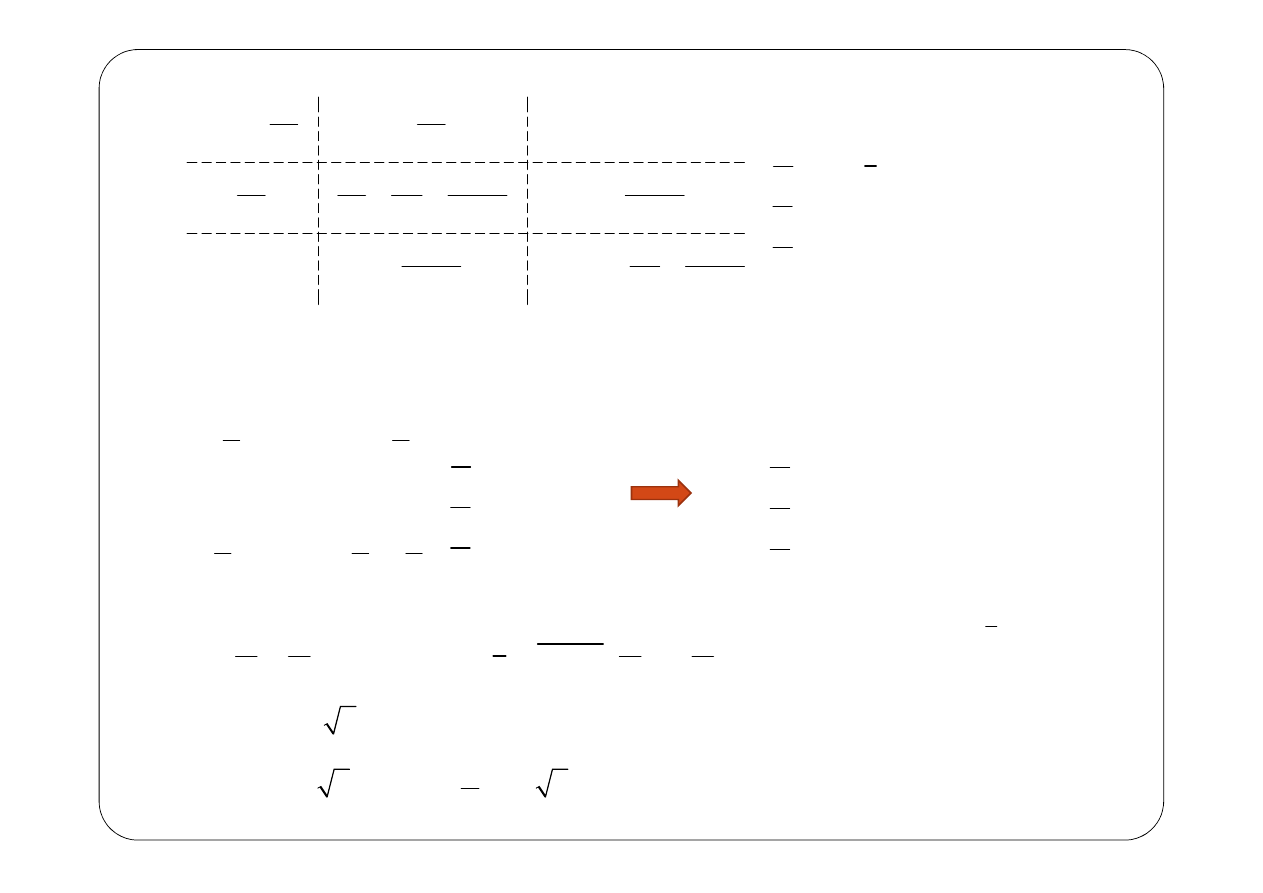
Metoda napięć węzłowych
( )
i t
1
R
R
R
C
L
( )
i t
( )
u t
( )
( )
( )
z
0
0
1
2
3
1
1
2
2
rad
2 2 sin
A,
1
s
1Ω,
1Ω,
2 Ω,
H,
F.
i t
t
R
R
R
L
C
=
=
=
=
=
=
=
=
=
ω
ω
( )
z
i t
2
R
3
R
( )
u t
( )
( )
?
?
u t
i t
=
=
j0
z
2e
2
I
=
=
z
I
1
R
C
L
2
R
3
R
I
U
1
2
3
n1
U
n2
U
n3
U
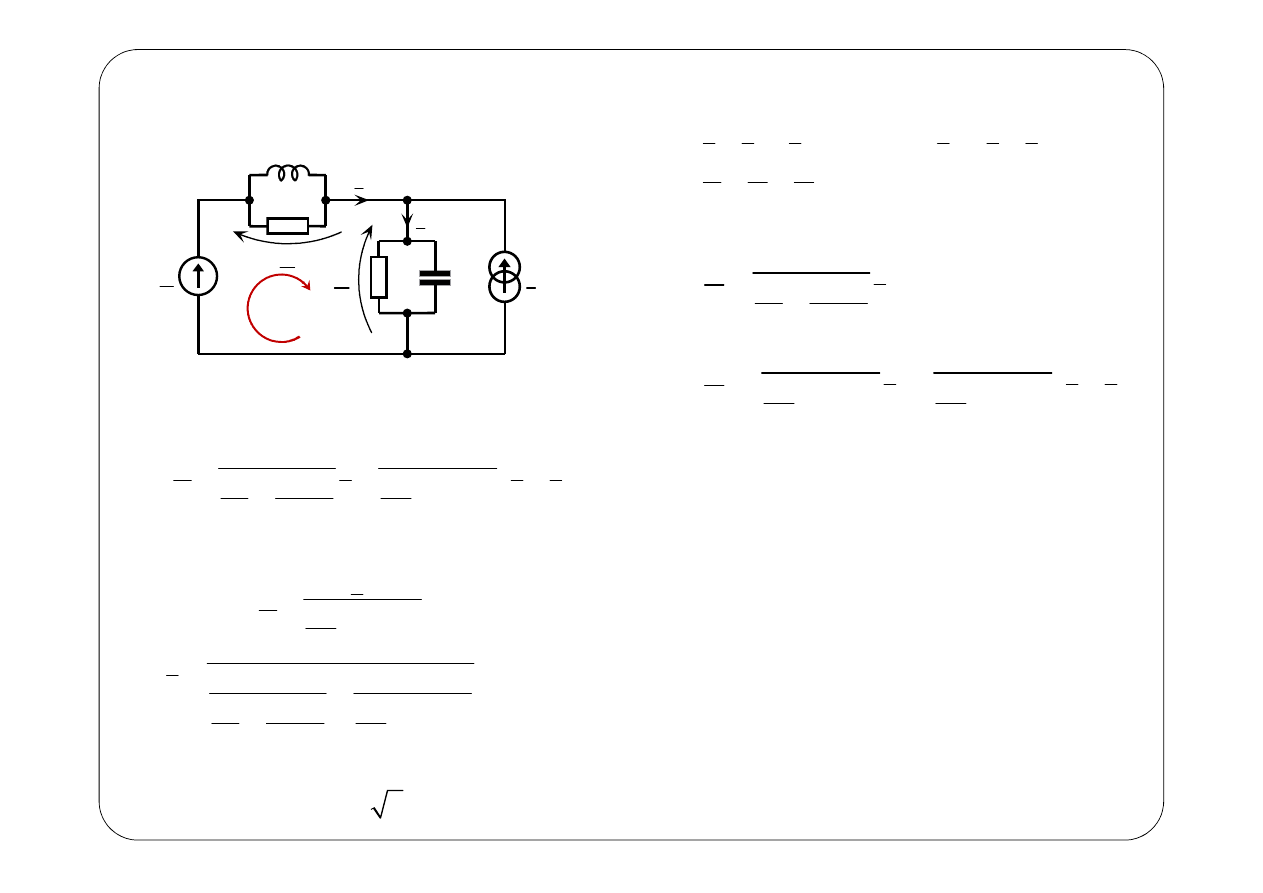
Symboliczny schemat zastępczy:
(
)
(
)
z
n1
n2
n1
n3
0
1
1
j
0
I
U
U
C U
U
R
− +
−
+
−
=
ω
1.
2.
3.
(
)
(
)
n1
n2
n2
n2
n3
1
2
0
1
1
1
0
j
U
U
U
U
U
R
R
L
−
−
+
+
−
=
ω
(
)
(
)
n2
n3
n1
n3
n3
0
0
3
1
1
j
0
j
U
U
C U
U
U
L
R
−
−
−
−
+
=
ω
ω
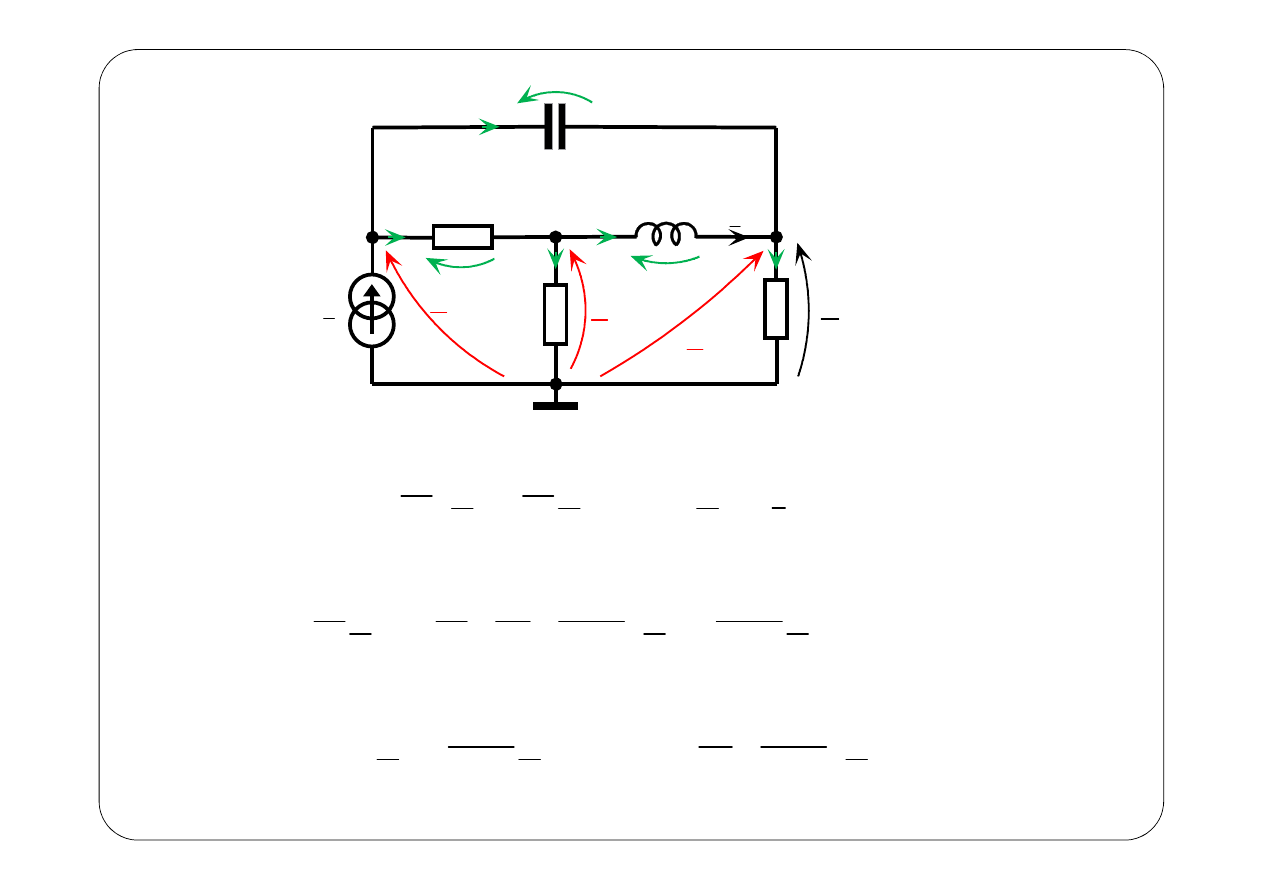
z
I
1
R
C
L
2
R
3
R
I
U
1
2
3
n1
U
n2
U
n3
U
z
n1
n2
n3
0
0
1
1
n1
n2
n3
1
1
2
0
0
n1
n2
n3
0
0
0
3
0
1
1
j
j
1
1
1
1
1
0
j
j
1
1
1
j
j
0
j
j
C
U
U
CU
I
R
R
U
U
U
R
R
R
L
L
CU
U
C
U
L
R
L
+
−
−
=
−
+
+
+
−
=
−
−
+
+
+
=
ω
ω
ω
ω
ω
ω
ω
ω
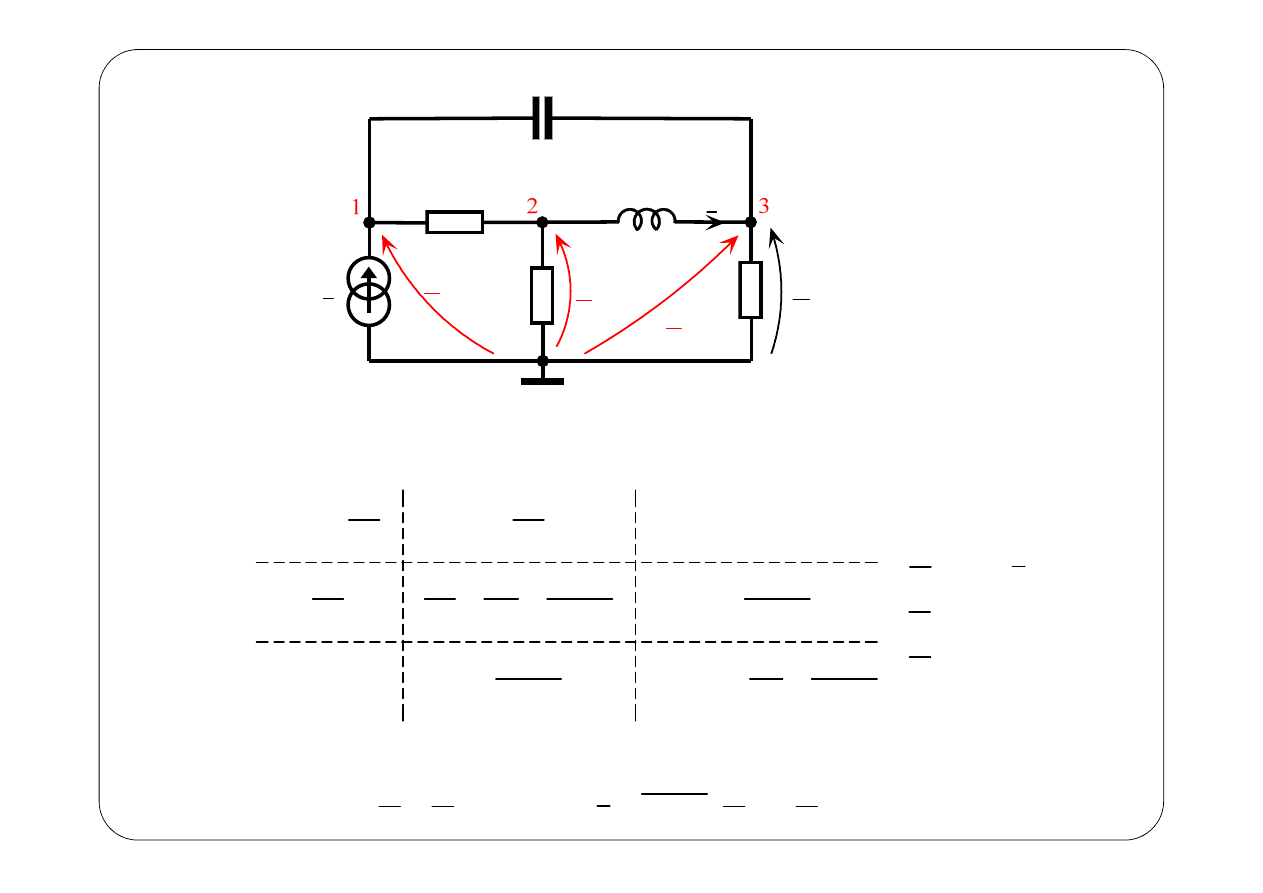
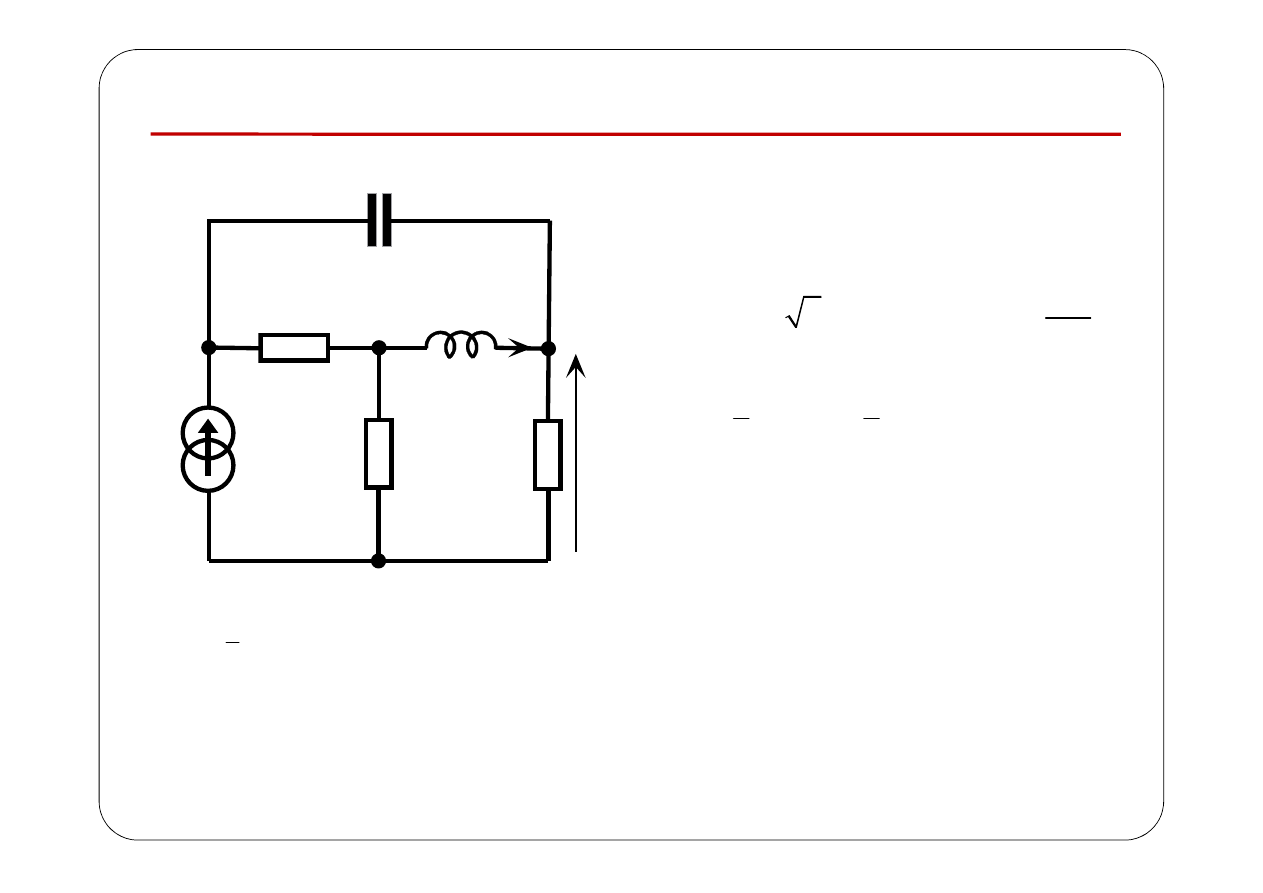
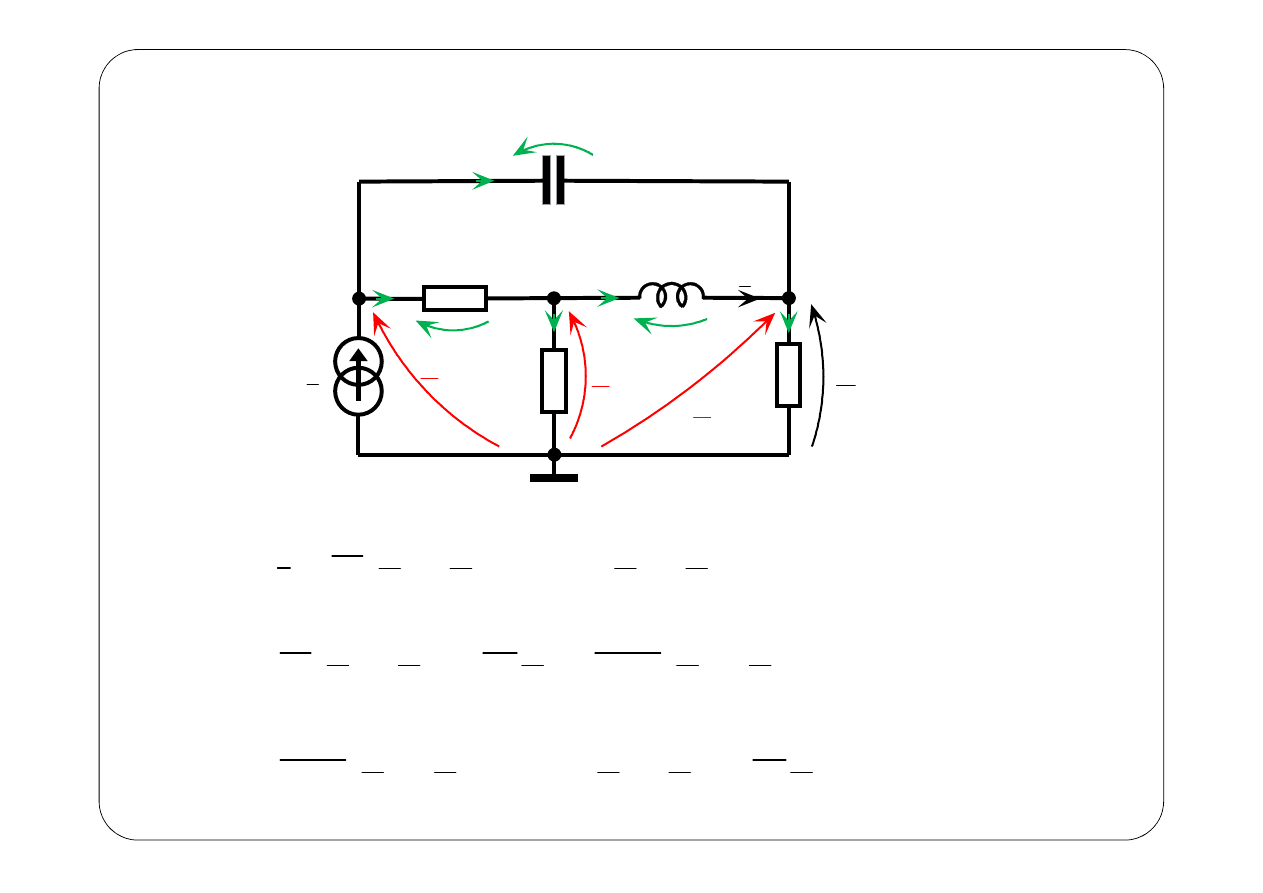
z
I
1
R
C
L
2
R
3
R
I
U
n1
U
n2
U
n3
U
1
2
3
0
0
1
1
z
n1
n2
1
1
2
0
0
n3
0
0
0
3
0
1
1
j
j
1
1
1
1
1
0
j
j
0
1
1
1
j
j
j
j
C
C
R
R
U
I
U
R
R
R
L
L
U
C
C
L
R
L
+
−
−
−
+
+
−
=
−
−
+
+
ω
ω
ω
ω
ω
ω
ω
ω
(
)
n3
n2
n3
0
1
j
U
U
I
U
U
L
=
=
−
ω
1
1
2
2
3
3
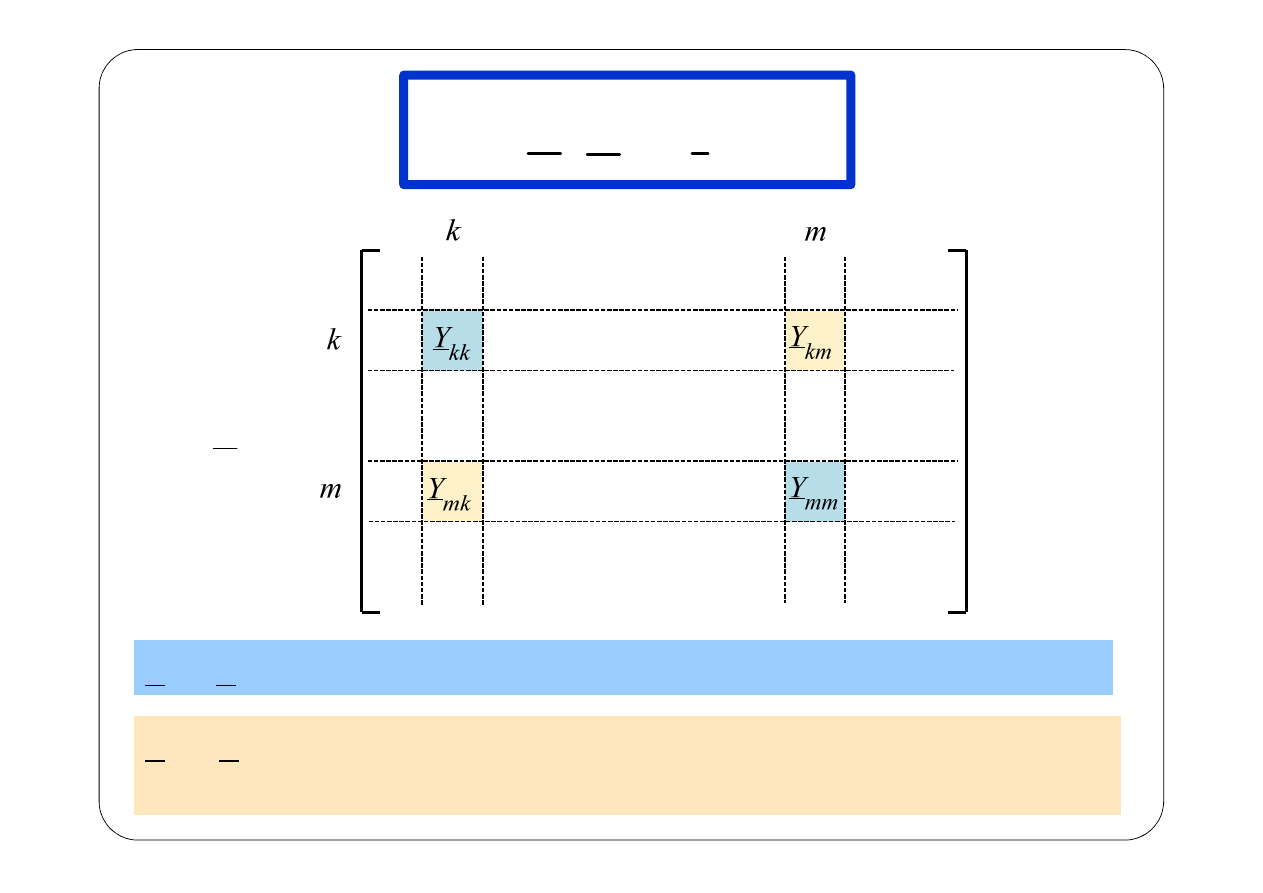
n
n
n
=
Y U
I
n
=
Y
n
=
Y
Y
kk
, (Y
mm
) — suma admitancji gałęzi połączonych z węzłem k, (m)
Y
mk
, Y
km
— suma admitancji gałęzi łączących węzły k i m
wzi
ęta ze znakiem minus
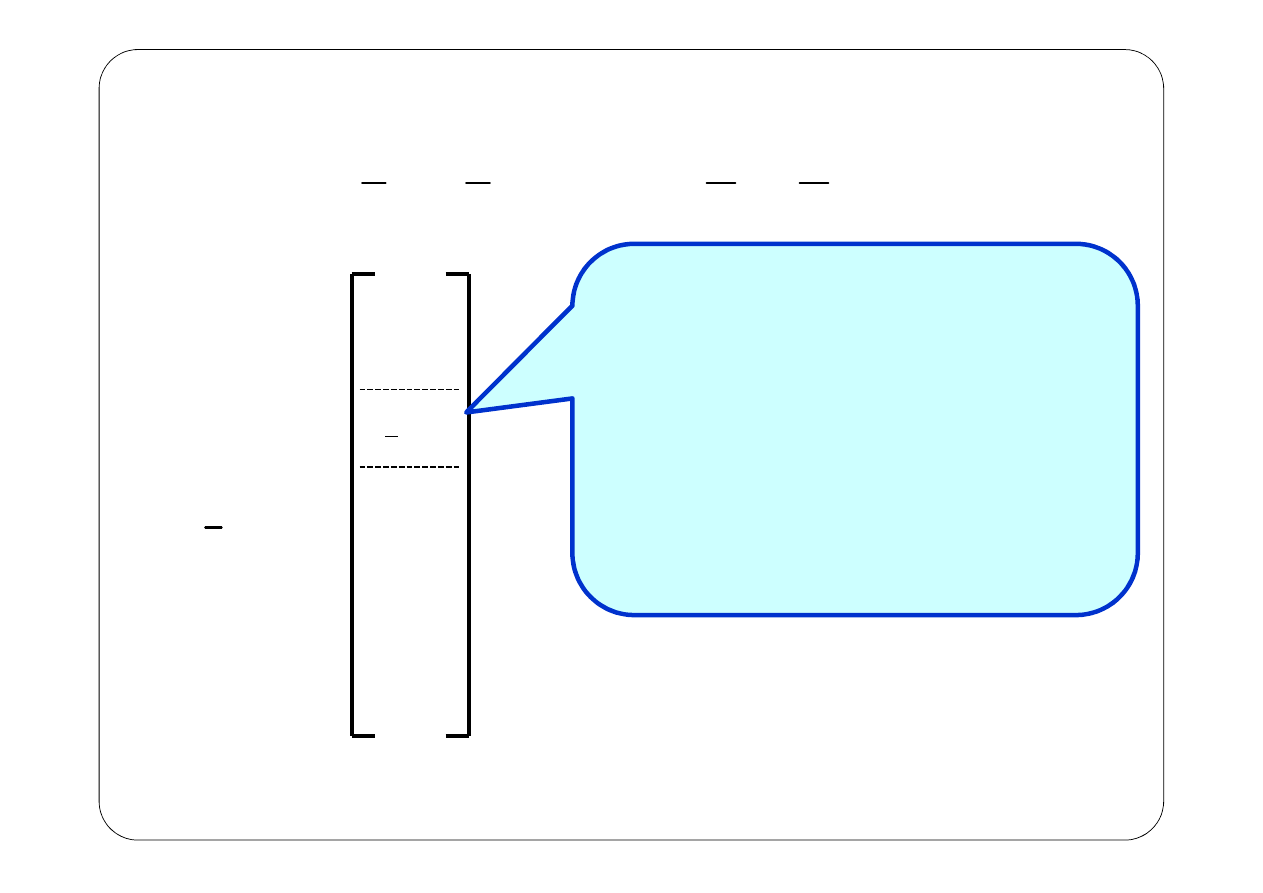
Układ RLC, i
z
t
n
n
,
czyli
km
mk
Y
Y
=
=
Y
Y
k
I
nk
Algebraiczna suma wartości
skutecznych zespolonych prądów
źródłowych (wydajności
prądowych źródeł prądowych)
dopływających do węzła k, przy
nk
n
=
I
dopływających do węzła k, przy
czym prądy dopływaj
ące
bierzemy ze znakiem plus,
a wypływaj
ące ze znakiem minus
0
0
1
1
z
n1
n2
1
1
2
0
0
n3
0
0
0
3
0
1
1
j
j
1
1
1
1
1
0
j
j
0
1
1
1
j
j
j
j
C
C
R
R
U
I
U
R
R
R
L
L
U
C
C
L
R
L
+
−
−
−
+
+
−
=
−
−
+
+
ω
ω
ω
ω
ω
ω
ω
ω
Po podstawieniu danych liczbowych
1
1
1
j
1
j
2
2
2
U
+
−
−
3
j
U
= −
n1
n2
n2
1
j
1
j
2
2
2
1
2
j2
j2
0
1
1
3
0
j
j2
j
2
2
2
U
U
U
+
−
−
−
−
=
−
−
n1
n2
n3
3
j
1,5
1
U
U
U
= −
=
=
(
)
π
j
2
n3
n2
n3
0
1
1
j2 0,5
j=e
j
U
U
I
U
U
L
−
=
=
=
−
= − ⋅
= −
ω
( )
( )
0
0
0
2 sin
V,
π
2 sin
2 cos
A
2
u t
ω t
i t
ω t
ω t
=
=
−
= −
Przykład 1.
( )
e t
1
R
2
R
3
R
L
1
C
2
C
3
C
( )
z
i t
( )
u t
( )
( )
( )
0
6
0
3
z
0
1
2
3
1
2
3
4 2 sin
V,
rad
10
,
s
5 10
2 cos
A,
500 Ω,
1 kΩ,
2 kΩ,
2 mH,
1nF,
500 pF,
500 pF.
?
e t
t
i t
t
R
R
R
L
C
C
C
u t
−
=
=
= ⋅
=
=
=
=
=
=
=
=
ω
ω
ω
3
z
4
j 5 10
E
I
−
=
=
⋅
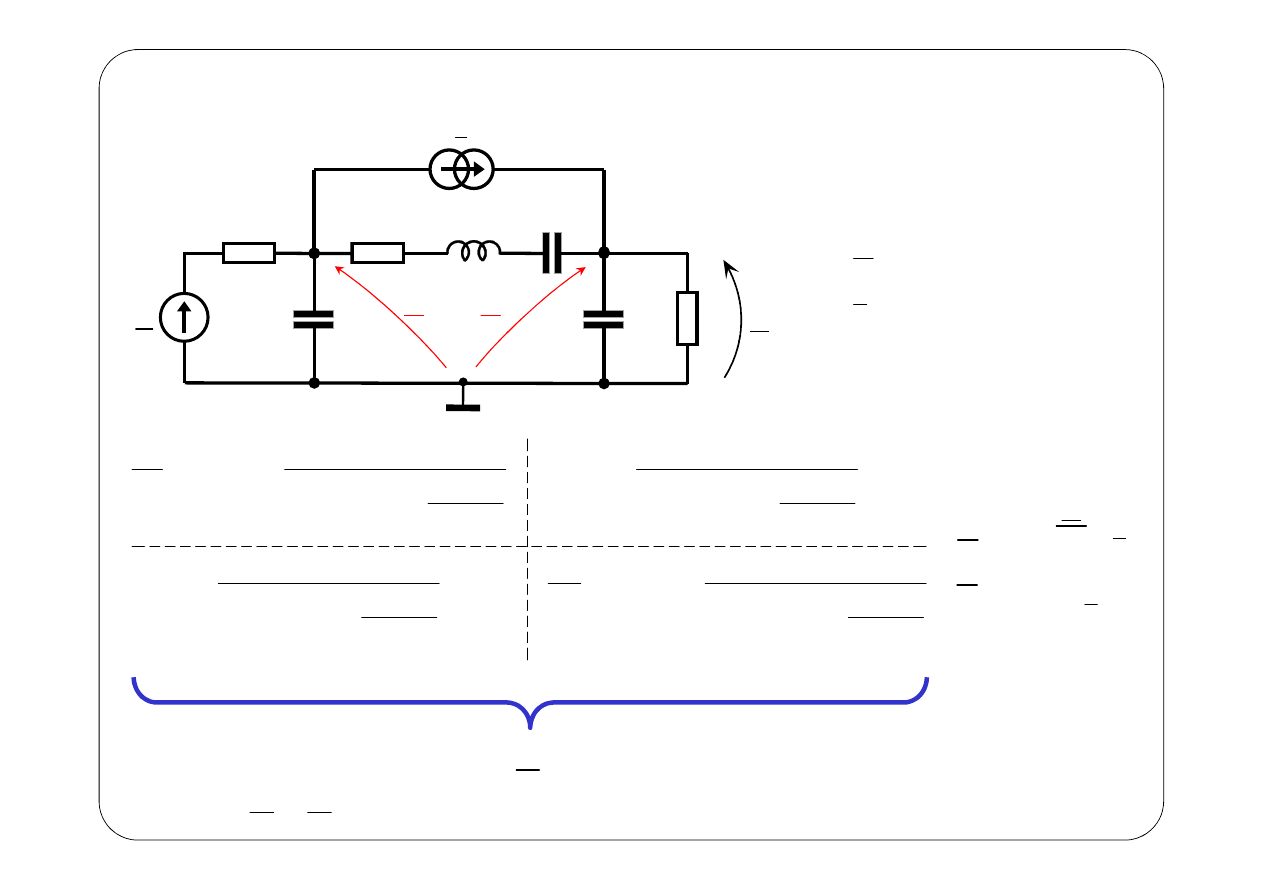
E
1
R
2
R
3
R
L
1
C
2
C
3
C
z
I
U
1
2
n1
U
n2
U
3
z
4
j 5 10
E
I
−
=
=
⋅
1
1
1
Symboliczny schemat zastępczy:
0
1
1
2
0
2
0
0
2
0
2
z
n1
1
n2
0
3
z
3
2
0
2
0
0
2
0
2
1
1
1
j
1
1
j
j
j
j
1
1
1
j
1
1
j
j
j
j
C
R
R
L
R
L
E
C
C
I
U
R
U
C
I
R
R
L
R
L
C
C
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
−
+
+
+
+
−
=
−
+
+
+
+
+
+
n2
U
U
=
n
Y

3
3
3
3
3
n1
3
3
3
3
n2
3 10
j10
10
8 10
j 5 10
10
1,5 10
j 0,5 10
j 5 10
U
U
−
−
−
−
−
−
−
−
−
⋅
+
−
⋅
−
⋅
=
−
⋅
+
⋅
⋅
Po uproszczeniu przez 10
–3
n1
n2
3
j
1
8
j 5
1
1,5
j 0,5
j 5
U
U
+
−
−
=
−
+
2
n2
U
U
∆
=
=
∆
n2
n
2
n
n
j0,494
3
j
8
j5
det
3
j10
1
j5
det
3
j3
3
j10
2,167
j1,167
2, 46 e
3
j3
U
U
U
=
=
∆
+
−
∆ =
= +
−
∆ =
= +
+
=
=
+
=
+
Y
( )
(
)
0
2, 46 2 sin
0, 494 V.
u t
t
ω
=
+
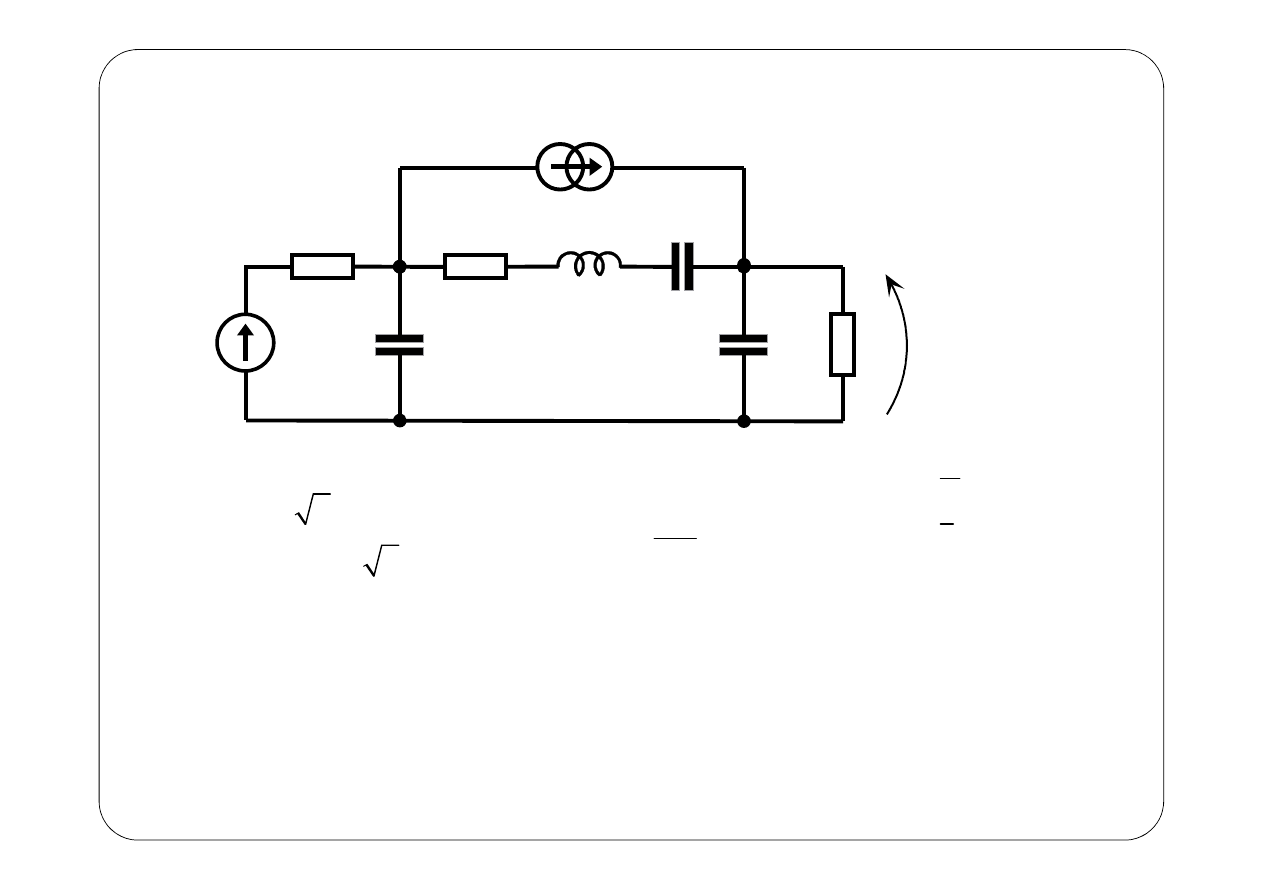
Przykład 2.
( )
e t
1
R
2
R
1
C
2
C
1
L
2
L
( )
i t
( )
u t
( )
i t
α
( )
( )
0
0
1
2
1
2
1
2
rad
2 2 cos
V,
1
,
s
1
1
Ω,
1Ω,
1H,
H,
2 F,
1F,
2.
2
2
?
e t
t
R
R
L
L
C
C
u t
=
=
=
=
=
=
=
=
=
=
ω
ω
α
2 j
E
=
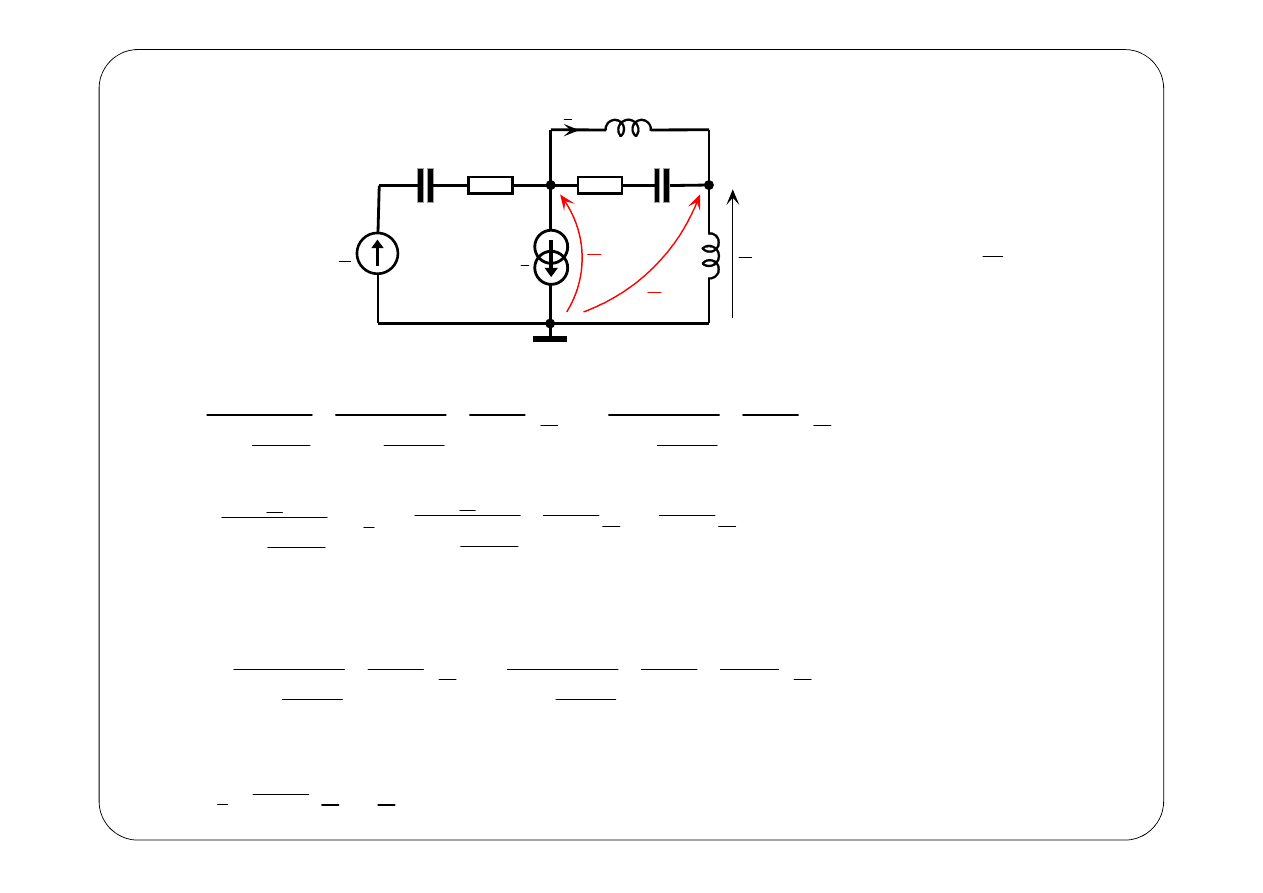
E
1
R
2
R
1
C
2
C
1
L
2
L
I
U
I
α
1
2
n1
U
n2
U
2 j
E
=
n1
n2
0
1
0
1
1
2
2
1
1
1
1
1
1
1
1
j
j
.
1
U
U
ω L
ω L
R
R
R
+
+
−
+
=
+
+
+
Symboliczny schemat zastępczy:
0
1
0
1
1
2
2
0
1
0
2
0
2
1
0
1
j
j
j
1
j
R
R
R
ω C
ω C
ω C
E
αI
R
ω C
+
+
+
=
−
+
n1
2
0
1
0
1
0
2
2
2
0
2
0
2
1
1
2
1
1
1
0
1
1
j
j
j
j
.
j
U
U
ω L
ω L
ω L
R
R
ω C
ω C
−
+
+
+
+
=
+
+
(
)
n1
n2
0
1
1
j
I
U
U
ω L
=
−
n1
n2
0
1
0
1
1
0
1
1
j
j
j
E
α
α
U
U
ω L
ω L
R
ω C
=
−
+
+
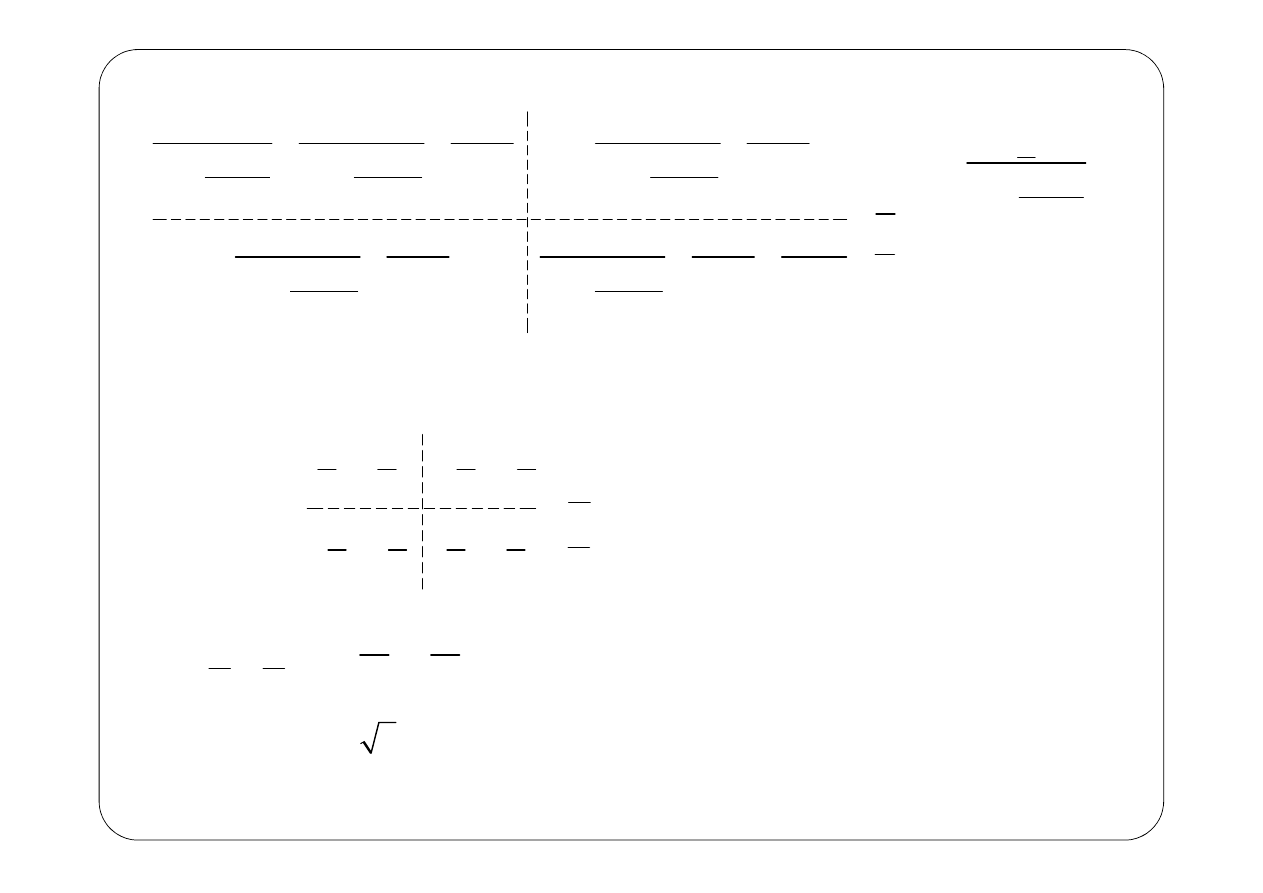
0
1
0
1
1
2
2
1
0
1
0
2
0
2
n1
0
1
n2
0
1
0
1
0
2
2
2
0
2
0
2
1
1
1
1
1
1
1
1
j
j
1
j
j
j
j
1
1
1
1
1
1
1
j
j
j
0
j
j
α
α
E
ω L
ω L
R
R
R
R
ω C
ω C
ω C
U
ω C
U
ω L
ω L
ω L
R
R
ω C
ω C
+
+
+
+
−
−
+
+
+
+
=
−
−
+
+
+
+
Po podstawieniu danych liczbowych
3
1
1
5
n1
n2
3
1
1
5
j
j
2
j2
2
2
2
2
1
1
1
5
0
j
j
2
2
2
2
U
U
−
− +
− +
=
− +
−
j2,5536
n2
6
4
j
0, 5547e
13
13
U
U
−
=
= −
−
=
( )
(
)
0, 5547 2 sin
2, 5536 V.
u t
t
=
−
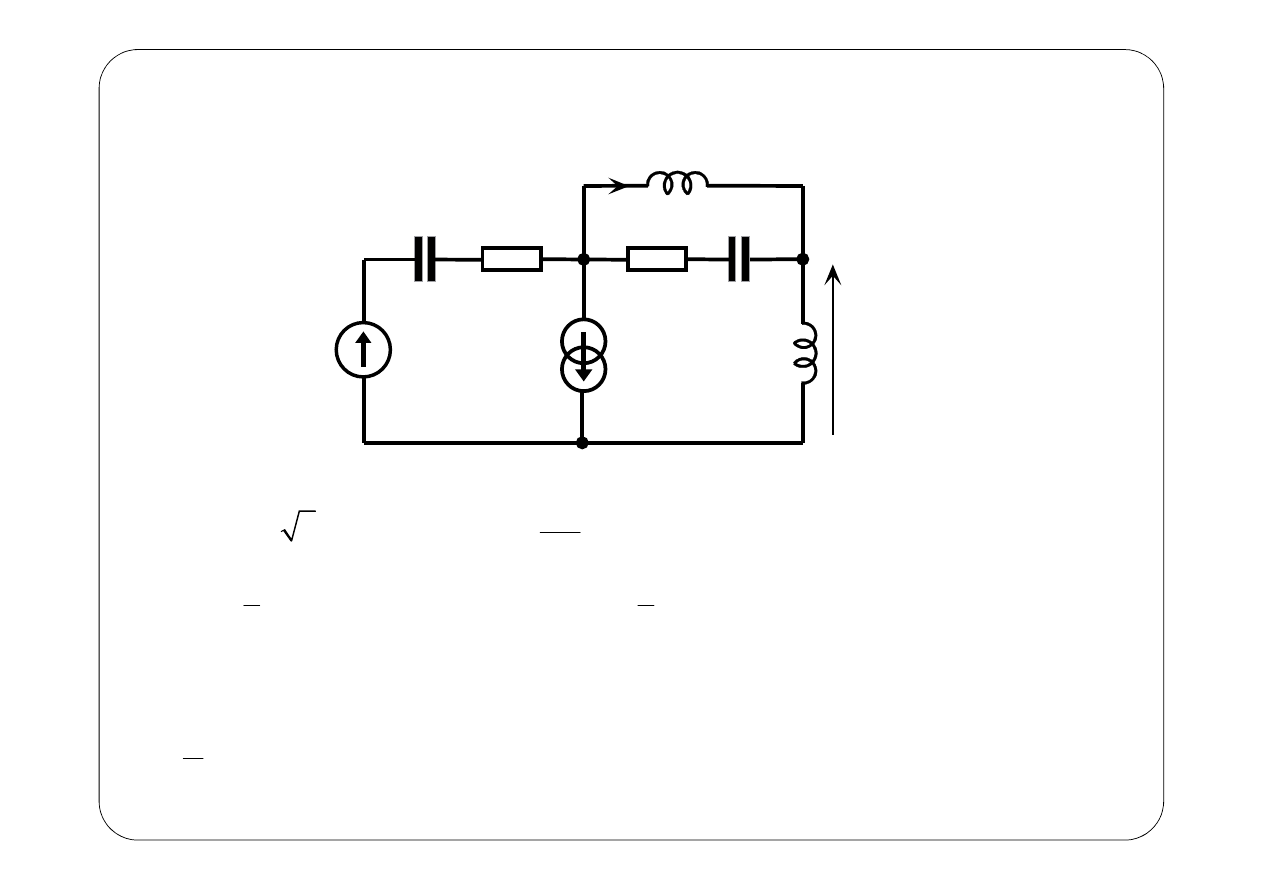
Przykład 3.
( )
e t
1
R
2
R
3
R
L
C
( )
u t
( )
( )
0
0
1
2
3
1
2
π
6sin
V,
1,
4
1Ω,
1Ω,
1Ω,
H,
e t
t
R
R
R
L
=
−
=
=
=
=
=
ω
ω
2
H,
1F.
L
C
=
=
( )
?
u t
=
3
j3
E
= −
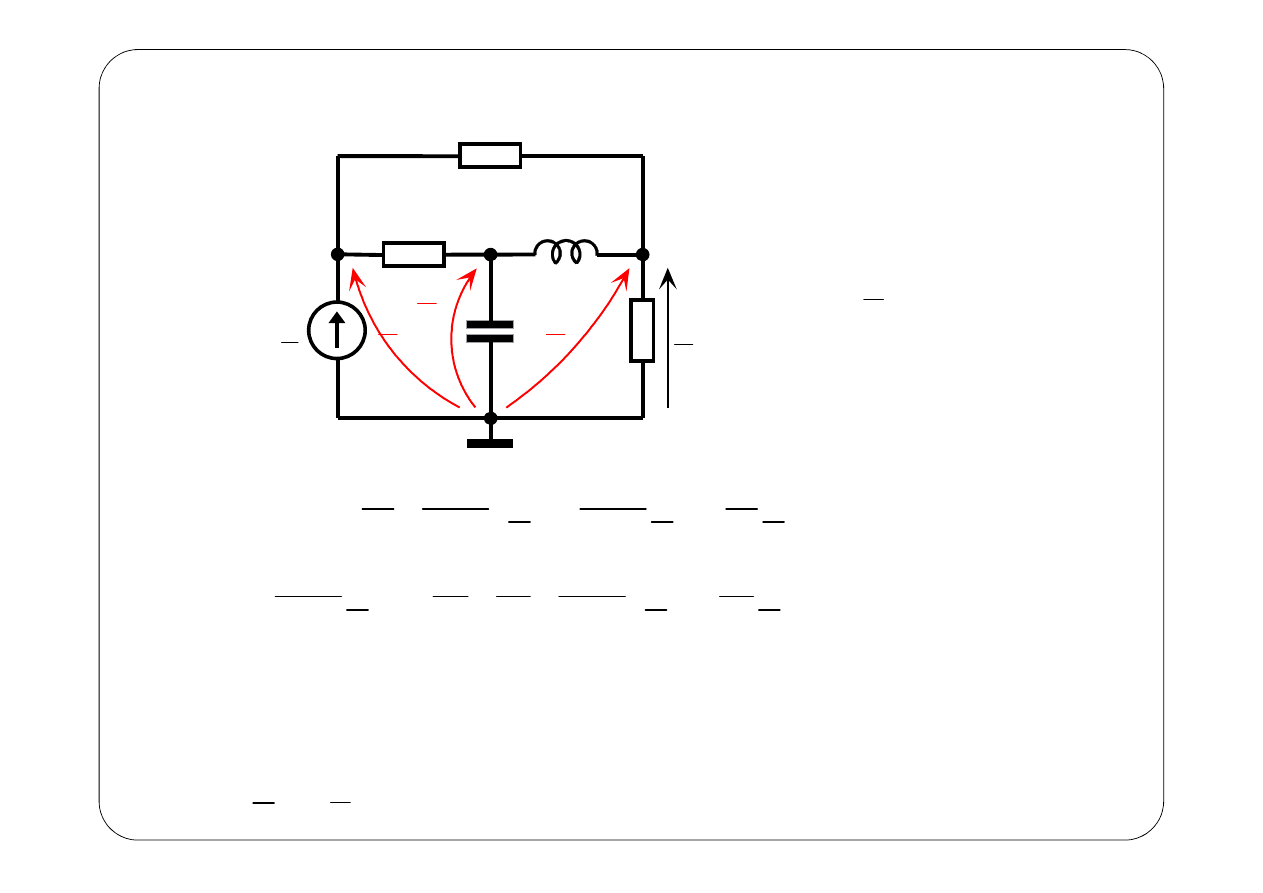
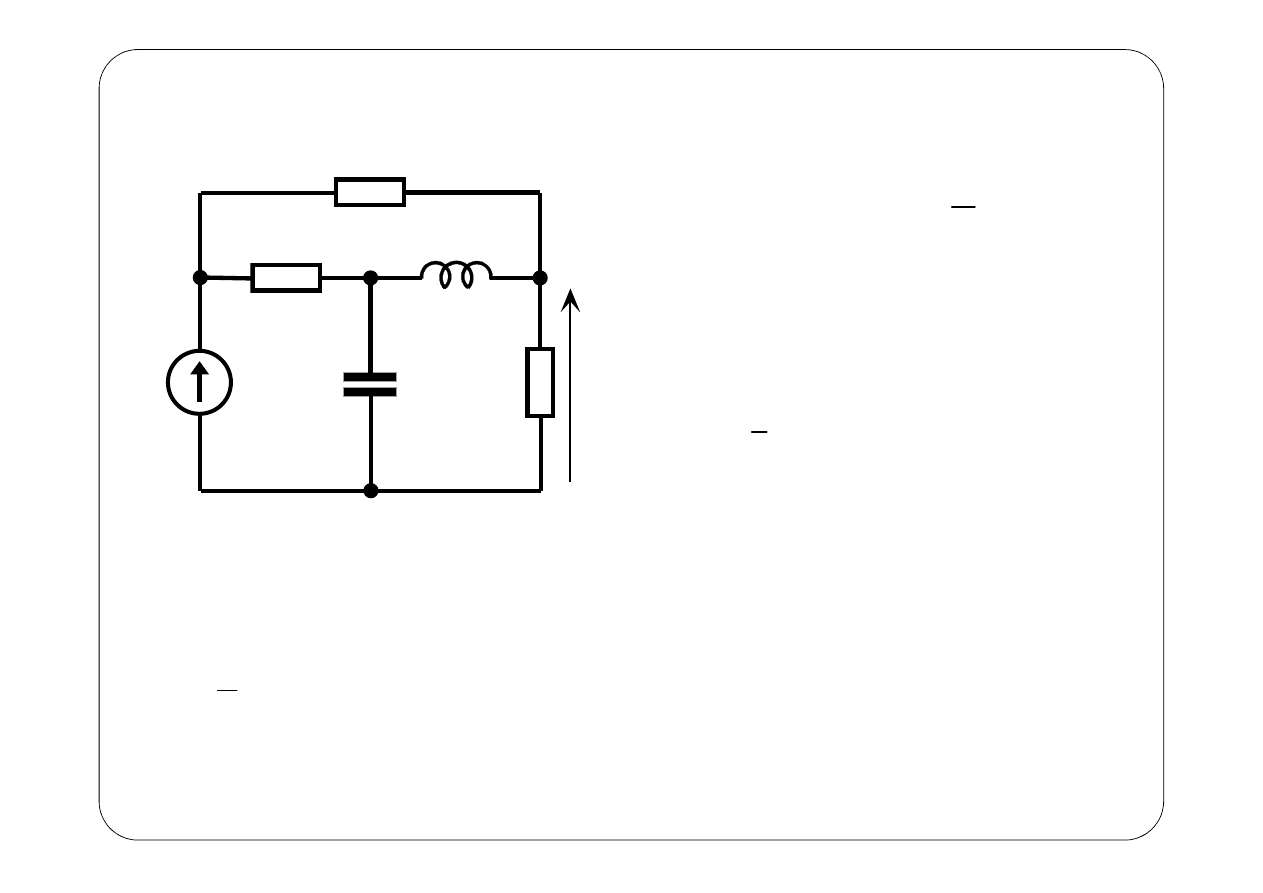
1
2
3
E
1
R
2
R
3
R
L
C
U
n1
U
n2
U
n3
U
3
j3
E
= −
Symboliczny schemat zastępczy
0
n1
n 2
n3
1
0
0
1
n1
n 2
n3
0
2
3
0
3
1
1
1
1
j
0
j
j
1
1
1
1
1
0
j
j
C
U
U
U
R
L
L
R
U
U
U
L
R
R
L
R
ω
ω
ω
ω
ω
+
+
−
−
=
−
+
+
+
−
=
1.
2.
W węźle 3: (nie jest to równanie z I prawa Kirchhoffa)
n3
U
E
=
3.
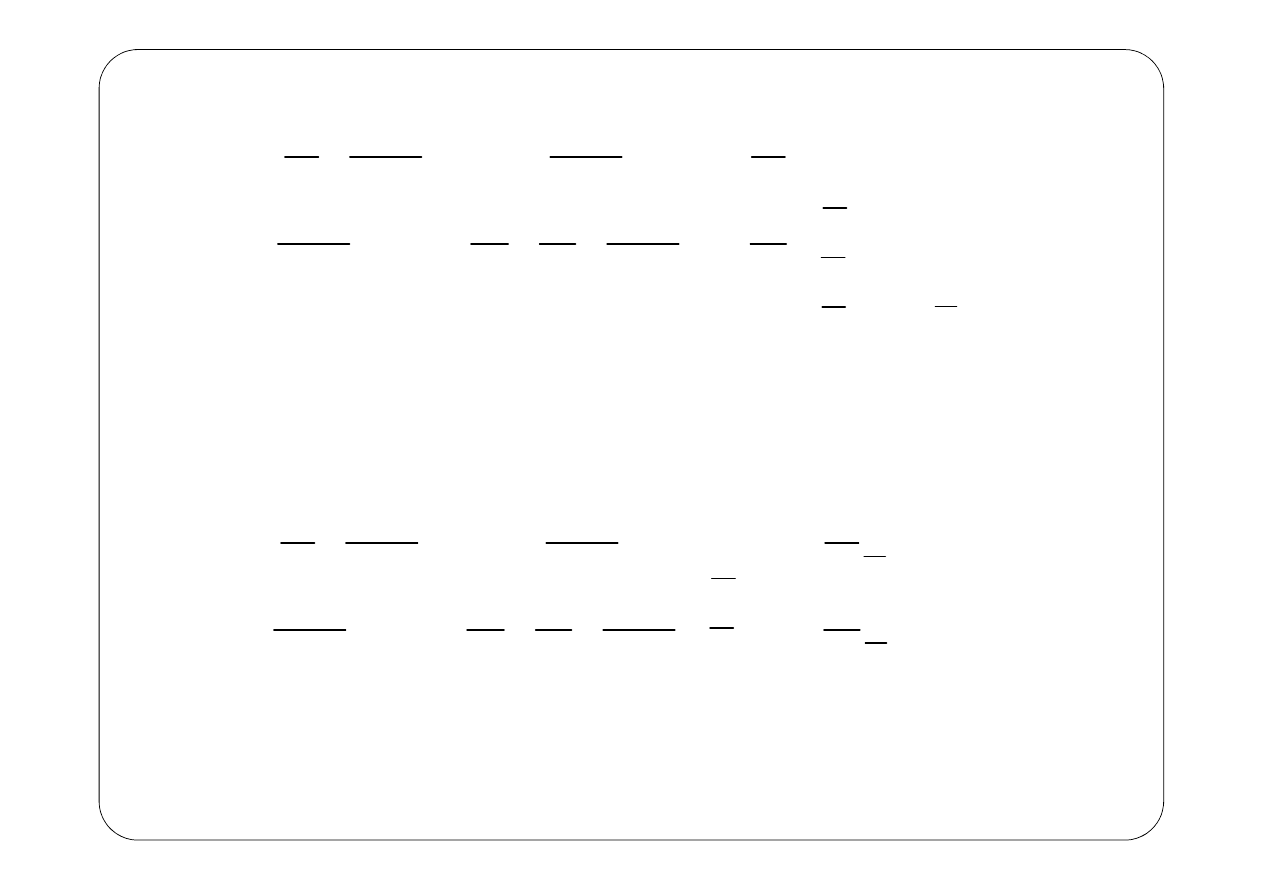
Równania można uporządkować tak
0
1
0
0
1
n1
n 2
0
2
3
0
3
n3
1
1
1
1
j
j
j
0
1
1
1
1
1
0
j
j
0
0
1
C
R
L
L
R
U
U
L
R
R
L
R
U
E
+
+
−
−
−
+
+
−
=
ω
ω
ω
ω
ω
lub, po uwzględnieniu równania
3
, tak
lub, po uwzględnieniu równania
3
, tak
0
1
0
0
1
n1
n 2
3
0
2
3
0
1
1
1
1
j
j
j
1
1
1
1
1
j
j
C
E
R
L
L
R
U
U
E
R
L
R
R
L
+
+
−
=
−
+
+
ω
ω
ω
ω
ω

Po podstawieniu danych liczbowych
n1
n2
1
j
j2
3
j3
j2
2
j2
3
j3
U
U
−
−
=
−
−
j1,249
n2
3
9
j
2,372e
4
4
U
U
−
=
= −
=
( )
(
)
2,372 2 sin
1, 249 V.
u t
t
=
−
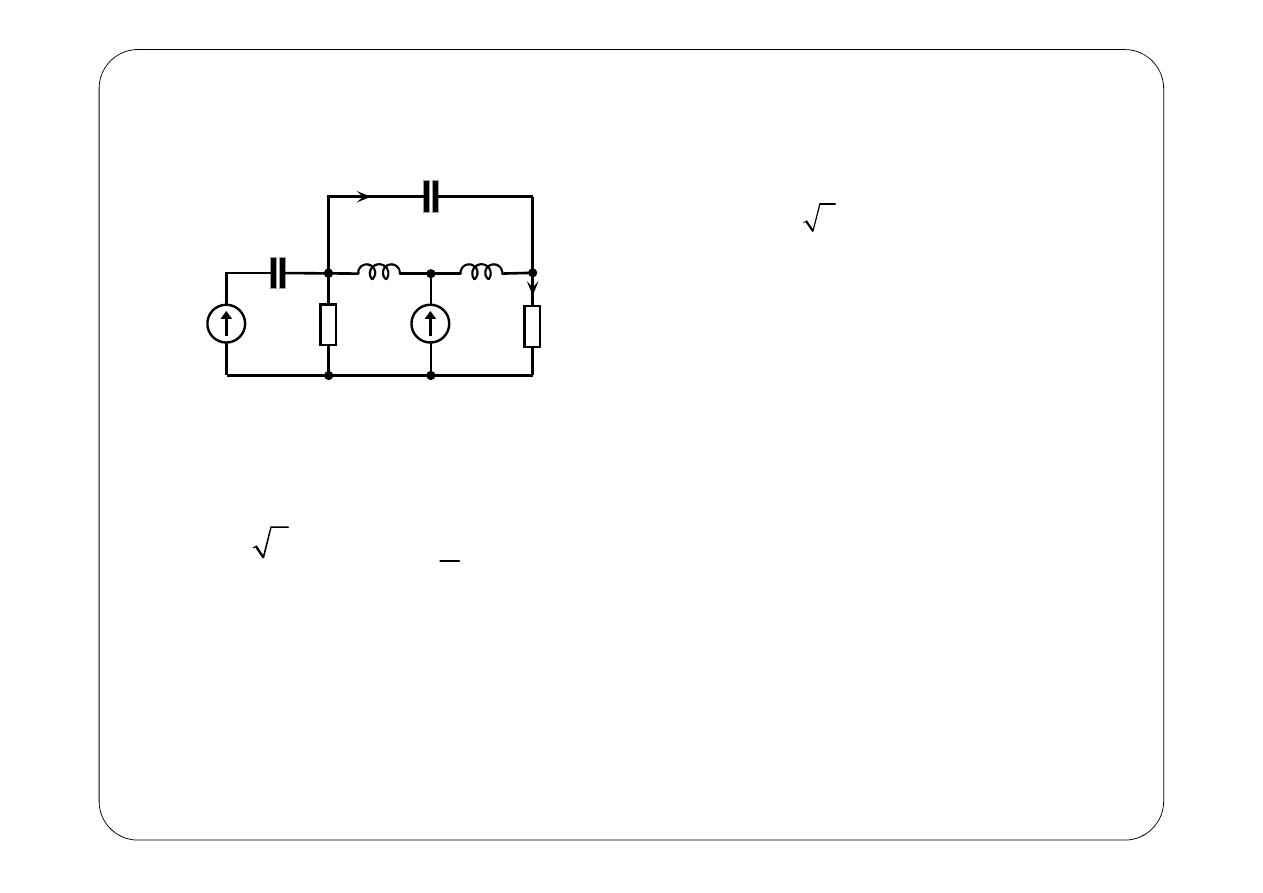
Przykład 4.
( )
e t
( )
i t
ρ
1
C
2
C
1
L
2
L
1
R
2
R
( )
i t
( )
0
i t
( )
1
2
1
2
1
2
5 2 cos V,
1Ω,
2Ω,
2 H,
1H,
1F,
2 F,
2 Ω
e t
t
R
R
L
L
C
C
ρ
=
=
=
=
=
=
=
=
Wyznaczyć prąd
( )
0
i t
Wyznaczyć prąd
( )
0
i t
( )
0
5 2 cos
j5,
1
e t
t
E
ω
=
=
=
⇌
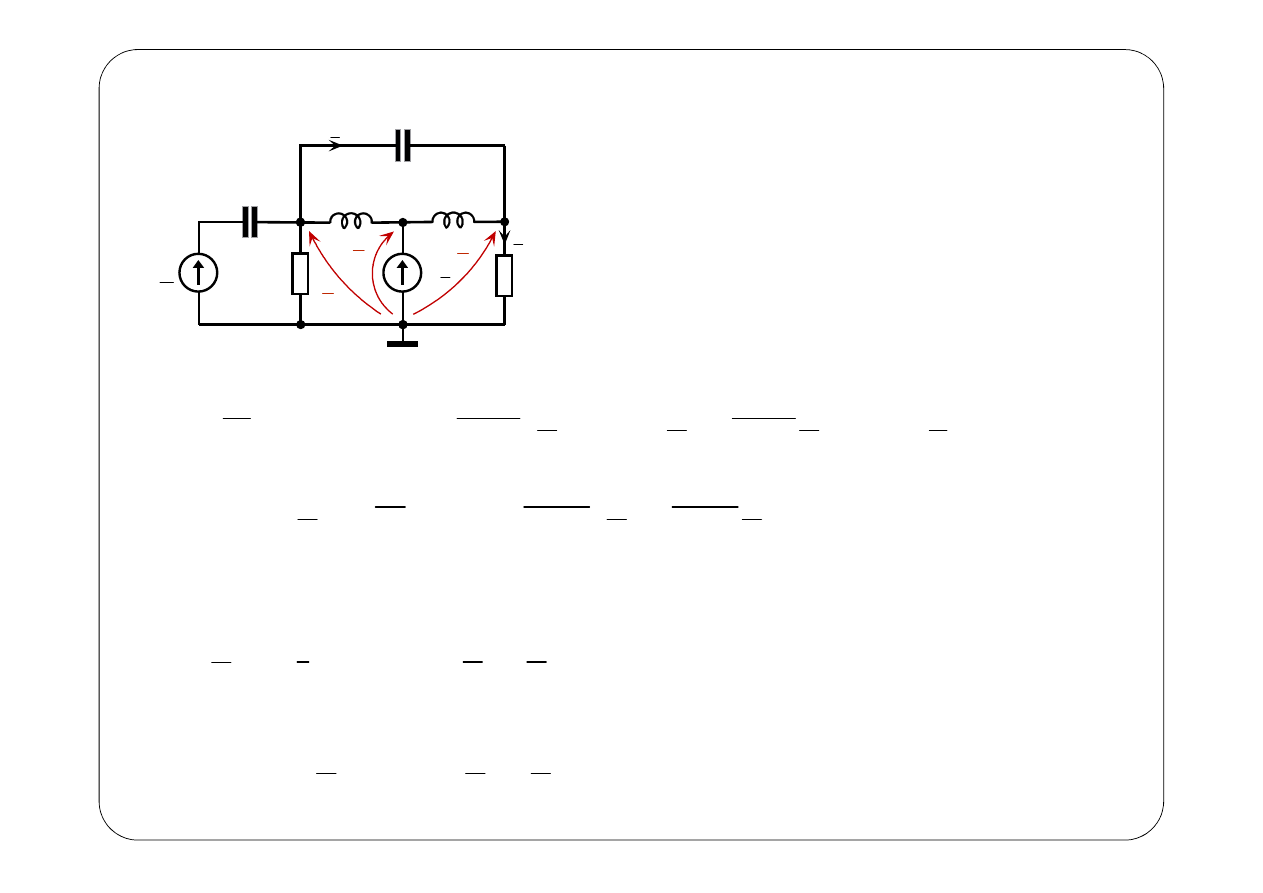
E
I
ρ
1
C
2
C
1
L
2
L
1
R
2
R
I
0
I
1
2
3
n1
U
n2
U
n3
U
0
1
0
2
0
2
0
1
n1
n2
n3
1
0
1
0
1
1
1
1
j
j
j
j
j
j
C
C
U
C U
U
C E
R
L
L
ω
ω
ω
ω
ω
ω
+
+
+
−
−
=
1.
Symboliczny schemat zastępczy
1
0
1
0
1
0
2
0
2
n1
n2
n3
2
0
2
0
2
j
j
1
1
1
j
j
0
j
j
R
L
L
C U
C
U
U
R
L
L
ω
ω
ω
ω
ω
ω
−
+
+
+
−
=
2.
n3
U
I
ρ
=
3.
W węźle 3 (nie jest to równanie na podstawie I prawa Kirchhoffa!)
czyli, po uporządkowaniu
0
2
0
2
n1
n2
n3
j
j
0
C
U
C
U
U
ω ρ
ω ρ
−
+
+
=
3.
(
)
0
2
n1
n2
j
C U
U
ρ ω
=
−
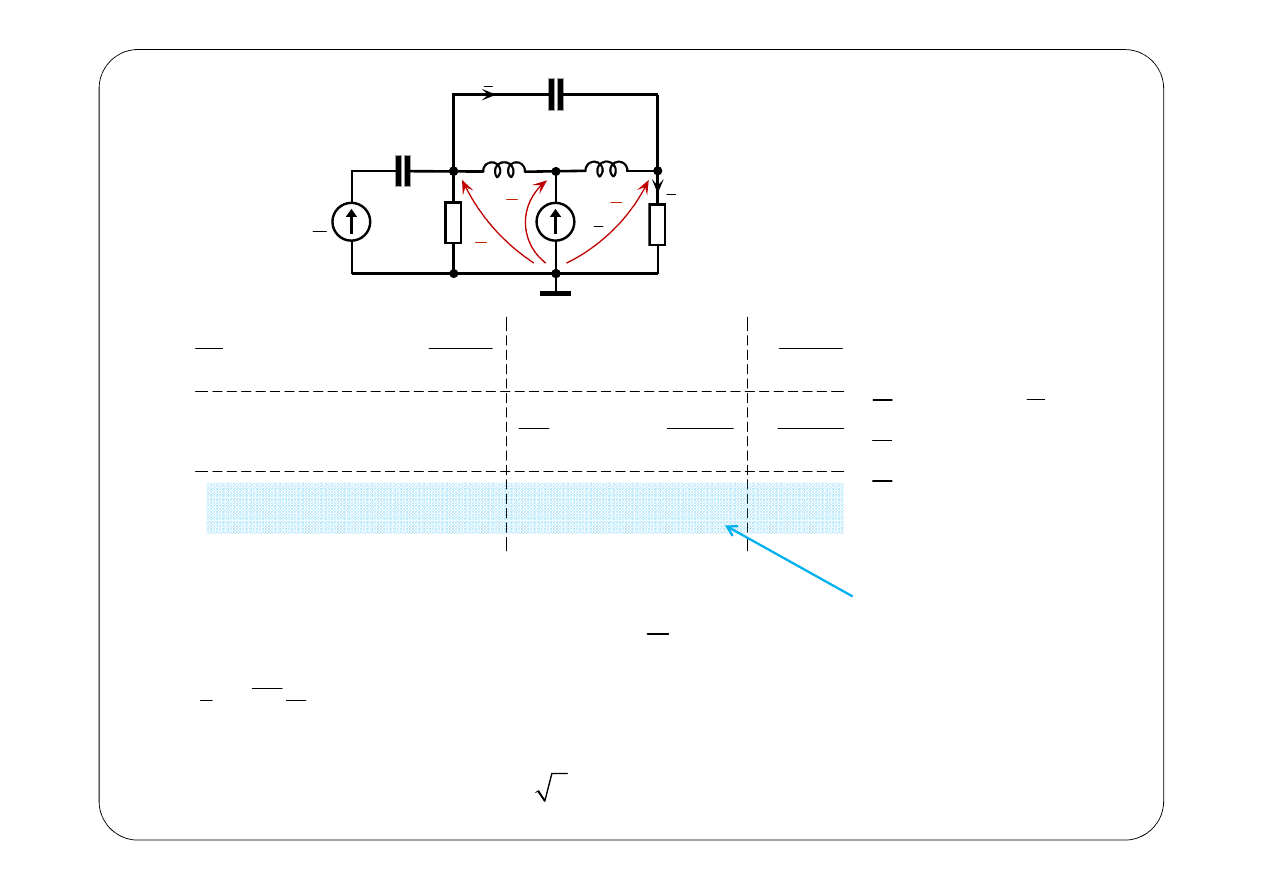
0
1
0
2
0
2
1
0
1
0
1
0
1
n1
0
2
0
2
n2
1
1
1
j
j
j
j
j
j
1
1
1
j
j
0
j
j
C
C
C
R
L
L
U
C E
C
C
U
R
L
L
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
+
−
−
−
+
+
−
=
E
I
ρ
1
C
2
C
1
L
2
L
1
R
2
R
I
0
I
1
2
3
n1
U
n2
U
n3
U
2
0
2
0
2
n3
0
2
0
2
j
j
0
j
j
1
R
L
L
U
C
C
ω
ω
ω ρ
ω ρ
−
To nie są admitancje!
Po podstawieniu danych i wyznaczeniu obliczamy
n2
U
j 2,709
0
n2
2
1
2,537
j1,171
2,794 e
I
U
R
=
= −
+
=
i ostatecznie
( )
(
)
0
2,794 2 sin
2,709 A.
i t
t
=
+
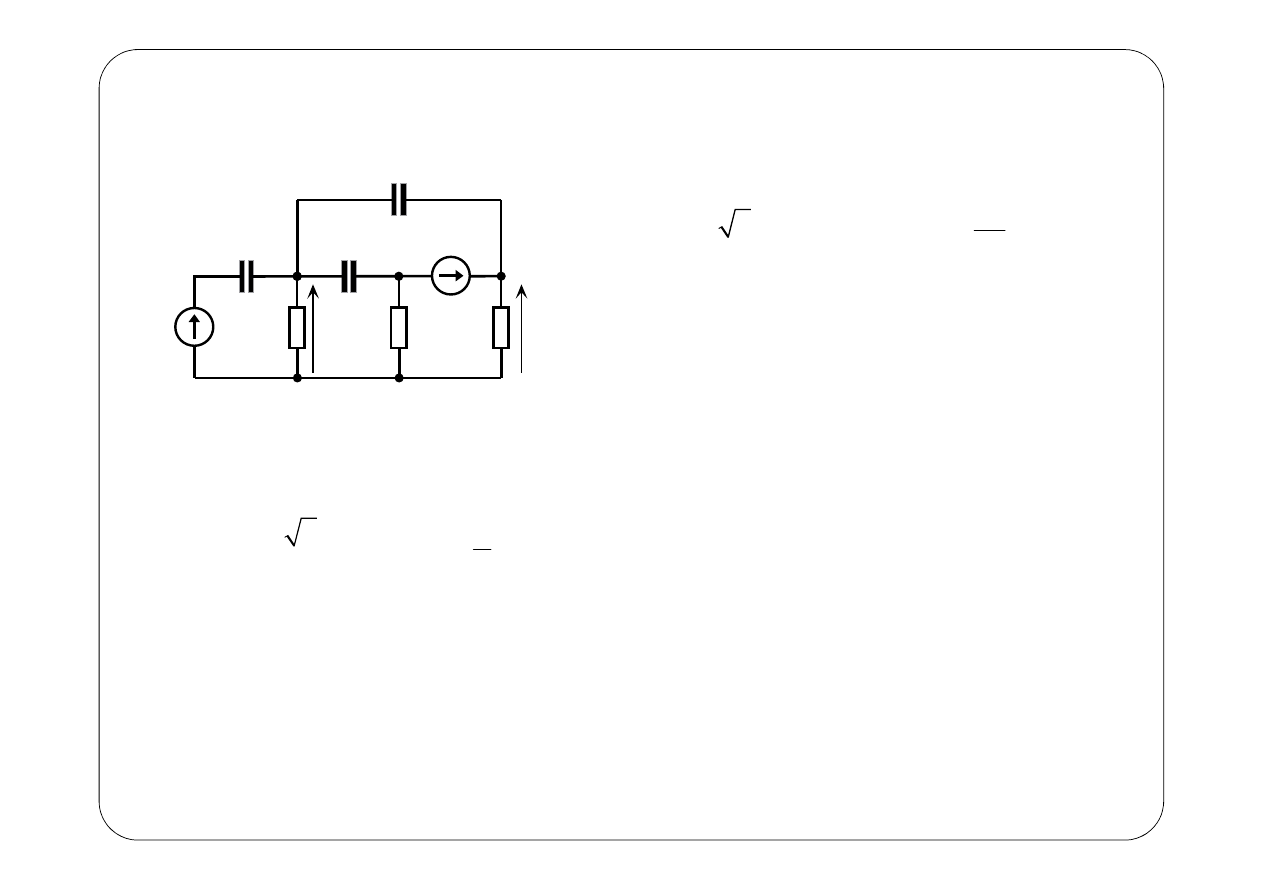
Przykład 4.
( )
e t
1
C
2
C
3
C
1
R
2
R
3
R
( )
u t
β
( )
u t
( )
0
u
t
( )
( )
3
0
0
1
2
3
1
2
3
0
rad
s
5 2 sin
V,
10
,
500Ω,
2 kΩ,
1kΩ,
1µF,
1µF,
0,5µF,
2.
?
e t
t
R
R
R
C
C
C
u t
=
=
=
=
=
=
=
=
=
=
ω
ω
β
Wyznaczyć napięcie
( )
0
u t
Wyznaczyć napięcie
( )
0
u t
( )
0
5 2 sin
5
e t
t
E
ω
=
=
⇌
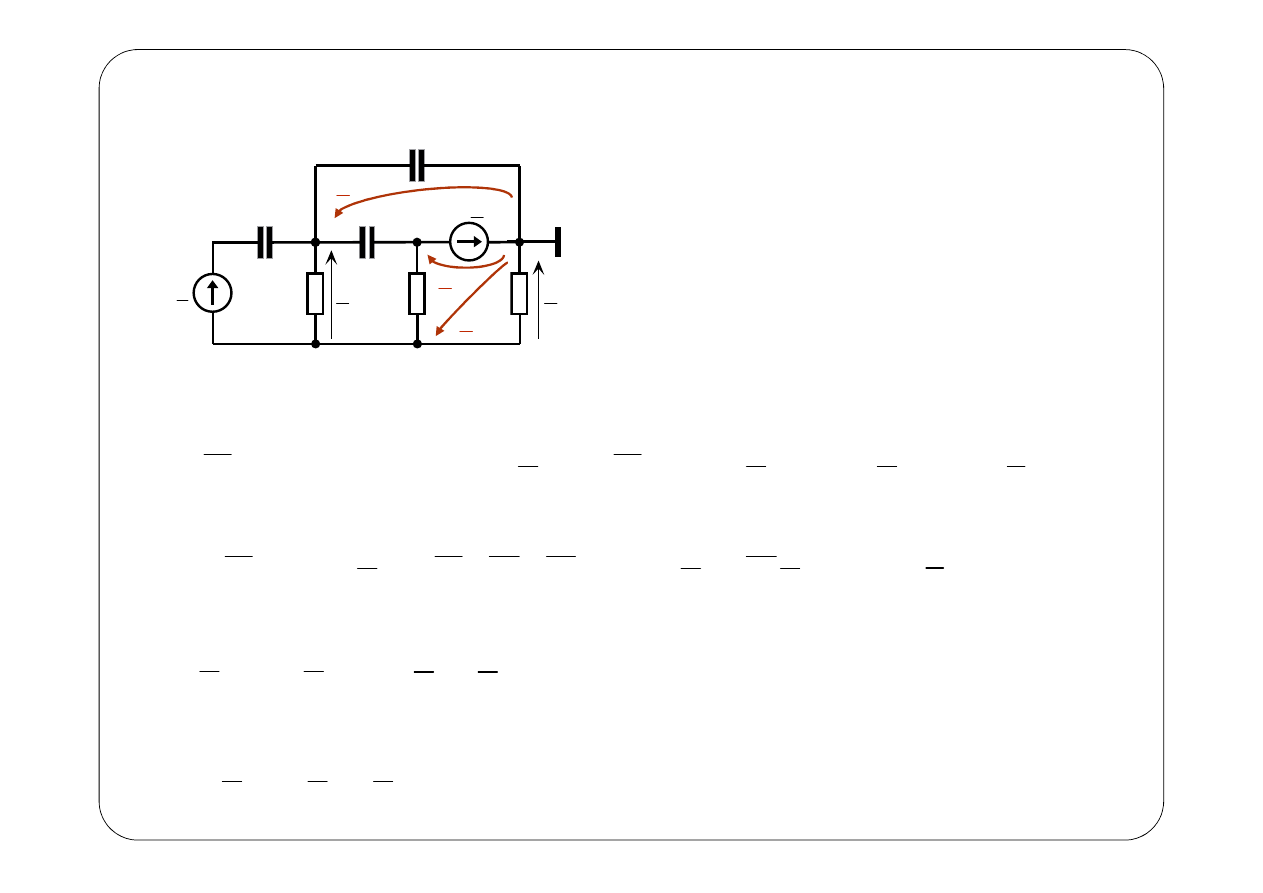
E
1
C
2
C
3
C
1
R
2
R
3
R
U
β
U
0
U
Symboliczny schemat zastępczy
1
2
3
n1
U
n2
U
n3
U
1
1
j
j
j
j
j
j
1.
C
C
C U
C U
C U
C E
ω
ω
ω
ω
ω
ω
+
+
+
+ −
−
−
=
0
1
0
2
0
3
0
1
0
2
0
1
n1
n2
n3
1
1
0
1
0
1
0
1
n1
n2
n3
1
1
2
3
2
1
1
j
j
j
j
j
j
1
1
1
1
1.
2.
1
j
j
j
C
C
C U
C U
C U
C E
R
R
C U
C U
U
C E
R
R
R
R
R
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
+
+ −
−
−
=
−
−
+
+
+
+
−
= −
n3
3.
U
U
β
= −
(
)
n1
n2
U
U
β
= −
−
czyli
n1
n2
n3
0
U
U
U
β
β
−
+
=
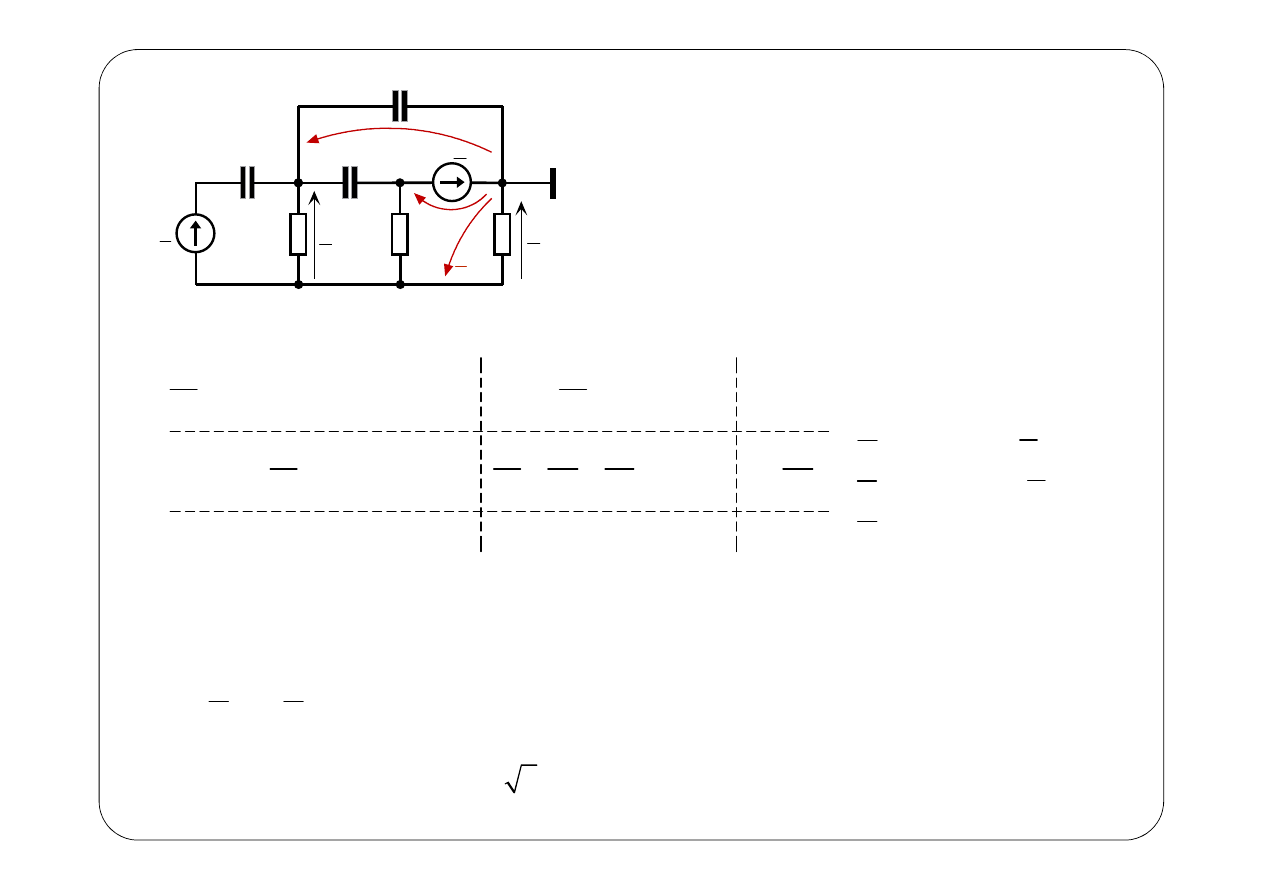
0
1
0
2
0
3
0
1
0
2
1
1
0
1
n1
1
1
j
j
j
j
j
j
1
1
1
1
1
C
C
C
C
C
R
R
U
C E
ω
ω
ω
ω
ω
ω
+
+
+
−
−
−
E
1
C
2
C
3
C
1
R
2
R
3
R
U
β
U
0
U
1
2
3
n2
U
0
1
0
1
0
1
n2
1
1
2
3
2
n3
1
1
1
1
1
j
j
j
0
1
C
C
U
C E
R
R
R
R
R
U
ω
ω
ω
β
β
−
−
+
+
+
−
= −
−
Po podstawieniu danych liczbowych i rozwiązaniu otrzymujemy
j1,651
0
n2
0,168
j2,091
2,0974e
U
U
= −
= −
+
=
czyli
( )
(
)
0
0
2, 0974 2 sin
1,651 V
u t
t
ω
=
+
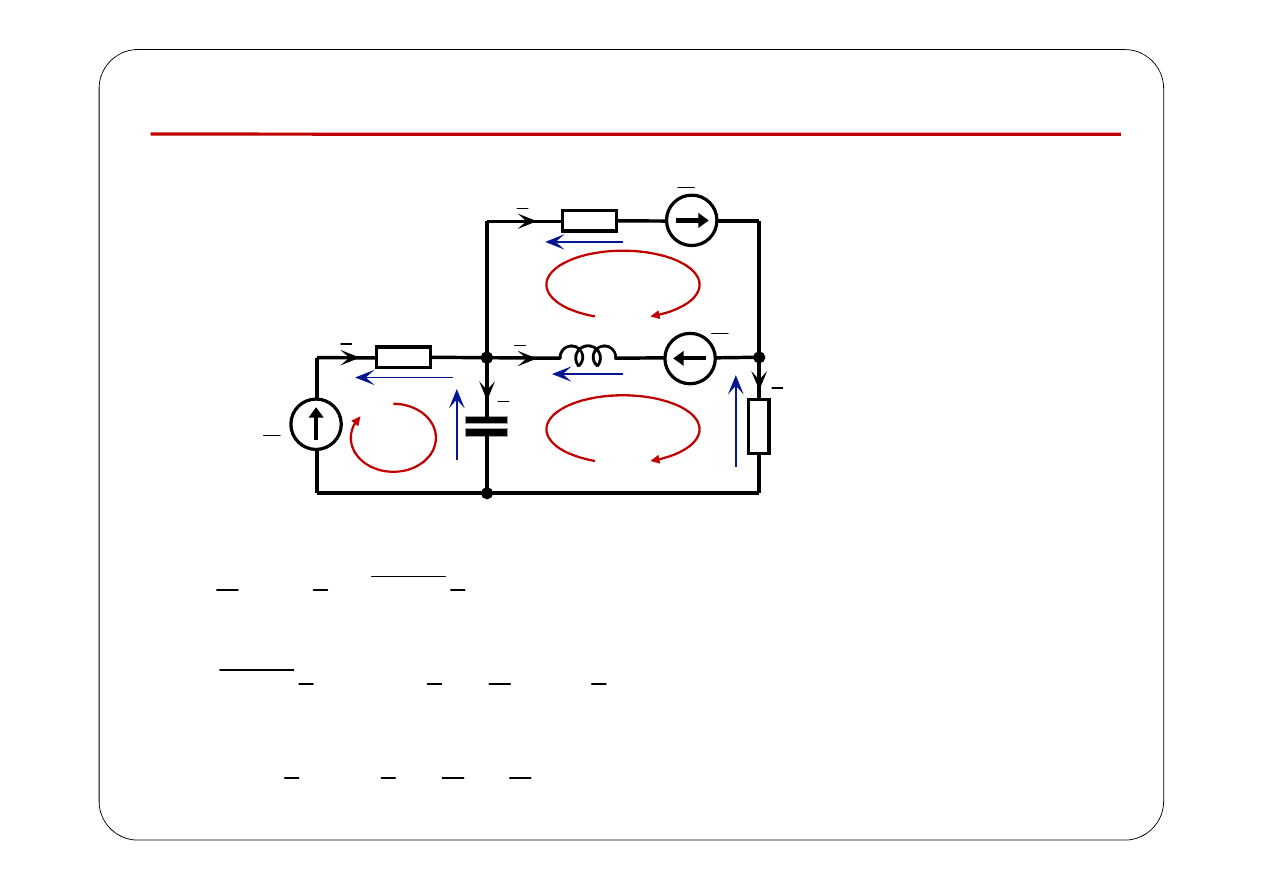
Metoda prądów oczkowych
1
E
2
E
3
E
1
R
2
R
3
R
C
L
1
I
2
I
3
I
4
I
5
I
1
2
3
1
1
3
1
0
1
0
j
E
R I
I
C
ω
− +
+
=
1.
3
2
2
5
0
3
0
1
j
0
j
I
LI
E
R I
C
ω
ω
−
+
+
+
=
2.
2
4
3
2
0
2
j
0
LI
R I
E
E
ω
−
+
−
−
=
3.
1
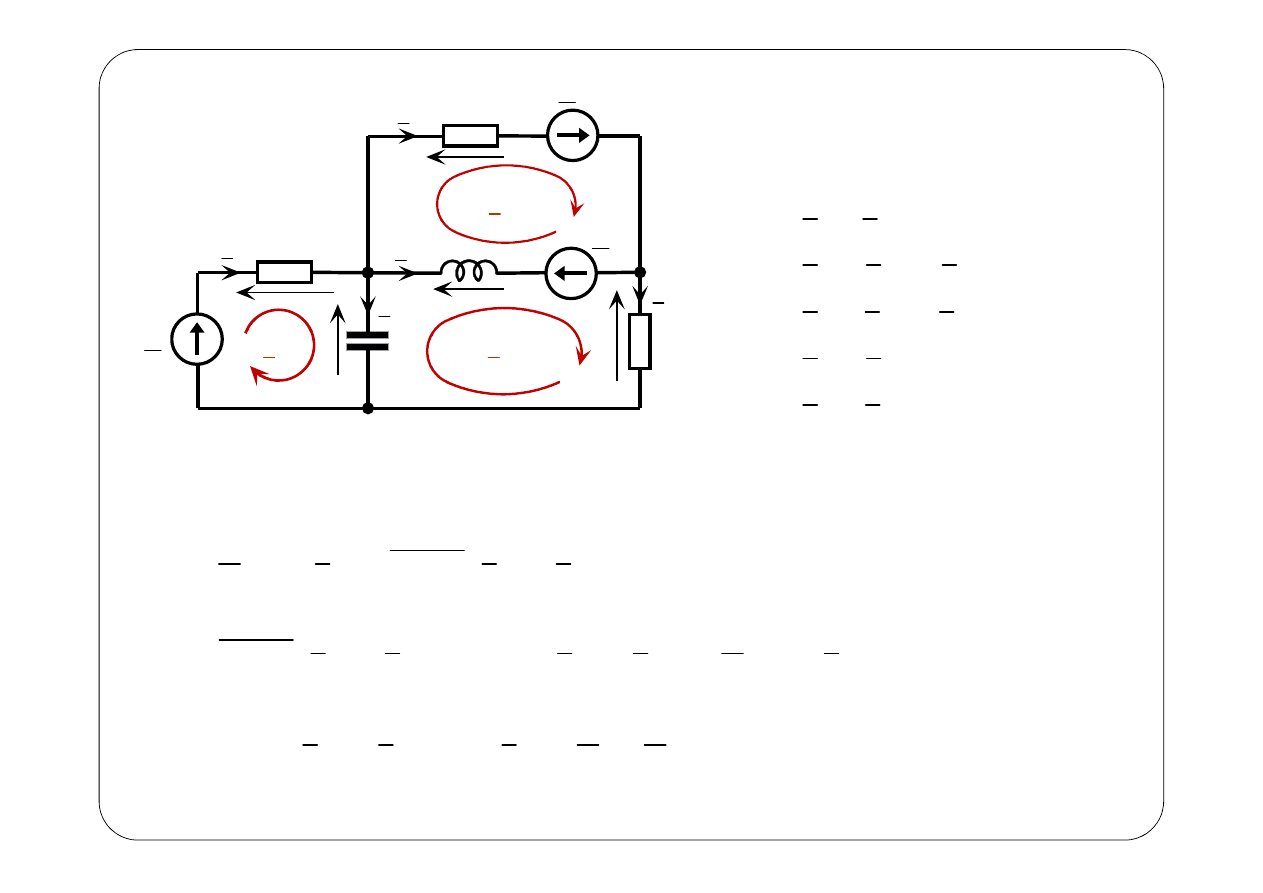
1
E
2
E
3
E
1
R
2
R
3
R
C
L
m1
I
m2
I
m3
I
1
I
2
I
3
I
4
I
5
I
1
m1
2
m2
m3
3
m1
m2
4
m3
5
m2
I
I
I
I
I
I
I
I
I
I
I
I
=
=
−
=
−
=
=
(
)
1
m1
m1
m2
1
0
1
0
j
E
R I
I
I
C
ω
− +
+
−
=
1.
(
)
(
)
m1
m2
m2
m3
2
m2
0
3
0
1
j
0
j
I
I
L I
I
E
R I
C
ω
ω
−
−
+
−
+
+
=
2.
(
)
m2
m3
m3
3
2
0
2
j
0
L I
I
R I
E
E
ω
−
−
+
−
−
=
3.
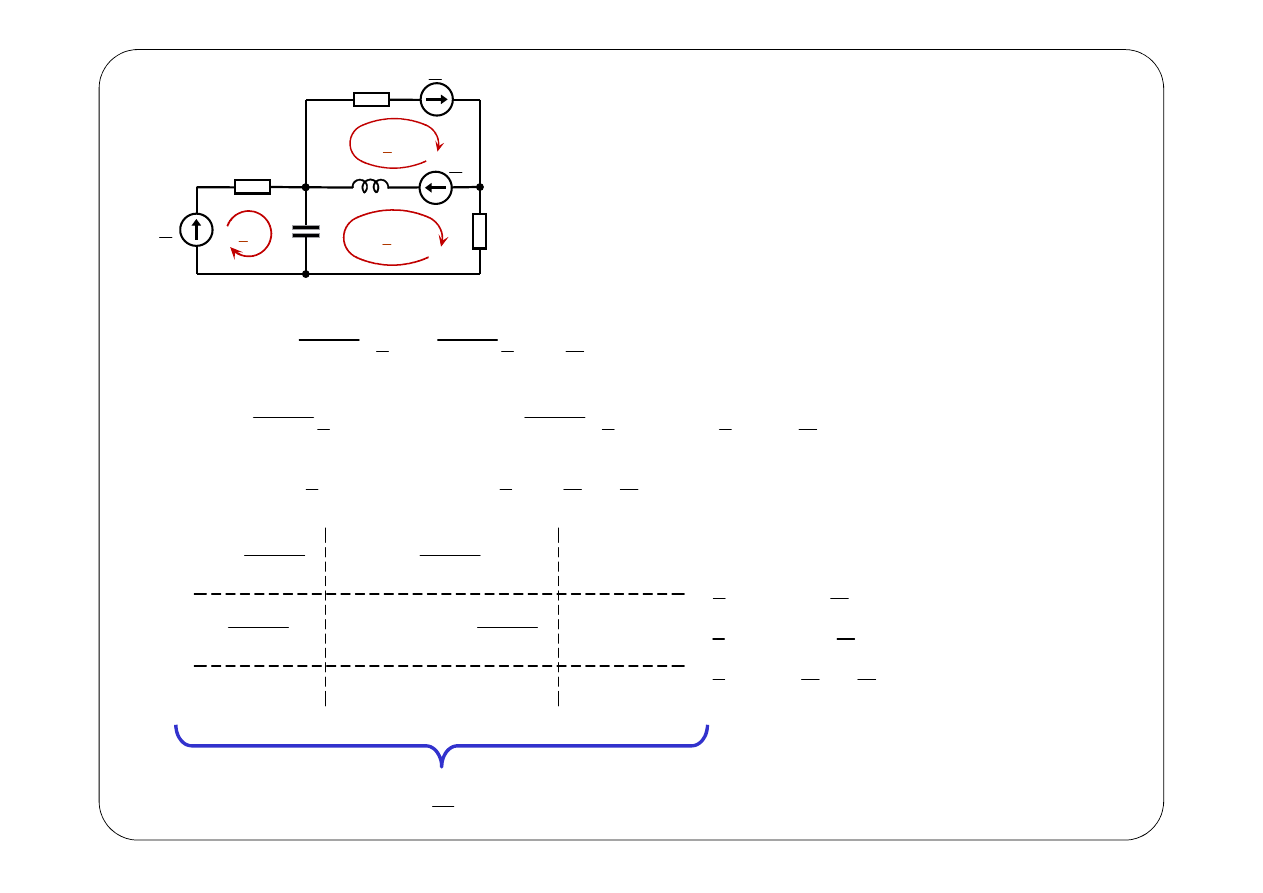
1
E
2
E
3
E
1
R
2
R
3
R
C
L
m1
I
m2
I
m3
I
m1
m2
1
1
0
0
m1
m2
m3
2
3
0
0
0
0
1
1
j
j
1
1
j
j
j
j
R
I
I
E
C
C
I
R
L
I
LI
E
C
C
ω
ω
ω
ω
ω
ω
+
−
=
−
+
+
+
−
= −
1.
2.
(
)
0
0
m2
m3
2
3
0
2
0
j
j
j
j
C
C
LI
R
L I
E
E
ω
ω
ω
ω
−
+
+
=
+
3.
1
0
0
m1
1
m2
2
3
0
0
0
0
m3
2
3
0
2
0
1
1
0
j
j
1
1
j
j
j
j
0
j
j
R
C
C
I
E
R
L
L
I
E
C
C
I
E
E
L
R
L
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
+
−
=
−
+
−
+
m
Z
— macierz zespolonych impedancji oczkowych
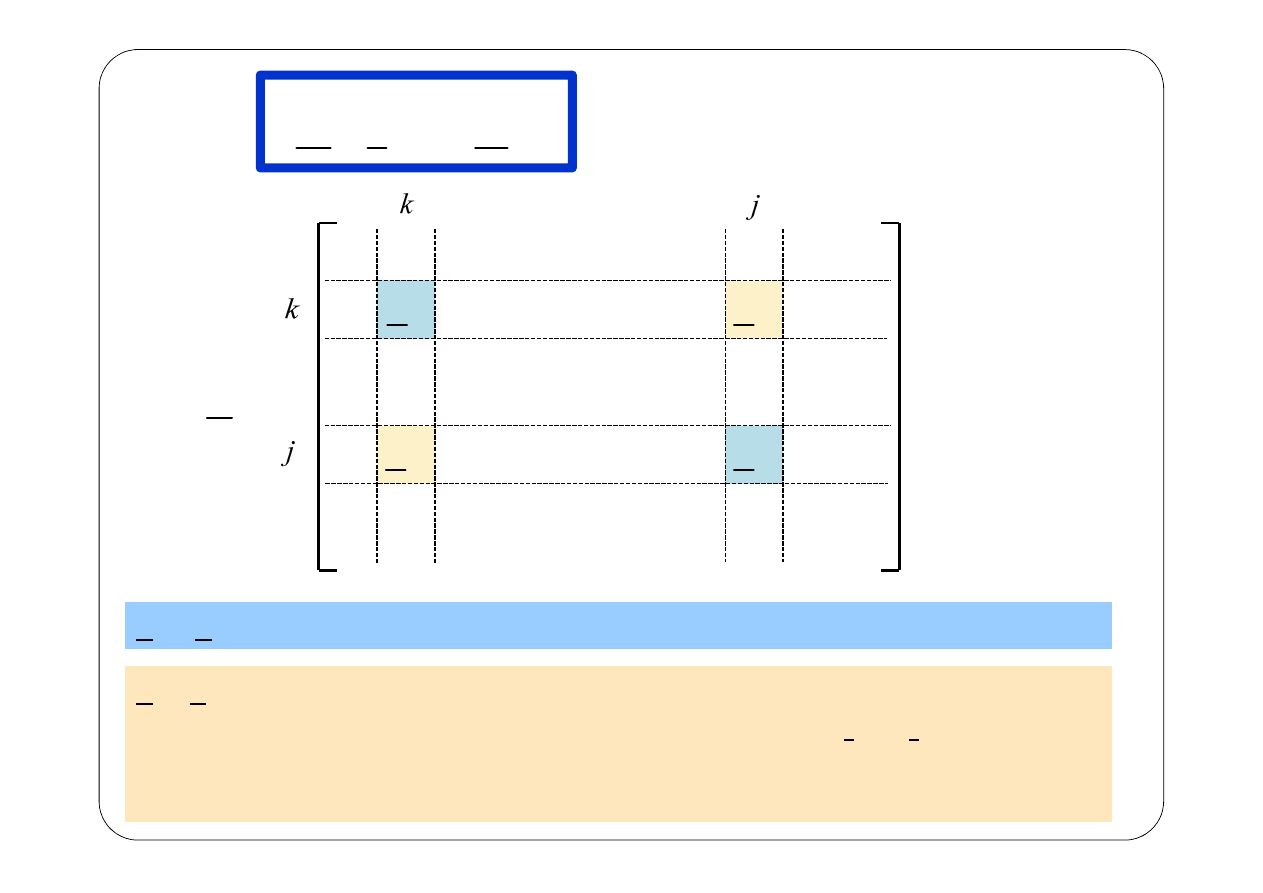
m
m
m
=
Z I
E
m
=
Z
Z
kk
Z
kj
Z
Z
jk
Z
jj
Z
Z
kk
, (Z
jj
) — suma impedancji zespolonych gałęzi tworzących oczko k, (j)
Z
jk
, Z
kj
— impedancje zespolone gałęzi należących jednocze
śnie do
oczek k i j, wzięte ze znakiem „+” gdy prądy I
mk
i I
mj
płyną we
wspólnej gałęzi w tym samym kierunku, lub ze znakiem „–” gdy
płyną w kierunkach przeciwnych
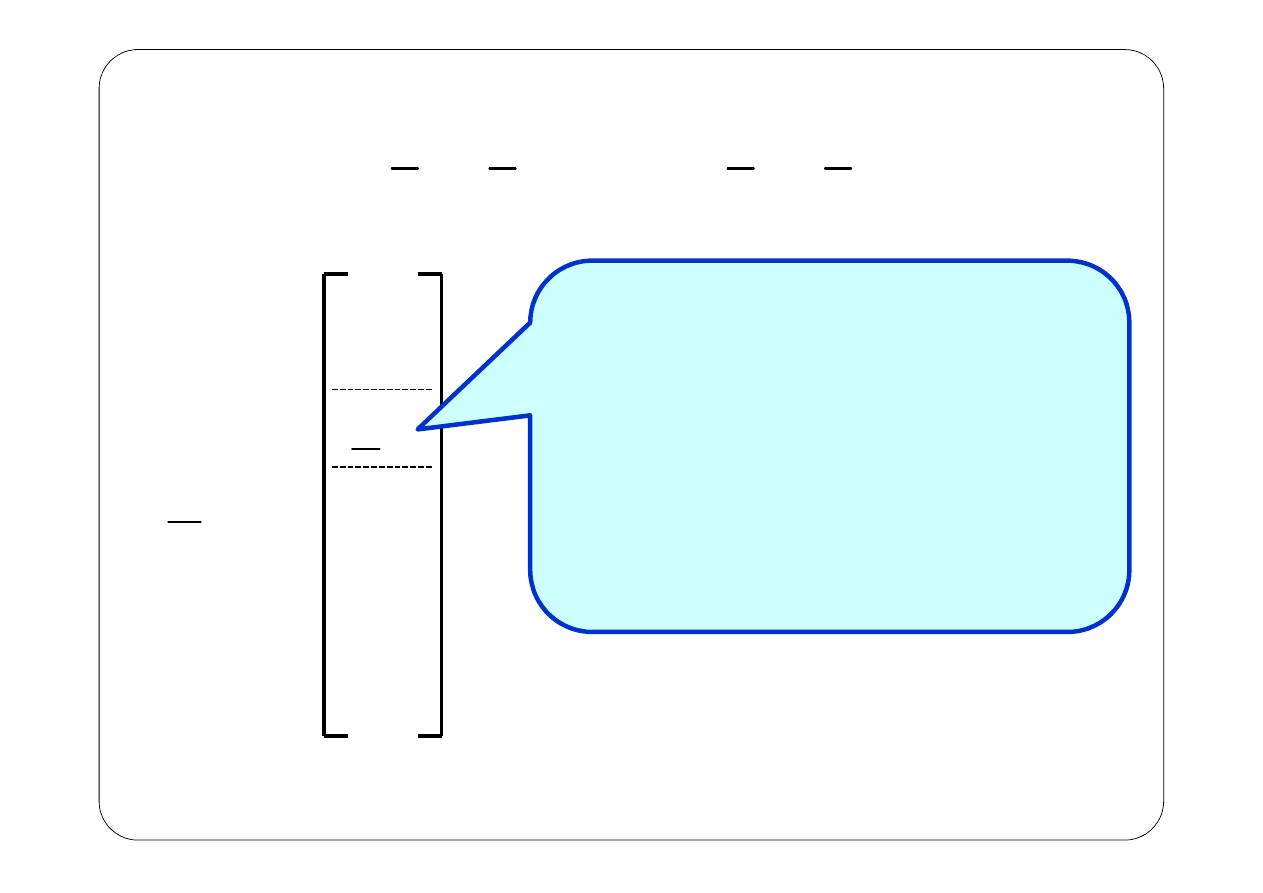
Układ RLC, e
t
m
m
,
czyli
kj
jk
Z
Z
=
=
Z
Z
k
mk
E
Algebraiczna suma wartości
skutecznych zespolonych SEM
źródeł napięciowych, znajdujących
się w oczku k, przy czym SEM
m
=
E
mk
E
skierowaną zgodnie z orientacją
oczka bierzemy ze znakiem plus,
a skierowaną przeciwnie — ze
znakiem minus
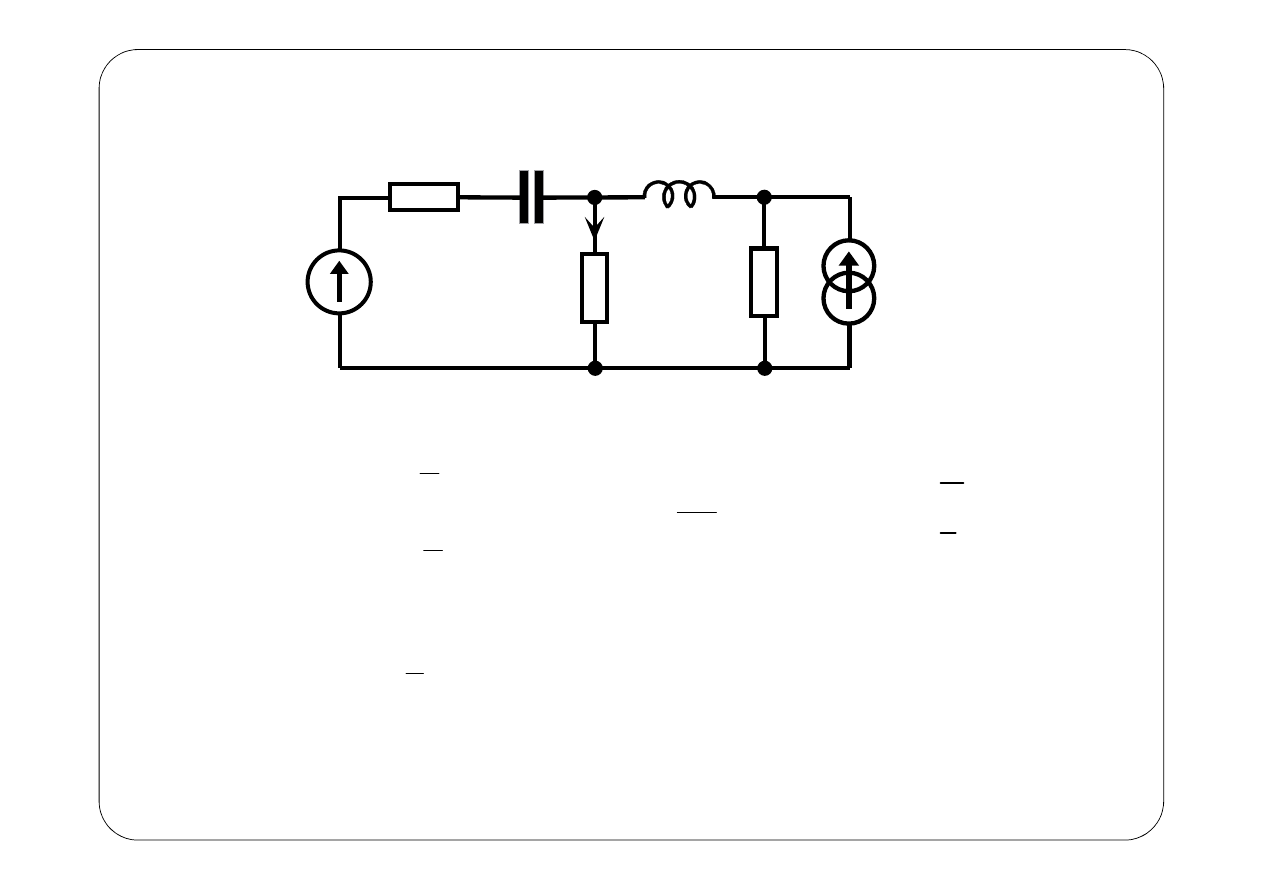
Przykład 1.
( )
e t
( )
z
i t
1
R
2
R
3
R
C
L
( )
i t
( )
( )
π
=
+
( )
( )
( )
( )
(
)
( )
0
z
1
2
3
π
4
rad
s
π
4
1
2
2sin
V,
1
2 sin
A,
1Ω,
1Ω,
2 Ω,
2 H,
F.
?
e t
t
i t
t
R
R
R
L
C
i t
ω
=
+
=
=
−
=
=
=
=
=
=
z
1
j
1 j
E
I
= +
= −
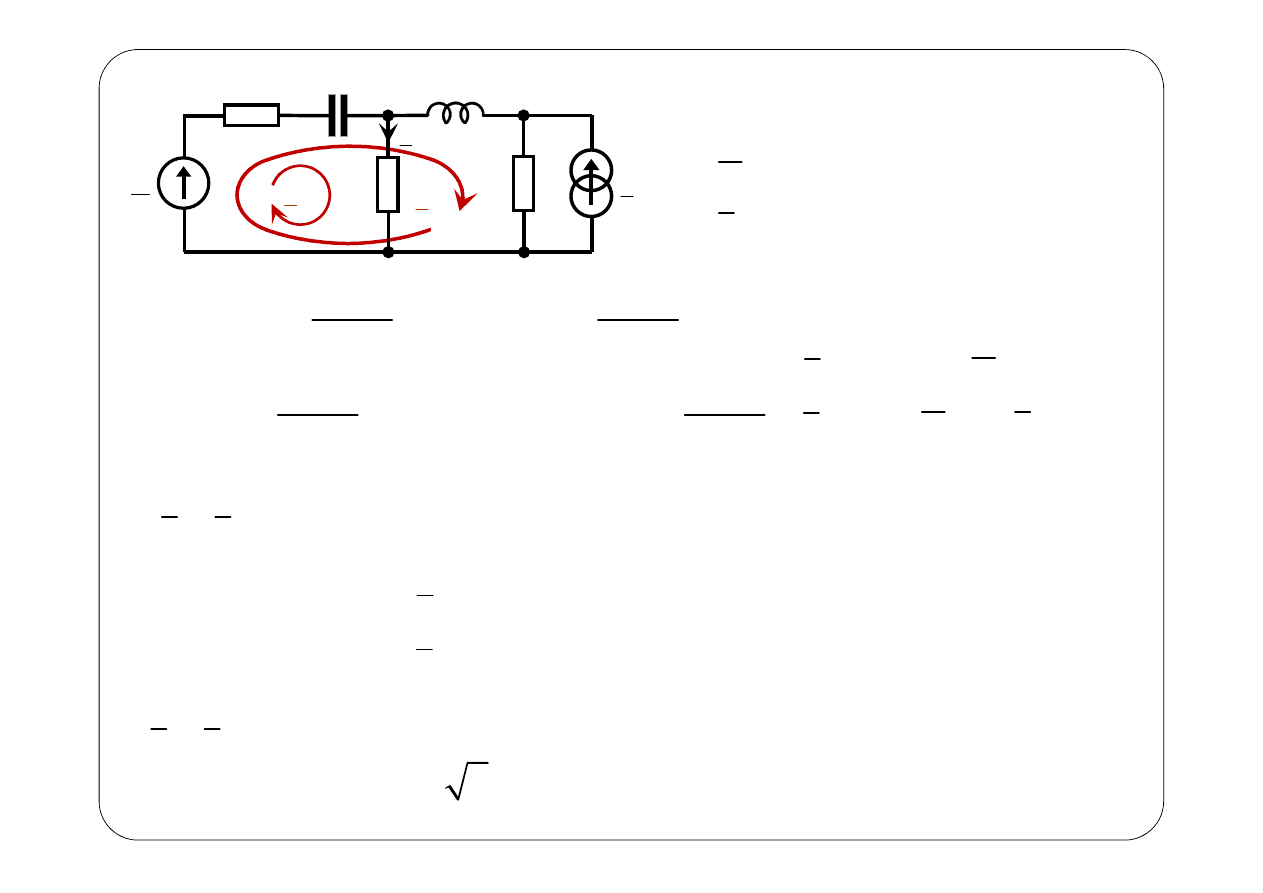
E
z
I
1
R
2
R
3
R
C
L
I
m1
I
m2
I
z
1
j
1 j
E
I
= +
= −
1
2
1
0
0
m1
z
m2
3
1
1
3
0
0
0
1
1
j
j
1
1
j
j
j
R
R
R
C
C
E
I
E
R I
I
R
R
R
L
C
C
ω
ω
ω
ω
ω
+
+
+
=
−
+
+
+
+
0
0
j
j
C
C
ω
ω
m1
I
I
=
m1
m2
j2,138
m1
2
j2
1 j2
1
j
1 j2
3
1
j3
0,1647
j0, 2588
0, 3068 e
I
I
I
I
−
−
−
+
=
−
− +
=
= −
−
=
( )
(
)
0, 3068 2 sin
2,138 A.
i t
t
=
−
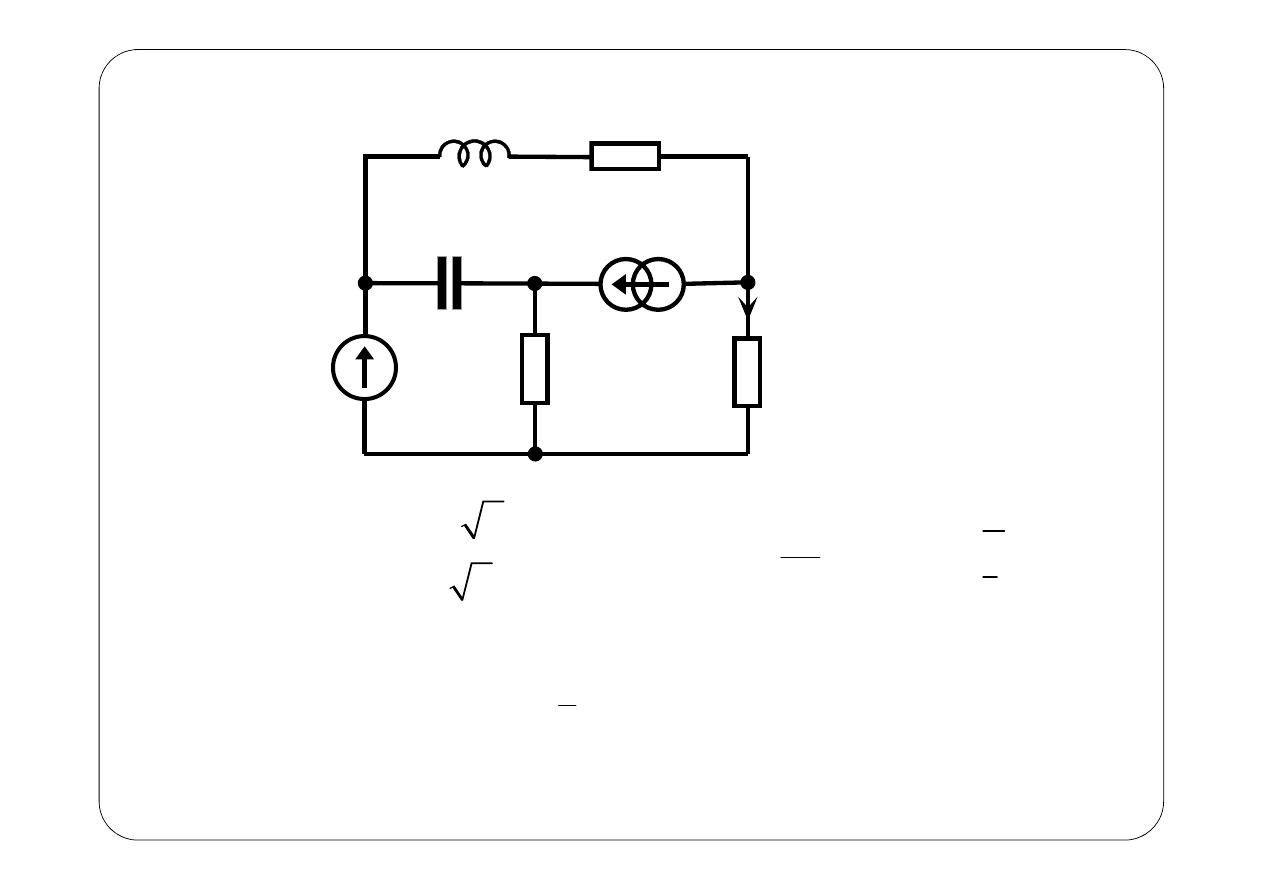
Przykład 2.
( )
e t
( )
z
i t
1
R
2
R
3
R
L
C
( )
i t
( )
( )
(
)
( )
0
z
1
2
3
rad
s
1
2
2 2 sin V,
1
2 cos A,
2 Ω,
1Ω,
3Ω,
2 H,
F.
?
e t
t
i t
t
R
R
R
L
C
i t
ω
=
=
=
=
=
=
=
=
=
z
2
j
E
I
=
=
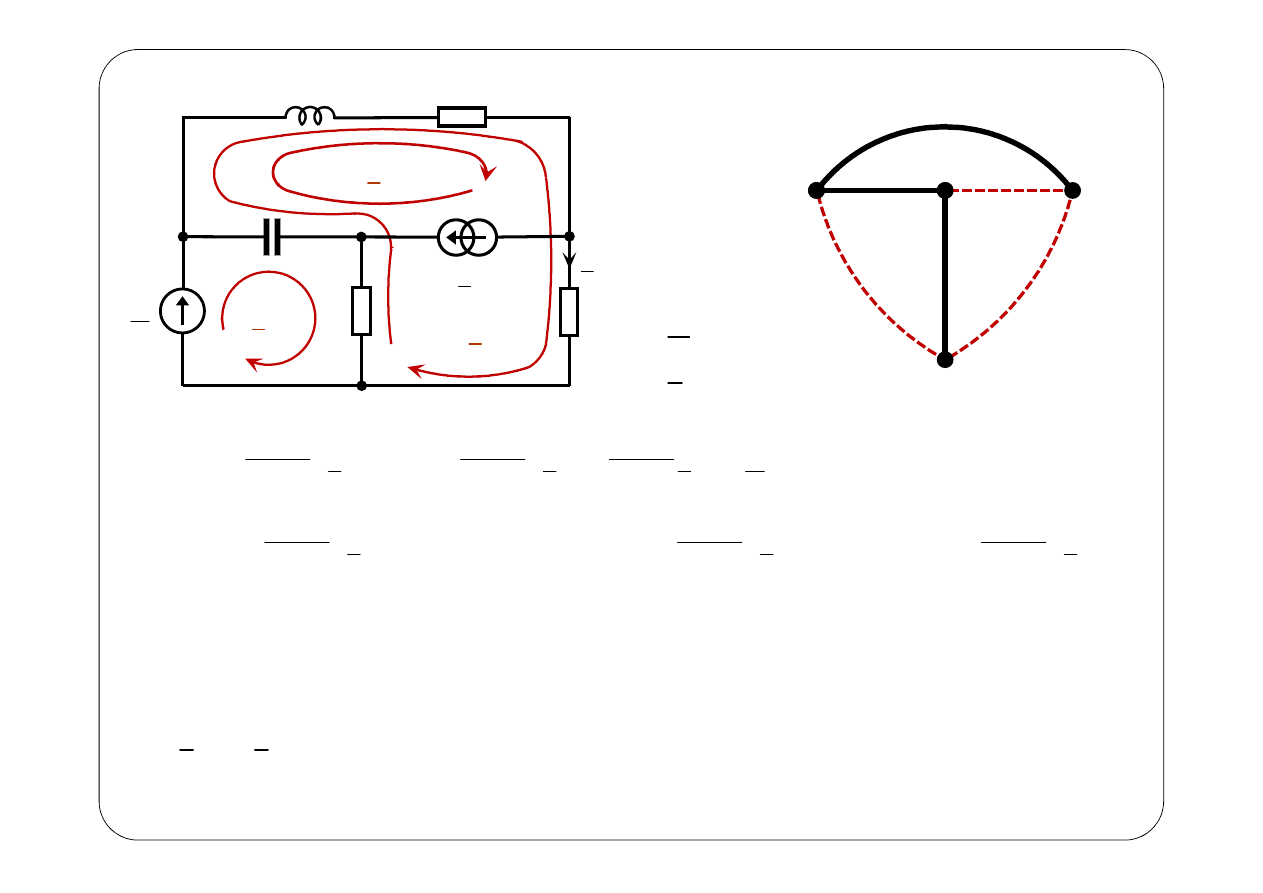
E
z
I
1
R
2
R
3
R
L
C
I
m1
I
m2
I
m3
I
z
2
j
E
I
=
=
1
1
1
R
I
R
I
I
E
+
−
+
−
=
1.
m1
m2
m3
1
1
0
0
0
m1
m2
m3
1
1
2
3
0
3
0
0
0
0
1
1
1
j
j
j
1
1
1
j
j
0
j
j
j
R
I
R
I
I
E
C
C
C
R
I
R
R
R
L
I
R
L
I
C
C
C
ω
ω
ω
ω
ω
ω
ω
ω
+
−
+
−
=
−
+
+
+
+
+
+
+
+
+
=
1.
2.
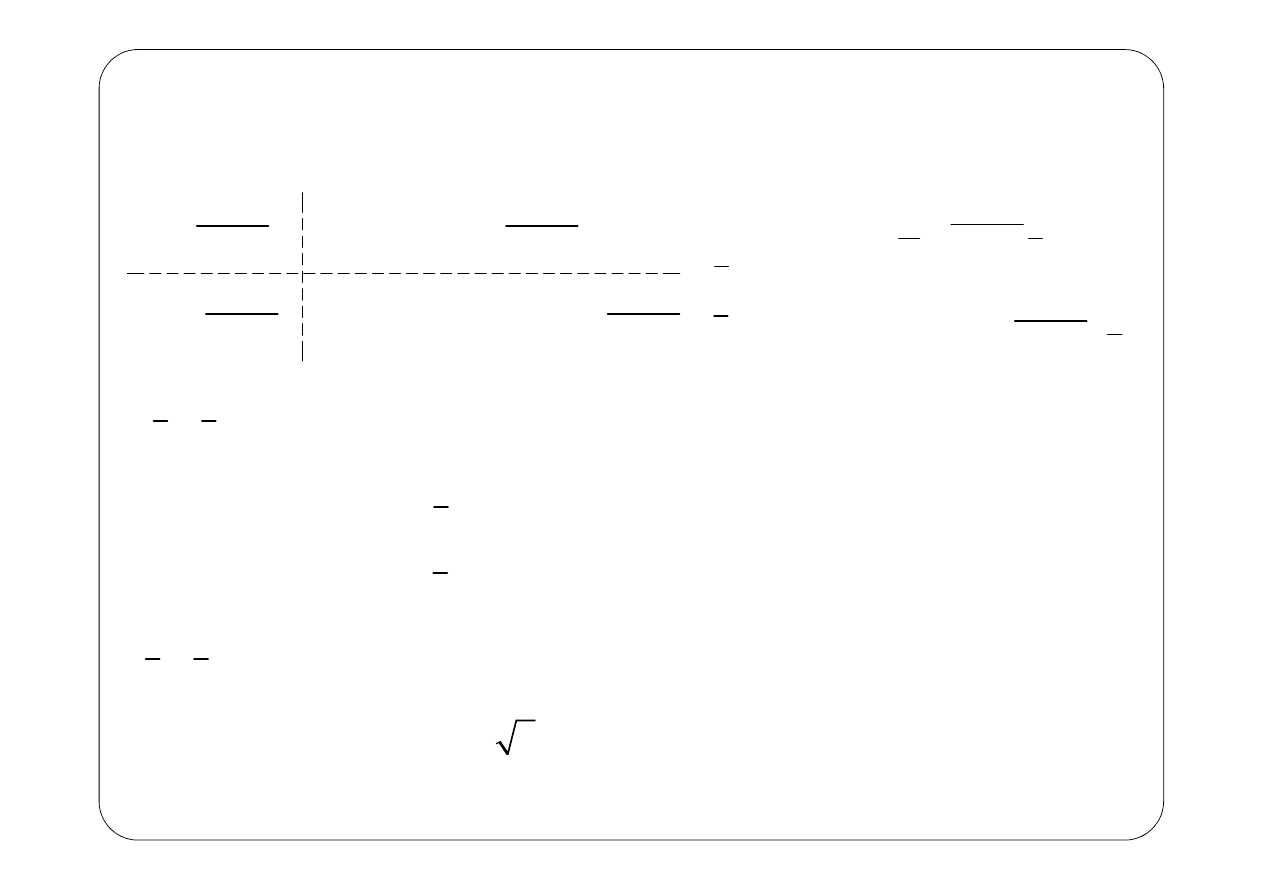
Dla oczka 3. nie potrafimy napisać równania na podstawie II prawa Kirchhoffa
(nie znamy napięcia na źródle prądowym). Zastępujemy je równaniem
m3
z
I
I
=
3.
Po podstawieniu równania
3.
do
1.
i
2.
i uporządkowaniu
z
1
1
0
0
0
m1
m2
1
1
2
3
0
z
3
0
0
0
0
1
1
1
j
j
j
1
1
1
j
j
j
j
j
E
I
R
R
C
C
C
I
I
R
R
R
R
L
R
L
I
C
C
C
ω
ω
ω
ω
ω
ω
ω
ω
+
+
− −
=
− −
+
+
+
+
−
+
+
m2
I
I
=
m1
m2
j1,107
m2
2
j2
2
j2
4
2
j2
6
j3
0,5
j 1,118e
I
I
I
I
−
−
− +
=
− +
−
=
=
− =
( )
(
)
1,118 2 sin
1,107 A.
i t
t
=
−
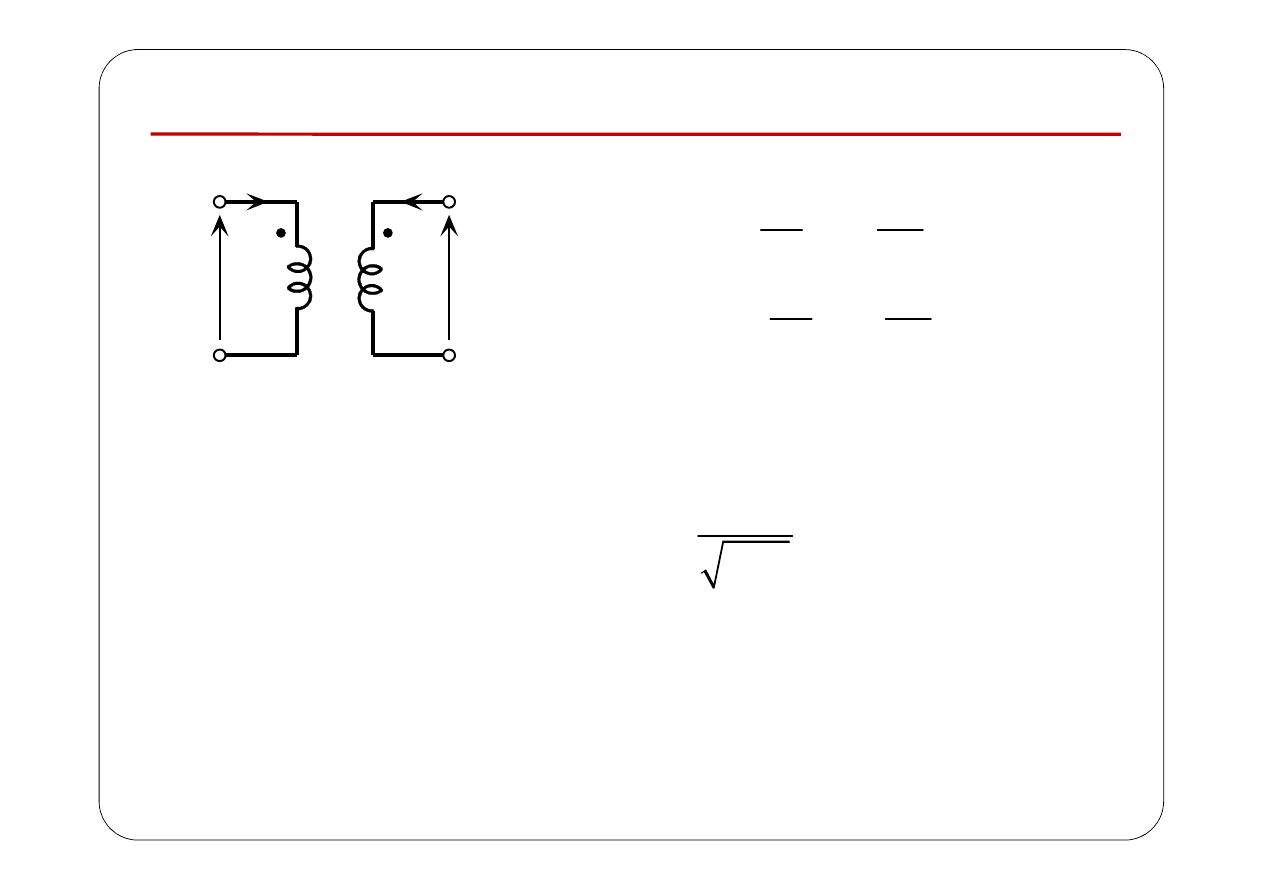
Induktory sprzężone magnetycznie
( )
1
u t
( )
2
u
t
( )
1
i t
( )
2
i t
1
L
2
L
M
( )
( )
1
2
1
1
1
2
2
2
d
d
d
d
d
d
d
d
i
i
u t
L
M
t
t
i
i
u
t
M
L
t
t
=
+
=
+
M — indukcyjność wzajemna, [M] = H
Warunek fizycznej realizowalności:
2
1
2
0
L L
M
−
≥
1
2
1
M
k
L L
=
≤
Zaciski jednoimienne (zaznaczone na schemacie np. kropkami) — początki
(lub końce) uzwojeń. Jeżeli prądy i
1
(t) i i
2
(t) jednocześnie wpływają do
zacisków
jednoimiennych
(lub
wypływają
z
nich),
to
strumienie
magnetyczne wytworzone przez te prądy sumują się.
Warunek fizycznej realizowalności:
lub
k — współczynnik sprzężenia
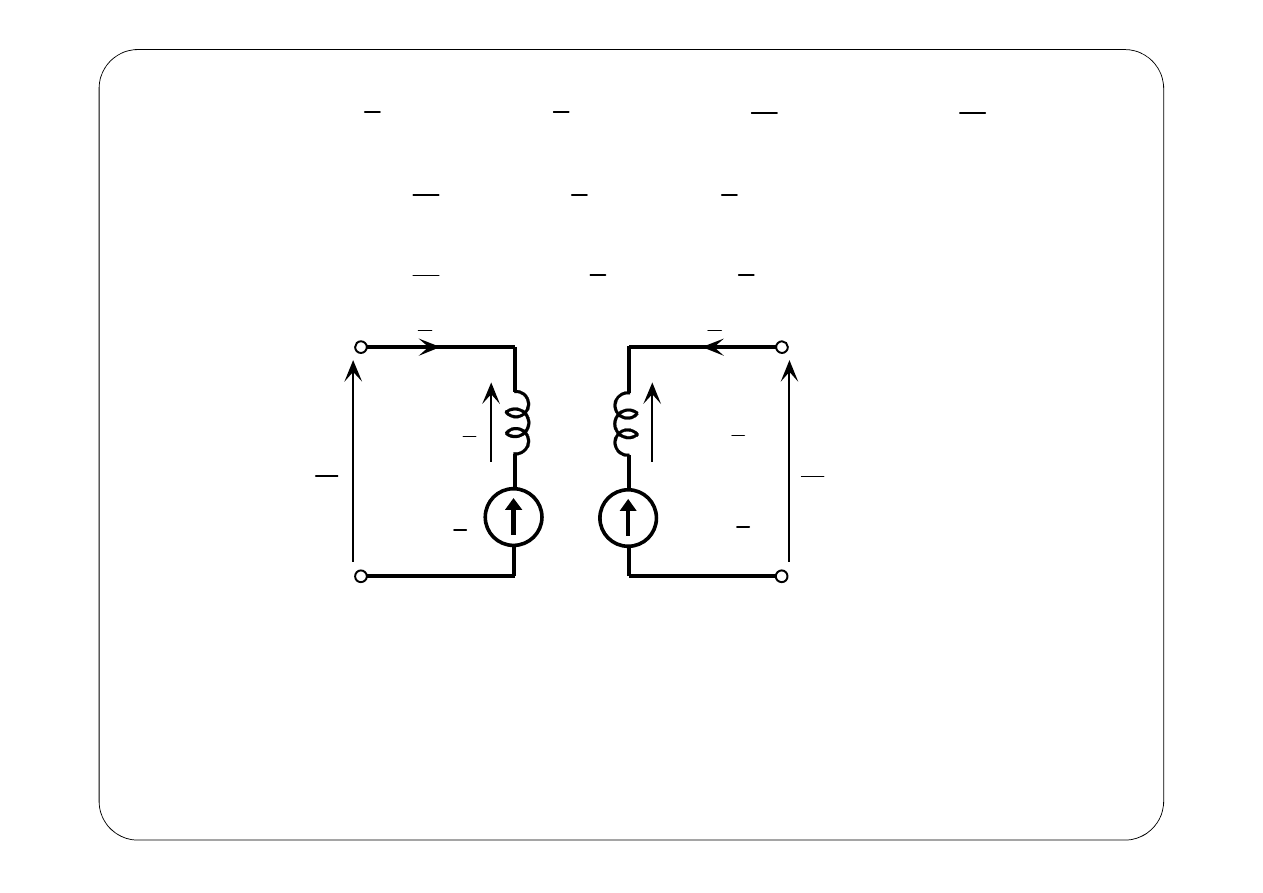
( )
( )
( )
( )
1
2
1
2
1
2
1
2
i t
I
i t
I
u t
U
u
t
U
⇌
⇌
⇌
⇌
1
2
1
0
1
0
1
2
2
0
1
0
2
j
j
j
j
U
L I
M I
U
M I
L I
ω
ω
ω
ω
=
+
=
+
U
U
1
I
2
I
1
L
2
L
1
0
1
j
L I
ω
2
0
2
j
L I
ω
1
U
2
U
2
0
j
M I
ω
1
0
j
M I
ω
Reguła strzałkowania źródeł sterowanych pochodzących od sprzężenia:
jeżeli prądy
i
1
(t)
i
i
2
(t)
jednocześnie wpływają do zacisków
jednoimiennych (lub wypływają z nich), to źródła sterowane strzałkujemy
przeciwnie do prądu w gałęzi, w której się znajdują.
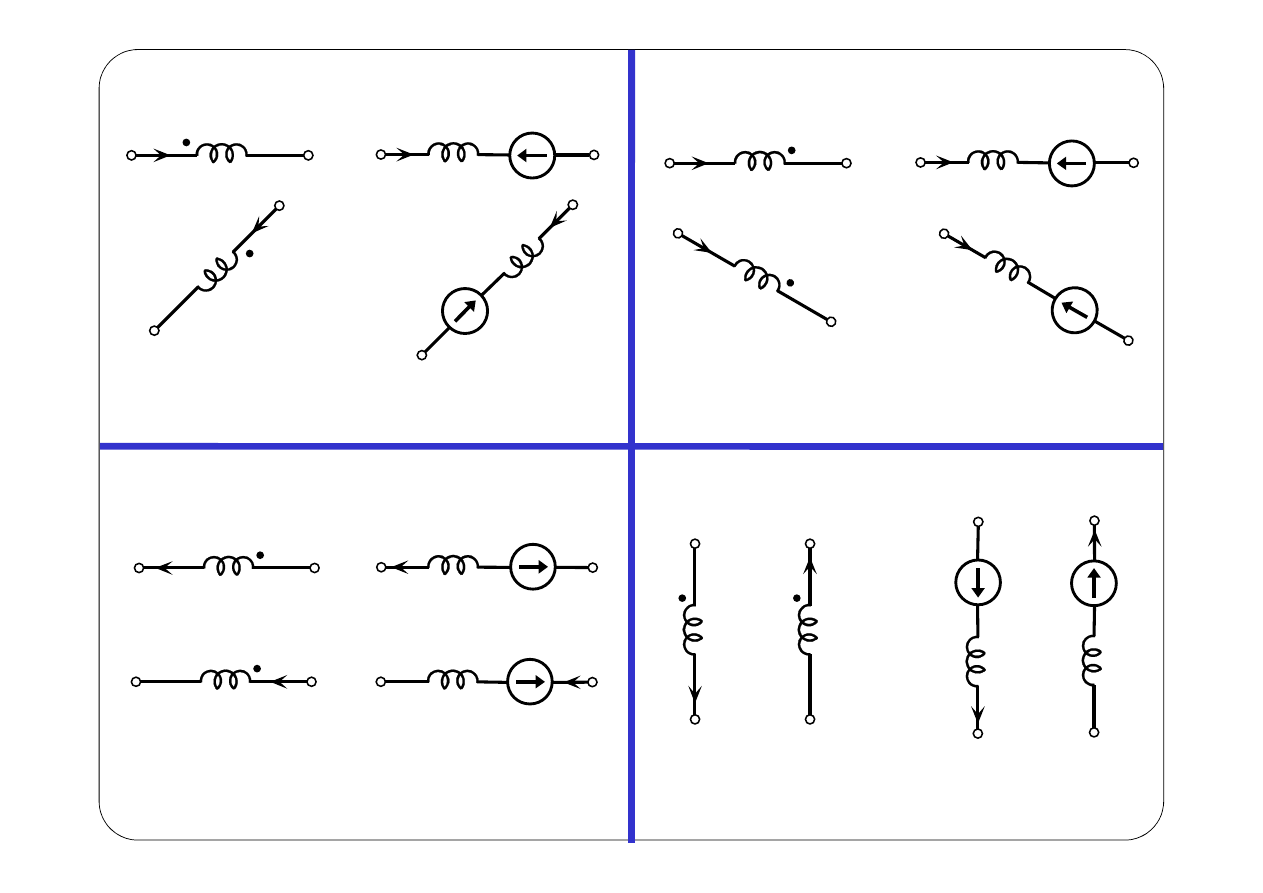
⇌
⇌
⇌
⇌
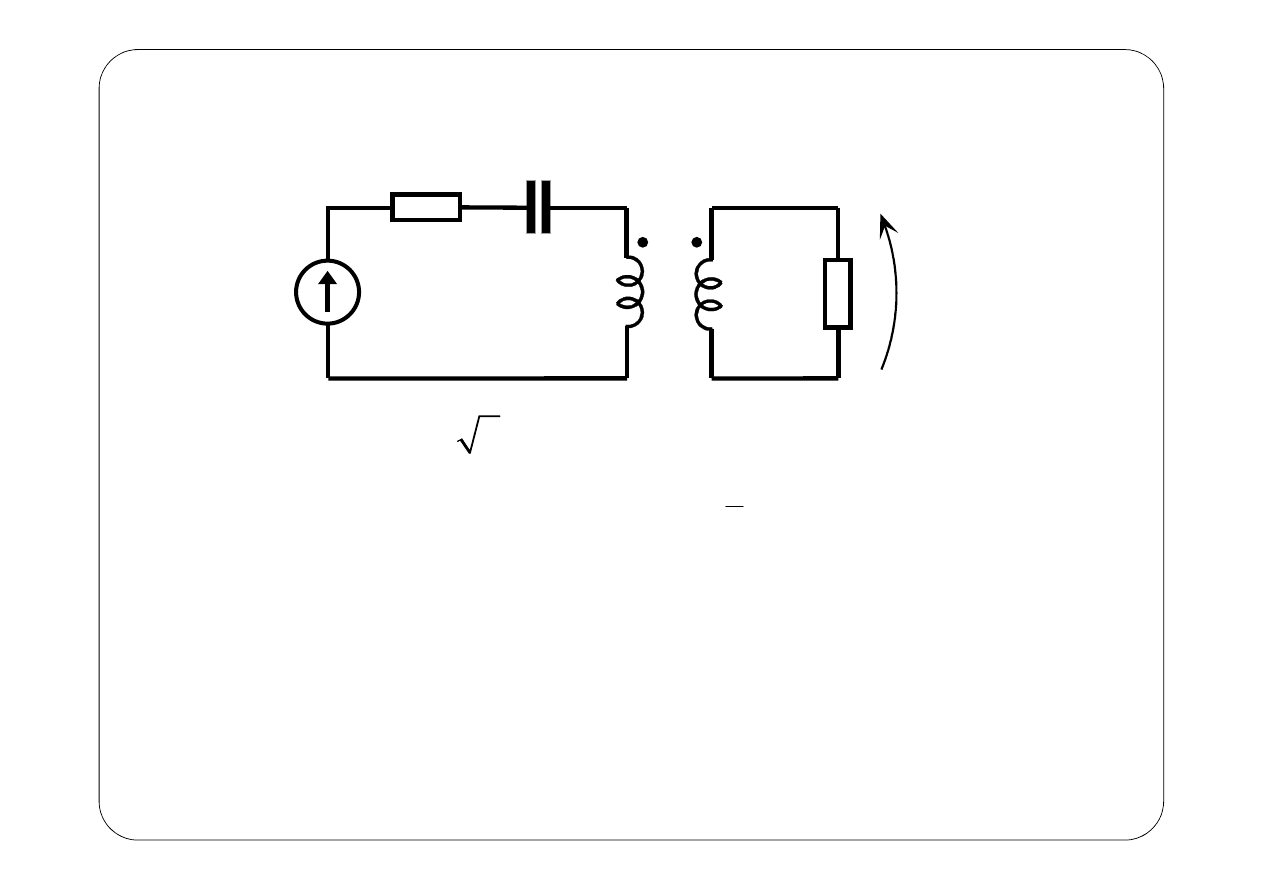
Przykład 1.
( )
e t
1
R
2
R
C
1
L
2
L
M
( )
u t
( )
5 2 sin V,
e t
t
=
( )
( )
1
2
1
2
1
4
5 2 sin V,
2 Ω,
1Ω,
F,
4 H,
2 H,
1H,
?
e t
t
R
R
C
L
L
M
u t
=
=
=
=
=
=
=
=
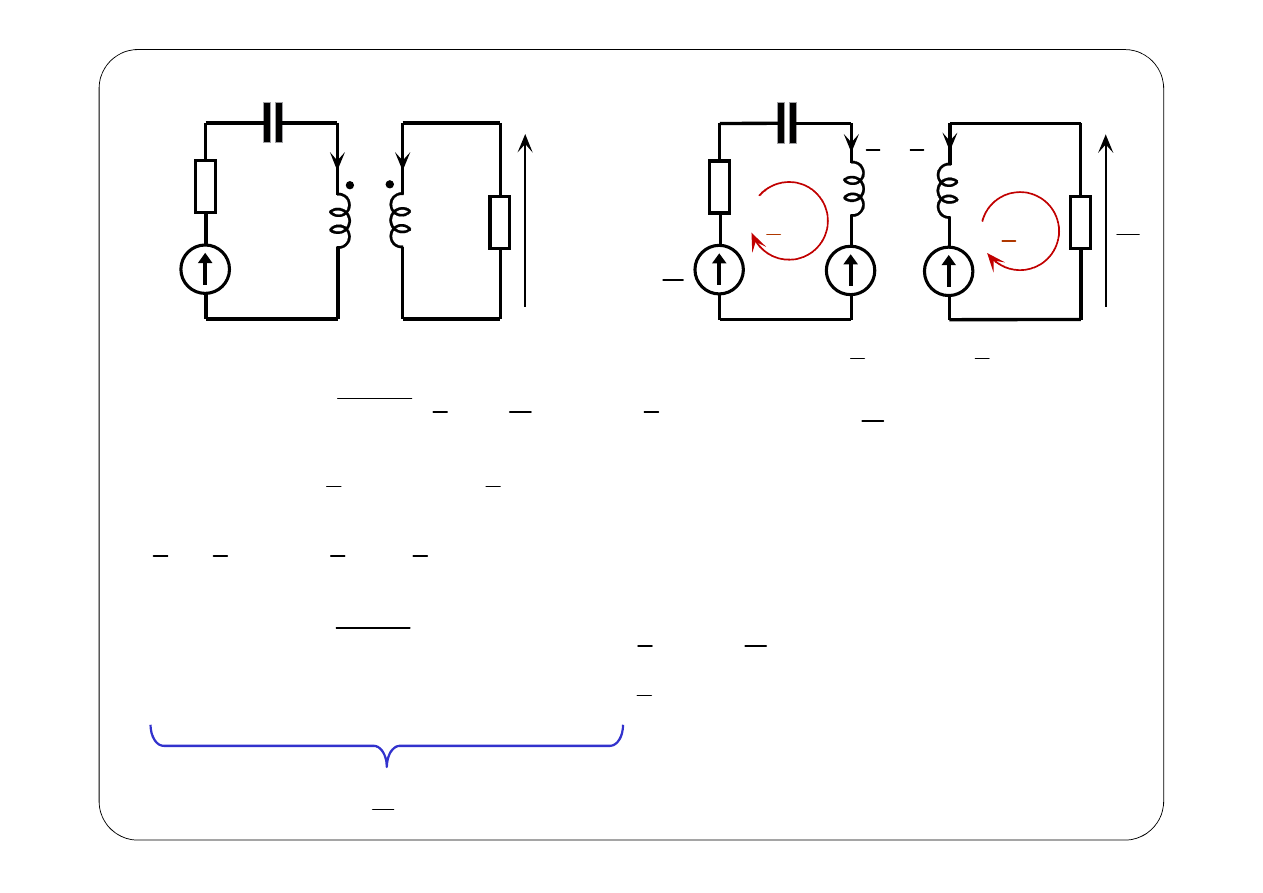
( )
e t
1
R
2
R
C
1
L
2
L
M
( )
u t
( )
1
i t
( )
2
i t
(
)
m1
2
1
0
1
0
0
1
j
j
j
R
L
I
E
M I
C
ω
ω
ω
+
+
= −
E
1
R
2
R
C
1
L
2
L
U
1
I
2
I
2
0
j
M I
ω
1
0
j
M I
ω
m1
I
m2
I
5
E
=
(
)
m2
1
2
0
2
0
j
j
R
L
I
M I
ω
ω
+
=
1
m1
2
m2
,
I
I
I
I
=
= −
1
0
1
0
m1
0
m2
0
2
0
2
1
j
j
j
0
j
j
R
L
M
I
E
C
I
M
R
L
ω
ω
ω
ω
ω
+
+
−
=
−
+
m
Z

( )
(
)
m1
m2
m2
j 0,6435
m2
2
2
j
5
j
1 2 j
0
0,8
j0, 6
0,8
j0, 6
e
2 sin
0, 6435 V.
I
I
I
U
R I
u t
t
−
=
−
+
=
+
=
=
+
=
=
+
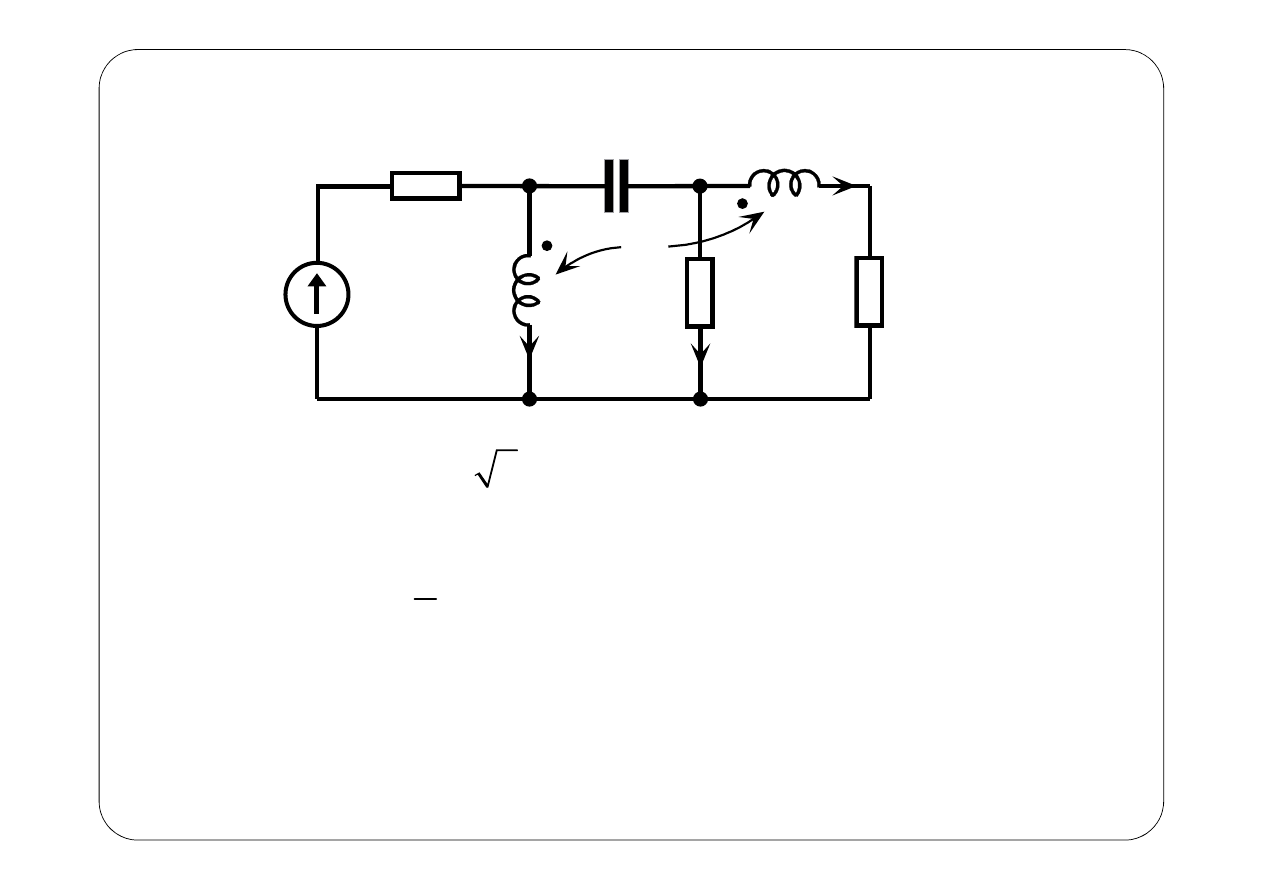
Przykład 2.
M
( )
e t
1
R
1
L
C
2
R
3
R
2
L
( )
1
i t
( )
2
i t
( )
i t
( )
( )
1
2
3
1
2
15 2 sin V,
1Ω,
1Ω,
1Ω,
2 F,
1
H,
4 H,
1H.
2
?
e t
t
R
R
R
C
L
L
M
i t
=
=
=
=
=
=
=
=
=
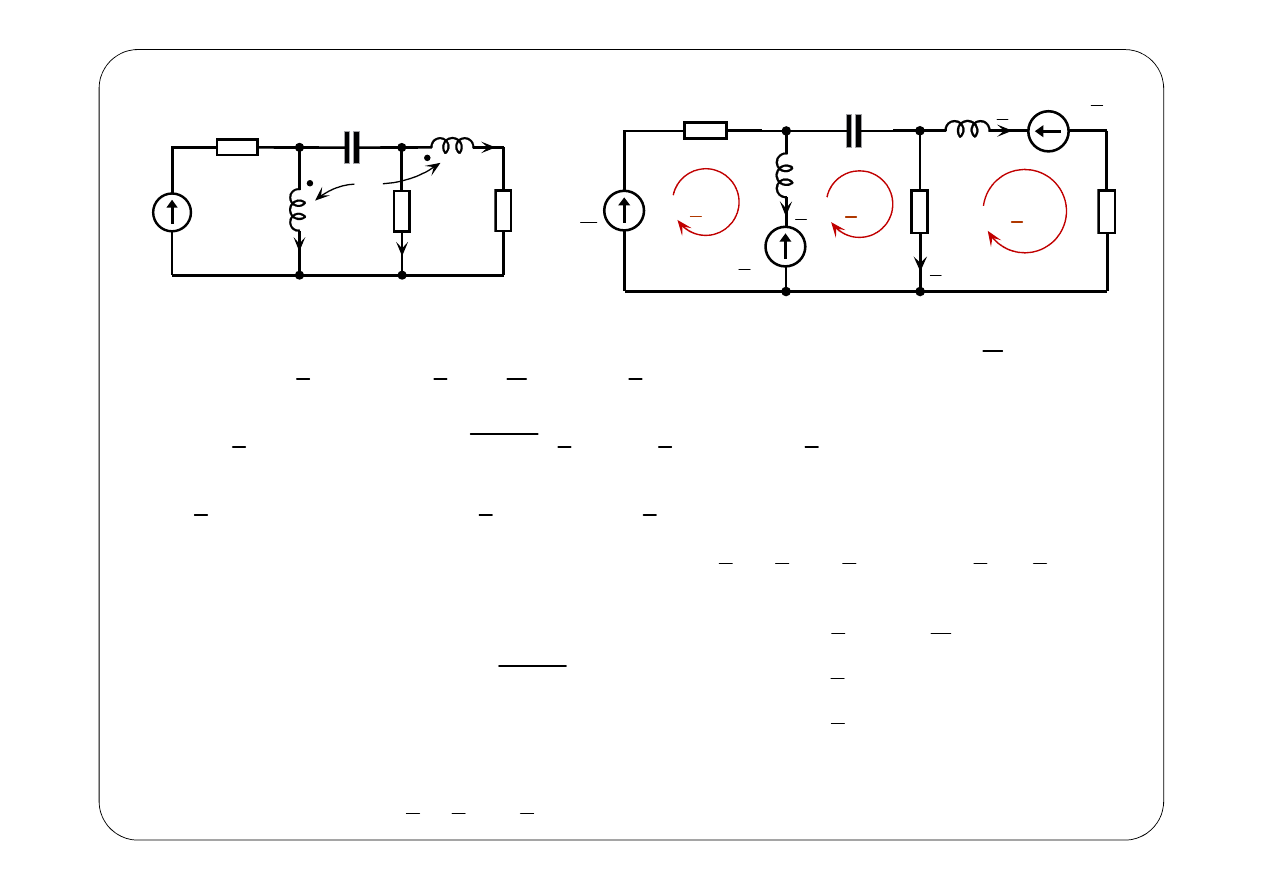
1
R
E
C
1
L
2
L
2
R
3
R
1
I
2
I
1
0
j
M I
ω
2
0
j
M I
ω
m1
I
m2
I
m3
I
I
15
E
=
(
)
m1
m2
2
1
0
1
0
1
0
m1
m2
m3
2
0
1
2
0
1
2
0
j
j
j
1
j
j
j
j
R
L I
L I
E
M I
L I
R
L
I
R I
M I
C
ω
ω
ω
ω
ω
ω
ω
+
−
= −
−
+
+
+
−
=
M
( )
e t
1
R
1
L
C
2
R
3
R
2
L
( )
1
i t
( )
2
i t
( )
i t
(
)
m1
m2
m3
2
0
1
2
0
1
2
0
0
m2
m3
1
2
2
3
0
2
0
j
j
j
j
j
j
L I
R
L
I
R I
M I
C
R I
R
R
L
I
M I
ω
ω
ω
ω
ω
ω
−
+
+
+
−
=
−
+
+
+
= −
1
m1
m2
2
m3
I
I
I
I
I
=
−
=
1
0
1
0
1
0
m1
m2
0
1
2
0
1
2
0
0
m3
0
2
0
2
3
0
2
j
j
j
1
j
j
j
0
j
0
j
j
j
R
L
L
M
I
E
L
R
L
R
M
I
C
I
M
R
M
R
R
L
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
+
− −
=
− −
+
+
m2
m3
I
I
I
=
−

m1
m2
m3
1
j0,5
j0,5
j
15
j0,5
1
1
j
0
j
1
j
2
j4
0
I
I
I
+
−
−
− −
=
− −
+
m2
m3
2
j4
3
j
I
I
= − +
= − +
j1,249
1
j3
3,162e
I
I
I
=
−
= +
=
j1,249
m2
m3
1
j3
3,162e
I
I
I
=
−
= +
=
( )
(
)
3,162 2 sin
1, 249 A.
i t
t
=
+
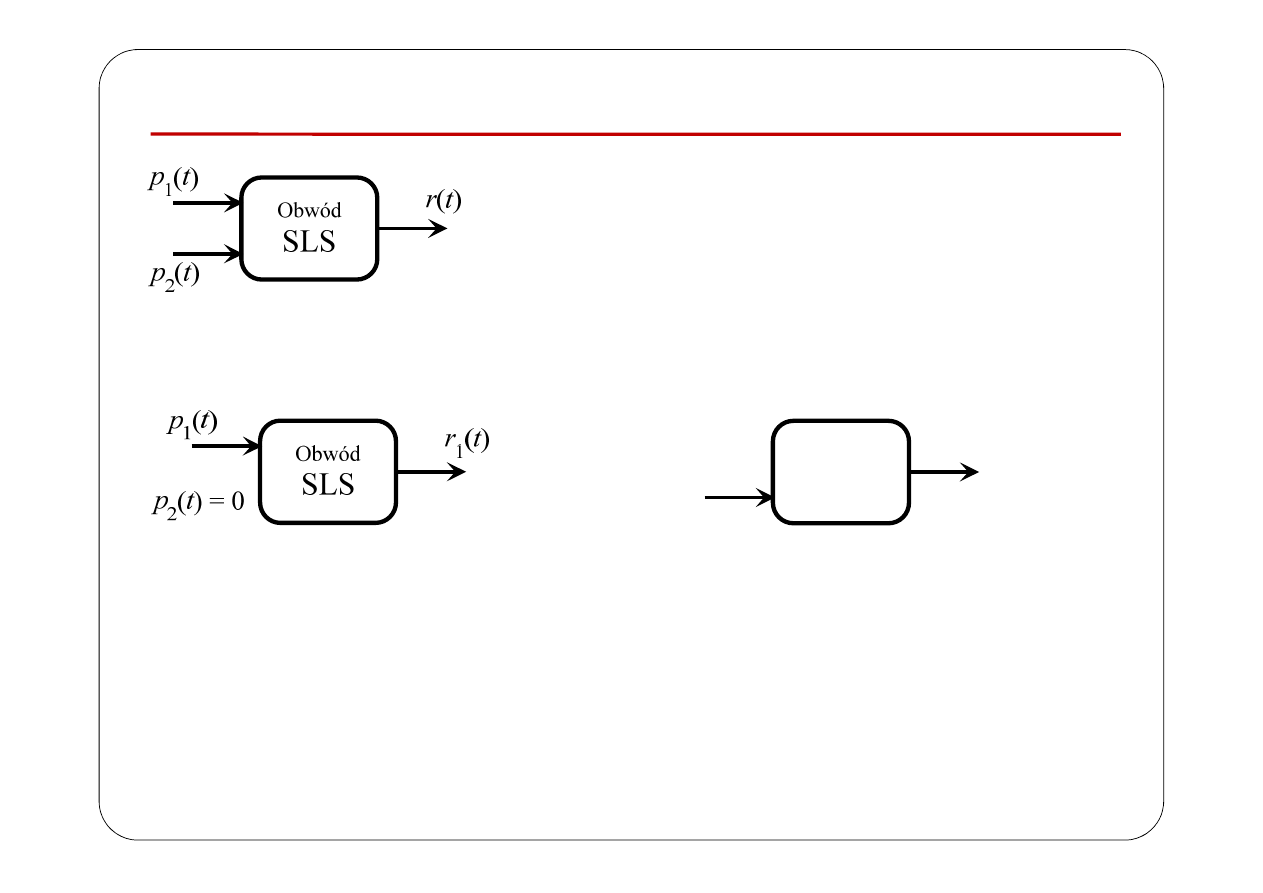
Zasada superpozycji
( ) ( ) ( )
1
2
r t
r t
r t
=
+
gdzie
Obwód
p (t) = 0
r
2
(t)
Obwód
SLS
p
1
(t) = 0
p
2
(t)
r
2
(t)
Wyłączanie pobudzeń:
autonomiczne
źródło napięciowe usuwamy z obwodu i zwieramy zaciski do
których było ono dołączone;
autonomiczne
źródło prądowe usuwamy z obwodu i pozostawiamy rozwarte
zaciski do których było ono dołączone.
Nie wolno usuwa
ć źródeł sterowanych — to nie są pobudzenia!
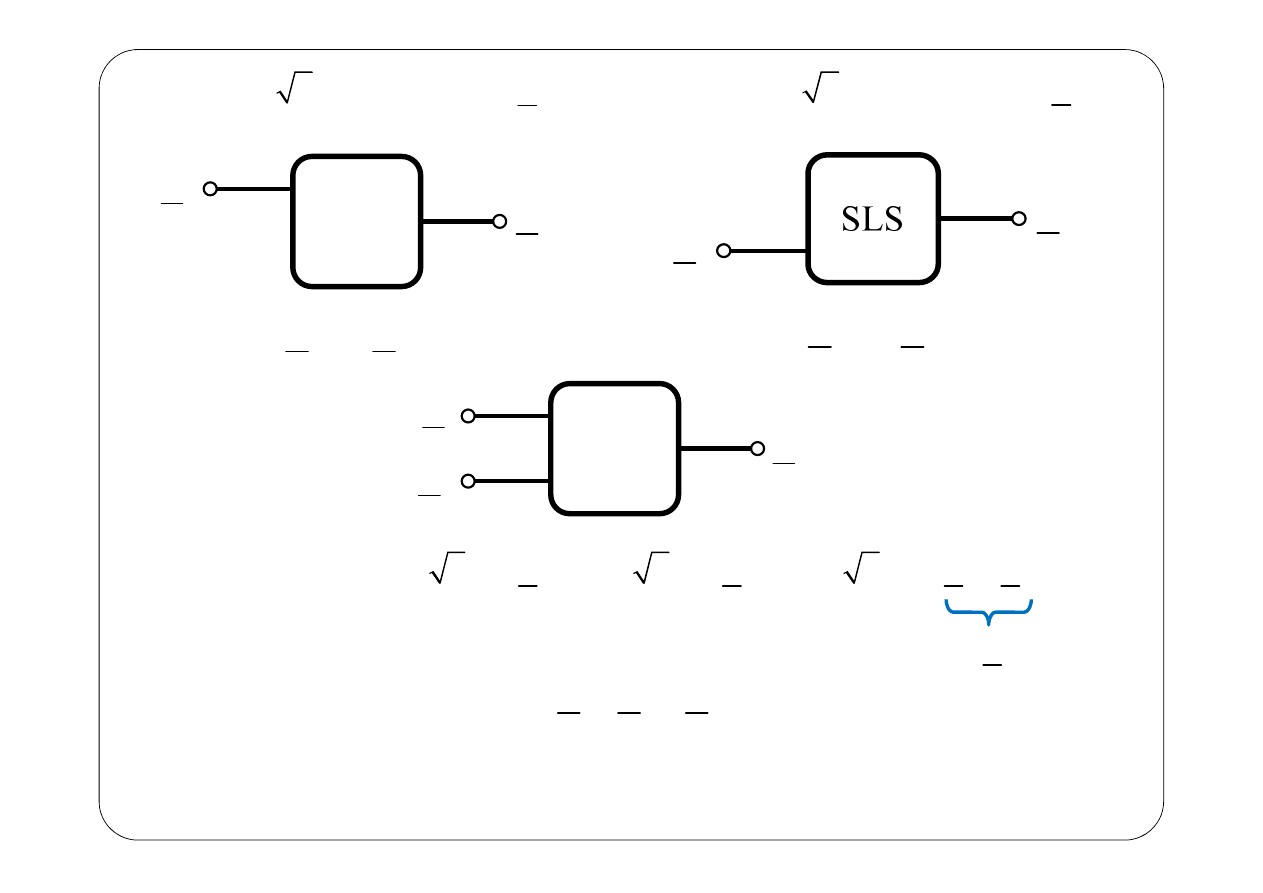
SLS
1
P
1
R
( )
(
)
1
1
1
0
1
2 sin
p t
P
t
P
=
+
⇌
ω
θ
1
1
P
R
→
( )
(
)
2
2
2
0
2
2 sin
p
t
P
t
P
=
+
⇌
ω
θ
2
P
2
R
2
2
P
R
→
SLS
1
P
R
SLS
2
P
R
( ) ( ) ( )
{
}
{
}
(
)
{
}
0
0
0
j
j
j
1
2
1
2
1
2
2 Im
e
2 Im
e
2 Im
e
ω t
ω t
ω t
r t
r t
r t
R
R
R
R
=
+
=
+
=
+
R
1
2
R
R
R
=
+
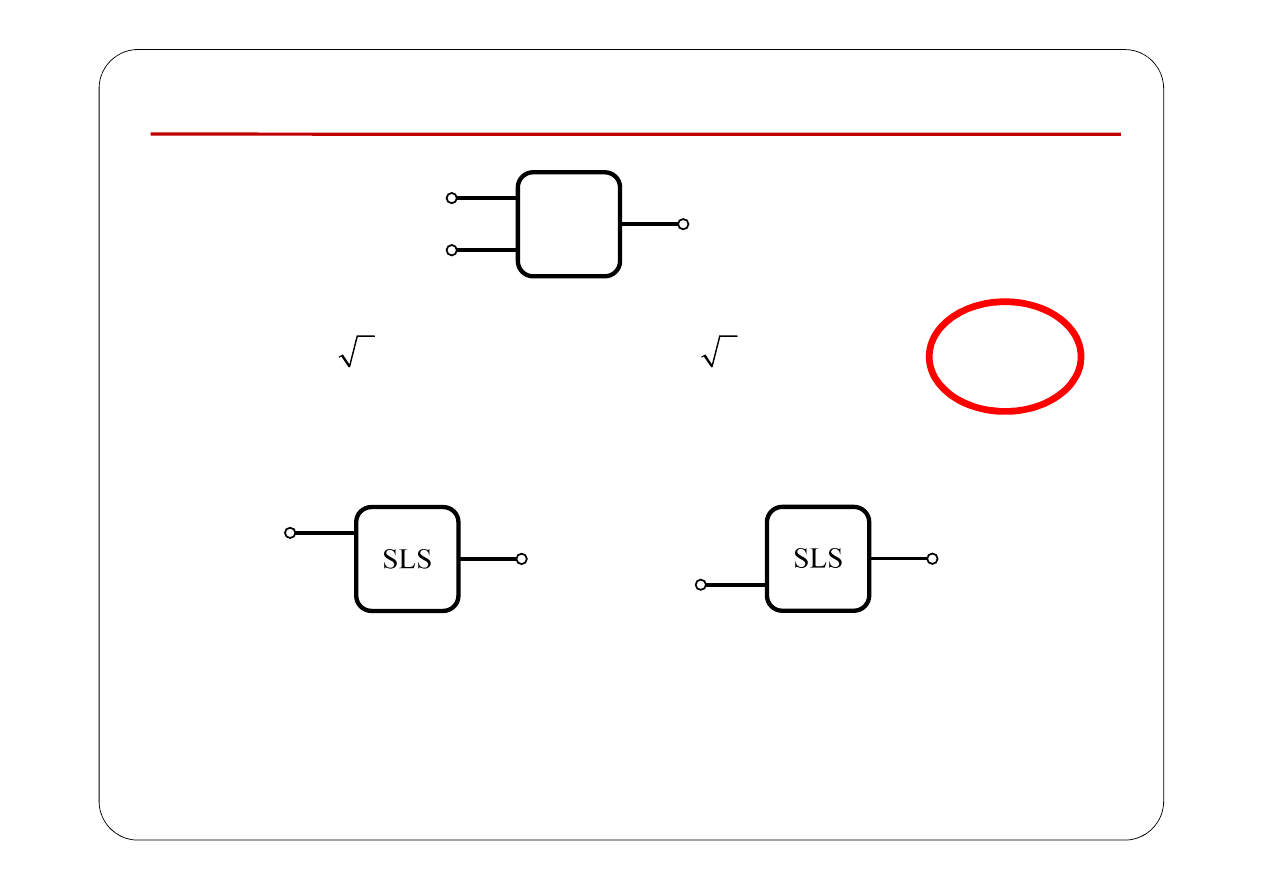
Pobudzenia sinusoidalne o różnych pulsacjach
SLS
( )
1
p t
( )
2
p
t
( )
r t
( )
(
)
( )
(
)
1
1
01
1
2
2
02
2
01
02
2 sin
,
2 sin
,
p t
P
t
p t
P
t
ω
θ
ω
θ
ω
ω
=
+
=
+
≠
Nie wolno zastosowa
ć metody symbolicznej!
Nie wolno zastosowa
ć metody symbolicznej!
( )
1
p t
( )
1
r t
( )
2
p t
( )
2
r t
( )
2
0
p
t
=
( )
1
0
p t
=
Każdy z powyższych układów można analizować metodą symboliczną
Zgodnie z twierdzeniem o superpozycji:
( ) ( ) ( )
1
2
r t
r t
r t
=
+
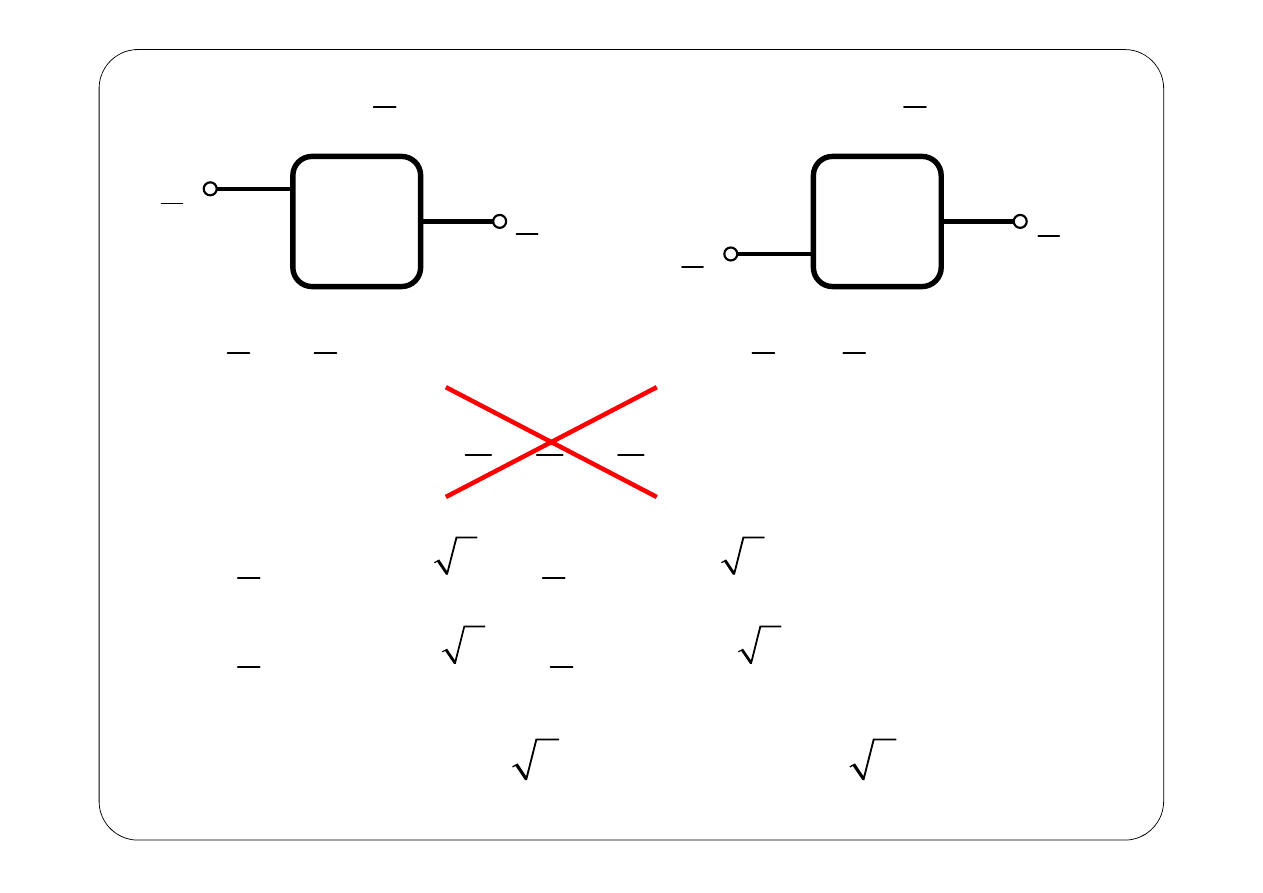
SLS
1
P
1
R
( )
1
1
01
;
p t
P
ω
⇌
1
j
1
1
1
e
P
R
R
→
=
η
( )
2
2
02
;
p t
P
ω
⇌
SLS
2
P
2
R
2
j
2
2
2
e
P
R
R
→
=
η
1
2
R
R
R
=
+
Źle!!!
1
2
R
R
R
=
+
Źle!!!
( )
{
}
(
)
( )
{
}
(
)
01
02
j
1
1
1
1
01
1
j
2
2
2
2
02
2
2 Im
e
2 sin
2 Im
e
2 sin
R
r t
R
R
t
R
r t
R
R
t
ω
ω
ω
η
ω
η
=
=
+
=
=
+
⇌
⇌
( ) ( ) ( )
(
)
(
)
1
2
1
01
1
2
02
2
2 sin
2 sin
r t
r t
r t
R
t
R
t
ω
η
ω
η
=
+
=
+
+
+
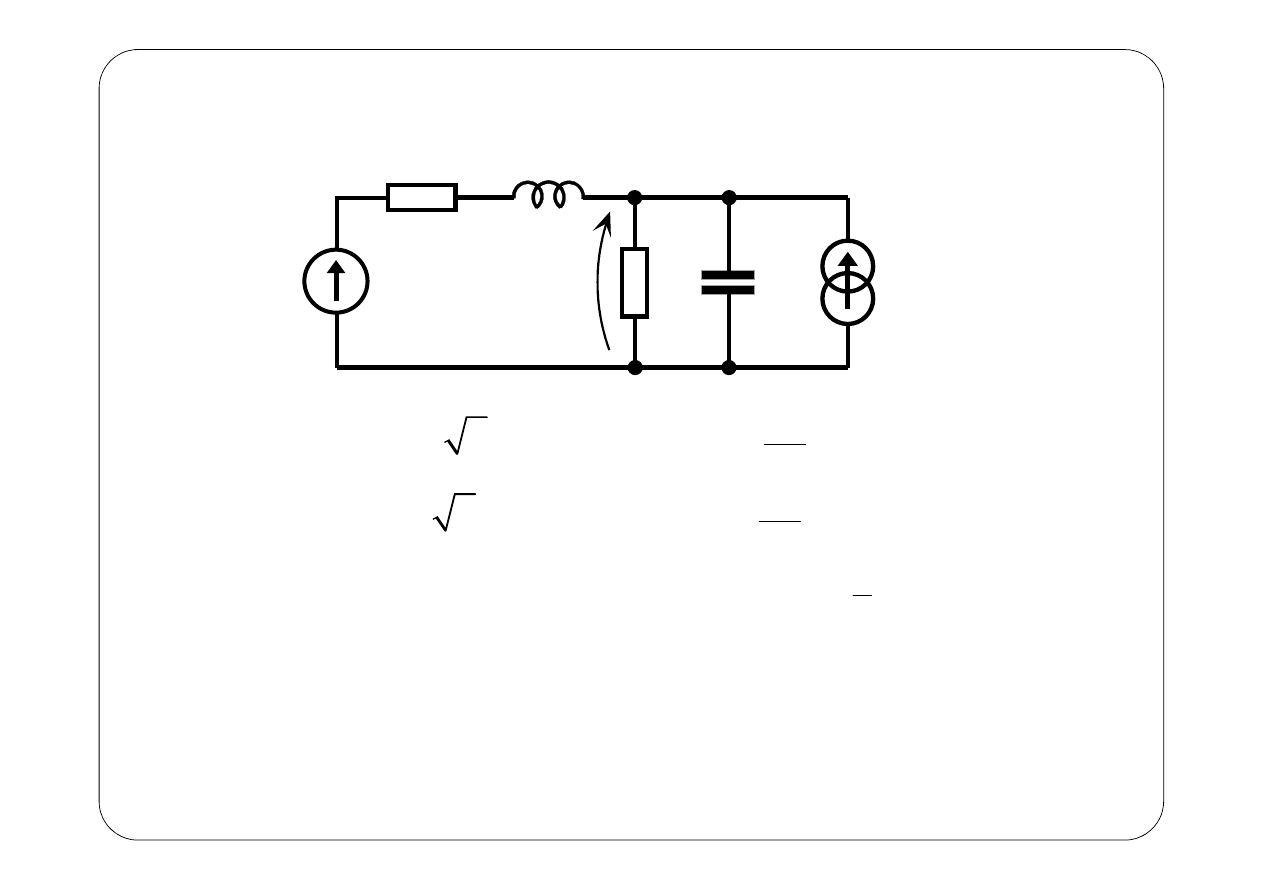
Przykład 1.
( )
e t
( )
z
i t
1
R
2
R
L
C
( )
u t
( )
(
)
01
rad
s
2 2 sin 2 V,
2
e t
t
ω
=
=
( )
(
)
( )
(
)
( )
01
z
02
1
2
s
rad
s
1
2
2 2 sin 2 V,
2
2 cos A,
1
1Ω,
2Ω,
1H,
F.
?
e t
t
i t
t
R
R
L
C
u t
ω
ω
=
=
=
=
=
=
=
=
=
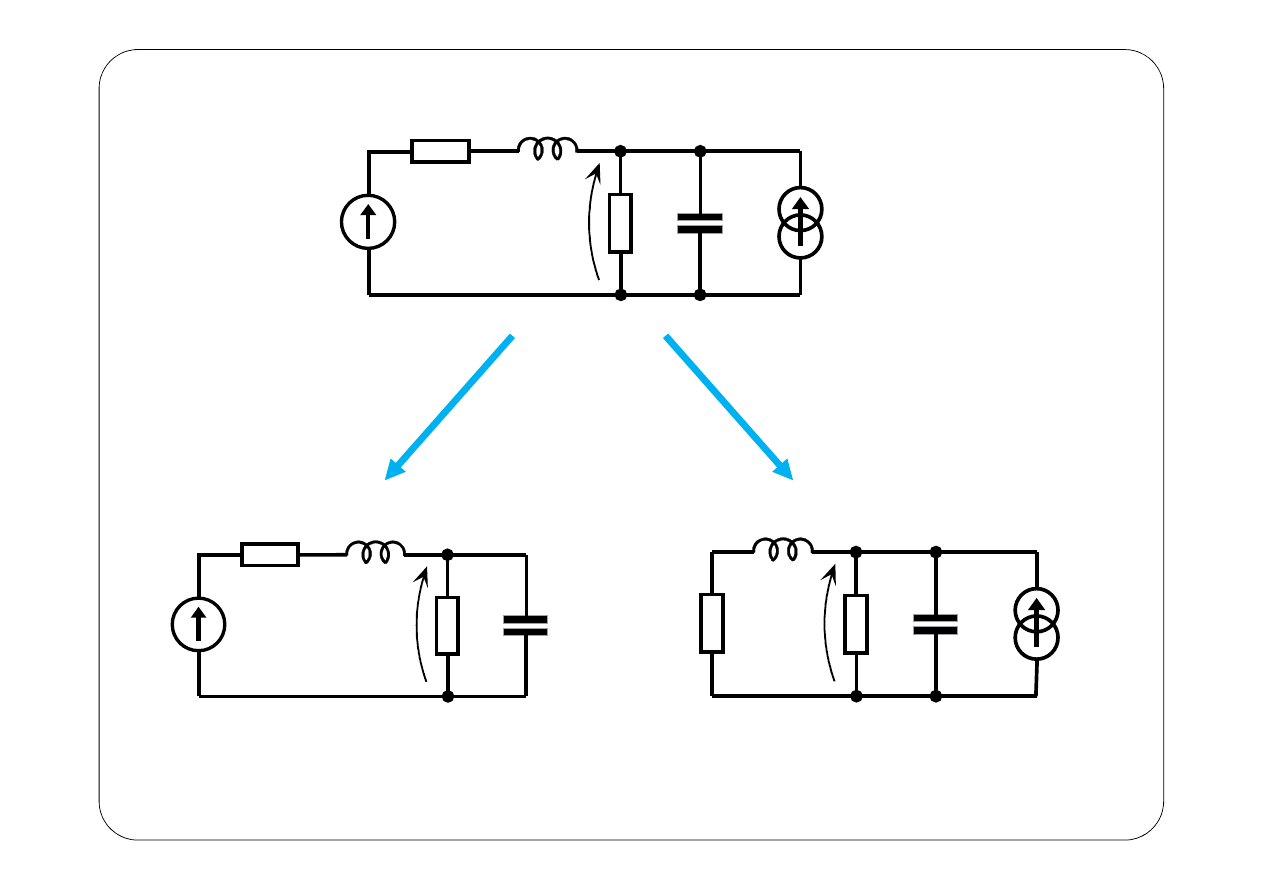
( )
e t
( )
z
i t
1
R
2
R
L
C
( )
u t
A
B
( )
e t
1
R
2
R
L
C
( )
u t
′
( )
z
i t
1
R
2
R
L
C
( )
u t
′′
( )
( )
( )
u t
u t
u t
′
′′
=
+
A
B
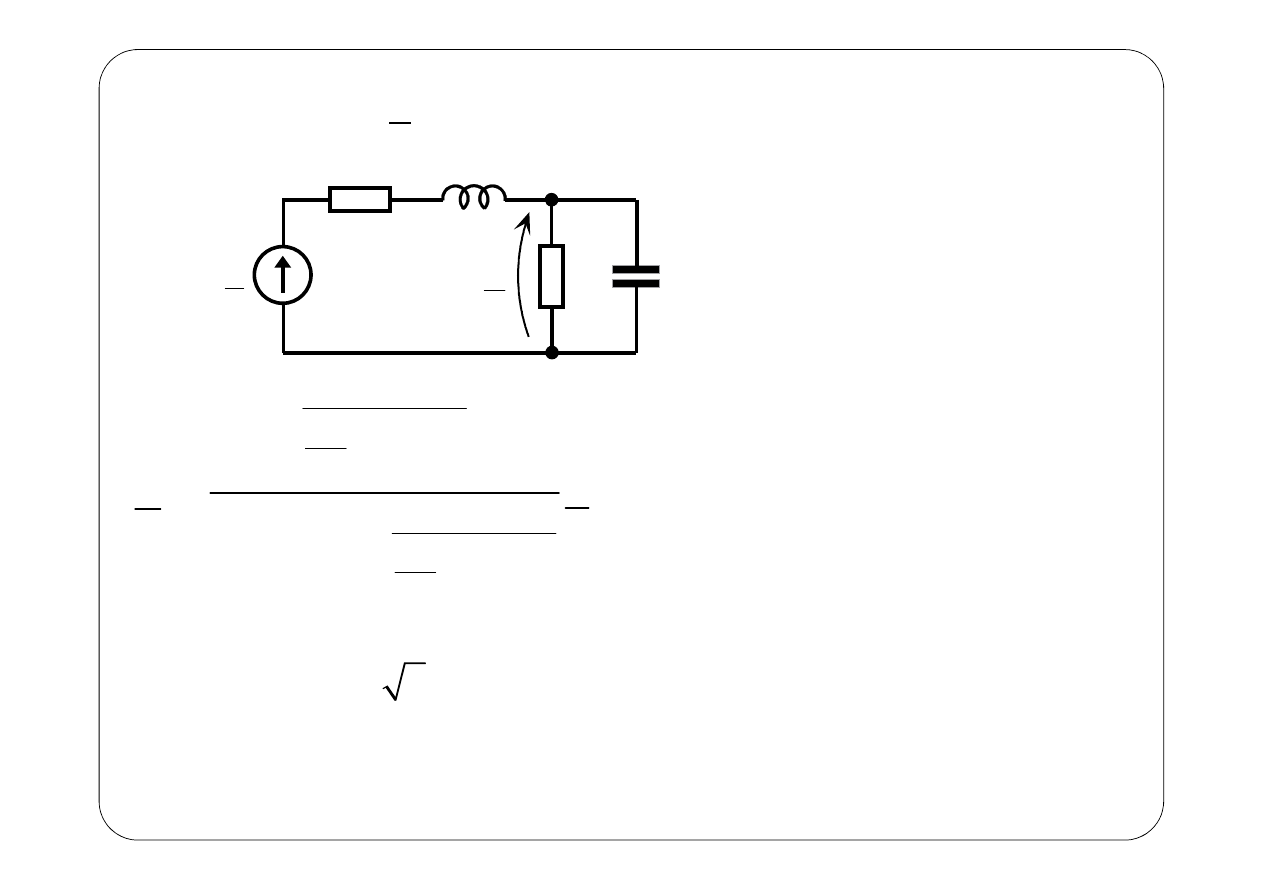
A.
i
z
(t) = 0, E = 2;
ω
01
= 2
E
1
R
2
R
L
C
U
′
1
1
j
C
ω
+
01
j1,816
2
1
01
01
2
1
j
0, 2353
j0, 9412
0, 9702e
1
j
1
j
C
R
U
E
R
L
C
R
ω
ω
ω
−
+
′ =
= −
−
=
+
+
+
( )
(
)
0, 9702 2 sin 2
1,816
u t
t
′
=
−
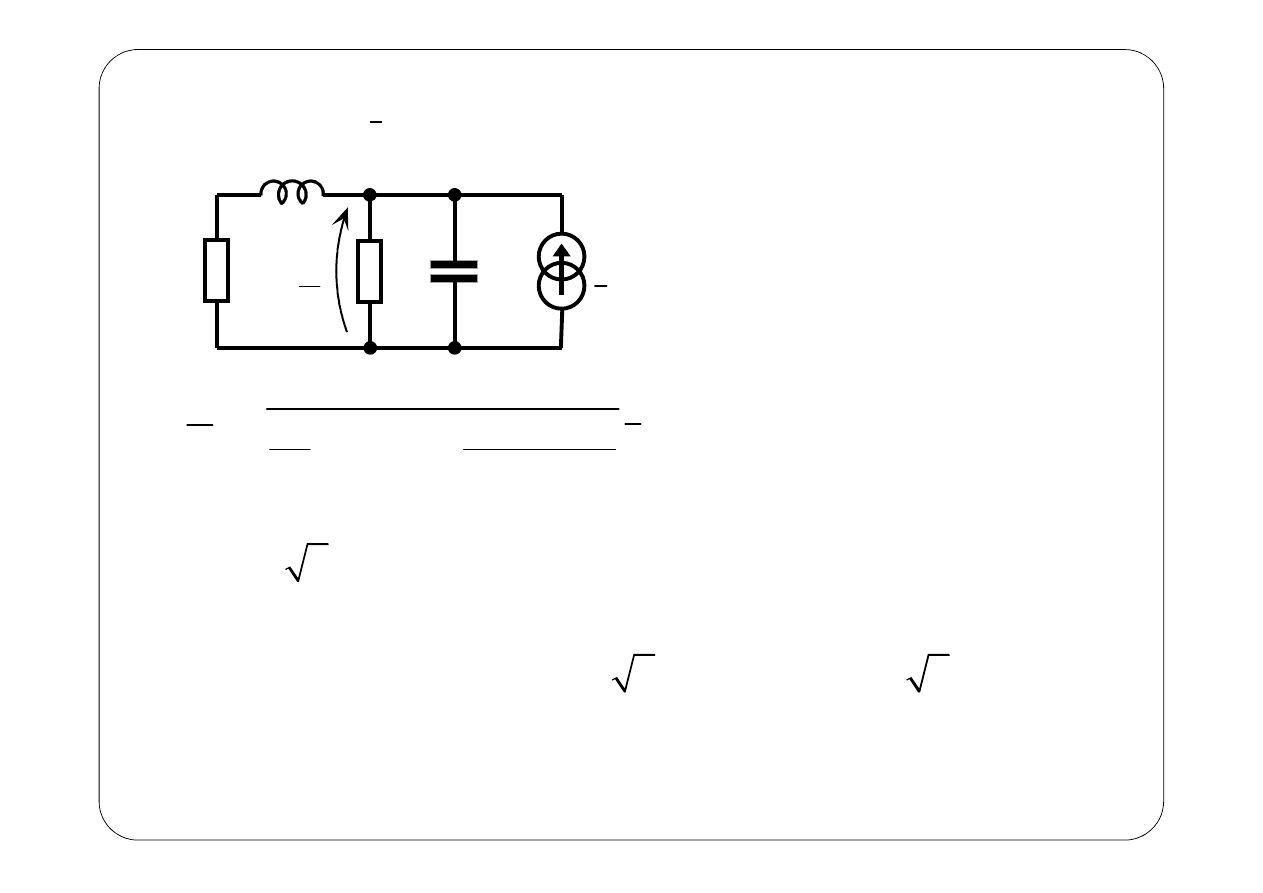
B.
e(t) = 0, I
z
= j;
ω
02
= 1
z
I
1
R
2
R
L
C
U
′′
z
1
j
1
1
j
U
I
C
ω
ω
′′ =
=
+
+
+
02
2
1
02
1
1
j
j
C
R
R
L
ω
ω
+
+
+
( )
2 cos
u t
t
′′
=
( )
( )
( )
(
)
0, 9702 2 sin 2
1,816
2 cos V.
u t
u t
u t
t
t
′
′′
=
+
=
−
+
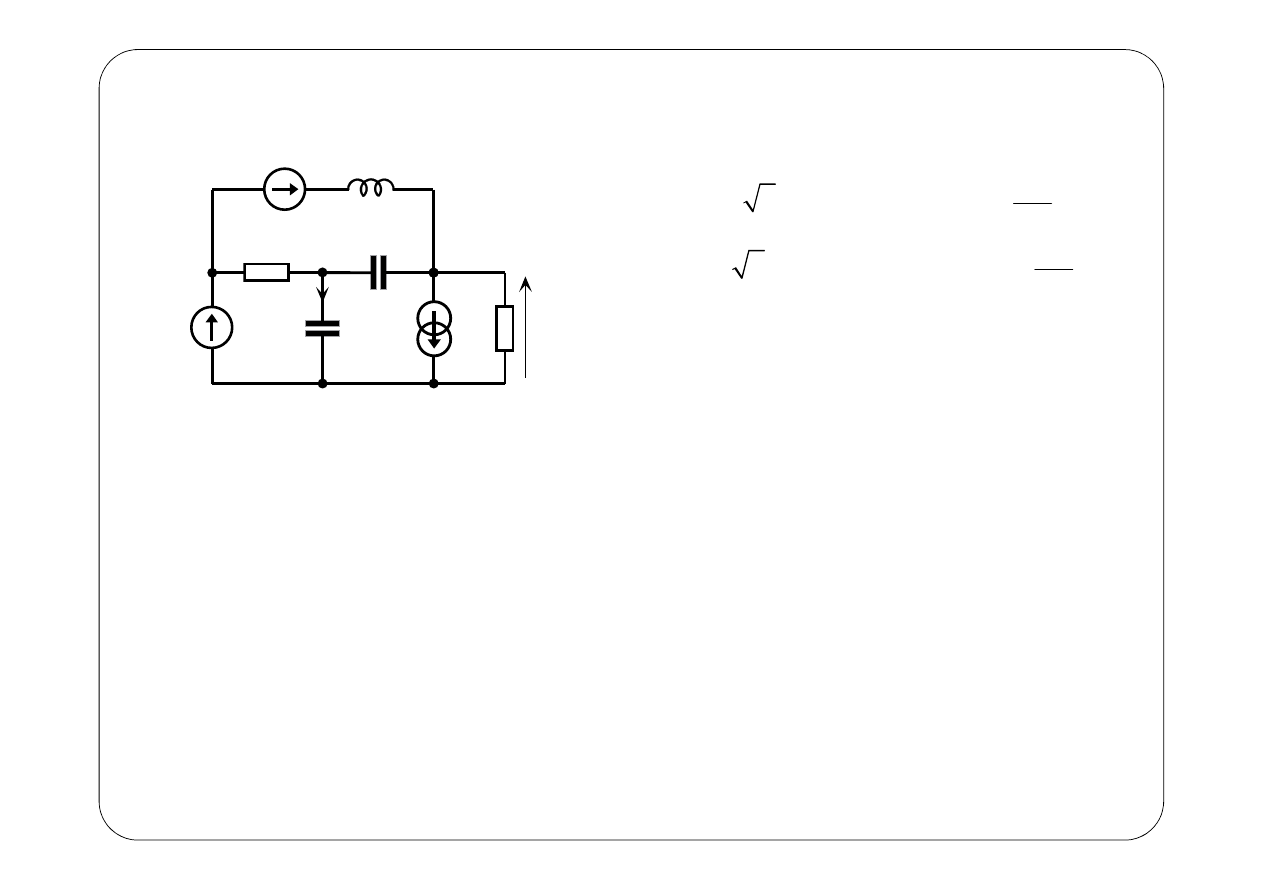
Przykład 2.
( )
1
e t
( )
2
e t
( )
i t
L
1
C
2
C
1
R
2
R
( )
i t
α
( )
u t
( )
( )
4
1
01
01
3
2
02
02
1
2
1
2
rad
2 2 sin
V,
10
,
s
rad
2 cos
V,
5 10
,
s
200Ω,
1kΩ,
20 mH,
0,1µF,
0, 25µF,
2.
e t
t
e t
t
R
R
L
C
C
=
=
=
= ⋅
=
=
=
=
=
=
ω
ω
ω
ω
α
Wyznaczyć napięcie
( )
u t
Pulsacje pobudzeń są różne!
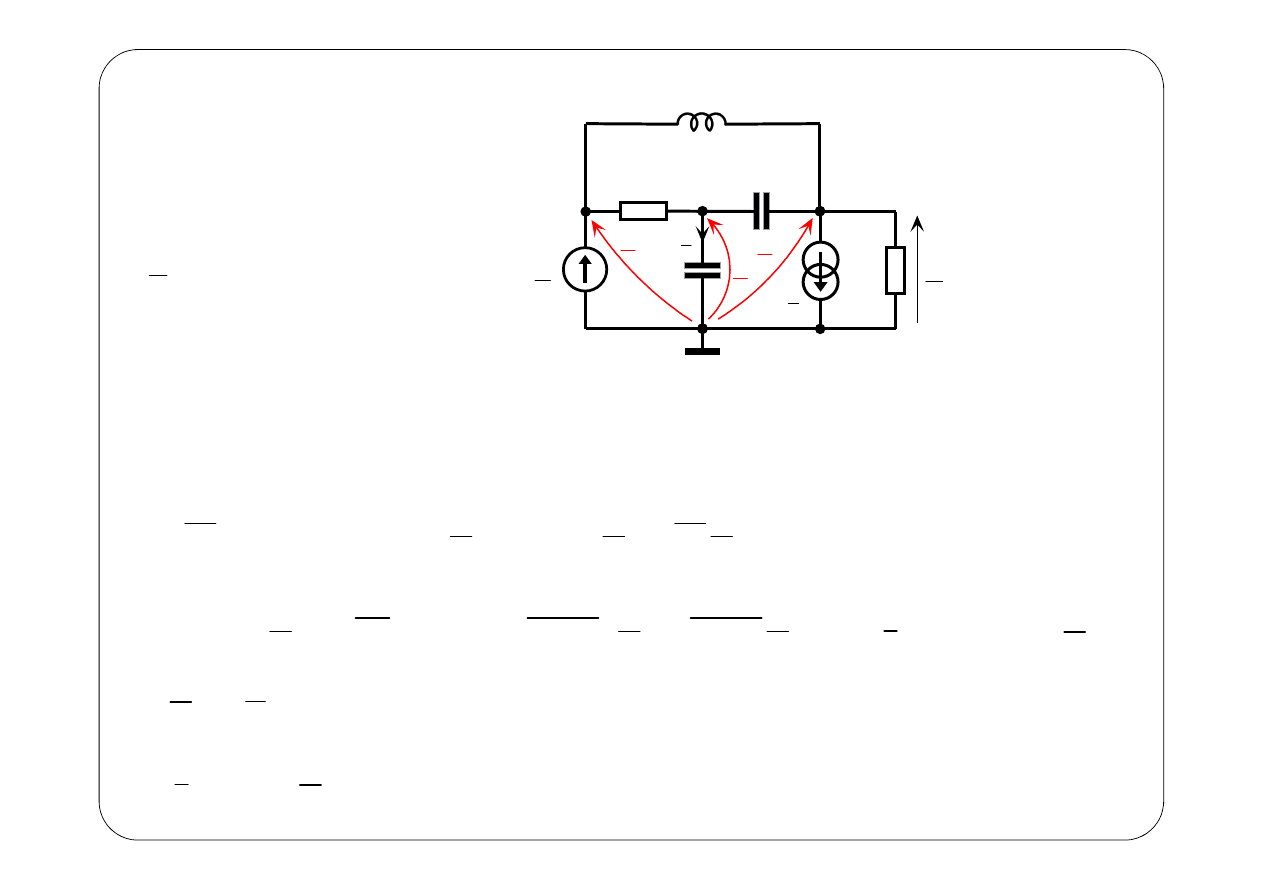
1
E
I
L
1
C
2
C
1
R
2
R
I
α
U
′
n1
U
n2
U
n3
U
3
1
2
( )
2
0
.
e t
=
A
4
1
01
2;
10
E
ω
=
=
Układ równań na napięcia węzłowe:
Nie wolno usunąć źródła sterowanego!!!
01
1
01
2
n1
01
2
n2
n3
1
1
01
2
n1
01
2
n2
n3
2
01
01
1
n3
1
1
j
j
j
0,
1
1
1
j
j
j
j
.
C
C
U
C U
U
R
R
C U
C
U
U
I
R
L
L
U
E
+
+
−
−
=
−
+
+
+
−
= −
=
ω
ω
ω
ω
ω
α
ω
ω
Układ równań na napięcia węzłowe:
01
1
n1
j
I
C U
=
ω
01
1
n1
j
,
C U
= −
α ω
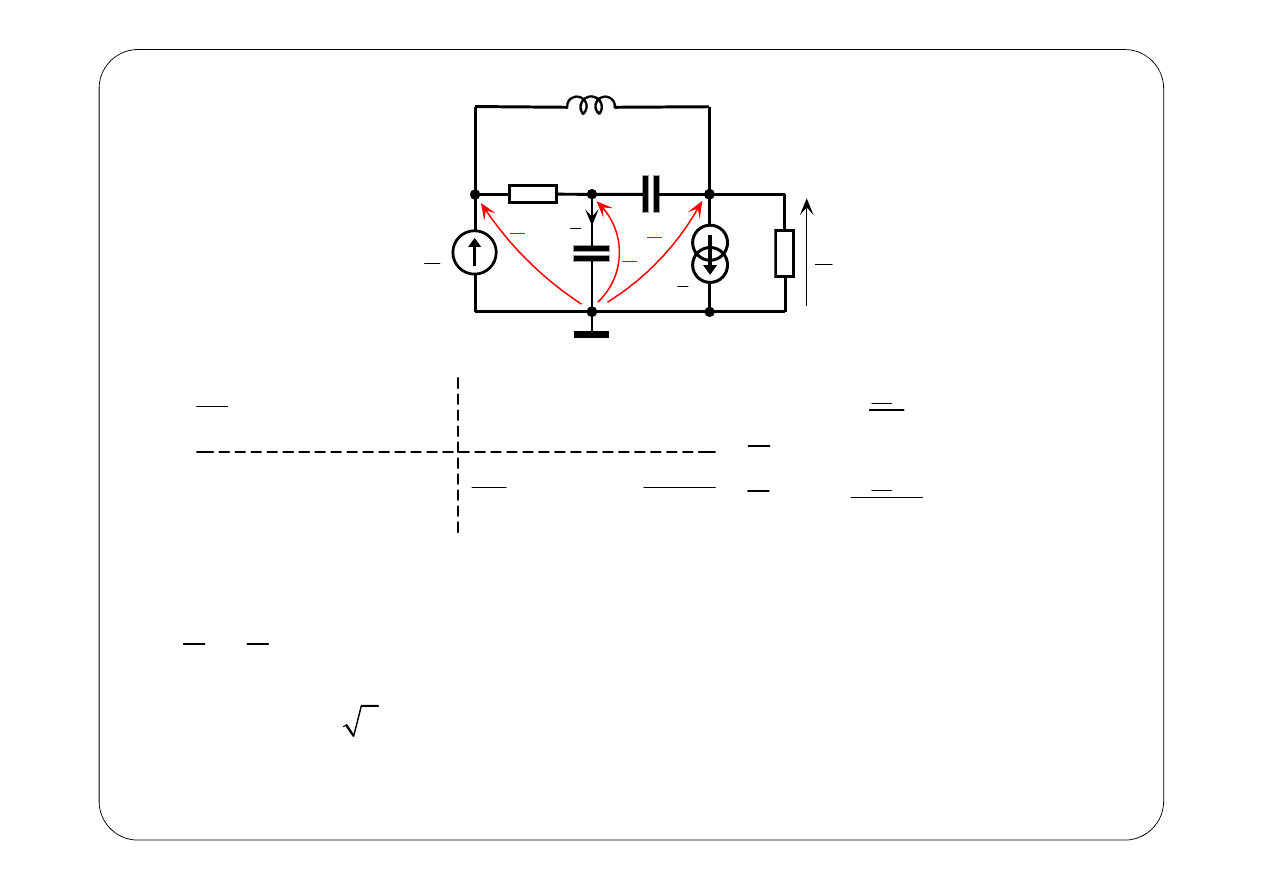
1
E
I
L
1
C
2
C
1
R
2
R
I
α
U
′
n1
U
n2
U
n3
U
3
1
2
1
01
1
01
2
01
2
1
1
n1
1
j
j
j
E
C
C
C
R
R
U
+
+
−
=
ω
ω
ω
1
1
n1
1
n2
01
2
01
1
01
2
2
01
01
1
1
j
j
j
j
j
R
U
U
E
C
C
C
R
L
L
=
−
+
+
+
ω
α ω
ω
ω
ω
j0,3692
n2
3, 039
j1,176
3, 259e
U
U
−
′ =
=
−
=
( )
(
)
01
3, 259 2 sin
0, 3692 V
u t
t
′
=
−
ω
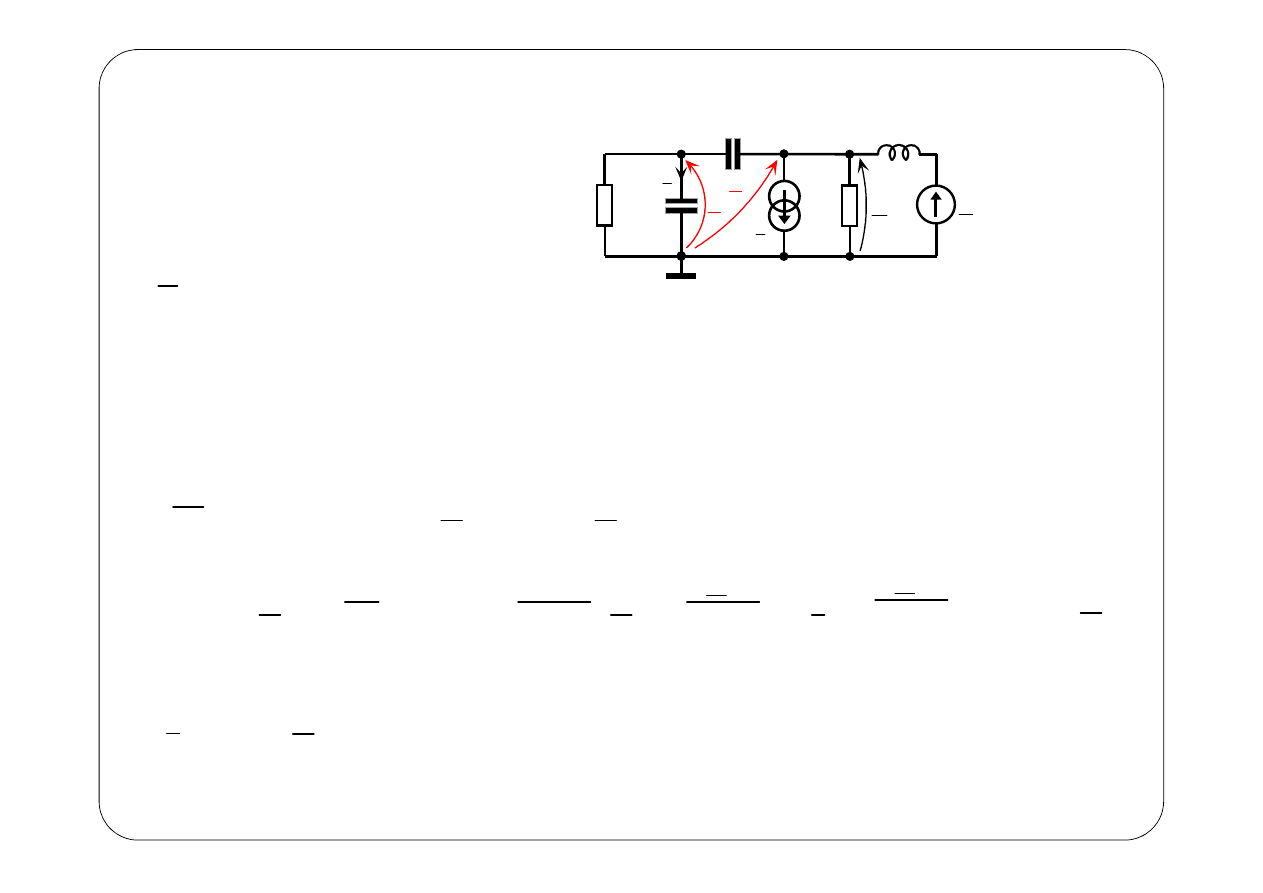
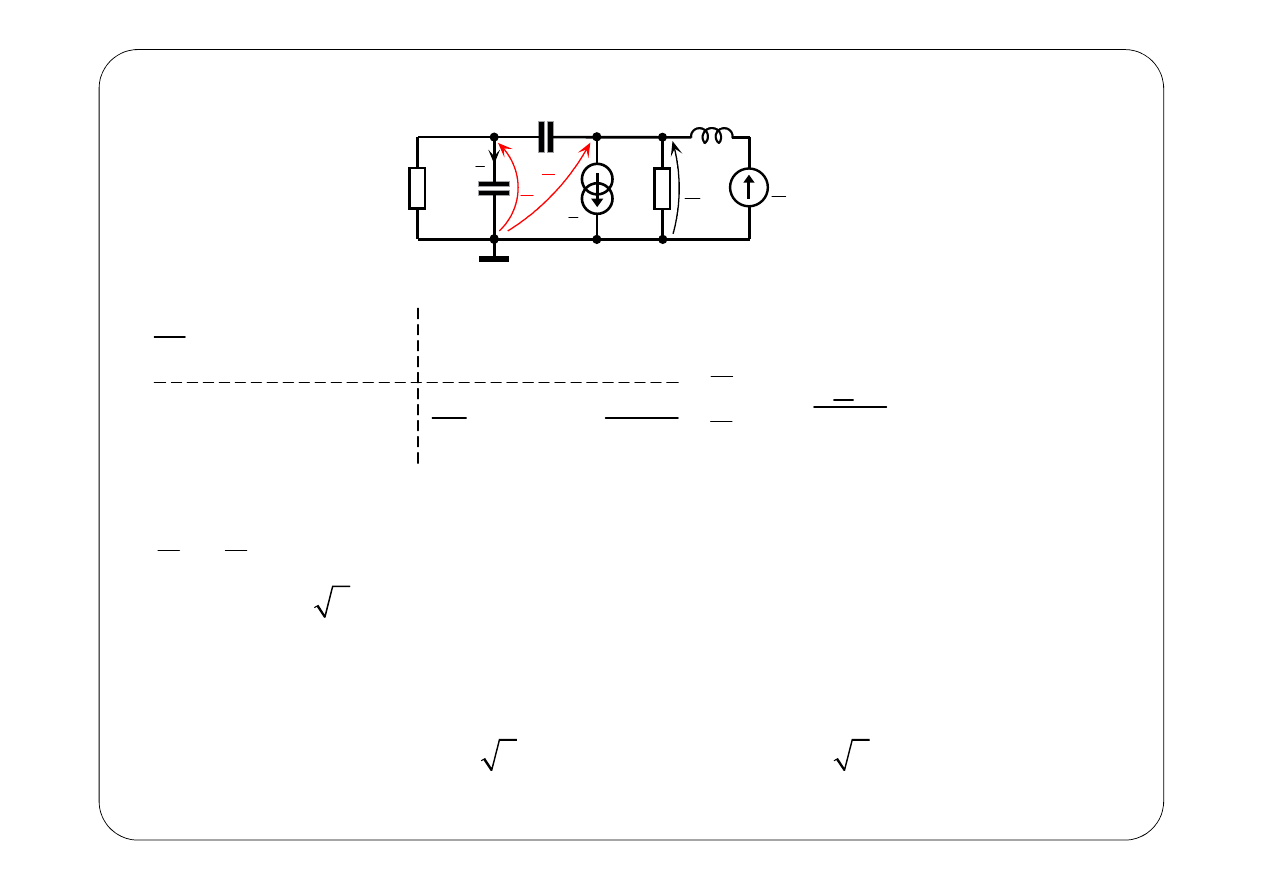
( )
1
0
e t
=
B.
3
2
02
j,
5 10
E
=
= ⋅
ω
I
L
1
C
2
C
1
R
2
R
I
α
U
′′
n1
U
n2
U
1
2
2
E
Układ równań na napięcia węzłowe:
02
1
02
2
n1
02
2
n2
1
2
02
2
n1
02
2
n2
2
02
02
1
j
j
j
0,
1
1
j
j
j
j
C
C
U
C U
R
E
C U
C
U
I
R
L
L
+
+
−
=
−
+
+
+
=
−
ω
ω
ω
ω
ω
α
ω
ω
02
1
n1
j
I
C U
=
ω
2
02
1
n1
02
j
,
j
E
C U
L
=
−
α ω
ω
02
1
02
2
02
2
1
n1
2
n2
02
2
02
1
02
2
02
2
02
1
j
j
j
0
1
1
j
j
j
j
j
C
C
C
R
U
E
U
C
C
C
L
R
L
+
+
−
=
−
+
+
+
ω
ω
ω
ω
α ω
ω
ω
ω
I
L
1
C
2
C
1
R
2
R
I
α
U
′′
n1
U
n2
U
1
2
2
E
02
2
02
j
R
L
ω
j1,451
n2
0,1353
j1,124
1,132e
U
U
′′ =
=
+
=
( )
(
)
02
1,132 2 sin
1, 451 V.
u t
t
′′
=
+
ω
Ostatecznie
( )
( )
( )
(
)
(
)
01
02
3, 259 2 sin
0, 3692
1,132 2 sin
1, 451 V.
u t
u t
u t
t
t
′
′′
=
+
=
−
+
+
ω
ω
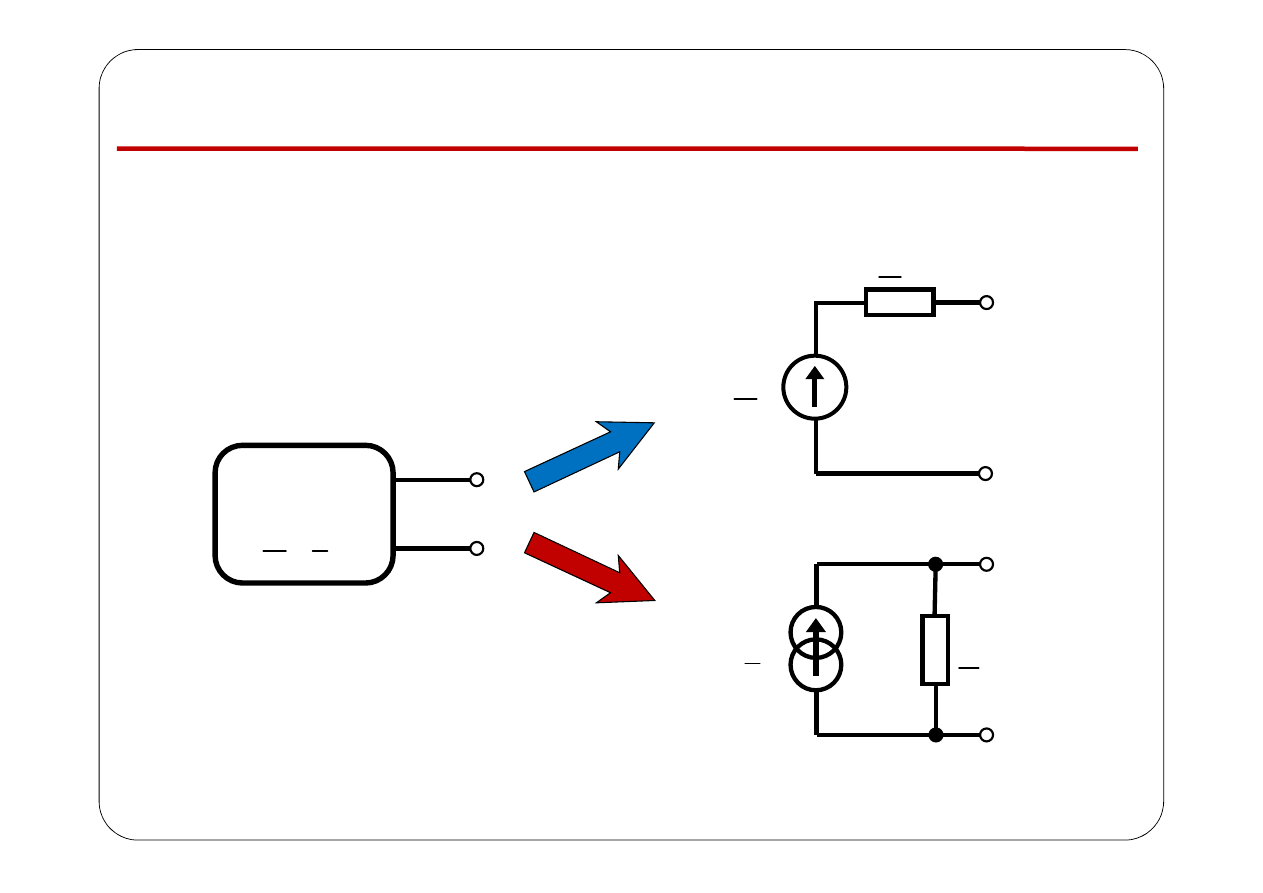
Twierdzenie Thévenina i Nortona
A
T
E
T
Z
Twierdzenie
Thévenina
A
B
A
B
B
z
SLS
,
E I
N
Y
N
I
Twierdzenie
Nortona
0
U
z
,
E I
T
E
T
Z
T
0
U
E
=
T
Z
T
zw
T
E
I
Z
=
z
,
E I
zw
I
T
E
0
T
T
0
zw
U
E
U
Z
I
=
=
N
0
N
I
U
Y
=
z
,
E I
0
U
N
I
N
Y
z
,
E I
zw
I
N
I
N
Y
zw
N
I
I
=
zw
N
zw
N
0
I
I
I
Y
U
=
=
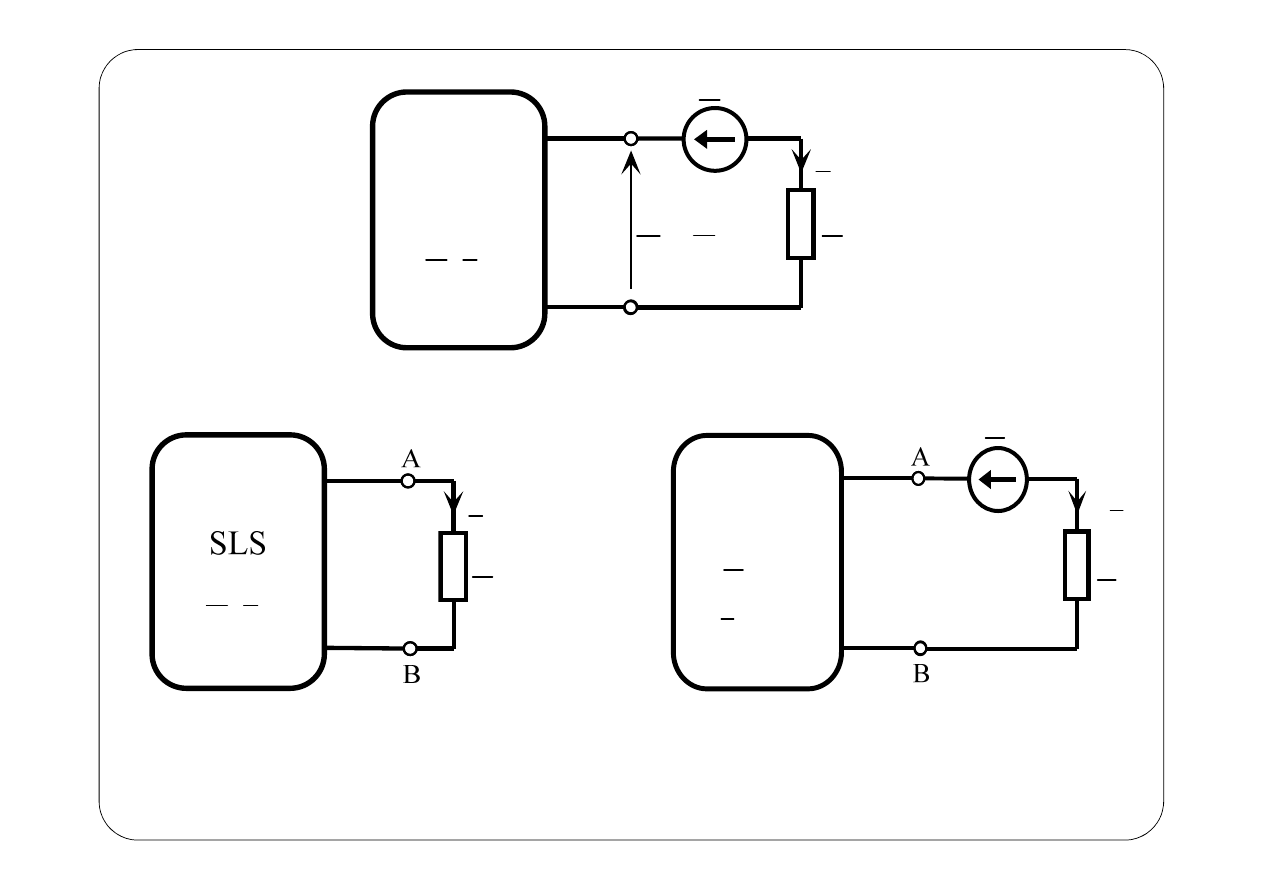
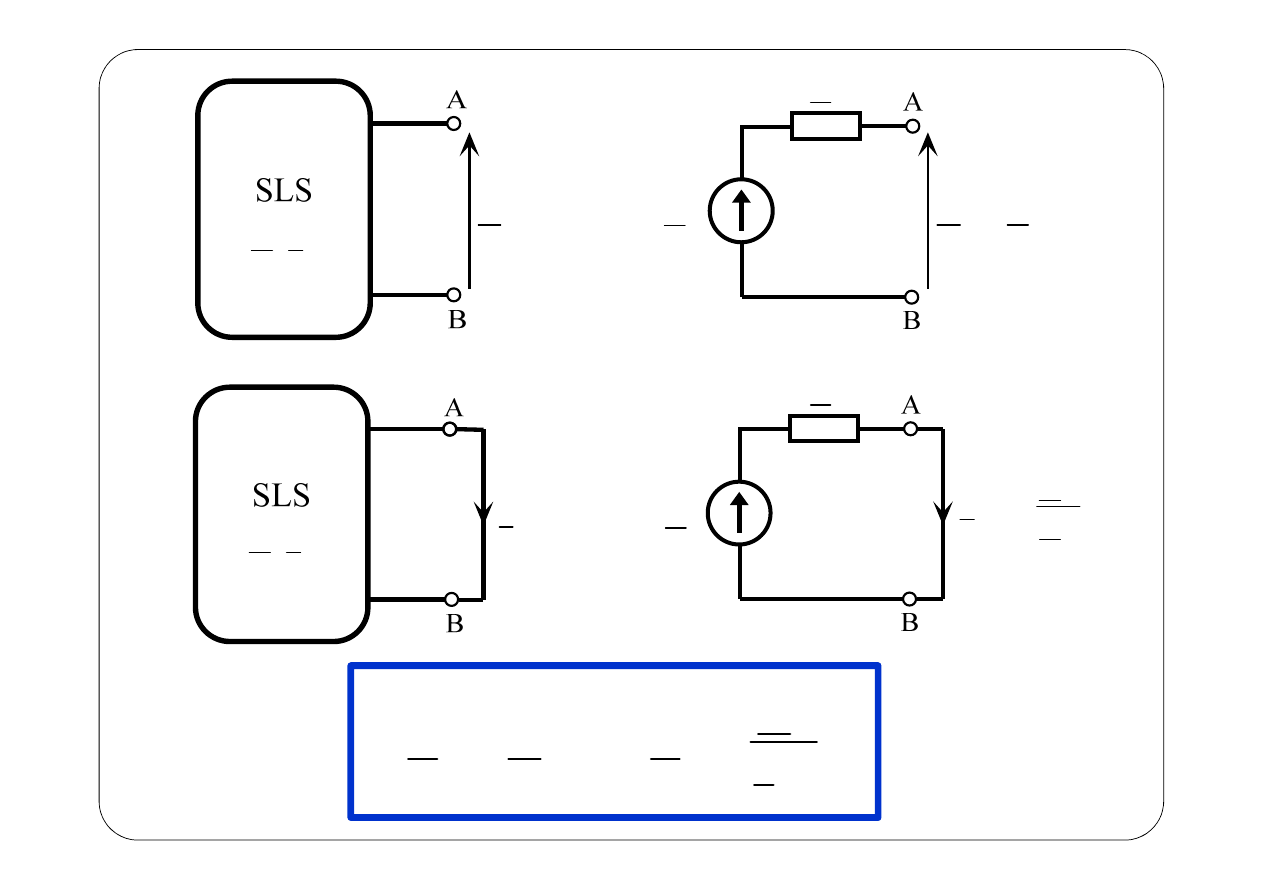
SLS
A
B
z
,
E I
T
U
E
=
T
E
0
I
=
0
Z
T
E
z
,
E I
0
I
0
Z
z
SLS
0
0
E
I
=
=
0
I
−
0
Z
+
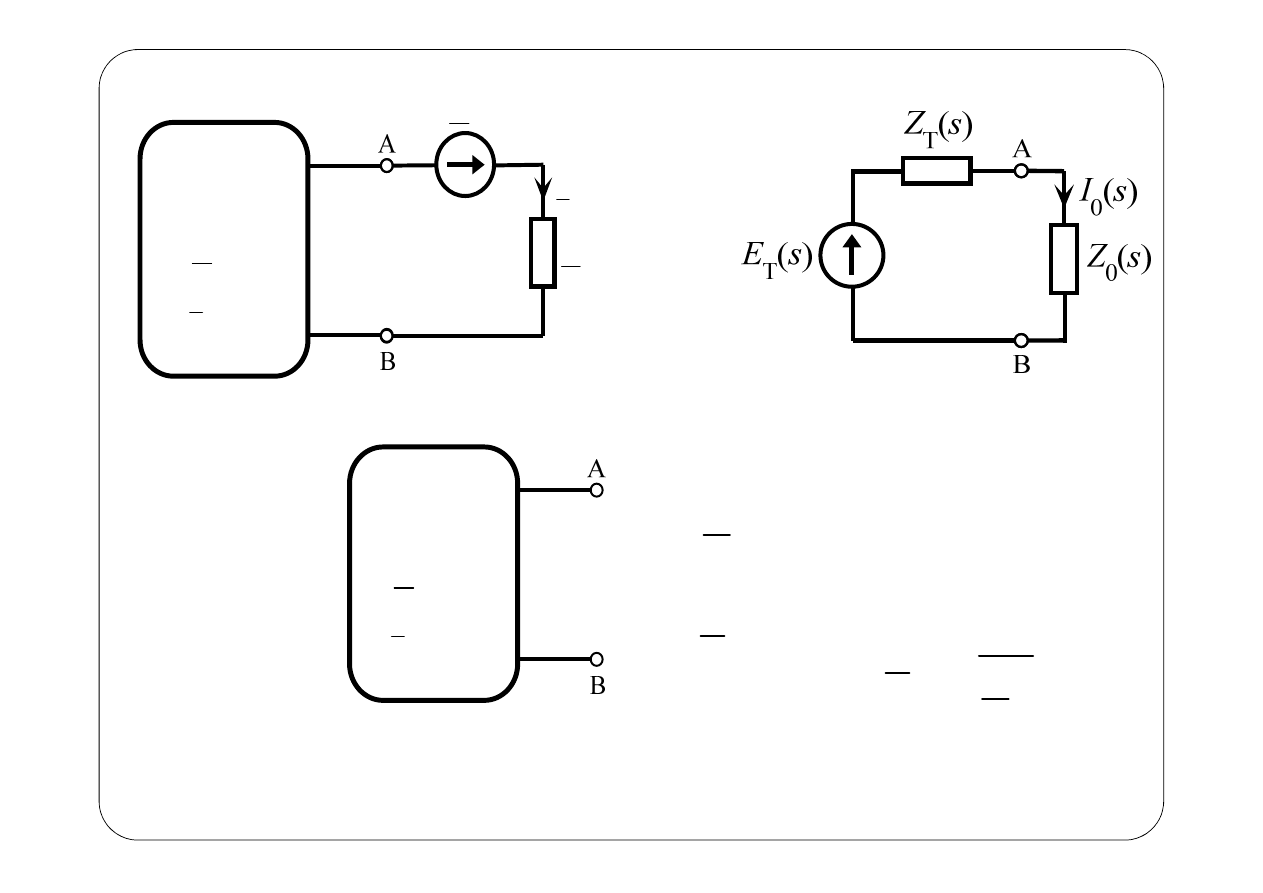
z
SLS
0
0
E
I
=
=
T
E
0
I
0
Z
⇒
z
SLS
0
0
E
I
=
=
⇐
T
Z
N
Y
N
T
1
Y
Z
=
Nie usuwamy z układu
źródeł sterowanych!!!
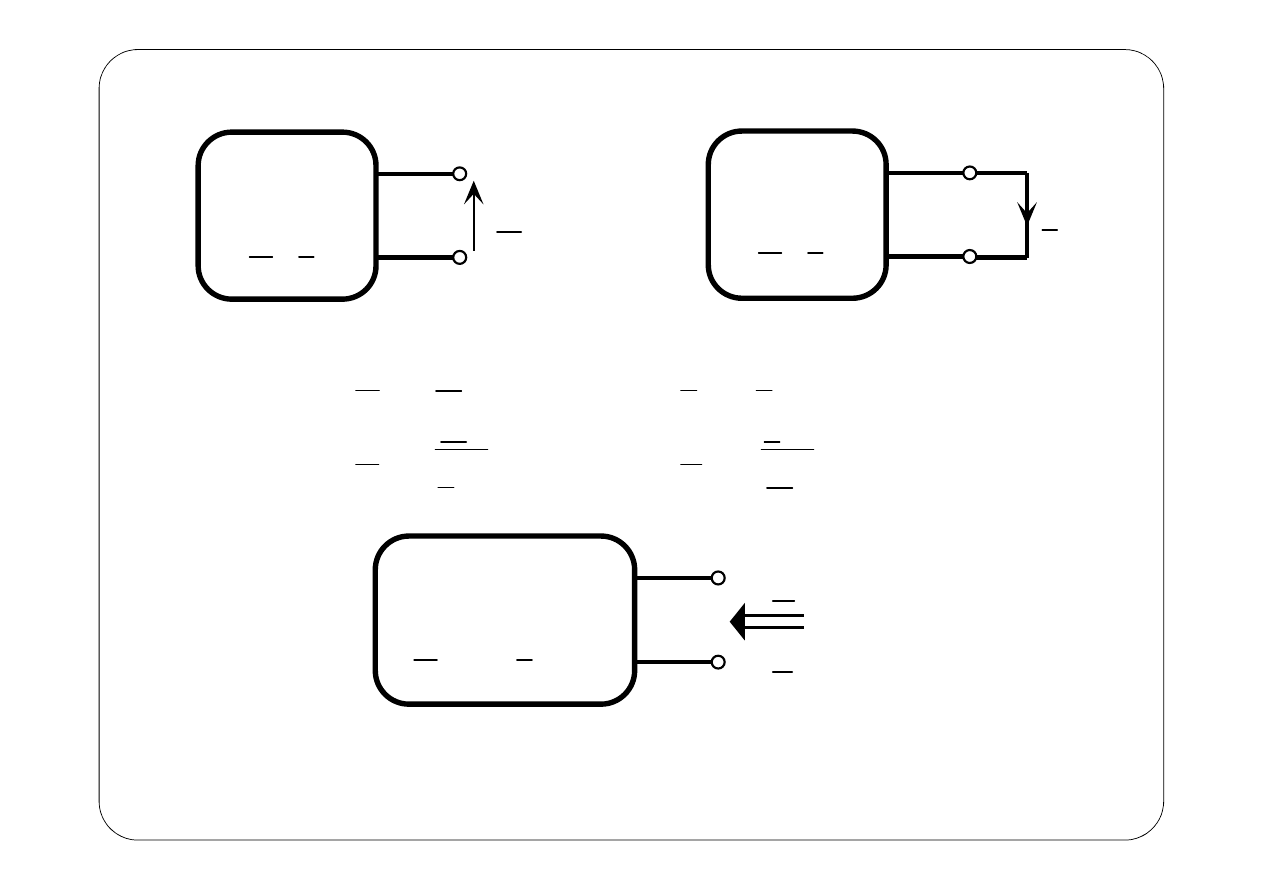
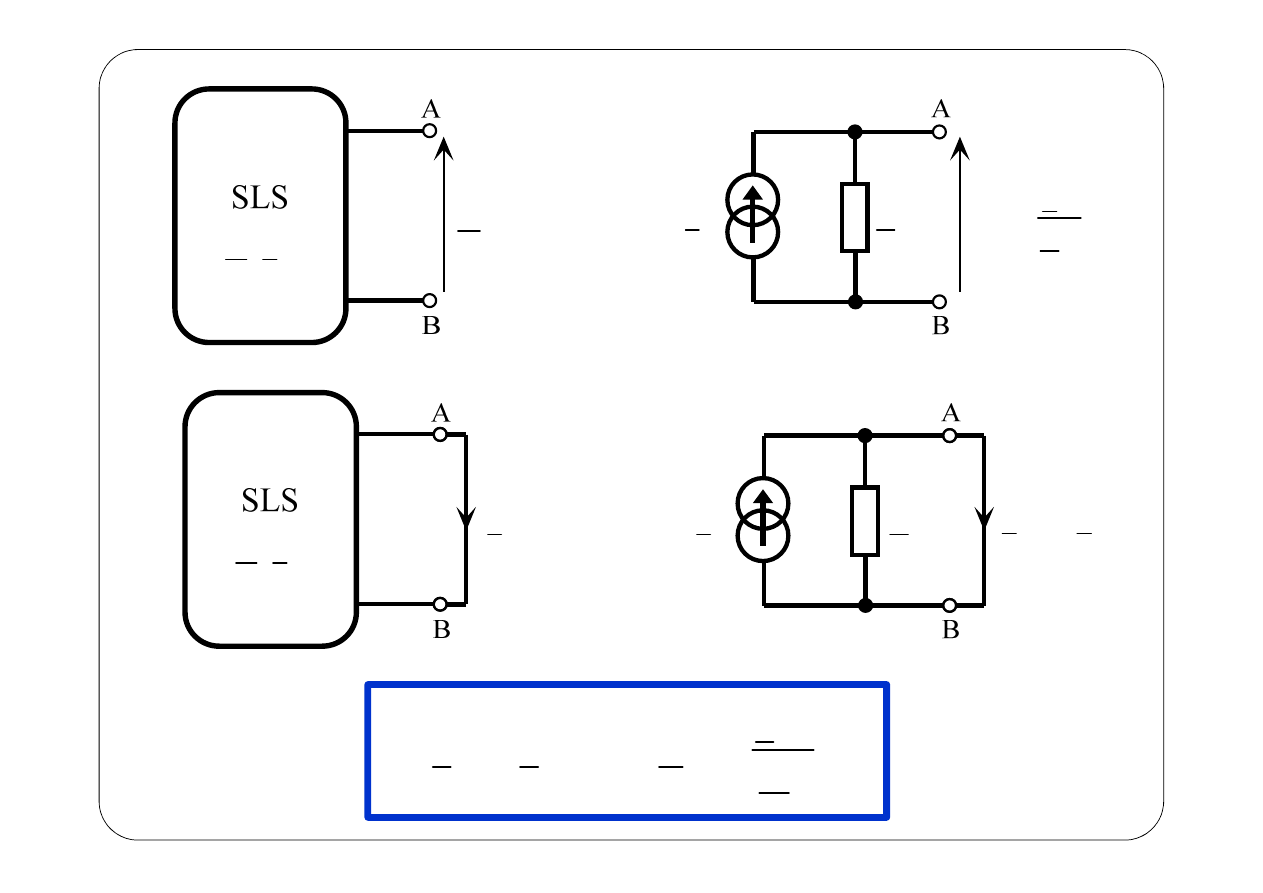
z
SLS
,
E I
z
SLS
,
E I
0
U
zw
I
T
N
zw
0
0
zw
E
U
I
I
U
I
Z
Y
=
=
=
=
0
zw
T
N
zw
0
Z
Y
I
U
=
=
z
SLS
0,
0
E
I
=
=
T
N
Z
Y
Nie wył
ączamy źródeł sterowanych!!!
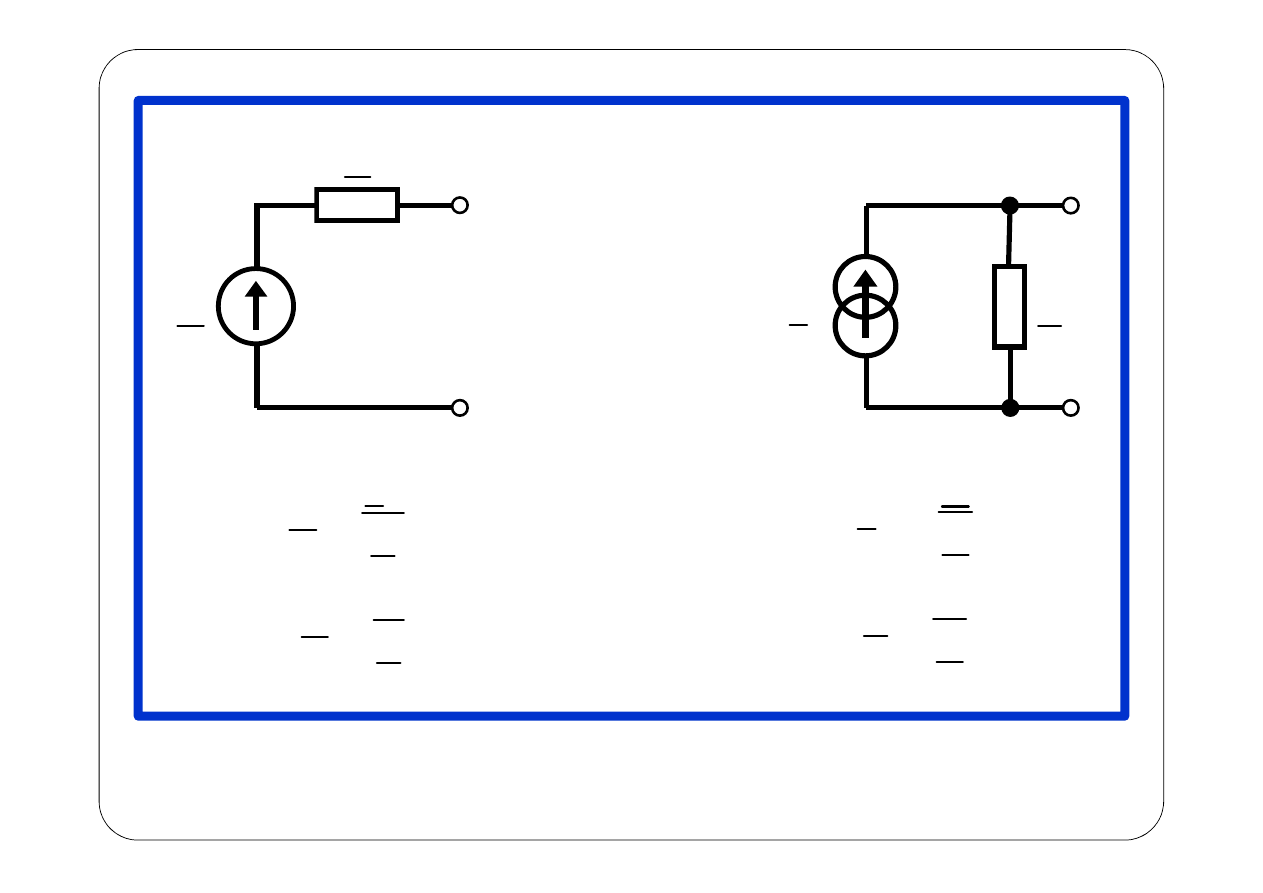
E
Z
z
I
Y
Norton
Thévenin
→
←
z
1
I
E
Y
Z
Y
=
=
⇐
z
1
E
I
Z
Y
Z
=
=
⇒
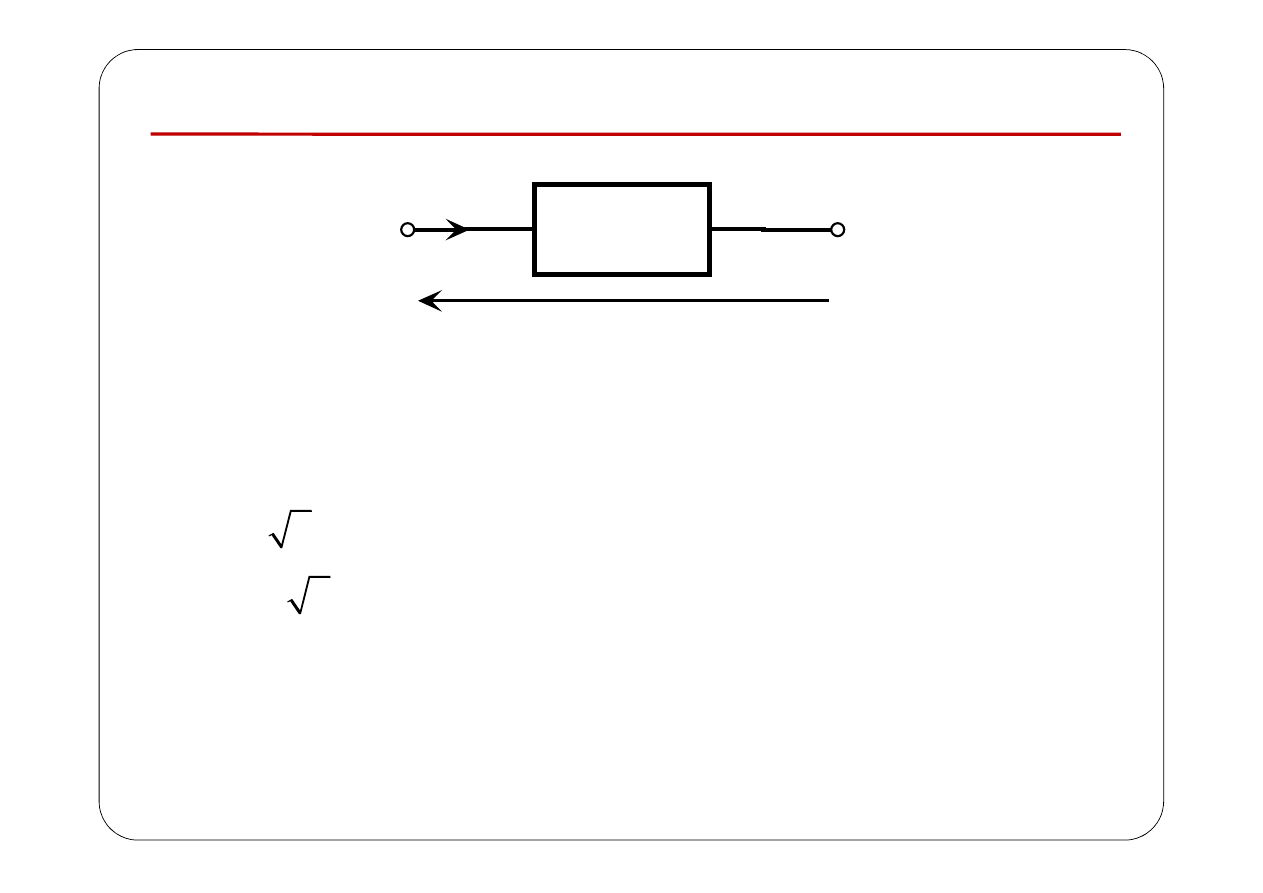
Moc w obwodzie przy pobudzeniu sinusoidalnym
Dwójnik
SLS
( )
u t
( )
i t
Moc chwilowa dostarczona do dwójnika:
( ) ( ) ( )
p t
u t i t
=
Zakładamy, że prąd i napięcie mają postać:
( )
(
)
( )
(
)
0
i
0
u
2 sin
2 sin
i t
I
t
u t
U
t
ω
ψ
ω
ψ
=
+
=
+
Zakładamy, że prąd i napięcie mają postać:
( )
(
) (
)
0
u
0
i
2
sin
sin
p t
UI
t
t
ω
ψ
ω
ψ
=
+
+
=
(
)
(
)
2 sin sin
cos
cos
x
y
x
y
x
y
=
− −
+
(
)
(
)
u
i
0
u
i
cos
cos 2
UI
UI
t
ψ ψ
ω
ψ ψ
=
−
−
+
+
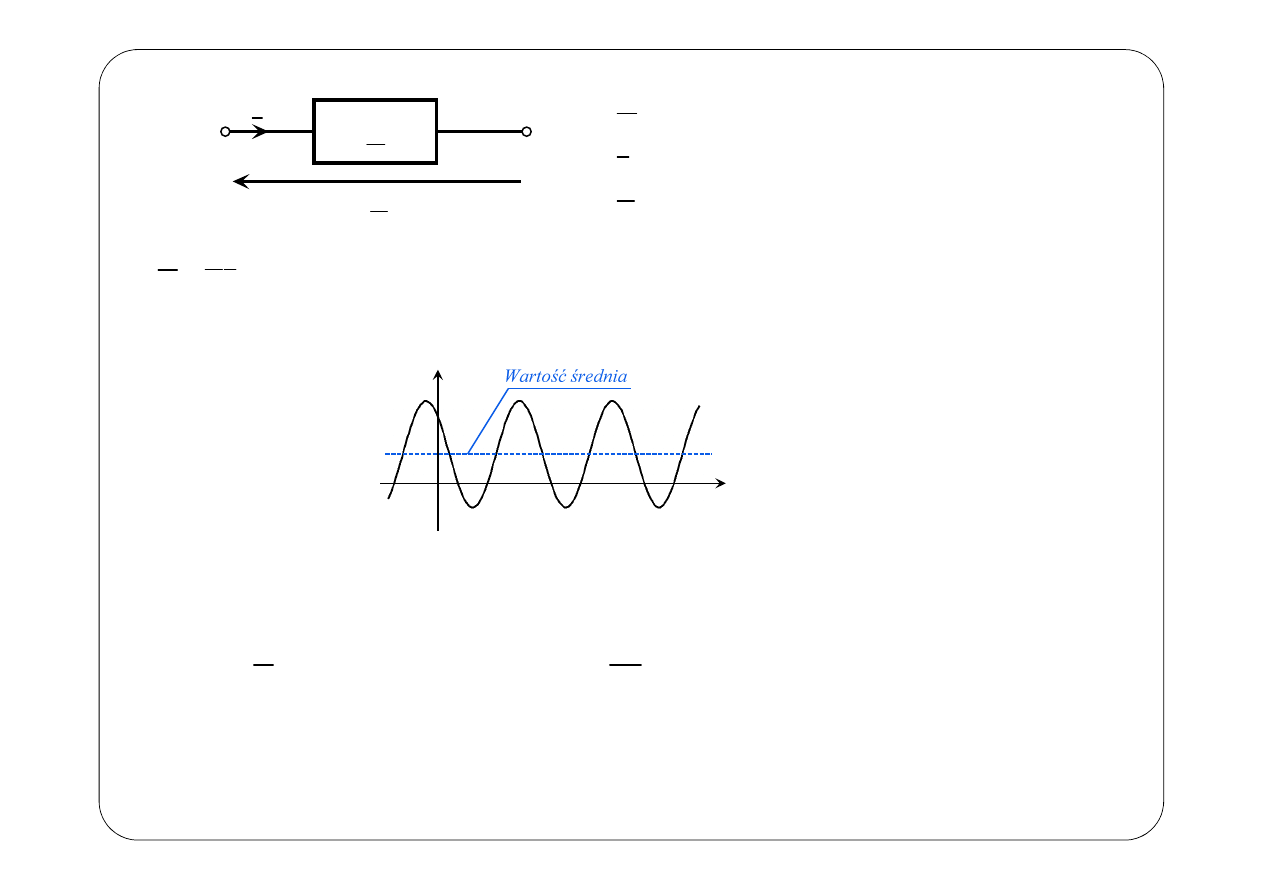
U
I
Z
u
i
j
j
j
e
e
j
e
U
U
I
I
Z
R
X
Z
=
=
= +
=
ψ
ψ
ϕ
(
)
u
i
j
j
j
j
u
i
e
e
e
e
,
,
i
U
Z I
Z
I
ZI
U
U
ZI
+
=
=
=
=
=
= +
ϕ ψ
ψ
ψ
ϕ
ψ
ϕ ψ
( )
(
)
0
i
cos
cos 2
2
p t
UI
UI
t
=
−
+
+
ϕ
ω
ψ ϕ
( )
p t
P
t
P
Wartość średnia mocy chwilowej
( )
0
0
0
1
2π
d
cos
,
t
T
t
P
p t
t
UI
T
T
+
=
=
=
∫
ϕ
ω
P — moc czynna, [P] = W
cos
ϕ
— współczynnik mocy
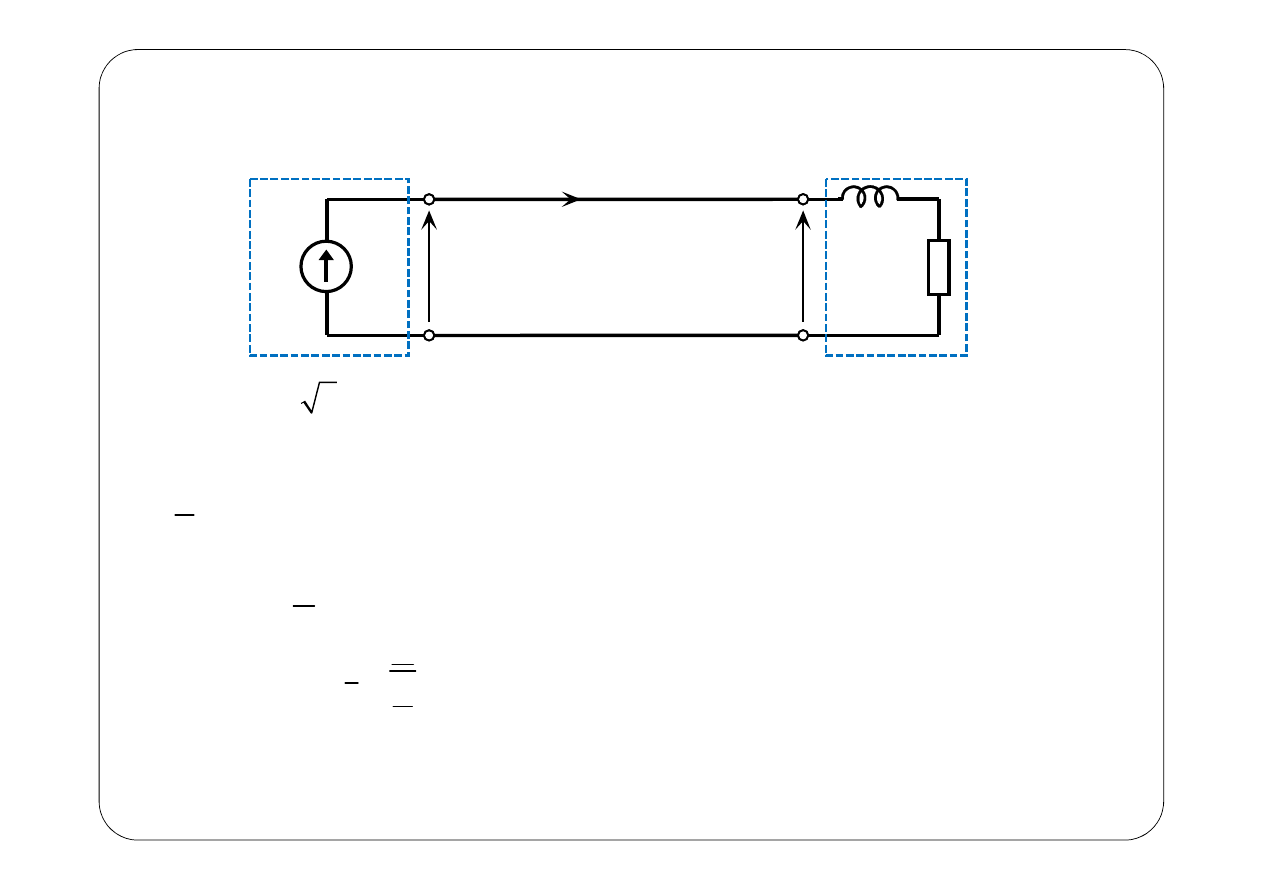
Przykład
( )
e t
L
R
( )
u t
( )
u t
( )
i t
Dostawca energii
Odbiornik
( )
0
0
2 sin
V,
230 V,
50 Hz,
100 Ω,
1 H.
e t
E
ω t
E
f
R
L
=
=
=
=
=
j1,2625
0
j2π
100
j314
329,5e
Z
R
f L
= +
=
+
=
1, 2625
cos
0,303
φ
φ
=
=
⇒
,
230
U
E
U
=
=
1,2625
0, 2118
j0,665
0, 698e
U
I
Z
−
=
=
−
=
0, 698
cos
48,7 W
I
P
UI
φ
=
=
=
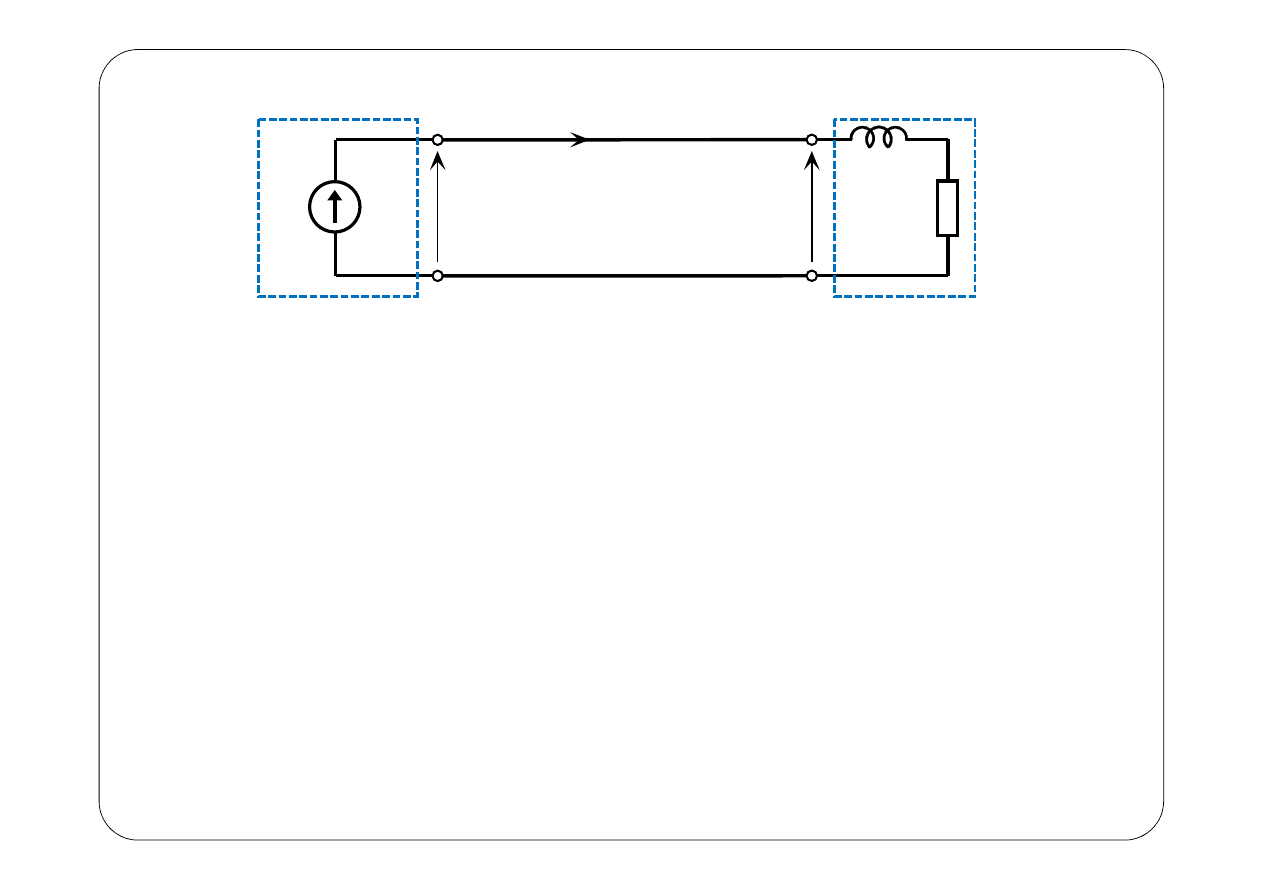
( )
e t
L
R
( )
u t
( )
u t
( )
i t
Dostawca energii
Odbiornik
230 V,
0, 698 A,
48, 7 W
U
I
P
=
=
=
Z punktu widzenia dostawcy pobierany prąd jest zbyt duży — jakby
Z punktu widzenia dostawcy pobierany prąd jest zbyt duży — jakby
odbiorca pozornie pobierał większą moc:
160,5
S
UI
=
=
S nazywa się moc
ą pozorną
[ ]
VA
S
=
u
i
j
j
j
e
e
e
cos
j
sin
j
S
U I
U
I
UI
UI
UI
P
Q
ψ
ψ
ϕ
ϕ
ϕ
−
∗
=
=
=
+
= +
≜
S — moc pozorna zespolona
{ }
{ }
Re
Re
cos
S
S
UI
P
S
U I
UI
∗
=
=
=
=
=
ϕ
{ }
{ }
{ }
{ }
Re
Re
cos
Im
Im
sin
P
S
U I
UI
Q
S
U I
UI
∗
=
=
=
=
=
=
ϕ
ϕ
Q — moc bierna
[ ]
[ ]
[ ]
VA
W
VAr
S
P
Q
=
=
=
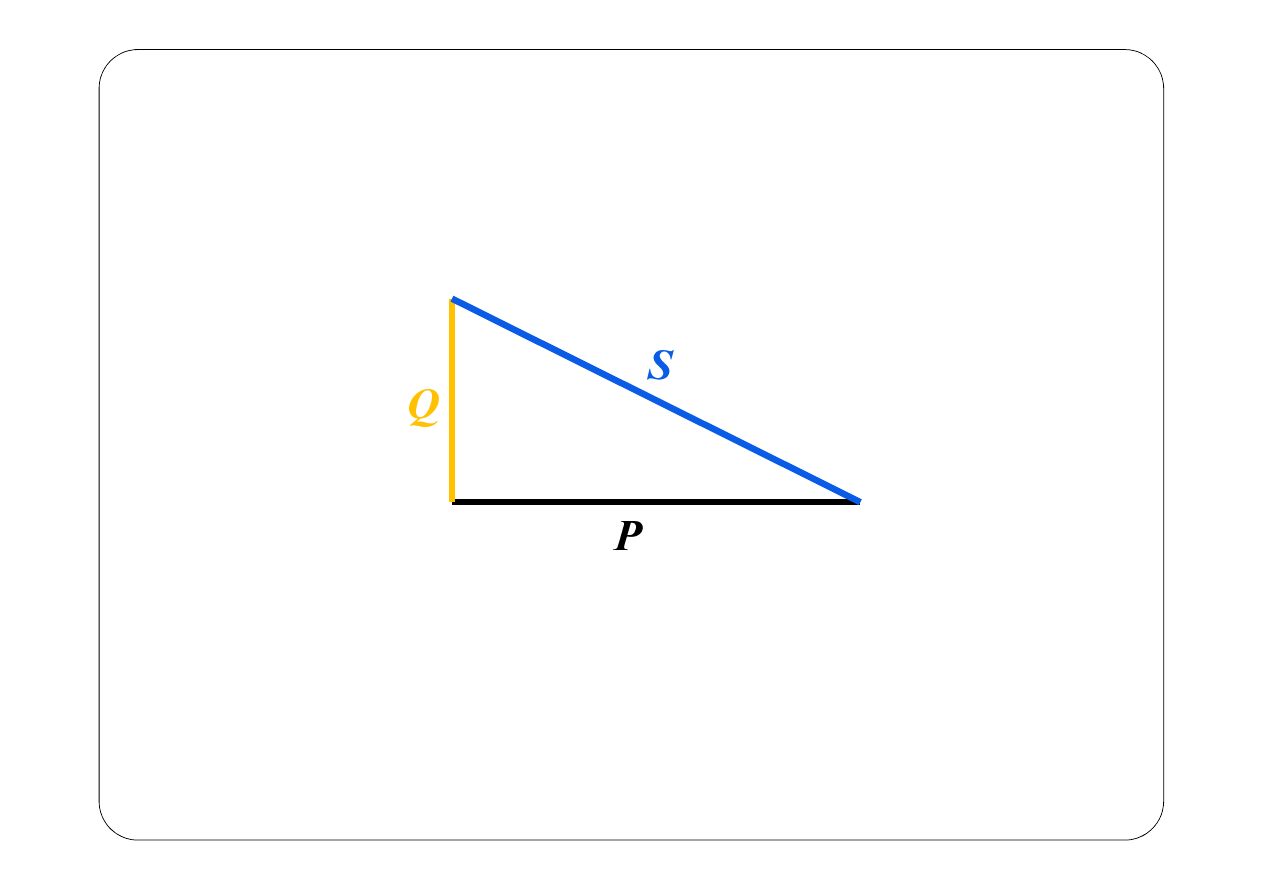
2
2
2
S
P
Q
=
+
„Trójkąt mocy”
cos
sin
S
I
U
I
U
I
Q
P
U
ϕ
ϕ
=
=
=
moc pozorna
moc czynna
moc bierna
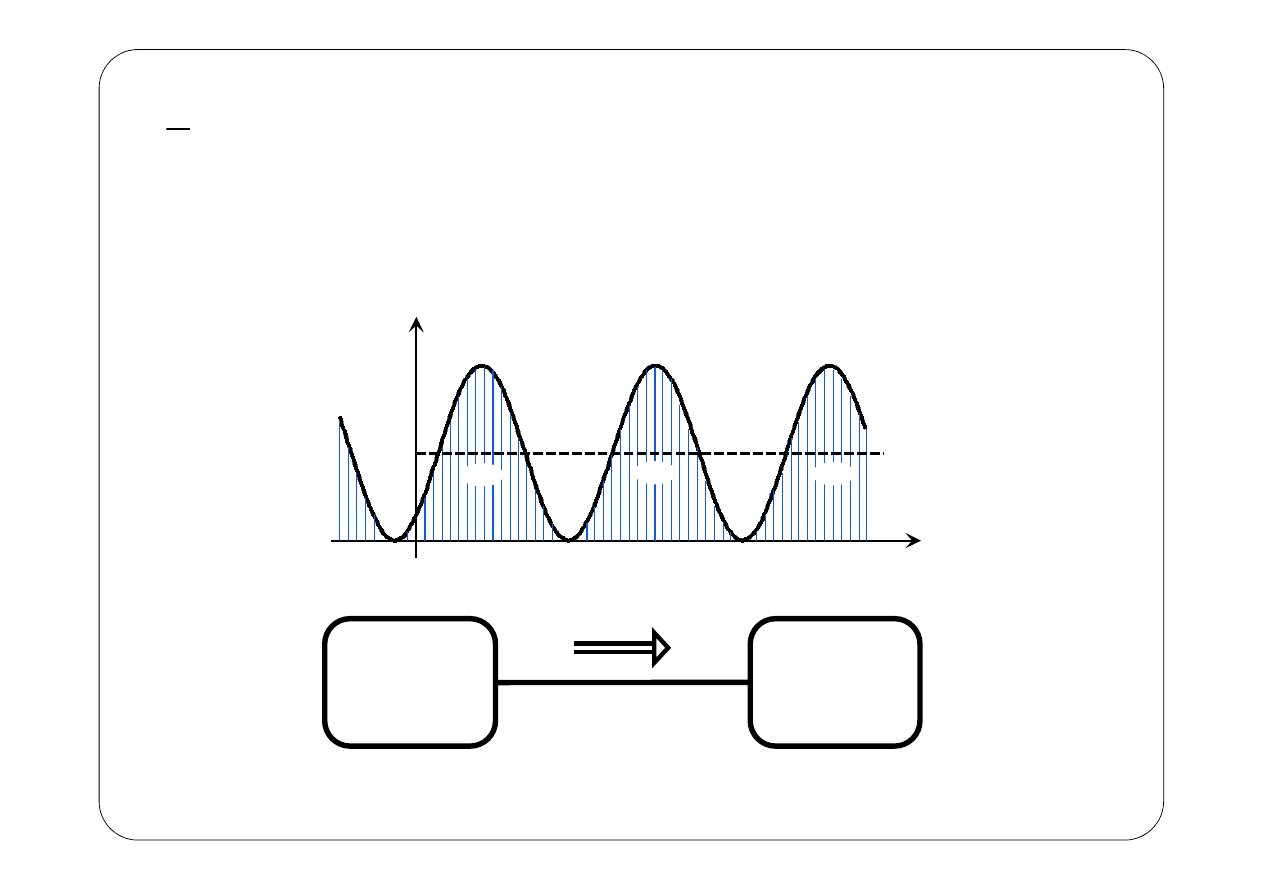
0
0,
cos
1
Z
R
ϕ
ϕ
= >
⇒
=
=
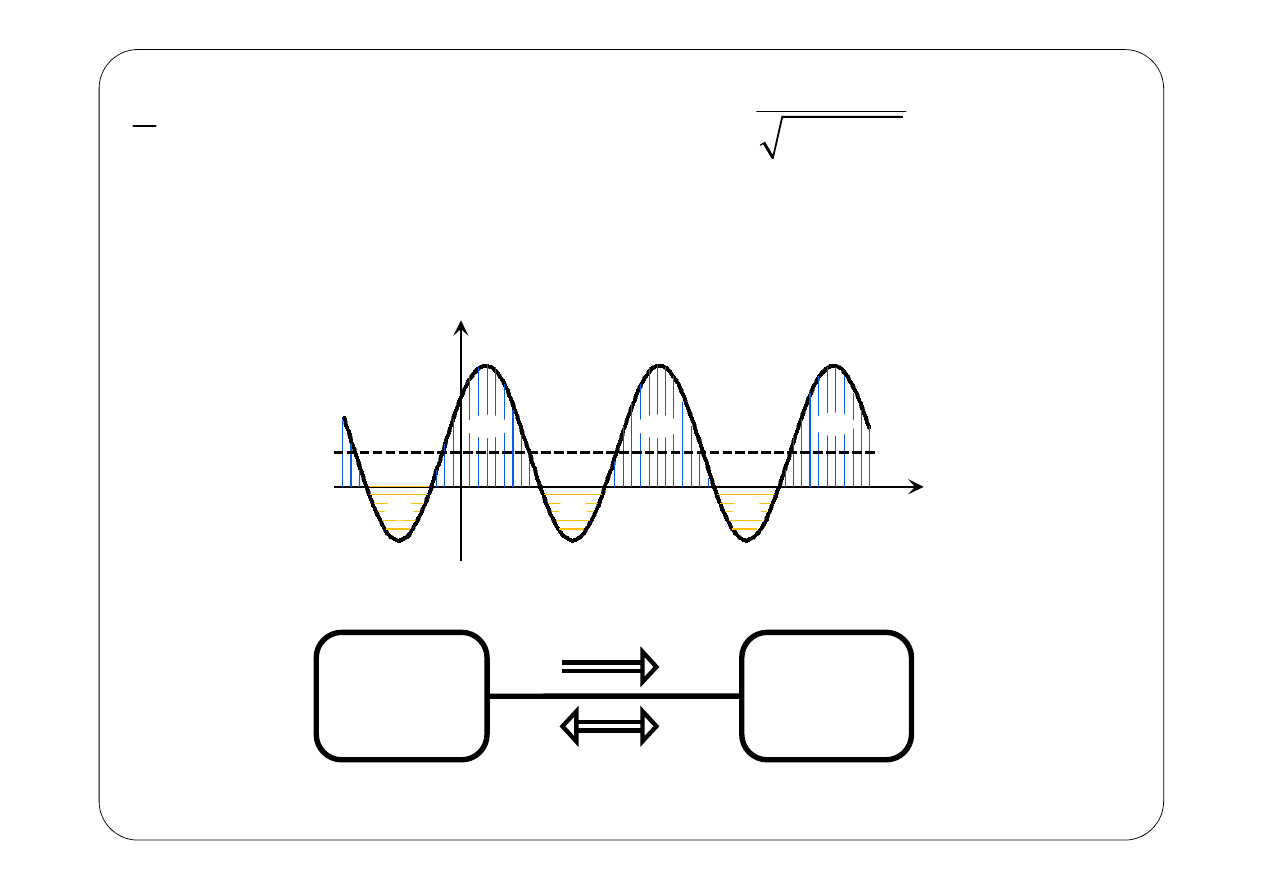
( )
(
)
0
i
cos 2
2
p t
UI
UI
t
P
UI
ω
ψ
=
−
+
=
( )
p t
P
+
+
+
t
P
Generator
Odbiornik
P
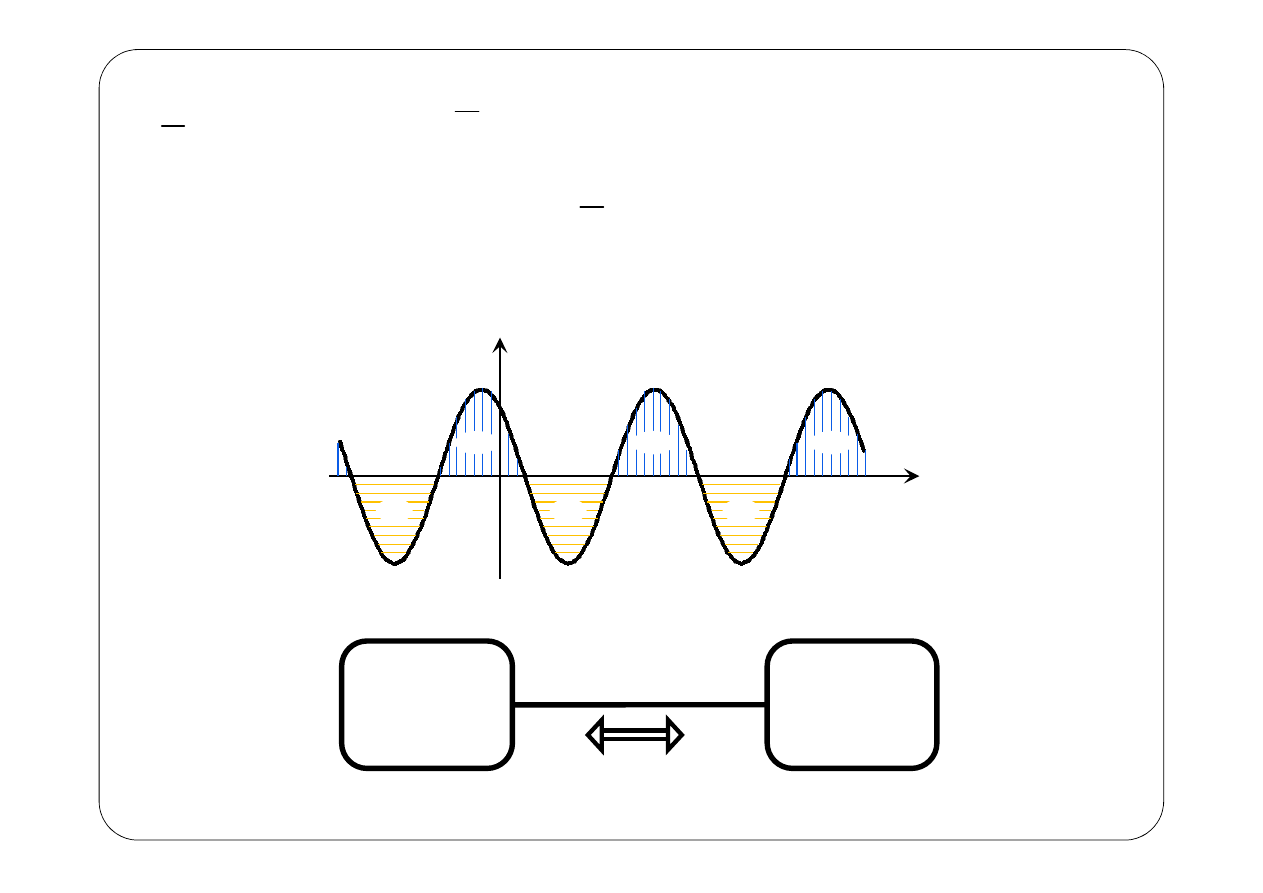
π
j
,
cos
0
2
Z
X
ϕ
ϕ
=
⇒
= ±
=
( )
(
)
0
i
0
i
π
cos 2
2
sin 2
2
2
0
p t
UI
t
UI
t
P
ω
ψ
ω
ψ
= −
+
±
= ±
+
=
+
+
+
( )
p t
t
+
+
+
t
−−−−
−−−−
−−−−
Generator
Odbiornik
0
P
=
Q
2
2
j
,
0,
0
cos
,
0
cos
1
R
Z
R
X
R
X
R
X
ϕ
ϕ
= +
>
≠
⇒
=
<
<
+
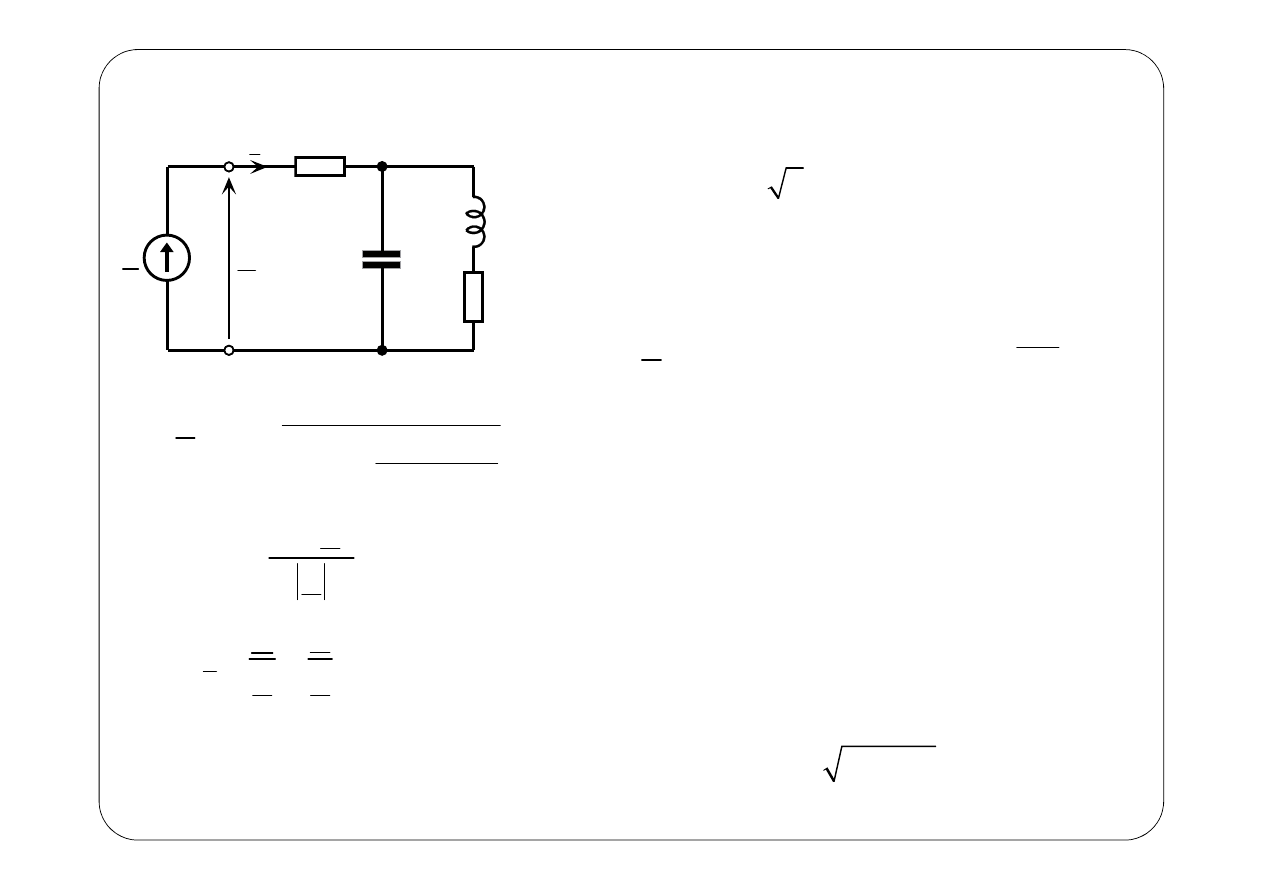
( )
(
)
0
i
cos
cos 2
2
cos
p t
UI
UI
t
P
UI
ϕ
ω
ψ ϕ
ϕ
=
−
+
+
=
+
+
+
( )
p t
P
t
−−−−
−−−−
−−−−
Generator
Odbiornik
P
Q
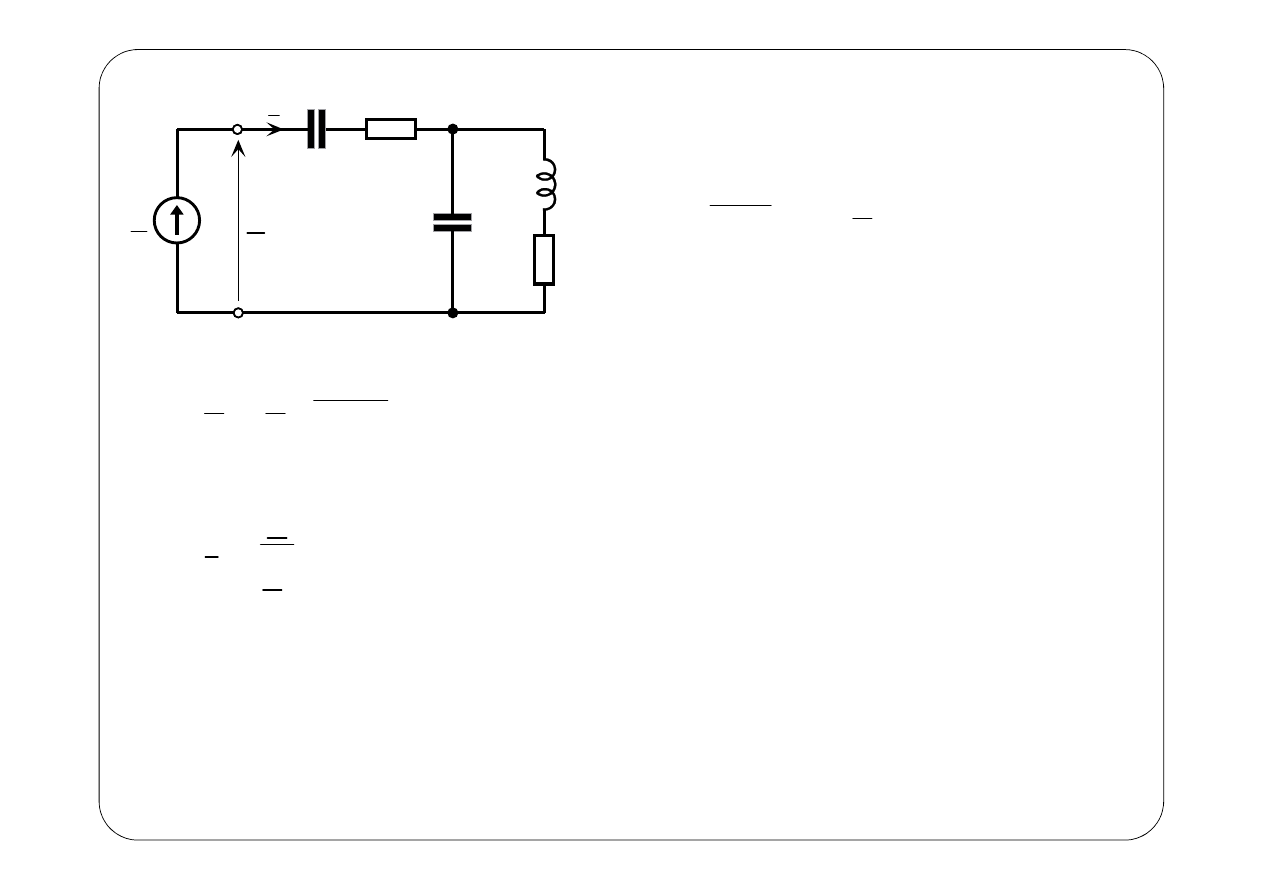
Przykład
E
1
R
2
R
L
C
I
U
( )
0
0
1
2
0
0
230 2 sin
V,
50 Hz,
1kΩ,
100 Ω,
5 H,
20 nF.
rad
230 V,
2π
100π
e t
t
f
R
R
L
C
E
f
s
ω
ω
=
=
=
=
=
=
=
=
=
(
)
1
1
1102
j1587 Ω
1
j
Z
R
C
ω
=
+
=
+
+
{ }
0
2
0
1
j
j
Re
cos
0, 5074
C
R
L
Z
Z
ω
ω
ϕ
+
+
=
=
j
j0,964
0, 0679
j0,978
0,119e
e
i
U
E
I
I
Z
Z
ψ
−
=
=
=
−
=
=
2
2
27, 4 VA,
cos
15, 6 W,
22, 5 VAr
S
EI
P
EI
Q
S
P
ϕ
=
=
=
=
=
−
=
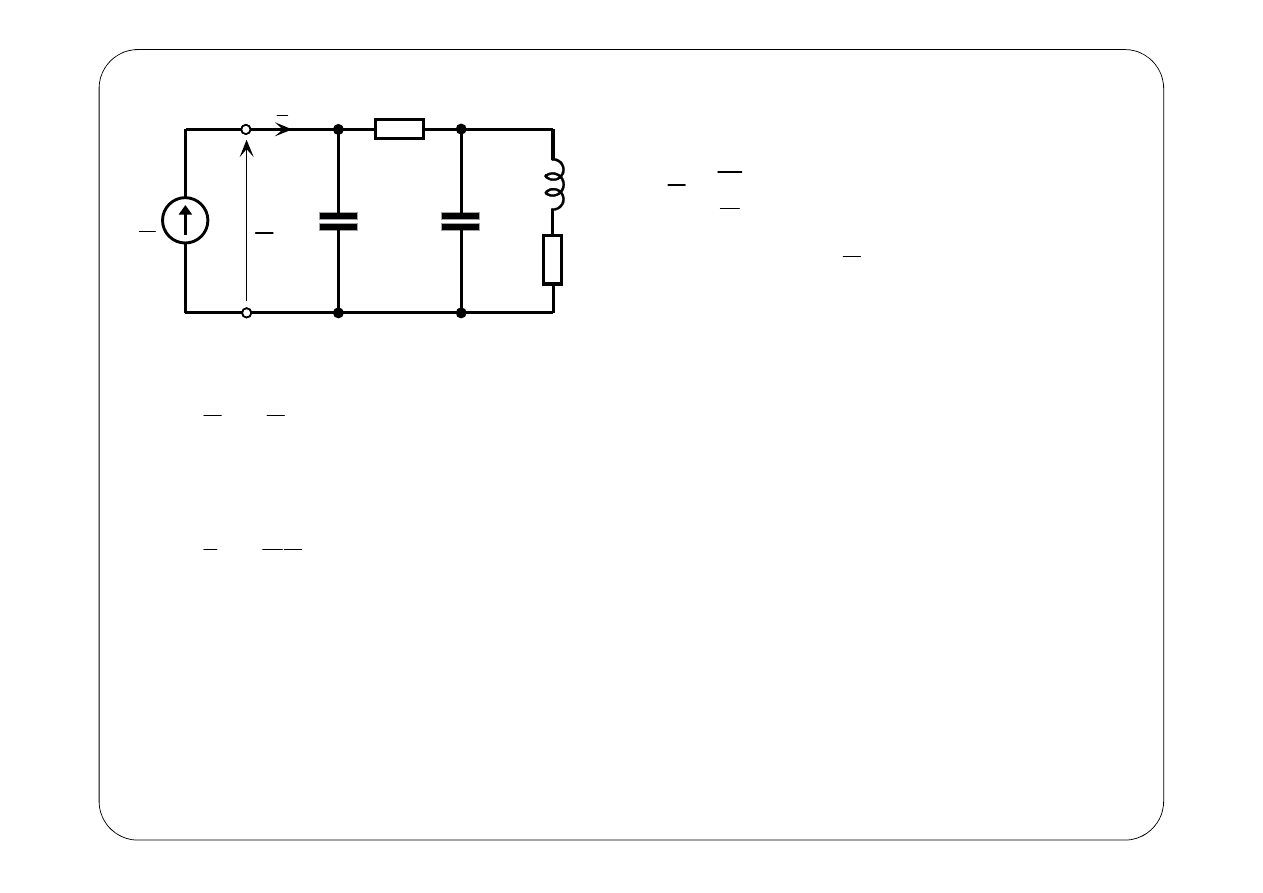
E
1
R
2
R
L
C
I
′
U
C
′
{ }
0
6
1
Im
1587
2 10 F
Z
C
C
ω
−
=
=
′
′ ≈ ⋅
0
1
1102 Ω
j
Z
Z
C
ω
′ = +
=
′
cos
1
ϕ
=
0, 209 A
E
I
Z
′ =
=
′
48 VA,
cos
48 W,
0
S
EI
P
EI
Q
ϕ
′
′
′
′
′
=
=
=
=
=
,
I
I
P
P
′
′
>
>
E
1
R
2
R
L
C
I
′′
U
C
′′
(
)
{ }
3
3
0
6
1
0, 295
j0, 425 10 S
j
Im
0, 425 10
1, 35 10 F
Y
Z
C
Y
C
ω
−
−
−
=
=
−
⋅
′′ = −
=
⋅
′′ =
⋅
3
0
j
0, 295 10 S
cos
1
Y
Y
C
ω
ϕ
−
′′
′′
= +
=
⋅
=
cos
1
ϕ
=
0, 0679 A
I
EY
′′
′′
=
=
15, 6 VA,
cos
15, 6 W,
0
S
EI
P
EI
Q
ϕ
′′
′′
′′
=
=
=
=
=
,
I
I
P
P
′′
′′
<
=
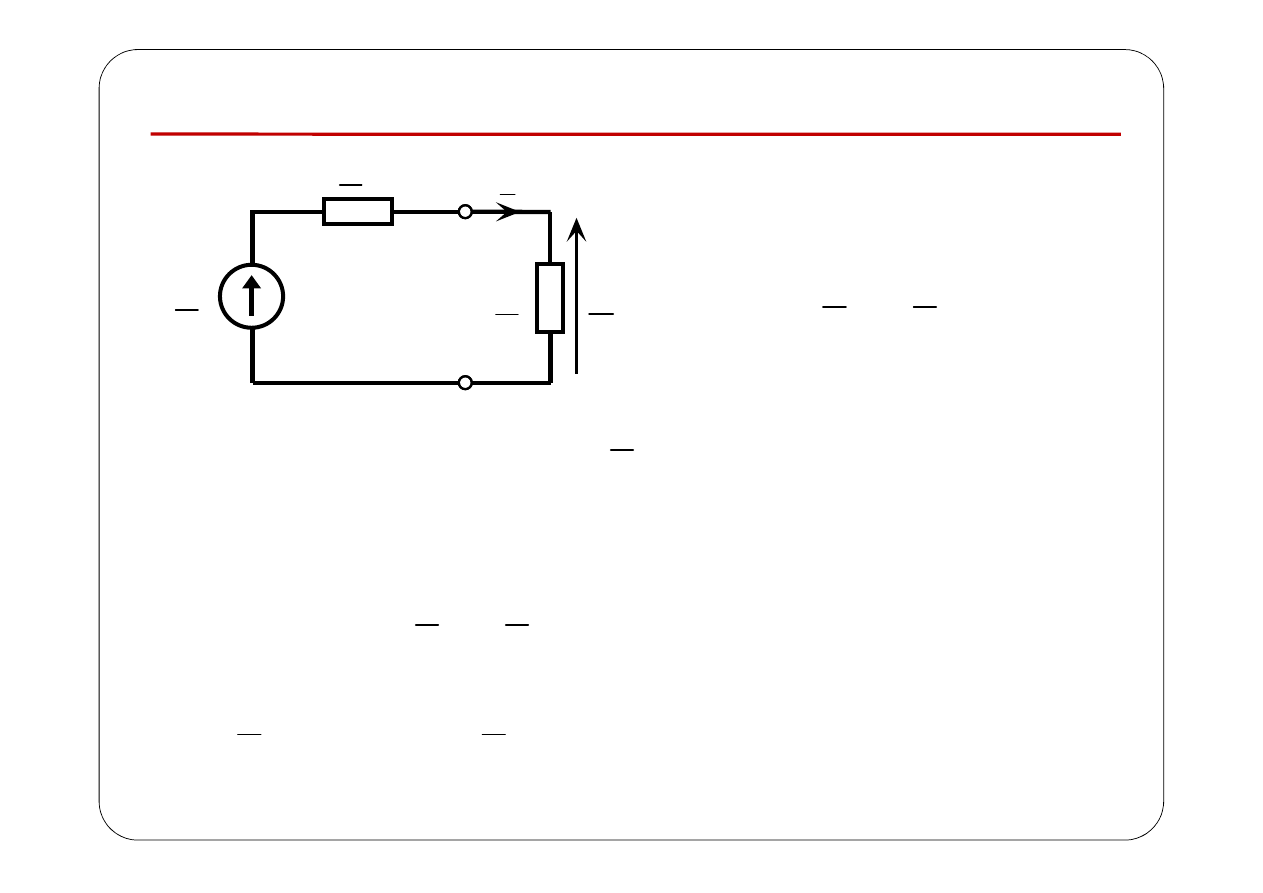
Dopasowanie obciążenia do generatora
Zadane
g
g
i
E
Z
Należy znaleźć impedancję
dwójnika reprezentującego
0
Z
g
E
g
Z
0
Z
I
U
Należy znaleźć impedancję
dwójnika reprezentującego
obciążenie, taką, aby do obciążenia przekazana została
maksymalna moc czynna.
0
Z
Zakładamy, że są impedancjami dwójników ściśle
pasywnych, czyli
g
0
i
Z
Z
{ }
{ }
g
0
Re
0
i
Re
0
Z
Z
>
>
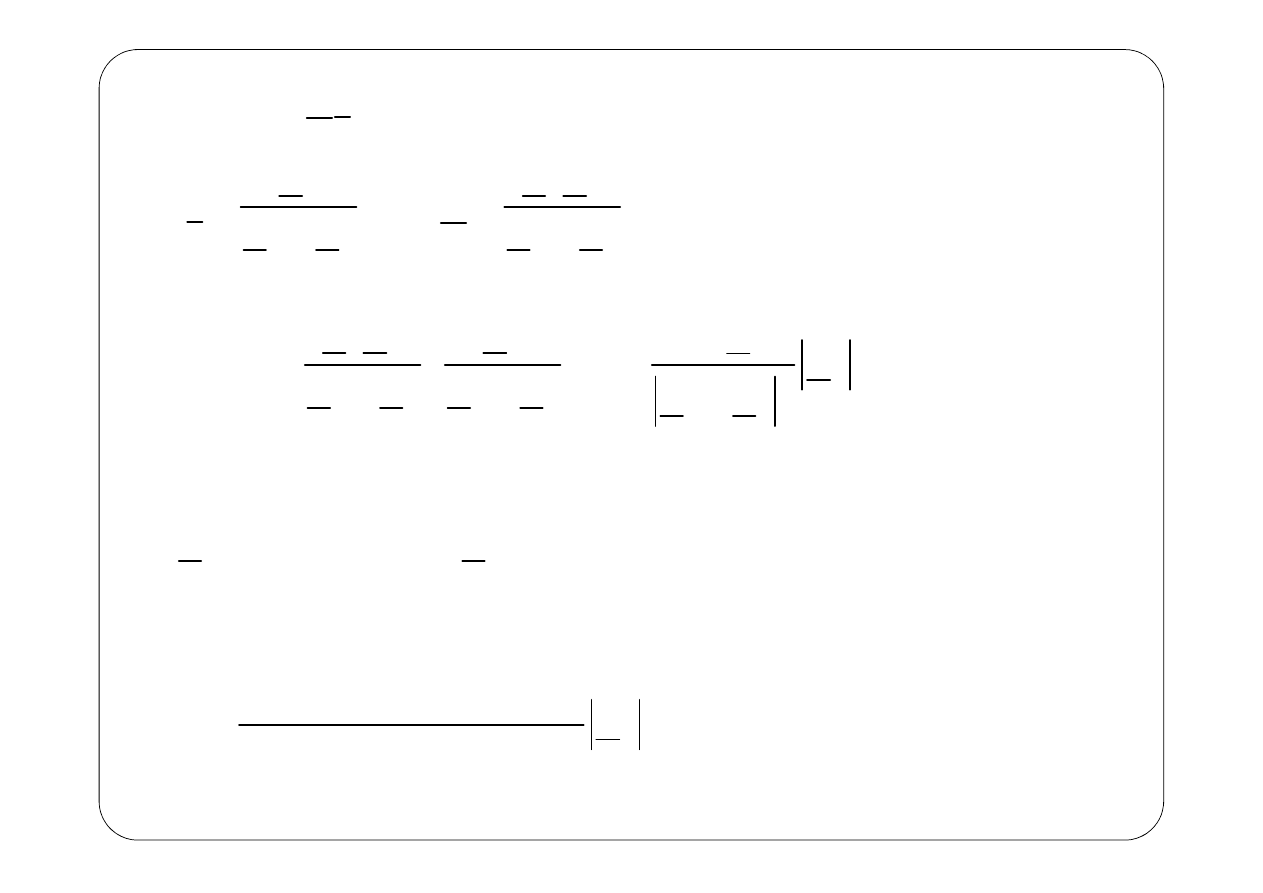
{ }
2
0
g
g
0
g
2
g
0
g
0
g
0
Re
Re
Z E
E
Z
P
E
Z
Z
Z
Z
Z
Z
∗
=
=
+
+
+
g
0
g
g
0
g
0
,
E
Z E
I
U
Z
Z
Z
Z
=
=
+
+
{ }
Re
P
U I
∗
=
Oznaczmy:
g
0
g
g
0
0
j
,
j
Z
R
X
Z
R
X
=
+
=
+
Wówczas
(
) (
)
2
0
g
2
2
g
0
g
0
R
P
E
R
R
X
X
=
+
+
+
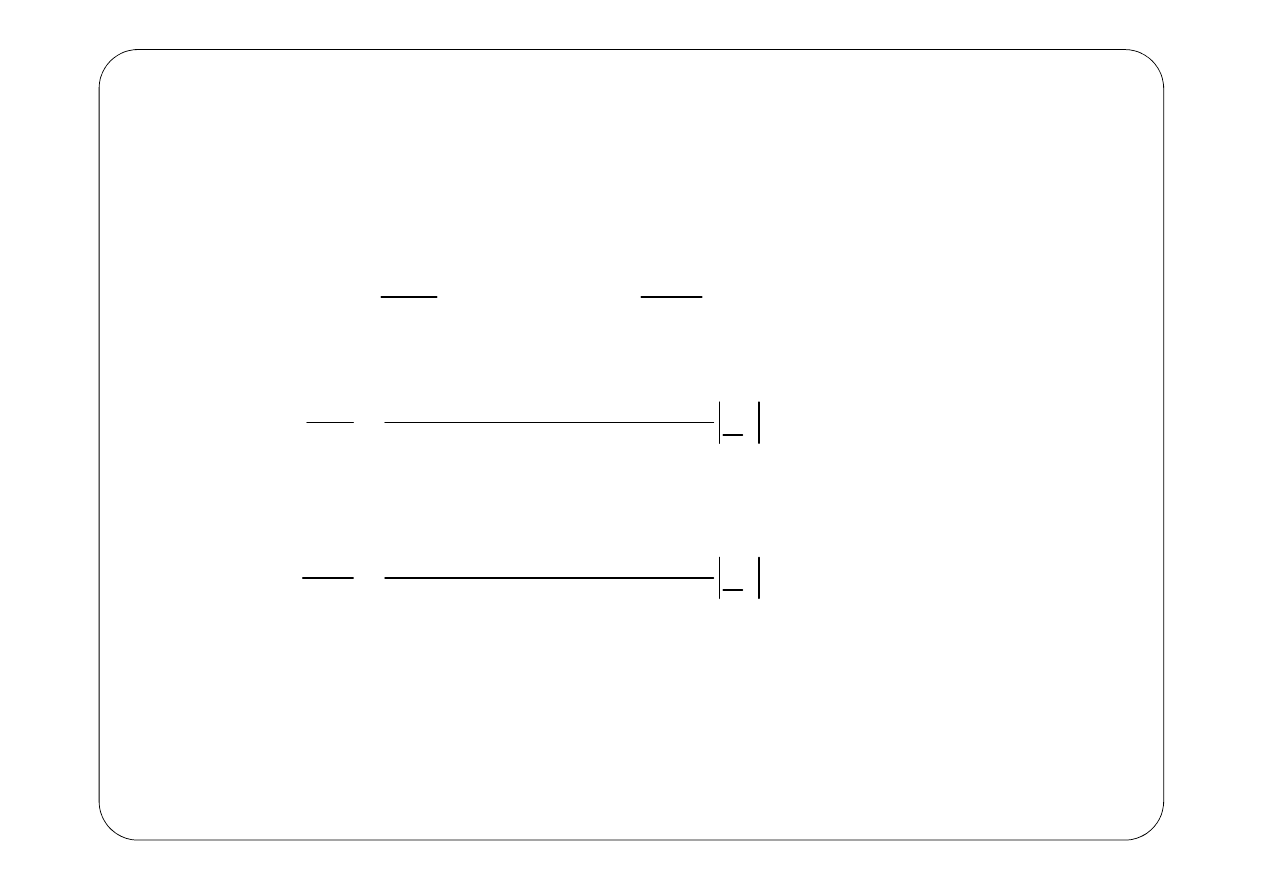
Należy znaleźć maksimum funkcji w obszarze
(
)
0
0
,
P R X
0
0
0
,
R
X
<
< ∞
− ∞ <
< ∞
Warunkami koniecznymi istnienia lokalnego ekstremum są:
0
0
0
i
0
P
P
R
X
∂
∂
=
=
∂
∂
(
)
(
) (
)
2
2
2
2
g
0
g
0
g
2
2
2
0
0
R
R
X
X
P
E
R
R
R
X
X
−
+
+
∂ =
=
∂
+
+
+
(
) (
)
(
)
(
) (
)
2
2
0
g
0
g
0
2
g
0
0
g
2
2
2
0
g
0
g
0
2
0
R
R
R
X
X
X
X
R
P
E
X
R
R
X
X
∂
+
+
+
−
+
∂ =
=
∂
+
+
+
Jedynym rozwiązaniem w rozważanym obszarze jest
0
g
0
g
i
R
R
X
X
=
= −
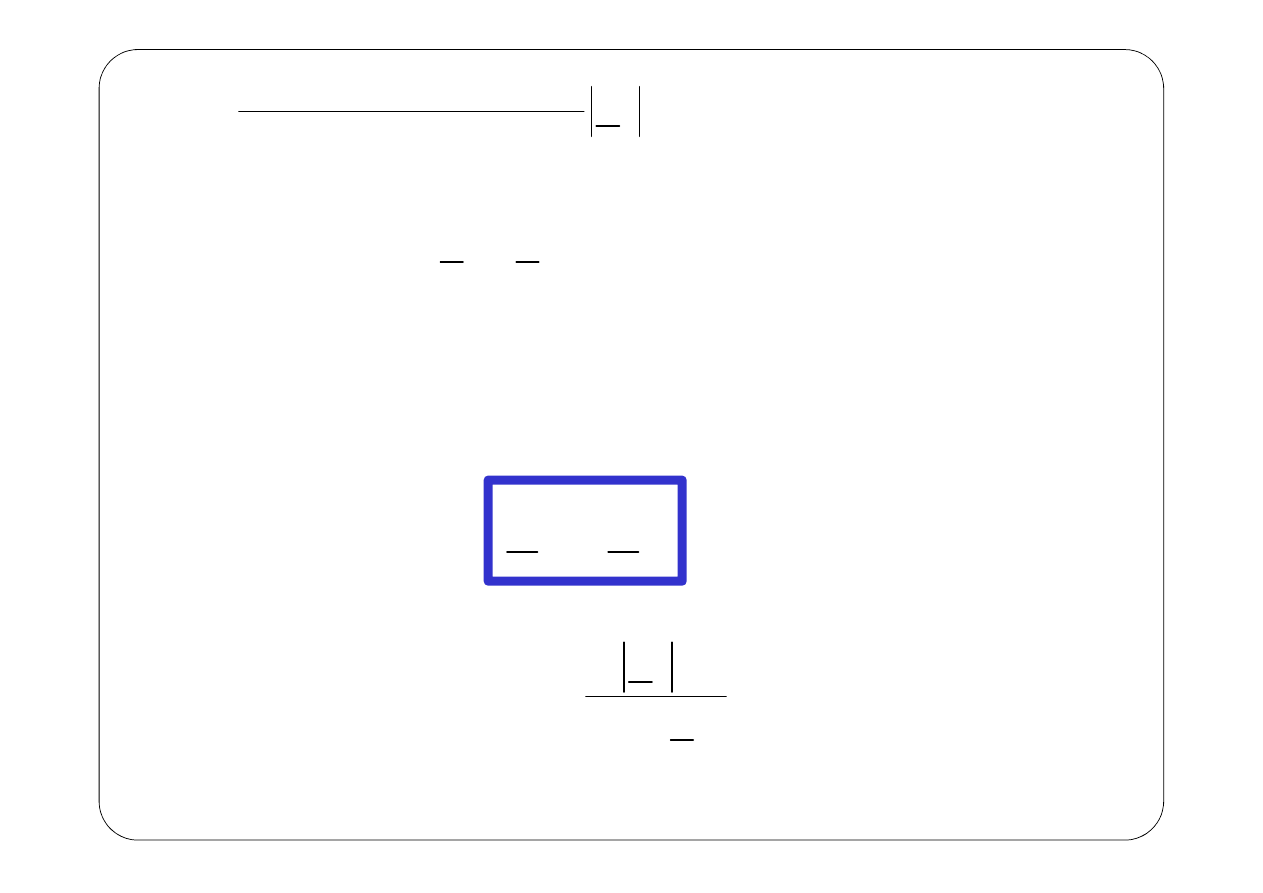
(
) (
)
2
0
g
2
2
g
0
g
0
R
P
E
R
R
X
X
=
+
+
+
0
g
0
g
0
g
R
R
Z
Z
X
X
∗
=
⇒
=
= −
Z przesłanek fizycznych wynika, że w wyznaczonym punkcie funkcja
ma lokalne maksimum, które jest jednocześnie największą
wartością funkcji w rozważanym obszarze.
Warunkiem dopasowania jest więc
(
)
0
0
,
P R X
Warunkiem dopasowania jest więc
0
g
Z
Z
∗
=
W warunkach dopasowania
{ }
2
g
max
g
4 Re
E
P
P
Z
=
=
Moc P
max
nazywa się moc
ą dysponowaną generatora
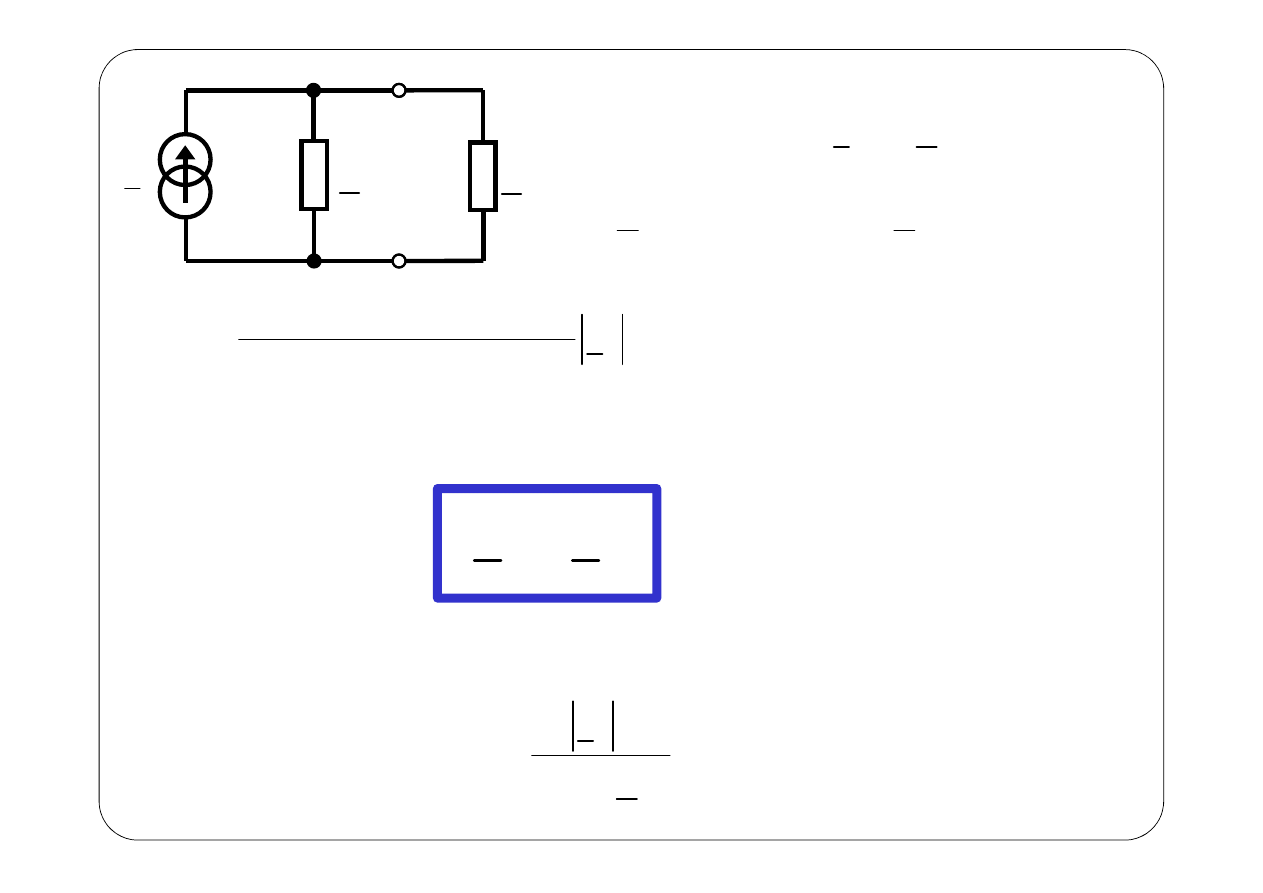
g
I
g
Y
0
Y
Zadane
g
g
i
I
Y
g
0
g
g
0
0
j
,
j
Y
G
B
Y
G
B
=
+
=
+
(
) (
)
2
0
g
2
2
g
0
g
0
G
P
I
G
G
B
B
=
+
+
+
Warunek dopasowania
Warunek dopasowania
0
g
Y
Y
∗
=
Moc dysponowana generatora
{ }
2
g
max
g
4 Re
I
P
Y
=
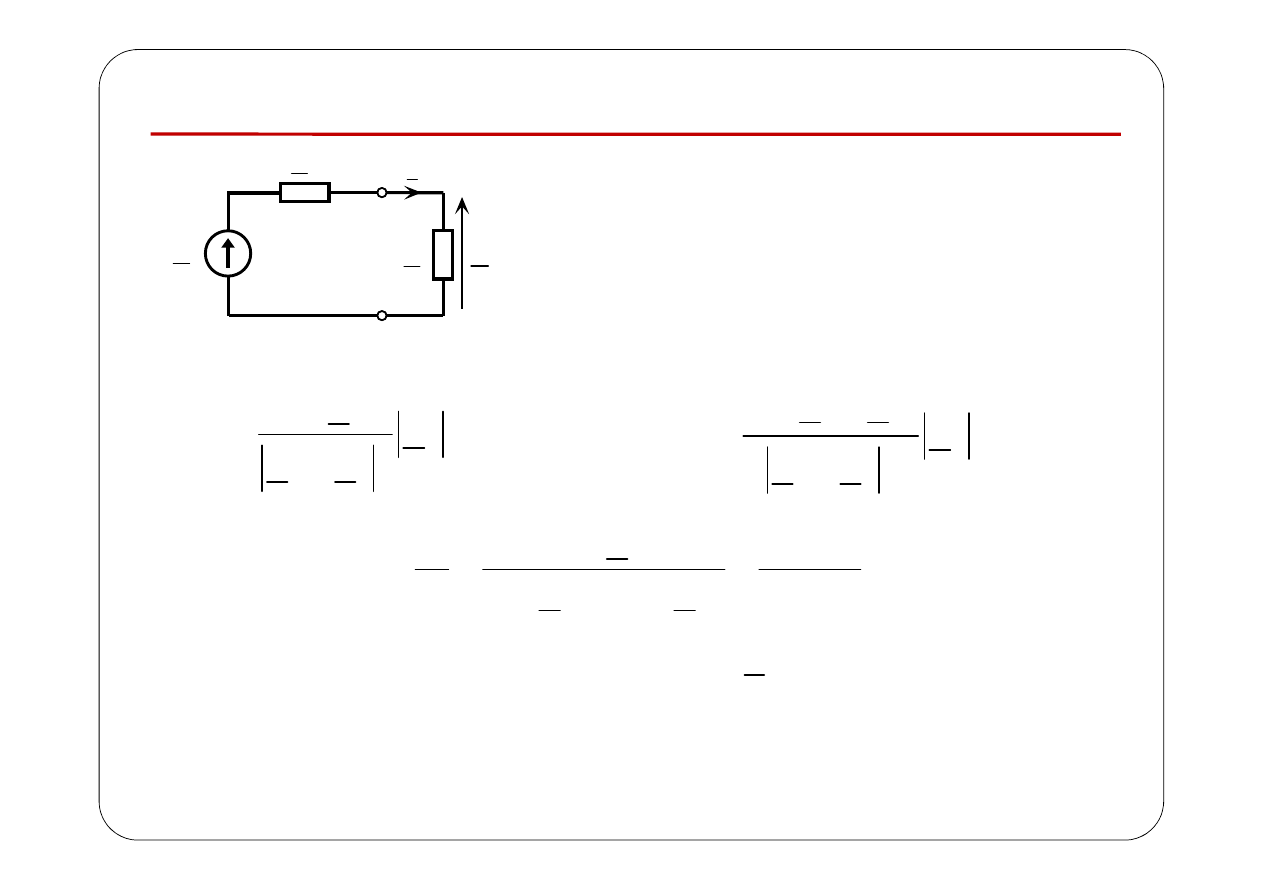
Sprawność przekazywania mocy
g
E
g
Z
0
Z
I
U
{ }
2
0
g
2
Re Z
P
E
=
+
{
}
2
g
0
g
g
2
Re Z
Z
P
E
+
=
+
Moc wydzielona w obciążeniu
Moc wytworzona w generatorze
g
2
g
0
P
E
Z
Z
=
+
g
g
2
g
0
P
E
Z
Z
=
+
{ }
{ }
{ }
0
0
g
g
0
g
0
Re
Re
Re
Z
R
P
P
R
R
Z
Z
η
=
=
=
+
+
W warunkach dopasowania (R
0
= R
g
):
1
2
η
=
Dopasowania na maksimum mocy czynnej nie stosuje si
ę w energetyce!!!
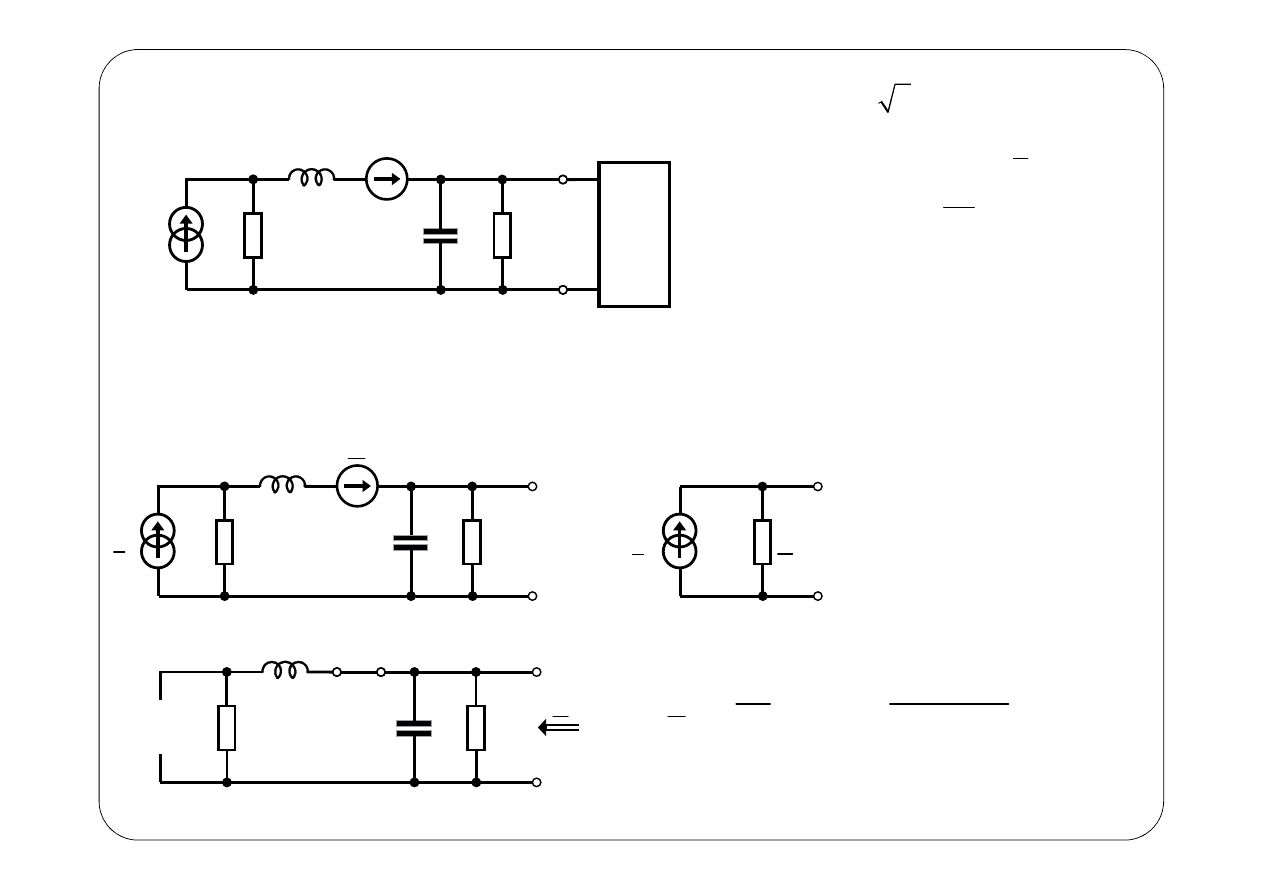
Przykład 1.
N
( )
e t
( )
z
i t
1
R
L
C
2
R
( )
( )
(
)
0
z
0
6
0
1
2
π
4
rad
5 2 cos
V,
0, 2sin
A,
10
,
50Ω,
100Ω,
50µH,
50 nF.
s
e t
t
i t
t
R
R
L
C
ω
ω
ω
=
=
−
=
=
=
=
=
Należy zaprojektować taki dwójnik N, aby wydzieliła
się w nim maksymalna moc czynna
E
E
z
I
1
R
L
C
2
R
≡
N
I
N
Y
1
R
L
C
2
R
N
Y
(
)
N
0
2
1
0
1
1
j
j
0, 02
j0, 04 S
Y
C
R
R
L
ω
ω
=
+
+
=
+
=
+
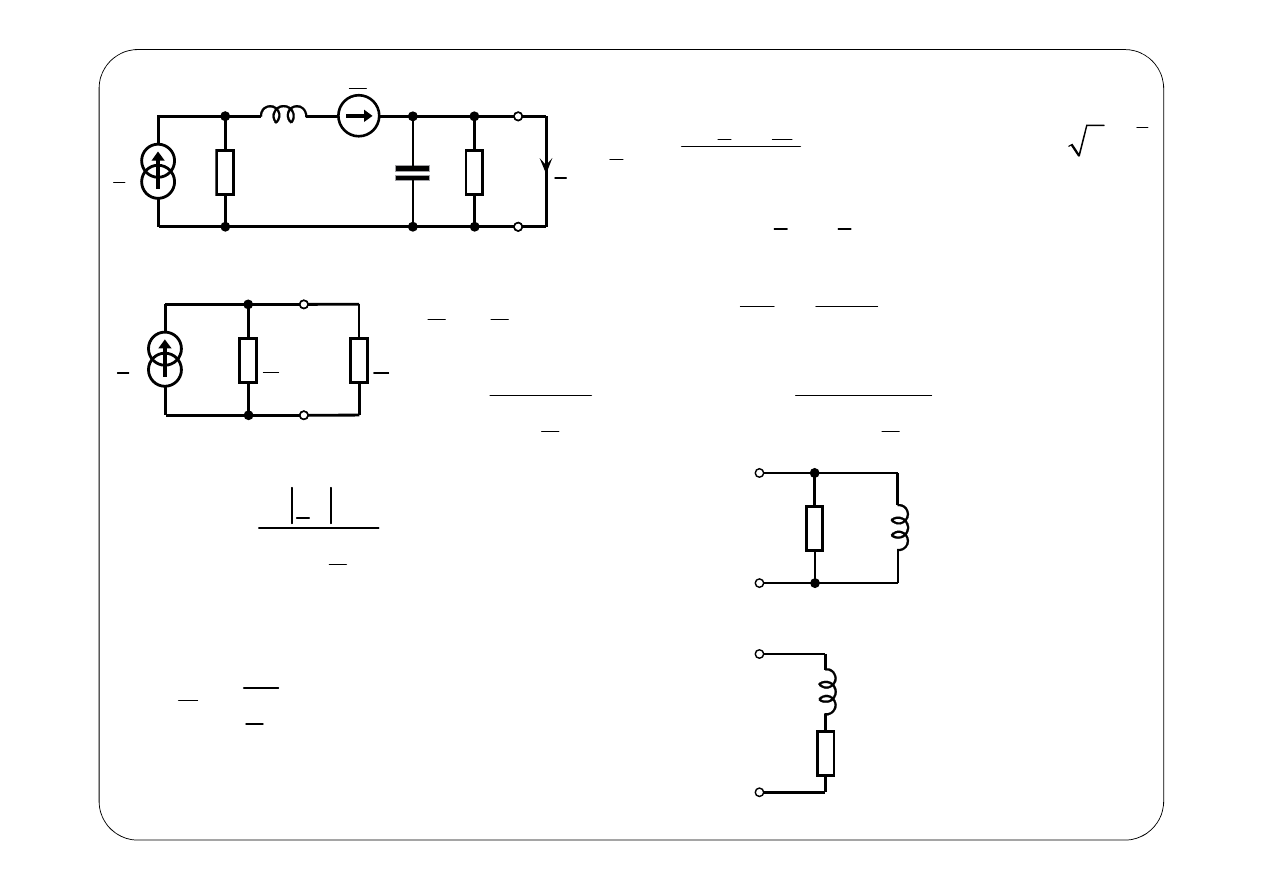
E
z
I
1
R
L
C
2
R
zw
I
π
j
z
1
4
zw
1
0
N
zw
0, 05
j0, 05
0, 05 2e
j
R I
E
I
R
L
I
I
ω
−
+
=
=
−
=
+
=
N
I
N
Y
0
Y
{ }
{ }
0
N
0
0
0
6
0
0
N
N
0
1
1
0, 02
j0, 04
j
1
1
50 Ω,
25 10 H.
Re
Im
Y
Y
R
L
R
L
Y
Y
ω
ω
−
∗
=
=
−
=
−
=
=
= −
=
⋅
0
R
0
L
{ }
2
N
max
N
0, 0625 W
4 Re
I
P
Y
=
=
0
0
0
0
0
6
0
0
1
10
j20
j
10
Ω
,
20 10 H
Z
R
L
Y
R
L
ω
−
′
′
=
=
+
=
+
′
′
=
=
⋅
0
R
′
0
L
′
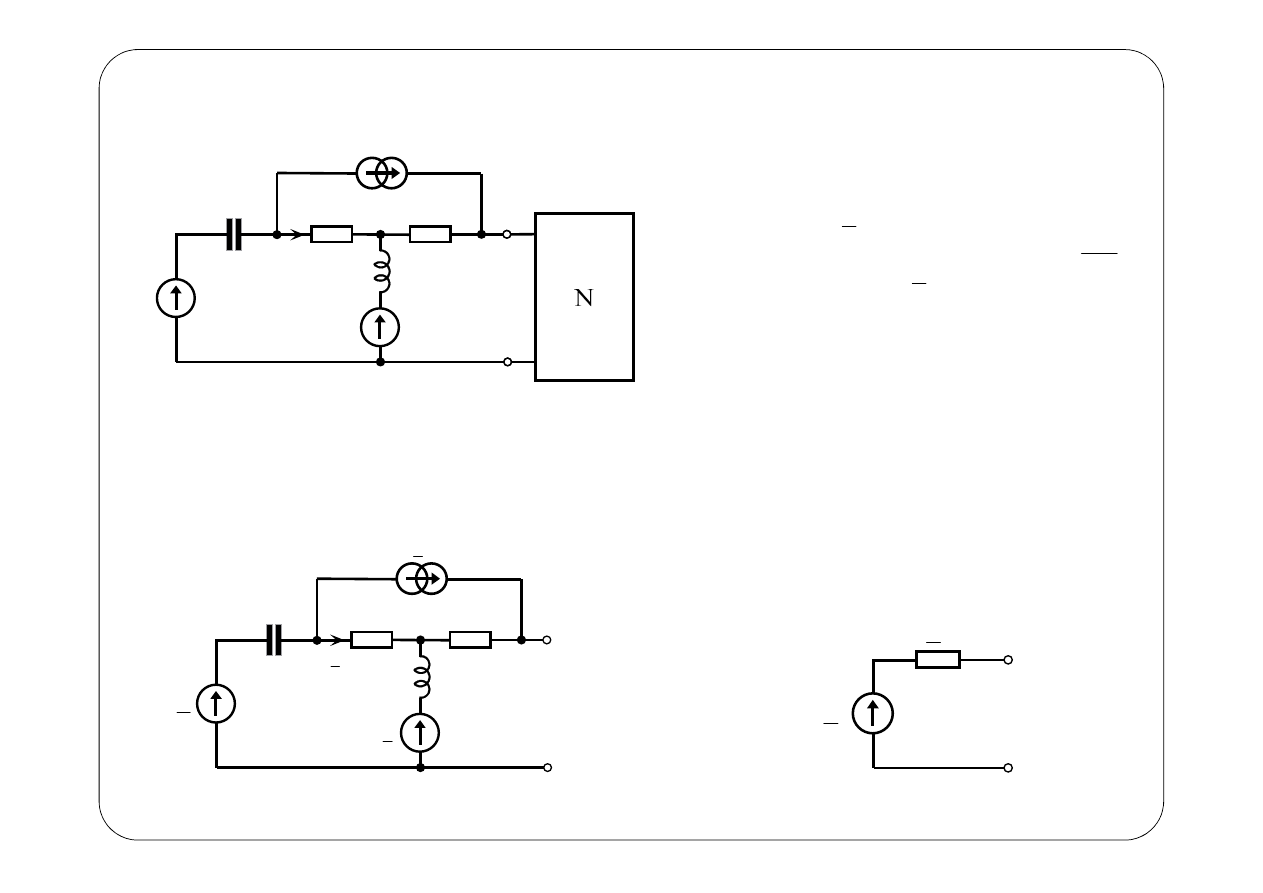
Przykład 2.
( )
e t
( )
z
i t
1
R
2
R
C
L
( )
i t
( )
i t
ρ
( )
(
)
( )
(
)
0
5
0
3
z
0
1
2
π
4
π
4
4sin
V,
rad
10
,
s
20 10 sin
A,
200 Ω,
100 Ω,
600 Ω,
2 mH,
50 nF.
e t
t
i t
t
R
R
L
C
ω
ω
ω
ρ
−
=
+
=
=
⋅
−
=
=
=
=
=
Należy zaprojektować taki dwójnik N, aby wydzieliła się w nim
Należy zaprojektować taki dwójnik N, aby wydzieliła się w nim
maksymalna moc czynna
E
z
I
1
R
2
R
C
L
I
I
ρ
T
E
T
Z
⇒
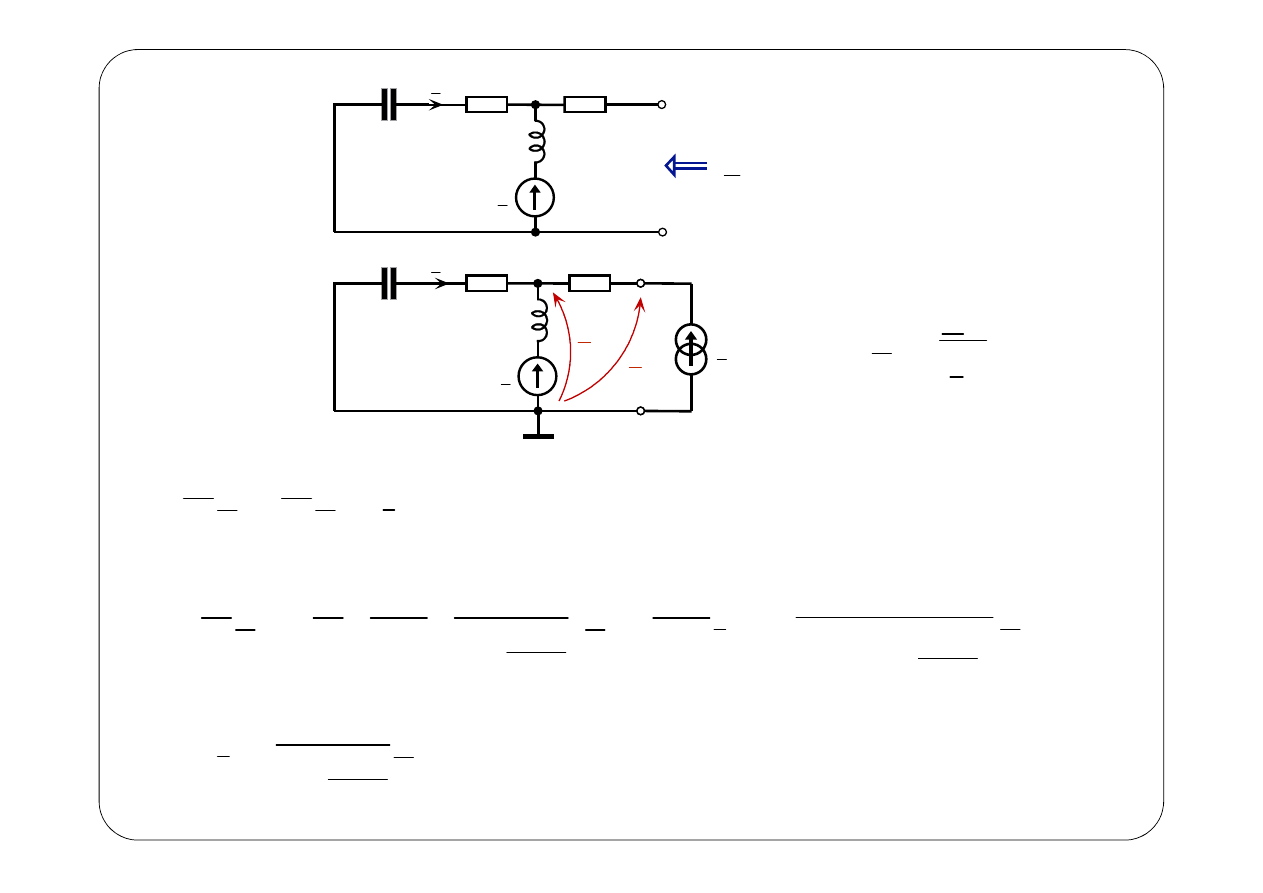
1
R
2
R
C
L
I
I
ρ
T
Z
1
R
2
R
C
L
I
I
ρ
1
2
n1
U
n2
U
0
I
n1
T
0
U
Z
I
=
0
n1
n2
2
2
n1
n2
2
2
0
0
1
0
1
1
1
1
1
1
1
j
j
j
U
U
I
R
R
U
U
I
R
R
L
L
R
C
ρ
ω
ω
ω
−
=
−
+
+
+
=
+
n2
1
0
1
1
j
I
U
R
C
ω
= −
+
n2
0
1
0
1
j
j
U
L R
C
ρ
ω
ω
= −
+
2
2
n1
0
n2
2
2
0
1
0
1
0
0
1
1
1
1
1
1
0
1
j
1
j
j
j
R
R
U
I
U
R
R
L
R
L R
C
C
ρ
ω
ω
ω
ω
−
=
−
+
+
+
+
+
n1
T
0
U
Z
I
=
1
n1
n
U
∆
=
∆
0
1
I
R
n
n
det
∆ =
Y
0
2
1
2
0
1
0
1
0
0
0
0
n11
2
0
1
0
1
0
0
1
1
1
det
0
1
j
1
j
j
j
1
1
1
1
j
1
j
j
j
R
R
L
R
L R
C
C
I
I
R
L
R
L R
C
C
ρ
ω
ω
ω
ω
ρ
ω
ω
ω
ω
∆ =
=
+
+
+
+
+
=
+
+
+
= ∆
+
+
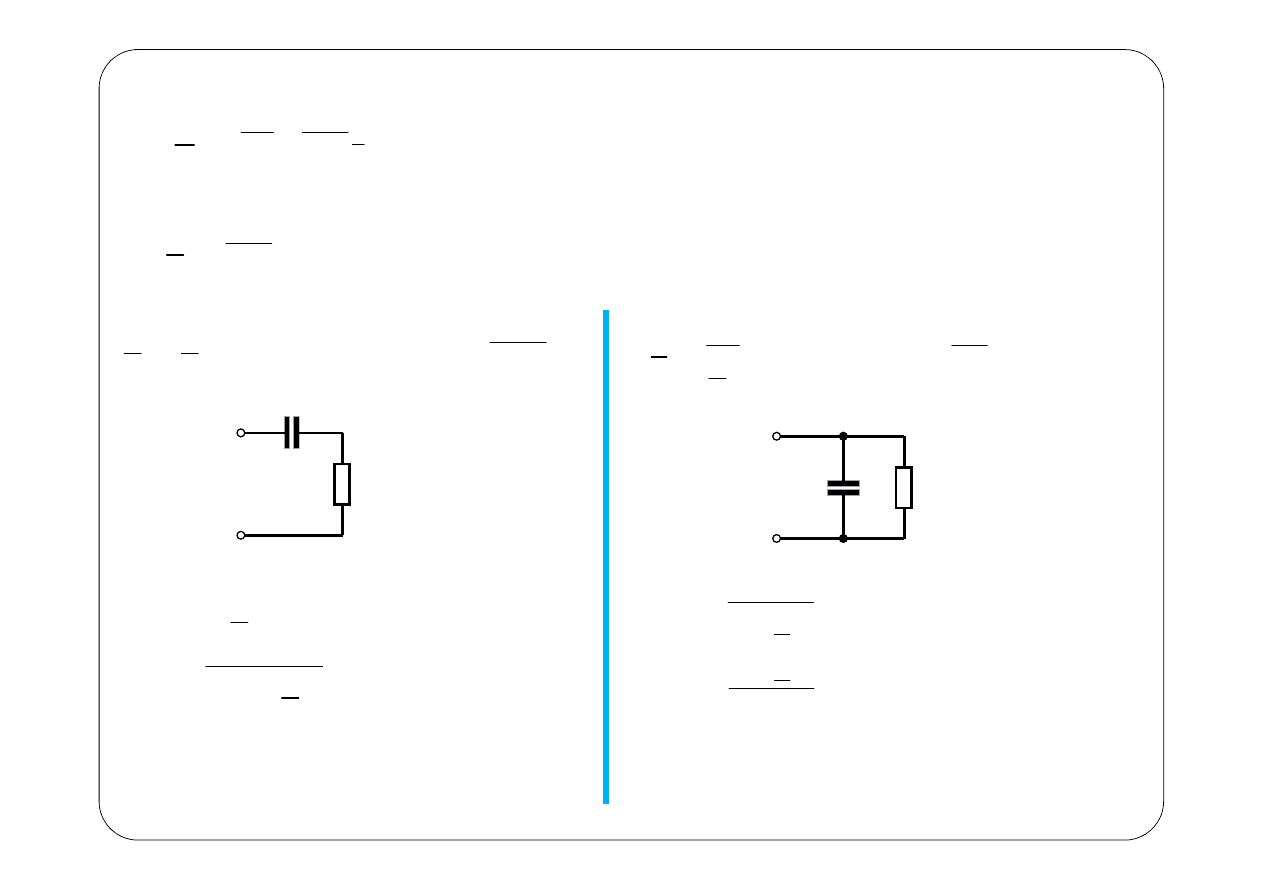
1
n11
0
n1
n
n
U
I
∆
∆
=
=
∆
∆
n11
T
n
Z
∆
=
∆
(
)
150
j50
=
+
Ω
(
)
0
T
150
j50
Z
Z
∗
=
=
−
Ω
0
C
0
0
0
1
j
R
C
ω
=
−
(
)
3
0
0
0
0
0
1
1
6
j2 10 S
j
Y
C
Z
R
ω
−
′
=
= +
⋅
=
+
′
0
R
{ }
{ }
0
0
6
0
0
0
Re
150Ω,
1
0, 2 10 F
0, 2 µF
Im
R
Z
C
Z
ω
−
=
=
= −
=
⋅
=
0
C
′
0
R
′
{ }
{ }
0
0
0
9
0
0
1
166,7 Ω,
Re
Im
20 10 F
20 nF.
R
Y
Y
C
ω
−
′ =
=
′ =
=
⋅
=
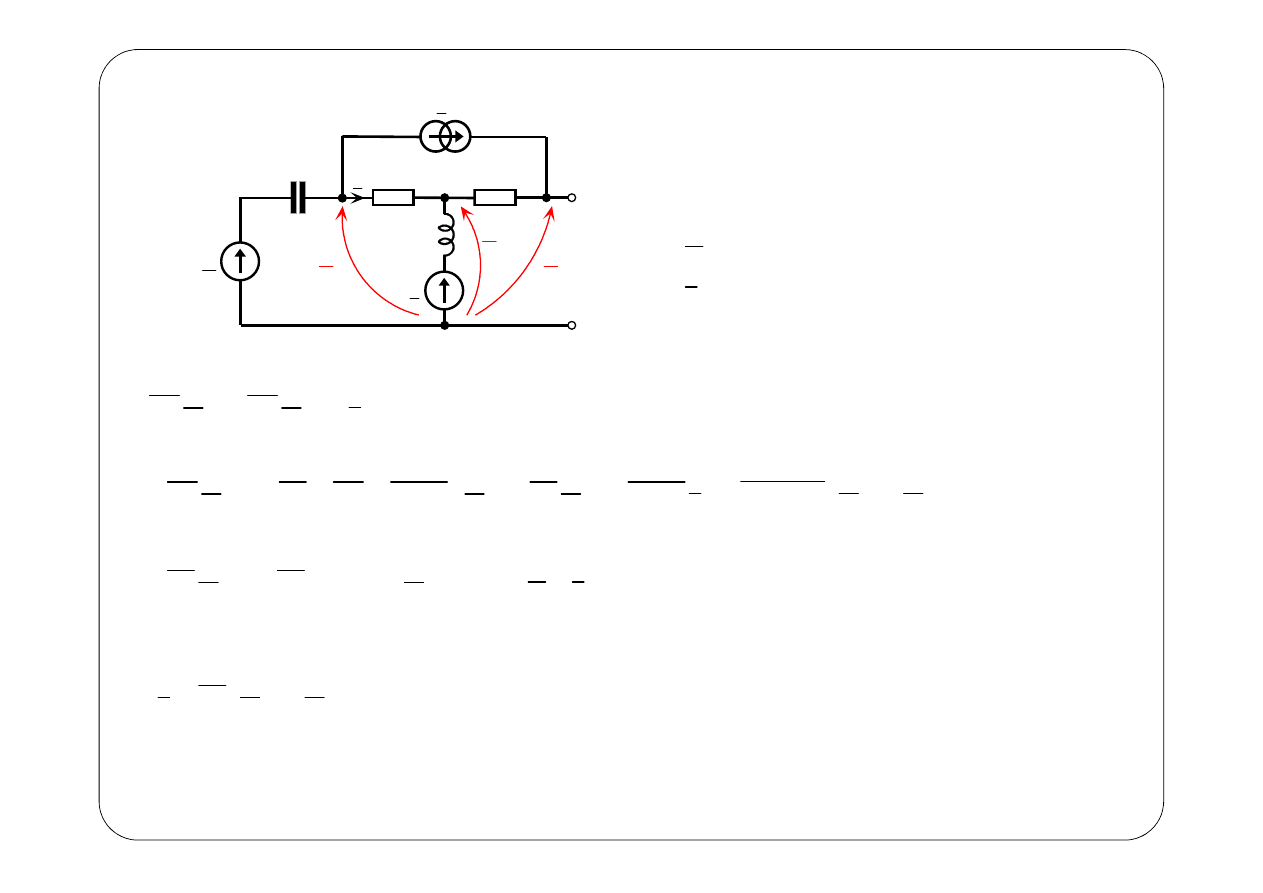
E
z
I
1
R
2
R
C
L
I
I
ρ
1
2
3
n1
U
n2
U
n3
U
z
2
j2,
0,01
j0,01
E
I
= +
=
−
z
n1
n2
2
2
1
1
U
U
I
R
R
ρ
−
=
n1
n2
n3
2
1
2
0
1
0
z
0
0
n2
n3
1
1
1
1
1
1
1
j
j
1
1
j
j
U
U
U
I
R
R
R
L
R
L
U
C U
C E
I
R
R
ρ
ω
ω
ω
ω
−
+
+
+
−
=
−
+
+
=
−
(
)
n3
n2
1
1
I
U
U
R
=
−
(
)
n3
n2
0
1
j
U
U
L R
ρ
ω
=
−
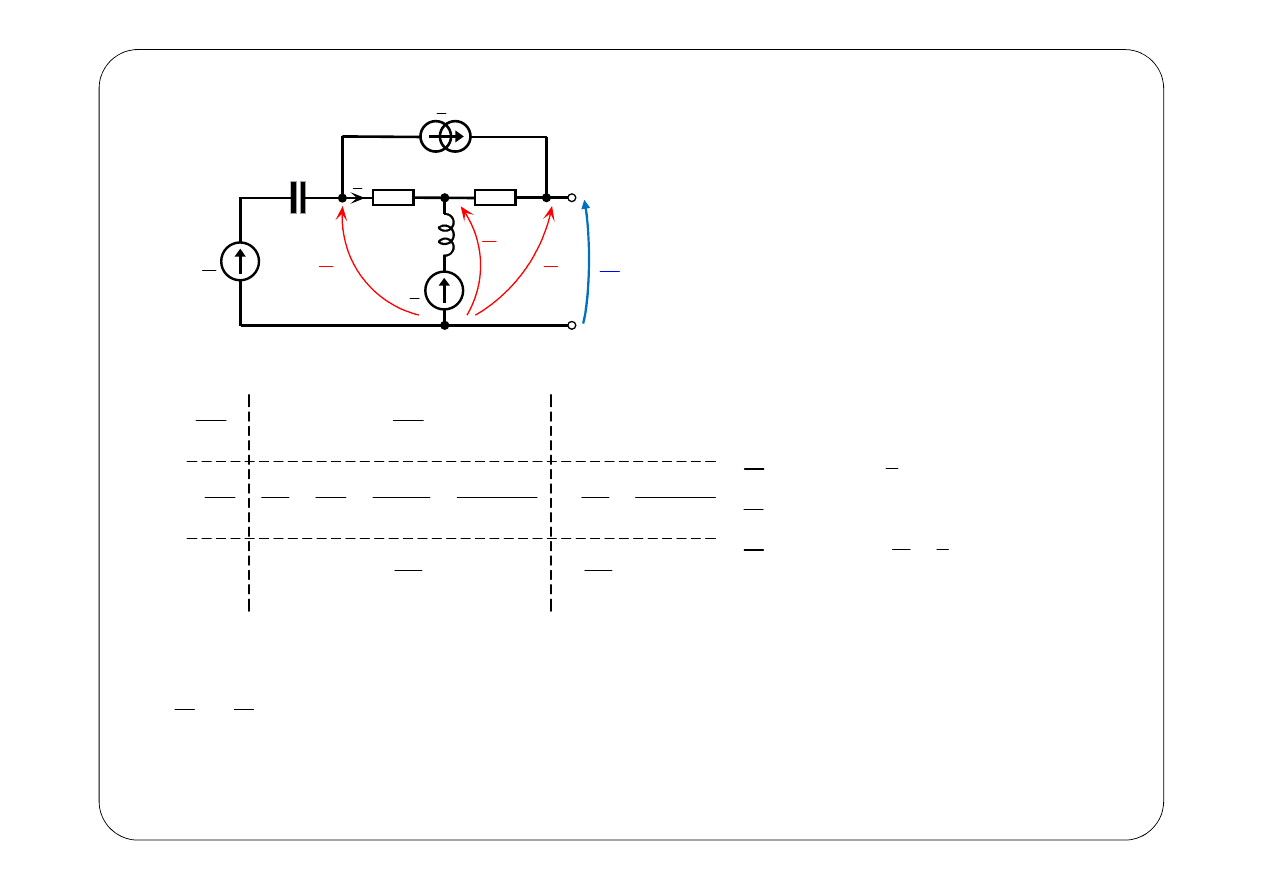
E
z
I
1
R
2
R
C
L
I
I
ρ
1
2
3
n1
U
n2
U
n3
U
2
2
1
1
0
R
R
U
I
−
0
U
2
2
z
n1
n2
2
1
2
0
0
1
1
0
1
z
0
n3
0
1
1
1
1
1
1
1
0
j
j
j
j
1
1
0
j
R
R
U
I
U
R
R
R
L
LR
R
LR
U
C E
I
C
R
R
ρ
ρ
ω
ω
ω
ω
ω
−
+
+
+
−
−
=
−
−
+
j 0,6435
0
n1
3
j4
5e
V.
U
U
=
= +
=
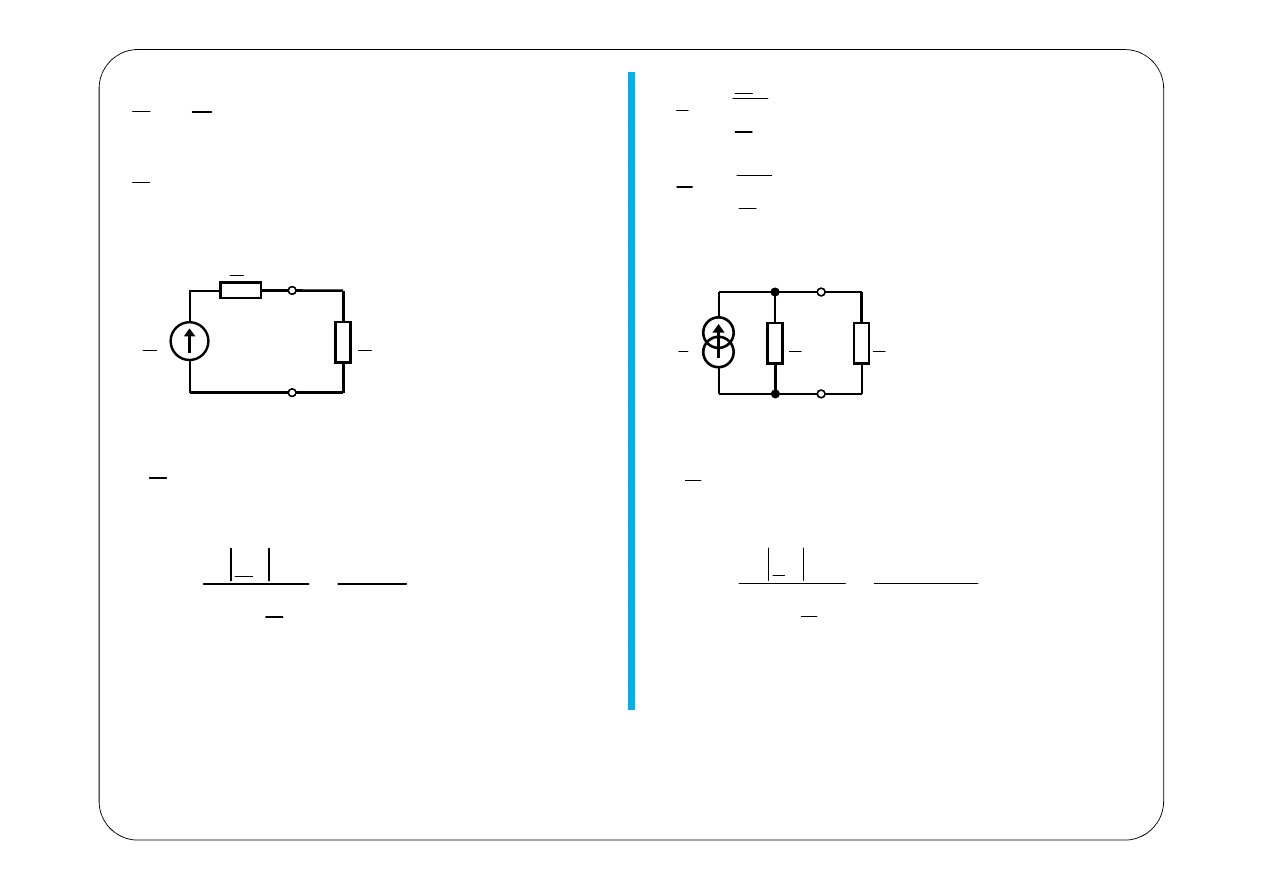
(
)
j0,6435
T
0
T
3
j4
5e
V
150
j50 Ω
E
U
Z
=
= +
=
=
+
T
E
T
Z
0
Z
j0,6055
T
N
T
0,026
j0,018
0,03162e
E
I
Z
=
=
+
=
(
)
3
N
T
1
6
j2 10 S
Y
Z
−
=
= −
⋅
N
I
N
Y
0
Y
(
)
0
150
j50
Z
=
−
Ω
{ }
2
2
T
3
max
T
5
41,6 10 W.
4 Re
4 150
E
P
Z
−
=
=
=
⋅
⋅
(
)
3
0
6
j2 10 S
Y
−
= +
⋅
{ }
2
2
N
3
max
3
N
0,03162
41,6 10 W.
4 Re
4 6 10
I
P
Y
−
−
=
=
=
⋅
⋅ ⋅
Wyszukiwarka
Podobne podstrony:
Zastosowanie metody problemowej w nauczaniu
Biznes plan, Biznes plan - hotel Hellena, III Analiz? strategiczn? firmy przeprowadzono przy zastoso
67 PNF – omów zasady i zastosowanie metody
NI 4 ZASTOSOWANIE METODY POZOSTAŁOŚCIOWEJ
Zastosowane metody statystyczne przykładowy wzorzec
Przykłady praktycznego zastosowania metody Bobath, 23.09.2016
Zestaw zabaw z zastosowaniem metody Weroniki Sherborne
zabawy ruchowe, Scenariusze zajęcia z zastosowaniem metody twórczej R, Scenariusze zajęcia z zastoso
Scenariusze zaj z zastosowaniem metody twórczej R.Labana, ćwiczenia i zabawy gimnastyczne
ZASTOSOWANIE METODY Kwadrant EKO-System w gosp. komunalnej, Inżynieria środowiska, EM- Ekologia
ZASTOSOWANIE METODY OWAS DO OCENY ZAGROE ZDROWOTNYCH DLA WYBRANYCH STANOWISK ROBOCZYCH OWAS
Optymalizacja wykorzystania zasobów przy zastosowaniu metody graficznej programowania liniowegox
Możliwość zastosowania metody biograficznej w pracy z człowiekiem dorosłym, andragogika
Komunikacja rynkowa ?finicja i zastosowanie metody GRP
Możliwości zastosowania metody PNF i kinesiotapingu w leczeniu młodzieńczej kifozy piersiowej ppt
więcej podobnych podstron