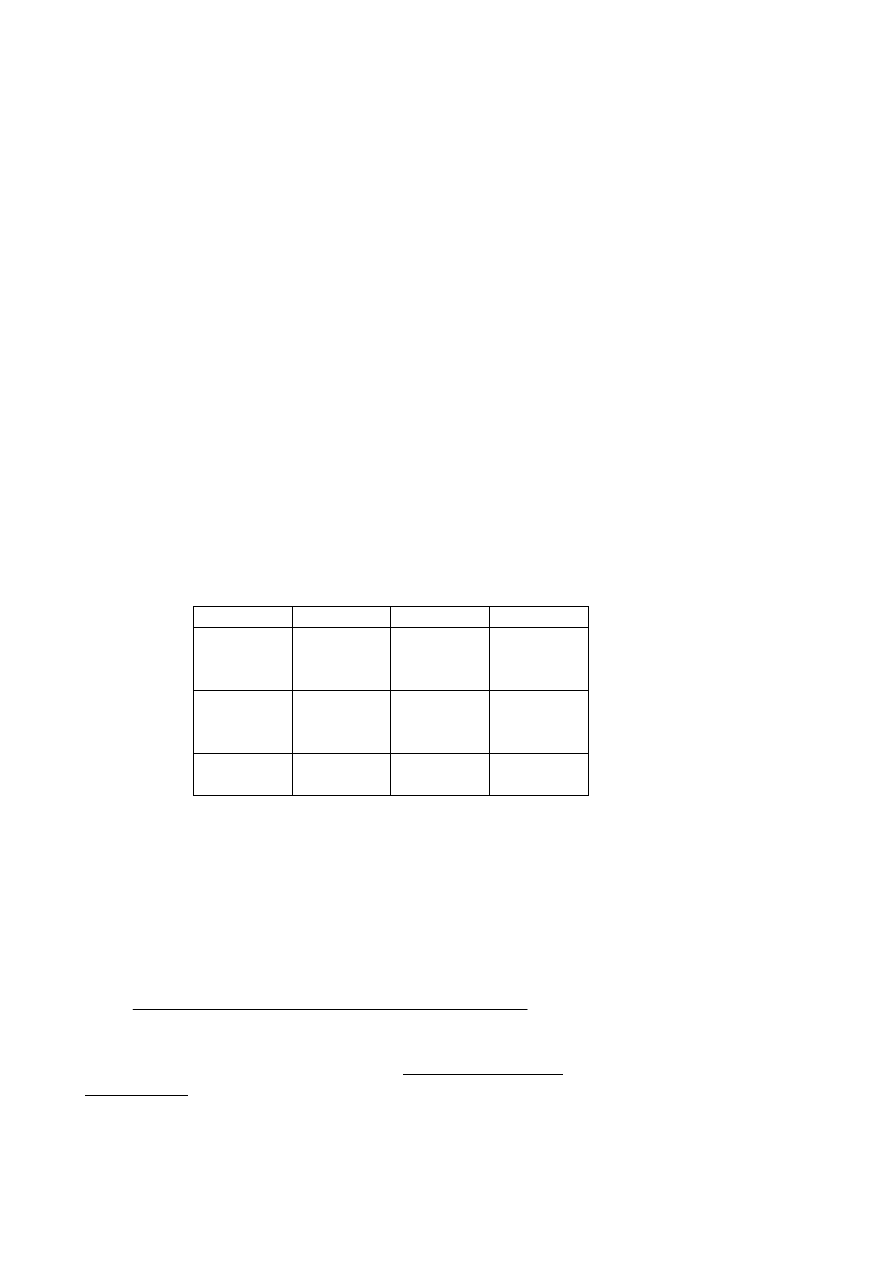
Test χ
2
(test niezależności dwóch zmiennych nominalnych)
Mamy dwie zmienne nominalne: X o w-kategoriach wartości i Y o k-kategoriach wartości.
Dane z n-elementowej próby mają postać dwudzielnej tablicy frekwencji (o w wierszach i k
kolumnach). Przy założeniu, że X i Y są niezależne w populacji, prawdopodobieństwo jednoczesnej
realizacji kategorii ‘i’ zmiennej X oraz kategorii ‘j’ zmiennej Y (dla i = 1,2…w, j = 1,2…,k)
wynosi:
P
ij
= P(X = i, Y = j) = P(X=i)*P(Y=j).
Zatem każdej parze kategorii zmiennej (X, Y), poza frekwencją otrzymaną w badaniu (f
o
) można
przyporządkować frekwencję oczekiwaną (f
e
) przy założeniu, że hipoteza zerowa jest prawdziwa.
Problem: Czy w populacji młodzieży akademickiej istnieje zależność pomiędzy zadowoleniem z
własnych osiągnięć a umiejscowieniem poczucia kontroli?
Mamy dwie zmienne nominalne, każda z ma dwie kategorie: zadowolenie z własnych osiągnięć →
zadowolony i niezadowolony; umiejscowienie poczucia kontroli → zewnątrzsterowni i
wewnątrzsterowni. Zależność pomiędzy zmiennymi nominalnymi nazywamy kontyngencją.
H
0
: zadowolenie z osiągnięć i umiejscowienie kontroli są niezależne
H
1
: ~H
0
Zbadaliśmy n = 200 osób, a ich wyniki rozłożyły się w następujący sposób w tabeli o liczbie
wierszy w = 2 i liczbie kolumn k = 2, czyli w tabeli 2x2, czteropolowej:
Zadow.
Niezadow.
Σ
Zewnątrz
a
(40)
30
b
(40)
50
a+b
= 80
Wewnątrz
c
(60)
70
d
(60)
50
c+d
= 120
Σ
a+c
=
100
b+d
=
100
n = 200
Weryfikacja hipotezy zerowej: porównanie frekwencji oczekiwanych (f
e
) i otrzymanych (f
o
).
Jak wyglądałyby frekwencje w poszczególnych kratkach, gdyby zmienne były niezależne – czyli
gdyby była prawdziwa hipoteza zerowa.
W tym celu obliczamy frekwencje oczekiwane – f
e
dla każdej kratki w tabeli:
n
kratki
danej
dla
brzegowych
sum
iloczyn
f
i
e
_
_
_
_
_
=
A następnie sprawdzamy, na ile frekwencje otrzymane w badaniu różnią się od frekwencji
oczekiwanych przy braku zależności pomiędzy zmiennymi. Dla każdej kratki w tabeli obliczamy
kwadratowe odległości pomiędzy frekwencjami otrzymanymi (f
o
) i oczekiwanymi (fe),
zrelatywizowane do wielkości frekwencji oczekiwanej (żeby nie nadważyć dużych kategorii).
∑
=
−
=
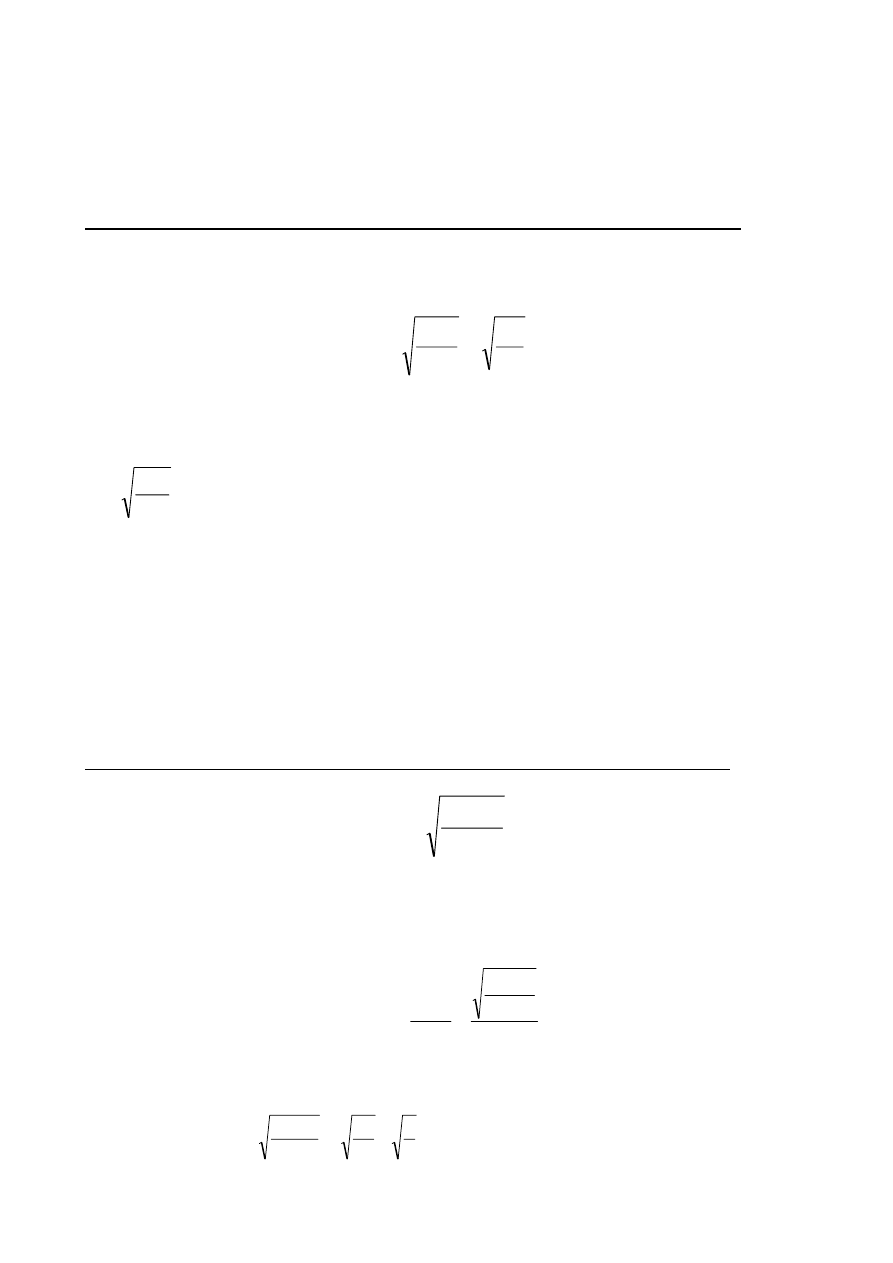
k
i
ei
ei
oi
f
f
f
1
2
2
)
(
χ
Dla naszego przykładu:
34
,
8
67
,
1
67
,
1
5
,
2
5
,
2
60
)
60
50
(
60
)
60
70
(
40
)
40
50
(
40
)
40
30
(
2
2
2
2
2
=
+
+
+
=
−
+
−
+
−
+
−
=
χ
Otrzymaną wartość porównujemy z wartością krytyczną dla danych stopni swobody:
df = (w-1) · (k-1)
gdzie k – liczba kolumn, w – liczba wierszy w tabeli (stopnie swobody zależą więc od ilości
poziomów zmiennych – ilości kratek w tabeli dwudzielnej).
Jeżeli
Æ H
2
,
2
df
α
χ
χ
>
0
odrzucamy (przy przyjętym poziomie istotności
α)
Jeżeli
Æ nie ma podstaw do odrzucenia H
2
,
2
df
α
χ
χ
≤
0
W naszym przykładzie:
df = (2-1) · (2-1) = 1
Wartość krytyczna testu χ
2
dla α = 0,05 wynosi 3,841 (
) (por. tabela C w podręczniku
F& T: wartości krytyczne chi-kwadrat).
841
,
3
2
3
,
05
,
0
=
χ
8,34 > od wartości krytycznej Æ H
0
odrzucamy.
W populacji młodzieży akademickiej istnieje związek pomiędzy umiejscowieniem poczucia
kontroli a zadowoleniem z własnych osiągnięć.
Względem jakiego rozkładu porównujemy wartość statystyki chi-kwadrat?
ZMIENNA O ROZKŁADZIE χ
2
Weźmy k zmiennych losowych, z
1
, z
2
, z
3
, … z
k
. Każda z nich ma rozkład normalny o średniej
równej zero i odchyleniu standardowym równym 1 (zmienne normalne wystandaryzowane: Z
i
Æ
N(0; 1)). Niech zmienne te będą nieskorelowane. Rozkład zmiennej Y
(k)
będącej sumą kwadratów k
zmiennych z
i
nazywamy rozkładem χ
2
o k stopniach swobody. Każdą zmienną mającą taki rozkład
będziemy nazywać zmienną o rozkładzie χ
2
i k stopniach swobody.
Y
(k)
=
∑
=
k
i
i
z
1
2
Przebieg funkcji gęstości prawdopodobieństwa zmiennej o takim rozkładzie zależy tylko od
jednego parametru – liczby stopni swobody k; μ = k, σ
2
= 2k. Funkcja gęstości rozkładu χ
2
jest
bardzo asymetryczna dla małych wartości k. W miarę wzrostu k asymetria rozkładu maleje i
rozkład chi-kwadrat upadania się do rozkładu normalnego (w praktyce dla k > 30 dystrybuanta
zmiennej o rozkładzie χ
2
jest dostatecznie podobna do dystrybuanty zmiennej o odpowiednim
rozkładzie normalnym, by je utożsamić i traktować jedną jako przybliżenie drugiej).
Statystyka testu χ
2
ma asymptotyczny rozkład χ
2
z df = (w-1) · (k-1) – co oznacza, że w miarę
wzrostu n, rozkład statystyki testu zbliża się do rozkładu χ
2
, im n większe, tym większa bliskość.
Testem chi-kwadrat weryfikujemy hipotezę zerową o niezależności dwóch zmiennych
nominalnych. W przypadku odrzucenia H
0
możemy ocenić siłę tej zależności przy pomocy
współczynników kontyngencji.
MIARY KONTYNGENCJI
Współczynnik kontyngencji dla tabeli 2x2 (czteropolowej) – współczynnik φ – Yule’a
Jest to pierwiastek z ilorazu danej wartości chi-kwadrat przez maksymalne chi-kwadrat, które dla
tabeli 2x2 wynosi tyle, ile n.
n
2
2
max
2
χ
χ
χ
ϕ
=
=
Tak obliczony współczynnik przyjmuje wartości z zakresu <0;1>.
Dla naszego przykładu:
204
,
0
200
3
,
8
=
=
ϕ
Współczynnik kontyngencji φ jest tożsamy z współczynnikiem korelacji r-Pearsona. Zatem także
przypadku dychotomicznych skal nominalnych możemy operować pojęciem zróżnicowania
wyjaśnionego i niewyjaśnionego.
φ
2
– część całkowitego zróżnicowania zmiennej Y wyjaśniona przez zmienność zmiennej X
(dla naszego przykładu φ
2
= (0,204)
2
= 0,04; 4% zmienności X jest wyjaśniona przez Y). φ Yule’a
osiąga wartość max = 1 tylko gdy rozkłady brzegowe frekwencji odpowiadają sobie, czyli gdy
niezerowe frekwencje układają się na jednej z przekątnych tabeli (na drugiej mamy zera), co zdarza
się niezwykle rzadko, mimo tego NIE KORYGUJEMY WARTOŚCI φ, gdyż poprawka
utrudnia interpretację wskaźnika (poprawka jest niewrażliwa na różnice rozkładów zmiennych).
Współczynnik kontyngencji dla wszystkich innych tabel – współczynnik C-Pearsona
n
C
+
=
2
2
χ
χ
Przyjmuje wartości z zakresu <0;1>, ale z definicji NIE OSIĄGA 1!!!
Z tego powodu wartość współczynnika C-Pearsona musi być ZAWSZE KORYGOWANA.
MAX
MAX
KOR
C
n
C
C
C
+
=
=
2
2
χ
χ
χ
2
max dla tabeli k x k (ilość kolumn = ilość wierszy; k ≥ 3) = (k-1)n , czyli n.p.: dla tabeli 3x3 Æ
max χ
2
= 2nÆ Cmax =
n
n
n
+
2
2
=
n
n
3
2
=
3
2
= 0,816; dla tabeli 4x4 Æ max χ
2
= 3nÆ Cmax =
n
n
n
+
3
3
=
n
n
4
3
=
4
3
= 0,866; itd. Gdy tabela jest prostokątna (w ≠ k), C
MAX
= [C
MAX
(k x k) +
C
MAX
(w x w)] / 2, np.: dla tabeli 3 x 4, C
MAX
= (0,816 + 0,866) / 2 = 1,682 / 2 = 0,841.