
POLITECHNIKA WARSZAWSKA
Wydział Elektroniki i Technik Informacyjnych
Instytut Automatyki i Informatyki Stosowanej
Zakład Sterowania i Systemów
Maciej Staniak, Tomasz Winiarski
NAWIGACJA ROBOTEM MOBILNYM
Praca magisterska wykonana
pod kierunkiem dr Jarosława Arabasa
Warszawa 2002

Pragniemy podziękować:
naszemu promotorowi
dr Jarosławowi Arabasowi
za opiekę, wyrozumiałość i miłą współpracę,
oraz dr Wojciechowi Szynkiewiczowi
za cenne wskazówki i pomoc

Spis treści
1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
Zakres pracy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
Przyczyny wyboru tematu pracy . . . . . . . . . . . . . . . . . . . . . . . . .
1
Układ pracy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
3
Tworzenie mapy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
Mapy topologiczne . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Mapy geometryczne . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Samolokalizacja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Podział podejść do problemu samolokalizacji . . . . . . . . . . . . . .
4
Metody pomiaru pozycji robota . . . . . . . . . . . . . . . . . . . . .
5
Wady metod lokalnych . . . . . . . . . . . . . . . . . . . . . . . . . .
6
Sposoby wyznaczania trajektorii
8
Metody deterministyczne . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
Metody bazujące na grafach . . . . . . . . . . . . . . . . . . . . . . .
8
Inne metody deterministyczne . . . . . . . . . . . . . . . . . . . . . .
11
Metody niedeterministyczne . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Algorytm ewolucyjny . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Symulowane wyżarzanie . . . . . . . . . . . . . . . . . . . . . . . . .
15
Metody nie wymagające mapy . . . . . . . . . . . . . . . . . . . . . . . . . .
15
Metody labiryntowe . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
Kryteria wyboru metody wyznaczania trajektorii
. . . . . . . . . . . . . . .
16
Podstawy projektowania robotów mobilnych
18
Wprowadzenie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
Baza jezdna . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
Rodzaje napędu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19

SPIS TREŚCI
ii
Podejścia do problemu sterowania . . . . . . . . . . . . . . . . . . . . . . . .
20
. . . . . . . . . . . . . . . . . . . . . . . . . . .
20
Podejście oparte na modelu . . . . . . . . . . . . . . . . . . . . . . .
20
Podejście hybrydowe . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
Podejście behawioralne . . . . . . . . . . . . . . . . . . . . . . . . . .
21
Właściwości środowiska Mindstorms
22
Środowisko sprzętowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
. . . . . . . . . . . . . . . . . . . . . . . . .
22
Główny element zestawu Mindstorms — RCX . . . . . . . . . . . . .
23
Czujniki . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
Elementy wykonawcze . . . . . . . . . . . . . . . . . . . . . . . . . .
25
Urządzenia do transmisji w podczerwieni . . . . . . . . . . . . . . . .
26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
System operacyjny legOS . . . . . . . . . . . . . . . . . . . . . . . . .
27
Programy wspomagające projektowanie robota . . . . . . . . . . . . .
30
Ogólna postać systemu wykonującego zadanie
32
Wprowadzenie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Moduł w komputerze PC . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Moduł w robocie MindStorms . . . . . . . . . . . . . . . . . . . . . . . . . .
34
35
Budowa planszy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
Wykorzystywane plansze . . . . . . . . . . . . . . . . . . . . . . . . .
38
Budowa robota . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
. . . . . . . . . . . . . . . . . . . . . . . . .
39
Baza jezdna . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
Układ napędowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
Zastosowane czujniki . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
Urządzenie nadawczo-odbiorcze w podczerwieni . . . . . . . . . . . .
49
50
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
Architektura programu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51

SPIS TREŚCI
iii
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
Trudności związane z umieszczeniem fug na zewnątrz pojazdu . . . .
56
Sposób sterowania silnikami . . . . . . . . . . . . . . . . . . . . . . .
59
. . . . . . . . . . . . . . . . . . . . . . .
60
Warstwa nadzoru . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
Model środowiska i robota . . . . . . . . . . . . . . . . . . . . . . . .
61
Opis automatu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
Mechanizmy komunikacji i synchronizacji międzywarstwowej . . . . . . . . .
64
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
Pierwsza transmisja . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
Implementacja mechanizmów komunikacji
. . . . . . . . . . . . . . .
68
Moduł aktualizacji mapy . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
69
Moduł przetwarzania trajektorii . . . . . . . . . . . . . . . . . . . . . . . . .
69
Właściwości trajektorii przesyłanej z komputera PC . . . . . . . . . .
69
Definicja jak najwierniejszego wykonania założonej trajektorii . . . .
70
Użyte struktury danych i zmienne sterujące
. . . . . . . . . . . . . .
71
Architektura modułu . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
Etap wyznaczania wektora manewrów
. . . . . . . . . . . . . . . . .
73
Etap przebudowy trajektorii i aktualizacji zmiennych sterujących
. .
78
Modyfikacje jądra systemu legOS . . . . . . . . . . . . . . . . . . . . . . . .
81
Cel przeprowadzonych zmian . . . . . . . . . . . . . . . . . . . . . . .
81
Odczyt barwy podłoża za pomocą osobno podłączonego czujnika światła 82
Odczyt barwy podłoża i obsługa odometrii dla czujnika światła i czuj-
nika odometrycznego podłączonych wspólnie do jednego wejścia RCX
82
Wyznaczanie trajektorii algorytmem ewolucyjnym
84
Opis algorytmu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
84
Reprezentacja rozwiązania . . . . . . . . . . . . . . . . . . . . . . . .
84
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
Operatory genetyczne . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
. . . . . . . . . . . . . . . . . . . . . . . . .
87
. . . . . . . . . . . . . . . . . . . . . . . . . . .
89
Sukcesja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
Uwagi na temat kodowania osobników
. . . . . . . . . . . . . . . . . . . . .
90
Rola zasięgu mutacji pozycji węzła . . . . . . . . . . . . . . . . . . .
90
Rola mutacji sposobu łączenia węzłów
. . . . . . . . . . . . . . . . .
90
Dobór parametrów algorytmu ewolucyjnego
. . . . . . . . . . . . . . . . . .
93

SPIS TREŚCI
iv
Ustalenie zasięgu mutacji . . . . . . . . . . . . . . . . . . . . . . . . .
93
. . . . . . . . . . . . . . . . . . . . . . . . . . .
97
Wybór metody reprodukcji . . . . . . . . . . . . . . . . . . . . . . . .
98
Testowanie zdolności omijania minimów lokalnych przez algorytm ewolucyjny 100
Wnioski z symulacji . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
10 Wyznaczanie trajektorii algorytmem deterministycznym
102
10.1 Model matematyczny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
10.2 Opis algorytmu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
11 Porównanie algorytmów: ewolucyjnego i deterministycznego
108
11.1 Symulacje systemu nawigacyjnego . . . . . . . . . . . . . . . . . . . . . . . . 108
11.1.1 Symulacje współdziałania algorytmu wyznaczającego ścieżkę z algo-
rytmem omijania przeszkód . . . . . . . . . . . . . . . . . . . . . . . 108
11.1.2 Badanie wpływu parametrów otoczenia . . . . . . . . . . . . . . . . . 111
11.2 Porównanie właściwości algorytmu ewolucyjnego i A* . . . . . . . . . . . . . 112
11.2.1 Badanie złożoności obliczeniowej
. . . . . . . . . . . . . . . . . . . . 112
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
11.3 Porównanie właściwości algorytmu ewolucyjnego i A* dla metryki czasowej . 117
11.3.1 Badanie złożoności obliczeniowej
. . . . . . . . . . . . . . . . . . . . 118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
121
125

Rozdział 1
Wstęp
Robot mobilny jest typem robota posiadającym zdolności lokomocyjne [19]. Jak każdy inny
robot potrafi wykonać konkretne zadanie dla niego przeznaczone. Wybór rodzaju zadania i
środowiska, w którym zostanie ono wykonane, implikuje konstrukcję robota i program nim
sterujący. Typowym zadaniem przed którym staje wiele konstruowanych robotów mobil-
nych jest nawigacja. Pokonanie danej trasy może oznaczać przejechanie jej na lądzie, lub
przepłynięcie, jeżeli będzie to środowisko wodne.
1.1
Cel pracy
Celem pracy jest weryfikacja eksperymentalna właściwości algorytmów ewolucyjnego i deter-
ministycznego wykorzystywanych do wyznaczania trajektorii optymalnej robota mobilnego
w środowisku zmiennym w czasie.
1.2
Zakres pracy
Zakresem niniejszej pracy jest nawigowanie robotem mobilnym w środowisku zmiennym
w czasie. Zadanie, które przed nim stawiamy będzie więc polegało na pokonaniu ścieżki
od jednego założonego punktu do drugiego, z ominięciem nieznanych wcześniej przeszkód.
Trajektoria zostanie wyznaczona za pomocą algorytmów ewolucyjnego i deterministycznego.
Robot mobilny, zbudowany w oparciu o zestaw Lego Mindstorms, będzie poruszał się po
planszy składającej się z kwadratowych kafelków.
1.3
Przyczyny wyboru tematu pracy
Wyznaczanie optymalnej trajektorii jest jednym z głównych zadań nawigacji. Powszechne w
robotyce jest wykorzystanie do tego celu metod sieciowych takich jak np. graf widoczności

ROZDZIAŁ 1. WSTĘP
2
[12]. Metody te umożliwiają robotowi uniknięcie przeszkód, natomiast nie dają możliwo-
ści uwzględnienia kosztu przejazdu przez dany obszar. Do znajdywania optymalnej ścieżki
w anizotorpowym środowisku używane są w praktyce deterministyczne algorytmy przeszu-
kiwania przestrzeni (jak np. A*). Jednak są propozycje, by optymalną ścieżkę wyznaczać
algorytmem ewolucyjnym [11] [12]. Istotne jest więc porównanie obu rodzaju algorytmów,
po to by sprawdzić, który lepiej nadaje się do wyznaczenia optymalnej trajektorii.
1.4
Układ pracy
Kolejny (drugi) rozdział będzie poświęcony teorii nawigacji. Rozdział trzeci jest rozwinięciem
jednego z aspektów nawigacji — wyznaczania trajektorii. Zawiera on przegląd stosowanych
metod. Stanowi on też ustosunkowanie się do wcześniejszych badań poświęconych algoryt-
mom ewolucyjnym. Rozdział czwarty opisuje metody sterowania robotami w aspekcie podejść
do problemu sterowania i organizacji struktury programu robota. W dalszej części (rozdział
piąty) opisane zostaną możliwości i ograniczenia robota budowanego z zestawu Mindstorms.
Kolejne rozdziały zostaną poświęcone zbudowanemu systemowi eksperymentalnemu, skła-
dającemu się z komputera PC, robota i planszy. Rozdział szósty zawiera krótki, całościowy
opis tego systemu. Rozdział siódmy traktuje o budowie planszy i robota, a ósmy o programie
robota. Rozdział dziewiąty prezentuje wykorzystywany algorytm ewolucyjny. Zaimplemen-
towany algorytm deterministyczny opisany zostanie w rozdziale dziesiątym. W rozdziale
jedenastym zostaną przedstawione symulacje ilustrujące współdziałanie algorytmów ewolu-
cyjnego i deterministycznego przy wyznaczaniu trajektorii robota mobilnego, a następnie
oba te algorytmy zostaną porównane.
Pracę zakończą podsumowanie i wnioski.

Rozdział 2
Problem nawigacji
Rozwiązanie problemu zaczniemy od definicji nawigacji:
Nawigacja (łac. navigatio - żegluga; navis - statek) to nauka traktująca o prowadzenia
statku wodnego albo latającego, metod określania jego pozycji i wyboru kursu [17].
Mimo że nazwa odnosiła się pierwotnie do okrętów, odnosi się obecnie także do obiektów
latających i pojazdów mechanicznych a w szczególności robotów mobilnych. Elementami
składowymi nawigacji robotów są:
• tworzenie mapy,
• samolokalizacja,
• wyznaczanie trajektorii.
Elementy te są od siebie niezależne, ale wykonanie zadania zależy od prawidłowego wyko-
nania każdego z nich. Zostaną one pokrótce omówione, by można było potem skonkretyzować
zadanie i wybrać odpowiednie środowisko pracy dla robota.
2.1
Tworzenie mapy
Dzięki mapie robot potrafi efektywnie planować trajektorie czy też samolokalizować się w
środowisku, w którym się porusza. Zasadniczo wyróżnia się trzy rodzaje map [15].
• topologiczne,
• geometryczne,
• hybrydowe - będące połączeniem dwóch powyższych rodzajów map.

ROZDZIAŁ 2. PROBLEM NAWIGACJI
4
2.1.1
Mapy topologiczne
Mapy topologiczne budowane są jako grafy, których węzły są pewnymi obiektami występują-
cymi w środowisku, a łuki relacjami przyległości pomiędzy tymi obiektami. Mapa topologicz-
na nie musi zawierać informacji o rozmiarach obiektów czy też odległościach pomiędzy nimi.
Człowiek, poruszając się w terenie, opiera się tak naprawdę na mapie topologicznej, gdyż
pamięta jakie obiekty ze sobą sąsiadują, nie znając często ich rozmiarów. Mapa taka okazuje
się w wielu przypadkach wystarczającą, ale jej interpretacja jest bardzo skomplikowana. Jej
niewątpliwą zaletą jest agregacja informacji, a wadą niejednokrotny brak istotnych danych
szczegółowych, takich jak odległości.
Łuki grafu mapy topologicznej mogą być tworzenie w oparciu o grafy widoczności i diagra-
my Voronoi. Metody te nie zostaną zaprezentowane, gdyż wykraczają poza zakres niniejszej
pracy. Ich opis znajduje się między innymi w [15].
2.1.2
Mapy geometryczne
Mapy geometryczne zawierają informację o bezwzględnych relacjach, takich jak odległość
i rozmiar, pomiędzy występującymi w środowisku obiektami. Najczęstszą realizacją takiej
mapy jest siatka zajętości. Rozmiar poszczególnych pól siatki, a także odległości pomiędzy
nimi są przeskalowanymi relacjami z rzeczywistego środowiska. Siatka zajętości jest łatwa w
interpretacji ale wymaga dużych zasobów pamięciowych. Powstaje ona dzięki interpretacji
odczytów z czujników robota w sytuacji jednoznacznego wyznaczenia jego pozycji dzięki
skorygowanym odczytom z czujników odometrycznych czy też triangulacji.
Mapa geometryczna znalazła zastosowanie w zbudowanym systemie nawigacyjnym, któ-
rego opis zaczyna się począwszy od pkt. 6.
2.2
Samolokalizacja
Samolokalizacja robota jest to określenie pozycji robota w danym układzie odniesienia. Po-
zycja ta jest estymowana na podstawie danych — modelu środowiska w postaci mapy geo-
metrycznej lub mapy topologicznej (przechowywanych w pamięci robota) i obserwacji (z
czujników).
2.2.1
Podział podejść do problemu samolokalizacji
Można wyróżnić trzy sposoby klasyfikacji metod samolokalizacji [16]:

ROZDZIAŁ 2. PROBLEM NAWIGACJI
5
a) metody lokalne i globalne
- metody lokalne — polegają na tym, że pozycja robota obliczana jest na podstawie
jego pozycji poprzedniej; są one dość efektywne i dokładne, jednak na ograniczonym
obszarze (co wynika z sumowania się błędów);
- metody globalne — wyznaczenie pozycji robota wykonywane jest bez znajomości jego
poprzedniej pozycji; metody te mają dużo większą złożoność obliczeniową, lecz nie
zachodzi zjawisko kumulacji błędów estymacji położenia;
b) związane ze środowiskiem statycznym i dynamicznym
- środowisko statyczne to takie, w którym porusza się tylko robot lub czujniki robota
nie potrafią wykryć ruchu innych obiektów;
- środowisko dynamiczne to takie, w którym inne obiekty poza robotem są ruchome i
robot potrafi wykryć ten ruch;
c) metody bierne i aktywne
- metody bierne to takie, kiedy robot nie wykonuje dodatkowych ruchów, ani nie steruje
czujnikami w celu wyznaczenia swojego położenia;
- metody aktywne to takie, gdy robot musi się przemieścić, by określić swoje położenie.
2.2.2
Metody pomiaru pozycji robota
a) względne
- metody odometryczne — polegają na obliczaniu względnego przemieszczenia pojazdu
na podstawie pomiaru kąta obrotu kół napędowych (wałów silników);
- metody inercyjne — polegają na wykorzystaniu żyroskopów i akcelerometrów do po-
miaru prędkości i przyspieszenia (pozycję uzyskuje się przez całkowanie);
b) bezwzględne
- aktywne latarnie kierunkowe — wyznaczanie pozycji na podstawie sygnałów wysyła-
nych przez trzy lub więcej nadajniki o znanych położeniach; jeśli określana jest odle-
głość od źródła jest to triatelacja, gdy kąty między nimi - triangulacja;
- rozpoznawanie sztucznych lub naturalnych znaczników — wyznaczanie pozycji na pod-
stawie znaczników, których pozycje zna robot;

ROZDZIAŁ 2. PROBLEM NAWIGACJI
6
- dopasowanie modelu — dane z czujników porównywane są z mapą terenu i na tej
podstawie wyznaczana jest pozycja robota.
2.2.3
Wady metod lokalnych
Przedstawione wcześniej metody samolokalizacji wskazują na zależności między środowi-
skiem a możliwościami technicznymi robota. Zostaną teraz opisane wady odometrii (która
jest najbardziej wyrafinowaną metodą jaką można zastosować korzystając z robota, któ-
ry wykonuje zadanie) i algorytm markowskiej lokalizacji, wykorzystywany przy względnym
pomiarze pozycji.
a) błędy w odometrii
- systematyczne (ciągła kumulacja) — nierówne średnice kół, rzeczywiste średnice kół są
różne od podanych wartości nominalnych, rzeczywisty rozstaw kół różni się od nominal-
nego, niewspółosiowość kół, skończona rozdzielczość enkodera, skończona częstotliwość
próbkowania enkodera;
- niesystematyczne (pojawiają się przypadkowo) — ruch po nierównym podłożu, ślizga-
nie się (śliskie podłoże, gwałtowne przyspieszanie lub skręcanie, interakcje z innymi
obiektami, powierzchniowy kontakt koła z podłożem);
Tak więc sama odometria nie jest wystarczająca przy lokalizacji robota. Przyczyną tego
są kumulujące się błędy. Oznacza to, że pozycja wyznaczona przez robota po jakimś czasie
może się diametralnie różnić od faktycznej.
b) algorytm lokalizacji markowskiej
Pewnym rozwiązaniem problemu kumulacji błędów w odometrii może być opisanie pozycji
robota rozkładem prawdopodobieństwa i z tego korzysta wspomniany algorytm markowskiej
lokalizacji. Poziom zaufania pozycji robota może być wtedy opisany wzorem:
P (L
t
= l) =
P (s
t
|l)P (L
t
= l|L
t−1
, a
t−1
)
P (s
t
|L
t
)
(2.1)
gdzie:
P (L
t
= l) - prawdopodobieństwo, że w chwili t robot znajduje się w pozycji l;
L
t
- zmienna losowa reprezentująca pozycję robota w chwili t;
S
i
- zmienna losowa reprezentująca pomiar zewnętrzny w dyskretnej chwili i;
A
i
- zmienna losowa reprezentująca działanie - pomiar wewnętrzny (czujniki odometryczne)
w dyskretnej chwili i;

ROZDZIAŁ 2. PROBLEM NAWIGACJI
7
Mimo markowskiego założenia, że pozycja robota zależna jest tylko od położenia poprzed-
niego i wykonanej akcji wystarcza to, aby pozycja robota coraz bardziej się rozmywała, gdyż:
P (L
t
= l|L
t−1
, a
t−1
) =
X
l
0
P (L
t
= l|L
t−1
= l
0
, a)P (L
t−1
= l
0
)
(2.2)
Dzieje się tak dlatego, gdyż prawdopodobieństwo P (L
t
= l) wyznaczane jest rekuren-
cyjnie w zależności od chwili poprzedniej. Tak więc rozkład Diraca opisujący początkową
pozycję robota (dokładnie znaną) - zmieni się po pewnym skończonym czasie (ze względu
na skończoną rozdzielczość reprezentacji liczb - teoretycznie powinno to nastąpić w nieskoń-
czoności) w rozkład jednostajny (całkowicie nieznana pozycja robota).
Przytoczone zostały przykłady względnego pomiaru pozycji robota i algorytmu wykorzy-
stującego względne informacje na temat pozycji robota (zmiany tej pozycji). Przedstawione
zostały ich wady, które wykluczają wyłączne zastosowanie ich do lokalizacji robota. Analo-
giczne wady mają inne metody lokalizacji względnej - a ich podstawą jest kumulacja błędów
pomiarowych. Wady metod lokalnych zostały uwzględnione w charakterystyce środowiska.

Rozdział 3
Sposoby wyznaczania trajektorii
Metoda użyta do wyznaczenia trajektorii zależy przede wszystkim od reprezentacji mapy
i holonomiczności bądź nieholonomiczności robota. Planery trajektorii można podzielić na
deterministyczne i niedeterministyczne. Ich szczególnym rodzajem są planery, które możemy
stosować w sytuacji, kiedy mapa środowiska jest nieznana, a końcowy punkt trajektorii
można zidentyfikować jedynie w jego bezpośrednim sąsiedztwie.
3.1
Metody deterministyczne
Metody deterministyczne wyznaczają trajektorię według ściśle określonego, deterministycz-
nego algorytmu.
3.1.1
Metody bazujące na grafach
W praktyce większość metod deterministycznych operuje na grafach. Wśród nich są takie,
które zostały zdefiniowane, jako strategie przeszukujące grafy. Ich charakterystyczną cechą
jest przyrostowy sposób generowania trajektorii; począwszy od stanu początkowego, a skoń-
czywszy na stanie terminalnym. Metody grafowe opisuje następujący model:
Model: hS, A, s
0
, T i
S - przestrzeń (zbiór) stanów. Pojedynczy stan może być utożsamiany z polem mapy wraz
z drogą do niego prowadzącą;
A - zbiór operatorów (akcji) (A : S 7−→ S);
s
0
- stan początkowy (s
0
∈ S);
T - zbiór stanów końcowych (terminalnych) (s
t
∈ T, T ⊂ S);
Strategie przeszukujące grafy można charakteryzować przez pojęcia zupełności i opty-
malności:

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
9
• Strategia jest zupełna, jeśli potrafi znaleźć drogę z s
0
do s
t
(jeśli taka istnieje).
• Strategia jest optymalna, jeśli potrafi znaleźć optymalną drogę z s
0
do s
t
.
Strategie różnią się również złożonością czasową i zajętością pamięci, zależnych od para-
metrów drzewa tworzonego podczas przeszukiwania:
b - współczynnik rozgałęzienia (średnia ilość dostępnych stanów następnych z danego sta-
nu),
d - głębokość najlepszego rozwiązania,
m - maksymalna głębokość drzewa.
Strategie niepoinformowane
Strategie niepoinformowane są algorytmami, które nie wykorzystują informacji o koszcie wy-
konania akcji w danym stanie (przejścia z tego stanu do następnego) podczas przeszukiwania
przestrzeni. Co najwyżej mogą uwzględnić łączny koszt wykonania ciągu akcji prowadzących
do stanu końcowego. Optymalny jest ciąg akcji o najmniejszym koszcie (w zadaniu wyzna-
czania trajektorii jest to ścieżka optymalna). Ponieważ strategie te nie wymagają informacji
o koszcie wykonania akcji, nadają się do przeszukiwań, w których interesujące jest znalezie-
nie dowolnego ciągu akcji prowadzącego do stanu końcowego (przykładem jest automatyczne
dowodzenie twierdzeń).
Strategie niepoinformowane działają według następującego algorytmu:
1. Utwórz listy L
o
(stanów otwartych) i L
z
(stanów zamkniętych);
wpisz s
0
do L
o
;
2. Rozwiń pierwszy stan z L
o
w sekwencję S
i
i przesuń go do L
z
;
Usuń z S
i
stany obecne w L
z
tworząc S
0
i
;
3. Jeśli s
t
∈ S
0
i
- STOP;
Jeśli nie - dopisz S
0
i
do L
o
i skocz do 2;
Poszczególne realizację różnią się postacią punktu 3 algorytmu.
przeszukiwanie wszerz -S
0
i
dodawane jest na końcu L
o
. Metoda ta jest optymalna
i zupełna. Jej złożoność czasowa wynosi - b
d
, a złożoność przestrzenna - b
d
. Na mapie
geometrycznej przeszukwianie wszerz bywa realizowane pod postacią algorytmu fali
(pożarowego).
przeszukiwanie w głąb - S
0
i
dodawane jest na początku L
o
. Metoda ta jest nieopty-
malna i niezupełna. Jej złożoność czasowa wynosi - b
m
, a złożoność przestrzenna jest
dalece mniejsza niż dla przeszukiwania wszerz i wynosi - bm

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
10
Strategie z informacją lokalną
Strategie z informacją lokalną opierają się na założeniu, że znany jest koszt wykonania danej
akcji w danym stanie, czyli przejścia ze stanu bieżącego do następnego.
Załóżmy, że:
s
∗
- lokalnie wybierany stan,
c(s
i
, s
0
i+1
), c(s
i
, s
00
i+1
)... to koszty przejścia z s
i
do s
0
i+1
, s
00
i+1
..., gdzie s
0
i+1
, s
00
i+1
... alternatywne
stany następne.
g(s
n
) = (s
0
, s
n
) to koszt przejścia ze stanu początkowego do bieżącego,
G
i
- zbiór kosztów g(s
0
, s
n
) dla wszystkich dotychczas rozwijanych stanów w i-tej iteracji
algorytmu.
Poniżej opisane zostaną dwie popularne realizacje strategii z informacją lokalną:
strategia wspinaczkowa (zachłanna) - W strategii tej rozwijane są stany o naj-
mniejszym koszcie ich osiągnięcia ze stanu poprzedniego. Ilustruje to algorytm:
1. i:=0;
2. Rozwiń stan s
i
i oblicz c(s
i
, s
0
i+1
), c(s
i
, s
00
i+1
), ...;
3. Wybierz stan s
∗
o najmniejszym koszcie c,
gdzie s
∗
jest jednym ze stanów s
0
i+1
, s
00
i+1
4. Jeśli s
∗
= s
t
to STOP; jeśli nie - i:=i+1 oraz skok do 2;
Metoda ta jest nieoptymalna i niezupełna. Jej zaletą jest prostota i mała złożoność
czasowa - bd i przestrzenna - bd.
strategia pierwszy najtańszy - Jest analogiczna do opisanej powyżej, z tą różnicą,
że uwzględniany jest koszt osiągnięcia rozwijanego stanu począwszy od stanu począt-
kowego. Ilustruje to algorytm:
1. i:=0, G
0
:= φ;
2. Rozwiń s
i
i wylicz G
∗
:= g(s
0
i+1
), g(s
00
i+1
), ...;
3. G
i
:= G
i
∪ G
∗
;
4. Wybierz na podstawie G
i
stan s
∗
o najmniejszym koszcie
jeśli s
∗
= s
t
to STOP;
jeśli nie - s
i
= s
∗
, i:=i+1 oraz skok do 2;
Ta pozornie niewielka modyfikacja powoduje, że strategia pierwszy najtańszy jest opty-
malna i zupełna. Niestety, złożoności czasowa i obliczeniowa rosną osiągając, w naj-
gorszym przypadku, poziom - b
d
.

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
11
Strategie heurystyczne
Strategie heurystyczne opierają się na założeniu, że znany jest szacunkowy koszt przejścia
od stanu aktualnego do stanu końcowego (koszt ciągu akcji do niego prowadzący). Dla pra-
widłowego działania szacowany koszt musi być zawsze mniejszy od rzeczywistego.
Załóżmy, że:
h(s
i
) jest funkcją heurystyczną, która określa szacunkowy koszt przejścia od stanu s
i
do
stanu s
t
;
H
i
- zbiór wartości funkcji heurystycznych h(s
i
) w i-tej iteracji algorytmu.
Poniżej omówiony zostanie algorytm A*, który jest najpopularniejszą realizacją stra-
tegii heurystycznej:
Założenia:
f (s
i
) = g(s
i
) + h(s
i
);
F
i
- zbiór sum f (s
i
) dla wszystkich stanów badanych w i-tej iteracji algorytmu.
1. i:=0, F
0
:= φ;
2. Rozwiń s
i
i wylicz F
∗
:= f (s
0
i+1
), f (s
00
i+1
), ...;
3. F
i
:= F
i
∪ F
∗
;
4. Wybierz na podstawie F
i
stan s
∗
o najmniejszym koszcie
jeśli s
∗
= s
t
to STOP;
jeśli nie - s
i
= s
∗
, i:=i+1 oraz skok do 2;
Metoda ta jest optymalna i zupełna. Jej złożoność zależy m. in. od postaci funkcji heu-
rystycznej. W praktyce, dla rozsądnie przyjętych funkcji heurystycznych, algorytm A* jest
znacznie wydajniejszy od strategii poinformowanej — pierwszy najtańszy. Możliwości dosto-
sowywania algorytmu do konkretnego zadania wykraczają poza zdefiniowanie funkcji heury-
stycznej. Istotną kwestią, jest bowiem także, wybór stanu do rozwinięcia (punkt 4 algorytmu)
spośród zbioru stanów, których wartość F
i
jest najmniejsza.
3.1.2
Inne metody deterministyczne
Istnieją też metody nie wykorzystujące podanego wcześniej modelu matematycznego. Dwie
z nich zostały opisane poniżej:
graf widoczności - stosowany jest na mapach na których występują przeszkody w
postaci wieloboków wypukłych. Trajektorie wyznaczane są począwszy od punktu po-
czątkowego poprzez połączenie go z widocznym krawędziami otaczających go prze-
szkód. Końce tak wyznaczonych odcinków są nowymi punktami, z których określane

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
12
są kolejne elementarne połączenia wyznaczane aż do momentu osiągnięcie punktu koń-
cowego. Dopuszczalne trajektorie powstają poprzez złożenie tak wyznaczonych odcin-
ków. Trajektoria optymalna wybierana jest jako najlepsza ze wszystkich wyznaczonych
trajektorii.
metoda pól potencjałowych - zakłada, że na robota działają siły dwojakiego ro-
dzaju: odpychające od przeszkód i przyciągające od punktu docelowego. Ruch robota
wyznaczany jest na podstawie analizy takiego układu dynamicznego. Metoda ta jest w
ogólności nieoptymalna, ale posiada szereg zalet, do których zaliczyć można jej dobre
działanie niezależnie od kształtu przeszkód.
3.2
Metody niedeterministyczne
Planowanie trajektorii przez metody niedeterministyczne ma w swoim przebiegu pewien
aspekt losowości, zależny od konkretnie zastosowanego algorytmu.
3.2.1
Algorytm ewolucyjny
Algorytm ewolucyjny należy do klasy metod inspirowanych biologicznie. Wybranym typem
algorytmu ewolucyjnego będzie schemat zwany obecnie prostym algorytmem genetycznym.
Działanie algorytmu rozpoczyna się od inicjacji populacji bazowej losowo wybranymi
tzw. osobnikami (reprezentującymi propozycje rozwiązań problemu). Następnie populacja
jest oceniana zgodnie z postawionym kryterium zadania. Ocenę osobnika nazywamy jego
przystosowaniem. Potem następuje reprodukcja — promująca lepsze rozwiązania — do po-
pulacji tymczasowej. W wyniku krzyżowania i mutacji osobników populacji tymczasowej
otrzymujemy populację potomną, która staje się populacją bazową w następnej iteracji al-
gorytmu i opisane powyżej operacje powtarzamy do osiągnięcia kryterium stopu. Kryterium
stopu może być ustalona maksymalna ilość iteracji, zbliżenie się do szacowanego wyniku
(z założonym dopuszczalnym błędem), brak poprawy najlepszego rozwiązania przez usta-
loną ilość iteracji lub degeneracja populacji (zanik jej różnorodności). Schemat algorytmu
ewolucyjnego znajduje się na rys. 3.1.
W biologicznej nomenklaturze genotyp to zestaw genów danego osobnika a fenotyp to
zespół jego cech, jakimi genotyp się objawia „zewnętrznie”. Podobnie jest w nomenklatu-
rze algorytmów ewolucyjnych z tym, że cechą „zewnętrzną”, jaką objawia genotyp danego
osobnika jest wartość funkcji przystosowania tegoż osobnika. Funkcja przystosowania jest
więc odwzorowaniem przestrzeni genotypu na przestrzeń fenotypu. Zasadniczym kryterium
jakości działania algorytmu ewolucyjnego to pytanie jak bardzo są zgodne metryki geno-
typu i fenotypu. Pytanie dlatego jest ważne, gdyż działamy operatorami genetycznymi na
przestrzeni genotypu a szukamy rozwiązania w przestrzeni fenotypu. Tak więc niejawnym

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
13
n := 0;
inicjacja P
0
;
ocena P
0
;
while (not warunek stopu) do
begin
T
n
:= reprodukcja P
n
;
O
n
:= krzyżowanie i mutacja T
n
;
ocena O
n
;
P
n+1
:= O
n
;
n := n + 1;
end;
gdzie:
P
n
- populacja bazowa;
O
n
- populacja potomna;
T
n
- populacja tymczasowa;
Rysunek 3.1: Schemat algorytmu ewolucyjnego
założeniem algorytmu jest to, że w otoczeniu danego punktu (jeśli nie jest on maksimum)
spodziewamy znaleźć się rozwiązanie lepsze [1].
Uwaga: drugim założeniem algorytmu jest to, że znajdywanie rozwiązań gorszych od obec-
nych pozwoli nam omijać maksima lokalne funkcji celu.
Poniższy przykład pokazuje rozbieżność metryki genotypowej i fenotypowej:
Przykład:
Rozważmy kodowanie binarne (jeden gen to jeden bit) i chromosomy o długości 3 bitów.
Wybierzmy trzy genotypy (A=a1,a2,a3)
A = 100
B = 110
C = 011
Odległość A od B w metryce Hamminga wynosi |A − B| = 1, A od C - |A − C| = 3 i B od

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
14
C - |B − C| = 2. Jeśli przyjmiemy fenotyp jako dziesiętną wartość genotypu traktowanego
jako liczba binarna otrzymamy:
F(A)=4
F(B)=6
F(C)=3
Odległość F(A) od F(B) w metryce euklidesowej wynosi |F (A) − F (B)| = 2, F(A) od F(C)
- |F (A) − F (C)| = 1, F(B) od F(C) - |F (B) − F (C)| = 3.
Relacje w odległościach wynoszą więc:
|A − B| < |B − C| < |A − C|;
|F (A) − F (C)| < |F (A) − F (B)| < |F (B) − F (C)|.
Powyższy przykład pokazuje „zachwianie” między odległościami w metryce genotypu a
odległościami w metryce fenotypu i jest ilustracją problemu o wiele szerszego niż anoma-
lie w kodowaniu binarnym. Powyższe omówienie będzie też stanowiło punkt wyjściowy dla
rozważań na temat genotypu i fenotypu w zadaniu planowania ścieżki robota.
Algorytm ewolucyjny został zaproponowany m. in. przez K. Trojanowskiego i Z. Michale-
wicza jako sposób planowania ścieżki robota [11]. Ścieżka (chromosom) jest reprezentowana
jako łamana a jej wierzchołki (dalej zwane węzłami) - punkty w przestrzeni euklidesowej
- są genami. Populacja chromosomów (osobników) w każdej iteracji algorytmu jest podda-
wana operatorom genetycznym m. in. mutacji (przesunięcie danego węzła o losowy wektor
z danym rozkładem) i krzyżowaniu (połączenie części jednej ścieżki z fragmentem drugiej),
dodania lub usunięcia węzła, po czym następuje sukcesja najlepszych osobników. Wartość
osobnika mierzy się funkcją przystosowania, która może być np. odwrotnością długości ścieżki
(promujemy ścieżki najkrótsze). Wykonując pewną ilość iteracji mamy nadzieję, że w końcu
zostanie znaleziona najlepsza ścieżka. Oczywiście nie wyklucza to generowania osobników re-
prezentujących ścieżki przechodzące przez obszar niedopuszczalny. Aby tego uniknąć stosuje
dodatkowy operator naprawy, który omija przeszkodę dodając nowe węzły. Dodatkowo by
zoptymalizować działanie algorytmu można wykorzystać operator wygładzania ścieżki.
K. Trojanowski i Z. Michalewicz następnie pokazali [12], że za optymalizację odpowie-
dzialne są głównie operatory naprawy i wygładzania. Wynika z tego, że najprościej jest
poprowadzić linię prostą łączącą punkt początkowy z punktem docelowym i najpierw pod-
dać ją naprawie a potem wygładzeniu. Tak jednak nie będzie, gdy założymy środowisko
anizotropowe lub niestacjonarne.
Powyższy sposób rozwiązania planowania ścieżki planowania robota przeznaczony jest
dla geometrycznej mapy, gdyż wykorzystuje zawartą w niej metrykę. Metryka określa nam
odległość między dwoma punktami w przestrzeni — w tym wypadku pomiędzy kolejnymi
węzłami ścieżki — i jest długością odcinka łączącego te dwa węzły. Wyliczenie długości całej
ścieżki jako sumy kolejnych odcinków łączących kolejne węzły jest więc trywialne. Jeżeli jako

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
15
węzły ścieżki wybierane byłyby (losowo przez algorytm ewolucyjny) węzły grafu, obliczenie
odległości między nimi oznaczałoby znalezienie między nimi najkrótszej ścieżki w grafie.
Istniałaby więc potrzeba użycia metod do przeszukiwania przestrzeni topologicznych. Samo
użycie algorytmu ewolucyjnego nie wniosłoby żadnej nowej jakości.
Innym sposobem rozwiązania problemu mogłoby być zakodowanie ciągów kolejnych wy-
konywanych przez robota akcji jako chromosomu (akcja - gen) (na przykład określenie ką-
ta o jaki robot powinien się obrócić i długości jaką powinien przejechać prosto) jednak
wtedy mutacja pojedycznego genu (modyfikacja pojedynczej akcji) automatycznie wpły-
wałaby na zmianę następnej części trajektorii. Jeżeli s
i+1
= a
i
(s
i
), s
i+2
= a
i+1
(s
i+1
)... to
s
0
i+1
= a
0
i
(s
i
), s
0
i+2
= a
i+1
(s
0
i+1
).... Tak więc stosunkowo niewielka zmiana w przestrzeni gene-
topu dałaby dużo większą w przestrzeni fenotypu (analogicznie jak w powyższym przykła-
dzie). Nie jest to więc dobry sposób kodowania reprezentacji rozwiązania.
3.2.2
Symulowane wyżarzanie
Symulowane wyżarzanie okazuje się być metodą, która pomimo (a może dzięki) swej prostocie
stosunkowo często odnajduje optimum globalne funkcji celu. Idea symulowanego wyżarzania
jest bardzo prosta. W kolejnych iteracjach wyznaczane są kolejne punkty trajektorii. Nowy
punkt jest zawsze akceptowany jeśli wnosi on poprawę w sensie kosztu (np. odległości od
końca), i akceptowany z pewnym prawdopodobieństwem jeśli wprowadza pogorszenie. Praw-
dopodobieństwo akceptacji punktu pogarszającego koszt spada wraz z upływem czasu, tak
aby algorytm dążył w pierwszych iteracjach do eksploracji przestrzeni, a pod koniec swojego
działania do eksploatacji obszaru przyciągania optimum globalnego, w którym się znalazł.
3.3
Metody nie wymagające mapy
W sytuacji, w której brak jest jakiejkolwiek mapy i dostępna jest jedynie wiedza o najbliż-
szym otoczeniu trudno mówić o znalezieniu trajektorii optymalnej. Wystarczająco dużym
problemem jest znalezienie jakiejkolwiek ścieżki łączącej dwa zadane punkty.
Najprostszym rozwiązaniem jest wykonywanie losowych ruchów zgodnie z zasadą, że
w sytuacji w której pożądane jest osiągnięcie celu jakakolwiek aktywność jest lepsza od
braku aktywności. Niestety ruchy losowe nie dają żadnej gwarancji osiągnięcia celu o czym
przekonał się każdy, kto zgubił się w lesie i w panice zaczął szukać drogi. Tego rodzaju
aktywność może doprowadzić człowieka do utraty sił a robota do wyczerpania źródeł energii.
3.3.1
Metody labiryntowe
Niekiedy możliwe jest wykorzystanie reguły prawej bądź lewej ręki do znalezienia popraw-
nej trajektorii. Jej zasada jest bardzo prosta: należy podążać zawsze do przodu trzymając

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
16
się jedną ręką (w przypadku robota burtą) przy ścianie. Oczywiście metoda ta gwarantuje
odnalezienie rozwiązania tylko w labiryncie w którym brak jest cykli w sensie ścieżek sta-
nowiących obwód zamknięty. W przypadku wykrycia tego rodzaju cyklu istnieje możliwość
zmiany strony, której należy się trzymać. Zabieg ten rokuje pewną nadzieję na odnalezie-
nie poszukiwanej ścieżki. Jeśli jednak i w tym wypadku osiągnięty zostanie ten sam punkt
poszukiwaczowi nie pozostaje nic innego jak wykonanie losowego ruchu, który da szansę na
wyjście z cyklu.
Powyższa analiza pozwala stwierdzić, że metoda labiryntowa nie przystaje do większości
rzeczywistych środowisk, takich jak miasto czy las. Daje ona jednak pewne nadzieje na
znalezienie wyjścia z budynku takiego, jak gmach Elektroniki.
3.4
Kryteria wyboru metody wyznaczania trajektorii
Przy wyborze metody wyznaczania trajektorii można posługiwać się kryteriami takimi jak:
niezawodność - Niezawodność jest jasnym i bardzo istotnym kryterium. Jeżeli ko-
nieczne jest wyznaczenie jakiegokolwiek poprawnego rozwiązania (omijającego obszary
zabronione), to należy wybierać takie metody, które to gwarantują. Do metod, które w
ogólnym przypadku nie dają takiej gwarancji można zaliczyć między innymi algorytmy
ewolucyjne i metody potencjałowe.
nacisk na znalezienie rozwiązania optymalnego - Chcąc osiągnąć pełną gwa-
rancję wyznaczenia rozwiązania optymalnego należy zastosować odpowiednie meto-
dy, takie jak przegląd zupełny. Czasami jednak ważniejsze jest szybkie wyznaczenie
jakiegokolwiek poprawnego rozwiązania. Wówczas bardzo skuteczny może okazać się
algorytm ewolucyjny.
dostępna informacja, reprezentacja mapy - Reprezentacja mapy ma bardzo duży
wpływ na wybór metody planowania ścieżki. Dla grafów skuteczne są metody grafowe,
dla siatek zajętości metody takie jak algorytm widoczności. W przypadku braku mapy
niekiedy można skorzystać z reguły opuszczania labiryntu. Dostępność dodatkowej
informacji daje niekiedy możliwość zbudowania funkcji heurystycznych, pozwalających
na znaczne przyspieszenie procesu obliczeniowego.
złożoność obliczeniowa - Kryterium to można stosować stosunkowo rzadko, gdyż
wybór metody implikowany jest zwykle przez inne kryteria, które mają w stosunku do
złożoności obliczeniowej znaczenie nadrzędne.
Złożoność obliczeniowa będzie tym mniejsza im więcej informacji można wyekstraho-
wać z mapy. Przykładowo algorytm „pierwszy najtańszy” można zastąpić wydajniej-
szym obliczeniowo algorytmem A* w sytuacji, gdy uda się wyznaczyć odpowiednią

ROZDZIAŁ 3. SPOSOBY WYZNACZANIA TRAJEKTORII
17
funkcję heurystyczną. Przypadek taki miał miejsce w realizowanym projekcie magi-
sterskim.
ograniczenia implementacyjne — dostępne zasoby sprzętowe i programowe
- Ograniczenia implementacyjne niejednokrotnie uniemożliwiają wyznaczenie trajek-
torii optymalnej. Przykładowo zapisywanie dużych map wiąże się z alokacją dużych
obszarów pamięci, które mogą nie być dostępne.
aspekt holonomicznosci robota - Planery trajektorii stosowane dla robotów ho-
lonomicznych [19] operują na mapach geometrycznych lub topologicznych. Metody te
zwykle nie uwzględniają kinematyki i dynamiki robota, gdyż nie ma takiej potrzeby.
Robot holonomiczny może bowiem wiernie wykonać każdą trajektorię leżącą w obsza-
rze dozwolonym.
Sposób wyznaczania trajektorii dla robotów nieholonomicznych niezmiernie się kom-
plikuje. Problemem jest nie tylko znalezienie optymalnej trajektorii w sensie znanym
z robotów holonomicznych, ale dodatkowo spełnienie ograniczeń związanych z nieho-
lonomicznością robota. Oczywiście dla pewnej klasy systemów możliwe jest wykonanie
trajektorii optymalnej poprzez rozwiązanie odwrotnego zadania kinematyki. Nasuwa
się jednak wówczas pytanie, czy konieczność złożenia elementarnego odcinka tej tra-
jektorii z wielu przekraczających jej granice odcinków odpowiadającym rzeczywistym
ruchom pojazdu, nie czyni jej nieoptymalną.
W ogólnym przypadku zadanie planowania ścieżki dla robotów nieholonomicznych mu-
si uwzględniać ich kinematykę i dynamikę. Do jego rozwiązanie używa się różnorodnych
metod bazujący m. in. na metodzie Newtona i dążności do minimalizacji wydatkowa-
nej energii. Metody te nie były stosowane w projekcie magisterskim w związku z czym
pominięto ich szczegółowy opis, który można odnaleźć między innymi w [19].

Rozdział 4
Podstawy projektowania robotów
mobilnych
4.1
Wprowadzenie
Każdy robot jest narzędziem stworzonym do wykonania określonego zadania w określonym
środowisku. Projekt robota musi spełniać te założenia. Każdy projekt składa się z dwóch
nierozerwalnych części:
• konstrukcji mechanicznej,
• oprogramowania.
W ogólnym przypadku stworzenie konstrukcji mechanicznej robota wymaga zbudowania
modeli kinematycznego i dynamicznego, analizy obciążeń itp. Są to zagadnienia bardzo sze-
rokie i czasochłonne, co więcej, w realizowanym projekcie nie było konieczności posiłkowania
się takimi metodami. Klocki Lego okazały się wystarczająco sztywne i wytrzymałe, silni-
ki cechowały się pożądanym momentem, a do zbudowania reguł ruchowych wystarczająca
okazała się obserwacja działania prototypów.
Tworząc oprogramowanie należy uwzględnić charakterystyki poszczególnych elementów
konstrukcji. Jak już napisano powyżej sterowanie silnikami wyznaczono na podstawie obser-
wacji robota. Oddzielną kwestią jest dostosowanie oprogramowania do charakterystyk czuj-
ników. Czujniki mogą być różnorodne [16], w niniejszej pracy opisano te, które są dostępne
w zestawach Mindstorms pkt. 5.1.3.
W dalszej części tego rozdziału zostaną zaprezentowane wybrane aspekty projektowania
konstrukcji i oprogramowania robota, mające istotne znaczenie w realizowanym projekcie
magisterskim.

ROZDZIAŁ 4. PODSTAWY PROJEKTOWANIA ROBOTÓW MOBILNYCH
19
4.2
Baza jezdna
Baza jezdna jest najważniejszą częścią każdego robota mobilnego. Od niej zależą jego możli-
wości ruchowe i sposób zadawania tego ruchu. Również i w tym aspekcie tworzenie zaawan-
sowanych konstrukcji może być wspierane za pomocą złożonych modeli matematycznych.
Modele te nie były jednak wykorzystywane, wobec czego zostaną pominięte. Podobnie mo-
delowanie pojedynczych kół okazało się zbędne.
4.2.1
Rodzaje napędu
Rodzaj napędu jest najistotniejszą kwestią o której musi zadecydować projektant robota
mobilnego. Wybór rodzaju napędu zależy od środowiska w którym będzie poruszał się robot,
charakteru tego ruchu i możliwości konstrukcyjnych.
Napęd synchroniczny
Tego rodzaju napęd składa się najczęściej z trzech kół położonych na wspólnym okręgu. Koła
te są każdorazowo skierowane w tym samym kierunku i poruszają się z tą samą prędkością.
Dzięki temu robot może zmieniać kierunek jazdy w dowolnym momencie w dowolną stronę, z
tym że orientacja korpusu robota nie zmienia się. Konstrukcja napędu synchronicznego jest
bardzo skomplikowana. Ma on jednak pewne zalety. Napęd synchroniczny daje możliwość
stworzenia robota holonomicznego [19], którego sterowanie jest relatywnie proste.
Napęd dookólny (wielokierunkowy)
Oparty na tym samym układzie co napęd synchroniczny, jest od niego jeszcze bardziej skom-
plikowany. Każde z kół może być ustawiane niezależnie i obracać się z indywidualną prędko-
ścią. Taka konstrukcja umożliwia szybką zmianę orientacji bazy robota.
Napęd różnicowy
Składa się z dwóch niezależnych kół napędowych położonych na jednej osi, wspomaganych,
dla zachowania równowagi, jednym lub dwoma kółkami swobodnymi, położonymi z tyłu bądź
z przodu pojazdu. Napęd różnicowy jest prosty w konstrukcji i zapewnia dużą zwrotność,
ale oparty na nim robot nie jest holonomiczny. Umożliwia on poruszanie się do przodu i do
tyłu po łukach o dowolnym promieniu (w szczególności po prostej i obrót w miejscu). Taki
napęd wykorzystywany jest w wielu robotach oraz pojazdach gąsienicowych, np czołgach.

ROZDZIAŁ 4. PODSTAWY PROJEKTOWANIA ROBOTÓW MOBILNYCH
20
Napęd Akermana (samochód kinematyczny)
Pojazdy oparte na napędzie Akermana obserwujemy na co dzień na naszych ulicach. Dyspo-
nują one najczęściej dwoma kołami napędowymi leżącymi na jednej osi i dwoma kołami nie
napędzanym leżącymi na drugiej osi. Napęd Akermana jest w praktyce prostszy od różni-
cowego gdyż wymaga budowy pojedynczego układu przeniesienia napędu. Co więcej oparta
na nim konstrukcja podlega podczas jazdy mniejszym naprężeniom. Nie zapewnia on jednak
takiej zwrotności jak napęd różnicowy i jest podobnie jak on nieholonomiczny.
4.3
Podejścia do problemu sterowania
W zależności od stopnia komplikacji programu i stawianych przed nim oczekiwań, projektant
może wykorzystać przy jego projektowaniu różne podejścia do problemu sterowania robotem
4.3.1
Podejście reaktywne
Jest to najprostsze z możliwych podejść. Oparty na nim program składa się z prostych reguł
typu bodziec — reakcja. Reakcja na konkretny bodziec jest zawsze taka sama, brak jest ja-
kiejkolwiek pamięci czy też struktur opartych na automatach. Najczęściej jest to realizowane
w ten sposób, że określona wartość odczytana z czujnika powoduje wystawienie określonego
sterowania na elemencie wykonawczym. Niewątpliwymi zaletami tego podejścia są prostota,
szybkość działania i niezawodność. Wadami natomiast niemożność implementacji jakiego-
kolwiek planowania, czy też uczenia się.
4.3.2
Podejście oparte na modelu
Podejście to opiera się na zasadzie „wyczuwaj — planuj — działaj” (ang. SPA: sense —
plan — act ). Działanie jest efektem kolejno wykonywanych, następujących po sobie etapów.
Najpierw odczyty z czujników są interpretowane, po czym na podstawie modelu środowiska
następuje zaplanowanie działania. Proces ten wymaga dokładnego modelu środowiska. Co
więcej, jest czasochłonny i niezwykle wrażliwy na niedokładność tego modelu, czy też zmiany,
które zaszły w środowisku podczas planowania. W praktyce, podejście to nie sprawdza się
podczas działania w rzeczywistym środowisku, gdyż jest zbyt wolne i niedokładne.
4.3.3
Podejście hybrydowe
W podejściu tym łączą się dwa inne: reaktywne i oparte na modelu. Całość zorganizowana
jest w trzech warstwach: warstwa najniższa jest reaktywna, warstwa najwyższa opiera się na

ROZDZIAŁ 4. PODSTAWY PROJEKTOWANIA ROBOTÓW MOBILNYCH
21
modelu, warstwa środkowa pośredniczy zaś w komunikacji pomiędzy uprzednio wymieniony-
mi warstwami. Wszystkie te warstwy zwykle funkcjonują współbieżnie. Cała struktura jest
dosyć skomplikowana, co może negatywnie wpłynąć na szybkość działania programu i jego
niezawodność. Z drugiej strony, tego typu rozwiązanie pozwala na oprogramowanie robotów
w szerokiej klasie zadań.
4.3.4
Podejście behawioralne
Podejście to jest funkcjonalnie zbliżone do hybrydowego (także łączy podejścia: reaktywne
i oparte na modelu) ale ma od niego nieco inną strukturę. Program nie jest podzielony na
warstwy i ma jednolitą budowę. Z jednej strony, taka organizacja może przyspieszyć dzia-
łanie programu, z drugiej jednak, występująca przy podejściu hybrydowym dekompozycja
problemu ułatwia jego zaprojektowanie.
W podejściu behawioralnym poszczególne zachowania mogą mieć tak prostą strukturę
jak reakcje przy podejściu reaktywnym. Istnieje jednak możliwość budowy automatu (a więc
i wykorzystania pamięci), czy też sieci zachowań wiążącej poszczególne związki przyczynowo
skutkowe. Układy odpowiedzialne za realizację poszczególnych zachowań mogą wykorzysty-
wać sprzężenie zwrotne, co pozwala na ich prawidłową pracę w obliczu niedokładności modelu
i występujących zakłóceń. Poszczególne zachowania mogą być wykonywane współbieżnie. Do
ich opisu używa się zwykle języka wyższego poziomu niż ma to miejsce w przypadku reakcji.
Przykładowym opisem zachowania może być „podrzucenie piłeczki”, czy też „dojechanie do
ściany”.

Rozdział 5
Właściwości środowiska Mindstorms
5.1
Środowisko sprzętowe
5.1.1
Charakterystyka ogólna
Klocki Lego Mindstorms są rozwinięciem serii Technic idącym w kierunku integracji klocków
z komputerami. Pierwszy podobny zestaw powstał już w 1989 roku na MIT i był tam z po-
wodzeniem wykorzystywany w projektach laboratoryjnych przeznaczonych dla studentów.
Podobnie jak miało to miejsce u jego amerykańskiego prekursora, sercem zestawu Mind-
storms jest mikrokomputer jednoukładowy. Mikrokomputer ten może komunikować się z
komputerami klasy PC za pośrednictwem kanału transmisyjnego w podczerwieni. Roboty
budowane przy wykorzystywaniu opisywanego zestawu mogą przetwarzać informacje płyną-
ce z różnorakich czujników a wynik tej analizy wykorzystywać do sterowania elementami
wykonawczymi takimi jak silniki. Wszystkie klocki są w pełni kompatybilne z dotychczas
produkowanymi, co sprawia, że sposób konstruowania robotów jest bliźniaczo podobny do
budowania zamków i samochodów znanych z innych zestawów firmy Lego.
W projekcie magisterskim wykorzystywano dwa różne zestawy z rodziny Mindstorms,
liczące w sumie ponad 900 elementów. Ich opis można odnaleźć m. in. na witrynie [7] i w
instrukcjach dołączonych do klocków [2], [3]. Niewątpliwą zaletą przyjętej technologii two-
rzenia robota był niezwykle krótki czas dzielący początki projektu od zrealizowania finalnej
konstrukcji. Właściwości mechaniczne robota, który powstał, pozwalały na jego intensyw-
ną eksploatację. Do głównych wad wybranego środowiska sprzętowego zaliczyć można jego
ograniczenia. Stosunkowo niewielka różnorodność klocków sprawiała, że powstawanie final-
nej konstrukcji wiązało się z licznym kompromisami. Szczególnie istotne okazało się uzależ-
nienie od oryginalnych czujników, których charakterystyki daleko odbiegały od ideału. Na
wykonanie własnych elementów nie pozwolił ograniczony czas dostępny na realizację całego
projektu.
Zestaw Lego Mindstorms składa się z kilku zasadniczych grup elementów, z których

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
23
niektóre zostaną opisane w dalszej części tego rozdziału; są to:
• główny element zestawu Mindstorms — RCX,
• czujniki,
• elementy wykonawcze,
• urządzenia do komunikacji w podczerwieni.
Dodatkowym elementem koniecznym do stworzenia autonomicznego robota jest zestaw
oprogramowania opisany w pkt. 5.2.
Rysunek 5.1: Główny element zestawu Mindstorms — RCX
5.1.2
Główny element zestawu Mindstorms — RCX
RCX, rys. 5.1, jest głównym klockiem zestawu Mindstorms, w nim bowiem znajduje się kom-
puter sterujący całą konstrukcją. Źródłem zasilania komputera jest sześć znajdujących się
wewnątrz RCX szeregowo połączonych baterii 1,5 V, które mogą zostać z powodzeniem za-
stąpione przez akumulatory 1,2V. Wykorzystywane ogniwo pozwala na autonomiczną pracę
robota przez minimum kilka godzin. Na górnej powierzchni RCX widoczne są trzy wejścia
czujnikowe oznaczone cyframi 1,2,3 oraz trzy wyjścia oznaczone literami A, B i C. Pomiędzy
złączami znajduje się ekran ciekłokrystaliczny oraz cztery przyciski sterujące. Bardzo waż-
nym elementem jest umieszczone z przodu, za czarną szybką, urządzenie nadawczo-odbiorcze
w podczerwieni.
ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
24
Mikrokomputer Hitachi
Wewnątrz RCX’a znajduje się mikrokomputer jednoukładowy Hitachi serii H8/3297. Jed-
nostka obliczeniowa taktowana jest zegarem o częstotliwości 16MHz. Ilość pamięci typu ROM
wynosi 16KB, a pamięci typu RAM 32KB. Pamięć typu RAM zawiera system operacyjny
i uruchamiane w nim programy, w pamięci ROM znajdują się preinstalowane programy,
stworzone przez firmę Lego. W praktyce, szybkość procesora jest wystarczająca do większo-
ści zastosowań, natomiast stosunkowo niewielka pamięć niejednokrotnie staje się źródłem
problemów. Hitachi wyposażony jest w wejścia analogowe sprzężone z przetwornikami analo-
gowo — cyfrowymi. Trzy spośród nich podłączone są do wejściowych złącz RCX, a czwarte
odpowiedzialne jest za monitorowanie napięcia na akumulatorach. Wyjścia procesora Hita-
chi umożliwiają sterowanie efektorami za pomocą zmian wypełnienia sygnału prostokątnego
— PWM (ang. Pulse Width Modulation). Urządzenie nadawczo-odbiorcze w podczerwieni
posiada oddzielną obsługę. Szczegółowy opis mikrokomputera odnaleźć można w instrukcji
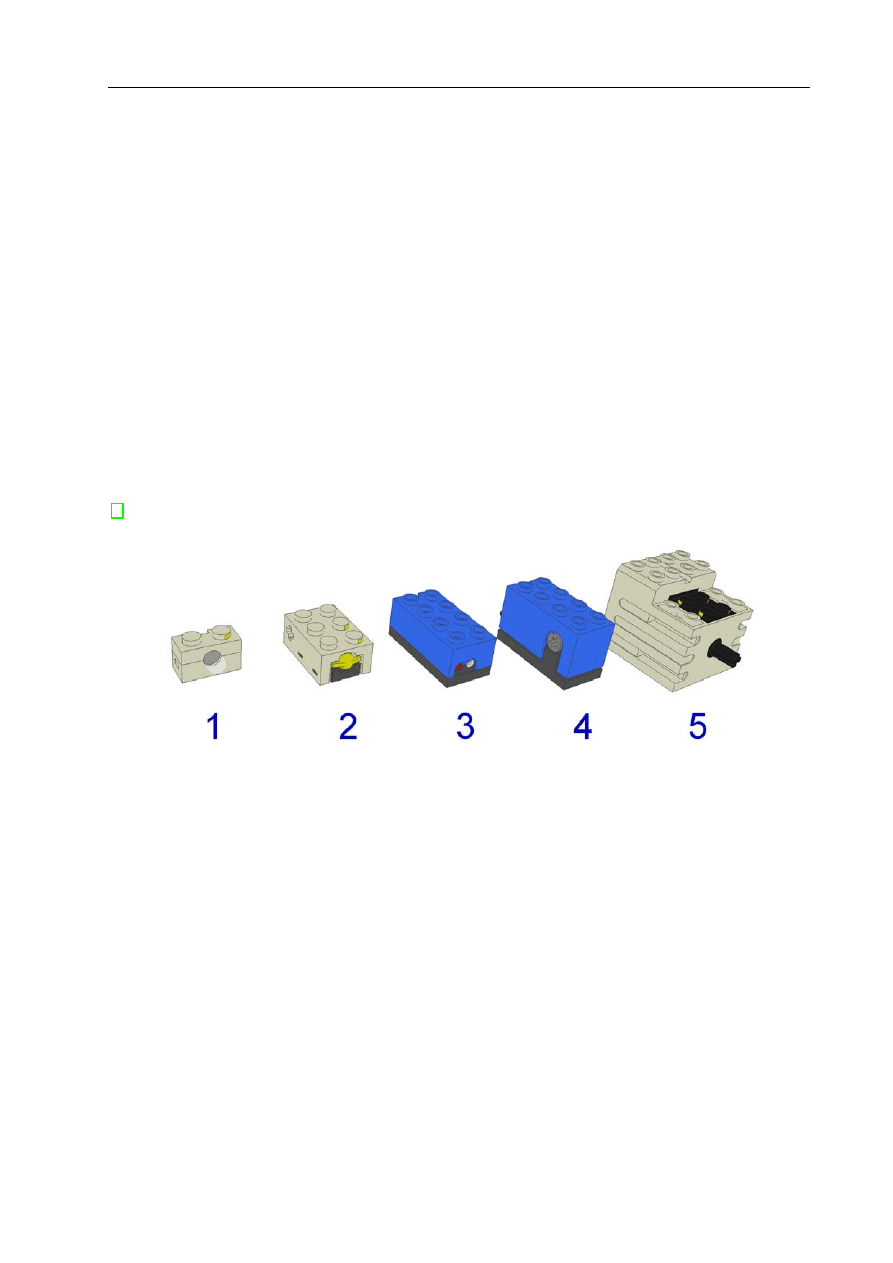
Rysunek 5.2: Wybrane klocki z zestawów Mindstorms 1 - lampa, 2 - czujnik dotyku, 3 -
czujnik natężenia światła, 4 - czujnik odometryczny, 5 - silnik prądu stałego
5.1.3
Czujniki
Zarówno czujniki jak i elementy wykonawcze połączone są z RCX za pomocą dwużyłowych
przewodów. Czujniki mogą być podłączane do każdego spośród trzech wejść RCX. Możliwe
są dwa tryby ich pracy:
bierny — wartość odczytu wynika bezpośrednio z rezystancji czujnika, dołączonego
równolegle do rezystora 10k zasilanego napięciem 5V.
aktywny — czujnik początkowo zasilany jest napięciem 8V przez okres około 150 µs,
po czym przez kolejne 32 µs dokonywany jest odczyt w sposób identyczny do tego,
który ma miejsce w biernym trybie pracy.

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
25
Czujnik dotyku
Czujnik dotyku oznaczony jest numerem 2 na rys. 5.2. Pracuje on w trybie aktywnym. Zasada
działania jest bardzo prosta. Jeżeli ruchoma końcówka czujnika, widoczna na rys. 5.2 jako
niewielki żółty element, zostanie wciśnięta, to zwierany jest mikroprzełącznik znajdujący się
wewnątrz czujnika, co może zostać natychmiast odczytane. Jeżeli brak jest takiego nacisku
to mikroprzełącznik jest rozwarty.
Czujnik natężenia światła
Czujnik światła oznaczony jest numerem 3 na rys. 5.2. Jego najistotniejszymi elementami
są widoczne na czołowej ściance czujnika: czerwona dioda oświetlająca badaną powierzchnię
i ukryty za przezroczystą szybką element światłoczuły. Czujnik światła może pracować w
trybie biernym, i aktywnym. W trybie aktywnym dioda umieszoczona w czujniku pali się a
w trybie biernym jest wyłączona. Praktyka wykazała, że praca w trybie biernym nie sprawdza
się, gdyż czujnik cechuje się wówczas niezwykle niską rozdzielczością.
Opisywany czujnik bada poziom natężenia docierającego do niego światła. Badanie bar-
wy podłoża nie jest bezpośrednio możliwe, gdyż brak jest pomiaru natężenia światła dla
poszczególnych długości fali.
Czujnik odometryczny
Czujnik odometryczny, oznaczony numerem 4, jest największym z czujników zaprezentowa-
nych na rys. 5.2. Pracuje on w trybie aktywnym. Oś, której zmiany kąta są badane, umiesz-
czana jest w jasnoszarej tulei, widocznej na bocznej ścianie czujnika. Czujnik odometryczny
przyjmuje cztery różne stany na każdą 1/4 obrotu osi, tak więc w sumie umożliwia odczyt
kąta z dokładnością do 1/16 obrotu.
Inne czujniki
Do zestawów Mindstorms dostępnych jest także wiele innych czujników dostarczanych przez
różnorakie firmy. Są to czujniki zarówno tak proste jak termistory, jak i tak skomplikowane
jak sondy ultradźwiękowe. Możliwości wzbogacania oryginalnego zestawu są praktycznie nie-
ograniczone, pod warunkiem, że nowe elementy będą zgodne z obowiązującymi standardami.
5.1.4
Elementy wykonawcze
Efektory mogą być podłączane do każdego spośród trzech wyjść RCX. Jak już napisano
wcześniej efektory sterowane są za pomocą zmiany wypełnienie sygnału prostokątnego.

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
26
Silniki prądu stałego
Silnik prądu stałego oznaczony jest numerem 5 na rys. 5.2. Cechuje go stosunkowo duży
moment począwszy od najmniejszych obrotów, w związku z czym może być z powodzeniem
wykorzystywany do napędu najróżniejszych konstrukcji. Opisywany silnik może pracować w
czterech trybach:
obracania się do przodu — moc silnika może być wówczas regulowana.
obracania się do tyłu — moc silnika może być wówczas regulowana.
zablokowania — wał silnika jest zablokowany i jego obrót jest niezwykle trudny. Tryb
ten może być używany do hamowania.
luzu — wał silnika obraca się niemalże swobodnie.
Eksperymenty wykazały, że funkcjonalna zależność pomiędzy prędkością wału a mocą
silnika jest silnie nieliniowa. Nawet po wyznaczeniu odwzorowania dla określonej konstrukcji
projektant staje przed koniecznością uwzględnienia wpływu poziomu napięcia na akumula-
torach. W praktyce nie możliwa jest więc płynna regulacja prędkości wału silnika.
Lampy
Lampa, oznaczona na rys. 5.2 numerem 1, to bardzo prosty element wykonawczy. Jej rola
sprowadza się do oświetlania przestrzeni w pewnym kącie bryłowym, który może być regu-
lowany za pomocą specjalnych nakładek.
5.1.5
Urządzenia do transmisji w podczerwieni
Do komunikacji w podczerwieni konieczne są dwa urządzenia nadawczo - odbiorcze. Ze stro-
ny robota urządzenie takie znajduje się w przedniej części RCX, ze strony komputera PC do
komunikacji używane jest specjalne urządzenie, zwane wieżą, podłączane do portu szerego-
wego. Nowsze, niewykorzystywane w realizowanym projekcie wieże, korzystają z magistrali
USB. Moment przesyłania danych jest najlepiej widoczny na rys. 8.9.
Maksymalna odległość pomiędzy obydwoma urządzeniami, przy której jest jeszcze za-
chowana poprawność przesyłania danych, zależy głównie od siły elektromotorycznej ogniwa
umieszczonego w RCX. Jest to jeden z nielicznych aspektów wykorzystania zestawu Mind-
storms, w którym baterie alkaliczne przewyższają akumulatory typu metal - wodór. W prak-
tyce odległość ta waha się w przedziale od jednego do trzech metrów. Komunikację mogą
uniemożliwić szumy tła w podczerwieni. Sytuacja taka miała miejsce zimą podczas reali-
zacji laboratorium ERO. Rozgrzane kaloryfery okazały się być skutecznym utrudnieniem w

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
27
wykorzystaniu RCX jako źródła promieniowania podczerwonego, gdyż poziom emitowanego
przez niego sygnału był niższy od poziomu tła związanego z emisją kaloryferów.
Kanał transmisyjny wykorzystywany jest do przesyłania systemu operacyjnego, progra-
mów w nim uruchamianych a także danych już podczas pracy robota. Transmisja może
przebiegać dwukierunkowo, ale nie jest możliwe przesyłania pakietów w obie strony w tym
samym czasie. Wysyłanie danych odbywa się poprzez wywołanie odpowiedniej funkcji, odbiór
natomiast następuje w wyniku uruchomienia programu obsługi przerwania.
Dodatkowym elementem zestawów Mindstorms jest pilot, który umożliwia sterowanie
robotami wyposażonymi w oryginalny system operacyjny firmy Lego. Pilot przekazuje RCX
dyrektywy w podczerwieni, które są interpretowane na poziomie systemu operacyjnego i
niezwłocznie wykonywane.
5.2
Środowisko programowe
Na środowisko programowe Mindstorms składają się:
— system operacyjny mikrokomputera Hitachi wraz z aplikacjami w nim uruchamianymi,
— interfejs programistyczny,
— programy wspomagające projektowanie robota.
Firma Lego dostarcza zestawy Mindstorms z własnym systemem operacyjnym i graficz-
nym środowiskiem do tworzenia aplikacji w systemach Microsoft Windows. Oprogramowanie
to jest dobrym rozwiązaniem dla dzieci, które stawiają pierwsze kroki w świecie robotyki,
dla profesjonalistów stanowi jednak bardzo poważne ograniczenie. Grupka zapaleńców przy-
stąpiła więc do tworzenia własnych systemów operacyjnych, z których do dziś pozostają w
użyciu dwa: napisany w C legOS i stworzony w Javie leJOS. Fakt że Java zadomowiła się
na dobre na platformie wyposażonej tylko w 32kB RAM może być pewnym zaskoczeniem.
Nie ulega jednak wątpliwości, że rozwiązanie to sprawdziło się w praktyce i nie wykluczone,
że w przyszłości zdobędzie większą popularność niż starszy historycznie legOS.
5.2.1
System operacyjny legOS
System operacyjny legOS został stworzony przez Markusa L. Noga. Obecnie rozwijany jest
jako jeden z projektów na sourceforge [4]. Jego kolejne wersje będą nosiły nazwę BrickOS.
LegOS obsługuje znakomitą większość funkcji możliwych do wykorzystania w zestawach
Mindstorms. obecnie (dla systemu legOS 2.6) jedynymi dwiema funkcjami, które nie zostały
jeszcze zaimplementowane, są sterowanie RCX za pomocą pilota i obsługa wieży podłączonej
do USB.

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
28
Zarówno system operacyjny legOS jak i tworzone dla niego aplikacje można kompilować
we wszystkich najważniejszych systemach operacyjnych, a w szczególności w Linux, z którego
korzystano podczas realizacji projektu magisterskiego.
LegOS a systemy czasu rzeczywistego
Do obsługi urządzeń działających w czasie rzeczywistym wskazane jest użycie systemów
czasu rzeczywistego. Takim urządzeniem jest niewątpliwie robot realizowany w projekcie
magisterskim. LegOS można nazwać systemem czasu quasi rzeczywistego. Dysponuje on
niektórymi mechanizmami znanymi z profesjonalnych systemów czasu rzeczywistego, takich
jak QNX. Są nimi:
obsługa wątków - Uruchamiane aplikacje mogą składać się z kilku wątków o okre-
ślonym priorytecie. Czas przełączania wątków wynosi 20ms, a więc jest bardzo długi.
Co więcej brak jest gwarancji określonej kolejności uruchamiania wątków, pomimo
nadanych im priorytetów.
semafory - Obsługa semaforów odbywa się w sposób znany z innych systemów.
funkcje oczekiwania na zdarzenie - Działają podobnie jak semafory z tą różnicą,
że odwieszenie wątku następuje w momencie spełnienia warunku logicznego zdefinio-
wanego w funkcji. Funkcje oczekiwanie na zdarzenie mają wyższy priorytet niż wątki
aplikacji, w związku z czym warunek ten sprawdzany jest relatywnie często.
W legOS brak jest zaawansowanych mechanizmów komunikacji pomiędzy procesami, ta-
kich jak kolejki wiadomości i spotkania. Można temu zaradzić wykorzystując do zsynchronizo-
wanego przesyłania danych zmienne globalne i semafory. Mechanizm ten został wykorzystany
w projekcie magisterskim.
Charakterystyka modułów
System operacyjny legOS składa się z kilkunastu modułów o określonej funkcjonalności.
Modularyzacja daje możliwość kompilowania, a następnie ładowania do RCX wersji syste-
mu przystających funkcjonalnością do potrzeb aplikacji. Wyspecjalizowany system zajmuje
mniej miejsca, co w sytuacji istotnych ograniczeń związanych z wielkością pamięci, pozwala
na stworzenie obszerniejszych aplikacji.
Poszczególne moduły zostały opisane w zestawieniu poniżej:
battery - interpretacja napięcia na bateriach.
conio - obsługa wejścia - wyjścia.
key - obsługa klawiszy znajdujących się na RCX’e.

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
29
dmotor - obsługa silników.
dsound - obsługa dźwięku. Dźwięk może być emitowany pod postacią melodii skła-
dającej się z sekwencji nut o określonej wysokości i długości trwania. Odtwarzanie
uprzednio nagranego dźwięku jest niemożliwe.
kmain - główny moduł jądra.
lcd - obsługa wyświetlacza znajdującego się na RCX’e.
lnp - obsługa protokołu komunikacji systemu legOS.
lnp-logical - warstwa logiczna protokołu komunikacji.
mm - zarządzanie pamięcią.
program - obsługa struktur i funkcji aplikacji uruchamianych w legOS’ie.
semaphore - obsługa semaforów.
systime - obsługa zegara systemowego.
tm - zarządzanie wątkami uruchomionymi w systemie.
Sposoby ograniczania długości kodu wynikowego programu
Napisanie złożonej funkcjonalnie aplikacji wymaga umiejętnego przygotowania jej kodu źró-
dłowego, tak aby skompilowany program był możliwie jak najkrótszy i zmieścił się w do-
stępnej pamięci RAM. Przygotowanie to wiąże się z zastosowaniem różnorodnych technik
programistycznych, z których część poprawia przejrzystość programu, a niektóre ją niestety
pogarszają:
Uwspólnianie możliwie jak największej części kodu - Korzystne jest przenie-
sienie do funkcji i procedur jak największej ilości kodu w sytuacji, gdy występuje on
kilkakrotnie. Zabieg ten zmniejsza długość kodu wynikowego, ale niekiedy może spo-
wolnić działanie programu.
Korzystanie ze zmiennych globalnych - Wykorzystanie zmiennych globalnych do
przekazywania danych do funkcji i procedur, zamiast korzystania z ich argumentów
zmniejsza objętość programu, ale negatywnie wpływa na przejrzystość kodu i jest złą
praktyką ze względu na niebezpieczeństwo niepożądanego oddziaływania jednej funkcji
na zmienną widoczną w innej funkcji.
ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
30
Zastępowanie kodu w C, kodem asemblerowym - Uzyskanie tą metodą krót-
szego kodu wynikowego programu wymaga doskonałej znajomości kompilatorów i jest
czasochłonne. Napisany kod staje się trudny w interpretacji.
Zastępowanie konstrukcji „switch” konstrukcjami „if-else” - Praktyka wyka-
zała, że dla zastosowanych kompilatorów zabiega ten znacząco skraca kod, który i tym
razem traci przez to na przejrzystości.
Odpowiednie dobieranie typów zmiennych - tak aby nie tracić miejsca na nie-
wykorzystywane bity zmiennych przechowujących dane.
Wielokrotne wykorzystywanie zmiennych - daje stosunkowo niewielką oszczęd-
ność miejsca i musi być przeprowadzane z niezwykłą uwagą.
Dokładne zaprojektowanie logicznej struktury programu - Daje zwykle naj-
większe oszczędności i pozwala na znaczną poprawę estetyki kodu.
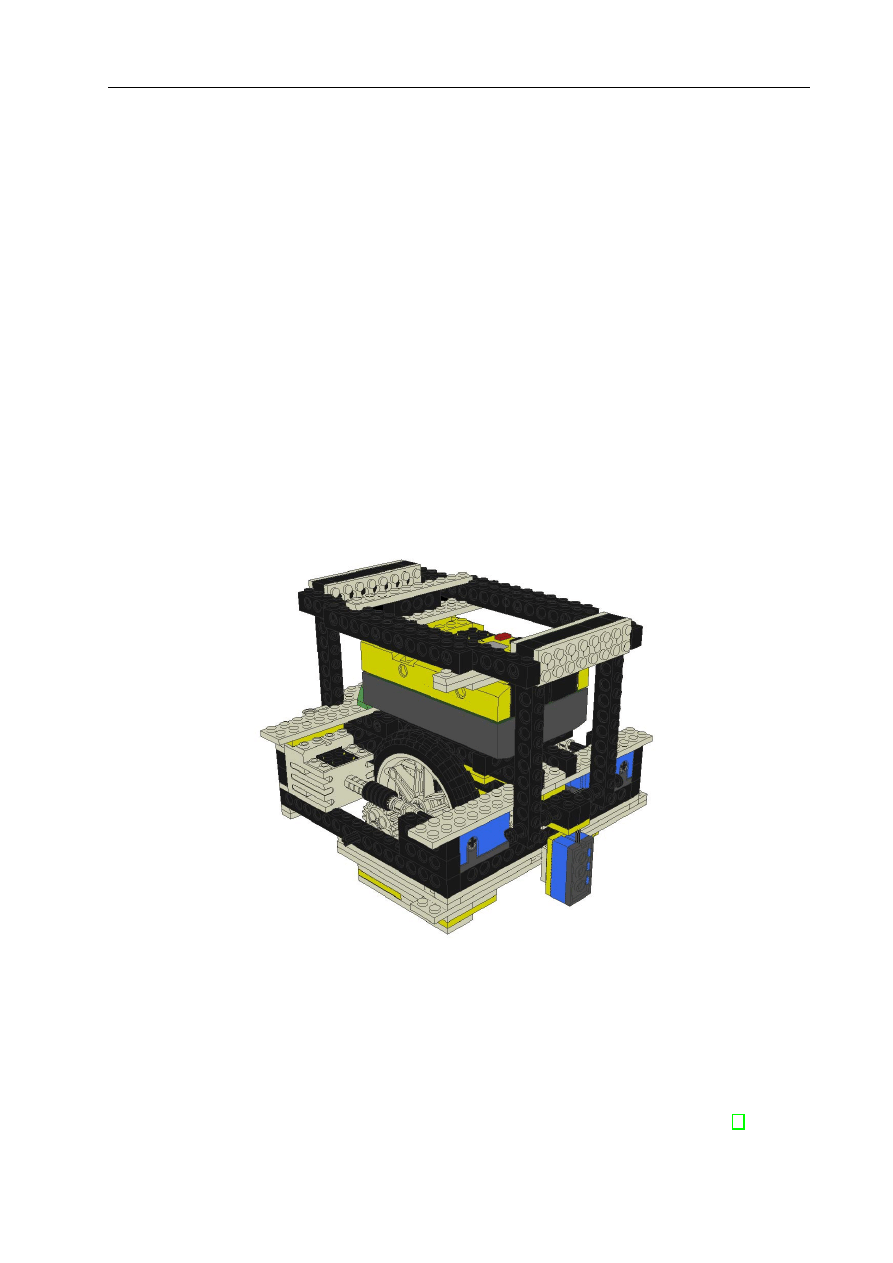
Rysunek 5.3: Robot MIŚ 4 wymodelowany za pomocą programu LeoCAD
5.2.2
Programy wspomagające projektowanie robota
Proces projektowania robota można usprawnić na wiele sposobów. Mario Ferrari [5] opraco-
wał emulator legOS’a, który umożliwia m. in. kontrolę zawartości pamięci mikrokomputera
Hitachi. Z drugiej strony możliwe jest projektowanie samej konstrukcji robota za pomocą

ROZDZIAŁ 5. WŁAŚCIWOŚCI ŚRODOWISKA MINDSTORMS
31
różnorodnych programów typu CAD. Najbardziej udanym z nich wydaje się być LeoCAD
[9]. Jest to darmowy edytor umożliwiający etapowe tworzenie trójwymiarowych modeli z
pojedynczych klocków. Dokładność odwzorowania jest bardzo wysoka. Program wraz z mo-
delem robota MIŚ 4 znajduje się na dołączonej do pracy płycie CD. Rysunek 5.3 przedstawia
jedno z ujęć zbudowanego modelu.

Rozdział 6
Ogólna postać systemu wykonującego
zadanie
6.1
Wprowadzenie
Jak to zostało już wspomniane, robot powinien być dopasowany do środowiska. Jest to pod-
stawowe założenie dotyczące konstrukcji i oprogramowania robota, tak by mógł wykonywać
powierzone mu zadanie. Jeśli chodzi o możliwości dostępnego nam robota to należy od razu
wykluczyć możliwość wyrafinowanej lokalizacji bezwzględnej. Robot nie ma możliwości tech-
nicznych wykrywania latarni (czujniki światła są nie dokładne), czy specjalnych znaczników
a tym bardziej lokalizacji na podstawie porównania posiadanej mapy z otoczeniem. Pozosta-
je jedynie lokalizacja względna, przez czujniki odometryczne dostarczane przez firmę Lego w
osobnym zestawie. Jednak, jak to zostało wcześniej napisane, sama odometria nie wystarcza
do dobrej lokalizacji. Kumulujące się błędy wykluczają jej wyłączne zastosowanie. Rozsąd-
nym wyjściem z tej sytuacji jest dyskretyzacja środowiska, zarówno przemierzanych długości,
jak i kątów, o które robot może się obrócić. Robot zajmuje konkretny kwadrat w przestrzeni
(oczko siatki) zwrócony przodem w jedną z czterech stron. Możemy więc abstrahować od
dokładnej odległości zajmowanej od krawędzi kwadratu, jak i kąta o jaki obrócony jest ro-
bot. Przyjęcie metryki miejskiej zamiast euklidesowej ułatwia lokalizację robota (a wręcz ją
umożliwia), która i tak wciąż nie jest trywialna (w dalszej części skupimy się na dalszych
jej aspektach technicznych); umożliwia też skoncentrowanie się na planowaniu ścieżki i jej
optymalizacji. Poza tym nic nie tracimy na ogólności testowanych w przyszłości algorytmów
optymalizacji.
Innym ograniczeniem jest niewielka dostępna pamięć operacyjna robota. Uniemożliwia to
zaimplementowanie algorytmu ewolucyjnego tak by wykonywany był przez robota. Do tego
celu został specjalnie napisany program uruchamiany na komputerze PC wykorzystujący
algorytm ewolucyjny do wyznaczenia optymalnej ścieżki (program też został wykorzystany

ROZDZIAŁ 6. OGÓLNA POSTAĆ SYSTEMU WYKONUJĄCEGO ZADANIE
33
do badania właściwości statystycznych algorytmu), która następnie jest przesyłana łączem
podczerwonym do robota wraz z mapą terenu. Alternatywną metodą jest algorytm A*.
Robot natomiast korzysta wyłącznie z algorytmu A*, do wyznaczania optymalnego ominięcia
nieznanych przeszkód. Po przejechaniu trasy, robot zwraca do komputera PC aktualną mapę.
6.2
Plansza
Stworzone środowisko składa się z czarnego kartonu z naklejonymi na niego, w równych od-
stępach, krzyżykami glazurniczymi, między którymi jest miejsce na ceramiczne, szkliwione
kafelki o wymiarach 10 × 10 mm. Kafelki są kwadratowe, więc spełniają założenia dotyczące
środowiska. Poza tym w przeciwieństwie do wykonanych z kartonu kwadratów są wystar-
czająco ciężkie, by robot ich nie przesuwał w czasie jazdy (są dodatkowo przytrzymywane
krzyżykami). Dwa kolory kafelków: biały i szary reprezentują różne koszty przejazdu i zapew-
niają niehomogeniczność środowiska, co czyni je ciekawym z punktu widzenia optymalizacji.
Czarna fuga między kafelkami jest rozpoznawana przez robota jako granica między obszara-
mi i informuje go o przekroczeniu granicy między polami (oczywiście robot jest nie większy
od kafelka i obraca się wokół środka własnej osi). Istniejące fugi można porównać do znacz-
ników jako metody samolokalizacji. Takie środowisko daje się w łatwy sposób modyfikować.
Wystarczy zdjąć kafelek — by powstał obszar zabroniony, zamiast niego położyć w to sa-
mo miejsce kafelek innego koloru — by zmodyfikować koszt przebycia tej części trasy, lub
też położyć kafelek na puste pole — by umożliwić robotowi przejazd tamtędy. W ten spo-
sób istnieje możliwość łatwego zademonstrowania przejazdu robota dla diametralnie różnych
ścieżek, jak również przekonania się, jak robot radzi sobie w warunkach wykrycia nieznanych
przeszkód, powstałych wskutek nieznacznej zmiany środowiska.
6.3
Moduł w komputerze PC
Na komputerze klasy PC wykonywany jest program XTiles (napisany przez Macieja Stania-
ka), który służy do wyznaczania optymalnych trajektorii algorytmem ewolucyjnym lub A*
(do wyboru). Program wyświetla aktualną mapę (kolorowe kwadraty odpowiadające kafel-
kom, po których jeździ robot), dla której poszukuje optymalnej ścieżki (przycisk „Start”).
Mapę można pobrać z pliku (przycisk „Open”) lub od robota - wysłaną łączem podczerwo-
nym (przycisk „Receive”). Mapę można też zachować do pliku (przycisk „Save”) lub przesłać
do robota łączem podczerwonym (przycisk „Send”) wraz z wyznaczoną trajektorią. Wyzna-
czona trajektoria jest pokazywana na mapie przez kółka. Krzyżyki natomiast informują,
gdzie znajdują się węzły ścieżki.
Program napisany jest w języku C++ przy wykorzystaniu obiektowej biblioteki Qt, za-

ROZDZIAŁ 6. OGÓLNA POSTAĆ SYSTEMU WYKONUJĄCEGO ZADANIE
34
pewniającej m. in. grafikę w systemie Linux.
6.4
Moduł w robocie MindStorms
Komputer sterujący robotem wykonuje program (autorstwa Tomasza Winiarskiego), którego
zadaniem jest wykonanie trajektorii wyznaczonej przez program XTiles. Robot porusza się
po wyznaczonej trajektorii do momentu gdy kolejny kafelek, na który będzie miał wjechać,
zacznie się różnić się od analogicznego na mapie przechowywanej w pamięci robota. Wtedy
to zostanie uruchomiony planer trajektorii (pkt. 10) i odcinek ścieżki zostanie przebudowany.
Robot wykrywa kolor kafelka lub jego brak, jak również fugi trzema czujnikami światła
skierowanymi w stronę planszy, po której jeździ. Równocześnie korzysta z z czujnika odo-
metrycznego do pomiaru kąta przy obrotach. Ponieważ są tylko trzy wejścia na czujniki —
dwa czujniki światła muszą być zwarte z odpowiednimi dwoma czujnikami odometrycznymi.
Robot odczytuje, więc de facto zbiorczą informację na temat pomiaru poziomu natężenia
światła i odometrii. Separacją odczytów zajmuje się napisana przez obu autorów obsługa
czujników w jądrze systemu operacyjnego LegOS.

Rozdział 7
Budowa planszy i robota
7.1
Budowa planszy
7.1.1
Założenia
Projektowana plansza musiała spełniać kilka założeń wynikających z ograniczeń robota mo-
bilnego i charakteru wykonywanego zadania. Ze względu na duże błędy czujników odome-
trycznych pojazdu przyjęto, że będzie on mógł się poruszać w dwóch ortogonalnych wzglę-
dem siebie kierunkach. Pozycja robota na planszy miała być dodatkowo zdyskretyzowana
co umożliwiało zaimplementowanie skutecznych algorytmów nawigacji, w sytuacji istotnych
ograniczeń sprzętowych. Błędy odometrii wymusiły też zastosowanie dodatkowych znacz-
ników na planszy, pełniących rolę punktów odniesienia, kalibrujących, a w tym przypad-
ku uściślających, pozycję pojazdu na planszy. Powyższe założenia implikowały zbudowanie
planszy z kwadratowych elementów utożsamianych z polami dyskretnej, geometrycznej siat-
ki mapy. Dodatkowo na planszy miały znajdować się znaczniki, położone pośrodku pól, bądź
pomiędzy nimi.
Względy praktyczne, związane z charakterem eksperymentów symulacyjnych, skłaniały
do zbudowania planszy z jednej strony prostej i taniej, a z drugiej trwałej i łatwej w re-
konfiguracji. Zastosowane materiały powinny być więc powszechnie dostępne, a więc i tanie.
Ważna jest ich wytrzymałość i przystosowanie do intensywnej eksploatacji. Wskazany była
wysoka masa pojedynczego pola, niwelująca ewentualne przesunięcia wynikające z przejazdu
robota czy nieostrożnej obsługi. Łatwość rekonfiguracji wiąże się głównie ze sposobem mo-
cowania pojedynczych pól do podstawy planszy. Pojedynczy element planszy nie mógł być
ani przyklejany ani mocowany w jakikolwiek inny trwały sposób.
Jak już wcześniej napisano właściwym kształtem pola jest kwadrat. Problemem pozosta-
je wyznaczenie jego optymalnej wielkości. Im z mniejszych pól będzie składała się plansza
tym więcej informacji znajdzie się na jej określonej powierzchni. Z drugiej strony wielkość
pola ograniczona jest przez możliwość skonstruowania bazy jezdnej robota zdolnej do po-

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
36
ruszania się po nim. Efektywna rozdzielczość czujnika natężenia światła montowanego w
robocie determinowała ilość możliwych do właściwego zaklasyfikowania barw podłoża. Roz-
miary planszy musiały być na tyle małe aby możliwy był swobodny dostęp do dowolnego jej
fragmentu.
Rysunek 7.1: Budowa planszy
7.1.2
Sposób wykonania
Projektowanie planszy rozpoczęto od zbudowania możliwie małej bazy jezdnej pojazdu, któ-
ra zdeterminowała długość boku kwadratowego pola planszy. Konstrukcja bazy zostanie
omówiona w sekcji dotyczącej budowy robota. Ostatecznie ustalono optymalne wymiary
pojedynczego pola na 10cm na 10cm. Doświadczenia płynące z poprzednich konstrukcji wy-
kluczały możliwość użycia papieru jako materiału, z którego zostaną wykonane pola. Papier
jest nietrwały, szybko się brudzi i nie można go skutecznie łączyć w sposób umożliwiają-
cy jego późniejsze rozdzielenie. Rozwiązaniem okazały się kafelki glazurnicze. Spełniały one
wszystkie, uprzednie założenia.
Jako podstawę planszy użyto kartonu. Zastosowanie takiego materiału było uzasadnio-
ne pomimo wad o których napisano wcześniej. Robot nie jeździ bezpośrednio po kartonie
a więc podstawa niszczy się w niewielkim stopniu. Co więcej, karton jest tani i ma wła-
ściwą barwę. Chcąc uczynić planszę łatwo modyfikowalną zdecydowano się na stworzenie
szkieletu w którym obsadzane będą kafelki. Szkielet ten ma postać ortogonalnej siatki. Je-
go głównym zadaniem jest uniemożliwienie kafelkom przesuwania się na boki. Naturalnym
budulcem szkieletu są, przyklejone na stałe do kartonu, krzyżyki glazurnicze, które ograni-
czają ruch kafelka klinując jego cztery wierzchołki. Chcąc usunąć kafelek po prostu wyjmuje
się go i odkłada na bok. Podobnie w dowolne puste pole można włożyć dodatkowy kafelek.

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
37
Szczeliny pomiędzy kafelkami, zwane dalej fugami, pełnią rolę znaczników lokalnych. Dzięki
nim pojazd może samolokalizować się. W toku długotrwałych eksperymentów mających na
celu zapewnienie dużej niezawodności wykonywania założonej trajektorii przyjęto szerokość
fugi wynoszącą 10mm. Przyczyny tego wyboru zostaną omówione dalej przy okazji opisu
bazy jezdnej robota. Szerokość fugi jest bezpośrednio zależna od szerokości krzyżyka, którą
wynosi także 10mm.
Ilość barw, które występują na planszy, wynika z faktycznej rozdzielczości czujników na-
tężenia światła. Warto podkreślić, że czujnik optyczny dostarczany w zestawach Mindstorms,
nie zwraca nominalnej informacji o barwie otoczenia, a jedynie wartość natężenia światła do
niego docierającego. Pomiar wspomagany jest diodą oświetlającą najbliższe sąsiedztwo czuj-
nika. W związku z tym odczyt zależy głównie od połyskliwości podłoża i odległości pomiędzy
oświetlanym obiektem a czujnikiem. Przykładowo błyszcząca czarna powierzchnia oddalona
od czujnika o 5mm może być tożsama z odległym o 10mm jasnoszarym, matowym wycin-
kiem papieru. Uzależnienie odczytu od odległości jest w tym wypadku niezmiernie istotne.
Pojazd w ruchu kołysze się, co powoduje, że odległość czujnika od podłoża jest zmienna w
czasie. Zależność ta jest trudna do uchwycenia i wykorzystania w celu korygowania odczytu.
Powyższe uwarunkowania spowodowały, że środowisko jest trójkolorowe.
Zarówno karton, który jest podstawą planszy, jak i przyklejone do niego krzyżyki są czar-
ne. Fragmenty kartonu znajdujące się pomiędzy sąsiadującymi kafelkami składają się wraz z
krzyżykami na fugi. Fugi mają więc także kolor czarny. Dodatkowo fugi są, z punktu widzenia
znajdujących się ponad nimi kafelków, zagłębieniami. Różnica odległości pogłębia dyspropor-
cję w natężeniu światła docierającego do czujnika. Kafelki mogą być białe bądź szare. Biały
jest naturalnym kolorem zakupionych kafelków. Jest to barwa znakomicie kontrastująca z
czarnymi fugami. Kolor szary, jest tak naprawdę barwą pośrednią pomiędzy białymi kafelka-
mi a czarnymi fugami, która można jeszcze poprawnie klasyfikować. Początkowo tę pośrednią
barwę uzyskiwano poprzez naklejanie fioletowego papieru na kafelki. Papier był niestety nie-
trwały a jego naklejanie pracochłonne. Szczęśliwie piąta z kolei zakupiona farba skutecznie
kryła kafelki, a odpowiadające jej natężenie światła plasowało się dokładnie pomiędzy zasto-
sowaną bielą i czernią. Pomalowane nią kafelki są matowoszare. Sposób przełożenia natężenia
światła na nominalną barwę podłoża zostanie omówiony w części poświęconej modyfikacji
jądra systemu operacyjnego legOS.
Fotografia 7.1 przedstawia proces budowy planszy. Początkowo na kartonie przyklejany
jest jeden, skrajny rząd krzyżyków. Przyklejanie kolejnych rzędów możliwie jest dzięki wy-
korzystaniu kafelków jako dystansów. Po zapełnieniu całej planszy kafelki są wyjmowane a
krzyżyki malowane na czarno. Po wyschnięciu całości można zapełniać planszę w dowolny
sposób, co umożliwia różnorakie testy. Na planszy widoczny jest, niestosowany już obecnie,
kafelek pokryty fioletowym papierem.

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
38
Rysunek 7.2: Mała plansza testowa
7.1.3
Wykorzystywane plansze
Pierwsza faza testów przebiegała na planszach o wymiarach 5 na 7 kafelków. Początkowo sze-
rokość fugi wynosiła 8mm. Na takiej planszy poruszał się robot MIŚ2. Plansza ta nie będzie
szerzej omówiona, gdyż została zastąpiona, dostosowaną do najnowszego pojazdu, planszą
o szerokości fugi 10mm. Przyczyną przebudowania całego systemu eksperymentalnego były
problemy z niezawodnością wykonywania zakrętów.
Plansza, na której przeprowadzono większość testów na etapie budowania robota i pisa-
nia sterującego nim programu, mierzyła także 5 na 7 kafelków, a jej fuga miała szerokość 10
milimetrów. Początkowo składała się z kafelków białych i pokrytych fioletowym papierem.
Obecnie wykorzystuje się te same białe kafelki, a pokrywanie papierem zastąpiono natryski-
waniem matowoszarej farby akrylowej. Zdjęcie 7.2 prezentuje małą planszę wraz ze stojącym
na jej skraju najnowszym modelem robota pobierającym dane z wieży Mindstorms.
Badania współdziałania programu wyznaczającego trajektorię w komputerze PC z robo-
tem mobilnym przeprowadzono na planszy analogicznej do poprzedniej, ale mierzącej 12 na
17 kafelków. Rys. 7.3 przedstawia jeden z testów przeprowadzanych na tej planszy.
7.2
Budowa robota
7.2.1
Założenia
Konstrukcja robota jest w pełni podporządkowana środowisku w którym się on porusza
i charakterowi wykonywanego przez niego zadania. Z drugiej strony, zaprojektowane śro-

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
39
Rysunek 7.3: Duża plansza testowa
dowisko eksperymentalne nie może przerastać możliwości robota. Doświadczenia płynące z
poprzednich projektów wskazywały na konieczność przyjęcia ortogonalnych kierunków ru-
chu. W punkcie 7.1 opisano szczegółowo planszę spełniającą to założenie. Robot, który miał
po niej jeździć, musiał posiadać dwie podstawowe umiejętności ruchowe:
• jazdy na wprost, nie przekraczając bocznych krawędzi kafelka,
• obracania się wokół własnej osi w zakresie 0 - 540
o
, przy możliwie małym przesunięciu
środka obrotu. Przyczyna wyboru takiego zakresu obrotu została omówiona w pkt. 8.3.
Współpraca z komputerem PC wymagała zbierania informacji o barwie napotkanych ka-
felków, a także przesyłania jej za pomocą łącza podczerwonego. Całość miała być wykonana
w oparciu o zestaw Mindstorms.
7.2.2
Charakterystyka ogólna
Powyższe założenia zdeterminowały konstrukcję robota. Najistotniejszym elementem każ-
dego pojazdu jest baza jezdna, decydująca o jego właściwościach motorycznych. Zostanie
ona opisana w punkcie 7.2.3. Za sterowanie kołami odpowiedzialny jest układ napędowy za-
prezentowany w punkcie 7.2.4. O możliwościach zbierania informacji o otoczeniu decydują
sensory pkt. 7.2.5. Komunikacja z komputerem PC nie byłaby możliwa bez wykorzystania
urządzenia nadawczo-odbiorczego w podczerwieni pkt. 7.2.6
Fotografie 7.4, 7.5, 7.8 prezentujące robota zawierają symbole ułatwiające identyfikację
poszczególnych elementów.

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
40
1 - Czujnik światła położony na przedzie prawej burty odpowiedzialny za kontrolowanie
najeżdżania na fugę położoną z prawej strony robota
2 - Czujnik światła umieszczony po środku przodu pojazdu kontroluje barwę podłoża, w
szczególności kafelka na który wjeżdża robot
3 - Czujnik światła położony na przodzie lewej burty odpowiedzialny za kontrolowanie
najeżdżania na fugę położoną z lewej strony robota
4 - Przednie kółko swobodne stabilizujące pojazd w osi podłużnej
5 - Tylne kółko swobodne stabilizujące pojazd w osi podłużnej
a - Prawo-burtowy czujnik odometryczny umieszczony na jednym wale z silnikiem A
b - Lewo-burtowy czujnik odometryczny umieszczony na jednym wale z silnikiem B
c - Lewo-burtowa przekładnia ślimakowa nasunięta na wał łączący czujnik odometryczny
b z silnikiem B
d - Koło zębate leżące na wspólnej osi z kołem e, przejmujące napęd z przekładni ślima-
kowej c
e - Lewe koło napędowe
A - Silnik położony na tyle prawej burty, napędzający prawe koło
B - Silnik położony na tyle lewej burty, napędzający lewe koło
IR - Urządzenie nadawczo-odbiorczo w podczerwieni
a)
b)
Rysunek 7.4: Lewa burta robota MIŚ 4: a) widok od przodu, b) widok od tyłu
Burty pojazdu są symetryczne, wobec czego wystarczające jest zaprezentowanie tylko
jednej z nich, w tym wypadku lewej. Tył robota nie zawiera żadnych istotnych elementów
wobec czego nie zamieszczono jego zdjęcia.

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
41
7.2.3
Baza jezdna
Baza jezdna zbudowana jest w układzie różnicowym. Składają się na nią cztery koła położone
w wierzchołkach rombu. Przekątne tego rombu pokrywają się z podłużną i poprzeczną osią
pojazdu. Dwa boczne koła są napędowe, kółko przednie i tylne stabilizują pojazd w osi
podłużnej. Rozkład kół w bazie jezdnej jest widoczny na zdjęciu 7.5. Kółko z numerem 4
zapobiega przechylaniu się pojazdu do przodu, kółko o numerze 5 zapobiega przechylaniu się
pojazdu do tyłu, koło oznaczone literą „e” jest lewym kołem napędowym. Po jego przeciwnej
stronie znajduje się nieoznaczone prawe koło napędowe. Kółka stabilizujące są swobodne.
Ustawiają się zgodnie z kierunkiem ruchu pojazdu. Każde z dwóch kół leżących na burtach
jest napędzane przez osobny silnik. Szczegóły przeniesienia napędu zostaną omówione w pkt.
a)
b)
Rysunek 7.5: Robot MIŚ4 a) widok z dołu pojazdu b) widok z góry pojazdu
Budowa bazy jezdnej została podyktowana założeniami opisanymi w pkt. 7.2.1. Jazda na
wprost odbywa się poprzez obracanie obu kół napędowych z tą samą prędkością w zgodnych
kierunkach. Obrót natomiast następuje w wyniku obracania kół z równymi prędkościami ale
w przeciwnych kierunkach. Eksperymenty wykazały że środek obrotu przesuwa się nie więcej
niż 5mm na 540
o
obrotu. Jest to wartość wystarczająca dla zapewnienia niezawodności tego
manewru. Szczegółowy sposób manewrowania zostanie opisany w pkt. 8.
Niewielkie rozmiary bazy jezdnej osiągnięto poprzez przeniesienie silników poza jej wnę-
trze. Dzięki temu możliwie było uzyskanie niewielkiego rozstawu, napędzanych od zewnętrz-
nej strony, kół napędowych. Kółka swobodne zostały umieszczone na przekątnej rombu pro-
stopadłej do cięciwy łączącej koła napędowe. Rozstaw kół swobodnych jest zbliżony do roz-
stawu kół napędowych. Dzięki temu podczas obrotu wszystkie koła zakreślają wspólny okrąg.
Przy takim rozmieszczeniu kół, rozmiary bazy jednej wynikają bezpośrednio z wielkości kloc-
ków zestawu Mindstorms. Ostatecznie osiągnięto bazę jezdną zdolną do poruszania się po
kafelkach o boku 10cm.
Szerszego omówienia wymaga zastosowana średnica kół napędowych. Nie ulega wątpliwo-
ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
42
ści, że zastosowanie dużych kół utrudnia zbudowanie małej bazy jezdnej. Pierwszy w pełni
funkcjonalny robot - MIŚ 2 - wyposażony był w koła napędowe o stosunkowo małej średni-
cy. Jego baza jezdna była wobec tego bardzo niewielka rys. 7.9. Niestety pomimo faktu, że
konstrukcja ta była bardzo udana, w szczególności znacznie mniejsza od obecnie stosowanej,
musiała zostać zastąpiona przez nową, wyposażoną w większe koła napędowe. Przyczyną tej
zmiany była konieczność zwiększenia szerokości fugi z 8mm do 10mm. Fuga 8mm okazała się
zbyt wąska. Długotrwałe testy ujawniły, że po zakończeniu niektórych obrotów robot usta-
wia się w niewłaściwym kierunku „przegapiając” 8mm fugę. Fakt ten wynikał bezpośrednio
z rozbieżności pomiędzy zakładaną a faktyczną wartością kąta wykonanego obrotu. Wartość
tego błędu była niekiedy zbyt wysoka. Taka sytuacja była niedopuszczalna, gdyż jednym
z najistotniejszych założeń projektu była bardzo wysoka niezawodność wykonywania zało-
żonej trajektorii. Fuga 10mm okazała się wystarczająco szeroka, żeby korygować kierunek
robota dla wszystkich, nawet najbardziej niedokładnych obrotów. Szczegółowy sposób uzy-
skania wysokiej dokładności obrotów zostanie omówiony dalej przy okazji opisu czujników
stosowanych w robocie pkt. 7.2.5 i układu napędowego pkt. 7.2.4. Niestety Robot MIŚ 2 nie
był przystosowany do jazdy po tak szerokiej fudze.
Akapity bieżący i poprzedni ilustrują niezwykle silną korelację pomiędzy konstrukcją
robota, programem sterującym i charakterystykami czujników. Fakt zastosowanie fugi sze-
rokości 10mm, podyktowany dokładnością wykonywanych obrotów, wymusił zastosowanie
kół napędowych dużej średnicy. Zależność tą ilustruje rys. 7.6. Użyte w nim symbole mają
następujące znaczenie:
Rysunek 7.6: Schemat momentu przejazdu przez fugę
k - płaszczyzna pokrywająca się z górna powierzchnią kafelka
p - równoległa do powierzchni ziemi płaszczyzna przechodzącą przez oś obrotu kół napę-
dowych
ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
43
h - odległość pomiędzy płaszczyzną p, a dolną krawędzią kółka swobodnego.
R - promień koła napędowego
W - szerokość fugi
y - odległość pomiędzy płaszczyzną p a płaszczyzną k
x - odległość pomiędzy płaszczyzną k a dolną krawędzią koła napędowego
Rysunek 7.6 pokazuje pojazd przejeżdżający prostopadle przez fugę, w momencie w któ-
rym koła napędowe znajdują się dokładnie ponad jej centrum. Przedstawiona sytuacja ma
charakter graniczny, kiedy to wartości y i h są sobie równe. Pojazd znajduje się wówczas na
granicy utraty przyczepności kół napędowych. W sytuacji kiedy y > h robot nieco się zapada
na granicy kafelków ale ostatecznie swobodnie przejeżdża przez fugę, natomiast kiedy y < h
zawisa w jej centrum lub przejedzie z rozpędu mając przez chwilę koła napędowe zawieszo-
ne w powietrzu. Pokonując fugę 10mm robot MIŚ 2 znajdował się w drugiej z opisanych
sytuacji.
Analiza rysunku prowadzi do następujących konkluzji: y
(7.1) R = y + x
z twierdzenia Pitagorasa:
(7.2) y =
s
R
2
− (
1
2
W )
2
(7.3) x = R − y = R −
s
R
2
− (
1
2
W )
2
przypadek graniczny
(7.4) y = h
Równanie (7.4) uzupełnione przez (7.2) daje
(7.5)
s
R
2
− (
1
2
W )
2
= h
Pełna przyczepność występuje w sytuacji kiedy
(7.6) y > h
Co daje w połączeniu z równaniem (7.2)
(7.7)
s
R
2
− (
1
2
W )
2
> h
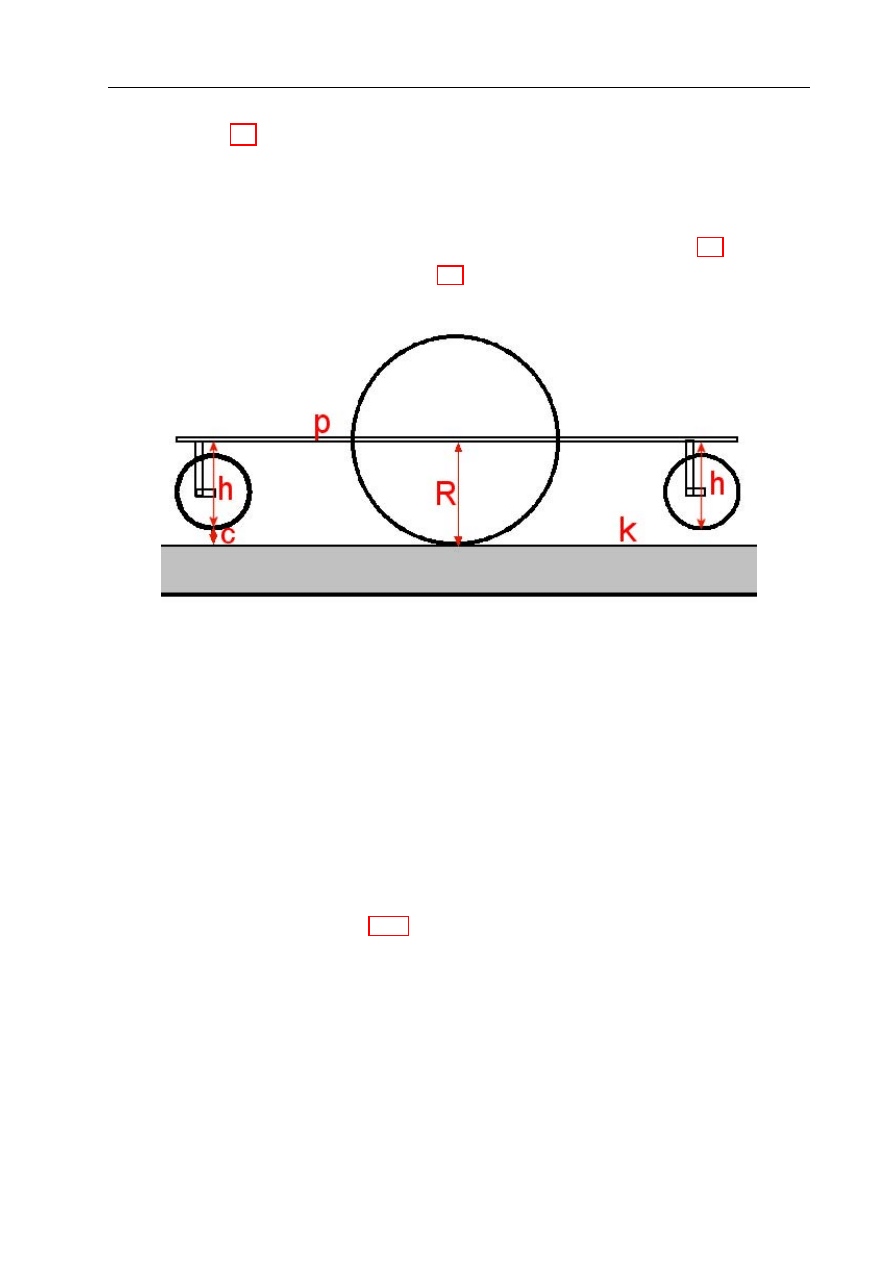
ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
44
Jak widać z (7.7) dla określonej szerokości fugi W poprawę przyczepności możemy uzyskać
zwiększając promień koła napędowego R bądź zmniejszając wartość h. Obydwie metody
są kłopotliwe i implikują niekorzystne następstwa. Jak napisano już wcześniej, duże koła
napędowe utrudniają zbudowanie zwartej bazy jezdnej. Pomniejszanie wartości h prowadzi
z kolei do kiwania się pojazdu wzdłuż osi podłużnej. Ilustruje to rysunek 7.7. Znaczenie
symboli jest zgodne zastosowanym na rys. 7.6 Nie występująca poprzednio litera c oznacza
średni prześwit pomiędzy dolnym krańcem kółka stabilizującego a powierzchnią kafelka.
Rysunek 7.7: Schemat jazdy po kafelku
Związek pomiędzy prześwitem c, promieniem R - wysokością h przedstawia poniższe
równanie:
(7.8) c = R − h
Korzystne jest wybranie możliwie najmniejszej wartości „c” dla której robot już się nie śli-
zga. Wartość prześwitu wpływa bowiem bezpośrednio na różnicę pomiędzy najmniejszą i
największą odległością czujników światła od podłoża. Im większe wahania w odległości czuj-
nika od podłoża tym większe różnice w wartości odczytu dla określonej barwy. Zagadnienie
to zostanie szerzej opisane w pkt. 7.2.5
Analiza przedstawiona powyżej pozwoliła na dobór optymalnych wartości średnicy koła
napędowego „R” i prześwitu „c” dla fugi o szerokości 10mm. Rozstaw kół napędowych
wynosi 57mm a ich średnica 85mm. Kółka swobodne dzieli odległość 78mm a ich średnica jest
znacznie mniejsza niż kół napędowych i wynosi 25mm. Prześwit „c” wynosi 3mm. Związane
z nim wahania odległości pomiędzy czujnikiem światła a podłożem zadecydowały o ilości
niezawodnie klasyfikowanych kolorów podłoża.
Przedstawiona baza jezdna jest nieholonomiczna. Nie przeszkadza to jednak w stosowaniu
metod planowania toru charakterystycznych dla holonomicznych robotów mobilnych. Wła-
ściwości dynamiczne pojazdu powodują, że droga hamowania robota z pełnej osiąganej przez

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
45
niego prędkości jest niezwykle krótka. Wynika to bezpośrednio z relatywnie niskiej, w stosun-
ku do mocy silników i przyczepności kół, prędkości ruchu pojazdu. Każda zmiana kierunku
wektora prędkości wiąże się z bardzo krótkim hamowaniem, obrotem i przyspieszaniem. Eks-
perymenty wykazały, że manewr ten zachodzi praktycznie w miejscu, choć pochłania pewien
czas, zależny głównie od rozbieżności pomiędzy początkową i końcową orientacją robota.
Towarzyszące manewrowi przesunięcie punktu zaczepienia wektora prędkości jest pomijalne.
Wpływają na to nie tylko opisane wcześniej właściwości dynamiczne pojazdu, ale i postać
środowiska, w którym się on porusza, a w szczególności relatywnie duża wielkość kafelków
i dodatkowa informacja płynąca z fug, która pozwala na skuteczne korygowanie ewentual-
nych przesunięć. Całość powoduje, że baza jezdna robota jest postrzegana przez warstwę
planowania toru sterującego nim programu tak, jak postrzegane są bazy jezdne robotów
holonomicznych. Sposób sterowania robotem zostanie szerzej opisany w pkt. 8
7.2.4
Układ napędowy
Konstruowany układ napędowy musiał spełniać kilka kryteriów:
• Posiadać niewielkie rozmiary i prostą możliwa do zastosowania konstrukcję.
• Luz pomiędzy wałem silnika a kołem napędowym powinien być jak najmniejszy.
• Moment generowany na kole napędowym powinien być relatywnie wysoki, tak aby
hamowanie i przyspieszanie odbywało się na bardzo krótkich odcinkach.
• Umieszczenie czujnika odometrycznego musi pozwalać na uzyskanie rozdzielczości od-
czytu adekwatnej do potrzeb związanych z pożądaną dokładnością wykonania założo-
nego kąta obrotu.
Układ napędowy robota MIŚ 2 przedstawionego na rys. 7.9 spełniał wszystkie powyższe
kryteria. Niestety nie mógł on zostać przeniesiony do robota MIŚ 4. Zastosowany w najnow-
szej konstrukcji układ napędowy jest, podobnie jak jego poprzednik, symetryczny względem
osi podłużnej robota; część lewo-burtowa napędza lewe koło napędowe a prawo-burtowa -
prawe koło napędowe. Obie części są identyczne. W dalszej części omówiona zostanie sekcja
położona po lewej stronie robota.
Rozmieszczenie poszczególnych elementów układu napędowego najlepiej ilustruje prawa
fotografia rysunku 7.8. Przyjęte oznaczenia są zgodne z objaśnionymi w pkt. 7.2.2. Silnik
„B” wprawia w ruch koło napędowe „e” za pośrednictwem przekładni ślimakowej „c” i koła
zębatego „d”. Przekładnia ślimakowa „c” leży na wspólnym wale z silnikiem „B” i czujni-
kiem odometrycznym ”b”, niewidocznym bezpośrednio na zdjęciu. Koło zębate „d” leży na
wspólnej osi z kołem napędowym „e”. Jak widać układ przeniesienia napędu jest bardzo

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
46
prosty i zwarty a jedyny istotny luz występuje między elementami „c” i „d”. Sumaryczne
luzy są mniejsze od obserwowanych w poprzedniej konstrukcji.
a)
b)
Rysunek 7.8: a) widok przodu pojazdu, b) widok lewej burty pojazdu
Oprócz luzów, na niedokładności w wykonaniu założonego kąta obrotu koła napędowego
wpływa też skręcanie się wału silnika i osi koła napędowego. O ile skręt wału silnika jest
bardzo niewielki, o tyle skręt osi koła napędowego nie może zostać pominięty. Sam fakt
skręcania się osi ma miejsce podczas hamowania, po manewrze zmiany orientacji całego
robota. Hamowanie jest niezwykle skuteczne co w dużej mierze wynika z właściwości prze-
kładni ślimakowej, która praktycznie uniemożliwia przenoszenie się ruchu obrotowego koła
na ruch obrotowy wału silnika, w sytuacji kiedy ten drugi jest zablokowany. Fakt ten powo-
duje, że część energii kinetycznej ruchu obrotowego całego pojazdu przechodzi, w sytuacji
braku poślizgu kół, w energię potencjalną naprężeń osi. Szczęśliwie koła nie tracą kontak-
tu z nawierzchnią i powstaje ruch oscylacyjny objawiający się naprzemiennym kołysaniem
się robota to zgodnie to przeciwnie do ruchu wskazówek zegara. Oscylacje mają charakter
gasnący i po pewnym czasie ustają, a cała energia przechodzi w ciepło. Warto podkreślić,
że fakt zachowania przyczepności wynika z właściwego doboru trących o siebie materiałów,
momentów występujących na kołach i prędkości ruchu obrotowego. Występowanie oscyla-
cji wpływa na sposób wykonywania obrotu, w którym to po hamowaniu następuje krótki
przestój, podczas którego koła są zablokowane, a oscylacje ustają, co pozwala na późniejsze
precyzyjne przyspieszenie we właściwym kierunku.
Na przeprowadzenie skutecznych manewrów przyspieszania i hamowania pozwala silnik
prądu stałego charakteryzujący się wysokim momentem i krótkim czasem reakcji na zadane
sterowanie. Moment generowany na wale silnika jest na tyle wysoki, że możliwa jest pra-
wie natychmiastowa zmiana prędkości koła napędowego, które z racji dużego promienia ma
niepomijalny moment bezwładności.
Silnik pracuje w czterech zasadniczych trybach:
1. Obracania się do przodu z zadaną mocą.

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
47
2. Obracania się do tyłu z zadaną mocą.
3. Zablokowania wału.
4. Luzu na wale.
Tryby luzu na wale i zablokowania wału funkcjonują bez większych zarzutów. W szcze-
gólności tryb zablokowania pozwala na szybkie hamowanie. Natomiast tryb obracania się z
założoną mocą nie pozwala na jazdę z różnymi prędkościami o czym pisano już w pkt. 5.1.4
Opisany w tym samym punkcie problem wpływu początkowego stanu na wejściu silnika
na opóźnienie reakcji na zadane sterowanie rozwiązano poprzez wyłączanie silnika na krótki
czas, około 100ms, w sytuacji konieczności zmiany kierunku jego obrotu.
Umieszczenie czujnika odometrycznego na wspólnej osi z silnikiem powoduje, że może
on wiernie odwzorowywać zmiany kąta bezpośrednio na wale silnika. Koło napędowe z kolei
dzieli od silnika tylko jedna przekładnia charakteryzująca się w dodatku niewielkimi luzami.
Dzięki temu czujnik odometryczny z niewielkim błędem odwzorowuje faktyczny kąt obrotu
koła napędowego. Funkcjonowanie pomiaru odometrii zostanie szerzej omówione w pkt. 7.2.5.
Rysunek 7.9: MIŚ 2
7.2.5
Zastosowane czujniki
W zbudowanym robocie zamontowano 5 czujników: 3 światłoczułe i 2 odometryczne.
Czujniki światła
Wszystkie czujniki światła zostały umieszczone z przodu pojazdu i są skierowane do dołu,
tak aby odczytywać barwę podłoża. Sensory pracują w trybie aktywnym, oświetlając swoje
otoczenie, co poprawia dokładność odczytów. Dwa czujniki umieszczono na burtach pojazdu.
Ich zadaniem jest wykrywanie momentu najeżdżania na fugę, dzięki czemu możliwe jest
utrzymanie kierunku jazdy na wprost. Trzeci czujnik umieszczono pośrodku przodu pojazdu.
ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
48
Musi on nie tylko wykrywać moment przejazdu przez fugę a więc i przekraczania kafelka,
ale także określać kolor kafelka, który się pod nim znajduje. Rozmieszczenie czujników jest
najlepiej widoczne na rysunku 7.5 przedstawiającym bazę jezdną pojazdu.
Poważnym problemem jest zmieniająca się w czasie odległość czujników od podłoża. Jej
wahania negatywnie wpływają na efektywną rozdzielczość czujników zwiększając przedział
wartości natężenia światła odpowiadający każdej barwie. Poprawna klasyfikacja wymaga
rozłączności przedziałów, co bezpośrednio wpływa na mniejszą ilość barw, które można nie-
zawodnie klasyfikować. Przyczyną różnic w odległościach pomiędzy podłożem a czujnikiem
jest kołysanie się pojazdu omówione w pkt. 7.2.3.
Charakterystyka czujników światła została omówiona w teoretycznej części pracy pkt.
5.1.3. Sposób translacji odczytu natężenia światła na barwę podłoża zostanie omówiony w
pkt. 8.9 poświęconym modyfikacjom systemu operacyjnego legOS. Wykorzystanie informacji
o barwie podłoża omówione zostanie w części traktującej o programie robota pkt. 8.
Czujniki odometryczne
Pierwsza wersja pojazdu MIŚ nie miała czujników odometrycznych. Pomiar kąta obrotu od-
bywał się poprzez pomiar czasu wykonania tego obrotu. Metoda ta była bardzo niedokładna
i niesłychanie wrażliwa na poziom napięcia na akumulatorach i temperaturę otoczenia. Wy-
mienione czynniki wpływały na moc silników co z kolei odbijało się na prędkości kątowej wału
silnika. Zastosowanie czasowych kryteriów ruchu nie pozwalało na poprawne wykonywanie
zadania. Wobec tego konieczny był zakup czujników odometrycznych.
Kolejne wersje pojazdu, aż do obecnej, wyposażone były w dwa czujniki odometryczne.
Każdy z nich mierzył kąt na jednym z kół napędowych. Umiejscowienie czujników zostało
omówione już wcześniej przy okazji opisu układu napędowego w pkt. 7.2.4. Rysunek 7.4
wydaje się najlepiej obrazować wzajemne położenie czujnika odometrycznego, silnika i prze-
kładni.
Sposób działania czujników odometrycznych został już opisany w pkt. 5.1.3. W budowa-
nym robocie każdemu pełnemu obrotowi koła napędowego odpowiadało około 384 zliczeń na
czujniku odometrycznym. Pełny obrót robota wokół własnej osi rejestrowany był jako 555
zliczeń. Taka rozdzielczość wystarcza do precyzyjnego skręcania.
Sposób podłączenia czujników
Komputer RCX ma trzy wejścia czujnikowe. W budowanym robocie zastosowano aż pięć
czujników, dlatego cztery z nich trzeba było połączyć w pary. Lewy czujnik odometryczny
zwarto z lewym czujnikiem światła i podłączono do lewego wejścia czujnikowego RCX. Środ-
kowy czujnik światła podłączono do środkowego wejścia, a prawe czujniki, po ich zwarciu,
do prawego wejścia. Podłączenie czujnika światła i odometrii do jednego wejścia RCX wy-

ROZDZIAŁ 7. BUDOWA PLANSZY I ROBOTA
49
musiło zmiany w jądrze systemu operacyjnego legOS, który nie był wcześniej przygotowany
do obsługi takiej pary. Zagadnienie to zostanie omówione w pkt. 8.9.
7.2.6
Urządzenie nadawczo-odbiorcze w podczerwieni
Komunikacja z komputerem PC jest możliwa dzięki wykorzystaniu urządzenia nadawczo-
odbiorczego w podczerwieni znajdującego się z przodu pojazdu. Jego umiejscowienie najle-
piej obrazuje rys. 7.8 Do nawiązania komunikacji konieczne jest zwrócenie RCX’a przodem
do wieży podłączonej do portu szeregowego komputera PC. Szczegóły przebiegu transmisji
zostały już opisane w teoretycznej części pracy w pkt. 5.1.5. Łącze podczerwone wykorzysty-
wane jest do ładowania systemu operacyjnego legOS i programu robota. Po uruchomieniu
programu robota kanał służy do przesyłania danych pomiędzy pojazdem a komputerem PC.

Rozdział 8
Program robota
8.1
Założenia
Program robota musiał spełniać szereg założeń wynikających z charakteru zadania i specyfiki
środowiska sprzętowego. Założenia wynikające z postawionego zadania sprowadzają się do
pewnych cech funkcjonalnych, które winien posiadać robot:
1. Pobranie z komputera PC mapy środowiska i trajektorii do pokonania.
2. Pokonanie trajektorii na planszy opisanej w pkt. 7.1
3. Inteligentne omijanie niespodziewanych przeszkód na planszy, przy wykorzystaniu pla-
nera trajektorii do poszukiwania najkrótszej drogi objazdu.
4. Aktualizowanie mapy na podstawie informacji zdobytej podczas pokonywania trajek-
torii.
5. Powrót do punktu startowego i przesłanie do komputera PC zaktualizowanej mapy
środowiska.
Warto nadmienić że plansza i robot powstawały równolegle a ich rozwój był silnie powią-
zany. Przykładowo rozpoznanie możliwości środowiska Mindstorms doprowadziło do opraco-
wania sposobu zaznaczania przeszkód na planszy. Najlepszą metodą okazało się wyjmowanie
kafelków. Taki sposób oznaczania ubytków nie wymagał stosowania dodatkowych czujników
dotykowych i był prosty w interpretacji przez program robota.
Ograniczenia środowiska sprzętowego opisane są w pkt. 5.1. Program robota musiał przy-
stawać do tych ograniczeń. Najistotniejsze założenia wypływające z tego faktu zostały przed-
stawione poniżej:
1. Konieczność napisania programu jako aplikacji systemu operacyjnego legOS.

ROZDZIAŁ 8. PROGRAM ROBOTA
51
2. Powstająca aplikacja musiała działać w czasie rzeczywistym sterując robotem podczas
wykonywania zadania.
3. Program robota musiał być dostosowany do charakterystyk czujników i elementów
wykonawczych.
4. Sumaryczny rozmiar programu i systemu operacyjnego nie mógł przekroczyć 32KB.
O ile pierwsze trzy założenia są naturalne i nie wpłynęły negatywnie na proces tworzenia
aplikacji o tyle ostatnie przysporzyło wielu trudności. Konieczność ograniczania zajętości pa-
mięci wpływała negatywnie na czas poświęcony na tworzenia kodu programu. Zmniejszanie
aplikacji wiązało się bowiem z zastosowaniem wielu czasochłonnych sztuczek programistycz-
nych takich jak zastępowanie konstrukcji „switch” konstrukcją „if-else”. Ta i inne metody
ograniczania długości kodu wynikowego opisane są w pkt. 5.2.1 Konsekwentne stosowanie
tych metod pozwoliło na połączenie wzrostu funkcjonalności programu z utrzymywanie jego
całkowitego rozmiaru w granicach 9 KB.
8.2
Architektura programu
Program, który powstał, spełnia wszystkie powyższe założenia, dzięki czemu robot popraw-
nie wykonuje postawione przed nim zadanie. Najlepszą organizacją programu okazało się
podzielenie go na warstwy. Metoda ta jest charakterystyczna dla nowoczesnych aplikacji
robotycznych. Jej zastosowanie wypływało z analizy założeń, a nie zapoznania się ze stosow-
ną literaturą, które nastąpiło później. Fakt, że samodzielna analiza doprowadziła do wnio-
sków zgodnych z opracowaniami teoretycznymi jest jeszcze jednym potwierdzeniem słuszno-
ści przyjętej metody.
Skuteczność i uniwersalność metody warstwowej wiąże się z możliwością dekompozycji
rozwiązywanego problemu. Pozwala to na rozwiązanie złożonych zadań. Taka sytuacja miała
też miejsce tutaj. Opisywany program składa się z dwóch warstw:
• podrzędnej warstwy ruchu,
• nadrzędnej warstwy nadzoru.
Tylko warstwa ruchu ma bezpośredni dostęp do funkcji jądra systemu operacyjnego od-
wołujących się do czujników i elementów wykonawczych. Warstwa nadzoru wykorzystuje in-
formacje zebrane przez warstwę ruchu i wyznacza sterowania dla niej. Korzysta też z szeregu
modułów realizujących poszczególne przypisane jej funkcje. Tak więc moduł komunikacyjny
odpowiada za przesyłanie danych na linii robot - komputer PC. Moduł przetwarzania trajek-
torii przygotowuje dyrektywy dotyczące ruchu robota. Modyfikacja trajektorii jest możliwa
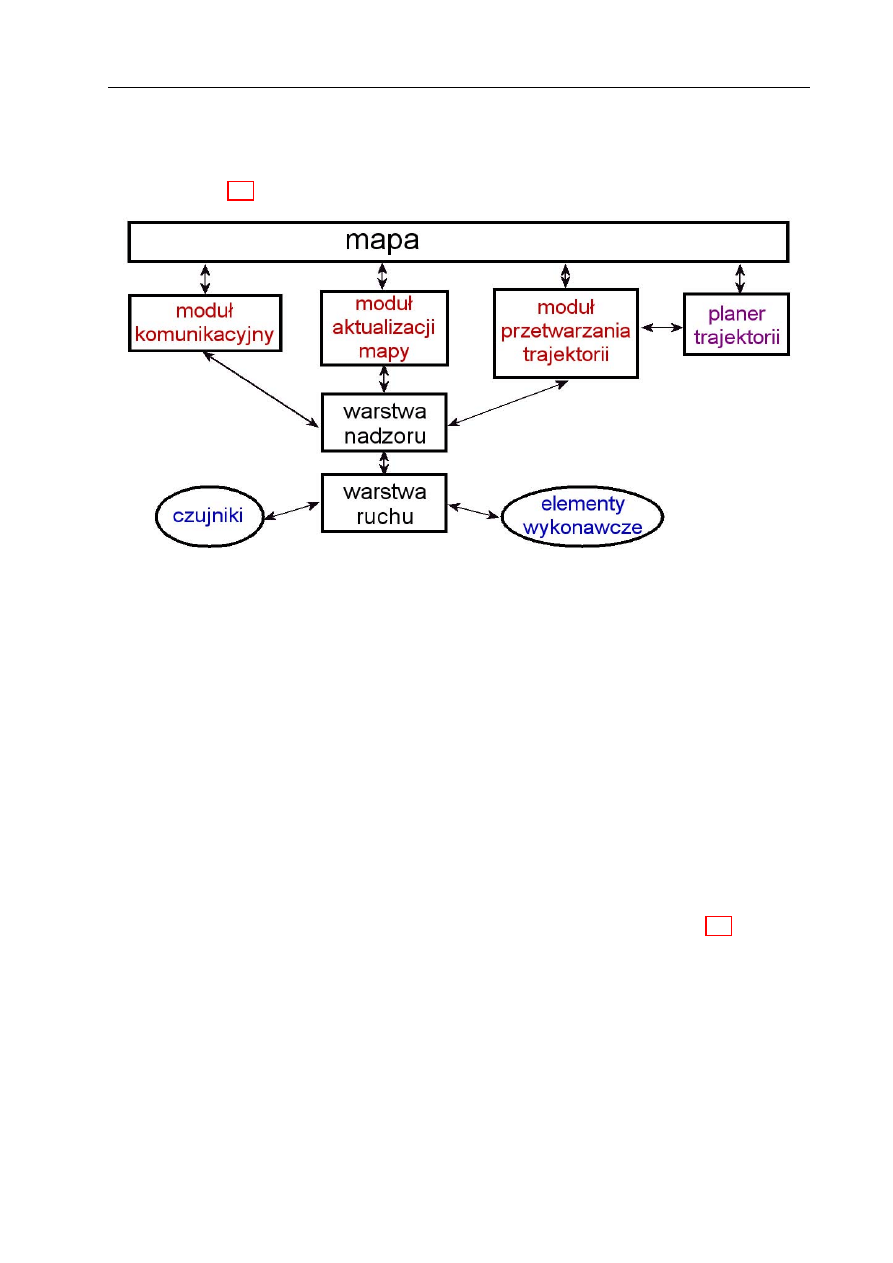
ROZDZIAŁ 8. PROGRAM ROBOTA
52
dzięki planerowi trajektorii wyznaczającemu objazdy. Uzyskane podczas jazdy informacje o
zmianach na planszy są przetwarzane w module aktualizacji mapy. Całość ilustruje schemat
blokowy na rys 8.1
Rysunek 8.1: Organizacja programu
8.3
Warstwa ruchu
Warstwa ruchu odpowiada za:
• Wszelkie aspekty związane z poruszaniem się robota, w szczególności prawidłowe wy-
konywanie dyrektyw ruchowych wydanych przez warstwę nadzoru;
• Zbieranie informacji o barwie kafelków znajdujących się na trasie robota i przekazywa-
nie jej do warstwy nadzoru.
Trzonem warstwy ruchu jest czterostanowy automat przedstawiony na rys. 8.2. Każdy ze
stanów odpowiada logicznie pewnemu rodzajowi ruchu wykonywanego przez pojazd.
Warstwa ruchu rozpatrywana na poziomie całego automatu ma charakter behawioralny,
gdyż sposób funkcjonowania robota zależny jest od stanu, w którym się on znajduje. Dla
konkretnego stanu program jest reaktywny a działanie robota sprowadza się do prostych
odpowiedzi na wejścia czujnikowe i stany semaforów. Zmiana stanu następuje w momencie, w
którym spełnione zostaną pewne warunki oznaczone symbolicznie małymi literami. Warunki
te związane są z odczytami z czujników światła a także dyrektywami warstwy nadzoru.
Poniżej zamieszczono objaśnienia każdego ze stanów i warunków przejść międzystano-
wych. I tak:
ROZDZIAŁ 8. PROGRAM ROBOTA
53
Rysunek 8.2: Automat realizowany w warstwie ruchu
0 - Stan pojazdu inicjowany jako pierwszy, zaraz po uruchomieniu robota. Pojazd w sta-
nie 0 jedzie na wprost po kafelku, starając się nie najeżdżać na fugi i badając czy nie
wjeżdża na nowy kafelek. Zasygnalizowanie czarnej barwy podłoża przez czujnik lewo-
burtowy powoduje niewielki skręt w prawo. Analogicznie znalezienie się ponad fugą
czujnika prawo-burtowego implikuje korektę kierunku w lewo. Środkowy czujnik świa-
tła bada barwę podłoża z przodu pojazdu. Fugi znajdujące się na zewnątrz pojazdu są
o wiele trudniejsze w interpretacji niż pojedyncza fuga biegnąca po środku pojazdu.
Zagadnienie to zostanie omówione w pkt. 8.3.1.
a - Warunkiem przejścia programu ze stanu 0 do 1 jest zarejestrowanie fugi przez środkowy
czujnik światła. Moment ten stanowi jednoznaczną informację o dokładnej pozycji ro-
bota. Od tej chwili rozpoczynają się przygotowania do ewentualnego wykonania obrotu.
Ostatnim manewrem wykonywanym jeszcze w stanie 0 jest jazda na wprost mająca na
celu zgranie środka obrotu pojazdu ze środkiem kafelka, przez który przejeżdża pojazd.
Pokrycie się obu punktów jest sygnalizowane przez funkcję badająca różnicę odczytów
kąta na kołach napędowych w momencie najechania na fugę i w chwili obecnej. W
momencie, w którym różnica przekroczy pewną wartość krytyczną pojazd jest zatrzy-
mywany. Mechanizm ten wykorzystywany jest także przy trzykrotnym badaniu barwy
podłoża znajdującego się pod środkowym czujnikiem światła. Trzy kolejne pomiary
mają miejsce tuż przed osiągnięciem końca odcinka przejazdu na wprost. Dzieląca je
odległość jest bardzo niewielka. Zastosowanie aż trzech pomiarów miało na celu zapew-
nienie wysokiej niezawodności określania barwy podłoża. O barwie przekazywanej do
warstwy nadzoru decyduje głosowanie. Zasada trzykrotnego odczytu wykorzystywana
jest przy wszystkich pomiarach koloru podłoża.

ROZDZIAŁ 8. PROGRAM ROBOTA
54
1 - Stan ten jest zdecydowanie najbardziej skomplikowany. Robot wykonuje w nim sze-
reg manewrów prowadzących do wykonania ruchu zaleconego przez warstwę nadzoru.
Operacjom tym towarzyszy zbieranie informacji o barwie kafelków napotkanych przez
środkowy czujnik światła.
Po wejściu w stan 1 robot znajduje się dokładnie po środku kafelka. Znana jest też bar-
wa kafelka pod środkowym czujnikiem światła. Zadaniem robota jest teraz wykonanie
szeregu manewrów przekazanych przez warstwę nadzoru. Manewry te sprowadzają się
do obrotów wokół własnej osi o całkowitą wielokrotność 90
o
. Mają one określoną hie-
rarchię. Najpierw wykonywany jest manewr pierwszy. Jeśli zakończy się on sukcesem
decyzję o dalszym ruchu podejmuje warstwa nadzoru. Porażka podczas wykonania
pierwszego manewru powoduje przystąpienie do wykonania drugiego. Manewry wy-
konywane są do chwili aż jeden z nich zakończy się sukcesem albo zostanie wykonany
ostatni z nich. Przez manewr zakończony sukcesem rozumie się taką operację, po której
zakończeniu środkowy czujnik optyczny robota znajduje się ponad kafelkiem. Następ-
stwem udanego manewru jest prawie zawsze jazda na wprost. Niepowodzenie ostatnie-
go z zaleconych manewrów implikuje konieczność wykonania nowej serii operacji, gdyż
wjechanie na pole planszy, na którym nie ma kafelka, jest niedopuszczalne.
Działanie funkcji wykonującej manewry zilustruje następujący przykład. Warstwa nad-
zoru daje następujące zalecenie: jedź na wprost, jeśli to się nie uda, to jedz w prawo;
jeśli i to się nie uda, to zawróć; Wszystkie kierunki określone są względem początkowej
orientacji robota. Pojazd przystępuje do wykonania zadania. Kolor podłoża znajdują-
cego się przed pojazdem niesie informację o tym, czy znajduje się tam kafelek. Stan
0 stwierdził, że podłoże przed robotem jest czarne, a więc w kierunku na wprost nie
ma kafelka. Warstwa ruchu przystępuje więc do wykonania kolejnego manewru, tym
razem do skrętu o 90
o
w prawo. Skręt ten jest realizowany w ten sam sposób co jazda
na wprost, opisana w poprzednim punkcie. Moment zakończenia skrętu sygnalizowany
jest przez funkcję badającą kąty obrotu kół napędowych. Podobnie jak to miało miej-
sce przy jeździe na wprost, wykonywaniu obrotu towarzyszy trzykrotny pomiar barwy
podłoża znajdującego się pod czołem pojazdu. Pomiar ten prowadzi do wyznaczenia
koloru kafelka leżącego na prawo od początkowej pozycji robota, bądź stwierdzenia
braku tego kafelka. Gdyby okazało się, że w badanym miejscu leży kafelek, warstwa
ruchu przekazałaby do warstwy nadzoru informację o fakcie powodzenia wykonanego w
prawo skrętu i dodatkowo barwy dwóch zbadanych kafelków. Brak kafelka oznaczałby
przystąpienie do ostatniego manewru - zawrócenia. Gdyby i ten manewr zakończył się
niepowodzeniem warstwa nadzoru otrzymałaby informację o bieżącej orientacji robo-
ta, fakcie niepowodzenia wszystkich manewrów i barwach trzech napotkanych podczas
obrotu kafelków.
Warstwa nadzoru może zalecić szereg manewrów będący dowolną kombinacją jazdy

ROZDZIAŁ 8. PROGRAM ROBOTA
55
na wprost, skrętu w prawo, skrętu w lewo i zawrócenia. Długość tej serii mieści się
w zakresie od jednego do czterech elementów. W szczególności zalecany może być po-
jedynczy manewr jazdy na wprost bądź zawrócenia. Funkcja wykonująca manewry
została napisana w taki sposób, żeby maksymalnie wykorzystywać zdobytą podczas
jazdy informację o fakcie występowania bądź nie otaczających pojazd kafelków. Dzięki
temu manewry z góry skazane na niepowodzenie nie są w ogóle wykonywane. Przy-
kładem może być wykonanie dyrektywy warstwy nadzoru w postaci: w prawo a w
przypadku niepowodzenia prosto. Pojazd najpierw skręci w prawo. Jeśli manewr ten
nie powiedzie się to obrót o kolejnych 270
o
zgodnie z ruchem wskazówek zegara nastąpi
tylko wówczas, jeśli wcześniej stwierdzono, że po jego zakończeniu czoło pojazdu stanie
ponad kafelkiem.
Pierwszy z manewrów różnych od jazdy na wprost wykonywanych w danej serii decy-
duje o kierunku w którym będzie obracał się pojazd. Skręt w prawo i zawrócenie wiąże
się z obrotem zgodnie z ruchem wskazówek zegara, skręt w lewo z obrotem przeciwnie
do ruchu wskazówek zegara. Kierunek obrotu dla danej serii manewrów nie zmienia
się. Maksymalny kąt o jaki obraca się pojazd podczas wykonywania jednej serii wy-
nosi 540
o
. Dokładność tego obrotu jest na tyle wysoka, że po jego zakończeniu pojazd
zawsze podąża we właściwym kierunku.
Po zakończeniu opisanych powyżej manewrów warstwa nadzoru odczytuje informacje
o ich przebiegu. Ich analiza prowadzi do podjęcia decyzji o następnym stanie w którym
znajdzie się warstwa ruchu.
b - Warstwa nadzoru może podjąć decyzję o pozostaniu warstwy ruchu w stanie 1 i wyko-
naniu kolejnej serii manewrów. Sytuacja taka ma miejsce w dwóch przypadkach:
1. Pojazd najpierw wykonuje zwrot w kierunku wieży podłączonej do komputera PC,
a następnie po zakończeniu przesyłania danych ponownie obraca się wjeżdżając
na początek trasy.
2. Wszystkie manewry z danej serii zakończyły się niepowodzeniem i pojazd ponow-
nie obraca się kierując się w stronę początku trasy.
c - Warstwa nadzoru podejmuje decyzję o przejściu pojazdu w stan uśpienia (stan 3) —
kiedy dalsze manewrowanie nie rokuje nadziei na wykonanie zadania.
d - Każdy udany manewr, za wyjątkiem zwrotu w kierunku wieży, pociąga za sobą przejście
warstwy ruchu w stan 2.
2 - Stan, w którym znajduje się pojazd zjeżdżający z kafelka. Po zakończeniu obrotu naj-
pierw silniki są blokowane i wyłączane na około 100ms. Pozwala to na precyzyjne ru-
szenie do przodu, następujące chwilę później. Ruch do przodu trwa do chwili spełnienia
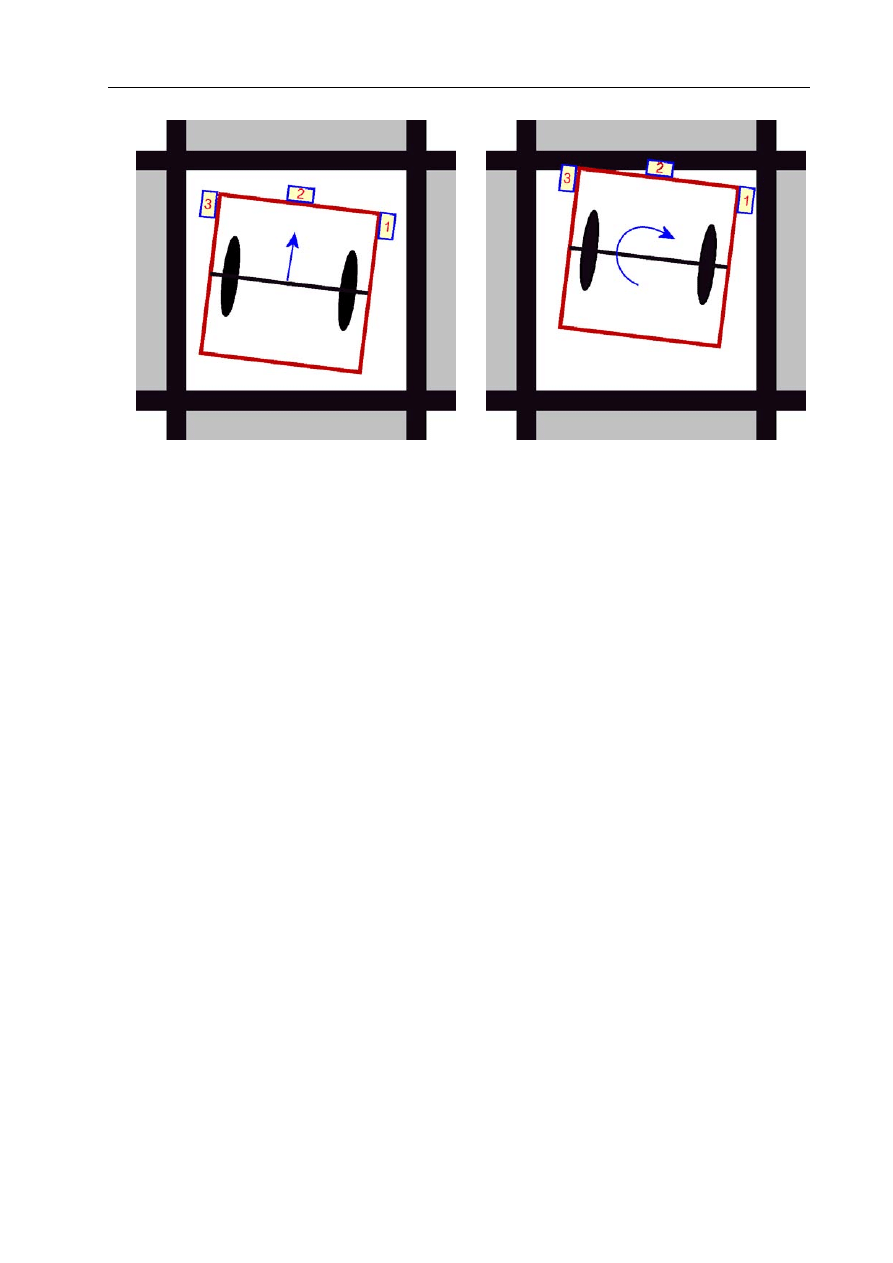
ROZDZIAŁ 8. PROGRAM ROBOTA
56
a)
b)
Rysunek 8.3: Niepoprawne przekraczanie fugi leżącej z przodu pojazdu wynikające z braku
pomiaru barwy podłoża pod środkowym czujnikiem światła: a) etap 1 , b) etap 2
warunku zmiany stanu. Stan 2 różni się od 0 jednym bardzo istotnym szczegółem. W
stanie 2 najechanie na fugę jednym z czujników nie pociąga za sobą korekty kursu.
Zagadnienie to zostanie omówione nieco dalej.
e - Przejście ze stanu 2 do 0 może nastąpić w dwóch przypadkach:
1. Kiedy oba burtowe czujniki światła znajdą się ponad fugą.
2. Po upływie pewnego maksymalnego czasu trwania stanu 2.
8.3.1
Trudności związane z umieszczeniem fug na zewnątrz pojaz-
du
Fugi znajdujące się na zewnątrz pojazdu są o wiele trudniejsze w interpretacji niż pojedyncza
fuga biegnąca po środku pojazdu. Główna trudność sprowadza się do momentu przekraczania
granicy między kafelkami. Pojazdy korzystające z fugi centralnej mają dwa czujniki leżące
z jej prawej i lewej strony. Najechanie na fugę lewym czujnikiem powoduje korektę kursu
w lewo, a prawym czujnikiem w prawo. Zmiana pola wiąże się z wykonaniem manewru na
linii przecięcia się dwóch fug. Manewr ten jest o tyle prosty, że stosowanie się do zasad
obowiązujących podczas jazdy na wprost prowadzi do prostopadłego ustawienia się do fu-
gi przecinającej tę, wzdłuż której dotychczas poruszał się pojazd. Prostopadłe ustawienie
powoduje najechanie na fugę obydwoma czujnikami barwy podłoża, co jest jednoznacznym
znakiem wjazdu na skrzyżowanie.
ROZDZIAŁ 8. PROGRAM ROBOTA
57
Zbudowanie planszy z kafelków pociągało za sobą konieczność korzystania z fug znajdu-
jących się na zewnątrz pojazdu. Jazda na wprost także i w tym przypadku jest stosunkowo
prosta. Najechanie lewym czujnikiem powoduje korektę kursu w prawo, a prawym czujnikiem
korektę kursu w lewo.
W dalszej części zostaną opisane dwa rozwiązania problemu przekraczania granicy po-
między kafelkami: z wykorzystaniem pomiaru barwy podłoża pod środkowym czujnikiem
światła i bez niego.
Brak pomiaru barwy podłoża pod środkowym czujnikiem światła
Kłopoty zaczynają się w momencie najechanie na prostopadłą fugę. Wszystkie fugi mają ten
sam kolor więc czujniki burtowe nie są w stanie stwierdzić czy znajdują się nad fugą leżące z
boku, czy też z przodu pojazdu. Stosowanie reguły reagowania na fugę obowiązującej podczas
jazdy na wprost prowadzi, w przypadku najechania na fugę leżącą z przodu pojazdu, do
obrotu w kierunku przeciwnym do pożądanego. Dopiero w chwili gdy oba czujniki znajdą się
ponad fugami pojazd ponownie pojedzie do przodu, „myśląc”, że przekracza granicę między
kafelkami. Niestety w momencie gdy oba czujniki znajdą się ponad kafelkami pojazd może
już znajdować się po niewłaściwej stronie którejś z fug. Sytuację taką ilustrują rysunki 8.3,
a)
b)
Rysunek 8.4: Niepoprawne przekraczanie fugi leżącej z przodu pojazdu wynikające z braku
pomiaru barwy podłoża pod środkowym czujnikiem światła: a) etap 3 , b) etap 4
Użyte symbole mają takie samo znaczenie jak na fotografiach 7.4, 7.5 i 7.8. Dla przypo-
mnienia:
1 - Czujnik światła położony na przodzie prawej burty odpowiedzialny za kontrolowanie
najeżdżania na fugę położoną z prawej strony robota
ROZDZIAŁ 8. PROGRAM ROBOTA
58
2 - Czujnik światła umieszczony po środku przodu pojazdu kontroluje barwę podłoża, w
szczególności kafelka, na który wjeżdża robot
3 - Czujnik światła położony na przodzie lewej burty odpowiedzialny za kontrolowanie
najeżdżania na fugę położoną z lewej strony robota
Poniżej zamieszczono analizę kolejnych etapów pokonywania fugi leżącej z przodu pojazdu,
nie wykorzystującego informacji dostarczanej przez środkowy czujnik światła. Warto pod-
kreślić, że jest to tylko jeden z możliwych przebiegów tego procesu, prowadzący do błędu w
ustawieniu pojazdu po jego zakończeniu.
1 - Etap przedstawiony na rys. 8.3 a. Pojazd jedzie do przodu. Jego oś podłużna jest nieco
obrócona w prawo w stosunku do osi podłużnej kafelka.
2 - Etap przedstawiony na rys. 8.3 b. Lewo-burtowy czujnik światła najeżdża na fugę i
robot zaczyna skręcać w prawo.
3 - Etap przedstawiony na rys. 8.4 a. Skręt w prawo prowadzi w pewnym momencie do
znalezienia się obu burtowych czujników światła ponad fugami. Robot przerywa wów-
czas obrót i zaczyna jechać na wprost myśląc że oba czujniki wykryły fugę leżąca z
przodu pojazdu. W rzeczywistości czujnik prawo-burtowy znalazł się ponad fugą leżąca
z prawej strony pojazdu.
4 - Etap przedstawiony na rys. 8.4 b. Jazda na wprost prowadzi do pokonania obu fug.
Niestety położenie pojazdu jest nieprawidłowe.
Dodatkowy pomiar barwy podłoża pod środkowym czujnikiem światła
Uniknięcia przedstawionej powyżej sytuacji jest możliwie jeśli pojazd wie o zbliżaniu się gra-
nicy pomiędzy kafelkami. O fakcie tym informuje środkowy czujnik światła. Czujnik ten jest
nieco wysunięty do przodu w stosunku do czujników burtowych, dzięki czemu jako pierwszy
wykrywa fugę leżącą z przodu pojazdu. Z chwilą wykrycia tej fugi pojazd przestaje reagować
na odczyty z czujników burtowych i jedzie na wprost. Jazda na wprost jest kontynuowana do
momentu aż oba czujniki burtowe najpierw znajdą się ponad fugami, a potem przynajmniej
jeden z nich z powrotem znajdzie się ponad kafelkiem. Alternatywnym kryterium zaprzesta-
nia bezwarunkowej jazdy na wprost jest upłynięcie pewnego maksymalnego odcinka czasu od
wykrycia fugi czołowej. Eksperymenty wykazały, że metoda ta jest niezawodna. Warunkiem
jej niezawodności jest gwarancja, że środkowy czujnik jako pierwszy wykryje fugę czołową,
a także odpowiednia szerokość fug i rozmieszczenie czujników burtowych. Rysunek 8.5 ilu-
struje przebieg etapu 2 i 3 pokonywania fugi z wykorzystaniem informacji ze środkowego
czujnika światła.
Etapy 2 i 3 mają następujący przebieg:
ROZDZIAŁ 8. PROGRAM ROBOTA
59
a)
b)
Rysunek 8.5: Poprawne przekraczanie fugi leżącej z przodu pojazdu z wykorzystaniem in-
formacji ze środkowego czujnika światła
2 - Etap przedstawiony na rys. 8.5 a. Środkowy czujnik światła wykrywa fugę leżącą z
przodu pojazdu, w związku z czym najechanie na fugę czujnika lewo-burtowego nie
powoduje zmiany kierunku ruchu pojazdu.
3 - Etap przedstawiony na rys. 8.5 b. Czujnik lewo-burtowy jako pierwszy zjeżdża z fugi.
Program robota reaguje więc na odczyt z czujnika prawo burtowego. Niewielki obrót
w lewo korzystnie koryguje kierunek ruchu pojazdu.
Powyższy mechanizm jest wykorzystywany przez pojazdy serii MIŚ. Rozmiary bazy jezd-
nej robota MIŚ 4 są w rzeczywistości nieco większe od przedstawionych na rysunkach 8.3,
8.4, 8.5. Nie wpływa to jednak na sens dotychczasowych rozważań.
8.3.2
Sposób sterowania silnikami
Warstwa ruchu steruje silnikami poprzez funkcje zaimplementowane w systemie operacyjnym
legOS. Sterowanie silnikami omówione jest szerzej w części teoretycznej 5.1.4. Robot porusza
się w następujących trybach:
• Obrotu ciągłego w lewo lub w prawo - Tryb ten używany jest do obracania robota
wokół własnej osi o wielokrotność 90
o
. Jeden z silników obraca się do przodu a drugi
do tyłu. Moc na silnikach wynosi 2/3 maksymalnej.
• Lekkiej korekty kursu w lewo lub w prawo - Tryb ten jest analogiczny do opisanego po-
wyżej z tą różnicą, że silniki pracują z małą mocą i po kilkudziesięciu µs są blokowane.
Dzięki takiemu wysterowaniu obrót jest bardzo niewielki, co umożliwia wykorzystanie
go do korygowania kursu podczas jazdy na wprost.

ROZDZIAŁ 8. PROGRAM ROBOTA
60
• Jazdy do przodu - Oba silniki obracają się wówczas do przodu.
• Zablokowania silników - Oba silniki są zablokowane, co prowadzi do wyhamowania
pojazdu. Zmiana trybu ruchu robota wiąże się z reguły z wyhamowaniem pojazdu.
• Wyłączenia silników - Oba silniki zostają wyłączone. Tryb ten używany jest w sytuacji
kiedy robot staje na dłuższy czas, np. podczas transmisji danych bądź w stanie uśpie-
nia warstwy ruchu robota. Dodatkowo silniki są wyłączane przy zmianie trybu ruchu
robota z obrotu ciągłego na jazdę na wprost. Zapewnia to wyeliminowanie ładunku
elektrycznego gromadzącego się w pojemnościach obwodu sterowania silnikami. Za-
bieg ten powoduje, że oba silniki po zainicjowaniu zaczynają się obracać z tym samym
przyspieszeniem, dzięki czemu pojazd rusza dokładnie do przodu.
Prędkość robota nie ma większego wpływu na poprawność wykonywania zadania, gdyż
kryteria odległościowe mają charakter odometryczny, a nie czasowy. Moc silników została
tak dobrana, żeby robot się nie ślizgał podczas przyspieszania i hamowania.
8.3.3
Odczyt danych z czujników
Warstwa ruchu odczytuje barwę z czujników światła i wartość kąta na czujnikach odometrycz-
nych. Odczyt ten następuje poprzez wywołanie odpowiednich funkcji systemu operacyjnego
legOS, które zwracają te wartości. Całość przetwarzania fizycznych odczytów z czujników
leży po stronie legOS’a co opisane zostanie w pkt. 8.9
8.4
Warstwa nadzoru
Warstwa nadzoru zawiera się w czterostanowym automacie. Poszczególne stany odpowia-
dają różnym etapom wykonywania zadania. W każdym stanie wywoływane są odpowiednie
moduły programu odpowiedzialne za komunikację z komputerem PC, aktualizację mapy i
przetwarzanie trajektorii. Rysunek 8.6 prezentuje opisywany automat. Stany noszą numery
0, 10, 20 i 30. Literami a do h oznaczono symbolicznie warunki przejścia pomiędzy stanami.
Wyjściem automatu jest stan, który osiąga warstwa ruchu, podczas zmiany stanu w warstwie
nadzoru.
Podobieństwo automatów warstwy ruchu i warstwy nadzoru ogranicza się do zbliżonego
układu stanów. Jak już napisano wcześniej automat warstwy ruchu ma charakter behawio-
ralny. Automat warstwy nadzoru funkcjonuje w oparciu o modele środowiska i robota. Cha-
rakterystyka poszczególnych stanów i warunki przejścia pomiędzy stanami zostaną opisane
nieco dalej.
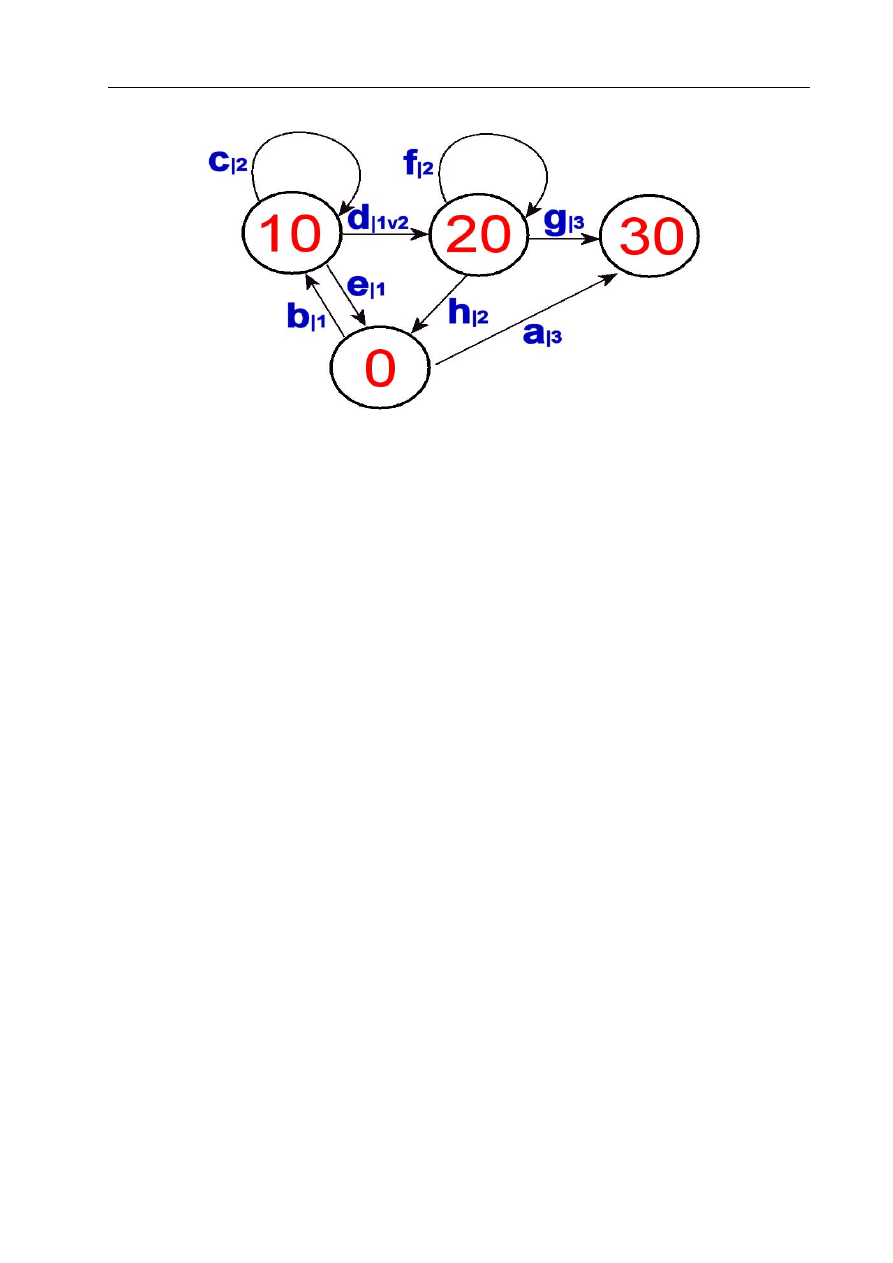
ROZDZIAŁ 8. PROGRAM ROBOTA
61
Rysunek 8.6: Automat realizowany w warstwie nadzoru
8.4.1
Model środowiska i robota
Na model środowiska składają się:
• mapa planszy,
• trajektoria do przebycia,
• lokalizacja wieży transmisyjnej.
Mapa planszy zapisana jest w tablicy dwuwymiarowej. Wartości poszczególnych komó-
rek są zgodne z kolorami kafelków na planszy. Dodatkowo tablica ta jest wykorzystywana w
planerze trajektorii. Prowadzi to do poważnej oszczędności pamięci w obliczu jej niedoboru.
Trajektoria jest wektorem współrzędnych jej kolejnych pól. Pierwsze pole jest punktem star-
towym, ostatnie metą. Wieża transmisyjna zlokalizowana jest w bezpośrednim sąsiedztwie
pola startowego. Komunikacja następuje po wjechaniu robota na pole startowe i wykonaniu
przez niego obrotu w celu uzyskania odpowiedniej orientacji.
Warstwa nadzoru posługuje się modelem robota. Model ten zakłada że:
• pojazd przemieszcza się pomiędzy środkami kafelków,
• ruch może odbywać się w czterech kierunkach,
• niemożliwe jest wjechanie na pole pozbawione kafelka,
• pojazd po wjechaniu na środek kafelka może obracać się wokół własnej osi o całkowitą
wielokrotność 90
o
; Obrót może być wielokrotnie powtarzany na tym samym kafelku,

ROZDZIAŁ 8. PROGRAM ROBOTA
62
• pojazd może uzyskać informację o barwie kafelka na którym się znajduje oraz kolorach
sąsiednich pól.
Powyższy model jest podstawą dla komunikacji z warstwą ruchu, analizy informacji na-
pływających z tej warstwy i procesu przetwarzania trajektorii.
8.4.2
Opis automatu
Rysunek 8.6 przedstawia automat zarządzający warstwą nadzoru. Dwucyfrowe nazwy po-
szczególnych stanów mają znaczenie historyczne. Ich występowanie wiąże się z genezą bie-
żącego automatu, którego poprzednie wersje miały znacznie więcej stanów i były na tyle
nieefektywne, że musiały zostać zastąpione przez prostszą strukturę. Poniżej znajduje się
opis poszczególnych stanów i warunków przejścia pomiędzy nimi:
0 - Stan, który przyjmuje warstwa nadzoru podczas inicjacji robota oraz wówczas kiedy po-
jazd wjeżdża na kafelek, z którego ma nastąpić komunikacja z komputerem PC. Robot
ustawia się pośrodku kafelka, po czym obraca się w kierunku wieży transmisyjnej, co
umożliwia transmisję danych, która następuje chwilę później. Mechanizm komunikacji
zostanie omówiony w pkt. 8.6. Po zakończeniu transmisji zostaje wykonana dyrektywa,
przekazana z komputera PC.
a - Operator programu uruchomionego w komputerze PC może podjąć decyzję o wyłącze-
niu robota. Jej konsekwencją jest przesłanie odpowiedniego rozkazu. Po jego odczytaniu
warstwa nadzoru przechodzi do stanu 30, a warstwa ruchu do stanu 3.
b - Operator z reguły decyduje się na wykonywanie założonej trajektorii. Warstwa nadzoru
przyjmuje wówczas stan 10, a warstwa ruchu wykonuje kolejny obrót, pozostając w
stanie 1.
10 - Zdecydowanie najbardziej złożony ze stanów warstwy nadzoru. Jego zadaniem jest
przeprowadzenie robota od pola początkowego trajektorii do, o ile jest to tylko możli-
we, jej pola końcowego. W tej fazie stan 10 jest uruchamiany każdorazowo po wjechaniu
na nowy kafelek. Pierwszą wykonywaną operacją jest analiza manewru wykonanego na
poprzednim kafelku. Znaczenie słowa „manewr” jest tożsame z użytym przy opisie sta-
nu 1 warstwy ruchu pkt. 8.3. Analiza ta jest przyczynkiem do wyznaczenie wektora
manewrów wykonywanego na obecnym kafelku. Po jego wykonaniu nowo zdobyta wie-
dza o otoczeniu zostaje wykorzystana do zaktualizowania mapy, a raport o wykonaniu
wektora manewrów do wyznaczenia kolejnego stanu. Realizacja wektora manewrów zo-
stała już opisana w części pracy poświęconej stanowi 1 warstwy ruchu pkt. 8.3. Moduł
przetwarzania trajektorii zostanie szczegółowo opisany w pkt. 8.8 a moduł aktualizacji
mapy w pkt. 8.7

ROZDZIAŁ 8. PROGRAM ROBOTA
63
c - Warunek ten jest spełniony jeśli manewr się powiódł i nie osiągnięto jeszcze mety.
Warstwa nadzoru pozostaje wówczas w stanie 10, warstwa ruchu przechodzi do stanu
2, a robot podąża w kierunku mety, którą ma jeszcze szansę osiągnąć. Pojęcie manew-
ru zakończonego powodzeniem jest objaśnione w części pracy poświęconej stanowi 1
warstwy ruchu pkt. 8.3.
d - Warstwa nadzoru przechodzi do stanu 20 w dwóch przypadkach:
1. jeśli manewr się powiódł i osiągnięto metę. Warstwa ruchu osiąga wówczas stan
2.
2. gdy manewr się nie powiódł i pojazd nie znajduje się na starcie. Warstwa ruchu
pozostaje wówczas w stanie 1.
Pierwszy z warunków charakteryzuje sytuację w której pojazd osiągnął punkt końcowy
trajektorii i rozpoczyna powrót w kierunku jej początku. Drugi warunek spełniony jest
w sytuacji braku możliwości osiągnięcia mety. Po serii manewrów zakończonej porażką
robot zawraca w kierunku startu.
e - Warstwa nadzoru osiąga stan 0 w przypadku, w którym manewr się nie powiódł i
pojazd znajduje się na starcie. Przechodzenie do stanu 20 nie ma wówczas sensu i
program niezwłocznie nawiązuje łączność z komputerem PC. Warstwa ruchu pozostaje
w stanie 1 co umożliwia kolejny obrót.
20 - Stan, w którym pojazd powraca do punktu początkowego trajektorii. Powrót może
odbywać się zarówno z pola końcowego trajektorii jak i, w przypadku braku możliwości
jego osiągnięcia, dowolnego innego pola. Stan 20 mógłby być obsługiwany w sposób w
pełni analogiczny do stanu 10. Niestety ze względu na ograniczoną wielkość pamięci
jego realizacja jest znacznie prostsza. Pojazd powraca po trajektorii, którą faktycznie
wykonał w poprzedniej fazie. Także i w tym stanie mapa jest aktualizowana. Prostota
implementacji nie dała możliwości omijania nieznanych dotąd przeszkód.
f - Warunek ten jest spełniony jeśli manewr się powiódł i nie osiągnięto jeszcze początko-
wego pola trajektorii. Warstwa nadzoru pozostaje w stanie 20 a warstwa ruchu prze-
chodzi do stanu 2. Pojazd z sukcesem pokonał kolejne pole trajektorii powrotnej i
kontynuuje jazdę.
g - Manewr zakończony niepowodzeniem uniemożliwia osiągnięcie pola początkowego. Ro-
bot przechodzi w stan uśpienia, poprzez osiągnięcie stanu 30 w warstwie nadzoru i stanu
3 w warstwie ruchu.
h - Osiągnięcie pola początkowego pozwala na komunikację z komputerem PC, która za-
chodzi w stanie 0 warstwy nadzoru. Warstwa ruchu pozostaje w stanie 1.

ROZDZIAŁ 8. PROGRAM ROBOTA
64
30 - Stan terminalny, w którym robot pozostaje uśpiony, aż do momentu ponownego uru-
chomienia programu.
8.5
Mechanizmy komunikacji i synchronizacji między-
warstwowej
Opis warstw ruchu i nadzoru byłby niekompletny bez zaprezentowania sposobu ich współ-
działania. System operacyjny legOS udostępnia zaledwie trzy mechanizmy, wzajemnego od-
działywania na siebie wątków, uruchomionej w nim aplikacji:
1. semafory,
2. wspólne obszary pamięci implementowane jako zmienne globalne,
3. funkcje oczekiwanie na zdarzenie.
Szczegółowy sposób działania tych mechanizmów został już opisany w części teoretycznej
pracy pkt. 5.2.1. Zarówno warstwa ruchu jak i warstwa nadzoru są uruchamiane jako wątki
programu robota. Do ich współdziałania wykorzystywane są pierwsze dwie z wymienionych
powyżej metod. Semafory służą do synchronizacji, zmienne globalne do przechowywania
danych a połączenie obu tych metod umożliwia kontrolowane przesłanie wiadomości.
Wysłanie wiadomości odbywa się w niezwykle prosty sposób. Pierwszy z wątków zapisuje
dane w zmiennych globalnych. Drugi zawiesza się na semaforze w oczekiwaniu na sygnał
przygotowania całej paczki danych. Gdy pierwszy wątek zapisze już wszystkie niezbędne
dane odwiesza semafor, na którym zawiesił się drugi wątek. Zmiana stanu semafora umożliwia
drugiemu wątkowi odczytanie danych.
Pomimo swoich niedoskonałości, mechanizm ten zapewniał wystarczający stopień komu-
nikacji pomiędzy warstwą nadzoru a warstwą ruchu. Kolejkowanie wiadomości szczęśliwie
nie było konieczne. Postać paczki danych była z góry zdeterminowana a wątek odczytujący
wiadomość odwoływał się do znanych apriori zmiennych globalnych.
Sposób synchronizacji warstw ruchu i nadzoru ilustruje sieć Petriego - rys. 8.7. Teorię sieci
Petriego można odnaleźć między innymi w publikacji [18]. Poniżej zaprezentowany zostanie
opis poszczególnych sekcji programu oznaczonych na rys.8.7 cyframi od 1 do 8.
1 - Fragment kodu warstwy ruchu odpowiedzialny za przejazd na wprost. W sytuacji wie-
lokrotnego powtarzania obrotu fragment ten będzie zawierał instrukcję pustą.
2 - Wykonanie manewru w stanie 1 warstwy ruchu.
3 - Instrukcja pusta.
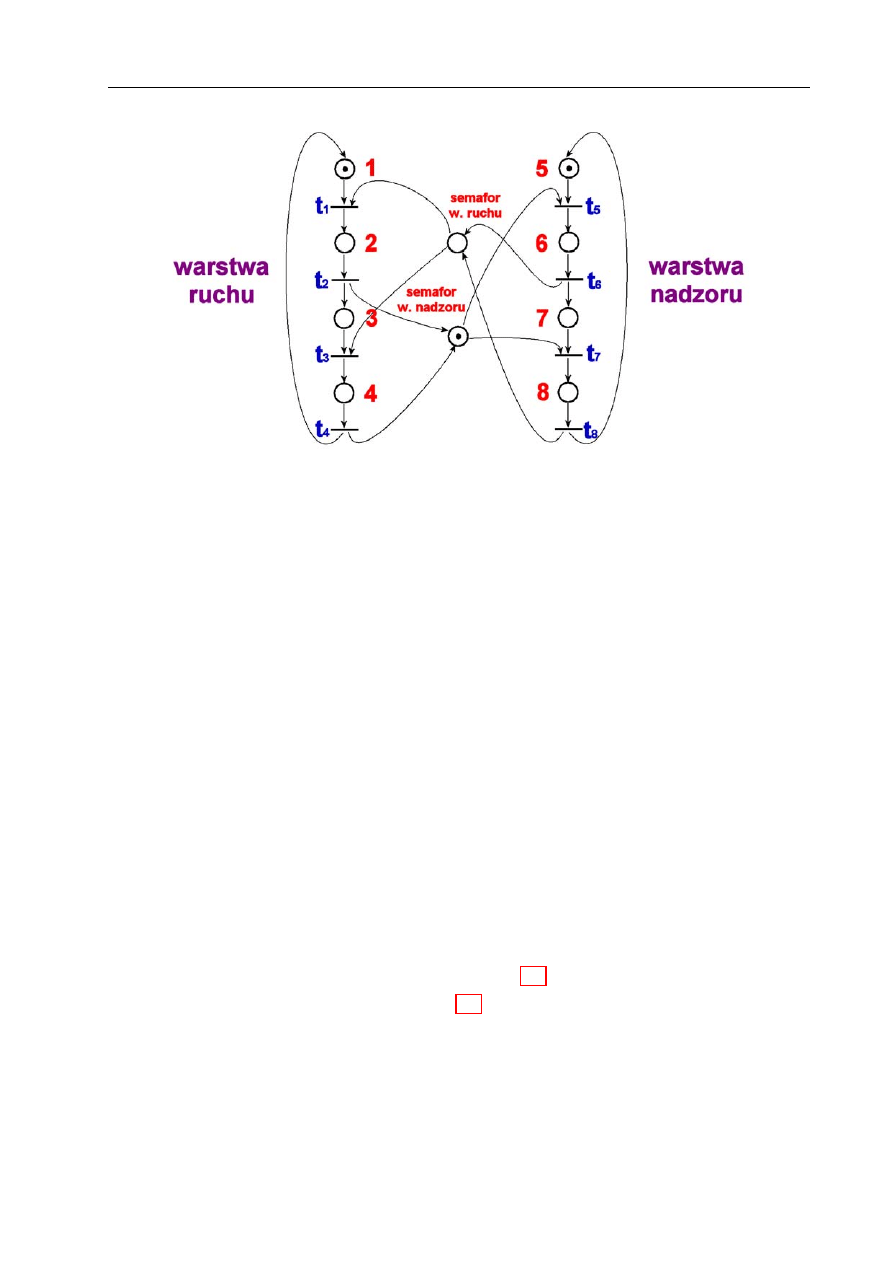
ROZDZIAŁ 8. PROGRAM ROBOTA
65
Rysunek 8.7: Synchronizacja pomiędzy warstwą ruchu i warstwą nadzoru
4 - Sekcja programu odpowiedzialna za interpretację dyrektyw warstwy nadzoru dotyczą-
cych zmiany stanu w warstwie ruchu. W sytuacji gdy warstwa ruchu przejdzie do stanu
2 dodatkowo fragment ten kontroluje zjeżdżanie pojazdu z kafelka.
5 - Instrukcja pusta.
6 - Ewentualne przetworzenie trajektorii. Przygotowanie wektora manewrów dla warstwy
ruchu.
7 - Instrukcja pusta.
8 - Interpretacja faktycznie wykonanego manewru. Ewentualna komunikacja. Podjęcie de-
cyzji o zmianie stanu w warstwie nadzoru i warstwie ruchu.
Dla konkretnego cyklu sekcje 1 - 4 mogą być uruchamiane w ramach różnych stanów
warstwy ruchu natomiast sekcje 5 - 8 zawierają się w jednym, konkretnym stanie warstwy
nadzoru.
Sposób obiegu znaczników w sieci Petriego z rys. 8.7 najłatwiej prześledzić budując jej
drzewo osiągalności zaprezentowane na rys. 8.8. Drzewo to jest zdegenerowane do jednej
gałęzi. Dziesięciocyfrowy wektor zer i jedynek informuje o lokalizacji znaczników. Cyfra „1”
reprezentuje obecność znacznika, a „0” jego brak. Wektor został dla wygody Czytelnika
podzielony na trzy części. Skrajna lewa części zawiera sekcje programu ponumerowane od 1
do 4, będące fragmentami warstwy ruchu. Część środkowa zawiera sekcje warstwy nadzoru
o numerach 5 - 8. Skrajny prawy fragment informuje o stanie semaforów: warstwy ruchu -
pozycja 9 i warstwy nadzoru - pozycja 10.
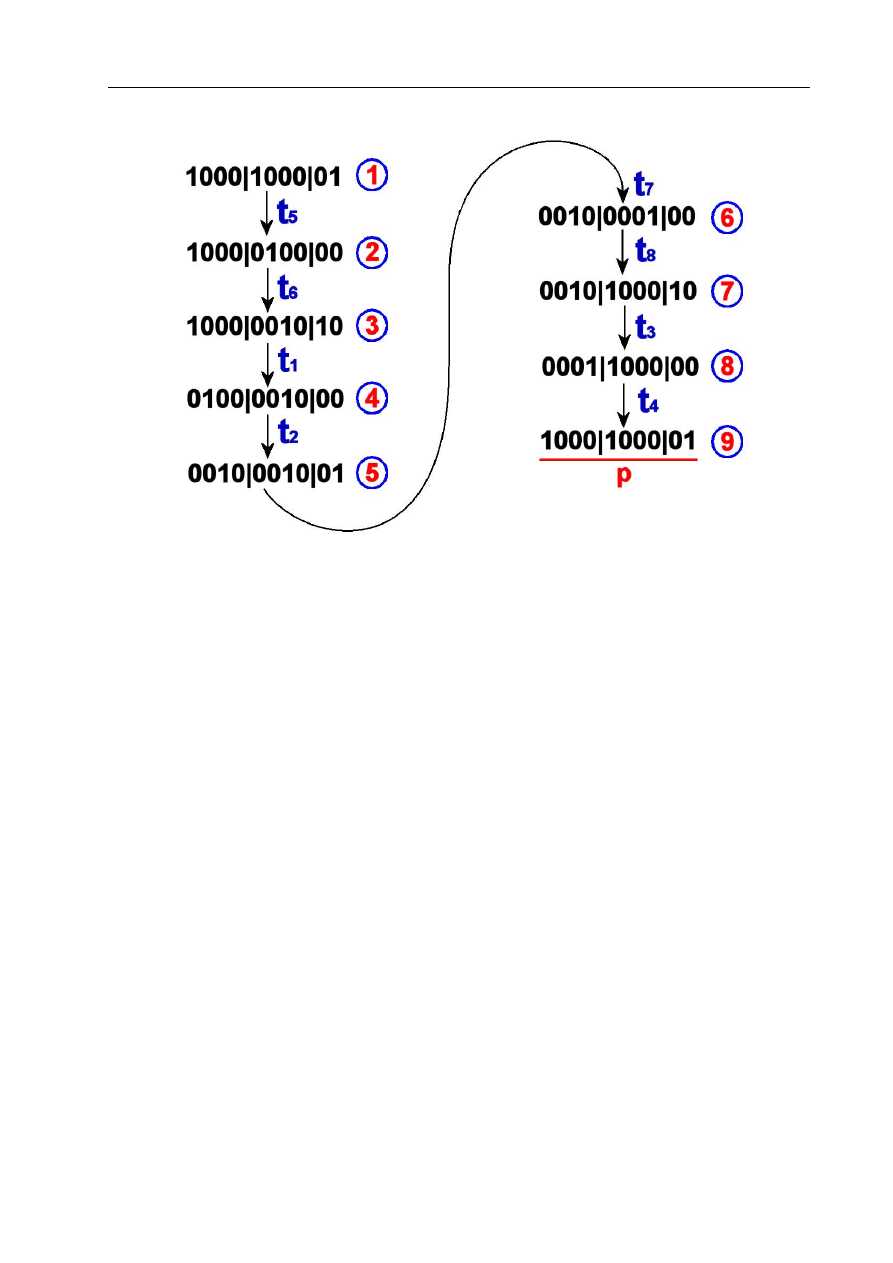
ROZDZIAŁ 8. PROGRAM ROBOTA
66
Rysunek 8.8: Drzewo osiągalności
Prześledzenie poszczególnych znakowań drzewa osiągalności pozwoli na lepsze zrozumie-
nie mechanizmów komunikacji między-warstwowej. Przedstawiona interpretacja dotyczy sy-
tuacji, w której robot przemieszcza się z kafelka na kafelek podążając od startu do mety.
Wykonywanie obrotów na jednym kafelków, czy też przechodzenie w stan uśpienia, ma nieco
inny przebieg charakteryzowany przez to samo drzewo osiągalności.
1 - Z takim znakowaniem inicjowany jest program. Utrzymuje się ono tylko przez chwilę,
gdyż stan semafora warstwy nadzoru powoduje natychmiastowe przejście do znakowa-
nia 2.
2 - Warstwa nadzoru odwiesza się, po czym następuje przebudowanie trajektorii. Zaktu-
alizowana trajektoria umożliwia wyznaczenie wektora manewrów dla stanu 1 warstwy
ruchu. Warstwa ruchu znajdując się w stanie 0 przeprowadza pojazd przez kafelek po
czym zawiesza się na początku stanu 1 w oczekiwaniu na dyrektywy z warstwy nadzoru.
3 - Warstwa nadzoru z powodzeniem wyznaczyła wektor manewrów sygnalizując ten fakt
zmianą stanu semafora warstwy ruchu. Chwilę później zawiesza się na semaforze war-
stwy nadzoru oczekując na raport o faktycznie wykonanym manewrze.
4 - Warstwa ruchu odwiesza się i odczytuje wektor manewrów po czym wykonuje go. Po
zakończeniu manewrów przygotowuje raport o ich przebiegu.

ROZDZIAŁ 8. PROGRAM ROBOTA
67
5 - Przygotowanie raportu sygnalizowane jest zmianą stanu semafora warstwy nadzoru.
Następnie warstwa ruchu zawiesza się ponownie na semaforze warstwy ruchu w ocze-
kiwaniu na dyrektywę warstwy nadzoru dotyczącą zmiany stanu niższej z warstw.
6 - Warstwa nadzoru odwiesza się, po czym przetwarza informację o faktycznie wykona-
nym manewrze. Na jej podstawie wyznaczany jest kolejny stan dla warstwy ruchu.
7 - Wyznaczenie następnego stanu warstwy ruchu implikuje zmianę stanu semafora tej
warstwy. Warstwa nadzoru zawiesza się w oczekiwaniu na sygnał możliwości rozpoczę-
cia wyznaczania kolejnego wektora manewrów.
8 - Warstwa ruchu odwiesza się i odczytuje wiadomość o zmianie stanu, która następuje
chwilę później. Zgodnie z założeniem o zmianie kafelka przechodzi do stanu 2. Z chwilą
przekroczenia granicy kafelka stan warstwy ruchu zmienia się na 0 a semafor warstwy
nadzoru zostaje zwolniony.
9 - Znakowanie to jest identyczne ze znakowaniem 1 wobec czego zostało oznaczone jako
powtórzenie.
Zaprezentowane drzewo sprowadza się do pojedynczej gałęzi. Jego prostota sprzyja wyso-
kiej niezawodności ściśle deterministycznego programu. Znakowania pierwsze i dziewiąte są
tożsame, wobec czego program ma charakter cykliczny. Komunikacja pomiędzy warstwami
odbywa się według jednego schematu. Warstwa ruchu zawiesza się na swoim semaforze w
oczekiwaniu na wiadomość od warstwy nadzoru. Warstwa nadzoru po przygotowaniu wiado-
mości zmienia stan semafora warstwy ruchu, po czym warstwa ruchu odwiesza się i odczytuje
wiadomość. Przesyłanie wiadomości z warstwy ruchu do warstwy nadzoru obsługiwane jest
analogicznie przy wykorzystaniu semafora warstwy nadzoru.
8.6
Moduł komunikacyjny
Moduł komunikacyjny uruchamiany jest w stanie 0 warstwy nadzoru opisanym w pkt. 8.4.2.
Transmisja danych rozpoczyna się niezwłocznie po chwili, w której pojazd ustawi się prawi-
dłowo względem wieży. Rys. 8.9 ilustruje ten moment. Robot i wieża znajdują się na jednej
linii i są zwrócone ku sobie.
Postać przekazywanych danych zależy od etapu realizowanego zadania.
8.6.1
Pierwsza transmisja
Jedną z pierwszych rzeczy, którą wykonuje, nowo uruchomiony program robota jest nawią-
zanie komunikacji z komputerem PC. Dane przesyłane są wówczas w następującej kolejności:

ROZDZIAŁ 8. PROGRAM ROBOTA
68
Rysunek 8.9: Pojazd komunikuje się z wieżą podłączoną do komputera PC
1. Komputer PC przesyła robotowi mapę planszy.
2. Komputer PC przesyła robotowi trajektorię do wykonania. Pierwsze pole trajektorii
jest jednocześnie bieżącą lokalizacją pojazdu.
3. Komputer PC przesyła do pojazdu jego obecną orientację. Orientacja jest informacją
o kierunku w którym zwrócony jest robot podczas transmisji.
4. Robot otrzymuje także dyrektywę dotyczącą jego dalszej pracy. Może ona mieć dwojaką
postać:
• nakaz rozpoczęcia wykonywania zadania.
• nakaz przejścia w stan uśpienia.
8.6.2
Kolejne transmisje
Kolejne wymiany danych pomiędzy komputerem PC a robotem mają nieco inny przebieg.
Robot wykonał już zadanie i przesyła na samym początku transmisji zaktualizowaną mapę
planszy. Pozostałe etapy komunikacji nie ulegają zmianie.
8.6.3
Implementacja mechanizmów komunikacji
W omawianym projekcie transmisja odbywa się pomiędzy pojedynczą wieżą i pojedynczym
robotem. Fakt ten zdeterminował użycie trybu bezpośredniego przesyłania danych. Tryb
ten jest prostszy od adresowego i jego użycie było naturalne w sytuacji braku konieczności
adresowania pakietów.

ROZDZIAŁ 8. PROGRAM ROBOTA
69
Obsługa nadawania i odbierania danych jest zrealizowana w robocie i komputerze PC
w sposób w pełni analogiczny. Odbiór odbywa się poprzez program obsługi przerwania a
nadawanie możliwe jest dzięki wywołaniu odpowiedniej funkcji z biblioteki liblnp.
8.7
Moduł aktualizacji mapy
Mapa planszy na której będzie się poruszał robot przesyłana jest do niego w trakcie trans-
misji opisanej w pkt. 8.6. Podczas wykonywania zadania plansza ulega jednak modyfikacjom
polegającym na wyjmowaniu niektórych kafelków. Zadaniem modułu aktualizacji mapy jest
nanoszenie tych zmian na mapę przechowywaną w programie robota. Aktualizacja mapy
zachodzi każdorazowo po otrzymaniu przez warstwę nadzoru raportu o barwie kafelków na-
potkanych podczas wykonywania manewru. Raport ten przygotowywany jest w stanie 1 war-
stwy ruchu. Zawiera on informacje o barwach niektórych kafelków sąsiadujących z kafelkiem
na którym wykonywany był manewr. W praktyce wykorzystywana jest jedynie informacja
o wyjęciu kafelków, które wcześniej były obecne na mapie. Aktualizacja mapy zachodzi w
stanie 10 i 20 warstwy nadzoru. Opis zawartości raportu opisany jest także w pkt. 8.3.
8.8
Moduł przetwarzania trajektorii
Moduł przetwarzania trajektorii jest zdecydowanie najbardziej skomplikowany spośród wszyst-
kich modułów wykorzystywanych w warstwie nadzoru. Jego zadaniem jest wyznaczanie ta-
kich wektorów manewrów dla stanu 1 warstwy ruchu, które pozwoliłyby na jak najwierniejsze
wykonanie trajektorii przesłanej z komputera PC.
8.8.1
Właściwości trajektorii przesyłanej z komputera PC
Trajektoria wyznaczona w komputerze PC musi spełniać kilka założeń:
• Rozpoczyna się polem, na którym znajduje się pojazd podczas transmisji danych.
• Pole końcowe jest różne od początkowego.
• Kolejne pola trajektorii sąsiadują ze sobą bokami.
• Wszystkie pola trajektorii przebiegają przez te pola na planszy, o których zakłada
się, że znajdują się na nich kafelki. Założenie to musi potwierdzać mapa przesyłana z
komputera PC do robota.
• Brak jest cykli. Żadne pole trajektorii nie występuje dwukrotnie.
Z drugiej strony nie jest wymagane aby trajektoria przesyłana z komputera PC była w
jakikolwiek sposób optymalna.
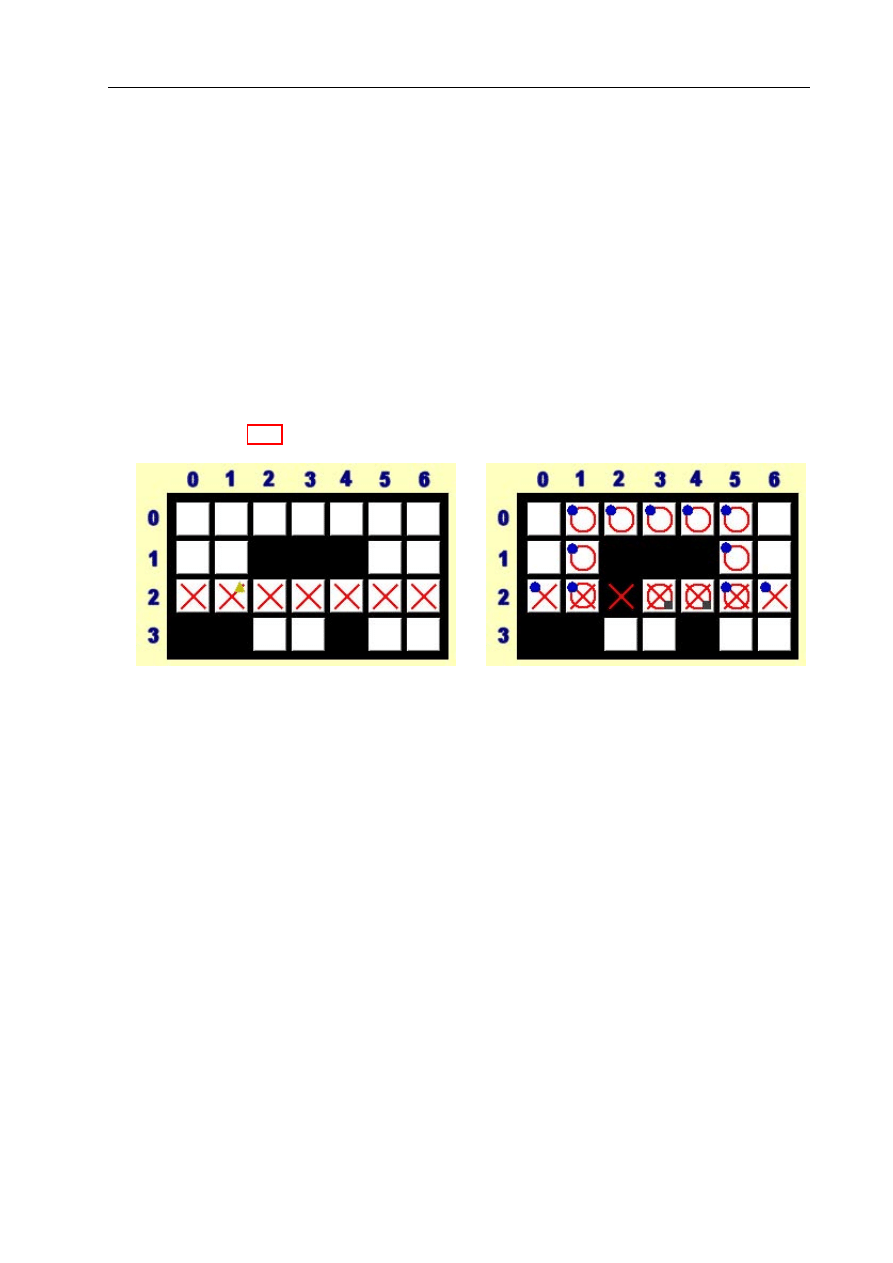
ROZDZIAŁ 8. PROGRAM ROBOTA
70
8.8.2
Definicja jak najwierniejszego wykonania założonej trajek-
torii
Moduł przetwarzania trajektorii stara się tak poprowadzić pojazd, aby przejechał on po jak
największej ilości pól znajdujących się na trajektorii PC. Przez trajektorię PC rozumiana
jest trajektoria wyznaczona przez algorytm uruchomiony w komputerze PC. Wykrycie bra-
ku kafelka na polu planszy należącym do trajektorii PC powoduje uruchomienie procedury
wykonania objazdu. Objazd jest tak wyznaczany aby jak najmniejszym kosztem dojechać
do kolejnego pola trajektorii PC. Z drugiej strony opisywany moduł dąży do unikania dwu-
krotnego odwiedzania tego samego pola. Oznacza to w praktyce, że niektóre pola trajektorii
PC mogą nie zostać odwiedzone pomimo faktu, że pojazd miał taką możliwość. Sytuację
taką ilustruje rys. 8.10.
a)
b)
Rysunek 8.10: Wykonanie objazdu z pominięciem cypla
Rysunek a) przedstawia trajektorię PC naniesioną na zakładaną mapę planszy a rysunek
b) trajektorię zrealizowaną naniesioną na mapę odwzorowującą faktyczny układ kafelków na
planszy. Trajektoria PC oznaczona jest krzyżykami. Przebiega on po odcinku linii prostej z
punktu o współrzędnych [0,2] do punktu o współrzędnych [0,6]. Pojazd z powodzeniem po-
konuje pola [0,2] i [1,2]. Na polu [1,2] wykrywa brak kafelka [2,2] leżącego na trajektorii PC.
Wyznaczony objazd oznaczony jest okręgami i biegnie z bieżącego kafelka - [1,2] do kolejnego
pola trajektorii PC - [3,2], o którym zakłada się, że leży na istniejącym kafelku. Trajektoria
PC ma 4 punkty wspólne z objazdem. Pierwszy punkt - [1,2] jest początkiem objazdu, kolej-
ny punkt - [5,2] punktem ponownego spotkania objazdu i trajektorii PC. Kolejne dwa punkty
wspólne - [4,2] i [3,2] leżą na swego rodzaju cyplu. Ich zaliczenie wymagałoby zawrócenia
w punkcie [3,2] w celu zrealizowania dalszego odcinka trajektorii PC rozpoczynającego się
w punkcie [6,2]. Wjechanie w cypel implikowałoby dwukrotne odwiedzenie pól [3,2], [4,2] i
[5,2]. Algorytm planowania trajektorii nie dopuszcza do takiej sytuacji. Ostatecznie pojazd
przejeżdża po polach oznaczonych w lewym górnym rogu niebieskimi kółkami. Są to w ko-
lejności odwiedzania: [0,2], [1,2], [1,1], [1,0], [2,0], [3,0], [4,0], [5,0], [5,1], [5,2] i [6,2]. Pola
oznaczone w prawym dolnym rogu szarym kwadratem [3,2] i [4,2] nie zostaną odwiedzone,

ROZDZIAŁ 8. PROGRAM ROBOTA
71
gdyż leżą na cyplu.
8.8.3
Użyte struktury danych i zmienne sterujące
Do zrozumienia mechanizmów kierujących działaniem modułu konieczne jest zapoznanie się
ze zmiennymi sterującymi i strukturami przechowującymi dane.
Sposób reprezentacji danych wynikał bezpośrednio z wykorzystania języka C do imple-
mentacji programu robota. Poniżej opisane są struktury przechowujące dane:
mapa planszy zapisana jest w tablicy dwuwymiarowej. Każda pojedyncza komórka
zawiera nie tylko informacje o barwie kafelka bądź jego braku ale także wykorzystywana
jest w planerze trajektorii. Zabieg ten wynika z konieczności oszczędzania pamięci.
pole trajektorii jest definicją typu będącego strukturą zawierającą współrzędne x i
y implementowanej zmiennej.
trajektoria PC jest tablicą typu pole trajektorii zawierającą trajektorię wyznaczoną
w komputerze PC. W przykładzie na rys. 8.10 trajektoria PC oznaczona jest krzyży-
kami.
trajektoria rzeczywista jest tablicą typu pole trajektorii zawierającą faktycznie wy-
konywaną trajektorię. Na rys. 8.10 trajektoria rzeczywista oznaczona jest niebieskimi
kółkami.
trajektorie obejść są tablicami typu pole trajektorii zawierającymi wszystkie możli-
we objazdy wyznaczone na wypadek braku kafelków sąsiadujących z bieżącym. Jedno
z obejść zostało oznaczone na rys. 8.10 okręgami.
start to zmienna typu pole trajektorii będąca pierwszym polem trajektorii PC.
meta jest zmienną typu pole trajektorii będącą ostatnim polem trajektorii PC.
bieżąca pozycja jest zmienną typu pole trajektorii określającą współrzędne pola na
którym znajduje się w danej chwili robot.
W programie użyte są również dodatkowe zmienne, które opisują powyższe dane i sterują
programem robota:
długość trajektorii rzeczywistej ma wartość równą indeksowi ostatniego pola tra-
jektorii rzeczywistej. Indeks pierwszego pola jest zerowy, wobec czego długość trajek-
torii rzeczywistej jest równa ilości jej pól pomniejszonej o jeden.
długość trajektorii PC jest zmienną o sensie analogicznym do poprzednio opisanej.

ROZDZIAŁ 8. PROGRAM ROBOTA
72
indeks trajektorii rzeczywistej określa indeks tablicy „trajektoria rzeczywista” od-
powiadający polu na którym znajduje się pojazd w chwili bieżącej.
indeks trajektorii PC określa indeks tablicy „trajektoria PC odpowiadający ostat-
niemu z pól trajektorii PC, na którym znajdował się robot.
indeks końca objazdu trajektorii PC jest indeksem trajektorii PC odpowiadają-
cym ostatniemu polu objazdu wyznaczanego na wypadek braku kafelka na jednym z pól
trajektorii PC. W przykładzie na rys. 8.10 końcem objazdu jest pole o współrzędnych
[3,2], a brakujące pole trajektorii PC ma współrzędne [2,2].
indeks spotkania trajektorii rzeczywistej jest indeksem trajektorii rzeczywistej
odpowiadającym pierwszemu wspólnemu, po zakończeniu objazdu, polu trajektorii rze-
czywistej i trajektorii PC. W przykładzie z rys. 8.10 pole to charakteryzują współrzędne
[5,2].
indeks spotkania trajektorii PC ma sens analogiczny do indeksu spotkania trajek-
torii rzeczywistej.
orientacja bezwzględna informuje o kierunku, w którym obrócony jest pojazd, wy-
znaczonym względem układu współrzędnych planszy. W przykładzie z rys. 8.10. Pojazd
zwrócony ku górze miałby orientację bezwzględną równą 0, zwrócony w prawo równą
1, do dołu równą 2, a w lewo równą 3.
orientacja względna ma sens analogiczny do bezwzględnej z tą różnicą, że określa
różnice pomiędzy bieżącym a planowanym kierunkiem w którym zwrócony jest pojazd.
Jeżeli kierunki te są zgodne to orientacja względna wynosi 0. Planowany kierunek
obrócony względem bieżącego o 90
o
w prawo daje orientację względną równą 1, obrót
o 180
o
daje orientację równą 2, a o 270
o
równą 3.
wektor manewrów został już po części opisany w pkt. 8.3. Jego kolejne współrzędne
są hierarchicznie uporządkowanymi zaleceniami warstwy nadzoru dla warstwy ruchu
określającymi orientacje względne pomiędzy planowanym a bieżącym kierunkiem w
którym zwrócony jest pojazd.
8.8.4
Architektura modułu
Moduł przetwarzania trajektorii uruchamiany jest każdorazowo wraz z kolejnymi wywołania-
mi stanu 10 warstwy nadzoru. Moduł ten można podzielić na kilka części będących zarazem
etapami jego działania. Poniżej zaprezentowano te etapy w porządku chronologicznym:
1. przebudowa trajektorii i aktualizacja zmiennych sterujących Wymienione ope-
racje możliwe są dzięki analizie manewru wykonanego na poprzednim kafelku.
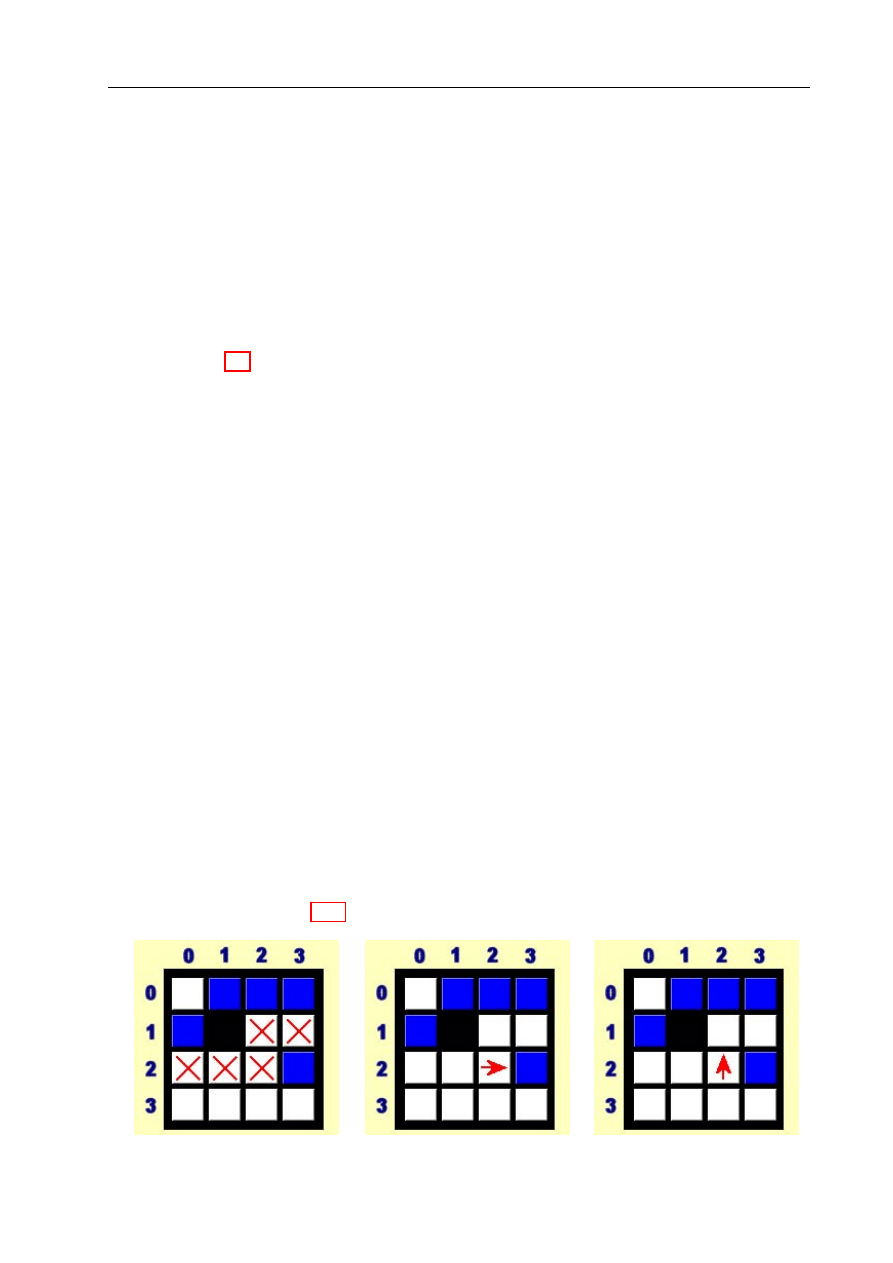
ROZDZIAŁ 8. PROGRAM ROBOTA
73
2. wyznaczenie wektora manewrów dla stanu 1 warstwy ruchu W etapie tym
wyznaczane są wszystkie możliwe objazdy na wypadek braku kafelków sąsiadujących z
bieżącym. Przebieg trajektorii rzeczywistej determinuje pierwszą współrzędną wektora
manewrów. Dalsze trzy współrzędne wyznaczane są na podstawie trajektorii objazdów.
3. aktualizacja orientacji bezwzględnej Wartość tej zmiennej zdeterminowana jest
przez raport warstwy ruchu o wykonaniu zleconego wektora manewrów.
Pierwsze dwa etapy wykonywane są w sekcji szóstej, a etap trzeci w sekcji ósmej, sieci
Petriego z rys. 8.7. Fakt ten ilustruje niezmiernie istotną właściwość opisywanego modułu.
Cały wektor manewrów wyznaczany jest zanim rozpocznie się manewr. Konieczne do te-
go obliczenia wykonywane są podczas przejazdu przez kafelek. Czas tego przejazdu jest w
praktyce wystarczająco długi aby obliczenia zakończyły się przed przejściem warstwy ruchu
do stanu 1. Dzięki temu wektor manewrów wykonywany jest płynnie i brak jest przestojów
związanych z dodatkowymi obliczeniami. Pojazd znajduje się cały czas w ruchu a wszystkie
obliczenia wykonywane są podczas jazdy. Jedynym momentem, w którym robot zatrzymu-
je się oczekując na wyznaczenie wektora manewrów jest nieoczekiwane przejście warstwy
nadzoru ze stanu 10 do stanu 20, mające miejsce w sytuacji niepowodzenia wykonywanego
manewru.
8.8.5
Etap wyznaczania wektora manewrów
Etap ten zostanie omówiony jako pierwszy, chociaż faktycznie wykonywany jest jako drugi.
Taka kolejność opisu pozwoli na lepsze zrozumienie działania całego modułu. Omawiany etap
prowadzi do wyznaczenia wektora manewrów dla warstwy ruchu. Pierwsza współrzędna tego
wektora zależna jest od bieżącej orientacji pojazdu a także charakteru sąsiedztwa pomiędzy
bieżącym polem trajektorii rzeczywistej a jej polem następnym. Jej wartość musi być tak
dobrana aby warstwa ruchu obróciła pojazd w kierunku, w którym znajduje się kolejne
pole trajektorii. Do opisu pojedynczego obrotu używana jest orientacja względna. Sposób jej
wyznaczania ilustruje rys. 8.11
a)
b)
c)
Rysunek 8.11: Sposób wyznaczania orientacji względnej
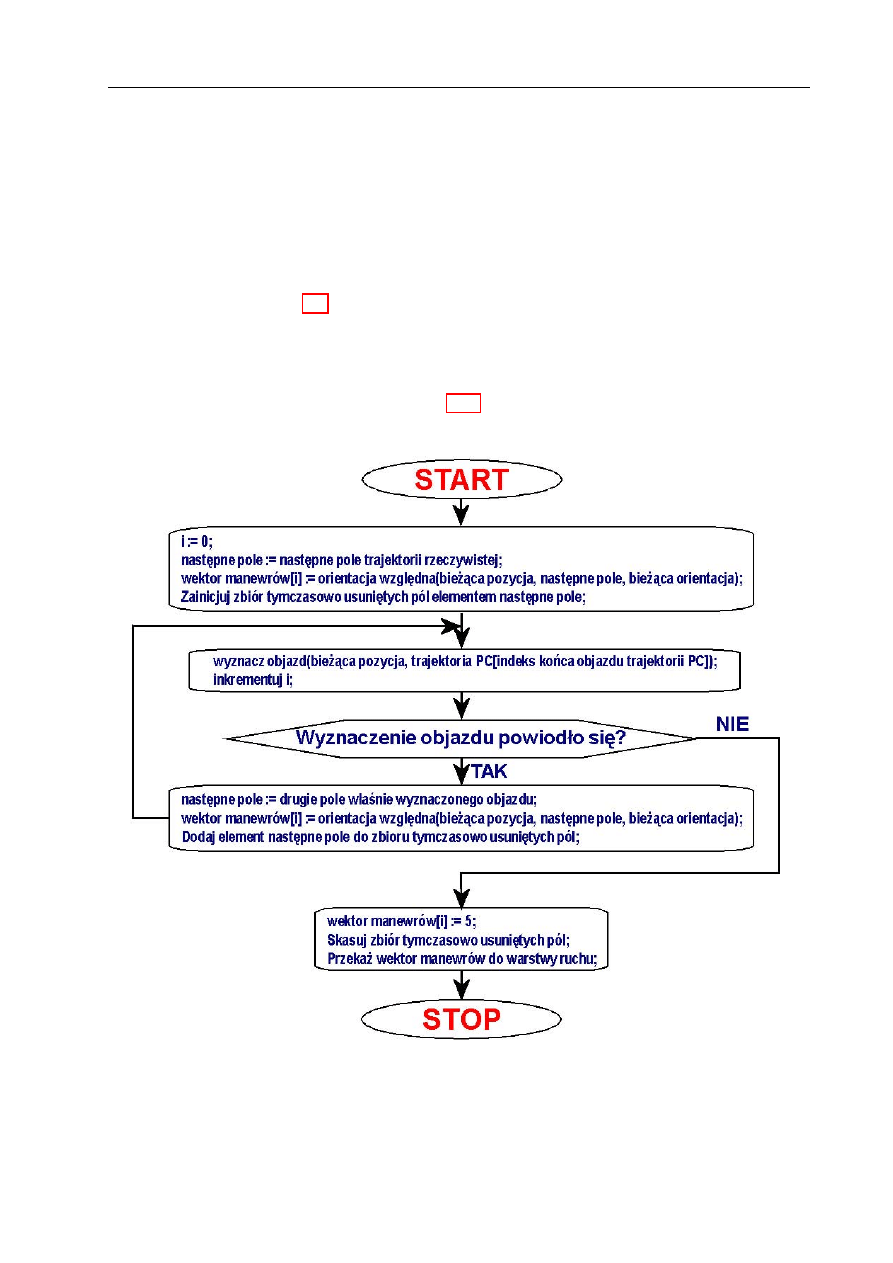
ROZDZIAŁ 8. PROGRAM ROBOTA
74
Na rysunkach znajduje się przykładowa mapa. Krzyżykami oznaczona jest trajektoria
do pokonania. Pojazd jedzie kolejno po polach: [0,2], [1,2], [2,2], [2,1], [3,1]. Wjeżdżając na
pole [2,2] robot zwrócony jest w prawo, wobec czego jego orientacja bezwzględna wynosi 1 -
rysunek b. Chcąc pojechać do góry musi obrócić się w lewo i osiągnąć orientację bezwzględ-
ną równą 0 - rysunek c. Obrót ten będzie zakodowany pod postacią orientacji względnej
wynoszącej 3 - co odpowiada skrętowi w lewo. W ogólnym przypadku orientację względną
pozwala wyznaczyć wzór 8.1.
(8.1) orientacja względna := (orientacja docelowa - orientacja początkowa + 4) mod 4
Schemat blokowy przedstawiony na rys. 8.12 ilustruje działanie algorytmu wyznaczania
wektora manewrów.
Rysunek 8.12: Schemat blokowy algorytmu wyznaczania wektora manewrów
Pierwsza współrzędna wektora manewrów zależna jest od następnego pola trajektorii rze-
czywistej, na które ma właśnie wjeżdżać pojazd. Kolejne współrzędne wektora wyznaczane
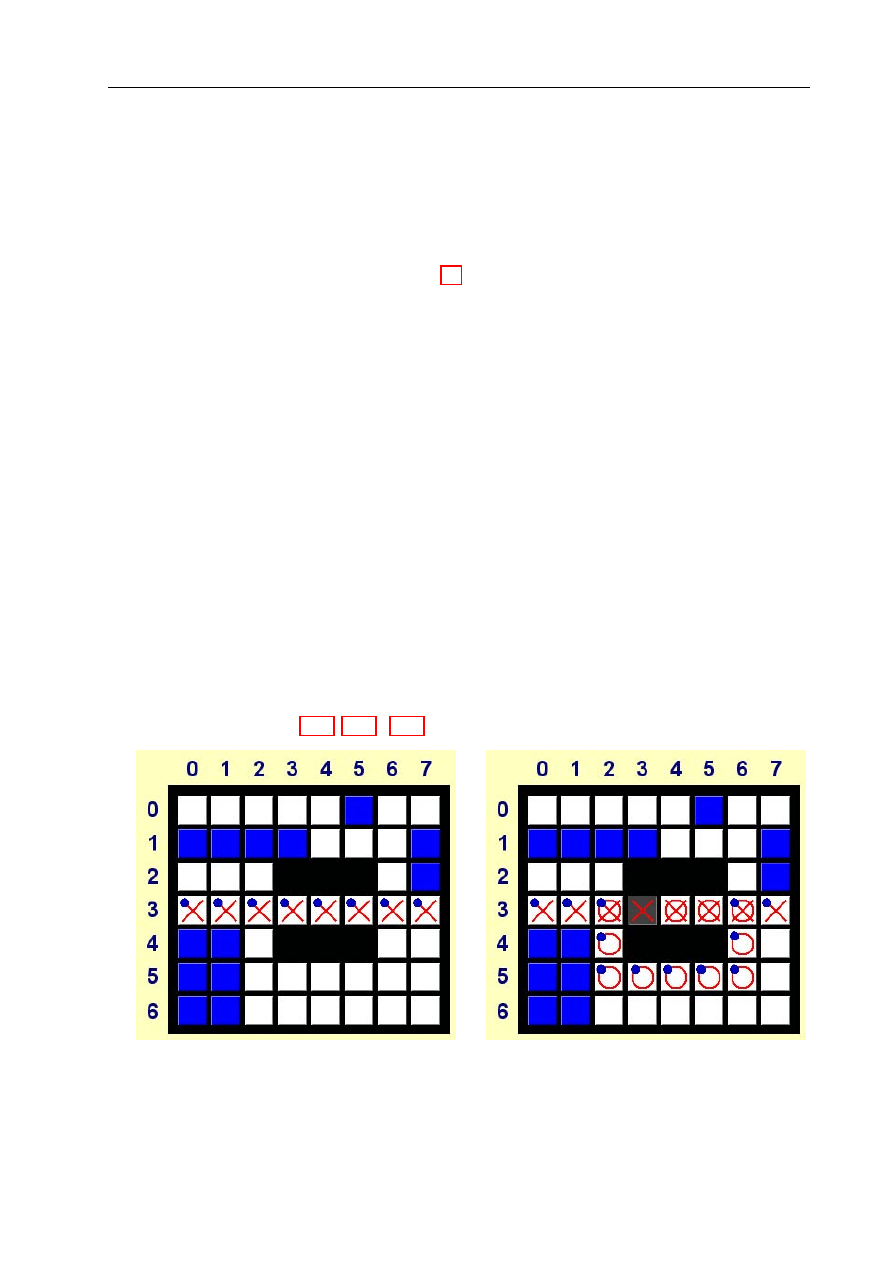
ROZDZIAŁ 8. PROGRAM ROBOTA
75
są na podstawie przebiegu ewentualnych objazdów. Jak już napisano wcześniej wektor ma-
newrów uwzględnia ewentualność ubytku kafelków sąsiadujących z bieżącym. Kafelki te są
zawarte w zbiorze tymczasowo usuniętych pól. Jako pierwszy za nieistniejący uważany jest
kafelek będący następnym polem trajektorii rzeczywistej. Moduł przetwarzania trajektorii
przystępuje do wyznaczania trajektorii objazdu. Jej wyliczenie możliwe jest dzięki wykorzy-
staniu planera trajektorii opisanego w pkt. 10.
Pierwszym polem objazdu jest bieżąca pozycja robota, a polem ostatnim element tra-
jektorii PC odpowiadający indeksowi końca objazdu trajektorii PC. Objazd wyznaczany
jest na podstawie mapy planszy a jego trajektoria zapisywana w odpowiedniej tablicy. Jeśli
wyznaczenie objazdu zakończyło się sukcesem, to znaczy możliwe było osiągnięcie zakła-
danego, ostatniego pola, to druga współrzędna wektora manewrów zostanie określona na
podstawie wzajemnego położenia bieżącego pola i sąsiadującego z nim drugiego pola właśnie
wyliczonego objazdu. W przeciwnym wypadku współrzędna ta przyjmie wartość 5, oznacza-
jącą niepowodzenie wyznaczenia objazdu, i kolejne objazdy nie będą już obliczane, a wektor
manewrów zostanie przekazany do warstwy ruchu. Jeśli udało się wyznaczyć pierwszy z ob-
jazdów, to moduł przystępuje do wyznaczania kolejnych objazdów, kierując się przy tym tymi
samymi zasadami, które obowiązywały dotychczas. Wyznaczanie każdego kolejnego objaz-
du poprzedzone jest uzupełnieniem zbioru tymczasowo wyeliminowanych kafelków drugim
polem objazdu poprzednio wyliczonego. Eliminowanie kolejnych pól może doprowadzić do
wyizolowania pola na którym znajduje się pojazd. Po wyliczeniu ostatniego z objazdów zbiór
tymczasowo wyeliminowanych pól zostaje usunięty.
Przykład z rysunków 8.13, 8.14 i 8.15 ilustruje działanie powyższego algorytmu.
a)
b)
Rysunek 8.13: Wyznaczanie wektora manewrów - współrzędne 1 i 2
Mapa wykorzystana w przykładzie składa się z czterech rodzajów pól. Pole białe odpowia-
da białemu kafelkowi, fioletowe — szaremu, a czarne — brakowi kafelka. Koszt wjechania na
biały kafelek wynosi 1, na szary (na mapie oznaczony kolorem fioletowym) — 2, a wjechanie
ROZDZIAŁ 8. PROGRAM ROBOTA
76
na czarne pole nie jest możliwe gdyż nie ma na nim kafelka. Pola oznaczone kolorem ciemno-
szarym należą do zbioru tymczasowo usuniętych pól. Krzyżykami oznaczona jest trajektoria
rzeczywista, która pierwotnie miał pokonać pojazd. W omawianym przykładzie trajektoria
ta pokrywa się z trajektorią PC, choć w ogólnym przypadku sytuacja taka nie musi mieć
miejsca. Planowo pojazd ma pokonywać pola w następującej kolejności: idąc po współrzęd-
nych - [0,3], [1,3], [2,3], [3,3], [4,3], [5,3], [6,3] i [7,3]. Przykład ilustruje wyznaczanie wektora
manewrów wykonywanego na polu [2,3].
Pierwsza współrzędna wektora manewrów wyliczana jest na podstawie bieżącej pozycji
pojazdu, następnego pola trajektorii rzeczywistej i bieżącej orientacji bezwzględnej. Pojazd
wjeżdżając na pole [2,3] zwrócony jest w prawo, wobec czego jego orientacja bezwzględna
wynosi 1. Następne pole trajektorii rzeczywistej ma współrzędne [3,3]. W celu wjechania na
nie pojazd musi osiągnąć orientację bezwzględna równą 1. Orientacje docelowa i bieżąca nie
różnią się wobec czego, zgodnie ze wzorem 8.1, pierwsza współrzędna wektora manewrów
wyniesie 0.
Jako pierwsze do zbioru tymczasowo usuniętych pól zostanie włączone pole trajektorii
rzeczywistej o wsp. [3,3]. Pierwszy z objazdów wyznaczany będzie przy założeniu, że na po-
lu tym brak jest kafelka. Pierwszym polem, tego i innych objazdów wyznaczanych w tym
przykładzie, będzie bieżąca pozycja robota wynosząca [2,3], polem ostatnim zaś element
trajektorii PC o wsp. [4,2]. Ostatnie pole objazdów wyznaczane jest na podstawie wartości
indeksu końca objazdu trajektorii PC. Indeks ten jest tak dobrany aby odpowiadać polu
trajektorii PC jak najbliższemu bieżącej pozycji robota. Pole to jest wybierane spośród nie-
odwiedzonych jeszcze pól trajektorii PC, o których zakłada się że znajdują się na nich kafelki.
Planer trajektorii wyznacza objazd kierując się kryterium jak najmniejszego kosztu osiągnię-
cia pola docelowego. Najmniejszym kosztem cechuje się objazd oznaczony kółkami na prawej
mapie rys. 8.13. Wyznaczenie tego objazdu zakończyło się sukcesem, gdyż osiągnięto pole
docelowe. Druga współrzędna wektora manewrów zależna będzie tym razem od drugiego pola
właśnie wyliczonego objazdu i wyniesie 1. W sytuacji, w której manewr faktycznie wykonany
przez warstwę ruchu odpowiadał by temu objazdowi nowo określona trajektoria rzeczywista
biegła by po polach oznaczonych niebieskimi kółkami: zaczynając od bieżącego pola - [2,3],
[2,4], [2,5], [3,5], [4,5], [5,5], [6,5], [6,4], [6,3], [7,3]. Przyczyna wyeliminowania z trajektorii
rzeczywistej niektórych pól trajektorii PC wyjaśniona jest w pkt. 8.8.2 poświęconym definicji
jak najwierniejszego wykonywania trajektorii.
Poprawne wyznaczanie pierwszego objazdu implikuje przystąpienie do wyznaczania kolej-
nego z nich. Zbiór tymczasowo usuniętych pól zostaje uzupełniony drugim polem poprzednio
wyliczonego objazdu o wsp. [2,4]. Pozostałe założenia nie ulegają zmianie. Planer trajekto-
rii wyznacza objazd oznaczony czerwonymi okręgami na rys. 8.14 a. Trzecia współrzędna
wektora manewrów przyjmuje wartość 3. Nowo wyliczona trajektoria rzeczywista biegnie po
polach oznaczonych niebieski kółkami.
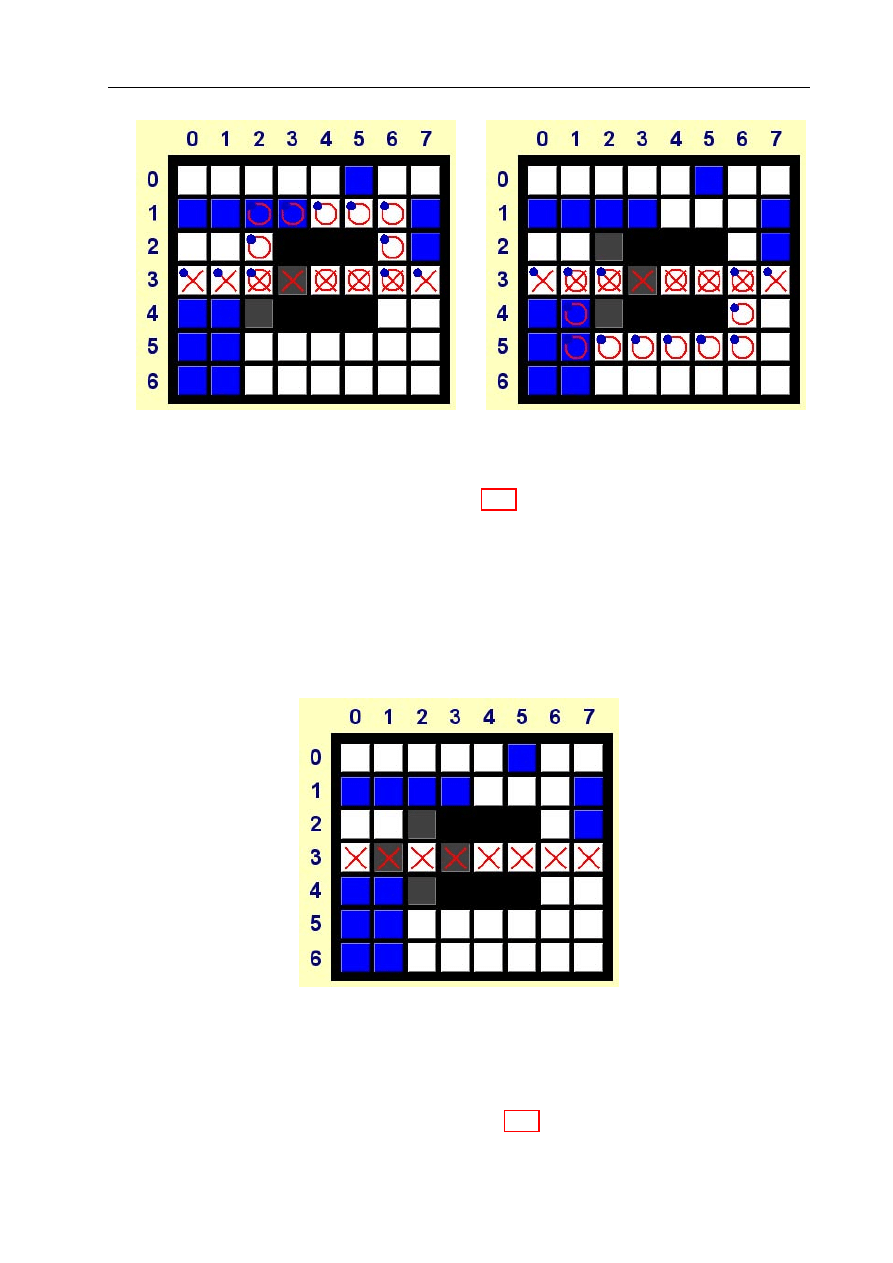
ROZDZIAŁ 8. PROGRAM ROBOTA
77
a)
b)
Rysunek 8.14: Wyznaczanie wektora manewrów - współrzędne 3 i 4
Przebieg ostatniego z objazdów ilustruje rys. 8.14 b. Pola [2,2], [3,3] i [2,4] należą już do
zbioru tymczasowo usuniętych pól, wobec czego objazd biegnie przez ostatnie pole umożli-
wiające opuszczenie początkowego kafelka, a czwarta współrzędna wektora manewrów osią-
gnie wartość 2. Pojazd pojedzie objazdem wyliczonym w tej fazie w przypadku, w którym
hipoteza o braku kafelków na szarych polach potwierdzi się, a pole [1,3] nadal będzie wypo-
sażone w kafelek. Przejazd ten będzie wiązał się z ponownym odwiedzeniem pola trajektorii
rzeczywistej o współrzędnych [1,3].
Rysunek 8.15: Wyznaczanie wektora manewrów - współrzędna 5
Wyznaczenie czwartej współrzędnej wektora manewrów pociąga za sobą dodanie pola
[1,3] do zbioru tymczasowo usuniętych pól - rys. 8.15. Fakt ten uniemożliwia skuteczne
wyznaczenie czwartego z kolei objazdu. Piąta współrzędna wektora manewrów przyjmie,
odpowiadającą takiej sytuacji, wartość 5. Ostatecznie wektor manewrów będzie miał postać:

ROZDZIAŁ 8. PROGRAM ROBOTA
78
[0,1,3,2,5].
Wektor manewrów wyliczany jest na każdym polu trajektorii rzeczywistej, w szczególności
kiedy pojazd jedzie już po wcześniej wyznaczonym objeździe. W ogólnym przypadku wektor
ten może składać się z 2 do 5 współrzędnych, gdyż nawet wyznaczanie pierwszego z objazdów
może zakończyć się niepowodzeniem.
Na przedostatnim polu trajektorii rzeczywistej wektor manewrów wyznaczany jest we-
dług uproszczonego algorytmu. Ze względu na fakt, że następnym polem jest ostatnie pole
trajektorii PC, jedynym manewrem, który ma sens, jest wjechanie bezpośrednio na nie. Żad-
ne objazdy nie są wyliczane, a wektor manewrów ma dwie współrzędne, z których druga jest
równa 5.
Warstwa ruchu zdaje warstwie nadzoru raport o wykonaniu zleconego wektora manew-
rów. Na jego podstawie moduł przetwarzania trajektorii aktualizuje orientację bezwzględną
pojazdu, a stan 10 warstwy nadzoru podejmuje decyzję o zmianach stanu warstwy ruchu
i warstwy nadzoru. Jeśli manewr zakończy się niepowodzeniem, czyli nie możliwy będzie
wjazd na którąkolwiek z zaplanowanych trajektorii, to pojazd rozpoczyna powrót do pola
początkowego trajektorii PC, co wiąże się z przejściem warstwy nadzoru do stanu 20. W
przypadku, w którym warstwa nadzoru pozostanie w stanie 10, zarówno raport o wykonaniu
wektora manewrów, jak i wyznaczone trajektorie objazdów, zostaną wykorzystane do póź-
niejszej przebudowy trajektorii rzeczywistej i aktualizacji zmiennych sterujących. Dodatkowo
indeks trajektorii rzeczywistej jest inkrementowany, gdyż pojazd z powodzeniem wjechał na
jej kolejne pole.
8.8.6
Etap przebudowy trajektorii i aktualizacji zmiennych steru-
jących
Etap przebudowy trajektorii uruchamiany jest każdorazowo na początku stanu 10 warstwy
nadzoru. Wykonywany algorytm nie potrzebuje bezpośredniej informacji o poprzednim sta-
nie tej warstwy. Wykorzystywany jest za to raport warstwy ruchu o faktycznie wykonanym
manewrze, a także trajektoria rzeczywista, trajektoria PC i trajektorie objazdów, wyzna-
czone na wypadek konieczności zjechania z wcześniej założonej trajektorii rzeczywistej oraz
indeksy charakteryzujące odpowiednie pola na tych trajektoriach. Wszystkie zmienne zostały
opisane w pkt. 8.8.3.
Schemat blokowy algorytmu wykorzystywanego w opisywanym etapie znajduje się na rys.
8.16. Dla ułatwienia analizy jego poszczególne sekcje zostały oznaczone czerwonymi literami
w zakresie od a do e. Poniżej znajduje się opis tych sekcji oraz warunków, które muszą zostać
spełnione, aby sekcje te zostały wykonane:
a - Fragment kodu uruchamiany w sytuacji kiedy pojazd jedzie po wcześniej zakładanej
trajektorii rzeczywistej. Faktycznie wykonany manewr odpowiada wówczas pierwszej
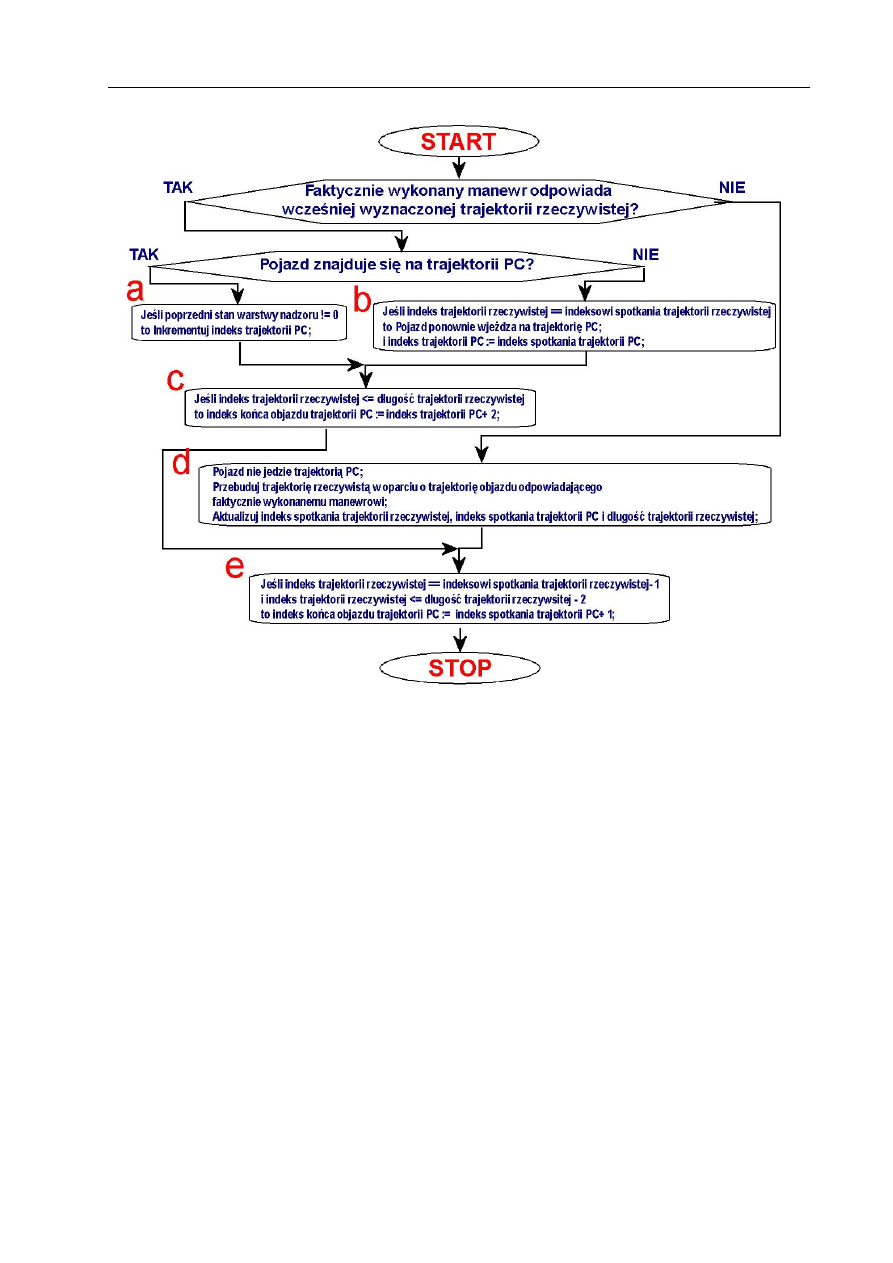
ROZDZIAŁ 8. PROGRAM ROBOTA
79
Rysunek 8.16: Schemat blokowy etapu przebudowy trajektorii i aktualizacji zmiennych ste-
rujących
współrzędnej wektora manewrów wyznaczonego w poprzedniej fazie. Dodatkowo, robot
musi znajdować się na trajektorii PC. Wówczas naturalnym krokiem jest inkrementacja
indeksu trajektorii PC, gdyż pojazd z powodzeniem pokonał kolejne jej pole.
b - Sekcja wykonywana w przypadku, w którym pojazd jedzie po wcześniej zakładanej tra-
jektorii rzeczywistej, ale nie znajduje się na trajektorii PC. Robot podąża którymś z
objazdów wyznaczonych co najmniej dwa pola wcześniej. Przypadek, w którym indeks
trajektorii rzeczywistej zrówna się z indeksem spotkania trajektorii rzeczywistej, świad-
czy o powrocie pojazdu na trajektorie PC. Indeks trajektorii PC przyjmuje wówczas
wartość indeksu spotkania trajektorii PC, a robot osiąga pola w którym trajektoria
rzeczywista i trajektoria PC spotykają się.
c - Sekcja uruchamiana każdorazowo po sekcjach a lub b. Jej zadaniem jest ustalenie war-
tości indeksu następnika objazdu trajketorii PC odpowiadającego polu leżącemu na
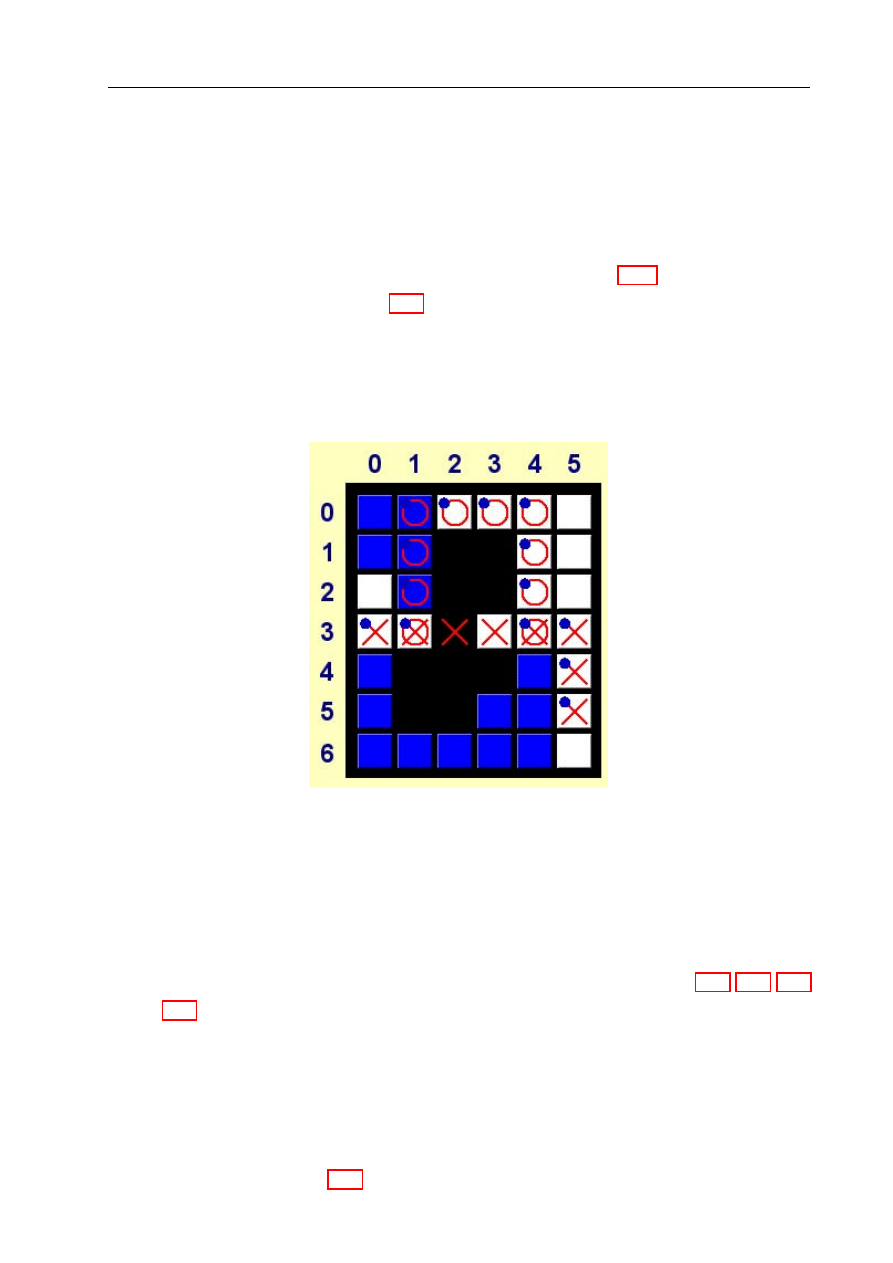
ROZDZIAŁ 8. PROGRAM ROBOTA
80
trajektorii PC do którego będą zmierzały objazdy budowane w etapie wyznaczania
wektora manewrów. Indeks ten określany jest tylko w sytuacji kiedy ma to sens, czy-
li wówczas kiedy pojazd znajduje się co najmniej dwa pola przed końcem trajektorii
rzeczywistej. Jego wartość jest powiększoną o 2 wartością indeksu trajektorii PC. Przy-
czyny takiego wyboru pola kończącego każdy z objazdów wypływają z dążenia do jak
najwierniejszego wykonania trajektorii PC opisanego w pkt. 8.8.2.
W przykładowej mapie na rys. 8.17 trajektoria rzeczywista oznaczona jest niebieskimi
kółkami. Rozpoczyna się na polu o współrzędnych [0,3], po czym biegnie przez pola
[1,3], [1,2], [1,1], [1,0], [2,0], [3,0], [4,0], [4,1], [4,2], [4,3], [5,3], [5,4], i kończy się po-
lem [5,5]. Indeks następnika objazdu trajektorii PC wyznaczany będzie na polach o
współrzędnych od [0,3] do [5,3].
Rysunek 8.17: Przykładowa mapa
d - Jeśli faktycznie wykonany manewr nie odpowiada wcześniej wyznaczonej trajektorii
rzeczywistej to pojazd wjechał na jeden z objazdów zbudowanych na poprzednim polu
i z pewnością nie jedzie już po trajektorii PC. Trajektoria rzeczywista zostaje przebu-
dowana w oparciu o trajektorię objazdu tak jak miało to miejsce na rys. 8.13, 8.14, 8.15
i 8.17. Trajektoria objazdu zostaje wstawiona w miejsce nie odwiedzonego fragmen-
tu trajektorii rzeczywistej. Indeks spotkania trajektorii PC przyjmuje wartość indeksu
pola trajektorii PC, będącego pierwszym wspólnym polem trajektorii PC i trajektorii
rzeczywistej, następującym po polu bieżącym. W analogiczny sposób wyznaczany jest
indeks spotkania trajektorii rzeczywistej odpowiadający polu leżącemu na trajektorii
rzeczywistej. Ponownie wyznaczana jest również długość trajektorii rzeczywistej.
W przykładzie na rys. 8.17 w momencie wjechania robota na objazd oznaczony czer-

ROZDZIAŁ 8. PROGRAM ROBOTA
81
wonymi kółkami omawiane indeksy przyjmą wartości odpowiadające polu o współrzęd-
nych [4,3].
e - Sekcja ta uruchamiana jest każdorazowo na końcu etapu przetwarzania trajektorii. Jej
celem jest ewentualna inkrementacja indeksu końca objazdu trajektorii PC następu-
jąca w sytuacja wjazdu na pole leżące na objeździe, poprzedzające pole leżące już na
trajektorii PC. Inkrementacja ta zachodzi w przypadku, gdy pojazd znajduje się co
najmniej dwa pola od końcowego pola trajektorii rzeczywistej.
W przykładzie na rys. 8.17 operacja ta zostanie wykonywana na polu o współrzędnych
[4,2].
8.9
Modyfikacje jądra systemu legOS
8.9.1
Cel przeprowadzonych zmian
Zmiany dokonane w jądrze systemu operacyjnego legOS miały dwa zasadnicze cele:
1. Umożliwienie aplikacji uruchomionej w systemie operacyjnym dokonania odczytu bar-
wy podłoża znajdującego się pod czujnikiem światła. Czujnik ten może być podłączony
niezależnie do jednego z wejść RCX’a lub zestawiony w parze z czujnikiem odometrycz-
nym.
2. Wprowadzenie obsługi czujnika odometrycznego zestawionego w parze z czujnikiem
natężenia światła.
Informacja o kolorze podłoża wykorzystywana jest w opisanej w pkt. 8.3 warstwie ruchu
programu robota. Kolor wyznaczany jest na podstawie natężenia światła docierającego do
odpowiedniego czujnika. Ekstrahowaniem barwy podłoża zajmuje się system operacyjny, a
nie uruchomiona w nim aplikacja. Taki podział funkcjonalny ma kilka przyczyn:
1. Funkcje systemu operacyjnego mają wyższy priorytet niż fragmenty kodu aplikacji,
wobec czego wyznaczanie barwy przebiega w systemie operacyjnym znacznie szybciej
niż poza nim.
2. Kod aplikacji bazującej bezpośrednio na kolorach jest krótszy i czytelniejszy.
3. Jeśli czujnik światła podłączony jest wraz z czujnikiem odometrycznym do jednego
wejścia RCX, to odczyt barwy podłoża staje się nierozerwalnie powiązany z obsługą
odometrii, w związku z czym naturalne jest stworzenie wspólnego kodu do obsługi
obydwu czujników.

ROZDZIAŁ 8. PROGRAM ROBOTA
82
Obsługa czujników odometrycznych musi być wykonywana w systemie operacyjnym, po-
nieważ tylko funkcje systemu operacyjnego mogą być wywoływane z wystarczająco dużą,
przekraczającą 100Hz, częstotliwością. Częstotliwość taka jest wymagana do nadążania za
zmianami stanu wejścia czujnikowego do którego podłączony jest czujnik odometryczny.
8.9.2
Odczyt barwy podłoża za pomocą osobno podłączonego czuj-
nika światła
Gdy czujnik światła podłączony jest pojedynczo do wejścia RCX, translacja natężenia świa-
tła na barwę podłoża jest bardzo prosta. Poszczególnym barwom odpowiadają wówczas
wyznaczone eksperymentalnie przedziały natężenia światła przedstawione w tab. 8.1. Prze-
działy te są charakterystyczne dla zbudowanego systemu symulacyjnego i przy jakiejkolwiek
jego istotnej zmianie muszą być weryfikowane.
zakres czerni
zakres szarości
zakres bieli
20 - 31
32 - 37
39 - 47
Tabela 8.1: Zakres odczytów dla poszczególnych barw przy zastosowaniu osobno podłączo-
nego czujnika światła
8.9.3
Odczyt barwy podłoża i obsługa odometrii dla czujnika świa-
tła i czujnika odometrycznego podłączonych wspólnie do
jednego wejścia RCX
Czujnik odometryczny przyjmuje normalnie cztery stany na każdą 1/4 obrotu jego wału,
co opisuje pkt. 5.1.3. Po zwarciu czujników odometrii i światła na jednym wejściu RCX
ich odczyty uwspólniają się. Czujnik odometryczny osiąga już tylko po trzy stany na każ-
dą 1/4 obrotu, a odczyty z czujnika światła ulegają przeskalowaniu w zależności od stanu,
w którym znajduje się czujnik odometryczny. Stany 1 i 2 czujnika odometrycznego nadal
odpowiadają 1/16 obrotu. Stan 3 odpowiada zaś 1/8 obrotu, gdyż powstaje z połączenia
dawnych stanów 3 i 4 i dlatego został oznaczony jako 34. Każdy ze stanów czujnika odome-
trycznego charakteryzowany jest przez pewien zakres odczytów, wynikający z wpływu zmian
rezystancji na czujniku światła. Barwę podłoża można określić tylko dla 1 i 2 stanu czujnika
odometrycznego, gdyż rozdzielczość w stanie 34 jest zbyt mała. Barwy podłoża zostały tak
dobrane, aby charakteryzujące je zakresy odczytów z wejścia czujnikowego były wzajemnie
rozłączne niezależnie od stanu w którym znajduje się czujnik odometryczny. Zakresy odczy-
tów dla poszczególnych stanów czujnika odometrycznego i odpowiadających im barw zostały
zamieszczone w tab. 8.2.
ROZDZIAŁ 8. PROGRAM ROBOTA
83
stan
zakres całego stanu
zakres czerni
zakres szarości
zakres bieli
1
15 - 46
15 - 32
33 - 37
39 - 46
2
50 - 83
50 - 66
67 - 73
74 - 83
34
88 - 100
nieokreślony
nieokreślony
nieokreślony
Tabela 8.2: Zakres odczytów dla poszczególnych stanów i odpowiadających im barw przy
równoległym połączeniu czujników światła i odometrycznego
Odczyty kąta obrotu wału czujnika odometrycznego są na 16 jednostek. Zmiany wartości
kąta ustalane są na podstawie bieżącego i poprzedniego stanu w którym znajdował się czujnik
odometryczny, co ilustruje tab. 8.3
1
2
34
1
0
1
-2
2
-1
0
1
34
2
-1
0
Tabela 8.3: Zmiany kąta obrotu wału czujnika odometrycznego podczas przejścia pomiędzy
poszczególnymi stanami czujnika odometrycznego (dla przejścia stanu z lewej kolumny w
stan z górnego wiersza)

Rozdział 9
Wyznaczanie trajektorii algorytmem
ewolucyjnym
9.1
Opis algorytmu
Jak to zostało ustalone w założeniach wstępnych (punkt 3.2.1) optymalna trajektoria dla
robota może być wyznaczona algorytmem ewolucyjnym. Poniżej zostaną omówione szczegóły
implementacji takie, jak: reprezentacja rozwiązania, inicjacja populacji, operatory genetycz-
ne, funkcja przystosowania, sposoby reprodukcji i sukcesja.
9.1.1
Reprezentacja rozwiązania
Każdy chromosom (osobnik) reprezentuje przykładową ścieżkę, po której porusza się robot
i jest listą genów. Pojedynczy gen jest uporządkowaną trójką (x, y, t), gdzie x i y są dys-
kretnymi współrzędnymi (w układzie współrzędnych z zerem w lewym górnym rogu) punktu
będącego węzłem ścieżki, a t oznacza sposób połączenia ścieżki z węzłem poprzednim. Pierw-
szy gen wyznacza zawsze początek ścieżki, a jego wartość t nie ma znaczenia (standardowo
przyjmowana jest jako 0), a ostatni - koniec. Oba te geny nie są poddawane operacjom ge-
netycznym - z wyjątkiem wartości połączenia t w ostatnim węźle - dlatego że współrzędne
punktów końcowego i początkowego nie mogą być zmienione przez algorytm.
X
i
= {(x
i
0
, y
i
0
, t
i
0
), . . . , (x
i
n
, y
i
n
, t
i
n
)} — i-ty chromosom w populacji.
Możliwe są dwa rodzaje połączenia (wartości t genu):
0) najpierw wykonywany jest ruch w pionie (wzdłuż osi Y) a potem w poziomie (wzdłuż
osi X) — na rysunku 9.1 przedstawione są wszystkie cztery możliwości („A” — węzeł
poprzedzający „B”, kółka — ścieżka łącząca węzły).
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
85
1) najpierw wykonywany jest ruch w poziomie (wzdłuż X) a potem w pionie (wzdłuż Y)
— na rysunku 9.2 przedstawione są wszystkie cztery możliwości.
Rysunek 9.1: 4 możliwości łaczenia węzłów dla wartości t=0
Rysunek 9.2: 4 możliwości łaczenia węzłów dla wartości t=1
Przykładowa ścieżka pokazana jest na rysunku 9.3 (krzyżyki — węzły, kółka — ścieżka
łącząca dwa kolejne węzły).
Rysunek 9.3: Przykładowa ścieżka
W końcówce ścieżki trzy węzły są w poziomie — ostatnie dwa geny pokazują, że w takim
wypadku wartość t nie ma znaczenia (wszystko jedno czy robot pojedzie najpierw 0 pól w
pionie a potem 2 pola w prawo - wartość t=0, czy najpierw 2 pola w prawo a potem 0 w
pionie - wartość t=1), analogicznie sytuacja wygląda, gdy dwa węzły łączą się w pionie (mają
tę samą współrzędną Y).
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
86
Wartość t jest istotna ze względu na sposób łączenia punktów wynikający z użytej tu-
taj metryki miejskiej. Sposób połączenia nie jest istotny w przypadku środowiska homoge-
nicznego i nie posiadającego przeszkód, co może zdarzyć się tylko lokalnie (wszystkie pola
prostokąta, którego wierzchołkami są dwa sąsiednie węzły mają ten sam koszt przejazdu).
Takie połączenie nie wpływa na ogólność rozwiązania, gdyby istniała inna potrzeba przej-
ścia od jednego węzła do drugiego zawsze może to zostać osiągnięte dzięki dodatkowym
węzłom (rysunek 9.4)
Rysunek 9.4: Sposoby realizacji ścieżek
Długość chromosomów w ogólności nie jest stała. Aby założona trasa mogła zostać wy-
konana przez robota musi być zapisana jako ciąg kolejnych punktów na mapie, przez które
robot powinien przejechać.
˜
X = {(˜
x
0
, ˜
y
0
), . . . , (˜
x
n
, ˜
y
n
)},
który to ciąg powstaje dzięki odpowiedniemu połączeniu węzłów w zależności od wartości t
(punkt 9.1.1).
9.1.2
Inicjacja populacji
Wartości x i y położenia kolejnych węzłów kolejnych osobników losowane są rozkładem rów-
nomiernym.
x
i
= a
i
; a
i
∈ h0, x
max
i , a
i
∈ Z
y
i
= b
i
; b
i
∈ h0, y
max
i , b
i
∈ Z
x
max
- maksymalna wartość współrzędnej x (szerokość pomniejszona o jeden)
y
max
- maksymalna wartość współrzędnej y (wysokość pomniejszona o jeden)
Wartości rodzaju łączenia węzłów t losowane są z rozkładem dwupunktowym.
t
i
= 0, z prawdopodobieństwem p = 0, 5;
t
i
= 1, z prawdopodobieństwem p = 0, 5;
Istnieje również możliwość zanicjowania wszystkich wartości t jedną, identyczną liczbą.

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
87
9.1.3
Operatory genetyczne
a) mutacja
- mutacja węzła z rozkładem równomiernym o danym zasięgu r; współrzędne x i y mutowane
są niezależnie:
x
i
[j + 1] = x
i
[j] + a
i
; a
i
∈ h−r, ri , a
i
∈ Z, gdy 0 ¬ x
i
[j] + a
i
¬ x
max
x
i
[j + 1] = 0, gdy x
i
[j] + a
i
< 0
x
i
[j + 1] = x
max
, gdy x
i
[j] + a
i
> x
max
y
i
[j + 1] = y
i
[j] + b
i
; b
i
∈ h−r, ri , b
i
∈ Z, gdy 0 ¬ y
i
[j] + b
i
¬ y
max
y
i
[j + 1] = 0, gdy y
i
[j] + b
i
< 0
y
i
[j + 1] = y
max
, gdy y
i
[j] + b
i
> y
max
- mutacja połączenia t z rozkładem dwupunktowym - z prawdopodobieństwem p zmie-
nienia tej wartości
t
i
[j + 1] = 1 − t
i
[j], z prawdopodobieństwem p;
t
i
[j + 1] = t
i
[j], z prawdopodobieństwem 1 − p;
b) krzyżowanie
- jednopunktowe - losowany jest gen z pierwszego osobnika poddawanego krzyżowaniu - gen
ten staje się jego ostatnim genem (reszta do końca jest kasowana), następnie losowany jest
gen z drugiego osobnika - ma on być pierwszym genem, który zostanie dołączony do pierw-
szego osobnika wraz z resztą kolejnych genów.
n
(x
0
0
, y
0
0
, t
0
0
), . . . , (x
0
k
, y
0
k
, t
0
k
), (x
0
k+1
, y
0
k+1
, t
0
k+1
), . . . , (x
0
n
, y
0
n
, t
0
n
)
o
⊕
n
(x
1
0
, y
1
0
, t
1
0
), . . . , (x
1
l
, y
1
l
, t
1
l
), (x
1
l+1
, y
1
l+1
, t
1
l+1
), . . . , (x
1
m
, y
1
m
, t
1
m
)
o
−→
n
(x
0
0
, y
0
0
, t
0
0
), . . . , (x
0
k
, y
0
k
, t
0
k
), (x
1
l+1
, y
1
l+1
, t
1
l+1
), . . . , (x
1
m
, y
1
m
, t
1
m
)
o
gdzie:
n - długość pierwszego chromosomu;
m - długość drugiego chromosomu;
k ∈ h0, ni - wylosowany punkt przecięcia pierwszego chromosomu;
l ∈ h0, mi - wylosowany punkt przecięcia drugiego chromosomu;
9.1.4
Funkcja przystosowania
Funkcją celu zadania optymalizacji jest całkowity koszt przejazdu robota od punktu począt-
kowego do końcowego. Całkowity koszt przejazdu jest sumą kosztów (c((˜
x
i
, ˜
y
i
))) przejechania

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
88
przez dane pole (kafelek). Różne typy pól (rozróżniane kolorami) mają odmienne koszty prze-
jazdu.
Zadanie optymalizacji:
min f ( ˜
X);
f ( ˜
X) =
n
X
i=0
c((˜
x
i
, ˜
y
i
));
(9.1)
przy ograniczeniach: ∀i, (˜
x
i
, ˜
y
i
) /
∈ D,
gdzie: D jest zbiorem pól zakazanych (obszarem zabronionym), przez które robot nie może
przejechać (z prostej przyczyny - nie ma tam kafelka).
Funkcja przystosowania jest zależna od całkowitego kosztu przejazdu ścieżki. Jej zada-
niem jest ocenianie osobników. Im trajektoria reprezentowana przez danego osobnika jest
krótsza, tym osobnik powinien mieć wyższe przystosowanie. W ten sposób algorytm ewolu-
cyjny podczas reprodukcji będzie promował najlepsze rozwiązania. Funkcja przystosowania
jest więc w algorytmie maksymalizowana (są faworyzowane osobniki o lepszym przystosowa-
niu).
max F (X);
F (X) = h − f ( ˜
X),
(9.2)
gdzie: h jest szacowanym maksymalnym kosztem przejazdu;
i przy założeniu:
∀i, (˜
x
i
, ˜
y
i
) ∈ D ⇒ c((˜
x
i
, ˜
y
i
)) = d,
gdzie d jest karą za przejście trajektorii przez pole zabronione
oraz ∀i, (˜
x
i
, ˜
y
i
) /
∈ D d > c((˜
x
i
, ˜
y
i
)).
Koszt przejazdu przez pole niedopuszczalne jest dużo większy niż przez pole dopuszczal-
ne. Celem tak dużego kosztu jest dyskredytowanie trajektorii przejeżdżających przez pola
zakazane. Koszt ten nie powinien być jednak zbyt wysoki, by osobniki miały możliwość prze-
kraczania obszarów niedopuszczalnych w poszukiwaniu lepszych trajektorii. Funkcja przy-
stosowania zawiera więc liniową funkcję kary.
Może się więc zdarzyć, że rozwiązanie podane przez algorytm będzie niedopuszczalne.
Wtedy to część trajektorii przechodząca przez obszar zabroniony jest wyznaczana algoryt-
mem deterministycznym (analogicznym jak został zaimplementowany w robocie, do omijania
nieznanych przeszkód pkt. 10).

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
89
9.1.5
Sposoby reprodukcji
Zadaniem reprodukcji jest wyłonienie populacji tymczasowej poddawanej operatorom gene-
tycznym. Reprodukcja promuje osobniki najlepiej przystosowane. Nie oznacza to, że zawsze
do populacji tymczasowej przechodzą osobniki najlepsze. Zazwyczaj mają tylko większą szan-
sę dostania się do niej [1].
a) ruletkowa (proporcjonalna)
Jest to rodzaj reprodukcji, w której szansa osobnika na poddanie go operacjom genetycznym
jest proporcjonalna do wartości jego funkcji przystosowania:
p(X) =
F (X)
P
Y ∈P
t
F (Y )
(9.3)
b) ruletkowa zmodyfikowana
Jest modyfikacją poprzedniego sposobu reprodukcji. Szansa osobnika na poddanie go opera-
cjom genetycznym jest proporcjonalna do wartości jego funkcji przystosowania pomniejszonej
o wartość funkcji przystosowania najgorszego osobnika w danej generacji.
p(X) =
F (X) − F
t
P
Y ∈P
t
(F (Y )) − F
t
,
(9.4)
gdzie:
F
t
= inf
X∈P
t
F (X)
(9.5)
Metoda ta w przeciwieństwie do poprzedniej nie jest wrażliwa na ustalaną stałą h (sza-
cowany maksymalny koszt przejazdu), ponieważ:
F (X)−F
t
= (h−
P
n
i=0
c((˜
x
i
, ˜
y
i
)))−(h−
P
n
i=0
c((˜
x
i
, ˜
y
i
)
t
)) =
P
n
i=0
c((˜
x
i
, ˜
y
i
)
t
)−
P
n
i=0
c((˜
x
i
, ˜
y
i
)),
gdzie: ˜
X
t
- ścieżka o najwyższym koszcie w danej generacji.
c) turniejowa
Reprodukowani osobnicy są wyłaniani w turniejach liczności q (dobieranej arbitralnie - jako
jeden z parametrów algorytmu) osobników wybieranych losowo z rozkładem równomiernym
(ze zwracaniem). W każdym turnieju wygrywa osobnik o najwyższej funkcji przystosowania.
Turniej przeprowadzany jest, aż zostanie wyłoniona populacja potomna o liczności populacji
bazowej. Oczywiście tak jak w przypadku reprodukcji ruletkowej część osobników będzie w
nowej populacji będzie posiadała swoje kopie.

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
90
9.1.6
Sukcesja
Sukcesja jest trywialna - tzn. cała populacja potomna staje się nową populacją bazową.
9.2
Uwagi na temat kodowania osobników
9.2.1
Rola zasięgu mutacji pozycji węzła
Zasięg mutacji węzła ma wpływ na właściwości eksploracyjne i eksploatacyjne algorytmu.
Im większy zasięg mutacji, tym większa eksploracja a mniejsza eksploatacja.
9.2.2
Rola mutacji sposobu łączenia węzłów
Wartość t w genie jest odpowiedzialna za sposób połączenia danego węzła z poprzednim. Jak
zostało ustalone liczba możliwości łączenia: pion-poziom i poziom-pion — jest wystarczają-
ca w ogólności. Warto jednak się zastanowić, czy nie dałoby się przedstawić chromosomu
dysponując tylko jednego rodzaju łączeniem (czyli de facto zrezygnować z kodowania bitu t
w ogóle) oraz jakie pociąga to za sobą konsekwencje.
Każda trasa jest ciągiem pól, przez które robot ma przejechać. Abstrahując od ilości
pól, przez które robot może jechać w jednym kierunku (w pionie lub w poziomie), można
trasę określić również jako ciąg kierunków. Zakładając, że robot nie może się cofać (takie
rozwiązanie jest z oczywistych przyczyn nie optymalne) ciąg ten będzie naprzemienny i
będzie wyglądał następująco:
pion - poziom - pion - poziom - pion . . .
lub
poziom - pion - poziom - pion - poziom . . . ,
Powyższe dwa przypadki wyczerpują wszystkie możliwości, ponieważ występuje natural-
na kontaminacja (wynikająca z abstrahowania od ilości przejechanych w jednym kierunku
pól):
poziom - poziom → poziom
pion - pion → pion.
Jeśli określimy a priori rodzaj skrętu jako pion-poziom (wartość t=0) to okaże się, że cała
ścieżka może być opisana ciąg punktów-węzłów łączonych właśnie w ten sposób:
(pion - poziom) - (pion - poziom) - (pion . . .
(nawiasy mają wyróżnić poszczególne segmenty)
Drugi rodzaj trasy:
poziom - pion - poziom - pion - poziom . . .
będzie mógł także zostać zakodowany, gdyż:
poziom = pion - poziom;
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
91
oczywiście w tym przypadku ruch w pionie będzie wynosił zero pól.
Wynika z tego, że rodzaj trasy można uogólnić do pierwszego rodzaju.
Dla skrętu poziom-pion sytuacja będzie wyglądać symetrycznie. W tym wypadku ogólność
stanowić będzie drugi rodzaj trasy.
Jak się można było przekonać wystarczyłby jeden rodzaj kodowania skrętu. Konsekwen-
cją tego byłoby to, że minimalna ilość genów dla zakodowania optymalnej ścieżki była by o
jeden w większa, kiedy „nie trafilibyśmy” w schemat ścieżki optymalnej (założylibyśmy np.
łączenie pion-poziom a ścieżka zaczynałaby się od poziomu).
Powstaje więc pytanie czy jest sens kodować rodzaj łączenia. Kosztem czasu algorytmu
potrzebnego na operacje genetyczne na 2/3 genu zmniejszamy analogiczny koszt o 1/3 na
każdy gen.
Z drugiej jednak strony może okazać się, że uproszczenie kodowania, czyli wyeliminowa-
nie zmiennej sposobu łączenia, spowoduje pogorszenie właściwości metrycznych przestrzeni
analogicznych do tych, jakie występują podczas kodowania binarnego opisane go w punkcie.
Zanim przedstawione zostaną wyniki eksperymentu zostaną przedstawione argumenty
zarówno za, jak i przeciwko kodowaniu sposobu połączenia.
Załóżmy, że dysponujemy trzema genami i następujące sposoby ustawienia węzłów i wza-
jemnych połączeń (rys. 9.5).
Rysunek 9.5: Sposoby realizacji ścieżek
Dwa pierwsze przypadki zakładają swobodę w wyborze rodzaju łączenia a w wypadku
jej braku zgodność rodzaju łączenia z kształtem ścieżki (trzeci węzeł pokrywa się z którymś
z dwóch pozostałych). Trzeci i czwarty przypadek pokazuje brak swobody łączenia i jego
niezgodność z kształtem ścieżki. Załóżmy teraz, że jedna z możliwych ścieżek jest częścią
trasy optymalnej (lub po prostu jej koszt przejazdu jest mniejszy), chcemy więc oszacować
prawdopodobieństwo znalezienia tej ścieżki, kiedy dysponujemy ścieżką alternatywną.
a) swobodny wybór łączenia - prawdopodobieństwo znalezienia lepszej ścieżki równa się
prawdopodobieństwu zmiany wartości t na przeciwną;
b) bez swobodnego wyboru łączenia - trzeci węzeł należy ustawić na wierzchołku kąta
prostego po przeciwnej stronie - prawdopodobieństwo znalezienia lepszej ścieżki równa się
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
92
więc prawdopodobieństwu, że węzeł trzeci zmutuje na tę pozycję;
Rozważenie przypadku b) daje też pogląd na temat wyboru zasięgu mutacji, który po-
winien być tak dobrany, żeby węzeł od razu wskoczył na swoje miejsce. Nie możemy a priori
ustalić optymalnego zasięgu mutacji kierując się odległością, o jaką ma być przesunięty wę-
zeł, gdyż za każdym razem będzie ona inna. Jedno, co możemy wiedzieć, że jednocześnie
węzeł nie może być przesunięty w pionie lub poziomie (w zależności czy wierzchołek, na
którym ma się znaleźć ma tę samą, co on współrzędną x lub y). Wynika z tego, że optymal-
nym zasięgiem mutacji byłaby jedynka (zakładając rozkład jednostajny), gdyż taka wartość
daje maksymalną szansę wylosowania zera z zachowaniem użyteczności mutacji (mutacja o
zasięgu zero dająca największe, bo stuprocentowe szanse wyboru zera, jest bezużyteczna z
oczywistych powodów).
Pojawia się jednak kolejna trudność. Zanim węzeł dotrze na miejsce koszt rozważanej
ścieżki może ulec zwiększeniu (np. ścieżka trafi na przeszkodę, którą ścieżka pierwotna i
docelowa omijają), a to będzie zmniejszało szanse reprodukcji takiej ścieżki, a co za tym
idzie, dotarcie jej do celu.
Z drugiej zaś strony najlepszą okazać się może ścieżka idąca przez wnętrze prostokąta
wyznaczanego przez dwie rozważane alternatywne ścieżki (przykład - rys. 9.6).
Rysunek 9.6: Sposoby realizacji ścieżek
Wtedy analogiczne rozumowanie pokazałoby wyższość braku swobody zmiany łączenia.
Powyższe rozważania nie rozstrzygają, czy bardziej opłaca się stosować bit zmiany łą-
czenia, czy też nie. W sposób teoretyczny trudno wyrokować, które z podanych powyżej
argumentów na rzecz obu stron, są bardziej istotne. Dopiero wyniki przeprowadzonych te-
stów wskażą statystyczną istotność któregoś z argumentów.
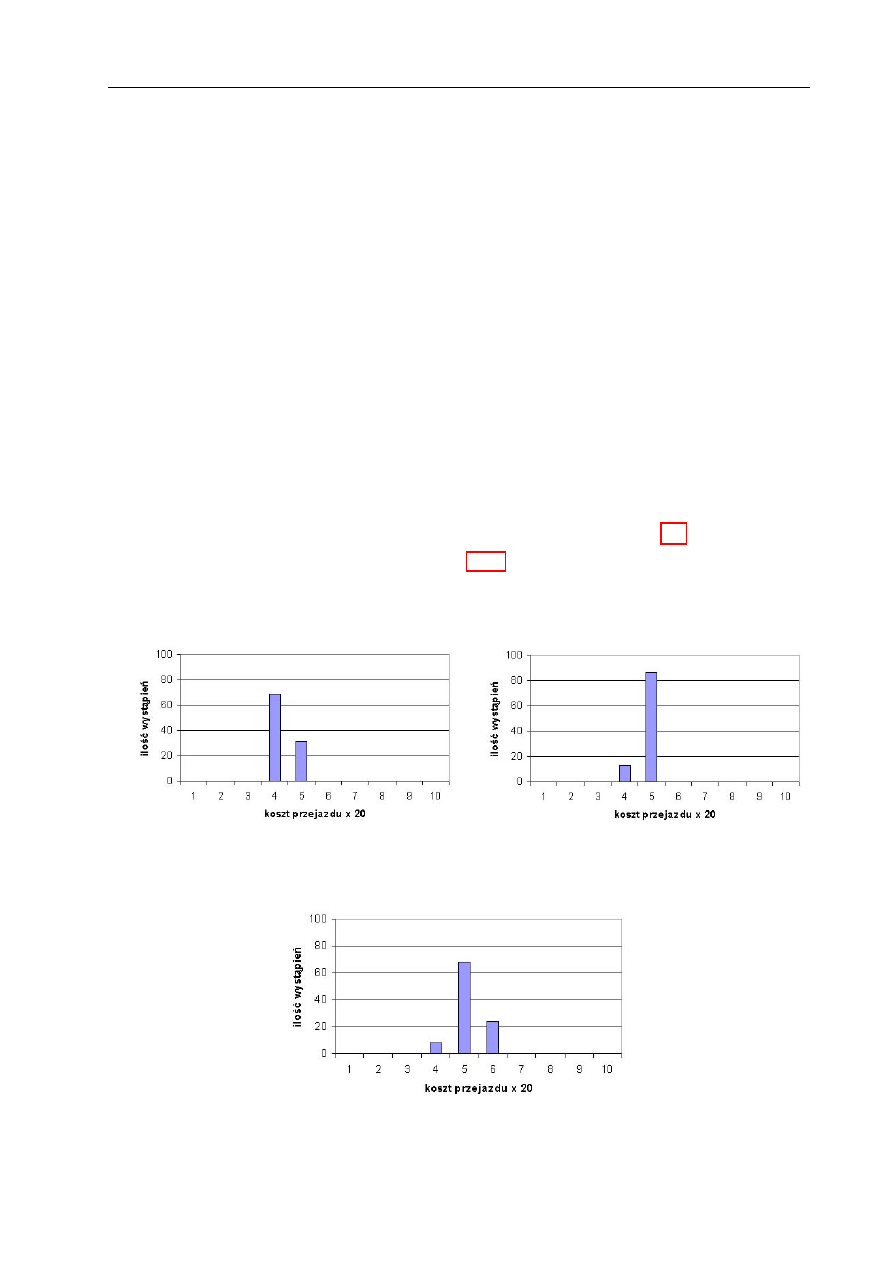
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
93
9.3
Dobór parametrów algorytmu ewolucyjnego
Do wyznaczania optymalnych parametrów algorytmu genetycznego zostały przeprowadzone
odpowiednie symulacje. Ich ilustracją są m. in. histogramy najlepszych osiągniętych trajek-
torii. Warunkiem stopu była ilość iteracji algorytmu, przyjęta na 100 000 - dla tej wartości
algorytm dawał rozsądne wyniki. Histogram był tworzony na podstawie 100 niezależnych
uruchomień. Testowane były głównie operatory genetyczne i reprodukcja.
9.3.1
Ustalenie zasięgu mutacji
Przeprowadzono szereg symulacji dotyczących zasięgu mutacji. Mutacja (zgodnie z założe-
niami) zachodziła z rozkładem równomiernym o danym zasięgu i rozkładem normalnym.
Symulacje przeprowadzono bez uwzględnienia wartości łączenia (t) (nie był mutowany,
a także inicjowany zerem), bez krzyżowania i z reprodukcją ruletkową. Ilość węzłów zosta-
ła ustawiona na 6 - tyle bowiem wystarczy do wykonania tego zadania. Najlepsze wyniki
dał operator mutacji o zasięgu jeden z rozkładem równomiernym (rys. 9.7 a.). Taki zasięg
przewidziany został też teoretycznie w punkcie 9.2.2. Generalnie stosunkowo niewielki zasięg
mutacji (niezależnie od rozwiązywanego problemu) daje najbardziej regularną przestrzeń
przeszukiwań.
a)
b)
Rysunek 9.7: a) Histogram dla zasięgu mutacji 1; b) histogram dla zasięgu mutacji 2
Rysunek 9.8: Histogram dla zasięgu mutacji 5
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
94
Rysunek 9.9: Mapa 1
Jak pokazują histogramy, im dalszy zasięg mutacji, tym bardziej pogarsza się działanie
algorytmu (rys. 9.7 - 9.8). Dla zasięgu mutacji równego jeden, najlepsze wyniki (o koszcie
przejazdu wyższym od optymalnego nie więcej niż o 20) uzyskiwane są w 69%.
Testowany był również wpływ na działanie algorytmu mutacji wartości łączenia (w tym
wypadku inicjacja wartości t odbywała się z rozkładem dwupunktowym - prawdopodobień-
stwo wylosowania zera lub jedynki wynosiło 0,5).
Symulacja została przeprowadzona przy wyznaczonej już optymalnej wartości zasięgu
mutacji równej jeden.
Jak się okazuje, najlepszą wartością prawdopodobieństwa mutacji sposobu łączenia jest
zero. Wynika z tego, że wartość ta nie powinna być w ogóle mutowana. Jeszcze lepszy wynik
zostaje uzyskany, gdy wartość sposobu łączenia zainicjowana jest jednakową wartością (w
tym wypadku zerem, odpowiadającym łączeniu typu pion-poziom. Oznacza to nie tylko
brak przydatności zmiennej kodującej sposób łączenia dla tej mapy, ale i zły wpływ tej
zmiennej na działanie algorytmu. Dzieje się tak dlatego, że całą optymalną trajektorię można
przedstawić za pomocą ciągu pion-poziom-pion-poziom. . . ), więc wartość sposobu łączenia
przy każdym węźle powinna być ustawiona na zero, losowe ustawienie tych wartości i ich
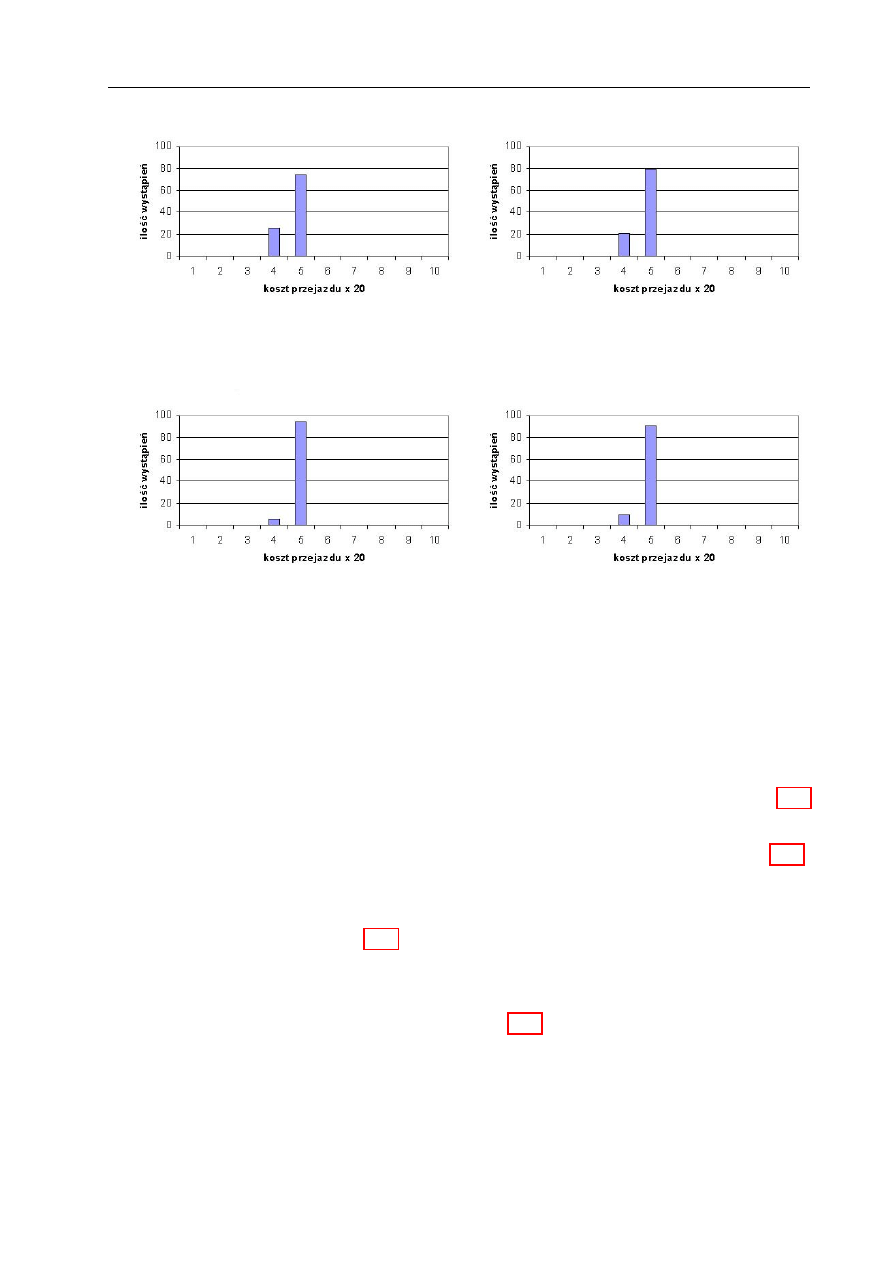
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
95
a)
b)
Rysunek 9.10: Histogram dla mutacji połączenia - a) z prawdopodobieństwem 0,1; b) z
prawdopodobieństwem 0,2
a)
b)
Rysunek 9.11: Histogram dla mutacji połączenia - a) z prawdopodobieństwem 0,4; b) z
prawdopodobieństwem 0,2 (7 węzłów)
mutacja prowadzi tylko do niepotrzebnej destabilizacji algorytmu. Przeprowadzone zostały
też sumulacje, które miały pokazać, czy zwiększenie ilości węzłów zrównoważyłoby zły wpływ
mutacji sposobu łączenia. Mogłoby tak być, gdyż mutując sposób łączenia algorytm bardzo
rozrzutnie dysponuje węzłami.
Jak pokazuje histogram zwiększenie ilości węzłów w tym wypadku nie pomaga (rys. 9.11
b.).
Teraz zostaną zaprezentowane wyniki działania algorytmu dla innej mapy (rysunek 9.12)
o alternatywnej konfiguracji dopuszczalnej trajektorii typu poziom-pion.
Jak można się przekonać, znowu najlepszym prawdopodobieństwem mutacji jest praw-
dopodobieństwo równe zero (rys. 9.13).
Jak pokazują histogramy, mimo „sprzecznej” konfiguracji (konfiguracja mapy - poziom-
pion, a sposób łączenia węzłów pion-poziom), wyniki są znacząco lepsze podczas jednakowej
inicjacji sposobu łączenia i braku jego mutacji (rys. 9.15).
Zaprezentowane powyżej wyniki symulacji wskazują na szkodliwy wpływ uwzględniania
sposobu łączenia poszczególnych węzłów w kodowaniu. Algorytm ma tendencję do wybie-
rania jednego rodzaju połączenia - wszystko jedno czy rodzaj jest zgodny z konfiguracją
trajektorii, czy nie - ważne, żeby był identyczny dla całego chromosomu. Wynika to rów-
nież z wcześniejszych rozważań dotyczących sprowadzania trajektorii do ciągów typu pion-
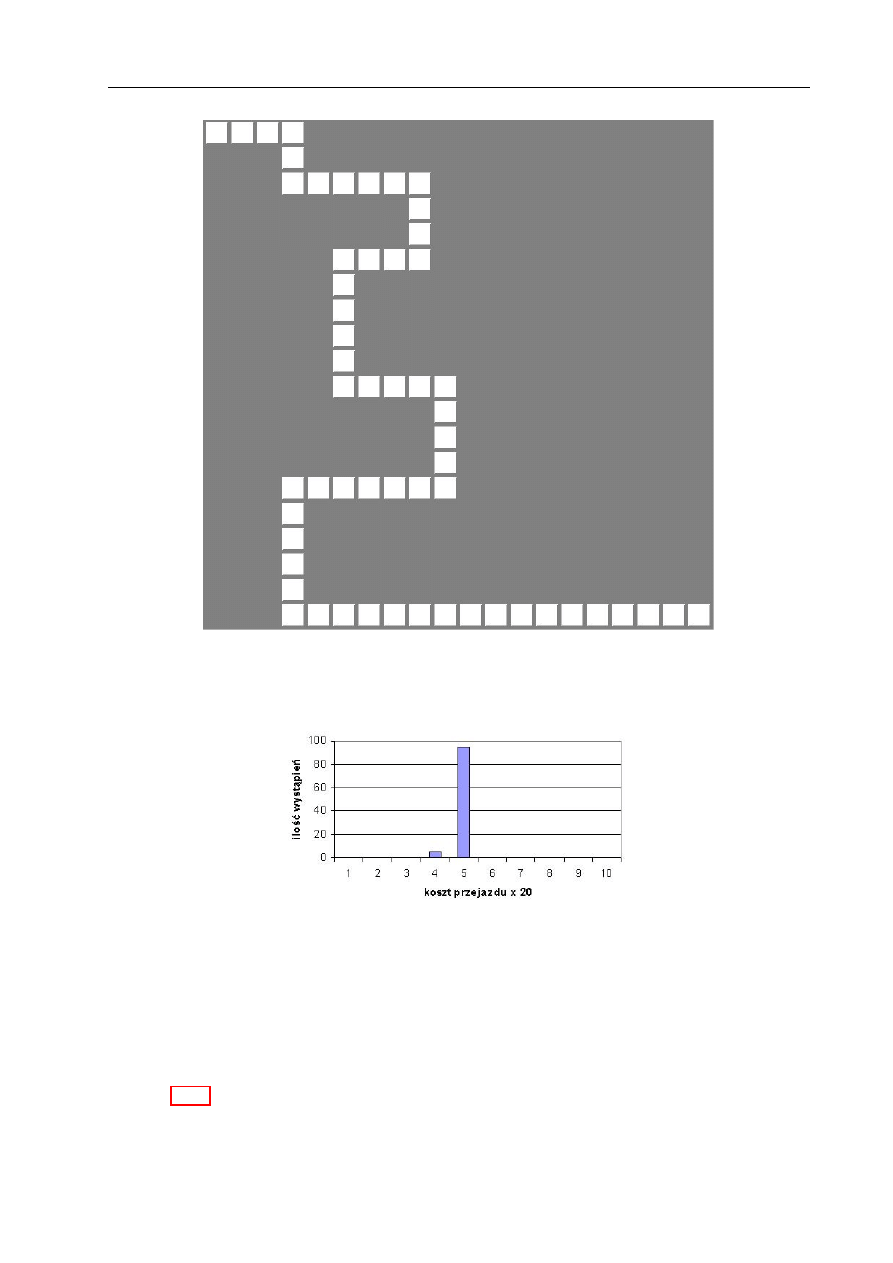
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
96
Rysunek 9.12: Mapa 2
Rysunek 9.13: Histogram dla mutacji połączenia z prawdopodobieństwem 0
poziom. . .
Wniosek, więc jest oczywisty: nie ma najmniejszego sensu stosowania różnego rodzaju
połączeń. Ewentualne zalety wynikające z kodowania sposobu łączenia węzłów rozważane w
punkcie 9.2.2 nie uzyskały potwierdzenia eksperymentalnego.
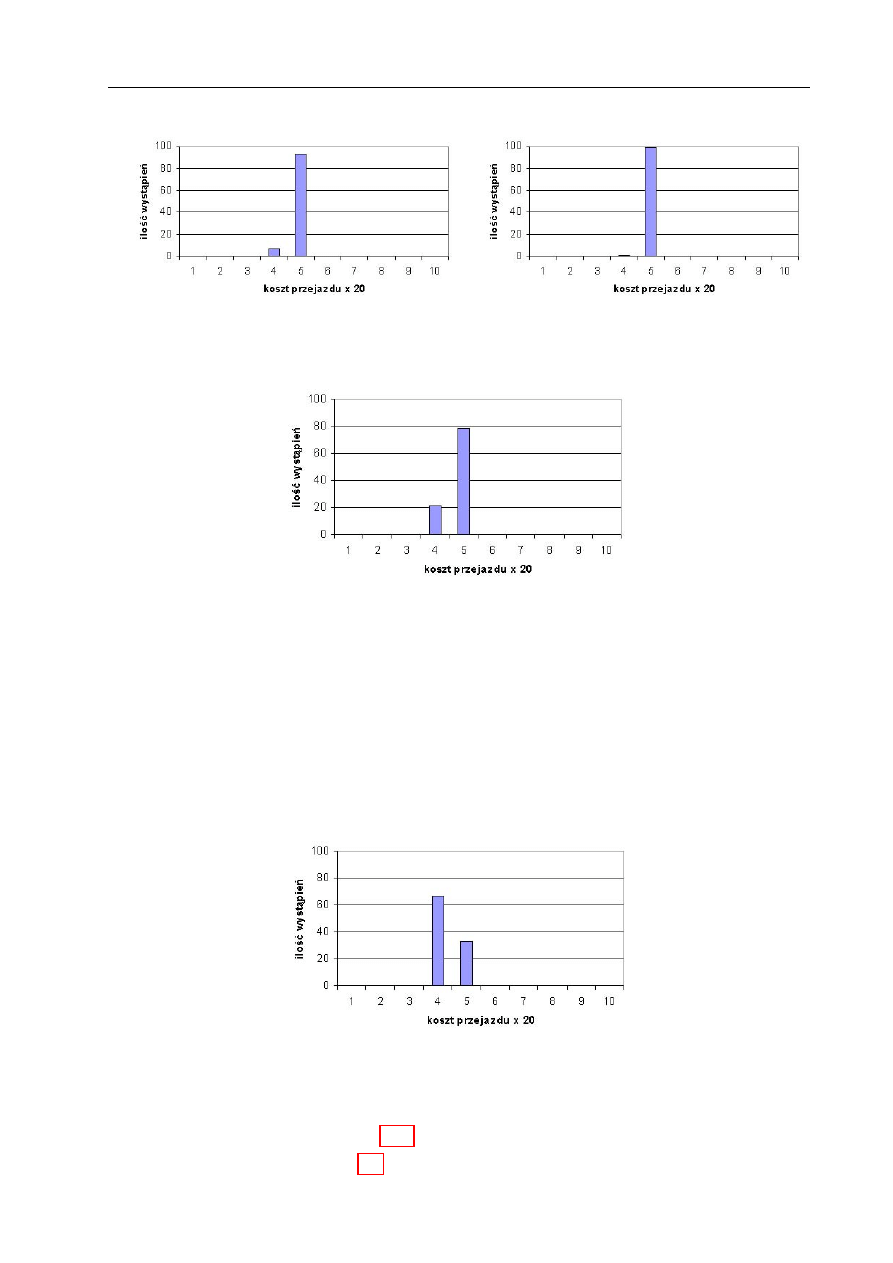
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
97
a)
b)
Rysunek 9.14: Histogram dla mutacji połączenia - a) z prawdopodobieństwem 0,1; b) z
prawdopodobieństwem 0,4
Rysunek 9.15: Histogram dla jednakowych połączeń
9.3.2
Wpływ krzyżowania
Po ustaleniu optymalnego zasięgu mutacji badany był wpływ krzyżowania. Symulacje prze-
prowadzona dla mapy nr 1, przy optymalnym zasięgu mutacji równym jeden i reprodukcji
ruletkowej zmodyfikowanej. Każdy osobnik był krzyżowany z losowo wybranym innym z po-
pulacji. Prawdopodobieństwo krzyżowania było stale równe jeden (tzn. zachodziło zawsze).
Rysunek 9.16: Histogram dla krzyżowania
Jak widać na histogramie (rys. 9.16) wynik jest minimalnie gorszy od tego, jaki został
osiągnięty bez krzyżowania (rys. 9.7 a.) - w zasadzie w granicy błędu statystycznego. Można

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
98
więc wnioskować, że krzyżowanie nie ma większego wpływu na wynik. Krzyżowanie można by
potraktować jako specyficzny rodzaj mutacji. Podczas krzyżowania część węzłów nie zosta-
nie w ogóle przesunięta, a reszta zostanie przesunięta w miejsce węzłów losowego osobnika
z populacji. Przy takim założeniu mutacja właściwa nakłada się na mutację-krzyżowanie.
Więc jeśli został wyznaczony odpowiedni zasięg mutacji, nie ma sensu go psuć poprzez do-
datkową mutację (krzyżowanie). Generalnie krzyżowanie nie jest operatorem koniecznym w
algorytmach ewolucyjnych (dowód zbieżności algorytmu wymaga jedynie istnienia mutacji),
aczkolwiek często stosowanym. W tym konkretnym przypadku eksperymenty wykazały brak
wpływu tego operatora na poprawę działania algorytmu. Można więc wyeliminować krzyżo-
wanie z algorytmu oszczędzając tym samym obliczeń.
9.3.3
Wybór metody reprodukcji
Operacje reprodukcji i sukcesji to selekcja. Z selekcją jest związany selektywny nacisk, który
jest tym większy, im większa jest wartość oczekiwana kopii lepszego osobnika w porówna-
niu z wartością oczekiwaną kopii gorszego osobnika. Ponieważ została założona równoliczość
populacji bazowej i potomnej sukcesja jest trywialna. Taki rodzaj sukcesji nie wprowadza
dodatkowego selektywnego nacisku (wartość oczekiwana kopii każdego osobnika nie jest mo-
dyfikowana). Jedyne co można zrobić to dobrać najlepszą metodę reprodukcji dla zadania.
Jak zostało to przedstawione w punkcie 9.1.5 metody reprodukcji różnią się prawdopodo-
bieństwem reprodukowania danego osobnika, a od prawdopodobieństwa zależy wartość ocze-
kiwana kopii tego osobnika w kolejnej populacji bazowej, więc selektywny nacisk zależy od
sposobu reprodukcji.
Selektywny nacisk określa stosunek eksploatacji do eksploracji. Eksploatacja to przeszu-
kiwanie obszaru przyciągania G( ˆ
X)w celu wyznaczenia maksimum lokalnego ˆ
X. Natomiast
eksploracja polega na wybraniu zbioru G(X
∗
), zawierającego maksimum globalne X
∗
, z ro-
dziny obszarów przyciągania ekstremów lokalnych.
Zmniejszenie prawdopodobieństwa reprodukcji lepszego osobnika w stosunku do gorszego
zwiększa szansę reprodukcji tego ostatniego i zmniejsza selektywny nacisk. Polepsza też
zdolności eksploracyjne algorytmu, gdyż dopuszczając osobniki słabsze mamy nadzieję na
opuszczenie obszaru przyciągania minimum lokalnego.
Reprodukcja ruletkowa nie jest więc dobrą metodą reprodukcji, gdyż wraz z kolejnymi
generacjami zmniejsza się selektywny nacisk z powodu zbliżonych wartości przystosowania
osobników w populacji. Na początku działania algorytmu, gdy populacja jest najbardziej
zróżnicowana selektywny nacisk jest największy. Dzieje się więc coś odwrotnego, od tego
czego należałoby oczekiwać od algorytmu optymalizacji globalnej, czyli właściwości eksplo-
racyjnych na początku i eksploatacji pod koniec. Reprodukcja ta może prowadzić do przed-
wczesnej zbieżności. Selektywny nacisk w reprodukcji ruletkowej zależy pośrednio od dodania
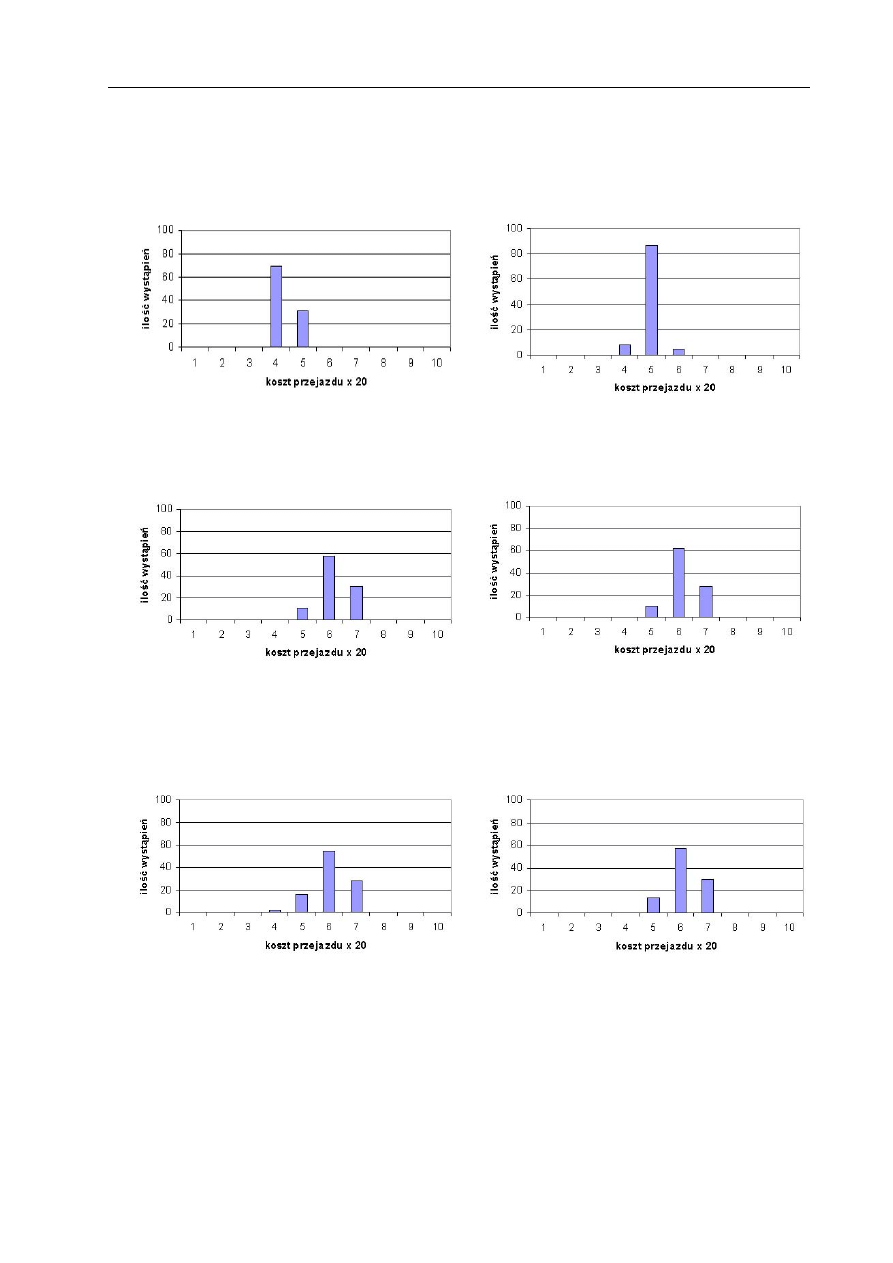
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
99
stałej do funkcji przystosowania. Tak jest w tym zadaniu, gdyż maksymalny koszt przejazdu
h jest szacowany.
Powyższych wad nie ma zmodyfikowana wersja reprodukcji ruletkowej.
a)
b)
Rysunek 9.17: Histogram dla reprodukcji - a) ruletkowej zmodyfikowanej; b) ruletkowej
a)
b)
Rysunek 9.18: Histogram dla reprodukcji turniejowej - a) liczności turnieju 2; b) liczności
turnieju 3
a)
b)
Rysunek 9.19: Histogram dla reprodukcji turniejowej - a) liczności turnieju 4; b) liczności
turnieju 5
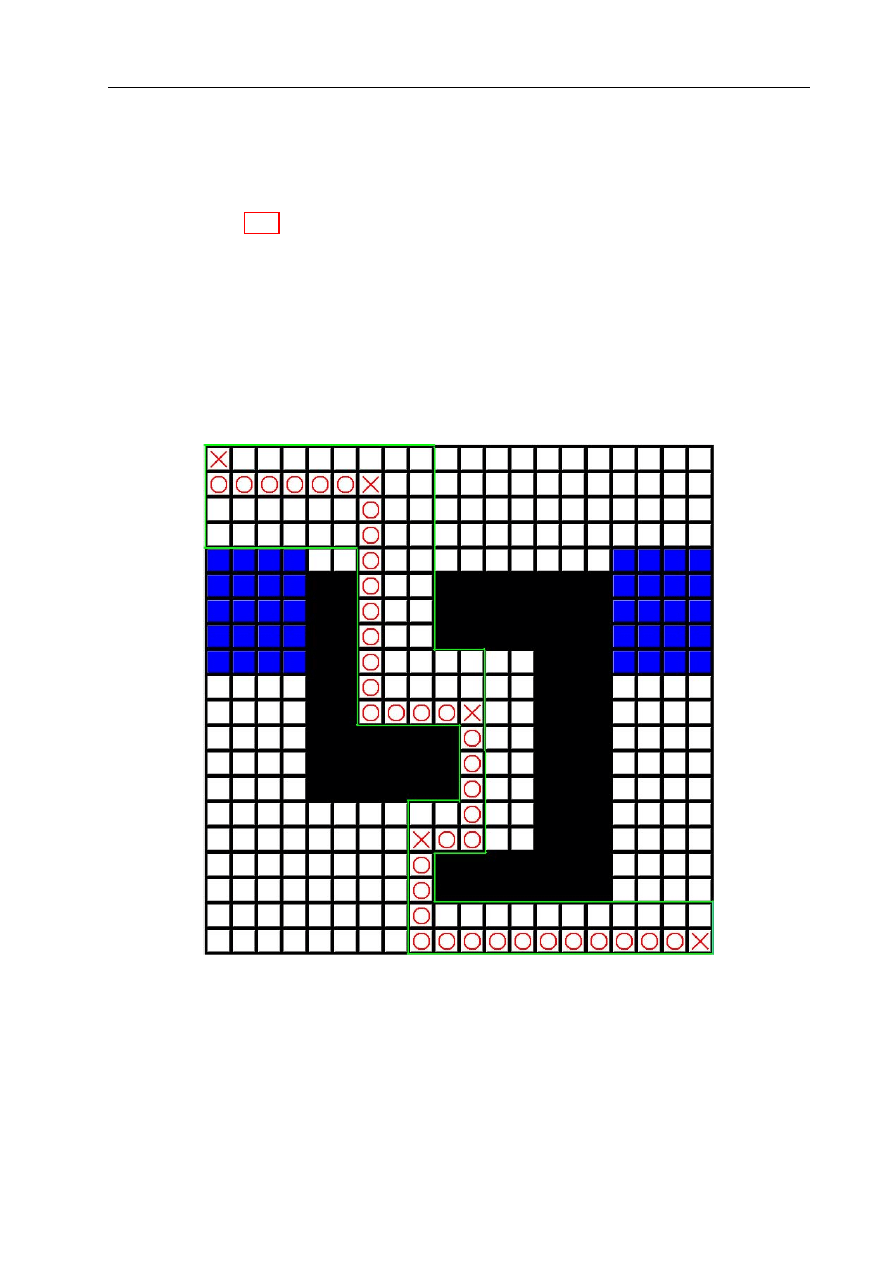
ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
100
9.4
Testowanie zdolności omijania minimów lokalnych
przez algorytm ewolucyjny
Mapa na rysunku 9.20 zawiera minimum globalne w postaci pasa białych kafelków (zakreślo-
nego zieloną obwiednią) o koszcie przejazdu równym 43 (koszt przejazdu przez biały kafelka
wynosi 1). Istnieją też dwa minima lokalne, prowadzące przez obszary składające się z sza-
rych kafelków (oznaczonych kolorem fioletowym, o koszcie przejazdu 2). Koszt przejazdu
dla każdego z dwóch minimów wynosi 44. Pokazana wyznaczona przez algorytm trajektoria
jest jedną z wielu optymalnych trajektorii mieszczących się w zielonym pasie. Świadczy to
o dobrych możliwościach optymalizacyjnych algorytmu i braku jego wrażliwości na minima
lokalne.
Rysunek 9.20: Mapa 3
9.5
Wnioski z symulacji
Jak pokazują wyniki symulacji algorytm ewolucyjny jest w stanie wyznaczyć optymalną
trajektorię, pod warunkiem, że zostaną dobrze dobrane parametry algorytmu. One też mają

ROZDZIAŁ 9. WYZNACZANIE TRAJEKTORII ALGORYTMEM EWOLUCYJNYM
101
wpływ na czas potrzebny na otrzymanie optymalnej trajektorii.
Symulacje wskazują, że przede wszystkim ważne są możliwości eksploatacyjne algoryt-
mu - czyli mutacja o niewielkim zasięgu oraz silny selektywny nacisk podczas fazy selekcji
(przynajmniej jeśli chodzi o mapy o tych wielkościach, co testowane).
O rzeczywistych możliwościach algorytmu ewolucyjnego w wyznaczaniu optymalnych
ścieżek świadczyć może jedynie porównanie z jednym z deterministycznych algorytmów wy-
znaczających rozwiązania optymalne. Porównanie takie znajduje się w pkt. 11.2.
Rozdział 10
Wyznaczanie trajektorii algorytmem
deterministycznym
Drugim algorytmem wyznaczania ścieżki dla robota na komputerze PC jest A*. Algorytm
ten służy również do wyznaczania optymalnych objazdów. Algorytm opisany w punkcie 3.1.1
przeznaczony jest dla map topologicznych (opartych na grafach). Poniżej przedstawiona jest
modyfikacja tego algorytmu na potrzeby mapy geometrycznej.
10.1
Model matematyczny
założenie:
f (x, y) = g(x, y) + h(x, y),
h(x, y) = k(x, y) − (x, y)
t
k = |x − x
t
| + |y − y
t
| - funkcja heurystyczna;
c(x, y) - koszt przejazdu przez kafelek w miejscu (x, y);
g(x, y) = c((x, y)
0
, (x, y)) - dotychczasowy koszt przejazdu od początku (x, y)
0
do miejsca
(x, y);
D - obszar zabroniony;
1. i:=0, F
0
:= φ; g((x, y)
0
) = c((x, y)
0
);
∀(x, y) − (x, y)
0
, g(x, y) = ∞;
2. Rozwiń (x, y) i wylicz:
F
i
:= F
i
∪ f ((x − 1), y), jeśli ((x − 1), y) /
∈ D;
F
i
:= F
i
∪ f (x, (y − 1)), jeśli (x, (y − 1)) /
∈ D;
F
i
:= F
i
∪ f ((x + 1), y), jeśli ((x + 1), y)) /
∈ D;
F
i
:= F
i
∪ f (x, (y + 1)), jeśli (x, (y + 1)) /
∈ D;
3. Wybierz na podstawie F
i
stan (x, y)
∗
o najmniejszej sumie kosztu i wartości sumy funkcji
heurystycznej
g((x, y)
∗
) = g(x, y) + c(x, y)

ROZDZIAŁ 10. WYZNACZANIE TRAJEKTORII ALGORYTMEM DETERMINISTYCZNYM
103
jeśli (x, y)
∗
= (x, y)
t
- STOP;
jeśli nie - (x, y) = (x, y)
∗
, i:=i+1 oraz skok do 2;
10.2
Opis algorytmu
Algorytm zaczyna działanie w punkcie początkowym trajektorii i sprawdza pola powyżej,
poniżej, na lewo i na prawo tego pola. Jeśli pola te leżą na mapie, nie jest to obszar za-
broniony i jeśli nie były one wcześniej rozwinięte to wyznacza sumaryczny koszt przejazdu
do tego kafelka i sumę tego kosztu i wartości funkcji heurystycznej dla tego kafelka. Potem
wybierany jest kafelek o najmniejszej tej sumie i jeśli nie jest on punktem docelowym jest
znowu rozwijany - sprawdzane są dalej jego pola sąsiednie - i tak dalej.
Metoda ta jest optymalna i zupełna. Swoją szybkość zawdzięcza istnieniu funkcji heury-
stycznej, która ukierunkowuje działanie algorytmu — nie szuka on punktu docelowego zata-
czając okręgi (w metryce miejskiej okrąg ma kształt kwadratu) wokół punktu początkowego
a stara się podążać właśnie w kierunku punktu docelowego. Oszczędza w ten sposób czas
nierozwijając pewnych pól. Funkcja heurystyczna została określona jako odległość w metryce
miejskiej punktu bieżącego od punktu docelowego. Wartość tej funkcji będzie mniejsza lub
równa od rzeczywistej odległości (liczonej jako sumy wag mijanych wszystkich kafelków) do
punktu docelowego. Taka sytuacja nazywana jest niedoszacowaniem funkcji heurystycznej.
A właśnie to niedoszacowanie sprawia, że algorytm A* jest optymalny [14].
W stosunku do ogólnej postaci A*, implemementowany algorytm, stosowany dla metryki
miejskiej, mógł ulec pewnemu uproszczeniu, bez utraty optymalności. Pola już odwiedzane
nigdy nie będą odwiedzone ponownie, nawet jeśli rozwijany będzie ich sąsiad, różny od
pola, z którego zostały rozwinięte. Modyfikacja ta mogła zostać wprowadzona, gdyż koszt
wjazdu na kafelek jest niezależny od kierunku, z którego następuje. Dla metryki czasowej,
uwzględniającej koszt skrętu (pkt. 11.3), modyfikacja ta nie została wprowadzona, gdyż
warunek ten nie jest wówczas spełniony.
Algorytm został też ulepszony w stosunku do oryginalnego w ten sposób, że jeśli mi-
nimalną wartość sumy dotychczasowego kosztu i funkcji heurystycznej posiada więcej niż
jeden kafelek to wybierany jest ten z nich, który ma największy koszt dotychczasowy. Przy-
spiesza to działanie algorytmu, jeśli na mapie występują duże jednolite obszary, na których
znajdujące się kafelki mają identyczną wartość tej sumy.
Rysunek 10.1 pokazuje działanie algorytmu dla funkcji heurystycznej h(s) ≡ 0 (de facto
strategii pierwszy najtańszy) — rozwijane są pola naokoło punktu początkowego.
Rysunek 10.2 pokazuje działanie algorytmu z heurystyką, która ukierunkowuje działanie
algorytmu w stronę punktu docelowego. Wszystkie pola leżące na kwadracie między polem
początkowym a docelowym mają tę samą wartość sumy kosztu dotychczasowego i wartości
funkcji heurystycznej — wszystkie są więc rozwijane (liczba 100 — nieobliczony koszt).
ROZDZIAŁ 10. WYZNACZANIE TRAJEKTORII ALGORYTMEM DETERMINISTYCZNYM
104
Rysunek 10.1: Wyznaczone wartości dotychczasowego kosztu dla h(s) ≡ 0
Rysunek 10.3 pokazuje działanie ulepszonej wersji algorytmu. Ponieważ przy jednako-
wych sumach wartości funkcji heurystycznej i dotychczasowego kosztu rozwijane są punkty
o najmniejszym dotychczasowym koszcie - nie jest przeszukiwany cały kwadrat między punk-
tem początkowym a docelowym, a najkrótsza ścieżka wyznaczana jest od razu.
Rysunek 10.4 pokazuje działanie ulepszonego algorytmu na mapie testowej. Najkrótsza
ścieżka prowadząca przez obszar fioletowy ma koszt o jeden większy niż optymalna ścieżka
wyznaczona przez algorytm (zaznaczona kółkami). Widać jak algorytm doszedł do końca
niebieskiego pola i stwierdził, że nie warto dalej rozwijać tej trajektorii.

ROZDZIAŁ 10. WYZNACZANIE TRAJEKTORII ALGORYTMEM DETERMINISTYCZNYM
105
Rysunek 10.2: Wyznaczone wartości dotychczasowego kosztu dla algorytmu A*
ROZDZIAŁ 10. WYZNACZANIE TRAJEKTORII ALGORYTMEM DETERMINISTYCZNYM
106
Rysunek 10.3: Wyznaczone wartości dotychczasowego kosztu dla algorytmu A*, jeśli przy
jednakowej wartości f (s
i
) rozwijane jest pole o najwyższym koszcie

ROZDZIAŁ 10. WYZNACZANIE TRAJEKTORII ALGORYTMEM DETERMINISTYCZNYM
107
Rysunek 10.4: Wyznaczone wartości dotychczasowego kosztu dla algorytmu A*, jeśli przy
jednakowej wartości f (s
i
) rozwijane jest pole o najwyższym koszcie

Rozdział 11
Porównanie algorytmów:
ewolucyjnego i deterministycznego
Jak zostało ustalone, algorytm uruchamiany na komputerze PC wyznacza robotowi optymal-
ną trajektorię, robot zaś w razie zmiany mapy wyznacza sobie optymalny objazd algorytmem
A*. W rozdziale tym opisana jest zarówno możliwość wyznaczania objazdu przez algorytm
A*, jak i porównanie tego algorytmu z algorytmem ewolucyjnym podczas wyznaczania opty-
malnej ścieżki. Opisane też zostaną fizyczne aspekty wykonywania zadania przez robota.
11.1
Symulacje systemu nawigacyjnego
11.1.1
Symulacje współdziałania algorytmu wyznaczającego ścież-
kę z algorytmem omijania przeszkód
W celu sprawdzenia niezawodności systemu przesymulowano jego działanie. Testy przepro-
wadzono na mapie na rys. 11.1, o wymiarach 12x17. Wymiary mapy są takie, gdyż taka
mapa nie jest zbyt wielka (niezbyt kosztowna, czas przejazdu robota nie jest nużąco długi
itd.) poza tym są na niej wszystkie elementy potrzebne do wykonania dobrego testu. Mapa
jest analogiczna do mapy 9.20 z punktu 9.4, w którym były testowane zdolności unikania
optimów lokalnych przez algorytm ewolucyjny. Zawiera więc dwa obszary zabronione mię-
dzy którymi trzeba wymanewrować i dwa obszary o wyższym koszcie przejazdu za kafelek,
przez które przejazd byłby prostszy (mniej zakrętów wykonanych przez robota, mniej węzłów
potrzebnych do wykorzystania przez algorytm ewolucyjny), ale za to nieoptymalny.
Algorytm ewolucyjny lub deterministyczny wyznacza optymalną ścieżkę zaznaczoną na
rys. 11.1 krzyżykami. Jest ona następnie przesyłana do robota wraz z informacją o mapie.
W razie potrzeby robot wyznacza objazd. Objazd jest taki, aby jak najwierniej wykonać
trajektorię wyznaczoną przez komputer PC 8.8.2. Tak więc objazd, plus reszta trajektorii
z komputera PC, nie muszą być optymalną trajektorią począwszy od punktu w którym
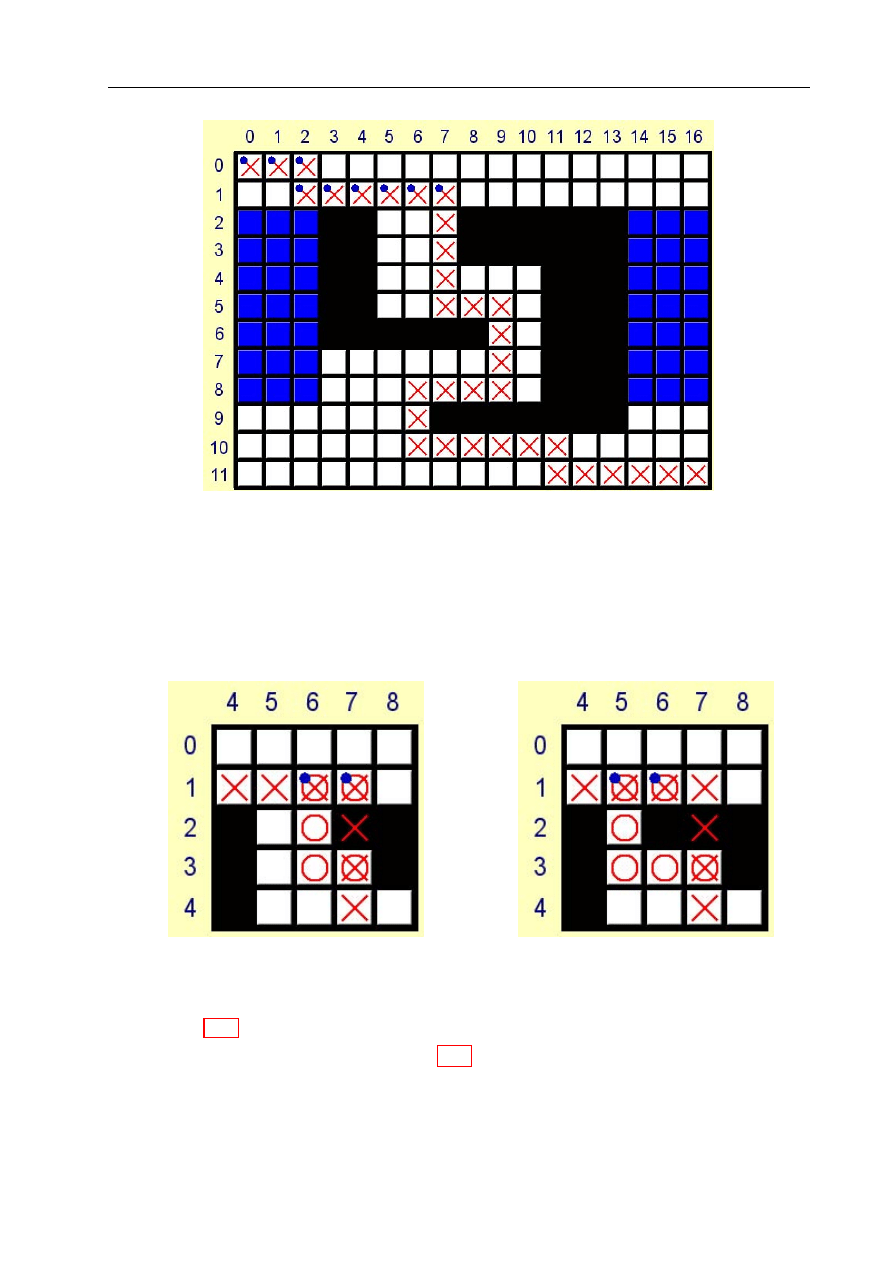
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
109
Rysunek 11.1: Trajektoria wyznaczona przez algorytm ewolucyjny naniesiona na mapę plan-
szy testowej
wyznaczany jest objazd a skończywszy na ostatnim polu trajektorii przesłanej z komputera
PC.
a)
b)
Rysunek 11.2: Pierwsze dwa krótkie objazdy, których fragmenty były wykonywane na trasie
Rysunek 11.3 pokazuje objazd wyznaczany przez robota w wypadku zabrania mu trzech
kafelków z pól [5,2], [6,2] i [7,2]. Na rys. 11.2 pokazano objazdy, które wykonałby robot
w wypadku zabrania mu kafelka [7,2] lub obu kafelków [7,2] i [6,2]. Planowane objazdy
zaznaczone są kółkami a wykonanie ich — niebieskimi kropkami. Rysunek ten pokazuje
jak zmienia się wiedza robota podczas wykonywania trajektorii. Robot po prostu próbuje
ominąć tworzący się w jego świadomości cypel, wciąż dowiadując się o nowych kafelkach.
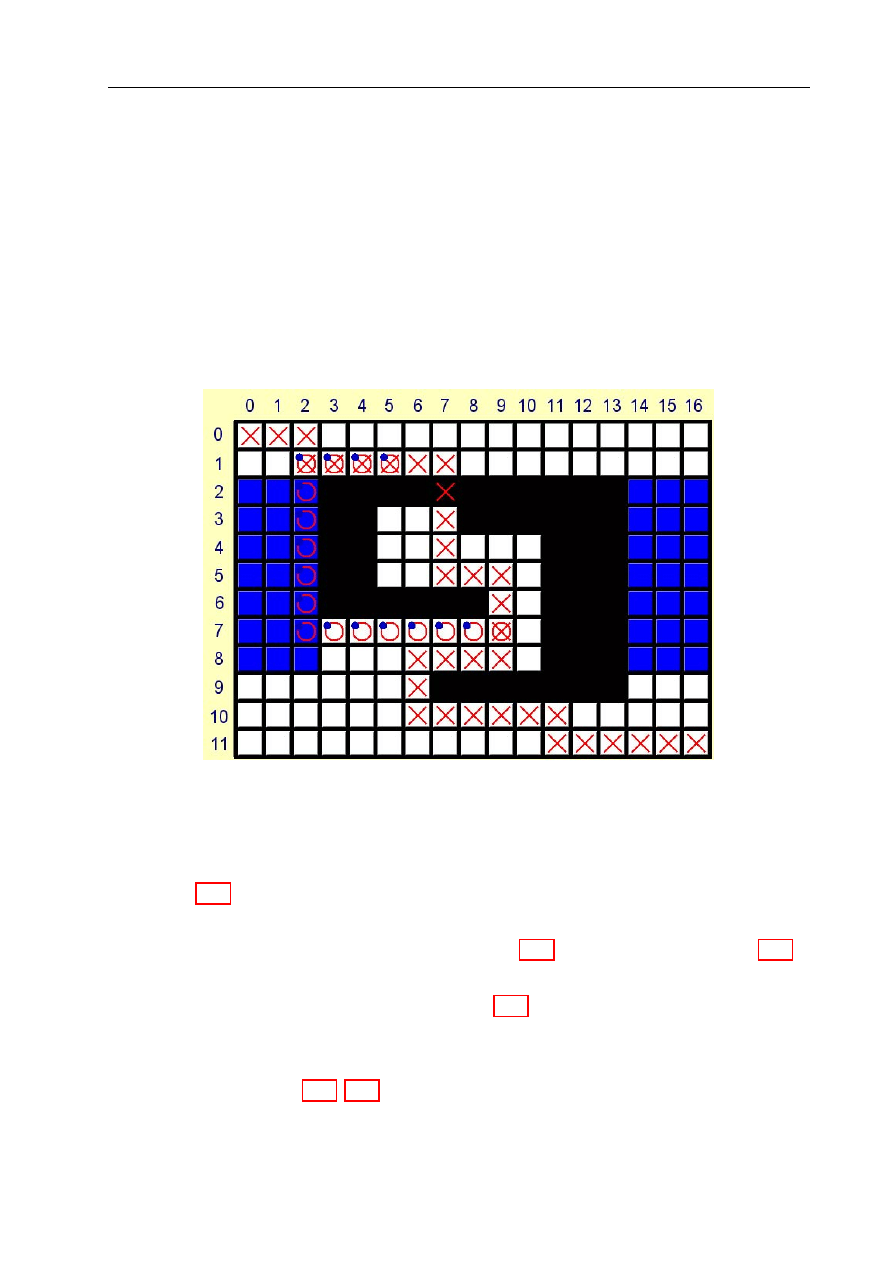
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
110
Kiedy zobaczy brak kafelka na polu [5,2] wie, że jest przesmyk znajdujący się między dwoma
obszarami zabronionymi. Jego wiedza jest kumulacją wiedzy zdobytej podczas jazdy i wiedzy
o mapie, którą wcześniej dostał z komputera PC. Ponieważ robot zna kształt i rozmiar
obszaru zabronionego po lewej stronie nie próbuje już tędy jechać a wykonuje długi objazd
tego obszaru do punktu [9,7]. Nie jest to optymalna trajektoria, jednak - jak to zostało
założone - celem robota nie jest znalezienie trajektorii optymalnej, a powrót na trajektorię
wyznaczoną w komputerze PC i jak najwierniejsze jej oddanie (oczywiście nie ma sensu
wracanie do punktu [7,3], gdyż odcinek trajektorii z komputera PC między punktem [7,3] a
[9,7] byłby niepotrzebnie przejechany dwukrotnie).
Rysunek 11.3: Długi objazd pozwala powrócić na trajektorię wyznaczoną przez algorytm
ewolucyjny
Na rys. 11.4 widać, że także kafelek na polu [9,7] został zabrany; widać też propozycję
objazdu i przejechanie kilku kolejnych kafelków leżących na trajektorii z komputera PC.
Teraz robot dowiaduje się o braku kafelka [9,10] (rys. 11.6 a.) i następnie [9,11] (rys. 11.5) -
wyznacza więc objazd najpierw na [10,10], a zaraz potem na [14,11].
Ponieważ ostatnie pole trajektorii [16,11] (rys. 11.6 b.) jest niedostępne, robot wraca do
punktu początkowego [0,0] tą samą trajektorią, którą jechał do tej pory. Po dojechaniu do
pola [0,0] wysyła do komputera PC informacje o zmianach w mapie.
Na kolejnych rysunkach (11.1, 11.6) można prześledzić jak się zmieniała wiedza robota, po
wykonaniu kolejnych odcinków trajektorii (zaznaczanych niebieskimi kropkami).
Podczas symulacji zostały sprawdzone różne aspekty działania systemu. Jeśli chodzi o
wyznaczenie trajektorii to mapa zawiera obszar zabroniony i trajektorie suboptymalne prze-

ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
111
Rysunek 11.4: Dodatkowy objazd wykonywany w sytuacji usunięcia ostatniego pola właśnie
wykonywanego objazdu
chodzące przez obszar fioletowych pól. Ze strony robota zostały przetestowane możliwości
omijania obszarów zabronionych i wyznaczania objazdów. Przeszkody spotykane przez ro-
bota były różnego rodzaju — zagrodzenie przesmyku między obszarami zabronionymi wraz
z odkrywaniem braku możliwości przejazdu podczas kolejnych prób objazdu, konieczność
wycofania się z objazdu, brak docelowego kafelka. Zarówno algorytm po stronie komputera
PC, jak i robot spełniły założenia dotyczące ich działania. Bezbłędna też była komunikacja
między komputerem PC a robotem — mapy i trajektorie były przekazywane poprawnie w
obie strony.
11.1.2
Badanie wpływu parametrów otoczenia
System był testowany w różnych warunkach. Robot był konstruowany i testowany dwa lata i
działał niezależnie od pory roku. Co prawda wahania temperatury były niewielkie, jednak na
robota niekorzystny wpływ mogło mieć działanie grzejników. Działanie poprzedniego robota
przez nas konstruowanego, naprowadzającego się na źródło podczerwieni, było zakłócane
właśnie przez grzejniki, gdyż do naprowadzania służyły czujniki światła, które reagują także
na podczerwień. Jednak w przypadku obecnego robota emisja podczerwieni przez grzejniki
nie miała istotnego znaczenia. Również brak światła nie miał wspływu na działanie robota,
gdyż czujniki są tak skonstruowane, że oświetlają obiekt, którego kolor badają. Czystość
kafelków też nie odgrywa wielkiej roli. Nawet, gdy kafelki są lekko przybrudzone, są dobrze
rozpoznawane przez robota. Obecnie poziomy światła odpowiedzialne za rozpoznawanie bar-
wy kafelka lub jego braku są tak dobrane, by wykluczyć powyżej opisane zakłócenia. Robot
dobrze jeździł po kafelkach - nie ślizgał się, nie zaczepiał o fugi. Komunikacja między kom-
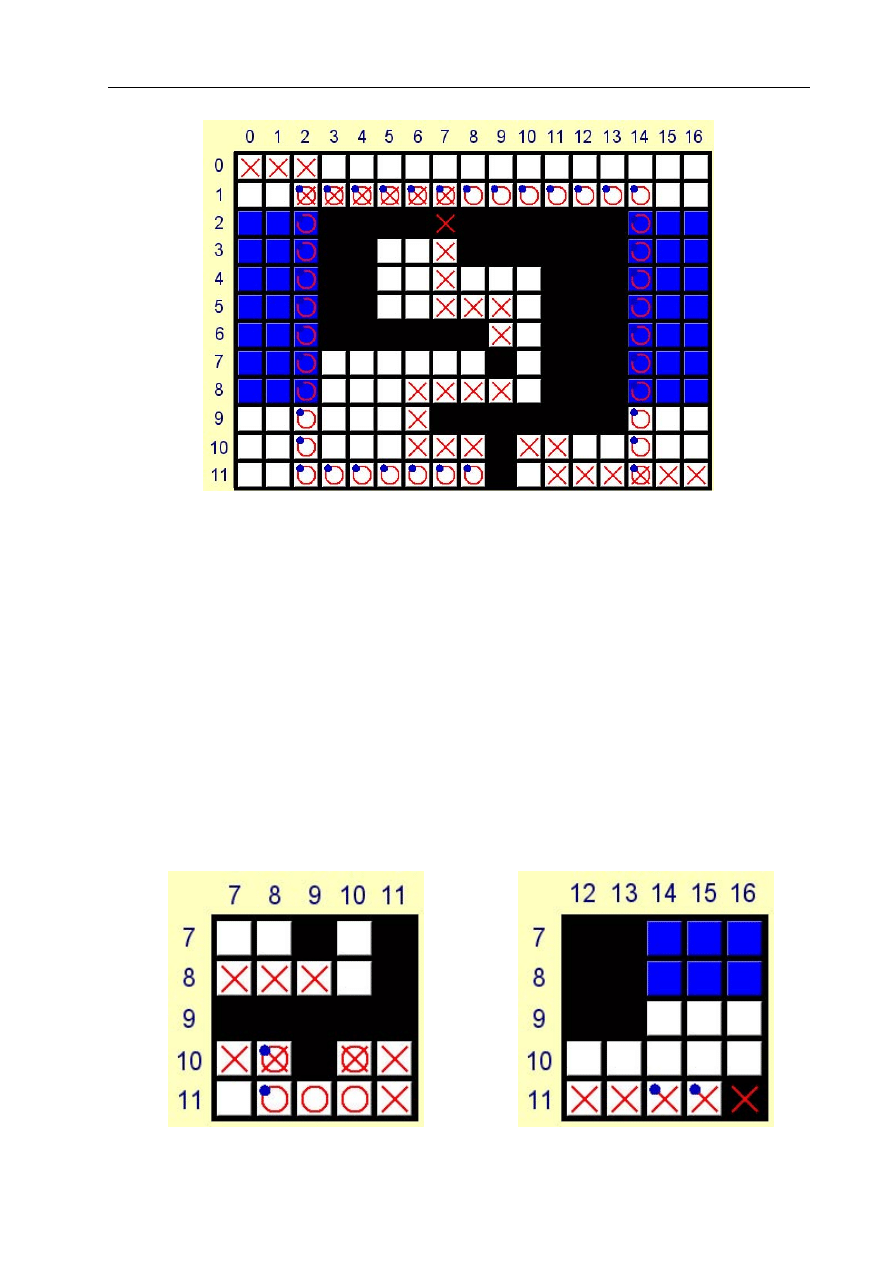
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
112
Rysunek 11.5: Najdłuższy z objazdów zrealizowanych na trasie
puterem PC a robotem przebiegała prawidłowo.
11.2
Porównanie właściwości algorytmu ewolucyjnego
i A*
11.2.1
Badanie złożoności obliczeniowej
Badanie złożoności obliczeniowej prowadzi się poprzez mierzenie czasów działania obu algo-
rytmów na tym samym procesorze (tutaj - Athlon 1.6GHz XP+). Liczba iteracji potrzeb-
a)
b)
Rysunek 11.6: a) Ostatni z krótkich objazdów; b) ostatni odcinek trajektorii

ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
113
nych do uzyskania wyniku nie jest miarodajna, gdyż w ogólności iteracje dwóch różnych
algorytmów mogą mieć różny nakład obliczeniowy. Aby porównać algorytm A* i ewolucyjny
wystarczy porównać ich działanie na mapach złożonych z pól jednego koloru (np. samych bia-
łych) z punktem startowym trajektorii w jednym rogu i końcowym w rogu przeciwstawnym;
jest tak dlatego, że takie mapy są najłatwiejsze dla algorytmu ewolucyjnego a najtrudniejsze
dla A* (wariant niezmodyfikowany). Dla jednolitej mapy (np. całej białej) czas potrzebny
algorytmowi ewolucyjnemu na wyznaczenie optymalnej ścieżki będzie oszacowaniem dolnym
czasu potrzebnego na znalezienie optymalnej ścieżki dla bardziej skomplikowanych map; na-
tomiast czas potrzebny algorytmowi A* będzie oszacowaniem górnym dla tego algorytmu.
Jednolita mapa jest najprostsza dla algorytmu ewolucyjnego (najszybciej znajduje rozwią-
zanie), z tego względu, że ma największą ilość optymalnych ścieżek spośród różnych map.
Każda trajektoria jest optymalna jeśli położenie jej węzłów względem siebie jest następu-
jące: (x
j
x
i
, y
j
y
i
; j > i (początek trajektorii jest w punkcie (0, 0), koniec w punkcie
(x
max
, y
max
) (oznaczenia z punktu 9.1.2). Jedynym zadaniem algorytmu ewolucyjnego jest
więc uporządkowanie węzłów w odpowiedniej kolejności. Ponieważ na takiej mapie jest naj-
większa ilość dróg optymalnych, algorytm ewolucyjny ma największą szansę na znalezienie
optymalnej drogi. Dla algorytmu A* takie zadanie jest najtrudniejsze, gdyż suma kosztu
dotychczasowego i wartości funkcji heurystycznej będzie dla każdego pola taka sama i bę-
dzie wynosiła tyle, co optymalny koszt przejazdu; w takim wypadku A* traci swoje wszelkie
atuty i ma taką złożoność obliczeniową jak zwykła strategią nieinformowana. Algorytm A*
musi więc w takim wypadku „odwiedzić” wszystkie pola na mapie. Nie robi tego na mapach
bardziej skomplikowanych, gdyż część pól wtedy omija, ponieważ nie dają one nadziei na
optymalne rozwiązanie.
Powyższe oszacowanie ma sens, jeśli algorytm ewolucyjny jest gorszy od A*. Rozumowa-
nie jest następujące - jeżeli algorytm ewolucyjny jest gorszy od A* dla swojego najłatwieszego
zadania, które jednocześnie jest najtrudniejsze dla A* — będzie gorszy od A* zawsze. Dla
bardziej skomplikowanej mapy, czas wykonywania algorytmu ewolucyjnego może się tylko
wydłużyć, a A* tylko skrócić. Warto też zaznaczyć, że ze względu na indeterminizm al-
gorytmu ewolucyjnego czas jego działania przedstawiony jest jako uśredniony czas w 100
niezależnych symulacjach (dokładnie jak podczas badania parametrów algorytmu). Algoryt-
my były testowane na kwadratowych mapach o długości boku - 25, 50, 75, 100 - kafelków.
Jak pokazuje zestawienie (tabela 11.1) — czas wykonywania A* rośnie proporcjonalnie do
powierzchni mapy (ilości pól). Ma to swoje uzasadnienie teoretyczne — algorytm za każdym
razem przechodzi przez wszystkie pola.
Algorytm ewolucyjny testowany był w zależności od liczby węzłów (9.1.1). Ta liczba
odzwierciedla skomplikowanie zadania. Również komplikacja zadania powinna rosnąć wraz
wielkością mapy. Wynika to stąd, że na większej mapie może znajdować się więcej nieza-
leżnych obiektów (obszarów zabronionych lub o wyższym koszcie przejazdu). W badaniach
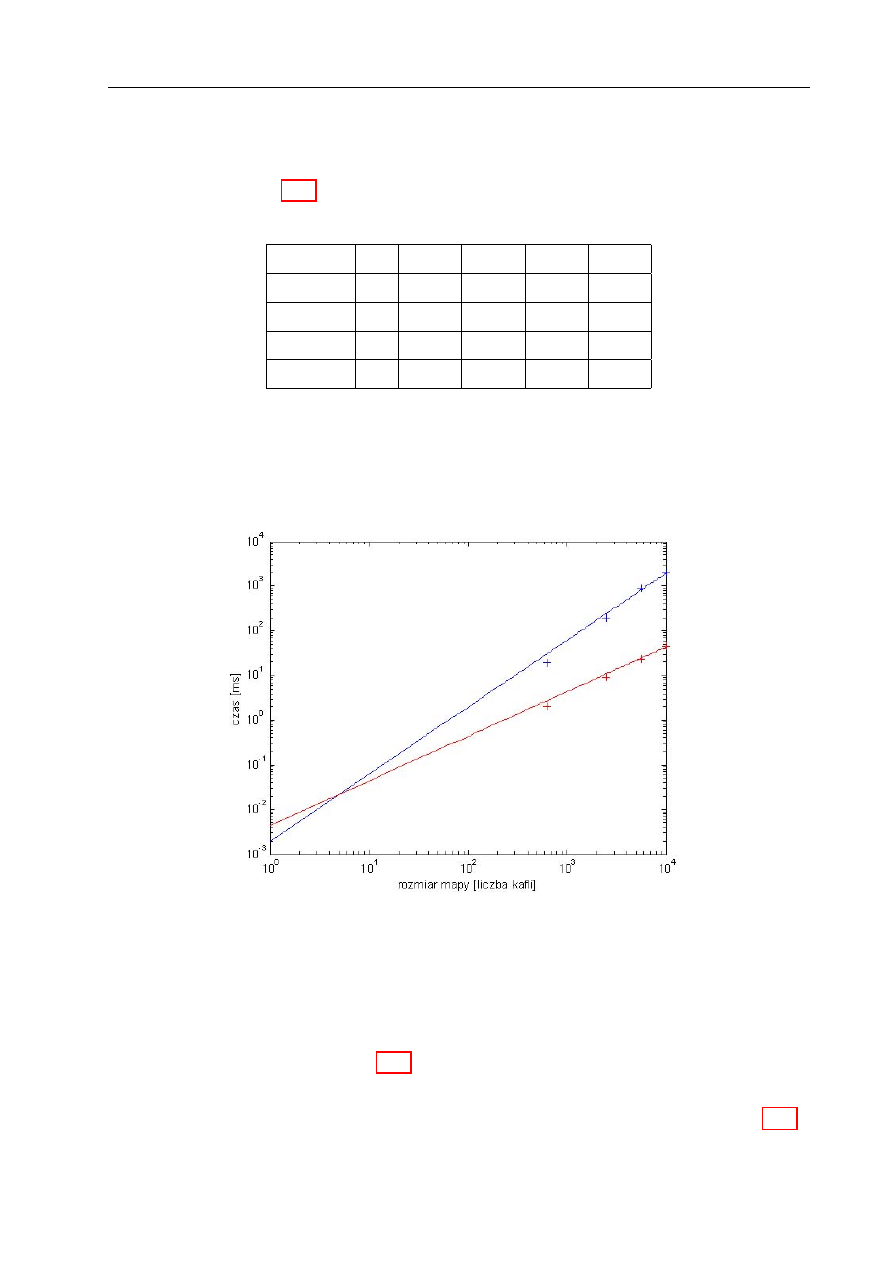
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
114
za podstawową ilość węzłów przyjęto 5. Jeden z nich koduje początek ścieżki, drugi koniec
i są niezmieniane przez algorytm; pozostałe 3 służą do wyznaczenia trajektorii. Jak widać
na mapie 20x20 (rys. 9.20) 5 węzłów wystarcza na rozwiązanie średnio skomplikowanego
zadania.
A*
AE-5
AE-6
AE-7
AE-8
25x25
2
19
215
1383
16112
50x50
9
191
2051
12900
n
75x75
23
875
8032
n
n
100x100
45
1846
19487
n
n
Tabela 11.1: Porównanie czasu działania (w ms) algorytmu A* i algorytmu ewolucyjnego dla
różnej liczby węzłów (n - nie symulowano).
Rysunek 11.7: Porównanie czasu działania na białych mapach algorytmu A* (czerwony) i
algorytmu ewolucyjnego o pięciu węzłach (niebieski); krzyżyki - wartości zmierzone; linie -
trend; skala podwójnie logarytmiczna.
Jak wykazały symulacje (tabela 11.1) algorytm genetyczny był średnio gorszy dla każdej z
czterech map. Rozkład wyników miał średnio wariancję 12486. Tendencja ta była niezależna
od liczby węzłów. Czas działania algorytmu ewolucyjnego jest rzędu O (n
1,5
) (wykres 11.7).
Wraz ze wzrostem liczby węzłów, rosła także gwałtownie złożoność obliczeniowa algo-
rytmu ewolucyjnego, co jest zrozumiałe, gdyż trudniej jest ustawić większą liczbę węzłów w
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
115
odpowiedniej kolejności.
Oba algorytmy zostały również przesymulowane na przykładowych anizotropowych ma-
pach 25×25, 50×50, 75×75 i 100×100 o konfiguracji analogicznej jak mapy 9.20. Nie wzrosła
więc złożoność tej mapy i zadanie rozwiązywalne było za pomocą pięciu węzłów. Algorytm
A* rozwiązał te zadania — znajdując oczywiście wartość optymalną — w czasach krótszych
niż dla białych map o danej wielkości (tabela - 11.2, wykres - 11.9). Zachował jednak zło-
żoność obliczeniową O (n). Natomiast czasy algorytmu ewolucyjnego wzrosły w stosunku do
jego czasów dla białej mapy. Dzieje się tak, dlatego że na jednolitej mapie jest najwięcej
ścieżek optymalnych, spośród wszystkich możliwych map. Złożoność obliczeniowa algorytmu
ewolucyjnego wzrosła zgodnie z przewidywaniami teoretycznymi i wynosi O (n
2,5
) (tabela -
A*
AE
25x25
2
1478
50x50
7
46521
75x75
15
370353
100x100
33
1528143
Tabela 11.2: Porównanie czasu działania (w ms) algorytmu A* i algorytmu ewolucyjnego dla
anizotropowych przykładowych map.
11.2.2
Dyskusja wyników
Jak pokazały symulacje algorytm ewolucyjny, w ogólności, radzi sobie gorzej od algorytmu
A*. Nakład obliczeniowy A* rośnie proporcjonalnie do ilości pól na mapie, zaś dla algorytmu
ewolucyjnego zależność ta jest wielomianowa rzędu O (n
2,5
). Dzieje się tak dlatego, że obszar
przeszukiwań algorytmu A*, to powierzchnia całej mapy, natomiast algorytm ewolucyjny
przeszukuje w przestrzeni dostępnych mu ścieżek, których jest (x
max
∗ y
max
)
n
(n - ilość
węzłów mutowanych, bez początkowego i końcowego). Zależność ilości dostęonych ścieżek
od wielkości mapy jest więc wielomianowa względem ilości pól, a wykładnicza względem
liczby węzłów. Osiągnięcie, więc zależności rzędu O (n
1,5
) (względem liczby pól) jest dobrym
wynikiem. Natomiast złożoność obliczeniowa algorytmu, względem ilości węzłów, jest rzędu
O (n
10
) i jest to zależność lepsza od wykładniczej zależności wielkości obszaru przeszukiwań
algorytmu względem ilości węzłów.
Wniosek ogólny jest taki: algorytm ewolucyjny działa sprawnie w swojej przestrzeni po-
szukiwań, jednak jest to dużo większa przestrzeń niż przestrzeń przeszukiwana przez A*,
mimo użycia kodowania (reprezentacji osobników) dla algorytmu ewolucyjnego zgodnego z
przyjętą metryką 3.2.1. Badania [11] [12], które pokazały użyteczność stosowania algoryt-
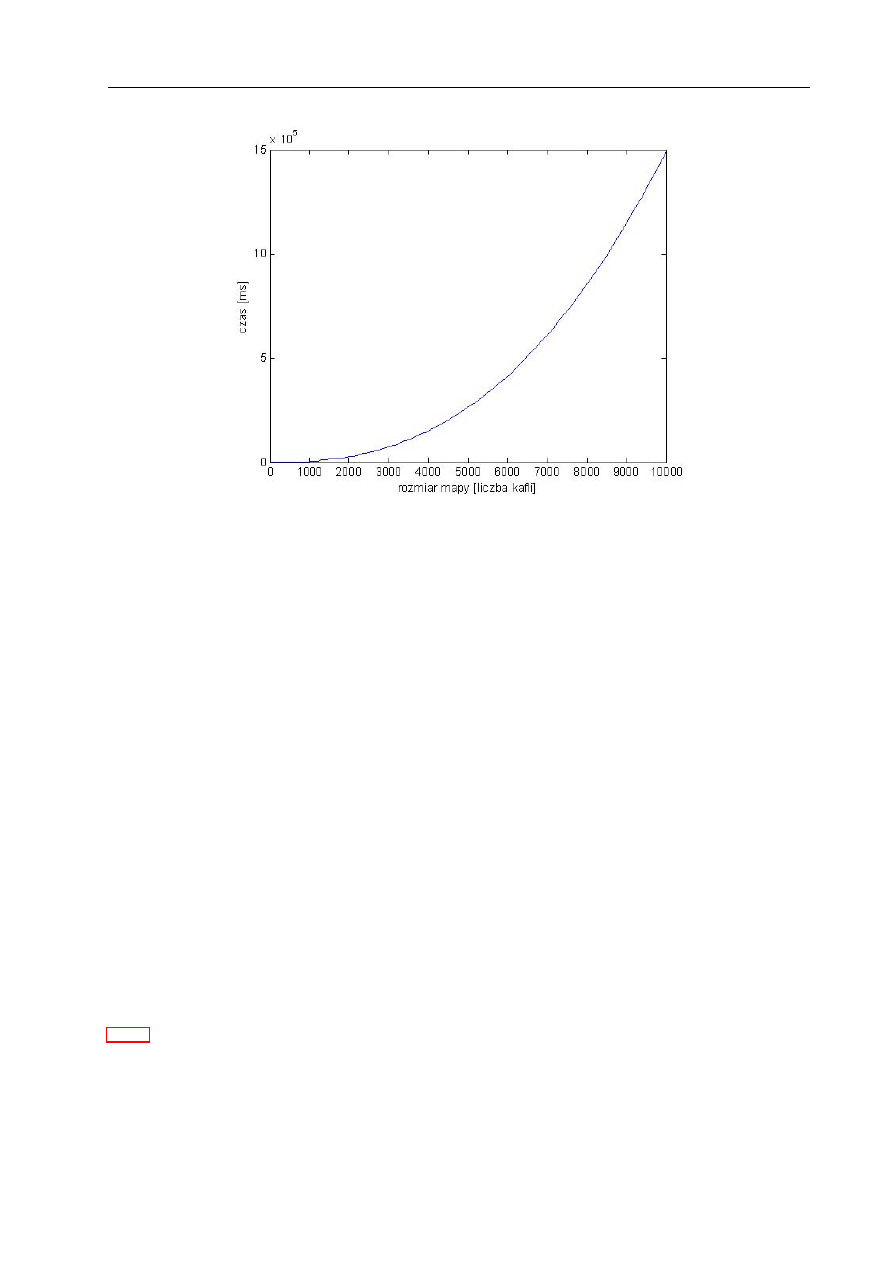
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
116
Rysunek 11.8: Wykres czasu działania (w ms) algorytmu ewolucyjnego, dla anizotropowych
przykładowych map.
mu ewolucyjnego, prowadzone były w środowisku ciągłym, w którym użycie algorytmu A*
nie jest możliwe. Ponadto algorytm ewolucyjny porównywany był z deterministycznym pla-
nerem, którego działanie polegało na: poprowadzeniu odcinka łączącego punkt początkowy
z docelowym, wyznaczenia objazdów przeszkód, z którymi przecina się ten odcinek i koń-
cowym wygładzeniu trajektorii. Planer ten nie miał informacji o koszcie przejazdu przez
obszar, przez który wyznaczył trajektorię — nie mógł więc, w ogólnym przypadku, wyzna-
czyć jej w sposób optymalny. Użycie algorytmu ewolucyjnego dla środowiska ciągłego było
więc uzasadnione.
Dla środowiska zdyskretyzowanego uzasadnione jest użycie algorytmu ewolucyjnego, gdy
szybko chcemy mieć dobre rozwiązanie - niekoniecznie optymalne. Jest to możliwe, dlatego że
algorytm na samym początku wyznacza już przykładowe rozwiązania (inicjacja osobników),
które następnie za pomocą operatorów genetycznych i reprodukcji są udoskonalane. Istnieje
więc możliwość zatrzymania algorytmu w dowolnym momencie i odczytania najlepszego do
tej pory znalezionego wyniku. Proces znajdywania najlepszego rozwiązania obrazuje wykres
Algorytm ewolucyjny wyznaczył już w 313. iteracji rozwiązanie bliskie optymalnemu
(równemu 43), a potem je już tylko poprawiał. Właściwości tej nie posiada algorytm A*,
który wyznacza rozwiązanie przyrostowo.
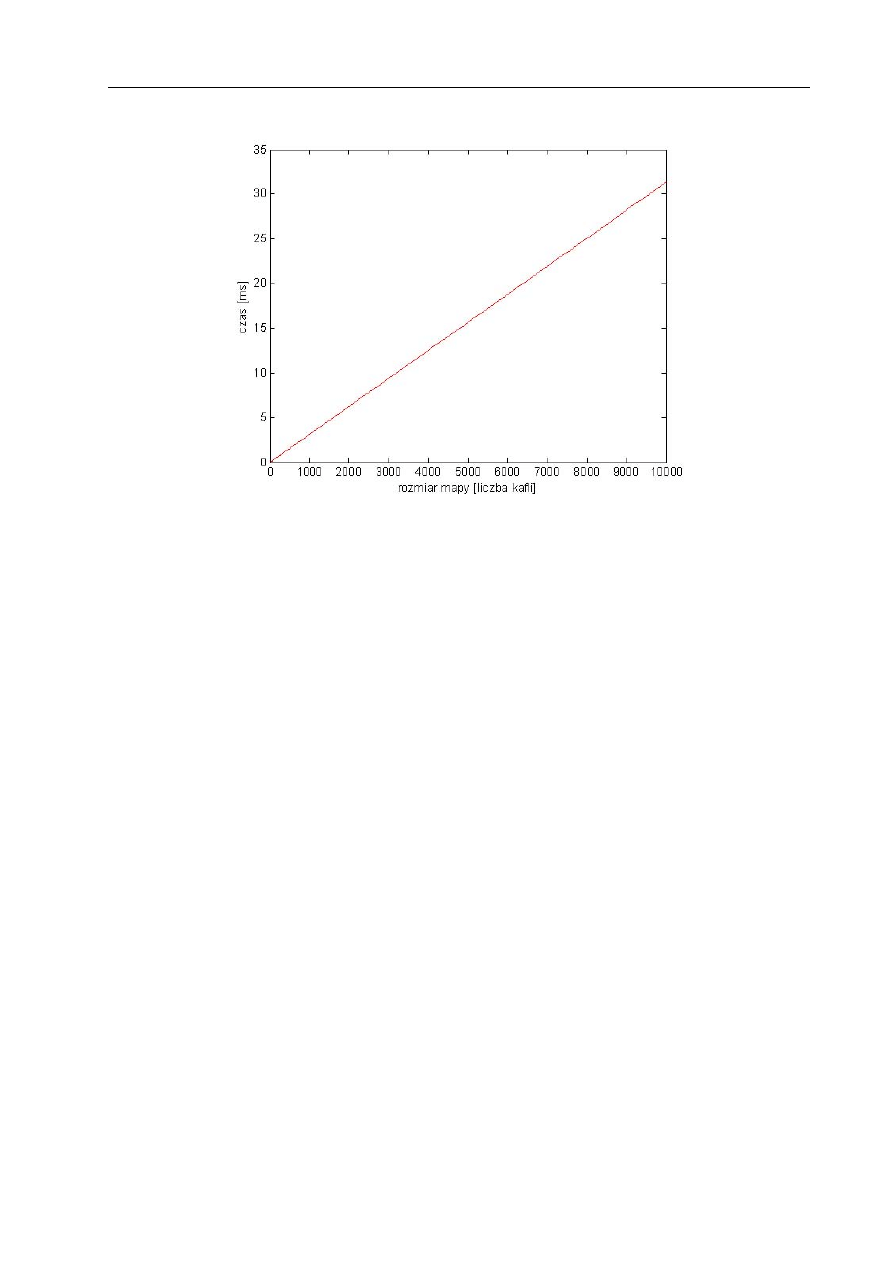
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
117
Rysunek 11.9: Wykres czasu działania (w ms) algorytmu A*, dla anizotropowych przykła-
dowych map.
11.3
Porównanie właściwości algorytmu ewolucyjnego
i A* dla metryki czasowej
Zarówno A*, jak i algorytm ewolucyjny, na których prowadzone były badania opisane w
poprzednim punkcie nie uwzględniają czasu przejazdu, a jedynie jego koszt. Oczywiście koszt
przejazdu przez dane pole może być utożsamiony z czasem, jednak nie uwzględnia on wówczas
czasu koniecznego na manewry robota, takie jak skręty. Przetestowane zostały więc jeszcze
raz oba algorytmu przy uwzględnieniu kosztu skrętu. Koszt skrętu (w lewo lub w prawo)
wynosi jeden, koszt zawrócenia — 2.
Jedyną zmianą wykonaną w algorytmie ewolucyjnym, w celu wprowadzenia metryki cza-
sowej, była modyfikacja funkcji przystosowania, która została wzbogacona o koszt skrętów
jakie musi wykonać robot.
W algorytmie A* dotychczasowy koszt pola, na którym robot wykonuje skręt jest po-
większony o jeden. W implementacji z poprzedniego punktu wystarczyło, by każde pole na
mapie zostało rozwinięte tylko raz — trajektoria prowadząca do niego była od razu optymal-
na. Złożoność tego algorytmu jest więc liniowa. Złożoność algorytmu A* uwzględniającego
koszt skrętu nie jest liniowa, gdyż może istnieć potrzeba wielokrotnego rozwinięcia danego
pola, dzieje się tak dlatego, że graf, po którym porusza się algorytm jest grafem skierowanym.
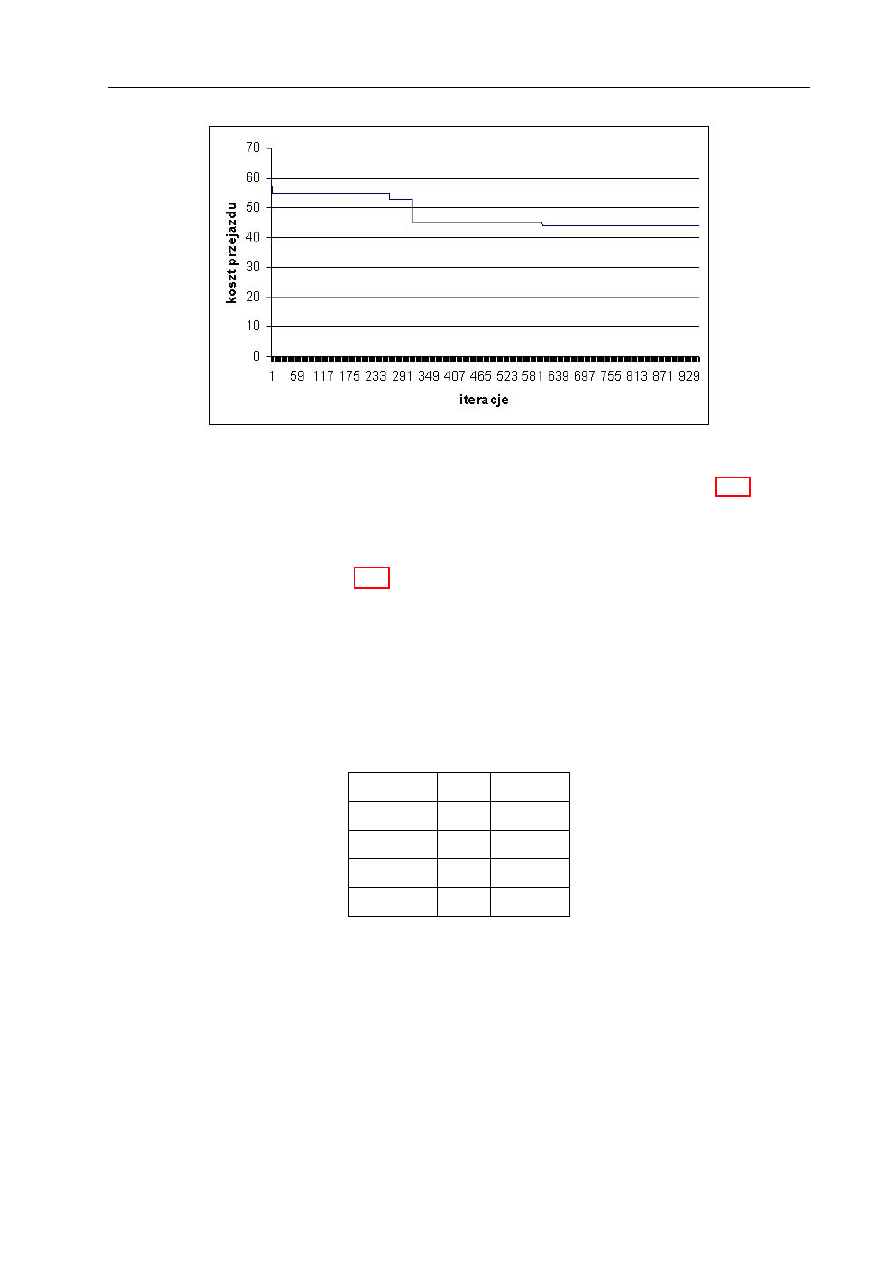
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
118
Rysunek 11.10: Najlepsze dotychczasowe rozwiązanie; wykres dla mapy 9.20.
11.3.1
Badanie złożoności obliczeniowej
Jak wykazały symulacje (tabela 11.3) nakład obliczeniowy algorytmu A* dla metryki czaso-
wej jest rzędu O (n
2
), a algorytmu ewolucyjnego rzędu O (n
2,5
). Badania prowadzone były dla
kilku anizotropowych przykładowych map zawierających obszary zakazane i minima lokalne.
Algorytm ewolucyjny utrzymał swój nakład obliczeniowy, nakład obliczeniowy algorytmu A*
wzrósł z O (n) do O (n
2
). Zmniejszyła się więc dysproporcja między obydwoma algorytmami.
Jednak A* wciąż wyznacza optymalne rozwiązania szybciej niż algorytm ewolucyjny.
A*
AE
25x25
3
1528
50x50
77
48921
75x75
409
371490
100x100
1294
1565472
Tabela 11.3: Porównanie czasu działania (w ms) algorytmu A* i algorytmu ewolucyjnego dla
metryki czasowej.
11.3.2
Dyskusja wyników
Przeprowadzone symulacje pokazały, że nakład obliczeniowy algorytmu ewolucyjnego wzglę-
dem ilości pól dla metryki czasowej jest niewiele większy niż miejskiej. Implementacje algoryt-
mu dla obu zadań różniły się tylko funkcją przystosowania (z uwzględnieniem czasu manewru
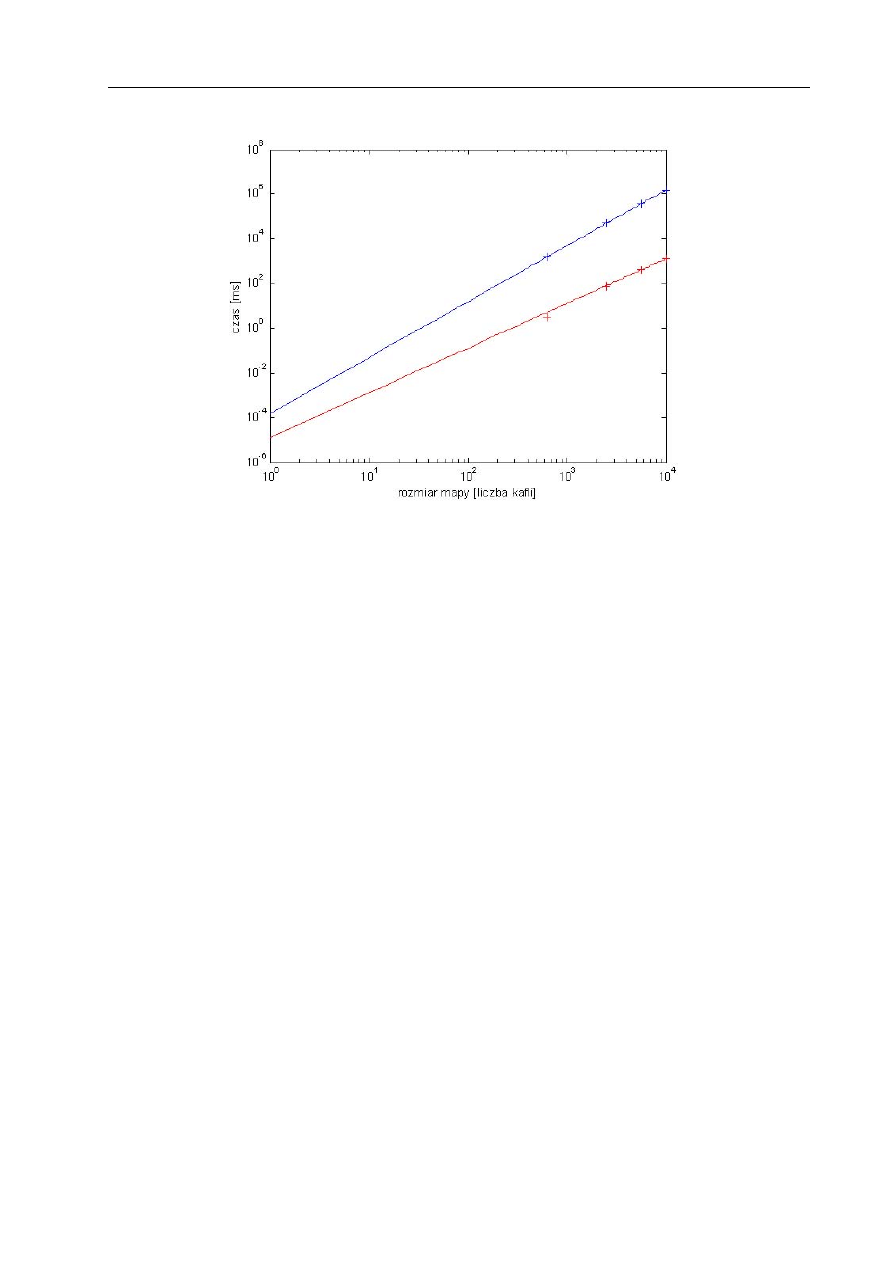
ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
119
Rysunek 11.11: Porównanie czasu działania algorytmu A* (czerwony) i algorytmu ewolucyj-
nego o pięciu węzłach (niebieski) dla metryki czasowej; krzyżyki - wartości zmierzone; linie
- trend; skala podwójnie logarytmiczna.
lub nie). Te dwa aspekty świadczą o małej wrażliwości algorytmu ewolucyjnego na zmiany
warunków zadania. Aspekty te są od siebie częściowo zależne. Ponieważ wystarczy zmienić
tylko funkcję przystosowania, parametry algorytmu, takie jak np. zakres mutacji, pozostają
bez zmian. Oznacza to, że przestrzeń poszukiwań w dziedzinie genotypu się nie zmienia.
Przestrzeń poszukiwań w dziedzinie fenotypu nie zmienia się ze względu na niezmienność
sposobu reprodukcji, ulega natomiast zmianie właśnie ze względu na zmianę funkcji przysto-
sowania. Skoro zmienia się tylko funkcja przystosowania, a dopasowana jest ona do nowego
zadania, zmiany w działaniu algorytmu nie powinny być istotne. I jak pokazują symualacje,
nie są.
Natomiast nakład obliczeniowy algorytmu A* jest znacznie gorszy dla metryki czasowej
niż dla metryki miejskiej. Dzieje się tak, dlatego że może istnieć potrzeba wielokrotnego
rozwinięcia danego pola. Algorytm A* dla metryki miejskiej każde pole rozwija raz albo
wcale.
Główną zaletą algorytmu ewolucyjnego jest więc jego uniwersalność. W przypadku nie-
wielkiej zmiany zadania wystarczające jest zmienienie tylko funkcji przystosowania. Jeśli
zadanie będzie się znacznie bardziej różniło (np. przestrzeń przestałaby być dyskretna), wy-
starczy zmienić tylko operatory genetyczne (na wersję dla przestrzeni ciągłych), bez zmiany
sposobu kodowania osobnika (osobnik dalej jest listą węzłów). W przypadku diametralnej
zmiany zadania powinna nastąpić również zmiana kodowania osobnika. Schemat algoryt-

ROZDZIAŁ 11. PORÓWNANIE ALGORYTMÓW: EWOLUCYJNEGO I DETERMINISTYCZNEGO
120
mu pozostaje jednak niezmieniony. Uniwersalność ta leży więc u podstaw idei algorytmów
ewolucyjnych; algorytmów, którymi możemy rozwiązywać praktycznie każde zadanie opty-
malizacji. Ceną, jaka jest płacona za ogólność algorytmu, jest często jego gorsze działanie w
przypadku zadań, dla których istnieją wyspecjalizowane algorytmy. Tak było np. w zadaniu
wyznaczania ścieżki robota. Jednak algorytmy ewolucyjne (jak i inne metody niedetermini-
styczne) sprawdzają się w sytuacjach, gdy konstrukcja dobrego derministycznego algorytmu
jest niemożliwa.

Rozdział 12
Podsumowanie
W ramach pracy został wykonany system nawigacyjny. System umożliwia wyznaczenie tra-
jektorii (algorytmem ewolucyjnym lub A*) i przesłanie jej wraz z mapą terenu robotowi.
Robot posługując się mapą i własnymi obserwacjami, w razie niemożliwości wykonania za-
danej trajektorii, wyznacza objazd algorytmem A*. W pracy zostały zbadane możliwości
obu algorytmów w wyznaczaniu optymalnych trajektorii. O możliwościach algorytmu ewolu-
cyjnego decydują przede wszystkim jego parametry (dobór operatorów genetycznych, model
reprodukcji etc.), które zostały starannie dobrane. Mimo to algorytm ewolucyjny okazał się
gorszy od A*. Jego złożoność obliczeniowa była nieliniowa. Algorytm A* szybko znajdował
rozwiązanie niezależnie od wielkości mapy i stopnia jej komplikacji. Klasyfikuje to A* jako
optymalny algorytm do wyznaczania trajektorii dla tego typu zadań. Mimo że robot korzy-
stając z zaimplementowanej A* sam mógłby wyznaczać całą trajektorię - a nie tylko objazdy
jak ma to miejsce w prezentowanym systemie, zbudowanie większego systemu nawigacyjnego
może mieć sens.
System mógłby być również stosowany, by przesyłać dane do robota i je otrzymywać.
Mimo że robot jest autonomiczny — aby był w pełni użyteczny - musi istnieć komunikacja
z nim. System służyłby wtedy do wysyłania celów misji, czyli np. odwiedzenia pewnych pól
przez robota. Wówczas robot samodzielnie decydowałby o sposobie wykonania tej misji (wy-
borze trajektorii). Istniała by też możliwość określenia trajektorii przez operatora systemu,
któremu zależałoby na jak najwierniejszym jej oddaniu - wtedy robot ograniczyłby się do
wykonywania objazdów. Oczywiście nie wykluczyłoby to wykonywania zadań algorytmizo-
walnych po stronie PC. Jeśli na przykład istniałaby potrzeba odwiedzenia kilku punktów na
mapie, należałoby rozwiązać zadanie komiwojażera, by odwiedzić te punkty w odpowiedniej
kolejności. Wtedy istniałoby, być może, uzasadnienie dla zastosowania algorytmu ewolucyj-
nego (ale to temat na następne badania). Algorytm działający na komputerze PC mógłby
przesyłać wtedy całą trajektorię (robot wyznaczałby tylko objazdy) lub tylko kolejność pól w
jakiej robot ma jej odwiedzić - robot musiałby wówczas samodzielnie wyznaczyć trajektorię
pomiędzy nimi.

ROZDZIAŁ 12. PODSUMOWANIE
122
Oprócz przeprowadzenia badań dotyczących możliwości algorytmów, zostały przebadane
aspekty fizyczne systemu —-jego możliwości w realnym środowisku. Złożył się na to m. in.
wybór środowiska dopasowanego do możliwości — głównie obserwacyjnych - robota. Duże
znaczenia — mimo że nie opisywane szeroko w pracy - miały możliwości samolokalizacyjne
robota. Nie bez znaczenia była też konstrukcja robota - ustawienie czujników światła i odo-
metrycznych. Wyeliminowane zostały niedogodności sprzętowe w postaci niedoboru wejść od
czujników, poprzez taką modyfikację jądra systemu operacyjnego LegOS, by możliwe były
odczyty mimo zwierania czujników. Nie bez znaczenia było też oprogramowanie robota zor-
ganizowane w dwóch wartwach: ruchu i nadzoru. Odpowiednio zostały też dobrane elementy
wykonawcze tak, żeby robot mógł wykonywać wszystkie potrzebne manewry. Przetestowana
została możliwość komunikacji robota z komputerem. Szereg problemów natury technicznej
został więc rozwiązany. Problemy te nie wystąpiłyby podczas zwykłej symulacji na kompu-
terze.
Zaletą tej pracy jest więc zarówno zbudowanie złożonego systemu do planowania misji,
wykonania jej i gromadzenia danych, jak i przeprowadzenie badań nad wyborem właściwego
algorytmu optymalizacji trajektorii.

Bibliografia
[1] Jarosław Arabas - „Wykłady z Algorytmów Ewolucyjnych”, WNT, Warszawa 2001
[2] Lego Mindstorms Constructopedia
[3] Lego Mindstorms User Guide
[4] http://legos.sourceforge.net/
[5] http://www.geocities.com/ marioferrari/emulegos.html
[6] Hitachi Single-Chip Microcomputer H8/3297 Series - Hardware Manual
[7] http://mindstorms.lego.com
[8] http://home.elka.pw.edu.pl/˜mbrudka/ERO/
[9] http://www.leocad.org/
[10] Zbigniew Michalewicz - „Algorytmy genetyczne + struktury danych = programy ewo-
lucyjne”, WNT 1999
[11] Krzysztof Trojanowski, Zbigniew Michalewicz - „Planowanie ścieżki mobilnego robota”,
Materiały I Krajowej Konferencji - Algorytmy Ewolucyjne
[12] Krzysztof Trojanowski, Zbigniew Michalewicz - „Evolutionary Algorithms and the
Problem-Specific Knowledge”, Materiały II Krajowej Konferencji - Algorytmy Ewo-
lucyjne i Optymalizacja Globalna
[13] Krzysztof Trojanowski, Zbigniew Michalewicz - „Extensions of Evolutionary Algorithms
for Non-Stationary Environments”, Materiały III Krajowej Konferencji - Algorytmy
Ewolucyjne i Optymalizacja Globalna
[14] Stuart Russel, Peter Norvig - „Artificial Inteligence: a modern approach”, Prentice-Hall,
Inc. 1995
[15] Wojciech Szynkiewicz - Materiały do wykładu Sterowanie i Programowanie Robotów

BIBLIOGRAFIA
124
[16] Wojciech Szynkiewicz - Materiały do wykładu Elementy Robotyki
[17] Władysław Kopaliński - „Słownik wyrazów obcych z almanachem”
[18] Krzysztof Sacha - „Sieci Petriego”, Materiały do wykładu Specyfikacja i Projektowanie
Oprogramowania
[19] Ignacy Dulęba - „Metody i algorytmy planowania ruchu robotów mobilnych i manipu-
lacyjnych”, Akademicka Oficyna Wydawnicza EXIT, Warszawa 2001

Dodatek A
Płyta CD
Do pracy dołączono płytę CD, zawierającą następujące elementy:
• program „Xtiles” wyznaczający trajektorię w komputerze PC,
• program robota,
• zmodyfikowane pliki źródłowe sytemu legOS,
• program służący do komunikacji robota z komputerem PC,
• model robota,
• zdjęcia robota,
• filmy z pokazu robota,
• pracę magisterską w formacie „pdf” wraz z plikami źródłowymi (format „latex”),
• programy narzędziowe.
Szczegółowy opis ww. elementów znajduje się w pliku „OPIS.TXT”.
Document Outline
- Wstep
- Problem nawigacji
- Sposoby wyznaczania trajektorii
- Podstawy projektowania robotów mobilnych
- Wlasciwosci srodowiska Mindstorms
- Ogólna postac systemu wykonujacego zadanie
- Budowa planszy i robota
- Program robota
- Wyznaczanie trajektorii algorytmem ewolucyjnym
- Wyznaczanie trajektorii algorytmem deterministycznym
- Porównanie algorytmów: ewolucyjnego i deterministycznego
- Podsumowanie
- Plyta CD
Wyszukiwarka
Podobne podstrony:
Prezentacja praca dyplom
Praca dyplomowa Strona tytułowa etc
PRACA DYPLOMOWA BHP - ORGANIZACJA PRACY W PSP, TEMATY PRAC DYPLOMOWYCH Z BHP
praca dyplomowa 1 strona wzor, Szkoła, prywatne, Podstawy informatyki
d druku BIBLIOGRAFI1, cykl VII artererapia, Karolina Sierka (praca dyplomowa; terapia pedagogiczna z
Praca dyplomowa(1)
streszczenie panelu, Prace dyplomowe i magisterskie, praca dyplomowa, materiały z internetu
praca dyplomowa BR5VQ5NYN263L77S7YKAVS66LCHECBHKF2E3GEQ
praca dyplomowa informatyka programowanie 7B5PTOE5KXERFXSEJISGCMFJDQ5X6LRRZEBNOJY
praca dyplomowa
praca dyplomowa edycja wbn1 2011
PRACA DYPLOMOWA MAGISTERSKA OCZ SC TYPU LEMMNA
Internet - UE prawo, Studia - IŚ - materiały, Semestr 07, Praca dyplomowa
do druku ROZDZIAŁ III, cykl VII artererapia, Karolina Sierka (praca dyplomowa; terapia pedagogiczna
PRACA DYPLOMOWA SPIS TREŚCI, TEMATY PRAC DYPLOMOWYCH Z BHP
strona tytulowa, WNPiD, moje, praca dyplomowa
inżynierska praca dyplomowa wzorzec
Wytwarzanie biogazu - wysypisak śmieci., Studia - IŚ - materiały, Semestr 07, Praca dyplomowa
więcej podobnych podstron