Ćwiczenie D6:

A

LGORYTMY

OBLICZANIA

MODUŁU

WEKTORA

,

PIERWIASTKA

KWADRATOWEGO

I

FUNKCJI

TRYGONOMETRYCZNYCH

PRZY

ZASTOSOWANIU

PROCESORÓW

SYGNAŁOWYCH

TMS320

opracował:

mgr inż. Tadeusz Białoń

[e-mail]

Cele ćwiczenia:

–

poznanie sposobów aproksymacji funkcji nieliniowych na
przykładzie funkcji sinus

–

analiza błędów procedur realizujących funkcje nieliniowe na
przykładzie procedur realizujących funkcję sinus

–

doskonalenie umiejętności obliczeniowych w arytmetyce
stałoprzecinkowej

Metody aproksymacji funkcji nieliniowych

Stałoprzecinkowe procesory sygnałowe są zoptymalizowane pod kątem wykonywania podstawowych
operacji arytmetycznych czyli dodawania i mnożenia. Niektóre procesory sygnałowe zawierają
w swojej strukturze dodatkowe urządzenia w sposób sprzętowy ułatwiające obliczanie wartości
funkcji nielinowych takich jak funkcje trygonometryczne czy pierwiastek kwadratowy. W przypadku
braku takich urządzeń w strukturze procesora, wartości funkcji nieliniowych należy obliczać przy
wykorzystaniu tylko operacji mnożenia i dodawania, stosując odpowiednie metody aproksymacji.

Aproksymacja za pomocą szeregu Taylora

Jedną z metod praktycznej realizacji funkcji nieliniowych jest aproksymacja za pomocą szeregu
Taylora, pozwalająca sprowadzić problem obliczania wartości funkcji nieliniowej do obliczania
wartości wielomianu.
Po rozwinięciu funkcji sinus w szereg Taylora w przedziale wartości kątów [0,

π

] radianów

i pominięciu wyrazów stopnia piątego i wyższych otrzymujemy:

sin( x ) = 0,0013 + 0,9826 * x +
+ 0,0544 * x

2

– 0,2338 * x

3

+ 0,0372 * x

4

Powyższy wzór pozwala obliczyć wartość funkcji sinus dla kątów z przedziału [0,

π

]. wartości

funkcji sinus dla katów z przedziału [-

π

, 0] obliczamy korzystając z nieparzystości funkcji sinus:

sin( -x ) = -sin( x )

Wartości dla pozostałych wartości kątów obliczamy korzystając ze wzorów redukcyjnych.
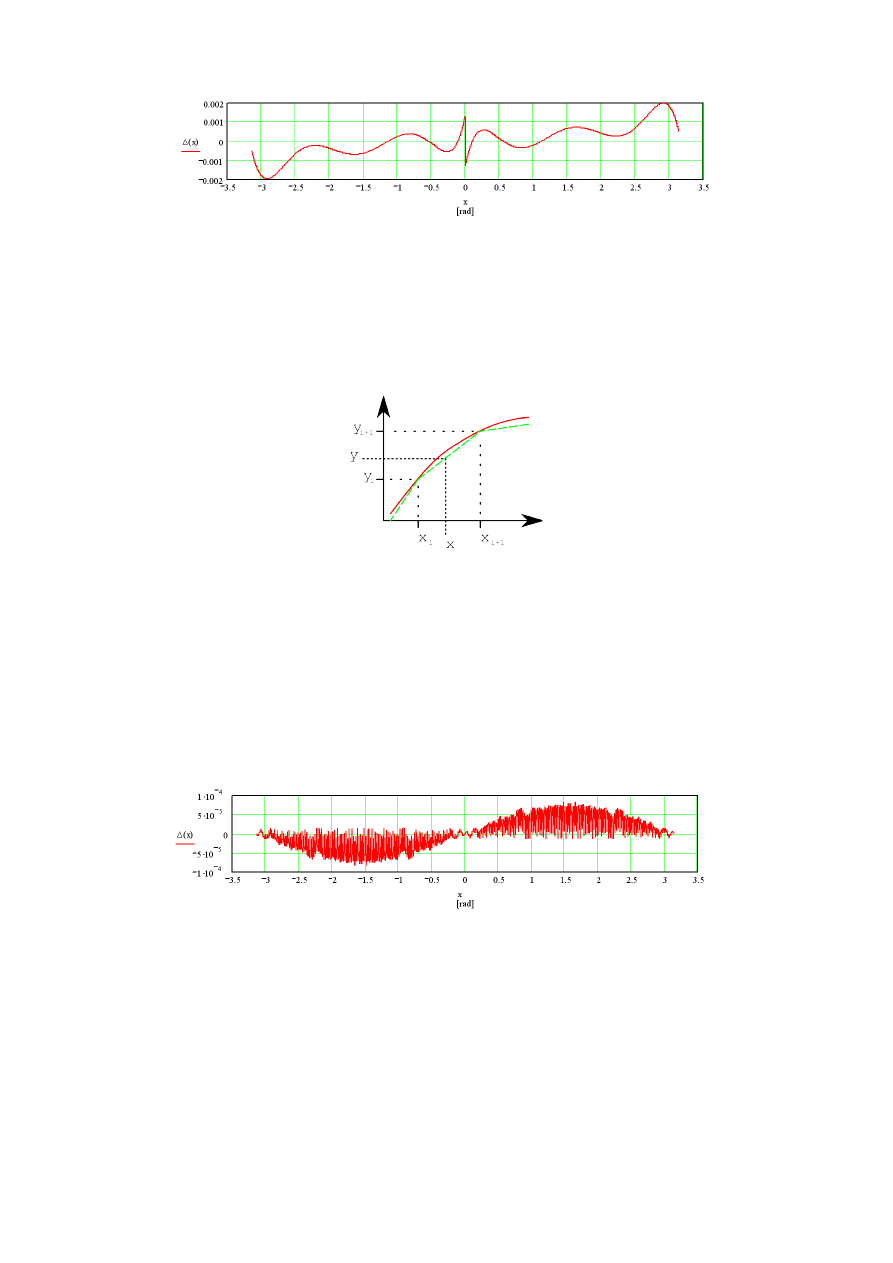
Bezwzględny błąd obliczania funkcji sinus za pomocą wyżej podanej aproksymacji szeregiem Taylora
przedstawia wykres poniżej. Jest to tylko błąd związany z metodą aproksymacji. Rzeczywiste błędy
obliczeniowe gotowej procedury będą większe ze względu na dodatkowe zaokrąglenia wynikające
z ograniczonej precyzji arytmetyki stałoprzecinkowej.

Tablica wartości funkcji i interpolacja

Inną metodą obliczania wartości funkcji nieliniowej jest utworzenie tablicy wartości tej funkcji
i umieszczenie jej w pamięci procesora. Procedura obliczająca wartość funkcji ma wtedy za zadanie
odnalezienie w tablicy wartości odpowiadających podanemu argumentowi, a następnie
przeprowadzenie odpowiedniej interpolacji, najczęściej liniowej. Ideę interpolacji liniowej
przedstawia poniższy rysunek.

−−−

rzeczywista wartość funkcji,

- - -

wartość interpolowana

Aby obliczyć wartość funkcji dla argumentu x należy odczytać z tablicy dwie wartości sąsiednie x

i

i x

i+1

oraz odpowiadające im wartości funkcji y

i

i y

i+1

, a następnie obliczyć wartość funkcji y ze

wzoru:

y = y

i

+ ( y

i+1

– y

i

) * ( x – x

i

) / ( x

i+1

– x

i

)

Bezwzględny błąd obliczania funkcji sinus za pomocą wyżej podanej interpolacji liniowej
przedstawia wykres poniżej. Jest to tylko błąd związany z interpolacją. Rzeczywiste błędy
obliczeniowe gotowej procedury będą większe ze względu na dodatkowe zaokrąglenia wynikające
z ograniczonej precyzji arytmetyki stałoprzecinkowej.

Skalowanie wartości i argumentu funkcji

Kolejnym problemem jest skalowanie argumentu i wartości funkcji. Wartości funkcji sinus należą do
przedziału [-1, 1] więc można je przedstawić w 16-bitowym kodzie uzupełnienia do dwóch

i skalowaniu Q15 bez żadnych dodatkowych zabiegów. Dziedziną funkcji sinus w rozpatrywanej
realizacji jest przedział [-

π

,

π

] niedający się zakodować w 16-bitowym skalowaniu Q15.

Przedział kątów wymaga więc przeskalowania polegającego na podzieleniu wszystkich jego wartości
przez

π

. Aby obliczyć wartość funkcji sinus dla przykładowego kąta 0,11

π

, należy jako wartość

wejściową dla badanych procedur podać liczbę 0,11 w 16-bitowym kodzie uzupełnienia do dwóch

i skalowaniu Q15.

Przebieg ćwiczenia

Ćwiczenie polega na uruchamianiu i testowaniu działania gotowego programu realizującego
obydwa opisane powyżej algorytmy obliczania funkcji sinus. Program ten, napisany w asemblerze,
oraz całe środowisko programistyczne zostanie przygotowany przez prowadzącego ćwiczenie.
W trakcie ćwiczenia należy zdjąć charakterystyki wartości funkcji sinus obliczane przez obydwa
algorytmy.

Sprawozdanie z ćwiczenia

Sprawozdanie powinno zawierać wykreślone charakterystyki błędów względnych i bezwzględnych
dla wyników działania obydwu algorytmów. Błędy względne należy obliczać w odniesieniu do
wartości funkcji sinus obliczonych na kalkulatorze lub w dowolnym programie matematycznym
zmiennoprzecinkowym, przy czym wartości te należy brać do obliczeń z dokładnością co najmniej
ośmiu znaczących pozycji dziesiętnych. W sprawozdaniu powinny się również znaleźć wnioski
i spostrzeżenia dotyczące działania i właściwości użytkowych obydwu procedur.