
Wykład 5
Weryfikacja modelu, cz. II

2
Procedura weryfikacji:
•
Dobro
ć
dopasowania do danych empirycznych
•
Istotno
ść
parametrów strukturalnych
•
Normalno
ść
, homoskedastyczno
ść
, brak autokorelacji
składników losowych
•
Dobór zmiennych obja
ś
niaj
ą
cych
•
Posta
ć
funkcyjna
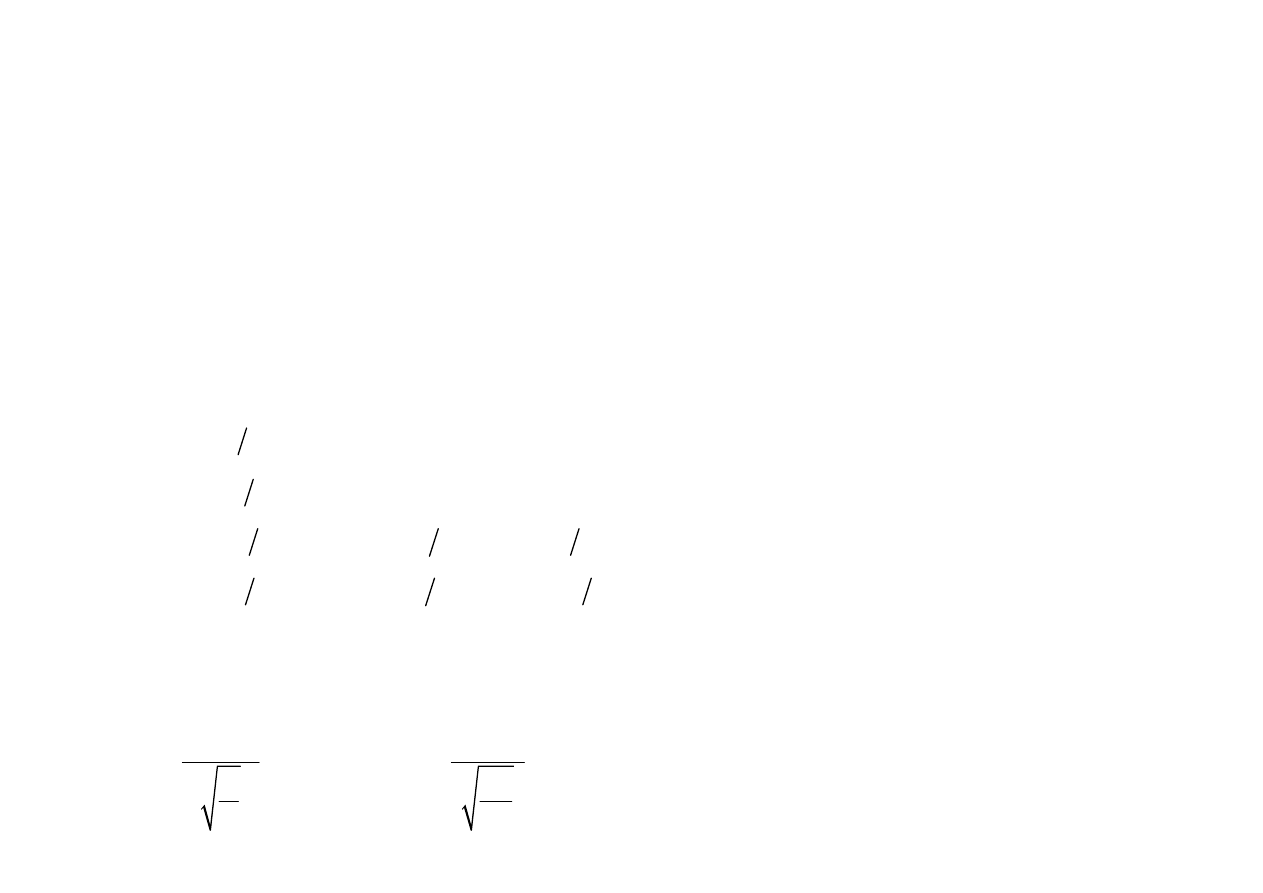
3
Normalno
ść
rozkładu składników losowych
Problemy w procedurze weryfikacji modelu w sytuacji, w której rozkład
składników losowych
t
ξξξξ
nie jest normalny!
Testy normalno
ś
ci znane z zaj
ęć
ze statystyki: rozkład zgodno
ś
ci
2
χχχχ
Pearsona?
Test Jarque-Bera (J-B)
Niech
2
t
X ~ N( ,
)
µ σ
µ σ
µ σ
µ σ
. Wówczas:
((((
))))
T
2
t
t 1
m
(1 T)
~ N
,
====
=
ξ
µ σ
=
ξ
µ σ
=
ξ
µ σ
=
ξ
µ σ
∑
∑
∑
∑
–
ś
rednia z próby
(((( ))))
T
2
2
2
2
t
t 1
S
(1 T 1)
(X
m) ~
(T 1) / T 1
====
=
−
−
σ χ
−
−
=
−
−
σ χ
−
−
=
−
−
σ χ
−
−
=
−
−
σ χ
−
−
∑
∑
∑
∑
– wariancja z próby
T
3
t
t 1
Sk
(1 T)
(X
m S) ~ N(0,6 T)
====
=
−
=
−
=
−
=
−
∑
∑
∑
∑
– sko
ś
no
ść
z próby
T
4
t
t 1
Kr
(1 T)
(X
m S) ~ N(3,24 T)
====
=
−
=
−
=
−
=
−
∑
∑
∑
∑
– kurtoza z próby
oraz
(((( ))))
Sk
0
~ N 0,1
6
T
−−−−
,
(((( ))))
Kr
3
~ N 0,1
24
T
−−−−
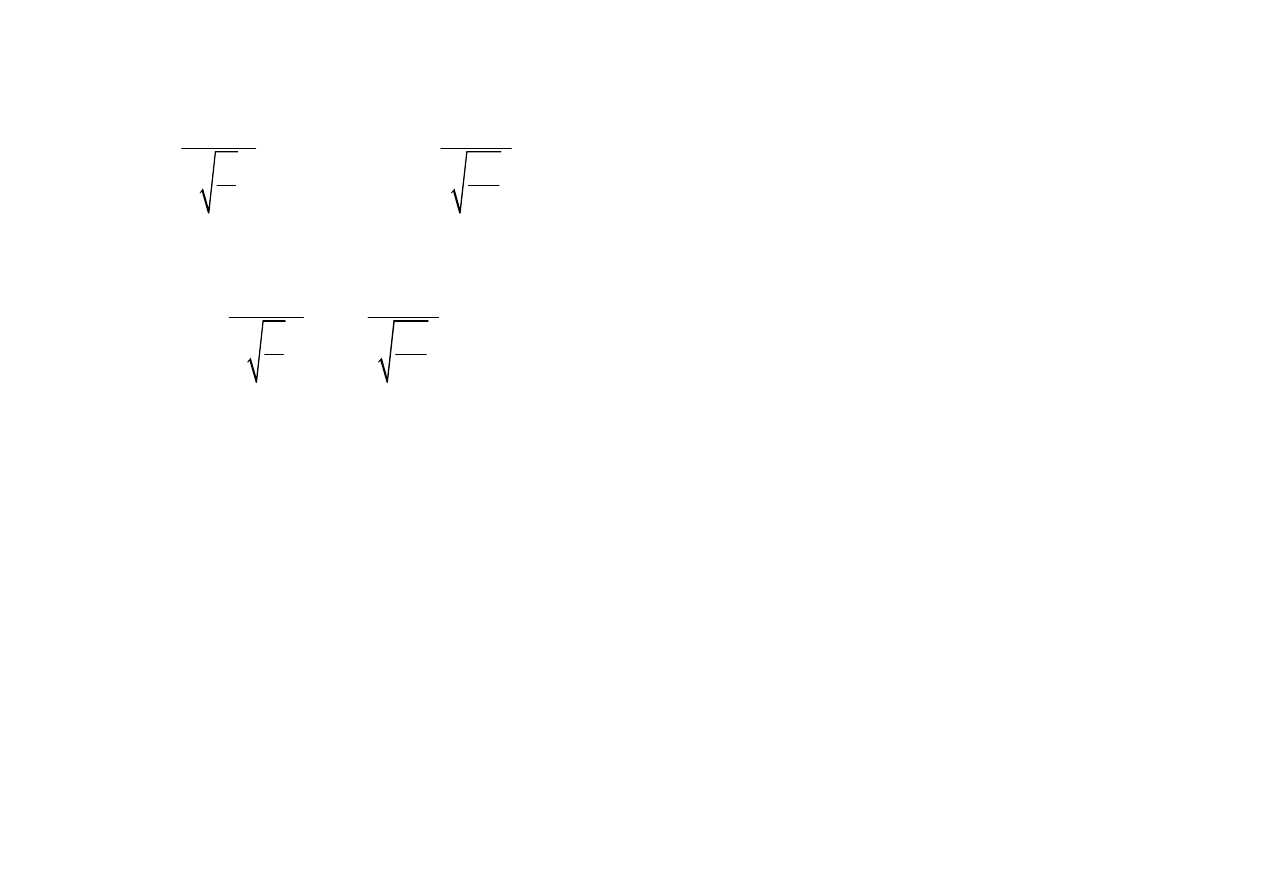
4
2
2
Sk
0
~
(1)
6
T
−−−−
χχχχ
,
2
2
Kr
3
~
(1)
24
T
−−−−
χχχχ
JB=
2
2
2
Sk
0
Kr
3
~
(2)
6
24
T
T
−
−
−
−
−
−
−
−
+
χ
+
χ
+
χ
+
χ
2
2
Pr[
(2)
(2)]
α
αα
α
χ
≥ χ
= α
χ
≥ χ
= α
χ
≥ χ
= α
χ
≥ χ
= α
Reguła decyzyjna:
2
0,05
0
t
JB
(2)
H :
~ N
≤ χ
≤ χ
≤ χ
≤ χ
⇒
⇒
⇒
⇒
ξξξξ
2
0,05
A
JB
(2)
H
> χ
> χ
> χ
> χ
⇒
⇒
⇒
⇒
Składniki (bł
ę
dy) losowe s
ą
nieobserwowalne. Test przeprowadza si
ę
na resztach z modelu!
Makroekonomiczna funkcja konsumpcji dla Wlk. Brytanii:
2
0,05
0
JB
2,9
5,99
H
=
<
= χ
=
<
= χ
=
<
= χ
=
<
= χ
⇒
⇒
⇒
⇒
5
Homoskedastyczno
ść
składników (bł
ę
dów) losowych
Nierch
2
t
Var( )
const
ξξξξ
ξ = σ ≠
ξ = σ ≠
ξ = σ ≠
ξ = σ ≠
. Przyczyny?
Konsekwencje:
j
b jest ci
ą
gle BLUE, niemniej nie jest najefektywniejszy
We wszystkich przypadkach wykorzystanie
j
S(b )
w procedurze weryfikacji mo
ż
e
prowadzi
ć
do bł
ę
dnych decyzji!
Procedura testowa:
2
2
2
t
t
t
t
t
Var( )
E[
E( )]
E(
0)
E(
)
ξ = ξ − ξ
= ξ −
= ξ
ξ = ξ − ξ
= ξ −
= ξ
ξ = ξ − ξ
= ξ −
= ξ
ξ = ξ − ξ
= ξ −
= ξ
2
t
0
1
t1
r
tr
t
u
Z
Z
= γ + γ
+
+ γ
+ ε
= γ + γ
+
+ γ
+ ε
= γ + γ
+
+ γ
+ ε
= γ + γ
+
+ γ
+ ε
K
K
K
K
0
1
r
H :
0
γ =
= γ =
γ =
= γ =
γ =
= γ =
γ =
= γ =
K
K
K
K
,
A
l
H : przynajmniej niektóre
0
γ ≠
γ ≠
γ ≠
γ ≠
(
l
1,2,
,r
====
K
K
K
K
);
(
2
t
0
t
u
= γ + ε
= γ + ε
= γ + ε
= γ + ε
)
Statystyki testowe:
2
2
T
(r
1) R
F
~ F[r,T
(r
1)]
r
1 R
− +
− +
− +
− +
=
− +
=
− +
=
− +
=
− +
−−−−
;
2
2
TR ~
(r)
χχχχ
2
2
R
U
R
U
U
R
2
U
U
U
(RSS
RSS ) /(df df )
(R
R ) /(K m)
F
~ F[K m,T (K 1)]
RSS / df
(1 R ) /(T (K 1)]
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
=
−
− +
=
=
−
− +
=
=
−
− +
=
=
−
− +
−
− +
−
− +
−
− +
−
− +

6
Homoskedastyczno
ść
składników (błedów) losowych, cd.
Makroekonomiczna funkcja konsumpcji dla Wlk. Brytanii:
2
t
0
1
t
t
u
Y
= α + α
+ ε
= α + α
+ ε
= α + α
+ ε
= α + α
+ ε
2
2
0,05
A
TR
38 0,23
8,74
3,84
(1)
H
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
⇒
⇒
⇒
⇒
0,05
A
38
2
0,23
F
36 0,299
10,75
4,11
F
(1,36)
H
1
1 0,23
−−−−
=
×
=
×
=
>
=
=
×
=
×
=
>
=
=
×
=
×
=
>
=
=
×
=
×
=
>
=
⇒
⇒
⇒
⇒
−−−−

7
Brak skorelowania skladsników (bł
ę
dów) losowych
Niech
t
s
t
t
s
s
t
s
t
s
Cov( ,
)
E{[
E( )][
E(
)]}
E[(
0)(
0)]
E[(
)]
0
ξ ξ =
ξ − ξ
ξ − ξ
=
ξ − ξ −
=
ξ ξ
≠
ξ ξ =
ξ − ξ
ξ − ξ
=
ξ − ξ −
=
ξ ξ
≠
ξ ξ =
ξ − ξ
ξ − ξ
=
ξ − ξ −
=
ξ ξ
≠
ξ ξ =
ξ − ξ
ξ − ξ
=
ξ − ξ −
=
ξ ξ
≠
. Przy-
czyny? Konsekwencje jak poprzednio
Procedura testowa:
t
0
1
t1
K
tK
1 t 1
r
t r
t
u
X
X
u
u
−
−
−
−
−
−
−
−
= α + α
+
+ α
+ γ
+
+ γ
+ ε
= α + α
+
+ α
+ γ
+
+ γ
+ ε
= α + α
+
+ α
+ γ
+
+ γ
+ ε
= α + α
+
+ α
+ γ
+
+ γ
+ ε
K
K
K
K
K
K
K
K
0
1
r
H :
0
γ =
= γ =
γ =
= γ =
γ =
= γ =
γ =
= γ =
K
K
K
K
,
A
l
H : przynajmniej niektóre
0
γ ≠
γ ≠
γ ≠
γ ≠
(l
1,2,
,r
====
K
K
K
K
)
Makroekonomiczna funkcja konsumpcji dla Wlk. Brytanii:
t
0
1
t
1 t 1
t
u
Y
u
−−−−
= α + α
+ γ
+ ε
= α + α
+ γ
+ ε
= α + α
+ γ
+ ε
= α + α
+ γ
+ ε
2
2
0,05
A
TR
37 0,385
14,245
3,84
(1)
H
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
⇒
⇒
⇒
⇒
A
(0,38536
0) / 1
F
0,627 34
21,317
4,13
H
(1 0,38536) / 34
−−−−
=
=
×
=
>
=
=
×
=
>
=
=
×
=
>
=
=
×
=
>
⇒
⇒
⇒
⇒
−−−−
t
0
1
t
1 t 1
2
t 2
t
u
Y
u
u
−
−
−
−
−
−
−
−
= α + α
+ γ
+ γ
+ ε
= α + α
+ γ
+ γ
+ ε
= α + α
+ γ
+ γ
+ ε
= α + α
+ γ
+ γ
+ ε
2
2
0,05
A
TR
36 0, 4
14, 4
5,99
(2)
H
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
⇒
⇒
⇒
⇒

8
Dobór zmiennych obja
ś
niaj
ą
cych
Niech
t
0
1
1t
2
2t
t
Y
X
X
= β + β
+ β
+ ξ
= β + β
+ β
+ ξ
= β + β
+ β
+ ξ
= β + β
+ β
+ ξ
Wówczas
2
t1
X
,
2
t2
X
and
1t
2t
X X
nie powinny mie
ć
zdolno
ś
ci obja
ś
niaj
ą
-
cych w regresji reszt
t
u
na
1t
X
i
2t
X
2
2
t
0
1
t1
2
t2
1
t1
2
t2
1
t1
t2
t
u
X
X
X
X
X X
= α + α
+ α
+ γ
+ γ
+ δ
+ ε
= α + α
+ α
+ γ
+ γ
+ δ
+ ε
= α + α
+ α
+ γ
+ γ
+ δ
+ ε
= α + α
+ α
+ γ
+ γ
+ δ
+ ε
0
1
2
1
H :
0
γ = γ = δ =
γ = γ = δ =
γ = γ = δ =
γ = γ = δ =
,
A
1
2
1
H : przynajmniej jeden z
,
,
0
γ γ δ ≠
γ γ δ ≠
γ γ δ ≠
γ γ δ ≠
Makroekonomiczna funkcja konsumpcji dla Wlk. Brytanii
2
t
t
t
t
u
974,6
0,035Y
0,0000002878Y
reszta
= −
+
−
+
= −
+
−
+
= −
+
−
+
= −
+
−
+
2
2
0,05
0
TR
36 0,0099152
0,377
3,84
(1)
H
=
×
=
<
= χ
=
×
=
<
= χ
=
×
=
<
= χ
=
×
=
<
= χ
⇒
⇒
⇒
⇒

9
Posta
ć
funkcyjna (Ramsey)
Niech
t
0
1
t1
K
tK
t
Y
X
X
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
K
K
K
K
. Wówczas
2
t
0
1
t1
K
tK
1
t
t
ˆ
Y
X
X
Y
= α + α
+
+ α
+ γ
+ ε
= α + α
+
+ α
+ γ
+ ε
= α + α
+
+ α
+ γ
+ ε
= α + α
+
+ α
+ γ
+ ε
K
K
K
K
0
1
H :
0
γ =
γ =
γ =
γ =
,
A
1
H :
0
γ ≠
γ ≠
γ ≠
γ ≠
Makroekonomiczna funkcja konsumpcji dla Wlk. Brytanii
2
t
t
t
t
ˆ
C
6017,0
0,83254Y
0,0000004582C
reszta
=
+
+
+
=
+
+
+
=
+
+
+
=
+
+
+
0,05
0
(0,99743
0,9974) / 1
0,00003 / 1
F
0,397
4,13
F
(1,34)
H
(1 0,99743) / 34
0,00257 / 34
−−−−
=
=
=
<
=
=
=
=
<
=
=
=
=
<
=
=
=
=
<
=
⇒
⇒
⇒
⇒
−−−−

10
Prosz
ę
przeprowadzi
ć
analogiczne obliczenia dla wcze
ś
niejszych przykładów (kształtowa-
nie si
ę
cen domów jednorodzinnych w miasteczku uniwersyteckim w San Diego, dochód i
wydatki na ochron
ę
zdrowia w USA)!
Wyszukiwarka
Podobne podstrony:
ekonomika w5
ekonomika w5
ekonometria W5
Przykładowe pytania do egzaminu W3 W5 i W7, Budownictwo PK, Ekonomika budownictwa
Ekonomia Drdrozdrowski, w5
geoeko-W5, Studia, Geologia i ekonomika złóż
EKONOMIKA MIAST I REGIONÓW W5
Spoleczno ekonomiczne uwarunkowania somatyczne stanu zdrowia ludnosci Polski
Ekonomia konspekt1
EKONOMIKA TRANSPORTU IX
Ekonomia II ZACHOWANIA PROEKOLOGICZNE
Ekonomia9
W5 Zawiesia
W5 sII PCR i sekwencjonowanie cz 2
więcej podobnych podstron