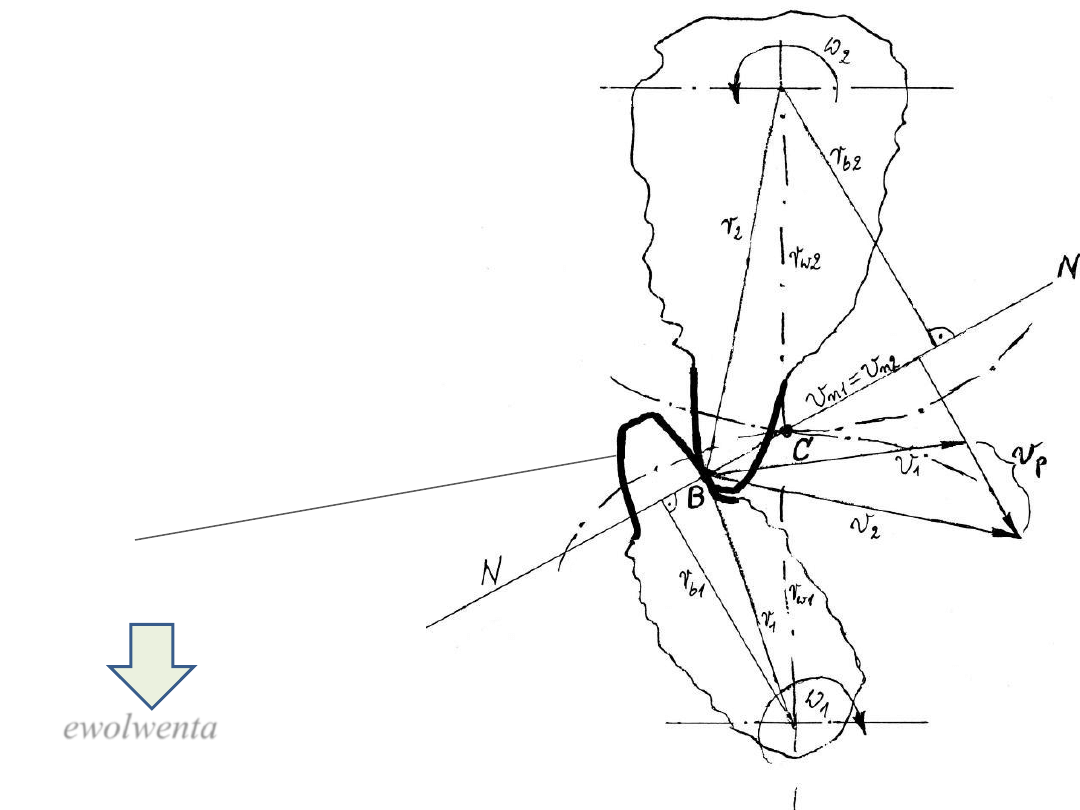
Opis geometrii zazębienia
i kół walcowych
o zębach prostych

C - punkt toczny
B - punkt przyporu
N-N - prosta przyporu
v

p

- prędkość poślizgu zębów

w p.B

zarys zęba (powierzchni
bocznej zęba)

ewolwenta

1

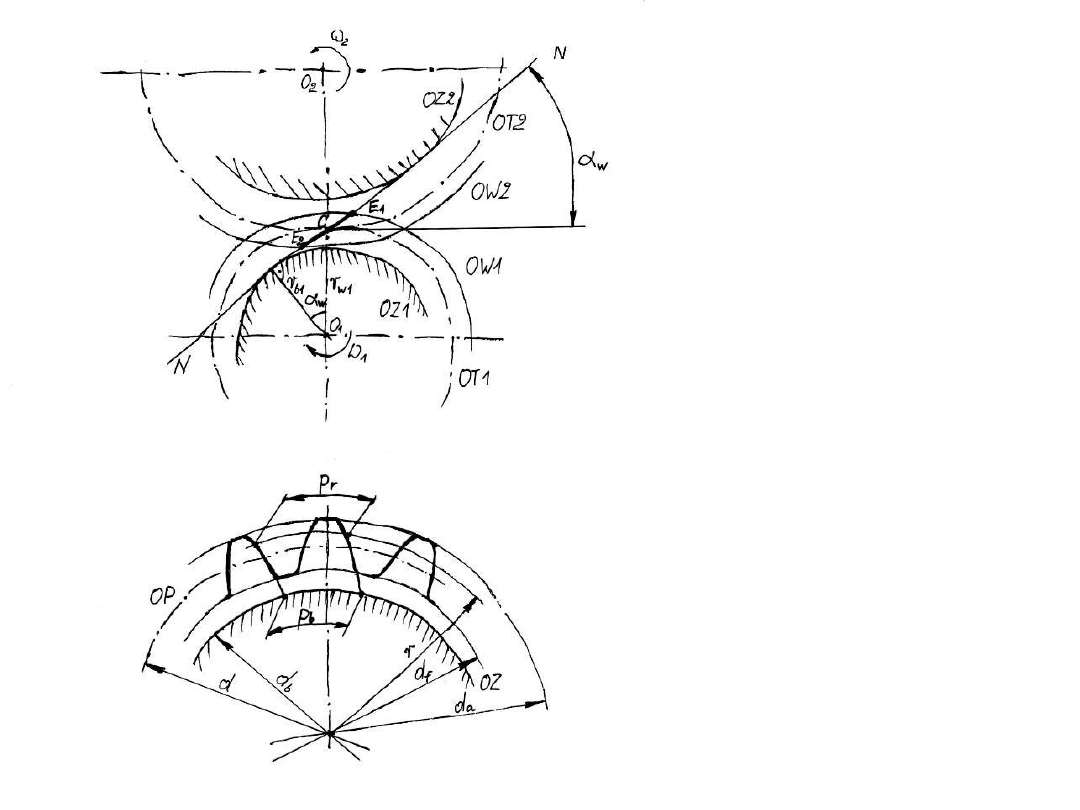
OT – okrąg toczny (d

w

)

OW – okrąg wierzchołkowy

(wierzchołków) (d

a

)

OZ – okrąg zasadniczy (d

b

)

E

2

E

1

- odcinek przyporu

α

w

– toczny kąt przyporu

OP – okrąg podziałowy (d)
p

r

- podziałka (na promieniu r)

p – podziałka nominalna

(na promieniu d/2)

2

3

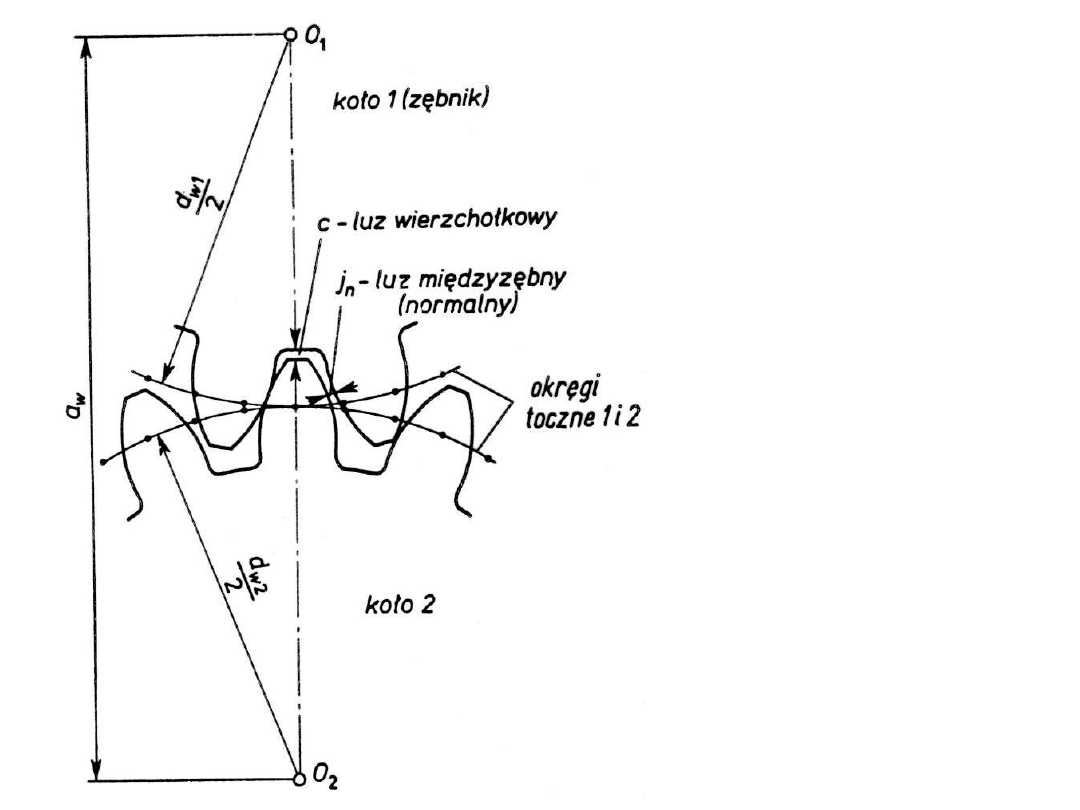
a

w

- odległość osi kół

a - nominalna (podstawowa)

odległość osi kół

a

w

≈ a

c = (0,20 - 0,25) m

m – moduł [mm]

j

n

> 0

4

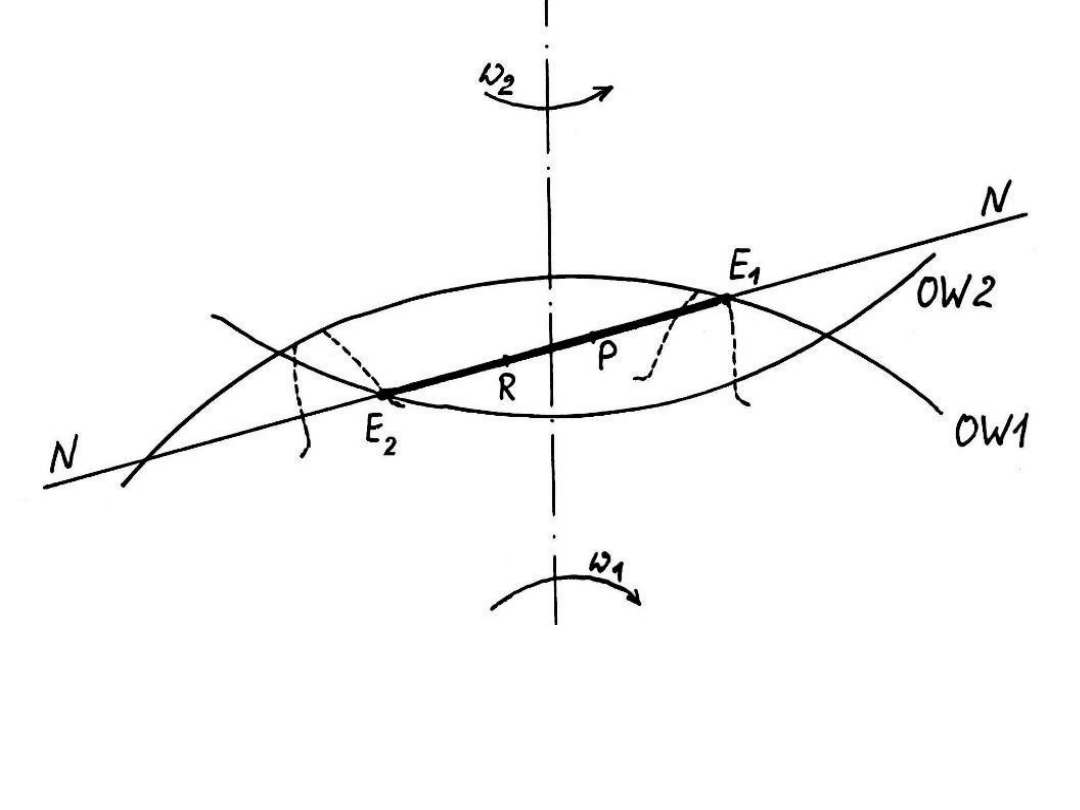
Przemieszczanie się
punktu przyporu (B)

RP – fragment odcinka przyporu, wzdłuż którego

współpracuje ze sobą najmniejsza liczba par zębów
( gdy zęby proste, zwykle – jedna para)

5

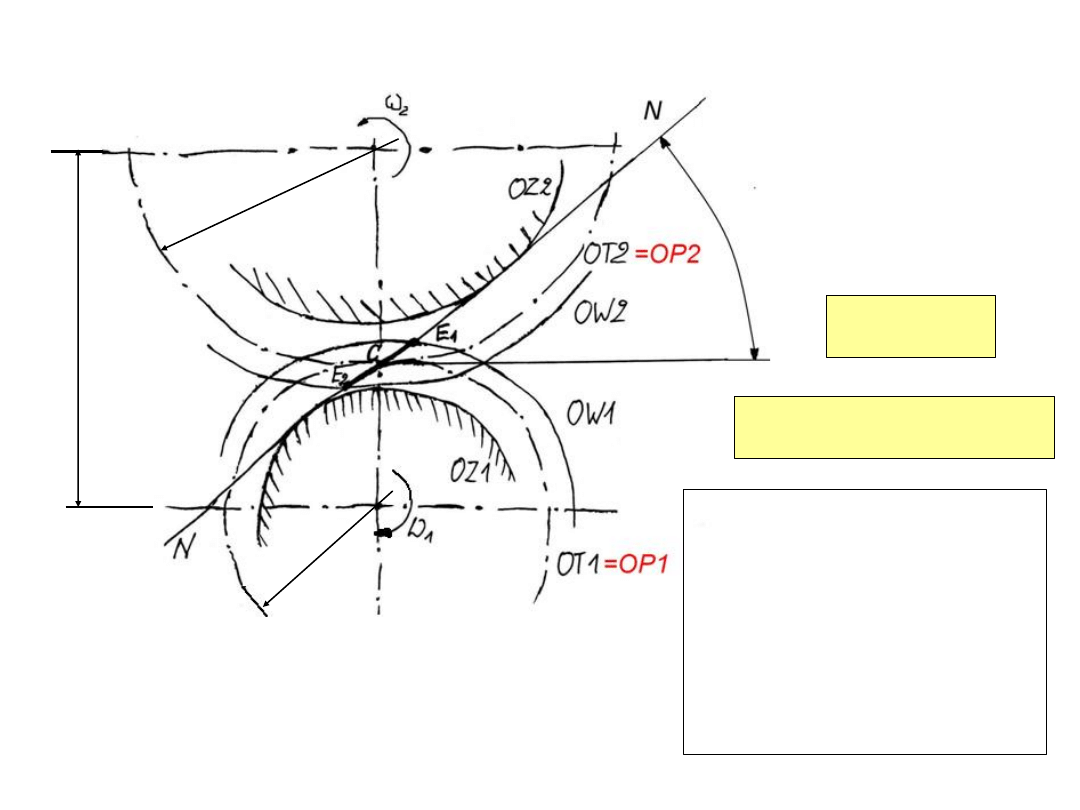
α

w

=α

a

w

= a

d

1

d

2

α

w

= α

O

1

O

2

Opis matematyczny geometrii (koła walcowe, zęby proste, x = 0)

d – średnica podziałowa
α – nominalny kąt przyporu
m – moduł [mm] (znormalizowany)
a – podstawowa odległość osi kół

d = m∙z

a = 0,5m(z

1

+ z

2

)

d

a

= d + 2h

a

d

f

= d – 2h

f

h

a

= ym

h

f

= ym + c

y – wsp.wys.zęba

6

Zwykle y = 1 - zęby normalne
Gdy : y > 1 - zęby wysokie

y < 1 - zęby niskie

y ≈ 1

Moduł znormalizowany, np. m = 1,5; 2,0; 2,5;

3,0; 3,5; 4,0;

. . .

Nominalny kąt przyporu

α = 20º

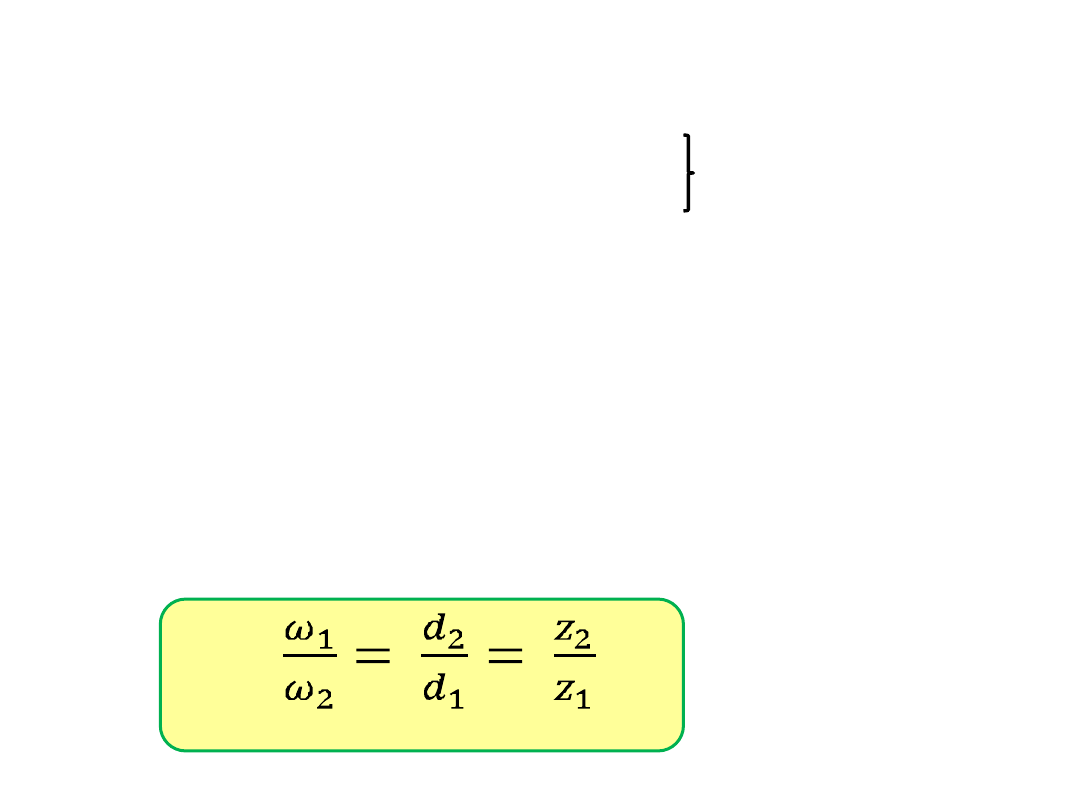
Przełożenie

i =

7

Zadanie

Przekładnia zębata walcowa o zębach prostych powinna mieć prze-
łożenie

i

= 5,2 i odległość osi

a

wym

= 176 mm. Moduł przyjęty

wstępnie

m

= 3 mm. Należy wyznaczyć wymiary poprzeczne kół

oraz odległość ich osi.

Zadanie

Dla przekładni zębatej walcowej o zębach prostych określono :

d

a1

= 66 mm,

d

a2

= 177 mm,

d

b1

= 56,4 mm,

d

b2

= 160,7 mm,

a =

115,5 mm. Należy wyznaczyć graficznie długość odcinka

przyporu.

8

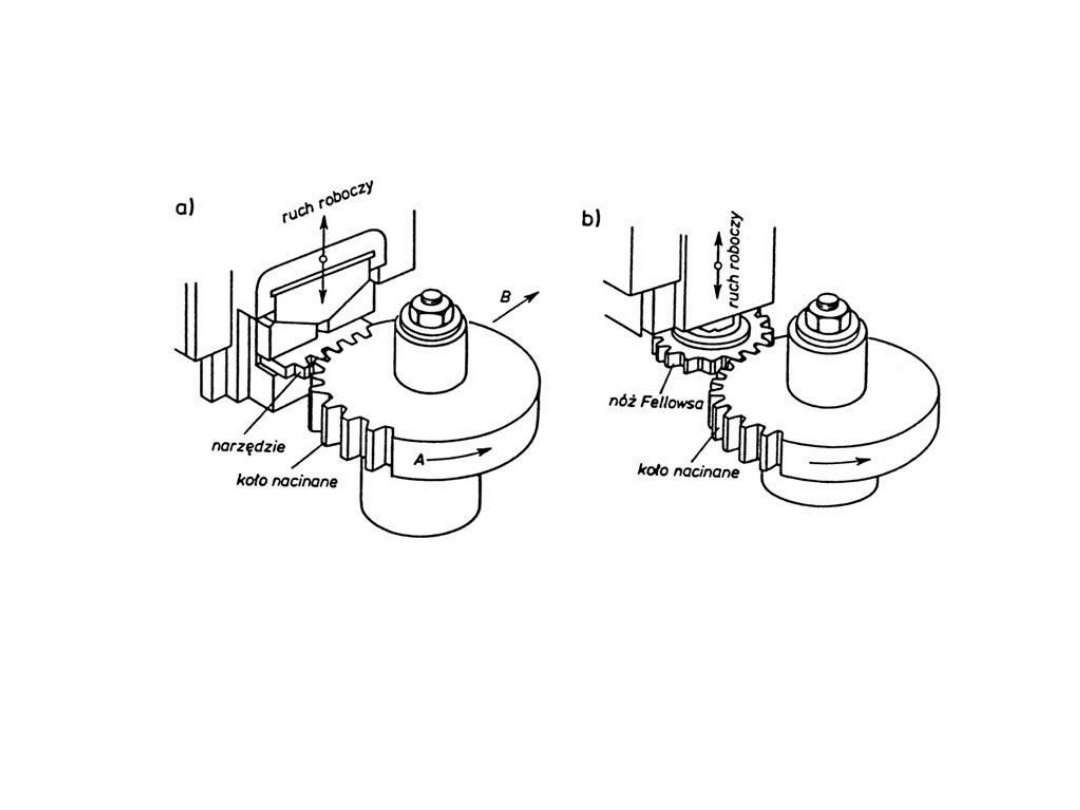
Wykonywanie zębów

Np.

a) metoda Maaga, b) metoda Fellowsa

Inne metody

9

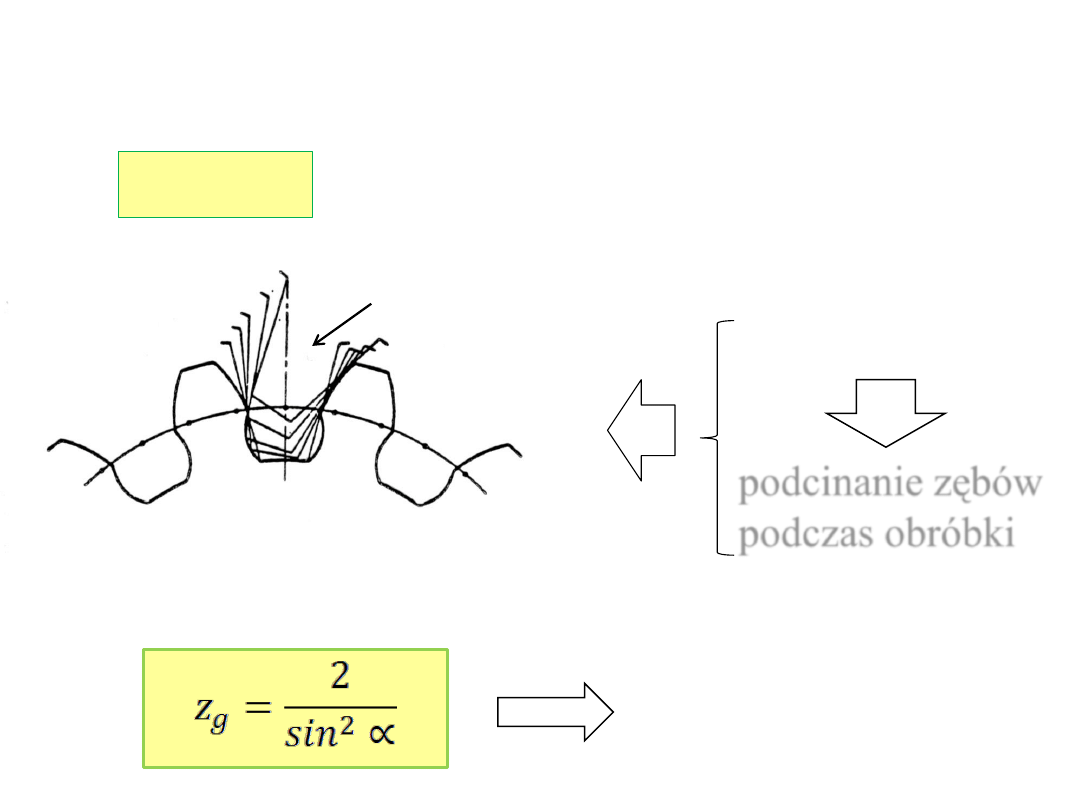
Ze względów technologicznych liczba zębów jest ograni-
czona od dołu. Powinien być spełniony warunek :

z ≥ z

g

Jeśli

z < z

g

podcinanie zębów
podczas obróbki

Dla kół walcowych o zębach prostych normalnych

z

g

=

17

ząb narzędzia

10

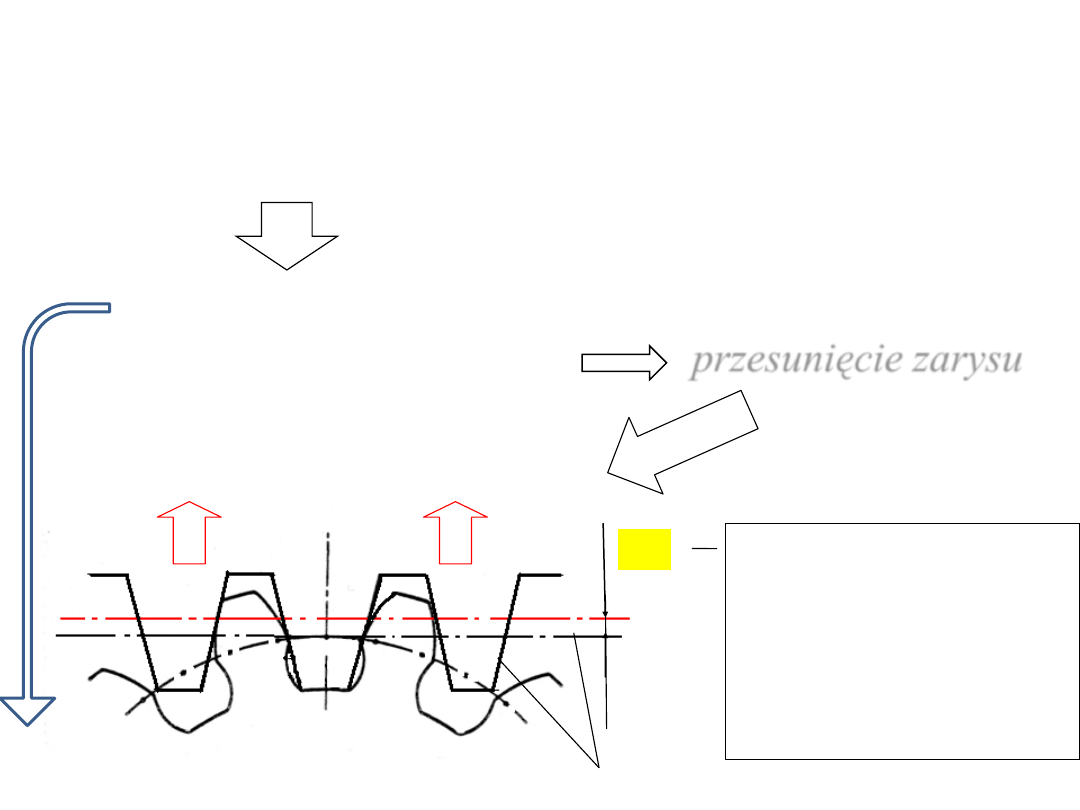
W celu uniknięcia podcinania zębów, gdy

z

<

z

g

• zęby skośne lub
• zabieg technologiczny

przesunięcie zarysu

Wykonywanie zębów z przesunięciem zarysu

x

∙m

narzędzie

odsunięcie narzędzia

x – wsp. przesunięcia

zarysu

Zwykle x < 0,5

wykonywane koło

nominalne położenie narzędzia

11

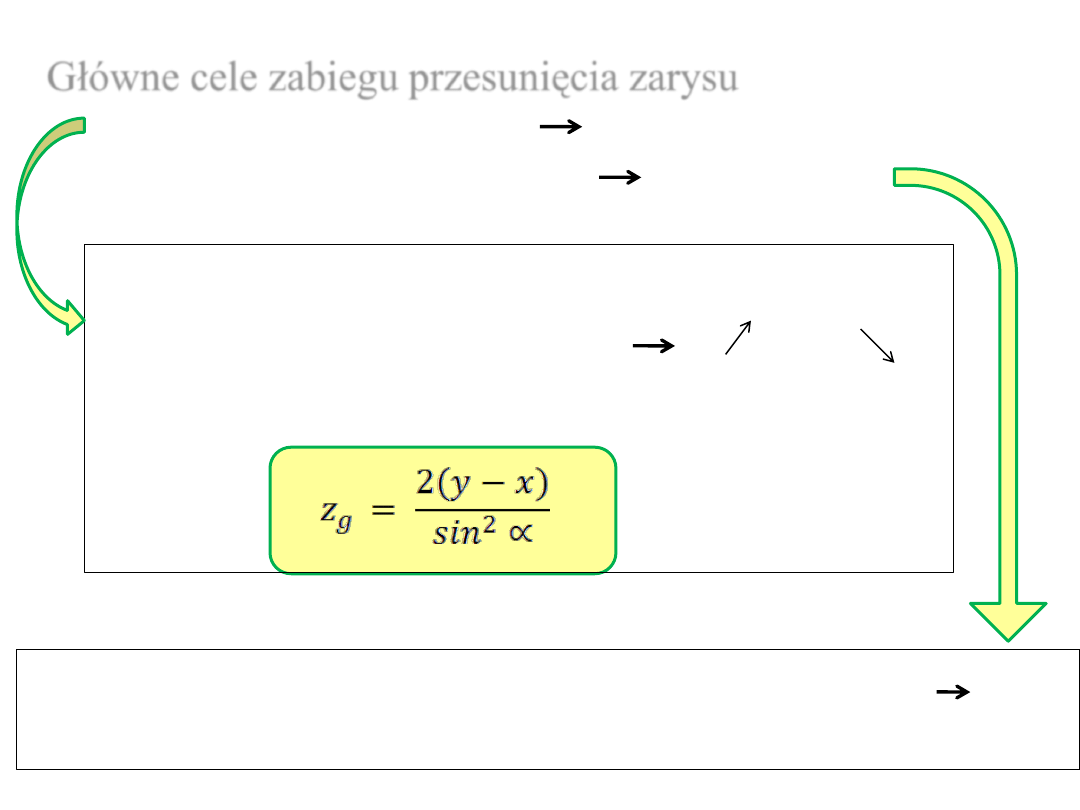
Główne cele zabiegu

przesunięcia zarysu

:

• niepodcinanie zębów ( koło)
• zmiana odległości osi kół ( przekładnia)

możliwość spełnienia warunku

z

>

z

g

przy małej liczbie zębów, gdyż

x ,

to

z

g

,

np. w metodzie Maaga

możliwość dopasowywania odległości osi do potrzeb

a

wym

(w niedużym zakresie)

12

Zabieg

przesunięcia zarysu

zmiana kształtu

i wymiarów zębów

Wymiary koła

• d = d
• d

a

= d + 2h

a

h

a

= (y +

x – k

)m

• d

f

= d – 2h

f

h

f

= (y -

x

)m + c

z projektu zabiegu
przesunięcia zarysu

założone

z obliczeń
wytrzymałościowych

k – współczynnik skrócenia

głowy zęba

13

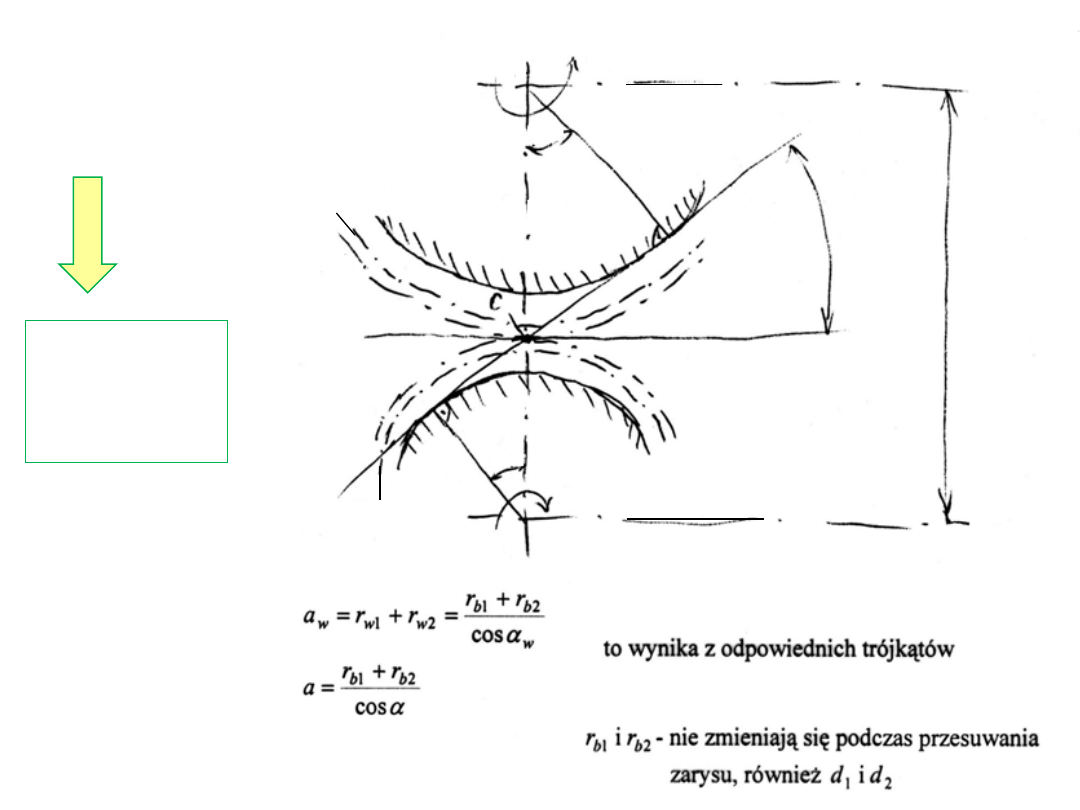
Projekt zabiegu

przesunięcia

zarysu

a

w

α

w

α

w

α

w

OZ2

OP2

OT2

r

b2

r

w2

ω

2

ω

1

O

2

O

1

OT1

OP1

OZ1

r

w1

r

b1

(śr. podział.)

x

1

= ?

x

2

= ?

(k = ?)

14

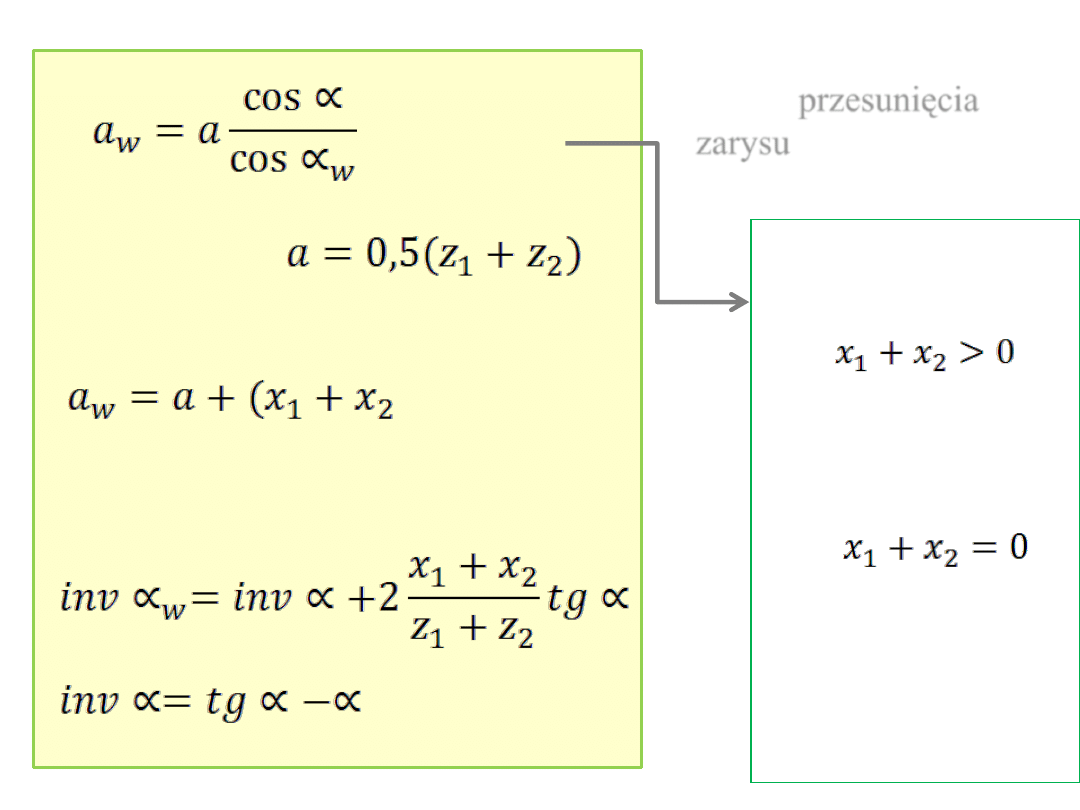
– k)m

Wyrażenia określające
zabieg

przesunięcia

zarysu

Jeśli

a

w

>

a,

to

α

w

>

α

Jeśli

a

w

=

a,

to

α

w

=

α

(p. rysunek)

15

Zadanie

Jednostopniowa przekładnia zębata jest utworzona z dwóch kół walco-
wych o zębach prostych i danych :

z

1

= 12,

z

2

= 30, m = 3 mm, y = 1,

α

= 20º. Odległość osi powinna wynosić

a

wym

= 63 mm. Wymaga się

również, by zęby były niepodcięte. Należy wyznaczyć potrzebne warto-
ści współczynników

x

1

i

x

2

przesunięcia zarysu zęba.

Uwaga : Z warunków ograniczających technologicznych ze względu na
niezaostrzenie wierzchołków zębów wynika, że powinno być x

1

≤ 0,4;

x

2

≤ 0,6.

16

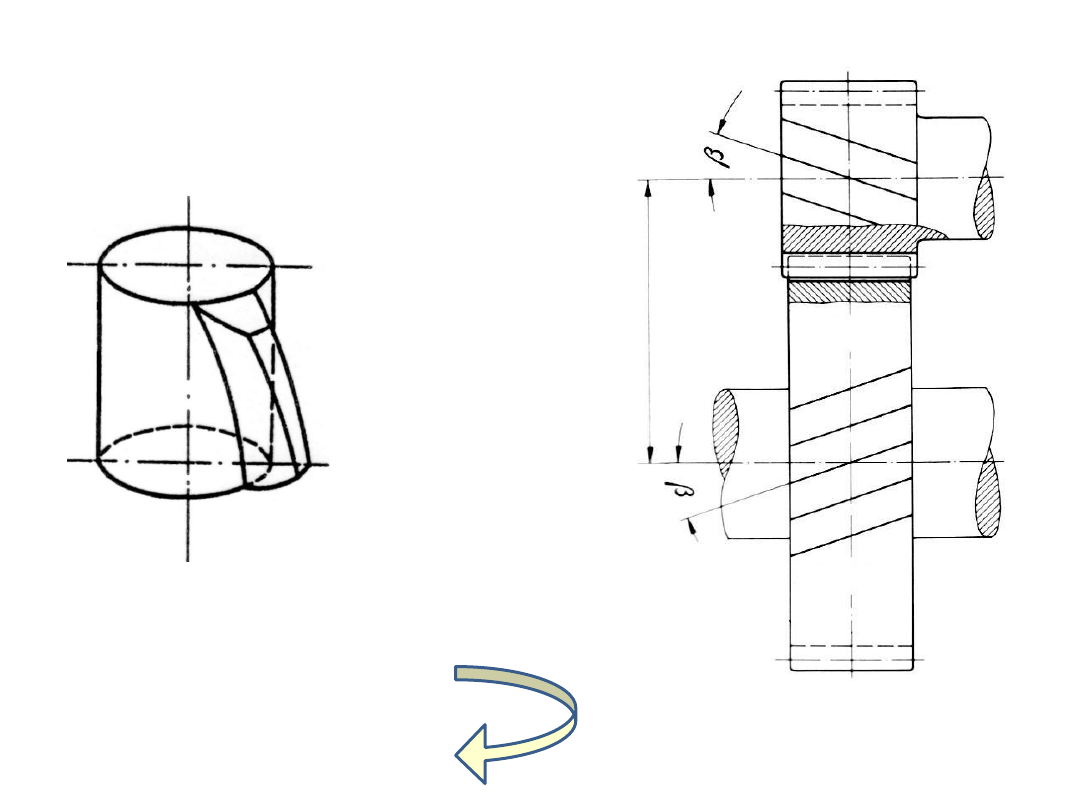
Opis geometrii zazębienia
i kół walcowych
o zębach skośnych

a

w

Zwykle

x

1

= 0 i x

2

= 0

a

w

= a

β – kąt pochylenia linii zęba

1

2

17

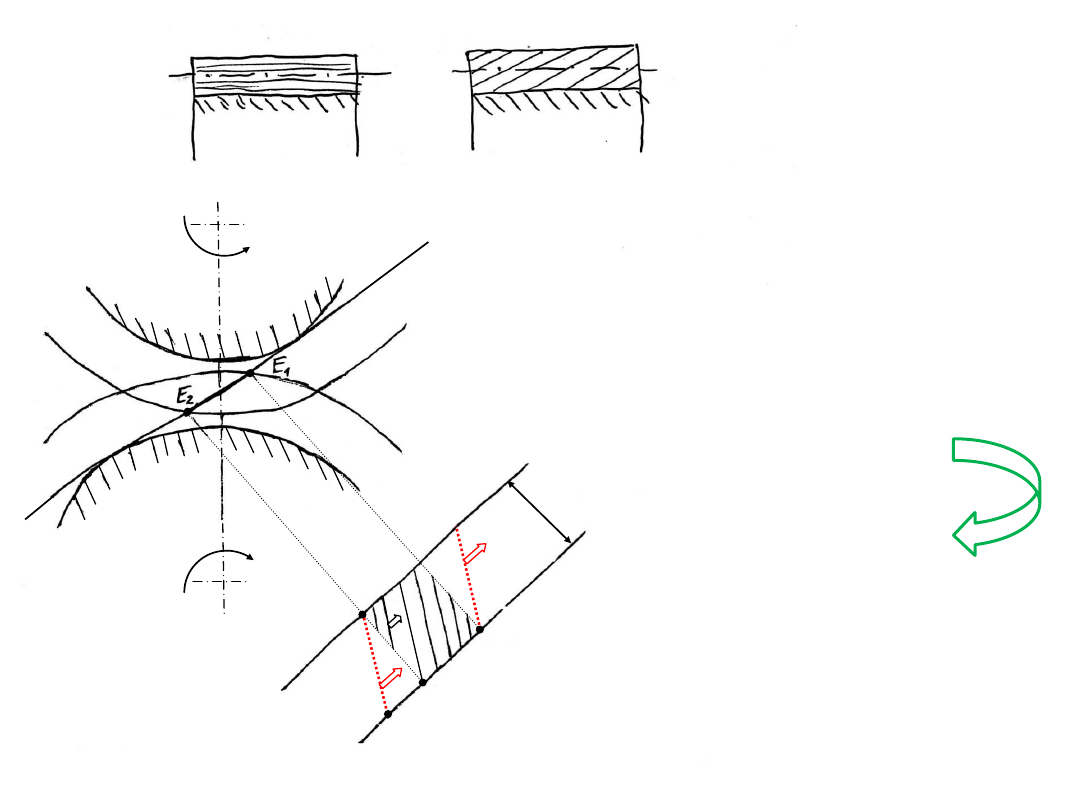
E

1

E

2

E

3

b

B

A

ω

2

ω

1

OZ1

OZ2

OW2

OW1

N

N

b – szerokość koła

E

3

– początek współpracy

E

1

- koniec współpracy

Współpraca kół
z zębami skośnymi

Dłuższy przypór

Większa liczba par
zębów w przyporze

zęby proste

zęby skośne

Linie styku zębów

18

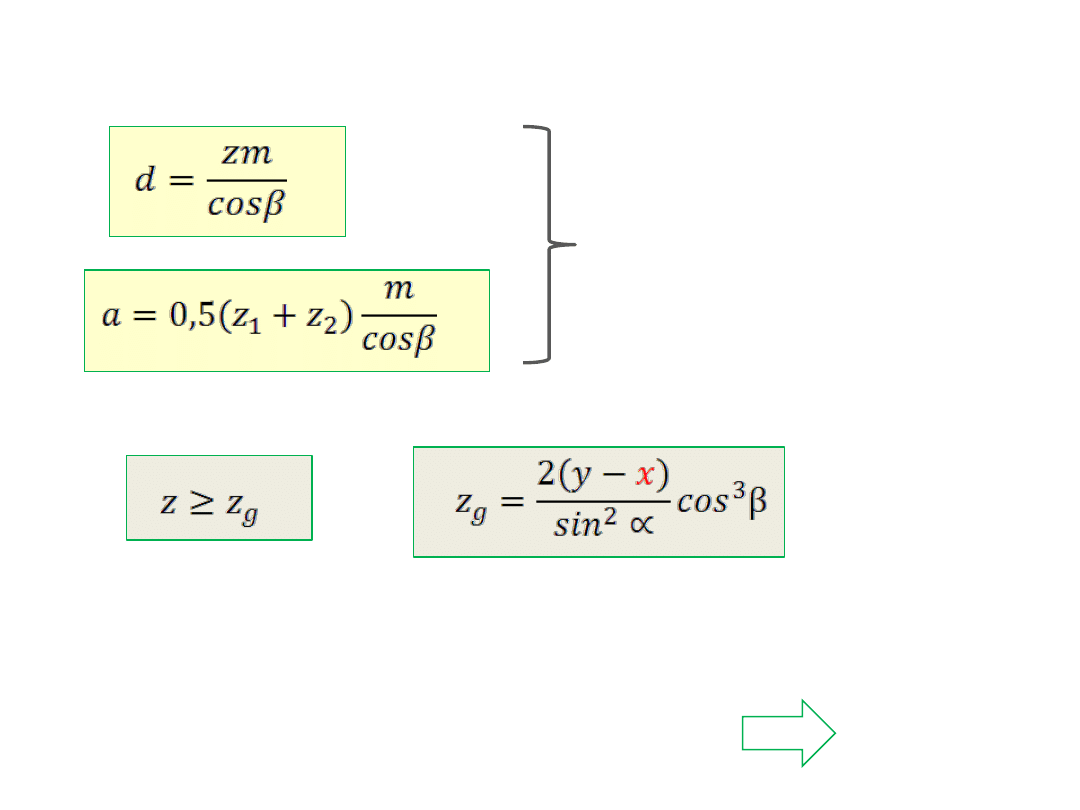
Opis matematyczny geometrii (koła walcowe, zęby skośne, x = 0)

Inne wielkości (

d

a

,d

f

,i,…) – jak

w kołach z zębami prostymi)

Np. dla β = 30º

z

g

≈ 11

• możliwość uniknięcia podcinania zębów
• dopasowywanie odległości osi do potrzeb

β

19

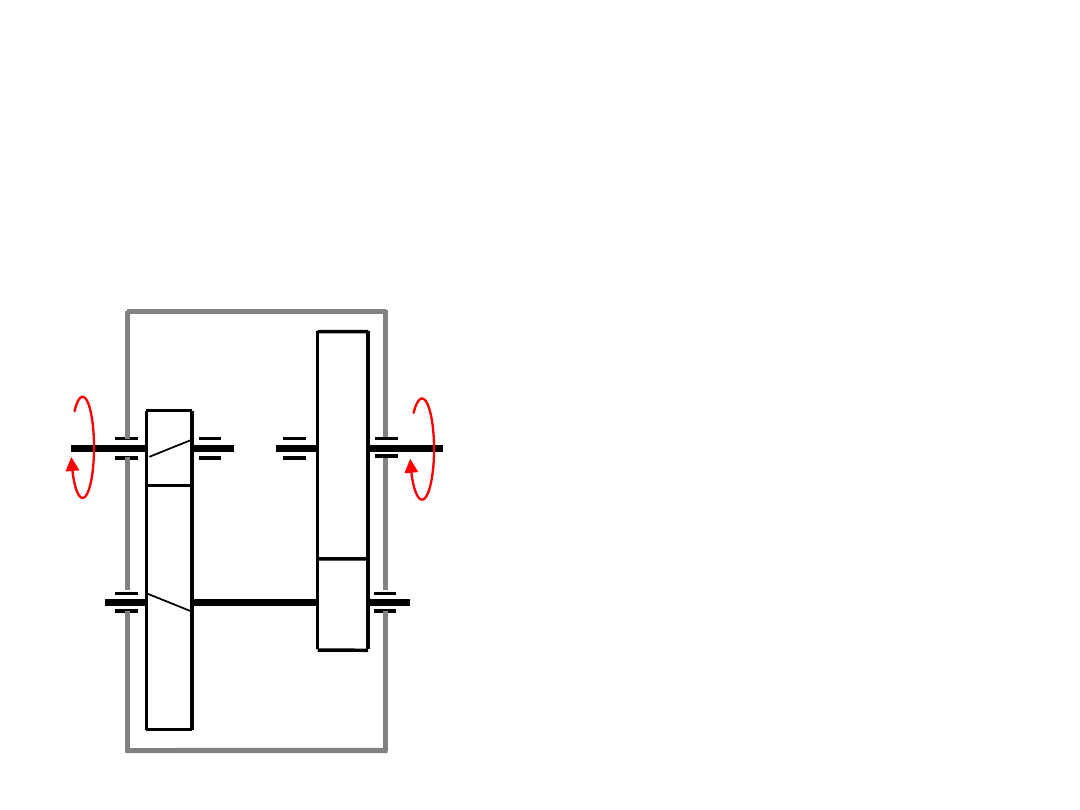
Zadanie

W dwustopniowej przekładni zębatej z kolami o zębach normalnych, wy-
konanymi bez przesunięcia zarysu : przełożenie i = 6,
Koło 2 jest osadzone na wspólnym wale z kołem 3, zazębionym z kołem
4. Koła 1 i 2 mają zęby skośne o module = 3,5 mm, a koła 3 i 4
mają zęby proste o module = 6 mm. Należy wyznaczyć:

z

1

= 20, z

2

=68.

z

1

z

2

z

3

z

4

ω

1

ω

4

m

12

m

34

a) najmniejsze liczby zębów kół 3 i 4,

zapewniające dokładną wartość
przełożenia oraz niepodcinanie bo-
ków zębów,

b) taki kąt pochylenia linii zębów kół

1 i 2, by odległości osi kół obydwu
stopni przekładni były jednakowe.

20

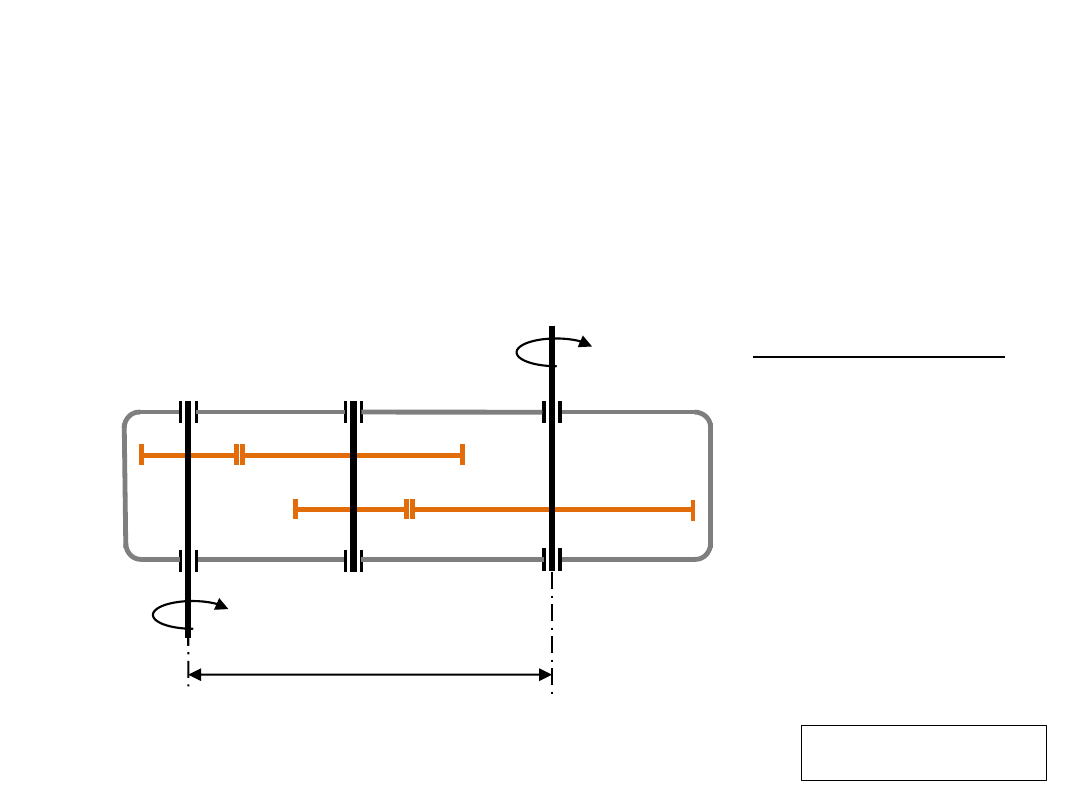
ω

1

ω

4

z

1

z

3

z

2

z

4

a

w

Zadanie

W dwustopniowym reduktorze są zastosowane koła walcowe wykonane
bez przesunięcia zarysu zębów. Koła 1 i 2 mają zęby skośne, a koła 3 i 4
-zęby proste. Odległość między osiami wałów - czynnego (wejścio-
wego) i biernego (wyjściowego) przekładni powinna wynosić 340 mm.
Należy wyznaczyć kąt β pochylenia zębów w kołach 1 i 2.

Dodatkowe dane :

z

1

=31, z

2

=96,

z

3

= 25, z

4

=44,

m

12

= 2,5 mm,

m

34

=5mm.

Odp.: 18,600 º

21

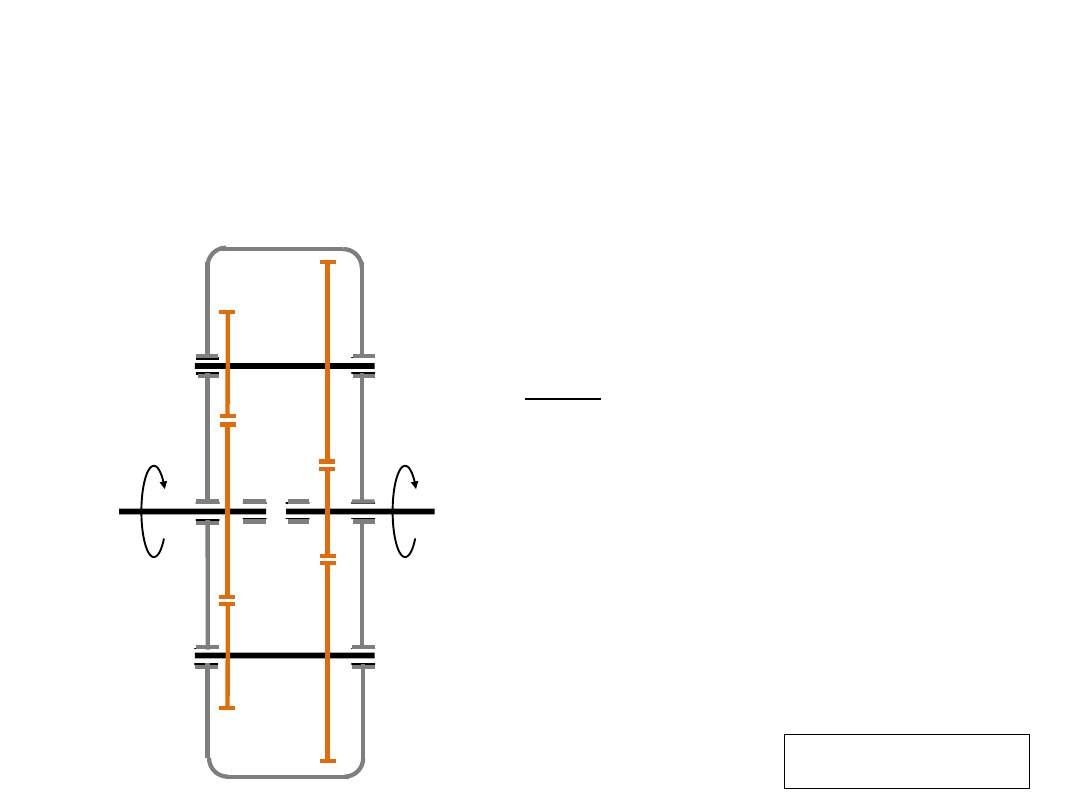
z

1

z

2

z

2

z

3

z

3

z

4

ω

1

ω

4

Zadanie

W dwustopniowej i dwudrożnej przekładni, pokazanej na rysunku, znane
są : liczby zębów poszczególnych kół, moduły w pierwszym
i w drugim stopniu przekładni oraz kąt β

12

pochylenia zębów kół 1 i 2.

Należy wyznaczyć kąt β

34

pochylenia zębów kół drugiego stopnia,

zapewniający prawidłową ich współ-
pracę.

m

12

i m

34

Dane :

z

1

= 18, z

2

= 61,

z

3

= 21, z

4

= 33,

m

12

= 3 mm, m

34

= 4 mm,

β

12

= 15º.

Odp.: 28,319º

22

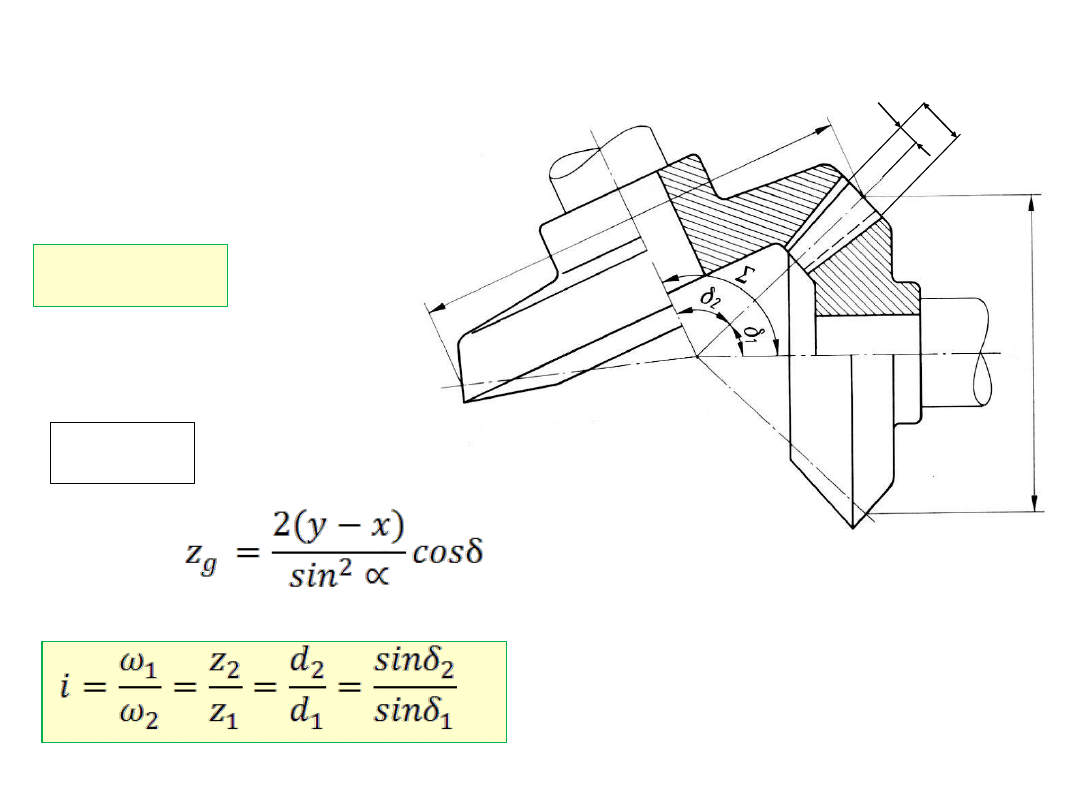
Opis geometrii zazębienia
i kół stożkowych
o zębach prostych

d

2

d

1

z

1

z

2

h

h

a

d = z∙m

h

a

= ym

z ≥ z

g

Zalety zębów skośnych
i zębów łukowych

23

24