Probabilistyczne podstawy wnioskowania statystycznego

Poj

ę

cia podstawowe:

• Definicje prawdopodobie

ń

stwa: klasyczna vs. cz

ę

sto

ś

ciowa

• Zmienna losowa

• Funkcja prawdopodobie

ń

stwa/g

ę

sto

ść

prawdopodobie

ń

stwa

• Rozkład prawdopodobie

ń

stwa

• Dystrybuanta

Rozkłady prawdopodobie

ń

stwa zmiennych skokowych i ci

ą

głych:

• Zero-jedynkowy

• Rozkład dwumianowy (Bernoulliego)

• Rozkład Normalny

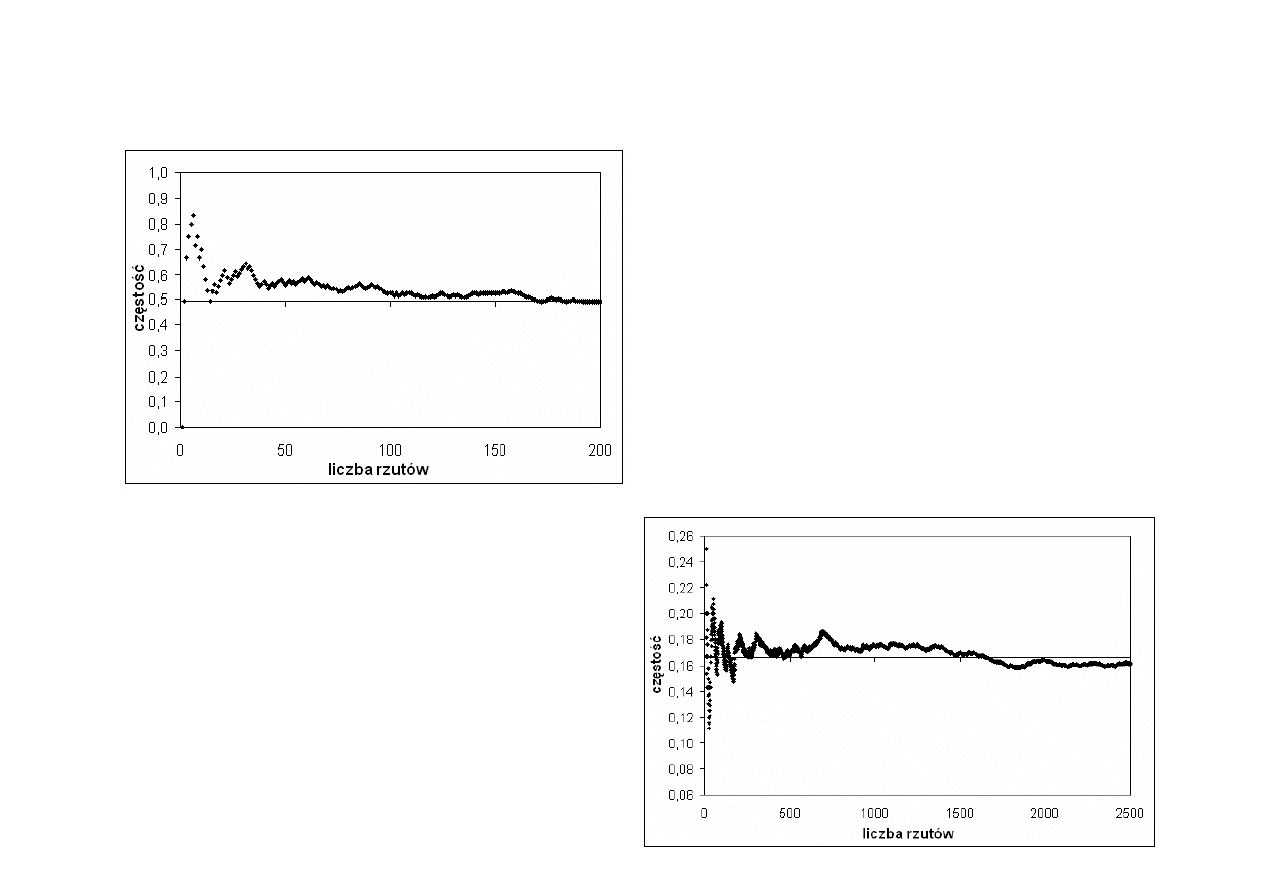
Eksperyment 1: Rzut monet

ą

Cz

ę

sto

ś

ciowa definicja prawdopodobie

ń

stwa

Eksperyment 2: Rzut kostk

ą

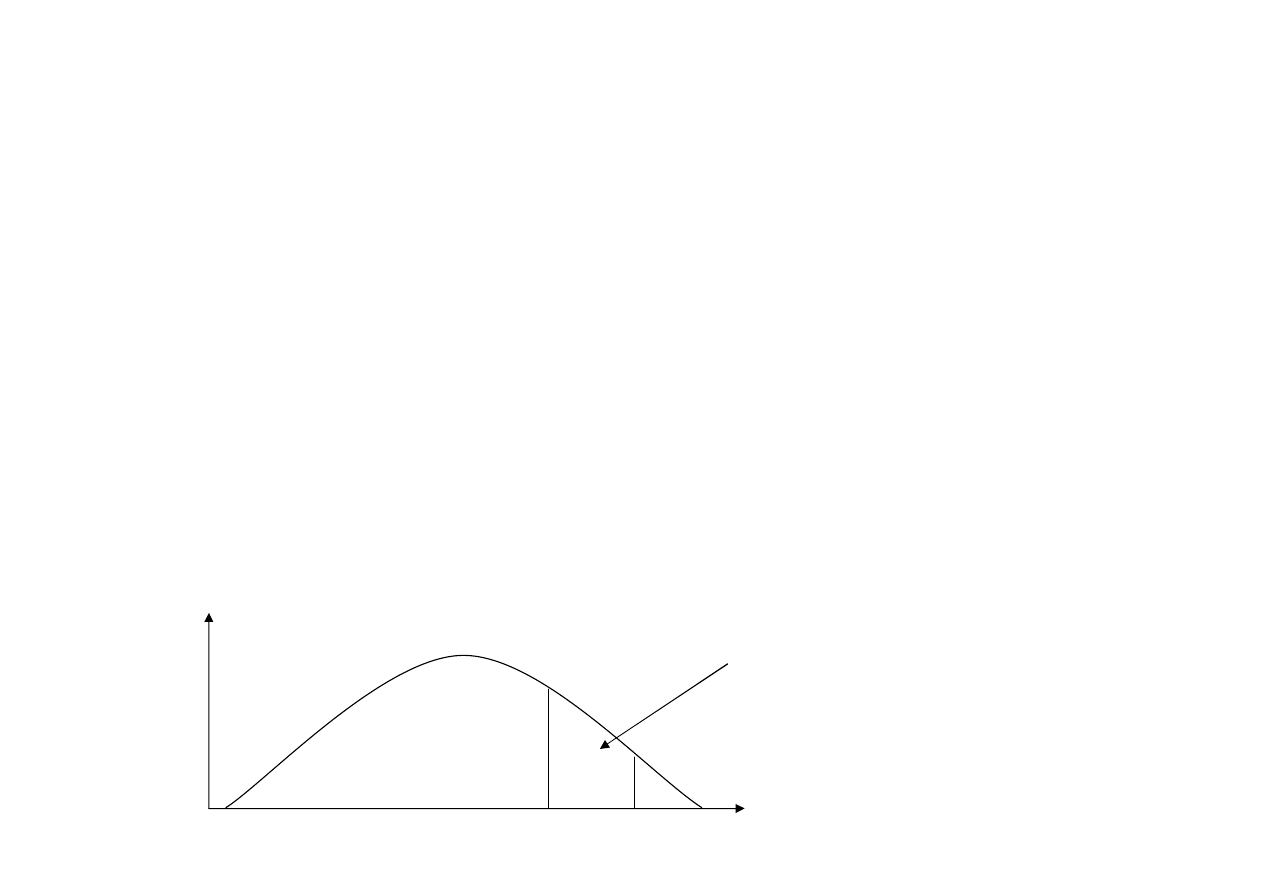
Dla zmiennej ci

ą

głej (funkcja g

ę

sto

ś

ci prawdopodobie

ń

stwa):

Funkcja prawdopodobie

ń

stwa/g

ę

sto

ś

ci:

Dla zmiennej skokowej

i

i

p

x

X

P

=

=

)

(

∫

∫

∞

+

∞

−

=

+∞

≤

<

∞

−

=

<

≤

<

=

≥

1

b

a

dowolnych

dla

)

(

)

(

0

)

(

)

X

P(

f(x)dx

b

X

a

P

dx

x

f

x

f

b

a

f(x)

x

a

b

∫

=

≤

<

b

a

dx

x

f

b

X

a

P

)

(

)

(

k

n

k

p

p

k

n

k

X

P

−

−

∗













=

=

)

1

(

)

(

)!

(

!

!

k

n

k

n

k

n

−

=









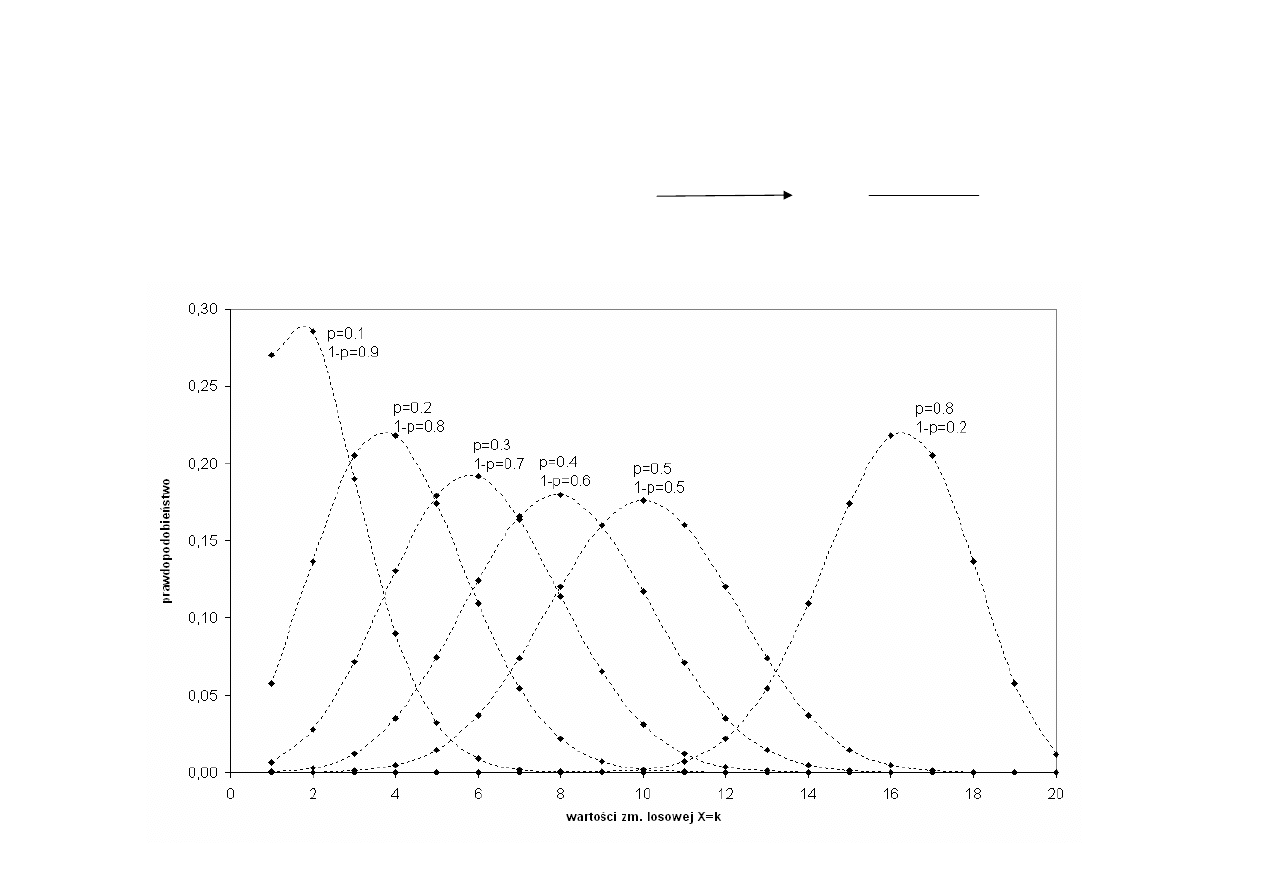
Rozkład dwumianowy

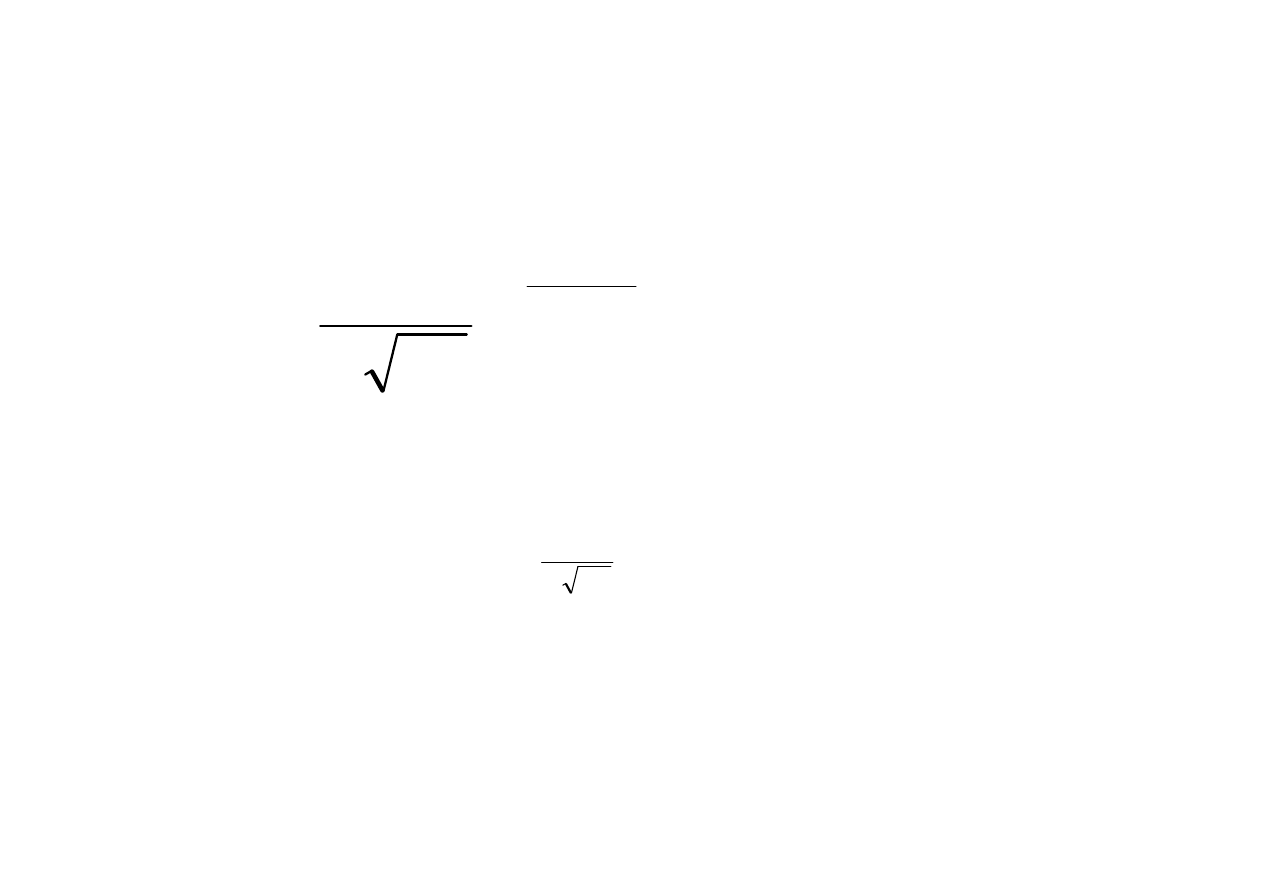
2

2

2

)

(

2

1

)

(

σ

π

σ

m

x

e

x

f

−

−

=

Rozkład normalny (krzywa Gaussa)

Zmienna losowa X ma rozkład normalny o parametrach m oraz

σ

co zapisujemy

w skrócie X: N(m,

σ

) je

ś

li funkcja g

ę

sto

ś

ci ma nast

ę

puj

ą

c

ą

posta

ć

:

Własno

ś

ci krzywej rozkładu normalnego:

1) Symetria wzg.

ś

redniej m

2) Maksimum osi

ą

ga w punkcie

3) Punkty przegi

ę

cia ramion rozkładu to: m-

σ

oraz m+

σ

π

σ

2

1

Własno

ś

ci

ą

rozkładu normalnego jest addytywno

ść

!!!

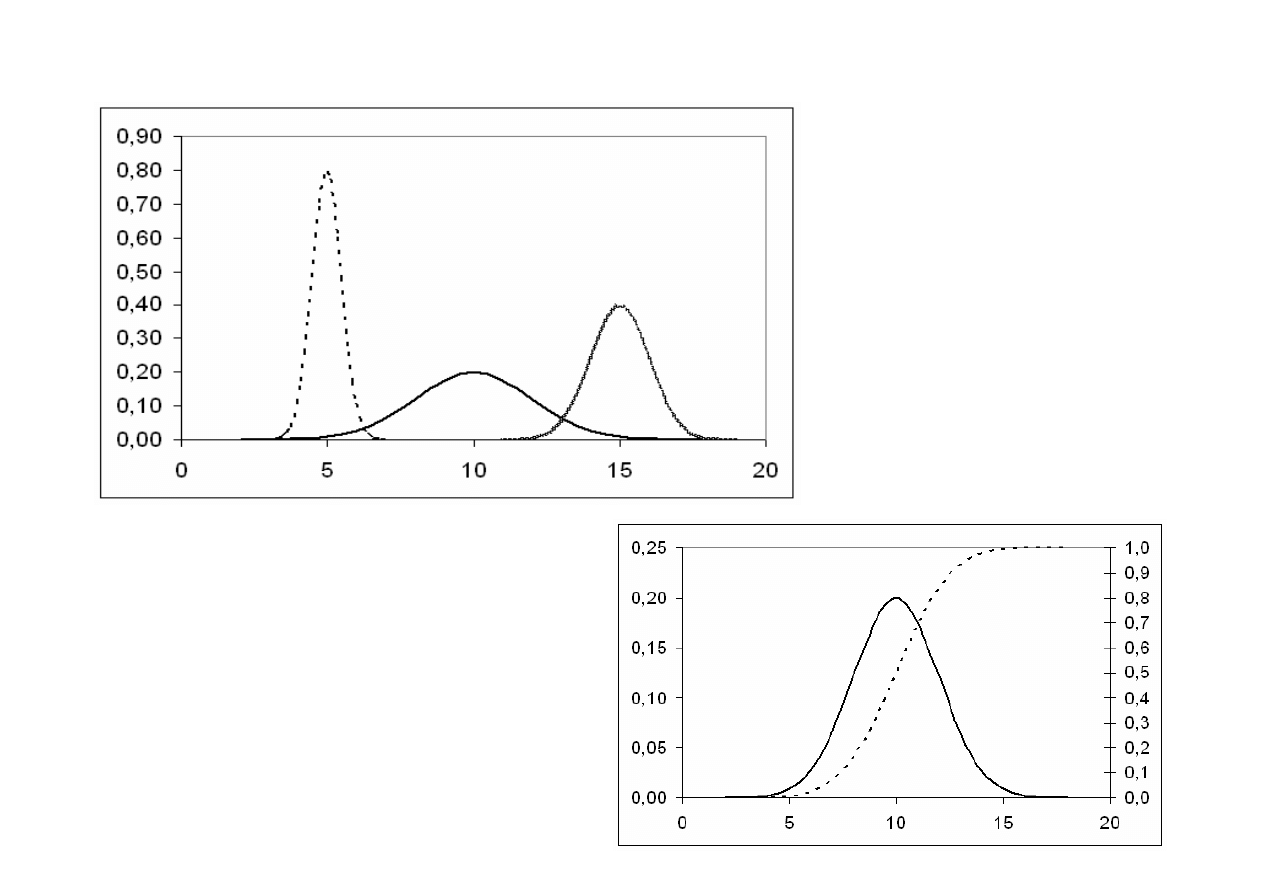
Funkcja g

ę

sto

ś

ci oraz dystrybuanta rozkładu normalnego

N(10,2)

N(5;0,5)

N(5;2)

N(15;1)

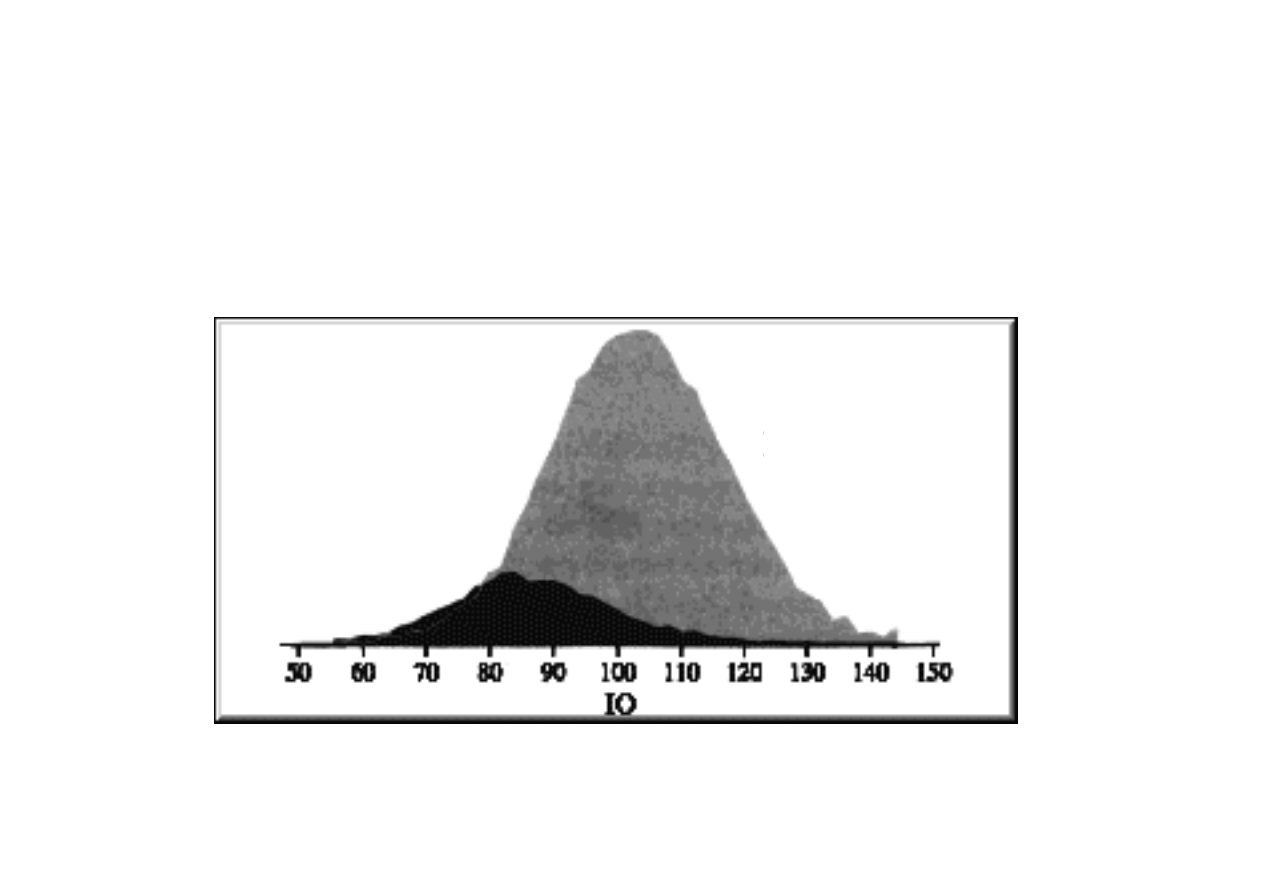
Black
distribution

White
distribution

Kontrowersyjne badanie inteligencji w populacji białych i
czarnych w USA

Intelligence and Class Structure in American Life (1994).

Co mo

ż

na powiedzie

ć

o rozkładzie inteligencji w populacji białych i czarnych na

podstawie poni

ż

szych wykresów?

Dlaczego wyst

ę

puje tak silna dysproporcja w rozkładzie inteligencji w tych

dwóch sub-populacjach?

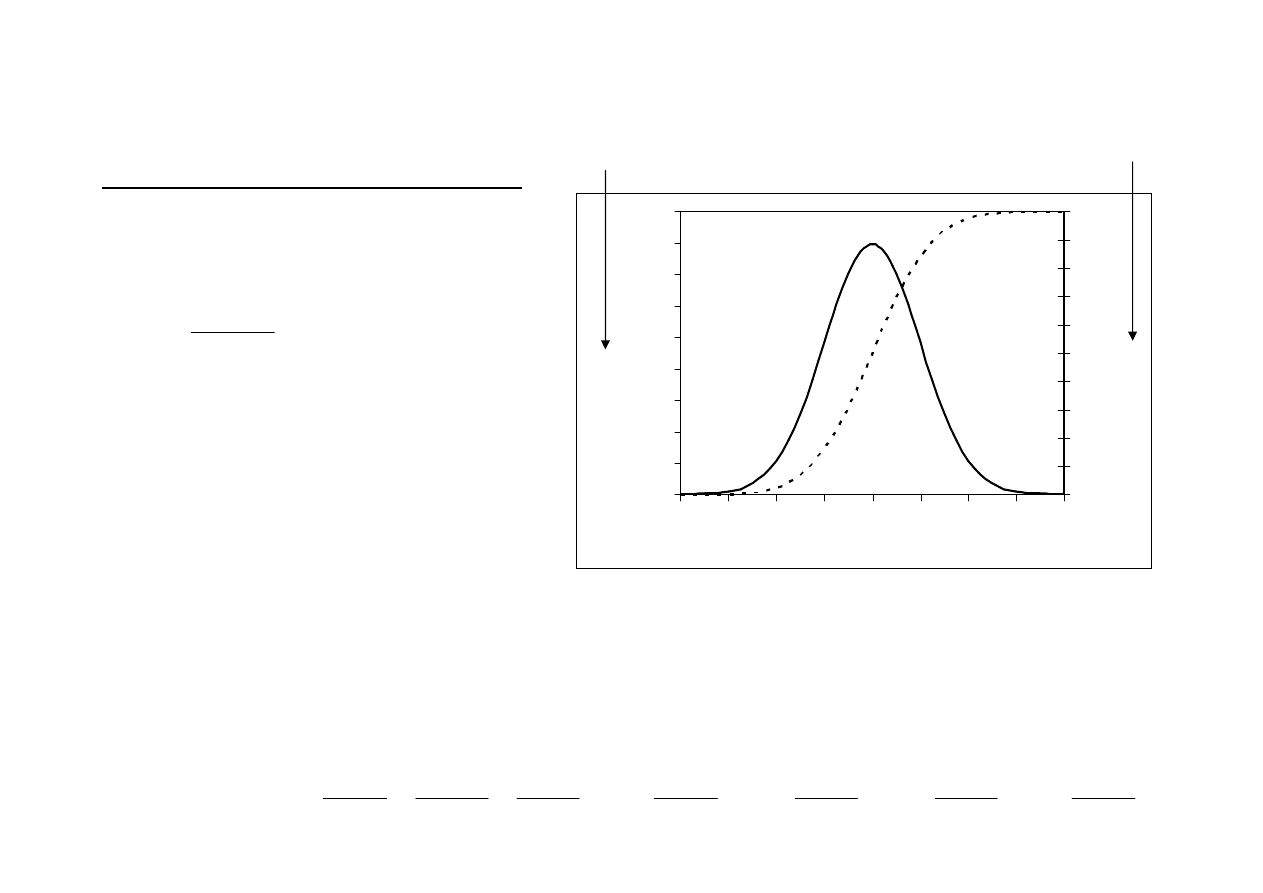
W jaki sposób wyznaczamy prawdopodobie

ń

stwo w

rozkładzie normalnym?

σ

m

X

U

−

=

)

(

1

)

(

oraz

)

(

)

(

u

u

u

u

−

Φ

−

=

Φ

−

=

ϕ

ϕ

Standaryzowany rozkład normalny:

Przekształcenie oryginalnych warto

ś

ci

zmiennej za pomoc

ą

reguły:

Nazywamy standaryzacj

ą

. Rozkład taki

ma parametry: N(1,0). Warto

ś

ci

dystrybuanty oraz funkcji g

ę

sto

ś

ci s

ą

stablicowane wiec nie musimy liczy

ć

całek!

0,00

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

-4

-3

-2

-1

0

1

2

3

4

u

φ

(u)

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Φ

(u)

F-cja
g

ę

sto

ś

ci

Dystrybuanta

Poniewa

ż

f-cja g

ę

sto

ś

ci jest symetryczna wzgl

ę

dem u=0 w tablicach mamy podane

warto

ś

ci obu funkcji tylko dla dodatnich u. Korzystamy zatem z własno

ś

ci:













−

Φ

−













−

Φ

=













−

≤

<

−

=













−

≤

−

<

−

=

≤

<

σ

σ

σ

σ

σ

σ

σ

m

a

m

b

m

b

U

m

a

P

m

b

m

X

m

a

P

b

X

a

P

)

(

Prawdopodobie

ń

stwo okre

ś

lamy:

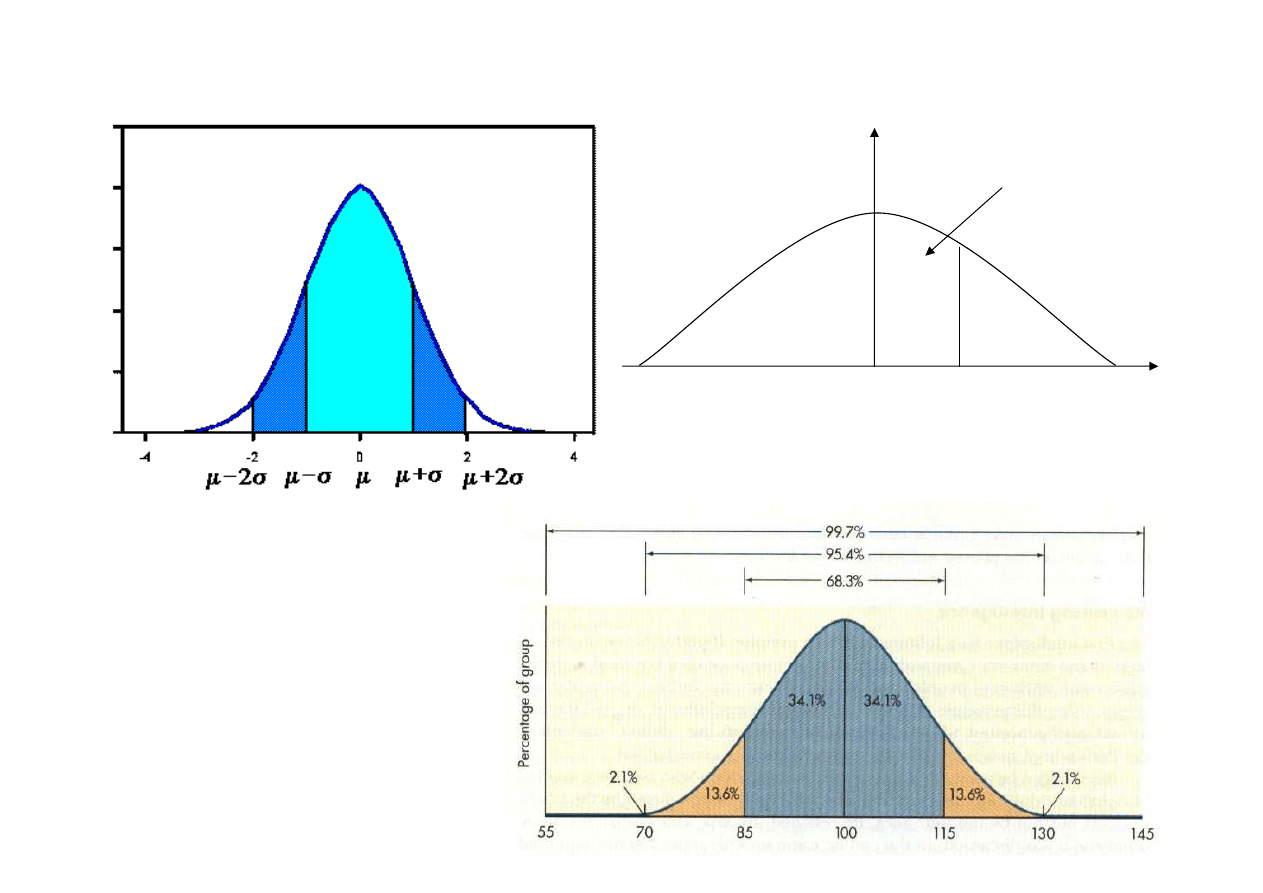
Inteligencja i reguła trzech sigm

0

u

)

(u

Φ