05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

1

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

K1B.1 Wiadomości ogólne

Kolokwium odbyło się w dniu 16 listopada 2005 r. Obejmowało ono następujący materiał z ćwiczeń

audytoryjnych:

1. analizę kinematyczną płaskich układów tarcz sztywnych,

2. analizę kinematyczną i statyczną kratownic płaskich,

3. wyznaczanie reakcji oraz wykresów sił przekrojowych w belkach,

4. wyznaczanie reakcji oraz wykresów sił przekrojowych w ramach płaskich.

K1B.2 Zadanie 1

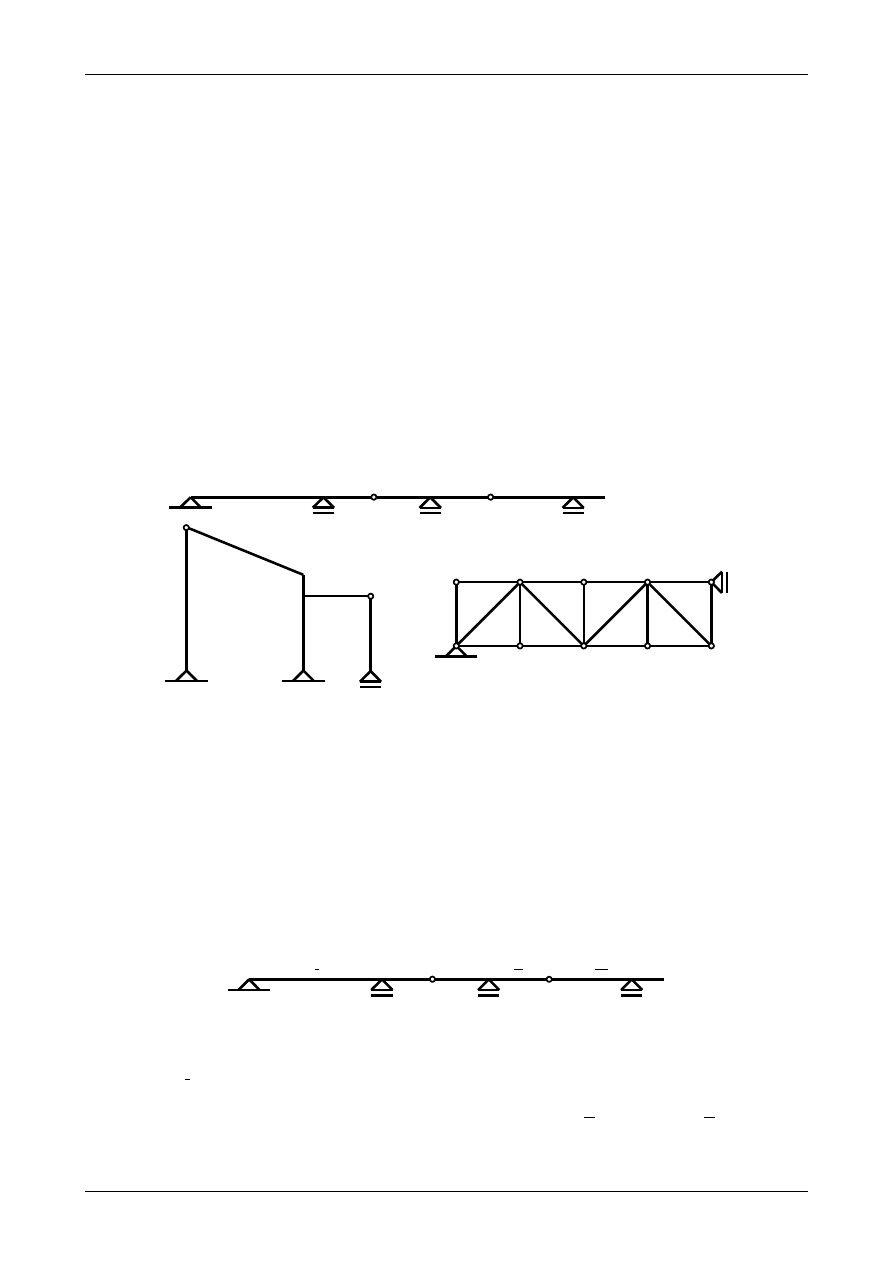
Dokonać analizy kinematycznej (sprawdzić warunek konieczny i warunki dostateczne geometrycznej

niezmienności) układów prętowych przedstawionych na rysunku K1B.1.

a)

b)

c)

Rys. K1B.1. Płaskie układy prętowe.

K1B.3 Rozwiązanie zadania 1

Rysunek K1B.2 przedstawia płaski układ prętowy z zaznaczonymi tarczami sztywnymi oraz więzami.

Jak widać składa się on z trzech tarcz sztywnych, które posiadają razem dziewięć stopni swobody. Podparte
one są za pomocą podpory przegubowo-nieprzesuwnej (A), która odbiera dwa stopnie swobody, trzech podpór
przegubowo-przesuwnych (B, D i F), które odbierają razem trzy stopnie swobody oraz dwóch przegubów (C i
E), które razem odbierają cztery stopnie swobody. Wszystkie więzy odbierają razem dziewięć stopni swobody.
Został więc spełniony warunek konieczny geometrycznej niezmienności.

I

II

III

A

B

C

D

E

F

Rys. K1B.2. Płaski układ prętowy.

Tarcza numer I jest podparta trzema prętami podporowymi, których kierunki nie przecinają się w jednym
punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tej tarczy. Jest ona więc
układem geometrycznie niezmiennym i stanowi podłoże dla tarczy numer II. Tarcza numer II jest podparta
prętem podporowym i przegubem i ponadto przegub nie znajduje się na kierunku pręta podporowego. Został
więc spełniony warunek dostateczny geometrycznej niezmienności dla tej tarczy. Jest ona więc układem

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

2

geometrycznie niezmiennym i stanowi podłoże dla tarczy numer III. Tarcza numer III jest podparta prętem
podporowym i przegubem i ponadto przegub nie znajduje się na kierunku pręta podporowego. Został więc
spełniony warunek dostateczny geometrycznej niezmienności dla tej tarczy. Jest ona więc układem
geometrycznie niezmiennym. Cały układ jest więc układem geometrycznie niezmiennym.

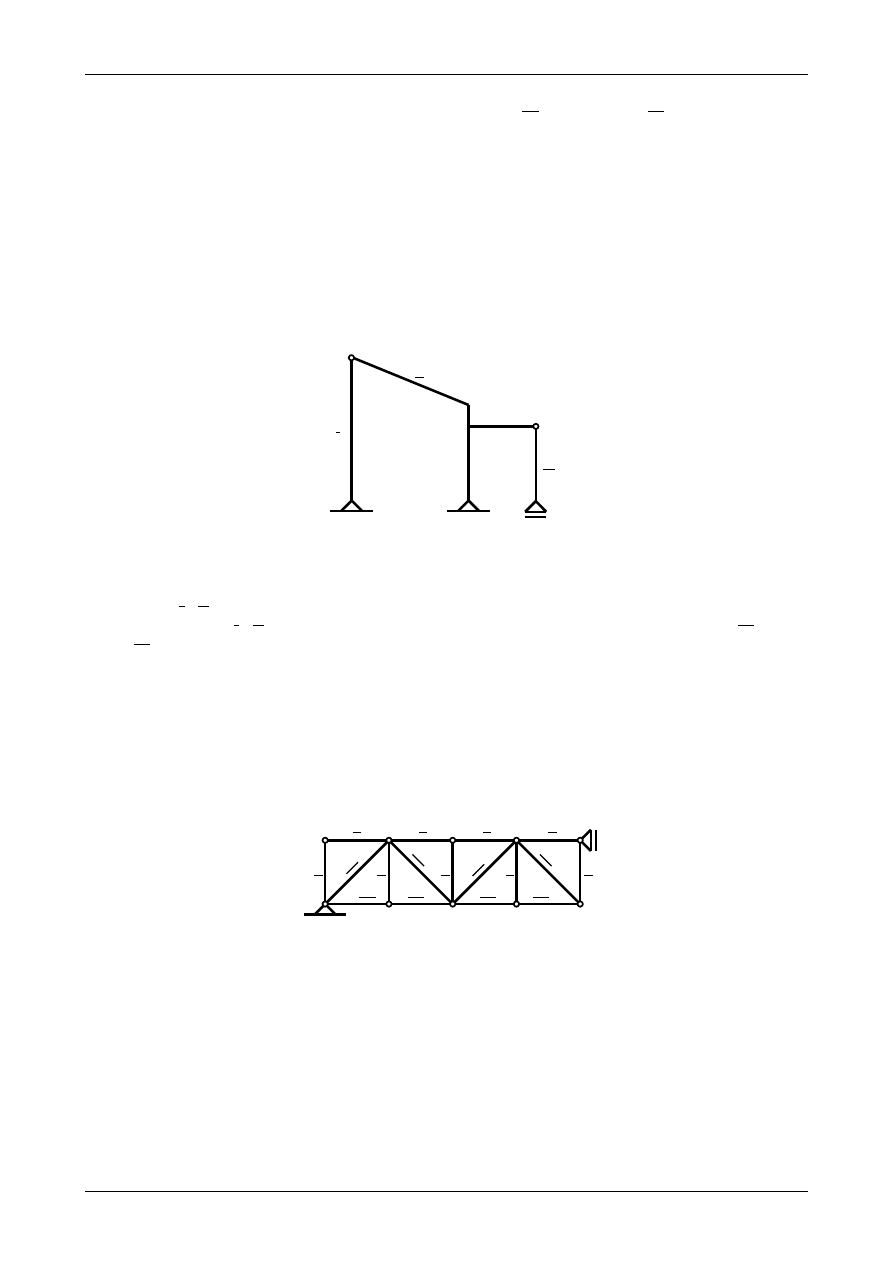
Rysunek K1B.3 przedstawia płaski układ prętowy z zaznaczonymi tarczami sztywnymi oraz więzami.

Jak widać składa się on z trzech tarcz sztywnych, które posiadają razem dziewięć stopni swobody. Podparte
one są za pomocą dwóch podpór przegubowo-nieprzesuwnych (A i C), które razem odbierają cztery stopnie
swobody, jednej podpory przegubowo-przesuwnej (E), która odbiera jeden stopień swobody oraz dwóch
przegubów (B i D), które razem odbierają cztery stopnie swobody. Wszystkie więzy odbierają razem dziewięć
stopni swobody. Został więc spełniony warunek konieczny geometrycznej niezmienności.

A

B

C

D

E

I

II

III

Rys. K1B.3. Płaski układ prętowy.

Tarcze numer I i II stanowią układ trójprzegubowy, w którym przeguby A, B oraz C nie znajdują się na jednej
prostej. Tarcze numer I i II są więc geometrycznie niezmienne i mogą stanowić podłoże dla tarczy III. Tarcza
numer III jest podparta przegubem i prętem podporowym lecz przegub D znajduje się na kierunku pręta
podporowego E. Nie został więc spełniony warunek dostateczny geometrycznej niezmienności dla tej tarczy.
Jest ona więc układem geometrycznie zmiennym. Cały układ jest więc układem geometrycznie zmiennym.

Rysunek K1B.4 przedstawia kratownicę płaską, która składa się z dziesięciu węzłów, które razem mają

dwadzieścia stopni swobody. Kratownica składa się z siedemnastu prętów kratownicy oraz trzech prętów
podporowych, które razem odbierają dwadzieścia stopni swobody. Został więc tym samym spełniony warunek
konieczny geometrycznej niezmienności dla tej kratownicy.

1

2

3

4

5=B

6

7

8

9

1

2

3

4

5

14

15

17

16

A=6

10

7

8

9

10

11

12

13

Rys. K1B.4. Kratownica płaska.

Kratownica jest zbudowana z trójkątów stanowi więc tarczę sztywną, która posiada trzy stopnie swobody.
Tarcza sztywna jest przymocowana do podłoża za pomocą trzech prętów podporowych, które odbierają jej
wszystkie stopnie swobody. Został więc tym samym spełniony warunek konieczny geometrycznej
niezmienności. Kierunki wszystkich trzech prętów podporowych nie przecinają się w jednym punkcie. Został
więc spełniony warunek dostateczny geometrycznej niezmienności. Kratownica jest więc układem
geometrycznie niezmiennym.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

3

K1B.4 Zadanie 2

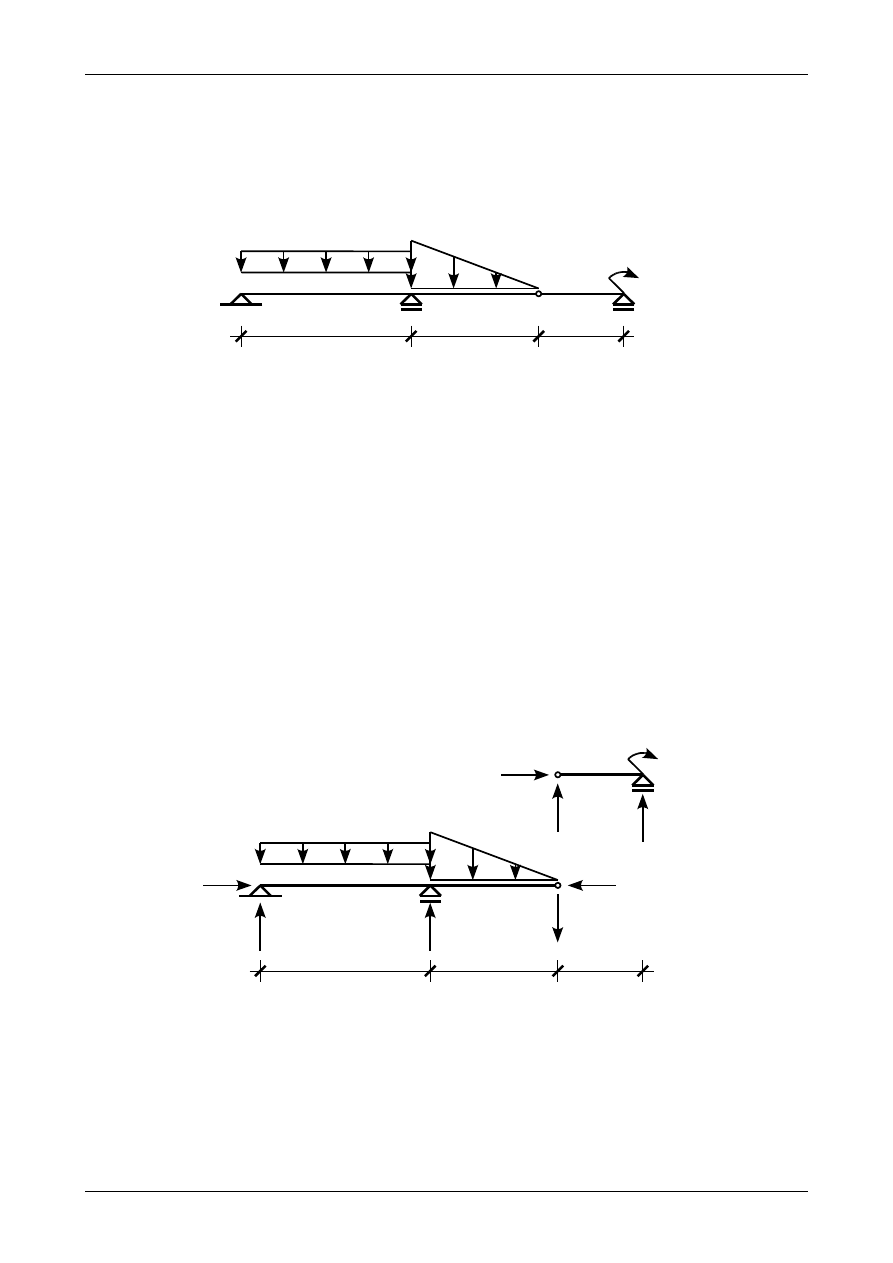
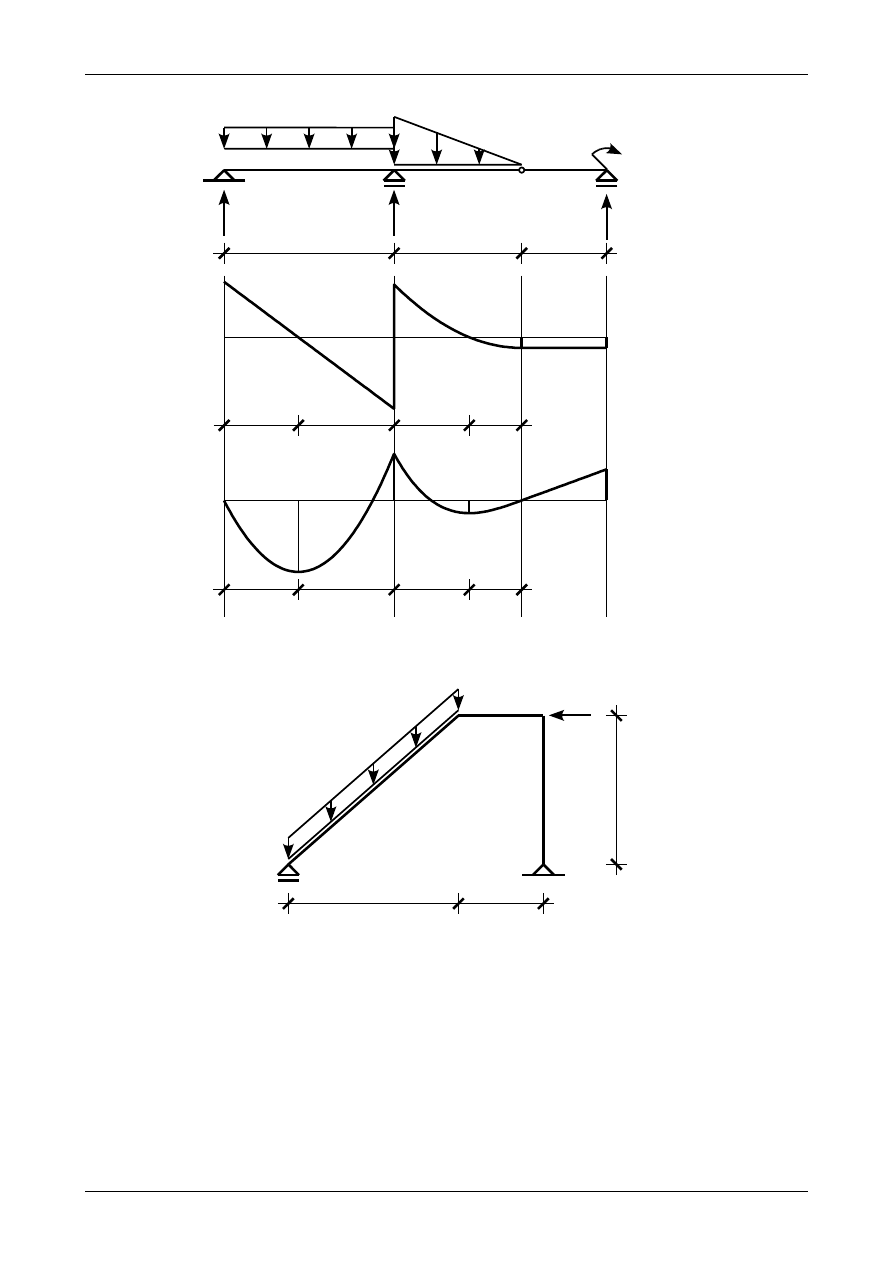
Narysować wykresy siły poprzecznej i momentu zginającego dla belki na rysunku K1B.5. Wymiary

belki podane są w metrach. Wartość 32,0 kN/m dotyczy obciążenia trójkątnego natomiast wartość 24,0 kN/m
dotyczy obciążenia równomiernie rozłożonego.

4,0

32,0 kN/m

24,0 kN/m

16,0 kNm

3,0

2,0

A

B

C

D

K1B.5. Belka złożona.

K1B.5 Rozwiązanie zadania 2

Belka złożona składa się z dwóch tarcz sztywnych, które posiadają sześć stopni swobody. Podpora

przegubowo-nieprzesuwna A odbiera dwa stopnie swobody, dwie podpory przegubowo-przesuwne B i D
odbierają razem dwa stopnie swobody natomiast przegub C odbiera dwa stopnie swobody. Razem wszystkie
więzy odbierają sześć stopni swobody. Został więc spełniony warunek konieczny geometrycznej
niezmienności. Belka AC podparta jest trzema prętami podporowymi, których kierunki nie przecinają się w
jednym punkcie został więc spełniony warunek dostateczny geometrycznej niezmienności. Belka AC jest
geometrycznie niezmienna i może stanowić podłoże dla belki CD. Belka CD jest podparta przegubem C oraz
prętem podporowym D i ponadto przegub C nie znajduje się na kierunku pręta podporowego D. Został więc
spełniony warunek dostateczny geometrycznej niezmienności. Belka CD jest geometrycznie niezmienna. Jeżeli
obie belki proste są geometrycznie niezmienne to i cała belka złożona jest geometrycznie niezmienna.

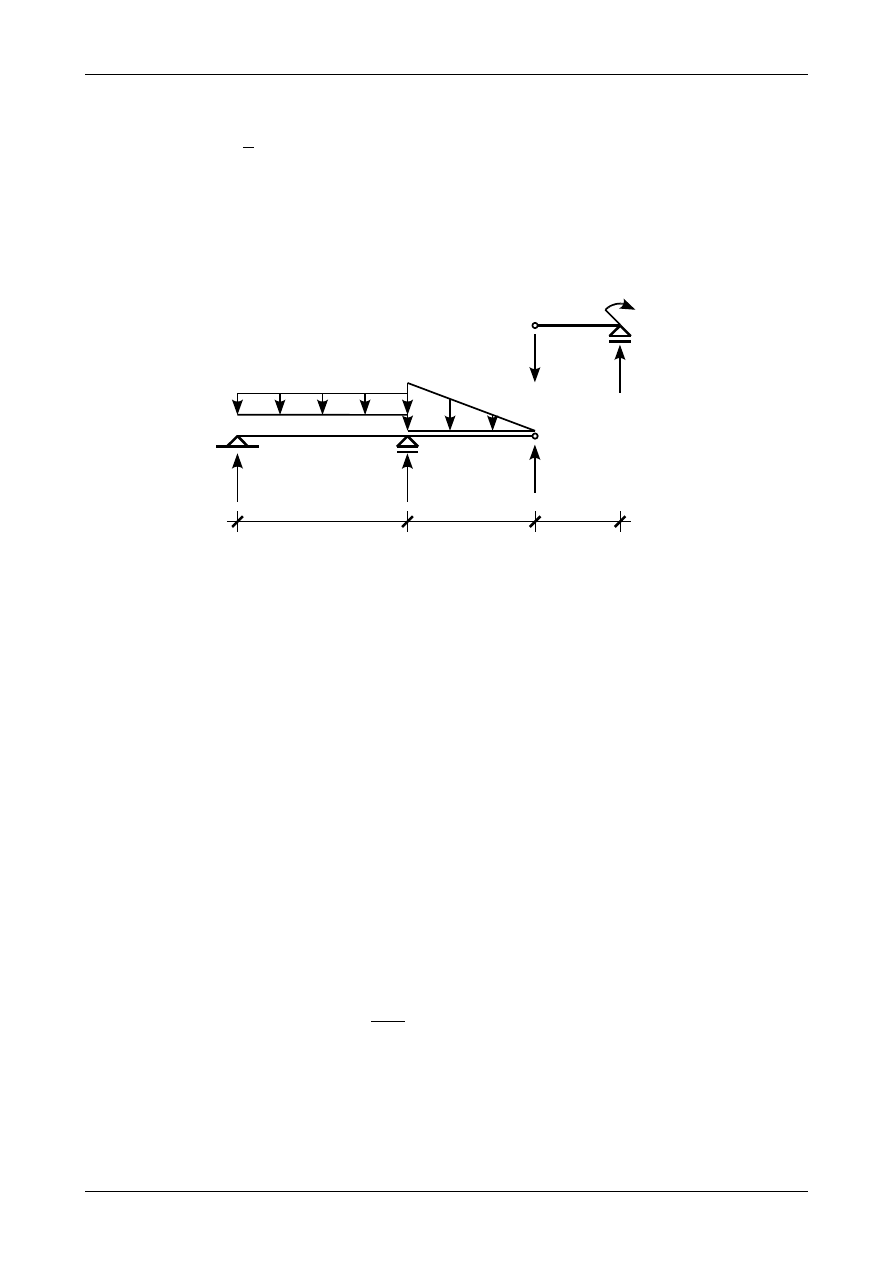
Rysunek K1B.6 przedstawia belkę złożoną rozłożoną na dwie belki proste z zaznaczonymi zwrotami

reakcji podporowych.

4,0

32,0 kN/m

24,0 kN/m

3,0

2,0

A

B

C

16,0 kNm

C

D

H

A

V

A

V

B

V

C

H

C

V

C

H

C

V

D

Rys. K1B.6. Założone zwroty reakcji podporowych.

Ponieważ na belce nie działa obciążenie czynne poziome obie poziome reakcje H

A

oraz H

C

wynoszą zero.

Wyznaczanie pionowych reakcji zaczniemy od belki CD. Reakcję V

C

wyznaczymy z warunku sumy

momentów wszystkich sił działających na belkę CD względem punktu D.

Dr inż. Janusz Dębiński

BDM

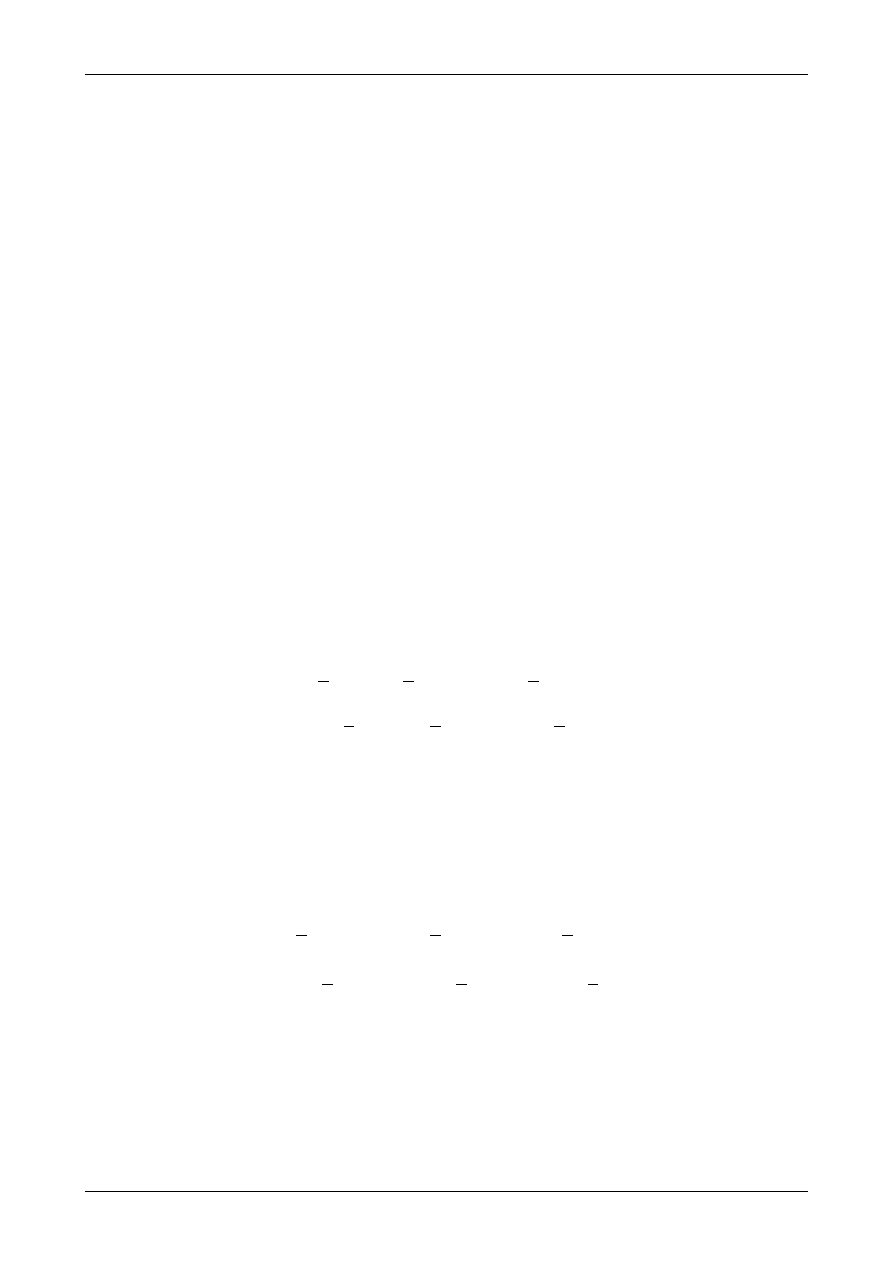
05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

4

 M

D

CD 

=0

V

C

⋅2,016,0=0

V

C

=−8,0 kN

.

(K1B.1)

Minus oznacza, że reakcja V

C

ma przeciwny zwrot do założonego. Reakcję V

D

wyznaczymy z warunku sumy

momentów wszystkich sił działających na belkę CD względem punktu C.

 M

C

CD 

=0

−V

D

⋅2,016,0 =0

V

D

=8,0 kN

.

(K1B.2)

Reakcja ma więc zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy warunek sumy rzutów
wszystkich sił działających na belkę CD na oś pionową Y.

Y

CD

=0

V

C

V

D

=−8,08,0 =0

.

(K1B.3)

Wszystkie siły działające na belkę CD znajdują się w równowadze. Reakcję V

A

wyznaczymy z warunku sumy

momentów wszystkich sił działających na belkę AC względem punktu B.

 M

B

 AC

=0

V

A

⋅4,0V

C

⋅3,0

1
2

⋅32,0⋅3,0⋅

1
3

⋅3,0 −24,0⋅4,0⋅

1
2

⋅4,0 =0

V

A

⋅4,0



−8,0



⋅3,0

1
2

⋅32,0⋅3,0⋅

1
3

⋅3,0−24,0⋅4,0⋅

1
2

⋅4,0=0

V

A

=42,0 kN

.

(K1B.4)

Reakcja ma więc zwrot zgodny z założonym. Reakcję V

B

wyznaczymy z warunku sumy momentów

wszystkich sił działających na belkę AC względem punktu A.

 M

A

 AC

=0

−V

B

⋅4,0V

C

⋅7,0

1
2

⋅32,0⋅3,0⋅



4,0



1
3

⋅3,0



24,0⋅4,0⋅

1
2

⋅4,0=0

−V

B

⋅4,0



−8,0



⋅7,0 

1
2

⋅32,0⋅3,0⋅



4,0



1
3

⋅3,0



24,0⋅4,0⋅

1
2

⋅4,0=0

V

B

=94,0 kN

.

(K1B.5)

Reakcja ma więc zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy warunek sumy rzutów
wszystkich sił działających na belkę AC na oś pionową Y.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

5

Y

AC

=0

V

A

V

B

−V

C

−

1
2

⋅32,0⋅3,0−24,0⋅4,0=42,094,0−



−8,0



−48,0−96,0=0

.

(K1B.6)

Wszystkie siły działające na belkę AC znajdują się w równowadze. Rysunek K1B.7 przedstawia prawidłowe
zwroty reakcji podporowych.

4,0

32,0 kN/m

24,0 kN/m

3,0

2,0

A

B

C

16,0 kNm

C

D

42,0 kN

94,0 kN

8,0 kN

8,0 kN

8,0 kN

Rys. K1B.7. Prawidłowe zwroty i wartości reakcji podporowych.

W przedziale AB działa obciążenie ciągłe równomiernie rozłożone więc siła poprzeczna będzie liniowa
natomiast moment zginający będzie parabolą. W celu narysowania paraboli potrzebować będziemy trzech
punktów natomiast aby narysować wykres liniowy będziemy potrzebowali dwóch punktów.

W punkcie A działa siłą skupiona o wartości 42,0 kN do góry więc siłą poprzeczna w tym punkcie wynosi

T

A

=42,0 kN

.

(K1B.7)

Obciążenie ciągłe działa w dół więc siła poprzeczne będzie maleć. W punkcie B z lewej strony siła poprzeczna
wynosi

T

B

L 

=42,0−24,0⋅4,0=−54,0 kN

.

(K1B.8)

Na obu końcach przedziału siłą poprzeczna ma wartości przeciwnych znaków więc w przedziale AB będzie
ona posiadała miejsce zerowe. Zgodnie ze wzorem (1.62) będzie się ono znajdowało w odległości

x

0

=

42,0
24,0

=1,75 m

(K1B.9)

od punktu A. Natomiast zgodnie ze wzorem (1.63) będzie ono w odległości

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

6

x

0

=

54,0
24,0

=2,25 m

(K1B.10)

od punktu B.

4,0

24,0 kN/m

A

42,0 kN

1,75

M

B

24,0 kN/m

A

42,0 kN

M

1

A

42,0 kN

M

A

a)

b)

c)

Rys. K1B.8. Równowagi odciętych części belki w przedziale AB.

Zgodnie z rysunkiem K1B.8 a) moment zginający w punkcie A wynosi

M

A

=0,0 kNm

.

(K1B.11)

Zgodnie z rysunkiem K1B.8 b) moment zginający w punkcie B wynosi

M

B

=42,0⋅4,0−24,0⋅4,0⋅

1
2

⋅4,0=−24,0 kNm

.

(K1B.12)

Znak minus oznacza, że moment ten rozciąga górną część przekroju pręta. Zgodnie z rysunkiem K1B.8 c)
ekstremalny moment zginający w przedziale AB wynosi

M

1

=42,0⋅1,75−24,0⋅1,75⋅

1
2

⋅1,75=36,75 kNm

.

(K1B.13)

Znak plus oznacza, że moment ten rozciąga dolną część przekroju pręta. Rysunek K1B.9 przedstawia wykresy
sił przekrojowych w przedziale AB.

W przedziale CD obciążenie ciągłe jest liniowe więc siła poprzeczna będzie parabolą natomiast moment
zginający będzie wielomianem trzeciego stopnia. W celu narysowania paraboli potrzebować będziemy trzech
punktów natomiast aby narysować wielomian trzeciego stopnia będziemy potrzebowali czterech punktów.

W punkcie B działa siłą skupiona o wartości 94,0 kN do góry więc siła poprzeczna w punkcie B z prawej
strony wynosi

T

B

P 

=−54,094,0=40,0kN

.

(K1B.14)

Dr inż. Janusz Dębiński

BDM

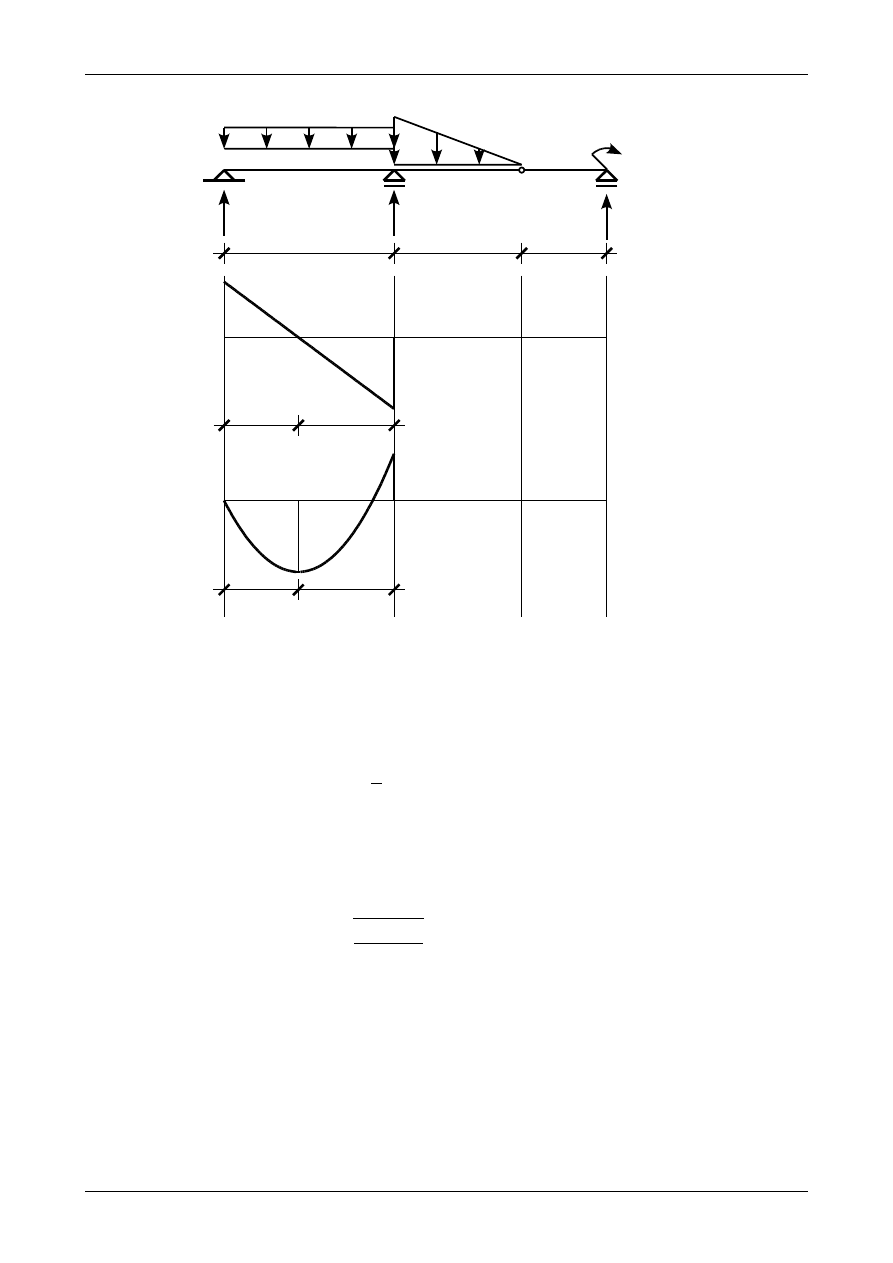
05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

7

4,0

32,0 kN/m

24,0 kN/m

16,0 kNm

3,0

2,0

A

B

C

D

42,0 kN

94,0 kN

8,0 kN

T [kN]

M [kNm]

+

42

,0

-5

4

,0

0,

0

24

,0

1,75

2,25

1,75

2,25

36

,7

5

Rys. K1B.9. Wykresy sił przekrojowych w przedziale AB.

W przedziale BC obciążenie ciągłe działa w dół czyli siła poprzeczna będzie maleć i w punkcie C z lewej
strony osiągnie wartość

T

C

L 

=40,0−

1
2

⋅32,0⋅3,0=−8,0 kN

.

(K1B.15)

Na obu końcach przedziału siła poprzeczna ma wartości przeciwnych znaków więc w przedziale AB będzie
ona posiadała miejsce zerowe. Zgodnie ze wzorem (1.65) będzie się ono znajdowało w odległości

x

0

=



2

⋅8,0⋅3,0

32,0

=1,225 m

(K1B.16)

od punktu C. Ponieważ obciążenie ciągłe w przedziale CD posiada miejsce zerowe w punkcie C więc siła
poprzeczna w tym punkcie będzie miała wartość ekstremalną. „Brzuszek” paraboli siły poprzecznej będzie
więc skierowany w dół.

Zgodnie z rysunkiem K1B.10 a) moment zginający w punkcie C wynosi

M

C

=0,0 kNm

.

(K1B.17)

Dr inż. Janusz Dębiński

BDM

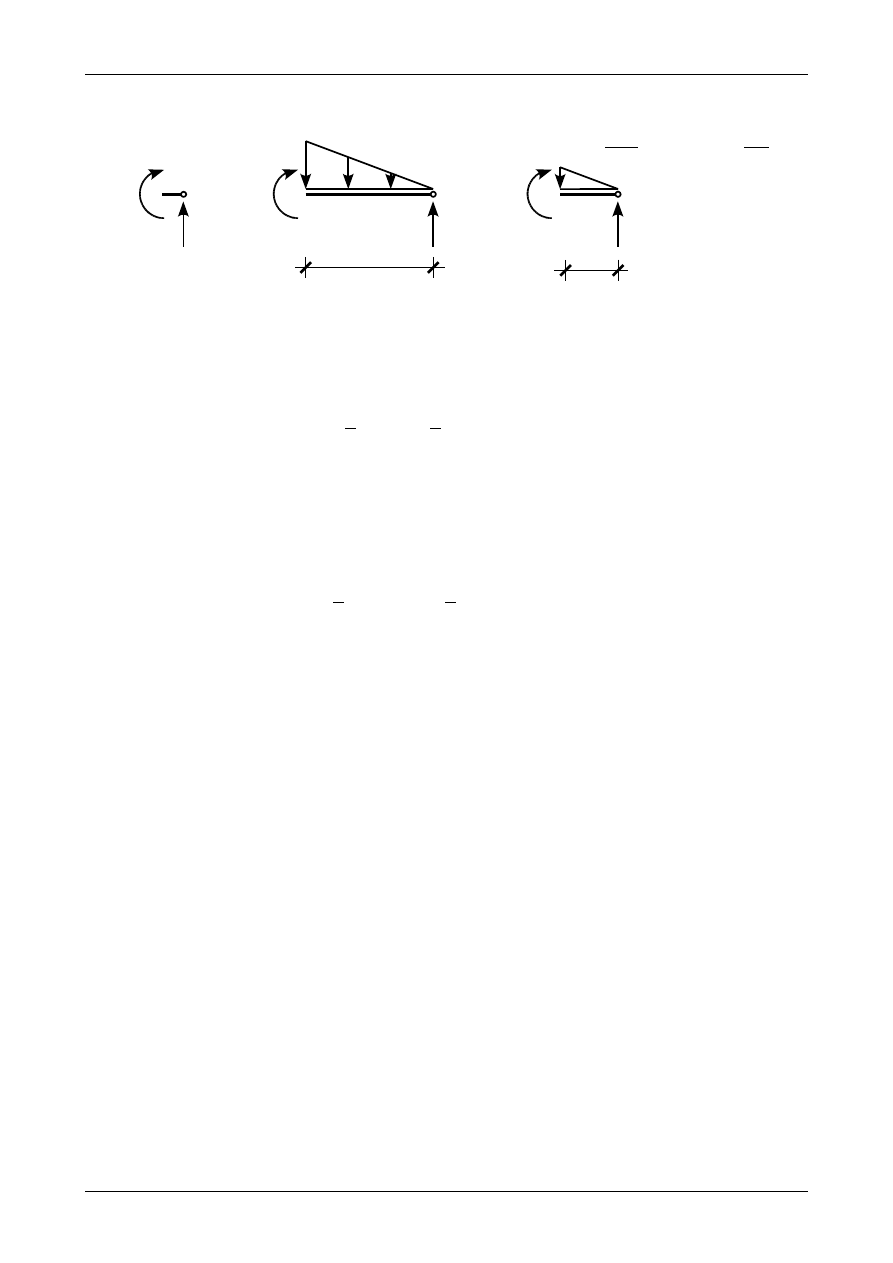
05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

8

32,0 kN/m

3,0

C

8,0 kN

M

B

C

8,0 kN

1,225

M

2

q

1,225=

32,0

3,0

⋅1,225=13,07

kN

m

C

8,0 kN

M

C

a)

b)

c)

Rys. K1B.10. Równowagi odciętych części belki w przedziale BC.

Zgodnie z rysunkiem K1B.10 b) moment zginający w punkcie B wynosi

M

B

=8,0⋅3,0−

1
2

⋅32,0⋅3,0⋅

1
3

⋅3,0=−24,0 kNm

.

(K1B.18)

Znak minus oznacza, że moment ten rozciąga górną część przekroju pręta. Moment zginający w punkcie B
wyznaczony ze wzoru (K1B.18) oczywiście równa się momentowi wyznaczonemu ze wzoru (K1B.12).
Zgodnie z rysunkiem K1B.10 c) ekstremalny moment zginający w przedziale BC wynosi

M

1

=8,0⋅1,225−

1
2

⋅13,07⋅1,225⋅

1
3

⋅1,225=6,531 kNm

.

(K1B.19)

Znak plus oznacza, że moment ten rozciąga dolną część przekroju pręta. Rysunek K1B.11 przedstawia
wykresy sił przekrojowych w przedziale BC.

W przedziale CD nie działa żadne obciążenie ciągłe więc siła poprzeczna będzie stała natomiast moment
zginający będzie liniowy. W celu narysowania wykresu liniowego potrzebować będziemy dwóch punktów.

W przegubie C działają dwie reakcje o tych samych wartościach lecz przeciwnych zwrotach. Razem obie
reakcje dają nam siłę zerową. Czyli siła poprzeczna w punkcie C z prawej strony wynosi

T

C

P 

=−8,0 kN

.

(K1B.20)

W punkcie D siła poprzeczna wynosi

T

D

=−8,0 kN

.

(K1B.21)

Zgodnie z rysunkiem K1A.12 a) moment zginający w punkcie C wynosi

M

C

=8,0⋅2,0−16,0 =0,0 kNm

.

(K1B.22)

Moment zginający w punkcie C wyznaczony ze wzoru (K1B.22) oczywiście równa się momentowi
wyznaczonemu ze wzoru (K1B.17). Zgodnie z rysunkiem K1A.12 b) moment zginający w punkcie D wynosi

Dr inż. Janusz Dębiński

BDM

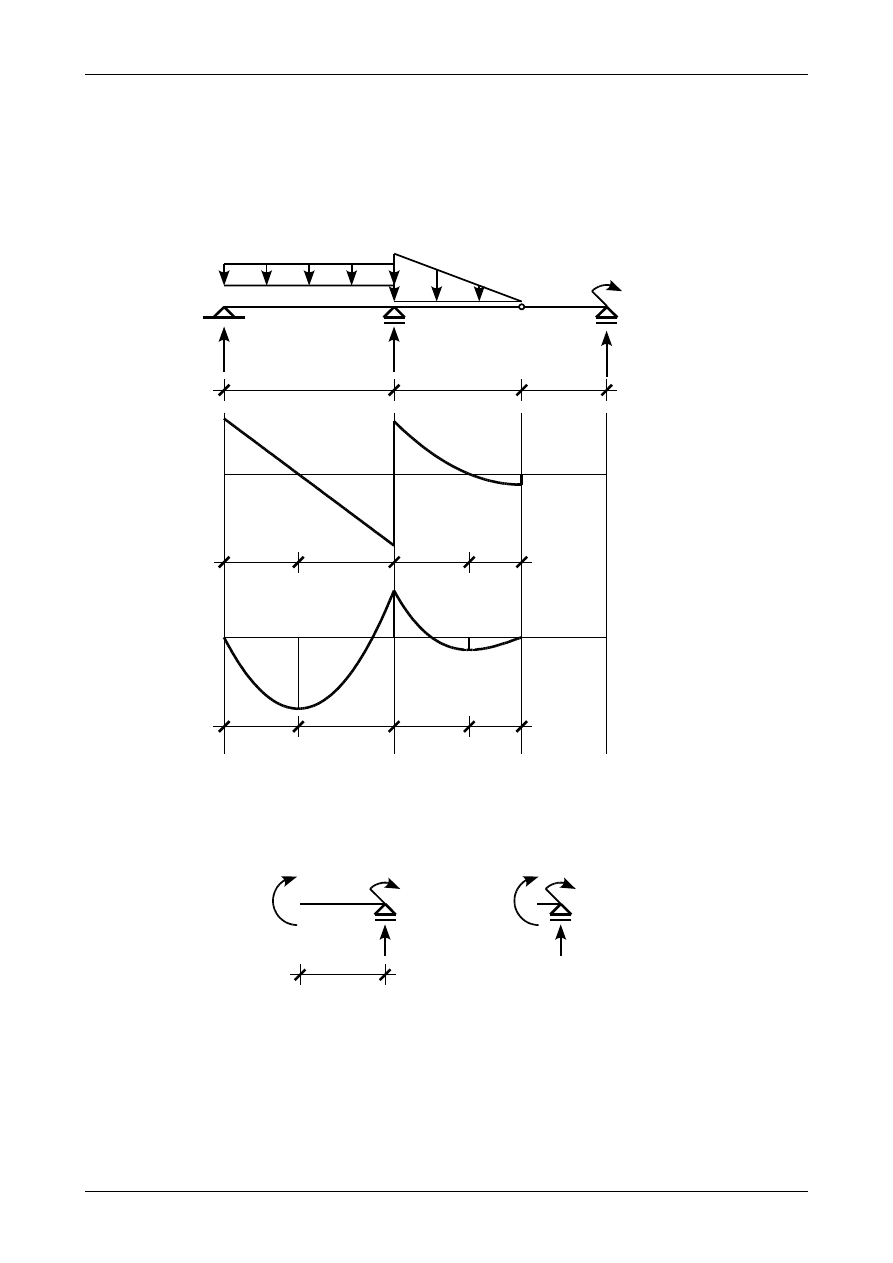
05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

9

M

D

=−16,0 kNm

.

(K1B.23)

Znak minus oznacza, że moment ten rozciąga górną część przekroju pręta. Rysunek K1B.13 przedstawia
wykresy sił przekrojowych w przedziale CD. Są to także ostateczne wykresy sił przekrojowych w belce.

4,0

32,0 kN/m

24,0 kN/m

16,0 kNm

3,0

2,0

A

B

C

D

42,0 kN

94,0 kN

8,0 kN

T [kN]

M [kNm]

+

42

,0

-5

4

,0

+

40

,0

0,

0

24

,0

0,

0

1,75

1,225

2,25

1,775

1,75

1,225

2,25

1,775

36

,7

5

6

,5

3

1

-8

,0

Rys. K1B.11. Wykresy sił przekrojowych w przedziale BC.

2,0

16,0 kNm

8,0 kN

M

C

16,0 kNm

8,0 kN

M

D

a)

b)

Rys. K1B.12. Równowagi odciętych części belki w przedziale CD.

K1B.6 Zadanie 3

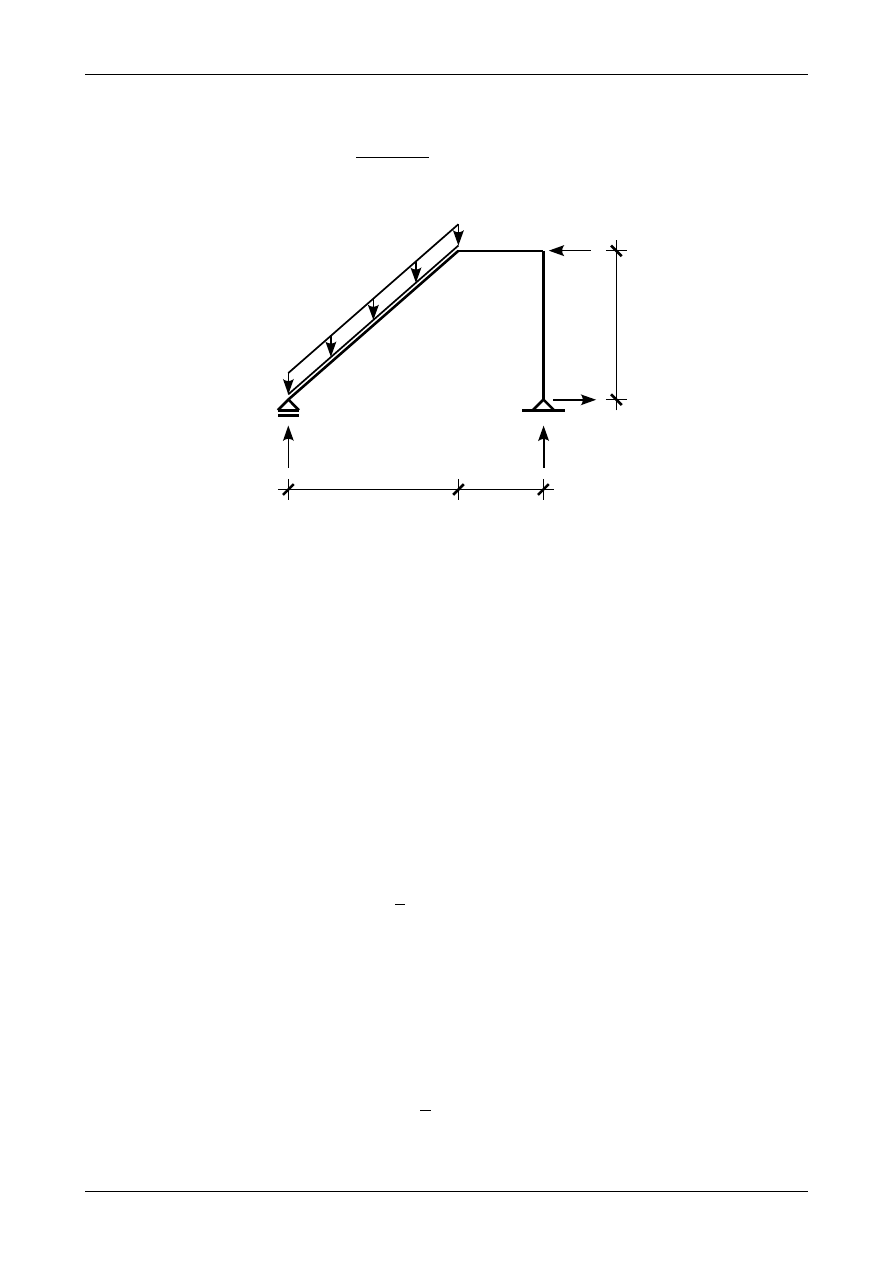
Narysować wykresy siły normalnej i poprzecznej oraz momentu zginającego dla ramy na rysunku

K1A.14. Następnie sprawdzić równowagę pręta ukośnego. Wymiary ramy są podane w metrach. Zwrócić
uwagę na podpory!

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

10

4,0

32,0 kN/m

24,0 kN/m

16,0 kNm

3,0

2,0

A

B

C

D

42,0 kN

94,0 kN

8,0 kN

T [kN]

M [kNm]

+

42

,0

-5

4

,0

+

4

0,

0

-8,0

0,

0

24

,0

0,

0

1

6,0

1,75

1,225

2,25

1,775

1,75

1,225

2,25

1,775

36

,7

5

6

,5

3

1

Rys. K1B.13. Ostateczne wykresy sił przekrojowych w belce.

4,0

2,0

3,

5

18

,0

kN

/m

8,0 kN

A

B

C

D

Rys. K1B.14. Rama płaska.

K1B.7 Rozwiązanie zadania 3

Rama płaska jest pojedynczą tarczą sztywną posiadającą trzy stopnie swobody. Podpora przegubowo-

nieprzesuwna D odbiera dwa stopnie swobody natomiast podpora przegubowo-przesuwna A odbiera jeden
stopień swobody. Razem obie podpory odbierają trzy stopnie swobody. Został tym samym spełniony warunek
konieczny geometrycznej niezmienności.

Tarcza sztywna jest podparta trzema prętami podporowymi, których kierunki nie przecinają się w jednym
punkcie. Został więc spełniony także warunek dostateczny geometrycznej niezmienności. Rama jest więc
układem geometrycznie niezmiennym.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

11

Długość pręta AB wynosi

L

AB

=



4,0

2

3,5

2

=5,315 m

.

(K1B.24)

4,0

2,0

3

,5

18

,0

kN

/m

8,0 kN

A

B

C

D

V

A

V

D

H

D

-5

,31

5-

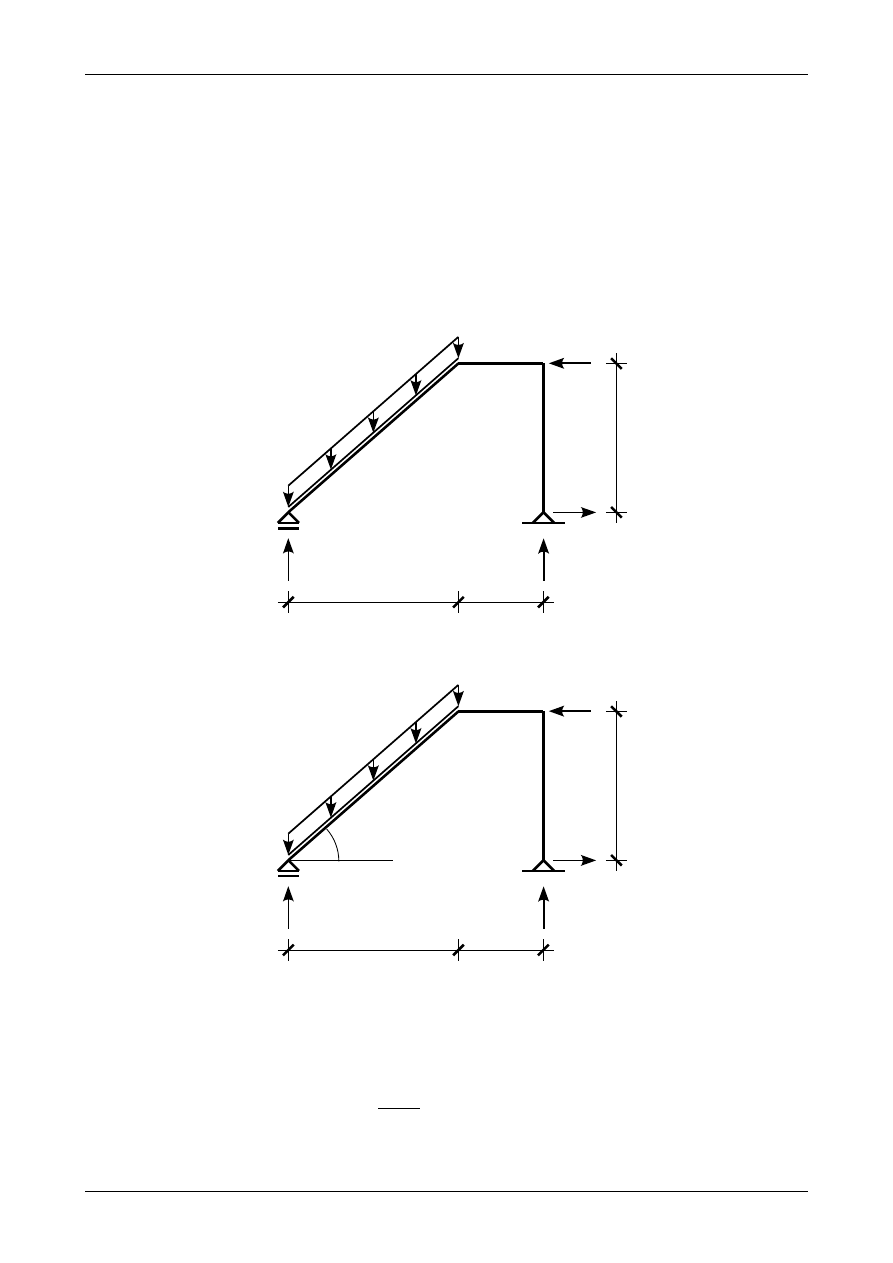
Rys. K1B.15. Założone zwroty reakcji podporowych.

Rysunek K1A.15 przedstawia założone zwroty reakcji podporowych.

Poziomą reakcję na podporze D wyznaczymy z warunku sumy rzutów wszystkich sił działających na ramę na
oś poziomą X.

 X =0
H

D

−8,0=0

H

D

=8,0 kN

(K1B.25)

Reakcja posiada zwrot zgodny z założonym. Reakcję V

A

wyznaczymy z warunku sumy momentów wszystkich

sił działających na ramę względem punktu D.

 M

D

=0

V

A

⋅6,0 −18,0⋅5,315⋅



1
2

⋅4,02,0



−8,0⋅3,5=0

V

A

=68,45 kN

.

(K1B.26)

Reakcja posiada zwrot zgodny z założonym. Reakcję V

D

wyznaczymy z warunku sumy momentów wszystkich

sił działających na ramę względem punktu A.

 M

A

=0

−V

D

⋅6,018,0⋅5,315⋅

1
2

⋅4,0−8,0⋅3,5=0

V

D

=27,22 kN

.

(K1B.27)

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

12

Reakcja posiada zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy warunek sumy rzutów
wszystkich sił działających na ramę na oś pionową Y.

Y =0

V

A

V

D

−18,0⋅5,315=68,4527,22−95,67=0

.

(K1B.28)

Wszystkie siły działające na ramę znajdują się w równowadze. Rysunek K1B.16 przedstawia ramę z
zaznaczonymi prawidłowymi zwrotami i wartościami reakcji podporowych.

4,0

2,0

3

,5

18

,0

kN

/m

8,0 kN

A

B

C

D

8,0 kN

27,22 kN

68,45 kN

Rys. K1B.16. Prawidłowe zwroty i wartości reakcji podporowych.

4,0

2,0

3,

5

18

,0

kN

/m

8,0 kN

A

B

C

D

8,0 kN

27,22 kN

68,45 kN

α

- 5

,31

5 -

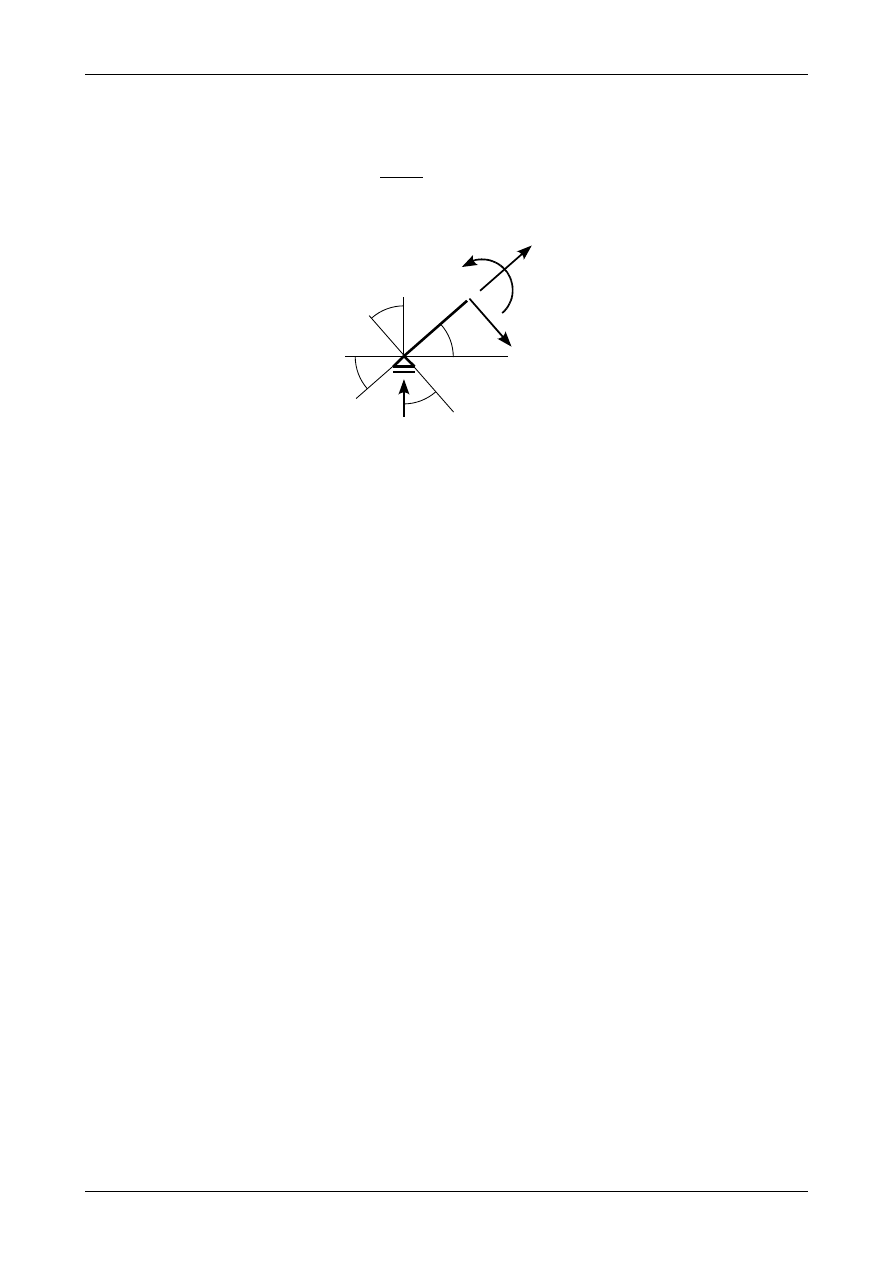
Rys. K1B.17. Kąt nachylenia pręta ukośnego AB.

Wartości sinusa i kosinusa kąta nachylenia pręta ukośnego AB zgodnie z rysunkiem K1B.17 wynoszą

sin







=

3,5

5,315

=0,6585

.

(K1B.29)

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

13

oraz

cos







=

4,0

5,315

=0,7526

.

(K1B.30)

A

68,45 kN

α

T

A

N

A

M

A

α

α

α

Rys. K1B.18. Równowaga sił w punkcie A.

Rysunek K1B.18 przedstawia równowagę sił w punkcie A. Siła normalna w punkcie A wynosi

N

A

=−68,45⋅sin







=−68,45⋅0,6585=−45,07 kN

.

(K1B.31)

Siła poprzeczna w punkcie A wynosi

T

A

=68,45⋅cos







=68,45⋅0,7526=51,52 kN

.

(K1B.32)

Moment zginający w punkcie A wynosi

M

A

=0,0 kNm

.

(K1B.33)

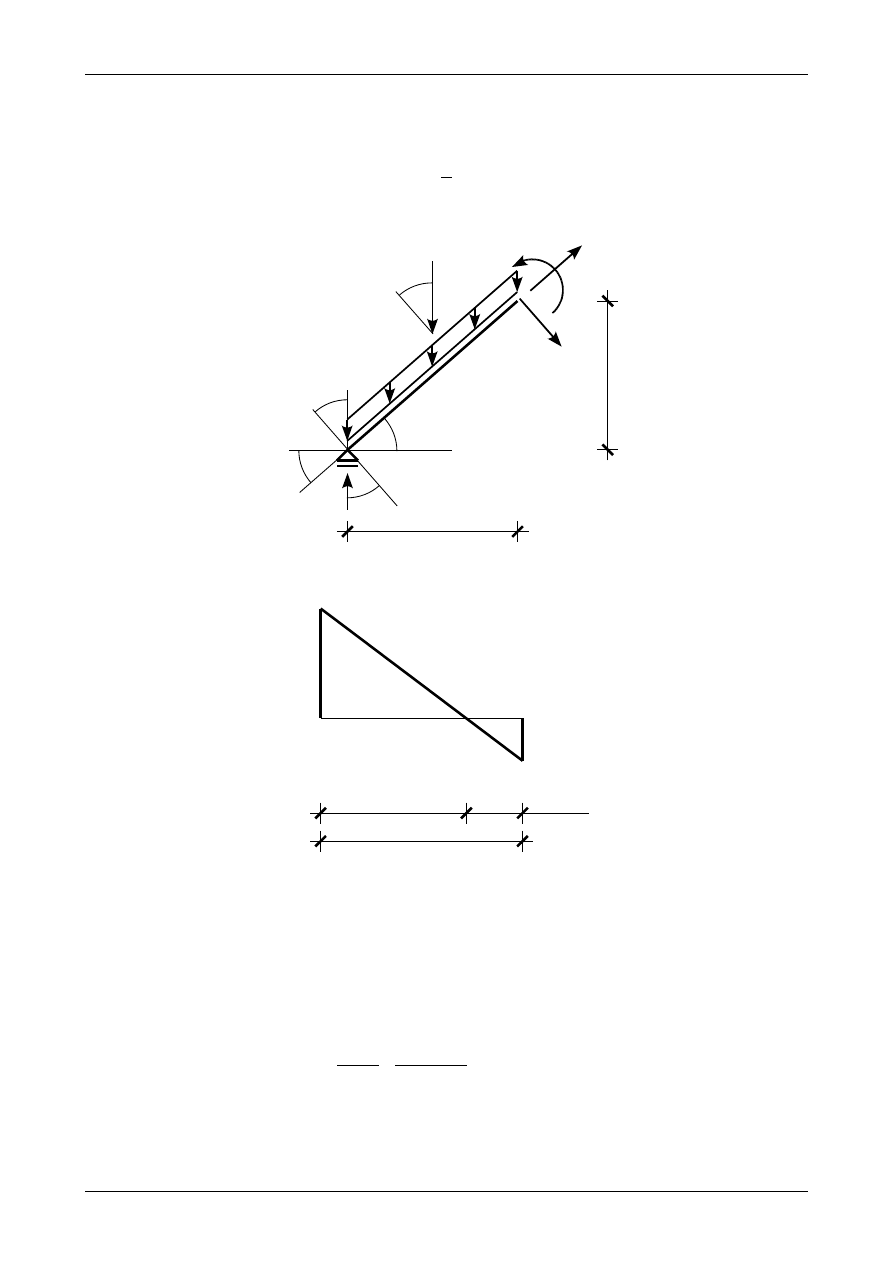
Rysunek K1A.19 przedstawia równowagę całego pręta ukośnego. Siła normalna w punkcie B z lewej strony
węzła wynosi

N

B

L 

=−68,45⋅sin







18,0⋅5,315⋅sin







=−68,45⋅0,658595,67⋅0,6585=17,92 kN

.

(K1B.34)

Siła poprzeczna w punkcie B z lewej strony węzła wynosi

T

B

L

=68,45⋅cos







−18,0⋅5,315⋅cos







=68,45⋅0,7526−95,67⋅0,7526=−20,49 kN

.

(K1B.35)

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

14

Moment zginający w punkcie B wynosi

M

B

=68,45⋅4,0−18,0⋅5,315⋅

1
2

⋅4,0=82,46 kNm

.

(K1B.36)

4,0

A

α

T

B (L)

3

,5

N

B (L)

M

B

α

α

α

α

- 5

,31

5 -

68,45 kN

18

,0

kN

/m

W

=18,0⋅5,315

Rys. K1B.19. Równowaga pręta ukośnego.

A

B

+

51

,5

2

kN

-2

0

,4

9

k

N

x

0

5,315-x

0

5,315

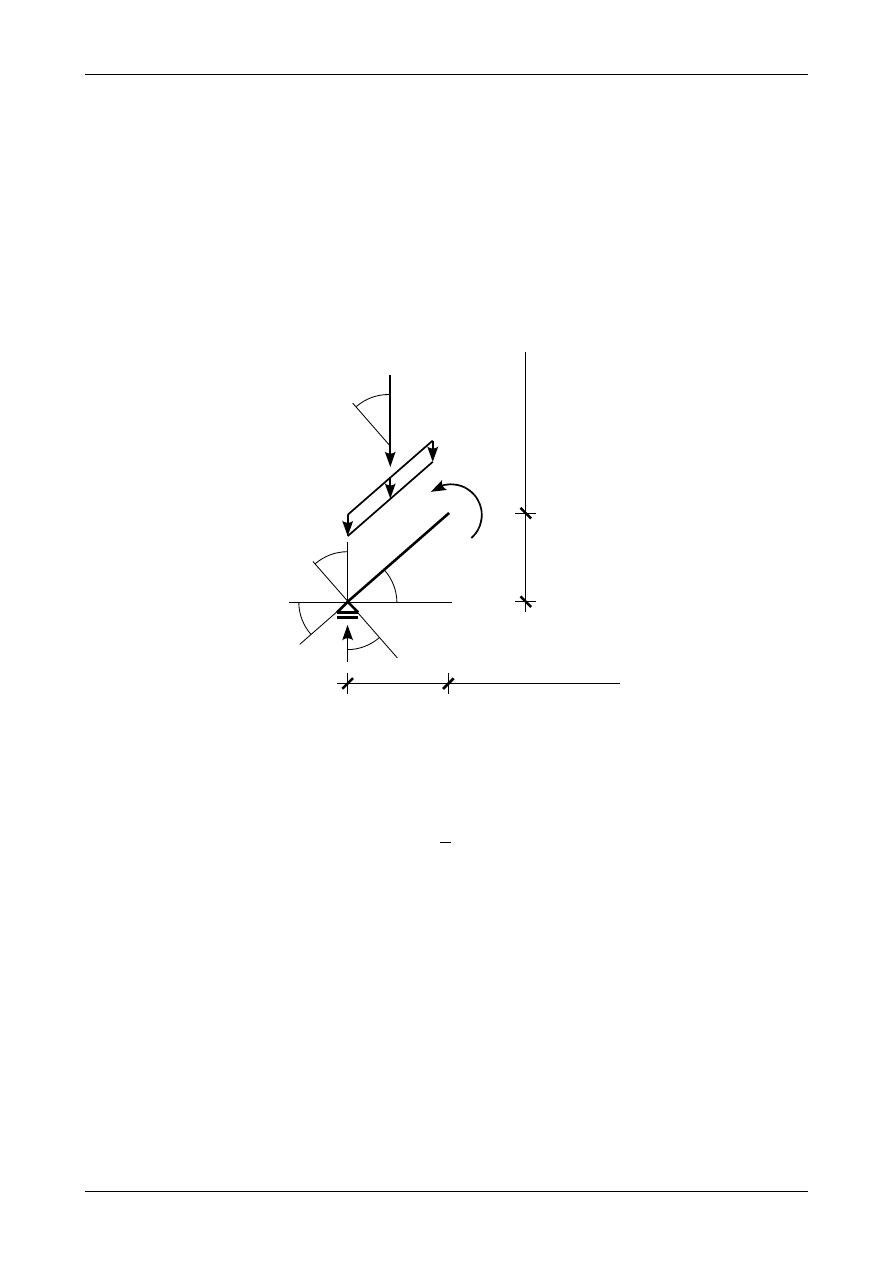
Rys. K1B.20. Wykres siły poprzecznej w przedziale AB.

Ponieważ siła poprzeczna na obu końcach przedziału AB posiada wartości przeciwnych znaków będzie ona
posiadała w tym przedziale miejsce zerowe. Rysunek K1B.20 przedstawia wykres siły poprzecznej w
przedziale AB.

Korzystając z twierdzenia Talesa możemy zapisać

51,52

x

0

=

20,49

5,315

−x

0

.

(K1B.37)

Po wymnożeniu możemy zapisać

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

15

273,8

−51,52⋅x

0

=20,49⋅x

0

.

(K1B.38)

Ostatecznie miejsce zerowe siły poprzecznej znajduje się w odległości

x

0

=3,802 m

.

(K1B.39)

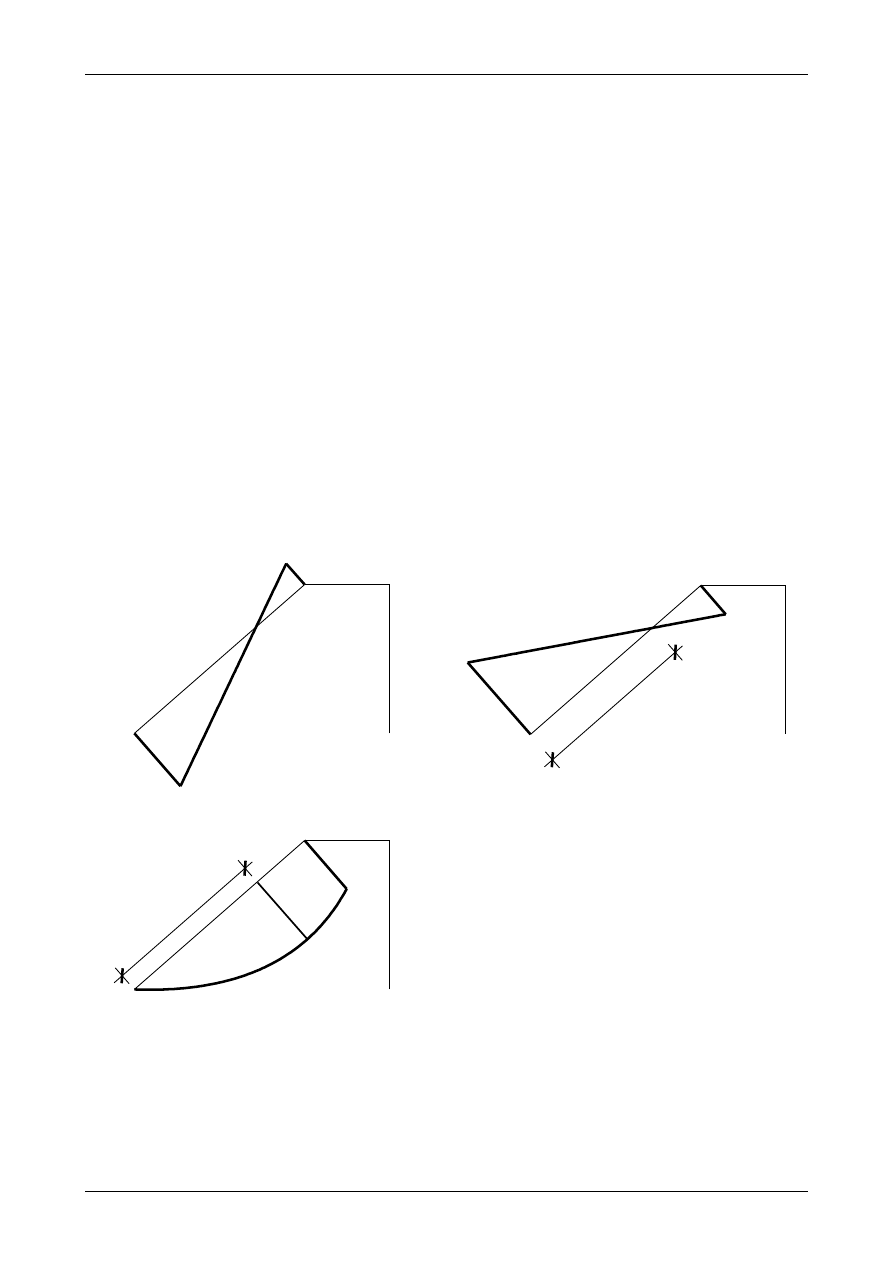
od punktu A. Rysunek K1B.21 przedstawia równowagę części pręta ukośnego dla obliczenia ekstremalnego
momentu zginającego.

A

α

M

1

α

α

α

α

- 3

,80

2 -

68,45 kN

18

,0

kN

/m

3,802

⋅0,6585

=

2,504

3,802

⋅0,7526=2,861

W

1

=18,0⋅3,802

Rys. K1B.21. Równowaga części pręta ukośnego dla obliczenia ekstremalnego momentu zginającego.

Moment ten wynosi

M

1

=68,45⋅2,861−18,0⋅3,802⋅

1
2

⋅2,861=97,94kNm

.

(K1B.40)

Znak plus oznacza, że ekstremalny moment zginający w przedziale AB rozciąga dolną część przekroju pręta.
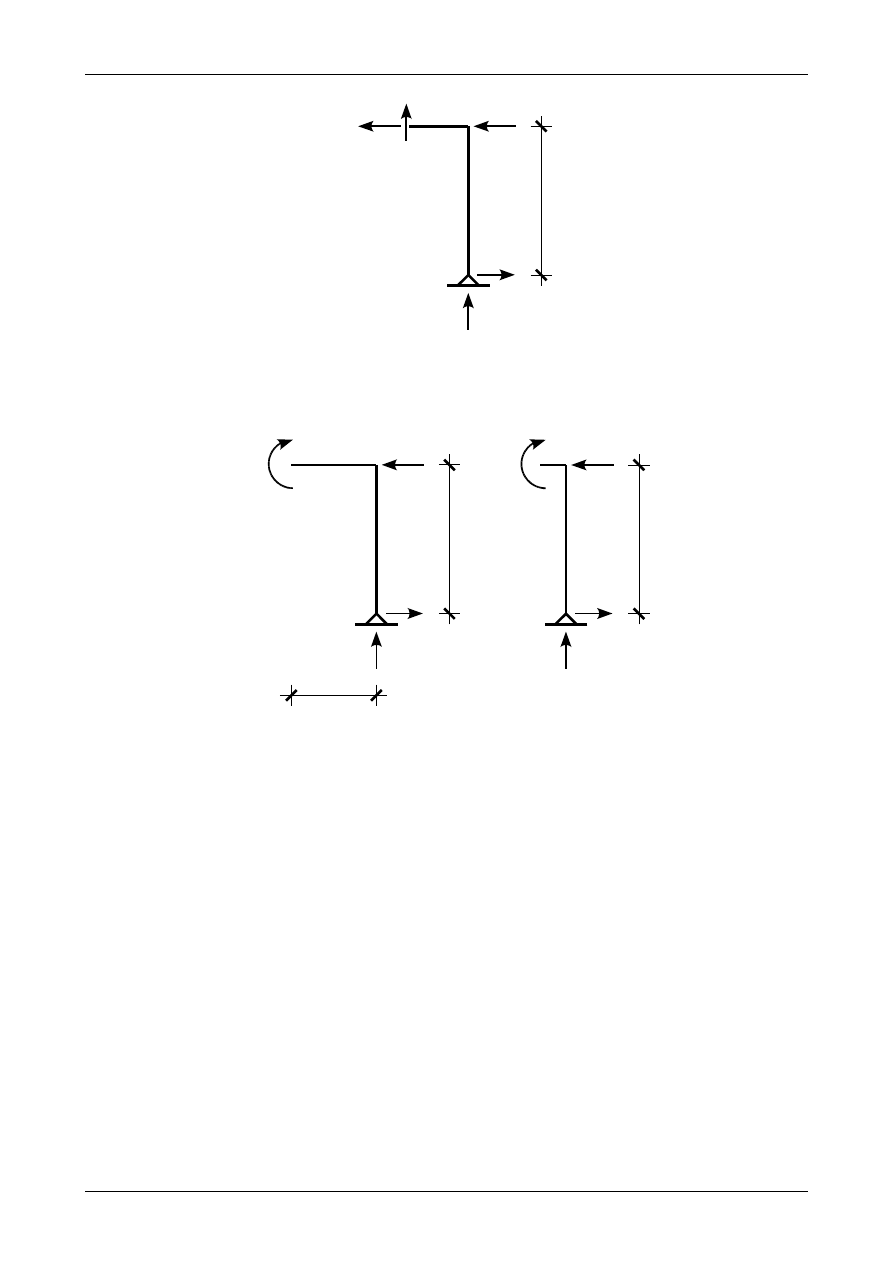
Rysunek K1B.22 przedstawia wykresy sił przekrojowych w przedziale AB.

W przedziale BC nie działa żadne obciążenie ciągłe więc siła normalna i poprzeczna będą stałe natomiast
moment zginający będzie liniowy. Rysunek K1B.23 przedstawia równowagę siły normalnej i poprzecznej w
przedziale BC.

Siła normalna w przedziale BC wynosi

N

BC

=8,0 −8,0=0,0 kN

.

(K1B.41)

Siła poprzeczna w przedziale BC wynosi

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

16

T

BC 

=−27,22 kN

.

(K1B.42)

Zgodnie z rysunkiem K1A.24 a) moment zginający w punkcie B wynosi

M

B

=27,22⋅2,08,0⋅3,5=82,44 kNm≈82,46 kNm

.

(K1B.43)

Znak plus oznacza, że moment ten rozciąga dolną część przekroju pręta. Moment zginający w punkcie B
wyznaczony ze wzoru (K1B.43) równa się oczywiście momentowi wyznaczonemu ze wzoru (K1B.36).

Zgodnie z rysunkiem K1A.24 b) moment zginający w punkcie C wynosi

M

C

=8,0⋅3,5=28,0 kNm

.

(K1B.44)

Znak plus oznacza, że moment ten rozciąga dolną część przekroju ramy. Rysunek K1A.25 przedstawia
wykresy sił przekrojowych w przedziale BC.

3,8

02

3,8

02

N [kN]

M [kNm]

-45

,07

+1

7,9

2

+5

1,5

2

-20

,49

82

,46

0,0

97

,94

T [kN]

Rys. K1B.22. Wykresy sił przekrojowych w przedziale AB.

W przedziale CD nie działa żadne obciążenie ciągłe więc siła normalna i poprzeczna będą stałe natomiast
moment zginający będzie liniowy. Rysunek K1A.26 przedstawia równowagę siły normalnej i poprzecznej w
przedziale CD.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

17

3

,5

8,0 kN

C

D

8,0 kN

27,22 kN

T

(BC)

N

(BC)

Rys. K1B.23. Równowaga siły normalnej i poprzecznej w przedziale BC.

2,0

3,

5

8,0 kN

C

D

8,0 kN

27,22 kN

M

B

3

,5

8,0 kN

C

D

8,0 kN

27,22 kN

M

C

a)

b)

Rys. K1B.24. Równowagi odciętych części ramy w przedziale BC.

Siła normalna w przedziale CD wynosi

N

CD 

=−27,22 kN

.

(K1B.45)

Siła poprzeczna w przedziale CD wynosi

T

CD

=−8,0 kN

.

(K1B.46)

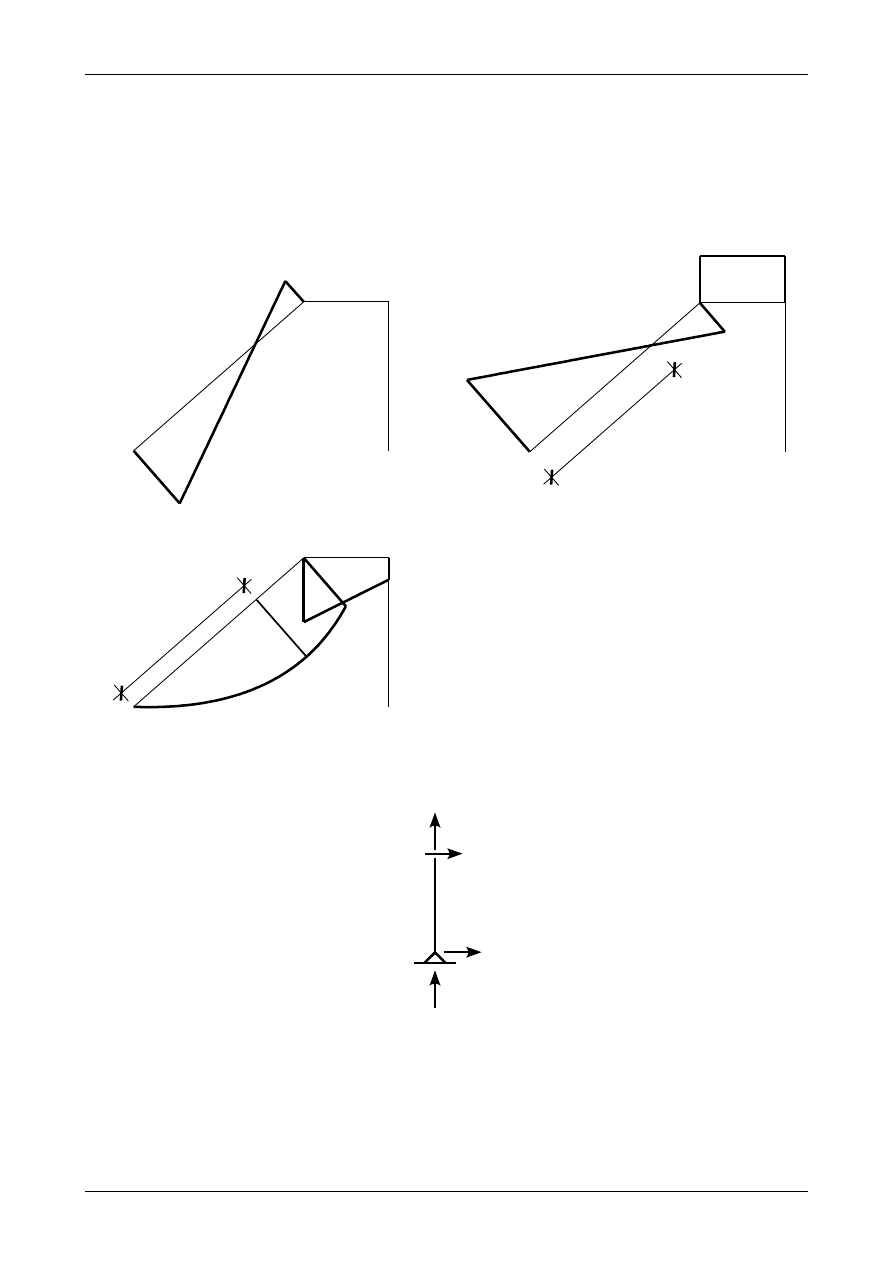
Zgodnie z rysunkiem K1A.27 a) moment zginający w punkcie C wynosi

M

C

=8,0⋅3,5=28,0 kNm

.

(K1B.47)

Znak plus oznacza, że moment ten rozciąga lewą część przekroju ramy. Zgodnie z rysunkiem K1A.27 b)
moment zginający w punkcie D wynosi

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

18

M

D

=0,0 kNm

.

(K1B.48)

Rysunek K1A.28 przedstawia wykresy sił przekrojowych w przedziale CD. Są to także ostatecznie wykresy
sił przekrojowych dla ramy.

3,8

02

3,8

02

N [kN]

M [kNm]

-45

,07

+1

7,9

2

+5

1,5

2

-20

,49

82

,46

0,0

97

,94

82

,4

6

2

8,

0

0,0

-27,22

T [kN]

Rys. K1B.25. Wykresy sił przekrojowych w przedziale BC.

D

8,0 kN

27,22kN

T

(CD)

N

(CD)

Rys. K1B.26. Równowaga siły normalnej i poprzecznej w przedziale CD.

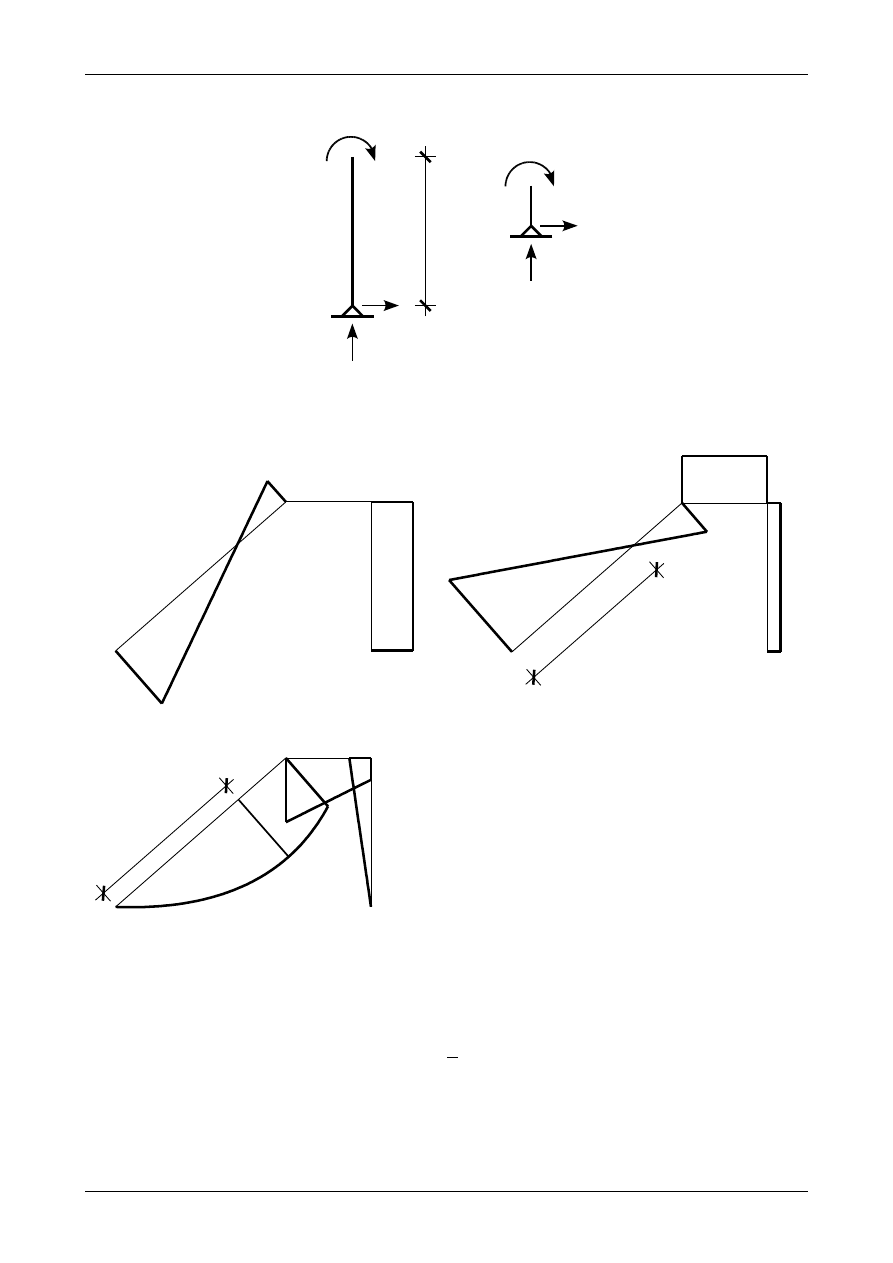
Rysunek K1A.29 przedstawia równowagę pręta ukośnego. Wartości sił przekrojowych w punkcie B
odczytamy na podstawie wykresów z rysunku K1A.28. Aby sprawdzić równowagę tego pręta należy
sprawdzić warunek sumy momentów wszystkich sił działających na ten pręt względem punktu A.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

19

3,

5

D

8,0 kN

26,0 kN

M

C

a)

D

8,0 kN

26,0 kN

M

D

b)

Rys. K1B.27. Równowagi odciętych części ramy w przedziale CD.

3,8

02

3,8

02

N [kN]

M [kNm]

-45

,07

+1

7,9

2

+5

1,5

2

-20

,49

82

,46

0,0

97

,94

82

,4

6

2

8,0

28,0

0,0

0,0

-27,22

-8

,0

-2

7

,2

2

T [kN]

Rys. K1B.28. Ostateczne wykresy sił przekrojowych dla ramy.

 M

A

 AB

=0

−20,49⋅5,315−82,4618,0⋅5,315⋅

1
2

⋅4,0=−0,024kNm≈0

.

(K1B.49)

Jak więc widać pręt ukośny znajduje się w równowadze.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

20

4,0

A

20

,49

kN

3,

5

α

- 5

,31

5 -

68,45 kN

18

,0

kN

/m

W

=18,0⋅5,315

17

,92

kN

82

,46

kN

m

Rys. K1B.29. Równowaga pręta ukośnego.

K1A.8 Zadanie 4

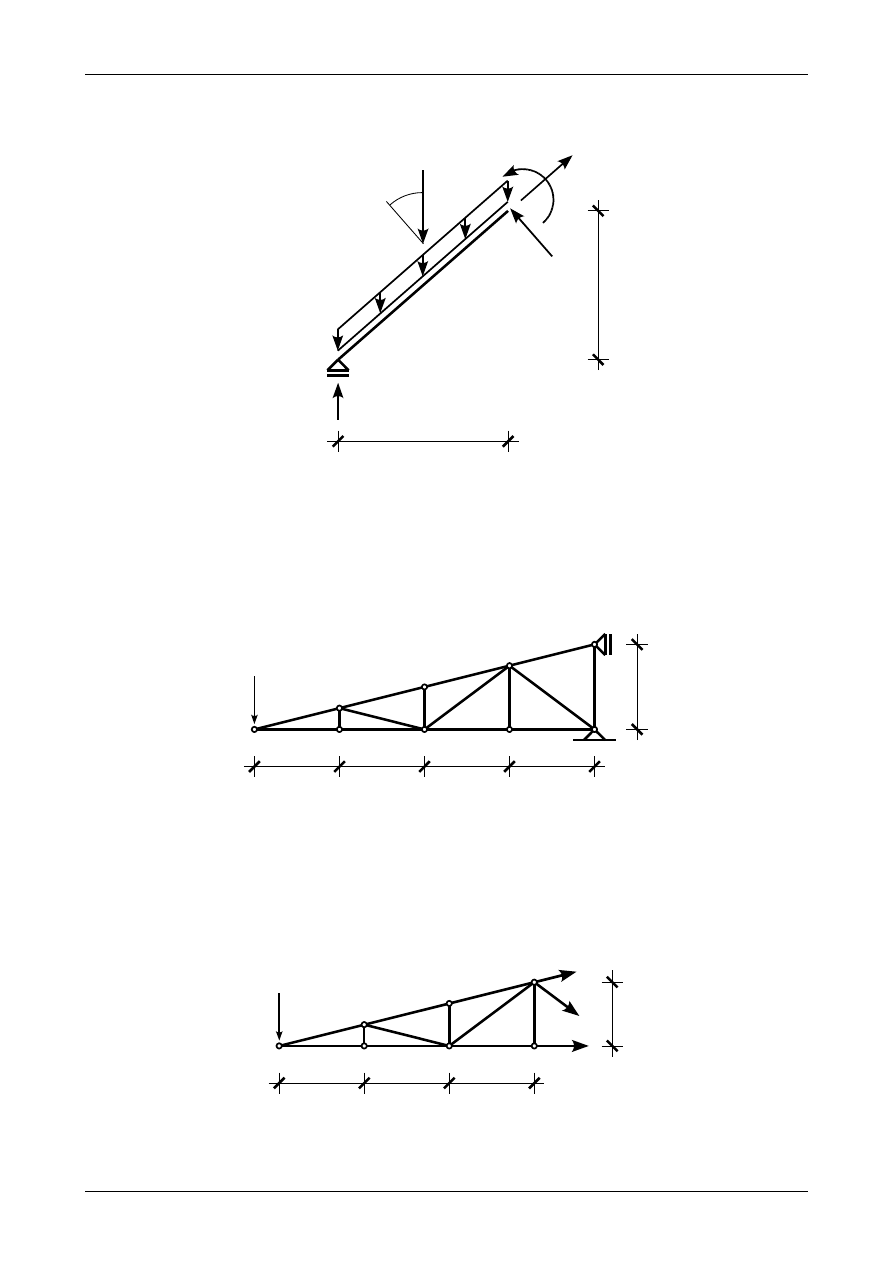
Wyznaczyć metodą Rittera siły w prętach oznaczonych literą R1 i R2 kratownicy na rysunku K1BA.30.

Wymiary kratownicy podane są w metrach. Pręty pasa górnego znajdują się na jednej linii.

3,0

3,0

3,0

3,0

3,

0

35,0 kN

R

1

R

2

Rys. K1B.30. Kratownica.

K1A.9 Rozwiązanie zadania 4

Rysunek K1B.31 przedstawia odciętą część kratownicy z zaznaczoną przyjętą dodatnią (rozciągającą)

siłą w pręcie R

1

.

3,0

3,0

3,0

2,

25

35,0 kN

R

1

1

Rys. K1B.31. Równowaga odciętej części kratownicy.

Dr inż. Janusz Dębiński

BDM

05/06

K1B. KOLOKWIUM NUMER 1 – ROZWIĄZANIA – RZĄD B

21

Punktem Rittera dla tej siły jest punkt numer 1. Siłę w pręcie R

1

wyznaczymy z warunku sumy momentów

wszystkich sił działających na część kratownicy względem punktu numer 1.

 M

1

=0

−R

1

⋅2,25−35,0⋅9,0=0

R

1

=−140,0 kN

.

(K1B.50)

Siła w pręcie R

1

jest ściskająca.

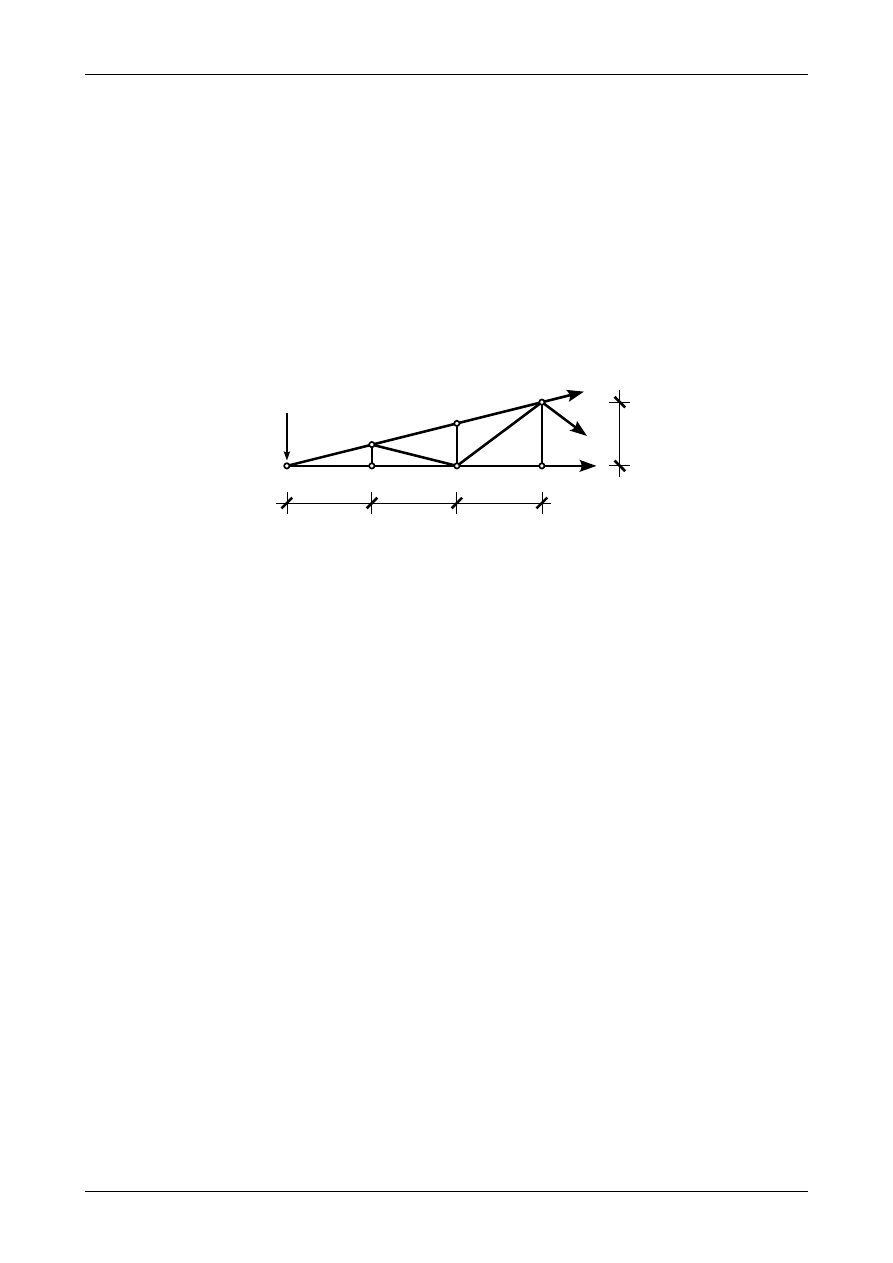
Rysunek K1B.32 przedstawia odciętą część kratownicy z zaznaczoną przyjętą dodatnią (rozciągającą) siłą w
pręcie R

2

.

3,0

3,0

3,0

2,

25

35,0 kN

2

R

2

Rys. K1B.32. Równowaga odciętej części kratownicy.

Punktem Rittera dla tej siły jest punkt numer 2. Siłę w pręcie R

2

wyznaczymy z warunku sumy momentów

wszystkich sił działających na część kratownicy względem punktu numer 2. Siłą ta jak widać wynosi zero.

(K1B.1)

Dr inż. Janusz Dębiński

BDM