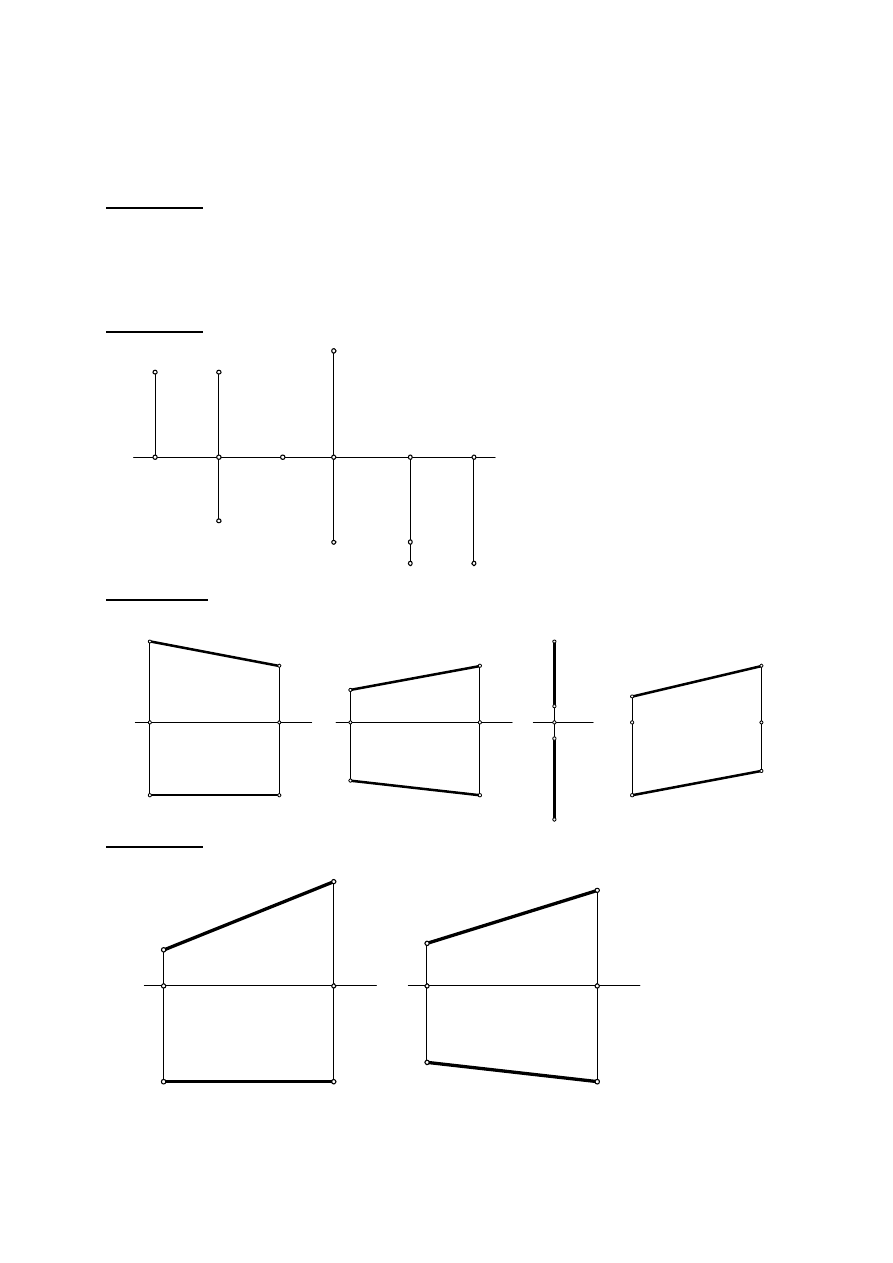
Rok akademicki 2008/2009

GEOMETRIA WYKREŚLNA – ĆWICZENIA
ZESTAW I

Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na
jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni są usytuowane.
A (10,20,30),

B (20,-10,30),

C (30,-20,-20),

D (15,30,-10),

E (40,0,-30),

F (50,0,0),

G (25,-20,20),

H (30,10,20),

J (10,-30,-10),

K (40,-30,10),

L (15,-10,-25),

Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty:

x

A''

A

x

A'

B'

B''

B

x

C

x

F

x

C'C''

F'

F''

E

x

E''

E'

D

x

D'

D''

Zadanie I. 3. Odcinek AB, CD, EF, GH rozdzielić w stosunku zaznaczonym na rysunkach

1:2

1:4

3:2

2:5

x

A''

B''

A

x

B

x

A'

B'

x

C''

D''

C

x

D

x

C'

D'

x

E''

F''

F

x

E

x

E'

F'

x

H''

G''

H

x

G

x

H'

G'

Zadanie I. 4. Na odcinkach AB i CD wyznaczyć punkt E oddalony od punktu A o 40 mm, a
od punktu C o 50 mm

x

A''

B''

A

x

B

x

A'

B'

x

C''

D''

C

x

D

x

C'

D'

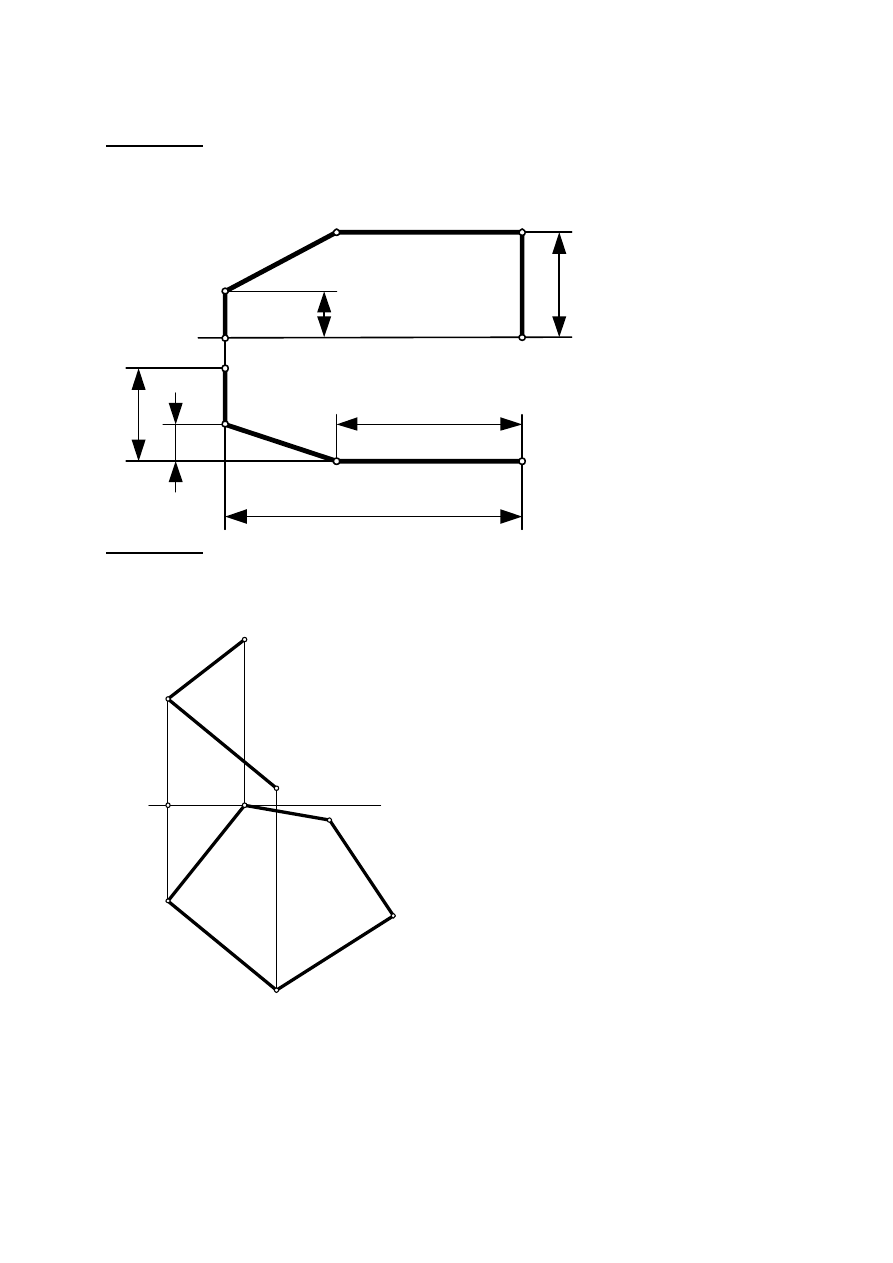
Zadanie I. 5. Określić graficznie rzeczywistą długość rurociągu / linii łamanej/. Wymiary
podano w metrach. Narysować rurociąg w aksonometrii.

x

A''B''

A'

B'

C''

C'

D''

D'

E'F'

E''

F''

13

20

2

5

,5

4

8

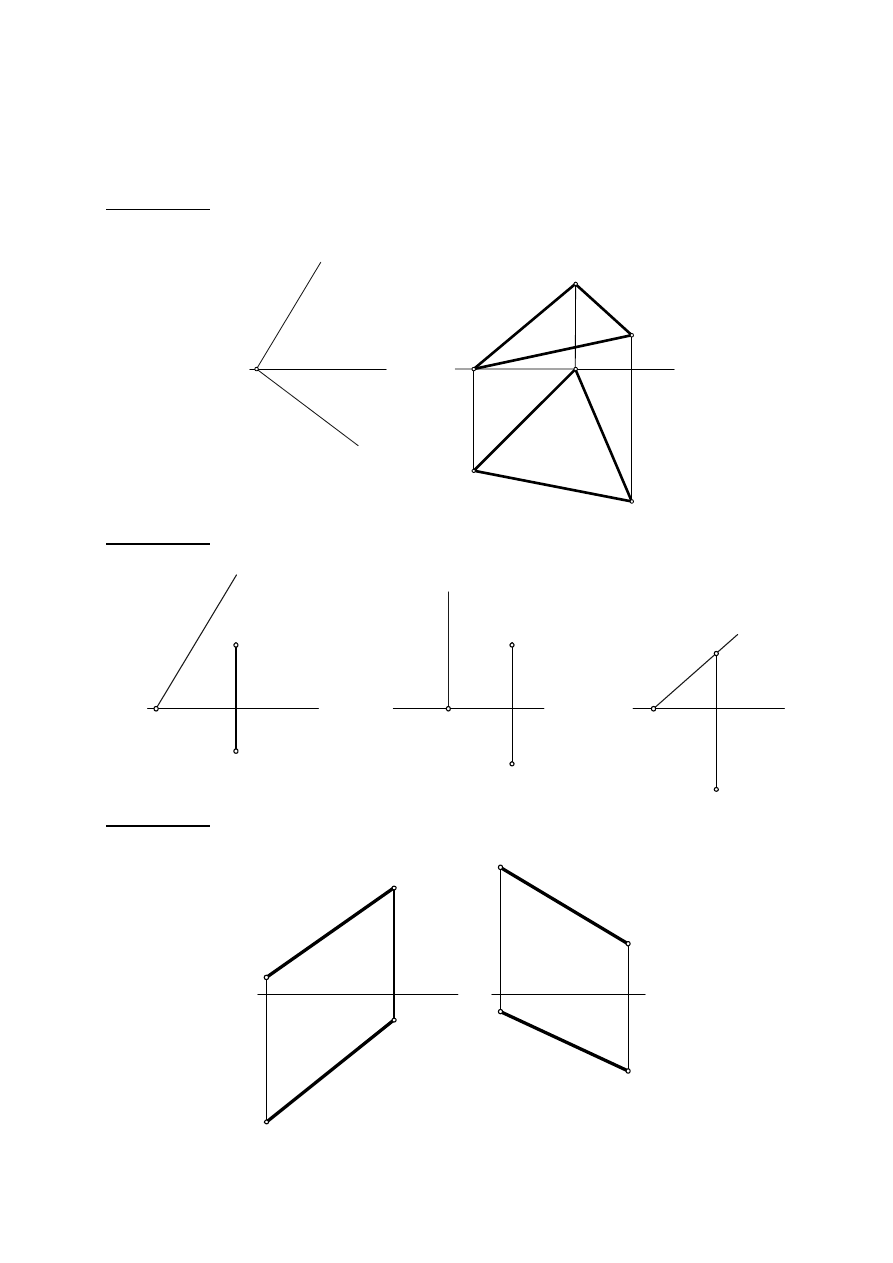
Zadanie I. 6. Wykreślić rzut pięcioboku na rzutni

Π

2

mając rzut tego pięcioboku na rzutni

Π

1

oraz dwa jego boki na rzutni

Π

2

. Narysować rzut tej figury na rzutni bocznej

Π

3

oraz

wykreślić rzeczywistą jej wielkość wykorzystując dwukrotną zmianę rzutni.

E''

x

A''

B''

A

x

B

x

A'

B'

C'

D'

E'

Rok akademicki 2008/2009

GEOMETRIA WYKREŚLNA – ĆWICZENIA
ZESTAW II

Zadanie II. 1. Na płaszczyźnie

α

narysować prostą poziomą w odległości a=30 mm od

powierzchni rzutni

Π

1

oraz narysować prostą czołową znajdującą się w odległości 45 mm od

Π

2

. To samo zadanie wykonać dla płaszczyzny określonej trójkątem ABC.

Π

2

ν

α

x

α

h

α

Π

1

A'

B''

C'

B'

A''

C''

Zadanie II. 2. Wykreślić brakujące ślady płaszczyzny zadanej jednym śladem i punktem
leżącym na tej płaszczyźnie.

ν

γ

x

γ

ν

α

x

α

A'

B''

C'

B'

A''

C''

ν

β

x

β

Zadanie II. 3. Prosta AB leży na płaszczyźnie poziomorzucającej a prosta CD na
płaszczyźnie pionoworzucającej. Wykreślić ślady tych płaszczyzn.

x

C''

C'

D''

D'

x

A''

m

'

A'

B''

B'

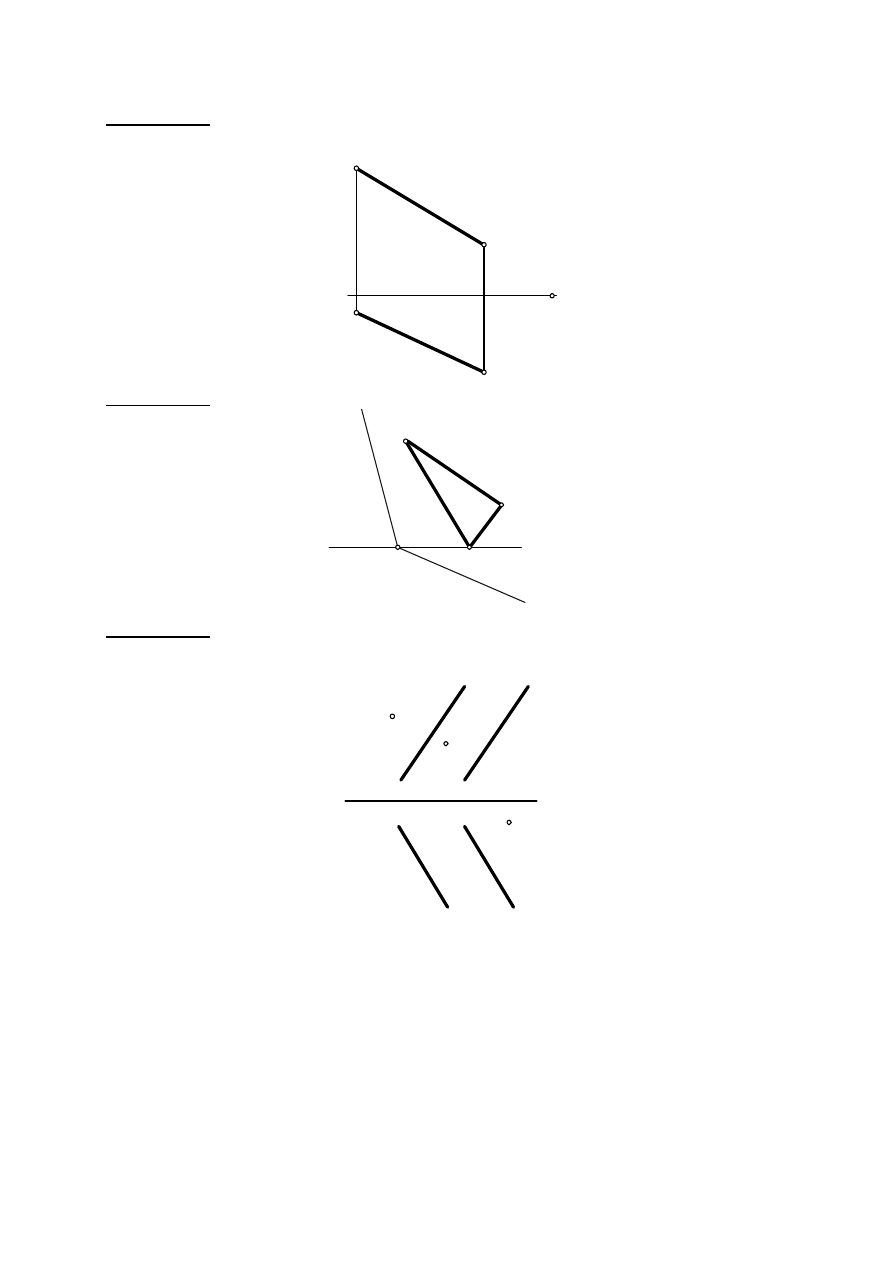
Zadanie II. 4. Prosta CD leży na dowolnej płaszczyźnie przecinającej się z osią x w punkcie
zbiegu x

α

. Wykreślić ślady tej płaszczyzny.

x

α

x

C''

C'

D''

D'

Zadanie II. 5. Wykreślić brakujące rzuty trójkąta ABC leżącego na płaszczyźnie

α

.

ν

α

x

α

h

α

B''

A''

C''

Zadanie II. 6. Znaleźć brakujące rzuty punktów A, B, C leżących na płaszczyźnie
wyznaczonej prostymi równoległymi l i m.

Π

1

B''

A''

C''

l''

m'

l'

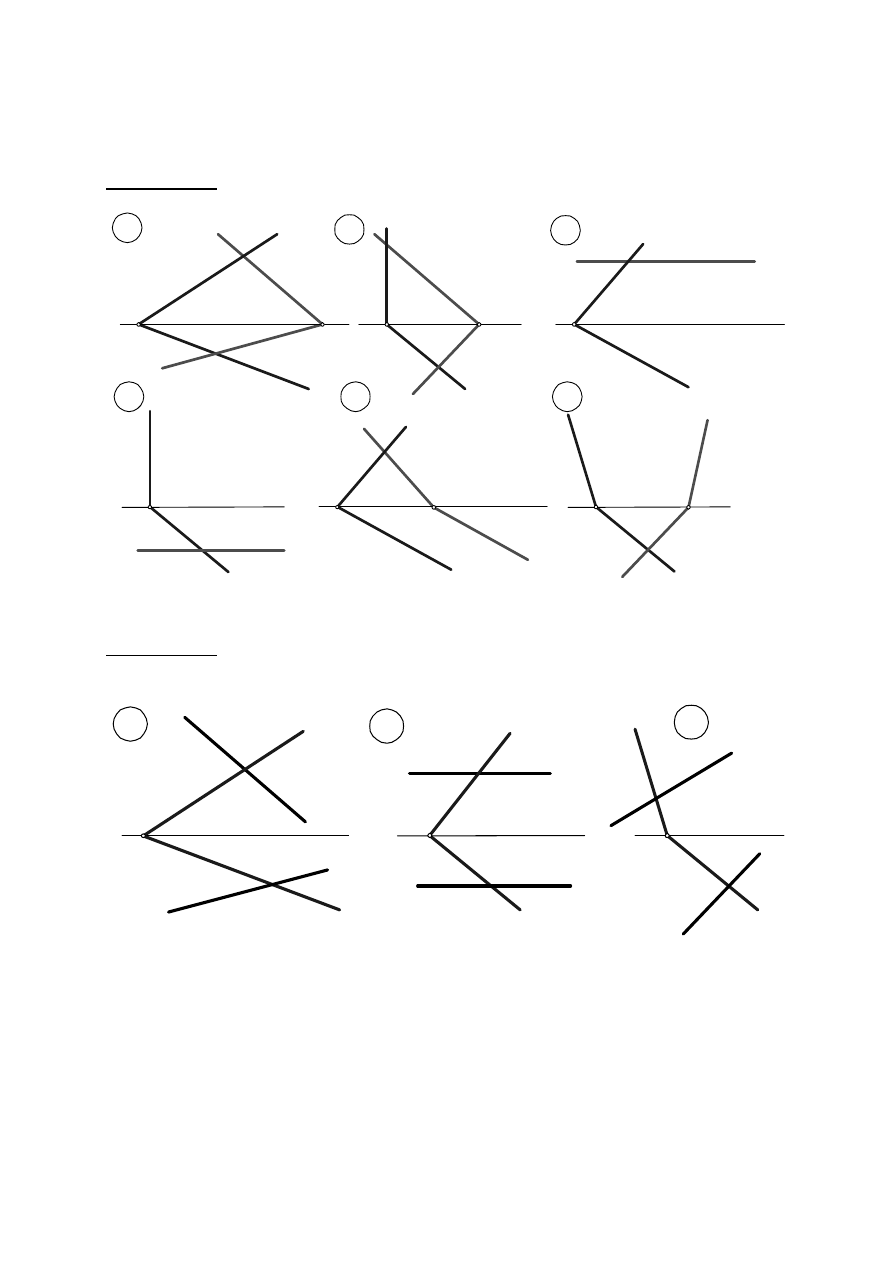
GEOMETRIA WYKREŚLNA – ĆWICZENIA

Rok akademicki 2008/2009

ZESTAW III

Zadanie III. 1. Wykreślić linię przecięcia się płaszczyzn

α

i

β

x

α

ν

β

h

β

x

β

ν

α

h

α

ν

β

h

β

x

β

ν

α

h

α

ν

β

x

α

ν

α

h

α

x

α

h

β

ν

α

h

α

ν

β

x

α

ν

α

h

α

x

α

x

β

h

β

ν

β

h

β

x

β

ν

α

h

α

x

α

1

2

3

6

5

4

Zadanie III. 2. Wyznaczyć punkt przebicia prostej z płaszczyzną. Określić widoczność
prostej

x

α

a'

x

β

ν

α

h

α

ν

α

h

α

x

α

ν

α

l'

h

α

x

α

1

2

3

l''

m'

m''

a''

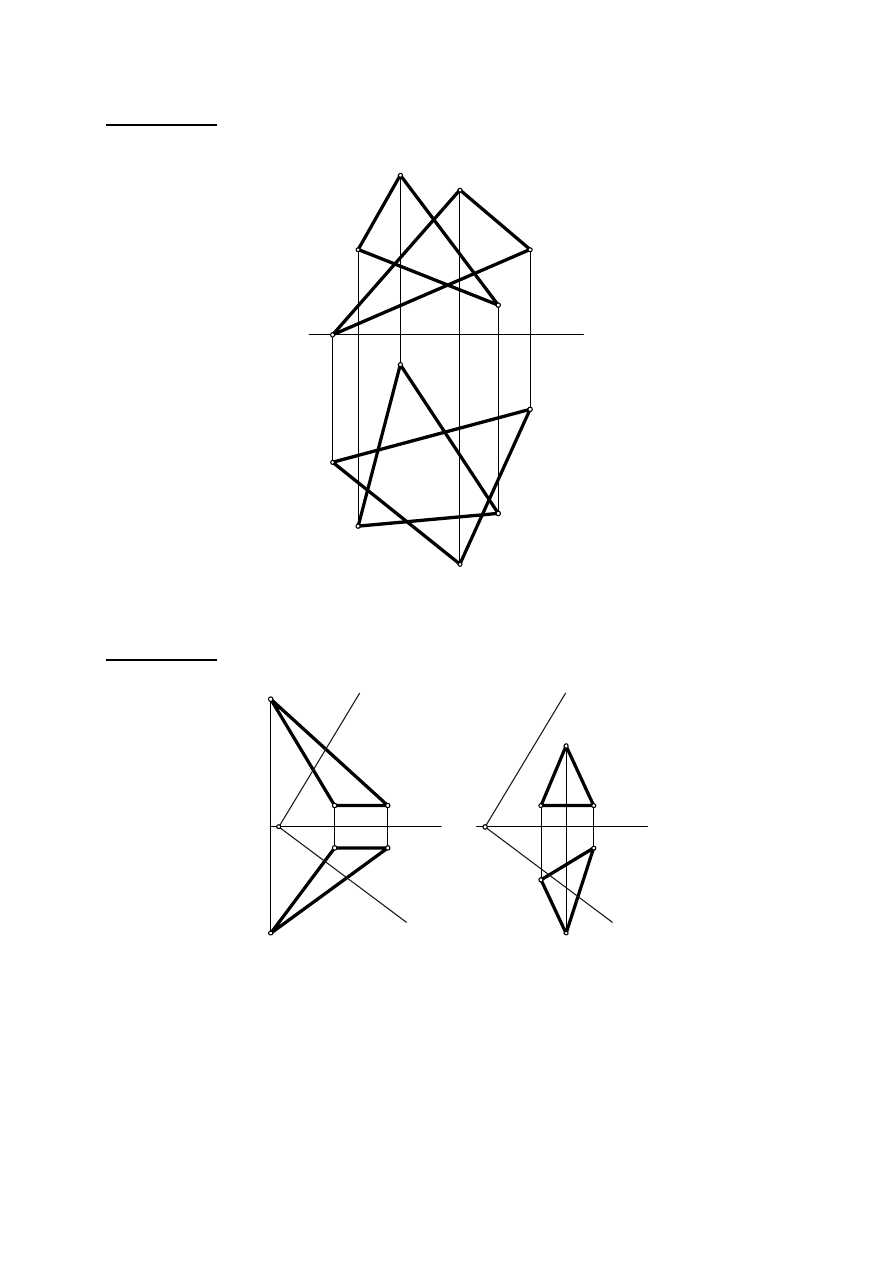
Zadanie III. 3. Wykreślić krawędź przecięcia dwóch trójkątów i określić ich widoczność.

A'

B''

C'

B'

A''

C''

E''

F''

G''

E'

G'

F'

Zadanie III. 4. Wykreślić linię przecięcia trójkąta ABC z płaszczyzną

α

. Określić

widoczność.

ν

α

x

α

h

α

C''

C'

A''

A'

B'

B''

ν

α

x

α

h

α

C''

C'

A''

A'

B'

B''

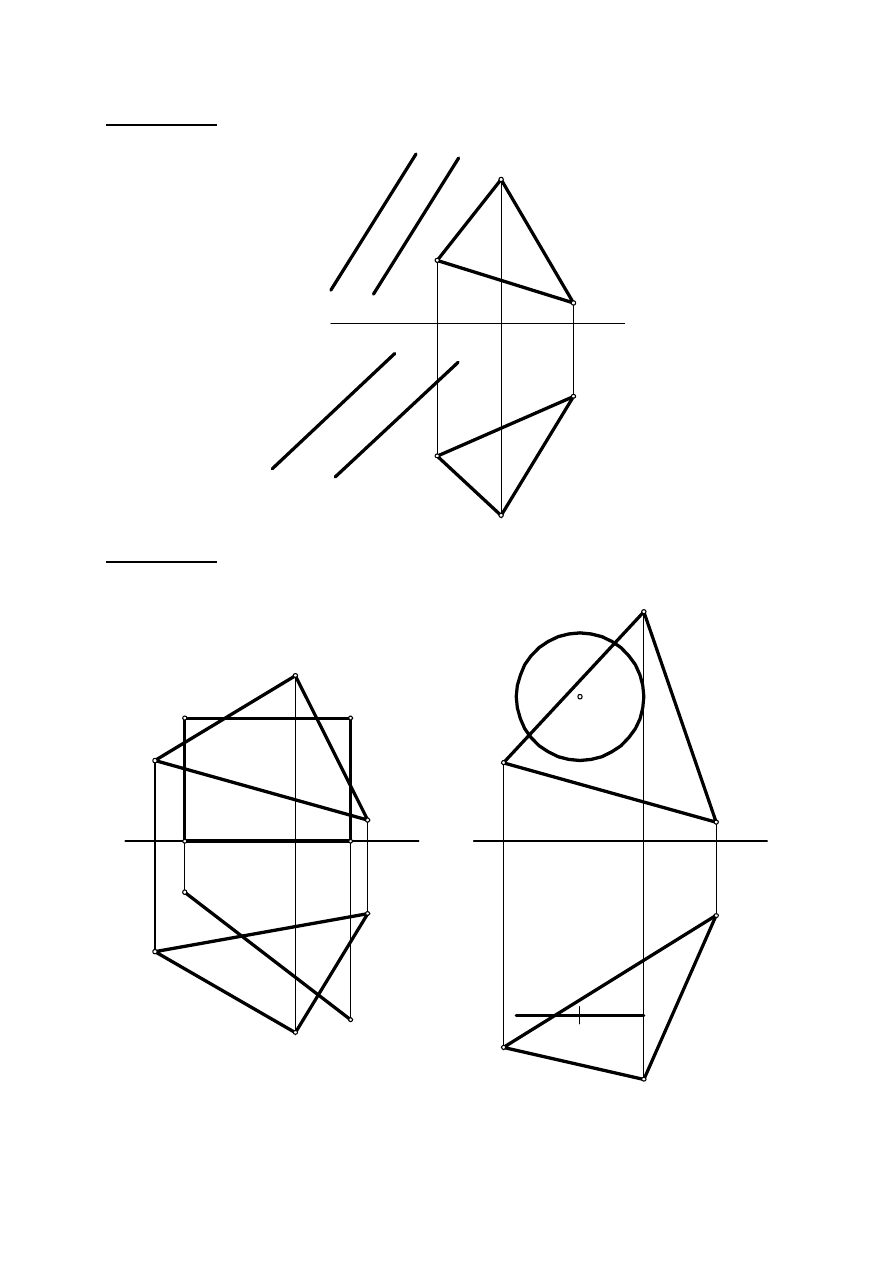
Zadanie III. 5. Wykreślić linię przecięcia dwóch płaszczyzn, utworzonych przez dwie proste
równoległe m i n oraz trójkąt ABC.

A'

B''

C'

B'

A''

C''

m''

n''

m'

n'

Zadanie III. 6. Wyznaczyć krawędź przecięcia figur płaskich i określić widoczność.

A'

B''

C'

B'

A''

C''

D''

E''

F''

G''

F'G'

D'E'

A'

B''

C'

B'

A''

C''

O'

O''

GEOMETRIA WYKREŚLNA – ĆWICZENIA

Rok akademicki 2008/2009

ZESTAW IV

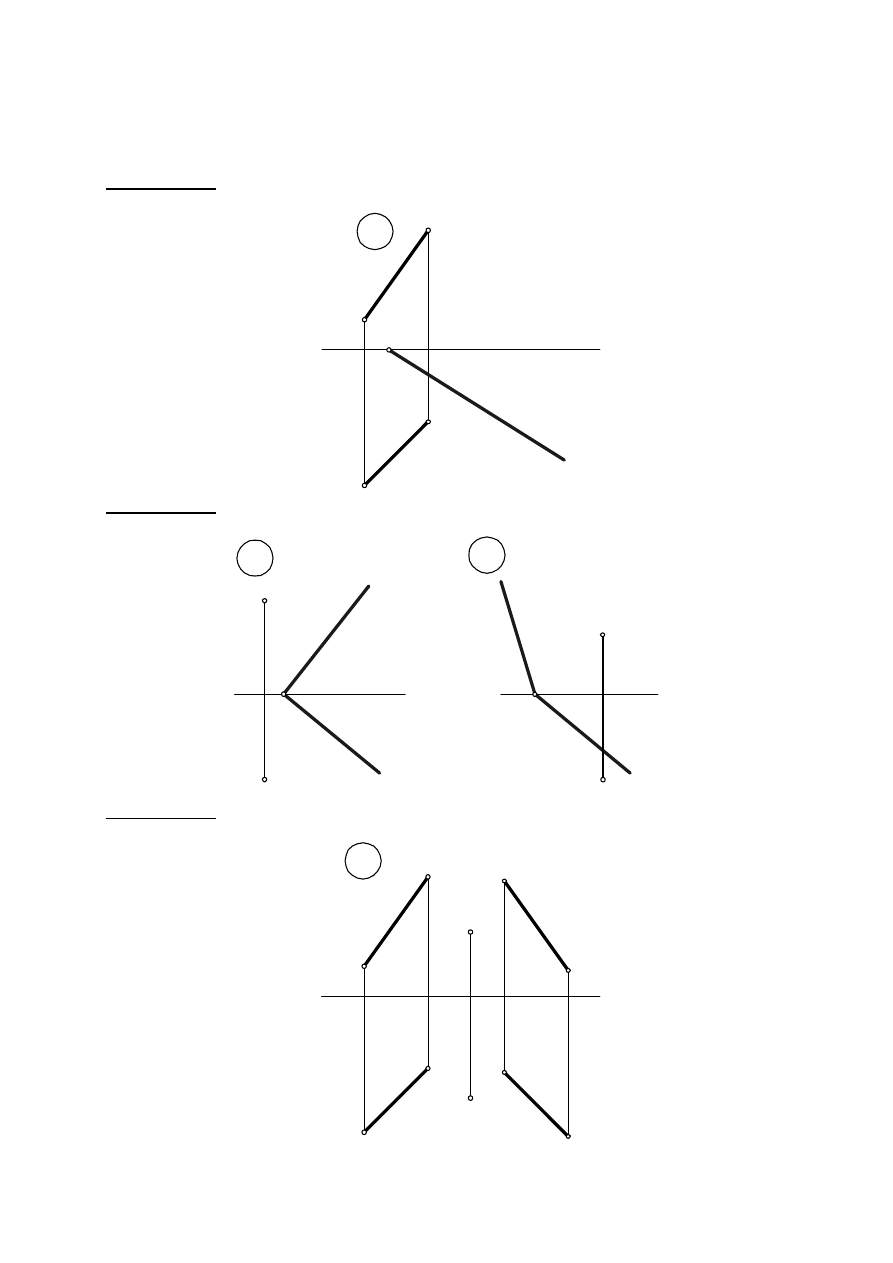
Zadanie IV. 1. Wykreślić pionowy ślad płaszczyzny

α

równoległej do prostej AB mając

zadany jeden ślad płaszczyzny

x

α

A'

h

α

1

B'

B''

A''

X

Zadanie IV. 2. Przez punkt A poprowadzić płaszczyznę

β

równoległą do płaszczyzny

α

.

Wyznaczyć jej ślady.

ν

α

h

α

x

α

ν

α

h

α

x

α

1

2

A'

A''

A'

A''

Zadanie IV. 3. Przez punkt A poprowadzić płaszczyznę

β

równoległą do odcinków prostych

BC i DE. Wyznaczyć jej ślady.

C'

1

B'

B''

C''

X

A'

D'

D''

A''

E'

E''

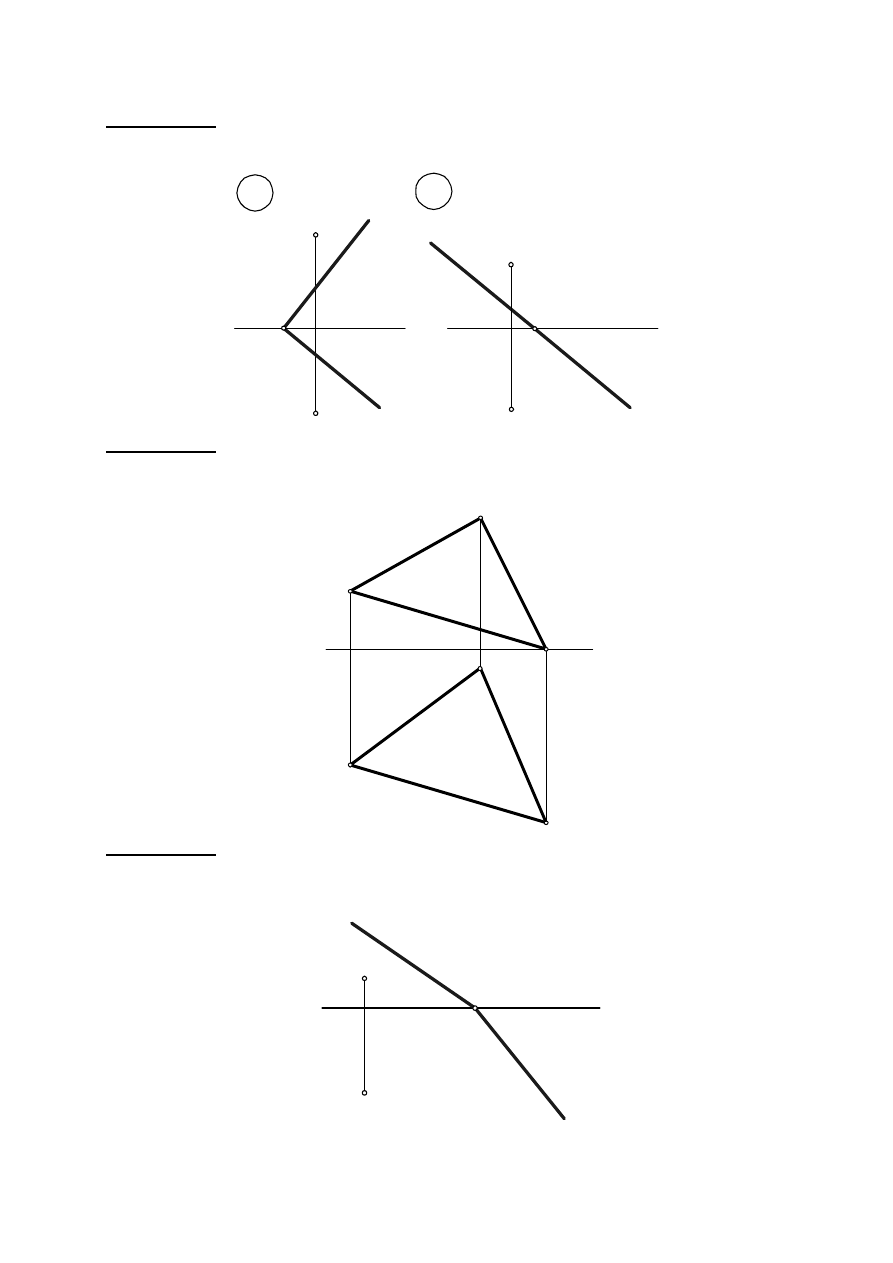
Zadanie IV. 4. Przez punkt A poprowadzić prostą prostopadłą do płaszczyzny

α

i wyznaczyć

punkt przebicia, określić odległość punktu A od płaszczyzny

α .

Określić widoczność prostej.

ν

α

h

α

x

α

ν

α

h

α

x

α

1

2

A'

A''

A'

A''

Zadanie IV. 5. Z punktu A wykreślić prostą prostopadłą do trójkąta ABC, wyznaczyć na niej
punkt D oddalony od punktu A o 50 mm. Punkt D jest punktem podstawy graniastosłupa o
podstawie trójkąta prawidłowego i ścianach prostopadłych do podstawy.

A'

B''

C'

B'

A''

C''

x

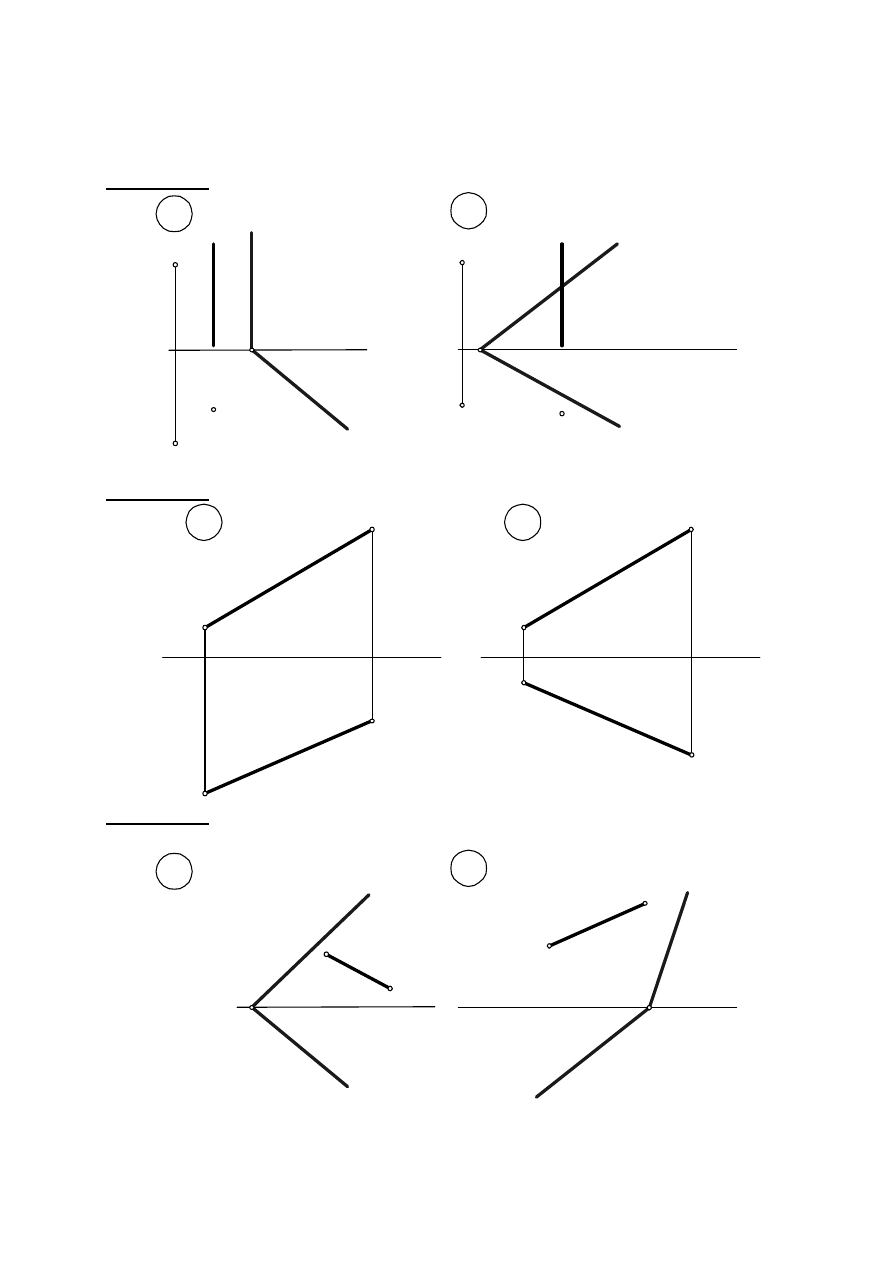
Zadanie IV. 6. Przez punkt A poprowadzić płaszczyznę

α

prostopadłą do płaszczyzny

β.

Punkt zbiegu płaszczyzny

α

z osią X jest dowolny. Wykreślić krawędź przecięcia

płaszczyzn.

x

β

A'

ν

β

h

β

A''

X

GEOMETRIA WYKREŚLNA – ĆWICZENIA

Rok akademicki 2008/2009

ZESTAW V

Zadanie V. 1. Obracając punkt A wokół osi o wprowadzić go na płaszczyznę

α

.

ν

α

h

α

x

α

ν

α

h

α

x

α

1

2

A''

A'

O''

O''

A''

A'

O''

O''

Zadanie V. 2. Określić rzeczywistą wielkość odcinka AB metodą obrotu.

1

B'

B''

X

A'

A''

2

B'

B''

X

A'

A''

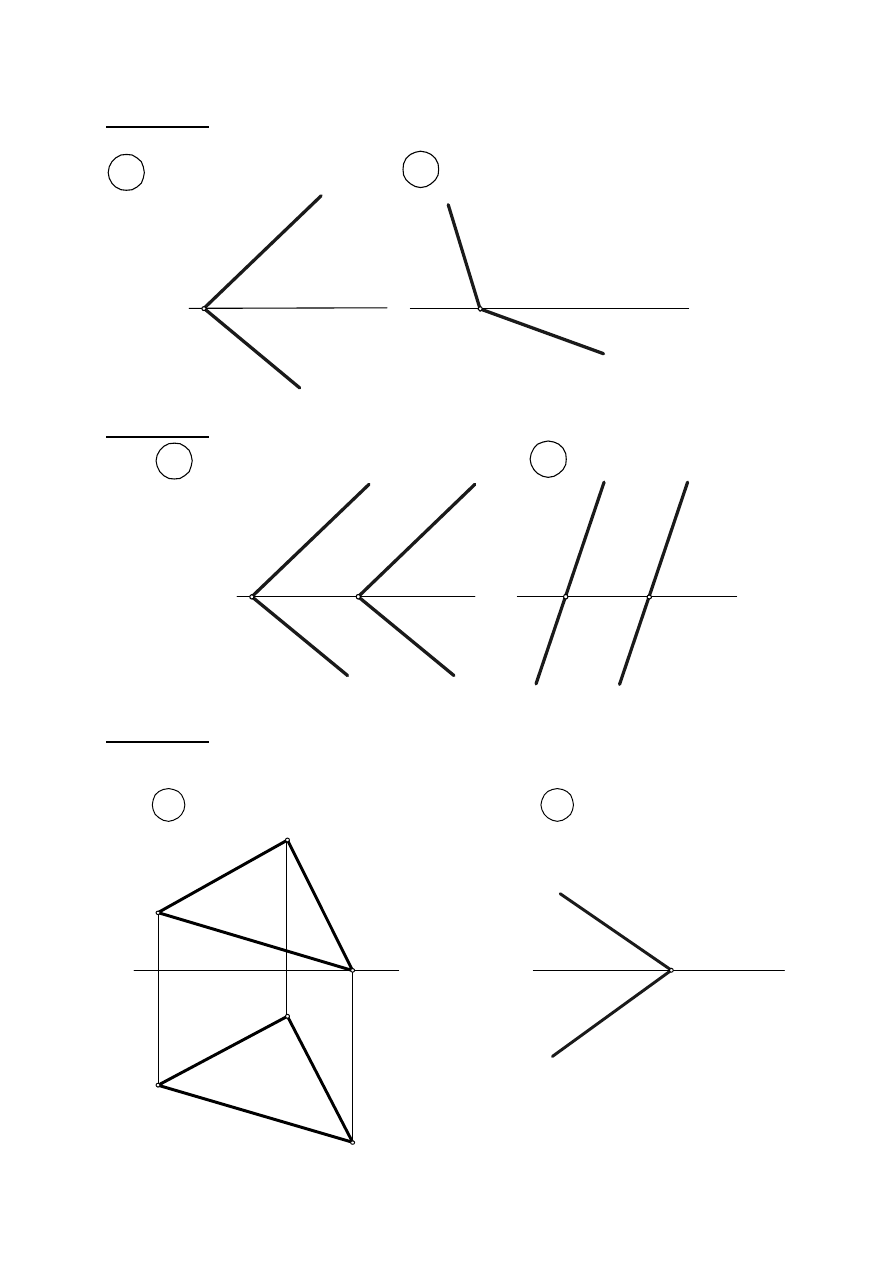
Zadanie V. 3. Wykreślić rzuty trójkąta równoramiennego leżącego na płaszczyźnie

α

z

wierzchołkiem C na śladzie poziomym. Dany jest bok trójkąta AB i ślady płaszczyzny

α.

ν

α

h

α

x

α

ν

α

h

α

x

α

1

2

A''

B''

A''

B''

Zadanie V. 4. Wykreślić rzuty okręgu o średnicy

∅

60 leżącego na płaszczyźnie

α

i

stycznego do śladów tej płaszczyzny.

ν

α

h

α

x

α

ν

α

h

α

x

α

1

2

Zadanie V. 5. Określić odległość między powierzchniami

α

i

β

.

ν

α

h

α

x

β

ν

β

h

β

x

α

1

2

x

α

ν

α

h

α

ν

β

h

β

x

β

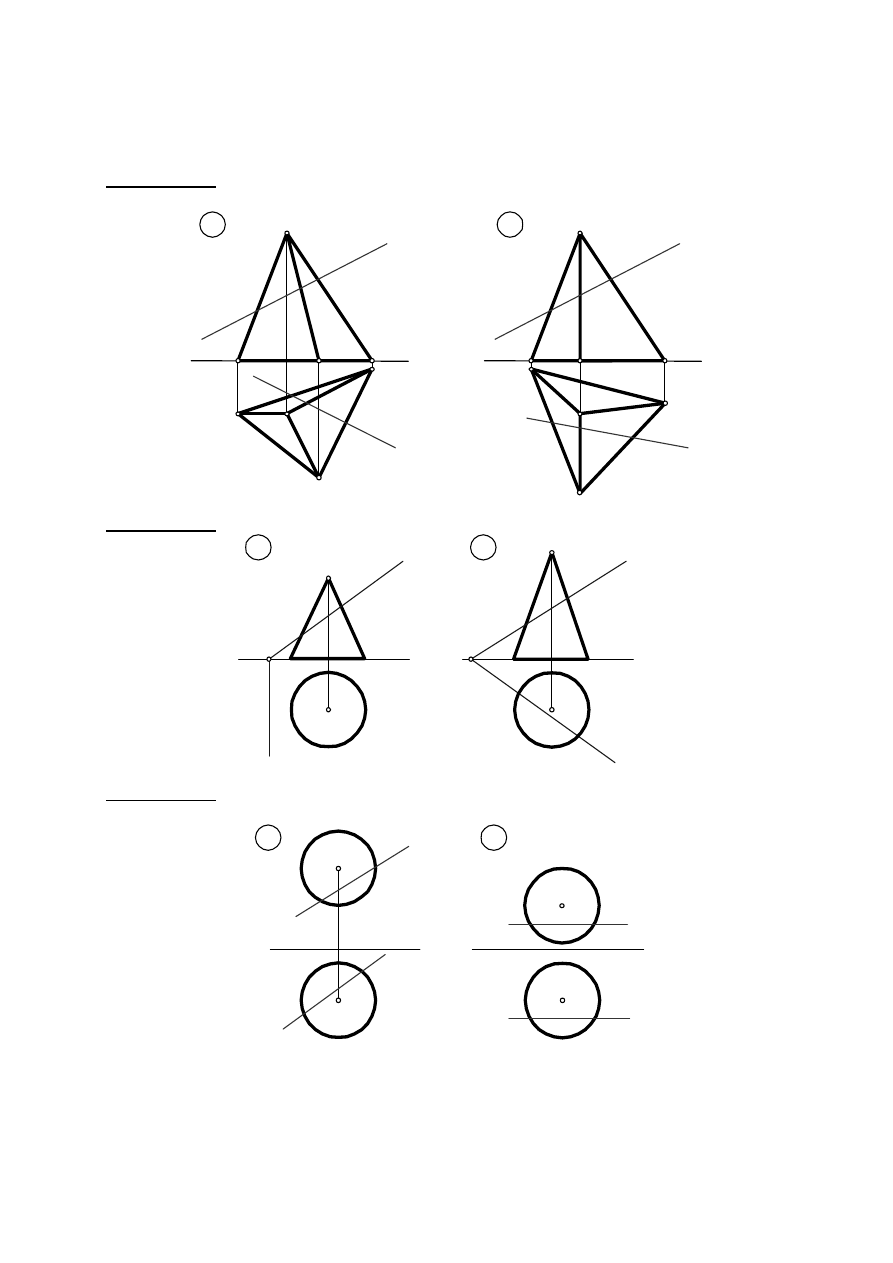
Zadanie V. 6. Określić rzeczywisty kąt pochylenia płaszczyzny trójkąta ABC względem
rzutni

Π

1

. Określić kąt rzeczywisty pochylenia płaszczyzny

β

względem rzutni

Π

2

.

A'

B''

C'

B'

A''

C''

x

x

β

ν

β

h

β

X

1

2

GEOMETRIA WYKREŚLNA – ĆWICZENIA

Rok akademicki 2008/2009

ZESTAW VI

Zadanie VI. 1. Wyznaczyć punkty przebicia powierzchni ostrosłupa prostą l. Określić
widoczność.

h

α

C''

C'

A''

A'

B'

B''

W''

W'

l''

l'

1

2

C''

C'

A''

A'

B'

B''

W''

W'

l''

l'

Zadanie VI. 2. Wykonać rozwinięcie stożka ściętego /model/.

h

α

W''

ν

α

W'

x

α

h

α

W''

ν

α

W'

x

α

1

2

Zadanie VI. 3. Wyznaczyć punkty przebicia kuli prostą l i określić widoczność.

O''

O'

x

O'

1

2

l'

l''

O''

l'

l''

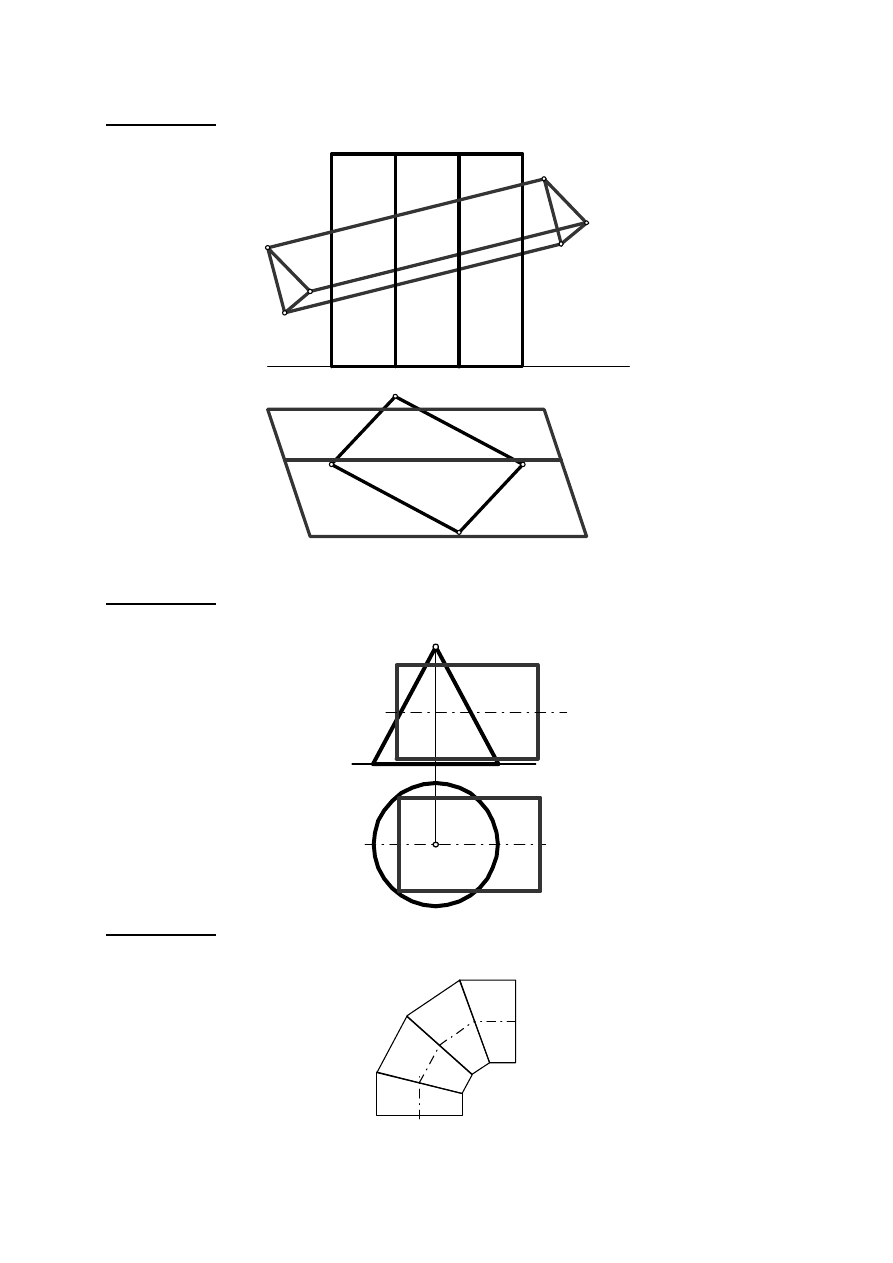
Zadanie VI. 4. Wyznaczyć linie przenikania się brył. Oznaczyć wszystkie wierzchołki brył,
określić widoczność – sporządzić siatkę widoczności oraz siatkę jednej bryły (do wyboru).

Zadanie VI. 5. Wyznaczyć linię przenikania walca ze stożkiem. Narysować trzeci rzut.

W''

W'

x

Zadanie VI. 6. Narysować kolanko rurociągu walcowego o średnicy

∅

800 mm składającego

się z 5/7/, /9/ segmentów. Wykonać rozwinięcie segmentów kolanka, określić kąt jednego
segmentu.