NAPÓR AERODYNAMICZNY

NAPÓR AERODYNAMICZNY

1.

Cel ćwiczenia

Celem ćwiczenia jest doświadczalne i teoretyczne

wyznaczenie wartości naporu aerodynamicznego na powierzchnie

o różnych kształtach.

2.

Podstawy teoretyczne

Naporem aerodynamicznym nazywamy siłę, z jaką

strumień gazu działa na przegrodę ustawioną w linii jego działania

w odległości mniejszej od długości zwartej części strumienia.

Całkowity napór aerodynamiczny strumienia jest sumą

geometryczną naporów elementarnych, wywieranych na zaporę

przez poszczególne cząstki poruszającej się masy gazu.

Z zasady ilości ruchu

(

)

dt

*

P

v

*

m

d

=

i z zasady stałości masy

const

m

=

wynika, iż szybkość geometrycznej zmiany (tj. pochodna

względem czasu) ilości ruchu wyodrębnionej w myśli masy gazu

strumienia jest równa naporowi, jaki ta masa gazu wywiera

na zaporę

dt

dv

m

dt

)

v

m

(

d

P

=

⋅

=

(1)

Nasze rozważania oparte są na następujących założeniach:

 gaz tworzący strumień swobodny jest doskonały

i nieważki, dzięki czemu pole prądu jest

symetryczne względem osi strumienia,

 rozkład prędkości w przekroju poprzecznym

strumienia jest równomierny,

 strumień porusza się w ośrodku, nie wywierającym

wyczuwalnego wpływu na przebieg zjawiska,

 ruch gazu jest ustalony,
 powierzchnia zapory, o którą strumień uderza, jest

doskonale gładka.

Z założeń tych wynika, iż szybkość cząstek gazu

są jednakowe i niezmienne pod względem wartości bezwzględnej,

a napór aerodynamiczny jest wywołany jedynie zmianą kierunku

prędkości pomiędzy przekrojem dopływowym i odpływowym

strumienia. Na rysunku 1 przedstawiono przypadek uderzenia

strumienia o przegrodę, na której rozdziela się on na dwa

strumienie.

Napór aerodynamiczny przedstawić można w postaci:

(

)

2

2

2

1

1

1

0

0

cos

v

Q

cos

v

Q

v

Q

cos

P

α

α

β

ρ

−

−

=

(2)

Uwzględniając, że

2

1

0

Q

Q

Q

+

=

vA

Q

=

oraz

2

1

0

v

v

v

=

=

otrzymamy

2

1

0

A

A

A

=

=

1

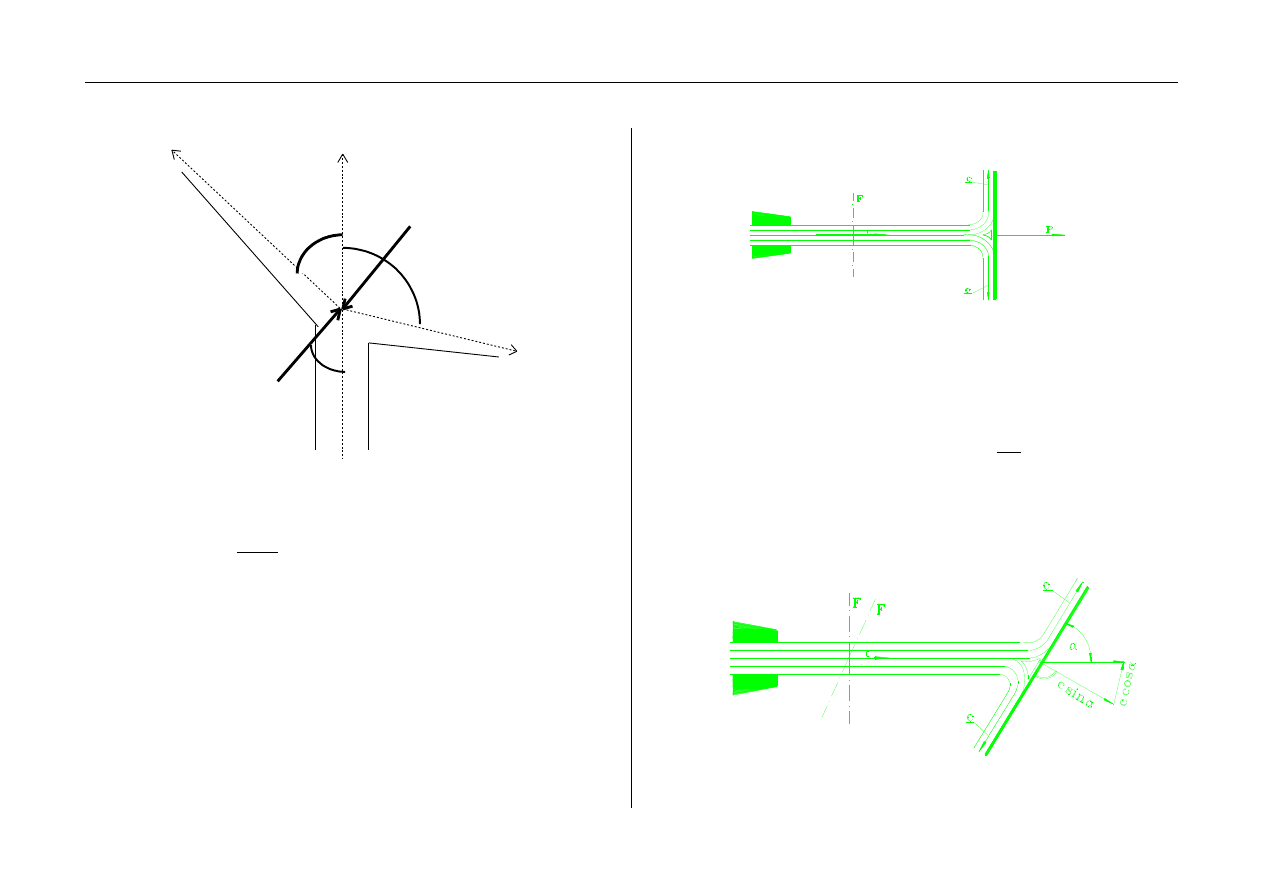
NAPÓR AERODYNAMICZNY

β

v

0

,A

0

α

2

Z

α

1

R

v

1

,A

1

v

2

,A

2

P

Rys. 1. Napór aerodynamiczny na przegrodę.

Równanie (1) przyjmuje postać

(

)

2

2

1

1

0

2

0

cos

A

cos

A

A

cos

v

P

α

α

β

ρ

−

−

⋅

=

(3)

Równanie (3) to ogólna zależność określająca napór

aerodynamiczny. Poniżej rozpatrzymy kilka przypadków

szczególnych.

I. Napór na ścianę płaską prostopadłą do kierunku

strumienia.

a.

ściana nieruchoma.

Strumień swobodny o przekroju F uderza o nieruchomą

ścianę płaską jak na rysunku.

Rys. 2. Napór aerodynamiczny na nieruchomą ścianę płaską prostopadłą

do kierunku strumienia.

Napór aerodynamiczny przedstawia się następująco:

0

2

0

0

0

0

2

0

A

Q

v

Q

A

v

P

ρ

ρ

ρ

=

=

⋅

=

(4)

II. Napór na ścianę płaską nachyloną do kierunku

strumienia

a.

ściana nieruchoma

Rys. 3. Napór aerodynamiczny na nieruchomą ścianę płaską nachyloną

do kierunku strumienia.

2

NAPÓR AERODYNAMICZNY

Gdy strumień gazu uderza o nieruchomą ścianę płaską,

nachyloną do kierunku strumienia pod kątem

α

, napór

aerodynamiczny rozkładamy na dwie składowe: normalną P

n

styczną P

t

. Składowa P styczna naporu wywieranego przez gaz

doskonałą z powodu braku lepkości nie istnieje; składowa

normalna przedstawia całkowity napór aerodynamiczny.

2

©

n

)

sin

v

(

A

P

α

ρ

⋅

⋅

=

(5)

Ponieważ

α

sin

A

A

©

=

zatem

α

ρ

sin

v

A

P

2

n

⋅

⋅

=

(6)

III. Napór na ścianę zakrzywioną

a.

ściana nieruchoma

Strumień gazu doskonałego wywiera napór aerodynamiczny na

nieruchomą ścianę łopatki, mającej kształt powierzchni walcowej,

utworzonej przez proste przechodzące przez łuk AB prostopadłe

do płaszczyzny wyznaczonej przez ten łuk.

)

sin

v

sin

v

(

Q

P

2

2

1

1

x

ε

ε

ρ

⋅

+

⋅

⋅

=

(7)

W przypadku łopatki symetrycznej względem płaszczyzny

przechodzącej przez oś x prostopadle do cięciwy AB.

Wówczas

v

v

v

;

2

1

2

1

=

=

=

=

ε

ε

ε

ε

ρ

sin

v

Q

2

P

x

⋅

⋅

⋅

=

(8)

Jeżeli

°

90

=

ε

, to składowa naporu

v

Q

2

P

⋅

⋅

=

ρ

(9)

Napór aerodynamiczny na półkulistą ścianę jest dwa razy

większy niż napór na ścianę płaską.

Rys. 4. Napór aerodynamiczny na nieruchomą ścianę zakrzywioną.

IV. Napór na ściany płaskie i zakrzywione o powierzchni

niewiele większej od przekroju strumienia

a.

ściana płaska

Gdy zaporę stanowi płytka okrągła, prostopadła do osi

strumienia, wówczas odpływający strumień gazu tworzy

powierzchnię stożkową okalającą całkowicie płytkę

3

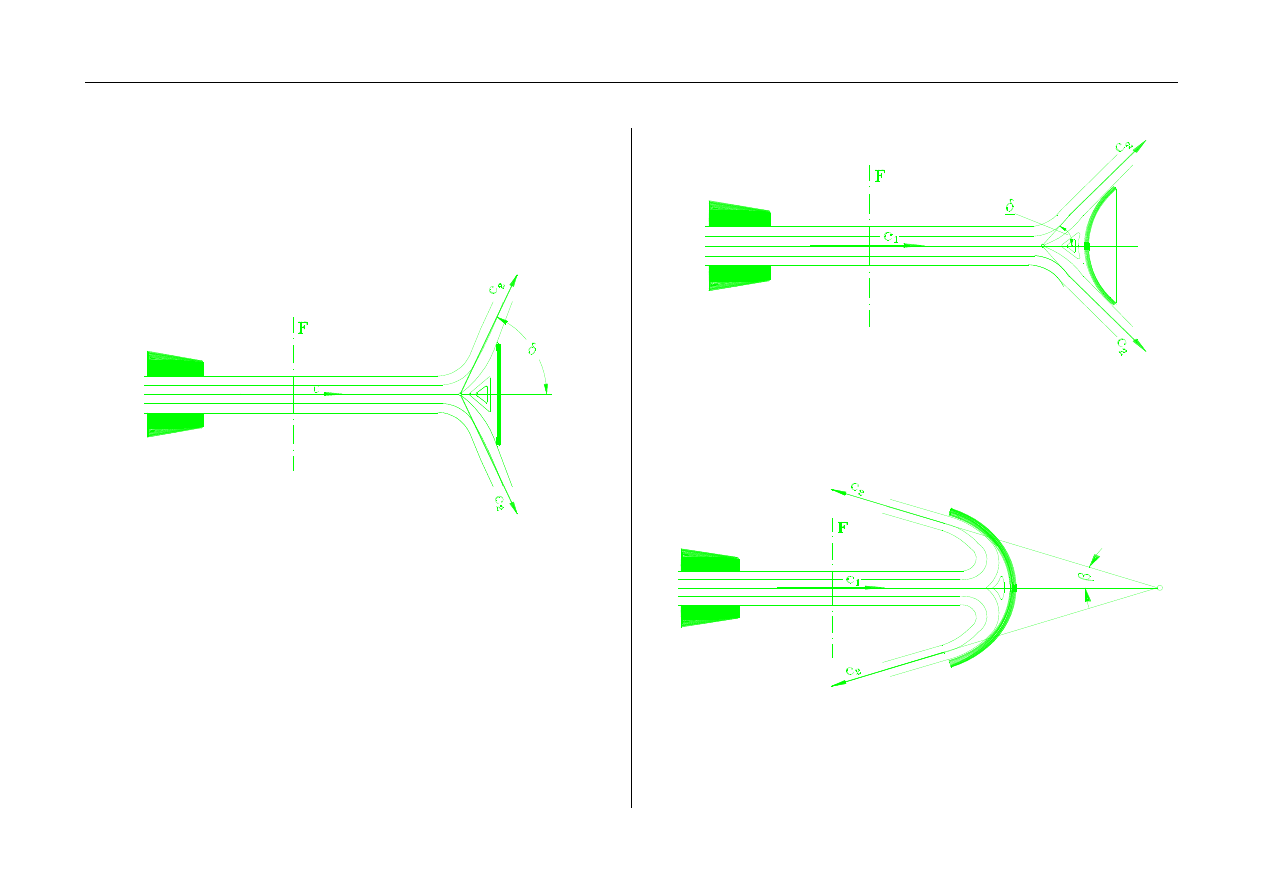
NAPÓR AERODYNAMICZNY

Oznaczając przez

δ

kąt, jaki odpływające strugi tworzą

z kierunkiem zasilania, napór aerodynamiczny określamy wzorem

)

cos

1

(

v

Q

P

δ

ρ

−

=

(10)

Ponieważ dla gazu doskonałego

c

c

c

2

1

=

=

.

Rys. 5. Napór aerodynamiczny na nieruchomą płytkę okrągłą prostopadłą do osi

strumienia.

b. Ściana zakrzywiona

Napór aerodynamiczny na ścianę wypukłą

)

cos

1

(

v

A

)

cos

1

(

v

Q

P

2

δ

ρ

δ

ρ

−

=

−

=

(11)

Rys. 6. Napór aerodynamiczny na nieruchomą ścianę zakrzywioną zwróconą

wypukłością przeciw prądowi.

Napór gazu na powierzchnię wklęsłą

)

cos

1

(

v

A

)

cos

1

(

v

Q

P

2

β

ρ

β

ρ

+

=

+

=

(12)

Rys. 7. Napór aerodynamiczny na nieruchomą ścianę zakrzywioną zwróconą

wklęsłością przeciw prądowi.

Napór maksymalny występuje przy zaporze w kształcie

wklęsłej czaszy półkulistej (

β

= 0).

4

NAPÓR AERODYNAMICZNY

2

max

v

A

2

v

Q

2

P

ρ

ρ

=

=

(13)

Jeżeli kulista czasza, zasilana przez strumień po stronie

wklęsłej, porusza się z prędkością u w kierunku osi strumienia,

wówczas napór aerodynamiczny

)

cos

1

(

)

u

v

(

Q

P

β

ρ

+

−

=

(14)

Napór maksymalny przy

β

= 0

)

u

v

(

Q

2

P

max

−

=

ρ

(15)

3.

Opis stanowiska pomiarowego

Podstawowymi elementami stanowiska laboratoryjnego są:

 układ zasilający z możliwością regulacji natężenia

przepływu UZ,

 dysza wypływowa D z pomiarem różnicy ciśnień

∆

p,

 rotametr R,
 wymienna przegroda,
 waga W,
 manometr M.

Rys. 8. Wymienne przegrody: płaska, cylindryczna

Rys. 9. Schemat stanowiska do wyznaczania naporu aerodynamicznego

5

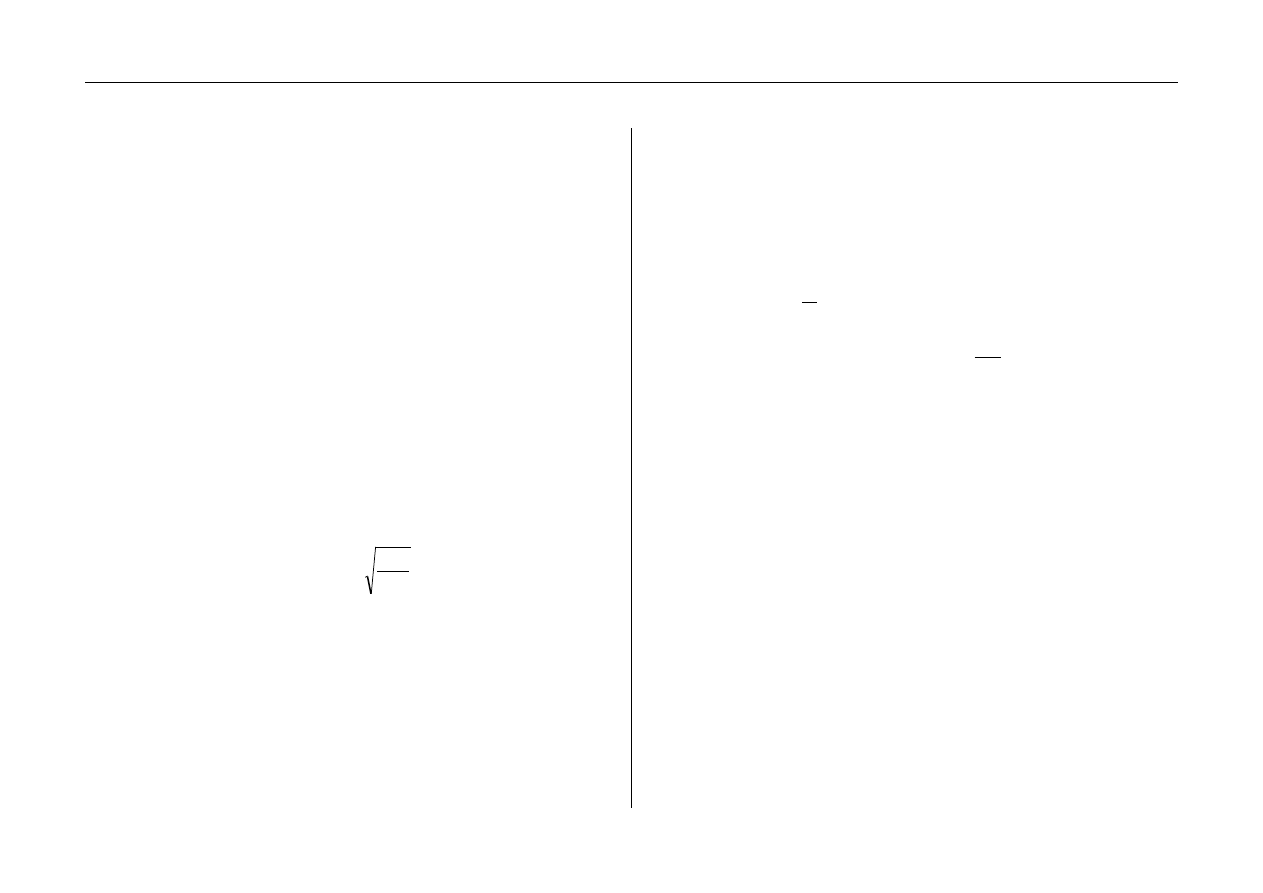
NAPÓR AERODYNAMICZNY

4.

Przebieg ćwiczenia

Ćwiczenie polega na pomiarze wielkości niezbędnych

do obliczenia naporu aerodynamicznego, a następnie na analizie

zebranych wyników. W części teoretycznej przedstawiono sposób

obliczania naporu aerodynamicznego dla różnych przegród,

natomiast część eksperymentalna polega na porównaniu naporu

aerodynamicznego obliczonego wg powyższych równań

z rzeczywistym naporem zmierzonym przy pomocy wagi

laboratoryjnej.

Aby porównać napór wyliczony z równań z naporem

zmierzonym musimy dysponować następującymi danymi:

 prędkość strugi na wylocie z dyszy - v,
 średnica wylotowa dyszy - d,
 kąt ustawienia wylotu dyszy do powierzchni płytki

β

oraz kąty wylotu strugi z obszaru płytki

α

 gęstość czynnika wypływającego z dyszy

ρ

.

W celu określenia prędkości strugi na wylocie wbudowano

w układ dyszę, której zadaniem jest spowodowanie spadku

ciśnienia. Spadek ciśnienia jest mierzony manometrem

różnicowym wypełnionym rtęcią. Prędkość strugi na wylocie

z dyszy v określa zależność:

ρ

∆

α

p

2

v

=

(16)

gdzie:

ρ

- gęstość czynnika wypływającego z dyszy [kg/m

3

],

α

- liczba przepływu dyszy.

Różnicę ciśnień

∆

p obliczymy uwzględniając wysokość

wychylenia się słupa rtęci w manometrze z zależności:

g

*

*

h

p

rt

rt

ρ

∆ =

(17)

gdzie:

h

rt

- wysokość słupa rtęci w manometrze [m],

ρ

r

-

gęstość rtęci [kg/m

3

]

g - przyspieszenie ziemskie [m/s

2

].

Liczba przepływu dla dyszy

α

wymaga wcześniejszego

ustalenia w oparciu o doświadczenie „Wyznaczanie współczynnika

przepływu

α

w pomiarowych urządzeniach zwężkowych”. Gęstość

czynnika (powietrze) wyznaczymy w oparciu o równanie stanu

gazu doskonałego:

mRT

pV

=

Wiedząc, że

V

m

=

ρ

otrzymujemy:

RT

p

=

ρ

(18)

gdzie:

p- ciśnienia atmosferyczne [Pa],

R- indywidualna stała gazowa dla powietrza [J/kg*K],

T- temperatura powietrza [K].

Należy pamiętać, że otrzymana wartość gęstości nie

uwzględnia zawartej w powietrzu wilgoci.

Wyniki pomiarów należy umieścić w tabeli, gdzie powinny

znajdować się następujące dane:

 ciśnienie atmosferyczne [Pa],
 temperatura powietrza [K],
 wysokości słupa rtęci dla różnych natężeń przepływu i dla

płytek o różnych kształtach,

 współczynnik przepływu dyszy,
 odczyt wartości naporu z wagi laboratoryjnej [kg],
 średnicę dyszy na wylocie [m].

Pomiar wartości niezbędnych do opracowania wyników

sprowadza się do jednoczesnej rejestracji wysokości słupa rtęci

i wartości naporu z wagi. Odczytany napór z wagi w kg należy

przekształcić na jednostkę siły, czyli N poprzez pomnożenie

wartości w kg przez przyspieszenie ziemskie. Dopiero tą wielkość

6

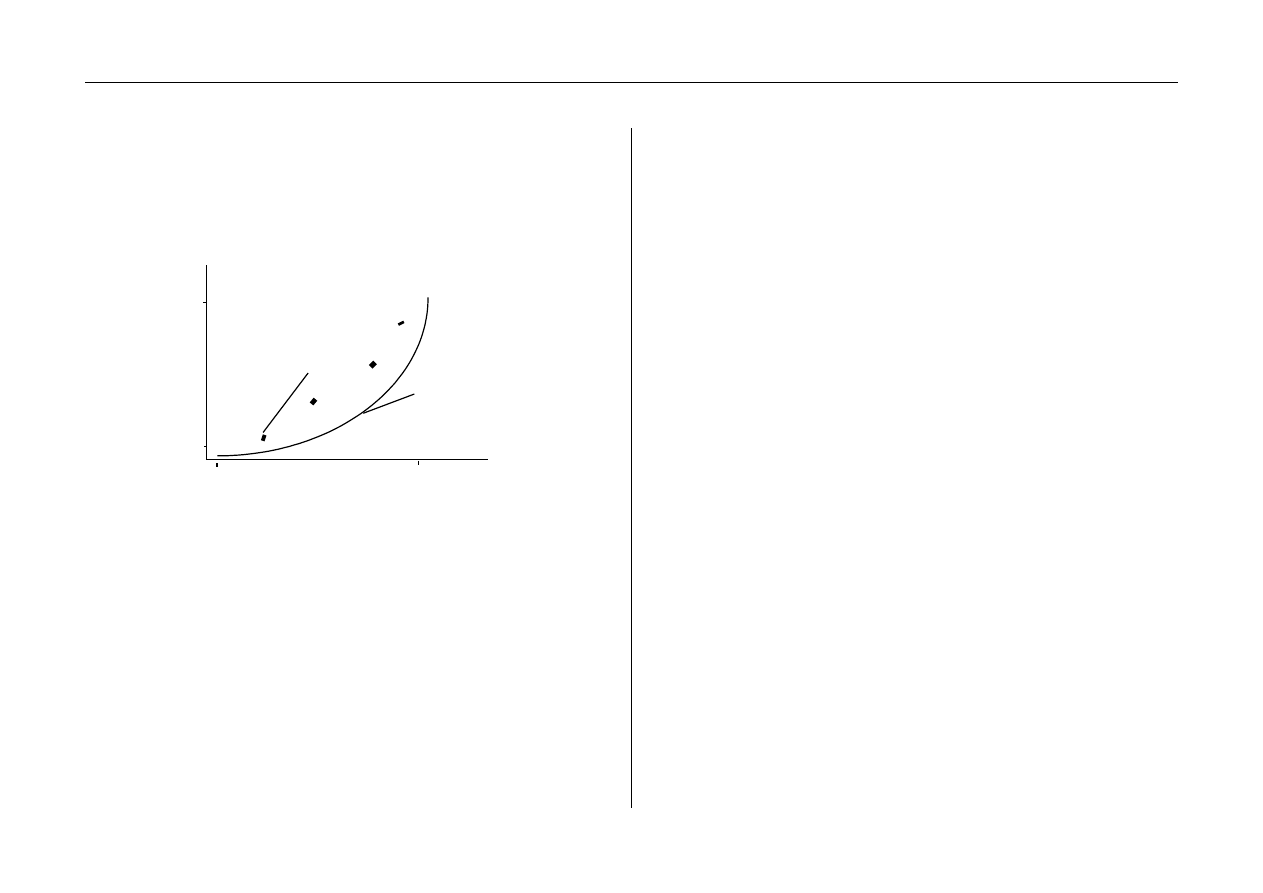
NAPÓR AERODYNAMICZNY

można zastosować w dalszych analizach. Wyniki ćwiczenia należy

przedstawić w postaci wykresów P=f(v) dla poszczególnych

płytek. Wykres powinien się składać z krzywej opisanej

zależnością naporu od prędkości wg podanych wcześniej równań

oraz z zaznaczonych punktów otrzymanych w trakcie pomiarów.

Pozostałe wielkości odczytuje się jednorazowo w trakcie ćwiczeń.

zale¿noœæ
P=f(v)

P

v

punkt otrzymany
w trakcie pomia-
rów

Rys. 10. Przykładowy wykres zależności naporu aerodynamicznego od prędkości

strugi

Kompletne sprawozdanie z ćwiczeń powinno zawierać wnioski z

analizowanego zagadnienia.

7

NAPÓR AERODYNAMICZNY

KARTA POMIAROWA

Imię i nazwisko ..............................................................................................................................................................................

Imię i nazwisko ..............................................................................................................................................................................

Kierunek

...........................................................................................

Rok.....................................

Grupa.......................

Ćw..........

...............................

(nr)

(data)

Ciśnienie atmosferyczne [Pa]

.......................................

h

rt

dla Q=0 [mmHg]

.......................................

m dla Q=0 [g]

.......................................

Średnica wew. wylotowa dyszy [mm]

.......................................

Temperatura powietrza [

o

C]

.......................................

Współczynnik

α

.......................................

Rodzaj powierzchni

.......................................

Lp.

Poziom cieczy

manometrycznej

Napór na wadze

h

rt

[mmHg]

m

[g]

1

2
3
4
5

8