1. Przedstaw i napisz jakie znaczenie ma całka Duhamela w teorii drgań.

(jej postać nie jest potrzebna ale na wszelki wypadek zamieszczam)

2. Wahadło matematyczne

Wahadło matematyczne składa się z masy m zawieszonej na lince. Okres drgań takiego
wahadła nie zależy od masy m i od początkowego wychylenia. Zależy on od długości
wahadła.

3. Podaj postać równania Lagrange’a II-go rodzaju,

4.

Wzór na częstość kołową drgań własnych układu, opisz jego parametry, podaj

jednostkę oraz podaj zależności pomiędzy ω, f i T.

ω-rad/s
c- N/m

f- częstotliwość [Hz= s^-1]
T- okres [s]

5. Przetworniki wielkości fizycznych (głównie związanych z procesami

wibroakustycznymi),



Rezystory, różnych postaci, np. potencjometry, tensometry,



Kondensatory



Cewki indukcyjne z rdzeniami ferromagnetycznymi lub magnesem,



Elementy piezoelektryczne,



Elementy halotronowe.

6. Kolejność działań podczas stosowania równania Lagrange’a,

.1. ustalić liczbę stopni swobody układu drgającego
.2. wybrać współrzędne uogólnione
.3. wyrazić energię kinetyczną i potencjalną w funkcji współrzędnych i prędkości
uogólnionych
.4. wykonać operacje różniczkowania
.5. obliczyć niepotencjalne siły uogólnione
.6. ułożyć równania ruchu w liczbie równej liczbie stopni swobody

7. Wyraź wzmocnienie w decybelach, jeśli dane są moce P1= 0.1 W, P2= 10 W, oraz

dla przypadku jeśli P1 i P2 zamienimy wartościami,

8. Narysuj schemat mechanizmu korbowo- tłokowego i napisz dlaczego położenie

tłoka nie jest jednoznacznie określane przez przemieszczenie s(t).

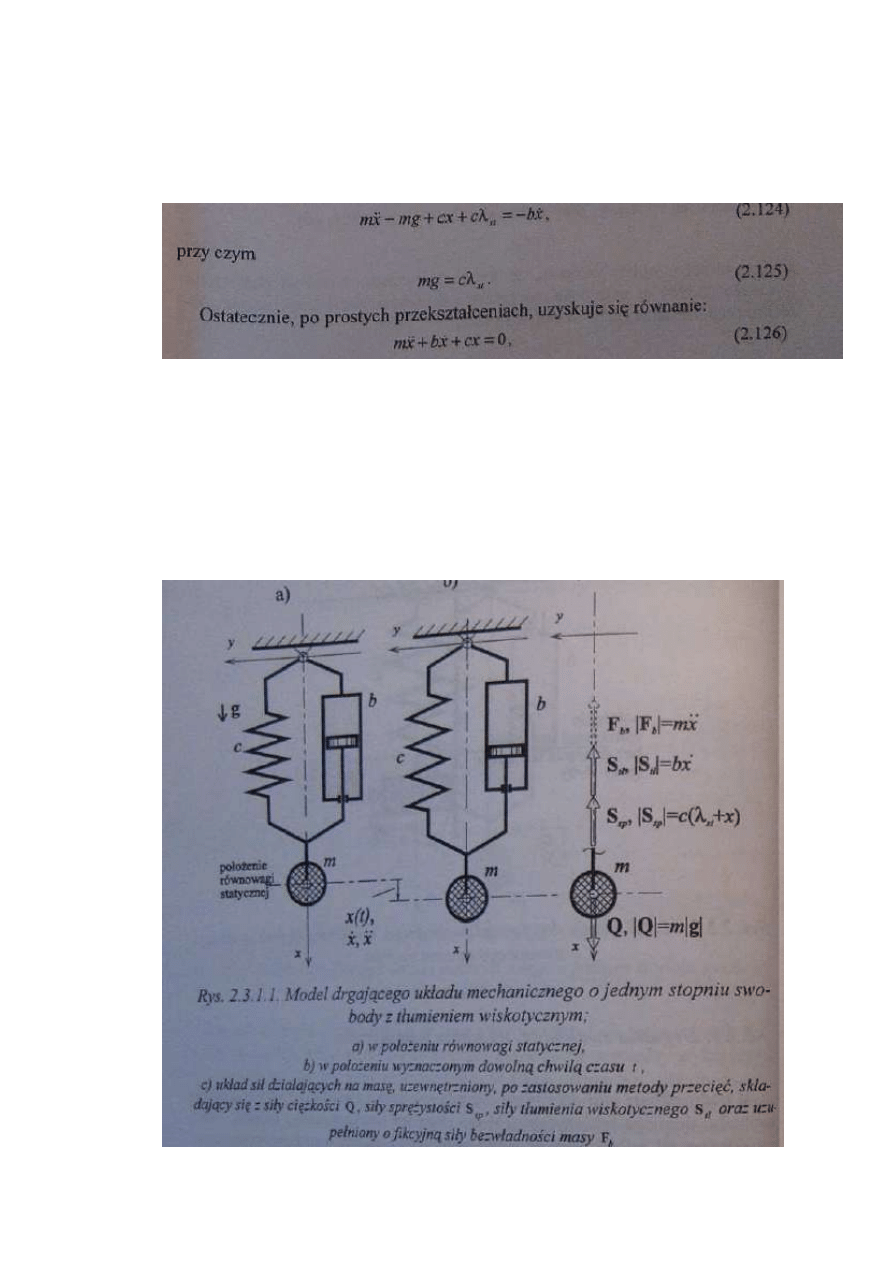
11. Podaj model matematyczny drgającego układu mechanicznego o jednym stopniu

swobody z tłumieniem wiskotycznym,

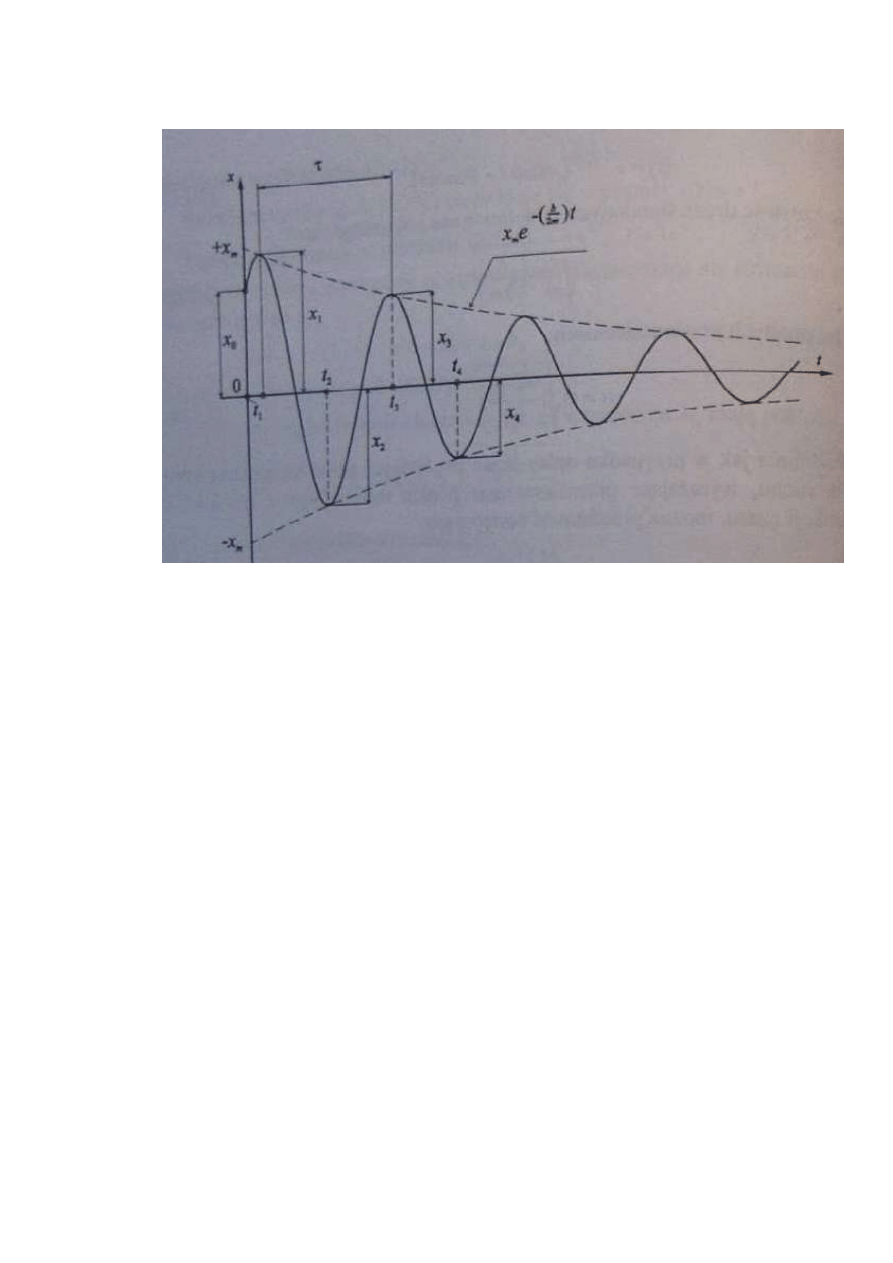
12. Narysuj układ mechaniczny o jednym stopniu swobody z tłumieniem wiskotycznym

wskazujący siły oraz wykres czasowego przebiegu swobodnych, zanikających drgań
punktu materialnego z podkrytycznym tłumieniem wiskotycznym przy zerowych
warunkach początkowych.

(najlepiej narysować a i c)

13. Wyjaśnij pojęcie częstość kołowa drgań i amplituda drgań.

Jest to prędkość kątowa, z jaką wiruje wektor, reprezentujący przemieszczenie punktu
materialnego w geometrycznej interpretacji ruchu oscylatora harmonicznego ω= 2πf.
Podstawową jednostką częstości kołowej jest jeden radian na jedną sekundę (rad/s).

Amplitudą drgań nazywa się maksymalne wychylenie punktu materialnego lub środka masy
ciała sztywnego od położenia równowagi podczas wykonywania harmonicznego ruchu
drgającego.