Rozdział 2

Dynamika

Dynamika jest działem mechaniki opisuj ˛

acym ruch układu materialnego

pod wpływem sił działaj ˛

acych na ten układ.

Dynamika opiera si ˛e na trzech zasadach Newtona:

1. Zasada bezwładno´sci:

Punkt materialny, na który nie działaj ˛

a ˙zadne siły lub wszystkie

działaj ˛

ace na´

n siły znosz ˛

a si ˛e, pozostaje w spoczynku lub porusza

si ˛e ruchem jednostajnym prostoliniowym wzgl ˛edem układu odniesienia.

Układ odniesienia, w którym słuszna jest ta zasada nazywamy i-

nercjalnym. Punkt w tym układzie nie mo˙ze udzieli´c sobie przyspieszenia.

2. W układzie inercjalnym zmiana ruchu punktu materialnego jest

proporcjonalna do siły działaj ˛

acej i odbywa si ˛e w kierunku dzia-

łania tej siły.

F = ma.

Równanie to jest podstawowym równaniem dynamiki.

3. Zasada akcji i reakcji.

Ka˙zdemu działaniu towarzyszy równe, lecz przeciwnie skierowane

przeciwdziałanie.

41

4. Pod wpływem układu sił punkt materialny uzyskuje przyspiesze-

nie równe sumie geometrycznej przyspiesze´

n, jakie uzyskałby w

wyniku niezale˙znego działania ka˙zdej z sił.

5. Zasada powszechnego ci ˛

a˙zenia.

Dwa punkty materialne o masach m

1

i m

2

działaj ˛

a na siebie z siła

proporcjonaln ˛

a do iloczynu tych mas, a odwrotnie proporcjonalnie

do kwadratu odległo´sci tych mas

F = k

m

1

m

2

r

2

,

gdzie k- stała grawitacji.

2.1

Zasada d’Alemberta dla punktu

Wyobra´zmy sobie, ˙ze pchaj ˛

ac wózek nadajemy mu przyspieszenie a.

Działamy oczywi´scie sił ˛

a F = ma. Na podstawie trzeciej zasady wózek

przeciwdziała z sił ˛

a B = −ma. (Pomijamy opory). Siła B nazywa si ˛e

sił ˛

a bezwładno´sci lub sił ˛

a d’Alemberta.

Podobnie na kamie´

n zawieszony na sznurku i poruszaj ˛

acy si ˛e po

okr ˛egu działa siła do´srodkowa F

r

= ma

n

, a siła od´srodkowa jest sił ˛

a

bezwładno´sci, itp.

St ˛

ad wniosek, ˙ze

F

= −B

(akcja i reakcja)

X

F

i

+ (−ma) = 0.

Zasada d’Alemberta

W ruchu punktu materialnego układ sił czynnych i reakcji wi ˛ezów równowa˙zy

si ˛e z pomy´slan ˛

a sił ˛

a bezwładno´sci.

X

F

i

+

X

R

i

+ (−ma) = 0

42

Przykład 1

Rozpatrzmy ruch masy m zawieszonej na ko´

ncu liny rozwi-

jaj ˛

acej si ˛

e z b ˛

ebna. Szukamy napi ˛

ecia liny.

G − siła ci ˛e˙zko´sci (czynna),

S − siła napi ˛ecia nici (reakcja),

B − siła bezwładno´sci.

Rzutuj ˛

ac wszystkie siły na o´s liny mamy

S − G + B

= 0,

S − mg + ma = 0,

S = m (g − a) .

Gdy spadek ciała b ˛

edzie swobodny, wówczas g = a i napi ˛

ecie S = 0.

2.2

P ˛

ed masy

Zgodnie z drug ˛

a zasad ˛

a dynamiki mo˙zemy napisa´c ruch ciała:

ma =

X

F

i

.

Pami ˛etaj ˛

ac jednak, ˙ze

a =

dv

dt

mamy

d

dt

(mv) =

X

F

i

.

Wielko´s´c mv = p nazywamy p ˛edem lub ilo´sci ˛

a ruchu punktu material-

nego.

Równanie

dp

dt

=

X

F

i

43

wyra˙za zasad ˛e p ˛edu dla punktu materialnego. Pochodna p ˛edu punktu

materialnego jest równa sumie sił działaj ˛

acych na dany punkt.

Równanie powy˙zsze jest ogólniejszym sformułowaniem drugiej zasady

dynamiki (jest prawdziwe w mechanice relatywistycznej).

Je˙zeli teraz

P

F

i

= 0, to

·

p = 0 ⇒ p = const. Jest to zasada

zachowania p ˛edu dla punktu.

Je˙zeli na punkt materialny nie działaj ˛

a ˙zadne siły, to p ˛ed punktu

jest zachowany, jest stały.

2.3

Kr ˛

et punktu materialnego

Kr ˛etem lub momentem p ˛edu punktu materialnego wzgl ˛edem punktu O

nazywamy wektor równy iloczynowi wektora poło˙zenia r przez p ˛ed p

poruszaj ˛

acego si ˛e punktu.

K

o def.

= r × mv.

Składowe kr ˛etu w układzie x, y, z:

K

o

x

= m (y ˙z − z ˙y) ,

K

o

y

= m (z ˙x − x ˙z) ,

K

o

z

= m (x ˙y − y ˙x) .

Zbadajmy zmian ˛e kr ˛etu K

o

w czasie

dK

o

dt

=

dr

dt

× mv + r ×

d

dt

(mv) ,

dK

o

dt

= v × mv

| {z }

=0

+ r × ma,

dK

o

dt

= M

o

.

44

Powy˙zszy zwi ˛

azek wyra˙za zasad ˛e kr ˛etu punktu materialnego:

Pochodna wektora kr ˛etu wzgl ˛edem czasu jest równa momentowi gł

ównemu wszystkich sił działaj ˛

acych na dany punkt.

je˙zeli teraz M

o

= 0, to

·

K

o

= 0 ⇒ K

o

= const. Jest to zasada zachowa-

nia kr ˛etu punktu materialnego:

Je˙zeli moment główny sił działaj ˛

acych na poruszaj ˛

acy si ˛e punkt jest

wzgl ˛edem jakiego´s bieguna równy zeru, to kr ˛et poruszaj ˛

acego si ˛e punktu

wzgl ˛edem tego bieguna jest zachowany, jest stały.

2.4

Dynamiczne równania ruchu punktu

Wychodzimy z wektorowej postaci

F = ma.

Uwzgl ˛edniaj ˛

ac

F

= F

x

i + F

y

j + F

z

k,

a =

¨

xi + ¨

yj + ¨

zk.

Mamy

m¨

x = F

x

,

m¨

y = F

y

,

m¨

z = F

z

lub

m¨

x =

X

F

ix

,

m¨

y =

X

F

iy

,

m¨

z =

X

F

iz

.

Poniewa˙z sił ˛

a w ogólnym przypadku jest funkcj ˛

a:

F = F (r, v, t)

45

st ˛

ad ogólna posta´c równa´

n b ˛edzie

⎧

⎪

⎪

⎪

⎨

⎪

⎪

⎪

⎩

m¨

x = F

x

(x, y, z, ˙x, ˙y, ˙z, t)

m¨

y = F

y

(x, y, z, ˙x, ˙y, ˙z, t)

m¨

z = F

z

(x, y, z, ˙x, ˙y, ˙z, t)

.

S ˛

a to ró˙zniczkowe równania drugiego rz ˛edu. Konieczne jest dwukrotne

całkowanie i wówczas pojawi si ˛e 6 stałych całkowania (3 równania). Aby

te stałe wyznaczy´c konieczne s ˛

a warunki pocz ˛

atkowe- musi ich by´c tyle,

ile stałych. Dla t = t

o

mamy

x = x

o

, ˙x = ˙x

o

,

y

= y

o

, ˙y = ˙y

o

,

z

= z

o

, ˙z = ˙z

o

.

Wykorzystuj ˛

ac warunki pocz ˛

atkowe otrzymujemy rozwi ˛

azania równa´

n:

⎧

⎪

⎪

⎪

⎨

⎪

⎪

⎪

⎩

x = f

1

(x

o

, y

o

, z

o

, ˙x

o

, ˙y

o

, ˙z

o

, t)

y = f

2

(x

o

, y

o

, z

o

, ˙x

o

, ˙y

o

, ˙z

o

, t)

z = f

3

(x

o

, y

o

, z

o

, ˙x

o

, ˙y

o

, ˙z

o

, t)

S ˛

a to kinematyczne równania ruchu.

46

2.5

Przykłady całkowania równa´

n ruchu

1. Ruch pod wpływem siły F = 0, z warunkami pocz ˛

atkowymi: t =

0,

·

r = v

o

, r = r

o

.

ma = 0,

m

··

r

= 0,

··

r

= 0,

·

r

= 0 + c,

·

r

= v

o

,

r

= v

o

t + c

1

,

r

= v

o

t + r

o

.

Jest to ruch jednostajny

2. Ruch pod wpływem stałej siły F = const., z warunkami pocz ˛

atkowymi:

t = 0,

·

r = v

o

, r = r

o

.

m

··

r

= F ,

··

r

=

1

m

F ,

·

r

=

1

m

F t + c,

·

r

=

1

m

F t + v

o

,

r

=

1

2m

F t

2

+ v

o

t + c

1

,

r

=

1

2m

F t

2

+ v

o

t + r

o

.

S ˛

a to wzory na ruch jednostajnie zmienny (przyspieszony lub

opó´zniony).

47

2.6

Drgania

2.6.1

Drgania swobodne punktu

Aby wyst ˛

apiły drgania, punkt musi porusza´c si ˛e ruchem prostoliniowym

pod wpływem siły F przyci ˛

agaj ˛

acej ten punkt do stałego punktu O

zwanego ´srodkiem drga´

n.

Siła spr ˛e˙zysto´sci jest proporcjonalna do wychylenia punktu

F = −kx, k- stała spr ˛e˙zysto´sci.

Równanie ruchu b ˛edzie miało posta´c

m¨

x = F,

m¨

x = −kx

lub

¨

x +

k

m

x = 0.

Oznaczmy

k

m

= ω

2

.

Otrzymujemy równanie ró˙zniczkowe drga´n swobodnych

¨

x + ω

2

x = 0, ω- cz ˛esto´s´c ruchu.

Otrzymane równanie jest równaniem liniowym, jednorodnym drugiego

rz ˛edu.

Rozwi ˛

azanie:

dokonujemy podstawienia x = e

αt

α

2

e

αt

+ ω

2

e

αt

= 0,

α = ±ıω.

48

Całka ogólna

x = Ae

ıωt

+ Be

−ıωt

.

Korzystaj ˛

ac z wzorów Eulera

sin ωt =

e

ıωt

− e

−ıωt

2ı

,

cos ωt =

e

ıωt

+ e

−ıωt

2

,

mamy

⎧

⎨

⎩

e

ıωt

= cos ωt + ı sin ωt

e

−ıωt

= cos ωt − ı sin ωt

.

St ˛

ad

x = A cos ωt + Aı sin ωt + B cos ωt − Bı sin ωt,

x = (A + B) cos ωt + ı (A − B) sin ωt.

Oznaczaj ˛

ac A + B = C

1

oraz ı (A − B) = C

2

, mamy

x = C

1

cos ωt + C

2

sin ωt.

Podstawiamy C

1

= a sin ϕ, C

2

= a cos ϕ.

x = a sin ϕ cos ωt + a cos ϕ sin ωt,

x = a sin (ωt + ϕ) - rozwi ˛

azanie

(2.1)

Stała a- amplituda (maksymalne wychylenie), ϕ- faza pocz ˛

atkowa ruchu,

drga´

n, (ωt + ϕ)- faza drga´

n.

Ruch okre´slony wzorem 2.1 jest okresowy o okresie

T

=

2π

ω

,

ω

=

r

k

m

,

T = 2π

r

m

k

49

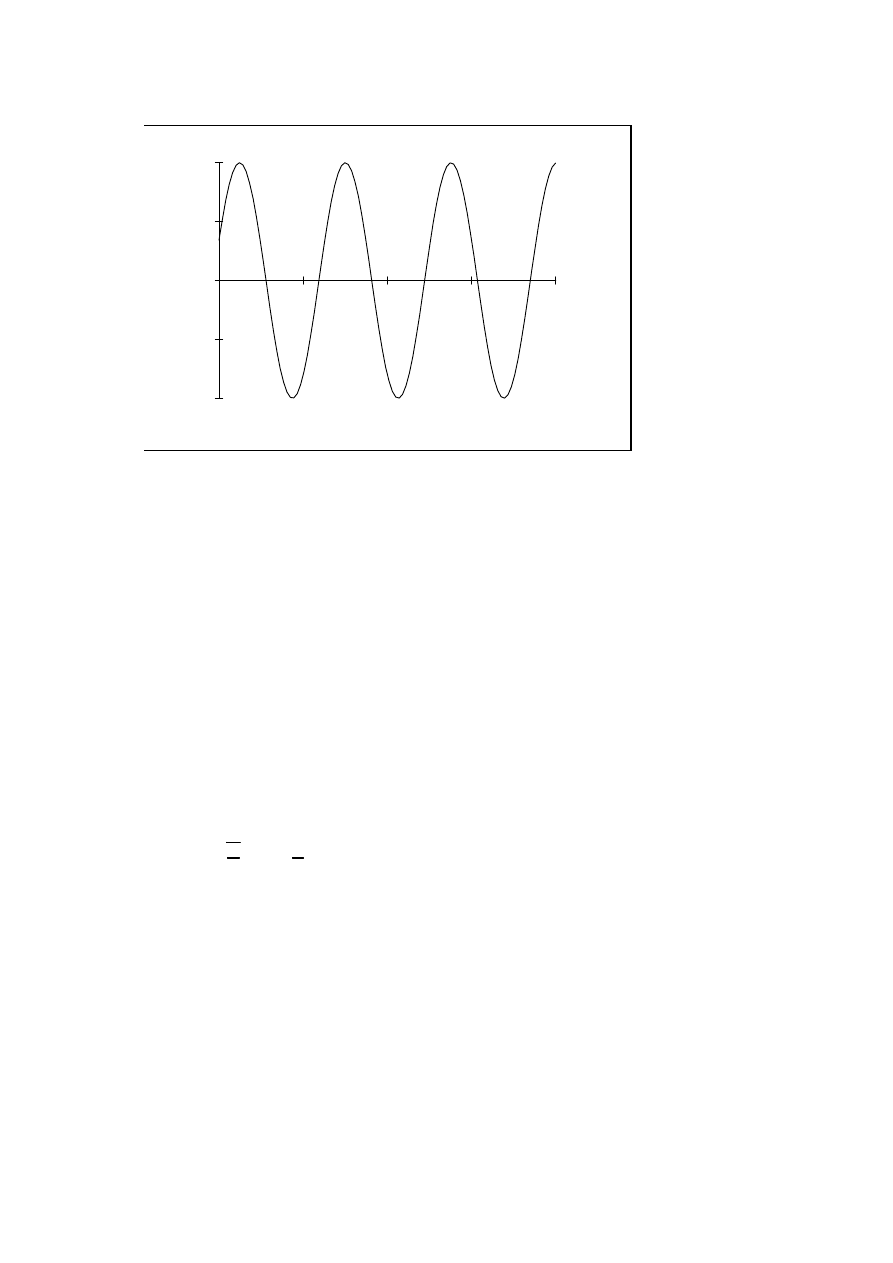
20

15

10

5

0

1

0.5

0

-0.5

-1

t

x

t

x

2.6.2

Drgania tłumione

Drgania tłumione wyst ˛epuj ˛

a w o´srodku stawiaj ˛

acym opór. Siły oporu

s ˛

a proporcjonalne do pr ˛edko´sci

R

∗

= −βv

x

= −β ˙x - siła tłumi ˛aca

Równanie ruchu:

m¨

x = −kx − β ˙x

¨

x + 2n ˙x + ω

2

x = 0

gdzie ω =

q

k

m

, 2n =

β

m

.

Poniewa˙z równanie charakterystyczne jest kwadratowe, to mog ˛

a zaj´s´c 3

przypadki rozwi ˛

aza´

n: ∆ > 0, ∆ = 0, ∆ < 0. Równanie charakterysty-

50

czne ma posta´c:

α

2

+ 2nα + ω

2

= 0,

∆ = 4n

2

− 4ω

2

,

√

∆ = 2

p

n

2

− ω

2

,

α

1

=

−2n − 2

√

n

2

− ω

2

2

= −n −

p

n

2

− ω

2

,

α

1

=

−2n + 2

√

n

2

− ω

2

2

= −n +

p

n

2

− ω

2

Rozpatrzmy przypadki

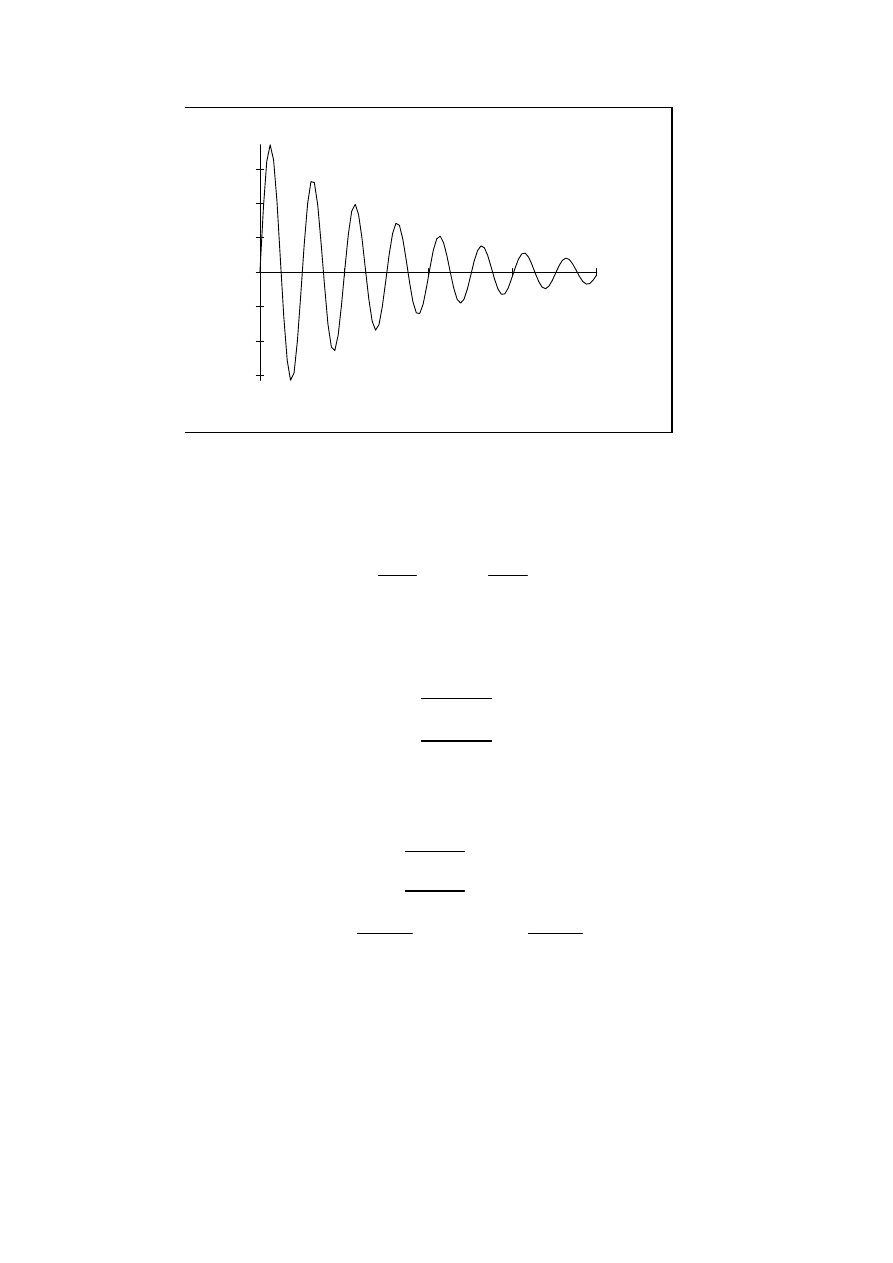
1. Małe tłumienie ω > n ⇒ ∆ < 0. Mamy rozwi ˛azania zespolone

(podobnie jak przy drganiach swobodnych).

Rozwi ˛

azanie

x = e

−nt

³

C

1

cos

p

ω

2

− n

2

t + C

2

sin

p

ω

2

− n

2

t

´

C

1

= a sin ϕ

C

2

= a cos ϕ

Ostatecznie

x = ae

−nt

sin

³p

ω

2

− n

2

t + ϕ

´

.

Je˙zeli t → ∞, to x → 0 - drgania zanikaj ˛a.

Okres

T =

2π

√

ω

2

− n

2

,

ω

t

=

p

ω

2

− n

2

51

50

37.5

25

12.5

0

0.75

0.5

0.25

0

-0.25

-0.5

-0.75

x

y

x

y

2. Du˙ze tłumienie ω < n ⇒ ∆ > 0. Mamy rozwi ˛azania rzeczywiste-

nie b ˛edzie drga´

n.

x = e

−nt

³

C

1

e

√

n

2

−ω

2

t

+ C

2

e

−

√

n

2

−ω

2

t

´

.

Korzystaj ˛

ac z wzorów na funkcje hiperboliczne

cosh (kt) =

e

kt

+ e

−kt

2

,

sinh (kt) =

e

kt

− e

−kt

2

oraz post ˛epuj ˛

ac podobnie jak przy drganiach swobodnych mamy

C

1

=

B

1

+ B

2

2

,

C

2

=

B

1

− B

2

2

x = e

−nt

³

B

1

cosh

³p

n

2

− ω

2

t

´

+ B

2

sinh

³p

n

2

− ω

2

t

´´

.

52

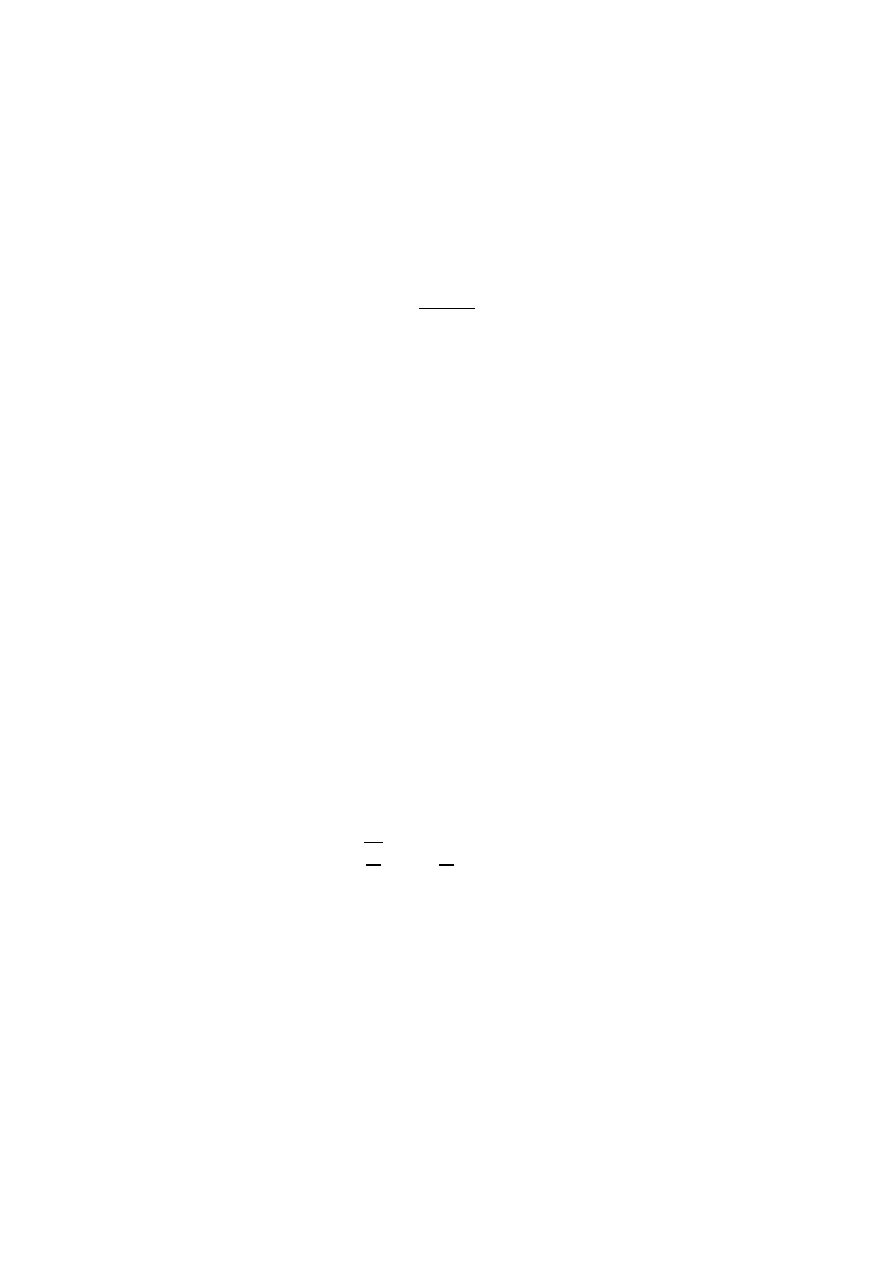
Wprowadzaj ˛

ac

B

1

= a sinh ϕ,

B

2

= a cosh ϕ

otrzymujemy

x = ae

−nt

sinh

³p

n

2

− ω

2

t + ϕ

´

.

Ruch ten nie jest ruchem okresowym, nie ma drga´

n.

3. Tłumienie krytyczne ω = n ⇒ ∆ = 0.Rozwi ˛azanie

x = e

−nt

(C

1

+ C

2

t)

Tutaj równie˙z mamy brak okresowo´sci- brak drga´n.

2.6.3

Drgania wymuszone

Je˙zeli na punkt dodatkowo działa siła wymuszaj ˛

aca okresowa- wys-

t ˛epuj ˛

a drgania wymuszone.

Siła wymuszaj ˛

aca S = H sin (pt), gdzie p - cz ˛esto´s´c siły wymuszaj ˛

acej.

Równanie ruchu tych drga´

n

m¨

x = −kx + H sin (pt)

¨

x + ω

2

x = h sin (pt)

ω =

r

k

m

,

h =

H
m

.

Rozwi ˛

azanie tego równania składa si ˛e z całki ogólnej równania jednorod-

nego

x

1

= a sin (ωt + ϕ)

53

i całki szczególnej równania niejednorodnego, któr ˛

a zakładamy tu w

postaci

x

2

= B sin (pt) .

Stał ˛

a B wyznaczamy wstawiaj ˛

ac x

2

do równania drga´

n

−Bp

2

sin (pt) + ω

2

B sin (pt) = h sin (pt) .

St ˛

ad

B =

h

ω

2

− p

2

.

Rozwi ˛

azanie ostateczne tych drga´

n

x = x

1

+ x

2

,

x = a sin (ωt + ϕ) +

h

ω

2

− p

2

sin (pt) .

Jest to zło˙zenie dwóch drga´n: własnych i wymuszonych.

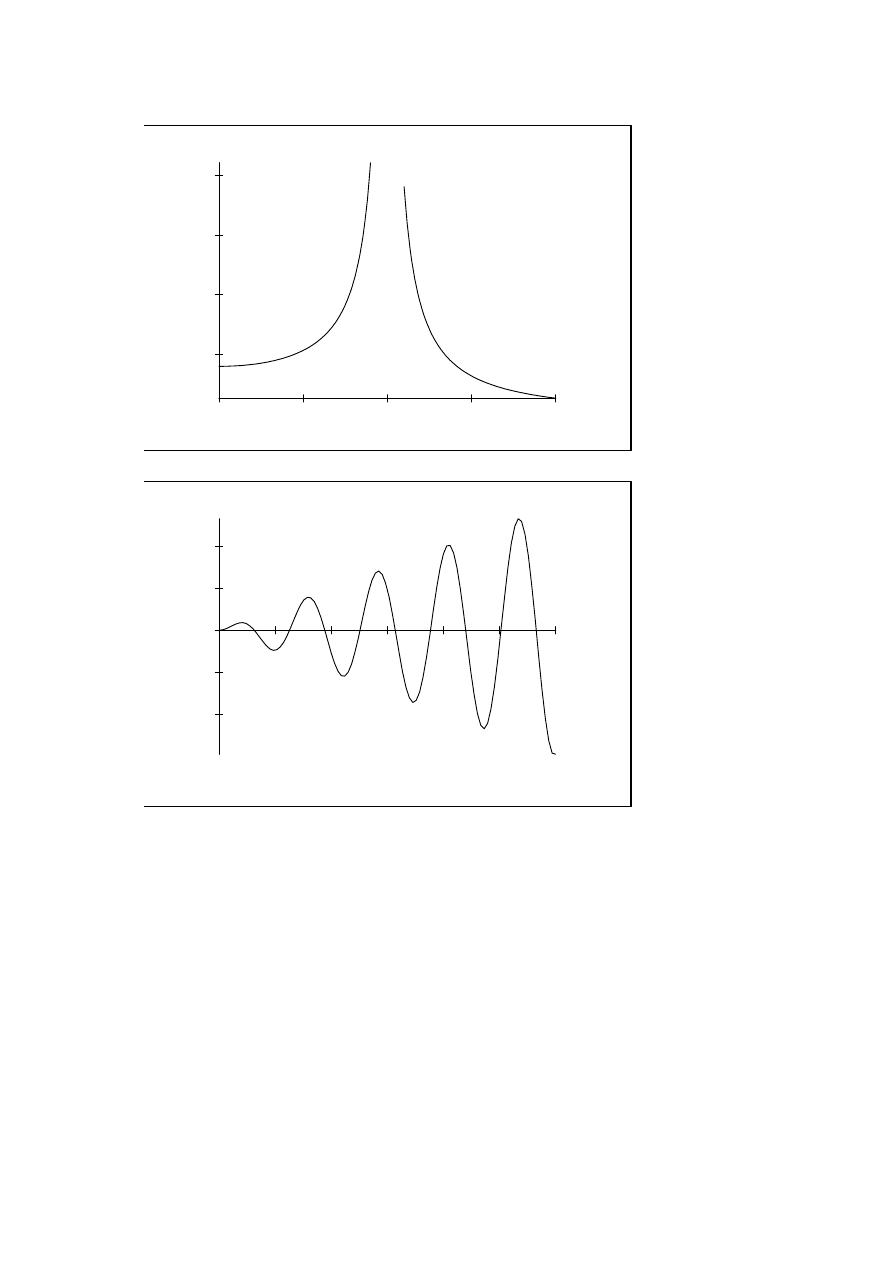
Widzimy, ˙ze amplituda drga´n wymuszonych

B =

h

ω

2

− p

2

zale˙zy od cz ˛esto´sci drga´n wymuszonych. Je˙zeli p → ω, to B → ∞ i

wyst ˛epuje rezonans.

W przypadku rezonansu rozwi ˛

azanie drga´

n b ˛edzie miało posta´c

x = a sin (ωt + ϕ) −

h

2ω

t cos (ωt)

54

2

1.5

1

0.5

0

5

3.75

2.5

1.25

p/w

|A|

p/w

|A|

30

25

20

15

10

5

0

1

0.5

0

-0.5

-1

x

x

2.7

Momenty bezwładno´sci

Momentem bezwładno´sci punktu materialnego wzgl ˛edem płaszczyzny,

osi lub bieguna nazywamy iloczyn masy tego punktu przez kwadrat

55

odległo´sci tego punktu od płaszczyzny, osi lub bieguna

I = mr

2

.

Momentem bezwładno´sci układu punktów materialnych wzgl ˛edem płaszczyzny,

osi lub bieguna nazywamy sum ˛e momentów bezwładno´sci wszystkich

punktów wzzgl ˛edem tej płaszczyzny, osi lub bieguna:

I =

X

i

m

i

r

2

i

.

Je˙zeli teraz mamy brył ˛e i potniemy j ˛

a na elementy ∆m

i

, to

I

i

=

X

i

r

2

i

∆m

i

.

W granicy dla o´srodka ci ˛

agłego otrzymujemy

I =

Z

V

r

2

dm.

Ka˙zdy moment bezwładno´sci mo˙zna przedstawi´c w posatci iloczynu

masy całego układu m przez kwadrat pewnej odległo´sci i zwanej promie-

niem bezwładno´sci

I = mi

2

,

st ˛

ad

i =

r

I

m

.

Równie˙z ka˙zdy moment bezwładno´sci mo˙zna przedstawi´c w postaci

iloczynu pewnej masy m

red

przez kwadrat pewnej przyj ˛etej odległo´sci

k.

I = m

red

k

2

.

St ˛

ad

m

red

=

I

k

2

.

56

W zale˙zno´sci od tego, czy układ jest lini ˛

a, powierzchni ˛

a czy brył ˛

a

okre´slamy dm:

dm = ρ

l

dl,

dm = ρ

S

dS,

dm = ρdV,

I

= ρ

l

Z

l

r

2

dl,

I = ρ

S

Z

S

r

2

dS,

I = ρ

Z

V

r

2

dV.

1. Moment bezwładno´sci wzgl ˛edem płaszczyzny

I

xy

=

Z

V

z

2

dm,

I

yz

=

Z

V

x

2

dm,

I

zx

=

Z

V

y

2

dm.

2. Moment bezwładno´sci wzgl ˛edem osi układu

I

x

=

Z

V

¡

y

2

+ z

2

¢

dm,

I

y

=

Z

V

¡

z

2

+ x

2

¢

dm,

I

z

=

Z

V

¡

x

2

+ y

2

¢

dm.

3. Moment bezwł ˛

adno´sci wzgl ˛edem punktu (biegunowy)

I

O

=

Z

V

¡

x

2

+ y

2

+ z

2

¢

dm

2.8

Momenty dewiacyjne

Mamy dwie płaszczyzny α i β i punkt m

1

odległy o r

1

i ρ

1

od tych

płaszczyzn. Momentem zboczenia punktu materialnego wzgl ˛edem płaszczyzn

wzajemnie prostopadłych nazywamy

D

αβ

= m

1

r

1

ρ

1

.

Momentem zboczenia wzgl ˛edem dwóch wzajemnie prostopadłych płaszczyzn

nazywamy wyra˙zenie

D

αβ

=

Z

V

rρdm.

57

W układzie kartezja´

nskim

D

xy

=

Z

V

xydm,

D

yz

=

Z

V

yzdm,

D

zx

=

Z

V

zxdm.

Twierdzenie 2 (Twierdzenie Steinera)

Moment bezwładno´sci wzgl ˛

e-

dem dowolnej osi jest równy momentowi wzgl ˛

edem osi równoległej prze-

chodz ˛

acej przez ´srodek masy powi ˛

ekszonemu o iloczyn masy całkowitej

układu przez kwadrat odległo´sci obu osi.

I

l

= I

s

+ md

2

.

Dowód.

Wzgl ˛edem osi l

Rysunek 2-1:

I

l

=

X

m

i

r

02

i

,

58

Wzgl ˛edem osi s

I

s

=

X

m

i

r

2

i

.

Mi ˛edzy r

0

i

i r

i

zachodzi zale˙zno´s´c

r

02

i

= r

2

i

+ d

2

+ 2dr

i

cos α

i

= r

2

i

+ d

2

+ 2dx

i

.

St ˛

ad

I

l

=

X

m

i

r

2

i

+

X

m

i

d

2

+

X

2m

i

x

i

,

I

l

= I

s

+ md

2

+ 2d

X

m

i

x

i

,

I

l

= I

s

+ md

2

+ 2d

Z

V

xdm,

gdzie

R

V

xdm jest momentem statycznym.

Poniewa˙z punkt S jest ´srodkiem masy, to

R

V

xdm = 0. Otrzymujemy

zatem

I

l

= I

s

+ md

2

.

2.9

Moment bezwładno´sci wzgl ˛

edem osi nachy-

lonej dowolnie wzgl ˛

edem osi układu

Zakładamy znajomo´s´c momentów I

x

, I

y

, I

z

oraz D

xy

, D

yz

, D

zx

.

Z rysunku mamy

r

= ρ sin ϕ,

r

2

= ρ

2

sin

2

ϕ = ρ

2

− ρ

2

cos

2

ϕ.

Rzut promienia ρ na o´s l jest równy sumie rzutów składowych tego

59

Rysunek 2-2:

60

promienia na t ˛

a o´s

ρ cos ϕ = x cos α + y cos β + z cos γ.

St ˛

ad

r

2

= ρ

2

− (x cos α + y cos β + z cos γ)

2

.

Uwzgl ˛edniaj ˛

ac, ˙ze

ρ

2

= x

2

+ y

2

+ z

2

i

cos

2

α + cos

2

β + cos

2

γ = 1

otrzymujemy

r

2

= x

2

+ y

2

+ z

2

− x

2

cos

2

α + y

2

cos

2

β + z

2

cos

2

γ

−2xy cos α cos β − 2yz cos β cos γ − 2zx cos γ cos α

= x

2

¡

cos

2

β + cos

2

γ

¢

+ y

2

¡

cos

2

α + cos

2

γ

¢

+ z

2

¡

cos

2

α + cos

2

β

¢

−2xy cos α cos β − 2yz cos β cos γ − 2zx cos γ cos α.

Grupuj ˛

ac wzgl ˛edem cosinusów

r

2

i

=

¡

y

2

+ z

2

¢

cos

2

α +

¡

z

2

+ x

2

¢

cos

2

β +

¡

x

2

+ y

2

¢

cos

2

γ −

−2xy cos α cos β − 2yz cos β cos γ − 2zx cos γ cos α.

Poniewa˙z moment bezwładno´sci wzgl ˛edem osi

I =

Z

V

r

2

dm,

to otrzymujemy

I

= I

x

cos

2

α + I

y

cos

2

β + I

z

cos

2

γ

−2D

xy

cos α cos β − 2D

yz

cos β cos γ − 2D

zx

cos γ cos α.

61

2.10

Elipsoida bezwładno´sci

Rysunek 2-3:

Na osi l odkładamy odcinek OQ (o´s ta mo˙ze si ˛e zmienia´c w przestrzeni

bo liczymy I dla całego p ˛eku osi)

Okre´slamy OQ co do długo´sci

OQ =

k

√

I

Okre´slamy miejsce geometryczne punktów Q

x = OQ cos α,

y = OQ cos β,

z = OQ cos γ,

cos α =

x

√

I

k

,

cos β =

y

√

I

k

,

cos γ =

z

√

I

k

.

Wstawiaj ˛

ac to do wzoru na moment I mamy

I

x

x

2

+ I

y

y

2

+ I

z

z

2

− 2D

xy

xy − 2D

yz

yz − 2D

zx

zx = k

2

62

Jest to równanie elipsoidy bezwładno´sci.

Elipsoid ˛

a bezwładno´sci nazywamy miejsce geometryczne punk-

tów, których odległo´sci od pocz ˛

atku układu s ˛

a odwrotnie proporcjon-

alne do pierwiastka z momentu bezwładno´sci wzgl ˛edem osi przechodz ˛

acej

przez dany punkt i pocz ˛

atek układu.

Mo˙zna te˙z przyj ˛

a´c układ współrz ˛ednych taki, ˙ze D

αβ

= 0. Wtedy

I

1

x

2

+ I

2

y

2

+ I

3

z

2

= k

2

,

gdzie I

1,2,3

- główne momenty bezwładno´sci.

Osie główne → D

αβ

= 0,

Osie centralne główne- główne przez ´srodek masy,

Osie główne- to osie elipsoidy.

2.10.1

Poło˙zenie osi głównej

Takimi osiami s ˛

a:

1. ka˙zda o´s symetrii,

2. ka˙zda prosta ⊥ do płaszczyzny symetrii,

3. ka˙zda prosta, na której le˙z ˛

a srodki mas warstw elementarnych,

otrzymanych przez podział ciała płaszczyznami prostopadłymi do

tej prostej.

2.11

Praca, energia, moc, pole sił

Je´sli na jaki´s punkt działa siła P i punkt przesuwa si ˛e o s, to mówimy,

˙ze P wykonała prac ˛

e

L = P ◦ s = P s cos α.

63

W układzie współrz ˛ednych

L = P ◦ s = P

x

s

x

+ P

y

s

y

+ P

z

s

z

Załó˙zmy teraz, ˙ze na punkt działa sił ˛

a wypadkowa

P

=

X

P

i

,

L = P ◦ s =

³X

P

i

´

◦ s = P

1

◦ s + P

2

◦ s + ...

Wynika st ˛

ad twierdzenie, ˙ze praca wypadkowej równa jest sumie prac

poszczególnych sił.

We´zmy teraz pod uwag ˛e prac ˛e elementarn ˛

a siły na łuku ds

dL = P ds cos α

Poniewa˙z

|dr| = ds,

to

dL = P |dr| cos α = P ◦ dr

St ˛

ad

dL = P

x

dx + P

y

dy + P

z

dz

Aby wyznaczy´c cał ˛

a prac ˛e wykonan ˛

a na łuku \

A

1

A

2

trzeba dL scałkowa´c

L =

Z

\

A

1

A

2

P ◦ dr =

Z

\

A

1

A

2

P

x

dx + P

y

dy + P

z

dz

Praca jest równa całce krzywoliniowej po łuku \

A

1

A

2

. Siła P jak wiemy

mo˙ze by´c postaci P = P (r, v, t). Je˙zeli dane s ˛

a równania ruchu r =

64

r (t), tzn.

x = x (t) ,

y

= y (t) ,

z

= z (t) .

Wówczas

dx = x

0

dt,

dy

= y

0

dt,

dz

= z

0

dt.

St ˛

ad

L =

Z

t

2

t

1

(P

x

˙x + P

y

˙y + P

z

˙z) dt =

Z

t

2

t

1

P ◦ vdt

W szczególnym przypadku, je´sli siła P zale˙zy tylko od poło˙zenia punktu

A na torze, wówczas miar ˛e rzutu siły na styczn ˛

a P cos α mo˙zna wyrazi´c

od współrz ˛ednej łukowej (długo´sci łuku) s:

L =

Z

s

2

s

1

P cos αds

Prac ˛e wykonan ˛

a przez sił ˛e w jednostce czasu nazywamy moc ˛

a siły

M

=

dL

dt

= P ◦

dr

dt

= P ◦ v,

M

= P ◦ v = P v cos α.

Jednostki pracy i mocy

1. 1J = 1N m = 1

kg m

2

s

2

= 10

7

ergów

2. 1W = 1

J

s

3. 1kGm = 1kG 1m = 9.81J

65

4. 1

kGm

s

1kM = 75

kGm

s

= 75 · 9.81

J

s

= 736W

2.12

Przykłady obliczania pracy sił

1. Praca siły ci ˛e˙zko´sci

L =

Z

\

A

1

A

2

P

x

dx + P

y

dy + P

z

dz,

P

x

= P

y

= 0,

P

z

= −mg

L = −mg

Z

\

A

1

A

2

dz = mg (z

1

− z

2

) = mgh

2. Praca siły spr ˛e˙zystej

P

x

= −kx

dL = P

x

dx = −kxdx

L = −k

Z

x

2

x

1

xdx =

k

2

¡

x

2

1

− x

2

2

¢

3. Praca siły centralnej

Siła centralna to siła, której kierunek bez wzgl ˛edu na punkt przyło˙ze-

nia przechodzi przez ten sam punkt. Punkt przyło˙zenia nazywa

si ˛e ´srodkiem sił centralnych (przyci ˛

aganie- odpychanie)

Zgodnie z zało˙zeniem mamy

P = P (r)

dL = P (r) cos αds

66

Z trójk ˛

ata AA

0

A” znajdujemy

dr = AA” = ds cos (π − α) − ds cos α

St ˛

ad

dL = −P (r) dr,

dL = −

Z

r

2

r

1

P (r) dr

Wynika st ˛

ad, ˙ze praca siły centralnej nie zale˙zy od drogi, lecz od

odległo´sci od punktu.

2.13

Praca sił i praca w polu sił

Je˙zeli w ka˙zdym punkcie pewnego obszaru działa siła zale˙zna od r i t,

P = P (r, t), to mówimy, ˙ze w tym obszarze jest okre´slone pole sił.

Je´sli siły te s ˛

a niezale˙zne od czasu, to pole jest stacjonarne. Wówczas

P = P (r)

P

x

= P

x

(x, y, z) ,

P

y

= P

y

(x, y, z) ,

P

z

= P

z

(x, y, z) .

Praca w tym polu sił

L =

Z

A

1

A

2

[P

x

(x, y, z) dx + P

y

(x, y, z) dy + P

z

(x, y, z) dz]

Na ogół praca ta zale˙zy od drogi.

Istniej ˛

a jednak pola, w których praca zale˙zy jedynie od skrajnych poło˙ze´n.

Tego typu pole nazywamy zachowawczymi lub potencjalnymi.

W polu potencjalnym mo˙zna zdefiniowa´c pewn ˛

a funkcj ˛e skalarn ˛

a za-

67

le˙zn ˛

a od poło˙zenia zwan ˛

a potencjałem pola:

P

= −gradV,

P

x

= −

∂V

∂x

,

P

y

= −

∂V

∂y

,

P

z

= −

∂V

∂z

.

dL = P

x

dx + P

y

dy + P

z

dz = −

µ

∂V

∂x

dx +

∂V

∂y

dy +

∂V

∂z

dz

¶

= −dV,

L = −

Z

A

1

A

2

µ

∂V

∂x

dx +

∂V

∂y

dy +

∂V

∂z

dz

¶

= −

Z

A

1

A

2

dV = V

1

− V

2

,

gdzie V

i

, i = 1, 2- potencjał w punkcie i.

Praca zatem nie zale˙zy od toru, czyli w tym polu

L =

I

P ◦ dr = 0.

Warunki istnienia potencjału

∂P

x

∂y

= −

∂

2

V

∂x∂y

,

∂P

y

∂x

= −

∂

2

V

∂y∂x

,

∂P

x

∂y

=

∂P

y

∂x

Podobnie uzyskujemy dalsze dwa warunki

∂P

x

∂z

=

∂P

z

∂x

,

∂P

y

∂z

=

∂P

z

∂y

.

Warunki powy˙zsze wynikaj ˛

a z warunków koniecznych i wystarczaj ˛

acych

na to, by wyra˙zenie podcałkowe było ró˙zniczk ˛

a zupełn ˛

a. W polu po-

tencjalnym wyra˙zenie to, dzi ˛eki potencjałowi, jest ró˙zniczk ˛

a zupełn ˛

a.

Je´sli V (x, y, z) jest potencjałem pola, to funkcja

V

0

= V (x, y, z) + C

68

jest równie˙z potencjałem (stała addytywna C pełni rol ˛e poziomu odniesienia).

Praca jest jednak ró˙znic ˛

a potencjałów, wi ˛ec

L = V

1

− V

2

= V

0

1

− V

0

2

Powierzchnia ekwipotencjalna

V (x, y, z) = a = const.

2.14

Rotacja pola sił

Je˙zeli pole sił jest polem wirowym, wówczas mo˙zna wprowadzi´c pewn ˛

a

funkcj ˛e wektorow ˛

a F , ˙ze

rotF =

¯

¯

¯

¯

¯

¯

¯

¯

¯

−

→

i

−

→

j

−

→

k

∂

∂x

∂

∂y

∂

∂z

P

x

P

y

P

z

¯

¯

¯

¯

¯

¯

¯

¯

¯

Pole jest wirowe je´sli rotF 6= 0 nie jest polem potencjalnym, np. pole

sił wiruj ˛

acej lepkiej cieczy, pole magnetyczne, itp. Linie sił tego pola s ˛

a

okr ˛egami. Je´sli pole jest potencjalne, to rotF = 0.

2.15

Przykłady zachowawczych pól sił

1. Jednorodne pole sił ci ˛e˙zko´sci

P

= mg

P

x

= P

y

= 0, P

z

= −mg

∂V

∂x

= −P

x

= 0,

∂V

∂y

= −P

y

= 0,

∂V

∂x

= −P

x

= mg.

St ˛

ad

V = mgz + C

69

Powierzchnie ekwipotencjalne- płaszczyzny

L = V

1

− V

2

= mg (z

1

− z

2

)

2. Potencjał siły spr ˛e˙zystej

P

x

= −cx,

V = V (x)

dV

dx

= −P

x

= cx

V

=

1
2

cx

2

3. Pole sił centralnych- przyci ˛

aganie

P

= P (r)

P

x

= −P (r)

x

r

,

P

y

= −P (r)

y
r

,

P

z

= −P (r)

z
r

,

r

=

p

x

2

+ y

2

+ z

2

.

Potencjałem jest funkcja

V =

Z

P (r) dr

L = V

0

− V =

Z µ

∂V

∂x

dx +

∂V

∂y

dy +

∂V

∂z

dz

¶

=

Z µ

∂V

∂r

∂r

∂x

dx +

∂V

∂r

∂r

∂y

dy +

∂V

∂r

∂r
∂z

dz

¶

=

Z

∂V

∂r

dr

∂V

∂x

=

∂V

∂r

∂r

∂x

= P (r)

x

p

x

2

+ y

2

+ z

2

= P (r)

x

r

= −P

x

70

Podobnie

∂V

∂y

= −P

y

,

∂V

∂z

= −P

z

.

4. Pole sił ci ˛

a˙zenia

P

= k

M m

r

2

,

V

=

Z

P dr = kM m

Z

dr

r

2

= −k

M m

r

+ C,

V

= −

kM m

r

.

Rozpatrzmy ruch punktu

m

..

r = P

Obliczamy prac ˛e wykonan ˛

a mi ˛edzy punktami A i B toru przez sił ˛e P

L

AB

=

Z

d

AB

P ◦ dr

L

AB

=

Z

d

AB

m

..

r ◦ dr =

Z

d

AB

m

..

r ◦

.

rdt =

Z

.

r

2

.

r

1

m

.

r ◦ d

.

r

=

Z

v

2

v

1

mv ◦ dv =

1
2

mv

2

¯

¯

¯

¯

¯

¯

v

2

v

1

=

1
2

mv

2

2

−

1
2

mv

2

1

Wyra˙zenie

1
2

mv

2

- energia kinetyczna

L

AB

= T

B

− T

A

Zasada równowa˙zno´sci pracy i energii kinetycznej:

Praca wykonana przez siły działaj ˛

ace na punkt przy przesuni ˛eciu tego

71

punktu z poło˙zenia A do poło˙zenia B jest równa przyrostowi energii

kinetycznej punktu

Praca w polu potencjalnym jest równa ró˙znicy potencjałów tego

pola sił

L

AB

= V

A

− V

B

Z ostatnich dwóch wzorów

T

B

− T

A

= V

A

− V

B

,

T

B

+ V

B

= T

A

+ V

A

Zasada zachowania energii mechanicznej

W zachowawczym polu sił suma energii kinetycznej i potencjalnej jest

stała.

Przykład ruchu w zachowawczym polu sił

Ruch punktu A po krzywej w jednorodnym polu sił ci ˛e˙zko´sci. Dzi-

ałaj ˛

a du˙ze siły mg i N reakcja normalna do krzywej (nie wykonuje

pracy)

T

=

mv

2

2

,

T

0

=

mv

2

0

2

,

V

= mgz,

V

0

= mgz

0

Z zasady zachowania energii

mv

2

2

+ mgz =

mv

2

0

2

+ mgz

0

St ˛

ad

v =

q

v

2

0

+ 2g (z

0

− z) =

q

v

2

0

+ 2gh

Pr ˛edko´s´c na torze nie zale˙zy od kształtu toru, tylko od ró˙znicy poziomów

i pr ˛edko´sci pocz ˛

atkowej

72

2.16

Ruch ´srodka masy układu punktów

Rozpatrzmy ruch układu n punktów materialnych

m

1

··

r

1

= P

0

1

m

2

··

r

2

= P

0

2

..

.

m

n

··

r

n

= P

0

n

⎫

⎪

⎪

⎪

⎪

⎪

⎪

⎪

⎬

⎪

⎪

⎪

⎪

⎪

⎪

⎪

⎭

⇒ m

i

··

r

i

= P

0

i

P

0

i

= P

i

+ W

i

,

gdzie P

i

- siły zewn ˛etrzne,

W

i

- siły wewn ˛etrzne

Dodajemy stronami pierwsze równania
P

i

m

i

··

r

i

=

P

i

P

0

i

inaczej

X

i

m

i

d

2

r

i

dt

2

=

X

i

P

i

+

X

i

W

i

X

i

m

i

d

2

r

i

dt

2

=

d

2

dt

2

X

i

m

i

r

i

´

Srodek masy okre´slony jest nast ˛epuj ˛

aco

r

0

=

P

i

m

i

r

i

M

st ˛

ad

X

i

m

i

d

2

r

i

dt

2

=

d

2

dt

2

(M r

0

) = M

··

r

0

Zgodnie z III zasad ˛

a Newtona

P

i

W

i

= 0 poniewa˙z wyst ˛epuj ˛

a parami.

St ˛

ad ostatecznie

M

··

r

0

=

X

i

P

i

73

Twierdzenie 3 (o ruchu ´srodka masy układu punktów materialnych)

´

Srodek masy porusza si ˛

e jak punkt materialny, w którym skupiona jest

całkowita masa układu i na który działaj ˛

a wszystkie siły zewn ˛

etrzne.

2.17

P ˛

ed układu punktów

X

i

m

i

d

2

r

i

dt

2

=

d

dt

X

i

m

i

dr

i

dt

=

d

dt

X

i

m

i

v

i

=

dQ

dt

gdzie Q =

P

i

m

i

v

i

- p ˛ed układu.

dQ

dt

=

X

i

P

i

- zasada p ˛edu

Zasada zachowania p ˛

edu. Je˙zeli na układ nie działaj ˛

a ˙zadne siły, to p ˛ed

układu jest stały

X

i

P

i

= 0 ⇒

dQ

dt

= 0 ∧ Q = const.

2.18

Kr ˛

et układu punktów materialnych

Kr ˛etem układu punktów materialnych wzgl ˛edem ´srodka S nazywamy

K

S

=

n

X

i=1

ρ

i

× (m

i

v

i

)

Twierdzenie 4 (Zasada zachowania kr ˛

etu)

Pochodna wzgl ˛

edem czasu

kr ˛

etu układu obliczonego wzgl ˛

edem punktu nieruchomego S lub wzgl ˛

edem

´srodka masy równa jest sumie momentów sił zewn ˛

etrznych działaj ˛

acych

na układ obliczonych wzgl ˛

edem punktu S lub ´srodka masy.

Dowód.

W układzie współrz ˛ednych obieramy punkt S

Wzgl ˛edem punktu S kr ˛et układu wynosi

K

S

=

n

X

i=1

ρ

i

× (m

i

v

i

)

74

dK

S

dt

=

d

dt

n

X

i=1

ρ

i

× (m

i

v

i

)

=

n

X

i=1

dρ

i

dt

× (m

i

v

i

) +

n

X

i=1

ρ

i

× (m

i

a

i

)

ale ρ

i

= r

i

− r

S

. St ˛

ad

dρ

i

dt

=

·

r

i

−

·

r

S

= v

i

− v

S

v

i

- pr ˛edko´s´c i-tego punktu, v

S

- pr ˛edko´s´c punktu S. Ponadto wiemy, ˙ze

m

i

a

i

= P

i

+ W

i

St ˛

ad

dK

S

dt

=

n

X

i=1

v

i

× (m

i

v

i

) −

n

X

i=1

v

S

× (m

i

v

i

) +

n

X

i=1

ρ

i

×

³

P

i

+ W

i

´

= −v

S

×

Ã

d

dt

n

X

i=1

m

i

r

i

!

+

n

X

i=1

ρ

i

× P

i

+

n

X

i=1

ρ

i

× W

i

v

S

×

Ã

d

dt

n

X

i=1

m

i

r

i

!

= v

S

×

d

dt

M r

0

= v

S

× Mv

0

v

0

- pr ˛edko´s´c ´srodka masy.

P

n
i=1

ρ

i

× W

i

= 0. St ˛

ad

dK

S

dt

= −v

S

× Mv

0

+

n

X

i=1

ρ

i

× P

i

Je˙zeli S jest punktem nieruchomym, to v

S

= 0 i pierwszy człon =

0. Je˙zeli v

S

= v

0

to S jest ´srodkiem masy. Wtedy v

0

× Mv

0

= 0.

Otrzymujemy zatem

dK

S

dt

=

n

X

i=1

ρ

i

× P

i

75

Zasada zachowania kr ˛

etu.

Je˙zeli na układ punktów nie działaj ˛

a

˙zadne momenty sił zewn ˛

etrznych wzgl ˛edem punktu S, to kr ˛et układu

wzgl ˛edem punktu S jest stały

M

S

=

n

X

i=1

ρ

i

× P

i

= 0 ⇒

dK

S

dt

= 0 ∧ K

S

= const.

We´zmy teraz ciało materialne, które obraca si ˛e wzgl ˛edem pewnej osi

z pr ˛edko´scia k ˛

atow ˛

a ω.

v = ωh

h- jest ramieniem p ˛edu elementu dm czyli vdm.

dK

0

= h v dm = ωh

2

dm

K

0

=

Z

ωh

2

dm = ω

Z

h

2

dm

K

0

= I

L

ω

2.19

Energia kinetyczna układu punktów

Energia kinetyczna układu punktów jest równa sumie energii poszczegól-

nych punktów

T =

X m

i

v

2

i

2

W ruchu post ˛epowym pr ˛edko´sci wszystkich punktów s ˛

a jednakowe wi ˛ec

T =

v

2

2

X

m

i

=

mv

2

2

2.19.1

Energia kinetyczna w ruchu obrotowym ciała sz-

tywnego

pr ˛edko´s´c v = ωh

dT =

1
2

v

2

dm =

1
2

ω

2

h

2

dm

76

St ˛

ad

T =

1
2

Z

v

2

dm =

1
2

Z

ω

2

h

2

dm =

1
2

ω

2

Z

h

2

dm =

1
2

I

L

ω

2

Twierdzenie 5 (Koeniga)

Energia kinetyczna układu punktów mate-

rialnych równa jest sumie energii kinetycznej, jak ˛

a miałby punkt mate-

rialny o masie całego układu, poruszaj ˛

acy si ˛

e z pr ˛

edko´sci ˛

a ´srodka masy

oraz energii kinetycznej tego˙z układu wzgl ˛

edem ´srodka masy.

Rozpatrzmy ruch układu wzgl ˛edem stałego układu. Wi ˛

a˙zemy na

stałe z układem punktów układ C, x

0

, y

0

, z

0

. Pr ˛edko´s´c dowolnego

punktu o masie m

i

wynosi

v

i

= v

0

i

+ v

C

v

2

i

= v

i

◦ v

i

= v

2

i

v

2

i

= v

2

i

=

¡

v

0

i

+ v

C

¢

2

= v

2

C

+ 2v

0

i

◦ v

C

+ v

02

i

= v

2

C

+ 2v

0

i

◦ v

C

+ v

02

i

St ˛

ad

T

=

X m

i

v

2

i

2

=

1
2

X

m

i

¡

v

2

C

+ 2v

0

i

◦ v

C

+ v

02

i

¢

=

1
2

v

2

C

X

m

i

+ v

C

◦

X

m

i

v

0

i

+

X m

i

v

02

i

2

Wyra˙zenie

P

m

i

v

0

i

- p ˛ed układu w jego ruchu wzgledem układu C, x

0

, y

0

, z

0

.

P ˛ed ten jest równy 0, bo układ jest sztywno zwi ˛

azany z primowanym

układem współrz ˛ednych

X

m

i

v

0

i

= 0

77

St ˛

ad

T =

1
2

mv

2

C

+

X m

i

v

02

i

2

Je˙zeli badamy energi ˛e kinetyczn ˛

a bryły, to energia kinetyczna wzgl ˛e-

dem ´srodka masy wynosi

T

0

=

1
2

I

L

ω

2

St ˛

ad

T =

1
2

mv

2

C

+

1
2

I

L

ω

2

2.19.2

Praca w ruchu obrotowym

dL = P

ϕ

ds

dL = P

ϕ

hdϕ

dL = M

l

dϕ

L =

Z

ϕ

2

ϕ

1

M

l

dϕ

2.20

Ruch post ˛

epowy ciała sztywnego

Równania ruchu jak dla punktu.

P ˛ed bryły

Q = mv

C

Kr ˛et bryły- bryła si ˛e nie obraca wzgl ˛edem ´srodka masy st ˛

ad K

C

= 0.

Praca: L =

R

d

AB

P ◦ dr.

Energia kinetyczna T =

1
2

mv

2

C

78

2.21

Ruch obrotowy ciała sztywnego

Równania ruchu

dK

Z

dt

=

X

M

iZ

K

Z

= I

Z

ω

d (I

Z

ω)

dt

=

X

M

iZ

I

Z

dω

dt

=

X

M

iZ

I

Z

ε =

X

M

iZ

I

Z

¨

ϕ =

X

M

iZ

- równanie ruchu bryły

Rozwi ˛

azanie równania ruchu I

Z

¨

ϕ =

P

M

iZ

:

ϕ =

M

Z

2I

Z

t

2

+ ω

0

t + ϕ

0

P ˛ed bryły.

Poniewa˙z w ruchu obrotowym ´srodek masy jest w spoczynku (o´s prze-

chodzi przez ´srdek masy), to p ˛ed Q = 0.

Kr ˛et bryły: K

Z

= I

Z

ω.

Praca: L =

R

ϕ

2

ϕ

1

M

l

dϕ.

Energia kinetyczna:

1
2

I

Z

ω

2

.

79

2.22

Wahadło matematyczne

M

z

= −mgl sin ϕ

ml

2

¨

ϕ = −mgl sin ϕ

¨

ϕ+

ml

ml

2

g sin ϕ = 0

¨

ϕ+

g

l

sin ϕ = 0

2.23

Wahadło fizyczne

Wahadłem fizycznym nazywamy swobodnie obracaj ˛

ace si ˛e ciało mate-

rialne wzgl ˛edem stałego punktu.

Ułó˙zmy równanie ruchu

M

z

= −F · y

M

z

= −mgs sin ϕ

I

z

¨

ϕ = −mgs sin ϕ

¨

ϕ+

ms

I

z

g sin ϕ = 0

Porównuj ˛

ac to równanie z wahadłem matematycznym

¨

ϕ +

g

l

sin ϕ = 0

otrzymujemy

l

red

=

I

z

ms

długo´s´c zredukowana

Okres wahadła

T = 2π

s

l

g

→ 2π

s

l

red

g

= 2π

s

I

z

mgs

.

80

Rozwi ˛

azanie

ϕ = A cos (ωt + ϕ

0

) .

2.24

Reakcje dynamiczne

ω = const.

R

A

, R

B

− reakcje dynamiczne

Korzystamy z zasady d’Alemberta

Siły od´srodkowe (bezwładno´sci) musz ˛

a si ˛e równowa˙zy´c z siłami reakcji.

Równania b ˛ed ˛

a

R

Ax

+ R

Bx

+ ω

2

Z

xdm = 0

R

Ay

+ R

By

+ ω

2

Z

ydm = 0

równania sił

−R

By

l − ω

2

Z

yzdm = 0

R

Bx

l + ω

2

Z

xzdm = 0

momenty

Oznaczaj ˛

ac

Z

xdm = mx

c,

Z

ydm = my

c

,

Z

yzdm = D

yz

,

Z

xzdm = D

xz

mamy

⎧

⎪

⎪

⎪

⎪

⎪

⎪

⎨

⎪

⎪

⎪

⎪

⎪

⎪

⎩

R

Ax

+ R

Bx

+ ω

2

mx

c

= 0

R

Ay

+ R

By

+ ω

2

my

c

= 0

R

By

l + ω

2

D

yz

= 0

R

Bx

l + ω

2

D

xz

= 0

81

st ˛

ad

R

Bx

= −ω

2

D

xz

l

R

By

= −ω

2

D

yz

l

R

Ax

= ω

2

µ

D

xz

l

− mx

c

¶

R

Ay

= ω

2

µ

D

yz

l

− my

c

¶

R

A

=

q

R

2

Ax

+ R

2

Ay

R

B

=

q

R

2

Bx

+ R

2

By

Reakcje znikaj ˛

a tylko wtedy, gdy

x

c

= 0,

y

c

= 0,

D

xz

= 0,

D

yz

= 0.

Aby reakcje dynamiczne były równe zeru o´s obrotu musi by´c centraln ˛

a

główn ˛

a osi ˛

a bezwładno´sci.

Je´sli o´s obrotu jest centraln ˛

a osi ˛

a, wówczas w ło˙zyskach działaj ˛

a pary

sił:

x

c

= 0,

y

c

= 0 =⇒

⎧

⎨

⎩

R

Ax

= −R

Bx

=

1

l

D

xz

ω

2

R

Ay

= −R

By

=

1

l

D

yz

ω

2

.

Przykład

Poniewa˙z płaszczyzna Oxz jest płaszczyzn ˛

a symetrii kr ˛

a˙zka, wi ˛ec D

yz

=

0 (tyle samo masy po obu stronach płaszczyzny), st ˛

ad

R

Ay

= R

By

= 0.

Osie x, y s ˛

a obrócone o k ˛

at ϕ w stosunku do głównych osi bezwładno´sci

1, 2. Nale˙zy wyznaczy´c moment D

xz

.

82

Wyprowadzenie wzoru ogólnego.

ξ

= x cos ϕ + y sin ϕ

η

= −x sin ϕ + y cos ϕ

ζ

= z

I

ξ

= I

x

cos

2

ϕ + I

y

sin

2

ϕ − D

xy

sin 2ϕ,

α = ϕ, β =

π

2

− ϕ, γ =

π

2

I

η

= I

x

sin

2

ϕ + I

y

cos

2

ϕ − D

zy

sin 2ϕ,

α = ϕ +

π

2

, β = ϕ, γ =

π

2

D

ξη

=

Z

ξηdm =

Z

(x cos ϕ + y sin ϕ) (−x sin ϕ + y cos ϕ) dm =

=

¡

cos

2

ϕ − sin

2

ϕ

¢ Z

xydm + sin ϕ cos ϕ

µZ

y

2

dm −

Z

x

2

dm

¶

.

Z

xydm = D

xy

i

Z

y

2

dm −

Z

x

2

dm =

Z ¡

y

2

+ z

2

¢

dm −

Z ¡

x

2

+ z

2

¢

dm = I

x

− I

y

czyli mamy

D

ξη

= D

xy

cos 2ϕ +

1
2

(I

x

− I

y

) sin 2ϕ.

Je´sli przyjmiemy, ˙ze teraz I

x

= I

1

i I

y

= I

2

s ˛

a momentami głównymi

(x, y - osie główne), to D

xy

= 0, st ˛

ad

D

ξη

=

1
2

(I

1

− I

2

) sin 2ϕ.

W naszym przypadku jest

D

xz

=

1
2

(I

1

− I

2

) sin 2α

83

st ˛

ad

R

Ax

= −R

Bx

=

1

2l

(I

1

− I

2

) ω

2

sin 2α.

2.25

Ruch płaski bryły

Zbadajmy p ˛ed i kr ˛et bryły w ruchu płaskim

dp

dt

=

X

F

i

p = p

c

dp

c

dt

=

X

F

i

dK

z

dt

=

X

M

iz

p

c

= m

·

r

c

= mv

c

K

z

= I

z

ω

z

st ˛

ad

⎧

⎨

⎩

m

··

r

c

=

P

F

i

I

z

¨

ϕ =

P

M

iz

równania ruchu płaskiego

Energia kinetyczna w ruchu płaskim

T =

1
2

mv

2

c

+

1
2

I

z

ω

2

.

84