1

Podaż na rynku doskonale konkurencyjnym,

równowaga rynkowa

i statyka porównawcza

1. Funkcje podaży ryku w SR

2. Równowaga na rynku doskonale konkurencyjnym w

SR

3. Równowaga w SR i w LR

4. Podaż rynku doskonale konkurencyjnego w LR

5. Dostosowania do zmian parametrów popytu i

podaży w SR i LR: statyka porównawcza rynków
doskonale konkurencyjnych

6. Zasięg podatku jednostkowego

7. Czysta strata wywołana podatkiem jednostkowym

☼

2

Funkcje podaży rynku w SR

Rynkową funkcję podaży opisuje wzór:

( )

( )

x

m

j

j

x

S

p

x

p

X

∑

=

=

1

dla m firm. (rys. 13.1).

Przykład: j-ta firma ma funkcję produkcji opisaną wzorem:
x

j

= K

j

1/2

L

j

1/2

i firmy zatrudniają różne ilości kapitału.

Wiemy, że

j

j

x

K

wx

p

2

=

to krzywa SRS firmy. Przekształcając to

równanie do postaci:

( )

w

K

p

p

x

j

x

x

j

2

=

otrzymujemy krzywą podaży

j-tej firmy i sumujemy podaż m firm:

( )

( )

∑

∑

=

=

=

=

m

j

j

x

x

m

j

j

x

S

w

K

p

p

x

p

X

1

1

2

i

następnie wyznaczamy rynkową funkcję podaży w SR:

( )

∑

=

=

m

j

j

x

x

S

K

w

p

p

X

1

2

.

Elastyczność podaży:

( )

x

S

x

x

S

p

X

dp

d

x

p

=

ε

Zmiany podaży rynkowej
Ilość firm w przemyśle i dystrybucja technik produkcji
między firmami stają się parametrami SRS rynkowej.
Wejście nowych firm podaż rynkowa rośnie, wprowadzenie
nowych technik produkcji i ich dyfuzja również prowadzi do
zwiększenia podaży na rynku.

3

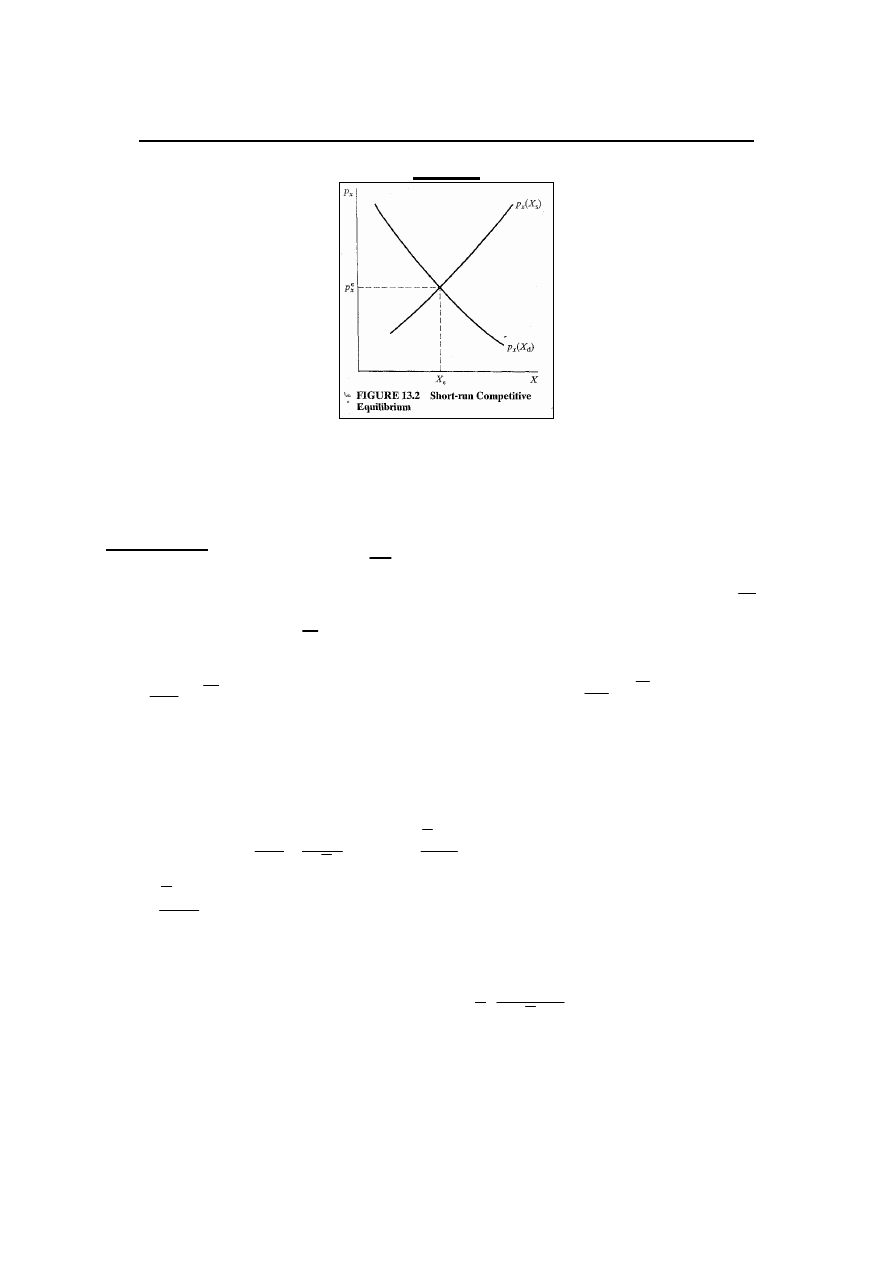
Równowaga na rynku doskonale konkurencyjnym

w SR

(rys. 13.2: dobro nie jest dobrem Giffen’a – krzywa popytu
opada, i są malejące przychody wszystkich zmiennych
czynników – krzywa podaży wznosi się)
Przykład: wszyscy konsumenci mają funkcję użyteczności:
U

i

= x

i

y

i

i dochody:

M

. Wszystkie firmy mają funkcje

produkcji: x

j

= K

j

1/2

L

j

1/2

i stałe zatrudnienie kapitału:

j

K

w

SR. Stawka płac: w . Funkcję popytu rynkowego opisuje wzór:

∑

=

=

n

i

i

x

D

M

p

X

1

2

1

, a podaży rynkowej:

∑

=

=

m

j

j

x

S

K

w

p

X

1

2

. Warunek

równowagi to: X

E

= X

D

= X

S

. Jeżeli przyjmiemy, że SM to

suma dochodów, a SK to suma kapitałów, to wzory na rynkowy
popyt i podaż można przeformułować i wstawić do warunku
równowagi:

( )

SK

SM

w

p

w

SK

p

p

SM

x

x

x

=

⇒

=

2

2

2

i rozwiązać go dla p

x

:

2

/

1















=

SK

SM

w

p

E

x

. Aby znaleźć wielkość popytu i podaży w

równowadze cenę równowagową wstawiamy do wzorów na
popyt i podaż rynkowe w SR:

( )( )

E

S

D

X

X

w

SK

SM

X

=

=













=

2

/

1

2

1

.

4

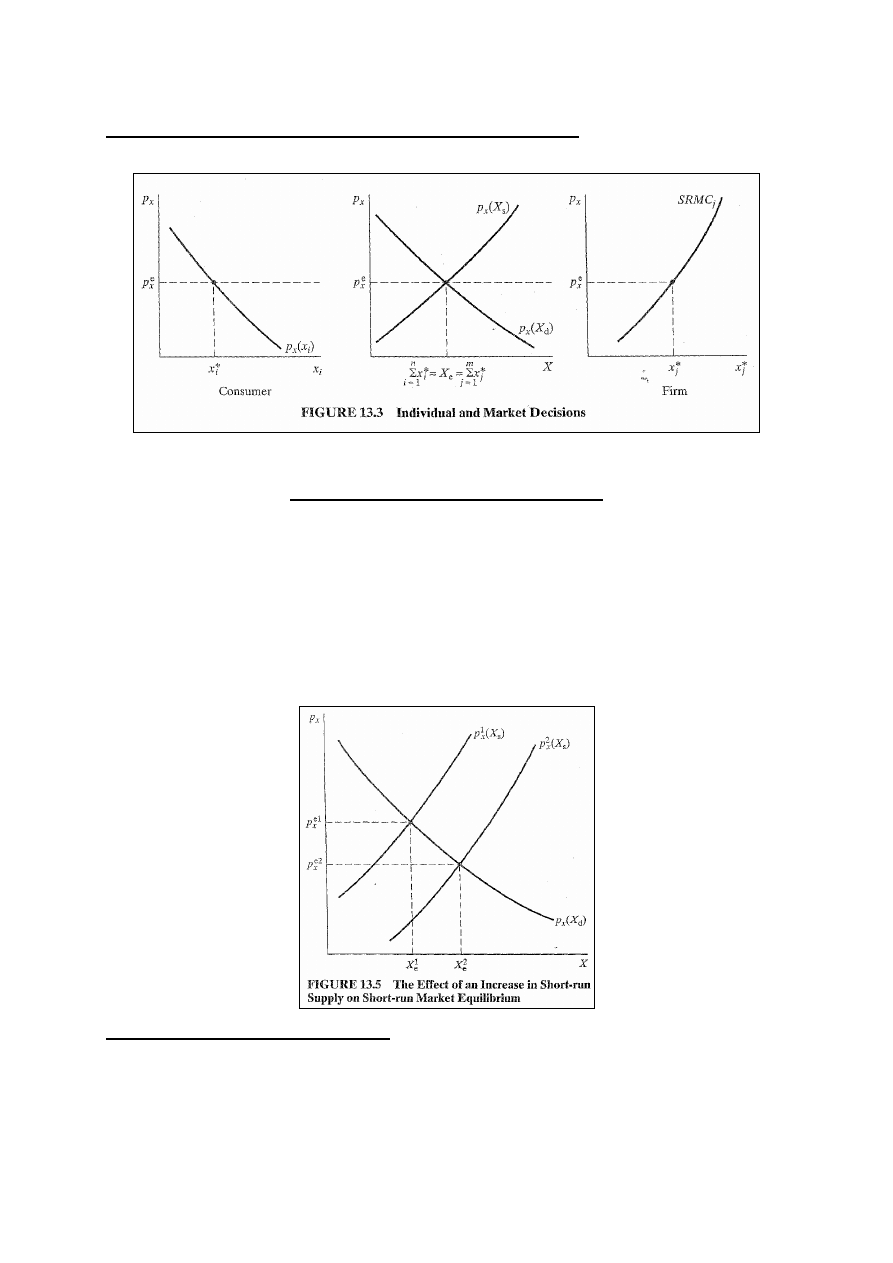
Decyzje indywidualne i równowagi rynkowe
Rys.13.3 – jednoczesność decyzji indywidualnych

Równowaga w SR i w LR

Na rys. 13.3 firma j-ta osiąga zyski, gdy

( )

( )

[

]

0

*

*

*

>

−

=

j

j

E

x

j

j

j

x

SRATC

p

x

x

π

. Jeżeli przyjmiemy, że nie ma barier na

wejściu dla nowych firm z warunków konkurencji wynika, że
nowe firmy wejdą na rynek i część firm już funkcjonujących
będzie się rozwijać. Prowadzi to do przesunięcia na prawo
krzywej rynkowej SRS - rys. 13.5.

Definicja równowagi w LR
Proces wchodzenia nowych firm spowodowany możliwością
osiągnięcia zysków w SR będzie trwał, aż ta możliwość
zostanie wyczerpana. Warunki rynkowe, w których zyski w

5

SR = 0 i nie ma żadnych możliwości ich osiągania określamy
mianem równowagi długookresowej w doskonałej konkurencji.
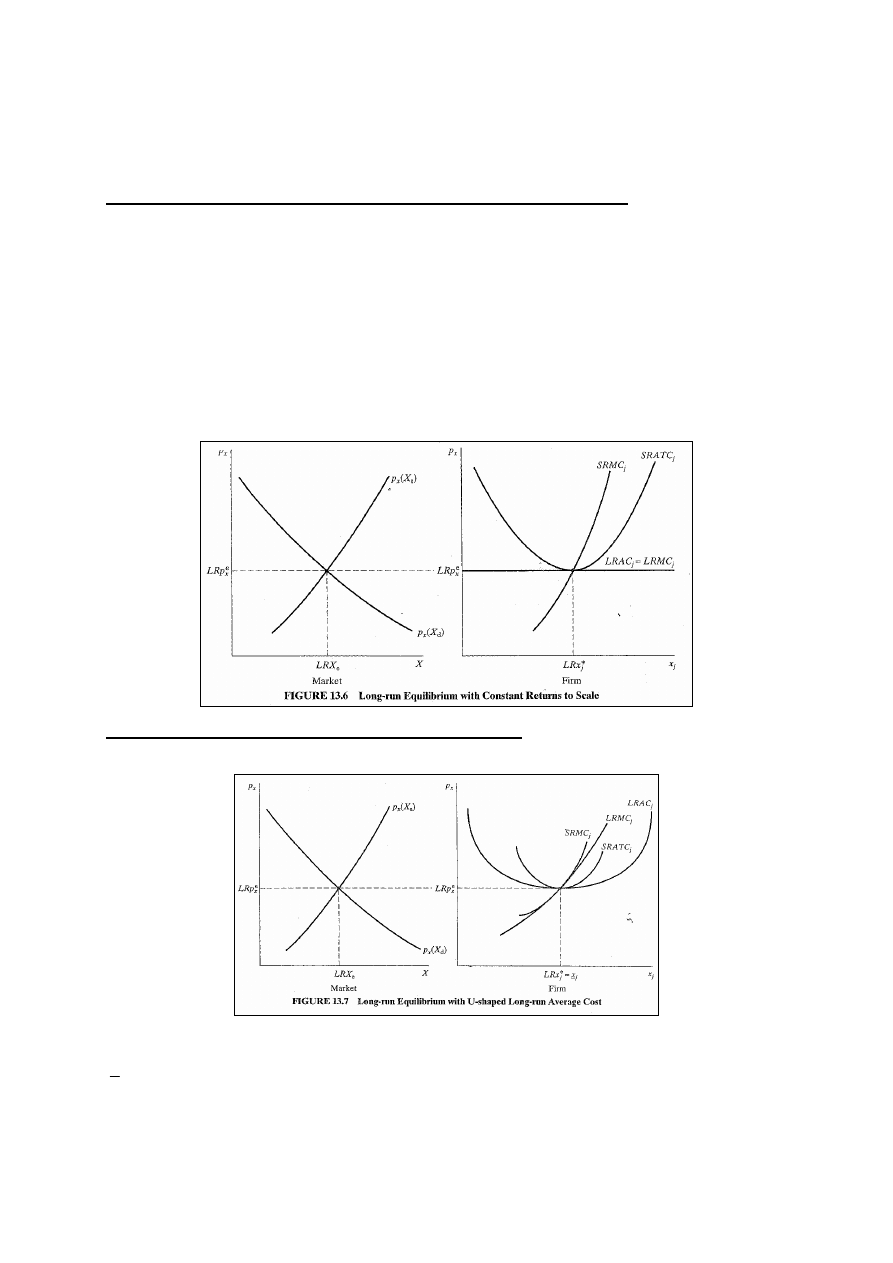
Równowaga w LR przy stałych korzyściach skali
(rys.13.6) Cena równowagowa w LR, LRp

x

E

, równa się SRMC i

minSRATC przy zerowych zyskach w SR dla LRx

j

*

:

SRπ

j

(LRx

j

*

) = LRx

j

*

[LRp

x

E

- SRATC

j

(LRx

j

*

)] = 0.

Co więcej, ponieważ minSRATC = LRATC przy stałych
korzyściach skali, to nie istnieją żadne możliwości dalszego
osiągania zysków przez rozwój w LR. Dlatego również w LR
zyski = 0: LRπ

j

(LRx

j

*

) = LRx

j

*

[LRp

x

E

- LRAC

j

(LRx

j

*

)] = 0.

Koszty przeciętne w LR w kształcie U
(rys.13.7)

Istnieje tylko jedna możliwa wielkość równowagowa w LR,

*

j

j

LRx

x

=

, gdyż jest to jedyny punkt, w którym SRMC

jednocześnie równa się minSRATC i minLRAC, czyli zyski w
SR i LR = 0.

6

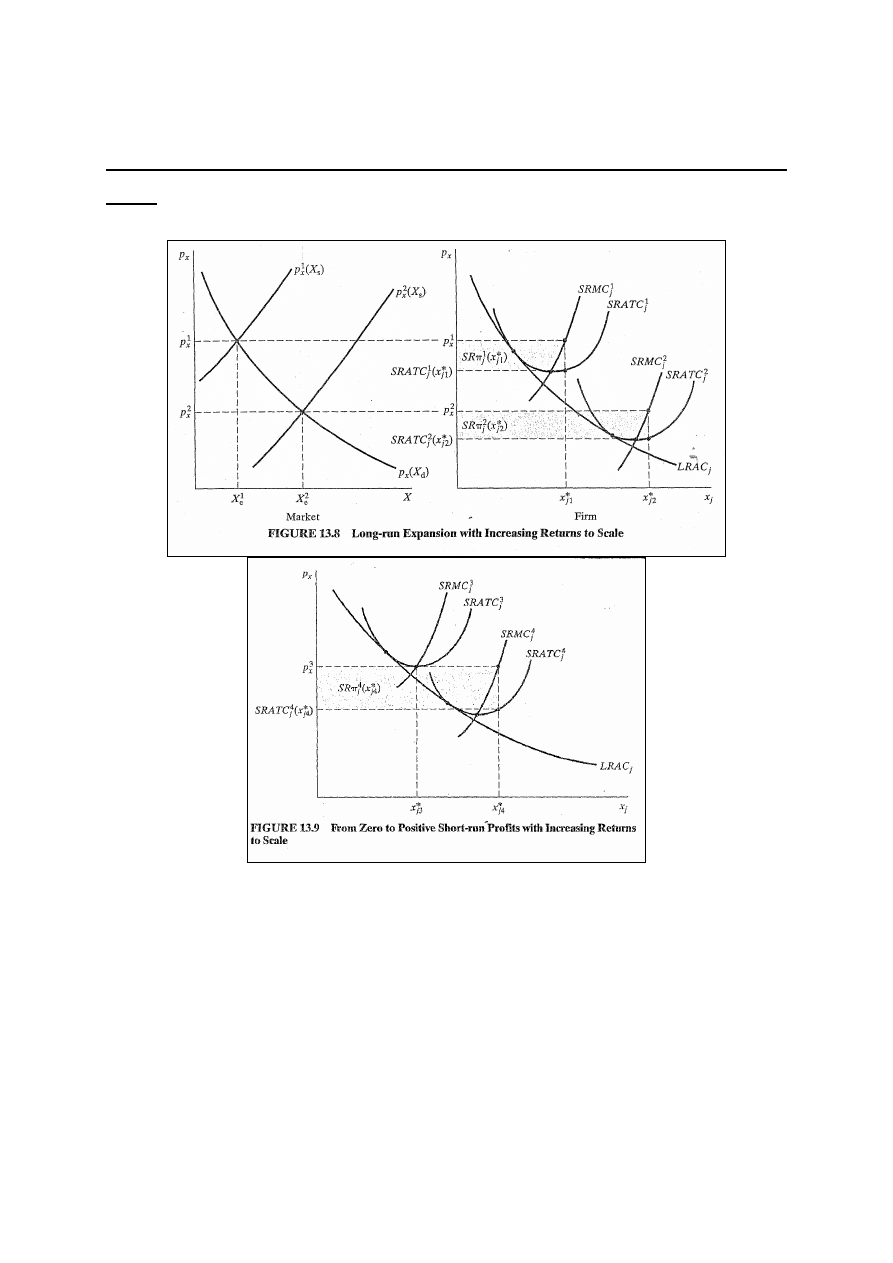
Nieistnienie równowagi w LR przy rosnących korzyściach
skali
(rys. 13.8 i rys. 13.9)

Załóżmy, że zaczynamy przy cenie p

x

1

gdy firma osiąga zyski

w SR:

( )

( )

[

]

0

*

1

1

1

*

1

*

1

1

>

−

=

j

j

x

j

j

j

x

SRAC

p

x

x

SR

π

. Istnienie tych zysków

stanowi zachętę dla innych firm do wchodzenia na ten rynek
i dla firm funkcjonujących do rozwoju. Prowadzi to do
przesunięcia krzywej SRS tego rynku z pozycji

( )

S

x

X

p

1

do

( )

S

x

X

p

2

i obniżenia ceny równowagi. Ale rozwój firmy j-tej

zmniejsza jej SRATC przesuwając krzywą do pozycji
SRATC

j

2

. Czyli zyski w SR są w dalszym ciągu dodatnie:

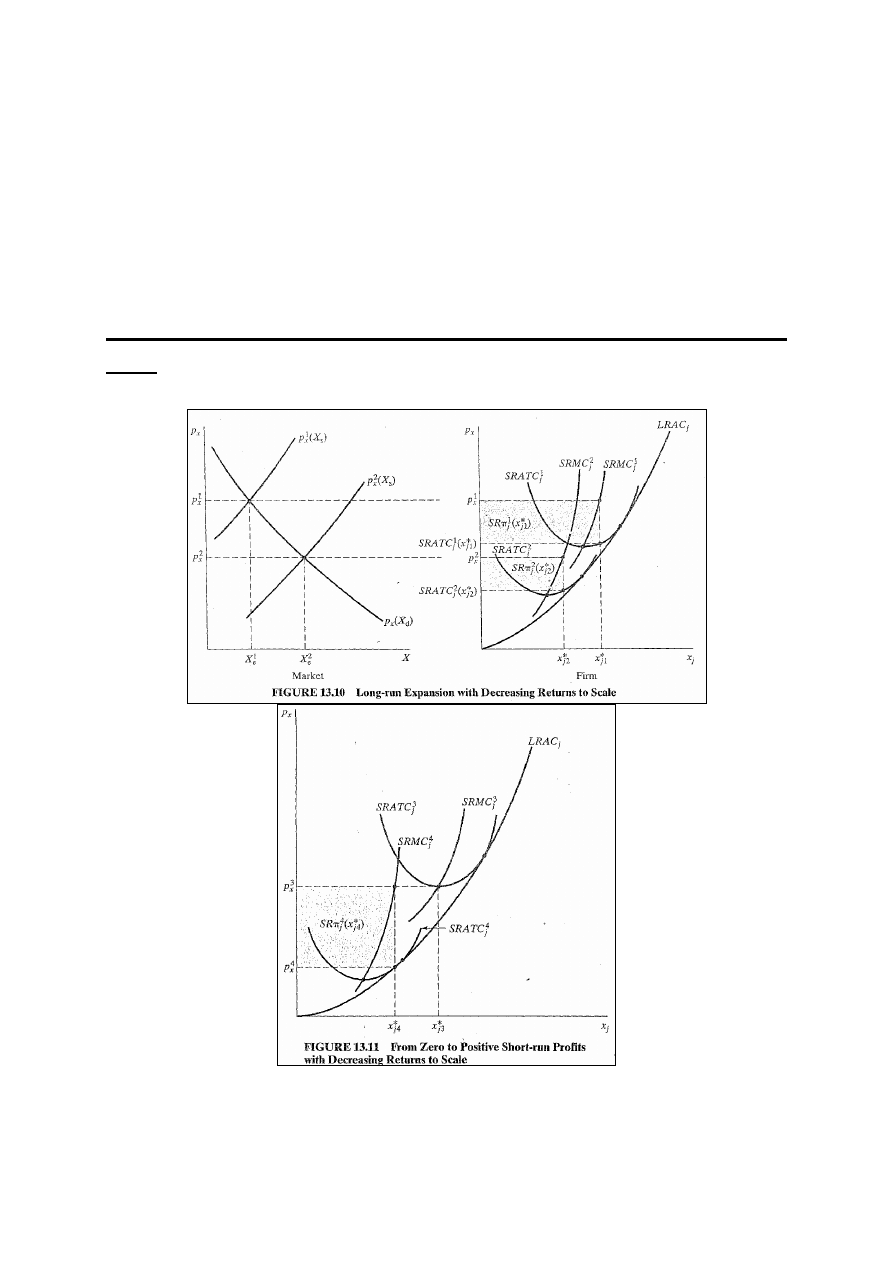
7

( )

( )

[

]

0

*

2

2

2

*

2

*

2

2

>

−

=

j

j

x

j

j

j

x

SRAC

p

x

x

SR

π

. Ponieważ minSRAC nigdy nie równa

się LRAC i ponieważ nie ma minLRAC, to nie ma punktu, w
którym wszystkie możliwości osiągania zysków zostają
wyczerpane. Nawet przy cenie p

x

3

równej minATC firma

może zwiększyć zyski zwiększając produkcję i zmniejszając
koszty do SRATC

j

4

.

Nieistnienie równowagi w LR przy malejących korzyściach
skali
(rys.13.10 i rys.13.11)

Jedyna możliwa równowaga LR zostałaby osiągana przy
zerowej produkcji.

8

Załóżmy, że na zaczynamy przy cenie p

x

1

gdy firma osiąga

zyski w SR:

( )

( )

[

]

0

*

1

1

1

*

1

*

1

1

>

−

=

j

j

x

j

j

j

x

SRAC

p

x

x

SR

π

. Firma nie ma bodźców

aby się rozwijać, gdyż wtedy zmniejszałaby swoje zyski.
Nowe firmy wchodzą na rynek powodując przesunięcie
krzywej SRS rynku na prawo z pozycji

( )

S

x

X

p

1

do

( )

S

x

X

p

2

.

Pomimo spadku ceny równowagi firma w dalszym ciągu osiąga
zyski ograniczając SRATC :

( )

( )

[

]

0

*

2

2

2

*

2

*

2

2

>

−

=

j

j

x

j

j

j

x

SRAC

p

x

x

SR

π

.

Jedyna równowaga: nieskończenie wiele firm, z których
każda wytwarza zero produktu.

Podaż rynku doskonale konkurencyjnego w LR

Z powyższych rozważań wynikają ważne cechy rynku
doskonale konkurencyjnego. Po pierwsze, jeżeli istnieją
rosnące korzyści skali, to konkurencja nie może utrzymać się
w długim okresie. Po drugie, jeżeli istnieją malejące korzyści
skali, to przemysł nie może funkcjonować w LR przy wolnym
wejściu na rynek. Rynki doskonale konkurencyjne
funkcjonujące w LR muszą mieć stałe korzyści skali lub
krzywą LRAC w kształcie U. Co więcej przy krzywej LRAC o
kształcie U, aby w przemyśle funkcjonowało wiele firm,
wielkość produkcji każdej z nich,

j

x

, musi być bardzo mała w

odniesieniu do wielkości produkcji osiąganej przez rynek w
równowadze w LR. Przy stałych korzyściach skali również
musi istnieć odpowiednio dużo firm aby spełnione były
warunki konkurencji doskonałej, pomimo ze każda firma o
dowolnej wielkości jednakowo zmniejsza koszty w LR.
Cena i wielkość produkcji w równowadze w LR
Cena w równowadze w LR wyznaczana jest przez technikę i
ceny czynników.
Przy stałych korzyściach skali:
LRp

x

E

= LRMC = LRAC = minSRATC.

9

Przy krzywej LRAC w kształcie U: LRp

x

E

= minLRAC.

W każdym przypadku podaż rynku jest sumą wielkości
podaży indywidualnych firm dostarczanych przy każdej
cenie. Przy krzywej LRAC w kształcie U podaż rynku jest
sumą wielkości podaży, jaką firmy są gotowe dostarczyć
przy minLRAC:

∑

=

=

m

j

j

S

x

LRX

1

.

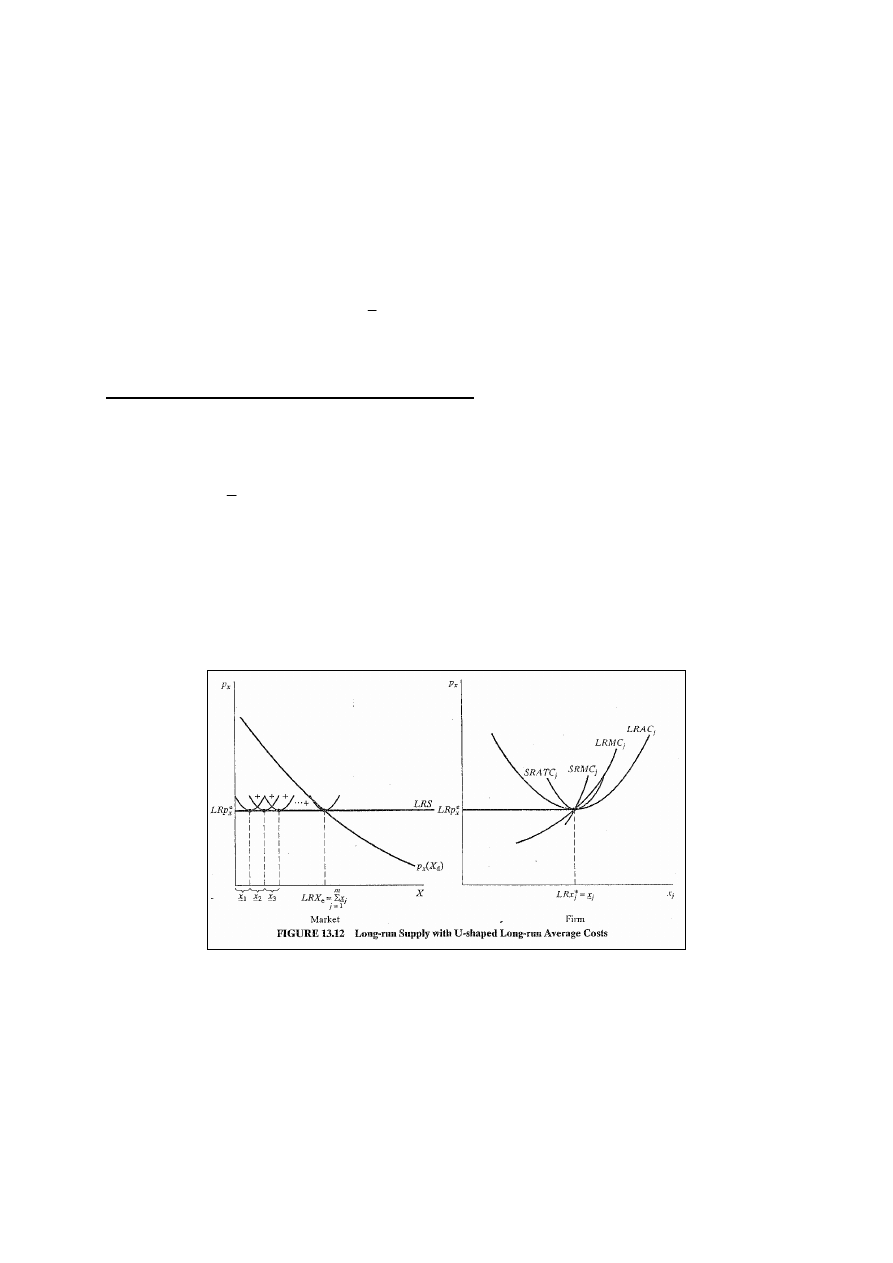
Doskonale elastyczna podaż w LR
Przemysł rozwija się lub kurczy w LR przez zwiększanie lub
zmniejszanie się ilości firm, z których każda produkuje
dokładnie

j

x

przy cenie równowagi w LR. Dlatego możemy

podaż przemysłu w LR traktować jako doskonale elastyczną
przy cenie równowagi w LR. Jeśli technika lub ceny
czynników nie zmienią się, to wielkość produkcji w
równowadze w LR rośnie lub maleje przy tej samej cenie.
(rys. 13.12).

Przy stałych korzyściach skali każda firma ma doskonale
elastyczną krzywą LRS, gdyż przy każdej swej wielkości
jednakowo zmniejsza koszty w LR. Tak więc rynkowa LRS
jest taka sama, jak LRS każdej firmy. Rynkowa podaż w LR
jest powiększeniem każdej firmy doskonale elastycznych
LRMC i LRAC. (rys.13.13) Zarówno firma, jak i rynek mogą

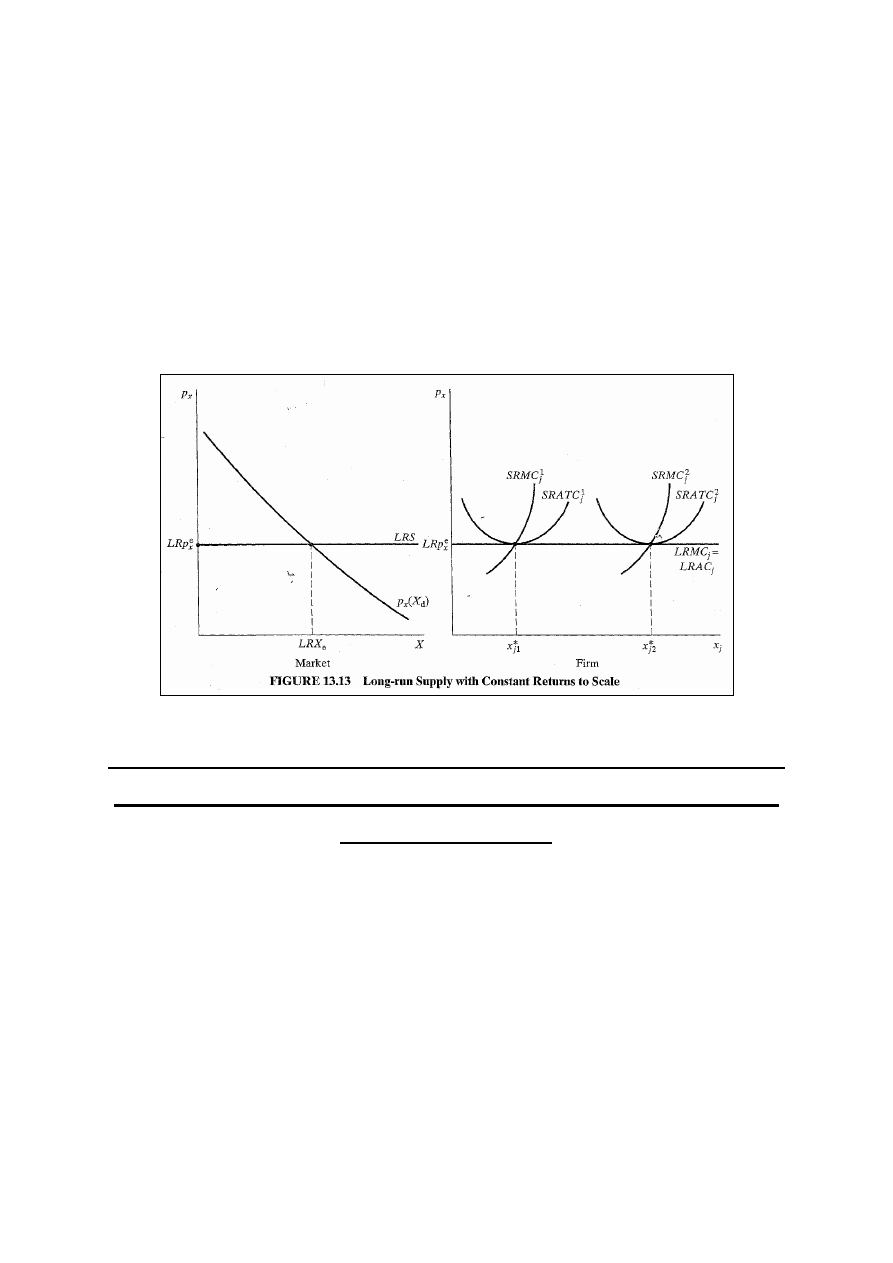
10

rozwijać się lub zmniejszać wzdłuż poziomej krzywej LRMC
firmy. Wielkość rynkowej produkcji w równowadze w LR jest
sumą optymalnych decyzji firm w SR przy cenie równowagi w
LR. Z rysunku wynika, że jedna firma może wybrać dowolną
wielkość produkcji wzdłuż krzywej podaży w LR. Z tego
wynika niemożność określenia, której nie było przy krzywej
kosztów w kształcie U: nigdy nie wiemy ile firm znajdzie się
w przemyśle o stałych korzyściach skali w LR.

Dostosowania do zmian parametrów popytu i podaży

w SR i LR: statyka porównawcza rynków doskonale

konkurencyjnych

Rys. 13.5 – statyka komparatywna SRS przy stałym D.

11

Zmiana popytu
Rys. 13.14 - statyka komparatywna D przy stałym SRS.

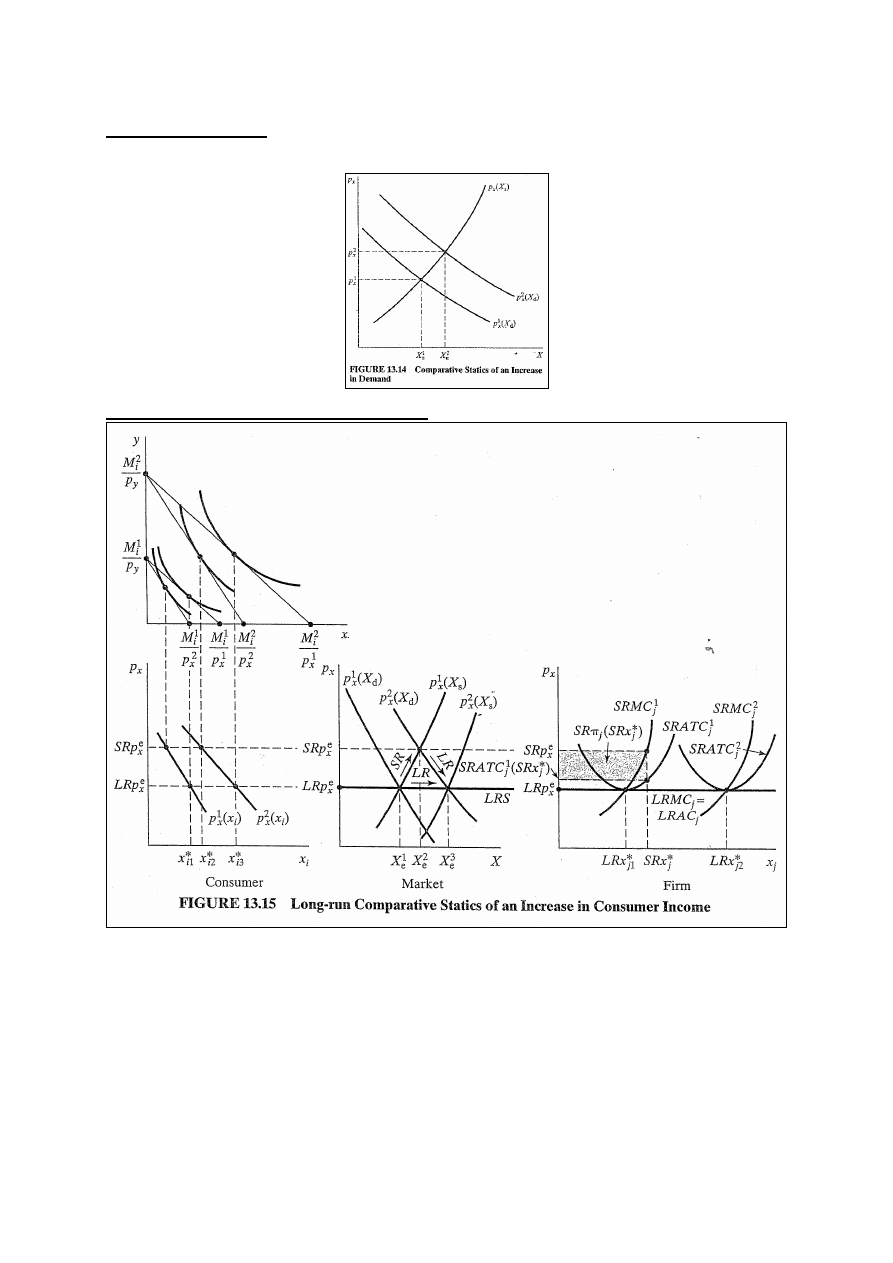
Wzrost dochodu konsumenta

Rys. 13.15 – przemysł o stałych korzyściach skali produkujący
dobro normalne znajduje się w równowadze w LR. Dochód
konsumenta ↑ z

1

i

M

do

2

i

M

⇒ krzywe popytu konsumenta na

dobro normalne ↑ z

( )

i

x

x

p

1

do

( )

i

x

x

p

2

. Wzrost dochodów

wszystkich konsumentów powoduje przesunięcie krzywej
popytu rynkowego na prawo z

( )

D

x

X

p

1

do

( )

D

x

X

p

2

. Cena w

12

równowadze w SR ↑ z

E

x

LRp

do

E

x

SRp

, a wielkość sprzedaży na

rynku ↑ z

1
E

X

do

2

E

X

. Przy wyższej cenie w równowadze w SR

firma zwiększa produkcję z

*

1

j

LRx

do

*

j

SRx

wzdłuż krzywej

SRMC i zaczyna osiągać zyski:

( )

( )

[

]

0

*

1

*

*

>

−

=

j

j

E

x

j

j

j

SRx

SRATC

SRp

SRx

SRx

SR

π

.

Zyski te stanowią zachętę dla innych firm do wejścia na ten
rynek i dla firm funkcjonujących na tym rynku do rozwoju.
Ten możliwy rozwój przedstawiony jest jako przesunięcie z
SRMC

j

1

i SRATC

j

1

do SRMC

j

2

i SRATC

j

2

. Łączny skutek

wejść i rozwoju powoduje przesunięcie krzywej rynkowej
SRS z

( )

S

x

X

p

1

do

( )

S

x

X

p

2

oraz obniżenie ceny. Proces rozwoju i

wchodzenia trwa tak długo aż ponownie cena równa się cenie
równowagi w LR i zyski równają się 0, czyli w

3

E

X

- punkcie

przecięcia

( )

D

x

X

p

2

i

( )

S

x

X

p

2

. Można również pominąć zmiany w SR

i patrzeć na dostosowania w LR jako przejście z

1
E

X

do

3

E

X

wzdłuż krzywej LRS przy niezmienionej cenie.

Zmiany techniki
Zmiany neutralne techniki produkcji w przemyśle o stałych
korzyściach skali są przykładem przesunięcia podaży w LR.
Wiemy, że LRTC są funkcją liniową wychodzącą z początku
układu współrzędnych: LRTC(x

1

) = bx

1

dla b > 0 i że LRMC:

LRMC

1

= b. Początkowa LRS jest doskonale elastyczna w

LRMC

1

. Jeżeli wielkość produkcji ma zwiększyć się o

arbitralnie wybrany mnożnik α > 1, dla każdej kombinacji
czynników, to nowa funkcja produkcji jest następująca:
x

2

(K, L) = αx

1

(K, L) ⇒ x

1

(K, L) = x

2

(K, L)/α.

Wstawiając za x

1

w LRTC = bx oraz w LRMC = LRAC = b

otrzymujemy: LRTC(x

2

) = b(x

2

/α) = (b/α)x

2

oraz

13

LRMC

2

= b/α < b. Z otrzymanych obliczeń wynika, że nowe

LRMC również są doskonale elastyczne i mniejsze od
starych. Jeżeli α = 2, to nowe MC stanowią ½ starych MC.

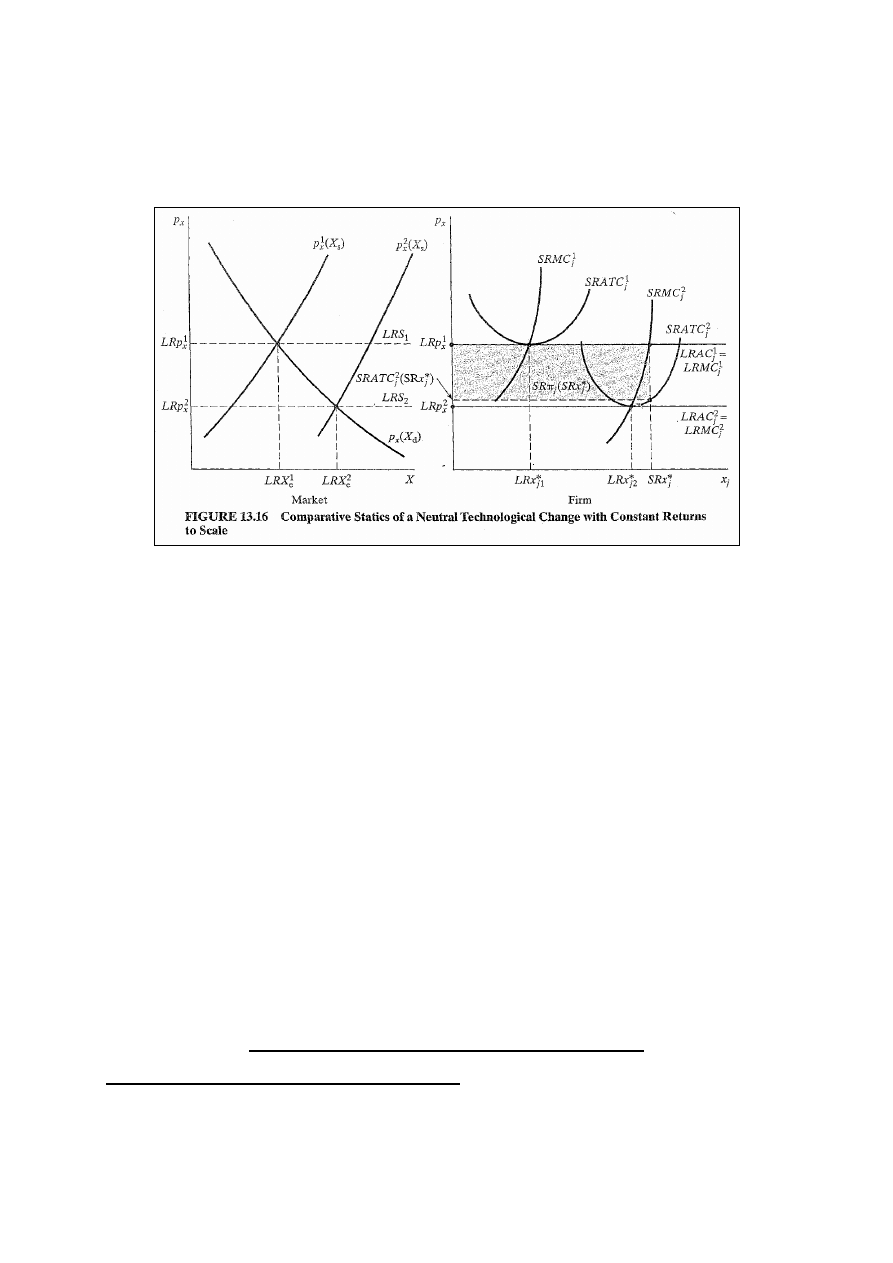
Rys. 13.16 – skutki neutralnej zmiany techniki produkcji dla
firmy i przemysłu przy założeniu, że na początku przemysł
znajduje się w równowadze w LR. Jeżeli firma j-ta
wprowadza nową technikę, to jej krzywe MC i AC w SR i w
LR przesuwają się do dołu. Ponieważ żadna firma
samodzielnie nie może wpłynąć na cenę w równowadze, to
cena rynkowa nie zmienia się aż inne firmy nie wprowadzą
nowej techniki. Firma j-ta osiąga zyski zrównując cenę z
nowymi SRMC:

( )

( )

[

]

0

*

2

1

*

*

>

−

=

j

j

x

j

j

j

SRx

SRATC

SRp

SRx

SRx

SR

π

. Jednakże te

zyski stanowią bodziec do wejścia i wprowadzania nowej
techniki, a to prowadzi do zwiększenia rynkowej SRS i
obniżania ceny. Trwa to aż zyski wyniosą 0 i wszystkie firmy
będą zatrudniać nową technikę.

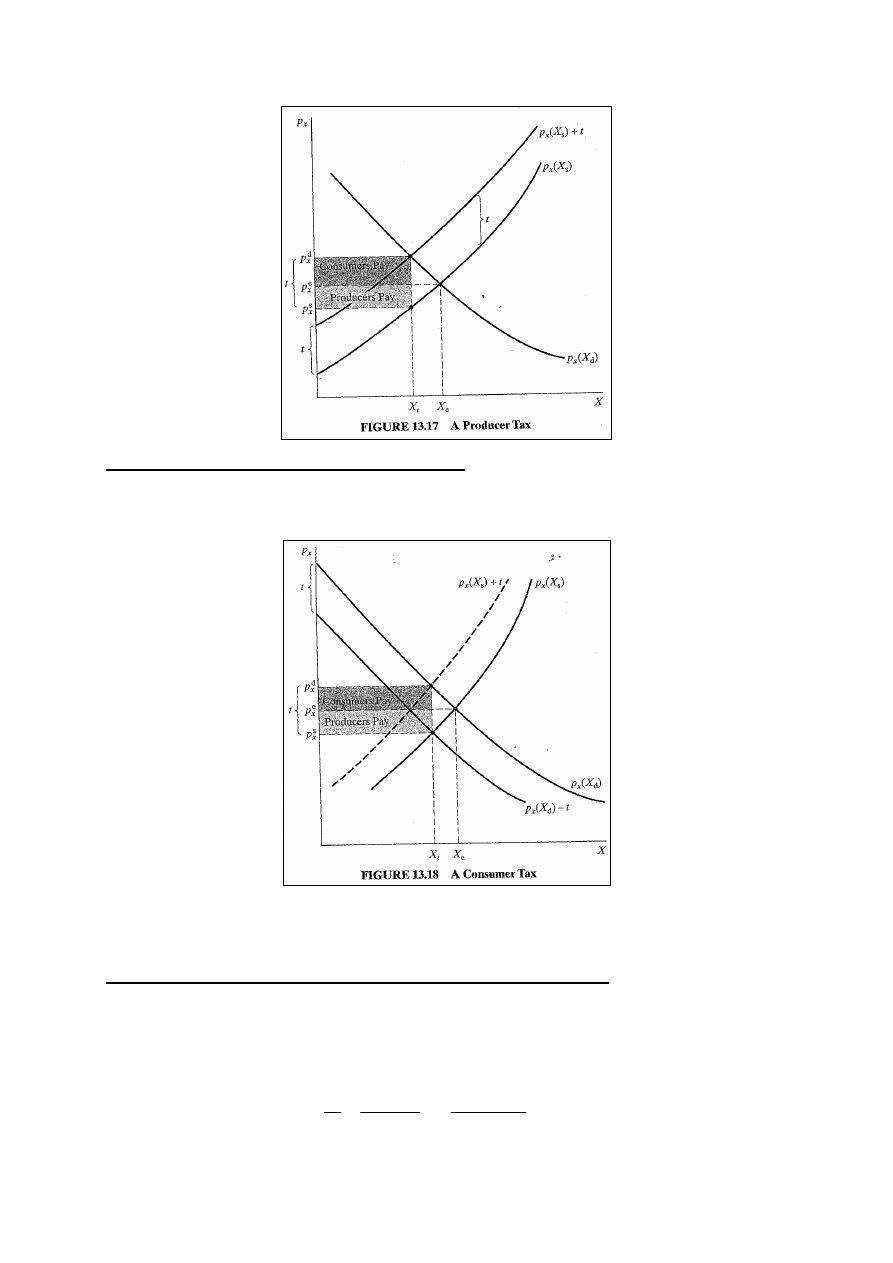
Zasięg podatku jednostkowego

Podatek nałożony na producenta
Podatek jednostkowy: podatek w wysokości określonej kwoty
od każdej jednostki sprzedanej – rys. 13.17.

14

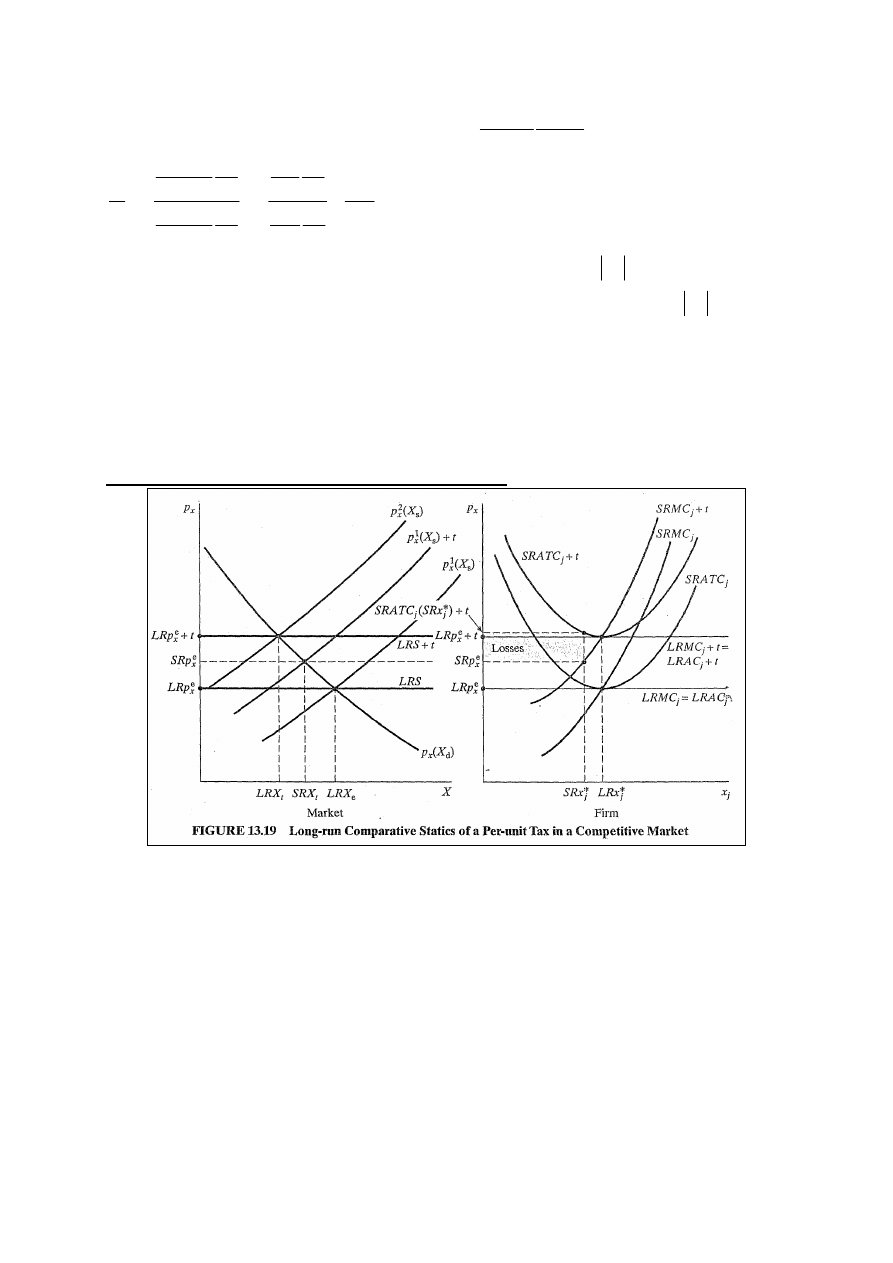
Podatek nałożony na konsumenta
Za każdą kupioną jednostkę konsument musi zapłacić kwotę
podatku – rys. 13.18.

Oba podatki są równoważne.

Elastyczność i zasięg podatku jednostkowego
Przy liniowych krzywych popytu i podaży względne
obciążenie podatkowe można przedstawić jako iloraz
podatku płaconego przez konsumenta i podatku płaconego
przez producenta:

d

x

e
x

s

x

e
x

s

x

e
x

e
x

d

x

s

d

p

p

p

p

p

p

p

p

t

t

−

−

−

=

−

−

=

/

1

/

1

. Mnożąc prawą stronę

15

tego wyrażenia przez:

e

e
x

e

e
x

t

e

t

e

X

p

X

p

X

X

X

X

/

/

−

−

otrzymujemy:

0

>

−

=

∆

∆

∆

∆

−

=

−

−

−

−

−

=

d

s

e

e
x

d

x

e

e
x

s

x

e

e
x

d

x

e
x

t

e

e

e
x

s

x

e
x

t

e

s

d

X

p

p

X

X

p

p

X

X

p

p

p

X

X

X

p

p

p

X

X

t

t

ε

ε

ponieważ

0

<

d

ε

.

Z powyższego równania wynika, że jeżeli

s

d

ε

ε

>

, to popyt

jest bardziej elastyczny od podaży i t

d

< t

s

. Jeżeli

s

d

ε

ε

<

, to

t

d

> t

s

. Powyższe spostrzeżenia można uogólnić dla

nieskończenie małych zmian wzdłuż nieliniowych krzywych
popytu i podaży: podmioty z mniej elastycznej strony rynku
płacą większą część podatku.
Skutki podatku jednostkowego w LR

Rys. 13.19. Zaczynamy w punkcie równowagi w LR przed
wprowadzeniem podatku. Skutki w SR pokazane zostały na
rys. 13.17 i 13.18. Cena dla sprzedającego maleje, a dla
kupującego rośnie, dla każdego o mniej niż wynosi sam
podatek. Jeżeli przemysł znajduje się w równowadze w LR i
cena dla sprzedającego maleje, to firmy będą ponosić straty
na skutek wprowadzenia podatku. Firmy zaczną wychodzić z
przemysłu, co spowoduje przesunięcie krzywej SRS dalej na
lewo. Wyjścia będą trwały aż firmy zaczną osiągać zerowe

16

zyski. Ponieważ poprzednio firmy pokrywały AC w minAC, to
cena musi wzrosnąć o całą wielkość podatku aby przywrócić
zerowe zyski. Na lewej części rysunku: skutki w SR nałożenia
podatku na producentów: przesunięcie krzywej podaży z

( )

S

x

X

p

1

do

( )

t

X

p

S

x

+

1

.Skutki w LR (po wyjściu): przesunięcie z

( )

S

x

X

p

1

do

( )

S

x

X

p

2

. Cena dla konsumentów w SR rośnie z

E

x

LRp

do

D

x

p

, a w LR do

t

LRp

E

x

+

. Tak więc w LR konsument musi

zapłacić cały podatek na rynku doskonale konkurencyjnym.
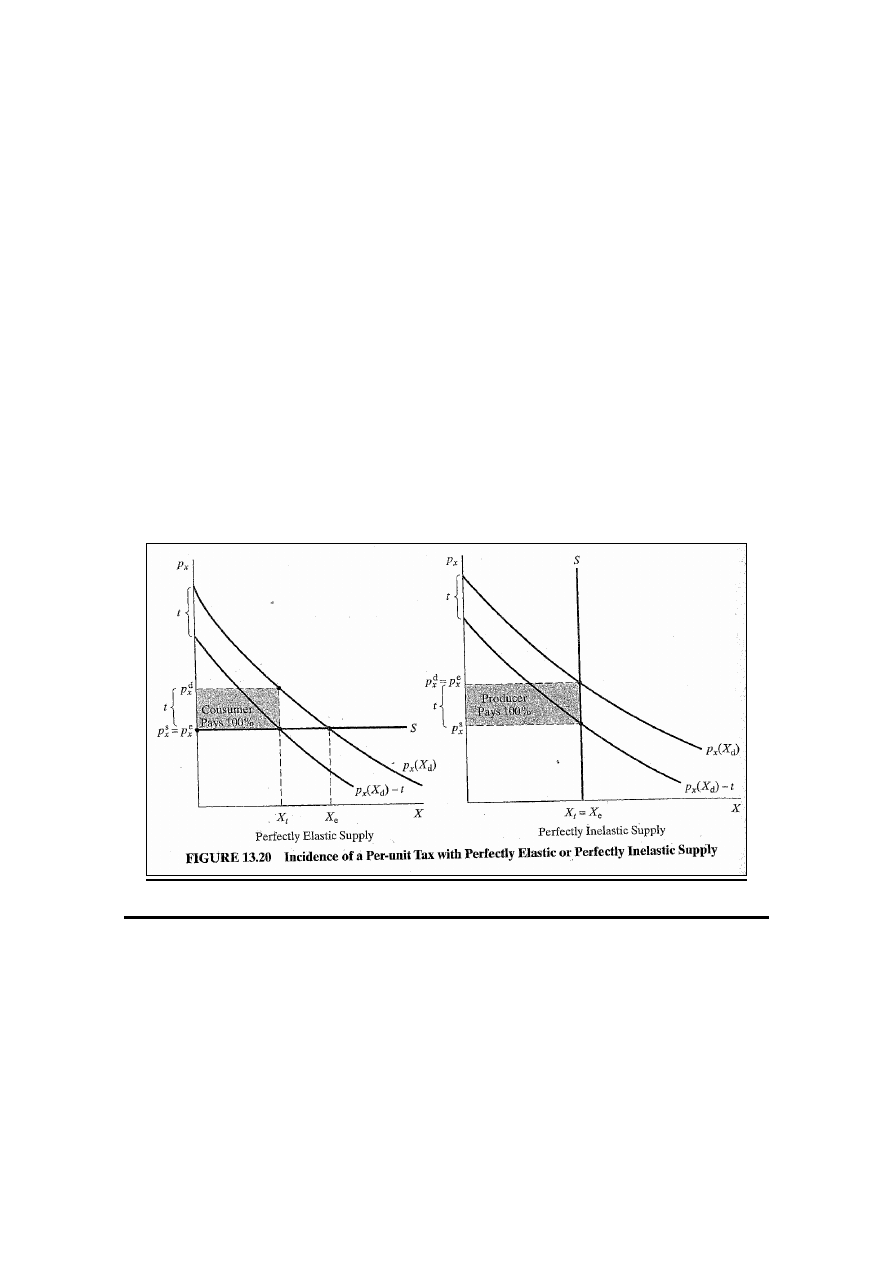
Skutek w LR pojawia się po jednej stronie rynku, gdyż LRS
jest doskonale elastyczna. Podmioty znajdujące się na
doskonale elastycznej stronie rynku nie płacą nic, a na
doskonale nieelastycznej – płacą podatek w całości (rys.
13.20)

Czysta strata wywołana podatkiem jednostkowym

Dla konsumentów korzystniejsze są podatki zryczałtowane
od podatków jednostkowych. Skutki po stronie dobrobytu
wywołane podatkiem jednostkowym można przeanalizować
biorąc pod uwagę opodatkowanie produktu, nadwyżkę
konsumenta i zyski przedsiębiorstw. Miarą zysków firm jest
suma zarobionych na każdej jednostce. Koszt każdej
następnej jednostki mierzy MC. Jeżeli firma sprzedaje

17

wszystkie wyprodukowane jednostki po jednej cenie, to zysk
zarobiony na każdej kolejnej jednostce będzie różnicą
między ceną i MC wyprodukowania tej jednostki. Całkowite
zyski będą całką:

( )

∫

=

=

x

p

MC

MC

dMC

MC

x

)

0

(

π

, gdzie MC(0) jest MC dla

zerowej produkcji. Na rynkach doskonale konkurencyjnych
zyski te są mierzone wzdłuż rynkowej krzywej podaży i są
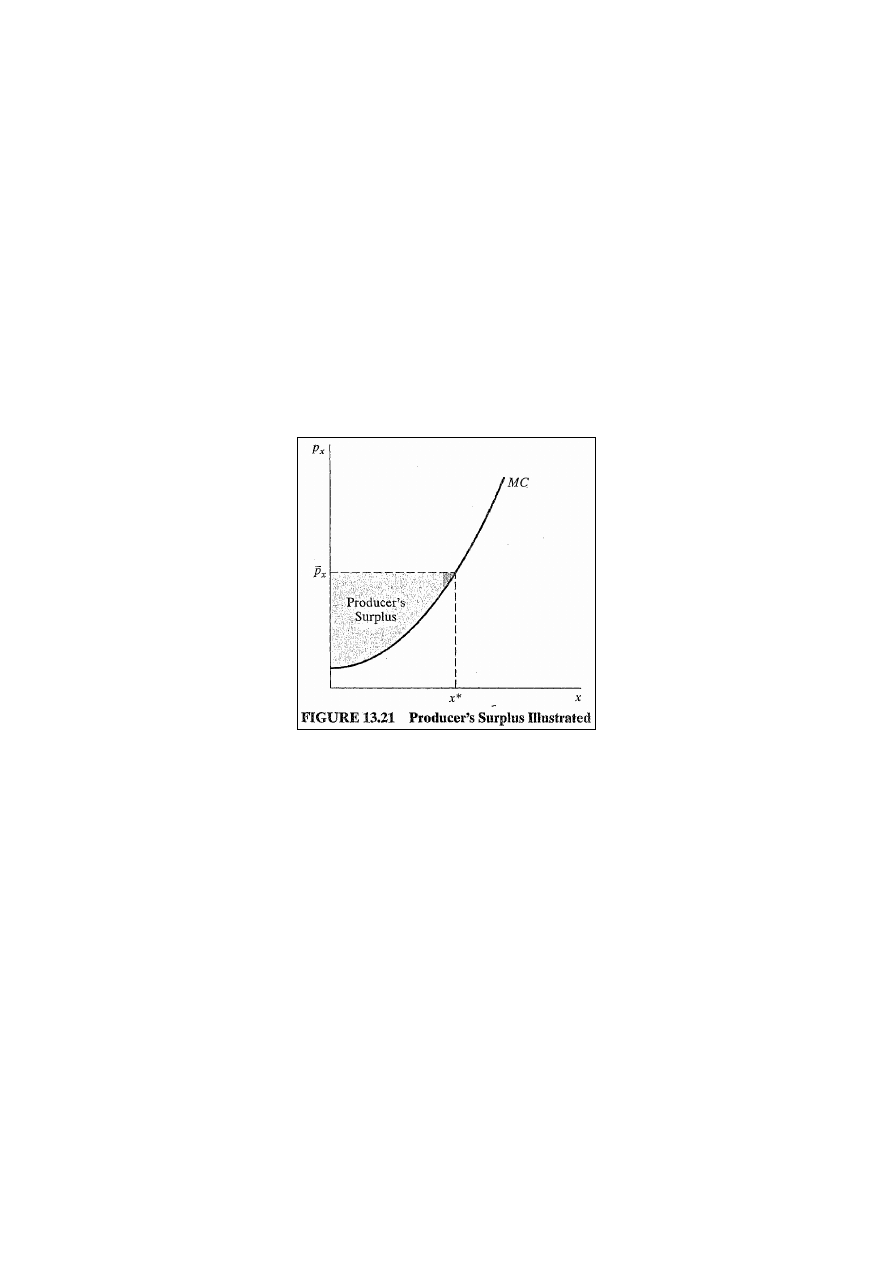
one określane mianem nadwyżki producenta:

(

)

∫

=

c

x

x

p

p

x

x

s

dp

p

x

PS

)

0

(

,

gdzie p

x

c

jest ceną na rynku doskonale konkurencyjnym – rys.

13.21.

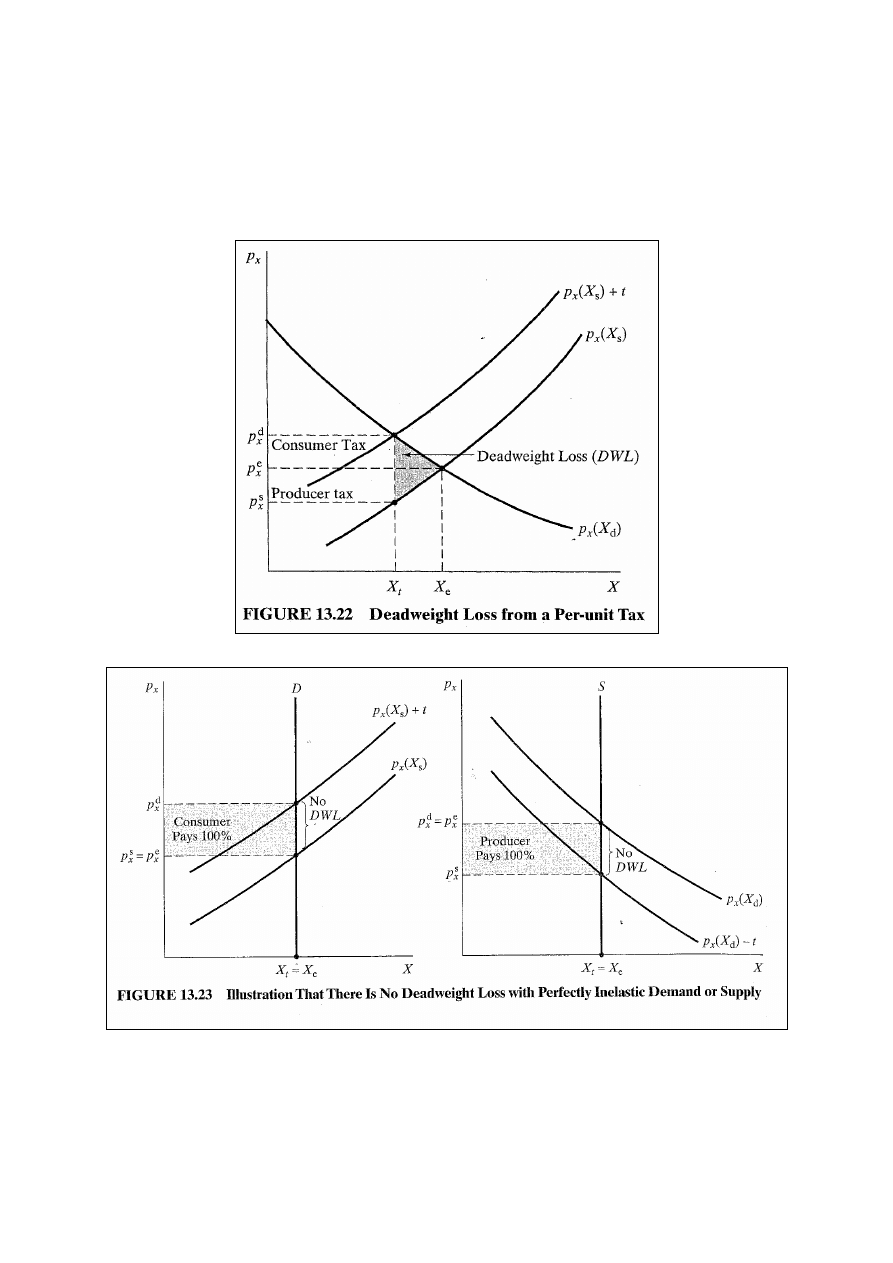
Po nałożeniu podatku jednostkowego pojawia się strata w
nadwyżce producenta i konsumenta. Część tej straty
przejmuje rząd w postaci dochodów podatkowych. Część jest
stratą netto dobrobytu (deadweight loss)– rys. 13.22:

t

p

p

x

s

p

p

x

d

t

tX

dp

x

dp

x

tX

PS

CS

DWL

d

x

e

x

d

x

e

x

−

+

=

−

∆

+

∆

=

∫

∫

.

Jeżeli efekty dochodowe są małe, czyli nieskompensowana
nadwyżka konsumenta przedstawia obliczenia straty
dobrobytu konsumenta, to stratę dobrobytu spowodowaną
jednostkowym podatkiem można interpretować jako stratę
społecznego dobrobytu wywołaną tym podatkiem.

18

Strata netto dobrobytu dla podatku jednostkowego nie
pojawi się, gdy podatek nie prowadzi do ograniczenia
wielkości produkcji, czyli gdy popyt lub podaż są doskonale
nieelastyczne – rys. 13.23.