
ZASADY OBLICZANIA PRZYCZÓŁKÓW MOSTÓW
DROGOWYCH WG PN-EN
Iwona JANKOWIAK
*)
, Krzysztof KARPIŃSKI
*)
*)
Politechnika Poznańska
1. WPROWADZENIE
Obliczanie przyczółków obiektów mostowych jest wieloaspektowe ze względu
na konieczność analizy elementów konstrukcyjnych, które z jednej strony
przenoszą wszystkie obciążenia działające z przęseł mostu, a z drugiej znajdują
się w ciągłej interakcji z gruntem, który dodatkowo również może być
obciążony. W procesie analizy statycznej oraz późniejszego wymiarowania
konstrukcji przyczółków zgodnie z wytycznymi norm PN-EN należy zatem
uwzględnić nowe, sugerowane przez normy obciążeniowe, schematy obciążeń
zmiennych oraz nowe zasady ustalania obciążeń stałych, przy jednoczesnym
przestrzeganiu zasad sugerowanych przez nowe normy geotechniczne.
Powoduje to konieczność korzystania z wielu norm już na etapie obliczeń
statycznych przyczółka, co może powodować znaczne utrudnienie i wydłużenie
czasu projektowania tego elementu. Celem niniejszej pracy jest zatem
przybliżenie zasad ustalania obciążeń działających na przyczółki mostów
drogowych, zasad ustalania kombinacji obciążeniowych dla podstawowych
stanów granicznych nośności oraz doboru odpowiednich do analizowanego
stanu granicznego współczynników częściowych. Zestawienie współczynników
częściowych zalecanych przez normy dotyczące mostów oraz normy dotyczące
zagadnień geotechnicznych powinno przysłużyć się poprawnemu ustalaniu
danych niezbędnych do wymiarowania przyczółków.
Projektowanie przyczółków zgodnie z nowymi normami europejskimi
PN-EN różni się znacząco od dotychczasowego, wykonywanego na podstawie
zasad zawartych w polskich normach PN. Podstawowe różnice w obliczeniach
statycznych przyczółków mostów drogowych wg PN-EN, w odniesieniu do
zasad obowiązujących dotychczas, to:
− brak różnicowania wartości obliczeniowych danego obciążenia stałego w
ramach schematu obciążenia - wprowadzono współczynniki obciążenia
zależne od analizowanego stanu granicznego, ale w ramach schematu
obciążenia dozwolono stosowanie tylko jednej z możliwych wartości
obliczeniowych,

− zaniedbanie sił hamowania i przyspieszania działających na przyczółki od
taboru samochodowego znajdującego się na nasypie (z wyjątkiem ścianek
zaplecznych),
− nowe zasady kombinowania obciążeń zmiennych: dotychczasowe układy
obciążeń zastąpiono współczynnikami kombinacyjnymi, które redukują
efekty jednoczesnego występowania kilku obciążeń zmiennych.
W tekście normy określającej obciążenia zmienne działające na mosty [4]
znajduje się zalecenie wydania załącznika krajowego, przeznaczonego do
stosowania w obliczeniach mostów i ich podpór przewidzianych do wykonania
w danym kraju. Załącznik ten mógłby zmieniać i precyzować zalecenia norm
PN-EN w pewnych ich punktach. Podobne uściślenie zapisów norm
geotechnicznych [5] w odniesieniu do obliczeń przyczółków mogłyby wnieść
załączniki do tej normy. W zakresie podstaw projektowania konstrukcji
wsporczych pod mosty uzupełnienia zatem mogłyby dotyczyć między innymi:
− określenia odpowiednich modeli do obciążenia jezdni położonej za
przyczółkami, ścianami skrzydeł, ścianami bocznymi i innymi częściami
mostu kontaktującymi się z gruntem,
− procedury wyboru właściwego sposobu projektowania części konstrukcji
wymagającego uwzględnienia odpowiednich oddziaływań geotechnicznych.
Wobec braku polskiego załącznika krajowego do [4], wiążące pozostają
zalecenia zapisów PN-EN. W pewnych sytuacjach zmusza to do prowadzenia
analiz obliczeniowych w zakresie szerszym niż byłoby to konieczne w
przypadku istnienia zaleceń szczegółowych w załączniku krajowym.
2. OBCIĄŻENIA STAŁE
2.1. Informacje ogólne
Obciążenia stałe konstrukcji mostowych, w tym przyczółków mostowych, jak
wszelkich innych konstrukcji budynków i konstrukcji inżynierskich, należy
określać zgodnie z normą [3].
Ciężar własny konstrukcji obejmuje elementy konstrukcyjne i
niekonstrukcyjne, łącznie z umiejscowionymi urządzeniami, jak również ciężar
ziemi i balastu. Norma zaleca, aby obciążenie stałe było uwzględniane w
kombinacjach obciążeń jako oddziaływanie pojedyncze.
Zalecane jest przedstawianie ciężarów własnych konstrukcji za pomocą
pojedynczej wartości charakterystycznej q
k
, obliczanej na podstawie
nominalnych wymiarów i charakterystycznych ciężarów objętościowych
materiałów. Jeśli ciężar własny elementów lub ciężar wyposażenia może
zmieniać się w czasie, co może mieć miejsce w przypadku eksploatacji
przyczółków mostowych, wówczas zaleca się, aby był on uwzględniony jako

górna i dolna wartość charakterystyczna – odpowiednio: q
k,sup
i q
k,inf
.
Uwzględnienie górnej i dolnej wartości charakterystycznej (odpowiednie
wartości mogą być podane w załączniku krajowym) w przypadku mostów
dotyczy sytuacji, w których materiał może zmienić swoje właściwości w czasie
użytkowania (np. wskutek konsolidacji zasypki przyczółka, nawodnienia gruntu
zasypki, itp.). W przypadku mostów drogowych dotyczy to ciężarów własnych
warstw izolacji wodoszczelnej, nawierzchni i innych warstw pokryciowych
mostów, w tym nadsypki gruntowej wtedy, kiedy zmienność ich grubości może
być duża. Przy braku załącznika krajowego należy przyjąć, że odchylenia
całkowitej grubości warstwy od wartości nominalnej (lub innych określonych
wartości) może być równe ±20% w przypadku, kiedy do wartości nominalnej
włączone jest pokrycie powykonawcze i +40% i -20% w przypadku, kiedy takie
pokrycie nie jest włączone. Odchylenie ±20% od wartości nominalnej należy
uwzględnić również przy rozpatrywaniu ciężarów własnych kabli, rurociągów i
przejść kontrolnych. Ciężary elementów niekonstrukcyjnych takich jak
balustrady, bariery, krawężniki i inne wyposażenie mostów, zaleca się (przy
braku załącznika krajowego) przyjmować jako równe wartościom nominalnym.
Zagadnienia dotyczące ustalania wartości obciążeń stałych szerzej
omówiono w pozycjach [8] i [9].
2.2. Parcie gruntu
Wartości parcia i odporu gruntu należy obliczać na podstawie Poprawki [7] do
PN-EN [5], która nakazuje w całości zastąpienie załącznika C (informacyjnego)
znajdującego się w [5] nowym załącznikiem C (informacyjnym) znajdującym się
w [7].
Graniczne wartości parcia i odporu gruntu należy wyznaczać z
następujących wzorów [7]:
− parcie graniczne:
[
]
ac
a
a
cK
u
u
q
dz
K
z
−
+
−
+
=
∫
γ
σ
)
(
(2.1)
gdzie całka od powierzchni terenu do głębokości z
[
]
a
a
ac
K
c
a
K
K
56
,
2
)
/
1
(
2
≤
+
=
(2.2)
− odpór graniczny:
[
]
pc
p
p
cK
u
u
q
dz
K
z
+
+
−
+
=
∫
γ
σ
)
(
(2.3)
gdzie całka od powierzchni terenu do głębokości z

[
]
a
a
pc
K
c
a
K
K
56
,
2
)
/
1
(
2
≤
+
=
(2.4)
gdzie:
a
- przyczepność (adhezja) pomiędzy gruntem a ścianą,
c
- spójność gruntu,
a
K
- współczynnik poziomego parcia granicznego gruntu,
p
K
- współczynnik poziomego odporu granicznego gruntu,
q
- pionowe obciążenie naziomu,
z
- odległość pionowa (głębokość) wzdłuż powierzchni ściany,
β
- kąt nachylenia powierzchni gruntu za ścianą (zwrot dodatni do góry),
δ
- kąt tarcia pomiędzy ścianą a gruntem,
γ
- całkowity ciężar objętościowy gruntu za ścianą,
)
(
z
a
σ
- całkowite naprężenie normalne do ściany na głębokości z (parcie
graniczne),
)
(z
p
σ
- całkowite naprężenie normalne do ściany na głębokości z (odpór
graniczny).
Wartość współczynnika efektywnego parcia gruntu K
a
oraz
współczynnika odporu K
p
można przyjmować na podstawie diagramów
zamieszczonych w [7] w zależności od kąta nachylania powierzchni terenu β,
efektywnego kąta tarcia wewnętrznego φ’ oraz kąta tarcia o ścianę oporową δ.
W przypadku gruntów uwarstwionych, niezależnie od wartości parametrów na
innych głębokościach, współczynniki K zaleca się określać na podstawie
parametrów na głębokości z [7].
Norma [5] dopuszcza zamiennie stosowanie analitycznej metody
obliczania granicznego parcia czynnego i odporu granicznego – metodę tę
doprecyzowano w Poprawce do Polskiej Normy [7]. Metoda analityczna zawiera
pewne przybliżenia na korzyść bezpieczeństwa i można ją stosować we
wszystkich przypadkach. Wykorzystuje ona parametry wytrzymałościowe takie
jak kąt tarcia wewnętrznego gruntu φ, spójność gruntu c, kąt tarcia δ oraz
przyczepność a pomiędzy ścianą a gruntem.
W poprawce do PN-EN [7] (także w samej PN-EN [5]) podano również
potrzebne do wystąpienia parcia i odporu granicznego przemieszczenia
konstrukcji oporowej. W odpowiednich tablicach podano przybliżone stosunki
v
a
/h (przemieszczenie ściany/wysokość ściany) dla całkowitego wzbudzenia
efektywnego czynnego parcia gruntu oraz dla całkowitego i połowicznego
efektywnego parcia biernego gruntu. Pośrednie wartości efektywnego parcia
czynnego można uzyskać przez interpolację liniową między wartościami z
tablic, natomiast w sytuacji wystąpienia parcia biernego wartości podane w
tablicy można interpolować na podstawie ogólnej krzywej zamieszczonej w [7].
3. OBCIĄŻENIA ZMIENNE DZIAŁAJĄCE NA PRZYCZÓŁKI
3.1. Informacje ogólne
Modele obciążeń zmiennych działających na przyczółki mostowe należy
przyjmować według PN-EN [4]. Przedstawione tam modele obciążeń zmiennych
zaleca się stosować w projektowaniu mostów drogowych o długościach
obciążanych mniejszych od 200 m. Założono, że modele obciążeń zmiennych
zawierają już w sobie tzw. nadwyżkę dynamiczną.
Modele obciążeń zmiennych mostów drogowych szerzej omówiono w
pracy [8].
3.2. Modele obciążeń przyczółków i ścian przyległych do mostów
Modele obciążeń zmiennych działających na przyczółki zostały określone w [4].
Przyjęto, że jezdnia położona za przyczółkami, ścianami skrzydeł, ścianami
bocznymi i innymi częściami mostu kontaktującymi się z gruntem powinna być
obciążona odpowiednimi modelami (mogą być określone w Załączniku
krajowym). Norma zaleca stosowanie modelu LM1 z tym, że obciążenia od
układu tandemowego można zastąpić równoważnym, równomiernie rozłożonym
obciążeniem „q
eq
”, rozłożonym na odpowiednio dobranej powierzchni
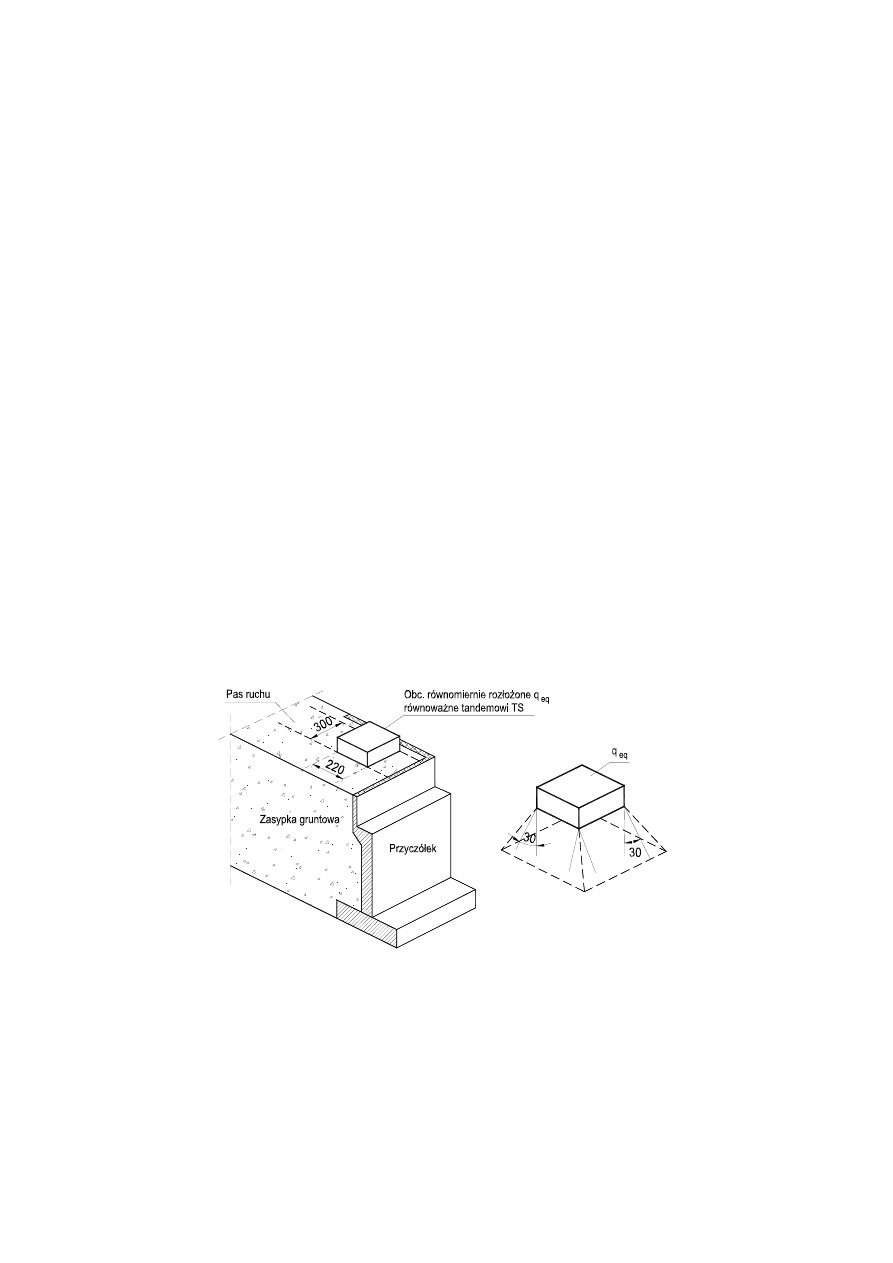
prostokąta zależnej od kąta rozkładu obciążeń poprzez zasypkę i grunt (Rys.1).
Rys.1. Obciążenie zmienne LM1 za przyczółkiem.
Rozkład obciążenia pionowego przez zasypkę gruntową powinien być
określony zgodnie z [5]. W przypadku braku innych reguł, jeżeli zasypka jest
właściwie zagęszczona, zalecana wartość kąta rozkładu w stosunku do pionu
wynosi 30º (Rys.1). Przy takiej wartości powierzchnia, na której q
eq
jest
położone, może być przyjęta za powierzchnię prostokątną o wymiarach
3,0x2,2m. Należy uwzględniać wartości charakterystyczne obciążeń pionowych.
W obliczaniu ścian przyczółków nie zaleca się uwzględniać jakiejkolwiek
siły poziomej działającej na poziomie pokrycia jezdni nad zasypką. Znacznie
upraszcza to zatem obliczenia statyczne.
3.3. Obciążenia ścianek zaplecznych
Choć siła pozioma na poziomie nawierzchni jezdni nad zasypka jest uznawana
za zbędną w analizie ściany przyczółka, to nie może być pomijana w analizie
ścianek zaplecznych. Jest to skutkiem tego, że pojazdy mogą hamować podczas
wjazdu na most. Zatem w projektowaniu ścianek zaplecznych [4] powinna być
uwzględniona podłużna siła hamowania o wartości charakterystycznej równej
0,6α
Q1
Q
1k
, działająca równocześnie z obciążeniem osiowym α
Q1
Q
1k
modelu LM1
oraz z parciem gruntu od strony zasypki (Q
1k
– obciążenie jedną osią tandemu
TS na paśmie o numerze 1, α
Q1
– współczynnik dostosowawczy). Zakłada się
jednocześnie, że zasypka nie jest jednocześnie obciążona.
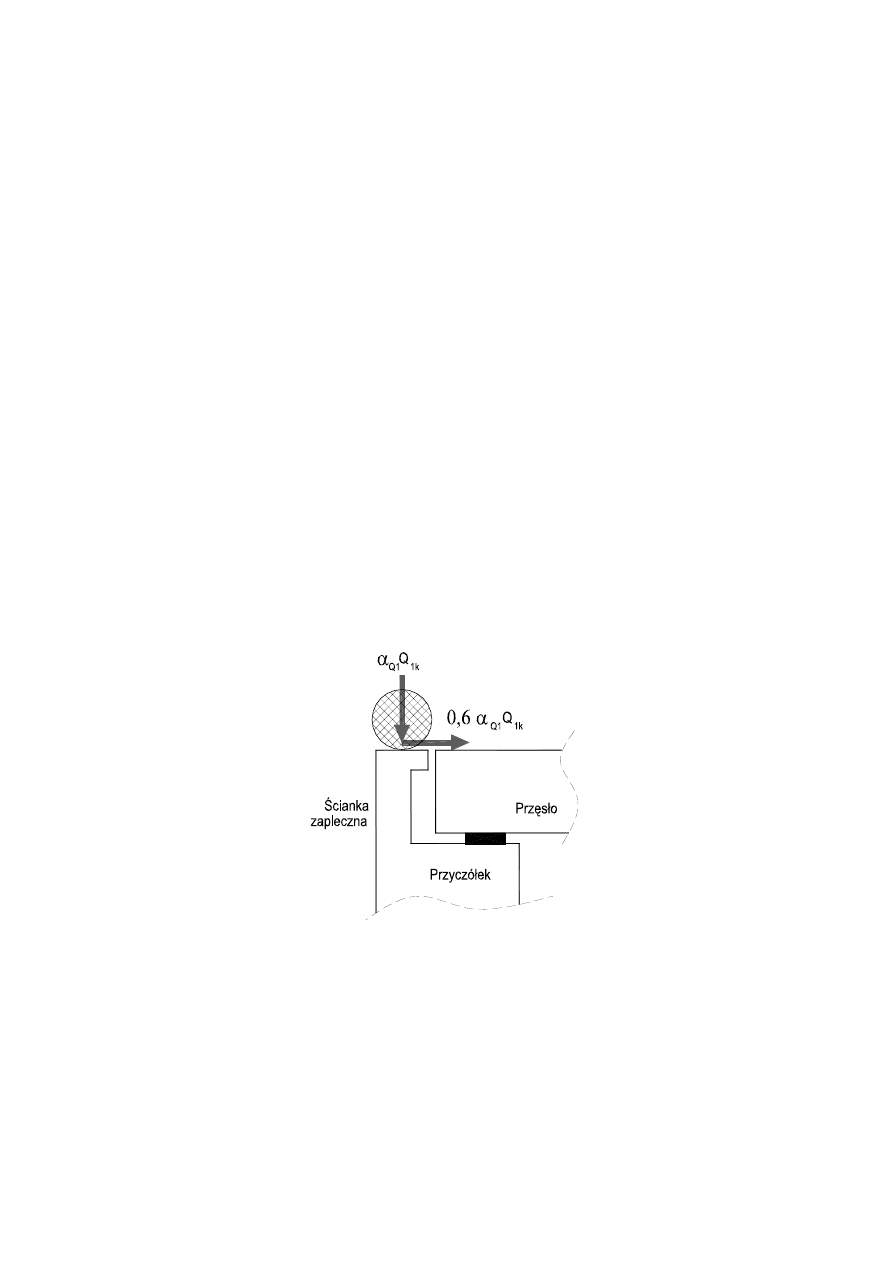
Zestawienie obciążeń zmiennych działających na ściankę zapleczną mostu
drogowego przedstawiono na Rys.2.
Rys.2. Obciążenia zmienne działające na ścianki zapleczne.

4. ZASADY ZESTAWIANIA OBCIĄŻEŃ W POSZCZEGÓLNYCH
STANACH GRANICZNYCH
4.1. Informacje ogólne
Normy [1] i [2] rozróżniają cztery stany graniczne nośności. Trzy z nich
powinny być rozpatrzone przy projektowaniu ścian oporowych, czyli
przyczółków:
− EQU – utrata równowagi statycznej konstrukcji lub jakiejkolwiek jej części,
uważanej za ciało sztywne (gdy wytrzymałość materiałów konstrukcyjnych
lub podłoża jest nieistotna dla zapewnienia nośności),
− STR – zniszczenie wewnętrzne lub nadmierne odkształcenie konstrukcji lub
elementów konstrukcji, łącznie z fundamentami; w tym przypadku
decydujące znaczenie ma wytrzymałość materiałów konstrukcji,
− GEO – zniszczenie lub nadmierne odkształcenie podłoża, kiedy istotne
znaczenie dla nośności konstrukcji ma wytrzymałość podłoża.
4.2. Stan graniczny równowagi statycznej konstrukcji
Przy sprawdzaniu równowagi statycznej konstrukcji (EQU) należy wykazać, że
efekty oddziaływań destabilizujących są mniejsze od efektów oddziaływań
stabilizujących [1]:
stb
d
dst
d
E
E
,
,
≤
(4.1)
gdzie:
E
d,dst
– wartość obliczeniowa efektu oddziaływań destabilizujących,
E
d,stb
– wartość obliczeniowa efektu oddziaływań stabilizujących.
Norma [5] rozszerza powyższy warunek do postaci:
d
stb
d
dst
d
T
E
E
+
≤
;
;
(4.2)
gdzie:
{
}
dst
d
M
k
rep
F
dst
d
a
X
F
E
E
;
/
;
,
γ
γ
=
oraz
{
}
stb
d
M
k
rep
F
stb
d
a
X
F
E
E
;
/
;
,
γ
γ
=
,
gdzie:
F
γ
– współczynnik częściowy do oddziaływania (patrz Tablica 2)
rep
F
– wartość reprezentatywna oddziaływania,
k
X
– wartość charakterystyczna właściwości materiału,
M
γ
– współczynnik częściowy do parametru geotechnicznego, uwzględniający
również niepewności modelu obliczeniowego (patrz Tablica 1),

d
a
– wartość obliczeniowa wielkości geometrycznej.
We wzorze (4.2) został dodatkowo uwzględniony czynnik:
T
d
– wartość obliczeniowa całkowitego oporu ścinania, jaki powstaje wokół
bloku gruntu, w którym jest umieszczona grupa pali wyciąganych albo
oporu na części konstrukcji stykającej się z gruntem.
W przypadku analizy stanu granicznego EQU współczynniki częściowe
do parametrów geotechnicznych przyjmują wartości zestawione w Tablicy 1:
Tablica 1. Współczynniki częściowe
γ
Μ
do parametrów geotechnicznych [5]
Parametr gruntu
Symbol
Wartość
Kąt tarcia wewnętrznego gruntu
a
'
ϕ
γ
1,25
Spójność efektywna
'
c
γ
1,25
Wytrzymałość na ścinanie bez odpływu
cu
γ
1,4
Wytrzymałość na jednoosiowe ściskanie
qu
γ
1,4
Ciężar objętościowy
γ
γ
1,0
a
– współczynnik ten stosuje się do wartości tanφ’
Norma [5] uznaje jednocześnie, że sprawdzenie równowagi statycznej
EQU jest istotne głównie w przypadku projektu konstrukcyjnego. W projekcie
geotechnicznym sprawdzanie stanu EQU jest ograniczone tylko do rzadkich
przypadków, np. sztywnego fundamentu opartego na skale. Utrata stateczności
konstrukcji lub podłoża (utrata równowagi pionowej) spowodowana ciśnieniem
wody lub innymi oddziaływaniami pionowymi powinna być wg [5] analizowana
jako stan graniczny UPL.
4.3. Stany graniczne zniszczenia lub nadmiernego odkształcenia przekroju
(STR lub/i GEO)
Sprawdzenie stanu granicznego zniszczenia lub nadmiernego odkształcenia
przekroju (STR lub/i GEO) sprowadza się do sprawdzenia warunku [1]:
d
d
R
E
≤
(4.3)
gdzie:
E
d
– wartość obliczeniowa efektu oddziaływań, takiego jak siła wewnętrzna,
moment lub wektor, reprezentujący kilka sił wewnętrznych lub momentów,
R
d
– wartość obliczeniowa odpowiedniej nośności.

Norma [5] uzupełnia powyższy warunek, opisując dokładnie
poszczególne jego składowe. Zatem:
{
}
d
M
k
rep
F
d
a
X
F
E
E
;
/
;
γ
γ
=
lub
{
}
d
M
k
rep
E
d
a
X
F
E
E
;
/
;
γ
γ
=
(4.4)
oraz
{
}
d
M
k
rep
F
d
a
X
F
R
R
;
/
;
γ
γ
=
lub
{
}
R
d
k
rep
F
d
a
X
F
R
R
γ
γ
/
;
;
=
lub
{
}
R
d
M
k
rep
F
d
a
X
F
R
R
γ
γ
γ
/
;
/
;
=
(4.5)
gdzie:
F
γ
– współczynnik częściowy do oddziaływania (patrz Tablica 3),
rep
F
– wartość reprezentatywna oddziaływania,
k
X
– wartość charakterystyczna właściwości materiału,
M
γ
– współczynnik częściowy do parametru geotechnicznego, uwzględniający
również niepewności modelu obliczeniowego,
d
a
– wartość obliczeniowa wielkości geometrycznej.
Sposób zastosowania powyższych wzorów powinien być określony przez
jedno z trzech podejść obliczeniowych [5], które zestawiono w Tablicy 2.
Podejścia obliczeniowe różnią się rozkładem współczynników częściowych, co
ma związek ze sposobem uwzględniania niepewności modelowania efektów
oddziaływań i wytrzymałości.
W stanach granicznych nośności STR i STR/GEO w trwałych i
przejściowych sytuacjach obliczeniowych, w zależności od stosowanego
podejścia obliczeniowego, należy dokonać wyboru odpowiedniego zestawu
współczynników częściowych, które zostały podzielone na następujące zestawy:
− Zestaw A – współczynniki do oddziaływań,
− Zestaw M – współczynniki do parametrów gruntowych,
− Zestaw R – współczynniki do oporów lub nośności.
Zasady wyboru właściwego podejścia obliczeniowego, jak i wartości
współczynników częściowych, mogą zostać podane w załącznikach krajowych.

W przypadku braku załącznika krajowego należy przyjmować zalecane wartości
współczynników częściowych, podane w [2] lub [5].
Poprawka [6] odnosi się do normy gruntowej [5], a wiec współczynniki
częściowe oraz podejścia obliczeniowe tam sprecyzowane mają zastosowanie
dla stanów granicznych związanych z projektowaniem geotechnicznym
(STR/GEO). Stany graniczne nośności konstrukcji (STR), które zależą od
zastosowanego materiału konstrukcyjnego (w przypadku przyczółków betonu)
należy analizować w oparciu o normy przedmiotowe (PN-EN 1992 do PN-EN
1996).
W pozycji [5] zostały zestawione współczynniki do oddziaływań lub
efektów oddziaływań zalecane dla budynków. Współczynniki te mają te same
wartości, co współczynniki częściowe przedstawione w normie podstawowej
[1]. W przypadku jednak obliczania podpór mostowych w stanie STR i GEO
współczynniki częściowe do oddziaływań lub efektów oddziaływań (γ
F
, γ
E
)
należy przyjmować na podstawie tablic zawartych w [2], zgodnie ze zbiorem B i
C. Z kolei współczynniki częściowe do parametrów geotechnicznych (γ
M
) oraz
współczynniki częściowe do nośności i oporu (γ
R
) zarówno dla budynków, jak i
dla mostów, należy przyjmować na podstawie [5].
W przypadku wyboru podejścia obliczeniowego 1 należy przeprowadzić
dwa oddzielne obliczenia z wykorzystaniem dwóch zestawów współczynników,
chyba że oczywiste jest, który z zestawów jest decydującym.
W tablicy 2 przedstawiono rozkłady współczynników częściowych w
zależności od przyjętego podejścia obliczeniowego.
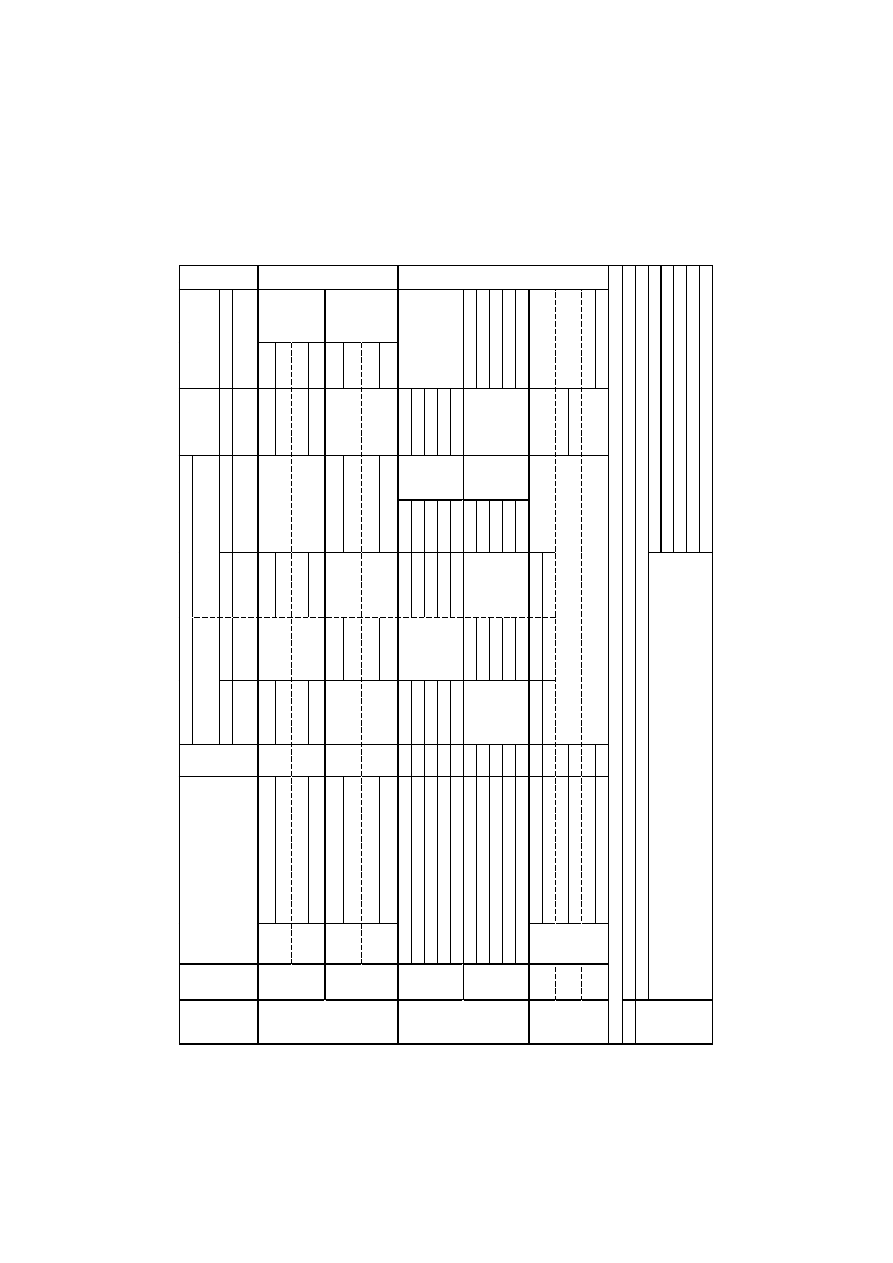
Tablica 2. Zestawienie współczynników częściowych (STR/GEO) [2], [5]
Ko
m
b
in
ac
ja
1K
o
m
bi
n
ac
ja
2
K
om
bi
na
cj
a
1K
o
m
b
in
ac
ja
A1
"+
"
M1
"+
"
R1
A2
"+
"
M2
"+
"
R1
A1
"+
"
M1
"+
"
R1
A
1
"+
"
M1
"+
"
R2
D
e
st
ab
iliz
u
ją
ce
1,
35
1,
35
1,
35
1,
35
St
ab
iliz
u
ją
ce
1,
00
1,
00
1,
00
1,
00
D
e
st
ab
iliz
u
ją
ce
1,
35/
1,
50
(1
)
1,
35/
1,
50
(1
)
1,
35/
1,
50
(1
)
1,
35/
1,
50
(1
)
St
ab
iliz
u
ją
ce
0,
00
0,
00
0,
00
0,
00
D
e
st
ab
iliz
u
ją
ce
1,
00
1,
00
St
ab
iliz
u
ją
ce
1,
00
1,
00
D
e
st
ab
iliz
u
ją
ce
1,
15/
1,
30
(1
)
1,
15/
1,
30
(1
)
St
ab
iliz
u
ją
ce
0,
00
0,
00
γ
φ '
1,
00
1,
00
1,
00
1,
00
γ
c
1,
00
1,
00
1,
00
1,
00
γ
cu
1,
00
1,
00
1,
00
1,
00
γ
qu
1,
00
1,
00
1,
00
1,
00
γ
f
1,
00
1,
00
1,
00
1,
00
γ
φ '
1,
25
1,
25
γ
c
1,
25
1,
25
γ
cu
1,
40
1,
40
γ
qu
1,
40
1,
40
γ
f
1,
00
1,
00
No
śno
ść
pod
ło
ża
γ
R;v
1,
00
1,
00
1,
00
P
rz
e
suni
ęci
e
(p
o
śliz
g)
γ
R;h
1,
00
1,
00
1,
00
No
śno
ść
pod
ło
ża
γ
R;v
1,
40
P
rz
e
suni
ęci
e
(p
o
śliz
g)
γ
R;h
1,
10
No
śno
ść
pod
ło
ża
γ
R;v
P
rz
e
suni
ęci
e
(p
o
śliz
g)
γ
R;h
(a
) ‐
Do opo
ru/no
śno
ści
(γ
R
)
Na po
dstaw
ie
PN‐EN
19
97
R1
fund
am
en
ty
bezp
ośre
dn
ie
‐‐
‐
R2
‐‐
R3
‐‐
1,
00
1,
00
‐
Spó
jno
ść
ef
ek
ty
w
n
a
Wy
tr
zy
m
ał
o
ść
na
ś
ci
n
an
ie
be
z
od
p
ływ
u
Wy
tr
zy
m
ał
o
ść
na
ś
ci
n
an
ie
je
dn
o
os
io
w
e
Ci
ęż
ar
ob
je
to
ści
o
w
y
M2
K
ąt
ta
rc
ia
we
wn
e
tr
zn
e
go
(a
)
‐‐
niek
orz
yst
ne
oddz
iływ
an
ia
na pa
le
‐
1,
25
Spó
jno
ść
ef
ek
ty
w
n
a
1,
25
Wy
tr
zy
m
ał
o
ść
na
ś
ci
n
an
ie
be
z
od
p
ływ
u
1,
40
Wy
tr
zy
m
ał
o
ść
na
ś
ci
n
an
ie
je
dn
o
os
io
w
e
1,
40
Ci
ęż
ar
ob
je
to
ści
o
w
y
1,
00
Do pa
ram
etr
ów
geo
tec
znic
zny
ch
(γ
M
)
M1
K
ąt
ta
rc
ia
we
wn
e
tr
zn
e
go
(a
)
‐
nośno
ść pa
li i
kote
w
Do odz
iał
ywa
ń ( γ
F
) lu
b ef
ektó
w
oddz
iał
ywa
ń (γ
E
)
A1
Sta
łe
γ
G
‐‐
do o
ddzia
ływ
ań
konstruk
cji
Na po
dsa
tw
ie
PN‐EN
1
990/A
1
Zm
ie
nn
e
γ
Q
‐‐
A2
Sta
łe
γ
G
‐‐
1,
00
‐
do o
ddzia
ływ
ań
geo
tec
hn
icz
ny
ch
1,
00
Zm
ie
nn
e
γ
Q
‐‐
1,
15/
1,
30
(1
)
‐
0,
00
Wspó
łcz
yn
nik
częś
cio
wy
Zest
aw
Od
dz
ia
ływ
an
ie
/
Pa
ra
m
e
tr
gr
un
tu
/
No
sn
o
ść
Sym
bol
Po
de
jś
ci
e
obl
ic
ze
ni
ow
e
1
Po
d
ej
sc
ie
obl
ic
ze
n
io
w
e
2
Po
de
jś
ci
e
obl
ic
ze
ni
o
w
e
3
Uwa
gi
Z
wy
ją
tk
ie
m
pr
o
je
kto
w
an
ia
pa
li
ob
ci
ąż
on
yc
h
osi
o
w
o
i ko
te
w
W
p
rz
ypa
dku
pr
o
je
kto
w
an
ia
pa
li
ob
ci
ąż
on
yc
h
osi
o
w
o
i kot
ew
Ko
m
b
in
ac
ja
2
K
om
bi
na
cj
a
A2
"+
"
(M
1
lu
b
M2
)
"+
"
R4
(A
1
lu
b
A2
) "+
"
M2
"+
"
R3
Ws
pó
łcz
yn
n
ik
te
n
stosuj
e
si
ę
do
wa
rt
o
ści
tan
φ
'
γ
Q
=
1,
35
lu
b
γ
Q
=
1,
15
w
pr
zy
pa
dk
u
ni
ek
or
zy
st
ne
go
odd
zi
ał
yw
an
ia
ru
ch
u
dr
og
ow
eg
o
i
pi
e
sz
e
go
,
U
W
AG
A:
γ
Q
=
1,
50
lu
b
γ
Q
=
1,
35
w
pr
zy
pa
dk
u
in
ny
ch
ni
e
ko
rzy
st
n
yc
h
odd
zi
ał
yw
ań
ru
ch
o
m
yc
h
i
zm
ie
nnyc
h
ta
ki
ch
ja
k:
(1
) ‐
‐ pozi
om
e
pa
rc
ie
g
run
tu
,
‐ pa
rc
ie
wo
d
y
gr
un
to
w
e
j,
‐ pa
rc
ie
wo
d
y
powi
e
rz
chni
ow
e
j i
po
d
sy
p
ki
‐ pa
rc
ie
g
runt
u
od
ob
ci
ąż
eń
ru
ch
o
m
yc
h
na
na
zi
omi
e
‐ it
d
.
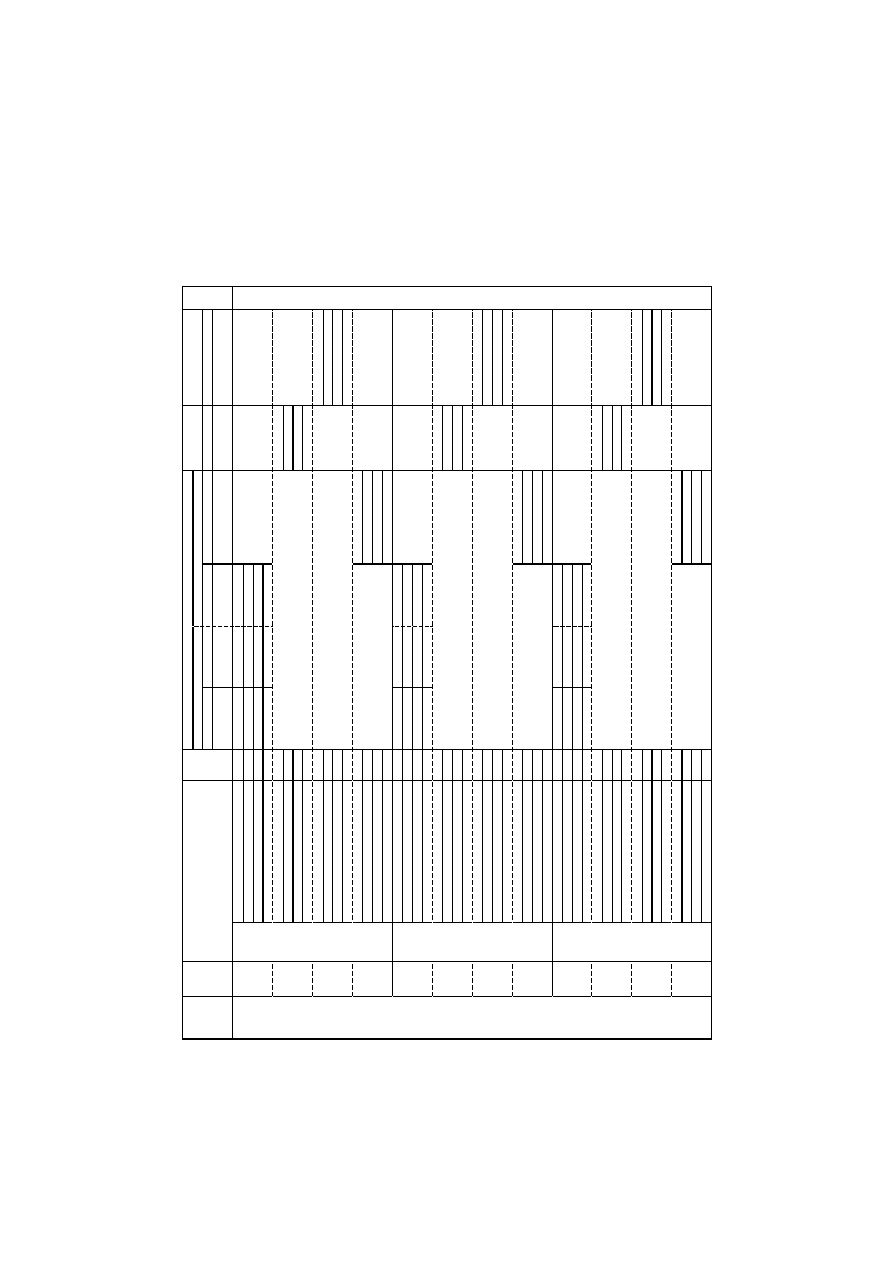
Tablica 2. C.d. Zestawienie współczynników częściowych (STR/GEO) [2], [5]
(do projektowania fundamentów głębokich)
Ko
m
b
in
a
cj
a
1K
o
m
b
in
a
cj
a
2
K
om
bi
na
cj
a
1
K
om
bi
na
cj
a
A1
"+
"
M1
"+
"
R1
A2
"+
"
M2
"+
"
R1
A1
"+
"
M1
"+
"
R1
A
1
"+
"
M1
"+
"
R2
No
śno
ść
pod
sta
w
y
γ
b
1
,00
1,
00
1
,00
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1
,00
1,
00
1
,00
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1
,00
1,
00
1
,00
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1
,25
1,
25
1
,25
No
śno
ść
pod
sta
w
y
γ
b
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1,
1
0
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1,
1
5
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
No
śno
ść
pod
sta
w
y
γ
b
1
,25
1,
25
1
,25
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1
,00
1,
00
1
,00
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1
,15
1,
15
1
,15
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1
,25
1,
25
1
,25
No
śno
ść
pod
sta
w
y
γ
b
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1,
1
0
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1,
1
5
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
No
śno
ść
pod
sta
w
y
γ
b
1
,10
1,
10
1
,10
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1
,00
1,
00
1
,00
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1
,10
1,
10
1
,10
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1
,25
1,
25
1
,25
No
śno
ść
pod
sta
w
y
γ
b
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
1,
1
0
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
1,
1
0
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
1,
1
5
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
No
śno
ść
pod
sta
w
y
γ
b
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
wc
is
k
a
n
iu
)
γ
s
No
śno
ść
ca
łkow
it
a
(p
rz
y
w
ci
ska
ni
u)
γ
t
No
śno
ść
pob
o
cz
ni
cy
(p
rz
y
w
y
ci
agani
u
)
γ
s;
t
D o
oporu/no
śno
ści
(γ
R
)
Na p
ods
taw
ie
PN ‐E
N 199
7
R1
Pa le
CF
A
‐‐
‐
R2
‐‐
R3
‐‐
1,
0
0
1,
0
0
1,
0
0
1,
1
0
R4
‐
1,
4
5
‐‐
1,
3
0
1,
4
0
1,
6
0
R1
Pale
w ie
rco
ne
‐‐
‐
R2
‐‐
R3
‐‐
1,
0
0
1,
0
0
1,
0
0
1,
0
0
R4
‐
1,
6
0
‐‐
1,
3
0
1,
5
0
1,
6
0
1,
0
0
1,
1
0
R4
‐
1,
3
0
‐‐
1,
3
0
1,
3
0
1,
6
0
R1
Pale
w bi
jan
e
‐‐
‐
R2
‐‐
R3
‐‐
1,
0
0
1,
0
0
W sp
ółc
zynni
k
częś
c io
w y
Ze st
aw
Oddz
ia
ływ
a
n
ie
/
Pa
ra
m
e
tr
g
runt
u
/
No
sn
o
ść
Sym
bol
Po
d
e
jś
ci
e
o
b
li
cz
en
io
w
e
1P
o
d
e
js
ci
e
obl
ic
ze
ni
ow
e
2
Po
d
e
jś
ci
e
obl
ic
ze
n
iow
e
3
Uw ag
i
Z
wy
ją
tki
e
m
pr
o
je
k
to
w
a
ni
a
pa
li
W
pr
zy
p
a
dku
pr
o
je
k
to
w
a
n
ia
pa
li
Ko
m
b
in
a
cj
a
2
K
om
bi
na
cj
a
A2
"+
"
(M
1
lu
b
M2
)
"+
"
R4
(A
1
lu
b
A2
)
"+
"
M2
"+
"
R3

4.4. Ustalanie wartości kombinacyjnych w zależności od analizowanego
stanu granicznego konstrukcji
We wszystkich analizowanych stanach granicznych nośności (STR, GEO i
EQU) obowiązuje ogólna kombinacja podstawowa obciążeń (konieczna do
rozpatrzenia w przypadku trwałych i przejściowych sytuacji obliczeniowych) w
postaci:
∑
∑
>
≥
⋅
ψ
⋅
γ
+
⋅
γ
+
⋅
γ
+
⋅
γ
1
i
i
,
k
i
,
0
i
,
Q
1
,
k
1
,
Q
P
1
j
j
,
k
j
,
G
Q
"
"
Q
"
"
P
"
"
G
(4.6)
Alternatywnie, ale tylko w przypadku stanów granicznych nośności STR i
GEO, konieczne jest sprawdzenie mniej korzystnego z dwóch wyrażeń
podanych poniżej (również obowiązujących w przypadku trwałych i
przejściowych sytuacji obliczeniowych):
⎪
⎩
⎪
⎨
⎧
⋅
ψ
⋅
γ
+
⋅
γ
+
⋅
γ
+
⋅
γ
⋅
ξ
⋅
ψ
⋅
γ
+
⋅
ψ
⋅
γ
+
⋅
γ
+
⋅
γ
∑
∑
∑
∑
>
≥
>
≥
1
i
i
,
k
i
,
0
i
,
Q
1
,
k
1
,
Q
P
1
j
j
,
k
j
,
G
j
1
i
i
,
k
i
,
0
i
,
Q
1
,
k
1
,
0
1
,
Q
P
1
j
j
,
k
j
,
G
Q
"
"
Q
"
"
P
"
"
G
Q
"
"
Q
"
"
P
"
"
G
(4.7)
(4.8)
gdzie:
γ – współczynniki obciążenia,
G – oznacza lub dotyczy (jeśli jest w indeksie) oddziaływań stałych,
P – oznacza lub dotyczy (jeśli jest w indeksie) oddziaływań od sprężenia,
Q – oznacza lub dotyczy (jeśli jest w indeksie) oddziaływań zmiennych,
ξ – współczynnik redukcyjny dla niekorzystnych oddziaływań stałych G (zaleca
się przyjmować:
ξ=0,85),
ψ – współczynniki kombinacyjne [1].
Oznaczenia użyte w podanych wzorach należy czytać następująco:
„+” – „należy uwzględnić w kombinacji z”,
Σ – „łączny efekt”(suma efektów oddziaływań).
W przypadku trwałych i przejściowych sytuacji obliczeniowych, wartości
obliczeniowe dla poszczególnych stanów granicznych oddziaływań przy
analizowaniu konstrukcji mostowych powinny być ustalane na podstawie trzech
zbiorów współczynników (A, B, C) zestawionych w odpowiednich tablicach w
normie [2]. Zatem:
− Przy sprawdzaniu równowagi statycznej EQU – przy ustalaniu wartości
obliczeniowych oddziaływań należy korzystać ze zbioru A,
−
Przy projektowaniu części konstrukcji w stanie STR, w których nie ma
miejsce oddziaływanie geotechniczne – należy korzystać ze zbioru B,

− Projekty części konstrukcji (stóp fundamentowych, pali, filarów, ścian
czołowych przyczółków, skrzydełek, ścianek utrzymujących podsypkę itd.)
(STR) wymagające uwzględnienia oddziaływań geotechnicznych i nośności
podłoża (GEO) należy sprawdzać, stosując tylko jeden z trzech
dodatkowych sposobów dotyczących oddziaływań geotechnicznych i
wytrzymałości.
Sposób
1 – stosowanie w oddzielnych obliczeniach wartości
obliczeniowych ze zbiorów B i C do oddziaływań geotechnicznych,
jak również do oddziaływań na konstrukcję i przekazywanych z
konstrukcji,
Sposób 2 – stosowanie wartości obliczeniowych ze zbiorów B do
wszystkich oddziaływań,
Sposób 3 – stosowanie wartości obliczeniowych ze zbioru C do
oddziaływań geotechnicznych oraz wartości obliczeniowych
oddziaływań ze zbioru B do oddziaływań na konstrukcję i
przekazywanych z konstrukcji,
Jest sugerowane, aby wybór sposobu dobierania wartości obliczeniowych
oddziaływań być dokonany na podstawie zaleceń załącznika krajowego – póki
co, załącznika brak.
Współczynniki obciążenia
γ zalecane dla wszystkich zbiorów
współczynników zgodnie z [2] zestawiono w Tablicy 3.
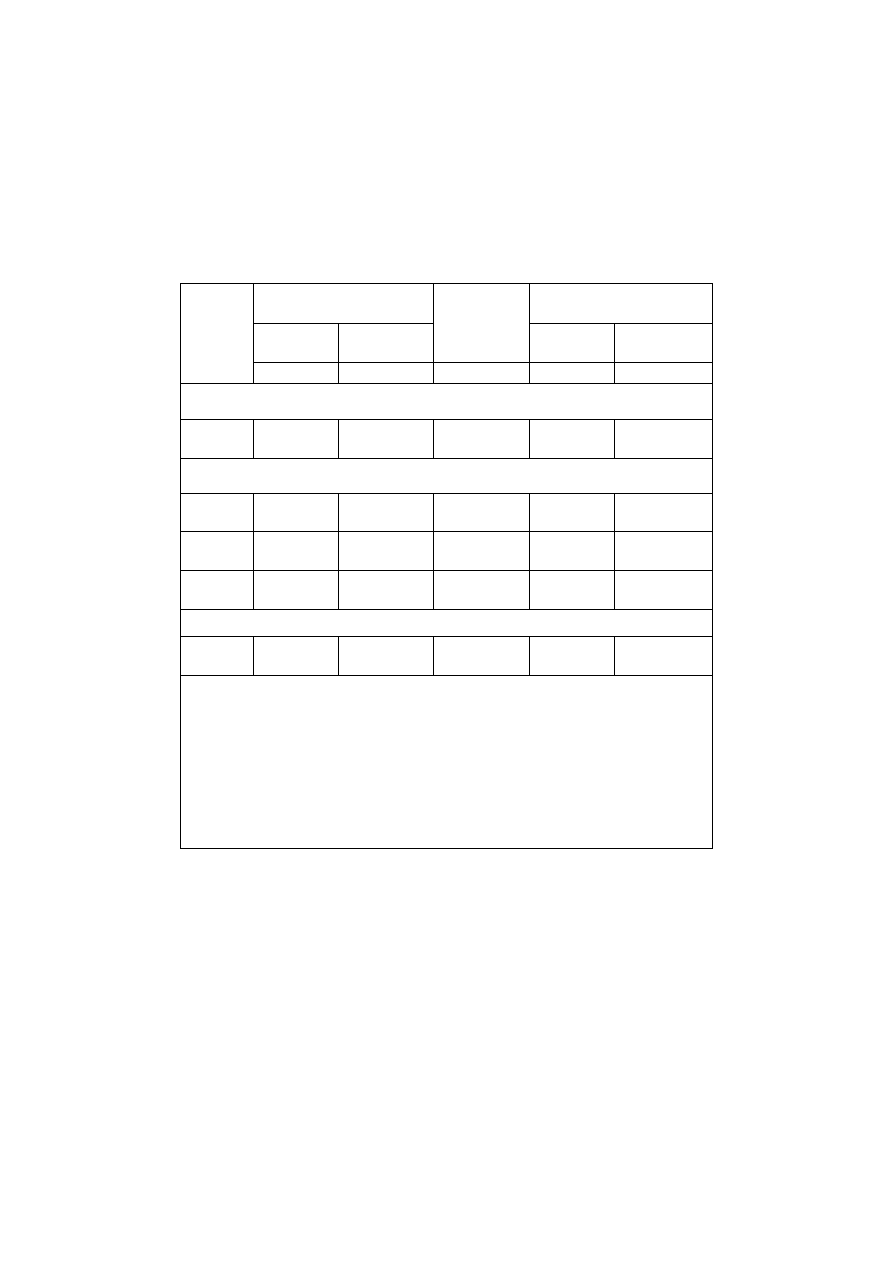
Tablica 3. Współczynniki obliczeniowe
γ obciążeń stałych i zmiennych w obliczeniach
przyczółków, w kombinacjach podstawowych
Wzór
opisu-
jący
kombi-
nację
Obciążenie stałe
(5)
Wiodące
oddzia-
ływanie
zmienne
Towarzyszące
oddziaływania zmienne
nieko-
rzystne
korzystne
główne
(jeśli są)
pozostałe
γ
Gj,sup
γ
Gj,inf
γ
Q,1
γ
Q,i
γ
Q,i
Zbiór A
4.6 1,05 0,95
1,35
(1) (4)
1,50
(2) (4)
1,35
(1)
1,50
(2)
Zbiór B
4.6 1,35 1,00
1,35
(1)
1,50
(2)
1,35
(1)
1,50
(2)
4.7 1,35 1,00
1,35
(1)
1,50
(2)
1,35
(1)
1,50
(2)
4.8 1,35
(3)
1,00
1,35
(1)
1,50
(2)
1,35
(1)
1,50
(2)
Zbiór C
4.6 1,00 1,00
1,15
(1)
1,30
(2)
1,15
(1)
1,30
(2)
(1)
dotyczy taboru samochodowego i pieszych (rowerzystów),
(2)
dotyczy innych oddziaływań ruchomych i innych oddziaływań zmiennych
(poziome parcie gruntu, wody gruntowej, wody przypowierzchniowej i
podsypki, parcie gruntu od obciążeń ruchomych),
(3)
do obciążeń z tej grupy stosuje się współczynniki redukcyjny
ξ,
(4)
w przejściowych sytuacjach obliczeniowych, podczas których występuje
ryzyko utraty równowagi statycznej, Q
k,1
przedstawia dominujące
obciążenie zmienne destabilizujące, a Q
k,i
odpowiednie towarzyszące
oddziaływania zmienne destabilizujące.
Wartości charakterystyczne wszystkich oddziaływań stałych
pochodzących z jednego źródła są mnożone przez γ
Gj,sup
, jeśli sumaryczny efekt
oddziaływania wypadkowego jest niekorzystny lub przez γ
Gj,inf
, jeśli sumaryczny
efekt oddziaływania wypadkowego jest korzystny.
LITERATURA
1. PN-EN 1990:2004/AC Eurokod. Podstawy projektowania konstrukcji

2. PN-EN 1990:2002/A1:2005 Eurokod. Podstawy projektowania konstrukcji
3. PN-EN 1991-1-1:2002 Eurokod 1: Oddziaływania na konstrukcje, Część 1-1:
Obciążenia ogólne. Ciężar objętościowy, ciężar własny, obciążenia użytkowe w
budynkach
4. PN-EN 1991-2:2003 Eurokod 1: Oddziaływania na konstrukcje, Część 2: Obciążenia
ruchome mostów
5. PN-EN 1997-1:2004 Eurokod 7: Projektowanie geotechniczne. Część 1: Zasady
ogólne
6. PN-EN 1997-1:2008/Ap2:2010: Poprawka do Polskiej Normy PN-EN 1997-1:2008
7. PN-EN 1997-1:2008/AC: Poprawka do Polskiej normy PN-EN 1997-1:2008
8. Jankowiak I., Siekierski W.: Obciążenia stałe i obciążenia taborem na mostach
drogowych według PN-EN, Archiwum Instytutu Inżynierii Lądowej, 8/2010,
Wydawnictwo Politechniki Poznańskiej
9. Karlikowski J., Madaj A.: Ogólne zasady ustalania oddziaływań na mosty według
PN-EN 1990:2004, Archiwum Instytutu Inżynierii Lądowej, 8/2010. Wydawnictwo
Politechniki Poznańskiej
PRINCIPLES OF DESIGNING THE ROAD BRIDGE ABUTMENTS
ACCORDING TO PN-EN STANDARDS
Summary
Calculation of bridge abutments is multi-faceted because there is a necessitate of
analysis the structural components, which on the one hand carry all loads from
the spans of the bridge into the foundation, on the other are in constant
interaction with the backfill behind the main wall of abutment, which
additionally also may be loaded. In the static analysis and the subsequent
designing of a bridge abutment in accordance with the guidelines of the PN-EN
standards some new live load models and new rules for determining the dead
weight should therefore be taken into account, with respect to the principles
suggested by the new geotechnical standard. This necessitates the use of
multiple standards at the stage of static calculations of abutments, which can
cause considerable difficulty and can extend the designing of this element. The
purpose of this study is, therefore, discuss the principles determining the loads
acting on the road bridge abutments, rules for determining combination for
actions and the selection of appropriate partial factors for the basic ultimate limit
states. Values statement of partial factors (for actions, materials and resistances)
recommended by both the load standard for bridges and geotechnical standard
should serve to determine of the necessary data for the dimensioning of
abutments.
Wyszukiwarka
Podobne podstrony:
04 22 PAROTITE EPIDEMICA
POKREWIEŃSTWO I INBRED 22 4 10
Wykład 22
22 Choroby wlosow KONSPEKTid 29485 ppt
22 piątek
plik (22) ppt
MAKROEKONOMIA R 22 popyt polityka fiskalna i handel zagr
PREZENTACJA UZUP 22 XII
22 Tydzień zwykłyxxxx, 22 środa
Prawo budowlane wykł 22 02 13
22 WdK
2011 09 22 Rozkaz nr 904 MON instrikcja doświadczenie w SZ RP
22 04 2010
2003 06 22
więcej podobnych podstron