Sygnały i systemy
- Pytania i zadania -
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
maslowski@prz.edu.pl
Sygnały dyskretne; Prosta i odwrotna transformata Z
2.1. Wykreślić sygnały dyskretne:
a)
2
5 [
3];
u n
−
(
)
2 [ ]
[
4] ;
u n
u n
−
−
[
2]
[
2] 2 [
7];
u n
u n
u n
+ +
− −
−
0,5 [2
3];
u n
−
3 2 [
1];
u n
−
−
b)
2 [ ];
nu n
[
3];
nu n
−
0,5 [
3];
nu n
−
0,5 [ ];
n
u n 0,5 [
2];
n
u n
−
1
2 0,5
[
2];
n
u n
−
⋅
−
4 [4
];
u
n
−
[ ]
u n
----------------------------------------------------------------------------------------------------------------------------------------
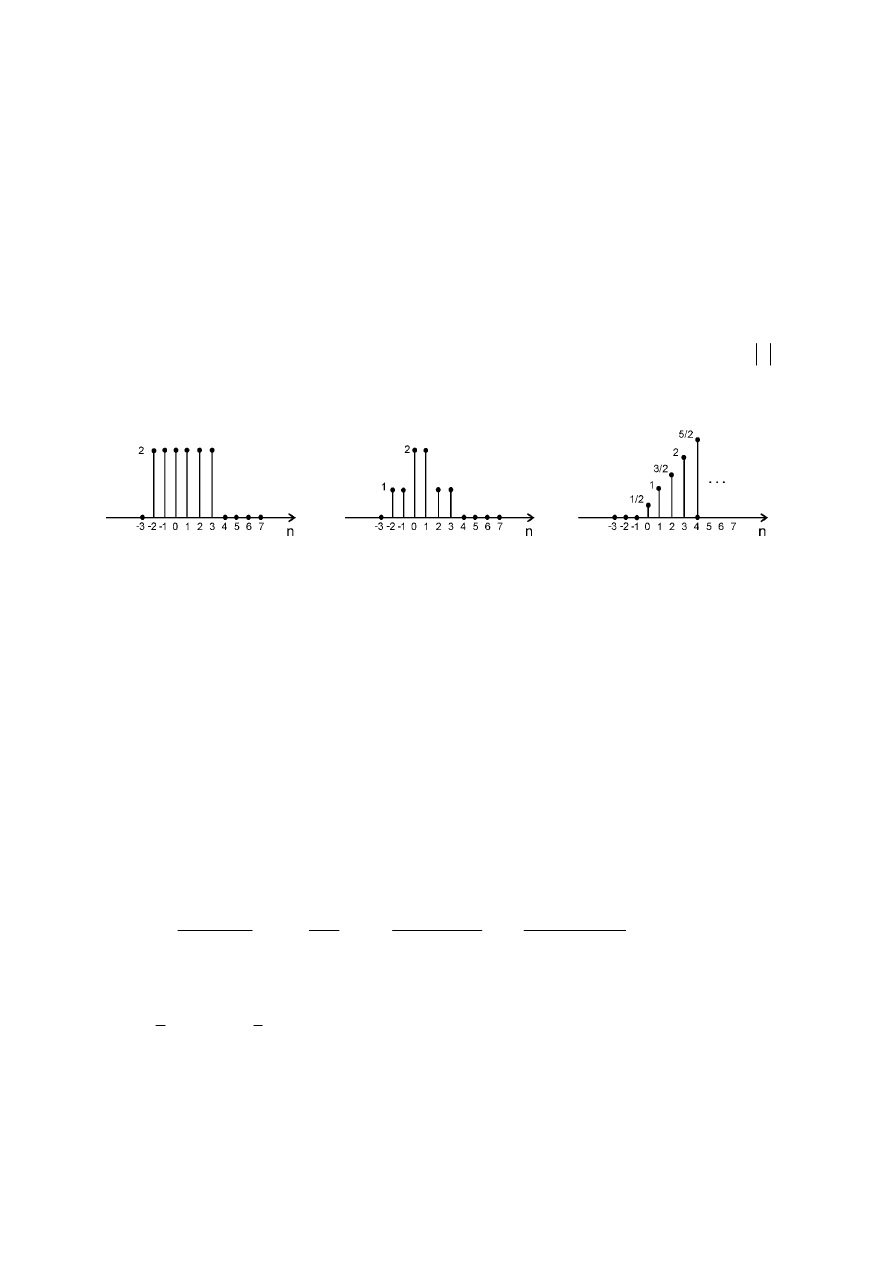
2.2. Znaleźć funkcje
[ ]
f n
określające sygnały dyskretne przedstawione na wykresach. Wyznaczyć ich
transformatę
Z
:
----------------------------------------------------------------------------------------------------------------------------------------
2.3. Wyznaczyć transformatę
Z
sygnałów dyskretnych :
a) delta Kroneckera:
[ ]
[ ]
x n
n
δ
=
;
[ ]
[
3]
x n
n
δ
=
−
lub
(
)
(
)
x nT
nT
δ
=
;
(
)
(
3)
(
)
n
T
x nT
δ
−
=
b) skok jednostkowy: [ ]
u n ; [
2]
u n
− lub (
)
(
)
x nT
u nT
=
;
(
)
(
2)
(
)
n
T
x nT
u
−
=
c) sygnał wykładniczy: [ ]
[ ]
n
x n
a u n
=
;
1
[
1]
[
1]
n
x n
a
u n
−
− =
− ;
d) próbkowana funkcja ekspotencjalna zanikająca do zera (
0
α
>
): (
)
(
)
nT
x nT
e
u nT
α
−
=
e)
1
2
[ ] (5 3
4 2
) [ ]
n
n
x n
u n
−
−
=
⋅
+ ⋅
lub
(
)
(
1)
(
2)
(
)
5 3
4 2
(
)
n
T
n
T
x nT
u nT
−
−
=
⋅
+ ⋅
f) sygnał liniowo narastający: [ ]
[ ]
x n
nu n
=
lub (
)
(
)
x nT
nT u nT
=
g)
2
[ ]
[ ]
x n
n u n
=
Wskazówka:
2
(
1)
n
n n
n
=
− +
h) funkcja sinusoidalna: [ ] sin[
] [ ]
x n
n u n
ω
=
lub (
) sin(
) (
)
x nT
n T u nT
ω
=
i) funkcja cosinusoidalna: [ ] cos[
] [ ]
x n
n u n
ω
=
lub (
) cos(
) (
)
x nT
n T u nT
ω
=
Czy zawsze transformata
Z
zależy od okresu próbkowania (częstotliwości próbkowania)?
----------------------------------------------------------------------------------------------------------------------------------------
2.4. Wyznaczyć odwrotną transformatę
Z
funkcji wymiernych:
a)
2
30
12
2
6
5
1
z
z
z
z
−
−
+
; b)
12
3
z
−
; c)
2
2
2
2
(
3)(
5)
z
z
z
z
−
−
−
; d)
5
8
3 5
9
2 7 12
z
z
z
z
−
−
+
−
+
+
Rozw.:
a)
1
1
3
[ ] 2
[ ]
2
3
n
n
u n
u n
⋅
+ ⋅
b) 4
[ ] 4 2
[ ]
n
n
u n
δ
− ⋅
+ ⋅
c)
1
(3
5
4
5
) [ ]
n
n
n
n
u n
−
−
+
⋅
d)
( )
( )
(
)
( )
( )
(
)
( )
( )
(
)
1
1
6
6
9
9
3
3
4
[
1] 5
3
4
[
6] 9
3
4
[
9]
n
n
n
n
n
n
u n
u n
u n
−
−
−
−
−
−
−
− −
⋅
− +
−
− −
⋅
− +
−
− −
⋅
−