
P
OLITECHNIKA
W
ARSZAWSKA
P
OMIARY PRZEMIESZCZEŃ I ANALIZA DEFORMACJI
Ćwiczenie nr 3
Temat: Wyznaczenie elementów tensora odkształceń poziomych przy użyciu
konstrukcji pomiarowej w formie gwiazdy regularnej – rozety gwiaździstej oraz
pomierzonych przemieszczeń.
Prowadzący: dr inż. Mieczysław Kwaśniak
Wykonawca: Jan Prusik
Grupa: I m2b
Rok akademicki: 2011/2012
Studia: stacjonarne drugiego stopnia sem. I mgr
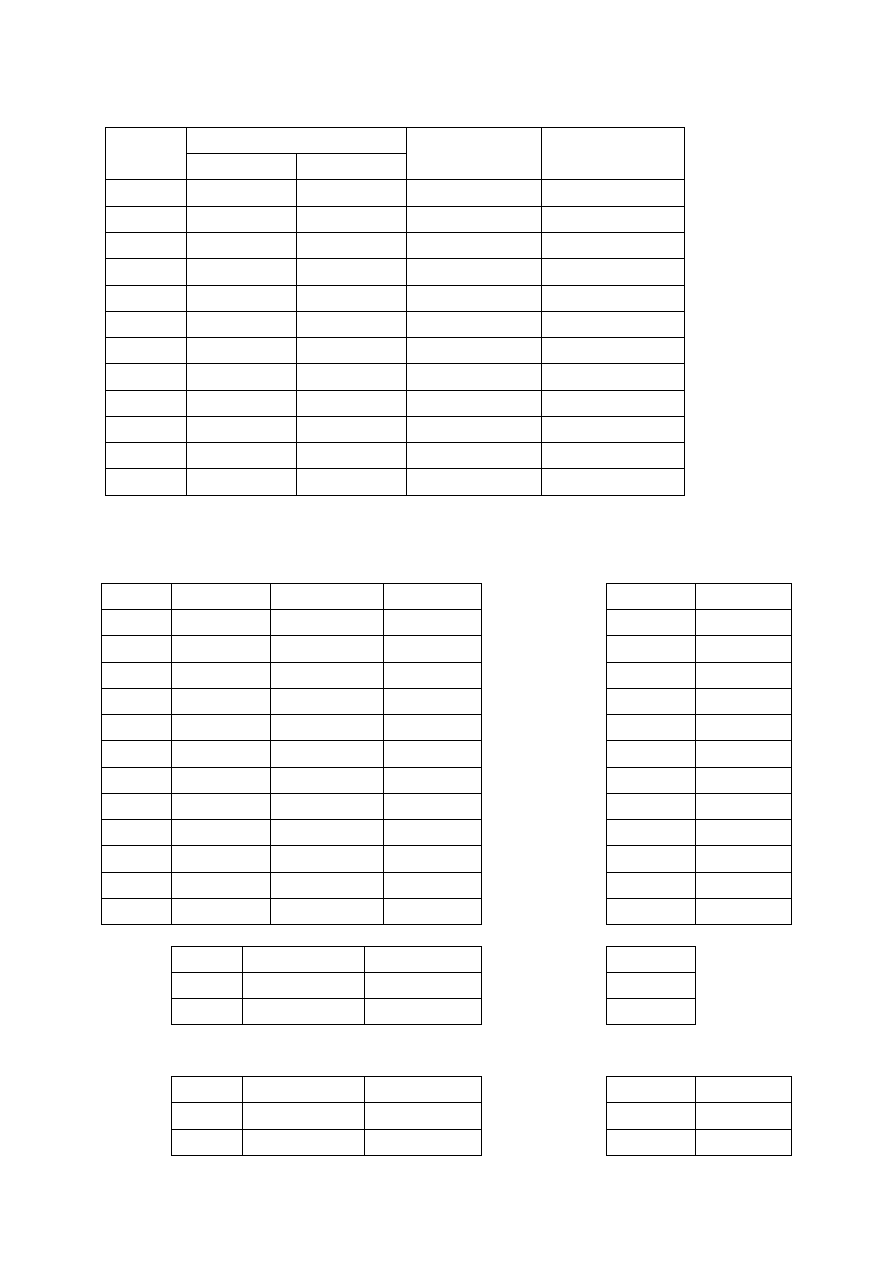
Dane do części pierwszej
Nr
Azymut - ϕ
L1
obs
L2
obs
grad
rad
1
0
0,000000
23,9998
23,9942
2
33,3333
0,523598
24,0004
24,0015
3
66,6667
1,047198
23,9994
24,0107
4
100
1,570796
24,0001
24,0115
5
133,3333
2,094395
24,0002
24,0041
6
166,6667
2,617994
23,9992
23,9955
7
200
3,141593
24,0001
23,995
8
233,3333
3,665191
24,0009
24,0012
9
266,6667
4,188791
24,0004
24,0099
10
300
4,712389
24,0007
24,0116
11
333,3333
5,235987
23,9997
24,0043
12
367,6667
5,775295
23,9998
23,9952
Znalezienie elementów tensora odkształceń za pomocą rozety gwiaździstej.
Rozwiązanie:
Współczynniki przy niewiadomych
Nr pkt
ε
xx
γ
xy
ε
yy
Nr pkt
ε
ϕi
1
1,000
0,000
0,000
1
0,00023
2
0,750
0,866
0,250
2
-0,00005
3
0,250
0,866
0,750
3
-0,00047
4
0,000
0,000
1,000
4
-0,00047
5
0,250
-0,866
0,750
5
-0,00016
6
0,750
-0,866
0,250
6
0,00015
7
1,000
0,000
0,000
7
0,00021
8
0,750
0,866
0,250
8
-0,00001
9
0,250
0,866
0,750
9
-0,00040
10
0,000
0,000
1,000
10
-0,00045
11
0,250
-0,866
0,750
11
-0,00019
12
0,763
-0,850
0,237
12
0,00019
4,520
0,001
1,493
0,000359
ATA
0,001
5,972
0,015
ATL
-0,000791
1,493
0,015
4,493
-0,001775
0,2485
0,0002
-0,0826
-0,000236
ε
xx
Q
0,0002
0,1674
-0,0006
X
0,000131
γ
xy
-0,0826
-0,0006
0,2500
0,000473
ε
yy
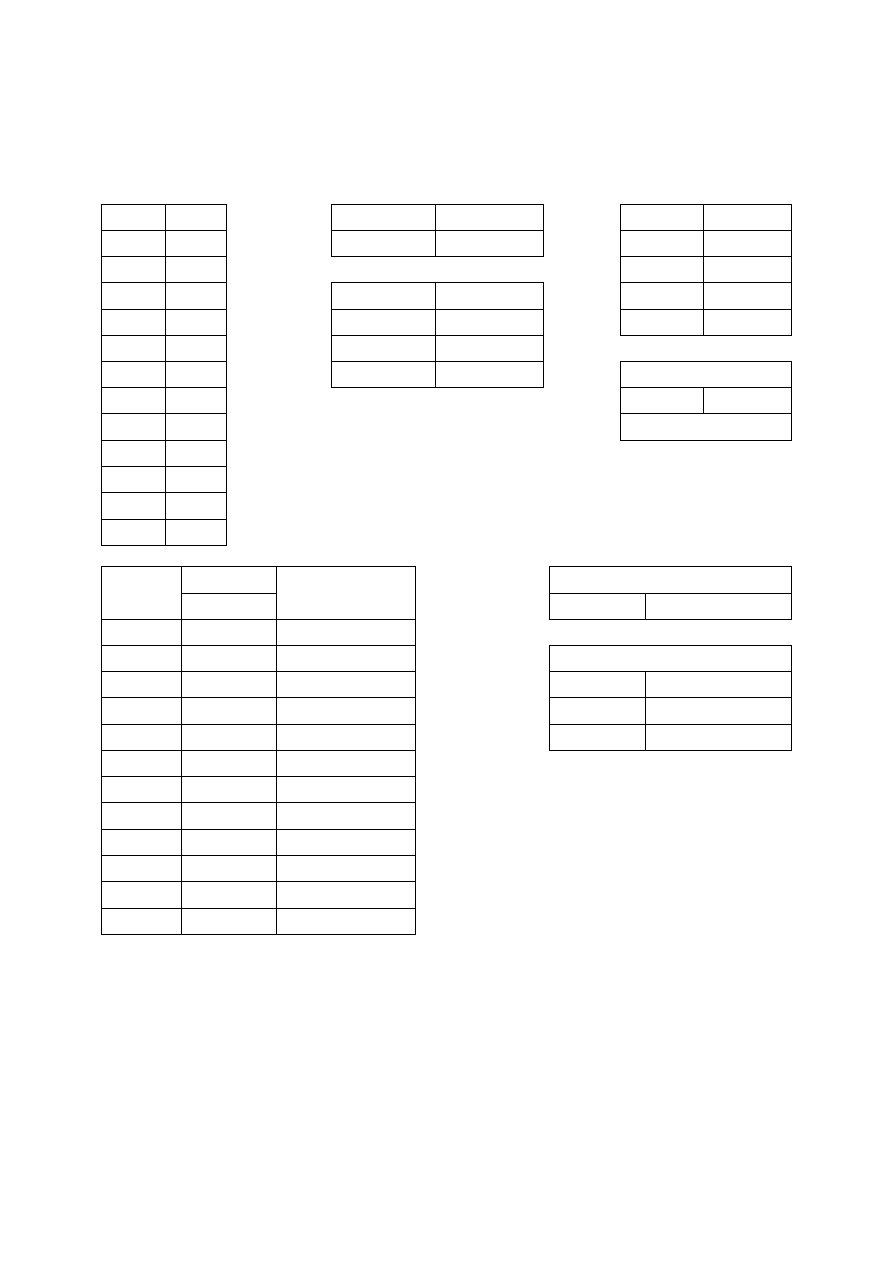
Kontrole
Nr pkt
V
VTV
VTL
n
12
1
0,000
0,00000000771 0,00000000771
u
3
2
0,000
d
0
3
0,000
σ
εϕ
0,0000295
f
9
4
0,000
σ
0,ϕ
0,0000293
α
0,05
5
0,000
σ
0,ϕ'
0,993
6
0,000
σ
kryt
1,371
Test glob
7
0,000
0,99
1,37
8
0,000
spełniony
9
0,000
10
0,000
11
0,000
12
0,000
Nr
Azymut - ϕ
γ
ϕ
Odkształcenie postaciowe
grad
γ
max
0,000378
1
0,0000
0,000131
2
33,3333
-0,000241
Odkształcenie liniowe
3
66,6667
-0,000372
ε
max
0,000496
4
100,0000
-0,000131
ε
min
-0,000259
5
133,3333
0,000241
ϕ
główne
188,2121
6
166,6667
0,000372
7
200,0000
0,000131
8
233,3333
-0,000241
9
266,6667
-0,000372
10
300,0000
-0,000131
11
333,3333
0,000241
12
367,6667
0,000370
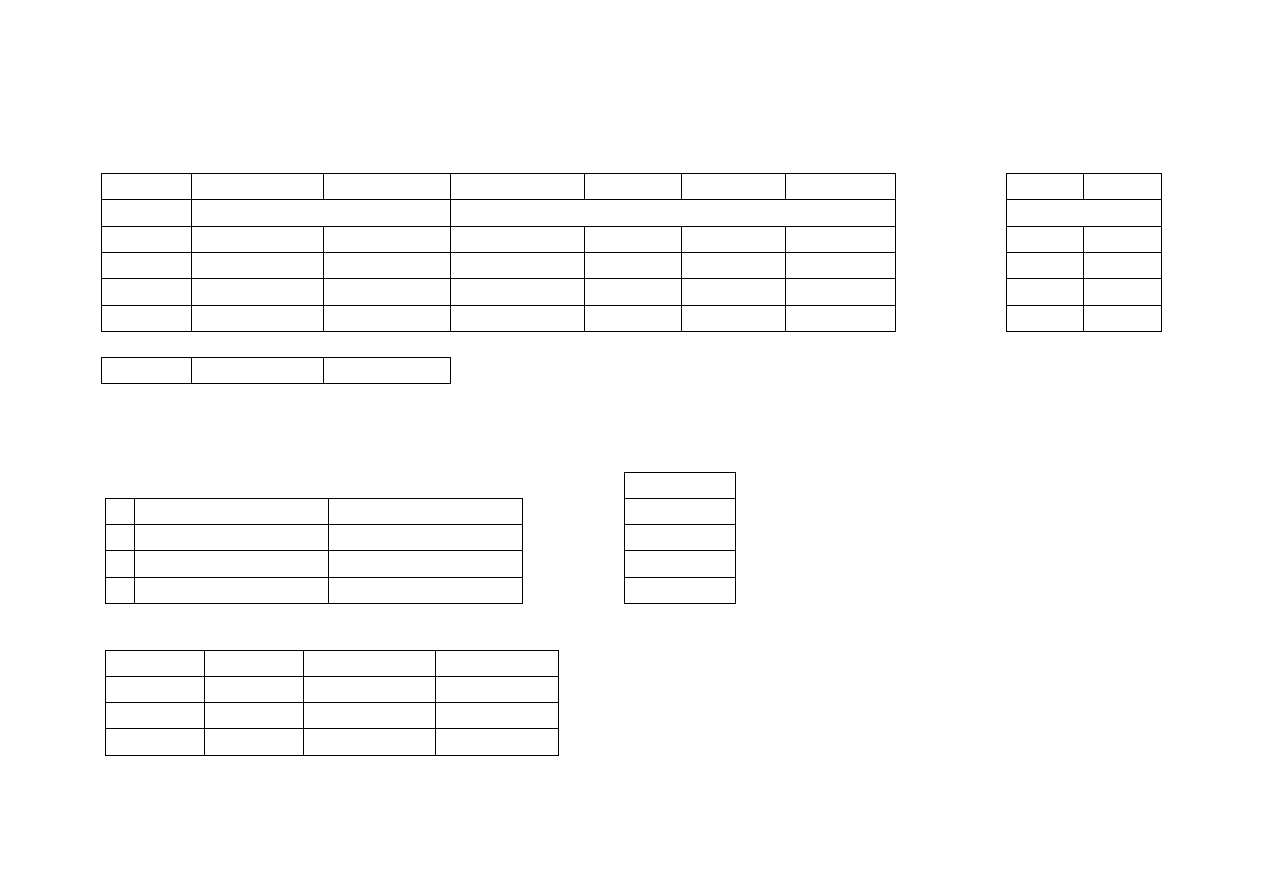
Znalezienie elementów tensora odkształceń za pomocą pomierzonych przemieszczeń.
Dane do części drugiej
punkt
x
y
∆x
∆y
σ
∆x
σ
∆y
X
Y
m
mm
mm
1
10,00
10,00
9,90
-3,90
0,80
0,70
-3882,50 14487,50
2
31,21
31,21
2,70
6,90
0,60
1,00
-25092,50 -6722,50
3
2,24
38,98
-5,00
-4,90
1,00
1,20
3877,50 -14492,50
4
-18,98
17,76
3,40
-15,10
1,20
0,80
25097,50
6727,50
średnia
6,12
24,49
Obliczenie współczynników aproksymacji dla równania p
x
=a
0
+a
1
x+a
2
y
a - współczynniki przy niewiadomych
∆x
1
-3882,50
14487,50
9,9
1
-25092,50
-6722,50
2,7
1
3877,50
-14492,50
-5
1
25097,50
6727,50
3,4
Macierz wag σ∆x
0,80
0
0
0
0
0,60
0
0
0
0
1,00
0
0
0
0
1,20
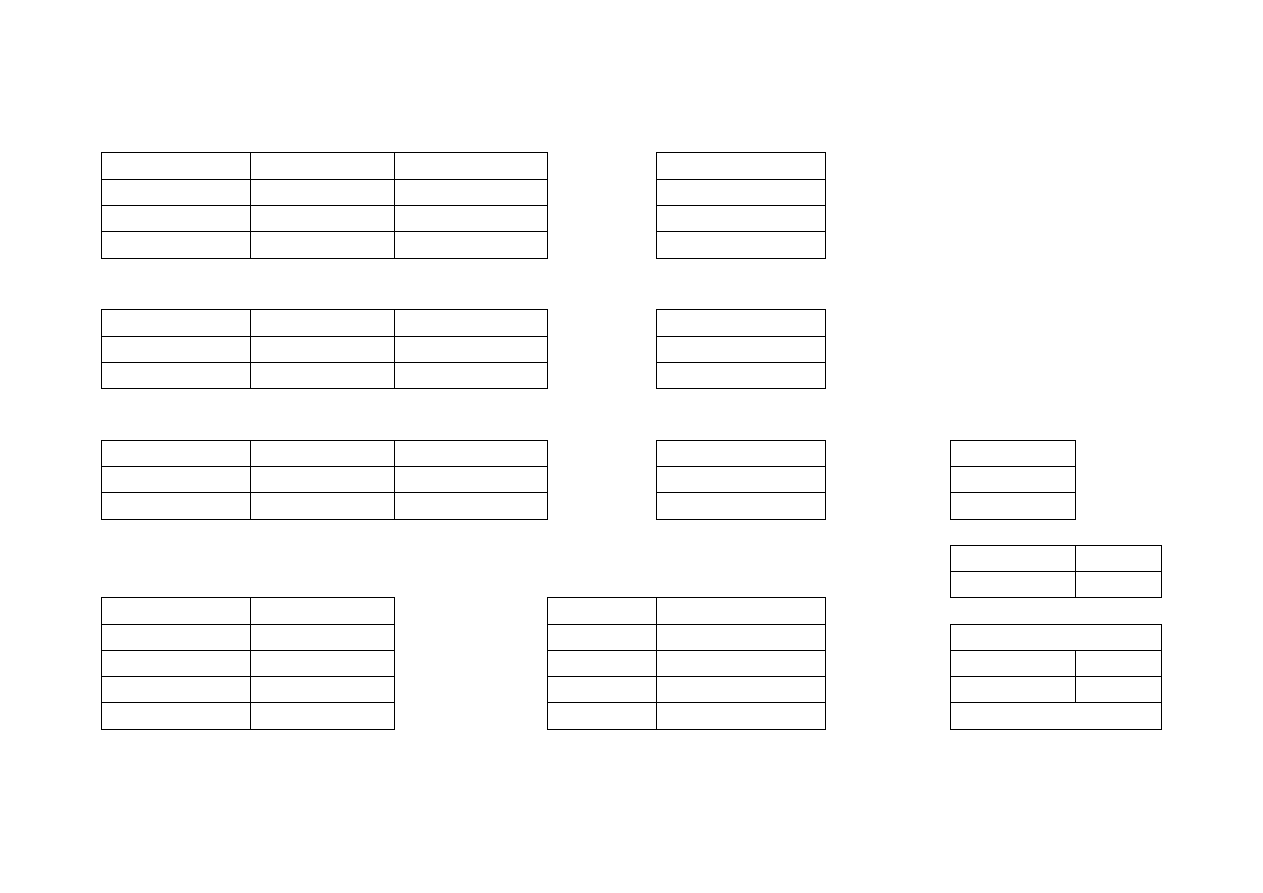
Macierz A
Macierz L
1,250
-4853,125
18109,375
12,375
1,667
-41820,833
-11204,167
4,500
1,000
3877,500
-14492,500
-5,000
0,833
20914,583
5606,250
2,833
Macierz A
T
A
Macierz A
T
L
6,035
-54461,476
-5857,517
20,330
-54461,476
2224989725,217
441738240,321
-208380,686
-5857,517
441738240,321
694945408,898
262031,641
Macierz Q
Macierz niewiadomych
σ
0,2145357782
0,0000055988
-0,0000017506
a0
-2,73610
0,463180
0,0000055988
0,0000000007
-0,0000000004
a1
0,00012
0,000026
-0,0000017506
-0,0000000004
0,0000000017
a2
-0,00048
0,000041
Kontrole
VTV
VTL
0,4161
0,4161
V
VTA
n
4
-0,278
0,00000
u
3
Test globalny
0,209
0,00000
d
0
σ
0
σ
kryt
-0,348
0,00000
f
1
0,645
1,960
0,417
0,00000
α
0,05
Spełniony
Obliczenie współczynników aproksymacji dla równania p
y
=a
0
+a
1
x+a
2
y
a - współćzynniki przy niewiadomych
∆y
1
-3882,50
14487,50
-3,9
1
-25092,50
-6722,50
6,9
1
3877,50
-14492,50
-4,9
1
25097,50
6727,50
-15,1
Macierz wag σ∆y
0,70
0
0
0
0
1,00
0
0
0
0
1,20
0
0
0
0
0,80
Macierz A
Macierz L
1,429
-5546,429
20696,429
-5,571
1,000
-25092,500
-6722,500
6,900
0,833
3231,250
-12077,083
-4,083
1,250
31371,875
8409,375
-18,875
Macierz A
T
A
Macierz A
T
L
5,298
8891,583
23291,309
-28,05571145
8891,583
1655031943,726
278686854,302
-747575,1308
23291,309
278686854,302
690107691,593
-271106,1196
Macierz Q
Macierz niewiadomych
σ
0,2216556800
0,0000000739
-0,0000075108
a0
4,23773
0,470803
0,0000000739
0,0000000006
-0,0000000003
a1
0,00042
0,000025
-0,0000075108
-0,0000000003
0,0000000018
a2
0,00008
0,000043
Kontrole
VTV
VTL
0,10252
0,10252
V
VTA
n
4
-0,119
0,0000
u
3
Test globalny
0,170
0,0000
d
0
σ
0
σ
kryt
-0,203
0,0000
f
1
0,320
1,960
0,136
0,0000
α
0,05
Spełniony
G=
0,00012
-0,00048
T=
0,00012145 -0,00003111
W=
0
-0,000446
0,00042
0,00008
-0,00003111 0,00008220
0,000446
0
ε
xx
0,00012145
γ
xy
-0,00003111
ε
yy
0,00008220
Nr
Azymut - ϕ
γ
ϕ
Odkształcenie postaciowe
grad
γ
max
0,000037
1
0,0000
-0,0000311
2
33,3333
0,0000014
Odkształcenie liniowe
3
66,6667
0,0000326
ε
max
0,00007071
4
100,0000
0,0000311
ε
min
0,00013293
5
133,3333
-0,0000014
ϕ
główne
349,5404
6
166,6667
-0,0000326
7
200,0000
-0,0000311
8
233,3333
0,0000014
9
266,6667
0,0000326
10
300,0000
0,0000311
11
333,3333
-0,0000014
12
367,6667
-0,0000331
-0,000400
-0,000300
-0,000200
-0,000100
0,000000
0,000100
0,000200
0,000300
0,000400
0,000500
0
5
10 15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
155
160
165
170
175
180
185
190
195
200
205
210
215
220
225
230
235
240
245
250
255
260
265
270
275
280
285
290
295
300
305
310
315
320
325
330
335
340
345
350
355
360
365
370
375
380
385
390395
400
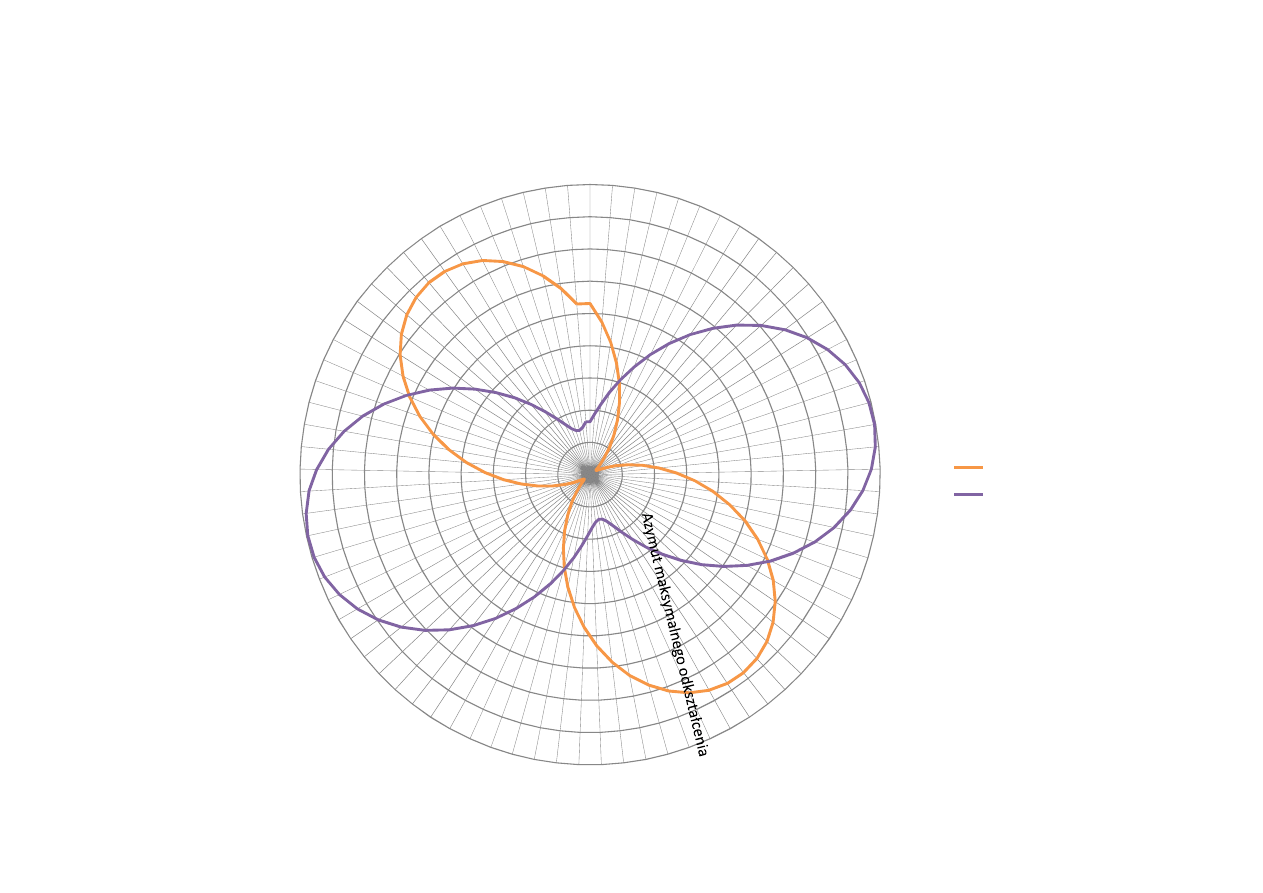
Wykres radialny odkształceń liniowych i postaciowych
γϕ
εϕi
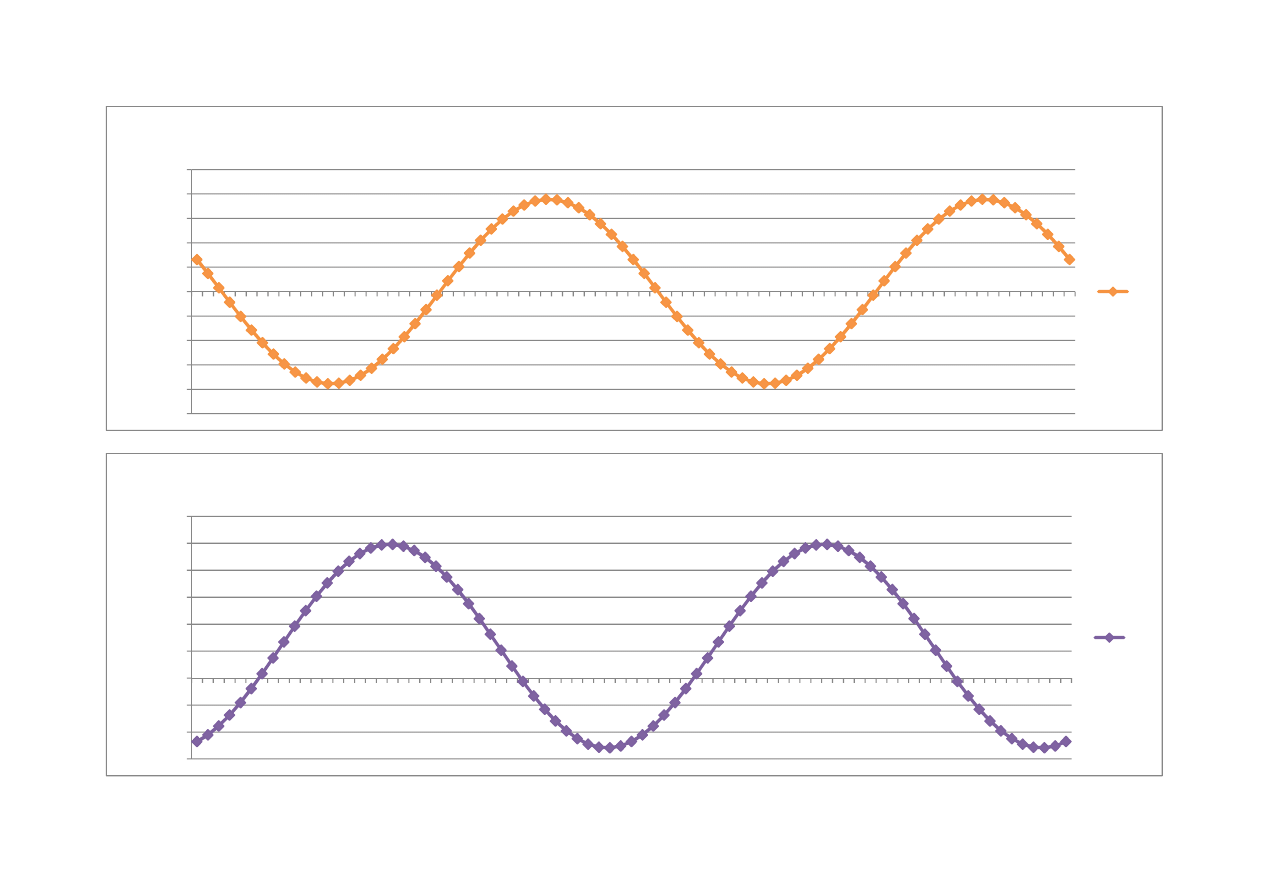
-0,000500
-0,000400
-0,000300
-0,000200
-0,000100
0,000000
0,000100
0,000200
0,000300
0,000400
0,000500
0
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
1
4
0
1
5
0
1
6
0
1
7
0
1
8
0
1
9
0
2
0
0
2
1
0
2
2
0
2
3
0
2
4
0
2
5
0
2
6
0
2
7
0
2
8
0
2
9
0
3
0
0
3
1
0
3
2
0
3
3
0
3
4
0
3
5
0
3
6
0
3
7
0
3
8
0
3
9
0
4
0
0
Odkształcenia postaciowe
γϕ
-0,000300
-0,000200
-0,000100
0,000000
0,000100
0,000200
0,000300
0,000400
0,000500
0,000600
0
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
1
4
0
1
5
0
1
6
0
1
7
0
1
8
0
1
9
0
2
0
0
2
1
0
2
2
0
2
3
0
2
4
0
2
5
0
2
6
0
2
7
0
2
8
0
2
9
0
3
0
0
3
1
0
3
2
0
3
3
0
3
4
0
3
5
0
3
6
0
3
7
0
3
8
0
3
9
0
4
0
0
Odkształceniia liniowe
εϕi
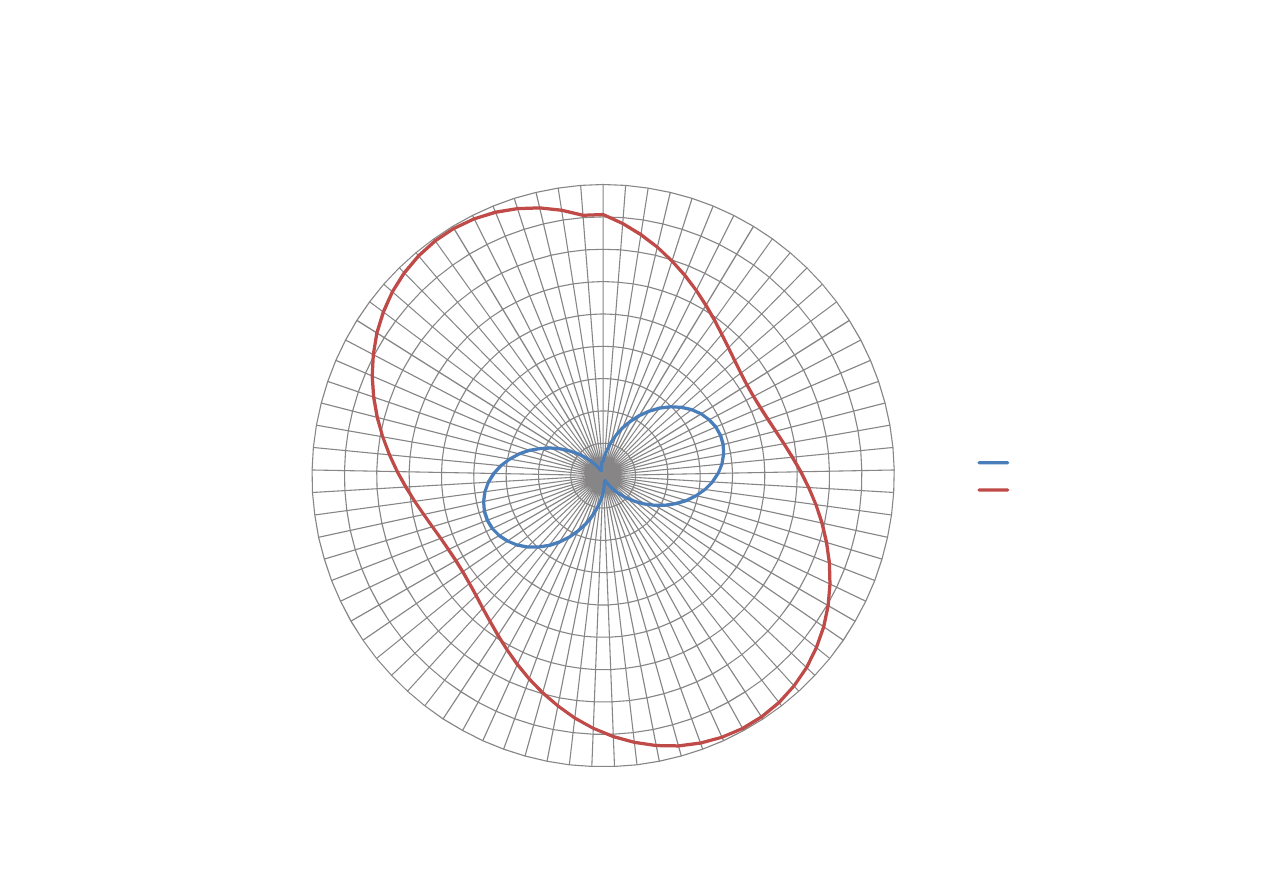
-0,0000400
-0,0000200
0,0000000
0,0000200
0,0000400
0,0000600
0,0000800
0,0001000
0,0001200
0,0001400
0
5
10 15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
155
160
165
170
175
180
185
190
195
200
205
210
215
220
225
230
235
240
245
250
255
260
265
270
275
280
285
290
295
300
305
310
315
320
325
330
335
340
345
350
355
360
365
370
375
380
385
390395
400
Wykres radialny odkształceń liniowych i postaciowych
γϕ
εϕi
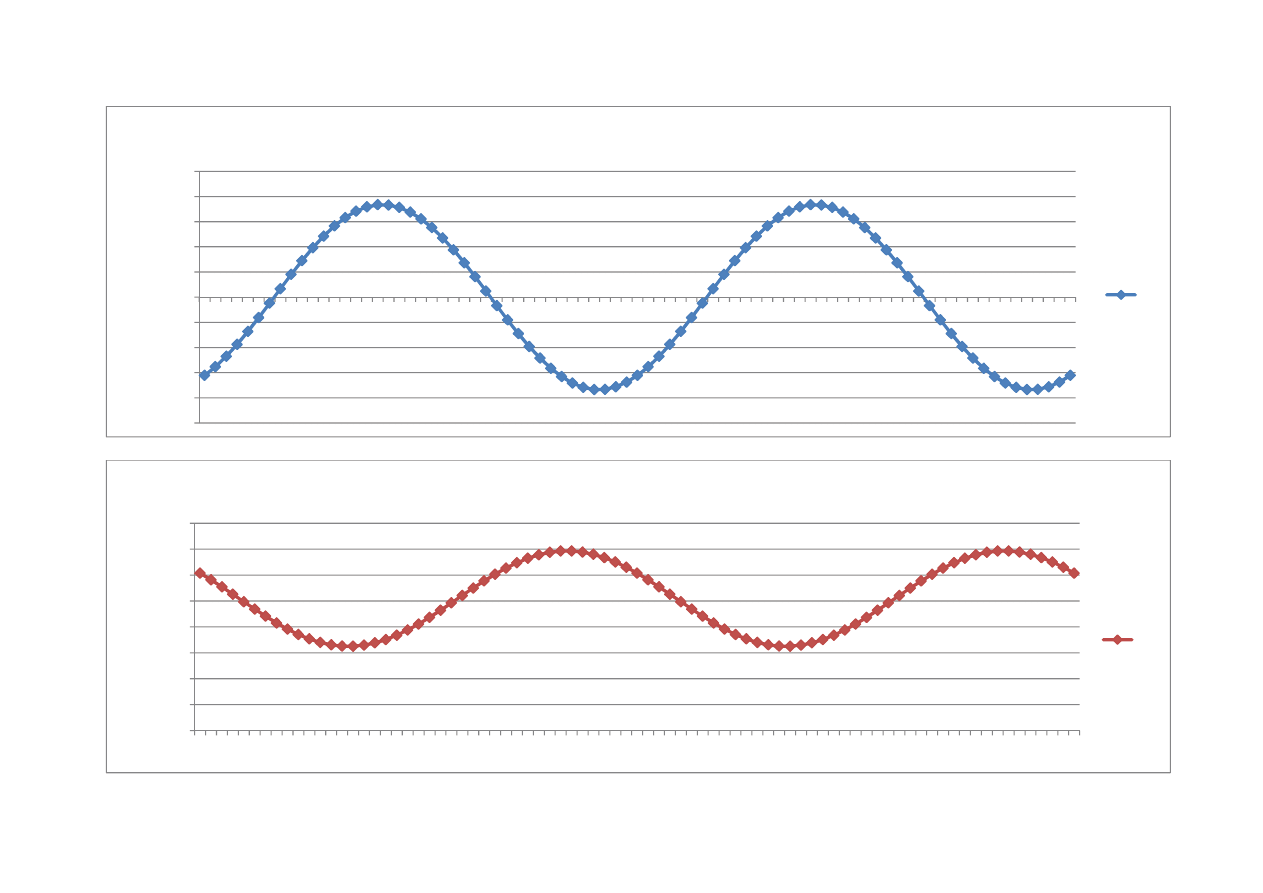
-0,0000500
-0,0000400
-0,0000300
-0,0000200
-0,0000100
0,0000000
0,0000100
0,0000200
0,0000300
0,0000400
0,0000500
0
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
1
4
0
1
5
0
1
6
0
1
7
0
1
8
0
1
9
0
2
0
0
2
1
0
2
2
0
2
3
0
2
4
0
2
5
0
2
6
0
2
7
0
2
8
0
2
9
0
3
0
0
3
1
0
3
2
0
3
3
0
3
4
0
3
5
0
3
6
0
3
7
0
3
8
0
3
9
0
4
0
0
Odkształcenia postaciowe
γϕ
0,0000000
0,0000200
0,0000400
0,0000600
0,0000800
0,0001000
0,0001200
0,0001400
0,0001600
0
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
1
4
0
1
5
0
1
6
0
1
7
0
1
8
0
1
9
0
2
0
0
2
1
0
2
2
0
2
3
0
2
4
0
2
5
0
2
6
0
2
7
0
2
8
0
2
9
0
3
0
0
3
1
0
3
2
0
3
3
0
3
4
0
3
5
0
3
6
0
3
7
0
3
8
0
3
9
0
4
0
0
Odkształcenia liniowe
εϕi
Wyszukiwarka
Podobne podstrony:
Cwiczenie nr 8 Teksty id 99954
Cwiczenia nr 2 RPiS id 124688 Nieznany
Cwiczenie nr 15 id 125710 Nieznany
Ćwiczenie nr 3 moje
Cwiczenia nr 6 RPiS id 124693 Nieznany
cwiczenie nr 2 instrukcja id 12 Nieznany
cwiczenie nr 9 sprawozdanie id 101106
Cwiczenie nr 10 id 125701 Nieznany
Cwiczenia nr 4 RPiS id 124689 Nieznany
cwiczenie nr 3 instrukcja id 12 Nieznany
Cwiczenia nr 5 RPiS id 124692 Nieznany
Cwiczenie nr 60 id 99947 Nieznany
Cwiczenia nr 1 RPiS id 124683 Nieznany
Cwiczenie nr 5 Wymiarowanie id 99941
Cwiczenia nr 9 (z 14) id 98690 Nieznany
cwiczenie nr 26 id 101103 Nieznany
CWICZENIE NR 8 moje
mzt 71 Cwiczenie nr 71 id 78283 Nieznany
więcej podobnych podstron