6. Osiadania podłoża gruntowego – zadania przykładowe
Zadanie 6.1
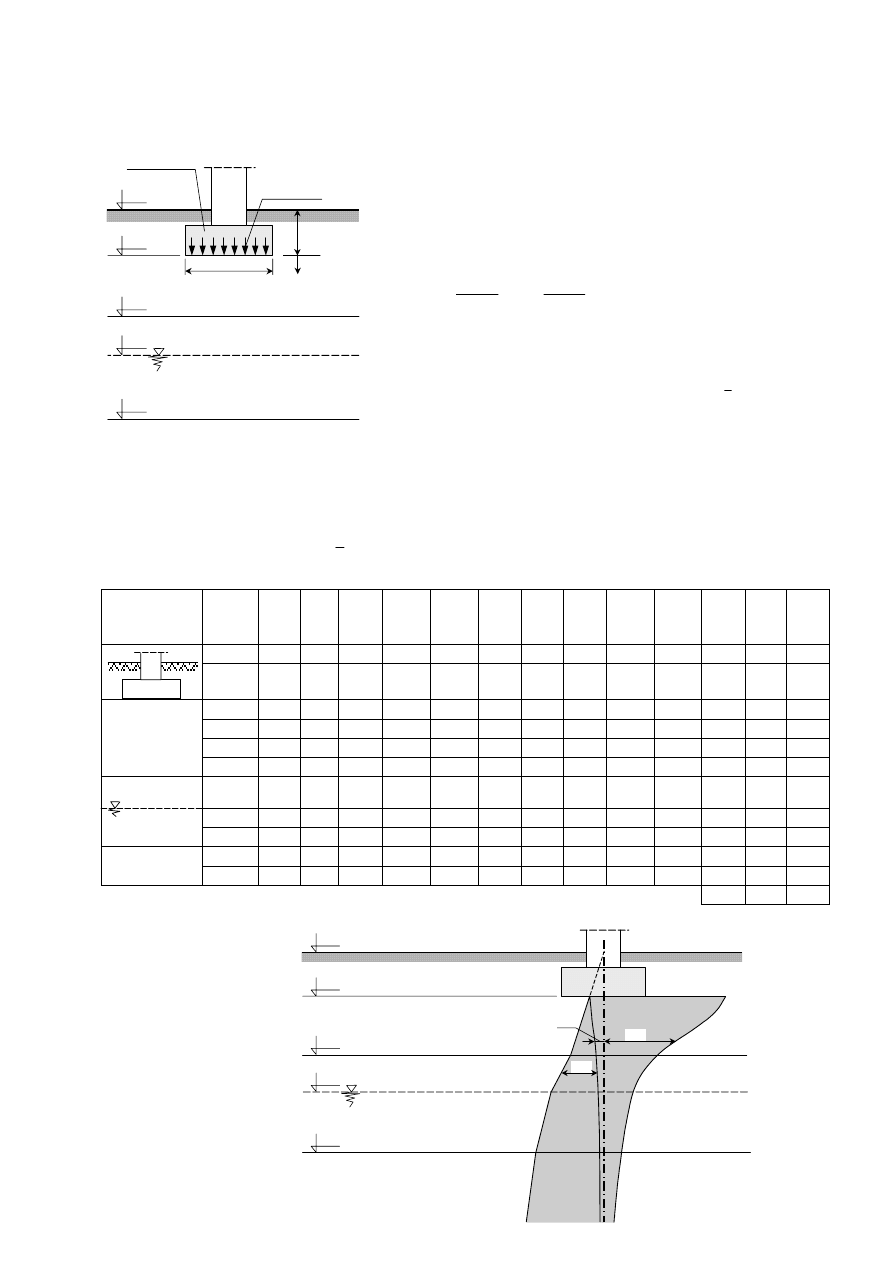
Wyznaczyć rozkład naprężeń w gruncie pod fundamentem przedstawionym na rysunku poniżej oraz
obliczyć wartość średnich osiadań podłoża gruntowego pod tym fundamentem.
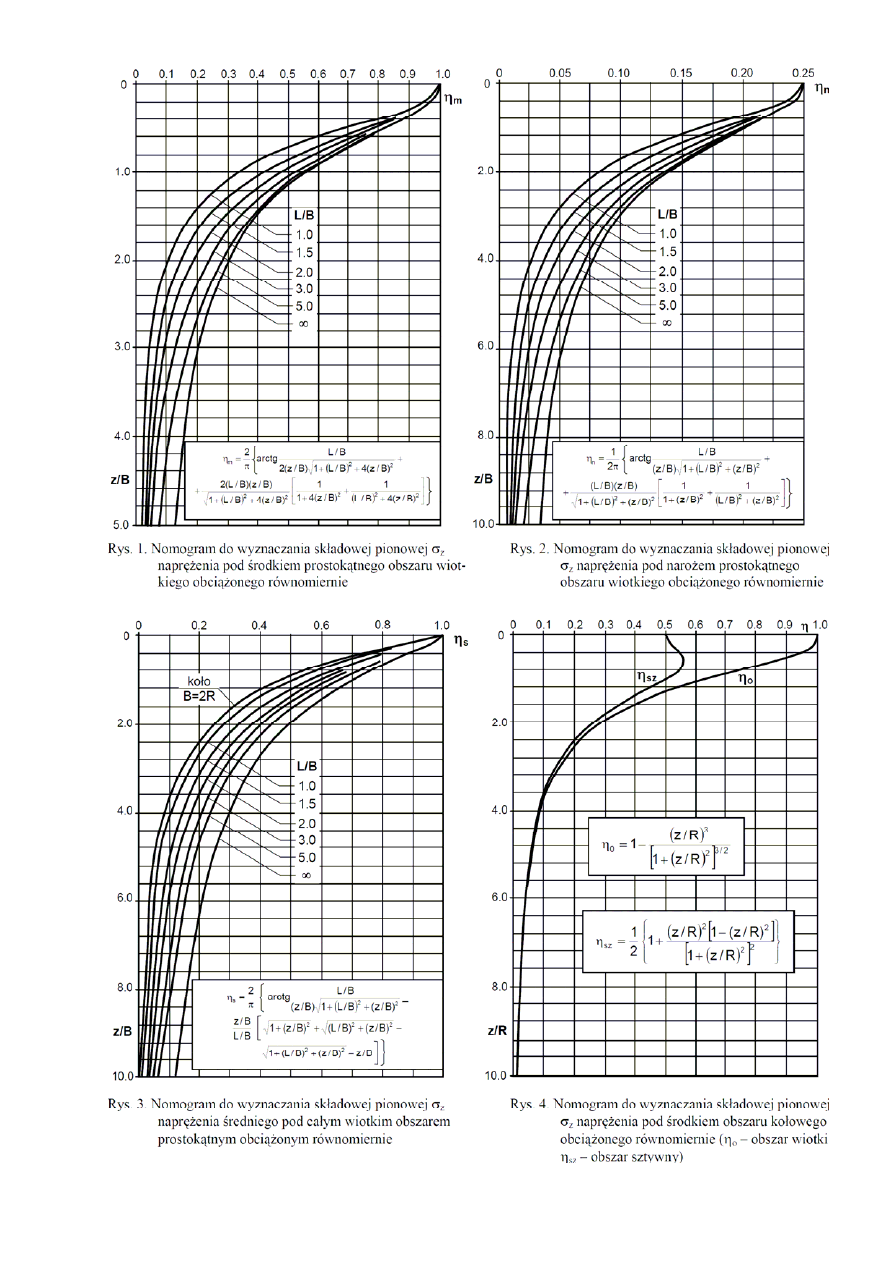
Rozkład naprężeń w gruncie pod fundamentem wyznaczony zostanie
z wykorzystaniem współczynnika
η
s
do wyznaczanie składowej pionowej
σ
z
naprężenia średniego pod całym wiotkim obszarem prostokątnym,
obciążonym równomiernie.
1) Obliczenie osiadań metodą odkształceń jednoosiowych
Wartość osiadania podłoża gruntowego obliczona zostanie ze wzoru:
∑
∑
⋅
⋅
+
⋅
=
+
=
i
i
szi
i
i
dzi
M
h
M
h
"
s
's
s
σ
λ
σ
0
[mm]
w którym:
s’ , s” - osiadania pierwotne i wtórne
M
0i
, M
i
– edometryczny moduł ściśliwości pierwotnej i wtórnej
h
i
– miąższość warstwy obliczeniowej (h
i
≤ B/2)
σ
dzi
– naprężenia dodatkowe na głębokości z
i
(
q
si
dzi
⋅
=
η
σ
)
σ
szi
– naprężenia wtórne na głębokości z
i
(
D
si
szi
q
⋅
=
η
σ
)
głębokość z
i
przyjmuje się w połowie miąższości h
i
.
λ – współczynnik uwzględniający stopień odprężenia gruntu w dnie
wykopu (
λ = 0 ÷ 1.0)
Sumowanie osiadań przeprowadza się do głębokości z
i
, na której spełnia się
warunek:
σ
dzi
< 0.3
⋅σ
γzi
.
Obliczenia pomocnicze:
q
D
=
γ
D
⋅D = 17.0⋅1.5 = 25.5 kPa, q = q - γ
D
⋅D = 300 – 25.5 = 274.5 kPa, L/B = 4.0/2.0 = 2.0, λ = 1.0
Tabela obliczeń naprężeń i osiadań
Profil
geotech.
Rzędna
spodu
warstwy
h
i
[m]
z
i
[m]
σ
γzi
[kPa]
0.3
σ
γzi
[kPa]
z
i
/B
η
si
σ
dzi
[kPa]
σ
szi
[kPa]
M
0i
[MPa]
M
i
[MPa]
i
's
[mm]
i
"
s
[mm]
i
s
[mm]
+1.5
0.0
0.0
0.0
0.0
25.5
7.7
0
1.0
274.5
25.5
60.0
75.0
0.0
0.0
0.0
-0.5 0.5
0.25
29.75
8.9 0.125
0.85
233.0
22.0 60.0 75.0 1.94 0.15 2.09
-1.0 0.5
0.75
38.25
11.5
0.375
0.72
198.0
18.0 60.0 75.0 1.65 0.12 1.77
-1.5 0.5
1.25
46.75
14.0
0.625
0.52
143.0
13.0 60.0 75.0 1.19 0.09 1.28
P
d
γ = 17 kN/m
3
-2.0 0.5
1.75
55.25
16.6
0.875
0.42
115.0
11.0 60.0 75.0 0.96 0.07 1.03
-3.0 1.0
2.50
69.00
20.7 1.25
0.30
82.0 8.0 35.0 47.0 2.34 0.17 2.51
-4.0 1.0
3.50
83.50
25.1 1.75
0.22
60.0 6.0 35.0 47.0 1.71 0.13 1.84
P
g,
γ =19 kN/m
3
γ’=10 kN/m
3
-5.0 1.0
4.50
93.50
28.1 2.25
0.15
41.0 4.0 35.0 47.0 1.17 0.09 1.26
-6.0 1.0
5.50
103.3
31.0 2.75
0.11
30.0 3.0 25.0 33.0 1.21 0.09 1.30
G
γ’ = 9.5 kN/m
3
-7.0 1.0
6.50
112.8
33.8 3.25
0.08 22.0 2.0 25.0 33.0 -
-
-
12.18
0.90 13.08
Rezultat: osiadania podłoża gruntowego wyniosą około s = 13.0 mm
zwg
Piasek drobny (P
d
)
γ = 17.0 kN/m
3
M
0
= 60 MPa, M = 75 MPa
stopa
B= 2m, L = 4m
0.00
+ 1.50
- 2.00
Piasek gliniasty (P
g
)
γ = 19.0 kN/m
3
γ’ = 10 kN/m
3
M
0
= 35 MPa, M = 47 MPa
Glina (G)
γ = 19.5 kN/m
3
γ’ = 9.5 kN/m
3
M
0
= 25 MPa, M = 33 MPa
- 3.00
- 5.00
D = 1.5 m
q = 300 kPa
B
zwg
z
Piasek drobny (P
d
)
γ = 17.0 kN/m
3
M
0
= 60 MPa, M = 75 MPa
0.00
+ 1.50
- 2.00
Piasek gliniasty (P
g
)
γ = 19.0 kN/m
3
γ’ = 10 kN/m
3
M
0
= 35 MPa, M = 47 MPa
Glina (G)
γ = 19.5 kN/m
3
γ’ = 9.5 kN/m
3
M
0
= 25 MPa, M = 33 MPa
- 3.00
- 5.00
zwg
σ
sz
σ
dz
σ
γz
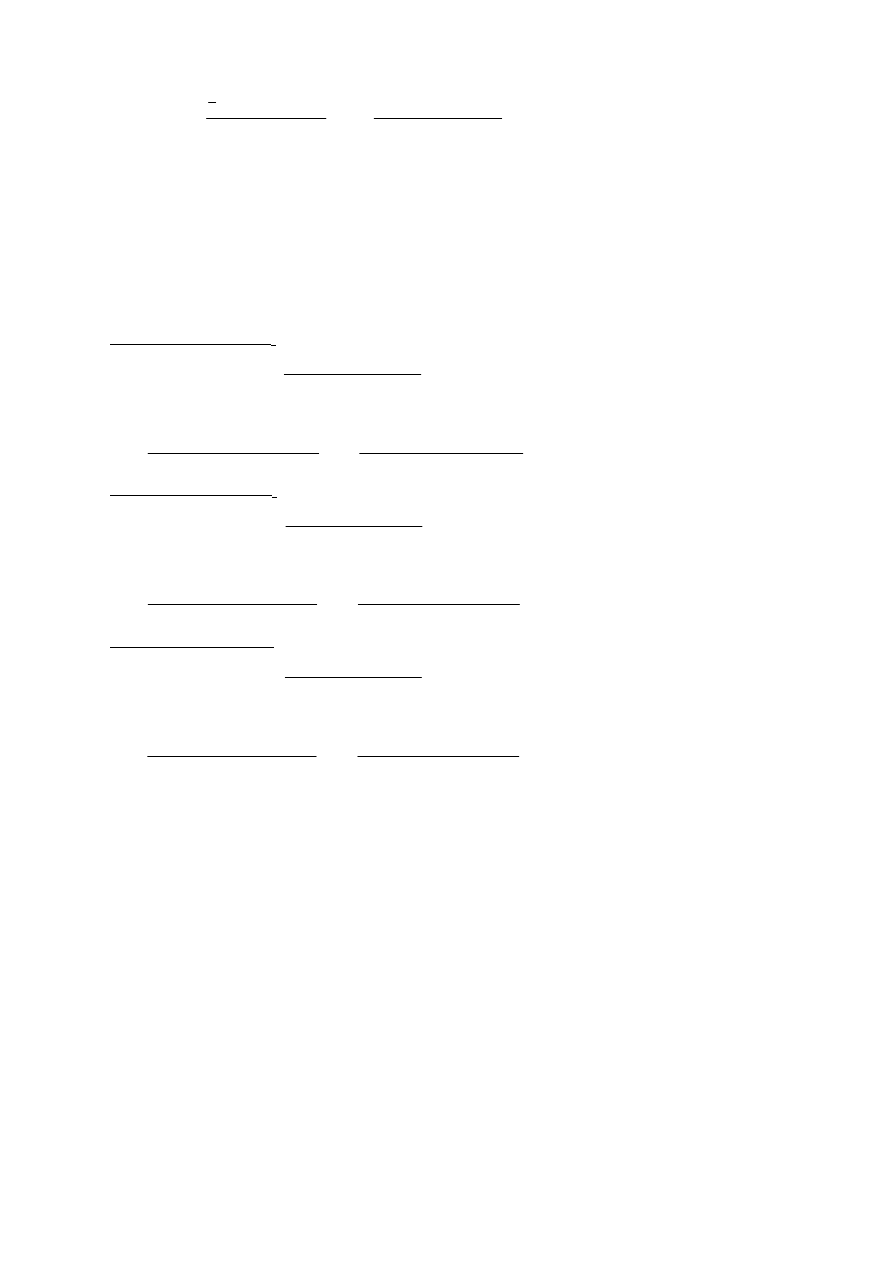
2) Obliczenie osiadań metodą odkształceń trójosiowych
Wartość osiadania podłoża gruntowego obliczona zostanie ze wzoru:
∑
∑
−
⋅
∆
⋅
⋅
⋅
+
−
⋅
∆
⋅
⋅
=
+
=
i
i
i
D
i
i
i
E
)
(
B
q
E
)
(
B
q
"
s
's
s
2
0
2
1
1
ν
ω
λ
ν
ω
[mm]
w którym:
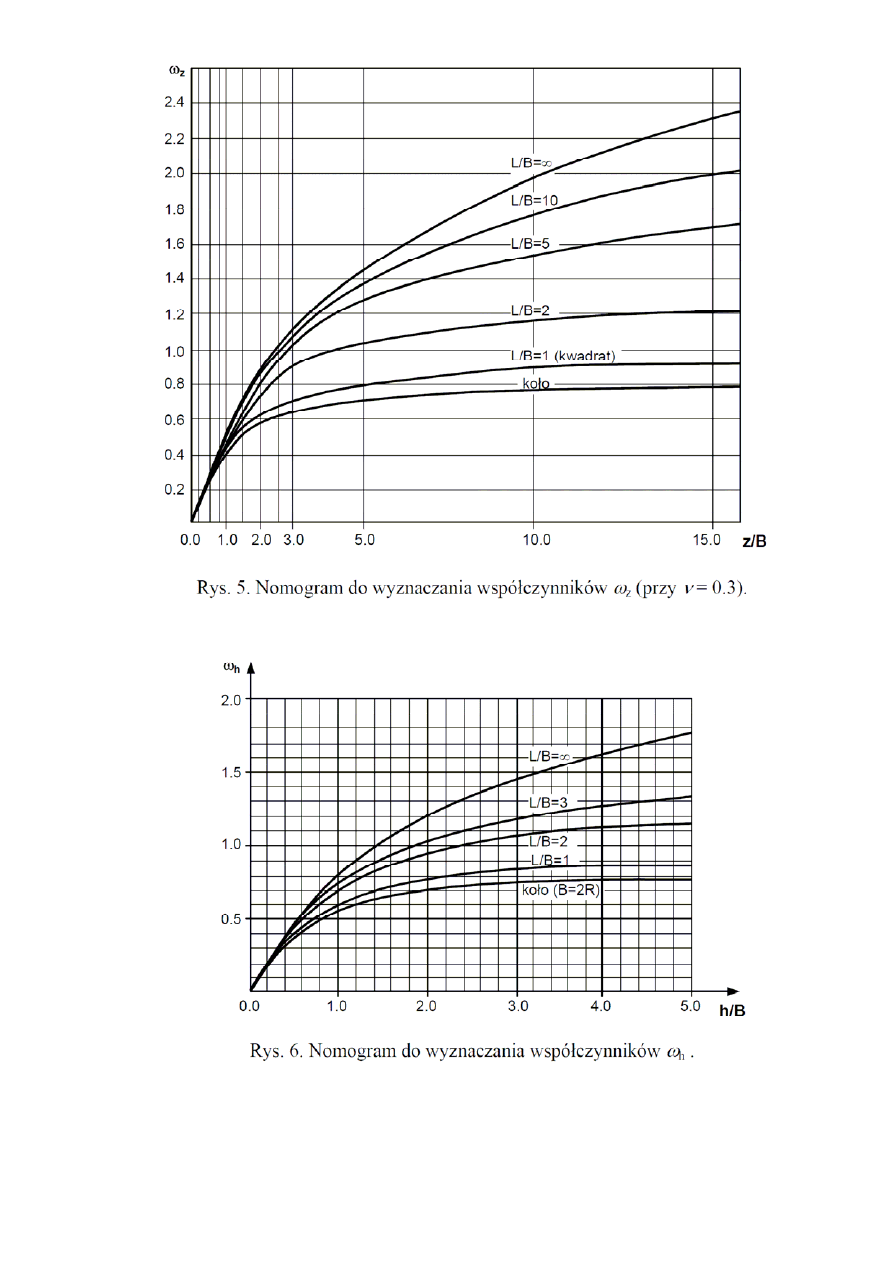
∆ω
i
=
ω
2i
–
ω
1i
(
ω
1i
– współczynnik wpływu dla stropu warstwy „i” na głębokości z
1i
,
ω
2i
– współczynnik wpływu dla
spągu warstwy „i” na głębokości z
2i
; współczynniki
ω
1
i
ω
2
zależą od z
1
/B i z
2
/B oraz L/B i odczyty-
wane są z nomogramu)
ν
i
– współczynnik Poissona dla gruntu w warstwie „i”,
E
0i
, E
i
- odpowiednio pierwotny i wtórny moduł odkształcenia ogólnego gruntu
B – szerokość fundamentu
a) osiadanie warstwy 1 – P
d
Przyjęto
ν
1
= 0.27
→
80
.
0
)
27
.
0
1
(
)
27
.
0
2
1
(
)
27
.
0
1
(
1
=
−
⋅
−
⋅
+
=
δ
→
48
60
80
.
0
01
=
⋅
=
E
MPa,
60
75
80
.
0
1
=
⋅
=
E
MPa
z
11
= 0
→ ω
11
= 0, z
21
= 2.0 m , z
21
/B = 2.0/2.0 = 1, L/B = 4.0/2.0 = 2
→
ω
21
= 0.47,
→
∆ω
1
= 0.47 – 0.0 = 0.47
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
37
0
98
4
60
27
0
1
47
0
0
2
5
25
0
1
48
27
0
1
47
0
0
2
5
274
2
2
1
.
.
)
.
(
.
.
.
.
)
.
(
.
.
.
s
5.35 mm
b) osiadanie warstwy 2 – P
g
Przyjęto
ν
2
= 0.30
→
74
.
0
)
30
.
0
1
(
)
30
.
0
2
1
(
)
30
.
0
1
(
2
=
−
⋅
−
⋅
+
=
δ
→
26
35
74
.
0
02
=
⋅
=
E
MPa,
35
47
74
.
0
2
=
⋅
=
E
MPa
z
21
= 2.0
→ ω
21
= 0.47, z
22
= 5.0 m , z
22
/B = 5.0/2.0 = 2.5, L/B = 2
→
ω
22
= 0.86,
→
∆ω
2
= 0.86 – 0.47 = 0.39
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
52
.
0
49
.
7
35
)
30
.
0
1
(
39
.
0
0
.
2
5
.
25
0
.
1
26
)
30
.
0
1
(
39
.
0
0
.
2
5
.
274
2
2
2
s
8.01 mm
c) osiadanie warstwy 3 – G
Przyjęto
ν
3
= 0.32
→
70
.
0
)
32
.
0
1
(
)
32
.
0
2
1
(
)
32
.
0
1
(
3
=
−
⋅
−
⋅
+
=
δ
→
5
.
17
25
70
.
0
03
=
⋅
=
E
MPa,
23
33
70
.
0
3
=
⋅
=
E
MPa
z
31
= 5.0
→ ω
31
= 0.86, z
32
=
∞ , z
32
/B =
∞, L/B = 2 →
ω
32
= 1.22,
→
∆ω
3
= 1.22 – 0.86 = 0.36
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
72
.
0
14
.
10
23
)
32
.
0
1
(
36
.
0
0
.
2
5
.
25
0
.
1
5
.
17
)
32
.
0
1
(
36
.
0
0
.
2
5
.
274
2
2
3
s
10.86 mm
d) osiadanie całkowite
s = s
1
+ s
2
+ s
3
= 5.35 + 8.01 + 10.86 = 24.22 mm
Wniosek:
Obliczenia metodą odkształceń trójosiowych dają większe wartości osiadań.
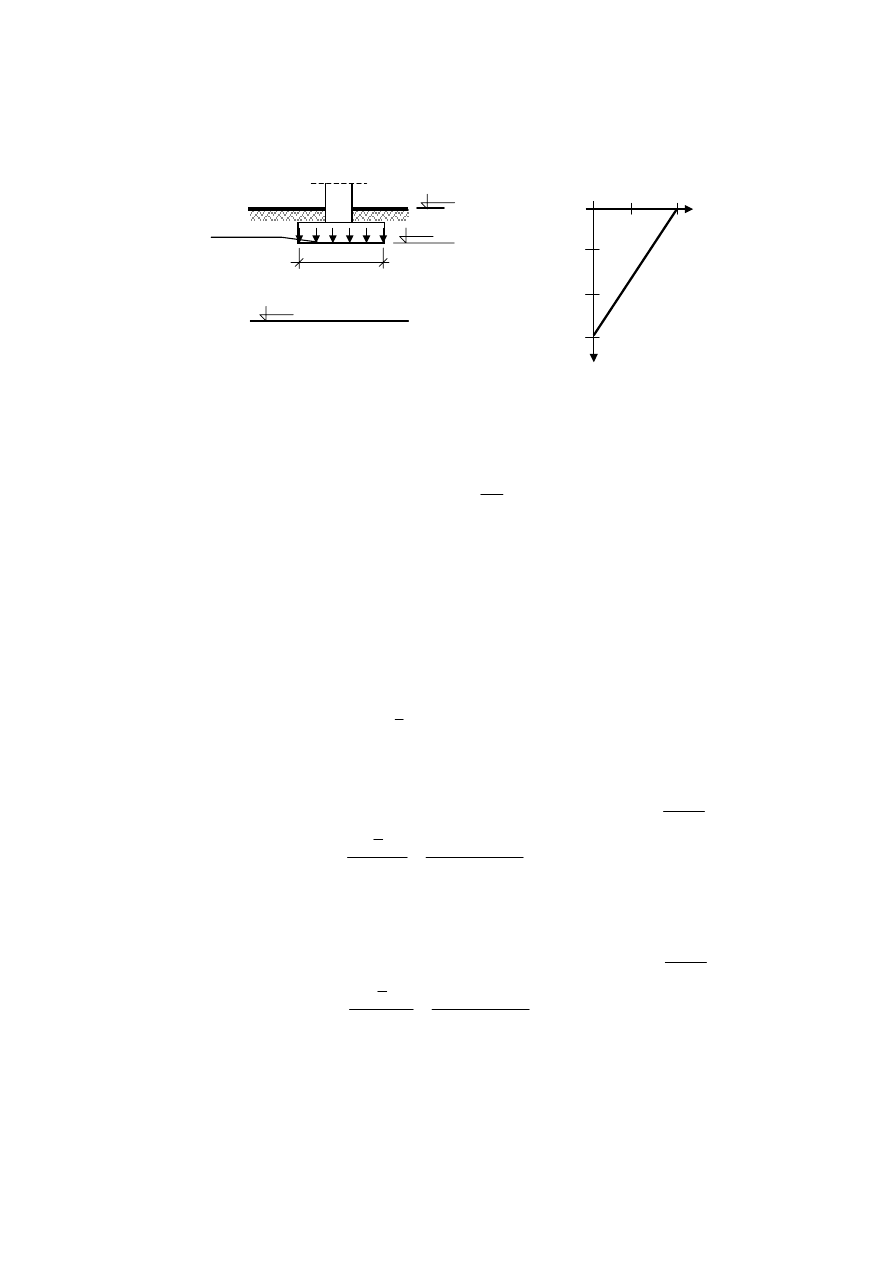
Zadanie 6.2
Obliczyć wartość osiadań podłoża gruntowego pod fundamentem przedstawionym na rysunku poniżej. Dla
uproszczenia przyjąć liniowy rozkład współczynnika
η
, jak pokazano na wykresie.
Rozwiązanie
Wzór na wartość
η
wyznaczono korzystając z prawa Talesa. Otrzymano następującą postać wzoru:
B
z
3
1
−
=
η
W związku z przyjęciem liniowego rozkładu współczynnika
η
nie trzeba dzielić podłoża gruntowego na
cienkie podwarstewki obliczeniowe. Można policzyć osiadania poszczególnych warstw rzeczywistych,
a następnie je zsumować.
W rozpatrywanym zadaniu nie mamy informacji o poziomie spągu warstwy drugiej. Należy to rozumieć, że
warstwa ta zalega do dużej głębokości. Jednak zasięg oddziaływania fundamentu sięga do ograniczonej
głębokości równej z
max
= 3B, na której wartość
η
równa jest zero.
Wartość z
max
wynosi: z
max
= 3B = 3
⋅ 2.0 m = 6.0 m
Wartość nacisków dodatkowych na grunt: q = 200 – 1.0
⋅ 18.0 = 182.0 kPa
1) osiadanie warstwy pierwszej
wysokość warstwy: h
1
= 3.0 m,
głębokość środka warstwy pod poziomem fundamentu: z
1
= 1.5 m, stąd
75
.
0
0
.
2
3
5
.
1
1
1
=
⋅
−
=
η
wartość osiadania warstwy:
mm
m
M
h
q
s
5
.
20
0205
.
0
10
20
0
.
3
182
75
.
0
3
01
1
1
1
=
=
⋅
⋅
⋅
=
⋅
⋅
=
η
2) osiadanie warstwy drugiej
wysokość warstwy: h
2
= z
max
– h
1
= 6.0 - 3.0 = 3.0 m,
głębokość środka warstwy pod poziomem fundamentu: z
2
= 4.5 m, stąd
25
.
0
0
.
2
3
5
.
4
1
2
=
⋅
−
=
η
wartość osiadania warstwy:
mm
m
M
h
q
s
55
.
4
00455
.
0
10
30
0
.
3
182
25
.
0
3
02
2
2
2
=
=
⋅
⋅
⋅
=
⋅
⋅
=
η
3) osiadanie całkowite podłoża pod fundamentem:
s = s
1
+ s
2
= 20.5 + 4.55 = 25.05 mm
± 0.00
q = 200 kPa
γ = 18 kN/m
3
M
0
= 20 MPa
B = 2.0 m
- 4.00
η
z/B
0
1
2
1
0.5
3
- 1.00
γ = 20 kN/m
3
M
0
= 30 MPa
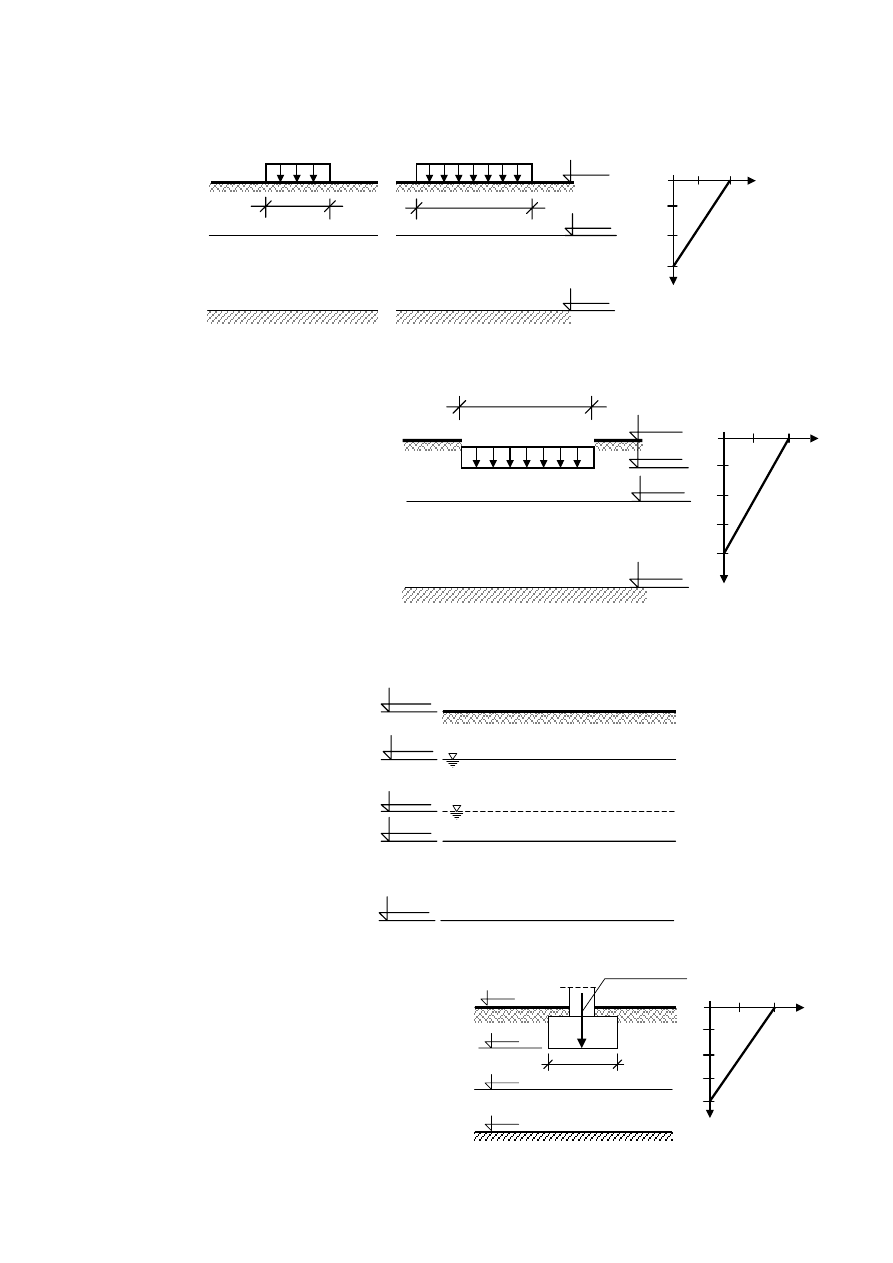
Zadania do rozwiązania
Zad. 6.3.
Który fundament osiądzie więcej? Spróbować powiedzieć najpierw bez obliczeń.
Policzyć wartości osiadań fundamentów. Rozkład
η przyjąć liniowy do głębokości z = 3B.
Odp.: więcej osiądzie fundament B, s
A
= 38.07 mm, s
B
= 57.8 mm.
Zad. 6.4.
Policzyć osiadanie warstwy
G
π
od nacisków dodatkowych q
przekazywanych przez fundament.
Rozkład
η przyjąć liniowy do
głębokości 4B.
Odp.: s
G
π
= 27.96 mm
Zad. 6.5.
Policzyć osiadanie warstwy namułu w wyniku obniżenia zwierciadła wody gruntowej
o 4.0 m. Przyjąć, że obniżenie wody wykonano na znacznym obszarze, stąd
η = 1 w całej
miąższości namułu.
Odp.: s
Nm
= 120 mm
Zad. 6.6.
Jaką szerokość powinna mieć
ława fundamentowa, aby osiadania podłoża
gruntowego nie przekroczyły 20 mm?
Obliczenia wykonać metodą odkształceń
jednoosiowych, przyjmując liniowy rozkład
współczynnika
η, jak pokazano na
wykresie.
Odp.: B
≥ 3.0 m.
- 2.0
q = 250 kPa
B = 3,0 m
± 0.0
- 6.0
M
0
= 25 MPa
z/B
0
1
2
3
1
0.5
η
- 1.0
G
π
,
Pd,
γ = 17 kN/m
3
4
podłoże nieściśliwe
B
- 2.0
q = 200
B = 3,0 m
A
q = 200
B = 1,5 m
± 0.0
- 6.0
M
0
= 10 MPa
M
0
= 20 MPa
M
0
= 10 MPa
M
0
= 20 MPa
z/B
0
1
2
3
1
0.5
η
podłoże nieściśliwe
podłoże nieściśliwe
± 0.0
- 2.0
- 6.0
- 7.0
P
d
,
γ = 18 kN/m
3
γ‘ = 11 kN/m
3
γ
sr
= 21 kN/m
3
zwg (pierw.)
zwg (obniż.)
- 10.0
Nm, M
0
= 1,0 MPa
η
z/B
0
1
2
4
1
0.5
± 0.00
- 3.5
M
0
= 25 MPa
- 1.0
3
B= ?
M
0
= 15 MPa
- 7.0
podłoże nieściśliwe
N = 250 kN/m?
