1

Mechanika ogólna

Wykład nr 13
Zjawisko tarcia. Prawa tarcia.

2

Więzy z tarciem

n

W więzach, w których nie
występuje tarcie, reakcja jest
prostopadła do płaszczyzny
styku ciał (nacisk).

n

W więzach z tarciem
dochodzi jeszcze jedna
reakcja, równoległa do
płaszczyzny styku.

mg

N

mg

N

T

P

3

Prawa tarcia statycznego
Coulomba i Morena

n

Siła tarcia jest zawsze przeciwna do

występującego lub ewentualnego

ruchu.

n

Wielkość siły tarcia jest niezależna

od pola powierzchni stykających się

ciał, zależy jedynie od rodzaju

powierzchni.

n

Zależność między naciskiem i siłą

tarcia:

T

N

µ

= ⋅

4

Współczynnik tarcia

Rodzaj powierzchni

µ

Stal-stal

0,15

Stal-żeliwo

0,18

Żeliwo-żeliwo

0,45

Metal-drewno

0,5-0,6

Drewno-drewno

0,65

Skóra-metal

0,6

5

Tarcie statyczne i
kinetyczne

n

Tarcie występuje w przypadku

układów poruszających

(kinetyczne) lub w układach,

w których ruch jest potencjalnie

możliwy, ale jeszcze do niego

nie dochodzi (statyczne).

6

Tarcie statyczne

n

Tarcie statyczne

przeciwdziałające wystąpieniu

ruchu zwiększa się w wyniku

przyłożenia siły od 0 do wartości

maksymalnej (tarcie całkowicie

rozwinięte).

7

Kąt tarcia

n

Kąt między reakcją pionową a siłą
tarcia nazywany jest kątem tarcia:

=tg

T

N

µ

φ

=

mg

N

mg

N

T

P

R

mg

N

T

P

R

8

Stożek tarcia

n

Linia działania wypadkowej reakcji zawarta
jest wewnątrz, lub w przypadku tarcia
całkowicie rozwiniętego, na powierzchni
stożka nazywanego stożkiem tarcia.

mg

N

T

P

R

mg

N

T

P

R

9

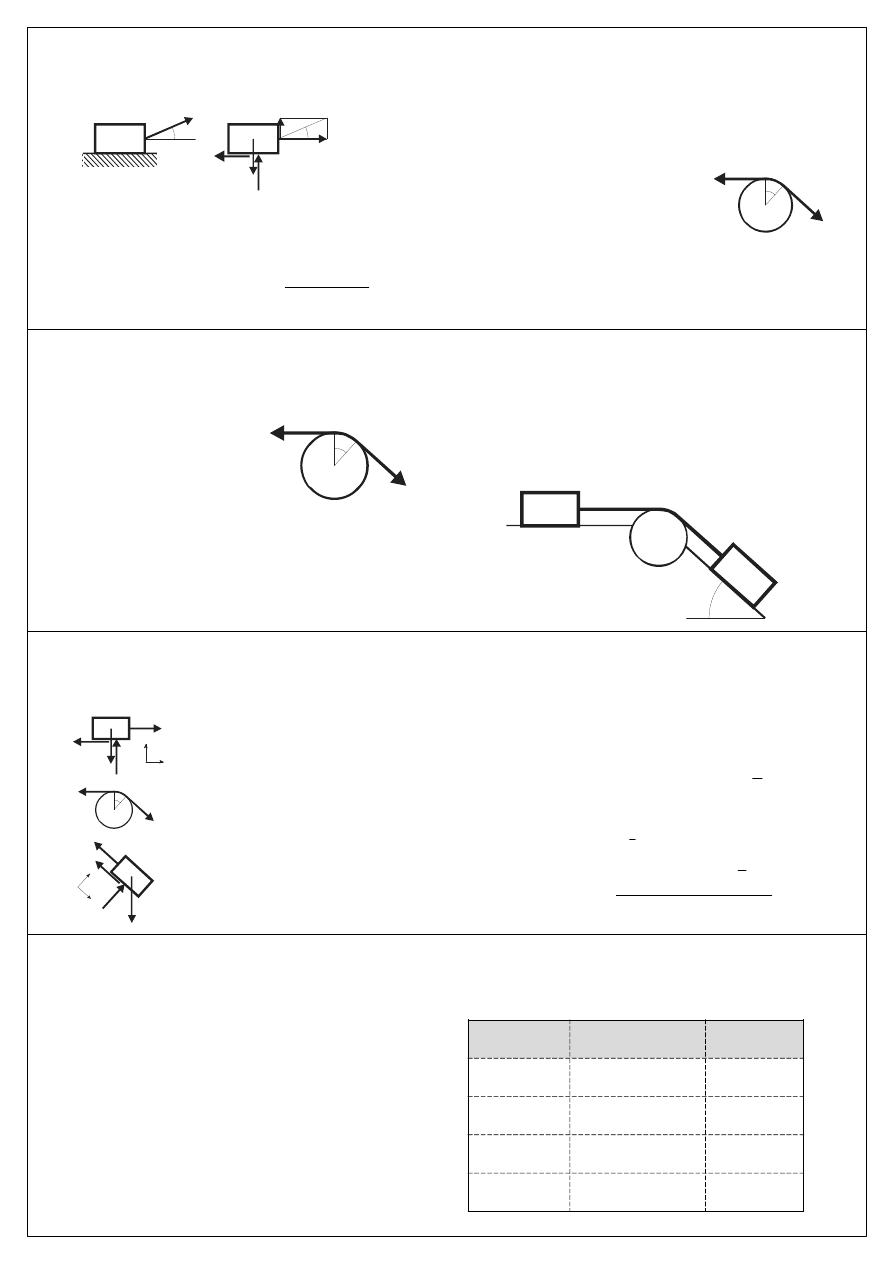
Tarcie ślizgowe - przykład

α

µ

m

α

mg

N

T

Pcos

α

Psin

α

P

0 :

cos

0

X

P

T

α

=

− =

∑

0 :

sin

0

Y

P

N

m g

α

=

+ − ⋅ =

∑

T

N

µ

= ⋅

n

Prawo tarcia:

sin

N

m g

P

α

= ⋅ −

(

)

sin

cos

m g

P

P

µ

α

α

⋅ −

=

sin

cos

m g

P

µ

µ

α

α

⋅ ⋅

=

+

10

Tarcie cięgien
o bloczek nieruchomy

(1)

n

Zależność miedzy siłami w cięgnie

przy całkowicie rozwiniętym

tarciu:

gdzie S

1

jest siła działającą

w cięgnie w kierunku

ewentualnego ruchu.

1

2

S

S

e

µα

= ⋅

S

1

S

2

α

11

Tarcie cięgien
o bloczek nieruchomy

(2)

n

Zależność odwrotna:

n

Kąt

α nazywany jest kątem

opasania i musi być wyrażany w

radianach.

2

1

S

S e

µα

−

= ⋅

S

1

S

2

α

12

Tarcie cięgien – przykład

(1)

n

Obliczyć masę graniczną m

2

, po

przekroczeniu której rozpocznie się ruch.

Miara kąta

α

=30

o

.

α

m

1

m

2

µ

1

µ

2

µ

3

13

Tarcie cięgien – przykład

(2)

T

1

m g

1

N

1

S

1

X

Y

S

1

S

2

α

m

2

S

2

m g

2

N

2

T

2

X

Y

2

2

1

S

S e

µ α

= ⋅

1

1

0 :

0

X

S

T

=

− =

∑

1

1

0 :

0

Y

N

m g

=

− ⋅ =

∑

1

1

1

T

N

µ

= ⋅

2

2

2

0 :

sin

0

X

m g

S

T

α

=

− − =

∑

2

2

0 :

cos

0

Y

N

m g

α

=

−

=

∑

2

3

2

T

N

µ

=

⋅

I

II

III

14

Przykład – rozwiązanie

1

1

1

1

1

S

N

m g

µ

µ

= ⋅

= ⋅ ⋅

2

6

2

1

1

S

m g e

π

µ

µ

= ⋅ ⋅ ⋅

2

6

2

1

1

3

2

sin

cos

0

m g

m g e

m g

π

µ

α µ

µ

α

− ⋅ ⋅ ⋅

− ⋅

=

2

6

1

1

2

3

sin

cos

m g e

m

g

g

π

µ

µ

α µ

α

⋅ ⋅ ⋅

=

− ⋅

I

II

III

1

1

S

T

=

1

1

N

m g

=

⋅

1

1

1

T

N

µ

= ⋅

2

2

1

S

S e

µ α

= ⋅

2

3

2

T

N

µ

=

⋅

2

2

cos

N

m g

α

=

2

2

2

sin

0

m g

S

T

α

− − =

15

Opór przy toczeniu

n

W rzeczywistych układach, w
przypadku ciał o przekrojach okrągłych,
reakcja pionowa przesunięta jest w
kierunku ewentualnego ruchu.

n

Wynika to z nierównomiernego
rozkładu sił pod ciałem. Mimo założenia
kołowości przekroju, w rzeczywistości
styk nie jest punktowy.

16

Wartości współczynnika
oporu toczenia

Koło

Rodzaj podłoża

f [cm]

Drewno

Drewno

0,05-0,8

Drewno

Stal

0,03-0,04

Stal

Stal

0,001-0,005

Żeliwo

Żeliwo

0,005

17

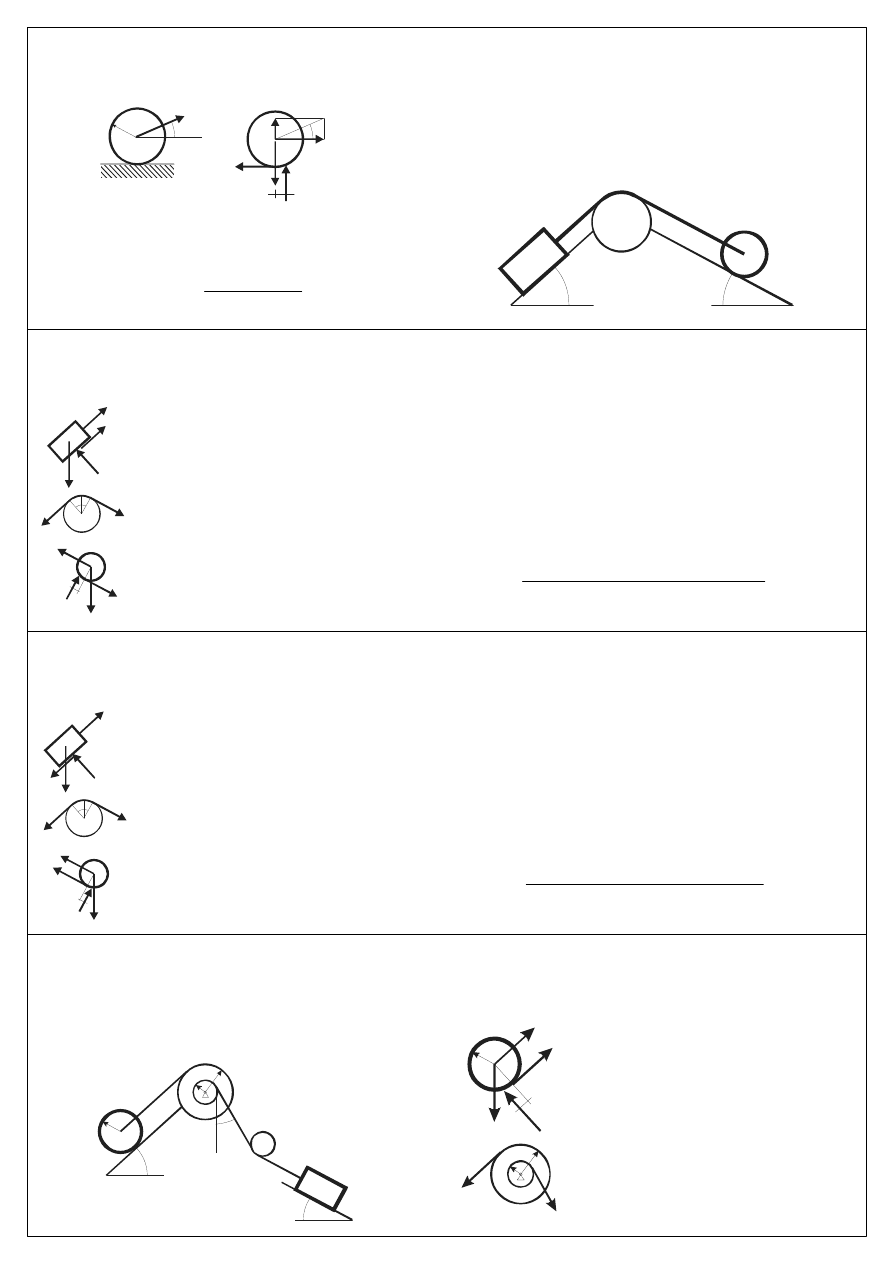
Opór toczenia - przykład

α

m

α

mg

N

T

Pcos

α

Psin

α

P

f

f

A

r

0 :

sin

0

Y

P

N

m g

α

=

+ − ⋅ =

∑

0 :

cos

0

A

M

P

r

N f

α

=

⋅ − ⋅ =

∑

sin

N

m g

P

α

= ⋅ −

(

)

cos

sin

0

P

r

m g

P

f

α

α

⋅ −

⋅ −

⋅ =

cos

sin

m g f

P

r

f

α

α

⋅ ⋅

=

⋅

+

18

Przykład A

α

m

2

µ

2

m

1

µ

1

β

f

n

Określić zakres, w jakim ma mieścić się
wielkość masy m

2

, aby nie wystąpił ruch.

α

=30

o

,

β

=45

o

19

Przykład A – wariant I
(ruch w lewo)

S

1

m g

1

N

1

T

1

S

1

S

2

α β

(

)

2

2

1

S

S e

µ α β

−

+

= ⋅

1

1

1

0 :

sin

0

X

m g

S

T

α

=

⋅ ⋅

− − =

∑

1

1

0 :

cos

0

Y

N

m g

α

=

− ⋅ ⋅

=

∑

1

1

1

T

N

µ

= ⋅

2

2

2

0 :

sin

0

A

M

N

f

S

r

m g

r

α

=

⋅ − ⋅ +

⋅ =

∑

2

2

0 :

cos

0

Y

N

m g

β

=

−

=

∑

S

2

m g

2

f

N

2

T

2

A

20

Wariant I - rozwiązanie

1

1

1

1

sin

cos

S

m g

m g

α µ

α

=

⋅ ⋅

− ⋅ ⋅ ⋅

1

1

cos

N

m g

α

=

⋅ ⋅

1

1

1

cos

T

m g

µ

α

= ⋅ ⋅ ⋅

(

)

(

)

2

2

1

1

1

sin

cos

S

m g

m g

e

µ α β

α µ

α

−

+

=

⋅ ⋅

− ⋅ ⋅ ⋅

⋅

(

)

(

)

2

1

1

1

2 min

sin

cos

cos

sin

m g

m g

e

r

m

g

f

g

r

µ α β

α µ

α

β

α

−

+

⋅ ⋅

− ⋅ ⋅ ⋅

⋅

⋅

=

⋅ +

⋅

2

2

cos

N

m g

β

=

21

Przykład A – wariant II
(ruch w prawo)

S

1

m g

1

N

1

T

1

S

1

S

2

α β

S

2

m g

2

f

N

2

T

2

A

(

)

2

2

1

S

S e

µ α β

+

= ⋅

1

1

1

0 :

sin

0

X

m g

S

T

α

=

⋅ ⋅

− + =

∑

1

1

0 :

cos

0

Y

N

m g

α

=

− ⋅ ⋅

=

∑

1

1

1

T

N

µ

= ⋅

2

2

2

0 :

sin

0

A

M

N

f

S

r

m g

r

α

=

⋅ + ⋅ −

⋅ =

∑

2

2

0 :

cos

0

Y

N

m g

β

=

−

=

∑

22

Wariant II - rozwiązanie

1

1

1

1

sin

cos

S

m g

m g

α µ

α

=

⋅ ⋅

+ ⋅ ⋅ ⋅

1

1

cos

N

m g

α

=

⋅ ⋅

1

1

1

cos

T

m g

µ

α

= ⋅ ⋅ ⋅

(

)

(

)

2

2

1

1

1

sin

cos

S

m g

m g

e

µ α β

α µ

α

+

=

⋅ ⋅

+ ⋅ ⋅ ⋅

⋅

(

)

(

)

2

1

1

1

2 max

sin

cos

sin

cos

m g

m g

e

r

m

g

r

g

f

µ α β

α µ

α

α

β

+

⋅ ⋅

+ ⋅ ⋅ ⋅

⋅

⋅

=

⋅ −

⋅

2

2

cos

N

m g

β

=

23

Przykład B-I

(1)

n

Określić maksimum masy m

1

, przy którym nie

wystąpi jeszcze ruch.

α

m

2

m

1

µ

1

γ

f

µ

2

β

r

r

1

r

2

24

Przykład B-I

(2)

1

1

1

0 :

sin

0

A

M

N

f

S r

m g

r

α

=

⋅ + ⋅ −

⋅ =

∑

1

1

0 :

cos

0

Y

N

m g

α

=

−

=

∑

m

1

r

S

1

m

1

g

f

A

T

1

N

1

1

1

2

2

0 :

0

O

M

S r

S

r

=

⋅ − ⋅ =

∑

S

2

S

1

r

1

r

2

25

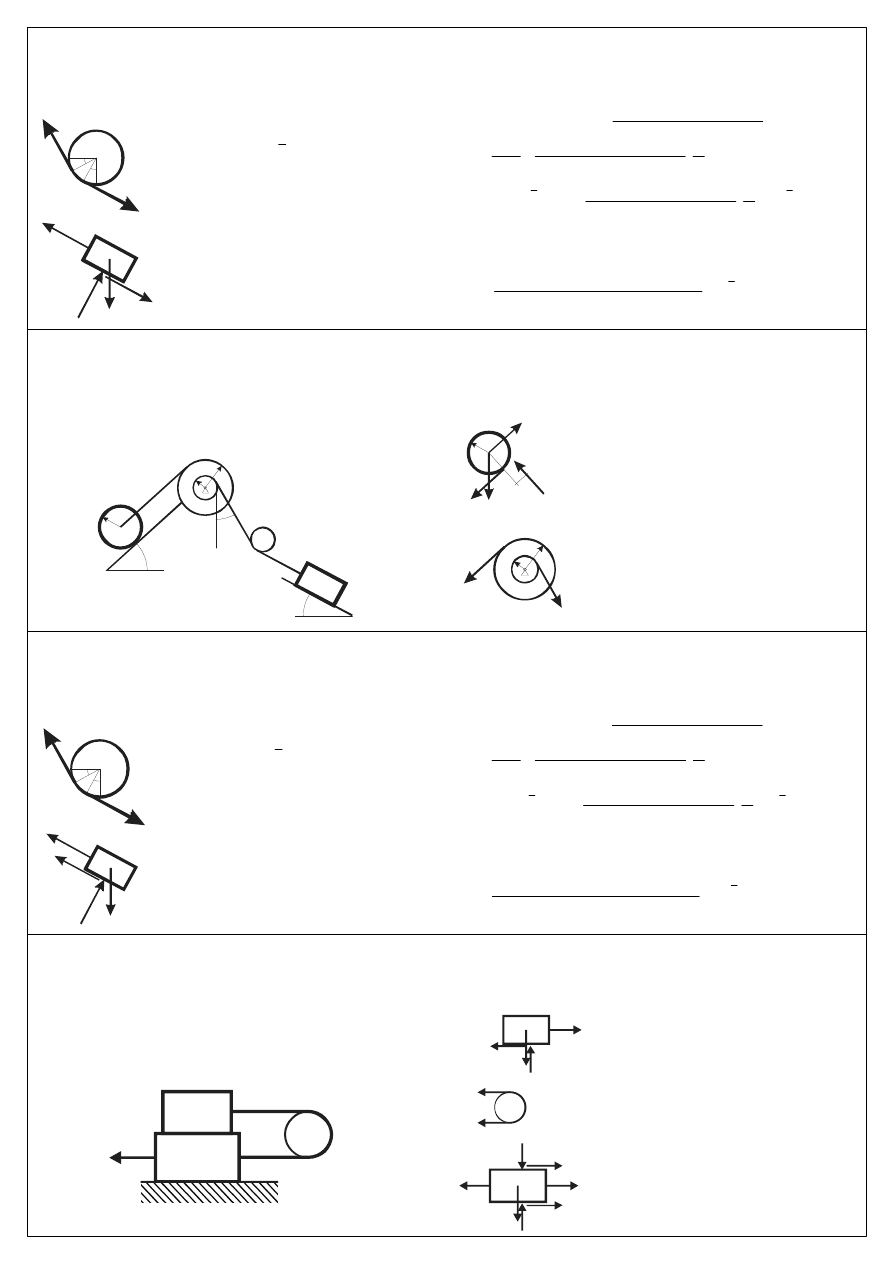
Przykład B-I

(3)

S

3

S

2

β

γ

(

)

1

2

3

2

S

S

e

π

µ

α β





−

− +









= ⋅

2

3

3

0 :

sin

0

X

m

g

S

T

γ

=

⋅ ⋅

− + =

∑

3

2

0 :

cos

0

Y

N

m

g

γ

=

−

⋅ ⋅

=

∑

3

2

3

T

N

µ

=

⋅

m

2

S

3

m

2

g

T

3

N

3

26

Przykład B-I - rozwiązanie

1

1

1

sin

cos

m g

r

m g

f

S

r

α

α

⋅ −

⋅

=

1

1

cos

N

m g

α

=

1

1

1

1

1

2

2

2

sin

cos

S r

m g

r

m g

f

r

S

r

r

r

α

α

⋅

⋅ −

⋅

=

=

⋅

(

)

(

)

1

1

2

2

1

1

1

3

2

2

sin

cos

m g

r

m g

f

r

S

S

e

e

r

r

π

π

µ

α β

µ

α β

α

α









−

− +

−

− +

















⋅ −

⋅

=

⋅

=

⋅ ⋅

(

)

(

)

(

)

1

2

2

2

2

2

1

1

sin

cos

sin

cos

m

g

m

g

r r

m

e

g

r

g

f

r

π

µ

α β

γ µ

γ

α

α





− +









⋅ ⋅

+

⋅

⋅ ⋅

⋅ ⋅

=

⋅

⋅ −

⋅

⋅

3

2

cos

N

m

g

γ

=

⋅ ⋅

3

2

2

cos

T

m

g

µ

γ

=

⋅

⋅ ⋅

27

Przykład B-II

(1)

n

Określić minimum masy m

1

, przy którym nie

wystąpi jeszcze ruch.

α

m

2

m

1

µ

1

γ

f

µ

2

β

r

r

1

r

2

28

Przykład B-II

(2)

1

1

1

0 :

sin

0

A

M

N

f

S r

m g

r

α

=

⋅ − ⋅ +

⋅ =

∑

1

1

0 :

cos

0

Y

N

m g

α

=

−

=

∑

1

1

2

2

0 :

0

O

M

S r

S

r

=

⋅ − ⋅ =

∑

m

1

r

S

1

m

1

g

f

A

T

1

N

1

S

2

S

1

r

1

r

2

29

Przykład B-II

(3)

(

)

1

2

3

2

S

S

e

π

µ

α β





− +









= ⋅

S

3

S

2

β

γ

m

2

S

3

m

2

g

T

3

N

3

2

3

3

0 :

sin

0

X

m

g

S

T

γ

=

⋅ ⋅

− − =

∑

3

2

0 :

cos

0

Y

N

m

g

γ

=

−

⋅ ⋅

=

∑

3

2

3

T

N

µ

=

⋅

30

Przykład B-II - rozwiązanie

1

1

1

cos

sin

m g

f

m g

r

S

r

α

α

⋅ +

⋅

=

1

1

cos

N

m g

α

=

1

1

1

1

1

2

2

2

cos

sin

S r

m g

f

m g

r r

S

r

r

r

α

α

⋅

⋅ +

⋅

=

=

⋅

(

)

(

)

1

1

2

2

1

1

1

3

2

2

cos

sin

m g

f

m g

r r

S

S

e

e

r

r

π

π

µ

α β

µ

α β

α

α









− +

− +

















⋅ +

⋅

=

⋅

=

⋅ ⋅

(

)

(

)

(

)

1

2

2

2

2

2

1

1

sin

cos

cos

sin

m

g

m

g

r r

m

e

g

f

g

r

r

π

µ

α β

γ µ

γ

α

α





−

− +









⋅ ⋅

−

⋅

⋅ ⋅

⋅ ⋅

=

⋅

⋅ +

⋅ ⋅

3

2

cos

N

m

g

γ

=

⋅ ⋅

3

2

2

cos

T

m

g

µ

γ

=

⋅

⋅ ⋅

31

Przykład C-I

(1)

n

Określić graniczną wartość siły, przy

przekroczeniu której może wystąpić

ruch.

m

1

µ

1

µ

3

m

2

µ

2

P

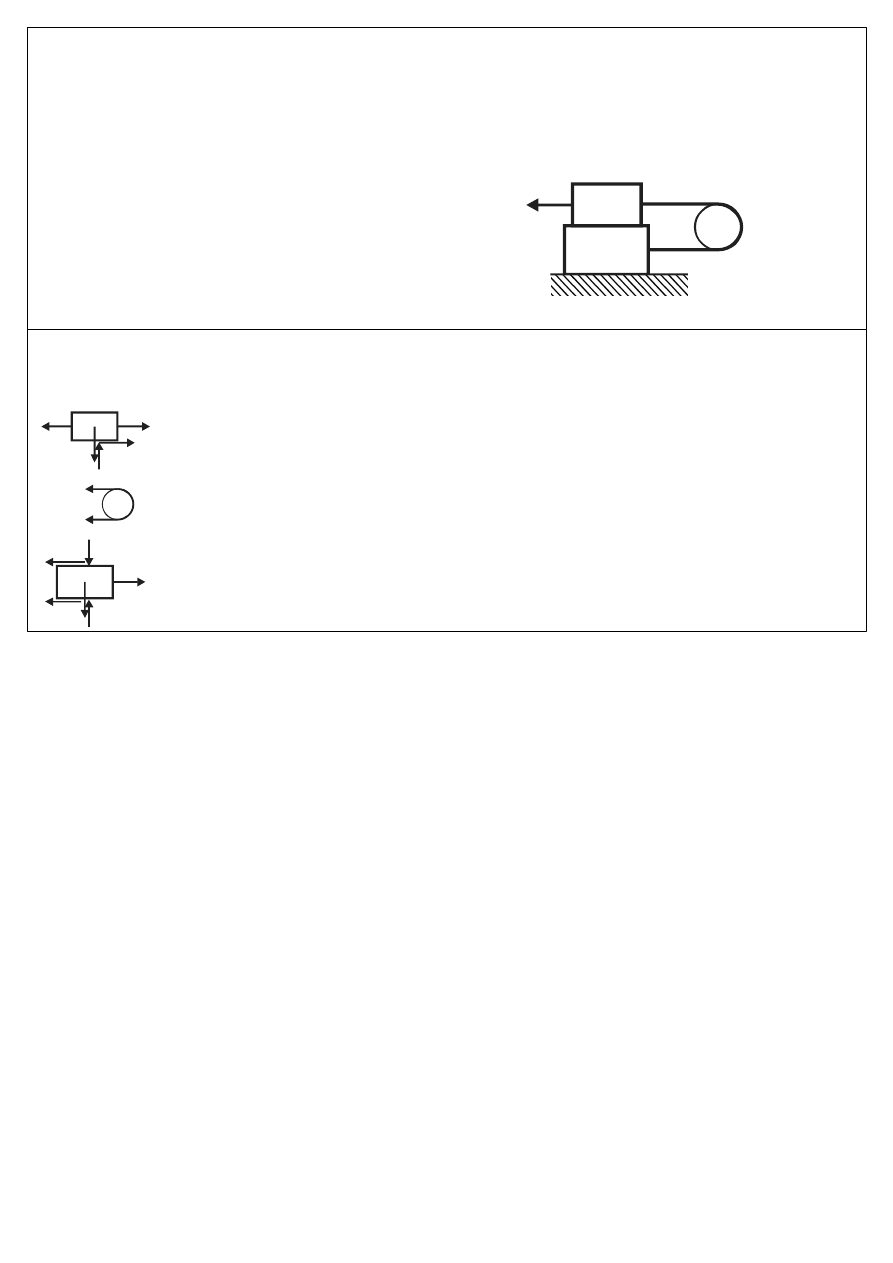
32

Przykład C-I

(2)

3

2

1

S

S e

µ π

= ⋅

1

1

0 :

0

X

S

T

=

− =

∑

1

1

0 :

0

Y

N

m g

=

− ⋅ =

∑

1

1

1

T

N

µ

= ⋅

T

1

m g

1

N

1

S

1

S

1

S

2

1

2

2

0 :

0

X

P T

T

S

=

− − −

=

∑

2

2

1

0 :

0

Y

N

m

g

N

=

−

⋅ −

=

∑

P

N

1

T

1

S

2

m g

2

N

2

T

2

2

2

2

T

N

µ

=

⋅

33

Przykład C-I - rozwiązanie

3

2

1

1

S

m g e

µ π

µ

= ⋅ ⋅ ⋅

1

1

1

S

m g

µ

= ⋅ ⋅

1

1

N

m g

=

⋅

1

1

1

T

m g

µ

= ⋅ ⋅

(

)

3

1

1

1

2

2

1

1

1

2

P

m g

m

g

m g

m g e

µ π

µ

µ

µ

= ⋅ ⋅ +

⋅

⋅ + ⋅

+ ⋅ ⋅ ⋅

2

2

1

N

m

g

m g

=

⋅ +

⋅

(

)

2

2

2

1

T

m

g

m g

µ

=

⋅

⋅ + ⋅

34

Przykład C-II

(1)

n

Określić graniczną wartość siły, przy

przekroczeniu której może wystąpić

ruch.

m

1

µ

1

µ

3

m

2

µ

2

P

35

Przykład C-II

(2)

T

1

m g

1

N

1

S

1

P

S

1

S

2

N

1

T

1

S

2

m g

2

N

2

T

2

3

2

1

S

S e

µ π

−

= ⋅

1

1

0 :

0

X

P

S

T

=

− − =

∑

1

1

0 :

0

Y

N

m g

=

− ⋅ =

∑

1

1

1

T

N

µ

= ⋅

2

1

2

0 :

0

X

S

T

T

=

− − =

∑

2

2

1

0 :

0

Y

N

m

g

N

=

−

⋅ −

=

∑

2

2

2

T

N

µ

=

⋅

36

Przykład C-II - rozwiązanie

(

)

(

)

3

1

1

1

2

2

1

S

m g

m

g

m g

e

µ π

µ

µ

=

⋅ ⋅ +

⋅

⋅ +

⋅

⋅

(

)

(

)

3

1

1

2

2

1

1

1

P

m g

m

g

m g

e

m g

µ π

µ

µ

µ

=

⋅ ⋅ +

⋅

⋅ +

⋅

⋅

+ ⋅ ⋅

1

1

N

m g

=

⋅

1

1

1

T

m g

µ

= ⋅ ⋅

(

)

2

1

1

2

2

1

S

m g

m

g

m g

µ

µ

= ⋅ ⋅ +

⋅

⋅ +

⋅

2

2

1

N

m

g

m g

=

⋅ +

⋅

(

)

2

2

2

1

T

m

g

m g

µ

=

⋅

⋅ + ⋅