WYKŁAD 13

1

POMIARY CZĘSTOTLIWOŚCI I CZASU

ANALOGOWE

Oscyloskopowe

- z użyciem liniowej podstawy czasu

- z użyciem sinusoidalnej podstawy

czasu

Integracyjne

Rezonansowe

Heterodynowe

WYKŁAD 13

2

POMIARY CZĘSTOTLIWOŚCI I CZASU

CYFROWE

Cyfrowy pomiar częstotliwości

- bezpośredni

- z przemianą częstotliwości

Cyfrowy pomiar odstępu czasu

- pomiar okresu sygnału

- pomiar wielokrotności okresu

WYKŁAD 13

3

POMIARY CZĘSTOTLIWOŚCI I CZASU

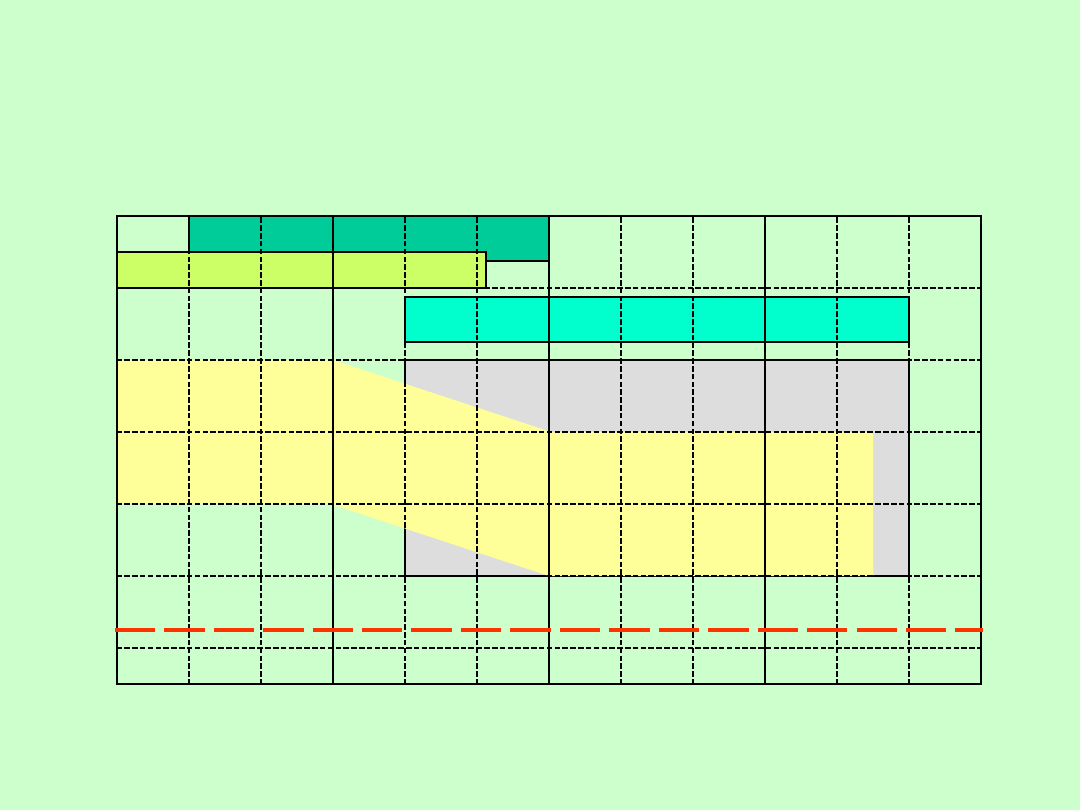
ZAKRES CZĘSTOTLIWOSCIOWY I DOKŁADNOŚĆ

WYBRANYCH METOD POMIARU CZĘSTOTLIWOŚCI I

CZASU

10

-

2

10

-

4

10

-

6

10

-

8

10

-10

10

-12

10

-14

Częstościomierze
integracyjne

Metody
oscyloskopowe

Falomierze
absorbcyjne

Częstościomierze
heterodynowe

Częstościomierze
cyfrowe

TEORETYCZNA GRANICA
DOKŁADNOŚCI

1 Hz

1 kHz

1 MHz

1 GHz

1

THz

WYKŁAD 13

4

POMIARY CZĘSTOTLIWOŚCI I CZASU

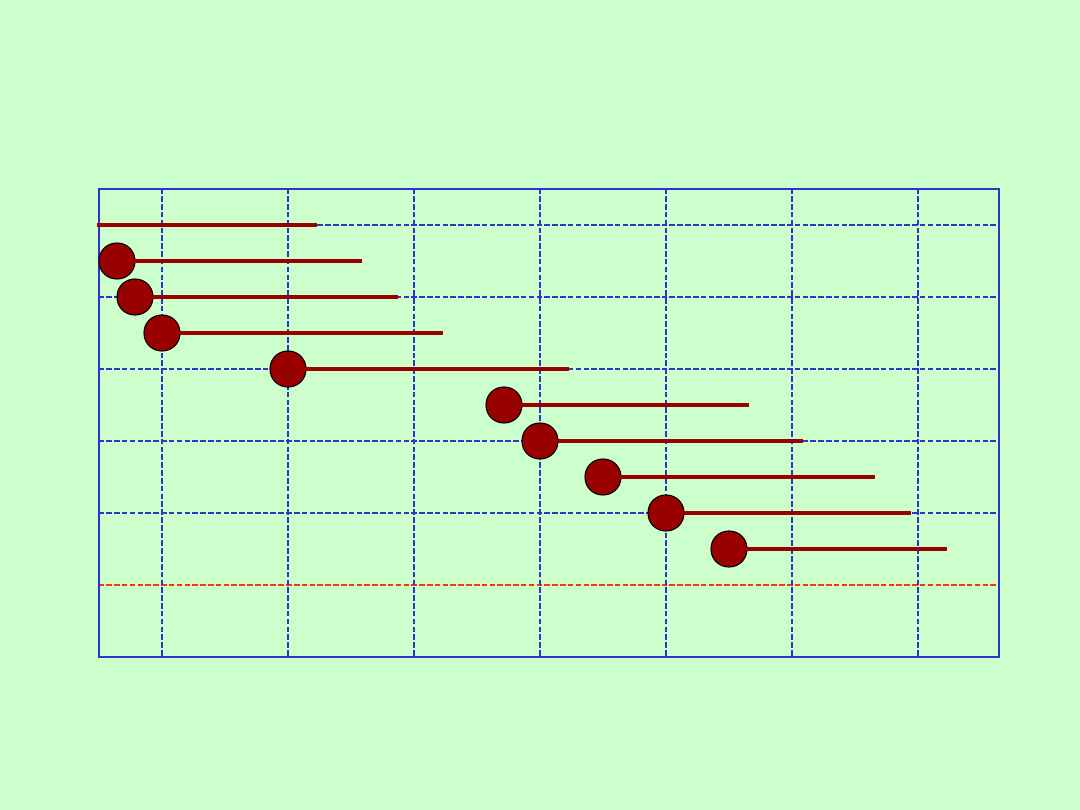
EWOLUCJA DOKŁADNOSCI WZORCÓW CZASU I

CZĘSTOTLIWOŚCI

10

-4

10

-6

10

-8

10

-

10

10

-

12

10

-

14

1930 1940 1950

1960 1970

1980 1990

rezonatory
LC

widełki stroikowe

zegar wahadłowy

średni czas
słoneczny generator

kwarcowy

czas efemerydowy

rezonator
rubidowy

rezonator
metanowy

mazer wodorowy

wzorzec
cezowy

GRANICA
TEORETYCZNA

WYKŁAD 13

5

POMIARY CZĘSTOTLIWOŚCI I CZASU

DEFINICJA SEKUNDY:

Sekunda jest to czas równy

9 192 631 770

okresów promieniowania
odpowiadającego przejściu między
dwoma nadsubtelnymi poziomami
stanu podstawowego

133

Cs (cezu 133).

Niedokładność tak ustalonej sekundy jest
rzędu 10

-13

, tzn. błąd t = 1 s na 317 098

lat.

WYKŁAD 13

6

POMIARY CZĘSTOTLIWOŚCI I CZASU

(definicje)

Częstotliwością f zjawiska okresowego nazywa
się liczbę jego całkowitych powtórzeń w
jednostce czasu



n

f 

Związek miedzy częstotliwością a okresem:

T

f

1



Pulsacja:

 = 2 f

Jednostką częstotliwości jest 1 herc (1 Hz)

WYKŁAD 13

7

POMIARY CZĘSTOTLIWOŚCI I CZASU

(definicje)

PRZEBIEG
QUASIHARMONICZNY:









0

)

(

2

sin

)

(

sin

)

(

















t

t

f

U

t

U

t

u

n

U – amplituda sygnału,
 - kąt fazowy,



0

– początkowy kąt fazowy,

f

n

– częstotliwość znamionowa przebiegu,

(t) – składowa kąta fazowego zmieniająca się

nieproporcjonalnie do czasu (przy czym d/dt

<< 2f

n

).

WYKŁAD 13

8

POMIARY CZĘSTOTLIWOŚCI I CZASU

(definicje)

CZĘSTOTLIWOŚĆ CHWILOWA:

CZĘSTOTLIWOŚĆ ŚREDNIA (w przedziale czasu  =

t

j

– t

i

):

dt

t

d

f

dt

d

f

n

t

)

(

2

1

































j

i

t

t

i

j

n

t

t

t

f

dt

t

f

f

)

(

)

(

2

1

)

(

1







WYKŁAD 13

9

POMIARY CZĘSTOTLIWOŚCI I CZASU

Oscyloskopowe pomiary częstotliwości – liniowa

podstawa czasu

L

T = L
C

X

BŁĘDY

T = L + C

X

f = T

WYKŁAD 13

10

POMIARY CZĘSTOTLIWOŚCI I CZASU

Oscyloskopowe pomiary częstotliwości – sinusoidalna

podstawa czasu

f

WE

= f

W

f

W

f

WE

= F

W

+ N

wir

/

(Figury
Lissajous)

WYKŁAD 13

11

POMIARY CZĘSTOTLIWOŚCI I CZASU

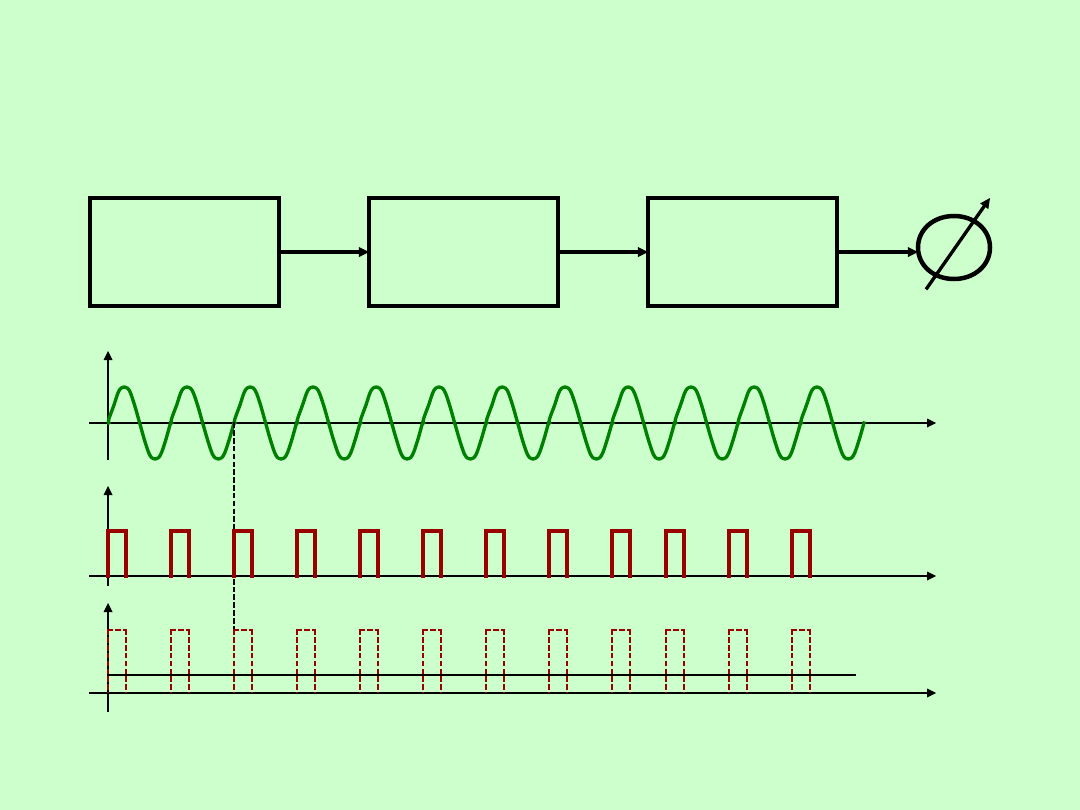
INTEGRACYJNY POMIAR CZĘSTOTLIWOŚCI

t

t

t

u

1

(

t)

u

1

(

t)

u

2

(

t)

u

2

(

t)

u(t
)

u(t
)

Źródło

sygnału

Układ

formowan

ia

Układ

uśredniaj

ący

U

m

U

0

U

0

= U

m

/T U

0

=

U

m

 f

WYKŁAD 13

12

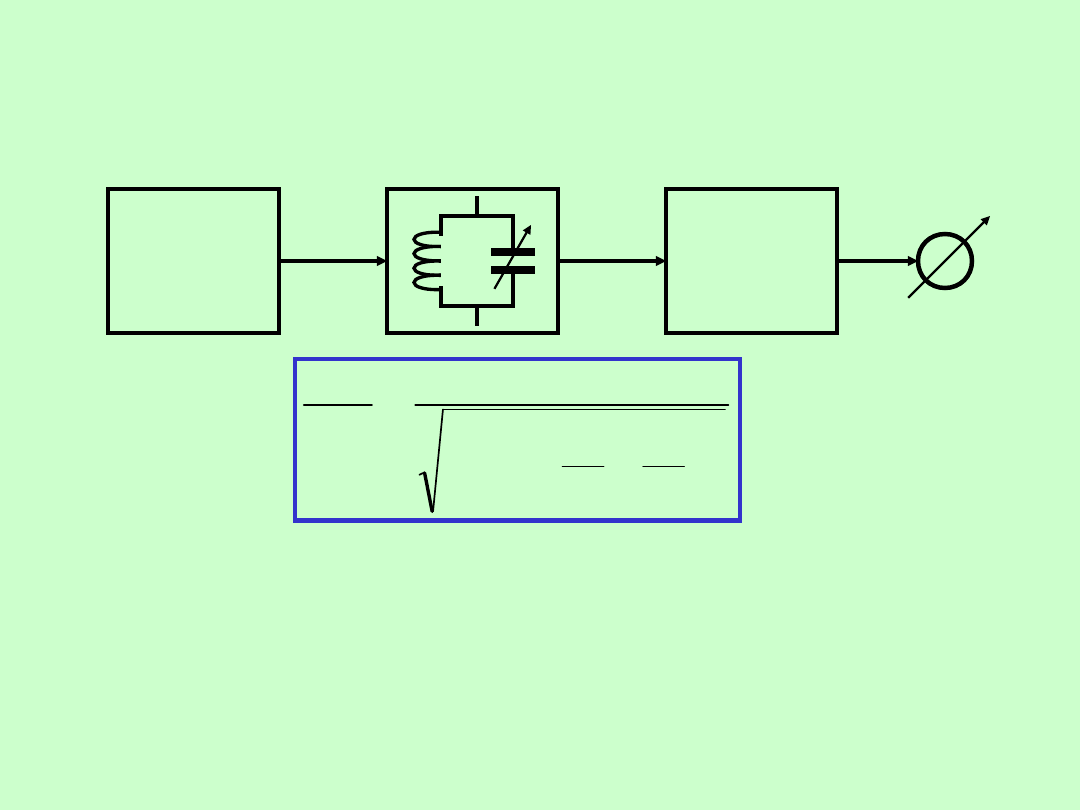
POMIARY CZĘSTOTLIWOŚCI I CZASU

METODA REZONANSOWA

Obwód

sprzęgają

cy

Wskaźnik

rezonans

u

2

0

0

2

max

1

1



















f

f

f

f

Q

I

I

I

max

- natężenia prądu przy częstotliwości

rezonansowej

I

- natężenie prądu przy częstotliwości f

Q

- dobroć obwodu

WYKŁAD 13

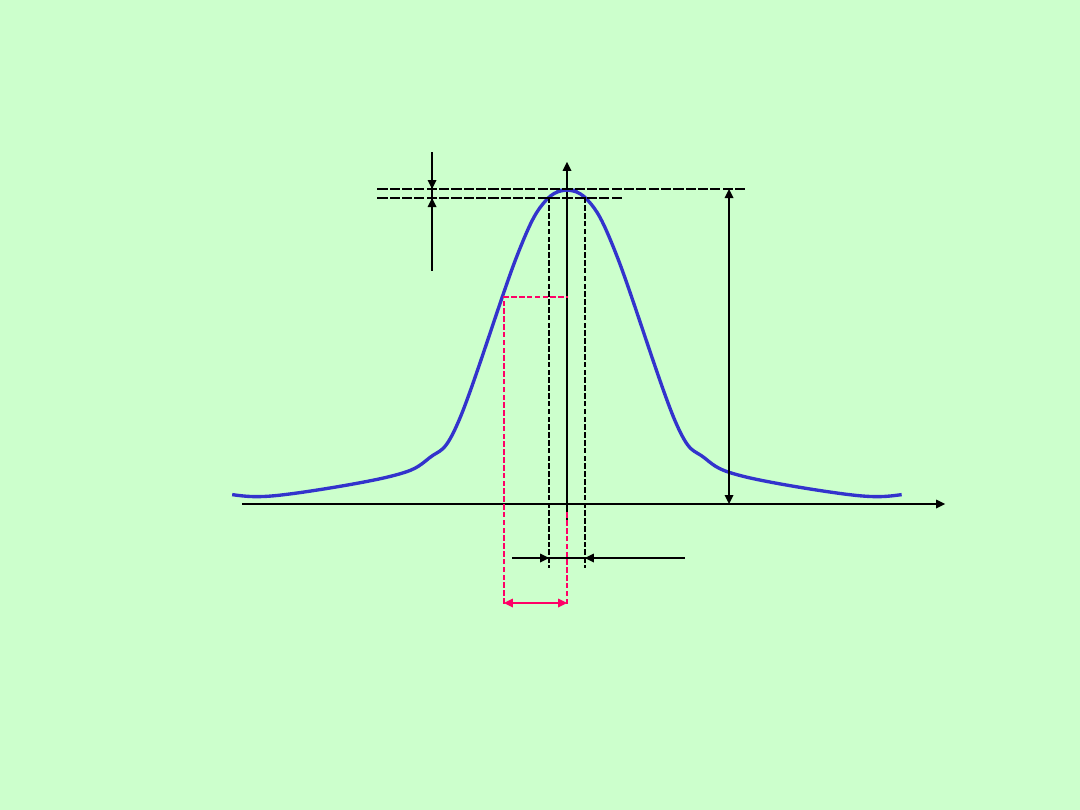
13

POMIARY CZĘSTOTLIWOŚCI I CZASU

METODA REZONANSOWA

f







*

f

2
f*



m

a

x



* - próg czułości

wskaźnika



f* -

przedział niepewności

przy

wyznaczaniu
punktu rezonansu

WYKŁAD 13

14

POMIARY CZĘSTOTLIWOŚCI I CZASU

METODA REZONANSOWA

Gdy

max

max

I

I







oraz

0

0

0

2

f

f

f

f

f

f







wted
y

1

2

1

max











Q

f

f

WYKŁAD 13

15

POMIARY CZĘSTOTLIWOŚCI I CZASU

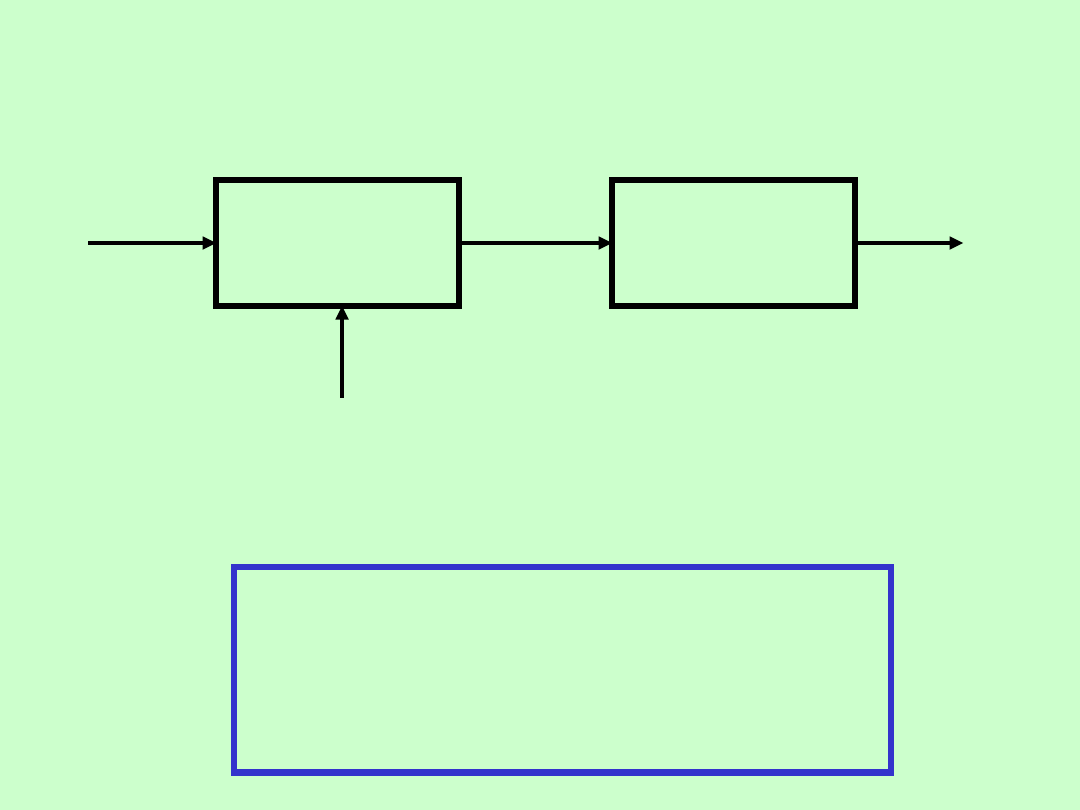
METODY HETERODYNOWE

SUMATOR

MIESZAC

Z

u

X

(t

)

u

W

(

t)

u(t)

i(t)

f

X

f

W

u

X

(t) = U

Xm

sin 2



f

X

t

u

X

(t) = U

Xm

sin 2



f

X

t

u(t) = u

X

(t) + u

W

(t) =

= U

Xm

sin 2



f

X

t + U

Wm

sin

2



f

W

t

WYKŁAD 13

16

POMIARY CZĘSTOTLIWOŚCI I CZASU

METODY HETERODYNOWE

i = a

0

+ a

1

U + a

2

U

2

i(t) = [a

0

+ ½ a

2

( U

Xm

2

+ U

Wm

2

)] +

+ a

1

( U

Xm

sin 2f

X

t + U

Wm

sin 2f

W

t ) +

+ ½ a

2

( U

Xm

2

cos 2 2f

X

t + U

Wm

2

cos 2

2f

W

t ) +

+ a

2

U

Xm

U

wm

[cos 2 (f

X

– f

W

) t - cos 2

(f

X

+ f

W

) t ]

i(t) = [a

0

+ ½ a

2

( U

Xm

2

+ U

Wm

2

)] +

+ a

1

( U

Xm

sin 2

f

X

t + U

Wm

sin 2

f

W

t ) +

+ ½ a

2

( U

Xm

2

cos 2

2f

X

t + U

Wm

2

cos 2

2f

W

t ) +

+ a

2

U

Xm

U

wm

[cos 2 (

f

X

– f

W

) t - cos 2

(

f

X

+ f

W

) t ]

WYKŁAD 13

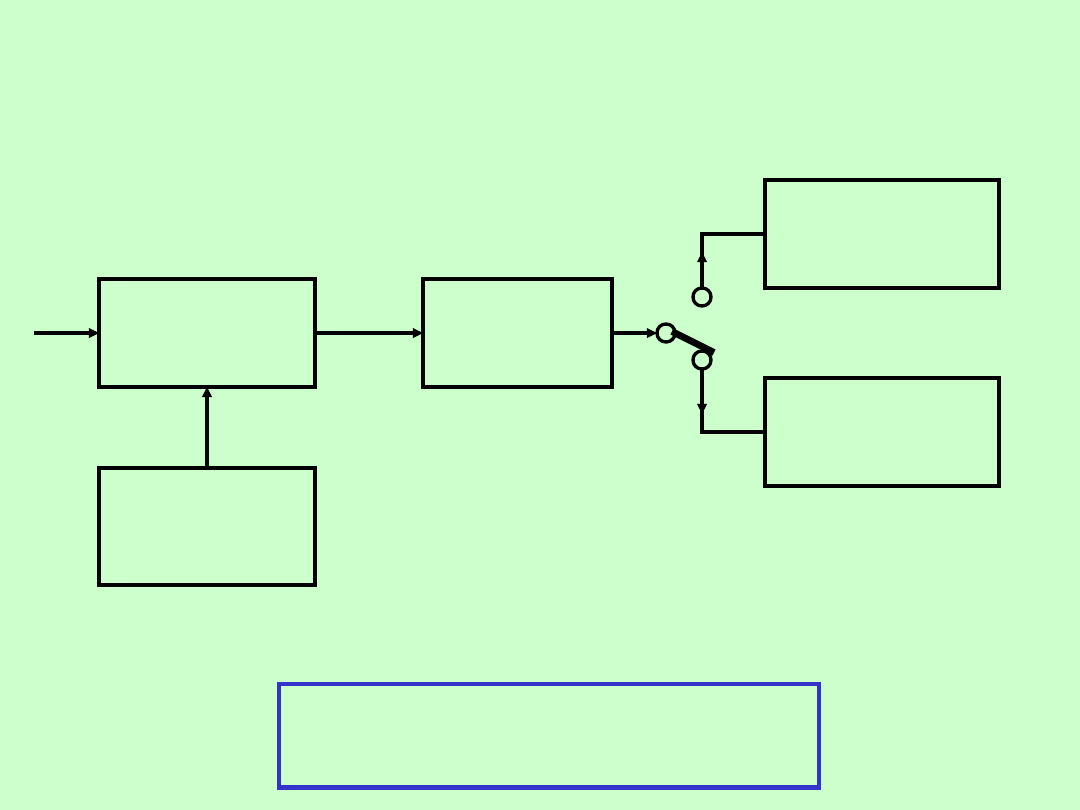
17

POMIARY CZĘSTOTLIWOŚCI I CZASU

METODY HETERODYNOWE

GENERATO

R

WZORCOW

Y

SUMATOR i

MIESZACZ

FILTR

Miernik

częstotliw

ości

Wskaźnik

zaniku

dudnień

f

X

-

f

W

f

X

f

W

f

X

, f

W

2f

X

, 2f

W

f

X

+ f

W

,

f

X

- f

W

-przy generatorze wzorowym o regulowanej
częstotliwości f

X

dążymy do uzyskania

warunku f

X

– f

W

= 0 (zanik dudnień)

- przy generatorze wzorcowym o stałej
częstotliwości f

W

mierzymy częstotliwość

różnicową F = f

X

– f

W

f

X

= f

W

+ F lub f

X

= f

W

-

F

WYKŁAD 13

18

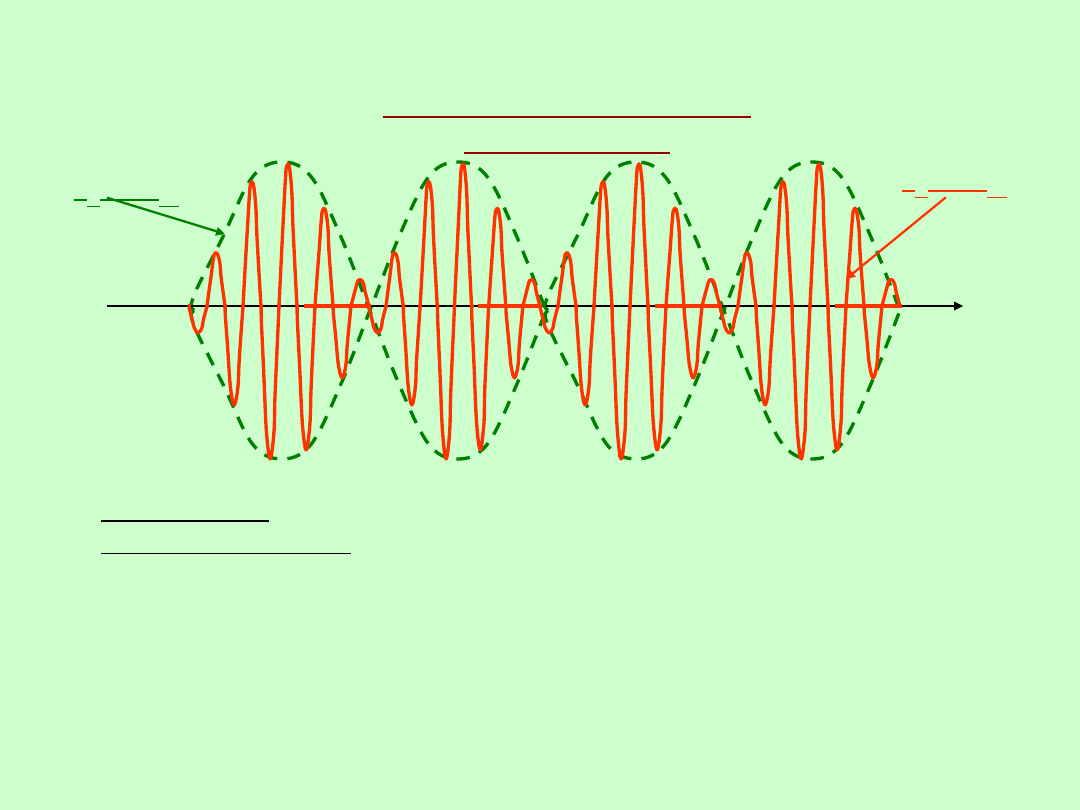
POMIARY CZĘSTOTLIWOŚCI I CZASU

SYGNAŁ NA WYJŚCIU

MIESZACZA

f

X

+ f

W

f

X

+ f

W

t

PRZYKŁAD
OBLICZENIOWY

f

X

= 10,001 000 MHz

f

W

= 10,000 000 MHz ;



g

f

W

= 10

-6

%

f

r

= f

X

– f

W

= 1000 Hz

WYKŁAD 13

19

POMIARY CZĘSTOTLIWOŚCI I CZASU

PRZYKŁAD OBLICZENIOWY
(c.d.)

Niech:



g

f

r

= 1 %

f

X

= f

W

+ f

r

= 10,001 000 MHz



g

f

X

=



g

f

W

+



g

f

r

= (0,1 + 10) Hz

%

10

4









X

X

g

X

g

f

f

f



WYKŁAD 13

20

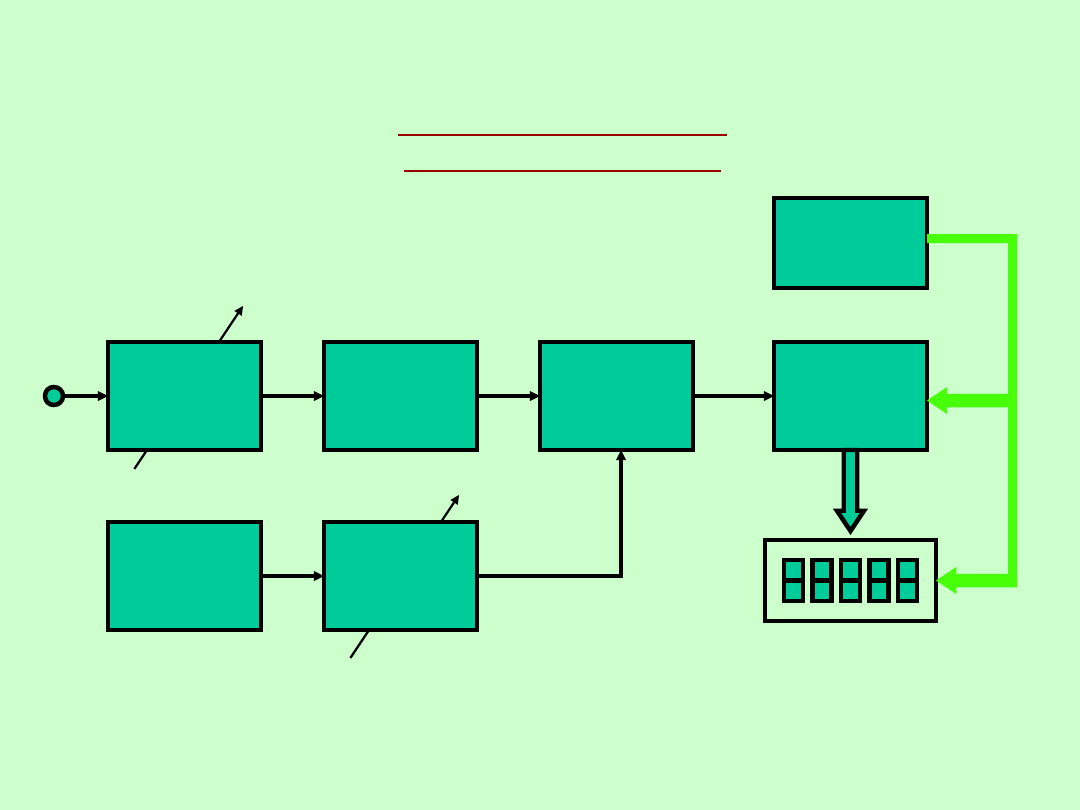
POMIARY CZĘSTOTLIWOŚCI I CZASU

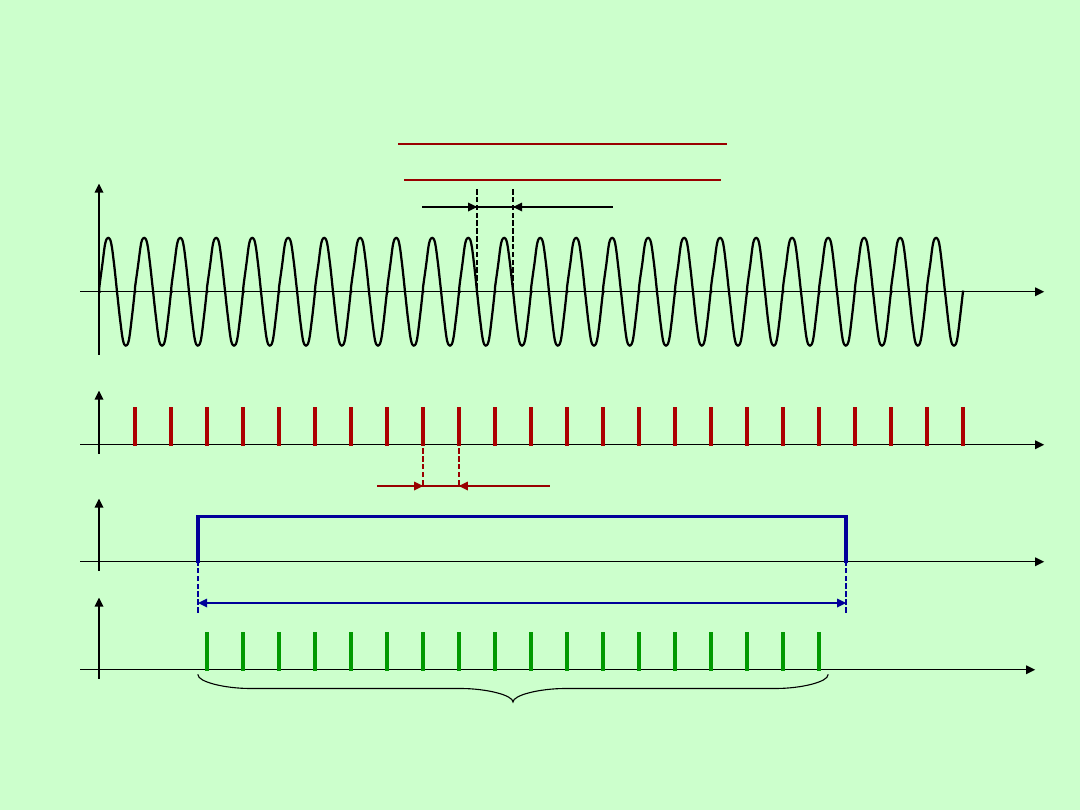
CYFROWY POMIAR

CZĘSTOTLIWOŚCI

UKŁAD

STEROWANIA

BRAMKA

LICZNIK

Układy

wejściowe

DZIELNIK

częstotli-

wości

Generator

wzorcowy

Układ

formowania

Wyświetlacz

u

we

u

1

u

3

u

4

WYKŁAD 13

21

POMIARY CZĘSTOTLIWOŚCI I CZASU

t

t

t

t

u

WE

u

1

u

3

u

4

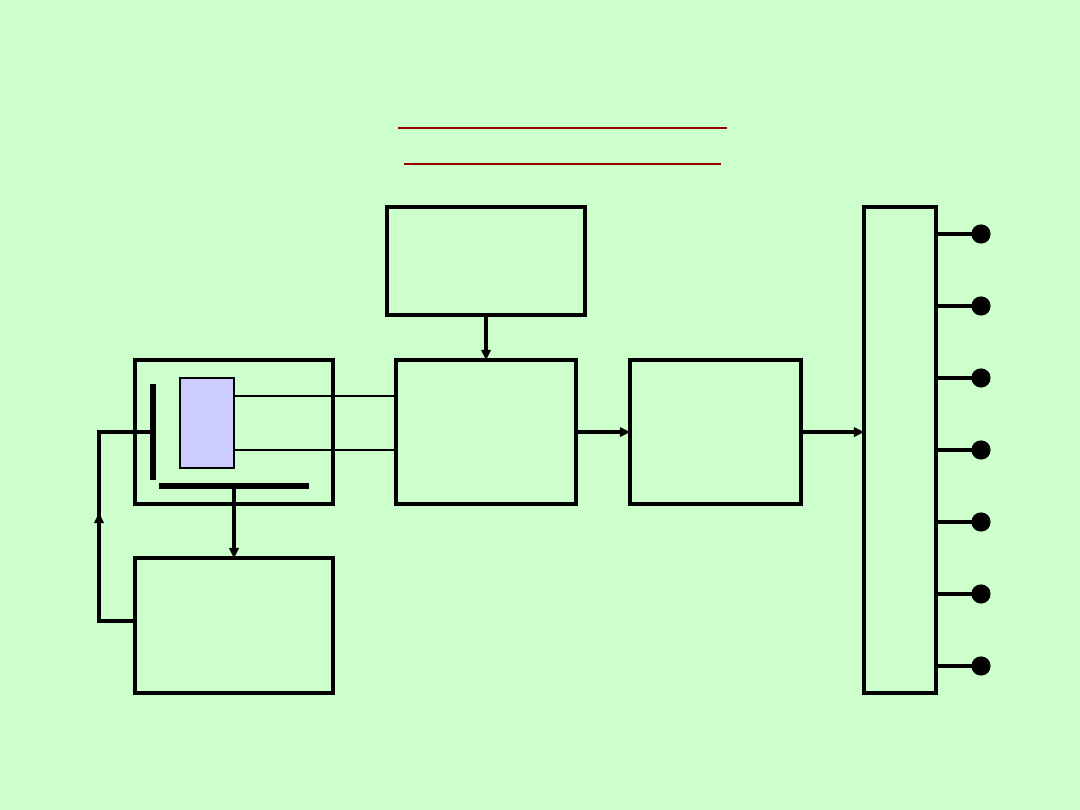
CYFROWY POMIAR

CZĘSTOTLIWOŚCI

N



T

X

T

X

WYKŁAD 13

22

POMIARY CZĘSTOTLIWOŚCI I CZASU

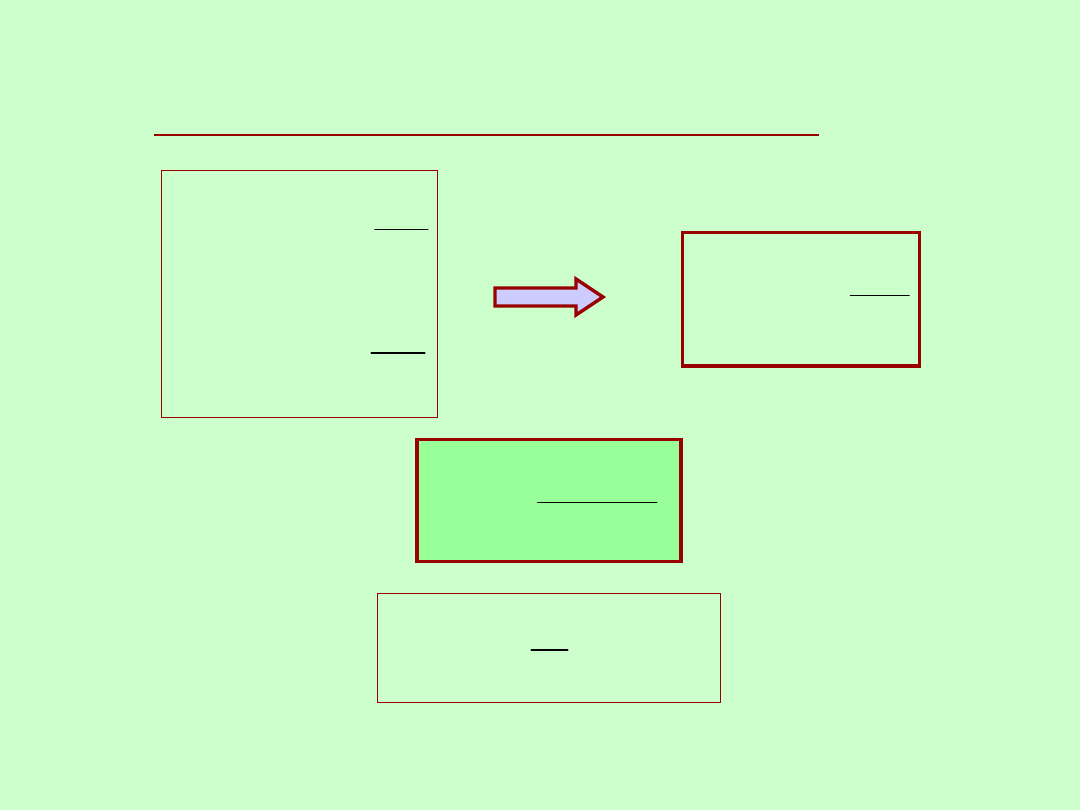
CYFROWY POMIAR

CZĘSTOTLIWOŚCI

kwarcowy wzorzec częstotliwości

K

Regulator

temperatu

ry

Regulacja

amplitudy

Generato

r 5 MHz

Separat

or i

dzielni

k f/5

D

zi

e

ln

ik

c

zę

st

o

tl

iw

o

śc

i:

f/

1

0

n

1
MHz

100
kHz
10 kHz

1 kHz

100 Hz

10 Hz

1 Hz

Niestabilność f:

długoterminowa: 10

-8

– 10

-

9

/miesiąc

krótkoterminowa: 10

-10

– 10

-

11

/godzinę

Krajowa

częstotliwość

wzorcowa;

225 kHz

(Warszawa 1)

WYKŁAD 13

23

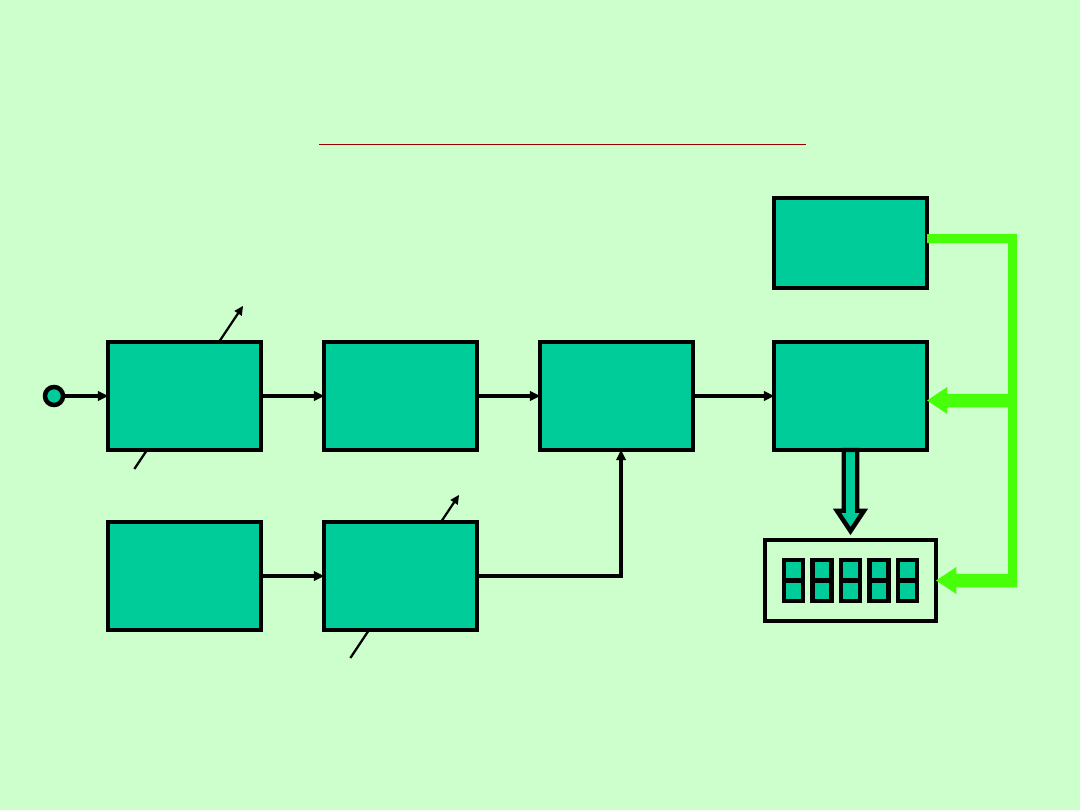
POMIARY CZĘSTOTLIWOŚCI I CZASU

CYFROWY POMIAR CZĘSTOTLIWOŚCI – błąd

pomiaru

W

W

X

X

f

m

T

m

f

N

T

N

















W

X

f

m

f

N





m

f

N

f

W

X





W

X

f

N

f









1

WYKŁAD 13

24

POMIARY CZĘSTOTLIWOŚCI I CZASU

UKŁAD

STEROWANIA

BRAMKA

LICZNIK

Układy

wejściowe

DZIELNIK

częstotli-

wości

Generator

wzorcowy

Układ

formowania

Wyświetlacz

u

we

u

1

u

3

u

4

CYFROWY POMIAR OKRESU

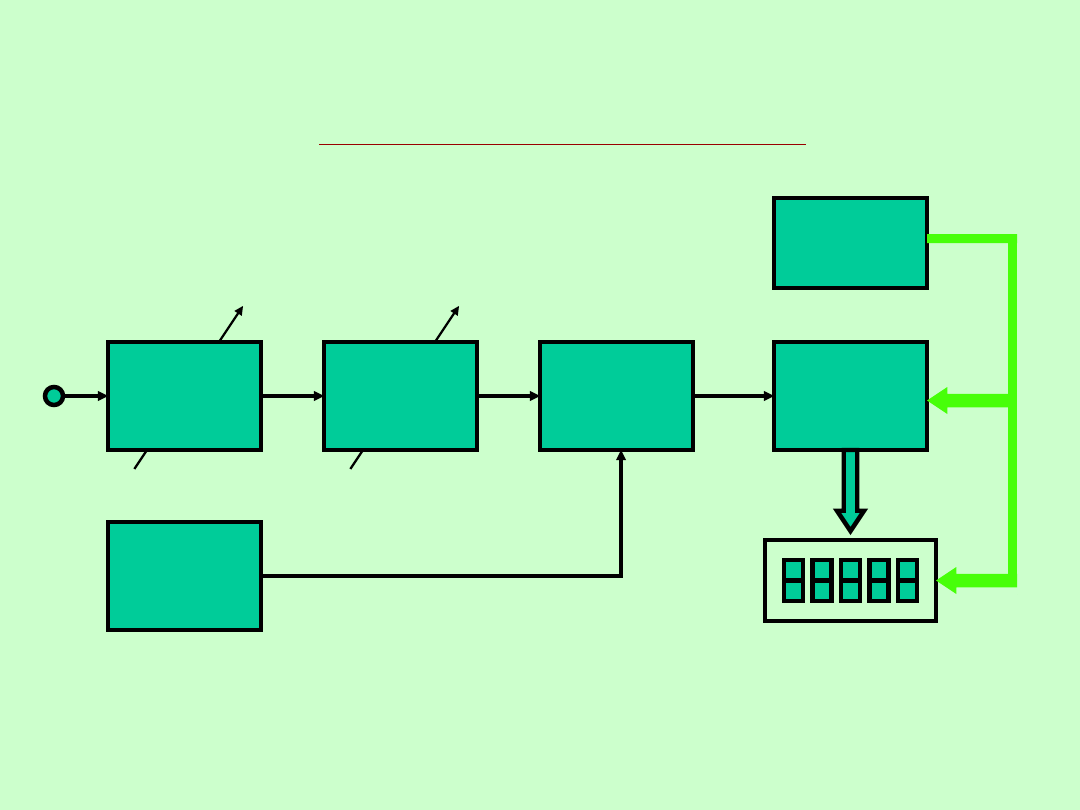
WYKŁAD 13

25

POMIARY CZĘSTOTLIWOŚCI I CZASU

CYFROWY POMIAR OKRESU

UKŁAD

STEROWANIA

BRAMKA

LICZNIK

Układy

wejściowe

DZIELNIK

częstotli-

wości

Generator

wzorcowy

Wyświetlacz

u

we

u

3

u

3

u

4

u

1

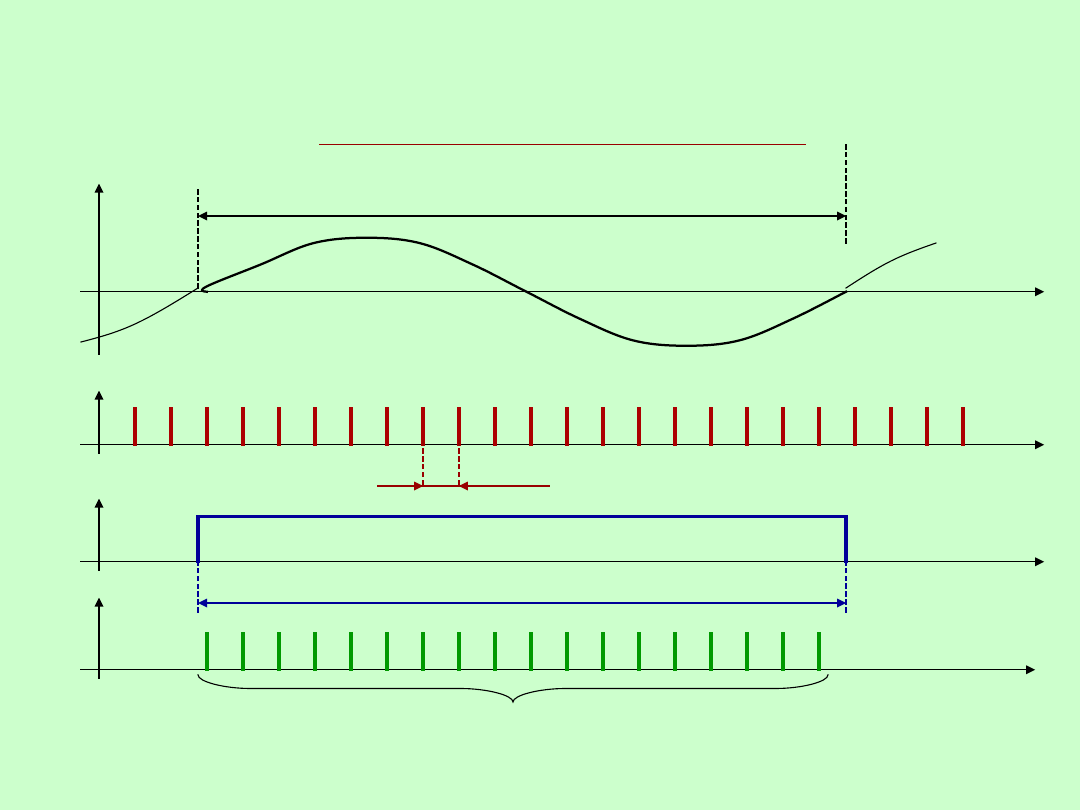
WYKŁAD 13

26

POMIARY CZĘSTOTLIWOŚCI I CZASU

t

t

t

t

u

WE

u

1

u

3

u

4

N



T

X

T

W

CYFROWY POMIAR OKRESU

WYKŁAD 13

27

POMIARY CZĘSTOTLIWOŚCI I CZASU

CYFROWY POMIAR OKRESU – błąd

pomiaru

 = k T

X

;

k – krotność

okresu

 = N T

W

W

W

W

X

f

m

T

T

T

k

N







m – współczynnik
podziału
częstotliwości
generatora
wzorcowego

N

f

m

k

T

W

X







1

W

X

f

N

T









1

WYKŁAD 13

28

POMIARY CZĘSTOTLIWOŚCI I CZASU

Przyczyny nieprawidłowego działania

częstościomierzy/czasomierzy cyfrowych

OBJAWY:

•Brak wskazania

•Wskazanie częstościomierza (czasomierza) znacznie
odbiegające od oczekiwanej wartości częstotliwości
(czasu)

•Niestabilny wynik pomiaru

•Ustawienia wejściowe silnie wpływają na wynik
pomiaru

WYKŁAD 13

29

POMIARY CZĘSTOTLIWOŚCI I CZASU

Przyczyny nieprawidłowego działania

częstościomierzy/czasomierzy cyfrowych

PRZYCZYNY:

 Nadmierne zakłócenia lub zniekształcenia sygnału

wejściowego

 Niewłaściwe ustawienia wejściowe

zbyt duże/zbyt małe wzmocnienie

niewłaściwy poziom wyzwalania

niewłaściwy rodzaj wejściowego układu

formującego

 Nieodpowiednie podłączenia wejścia

zbyt długie doprowadzenia

nieodpowiednie doprowadzenie masy

 Nadmierne obciążenie źródła sygnału

WYKŁAD 13

30

POMIARY CZĘSTOTLIWOŚCI I CZASU

Przyczyny nieprawidłowego działania

częstościomierzy/czasomierzy cyfrowych

SPOSOBY ZAPOBIEGANIA:

 Dobrać właściwe parametry układów wejściowych

częstościomierza

dostosować wzmocnienie do amplitudy sygnału

dobrać poziom wyzwalania

dobrać właściwy rodzaj wejściowego układu
formującego

 Zastosować prawidłowe połączenia masy i sygnałowe
 Zastosować sondę pomiarową
 Użyć oscyloskopu celem zbadania przebiegu sygnału,

co ułatwi znalezienie właściwych ustawień
częstościomierza

 Dokładnie przestudiować jeszcze raz instrukcję

obsługi przyrządu

WYKŁAD 13

31

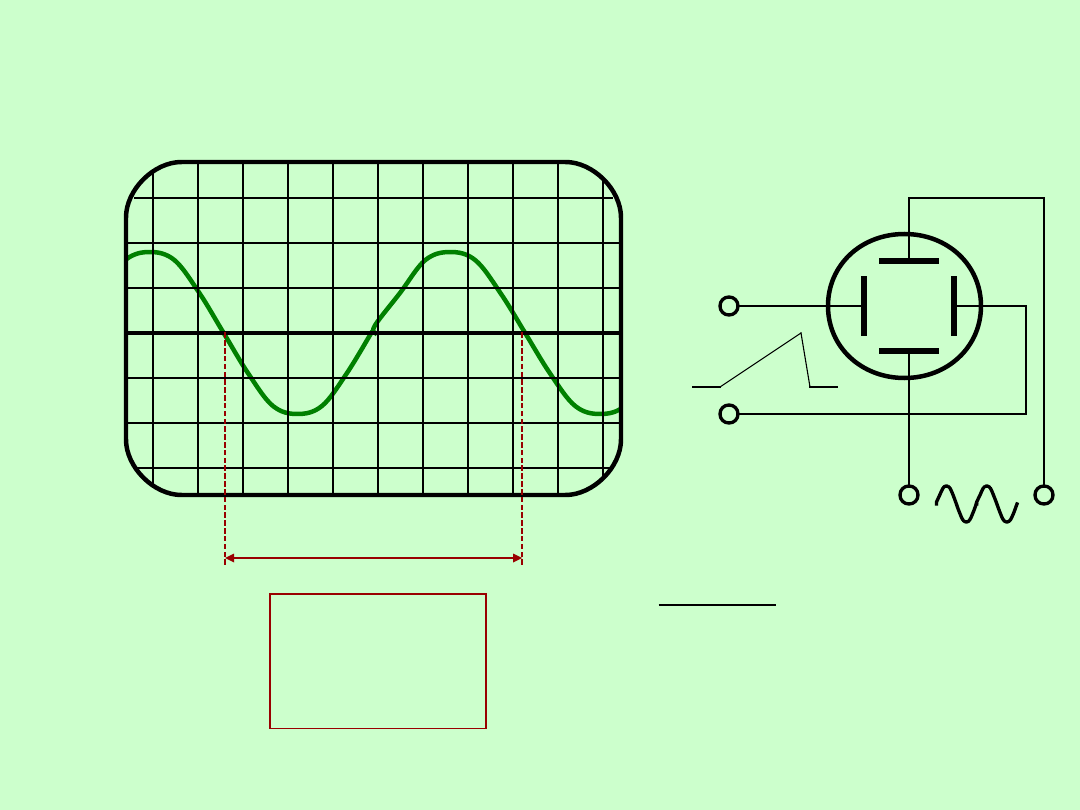
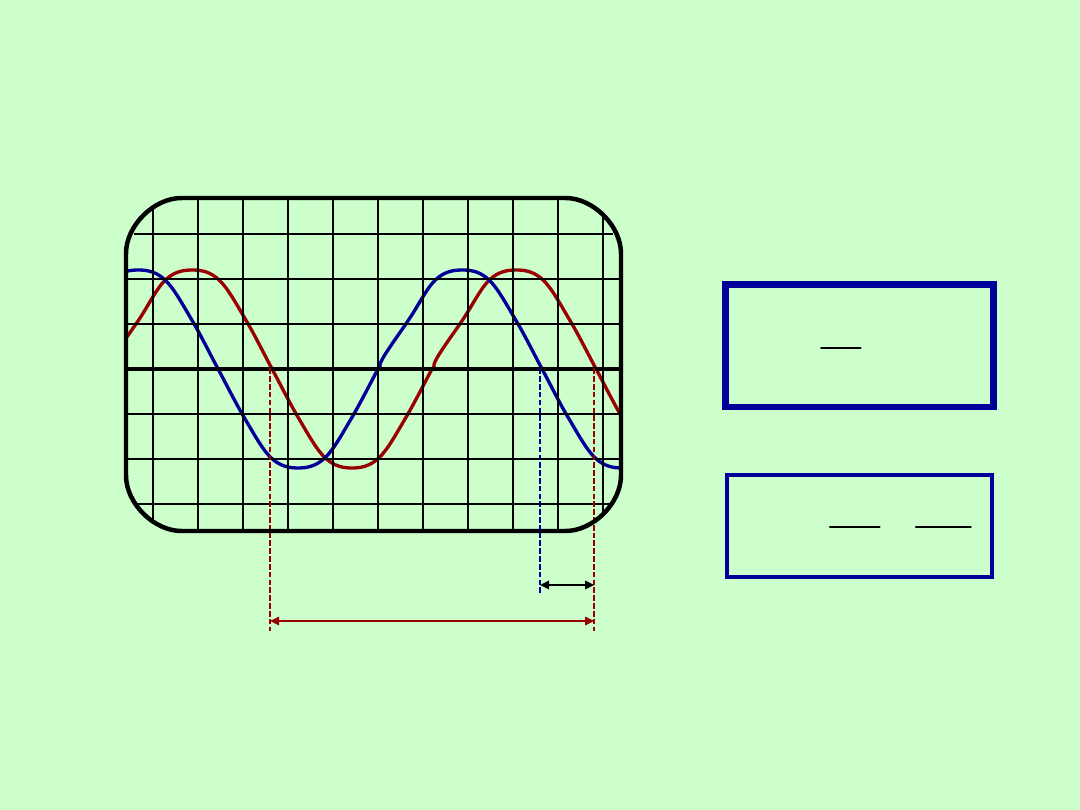
POMIARY PRZESUNIĘCIA FAZOWEGO

Pomiar oscyloskopowy – liniowa podstawa czasu

D

d

0

360





D

d



D

D

d

d 











WYKŁAD 13

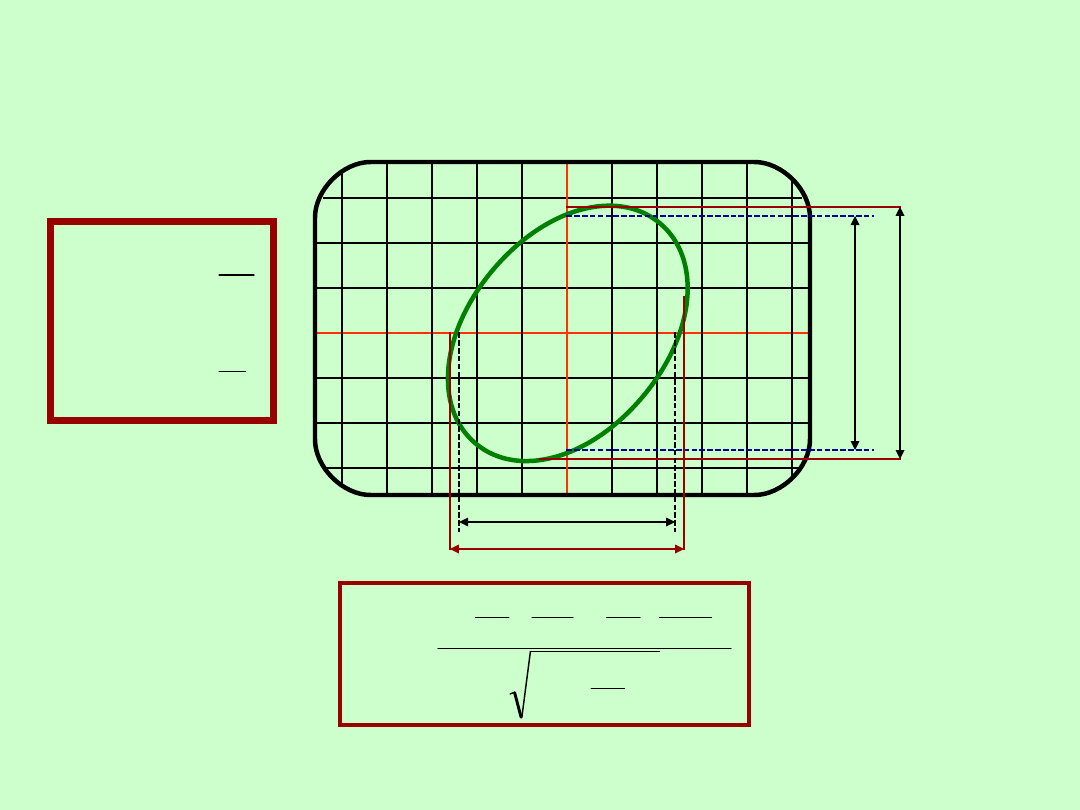
32

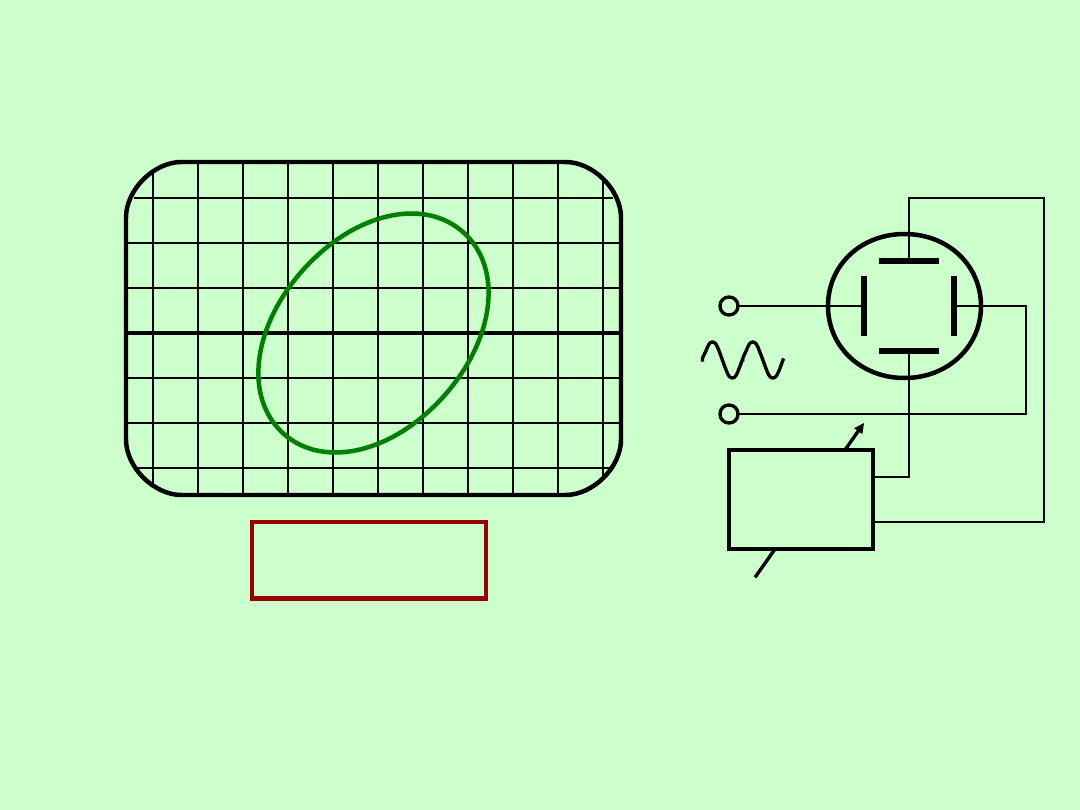
POMIARY PRZESUNIĘCIA FAZOWEGO

Pomiar oscyloskopowy – sinusoidalna podstawa czasu

X

x

Y

y

Y

y

X

x

arcsin

arcsin









2

1

2









































X

x

X

X

X

x

X

x

X

x



WYKŁAD 13

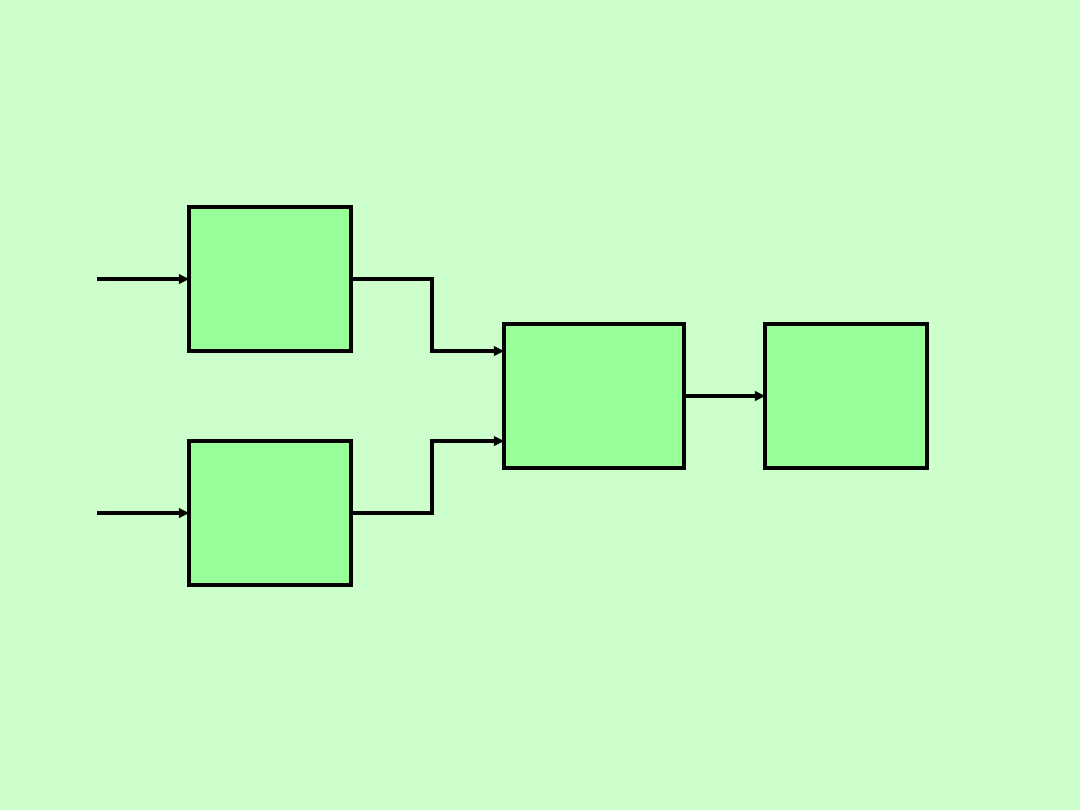
33

POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY Z SUMATOREM

UF
1

UF
2

SUMATO
R

V

u

5

u

4

u

3

u

2

u

1

WYKŁAD 13

34

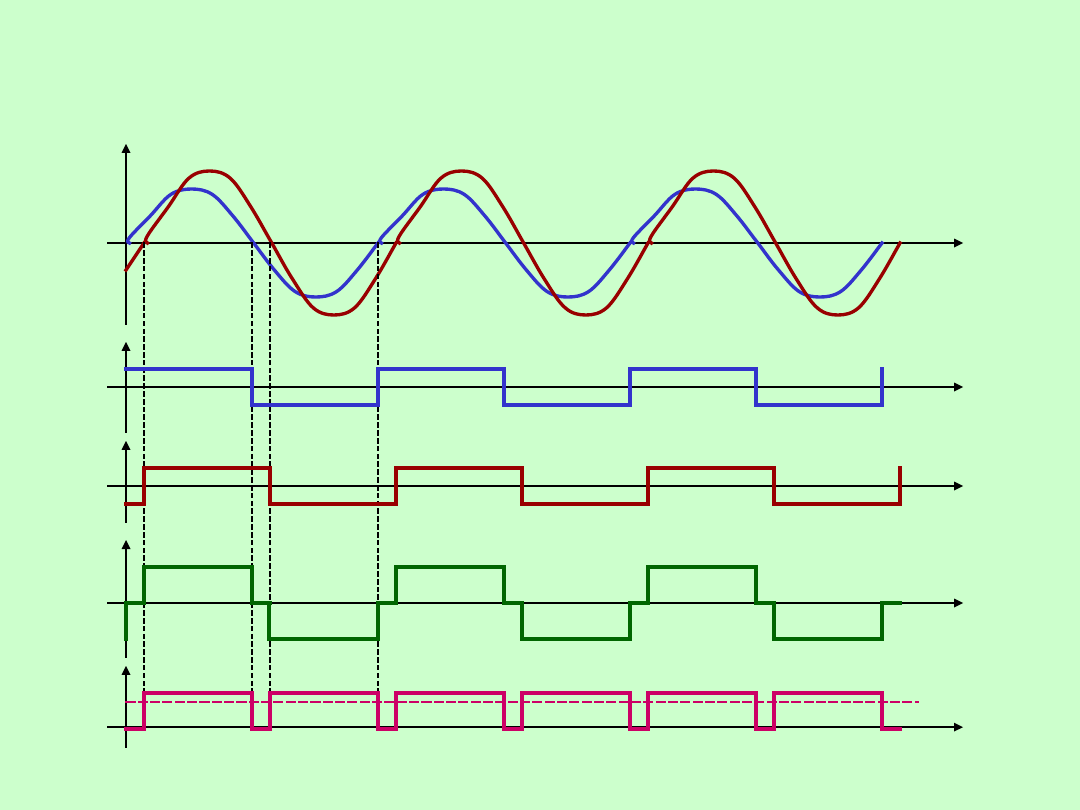
POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY Z SUMATOREM –

przebiegi sygnałów

t

t

t

t

t

u

2

u

1

u

3

u

4

u

5

u

50





2


U

V

WYKŁAD 13

35

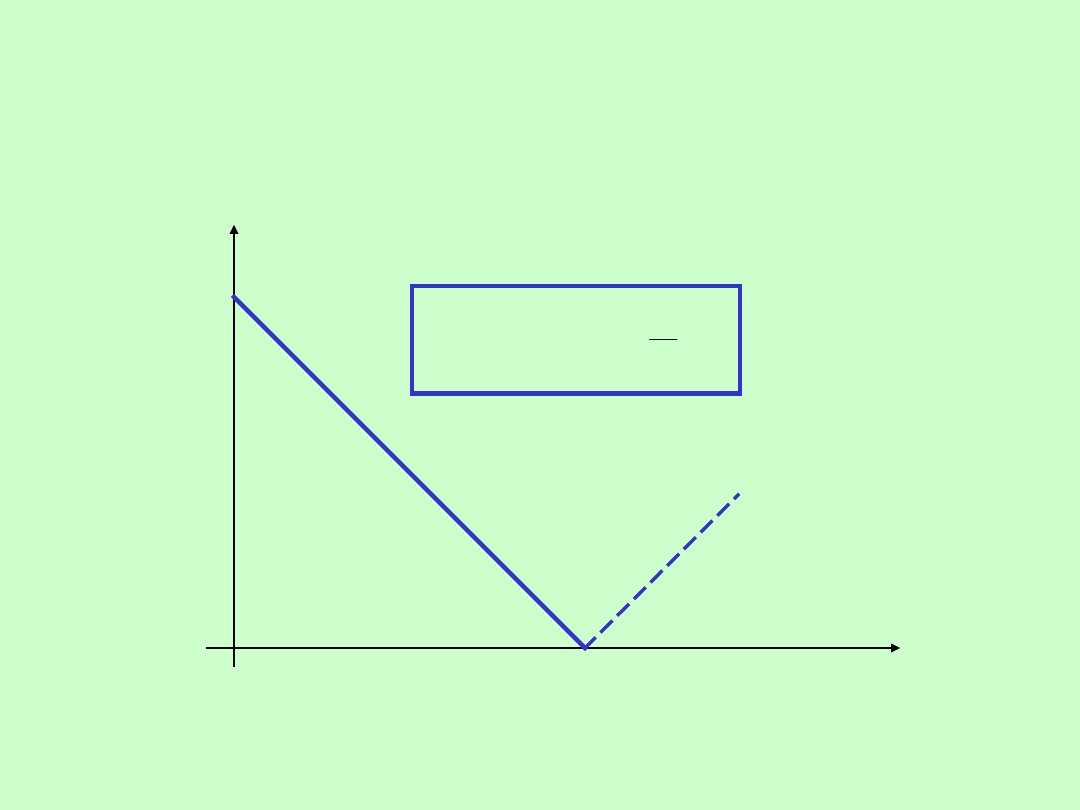
POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY Z SUMATOREM -

charakterystyka





0

U

M

U

V











 







1

M

V

U

U









0

0

0

2

1

















g

WYKŁAD 13

36

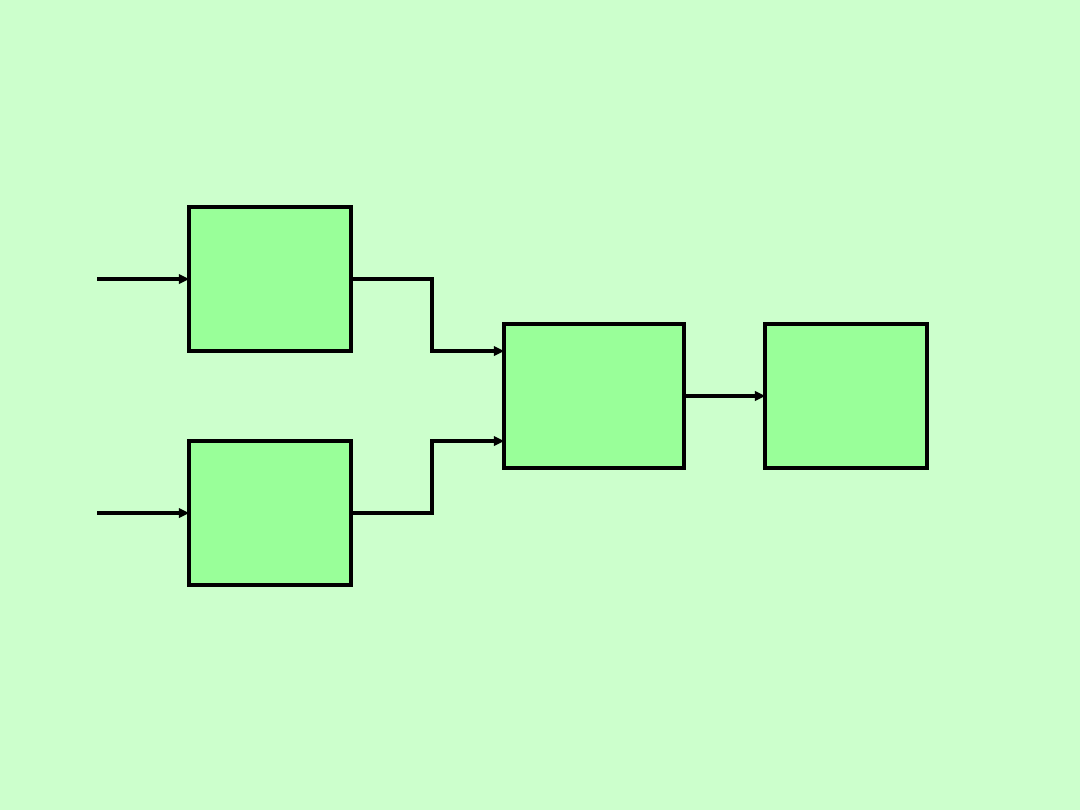
POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY

PRZERZUTNIKIEM

UF
1

UF
2

Przerzut
nik
dwustabi
lny

V

u

5

u

4

u

3

u

2

u

1

WYKŁAD 13

37

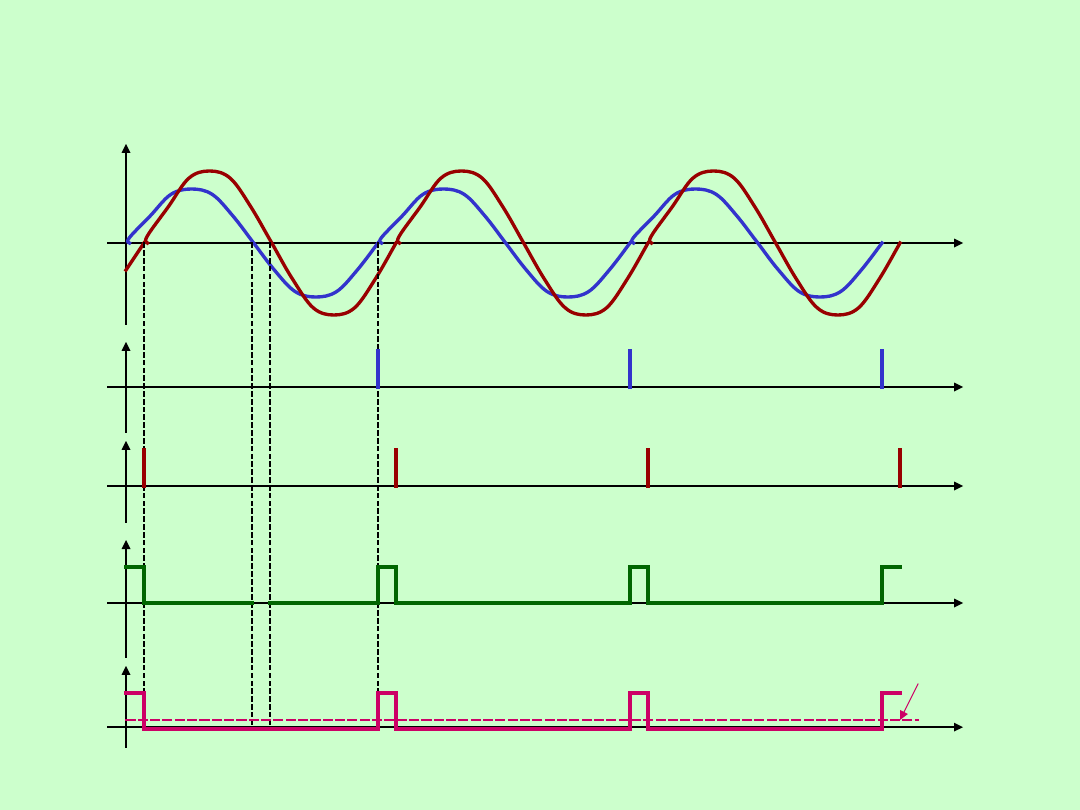
POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY Z PRZERZUTNIKIEM –

przebiegi sygnałów

t

t

t

t

t

u

2

u

1

u

3

u

4

u

5

u

50



2


U

V

WYKŁAD 13

38

POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ IMPULSOWY Z PRZERZUTNIKIEM –

charakterystyka



2



0

U

M

U

V





2





M

V

U

U









0

0

2

0

2

1

















g

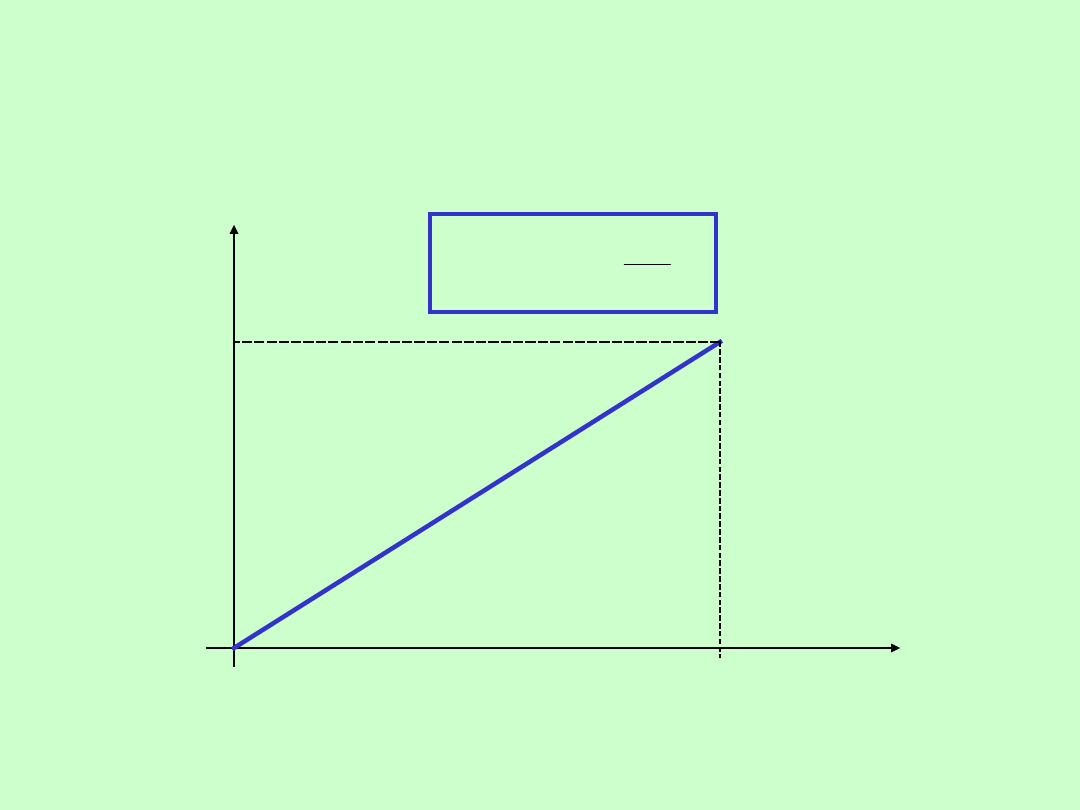
WYKŁAD 13

39

POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ CYFROWY – schemat blokowy

B

US

UF1

UF2

UF3

P
Cz

LICZNI

K

WSKAŹNI

K

u

2

u

1

sto
p

start

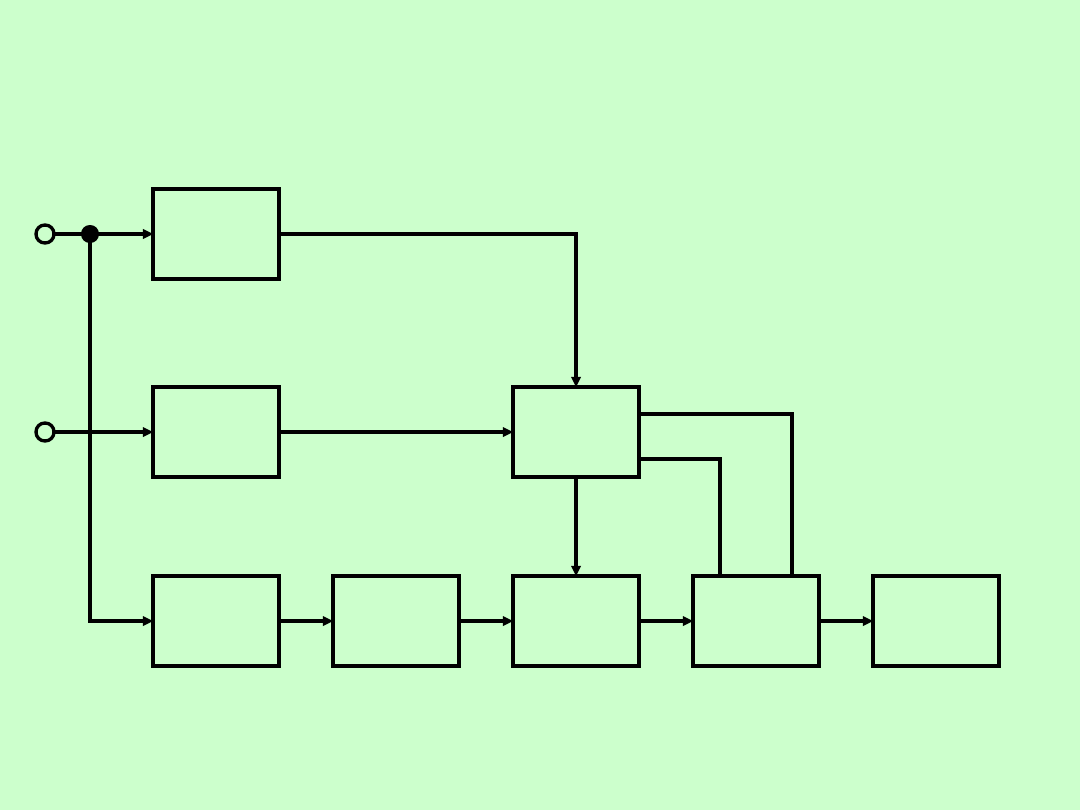
WYKŁAD 13

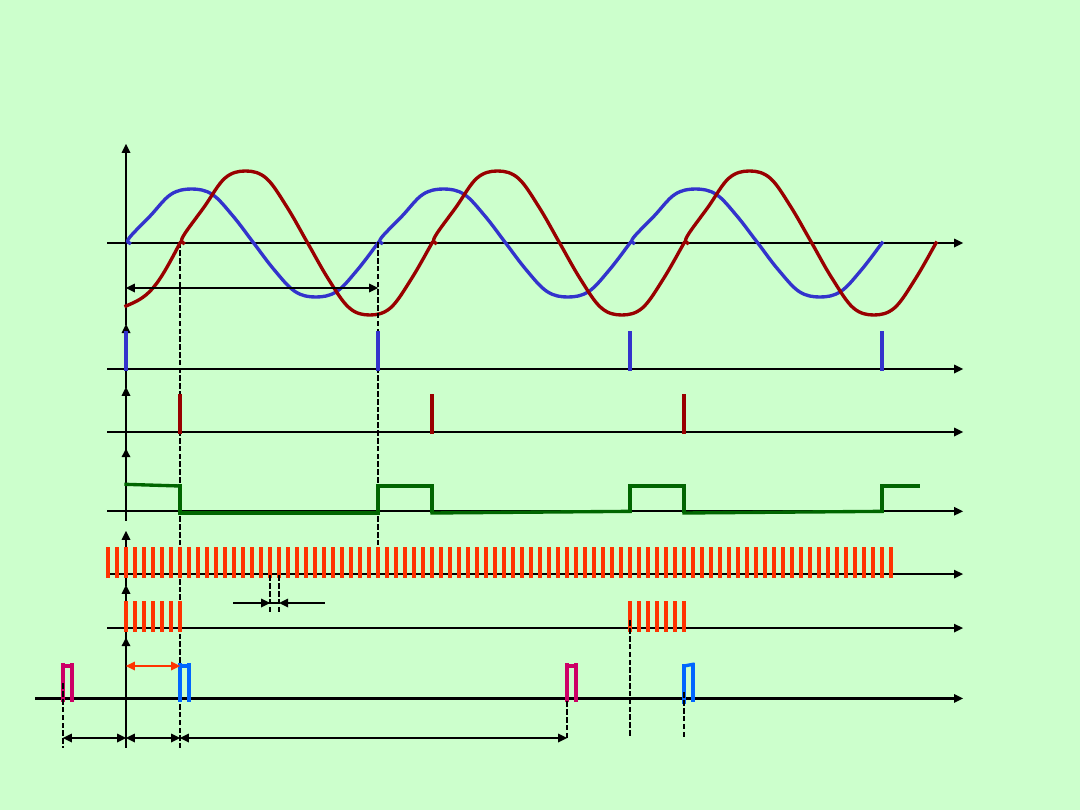
40

POMIARY PRZESUNIĘCIA FAZOWEGO

FAZOMIERZ CYFROWY

t

t

t

t

t

u

2

u

1

u

F1

u

F2

u

S

u

F3



2


t

t

u

L

GOTOWE

LICZENI
E

ODCZYT

n

T

X

T

X

/(36·10

k

)