2012-01-21 

1 

INŻYNIERIA BIOMEDYCZNA 

 
 

Plan 



Stan gazowy 



Prawa gazowe 



Gaz idealny a gaz rzeczywisty 



Oddziaływania międzycząsteczkowe 
 

Stan materii a stan skupienia  



Stan materii – podział  z punktu widzenia mikroskopowego 
(struktury jakie tworzą atomy, cząsteczki, jony) 



Stan skupienia - forma występowania materii (forma 
makroskopowa):  



Gazowy 



Ciekły 



Stały 

 

 

STAN GAZOWY            STAN CIEKŁY            STAN STAŁY 

uporządkowanie 

temperatura 

Opis stanu 



Objętość V: miara przestrzeni jaka zajmuje „próbka” [m

3

] 



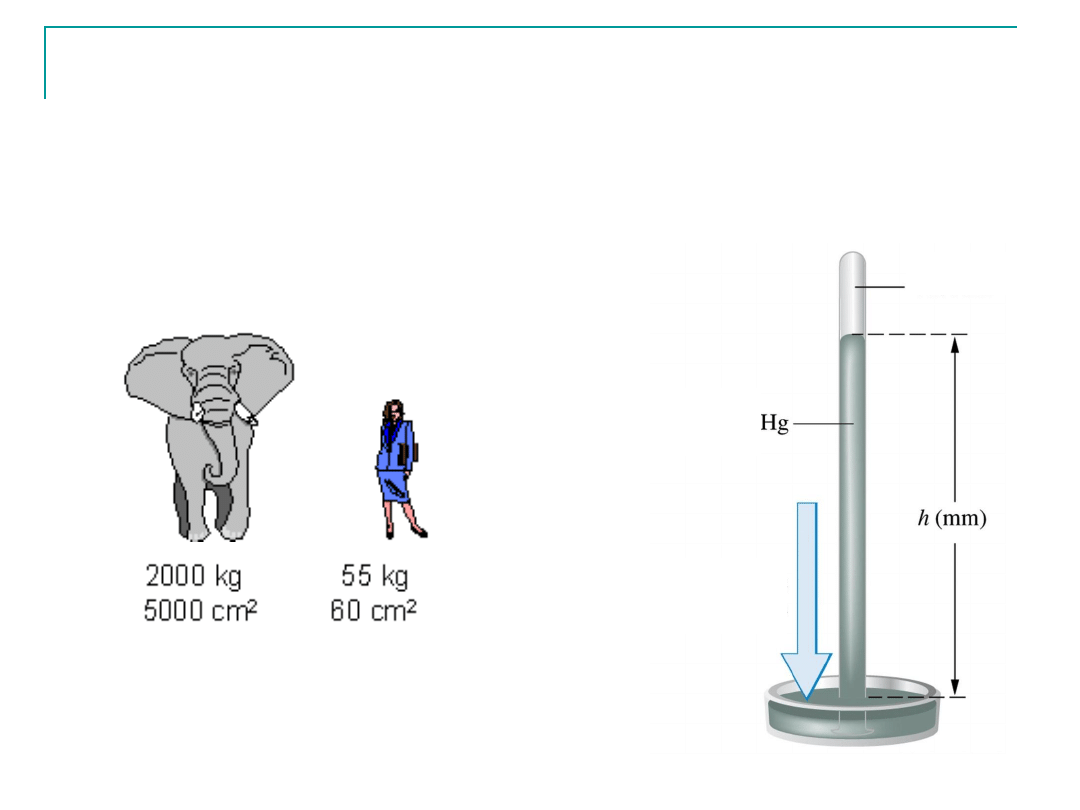
Ciśnienie: siła działająca na jednostkę powierzchni 



Jednostka w układzie SI [Pa]=[N

·m

-2

] 



1atm=760 mmHg=1013.25 hPa 

 

 

 

 

 

 

 



Temperatura T: [K] 



Ilość substancji n: [mol] 

próżnia 

ciśnienie 
atmosferyczne 

Cechy stanu gazowego  



Brak kształtu: 



Gaz przyjmuje kształt układu, w którym się znajduje 



Brak objętości: 



Gaz przyjmuje objętość układu, w którym się znajduje 



Średnia energia kinetyczna 

„elementów” tworzących gaz jest 

większa od 

średniej energii oddziaływania 

pomiędzy tymi 

„elementami” 
 

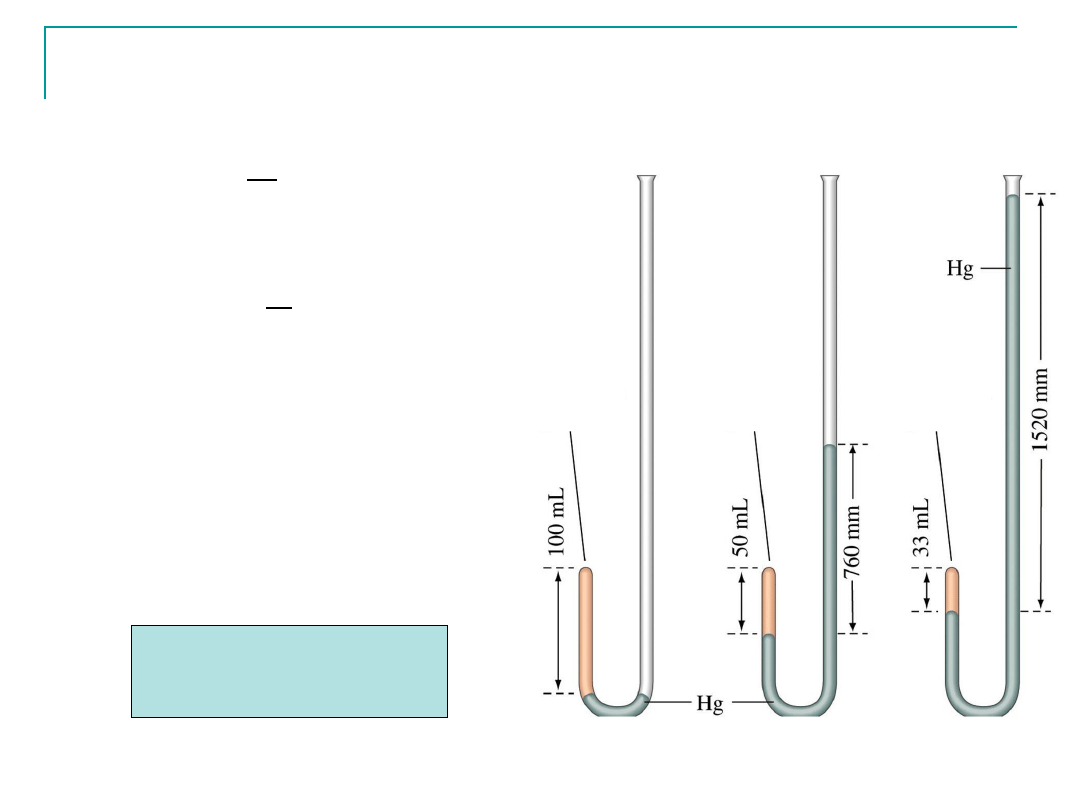
Prawa gazowe – prawo Boyle  

p

1

V



p

1

V

a



a



Vp

2

2

1

1

p

V

p

V





a

2

2

1

1

p

V

p

V



Gdzie     

V

-objętość,  

p

-ciśnienie, 

a

-stała 

Zamknięty 
gaz 

Zamknięty 
gaz 

Zamknięty 
gaz 

T=const, n=const 

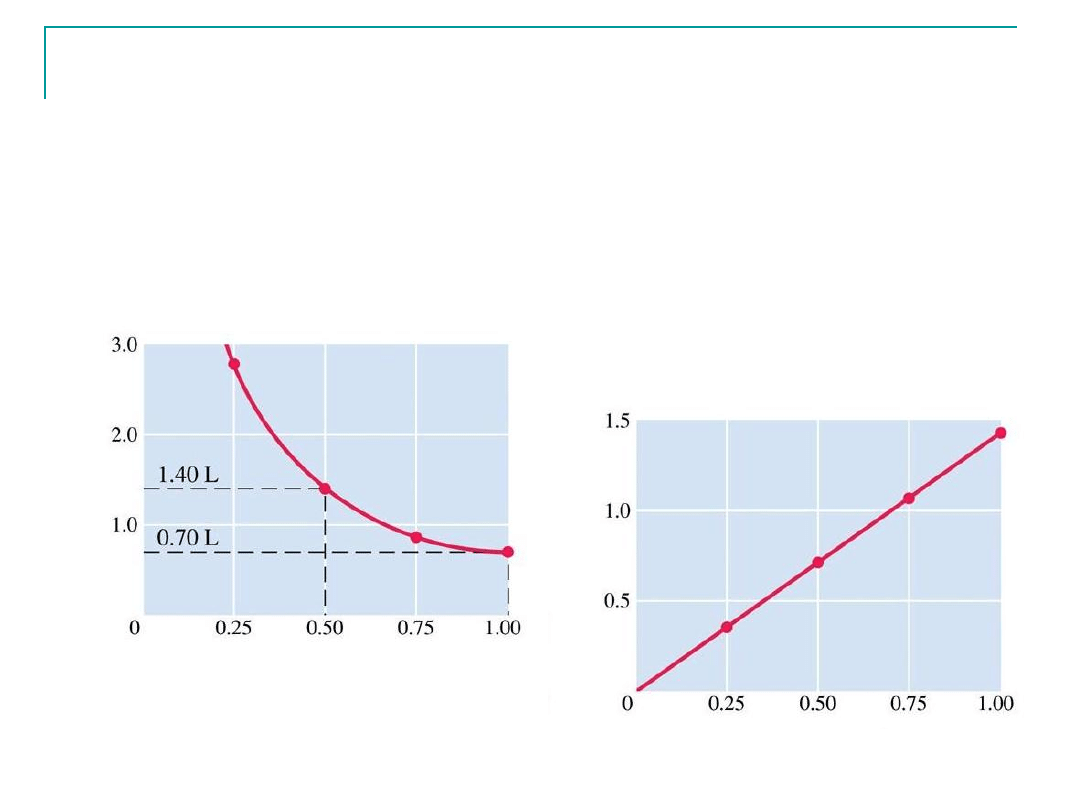
Prawo Boyle’a cd 



pV=const  jedynie w przybliżeniu opisuje relacje pomiędzy p i V  



Gaz który spełnia prawo Boyle’a nazywa się gazem idealnym 



Prawo to pozwala przewidzieć nową objętość gazu jeżeli 
zmienimy ciśnienie (przy T=const) lub vice versa: p

1

V

1

=p

2

V

2

 

ciśnienie (atm) 

ciśnienie (atm) 

Ob

jęto

ść 

(dm

3

) 

1

/V

 (

d

m

-3

) 

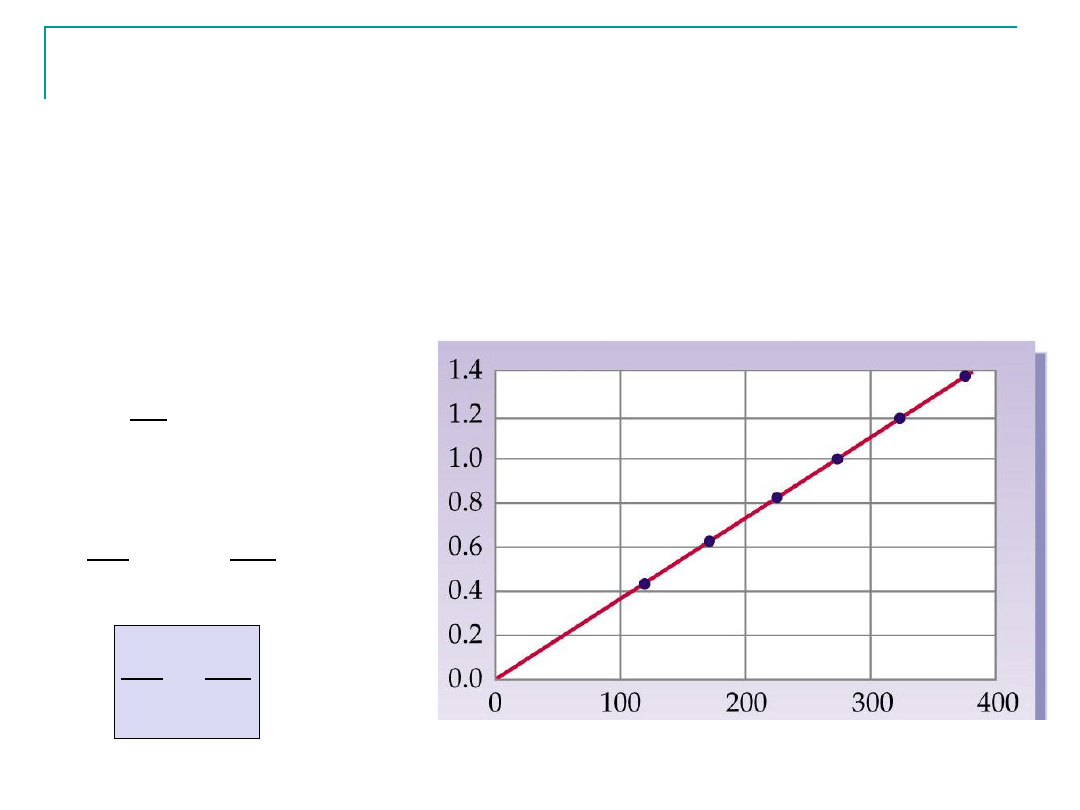
Prawo Charles’a 



J.Charles stwierdził, ze objętość gazu pod stałym ciśnieniem 
rośnie „liniowo” ze wzrostem temperatury dla określonej 
ilości gazu 

 

b



T

V

T

V



T

V

b



2

2

1

1

T

V

T

V





b

2

2

1

1

T

V

T

V



Gdzie     V-objętość,  
T-temperatura,       
b-stała 

Temperatura (K) 

Objęt

ość (m

3

) 

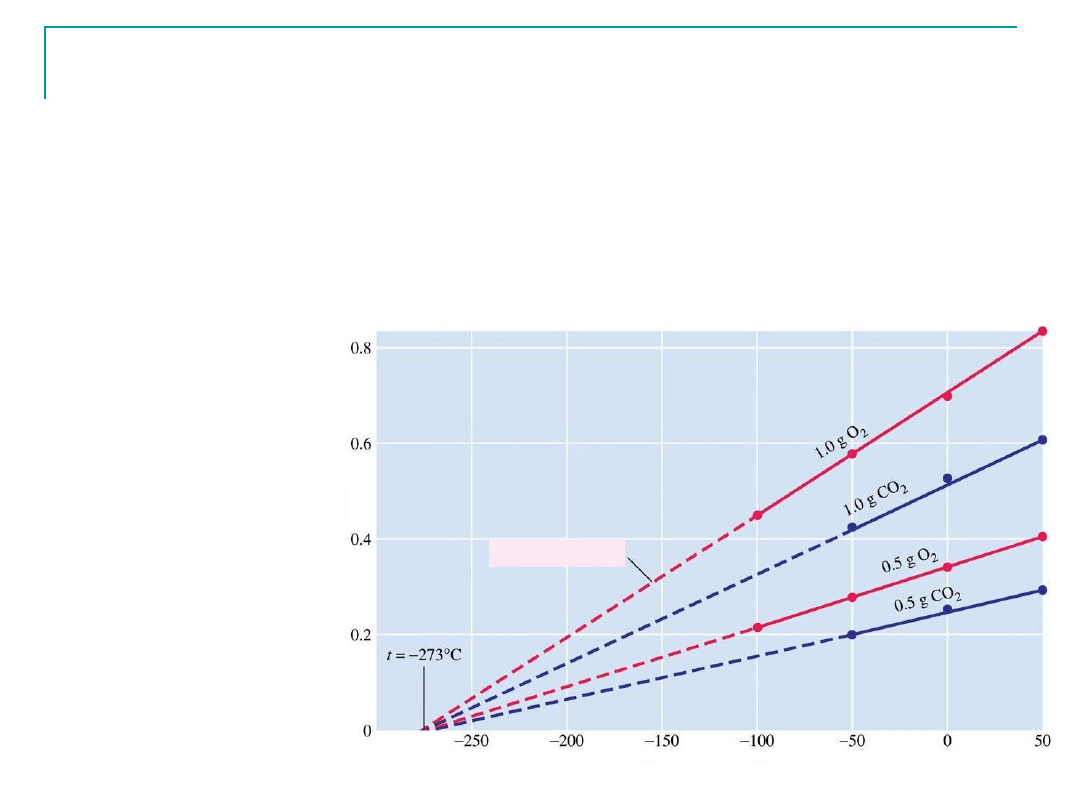
Prawo Charles’a cd 



Punkt charakterystyczny wykresu: dla wszystkich gazów 
objętość ekstrapolowana do zera jest w tym samym punkcie,    
-273.2

o

C  



W skali Kelwina, ten punkt definiowany jest jako 0 K (zero 
absolutne) 

 

 

Temperatura (

o

C) 

Ob

jęto

ść 

(dm

3

) 

Ekstrapolacja 

Kombinacja praw gazowych 



Każde z praw gazowych opisuje wpływ zmiany jednej z 
wielkości, jeżeli pozostałe dwa są stałe 



Dla stałej masy gazu 
 

 

p

T

V



p

T

d

V



d

T

Vp



2

2

2

1

1

1

T

p

V

d

T

p

V





2

2

2

1

1

1

T

p

V

T

p

V



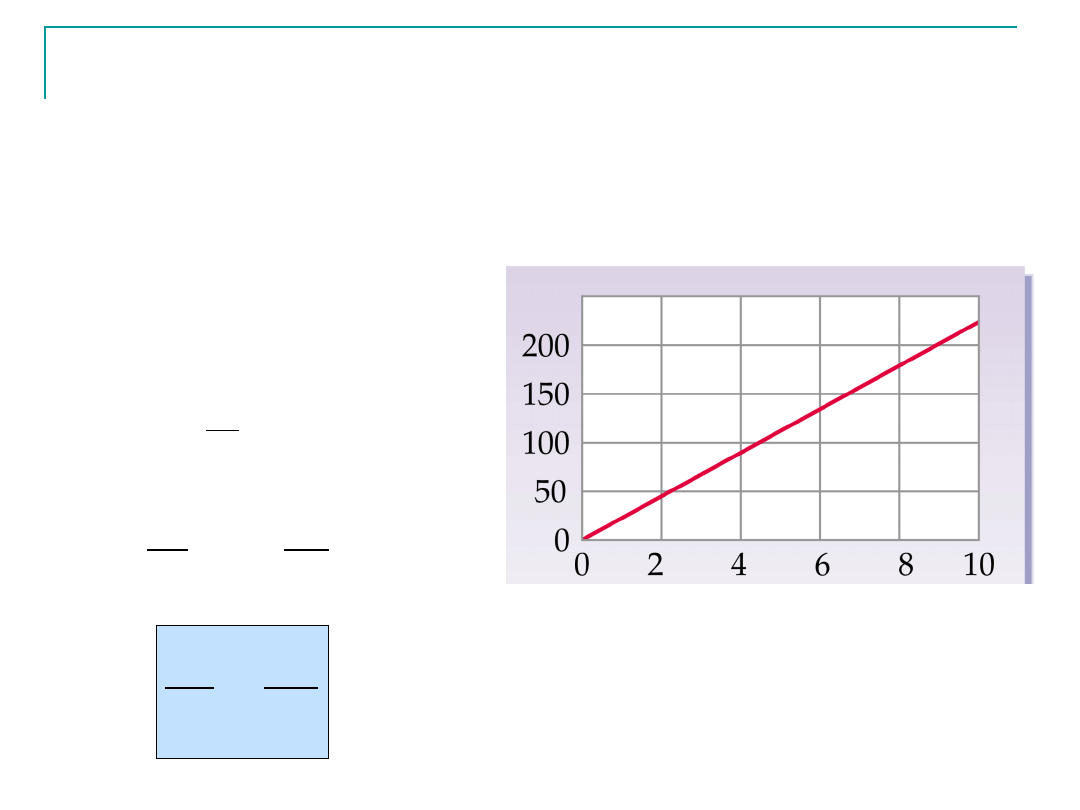
Prawo Avogadro 



A. Avogadro stwierdził, że równe objętości gazów w tej 
samej temperaturze i pod tym samym ciśnieniem  zawierają 
taka samą ilość „cząstek” 

 

n

V



n

V

c



c

n

V



2

2

1

1

n

V

c

n

V





2

2

1

1

n

V

n

V



Ilość moli 

Objęt

ość

 

Prawo gazu doskonałego 

p

T

n

V



p

T

n

R

V





nRT

pV



R- stała gazowa, 
R=8.314 J·(mol·K)

-1

 

2

2

2

2

1

1

1

1

T

n

V

p

T

n

V

p



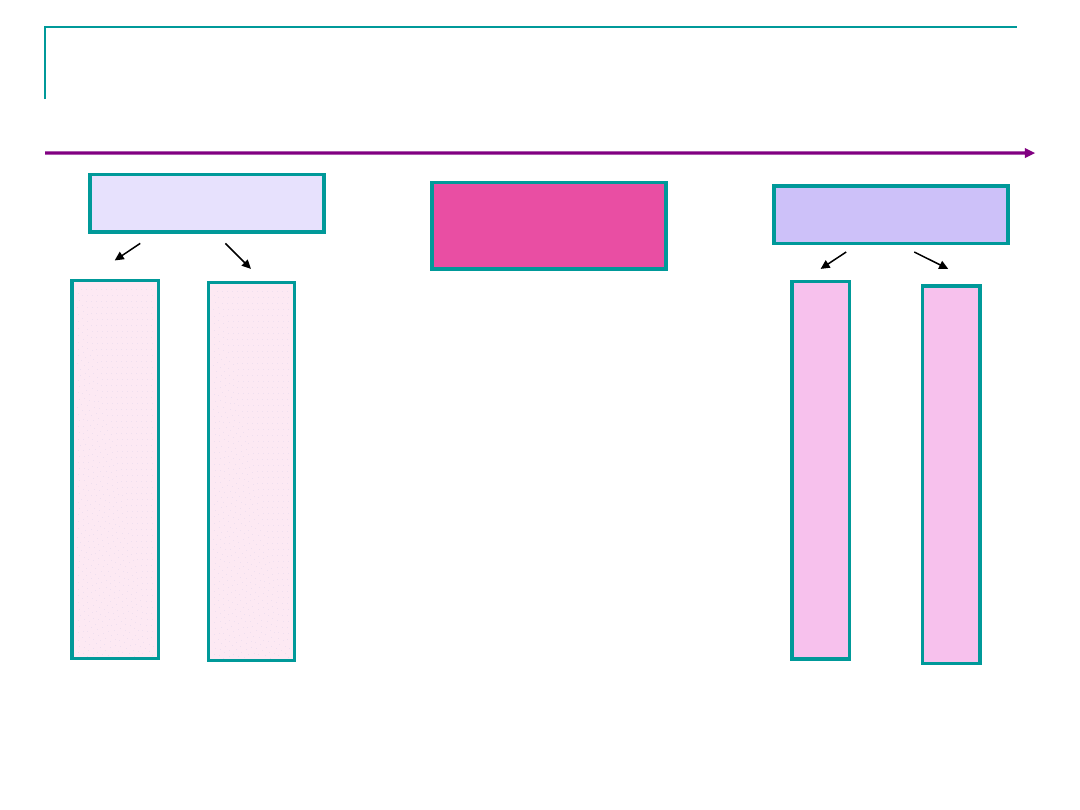
GAZOWY  STAN SKUPIENIA 

 

uporządkowanie 

STANY  MATERII W GRANICACH 

GAZOWEGO STANU SKUPIENI

A 

GAZ 

WŁAŚCIWY 

PLAZMA 

WY

SOK

O

-

TE

M

PERA

TURO

W

A

 

NIS

KO

-

TE

MPERA

TURO

W

A

 

NIENASYC

ON

A

 

NA

SYC

ONA

 

PARA 

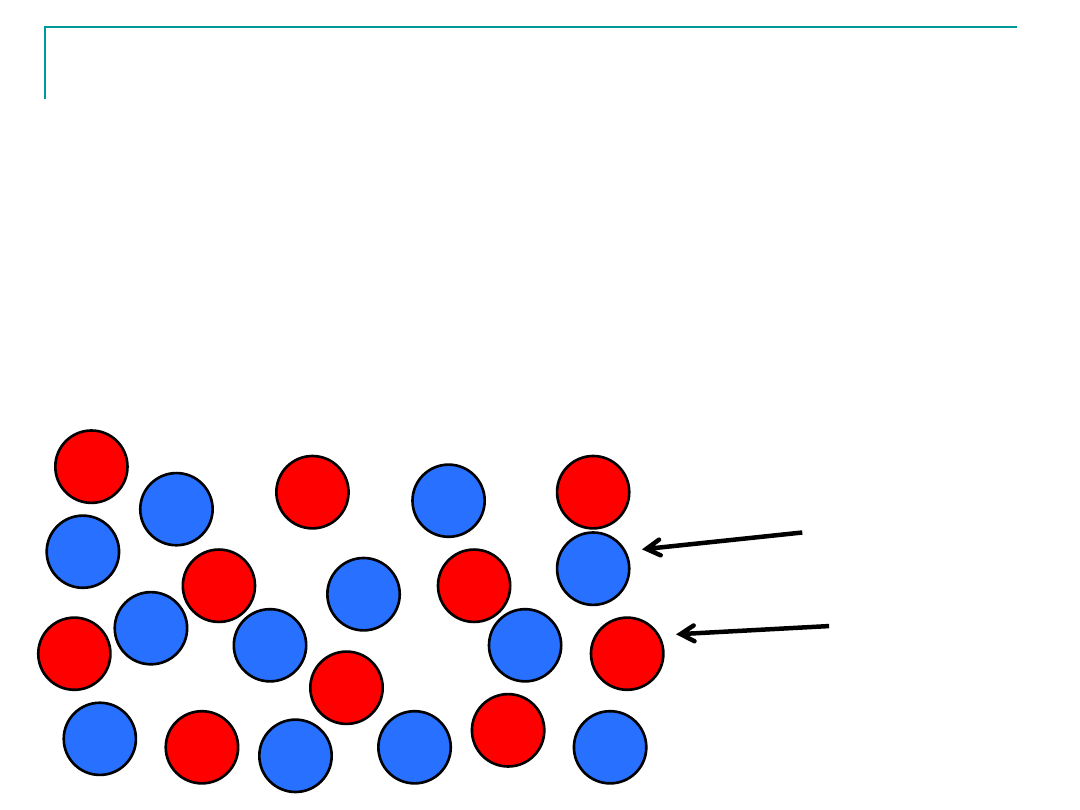
Plazma wysokotemperaturowa 

W  temperaturach  powyżej  10

5

-10

6

  K  atomy  ulegają 

całkowitej jonizacji tworząc nieuporządkowany stan 
materii  złożony  z  jąder  i  elektronów- 

PLAZMA 

WYSOKOTEMPERATUROWA 

 

 

elektron 
 
jadro 

Plazma wysokotemperaturowa 



Występowanie swobodnych ładunków elektrycznych 
o rozmiarach rzędu 10

-15

 m 



Silne oddziaływania elektrostatyczne i magnetyczne 
pomiędzy składnikami 

pV



nRT 



Emisja wyłącznie ciągłego widma fal 
elektromagnetycznych 

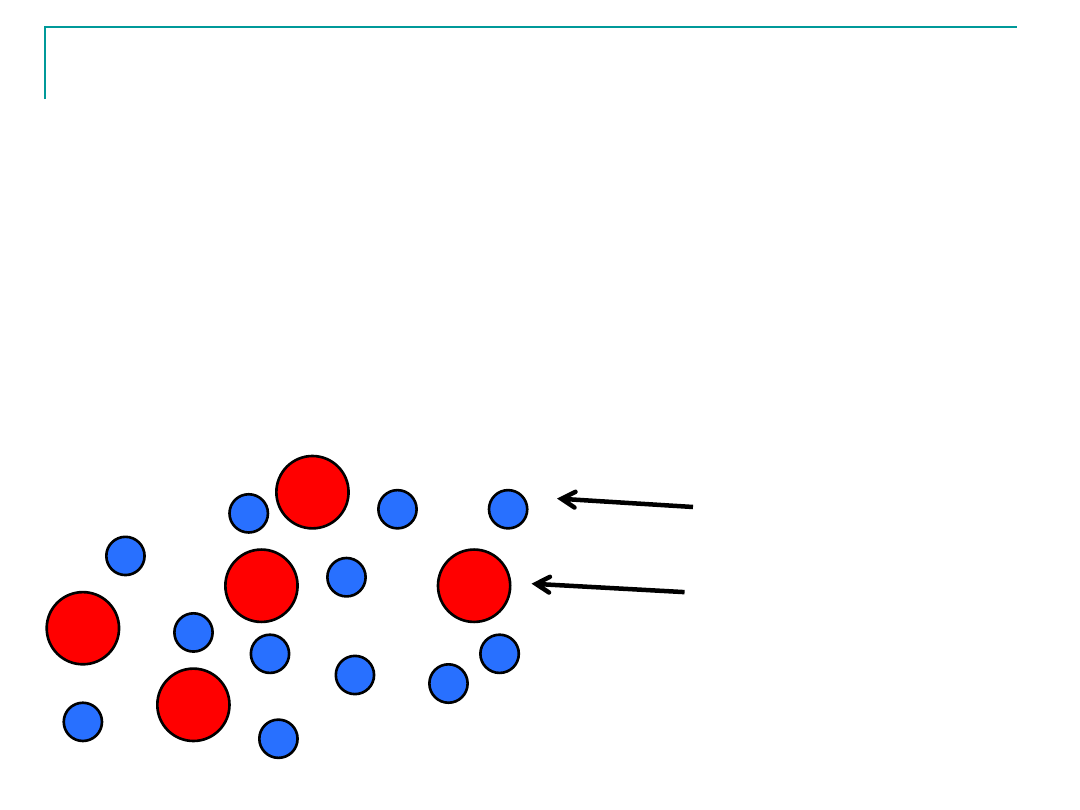
Plazma niskotemperaturowa 

W  temperaturach  >  10

3

K  atomy  ulegają  częściowej 

jonizacji  tworząc  nieuporządkowany  stan  materii 
złożony z jonów dodatnich i elektronów – 

PLAZMA 

NISKOTEMPERATUROWA 

 

 

elektron 
 
jon dodatni 

Plazma niskotemperaturowa 



Występowanie swobodnych ładunków elektrycznych 
o rozmiarach rzędu 10

-10

 m (jony dodatnie) i 10

-15

 m 

(elektrony) 



Silne oddziaływania elektrostatyczne i magnetyczne 
pomiędzy składnikami 

pV



nRT 



Emisja  ciągłego    i  charakterystycznego  widma  fal 
elektromagnetycznych 

 

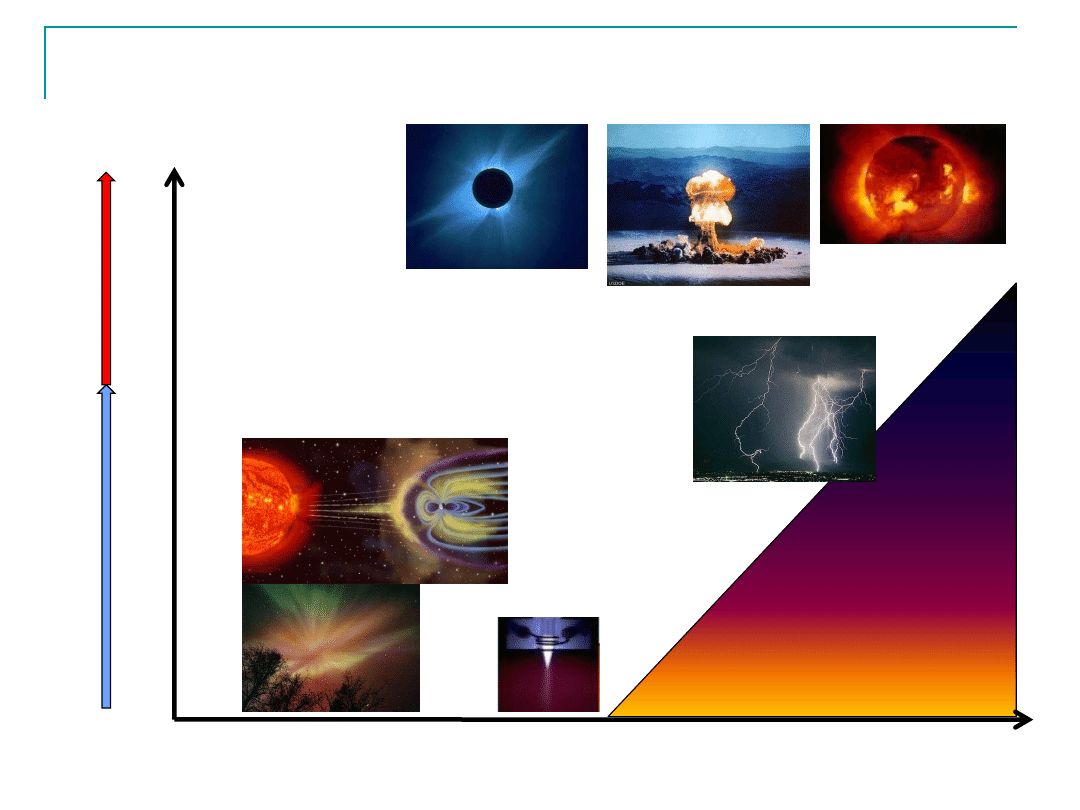
Plaz

m

a zi

m

na

 

niskote

m

per

at

urowa

 

Plaz

m

a gorąc

a 

wy

sokotempera

turowa

 

PLAZMA 

Koncentracja elektronów ( m 

-3

) 

10

3

  

           10

9

 

     10

15

                 10

21

 

     10

27

              10

33 

 

ciała stałe 

ciecze i gazy 

Niska temperatura 

Duża gęstość 

T

empera

tura

 [K]

 

10

6

 

 
   
 
 
10

5

 

 
 
 
 
10

4

 

 
 
 
 
10

3

 

 
 

Jądro słońca 

Synteza jądrowa 

Korona słońca 

Wiatr słoneczny 

Zorza 

Gaz właściwy 

 

W temperaturach od kilku do 1000-1500K atomy i cząsteczki 
praktycznie 

nie 

ulegają  jonizacji  mogąc  tworzyć 

nieuporządkowany  stan  materii  złożony  z  obojętnych 
atomów lub cząsteczek

 -  

GAZ  WŁAŚCIWY 

warunkiem istnienia stanu gazowego jest 

 

 

oddz

śr

kin

śr

E

E



Istnienie  silnych  oddziaływań  w  plazmie  było  wynikiem 
obecności  swobodnych  ładunków  elektrycznych  (dlatego  plazma 
nie może istnieć w niskich temperaturach) 

Słabe oddziaływania pomiędzy atomami i cząsteczkami 

gazów właściwych (co umożliwia ich istnienie w 

stosunkowo niskich temperaturach) są wynikiem 

istnienia 

sił międzycząsteczkowych 

zwanych 

siłami 

Van der Waalsa 

Siły międzycząsteczkowe 

Gaz właściwy składa się z atomów, których moment 

dipolowy 



=0, lub cząsteczek dla których 



0 

- 

 + 

atom   

cząsteczka   

cząsteczka 



=0    

   



=0  

 

 



0 

Oddziaływanie dipol-dipol 

- 

 + 

- 

 + 

F

4

 

F

3

 

F

1

 

F

2

 

F

1

+F

2

 

> 

F

3

+F

4

  

Oddziaływanie dipol- indukowany dipol 
 

duża odległość 

mała odległość 

indukowane 

dipole 

trwałe dipole 

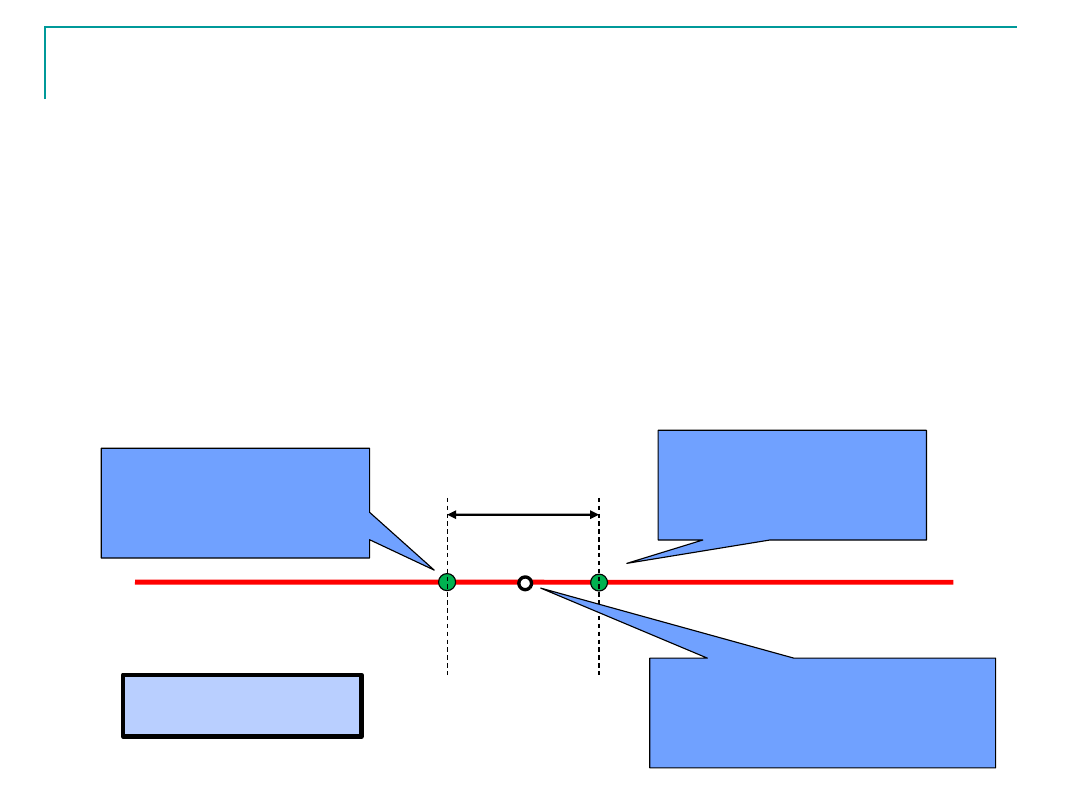
Siły międzycząsteczkowe: siły dyspersyjne Londona 

W każdym atomie lub cząsteczce środki ładunku dodatniego 
i  ujemnego  wykonują  ruch  drgający  wokół  położenia 
równowagi,  które  jest  wspólne  w  przypadku  cząsteczek 
(atomów) mających zerowy moment dipolowy (



=0) 

Chwilowe 
położenie q

(-)

  

Położenie równowagi 
dla q

(+)

 i  q

(-)

  

Chwilowe 
położenie q

(+)

  

l 



chwil

=q·l 

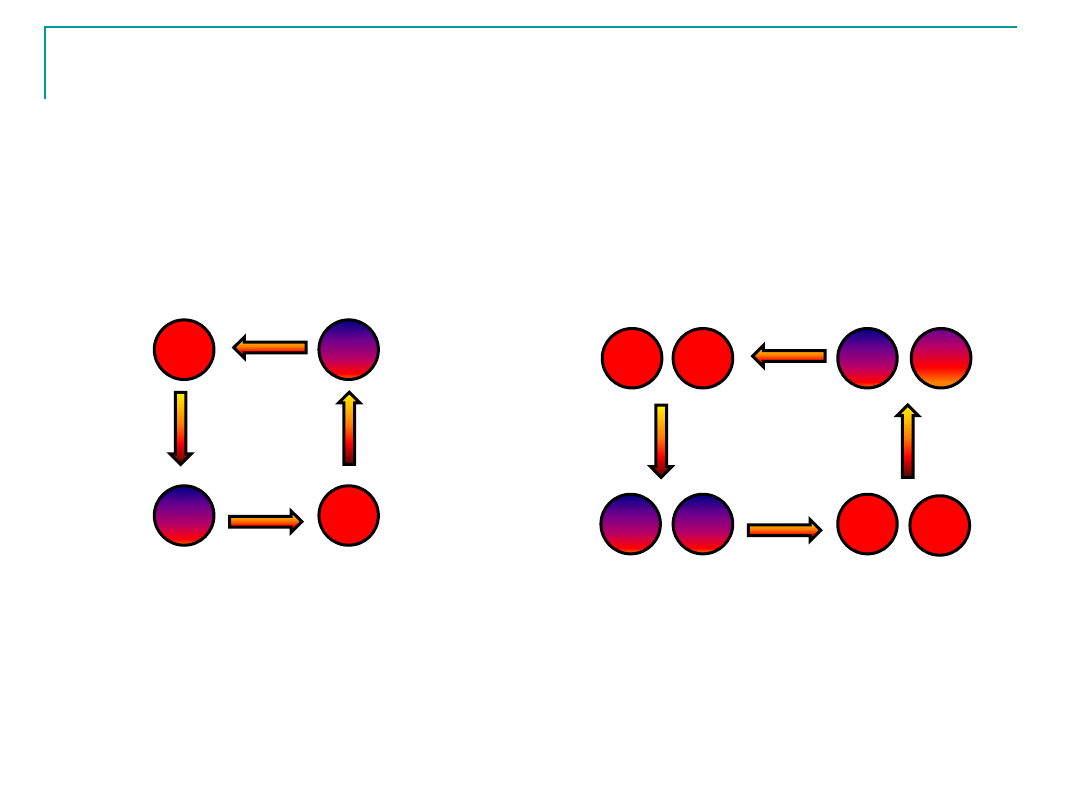
Siły międzycząsteczkowe: siły dyspersyjne Londona 

Każda cząsteczka (nawet taka, 
dla której 



=0) jest drgającym 

dipolem elektrycznym 

 

 

 

 

 

 

Czyli 



=0 oznacza tylko, 

że średni w czasie moment 
dipolowy wynosi zero 

Jeżeli dwie cząsteczki 
znajdują się blisko siebie… 

 

 

 

 

 

 

 

przyciąganie 

przyciąganie 

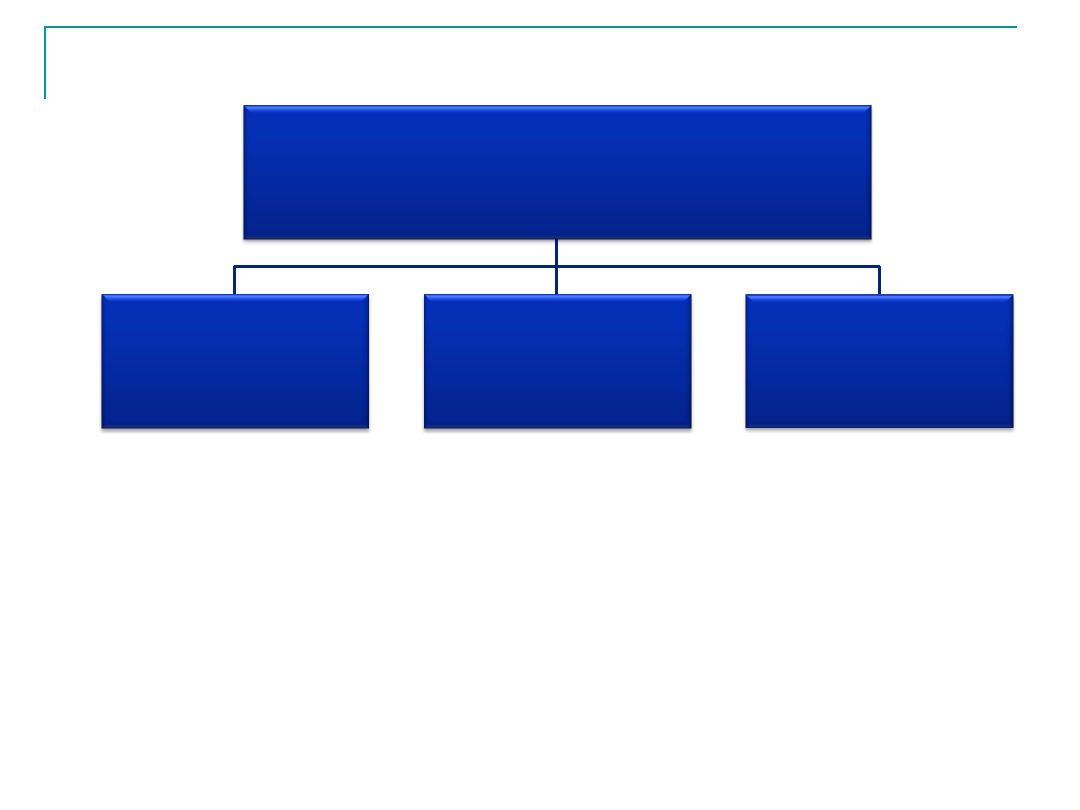
Siły międzycząsteczkowe 

Siły Van der Waalsa  

Oddziaływanie 

dipol-dipol 

Siły dyspersyjne 

(Londona) 

Oddziaływanie 

dipol-

indukowany dipol 

Teoria kinetyczna gazów 



Model stanu gazowego 



założenia 

1. Cząsteczki są punktami materialnymi (mają masę, nie 

posiadają wymiarów) 

2. Gaz składa się z cząsteczek, które znajdują się w 

ciągłym ruchu 

3. Cząsteczki nie oddziaływają na siebie za wyjątkiem 

momentu zderzeń (zderzenia sprężyste) 

Teoria kinetyczna gazów cd 



Jaki jest związek pomiędzy energią cząsteczek gazu a temperaturą 

w której się znajduje? 

 

Średnia energia kinetyczna ruchu postępowego cząsteczki gazu w temperaturze 
wynosi:  
 

 

 

 

 

gdzie   jest stałą Boltzmanna k=1.38

·10

-23 

J•K

-1

 



Średnia energia kinetyczna cząsteczki jest wprost 

proporcjonalna do temperatury bezwzględnej 



Średnia energia kinetyczna cząsteczki nie zależy od jej masy! 



 Na każdy stopień swobody ruchu cząstki przypada energia.      

W przypadku ruchu postępowego cząstka ma trzy stopnie 

swobody: związane z ruchem wzdłuż osi.  



Dla gazów jednoatomowych  jest to jedyny wkład do energii 
kinetycznej 

 

kT

2

3

E

śr



A

N

R

k



Teoria kinetyczna gazów cd 



W przypadku cząsteczki dwuatomowej cząsteczka ma 
również wkład do energii kinetycznej związany z jej ruchem 
obrotowym wokół dwóch osi prostopadłych do osi łączących 
atomy.  

  

 

 



W przypadku cząsteczki składającej się z trzech lub więcej 
atomów są trzy stopnie swobody związane z ruchem 
obrotowym (obroty wokół trzech prostopadłych osi), w 
związku z tym energia kinetyczna cząsteczki wynosi:  

 

 

kT

2

5

E

śr



3kT

kT

2

6

E

śr





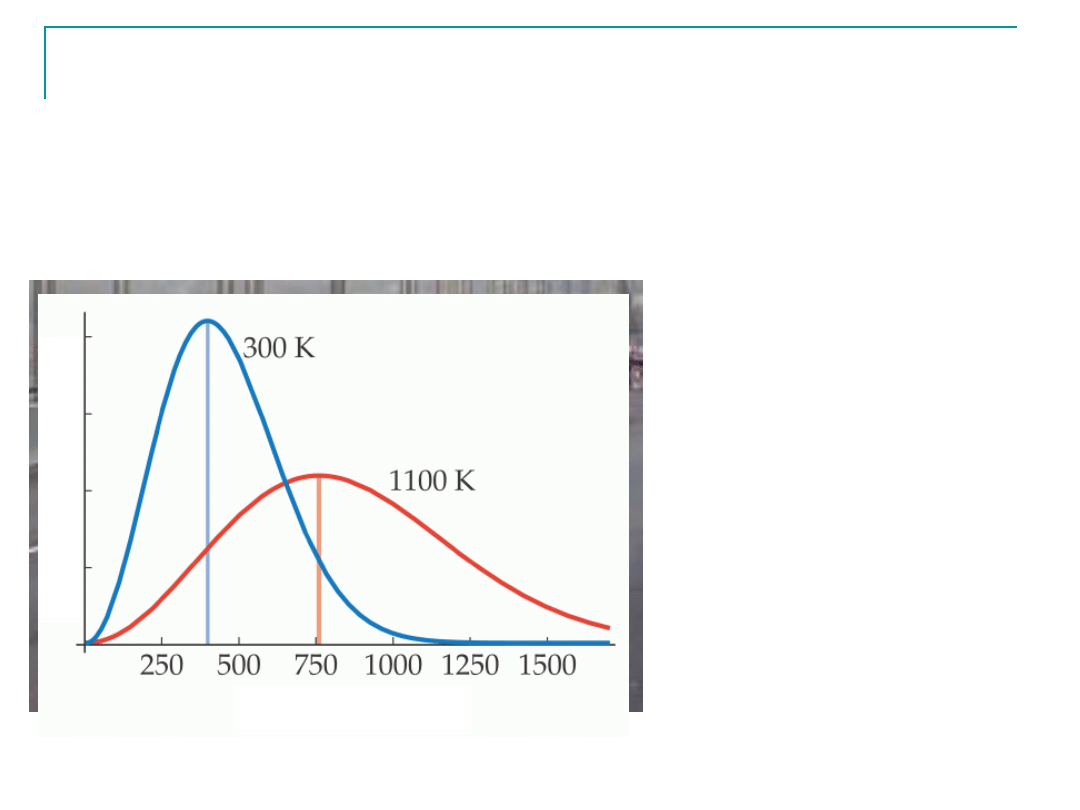
Rozkład prędkości Maxwella 



Rozkład szybkości cząsteczek- ułamek cząsteczek poruszających się z 
określoną szybkością 



J.M.Maxwell zaproponował matematyczną funkcji rozkładu (koniec XIX) 

 

 

•Jedynie niewielki ułamek 
cząsteczek porusza się z 
szybkościami znacznie 
mniejszymi lub znacznie 
większymi od szybkości 
średniej  

•Ze wzrostem temperatury 
następuje „poszerzenie” 
rozkładu i przesuniecie 
wartości średniej ku 
większym szybkościom 

prędkość (m/s) 

Li

cz

ba 

cz

ąste

k 

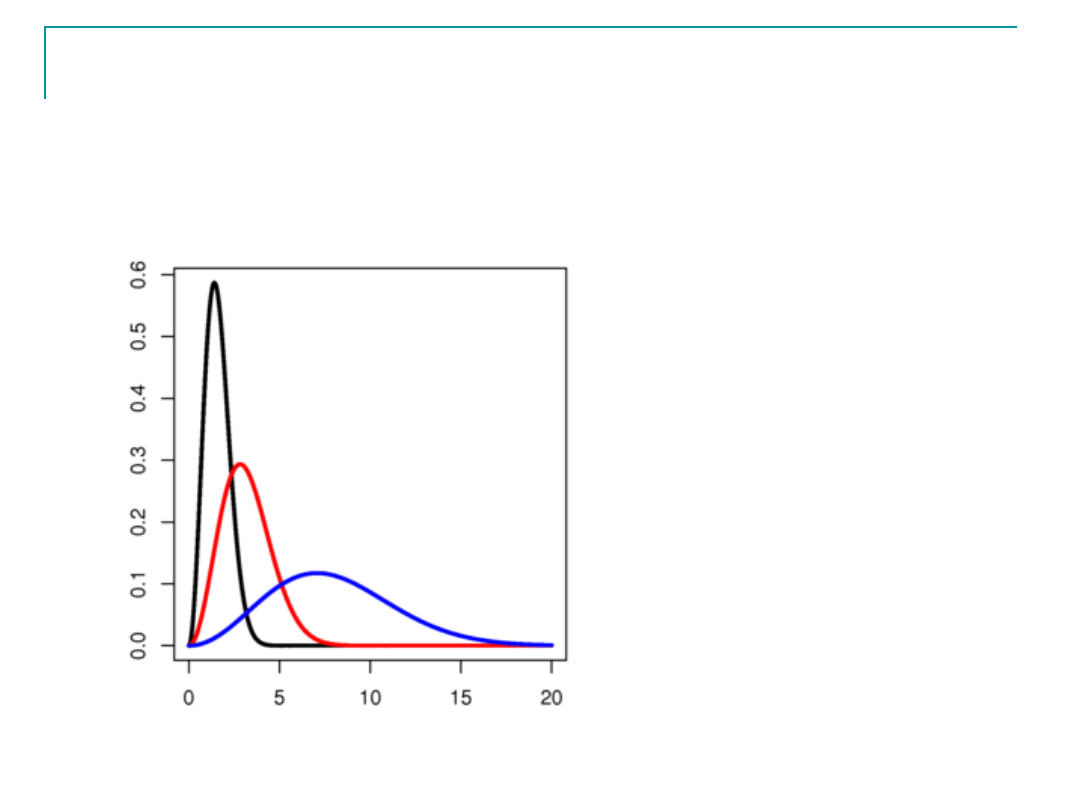
Rozkład szybkości Maxwella cd 



Rozkład szybkości dla cząsteczek o różnych masach molowych 

 

•Szybkość średnia ciężkich 
cząsteczek jest w danej 
temperaturze mniejsza niż 
szybkość średnia 
cząsteczek lekkich 

•Cząsteczki cięższe  
wykazują znacznie węższy 
rozkład szybkości, 
większość z nich porusza 
się z szybkościami 
zbliżonymi do średniej 

duża  masa 
molowa 

mała  masa 
molowa 

średnia  masa 
molowa 

prędkość (m/s) 

Li

cz

ba 

cz

ąstek

 

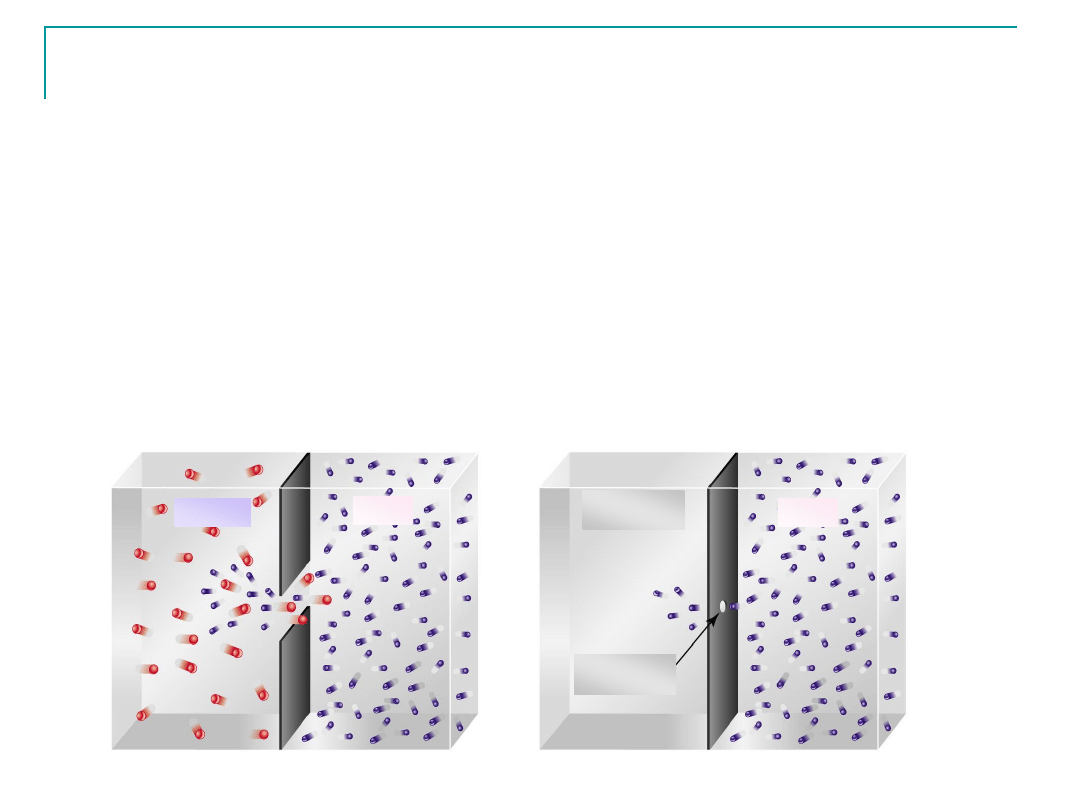
Dyfuzja i efuzja 



Dyfuzja - samorzutny proces mieszania się cząsteczek dwóch substancji 



Efuzja – proces  wypływu gazu ze zbiornika przez mały otwór  



Ze wzrostem temperatury następuje wzrost szybkości dyfuzji i efuzji 



Szybkości procesów dyfuzji i efuzji  są tym mniejsze im większe są masy 
molowe gazów 



Prawo efuzji Grahama: w danych warunkach temperatury i ciśnienia 
szybkość efuzji gazu jest odwrotnie proporcjonalna do pierwiastka 
kwadratowego z jego masy molowej 

 

otwór 

próżnia 

Gaz 2 

Gaz 1 

Gaz 

Gazy rzeczywiste 



Jakie są przyczyny odstępstwa od prawa gazu 
doskonałego? 



Istnienie oddziaływań międzycząsteczkowych 



Występowanie objętości cząsteczek 

 

nRT

pV



•Przybliżenie jest tym lepsze im średnie odległości 
cząsteczek gazu są większe od średnic cząsteczek 

•Warunek ten spełniony jest dla niskich wartości ciśnień i 
wysokich temperatur 

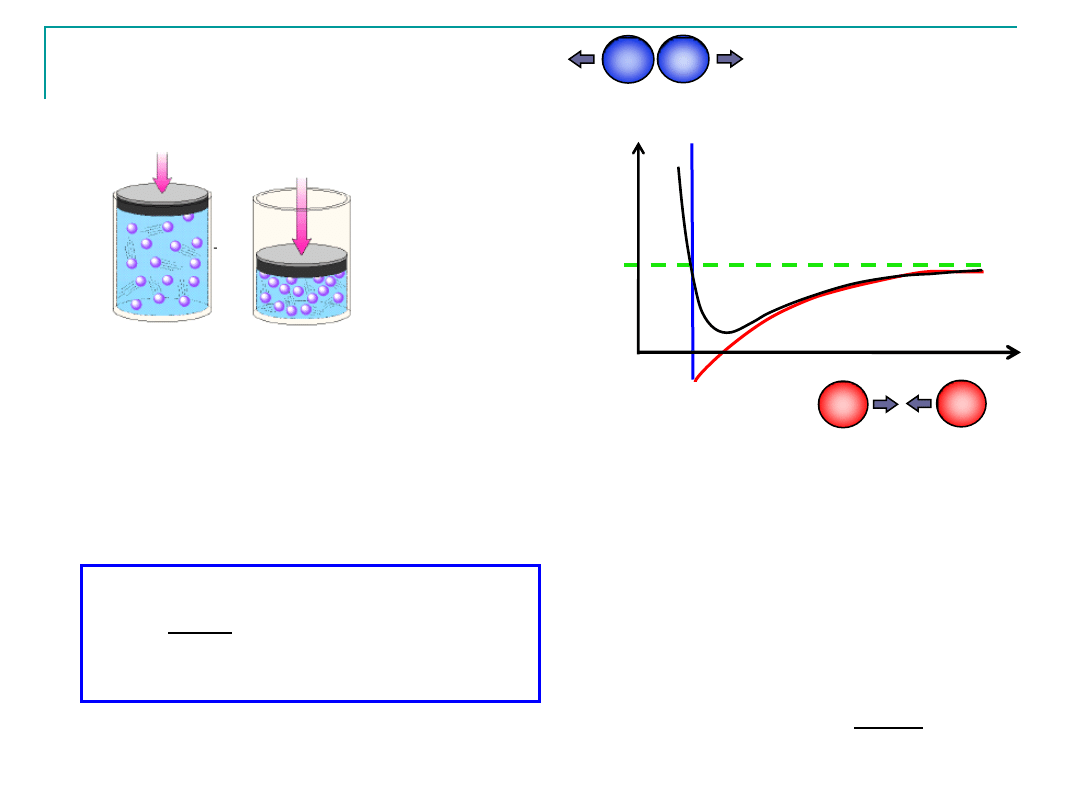
Gazy rzeczywiste 

2

2

eff

V

a

n

p

p





b

n

V

V

eff







nRT

V

p

ideal

ideal



U(r) 

Mała odległość 

odpychanie 

Duża odległość 

Przyciąganie

  

r 

Siły dalekiego zasięgu 

Siły przyciągania-tendencja do 
trzymania się razem 

Efektem jest dodatkowa kompresja 
gazu 

Siły krótkiego zasięgu  





nRT

b

n

V

V

a

n

p

2

2





















0 

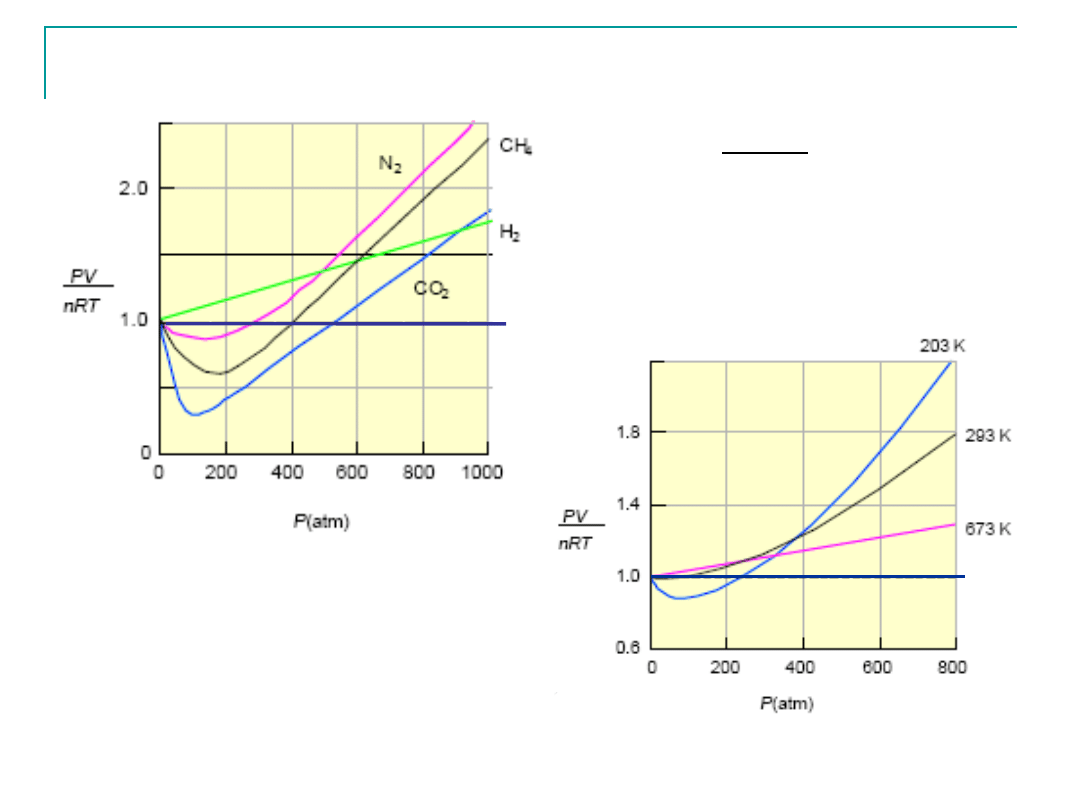
Gaz rzeczywisty 

Gaz 
idealny 

Gaz 
idealny 

1

nRT

pV



Gaz rzeczywisty cd 



azot N

2

 ................................  22,401 dm

3 



amoniak NH

3 

....................... 22,089 dm

3 



ditlenek siarki SO

2

 ............... 21,888 dm

3 



siarkowodór H

2

S .................. 22,145 dm

3 

W warunkach standardowych T=273K, p=1atm   
1 mol gazu idealnego zajmuje objętość 22.43 dm

3

 

Obniżamy temperaturę gazu rzeczywistego 
 



Średnia energia cząstek gazu maleje: 



Energia oddziaływań międzycząsteczkowych prawie nie 
ulega zmianie  

 



Gdy sprężymy gaz w którym  

  możliwe jest tworzenie się agregatów cząsteczek o 

rozmiarach nie przekraczających pewnej 

wartości 

krytycznej 



Taki stan gazowy materii nazywamy 

PARĄ 

NIENASYCONĄ  



Granicę pomiędzy gazem a parą nienasyconą określa T

K 

zwana temperaturą krytyczną 

 

kT

E

śr

2

3



oddz
śr

kin

śr

E

E



oddz
śr

kin

śr

E

E



oddz
śr

kin

śr

E

E



temperatura 

T

k

 

PARA

 

NIENASYCONA 

GAZ WŁAŚCIWY 

oddz
śr

kin

śr

E

E



oddz
śr

kin

śr

E

E



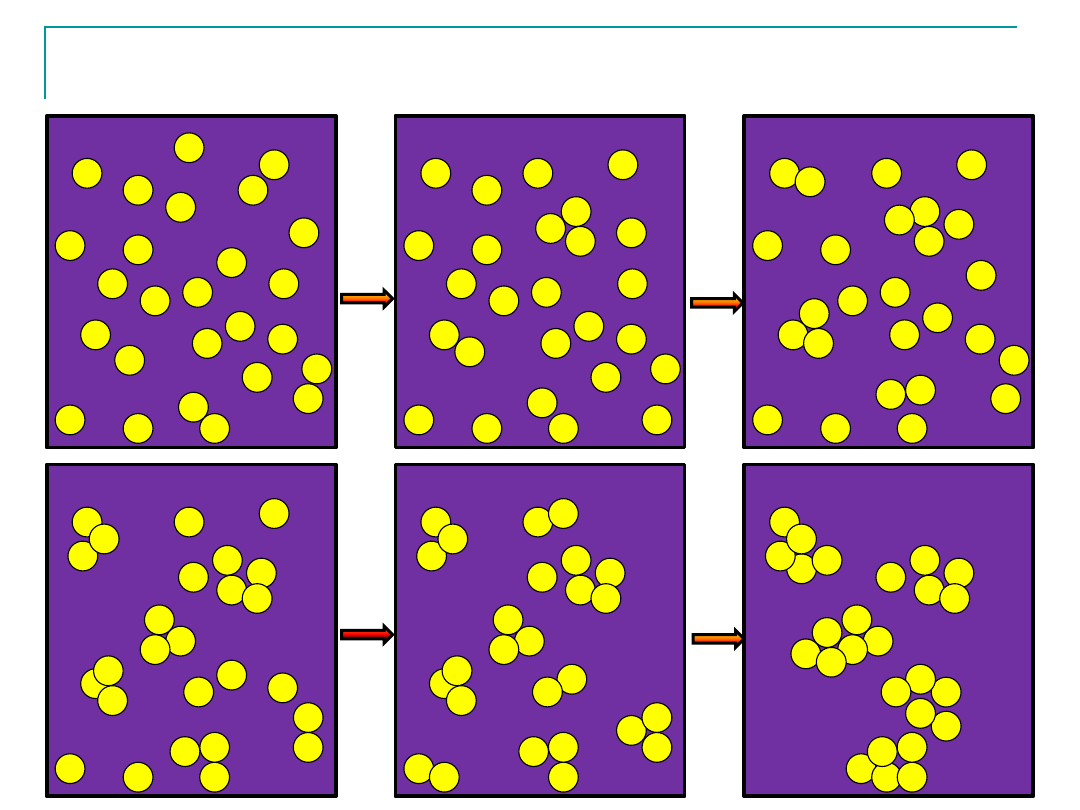
Jak zachowuje się para nienasycona przy podwyższaniu ciśnienia 
lub przy obniżaniu temperatury? 

2012-01-21 

40 

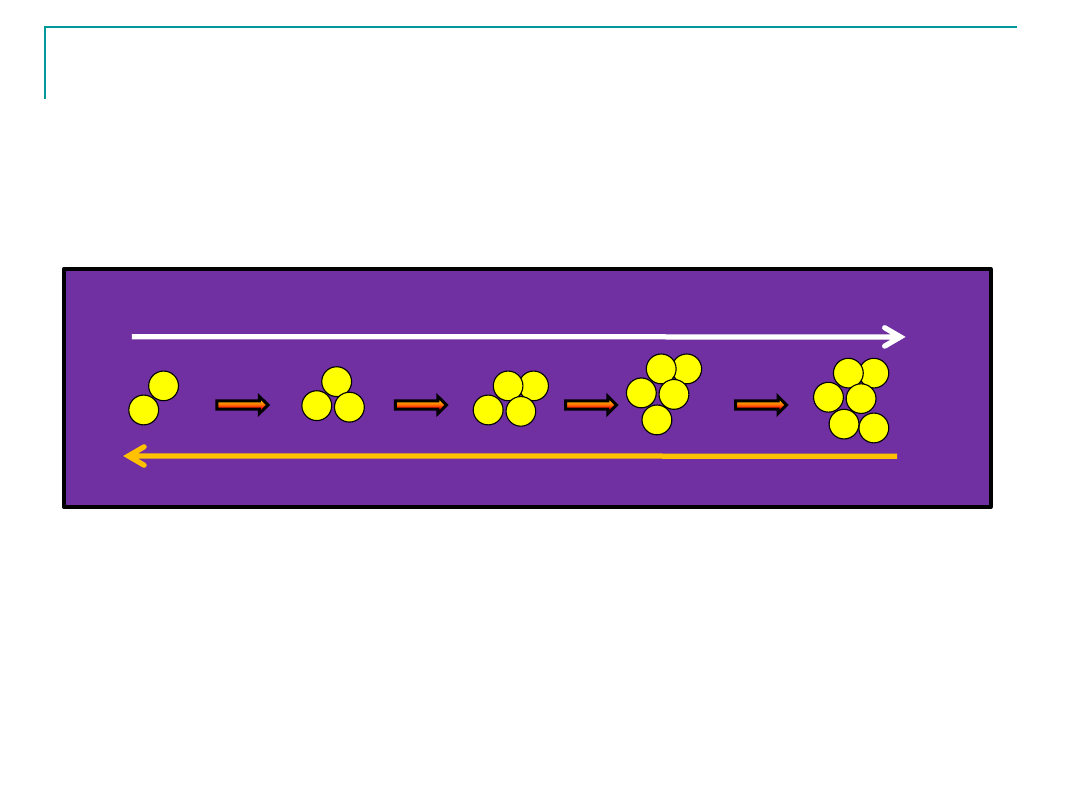
Para nienasycona 



 para nasycona 

 

Przy obniżaniu temperatury lub podwyższaniu 

ciśnienia pary nienasyconej wzrasta przeciętny 

rozmiar agregatów cząsteczek 

 

 

 

 

 

 

  ..agregaty  takie  tworzą  się  i  rozpadają  z  szybkością 

zależną od rodzaju cząsteczek, temperatury, ciśnienia 
oraz 

rozmiarów  agregatów  (czyli  od  liczby 

cząsteczek w agregacie),  

 

 

 

 

ciśnienie 

temperatura 

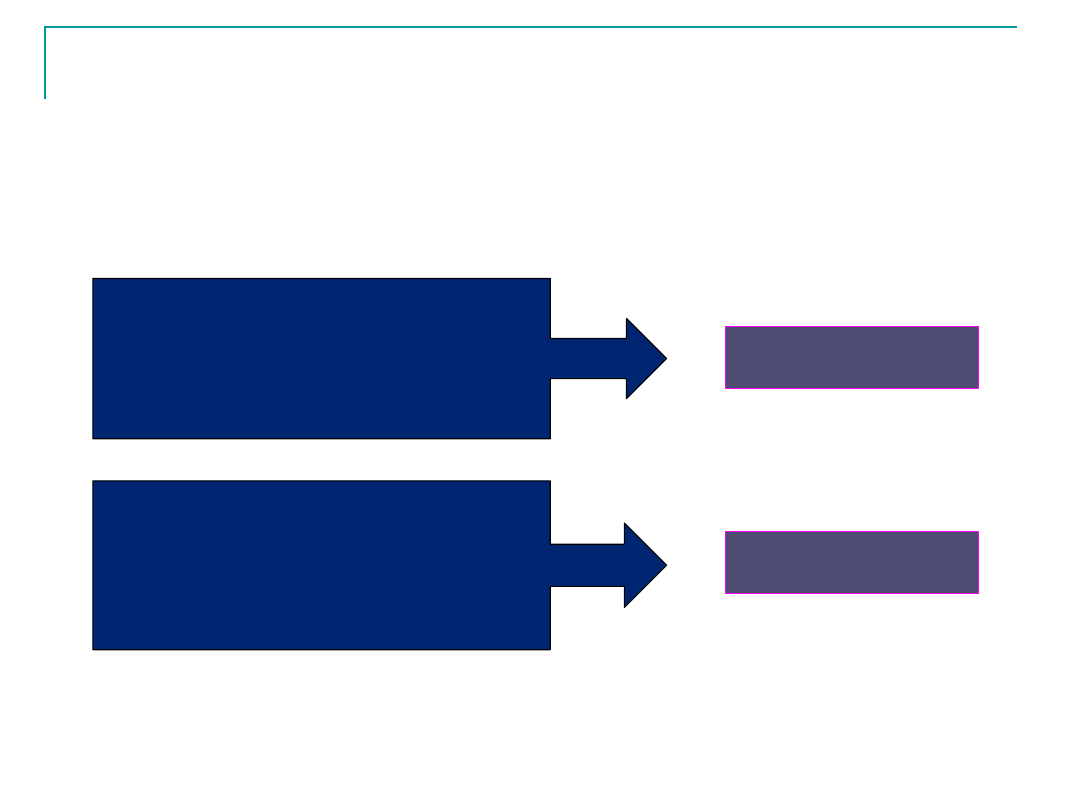
Dla każdej temperatury poniżej temperatury krytycznej T

K

 istnieje 

takie  ciśnienie,  przy  którym  rozmiary  agregatów  cząsteczek 
osiągają  wartość  krytyczną,  to  znaczy  taką  począwszy  od  której, 
szybkość  wzrostu  v

wzr

  agregatu    przewyższa  szybkość  jego 

rozpadu v

rozp

 

Rozmiary agregatów są 

MNIEJSZE 

od rozmiarów 

krytycznych   

Rozmiary agregatów są 

WIĘKSZE 

od rozmiarów 

krytycznych   

V

rozp

 >V

wzr

 

V

rozp

 <V

wzr

 

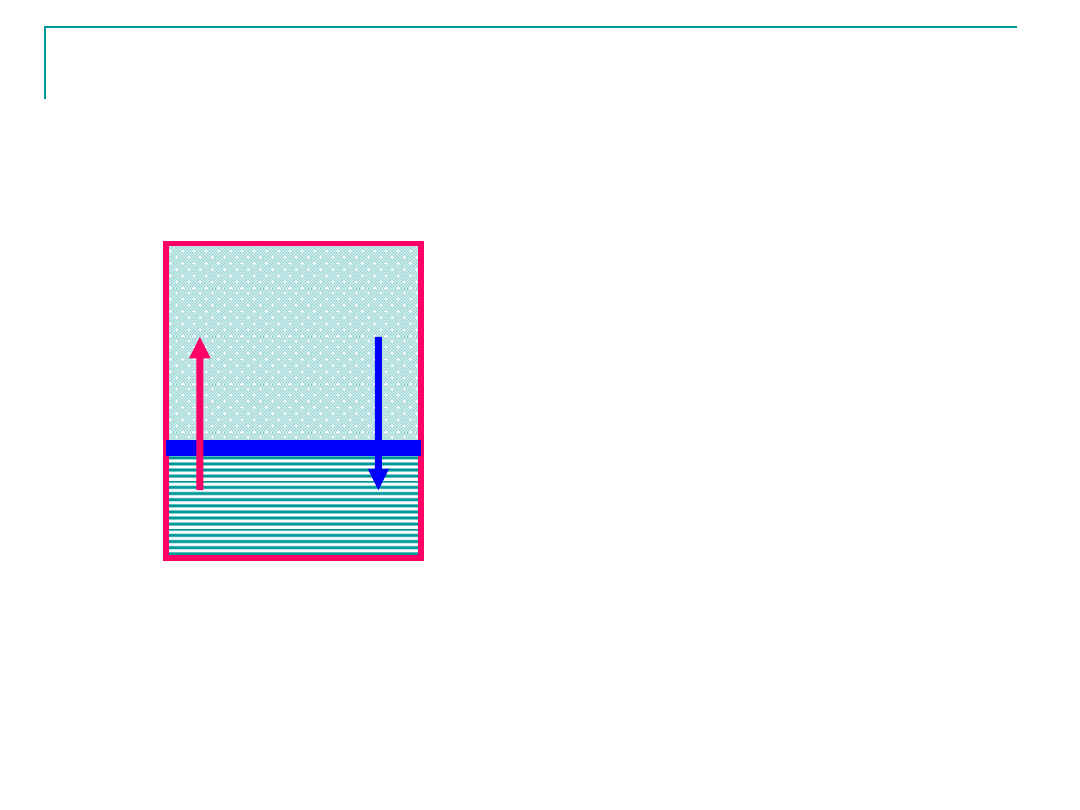
Równowaga ciecz-para 

Para 

 

 

 

Ciecz 

 

v

par 

v

kon 

V

par

 – szybkość parowania 

V

kon

 – szybkość kondensacji 

 

W stanie równowagi, w 
stałej temperaturze:  

V

par

=V

kon 

W takim stanie para nad cieczą osiąga maksymalne 
ciśnienie  p

R

  (w  stałej  temperaturze),  które  jest 

ciśnieniem pary nasyconej  

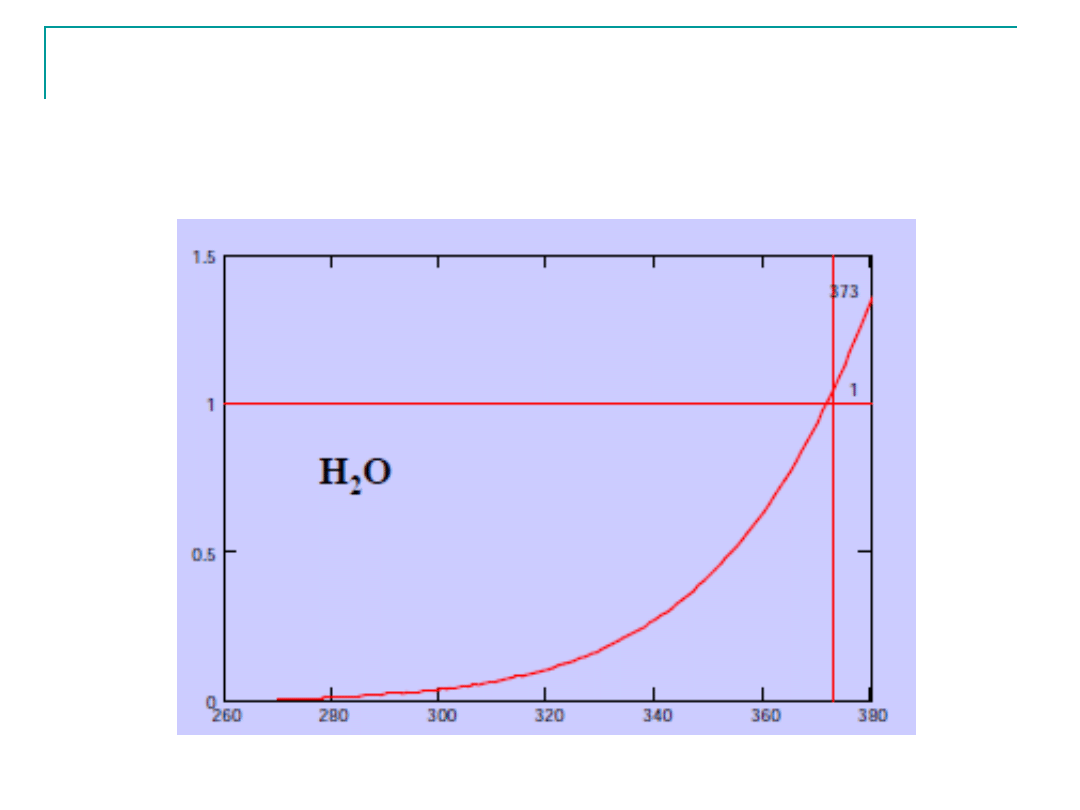
Para nasycona 

Para nasycona (definicja) to para, która w danej 

temperaturze osiągnęła maksymalne ciśnienie

 

Temperatura (K) 

Ciśni

eni

e 

(at

m

) 

 

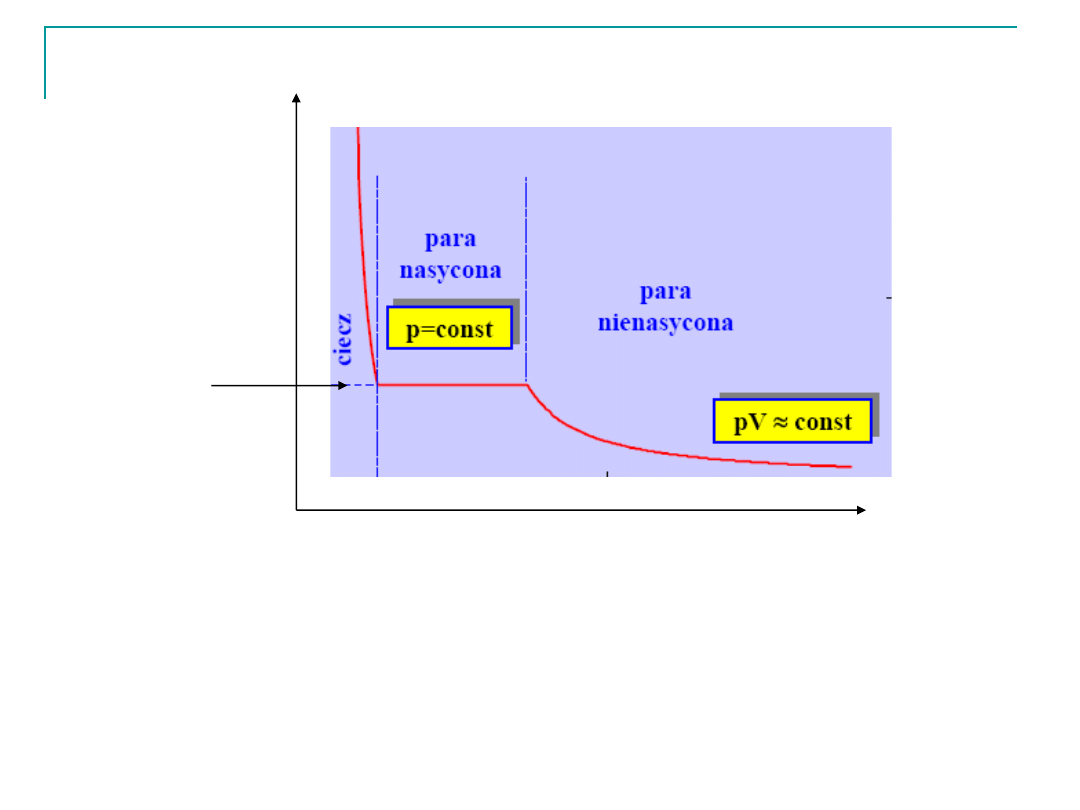
Rozważmy sytuację, w której para nienasycona o temperaturze 
T<T

K

 poddana jest sprężaniu 

objętość 

ci

śnie

nie

 

pk 

Para nasycona to para w równowadze z cieczą, z której powstała. 
Para  ta  ma  największe  możliwe  dla  danej  temperatury  ciśnienie  i  gęstość. 
Ciśnienie  pary  nasyconej  jest  niezależne  od  objętości.  Zmniejszanie 
objętości w stałej temperaturze powoduje skraplanie pary, a stan równowagi 
w  dalszym  ciągu  istnieje.  Zwiększanie  objętości  powoduje  wyparowanie 
cieczy bez obniżenia ciśnienia pary nasyconej.  

 

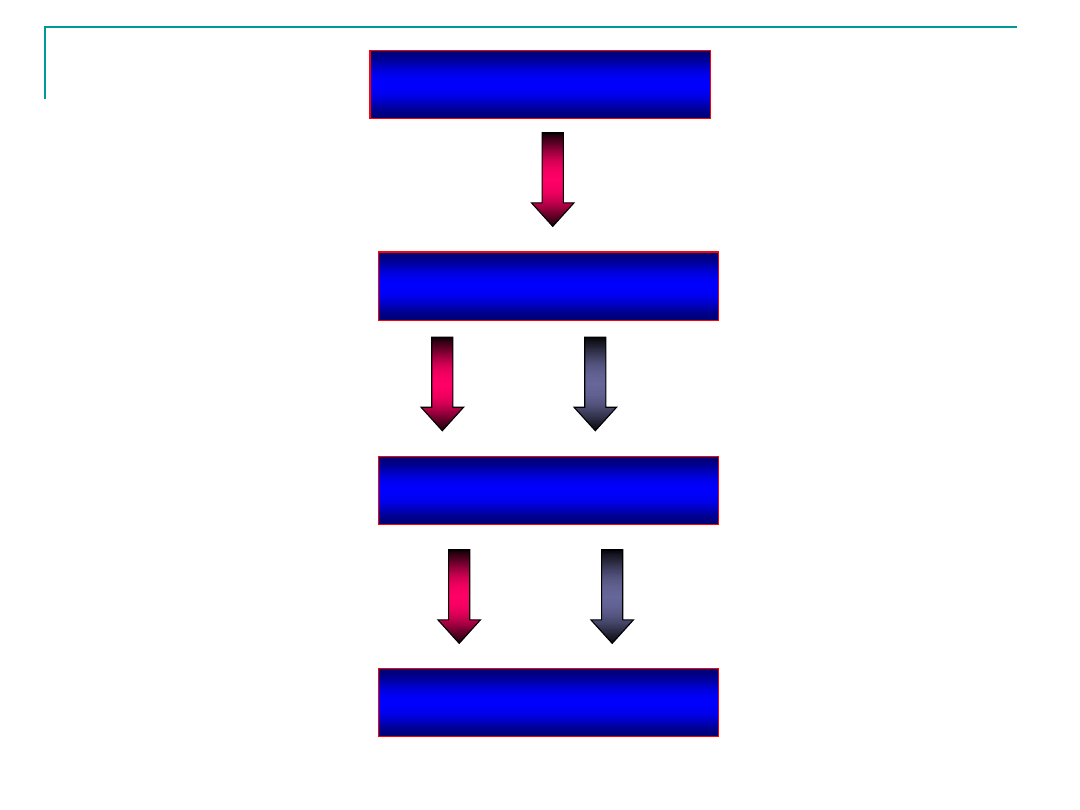
GAZ 

Obniżenie temperatury 

PARA NIENASYCONA 

Obniżenie temperatury 

Zmniejszenie objętości 

PARA NASYCONA 

Obniżenie temperatury 

Zmniejszenie objętości 

CIECZ 

Fizyczne stany materii 



Gaz 



Przyjmuje kształt naczynia w którym się znajduje 



Wypełnia naczynie w którym się znajduje 



Łatwo ulega kompresji 



Niska gęstość 



Ciała stałe 



Zachowuje własny kształt, niezależnie od kształtu naczynia w którym się 
znajduje 



Nie ulega kompresji 



Wysoka gęstość 



Ciecze 



Własności pośrednie pomiędzy własnościami gazów i ciał stałych, bardziej 
zbliżone do własności ciał stałych (gęstość wody i lodu są podobne) 

Fizyczne stany materii cd 

   

Gaz 

 

 

Ciecz   

 

Ciało stałe 

Oddziaływania międzycząsteczkowe 



Oddziaływanie wewnątrzcząsteczkowe 
  Oddziaływanie pomiędzy dwoma atomami „wewnątrz” 

cząsteczki (udział elektronów pomiędzy dwoma atomami- 
wiązanie kowalencyjne)  

Oddziaływania międzycząsteczkowe-oddziaływania pomiędzy 

cząsteczkami 



Jakie siły są odpowiedzialne za agregacje indywidualnych 
elementów tworzących ciecz lub ciało stałe? 
  Oddziaływania te mogą „wprowadzać” wiązania jonowe lub 

kowalencyjne lub słabsze wzajemne oddziaływania zwane 
oddziaływaniami międzycząsteczkowymi 



Zmiany w stanie skupienia są spowodowane przez zmiany  

 w oddziaływaniach pomiędzy cząsteczkami  a nie 

wewnątrzcząsteczkowych