1

Krystalografia II

Rzut stereograficzny

Rzut sferyczny (projekcja sferyczna)

„

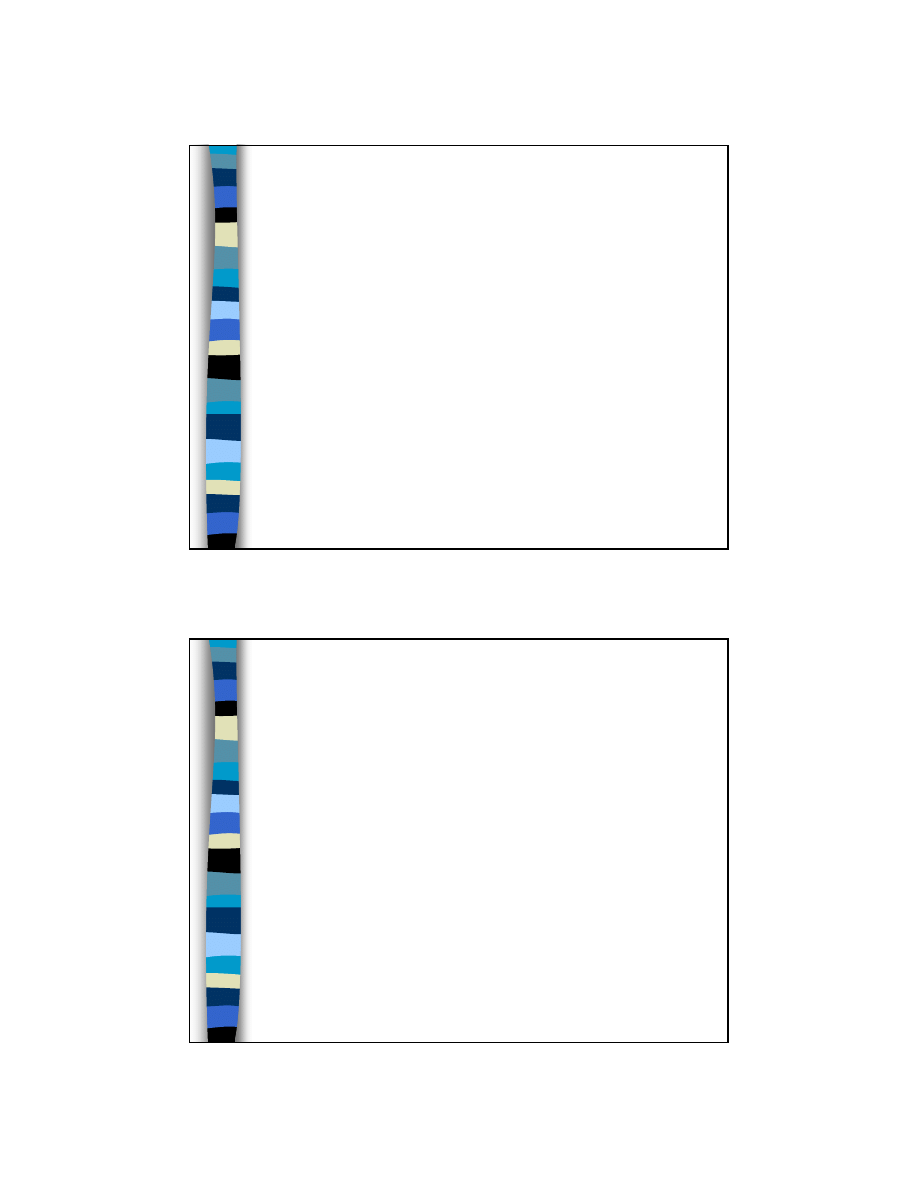
Kryształ zastępuje się zespołem płaszczyzn i
prostych równoległych do odpowiadających im
płaszczyzn i prostych krystalicznych w krysztale,
lecz przechodzących przez jeden punkt.

„

Ten punkt to środek zespołu, a całosć to zespół
krystaliczny. W zespole zachowane są
zależności między kątami.

2

Projekcja sferyczna bezpośrednia

„

Zespół umieszcza się w środku kuli o dowolnym
promieniu i przedłuża się proste i płaszczyzny aż
do przecięcia się z powierzchnią kuli. Powstałe
na sferze ślady przebicia są ich projekcjami.

„

Projekcją kierunku jest punkt, a płaszczyzny
koło.

Projekcja sferyczna pośrednia

„

Jeżeli w zespole zastąpimy płaszczyzny
prostymi do nich prostopadłymi, a kierunki –
płaszczyznami do nich prostopadłymi, to
otrzymamy projekcję sferyczną pośrednią.

„

Projekcją kierunku jest koło, a płaszczyzny
punkt.

3

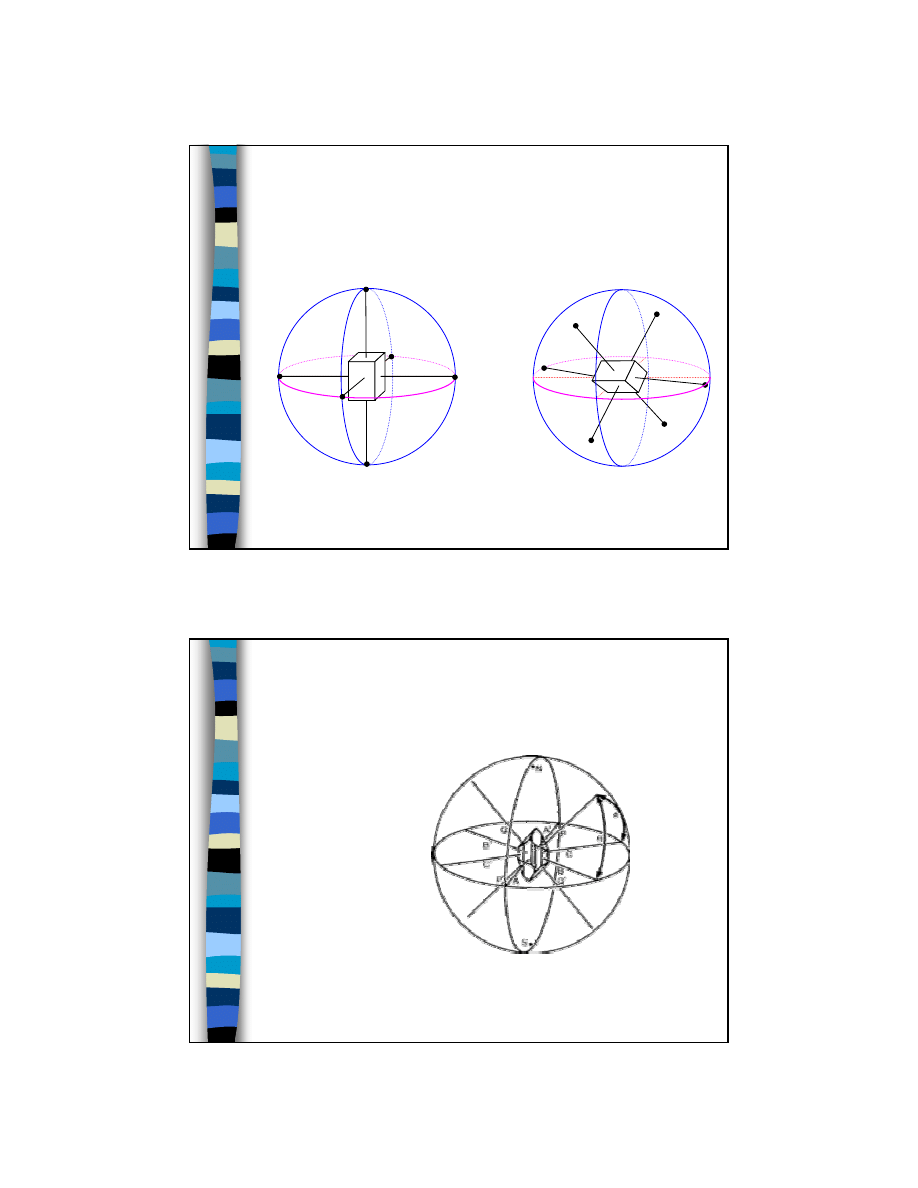
Projekcja sferyczna

Projekcja sferyczna

punkty przecięcia
prostych ze sferą –
bieguny (odpowiadają
płaszczyznom lub
kierunkom)

4

Projekcja stereograficzna i
cyklograficzna

„

Projekcja sferyczna daje wynik 3D, czyli trudny
do używania. Dlatego dalszym krokiem jest
wytworzenie płaskiego obrazu.

– globus

→ mapa

Projekcja stereograficzna i
cyklograficzna

„

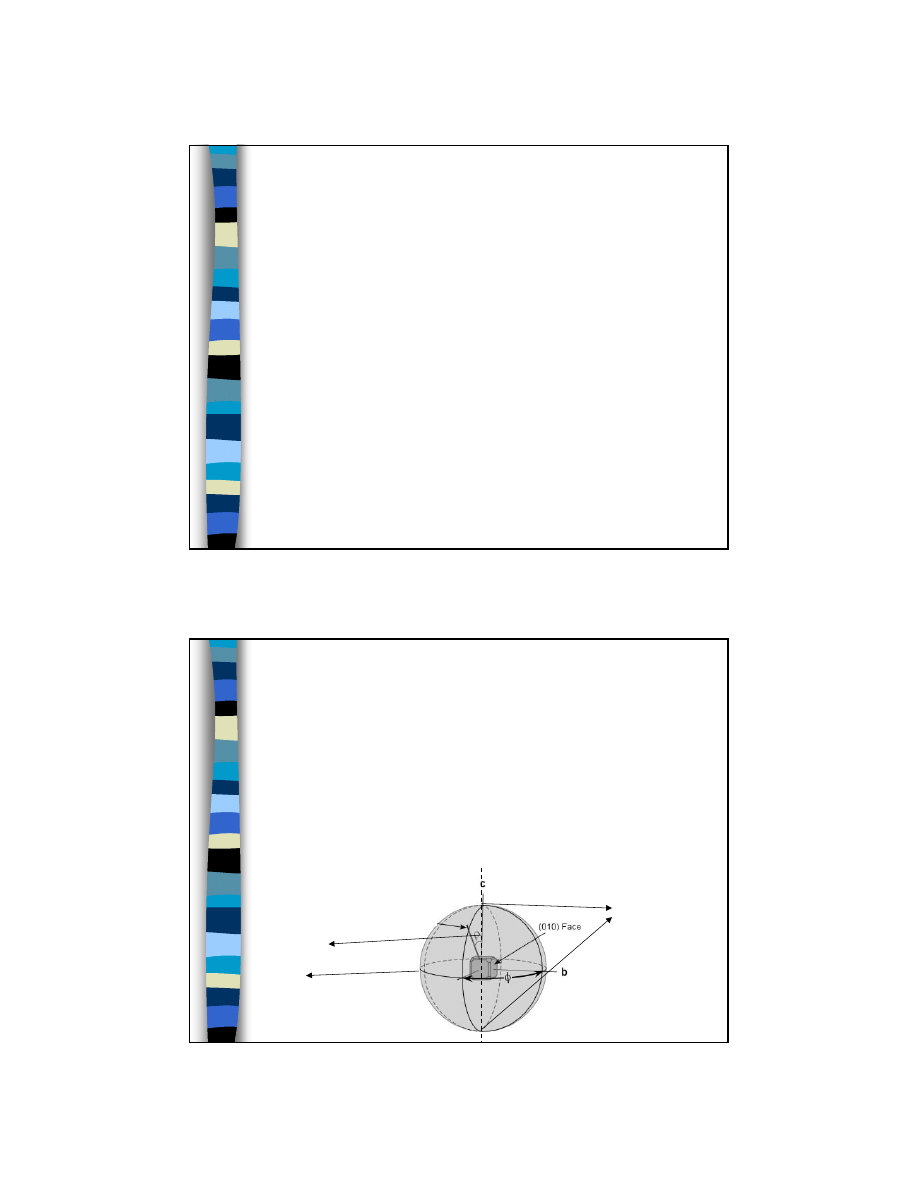
W tym celu:

– sferę projekcji przecinamy poziomą płaszczyzną

(płaszczyzną projekcji) przechodzącą przez środek sfery.
Wielkie koło wewnątrz sfery to koło projekcji.

oś projekcji

koło projekcji

punkty oczne

biegun

5

Projekcja stereograficzna i
cyklograficzna

„

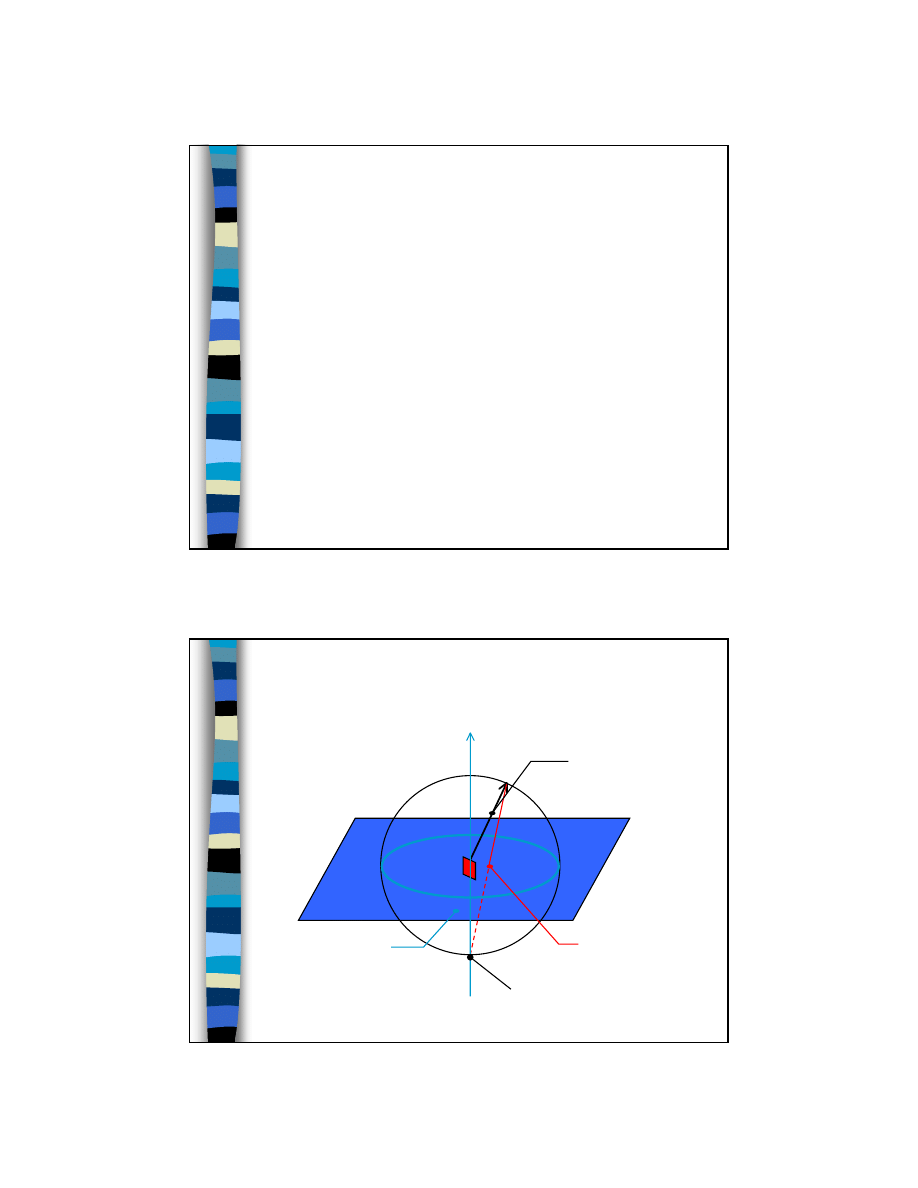
Następnie:

– Łączymy biegun z punktem ocznym na przeciwległej półkuli.

Punkt przecięcia tej prostej z kołem projekcji jest projekcją.

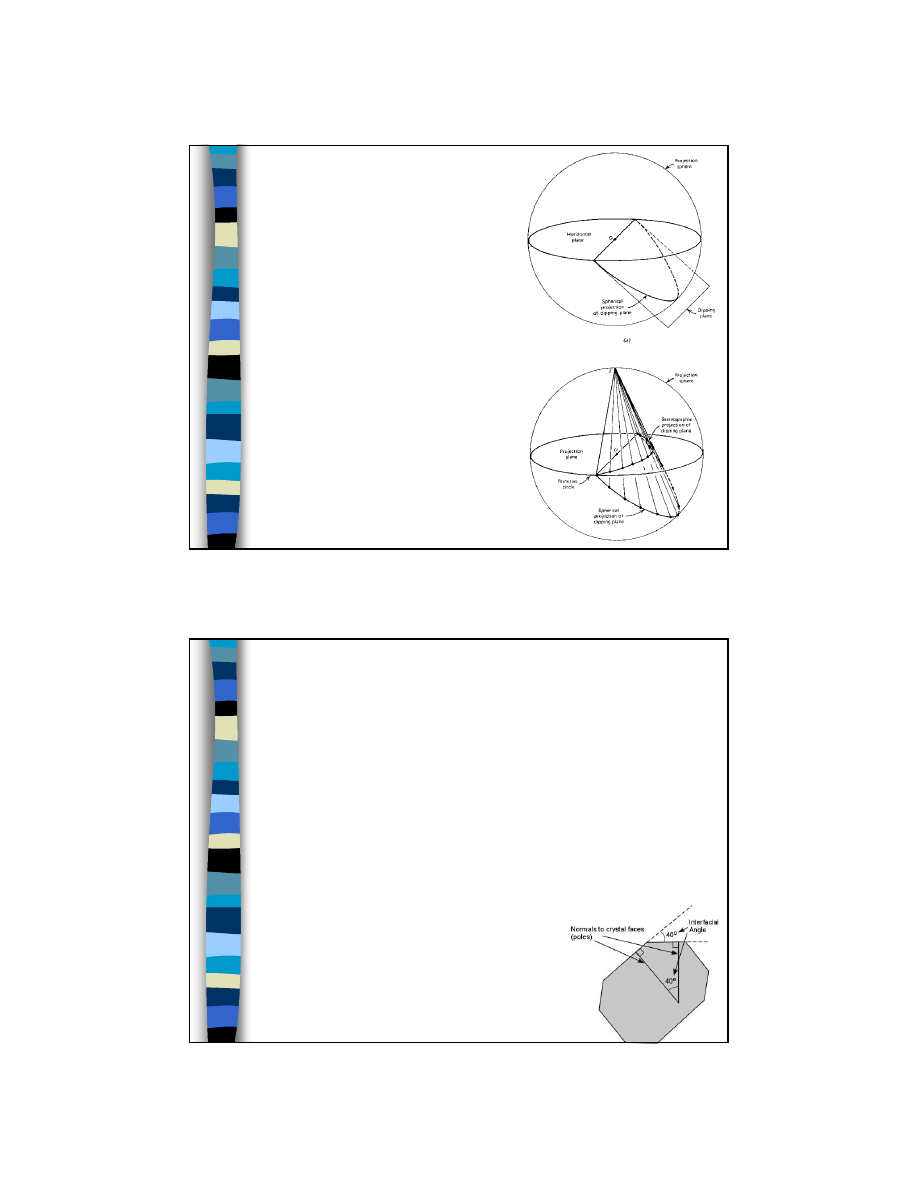
Zasada rzutu stereograficznego

normalna
do ściany hkl

rzut

płaszczyzna

rzutowania

z

obserwator

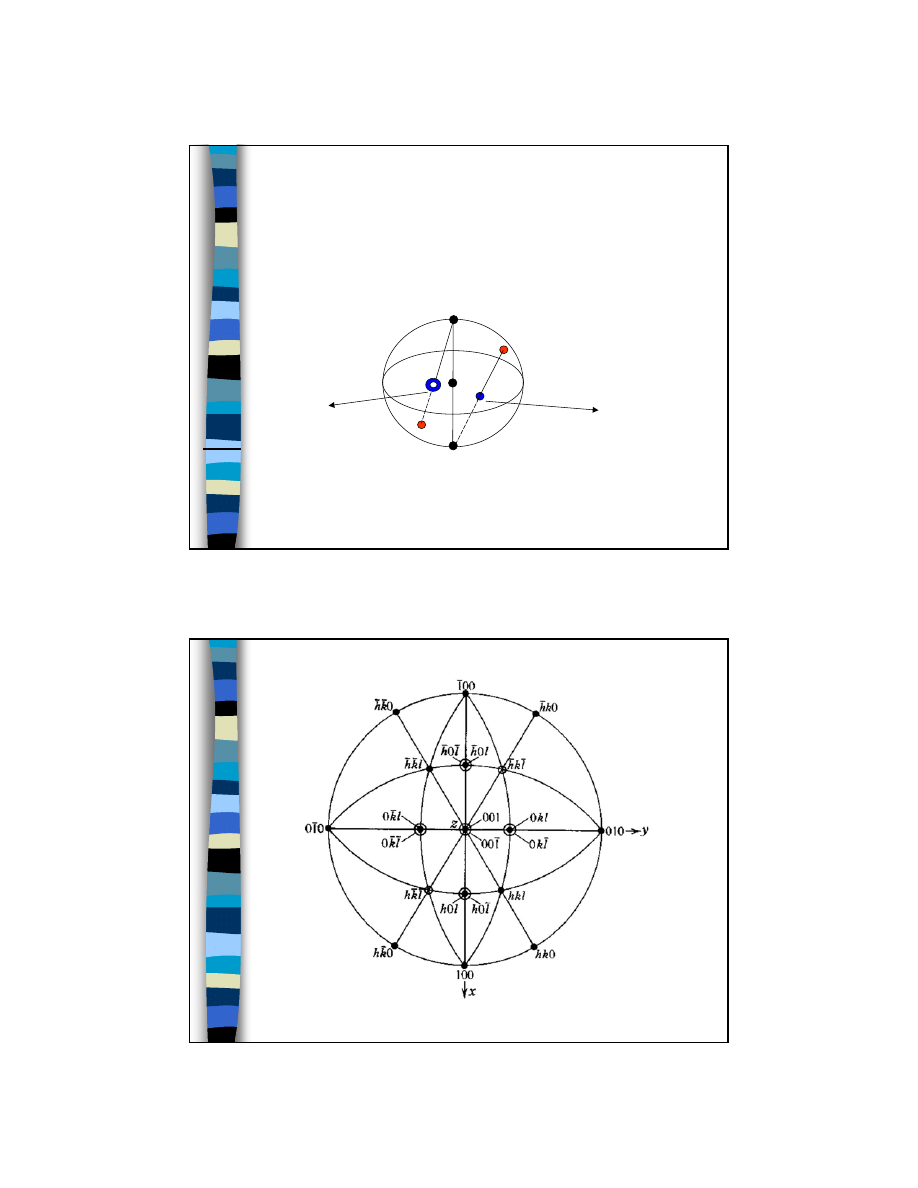
6

S

N

P

Q

Projekcja stereograficzna

punkt oznacza się
pełnym symbolem,
jeśli rzutowany
biegun jest ponad
kołem projekcji

punkt oznacza się
pustym symbolem,
jeśli rzutowany
biegun jest poniżej
koła projekcji

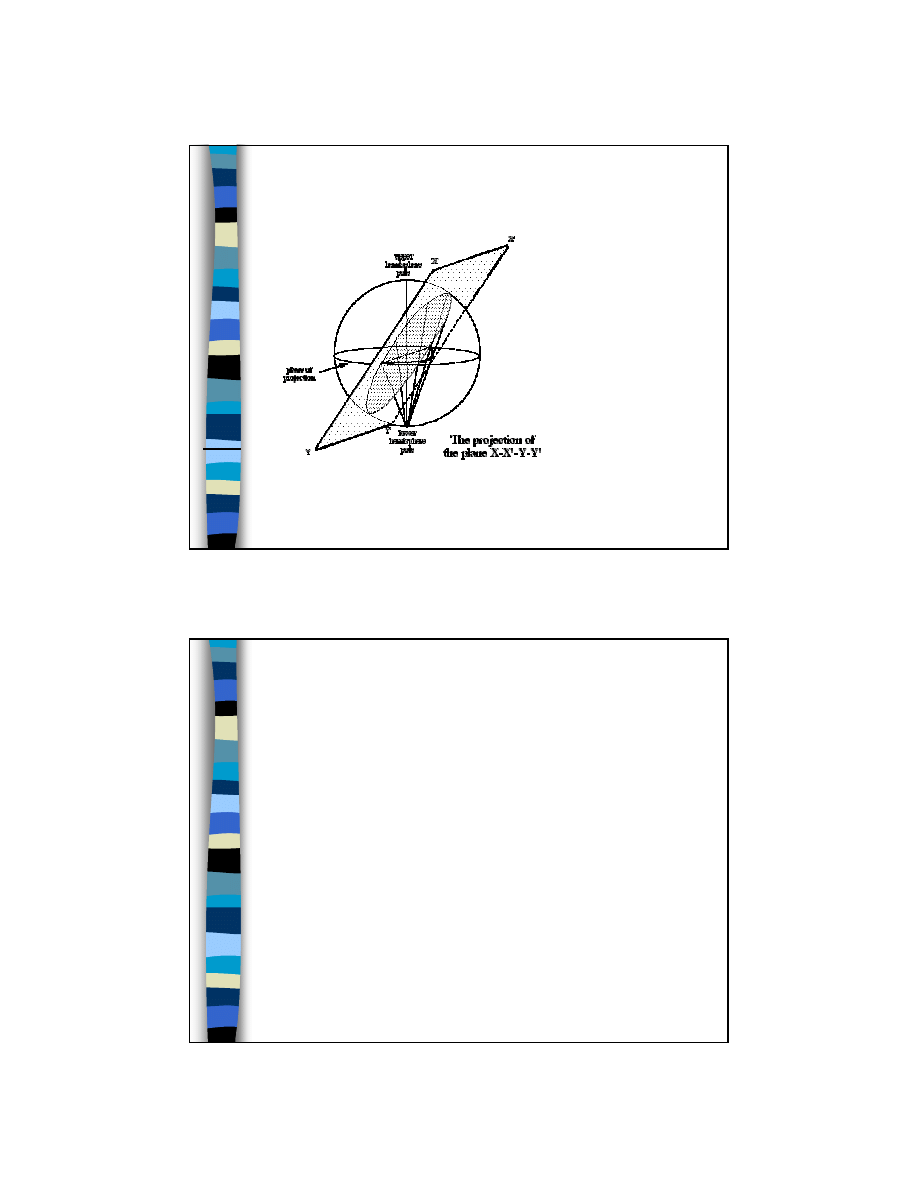
7

Projekcja stereograficzna

płaszczyzna X-X’-Y-Y’ odpowiada
kierunkowi krystalograficznemu do
niego prostopadłemu

Projekcja stereograficzna i
cyklograficzna

„

Projekcja cyklograficzna: jeżeli punktem wyjścia jest

projekcja sferyczna bezpośrednia;

„

Projekcja stereograficzna: jeżeli punktem wyjścia jest

projekcja sferyczna pośrednia;

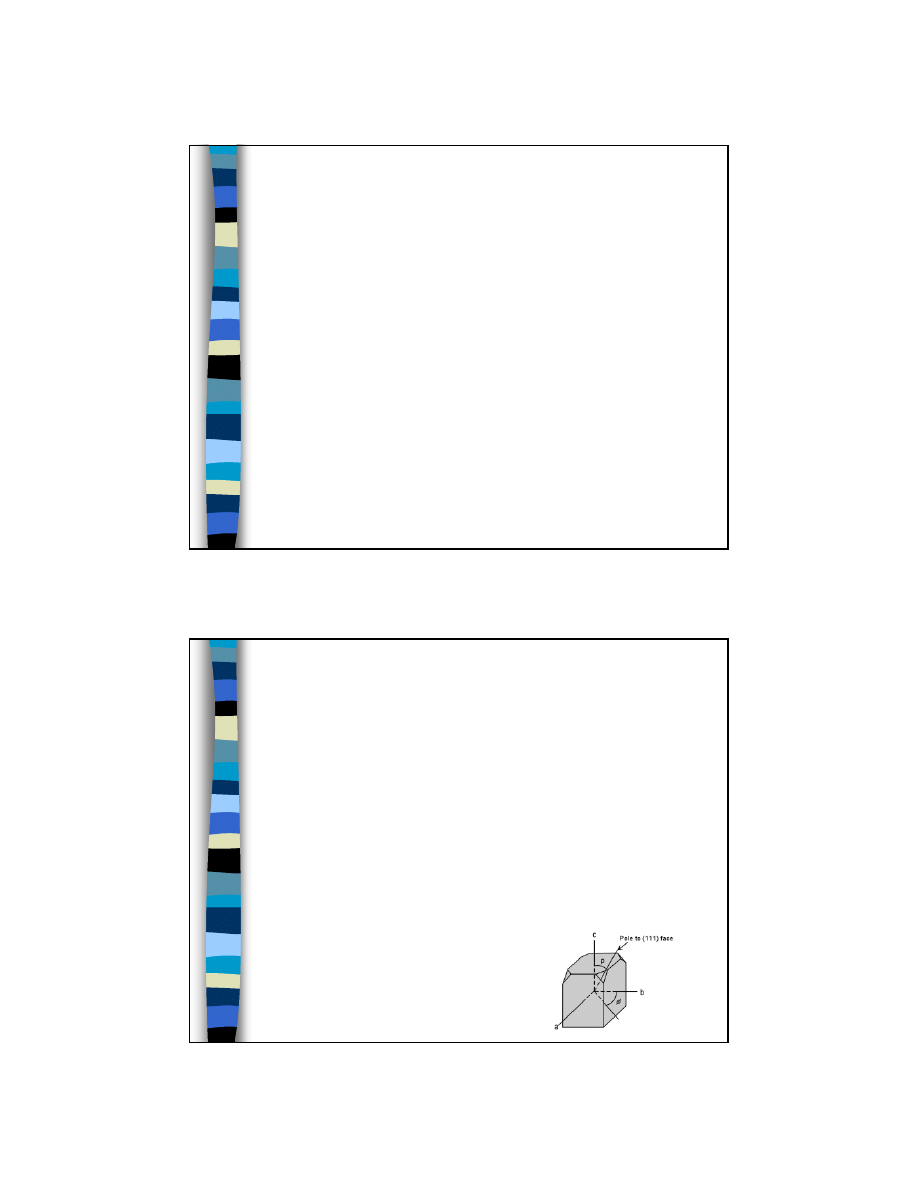
8

Projekcja stereograficzna i
cyklograficzna

„

projekcja stereograficzna:

– obrazem kierunków są elipsy i koła;
– obrazem płaszczyzn są punkty;

„

projekcja cyklograficzna:

– obrazem kierunków są punkty;
– obrazem płaszczyzn są elipsy i koła.

Przykład: projekcja stereograficzna
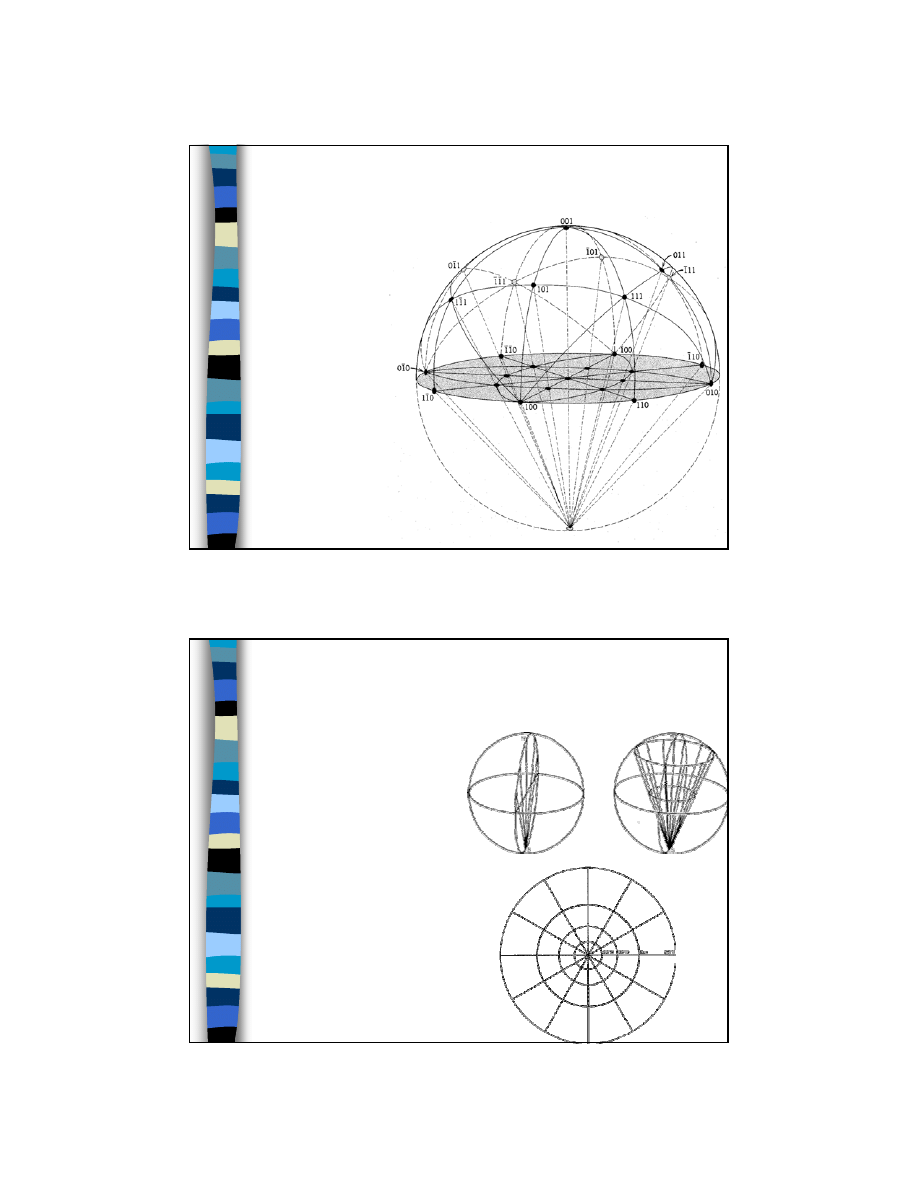
ścian sześcianu

Sześcian orientujemy tak, że
oś c jest skierowana pionowo
w gorę, w stronę punktu
ocznego N.

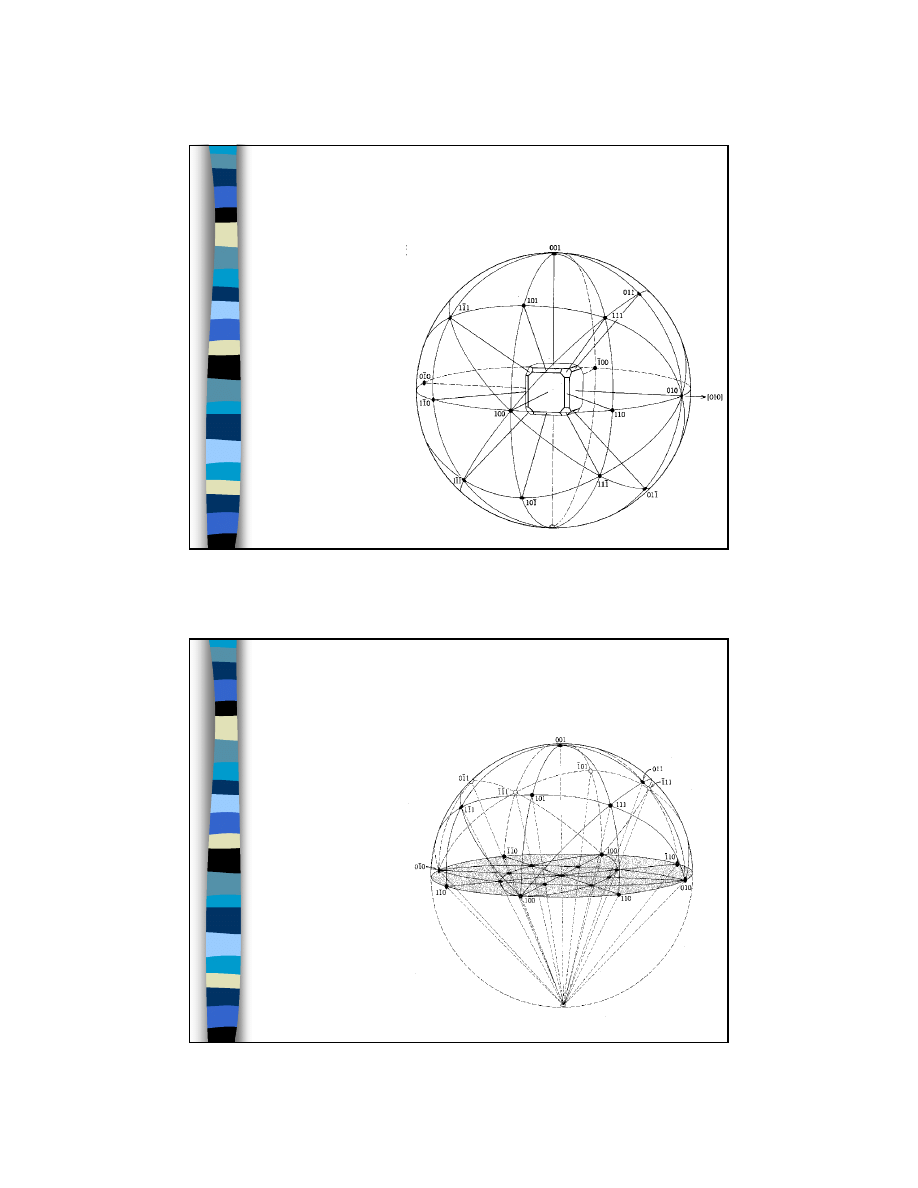
9

Przykład: projekcja stereograficzna
ścian sześcianu

„

Punkty i linie na
zewnętrznej
sferze to projekcja
sferyczna

„

Płaszczyzny =
punkty (bieguny)

Przykład: projekcja stereograficzna
ścian sześcianu

„

Szara
powierzchnia =
płaszczyzna
projekcji

Fig 6.5 of Klein (2002)

Manual of Mineral Science,

John Wiley and Sons

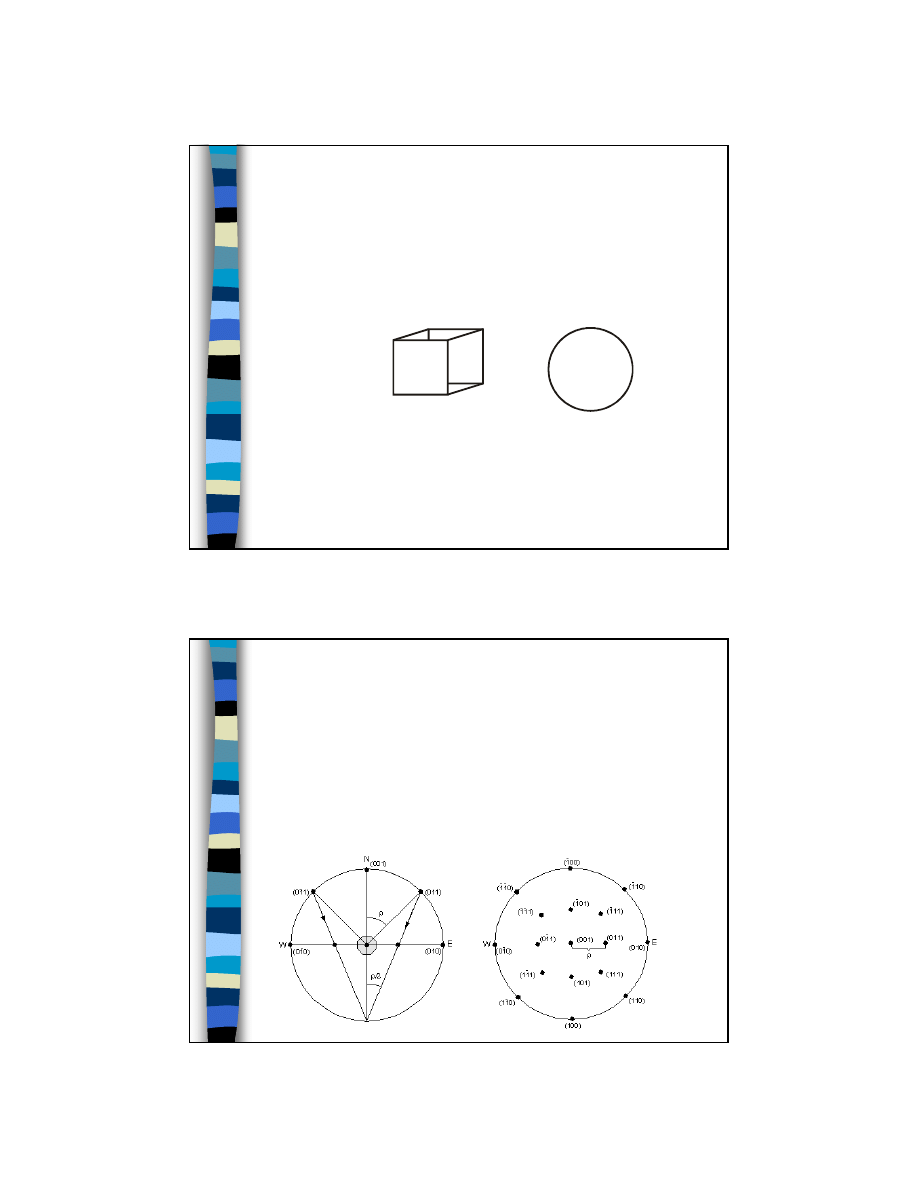
10

Przykład: projekcja stereograficzna
ścian sześcianu

A

B

C

°

°

°

A

°

C

°

B

Przykład: projekcja stereograficzna
ścian sześcianu

11

Przykład: projekcja
cyklograficzna ścian
sześcianu

Do czego służy ta zabawa:

„

Do graficznego opisywania kątów między
ścianami, kierunkami itd.

„

Kąt między płaszczyznami w krysztale = kąt
między kierunkami prostopadłymi do płaszczyzn.

„

Obie projekcje zachowuje kąty.

12

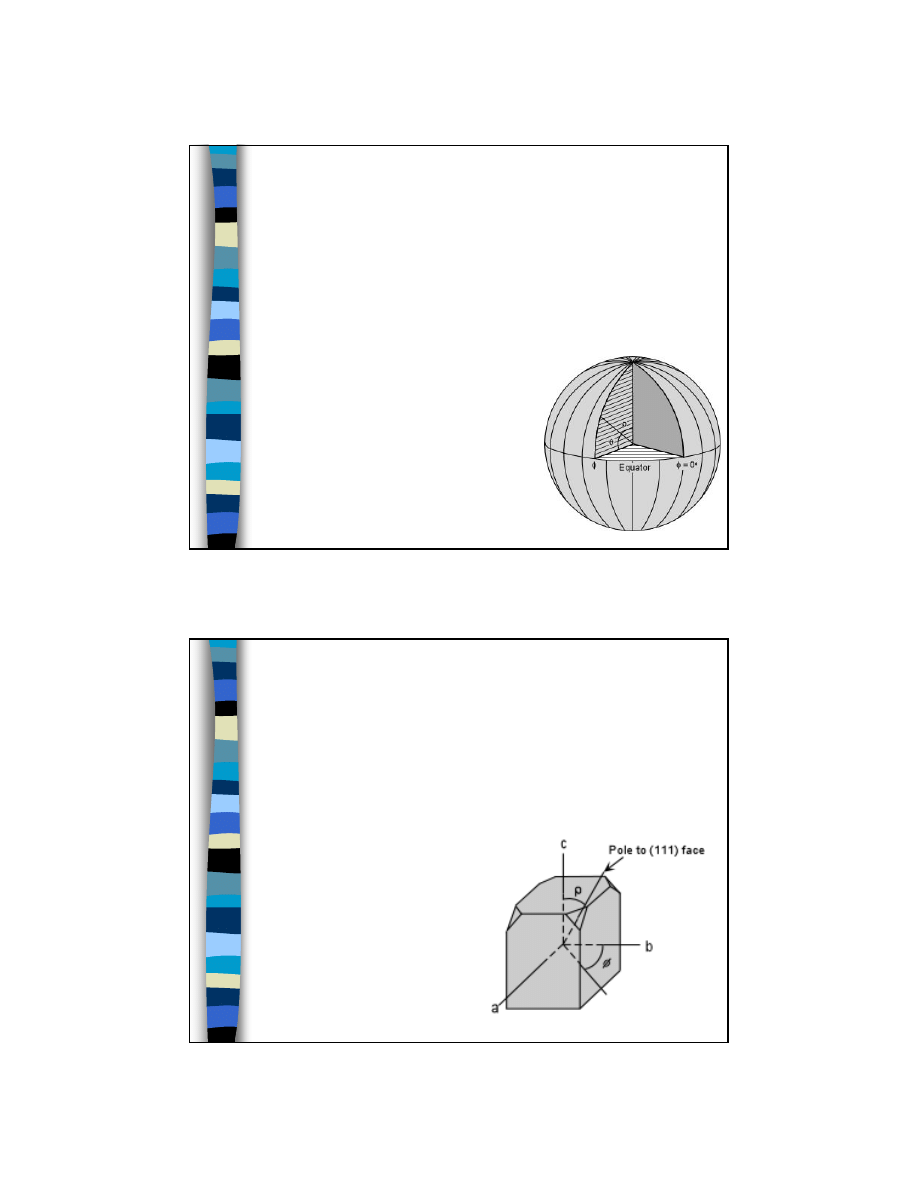
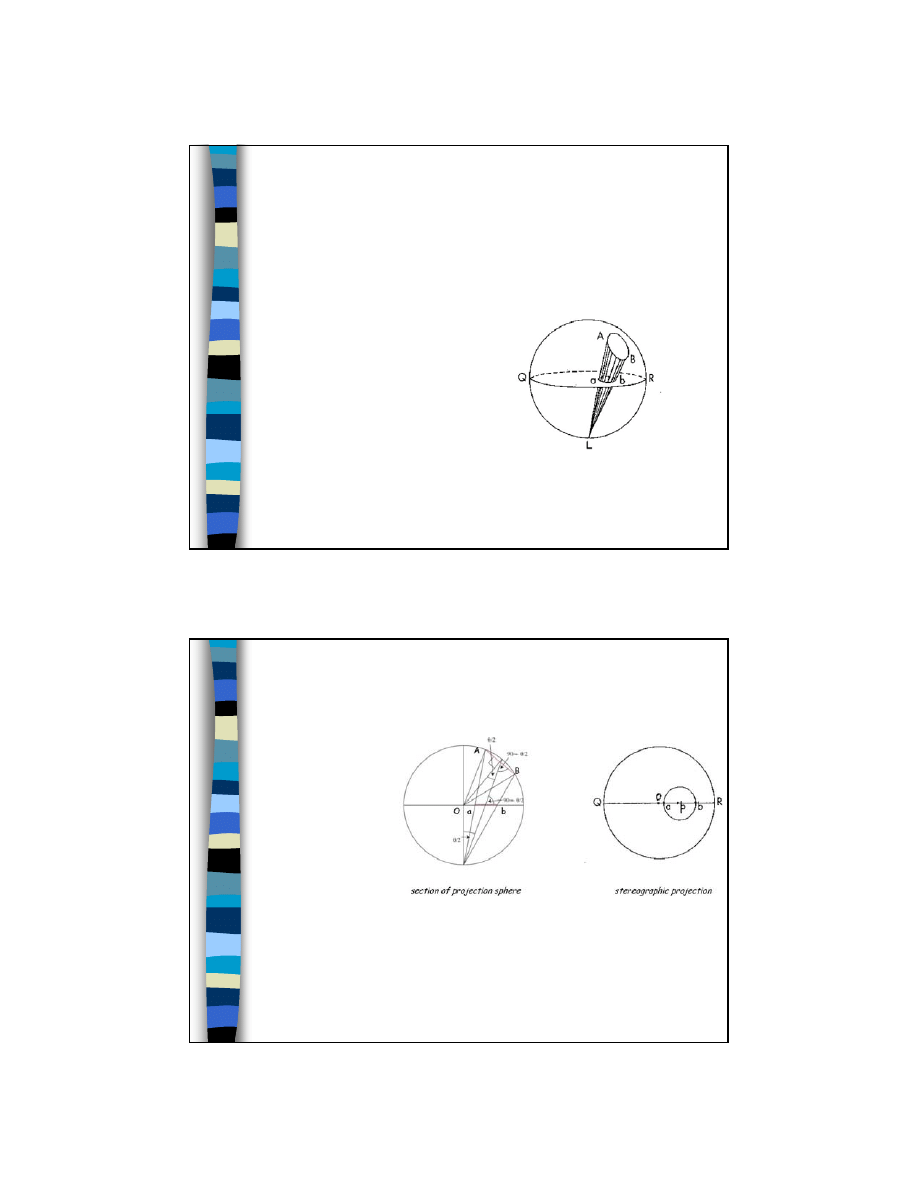
Jak odczytać kąty z projekcji
stereograficznej?

„

Kąt (biegunowy)

ρ - kąt między

osią c i biegunem
odpowiadającym płaszczyźnie
krystalicznej, mierzony w dół od
bieguna północnego.

„

Kąt

φ – kąt mierzony na

płaszczyźnie poziomej, od osi b
(zerowego południka) w kierunku
wskazówek zegara.

Jak odczytać kąty z projekcji
stereograficznej?

„

przykład:

– kąty

ρ i φ płaszczyzny (111)

w krysztale o strukturze
regularnej

13

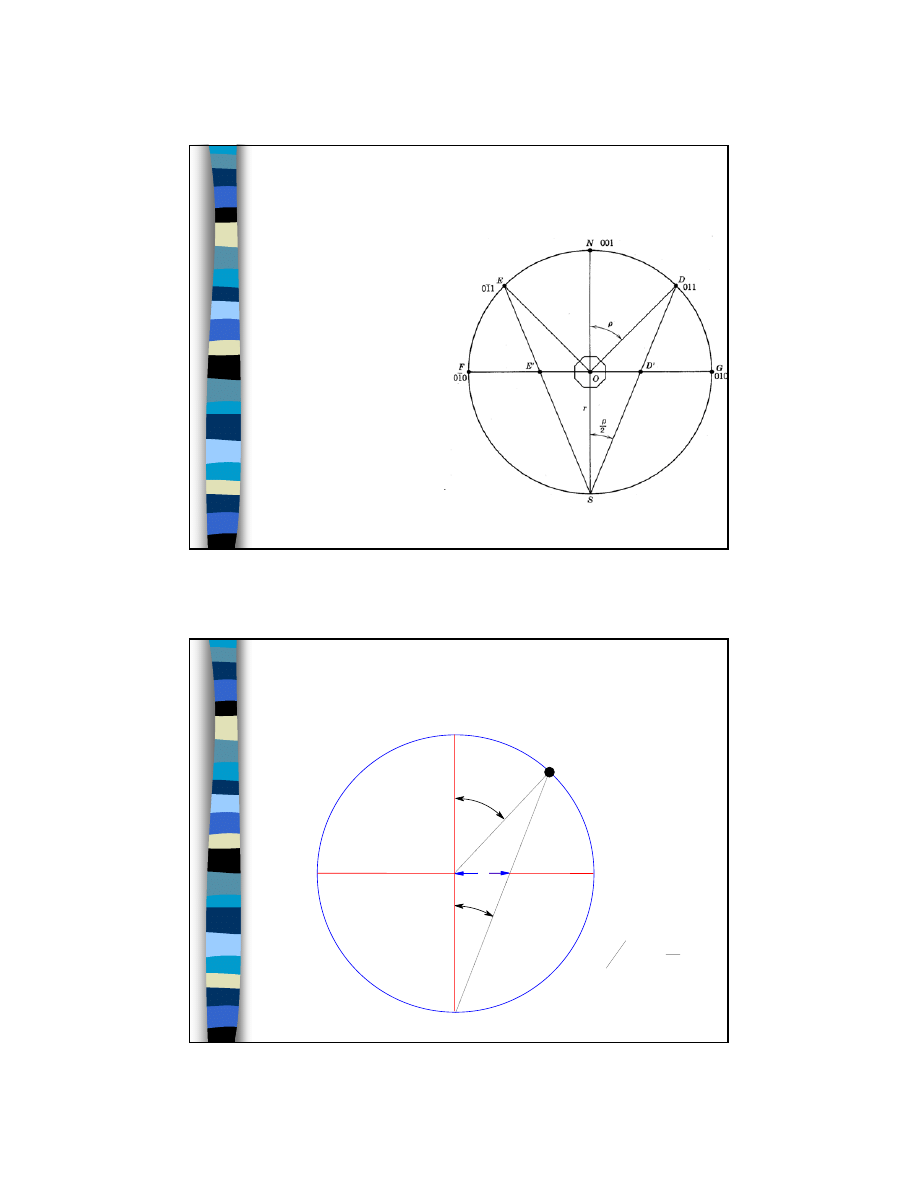
Jak odczytać kąty z projekcji
stereograficznej?

„

D i E – projekcja sferyczna

„

D' i E' – projekcja
stereograficzna

„

Odległość GD' = f(

ρ) gdy

ρ → 90 D’ → G

„

gdy

ρ → 0 D’ → O

Fig 6.6 of Klein (2002) Manual of Mineral Science, John Wiley and Sons

O

ρ/2

ρ

x

2

tg

ρ

=

R

x

Jak odczytać kąty z projekcji
stereograficznej?

Ściśle
mówiąc:

14

„

Zatem, 2-D
odległości od środka
płaszczyzny projekcji
i kąty są ze sobą
związane.

Fig 6.5 of Klein (2002)

Manual of Mineral Science,

John Wiley and Sons

Jak odczytać kąty z projekcji
stereograficznej?

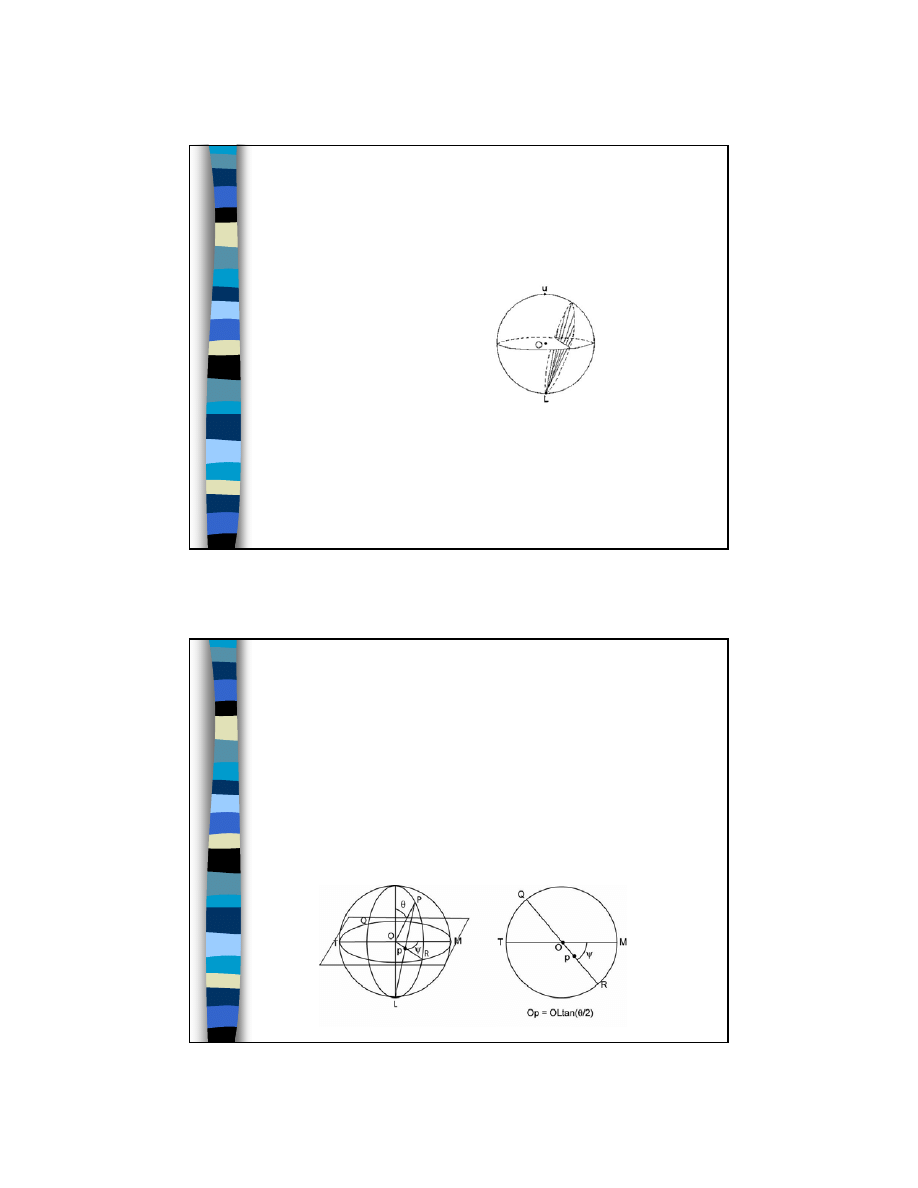
Jak odczytać kąty z projekcji
stereograficznej?

„

Małe koła:

– Tym samym kątom

ρ

odpowiadają okręgi o
różnym promieniu

15

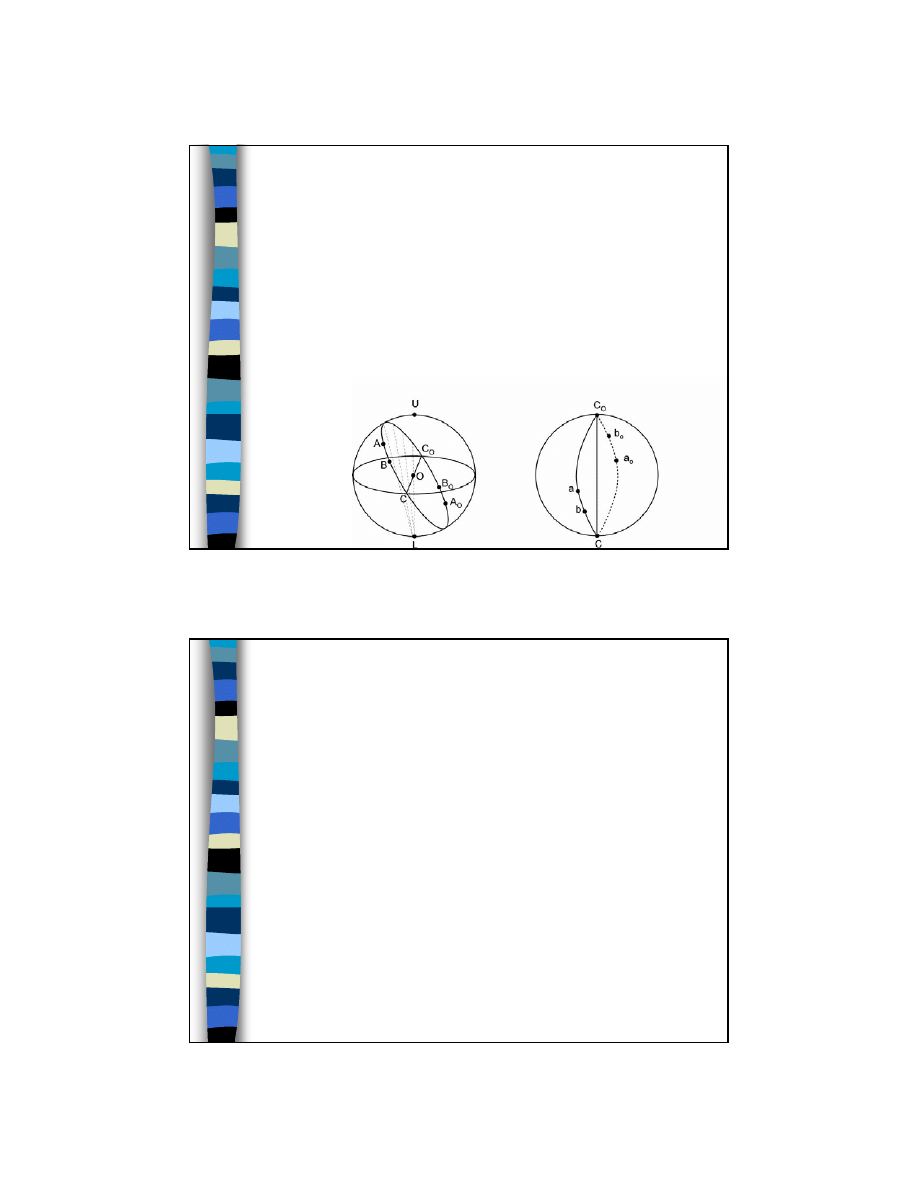
Jak odczytać kąty z projekcji
stereograficznej?

„

Małe koła:

– Gdy środek koła nie

leży na osi projekcji

Jak odczytać kąty z projekcji
stereograficznej?

„

Małe koła:

– Obrazem jest koło;

środkiem koła nie jest
obraz osi stożka.

16

Jak odczytać kąty z projekcji
stereograficznej?

„

Małe koła:

– Przypadek szczególny

Jak odczytać kąty z projekcji
stereograficznej?

„

Wielkie koła

– Obrazem wielkiego koła w płaszczyźnie równikowej jest koło

ograniczające płaszczyznę rzutu;

– Obrazem wielkiego koła pionowego jest linia prosta

17

Jak odczytać kąty z projekcji
stereograficznej?

„

Wielkie koła

– Obrazem wielkich kół

nachylonych pod kątem do
płaszczyzny równikowej są
krzywe (wycinki kół);

Jak odczytać kąty z projekcji
stereograficznej?

„

W praktyce do prezentacji rzutu stereograficznego
stosuje się siatkę „południków” i „równoleżników”
zwaną siatką Wulfa, mającą następujące cechy:

„

Oś z przebija siatkę w środku koła

„

Ściany równoległe do osi z - pas (hk0) stanowi
wielkie koło projekcji

„

Dodatni biegun osi x znajduje się pod płaszczyzną
projekcji

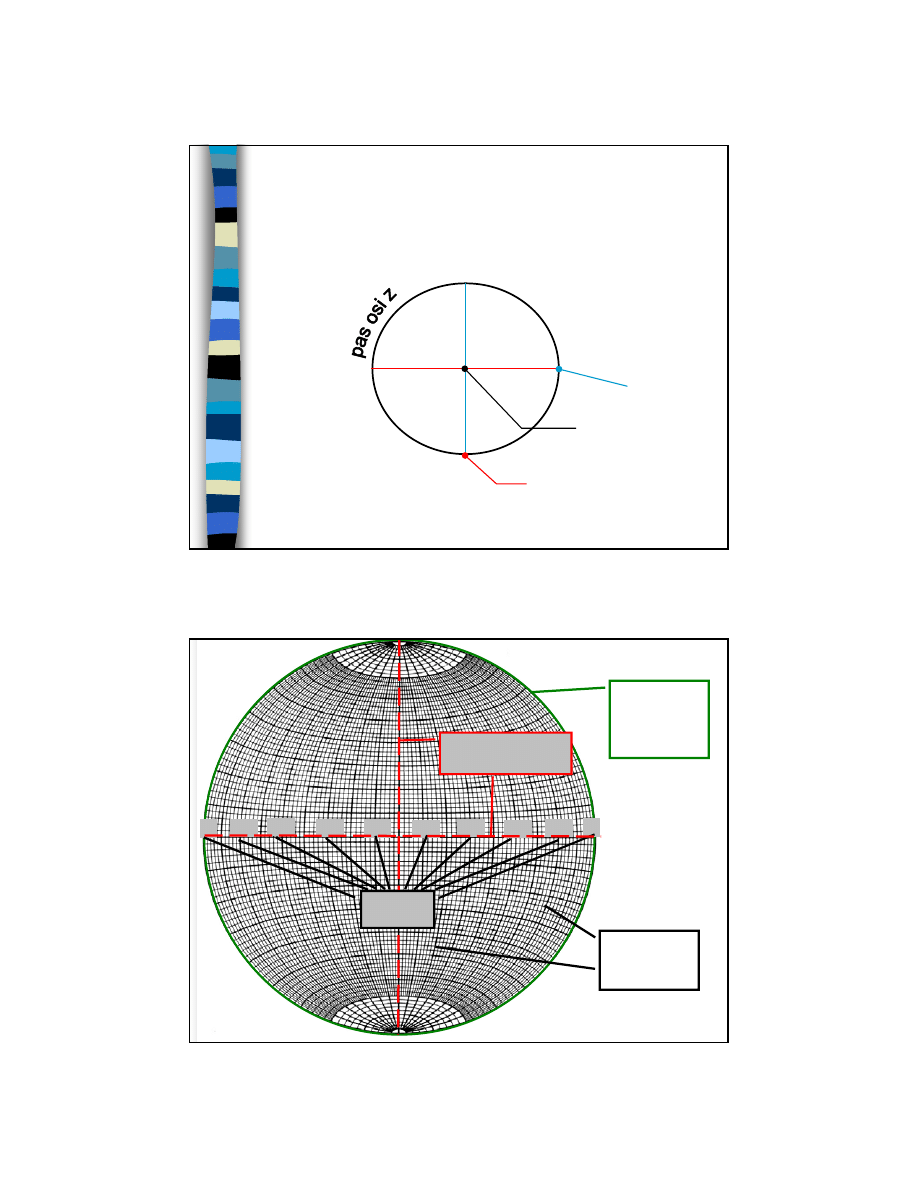
18

pas osi x

pas osi

y

oś y

oś x

oś z

Koło równikowe

= płaszczyzna

pozioma

0

20

40

60

80

0

20

40

60

80

ρ

Proste linie = pionowe

płaszczyzny

Wielkie koła =

nachylone

płaszczyzny

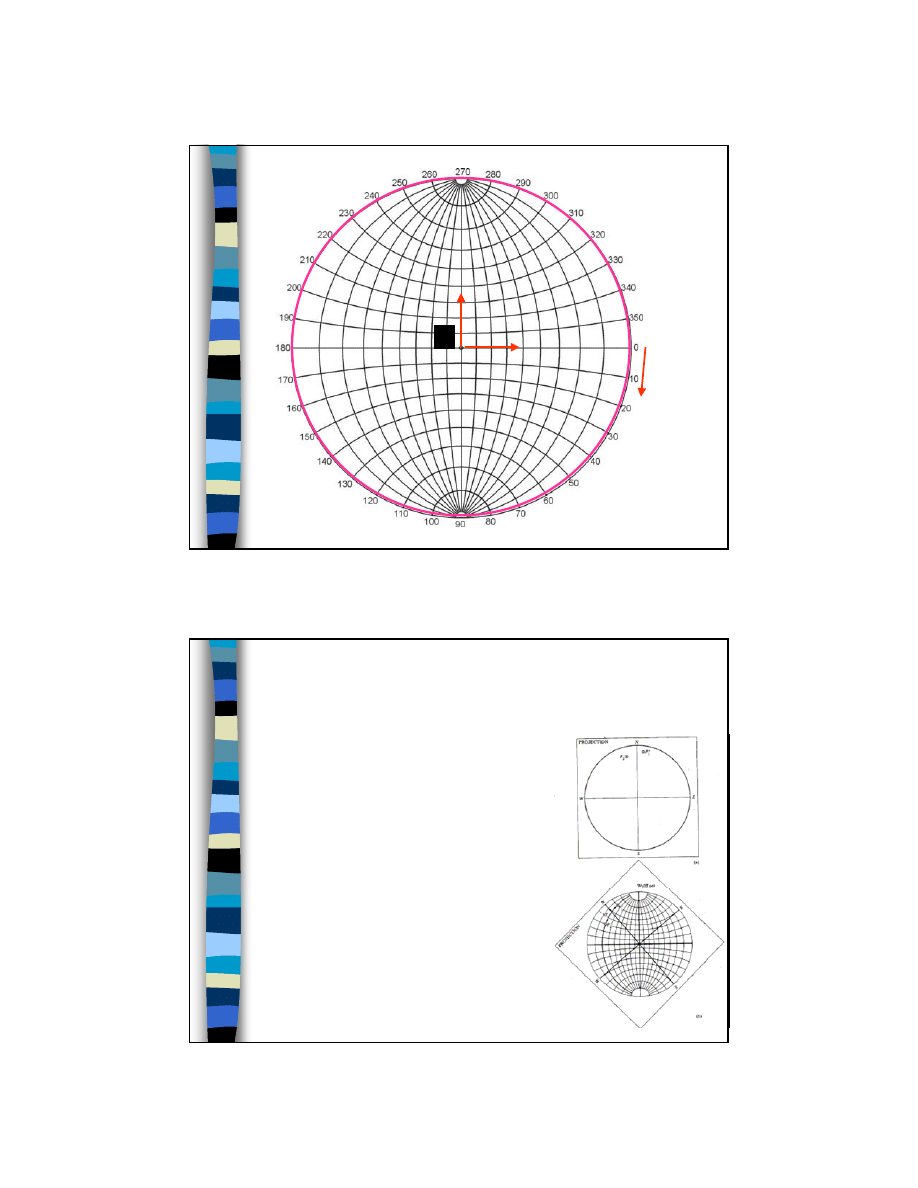
19

Siatka Wulfa

ϕ

ρ

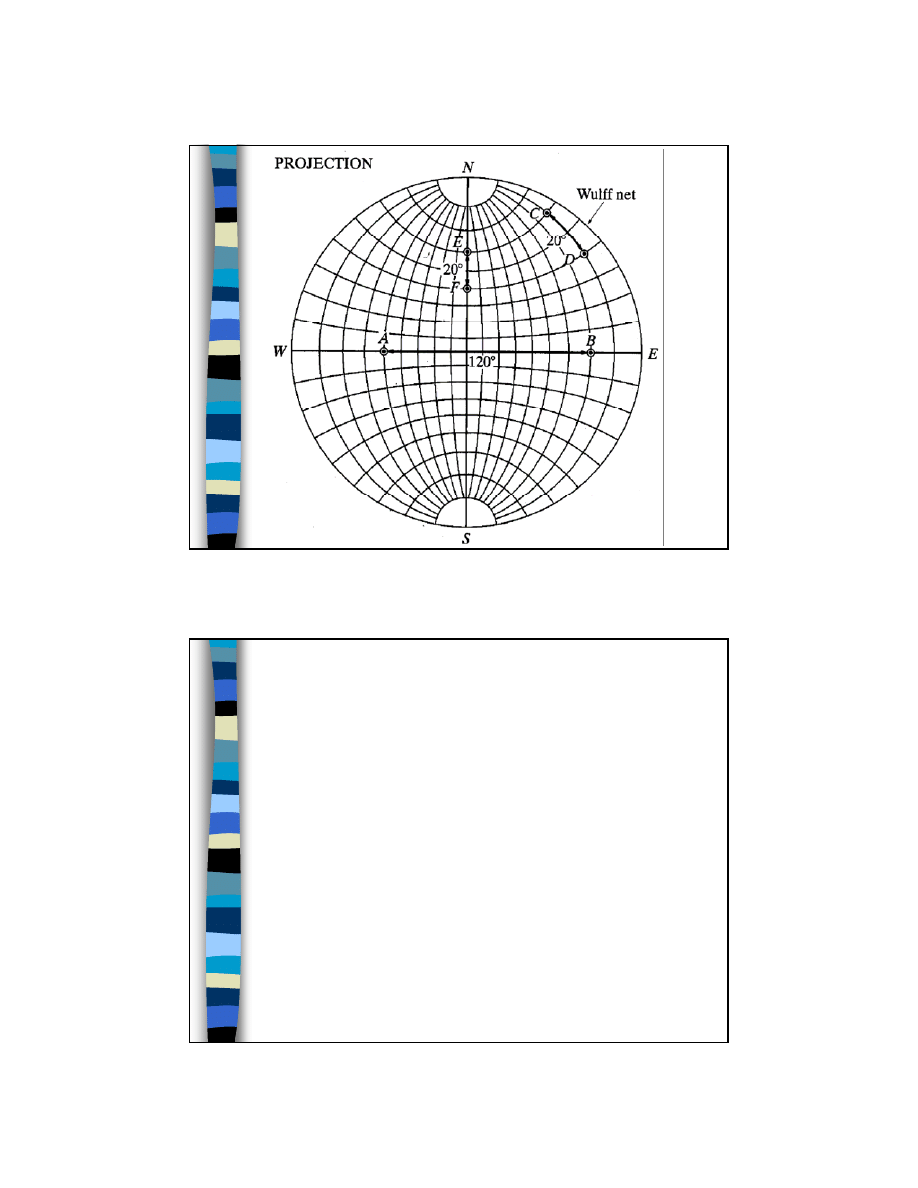
Znajdowanie kątów między
płaszczyznami

„

Aby znaleźć kąt między

płaszczyznami w krysztale

trzeba:

– zrobić rzut stereograficzny

kryształu;

– sprowadzić bieguny

odpowiednich płaszczyzn na

ten sam południk lub

równoleżnik (przez obrót);

20