Zad.9 

 
Zad.6 
Zasada Fermata (zasada najkrótszego czasu) 

Światło wybiera taką trajektorię, dla której czas przelotu jest elementarny (najkrótszy) 

Prawo odbicia światła 

Gdy światło ma za zadanie przejść między punktami A i B „dotykając” po drodze zwierciadła, rozchodzi się w 
jednorodnym ośrodku ze stałą prędkością v (c w próżni, przezroczystym ośrodku dielektrycznym v≤c i 𝑣 =

𝑐

√µ𝜀

 

gdzie ε,µ - względne przenikalności ośrodka – dielektryczna i magnetyczna). Czas przelotu światła po takiej 

drodze 

𝑡 =

√𝑥

2

+ℎ

2

𝑣

+

�𝐻

2

+(𝑑−𝑥)

2

𝑣

 

z warunku ekstremum 

𝑑𝑡

𝑑𝑥

= 0 , x to zmienna określająca punkt, w którym światło „dotyka” zwierciadła. Z 

ostatniego równania otrzymujemy więc  

𝑥

√ℎ

2

+𝑥

2

=

𝑑−𝑥

�𝐻

2

+(𝑑−𝑥)

2

 co jest równoważne z sinα=sinß, skąd znajdujemy 

prawo odbicia: α=ß 
 
 

 

 
 
Prawo załamania światła 
Rozpatrujemy dwa przezroczyste ośrodki z różnymi prędkościami rozchodzenia światła 𝑣

1

𝑖 𝑣

2

. Zadaniem jest 

znalezienie minimalnej trajektorii łączącej punkty A i B w obu ośrodkach. Trajektoria A-B będzie miała kształt 
łamanej. Czas ruchu światła dla takiej trajektorii (w funkcji zmiennej x) wynosi 𝑡 =

√𝑥

2

+ℎ

2

𝑣

1

+

�𝐻

2

+(𝑑−𝑥)

2

𝑣

2

 , z 

warunku ekstremum 

𝑑𝑡

𝑑𝑥

= 0 znajdujemy 

𝑥

𝑣

1

√ℎ

2

+𝑥

2

=

𝑑−𝑥

𝑣

2

�𝐻

2

+(𝑑−𝑥)

2

, czyli znaną nam postać prawa załamania 

światła 

𝑠𝑖𝑛𝛼
𝑠𝑖𝑛𝛽

=

𝑣

1

𝑣

2

= 𝑛

1,2

  gdzie n

1,2 

=v

1

/v

2

 nazywamy współczynnikiem załamania światła ośrodka II względem I.  

 

 

 

 

 

 

 

 

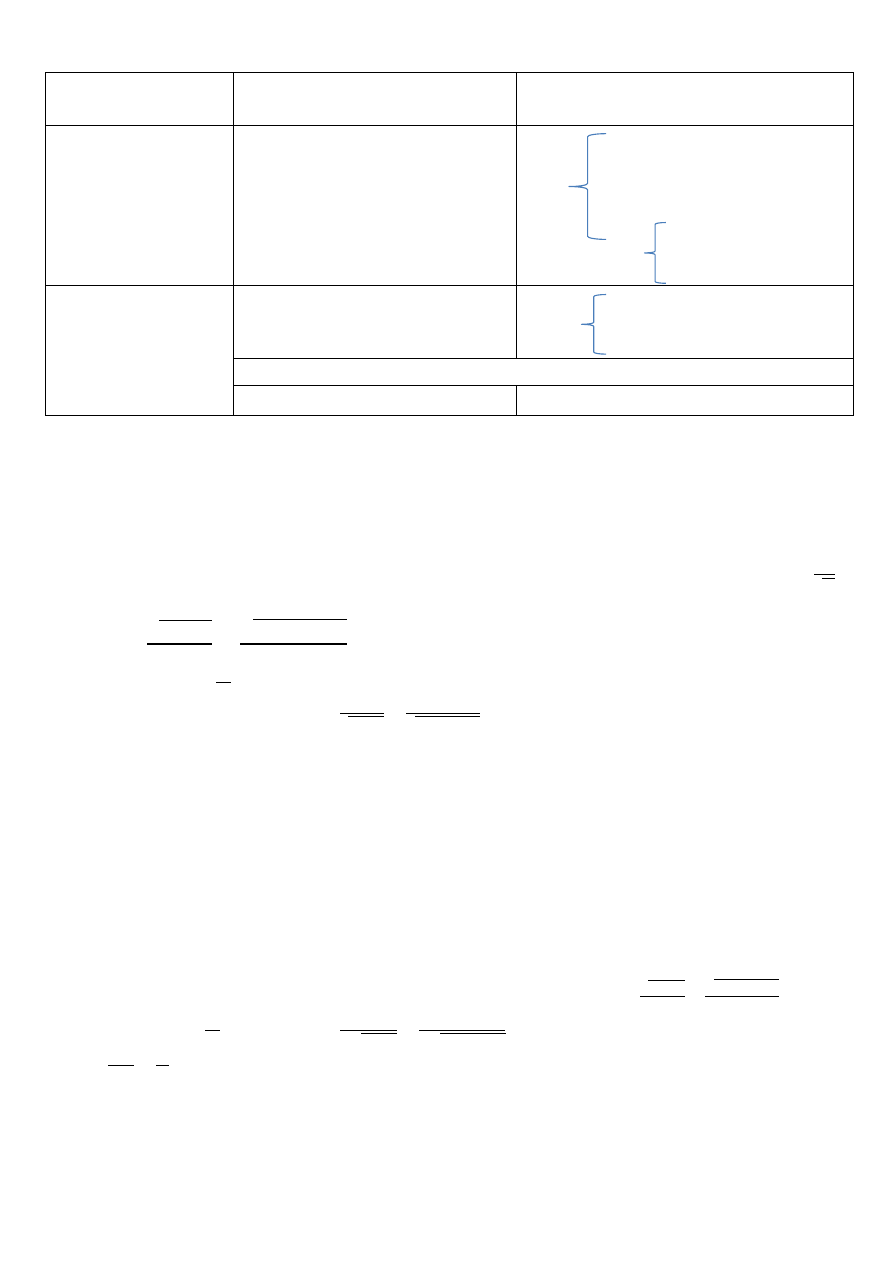
BOZONY 

 

FERMIONY 

 
NIE ODDZIAŁUJĄCE 

SILNIE 

Pośredniczące oddziaływań 
-elektromagnetycznych (foton) 
-słabych (cząstki Z i W) 
-grawitacyjnych (grawiton) 

                        

                  elektron 

Leptony    cząstka µ (mion) 
                  cząstka τ (taon) 
                  neutrina     elektronowe 

                                       mionowe 

                                     taonowe 

 
ODDZIAŁUJĄCE SILNIE 

Pośredniczące oddziaływań 

- silnych (między kwarkami – gluony) 

                     Górny, dolny 
Kwarki         dziwny, powabny 

                     piękny, prawdziwy 

hadrony 

Mezony (po 2 kwarki) 

Bariony (po 3 kwarki) 

 

 
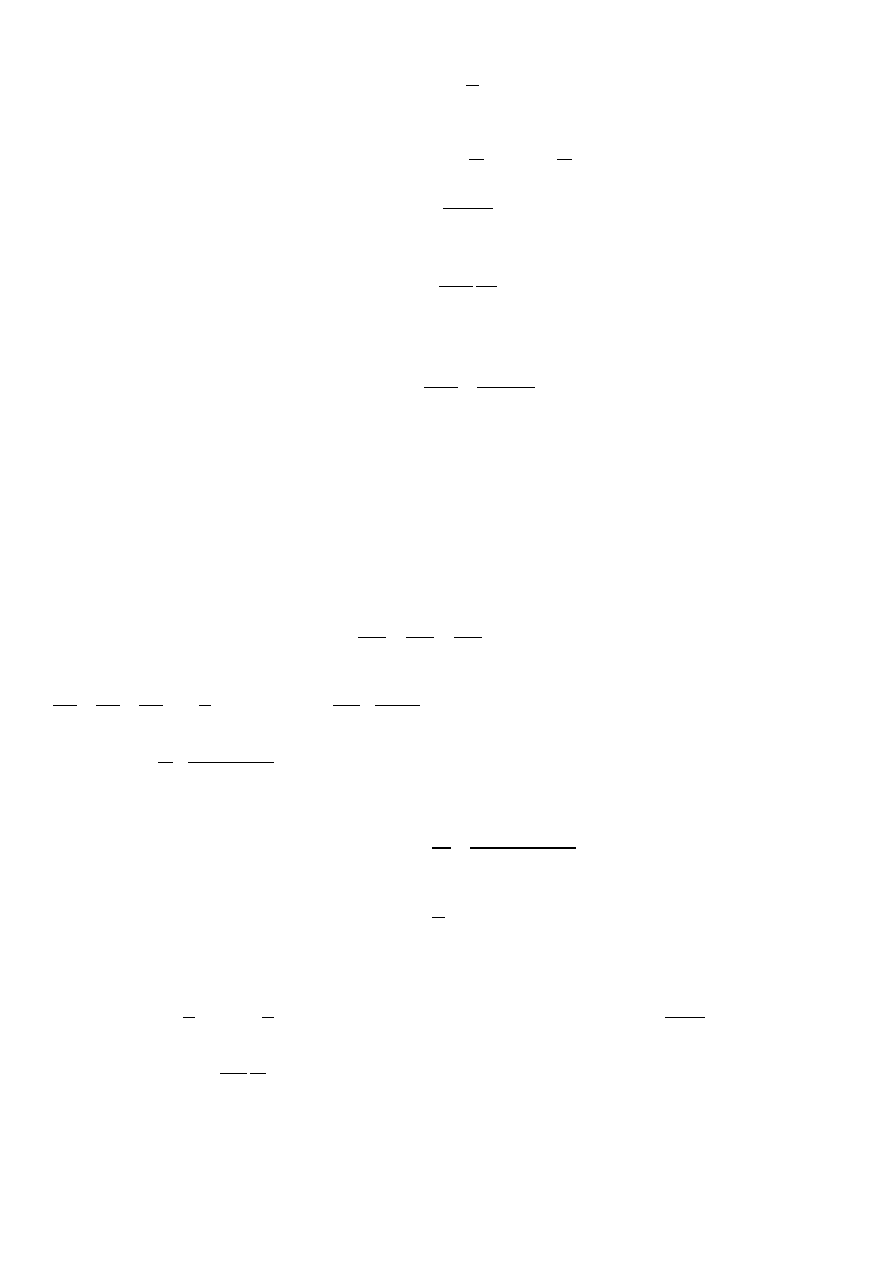
zad. 1                                                                                       𝑑𝑖𝑣𝐸 =

𝜌

𝜀

0

 

𝑟𝑜𝑡𝐸 = 0 

� 𝐸 𝑑𝑠 = 4𝜋𝑟

2

𝐸 =

1

𝜀

0

� 𝜌𝑑𝑉  =

𝑄

𝜀

0

 

𝐸 =

𝑄

4𝜋𝜀

0

𝑟

2

 

F=qE 

𝐹 =

1

4𝜋𝜀

0

𝑄𝑞

𝑟

2

 

Zad.4 
Potencjał pola elektrostatycznego pochodzącego od ciągłego rozkładu ładunku w danym punkcie jest równy 

𝜑(1) =

1

4𝜋𝜀

0

�

𝜌(2)𝑑𝑉

2

𝑟

12

 

Związek natężenia z potencjałem: 

𝐸 = −∇𝜑 

Wektor indukcji magnetycznej możemy przedstawić jako rotację pewnego wektora 

𝐵 = ∇𝑥𝐴 

Przez analogię do pola elektrostatycznego nazwiemy go POTENCJAŁEM WEKTOROWYM. Prawo Gaussa dla 

magnetyzmu jest spełnione:  

∇𝐵 = 0  → ∇(∇𝑥𝐴) = 0 

Ponieważ ∇𝑥𝐵 = µ

0

𝑗  →  ∇(∇𝑥𝐴) = µ

0

𝑗  

Po wykonaniu iloczynu wektorowego i różniczkowania otrzymujemy równanie: 

𝜕𝐴

𝑥

𝜕𝑦

2

+

𝜕𝐴

𝑥

𝜕𝑧

2

+

𝜕𝐴

𝑥

𝜕𝑥

2

= −µ

0

𝑗

𝑥

 

Równanie to ma postać taką jak równanie Poissona dla potencjału pola elektrostatycznego: 

𝜕

2

𝜑

𝜕𝑥

2

+

𝜕

2

𝜑

𝜕𝑦

2

+

𝜕

2

𝜑

𝜕𝑧

2

= −

𝜌

𝜀

0

                  𝜑(1) =

1

4𝜋𝜀

0

∫

𝜌(2)𝑑𝑉

2

𝑟

12

 

Składowa x potencjału wektorowego musi spełniać zależność: 
𝐴(𝑥

1

, 𝑦

1

, 𝑧

1

) =

µ

0

4𝜋

∫

𝑗

𝑥

(𝑥

2

,𝑦

2

,𝑧

2

)𝑑𝑉

2

𝑟

12

  

Dla pozostałych składowych otrzymamy podobne związki. Potencjał wektorowy możemy zapisać w postaci 

wektorowej: 

𝐴⃗(𝑥

1

, 𝑦

1

, 𝑧

1

) =

µ

0

4𝜋 �

𝑗(𝑥

2

, 𝑦

2

, 𝑧

2

)𝑑𝑉

2

𝑟

12

 

Zad.3  
Pole elektrostatyczne jest polem źródłowym (𝑑𝑖𝑣𝐸 =

𝜌

𝜀

0

) i potencjalnym(𝑟𝑜𝑡𝐸 = 0).Linie sił muszą więc 

wychodzić ze źródeł – ładunków i zachować symetrię rozkładu ρ. Dla ładunku punktowego (także naładowanej 

sfery, kuli lub warstwy sferycznej) nie może być zatem wyróżniony żaden kierunek, dlatego E musi być centralne 

. W przypadku symetrii sferycznej można łatwo obliczyć strumień E przez sferę o promieniu r. Wówczas 
∮ 𝐸𝑑𝑠 = 4𝜋𝑟

2

𝐸 =

1

𝜀

0

∫ 𝜌𝑑𝑉 =

𝑄

𝜀

0

 (z równania Maxwella i twierdzenia Gaussa). Stąd 𝐸 =

𝑄

4𝜋𝜀

0

𝑟

2

 (odnajdujemy 

postać prawa Coulomba).F działająca na ładunek punktowy q w polu E to F=qE i dla pola od punktowego 
ładunku Q wynosi  𝐹 =

1

4𝜋𝜀

0

𝑄𝑞

𝑟

2

. 

Dokładnie takie samo pole E otrzymujemy dla naładowanej kuli (sfery, powłoki sferycznej) dla r>R (R-promień 

sfery lub powłoki). Jeśli r<R, to możemy mieć do czynienia z następującymi przypadkami: 

a)Naładowana kula metalowa 

Ładunki gromadzą się na powierzchni- chcą być jak najdalej od siebie. Strumień pola E przez sferę o r<R jest 

równy zero, ponieważ wewnątrz sfery o tym promieniu nie ma ładunków. Pole elektrostatyczne wewnątrz 

naładowanej metalowej kuli znika. Ogólniej- pole elektrostatyczne wewnątrz kawałka przewodnika znika 

niezależnie od jego kształtu, ponieważ ładunek gromadzi się na powierzchni i strumień pola wewnątrz 

przewodnika jest równy zeru. 
b)naładowana kula izolatorowa 

Gdy kula jest izolatorem o równomiernie rozłożonym ładunku Q w całej objętości znajdujemy dla r<R 
4𝜋𝑟

2

𝐸 =

4𝜋𝑟

3

3𝜀

0

𝑄

4
3

𝜋𝑅

3 

 stąd 𝐸 =

1

4𝜋𝜀

0

𝑄𝑟
𝑅

3

. Konsekwencją wyrównywania potencjału w przewodnikach jest powstanie 

silnych pól elektrostatycznych w pobliżu ostrzy. Rozpatrując połączone kule 1 i 2 mamy 𝑉

1

=

𝑄

1

4𝜋𝜀

0

𝑟

1

= 𝑉

2

=

𝑄

2

4𝜋𝜀

0

𝑟

2

 

stąd 

𝑄

1

𝑄

2

=

𝑟

1

𝑟

2

 

Po obliczeniu stosunku natężeń pól obu kul otrzymamy 

𝐸

1

𝐸

2

=

𝑟

2

𝑟

1

 

c)płaszczyzna naładowana 
Linie sił nie mogą preferować żadnego kierunku na płaszczyźnie, wiec są skierowane prostopadle do niej. Gdy 
gęstość powierzchniowa ładunku 𝜎 =

𝑑𝑄

𝑑𝑆

= 𝑐𝑜𝑛𝑠𝑡, to  ∮ 𝐸𝑑𝑠 = 2𝑆𝐸 =

𝑄

𝜀

0

=

𝜎𝑆

𝜀

0

 , 𝐸 =

𝜎

2𝜀

0

 

 
Zad.8 
Cząstka swobodna 

𝑖ℎ�

𝜕𝛹

𝜕𝑡

= 𝐻́𝛹         𝐻́ =

𝑝́

2

2𝑚

+ 𝑉(𝑟)         V(r)=0   

𝑝́ = −𝑖ℎ�∇   

𝑖ℎ�

𝜕𝛹

𝜕𝑡 = −

ℎ

2

́

2𝑚 (

𝜕

2

𝛹

𝜕𝑥

2

+

𝜕

2

𝛹

𝜕𝑦

2

+

𝜕

2

𝛹

𝜕𝑧

2

) 

𝛹(𝑥, 𝑦, 𝑧, 𝑡) = 𝜑(𝑥, 𝑦, 𝑧)𝒳(𝑡) 

𝑖ℎ�

𝜕𝛹

𝜕𝑡 = 𝐸𝛹 

𝑑𝛹

𝛹 =

𝐸

𝑖ℎ�

𝑑𝑡 

𝛹 = 𝐶(𝑟)𝑒

−𝑖𝐸𝑡

ℎ

 

𝒳(𝑡) = 𝑒

−𝑖𝐸𝑡

ℎ

      

𝜑(𝑟) = 𝐶(𝑟) 
𝐻́𝜑(𝑟) = 𝐸𝜑(𝑟) 

−

ℎ

2

́

2𝑚 �

𝜕

2

𝜑

𝜕𝑥

2

+

𝜕

2

𝜑

𝜕𝑦

2

+

𝜕

2

𝜑

𝜕𝑧

2

� = 𝐸𝜑 

ℎ

2

𝑘

2

́

2𝑚 𝜑 = 𝐸𝜑 

ℎ

2

𝑘

2

́

2𝑚 = 𝐸 

𝛹(𝑟, 𝑡) = 𝐶𝑒

𝑖(𝑝𝑟−𝐸𝑡)

ℎ

 

Studnia 

𝑖ℎ�

𝜕𝛹

𝜕𝑡

= 𝐸𝛹 = −

ℎ

2

𝑑

2

𝛹

2𝑚𝑑𝑥

2

  ,    𝛹(0) = 𝛹(𝑎) = 0 

𝛹(𝑥, 𝑡) = 𝜑(𝑥)𝒳(𝑡),           𝒳(𝑡) = 𝑒

−𝑖𝐸𝑡

ℎ

 

−

ℎ

2

́

2𝑚

𝑑

2

𝜑(𝑥)

𝑑𝑥

2

= 𝐸𝜑(𝑥) 

𝜑(0) = 𝜑(𝑎) = 0 rozwiązania mają postać dla 0≤x≤a 

𝜑

𝑘

(𝑥) = 𝐶𝑠𝑖𝑛(𝑘𝑥) oraz 𝐸

𝑘

=

ℎ

2

𝑘

2

́

2𝑚

  

𝜑(0) = 𝜑(𝑎) = 0       ka=nπ    nϵC 

𝜑

𝑛

(𝑥) = 𝐶

𝑛

𝑠𝑖𝑛 �

𝑛𝜋

𝑎 𝑥� , 𝐸

𝑛

=

ℎ

2

𝑛

2

𝜋

2

2𝑚𝑎

2

 

𝐶

𝑛

= �

2
𝑎 

Zad.5 

𝑑𝑖𝑣𝐸 = 0

 

𝑟𝑜𝑡𝐸 = −

𝜕𝐵

𝜕𝑡

 

𝑑𝑖𝑣𝐵 = 0

 

𝑟𝑜𝑡𝐵 =

1

𝑐

2

𝜕𝐸

𝜕𝑡  

𝑟𝑜𝑡(𝑟𝑜𝑡𝐸) = −

𝜕𝑟𝑜𝑡𝐵

𝜕𝑡 = −

1

𝑐

2

𝜕

2

𝐸

𝜕𝑡

2

 

∇

2

𝐸 −

1

𝑐

2

𝜕

2

𝐸

𝜕𝑡

2

= 0

 

∇

2

𝐸 = (∇∇)𝐸 = �

𝜕

2

𝜕𝑥

2

+

𝜕

2

𝜕𝑦

2

+

𝜕

2

𝜕𝑧

2

� 𝐸

 

𝜕

2

𝐸

𝑥

𝜕𝑥

2

+

𝜕

2

𝐸

𝑥

𝜕𝑦

2

+

𝜕

2

𝐸

𝑥

𝜕𝑧

2

−

1

𝑐

2

𝜕

2

𝐸

𝑥

𝜕𝑡

2

= 0

 

𝐸 = �0, 𝐸

𝑦

(𝑥, 𝑡), 0�

 

𝜕

2

𝐸

𝑦

𝜕𝑥

2

−

1

𝑐

2

𝜕

2

𝐸

𝑦

𝜕𝑡

2

= 0

 

𝐸

𝑦

= 𝐶𝑅𝑒𝑒

𝑖(𝑘𝑥−𝜔𝑡)

= 𝐶𝑐𝑜𝑠(𝑘𝑥 − 𝜔𝑡) 

Jeśli równanie rozwiążemy na funkcjach zespolonych, to dowiemy się że prędkość rozchodzenia się fali jest 

prędkością światła. 
  
Zad.7 
𝑥� − 𝑜𝑝𝑒𝑟𝑎𝑡𝑜𝑟 𝑝𝑜ł𝑜ż𝑒𝑛𝑖𝑎 

 

𝑝̂ − 𝑜𝑝𝑒𝑟𝑎𝑡𝑜𝑟 𝑝ę𝑑𝑢

 

𝑥�Ψ(𝑥, 𝑡) = 𝑥Ψ(𝑥, 𝑡)

 

𝑝̂Ψ(𝑥, 𝑡) = −𝑖ℎ

𝑑

𝑑𝑥 Ψ

(𝑥, 𝑡)

 

𝑥�𝑝̂ ≠ 𝑝𝑥�

�

 

𝑥𝑖ℎ

𝑑

𝑑𝑥 Ψ

(𝑥, 𝑡) ≠ 𝑖ℎ

𝑑

𝑑𝑥 Ψ

(𝑥, 𝑡) = 𝑖ℎΨ(𝑥, 𝑡) + 𝑥𝑖ℎ

𝑑

𝑑𝑥 Ψ

(𝑥, 𝑡)