Podstawy Ochrony

Nazwisko: _______________________

Informacji

Rok/grupa: _______________________

Zima 2012/2013

Ć

wiczenie laboratoryjne I

Kryptoanaliza szyfrów mono- i polialfabetycznych

To jest laboratorium ćwiczeniowe. Należy jest wykonać w czasie trwania zajęć. Zadanie
to nie powinno zająć więcej czasu niż czas trwania laboratorium. Jeśli zadanie zostanie
zakończone wcześniej, to można kontynuować prace dotyczące poprzedniego
laboratorium lub pracy semestralnej.

1. Wstęp

System kryptograficzny nazywamy symetrycznym, gdy dla każdej pary kluczy (e, d)
„obliczeniowo łatwe” jest określenie na podstawie znajomości jednego z kluczy z pary,
np.klucza e - drugiego klucza d.

W większości praktycznych rozwiązań algorytmów kryptografii symetrycznej e = d.

Istnieją dwie klasy szyfrów symetrycznych:

•

szyfry blokowe

•

szyfry strumieniowe

Ponieważ w trakcie laboratoium będziemy zajmować sie tylko szyframi blokowmi,
dlatego informacje o szyfrach strumieniowych zostały pominięte.

Szyfr blokowy jest takim systemem szyfrującym, w którym tekst jawny dzielony jest na
ciągi równej długości t nad alfabetem A

M

, zwane blokami , a następnie każdy z bloków

jest kolejno szyfrowany.

Przemiotem ćwiczenia są szyfry blokowe podstawieniowe monoalbabetyczne
i polialfabetyczne (patrz rys. 1).

2. Proste szyfry podstawieniowe (monoalfabetyczne)

Niech A

A

A

A

będzie alfabetem zawierającym q symboli, zaś M

M

M

M

zbiorem wszystkich ciągów o

długości t nad alfabetem A

A

A

A

.

Niech K

K

K

K

będzie zbiorem wszystkich permutacji na zbiorze A

A

A

A

.

Dla każdego e

∈

∈

∈

∈

K

K

K

K

definiuje się przekształcenie szyfrujące:

E

e

(m) = ( e(m

1

) e(m

2

) e(m

3

) ... e(m

t

)) = ( c

1

c

2

c

3

...

c

t

) = c

gdzie:

m = ( m

1

m

2

m

3

...

m

t

)

∈

∈

∈

∈

M

M

M

M

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 2

Każdy symbol spośród t symboli tworzących blok zastępuje się (podstawia za niego)
innym symbolem ze zbioru A

A

A

A

, zgodnie z ustaloną permutacją e. Przekształcenie E

e

nazywa się prostym (monoalfabetycznym) szyfrem podstawieniowym.

Kluczem deszyfrującym odpowiadającym e jest permutacja d = e

-1

.

Szyfry

blokowe

przestawieniowe

podstawieniowe

homofoniczne

monoalfabetyczne

(proste)

polialfabetyczne

poligramowe

produktowe

(kaskadowe

)

Rys. 1 Klasyfikacja blokowych systemów kryptografii symetrycznej

Przekształcenie deszyfrujące:

D

d

(c) = ( d(c

1

) d(c

2

) d(c

3

) ... d(c

t

)) = ( m

1

m

2

m

3

...

m

t

) = m

Liczba różnych przekształceń szyfrujących wynosi q! i nie zależy od rozmiaru bloku t.
(np. dla alfabetu 26-literowego przestrzeń kluczy M

M

M

M

zawiera 26!

≈

≈

≈

≈

4

*

10

26

elementów).

Niestety, szyfry monoalfabetyczne są podatne na atak metodami analizy częstości
występowania znaków w kryptogramie.

Metody zmniejszania skuteczności kryptoanalizy częstotliwościowej

Konfuzja (nieład)

Dążenie do "wikłania" zależności Ee wiążącej klucz przekształcenia szyfrującego z
wiadomością jawną (a w konsekwencji także zależności Dd wiążącej klucz z
kryptogramem).

Rezultat konfuzji : Analiza statystycznych cech kryptogramu nie daje użytecznych
informacji o kluczu szyfrującym przekształcenia.

Dyfuzja (rozproszenie)

"Zacieranie" cech statystycznych tekstu jawnego w trakcie wykonywania przekształcenia
szyfrującego. Stosowane metody dyfuzji sprowadzają się zasadniczo do dwóch metod
postępowania :

•

stosowanie przestawień (mimo zachowania częstości występowania pojedynczych

znaków utrudnia się kryptoanalizę dzięki zaburzeniu częstości występowania
digramów, trigramów, etc.

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 3

•

uzależnienie każdego znaku kryptogramu od jak największej liczby znaków

wiadomości jawnej.

Operacją dodatkową, która może skutecznie wspomagać operację szyfrowania, jest
wstępna kompresja wiadomości jawnej przed poddaniem jej przekształceniu
szyfrującemu.

UWAGA : W tym przypadku odbiorca musi znać metodę dekompresji..

Z reguły w fazie pośredniej odwzorowuje się pierwotny alfabet jawny na zbiór kolejnych
nieujemnych liczb całkowitych, po czym po przeprowadzeniu operacji obliczeniowych
na liczbach i uzyskaniu ciągu liczb odpowiadających wiadomości zaszyfrowanej,
powraca do pierwotnego alfabetu.

Kluczem monoalfabetycznego szyfru podstawieniowego jest pewna permutacja, która w
przypadku dużej mocy alfabetu wiadomości jawnych jest „kłopotliwa” w zapisie.

Ze względu na łatwość implementacji stosuje się systemy z "mniejszą przypadkowością"
w wyborze klucza szyfrowania, tzw. systemy wielomianowe.

W systemach tych przekształcenie szyfrujące określone jest następująco :

f(m) = ( m t k t + m t-1 k t-1 + ... + m 1 k 1 + k 0 ) mod N

gdzie m jest nieujemną liczbą całkowitą < N , odpowiadającą literze alfabetu jawnego,
zaś zbiór:

{ k t , k t-1 , ... , k 1 , k 0 }

jest kluczem przekształcenia.

Dla wielomianów pierwszego rzędu kluczem jest para liczb k 1 i k 0 , a przekształcenie
nosi nazwę przekształcenia afinicznego.

f(m) = ( m k 1 + k 0 ) mod N

Szczególnymi przypadkami przekształcenia afinicznego są :

•

przekształcenie liniowe (tzw. "przerzedzone"): f(m) = m k 1 mod N

•

przesunięciowy "szyfr Cezara" : f(m) = ( m + k 0 ) mod N

Przykład szyfru Cezara:

Szyfr Cezara w wersji podstawowej polega na zastąpieniu każdej litery alfabetu literą
znajdującą się o trzy pozycje dalej (k

1

= 1, k

0

= 3):

C = E(m) = f(m) = (m+3) mod (26)

C to litera tekstu zaszyfrowanego odpowiadająca literze tekstu jawnego o indeksie m

Przesunięcie może mieć wielkość dowolną, więc ogólna postać algorytmu wygląda
następująco:

C = E(m) = (m+k) mod (26), 0<k<26

Algorytm deszyfrujący ma postać:

m = D(C) = (C-k) mod (26)

Dla szyfru Cezara (z przesunięciem o 3 znaki) klucz ma postać:

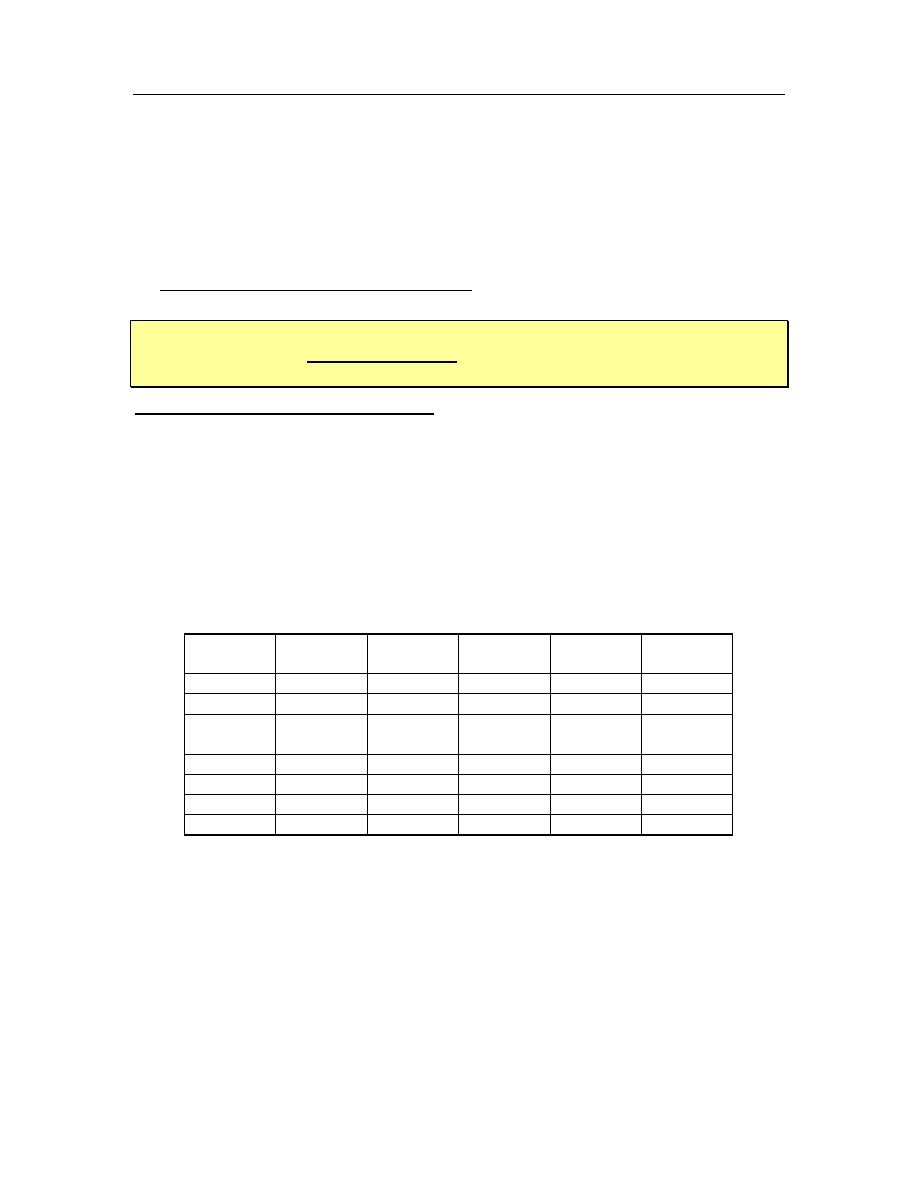
POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 4

a b c d e f g h i j k l m n o p q r s t u v w x y z
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Stąd przykładowy szyfrogram ma postać

tekst jawny : szyfr juliusza cezara
tekst zaszyfrowany: VCBIU MXOLXVCD FHCDUD

Dla szyfru Cezara łatwo można przeprowadzić kryptoanalizę metodą brutalną polegającą
na wypróbowaniu 25 możliwych kluczy k.

W afinicznych systemach kryptograficznych istotny jest właściwy dobór parametrów
klucza.

W szczególności parametr k

1

oraz liczba N określająca moc alfabetu wiadomości

jawnych muszą być względnie pierwsze. W przeciwnym przypadku nie istnieje
jednoznaczne przekształcenie deszyfrujące.

Przykład niewłaściwego wyboru klucza :

N = 26 (np. alfabet dużych liter łacińskich)

Wybierając k 1 = 13 i k 0 = 4 uzyskujemy :

f("A") = f(0) = ( 13 . 0 + 4 ) mod 26 = 4 mod 26 = 4 = "E"

f("C") = f(2) = ( 13 . 2 + 4 ) mod 26 = 30 mod 26 = 4 = "E"

Szyfry podstawieniow monalfabetyczne są podane na kryptoanlaizę częstotliwościową.
Dla każdego języka można bowiem określić względną częstość występowania liter.
Poniższa tabela prezentuje procentową częstość względną występowania poszczególnych
liter w tekście angielskim.

Litera

Częstość

(%)

Litera

Częstość

(%)

Litera

Częstość

E

12,75

L

3,75

W

1,50

T

9,25

H

3,50

V

1,50

R

8,50

C

3,50

B

1,25

N

7,75

F

3,00

K

0,50

I

7,75

U

3,00

X

0,50

O

7,50

M

2,75

Q

0,50

A

7,25

P

2,75

Z

0,25

D

4,25

G

2,00

3. Podstawieniowe szyfry polialfabetyczne

Polialfabetycznym szyfrem podstawieniowym jest szyfr blokowy o długości bloku t nad
alfabetem A

A

A

A

o następujących właściwościach:

•

przestrzeń kluczy K

K

K

K

zawiera wszystkie uporządkowane zbiory t permutacji ( p

1

,

p

2

, p

3

, ..., p

t

), przy czym każda permutacja p

i

jest określona na zbiorze A

A

A

A

;

•

szyfrowanie wiadomości m = ( m

1

m

2

m

3

...

m

t

)

∈

∈

∈

∈

M

M

M

M

przy pomocy klucza e = ( p

1

, p

2

, p

3

, ..., p

t

)

∈

∈

∈

∈

K

K

K

K

jest zdefiniowane przez:

E

e

(m) = ( p

1

(m

1

) p

2

(m

2

) p

3

(m

3

) ... p

t

(m

t

)) = ( c

1

c

2

c

3

...

c

t

) = c

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 5

•

przekształcenie deszyfrujące:

Dd (c) = (p

1

-1

(c

1

) p

2

-1

(c

2

) p

3

-1

(c

3

) ... p

t

-1

(c

t

))

zaś kluczem deszyfrującym d odpowiadającym kluczowi e jest uporządkowany
zbiór t permutacji odwrotnych:

d = (p

1

-1

, p

2

-1

, p

3

-1

, ..., p

t

-1

)

∈

∈

∈

∈

K

Przykład (szyfr Vigenere’a):

Niech A

A

A

A

= { a, b, c, ..., x, y, z } oraz t = 3. Wybierając jako klucz e zbiór trzech permutacji

( p

1

, p

2

, p

3

) takich, że p

1

przesuwa każdą literę o 3 pozycje w prawo (szyfr Cezara), p

2

-

o 7 pozycji w prawo, zaś p

3

- o 10 pozycji w prawo, uzyskuje się z wiadomości jawnej:

m = thi sci phe ris cer tai nly not sec ure

kryptogram:

c = E

e

(m) = wos vjs soo upc flb whs qsi qvd vlm xyo

Dużym ułatwieniem przy szyfrowaniu I deszyfrowaniu tekstu jest tablica Vigenere’a
(patrz niżej). Dla dowolnej litery tekstu jawnego a i dowolnej litery klucza k literą
kryptogramu c jest znak na przecięciu kolumny a i wiersza k. Deszyfrowanie działa
podobnie. Jak?

Szyfry

polialfabetyczne

są

także

trudniejsze

do

przełamania

od

szyfrów

monoalfabetycznych, lecz „odgadnięcie” długości bloku t sprowadza kryptoanalizę do
badania

t

przekształceń

monoalfabetycznych,

przy

czym

np.

do

analizy

częstotliwościowej zestawiane są podzbiory symboli kryptogramu określone zależnością:

C

i

= { c

i

, c

i+t

, c

i+2t

, ..., c

i+nt

} (i = 1, 2, ..., t -1)

Test Kasiski’ego:

Obserwacja: Powtarzalne fragmenty tekstu jawnego szyfrowane tymi samymi
fragmentami klucza dają w rezultacie identyczne segmenty kryptogramu.

Wniosek: Odstęp pomiędzy powtarzającymi się segmentami kryptogramu powinien być
wielokrotnością długości klucza t.

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 6

Metodyka:

Po

wyznaczeniu

zbioru

liczb,

będących

odległościami

między

powtarzającymi się segmentami kryptogramu należy wyznaczyć dla nich największy
wspólny podzielnik (gcd - greatest common divisor), który (po odrzuceniu
przypadkowych powtórzeń segmentów w krytpogramie) wskaże długość bloku (klucza) t.

Indeks koincydencji Friedmana (IC):

IC określa prawdopodobieństwo wystąpienia w kryptogramie dwóch jednakowych liter i
wyliczany jest z zależności :

(

)

(

)

1

1

1

0

−

−

∑

−

=

=

L

L

f

f

n

i

i

i

IC

gdzie f

i

jest liczbą wystąpień litery a

i

w tekście o długości L zaś sumowanie obejmuje

wszystkie litery alfabetu A

A

A

AC.

Tablica 1. Wartości oczekiwanych IC dla długiego tekstu angielskiego (26 symboli w
alfabecie A

M

)

t

1

2

3

4

5

10

∞

∞

∞

∞

IC

0,066

0,052

0,047

0,045

0,044

0,041

0,038

Wartość oczekiwana indeksu koincydencji:

( )

r

L

L

t

t

p

L

t

L

t

IC

E

κ

κ

1

1

1

1

−

−

−

−

+

=

gdzie:

L - długość kryptogramu;

t - okres (długość bloku);
k

p

- miara rozkładu prawdopodobieństwa (częstości) znaków w tekście jawnym (A

A

A

AM

zawiera N symboli):

∑

=

=

n

i

i

p

p

1

2

κ

Tablica 2. Przykładowe wartości współczynnika k

p

Język

k

p

francuski

0.0778

hiszpański

0.0775

niemiecki

0.0762

włoski

0.0738

angielski

0.0667

rosyjski

0.0529

k

r

- prawdopodobieństwo pojawienia się określonego symbolu w kryptogramie przy

„idealnie” płaskich charakterystykach częstotliwościowych:

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 7

n

r

1

=

κ

Przykład wykorzystania IC do oszacowania okresu szyfru :

Tekst angielski (duże litery bez spacji) po zaszyfrowaniu szyfrem podejrzewanym o to,
ż

e jest polialfabetycznym szyfrem okresowym, dał następujący szyfrogram :

"GPSNBMMBOHVBHFTIBWFCFFOQMBZJOHB

GVOEBNFOUBMQPMFJODPNQVUFSTDJFODF"

Długość zaszyfrowanego tekstu L = 63 znaki.

Liczba wystąpień poszczególnych liter w kryptogramie :

FA = FK = FL = FR = 0

FB = FC = FE = FI = FW = FZ = 1

FD = FH = FJ = FN = FP = FQ = FV = 3

FF = 9

FG = FS = FT = FU = 2

FM = 5

FO = 7

Wyliczony na podstawie powyższych danych wskaźnik zgodności :

IC = 0,061

A zatem należy podejrzewać, iż jest to szyfr monoalfabetyczny. Podstawiając d = 1,
I zakładając, iż litera F o największej liczbie powtórzeń odpowiada literze E o
największej częstotliwości występowania, otrzymuje się natychmiast rozwiązanie (gdyż
k1 = 1) :

"FORMALLANGUAGESHAVEBEENPLAYINGA

FUNDAMENTALROLEINCOMPUTERSCIENCE"

zaś po uzupełnieniu domyślnymi spacjami :

"FORMAL LANGUAGES HAVE BEEN PLAYING A

FUNDAMENTAL ROLE IN COMPUTER SCIENCE"

4. Ćwiczenie

W ramach ćwiczenia dostępne są dwie aplikacje (pracujące w środowisku MS-DOS).
Pierwsza z nich - Afin.exe – służy do krypotanalizy podstawieniowego szyfru
monoalfabetycznego, druga z kolei - Kasiski.exe - do kryptoanalizy szyfru
polialfabetycznego.

Przebieg ćwiczenia

1.

Kryptoanaliza szyfru monoalfabetycznego

Dla otrzymanych szyfrogramów należy odgadnąć klucz, a następnie odszyfrować
szyfrogram. Ponieważ szyfr afiniczny ma postać:

f(m) = ( m k 1 + k 0 ) mod N

stąd należy odgadnąć wartość k

1

, k

0

oraz N. Program Afin.exe umożliwia prowadzenie

ataku ze znanym tekstem, tzn. dla podanego znaku lub grupy znaków zwraca odpowiedni
kryptogram. Alfabetem tekstu jawnego oraz szyfrogramu mogą być znaki należące do

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 8

podstawowej (regularnej) i rozszerzonej tabeli kodów ASCII (patrz niżej). Pierwszym
znakiem tego alfabetu jest zawsze znak spacji.

2.

Kryptoanaliza szyfru Vigenere

W szyfrze Vigenere’a klucz tworzy sekwencja liter K = k

1

... k

t

przy czym k

i

(i=1, ..., t)

daje liczbę przesunięć w i-tym alfabecie, tj. każdy znak w kolejnych blokach o długości t
znaków jest przekształcany w znak szyfrogramu wg formuły:

f

i

(

m) = (m + k

i

) mod

N

Zadanie polega na odgadnięciu dla otrzymanych szyfrogramów klucza szyfrującego, a
następnie odszyfrowaniu szyfrogramu.

Program Kasiski.exe wspomaga prowadzenie kryptoanalizy, obliczając m.in. indeks
(współczynnik) koincydencji Friedmana, histogram oraz zbiór liczb, będących
odległościami między powtarzającymi się segmentami kryptogramu, które po
wyznaczeniu największego wspólnego podzielnik mogą pomóc (po odrzuceniu
przypadkowych powtórzeń segmentów w kryptogramie) w określeniu długości bloku
(klucza) t.

Przykład testowy:

Kryptogram o postaci

zhyme zvelk ojubw ceyin cusml ravsr yarnh ceari ujpgp vardu

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 9

qzcgr nncaw jaluh gjpjr ygegq fulus qffpv eyedq golka lvosj

tfrtr yejzs rvnci hyjnm zdcro dkhcr mmlnr fflfn qgolk alvos

jwmik qkubp sayoj rrqyi nrnyc yqzsy ednca leilx rchug iebko

ythgv vckhc jeqgo lkalv osjed weaks gjhyc llfty igsvt fvpmz

nrzol cyuzs fkoqr yryar zfgki qkrsv ircey uskvt mkhcr myqil

xrcrl gqarz olkhy ksnfn rrncz twuoc jnmkc mdezp irjej w

został uzyskany dla klucza ray i tekstu jawnego:

ihave beent oldby learn edsou rcest hatwh enatr ulygr eatmu

sicia nplay sandh ispla yings ounds sofre eands ponta neous

thatt helis tener hasno ideao fthea mount ofnon spont aneou

swork study schol arshi panal ysisa ndpla nning requi redto

achie vethe sespo ntane ousef fects ishal lnota rguet hepoi

ntion lywis htosa ythat ifiti strue itlea dsmet othea mazin

greal izati ontha tspon tanei tydoe snotc omeby itsel f

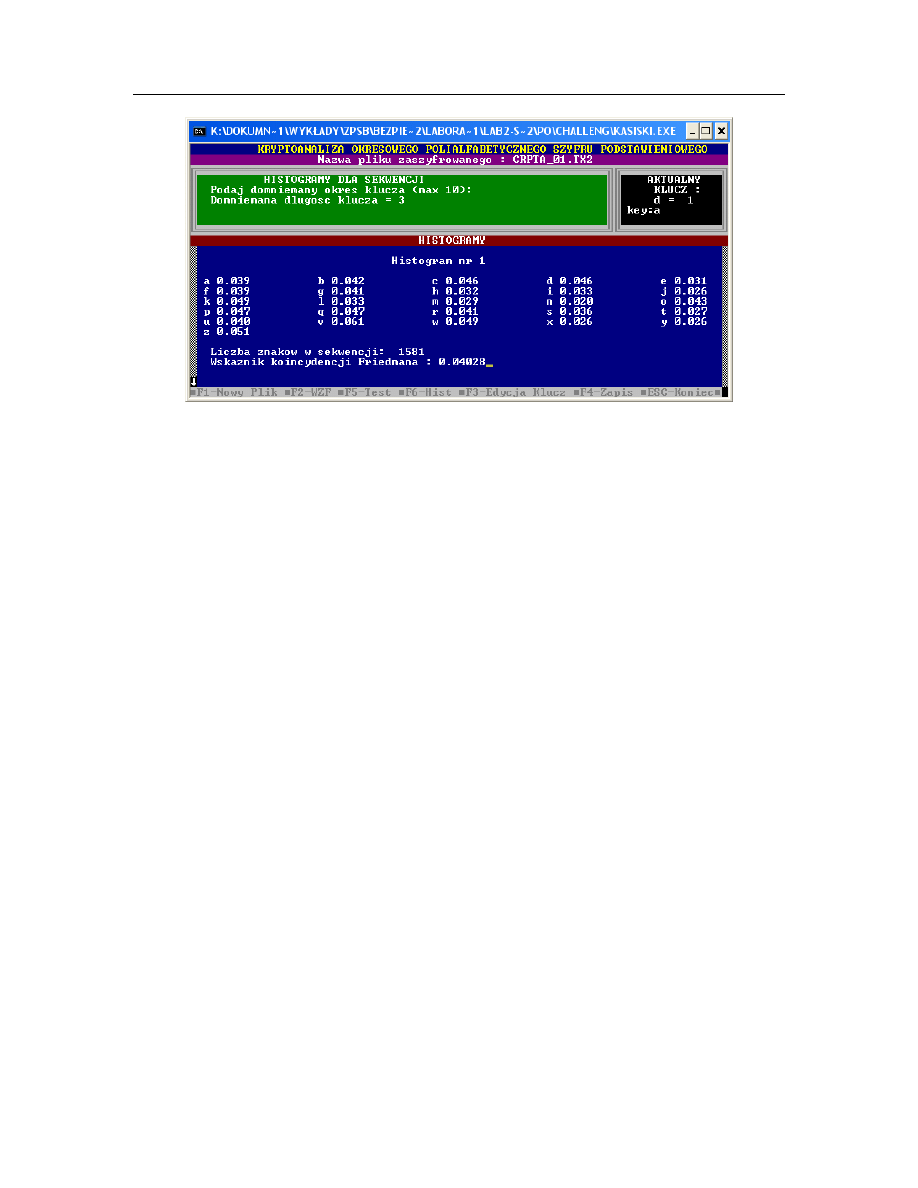
Przypomnijmy sobie, że w kryptoanalizie należy najpierw oszacować długość klucza
(długość bloku t, w programie Kasiski.exe parametr ten jest oznaczony przez d) - opcja
F2 programu, później dla wybranej liczby powtórzeń znaków w kryptogramie wykonać
test Kasisiego – opcja F5 programu i w końcu dla wybranej długości hasła t obejrzeć
histogramy (opcja F6 programu) dla każdej sekwencji z poniższych:

sekwencja 1: c

1

, c

1+t

, c

1+2t

, ..., c

1+nt

sekwencja 2: c

2

, c

2+t

, c

2+2t

, ..., c

2+nt

.......................................

sekwencja t: c

t

, c

t+t

, c

t+2t

, ..., c

t+nt

Na podstawie uzyskanych t histogramów można zidentyfikować kolejne znaki hasła.

Na przykład dla przedstawionego powyżej szyfrogramu prawdopodobna długość
szyfrogramu wynosi 6 (tak wynika z testu Freedmana, dla którego IC = 0.043, patrz także
Tabela 1). Testy Kasiskiego pokazują, że najczęstszymi podzielnikami odstępów
pomiędzy powtarzającymi się fragmentami szyfrogramu (o różnych długościach) jest
liczba 3. Przyjmijmy zatem, że długość hasła wynosi 3 i obejrzymy po kolei histogramy,
o których wspomniano powyżej (opcja F6 programu).

POI

Zima, 2012/2013

Ć

wiczenie laboratoryjne I

strona 10

W histogramie szukamy znaku, który najczęściej występuje w sekwencji pierwszej (jest
to znak v). Ponieważ w sekwencjach od 1 do t częstość występowania znaków jest taka
sama jak w tekście jawnym, to należy przyjąć, że znakom w sekwencji o największej
częstości odpowiada zaszyfrowana literka e (ten znak najczęściej występuje w
anglojęzycznych tekstach jawnych).

Stąd na podstawie tabeli Vigenere można znaleźć, że znakowi e tekstu jawnego i
znakowi v szyfrogramu odpowiada znak r (jest to pierwszy znak klucza). Pozostałe dwa
znaki klucza znajdujemy tak samo.

Uwaga! Czasami częstości wstępowania znaków w kryptogramie są bardzo zbliżone do
siebie. Wówczas należy znaleźć odpowiadające im znaki klucza, a następie zbadać
wszystkie możliwe klucze, które są kombinacją tych znaków, aż do momentu
odszyfrowania szyfrogramu.

Sprawozdanie z ćwiczenia

W trakcie ćwiczenia należy notować wszystkie czynności oraz uzyskiwane wyniki. Po
zakończeniu ćwiczenia należy przygotować sprawozdanie z przebiegu ćwiczenia,
zawierające m.in. krótki opis ćwiczenia, uzyskane wyniki oraz podsumowanie i wnioski
z ćwiczenia.

Sprawozdanie powinno zawierać opis sposobu przeprowadzenia ataku, odgadnięte klucze
oraz odszyfrowany tekst jawny.

Literatura

1. D. E. Robling Denning Kryptografia i ochrona danych, WNT 1982

2. J. Pieprzyk, T. Hardjono, J. Seberry Teoria bezpieczeństwa systemów

komputerowych

, Wydawnictwo Helion, 2005.