WYZNACZANIE STAŁEJ KERRA

Wstęp

Istnieją trzy zjawiska zwane zjawiskami Kerra, których wspólnym elementem jest 

pojawianie się dwójłomności substancji, które w normalnych warunkach jej nie wykazują:

•

optyczne zjawisko Kerra

 

  to zmiana współczynnika załamania materiału pod wpływem 

światła o bardzo dużym natężeniu;

•

m

   agnetooptyczne zjawisko Kerra

 

  (zjawisko Faradaya) jest podobne do efektu 

elektrooptycznego, ale jest wywołane polem magnetycznym;

•

elektrooptyczne zjawisko Kerra

 

  (kwadratowe elektrooptyczne zjawisko Kerra) to pojawianie 

się dwójłomności w ośrodku izotropowym pod wpływem przyłożonego pola elektrycznego.

W tym ćwiczeniu analizowane będzie zjawisko odkryte w 1875 przez szkockiego fizyka Johna 

Kerra, który badał zachowanie się promienia świetlnego przechodzącego przez płytę szkła, gdy 

prostopadle do biegu promieni świetlnych przykładane było wysokie napięcie. Dla pewnych 

wartości tego napięcia szkło okazywało się dwójłomne, by po wyłączeniu pola elektrycznego 

utracić tą właściwość. Wkrótce po tym odkryciu stało się jasnym, że efekt ten nie jest związany z 

deformacją szkła wymuszoną przez pole elektryczne, gdyż takie samo zjawisko zaobserwowano 

w cieczach. Doświadczenia z użyciem nitrobenzenu (cieczy szkodliwej) wymagają przyłożenia 

napięcia rzędu kilku kV, a obserwowane efekty elektrooptyczne są nawet o 2 rzędy wielkości 

mniejsze (wartość stałej Kerra) niż w ciałach stałych. W przypadku kwadratowego zjawiska 

elektrooptycznego ośrodek zyskuje dwójłomność w wyniku układania się polarnych cząsteczek 

ośrodka w kierunku zewnętrznego pola elektrycznego. Uporządkowaniu cząsteczek 

przeciwdziałają ich ruchy termiczne, dlatego efekt jest mniejszy przy wzroście temperatury. 

Opis teoretyczny

Poniżej przedstawiono uproszczony, skalarny opis zachowania się promienia światła 

przechodzącego przez ciało stałe (komórkę Kerra), które nie jest ośrodkiem centrosymetrycznym. 

Aby zaobserwować kwadratowe zjawisko elektrooptyczne można do promienia światła 

spolaryzowanego liniowo, padającego na badaną komórkę, przyłożyć prostopadle pole 

elektryczne. Przy braku pola elektrycznego komórka musi przepuszczać padające na nią światło, 

dlatego pole elektryczne przyłożymy pod kątem 45° do płaszczyzny polaryzacji światła. Na 

wyjściu komórki światło spolaryzowane będzie eliptycznie, a parametry tej elipsy będą zależne 

od drogi światła w ośrodku, natężenia pola elektrycznego i rodzaju substancji. 

Promień światła, którego wektor pola drga równolegle do przyłożonego pola 

elektrycznego nazywamy promieniem nadzwyczajnym, a promień światła, którego wektor pola 

drga prostopadle do tego pola nazywamy promieniem zwyczajnym. Różnica dróg optycznych 

pomiędzy promieniami zwyczajnym i nadzwyczajnym wyniesie:

 L = d(n

n

- n

z

)

(1)

gdzie:

n

n

 – współczynnik załamania promienia nadzwyczajnego

n

z

 – współczynnik załamania promienia nadzwyczajnego,

d – odległość pomiędzy okładkami komórki Kerra.

W związku z tym przesunięcie fazy wyniesie:

(

)

z

n

n

n

d

−

=

∆

λ

π

2

(2)

gdzie:

λ – długość fali promieniowania padającego na komórkę Kerra w próżni.

Można także pokazać, że przesunięcie fazy jest proporcjonalne do odległości d i kwadratu 

polaryzacji P. Jeżeli przyjmiemy, że polaryzacja jest liniową funkcją natężenie pola 

elektrycznego, a współczynnik proporcjonalności wynosi 2πK powyższą relację można zapisać 

jako:

2

2 KIE

π

=

∆

(3)

gdzie:

K – stała Kerna,

I – natężenie światła padającego na komórkę Kerra,

E – natężenie pola elektrycznego przyłożonego do komórki Kerra.

Zmiana fazy pomiędzy promieniami zwyczajnym i nadzwyczajnym, powstała w trakcie 

propagacji światła w komórce Kerra, jest proporcjonalna do kwadratu przyłożonego do niej 

napięcia, co tłumaczy pochodzenie nazwy zjawiska. Natężenie pola elektrycznego można 

wyrazić przez napięcie U przyłożone do elektrod i odległość między nimi w:

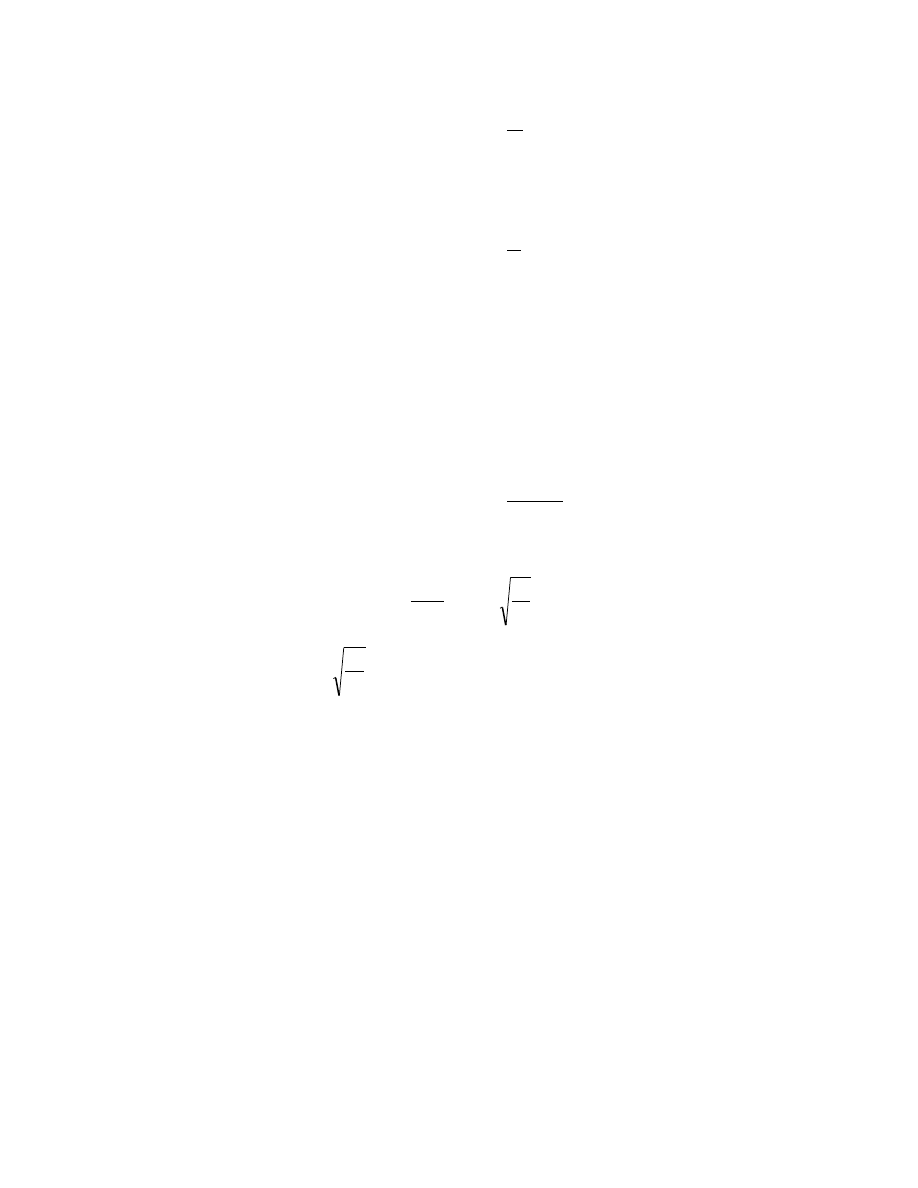
w

U

E

=

(4)

Natężenie światła I poza analizatorem jest wyznaczane dla układu laboratoryjnego (polaryzator i 

analizatora skręcone po 45

0

 względem kierunku pola elektrycznego w komórce) z relacji (1):











 ∆

=

2

sin

2

0

I

I

(5)

gdzie:

I

0

 – natężeni światła poza analizatorem gdy polaryzator i analizator są skręcone w tym samym 

kierunku, a pole elektryczne w komórce jest zerowe,

Δ – przesunięcie fazy między promieniami zwyczajnym i nadzwyczajnym.

Ze stałej proporcjonalności wyznaczana jest stała Kerra właściwa dla danego materiału z 

którego została wykonana komórka. Po podstawieniu (2) do (4) z użyciem (3) otrzymujemy:









=

2

2

2

0

sin

w

KdU

I

I

π

(6)

Rozwiązując to równanie względem U

2

 otrzymujemy









=

0

2

2

arcsin

I

I

Kd

w

U

π

(7)

Wykres funkcji 









=

0

2

arcsin

I

I

f

U

 będzie w przybliżeniu linią prostą. Z kąta nachylenia 

prostej wyznaczymy skalar - stałą Kerra K. Przy zastosowaniu pełnego opisu właściwości 

ośrodka stała ta jest wyrażana przez tensor. 

Opis układu laboratoryjnego

Najważniejszym elementem układu laboratoryjnego jest komórka Kerna wykonana z PLZT, 

ceramicznego kompozytu o wagowym udziale składników: Pb 0.9125, La 0.0875, Zr 0.65, Ti 

0.3503. Badany element PLZT jest przezroczysty dla fal elektromagnetycznych o długościach od 

0,4 do 5,6 um. Dla fali 633 nm (światło czerwone) współczynnik transmisji jest większy od 60%. 

Można przyjąć, że element PLZT zachowuje się jak przezroczysty polikryształ. Jednocześnie w 

stosunku do przyłożonego pola elektrycznego zachowuje się analogicznie do ferromagnetyka 

włożonego do pola magnetycznego. Domeny w elemencie PLZT są wstępnie spolaryzowane, a 

przyłożone napięcie powoduje wzrost ich objętości oraz zmianę orientacji zgodną z kierunkiem 

przyłożonego pola.

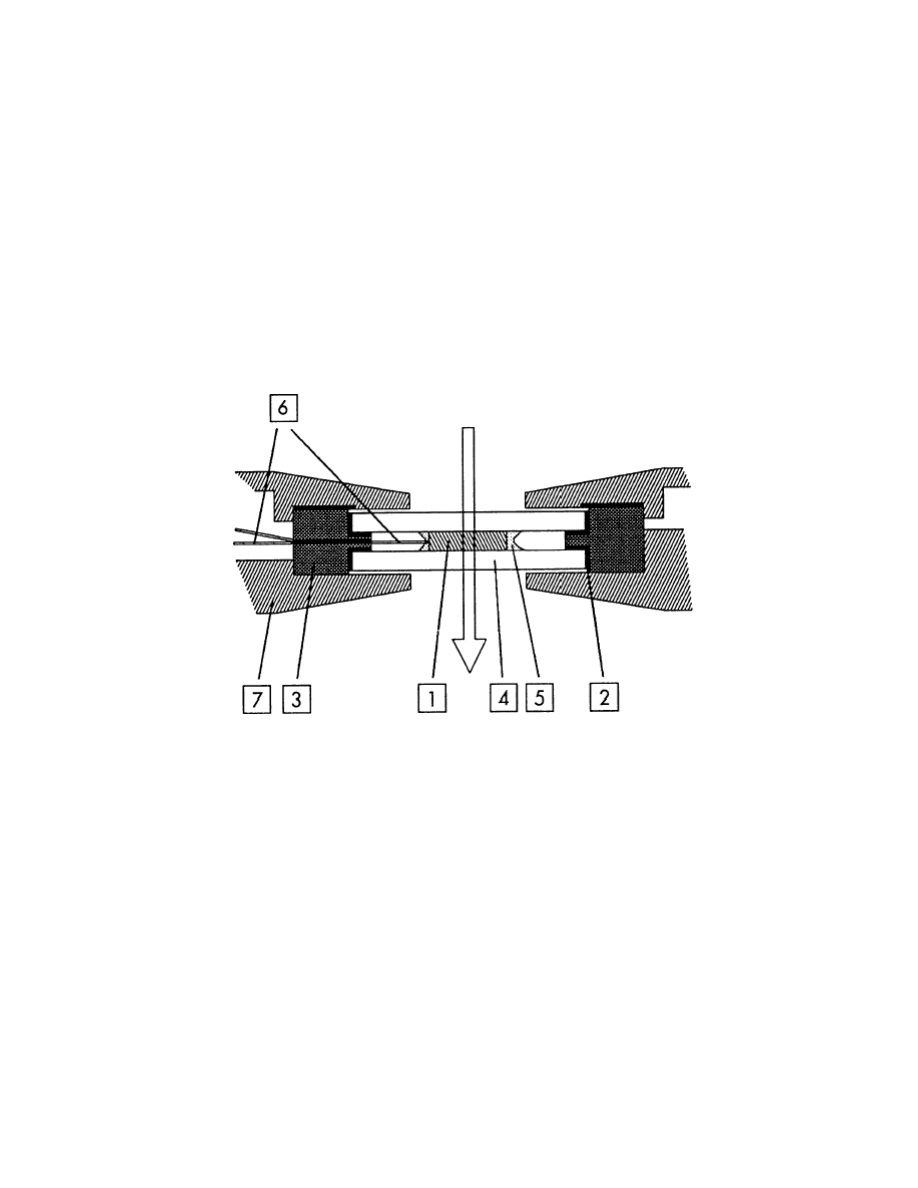
Element aktywny modulatora elektrooptycznego na bazie PLZT [1] pokazany na Rys.1. 

jest równoległościanem o wysokości 8 mm, długości (droga propagacji światła) w=1,5 mm i 

szerokości (odległość między elektrodami) d=1,4 mm. Element aktywny jest zamknięty 

hermetycznie z użyciem krzemowego pierścienia izolującego [3] i zaklejony pomiędzy dwiema 

płytkami szklanymi [4]. Dla zapewnienia przezroczystości optycznej jako klej [2] został użyty 

Balsam Kanadyjski. Druty [6] są przymocowane do elektrody od czoła elementu i łączą się z 

gniazdkiem BNC na obudowie [7].

Rys.1. Przekrój przez element PLZT w płaszczyźnie padania światła.

Układ laboratoryjny przedstawiony na Rys.2. zawiera następujące elementy:

1. komórkę Kerra (modulator elektrooptyczny na bazie PLZT);

2. zasilacz wysokiego napięcia (0-10 kV);

3. laser He-Ne 1.0 mW, z zasilaczem AC 230 V;

4. 2 filtry polaryzacyjne na stojakach: a) polaryzator, b) analizator;

5. ławę optyczna (dł. 60 cm) z 2 zestawami poziomujących podpórek;

6. uchwyty ślizgowe do ławy optycznej: 4 (wys. 30 mm) , 1 (wys. 80 mm);

7. fotodetektor;

8. uniwersalny wzmacniacz pomiarowy;

9. 2 cyfrowe multimetry pracujące jako woltomierze;

oraz kable i złącza: ekranowane kable BNC (750 mm); adapter: BNC-socket/4 mm (para 

zacisków wtykowych); 2 kable łączące czerwone (750 mm);  3 kable łączące niebieskie (750 

mm). 

Rys.2. Widok zestawu laboratoryjnego.

Element PLZT [1] jest podłączony bezpośrednio do zasilacza wysokonapięciowego [2]. 

Napięcie zasilające może być ustawiane od 0 do 10 000 V z precyzją większą niż zapewnia 

wyświetlacz zasilacza dzięki cyfrowemu woltomierzowi [9a] podłączonemu równolegle do 

zasilacza [2]. Nie wolno przekraczać napięcia 1000 V na zasilaczu, bo zniszczy to element PLZT. 

Źródłem światła jest laser He/Ne [3] o mocy 1 mW. Przed przystąpieniem do pracy z układem 

laboratoryjnym należy zapoznać się z warunkami BHP pracy z laserami.

Światło z lasera He/Ne [3] jest spolaryzowane liniowo przez polaryzator [4a]. Liniowo 

spolaryzowana fala świetlna może być rozpatrywana jako złożenie dwóch fal o jednakowych 

fazach spolaryzowanych tak, że jedna jest równoległa a druga prostopadła do kierunku pola 

elektrycznego przyłożonego do elementu PLZT. Monochromatyczne, pionowo spolaryzowane 

światło pada na element PLZT  który jest umocowany pod kątem 45° do pionu. Dwie fale 

świetlne przechodzą przez element PLZT z różnymi prędkościami. Fala nadzwyczajna jest 

1

2

3

4a

5

6

7

8

9b

9a

4b

relatywnie opóźniona w stosunku do fali zwyczajnej, co powoduje powstanie różnicy faz 

pomiędzy falami wychodzącymi z elementu PLZT. W efekcie na analizator [4b] pada światło 

spolaryzowane eliptycznie. Za analizatorem znajduje się fotodetektor [7], którym jest fotodioda 

krzemowa, używana wraz ze wzmacniaczem [8].

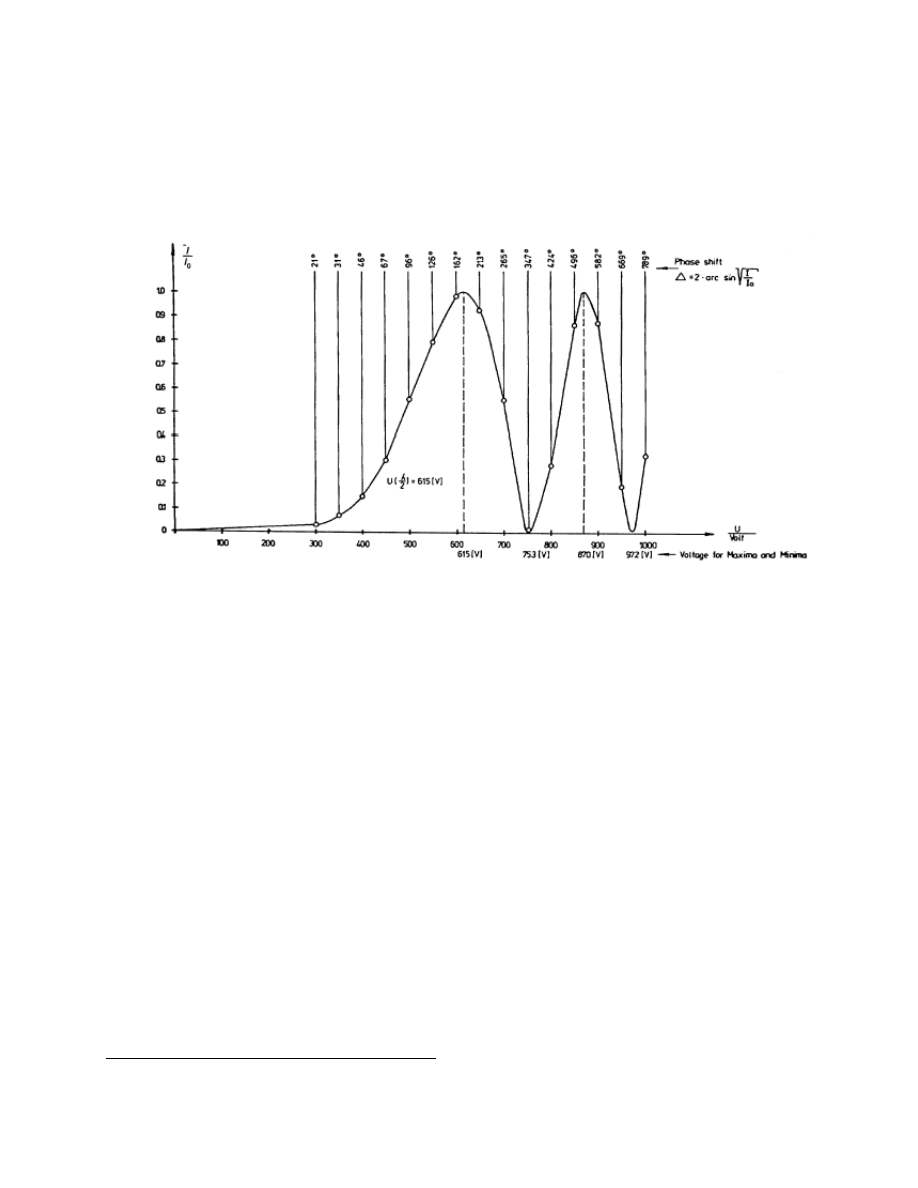
Rys.3. Względne natężenie światła poza analizatorem, jako funkcja napięcia U przyłożonego 

do elementu PLZT. Wyznaczone kąty zmiany fazy Δ pomiędzy promieniami zwyczajnym i 

nadzwyczajnym naniesiono w celu lepszego zobrazowania zjawiska

.

Obecność przesunięcia fazy jest dobrze widoczne poprzez maksima i minima 

obserwowanego natężenia światła w funkcji napięcia na fotodetektorze, co pokazano na Rys.3. 

Gdy do komórki Kerra nie przykładamy napięcia analizator i polaryzator wytłumią światło 

dochodzące do fotodetektora. Ze wzrostem napięcia następuje wzrost intensywności światła 

docierającego do fotodetektora. W przedstawionym przypadku maksimum natężenia widoczne 

jest po raz pierwszy dla napięcia 615 V. Jest to tak zwane napięcie półfalowe, gdy przesunięcie 

fazowe pomiędzy promieniami zwyczajnym i nadzwyczajnym wynosi 180

0

. Wartość stałej Kerra 

w tym przypadku wynosi K=2,7 10

-9

 (m/V

2

). Jest to wartość średnia podawana przez producenta 

dla fabrycznie nowych komórek. Ulega zmianie między innymi w związku z historią pracy.

Uwagi do wykonywania pomiarów

Ogólne wytyczne BHP przy pracy z laserami.

Każdy użytkownik winien przed uruchomieniem lasera lub urządzenia laserowego ustalić jego 

klasę i podstawowe dane o nim: długość emitowanej fali, moc lub energię, zalecenia użytkowe 

producenta. Laserem impulsowym nazywamy taki, którego czas świecenia jest krótszy niż 0,25 

sek. W przeciwnym wypadku jest uważamy go za pracujący w sposób ciągły.

Urządzenie laserowe klasy 1 jest bezpieczne, ponieważ wiązki laserowe nie są wyprowadzane na 

zewnątrz lub są dostatecznie słabe (odtwarzacz płyt kompaktowych). Po zdjęciu obudowy staje 

się urządzeniem wyższej klasy. 

Laser klasy 2 to laser emitujący promieniowanie widzialne (400 - 700 nm). Laser o działaniu 

ciągłym nie może mieć mocy większej niż 1mW, natomiast energia pojedynczego błysku lasera 

impulsowego może wynosić do 0,2uJ. Laser klasy 2 nie wymaga stosowania okularów 

ochronnych. Zabezpieczeń takich wymagają lasery klas wyższych od 2. 

Nie wolno pracować z żadnymi laserami jeżeli stosowało się leki wpływające na wielkość źrenic 

i odruch zamykania oczu. Za podstawową ochronę oczu przy pracy z laserami klasy 2 uważa się 

naturalne odruchy obronne zamykania oczu pod wpływem gwałtownego ich oświetlenia. W 

przypadku napromieniowania należy natychmiast zgłosić wypadek prowadzącemu oraz 

skorzystać z pomocy lekarskiej.

Bez względu na klasę lasera zabrania się patrzenia w wiązkę wychodzącą z lasera lub odbitą. 

Zabrania się zabaw wiązkami laserowymi polegającymi na oświetlaniu ludzi lub materiałów 

niebezpiecznych. W czasie ustawiania eksperymentu zaleca się pracować przy włączonym 

pełnym oświetleniu. Obowiązkiem eksperymentatora jest takie kierowanie wiązek, aby nie 

opuściły obszaru eksperymentu (ustawiając lustra, budując ekrany absorbujące lub 

rozpraszające). Wiązki laserowe należy prowadzić na poziomie różnym od poziomu oczu. 

Przed wykonywaniem jakichkolwiek pomiarów natężenia światła laser He/Ne musi być 

włączony na około 60 minut wcześniej, aby ustabilizować jego emisję. W tym czasie można 

dokonywać korekt ustawienia elementów układu i próbnych odczytów. Po każdej zmianie 

napięcia przykładanego do elementu PLZT lub zmianie warunków oświetlenia minie około 5 

minut zanim struktury krystaliczne zaadaptują się do nowych warunków i będzie można uzyskać 

wiarygodny odczyt. Konstrukcja fotodetektora wymaga aby wszystkie pomiary wykonywać w 

zaciemnionym pomieszczeniu.

Zadania do realizacji

Celem ćwiczenia jest zaplanowanie eksperymentu i sposobu jego analizy w wyniku którego 

wyznaczone zostanie napięcie półfalowe i stała Kerra oraz wykonany zostanie wykresu 

analogicznego do przedstawionego na Rys.3.

Każda osoba przystępująca do wykonania ćwiczenia laboratoryjnego jest zobowiązana 

opracować pisemnie i przedstawić prowadzącemu Sprawozdanie z wykonania ćwiczenia 

laboratoryjnego, w którym należy ująć: 

przed przystąpieniem do pomiarów:

a) harmonogram czynności na stanowisku laboratoryjnym z uwzględnieniem warunków 

bezpieczeństwa;

b) zestawienie wielkości zaplanowanych do pomiaru;

a po wykonaniu pomiarów uzupełnić o:

c) zapis procedur wyznaczania wielkości poszukiwanych i ich niepewności,

d) analizę niepewności oraz wnioski.

Przykładowe pytania kontrolne

1. Omówić zjawiska: polaryzacji, modulacji, dwójłomności, anizotropowości optycznej, Kerra.

2. Omówić zasady działania: lasera, modulatora elektrooptycznego, fotodetektora.

3. Omówić zasadę pomiaru stałej Kerra na stanowisku laboratoryjnym.

4. Omówić sposób wyznaczania stałej Kerra na bazie zaplanowanych pomiarów.

Literatura pomocnicza

[1] Katalog PHYWE LEP 2.6.02-00, www.phywe.de

[2] J.R.. Meyer-Arendt; Wstęp do optyki, PWN Warszawa 1977

[3] eds. T.G. Brown et al.; The optics encyklopedia: basic foundations and practical applications; 

Wiley-VCH Weinheim 2004

[4] E.R Mustiel, W.N. Parygin; Metody modulacji światła,  PWN Warszawa 1974

[5] M. Demianiuk; Własności fizyczne ciał stałych. Wykład z fizyki dla inżynierów. WAT 

Warszawa 2007