Fizyka statystyczna/Potencjały termodynamiczne

1

Fizyka statystyczna/Potencjały termodynamiczne

Fizyka statystyczna

Autor: Mirosław Makowiecki Email: [e-mail] Cała książka

Licencja: Creative Commons: uznanie autorstwa

[1]

Potencjałami termodynamicznymi, nazywamy takie wielkości fizyczne, których są
różniczkami zupełnymi, tzn. ich zmiana zależy od punktu początkowego do
końcowego, a nie zależy po jakiej drodze układ podążał między tymi punktami.
Różniczkami zupełnymi nazywamy wielkości, jeśli ją można zapisać w sposób (2.8).

Energia wewnętrzna

Jest to potencjał termodynamiczny, określa miarę do wykonania pracy. Na miarę tej
energii składa się energia oddziaływań między molekułami w tym ciele, energia
potencjalna elektronów a jądrem, i inne nie wymienione w tym ciele energie. Energia
wewnętrzna jest oznaczana przez U. Patrząc na wzór (1.4), który jest równaniem stanu,
ogólnie rzecz biorąc energia wewnętrzna U posiada różniczkę zupełną, czyli różniczkę
energii wewnętrznej można rozłożyć z definicji różniczki zupełnej podobnie jak w
punkcie (3.1) do postaci:

(3.1)

Wzór powyższy na różniczkę energii wewnętrznej jest rozłożony w sumę pewnych
infinitezymalnych składników, wykorzystując przy tym twierdzenie o różniczce
zupełnej, względem parametrów , którymi są niezależne parametry równania stanu
rozważanego układu. Jeśli chcemy policzyć zmianę energii wewnętrznej pomiędzy
punktami A,B, to wystarczy znać tą energię w tychże punktach.

Entalpia

Entalpia jest to potencjał termodynamiczny z definiowana jako sumę energii
wewnętrznej i iloczynu ciśnienia panującego w układzie przez jego objętość i
rozważamy ją jako:

(3.2)

••

gdzie:

•

- to entalpia.

•

- energia wewnętrzna

•

- ciśnienie w ciele w równowadze termodynamicznej

•

- objętość ciała

Entalpia

posiada różniczkę zupełną, ze względu że energia wewnętrzna posiada

różniczkę zupełną, czyli różniczkę entalpii można rozłożyć z definicji różniczki
zupełnej:

Fizyka statystyczna/Potencjały termodynamiczne

2

(3.3)

Wzór (3.3) jest rozłożony w sumę pewnych infinitezymalnych składników,
wykorzystując twierdzenie o różniczce zupełnej, względem parametrów , którymi są
niezależne parametry równania stanu rozważanego układu. Jeśli chcemy policzyć
zmianę entalpii pomiędzy punktami A,B, to wystarczy znać entalpię w tychże
punktach.

Entropia

Entropia określa miarę uporządkowania cząstek w danym układzie i wyraża się wzorem
względem dwóch parametrów niezależnych z trzech, bo jest spełnione równanie (1.4),
definicja infinitezymalnej zmiany entropii wyraża się wzorem (2.7). Entropia jest
wielkością addywną i posiada różniczkę zupełną, czyli różniczkę entropii można
rozłożyć z definicji różniczki zupełnej:

(3.4)

Wzór (3.4) jest rozłożony w sumę pewnych infinitezymalnych składników,
wykorzystując twierdzenie o różniczce zupełnej, względem parametrów , którymi są
niezależne parametry równania stanu rozważanego układu. Jeśli chcemy policzyć
zmianę entropii pomiędzy punktami A i B, to wystarczy znać entropię w tychże
punktach.

Energia swobodna

Energia swobodna jest potencjał termodynamiczny określanym wzorem:

(3.5)

Energia swobodna składa się z różnicy energii wewnętrznej  

 oraz z energii

związanej

jako iloczyn temperatury układu przez entropie posiadanej przez układ.

Energia swobodna posiada różniczkę zupełną, bo energia wewnętrzna posiada
różniczkę zupełną czyli różniczkę energii swobodnej można rozłożyć z definicji
różniczki zupełnej:

(3.6)

Wzór (3.6) jest rozłożony w sumę pewnych infinitezymalnych wielkości,
wykorzystując twierdzenie o różniczce zupełnej, względem parametrów , którymi są
niezależne parametry równania stanu rozważanego układu. Jeśli chcemy policzyć
zmianę energii swobodnej pomiędzy punktami A,B, to wystarczy znać energię
swobodną w tychże punktach.

Fizyka statystyczna/Potencjały termodynamiczne

3

Gibbsa-entalpia swobodna

Potencjał Gibbsa lub entalpia swobodna, której definicja jest jako różnicę entalpi
posiadanej przez ciało i energii związanej, jest określona:

(3.7)

Potencjał Gibbsa  

 posiada różniczkę zupełną, ponieważ jak wcześniej

udowodniliśmy entalpia posiada różniczkę zupełną, zatem różniczkę entropii można
rozłożyć z definicji różniczki zupełnej do postaci:

(3.8)

Wzór (3.8) jest rozłożony w sumę pewnych infinitezymalnych wyrazów, wykorzystując
twierdzenie o różniczce zupełnej, względem parametrów , którymi są niezależne
parametry równania stanu rozważanego układu. Jeśli chcemy policzyć zmianę
potencjału Gibbsa pomiędzy punktami A i B, to wystarczy znać potencjał Gibbsa w
tychże punktach.

Wyprowadzenie związków między potencjałami termodynamicznymi

Energia wewnętrzna

Różniczkę energii wewnętrznej

jest określana według pierwszej zasady

termodynamiki z definicją infinitezymalnej pracy (2.6) i infinitezymalnego ciepła
dostarczonego do naszego układu (2.7) uwzględniając definicję różniczki potencjału
termodynamicznego energii wewnętrznej, mówiąca ile cząstek wchodzi do układu z
otoczenia, co jest też związane ze zmiana energii wewnętrznej układu, oczywiście jest,
że:

(3.9)

Energię wewnętrzna posiada różniczkę zupełną, tzn. z definicji różniczki zupełnej,
można rozłożyć tą wielkość względem entropii, objętości i liczby cząstek jaki posiada
nasz badany układ:

(3.10)

Porównujemy wzór (3.9) ze wzorem (3.10), które oznaczają to samo, ale współczynniki
przy różniczkach przy drugim wzorze są zupełne inaczej napisanej za pomocą
pochodnych cząstkowych niż w pierwszym wzorze na różniczkę energii wewnętrznej,
zatem na podstawie porównania wspominanych tożsamości przyjmujemy wzory na
zmienne termodynamiczne:

(3.11)

(3.12)

(3.13)

Fizyka statystyczna/Potencjały termodynamiczne

4

Entalpia

Różniczkę entalpii można zapisać, korzystając przy tym (3.1) (definicji etalpi) i
podstawiając do niego tożsamość różniczkową (3.1) (definicji różniczki energii
wewnętrznej), można tą naszą różniczkę rozpisać ją, jak się przekonamy względem
różniczki zupełnej entropii, ciśnienia i liczby cząstek:

(3.14)

Ze wzoru (3.15) wynika wzór zdefiniowanych na różniczkach:

(3.15)

Entalpia posiada różniczkę zupełną, tzn. z definicji różniczki zupełnej, można rozłożyć
tą różniczkę względem entropii, ciśnienia i liczby cząstek jaki posiada nasz badany
układ:

(3.16)

Porównujemy wzór (3.16) ze wzorem (3.15), które oznaczają to samo, ale
współczynniki przy różniczkach przy drugim wzorze są zupełne inaczej napisane,
zdefiniowane za pomocą pochodnych cząstkowych niż w pierwszym wzorze na
różniczkę entalpii, zatem na podstawie porównania wspomnianych tożsamości
przyjmujemy wzory na zmienne termodynamiczne:

(3.17)

(3.18)

(3.19)

Energia swobodna

Różniczkę energii swobodnej można zapisać przy pomocy rozpisanej (3.9) różniczki
energii wewnętrznej, zatem:
Różniczkę energii swobodnej można zapisać, korzystając przy tym (3.9) i podstawiając
do niego tożsamość różniczkową (3.6) (definicji różniczki energii wewnętrznej), można
tą naszą różniczkę rozpisać ją, jak się przekonamy względem różniczki zupełnej
entropii, temperatury i liczby cząstek:

(3.20)

Wzór (3.17) można zapisać w sposób:

(3.21)

Entalpia posiada różniczkę zupełną, tzn. z definicji różniczki zupełnej, można rozłożyć
tą różniczkę względem entropii, ciśnienia i liczby cząstek jaki posiada nasz badany
układ:

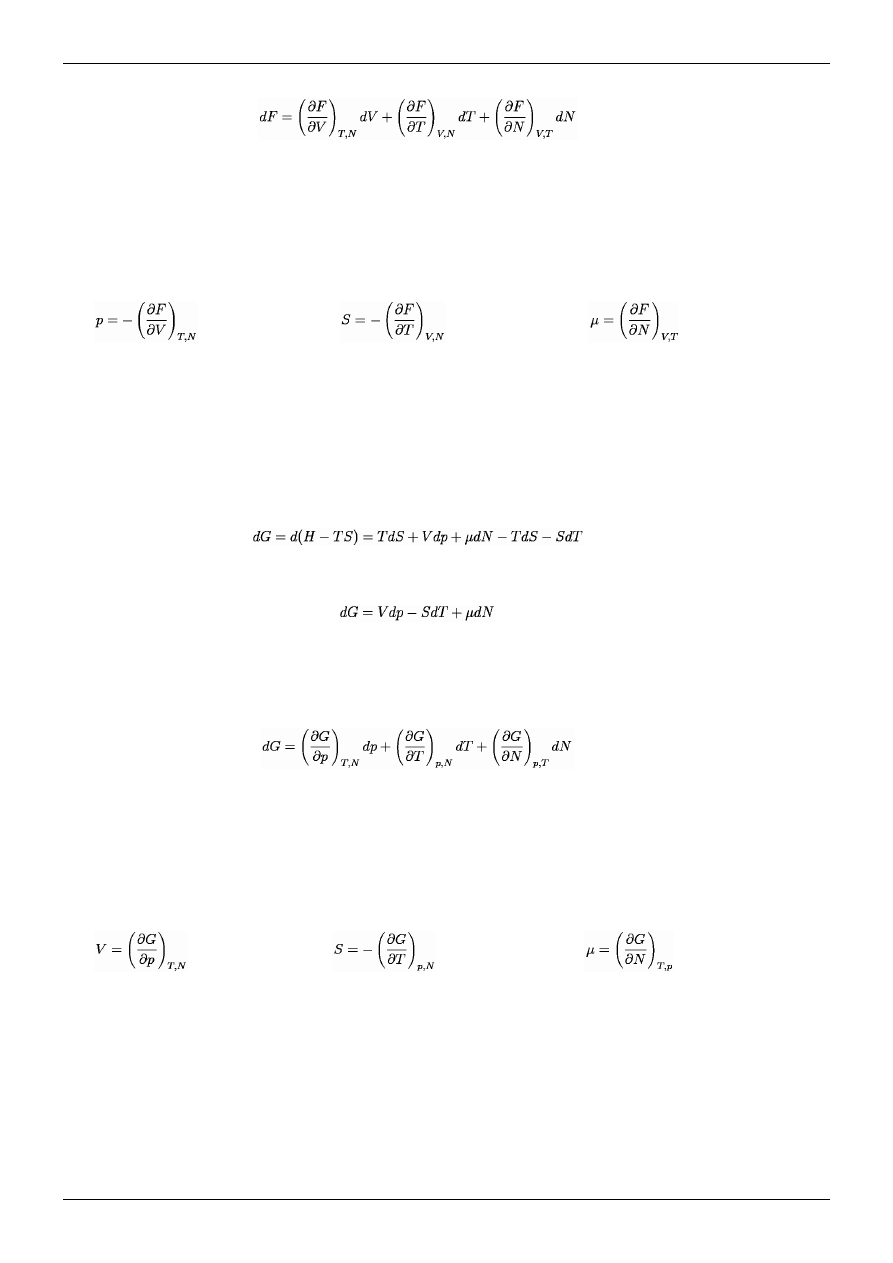
Fizyka statystyczna/Potencjały termodynamiczne

5

(3.22)

Porównujemy wzór (3.22) ze wzorem (3.21), które oznaczają to samo, ale
współczynniki przy różniczkach przy drugim wzorze są zupełne inaczej napisane za
pomocą pochodnych cząstkowych niż w pierwszym wzorze na różniczkę energii
swobodnej, zatem na podstawie porównania wspomnianych tożsamości przyjmujemy
wzory na zmienne termodynamiczne:

(3.23)

(3.24)

(3.25)

Potencjał Gibbsa

Różniczkę na potencjał Gibbsa można zapisać, korzystając przy tym (3.7) (definicji
potencjału Gibbsa) i podstawiając do niego tożsamość różniczkową (3.15) (definicji
różniczki etalpii), można tą naszą różniczkę rozpisać ją, jak się przekonamy względem
różniczki zupełnej ciśnienia, temperatury i liczby cząstek:

(3.26)

Ze wzoru (3.27) wynika wzór zdefiniowanych na różniczkach:

(3.27)

Entalpia posiada różniczkę zupełną, tzn. z definicji różniczki zupełnej, można rozłożyć
tą różniczkę względem entropii, ciśnienia i liczby cząstek jaki posiada nasz badany
układ:

(3.28)

Porównujemy wzór (3.28) ze wzorem (3.27), które oznaczają to samo, ale
współczynniki przy różniczkach przy drugim wzorze są zupełne inaczej zdefiniowane
za pomocą pochodnych cząstkowych niż w pierwszym wzorze na różniczkę potencjału
Gibbsa, zatem na podstawie porównania wspominanych tożsamości przyjmujemy
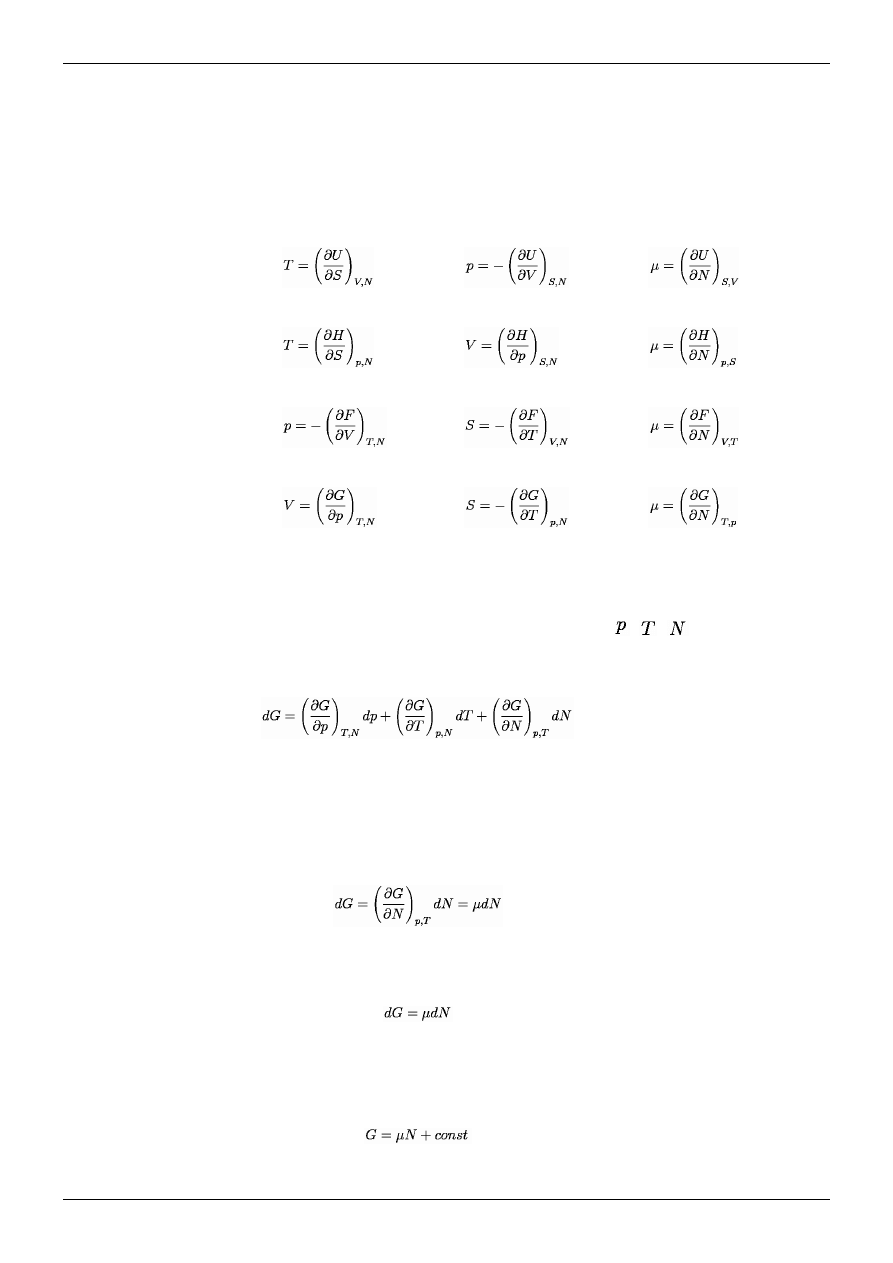
wzory na zmienne termodynamiczne:

(3.29)

(3.30)

(3.31)

Fizyka statystyczna/Potencjały termodynamiczne

6

Wzory między potencjałami a parametrami mierzalnymi

Zbierając wszystkie wyniki, to z definicji potencjałów termodynamicznych, tzn. energii
wewnętrznej, entalpii, energii swobodnej i potencjału Gibbsa, można wyznaczyć z
tychże parametrów ekstensywnych policzyć parametry termodynamiczne ekstensywne
(intensywne) wedle sposobu:

Energia wewnętrzna

(3.32)

(3.33)

(3.34)

Entalpia

(3.35)

(3.36)

(3.37)

Energia swobodna

(3.38)

(3.39)

(3.40)

Potencjał Gibbsa

(3.41)

(3.42)

(3.43)

Zależność między potencjałem chemicznym a potencjałem Gibbsa

Rozpiszemy różniczkę potencjału Gibbsa względem zmiennych , ,

, oczywiście

jest, że różniczka zupełna funkcji Gibbsa (ten potencjał posiada różniczkę zupełną)
można z definicji tejże różniczki zapisać wedle:

(3.44)

Jeśli we wzorze (3.44) będziemy rozpatrywać stałe ciśnienie (układ jest w równowadze
mechanicznej) i stałą temperaturę w układzie (układ jest w równowadzie
termodynamicznej), to wtedy dwa pierwsze wyrazy znikają, a pozostaje tylko trzeci,
który jest zależny od potencjału chemicznego i różniczki liczby cząstek jakie posiada
układ, zatem wspomniane równanie przechodzi w:

(3.45)

Wzór (3.45) przy postawionych warunkach brzegowych możemy przepisać dla
przejrzystości dalszych rozważań w postaci różniczkowej:

(3.46)

Całkujemy wzór (3.46) obustronnie z prawej strony względem ilości cząstek przy
stałym potencjale chemicznym, a z lewej względem potencjału Gibbsa, wtedy
dostajemy tożsamość ze stałą bliżej nieokreśloną:

(3.47)

Fizyka statystyczna/Potencjały termodynamiczne

7

Przyjmujemy, że stała jest równa zera w równaniu (3.47), bo potencjał Gibbsa nie ma
wartości absolutnej, tylko jest określona z dokładnością do pewnej stałej, czyli możemy
wyzerować tą stałą, nie zmniejszając ogólności znaczenia tego potencjału
ekstensywengo G, czyli przyjmijmy const=0, która występuje we wzorze (3.47), wtedy
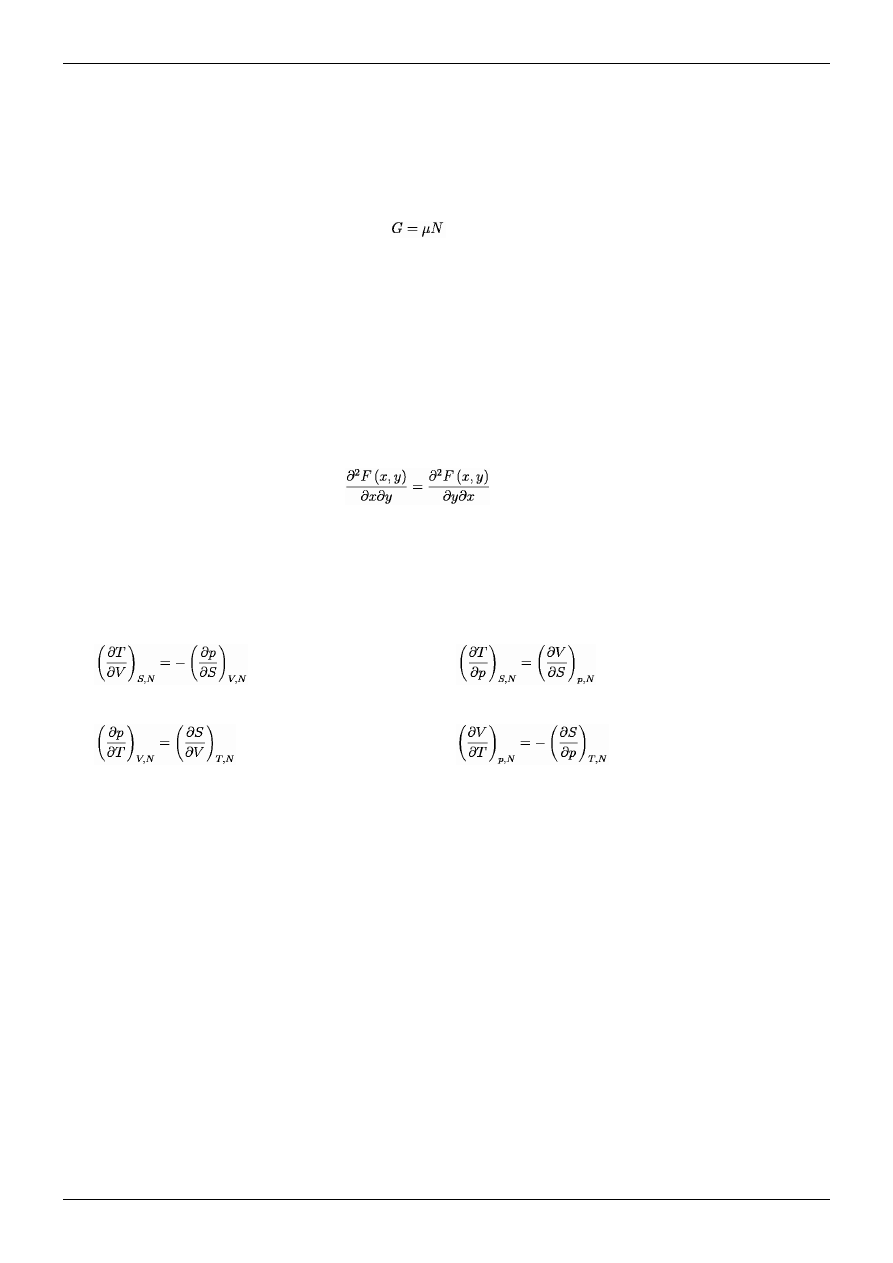
dochodzimy do wniosku:

(3.48)

Równanie (3.48) jest spełnione w stanie równowagi termodynamicznej, tzn. gdy
temperatura i ciśnienie w układzie nie zmieniają się, tylko liczba cząstek może się
zmienia zgodnie (3.46). W końcu w równanie (3.48) na potencjał Gibbsa jest zależny
od potencjału chemicznego i ilości cząstek w danej fazie.

Prawa Maxwella w statystyce fizycznej

Potencjały termodynamiczne posiadają różniczkę zupełną, zatem z definicji różniczki
zupełnej powinno zachodzić:

(3.49)

Wzory Maxwella można wyprowadzić korzystając z warunku, by różniczka była
różniczką zupełną (3.49) oraz ze wzorów w rozdziale"Wzory między potencjałami a
parametrami mierzalnymi", wtedy możemy napisać związki termodynamiczne, które są
nazywane związkami (prawami) Maxwella:

(3.50)

(3.51)

(3.52)

(3.53)

Fizyka statystyczna/Potencjały termodynamiczne

8

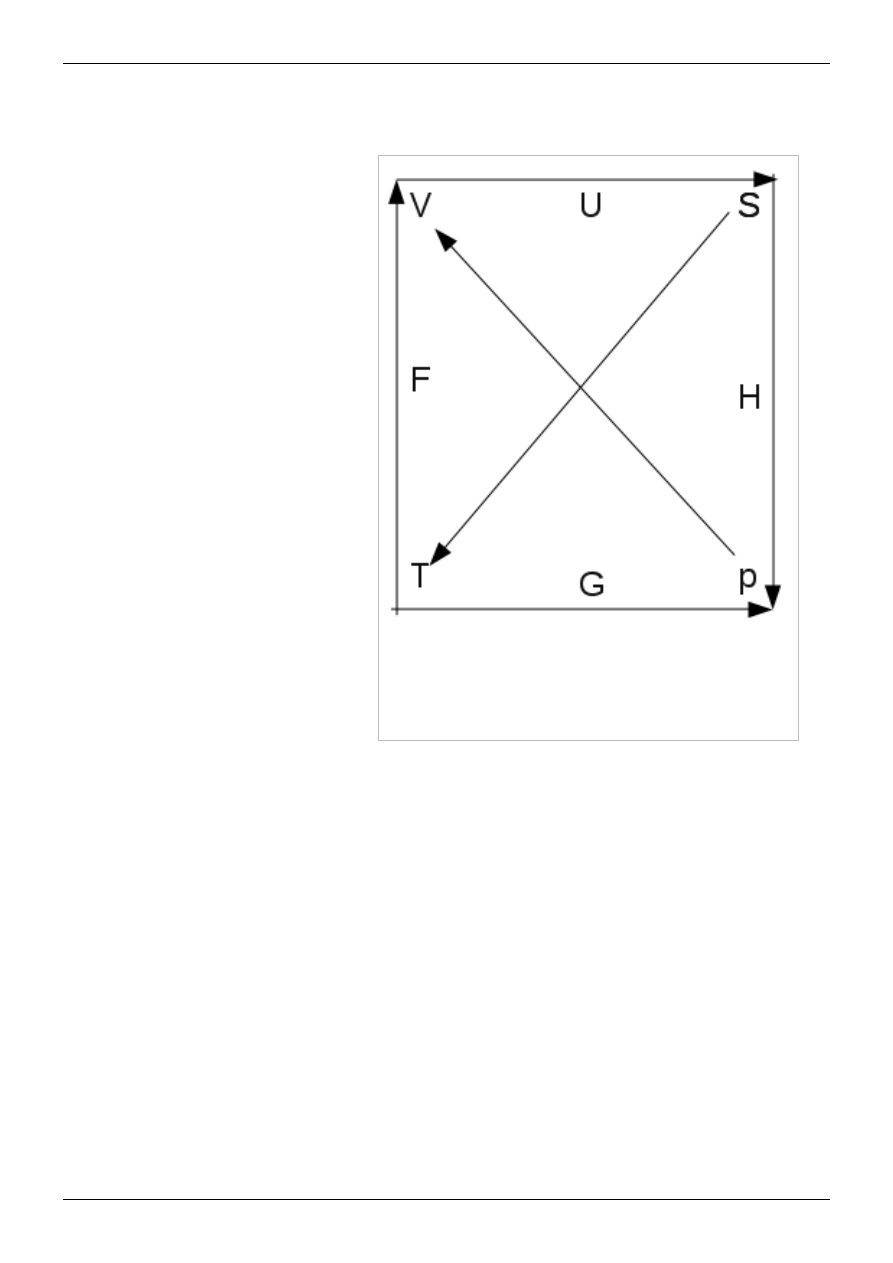
Łatwy sposób zapamiętania związków między potencjałami termodynamicznymi a
także praw Maxwella

Rysunek pozwala zapamiętać w łatwy sposób

związki między potencjałami

termodynamicznymi a parametrami nie będące

potencjałami termodynamicznymi a także prawa

Maxwella w fizyce statystycznej

Jak zapamiętać związki między
potencjałami
termodynamicznymi, a
mianowicie tak. Mamy cztery
potencjały termodynamiczne,
tzn. U,H,G,F. Jak widzimy na
rysunku z prawej i lewej strony
lub góra i dół występują
parametry mierzalne p,V,T,S. A
więc te wielkości, których
potencjał termodynamiczny
tworzy pochodną występujący w
środku danego boku według
naszego rysunku obok,
względem wielkości mierzalnej
występującym z prawej i z lewej
strony. W ten sposób dodarliśmy
do zmiennej mierzalnej , jeśli
przy tej zmiennej występuje
strzałka to ta pochodna
cząstkowa ma wartość ujemną, a
jego wartość występuje na
początku wektora, znak dodatni,
gdy dodarliśmy do miejsca,
który jest początkiem wektora, a
wartość tej pochodnej występuje
na końcu tego wektora. Jak
zapamiętać prawa Maxwella, a mianowicie tak. Na obrzeżach występują cztery
wektory, początek (koniec) tego wektora wskazuje względem jakiej wielkości
będziemy różniczkować, a koniec (początek) jaką wielkość różniczkujemy. Jeśli
wielkość którą różniczkujemy znajduje się na początku wektora, to wtedy znak naszego
wyrażenia jest dodatni, a w przeciwnym wypadku ujemny. To wyrażenie jest równe tak
samo nierozpatrywany wyrażeniu dla boku przeciwległego. Widzimy, że za pomocą
takiej metody można łatwo wywnioskować znak (minus lub plus) w tożsamości
Maxwella.

Przypisy

[1] http:/

/

creativecommons.

org/

licenses/

by-sa/

3.

0/

deed.

pl

Źródła i autorzy artykułu

9

Źródła i autorzy artykułu

Fizyka statystyczna/Potencjały termodynamiczne  Źródło: http://pl.wikibooks.org/w/index.php?oldid=169389  Autorzy: Kj, Lethern, Persino, 19 anonimowych edycji

Źródła, licencje i autorzy grafik

File:Thermodynamic potentials.png  Źródło: http://pl.wikibooks.org/w/index.php?title=Plik:Thermodynamic_potentials.png  Licencja: GNU Free Documentation License  Autorzy: Persino

Licencja

Creative Commons Attribution-Share Alike 3.0 Unported
//creativecommons.org/licenses/by-sa/3.0/