Zasada działania silnika i prądnicy prądu stałego:

Siła działająca na przewodnik z prądem w polu magnetycznym:

l

Bi

F

t

=

b- wartość chwilowa indukcji

i

t

– wartość prądu chwilowa prądu

l – długość przewodnika

Moment elektromagnetyczny jest równy:

2

D

F

Fr

M

e

=

=

M

e

– moment pojedynczego pręta

r – promień wirnika

D – średnica wirnika

2

Dl

Bi

M

t

e

=

dla z zwojów połączonych szeregowo:

z

Dl

Bi

M

t

e

2

=

Strumień magnetyczny:

BDl

BS

=

=

φ

Stąd:

t

t

e

i

k

zi

M

φ

φ

=

=

2

1

z

k

2

1

=

Siła elektromotoryczna pojedynczego pręta:

Blv

e

t

=

v –wartość chwilowa prędkości

2

D

r

v

ω

ω

=

=

ω - prędkość kątowa

2

D

Bl

e

t

ω

=

Dla z zwojów połączonych szeregowo:

φω

φω

ω

k

z

z

D

bl

e

t

=

=

=

2

1

2

Równanie obwodu twornika, zgodnie z prawami Kirchhoffa:

dt

di

L

e

i

R

u

t

t

t

t

t

t

+

+

=

Równanie obwodu wzbudzenia:

dt

di

L

i

R

u

w

w

w

w

w

+

=

W stanie ustalonym:

w

w

w

I

R

U

=

t

t

t

t

E

I

R

U

+

=

φω

k

I

R

U

t

t

t

+

=

φ

ω

k

I

R

U

t

t

t

−

=

Prądnica w stanach ustalonych:

t

t

t

t

I

R

E

U

−

=

t

t

t

I

R

k

U

−

Φ

=

ω

W nowszej literaturze występują równoznaczne oznaczenia związane

z modelami maszyny uogólnionej:

t

q

u

u

=

Φ

= k

d

ψ

t

q

i

i

=

q

d

e

i

M

ψ

=

dt

di

L

i

R

u

q

q

d

q

q

q

+

+

=

ωψ

dt

d

i

R

u

q

d

q

q

q

ψ

ωψ

+

+

=

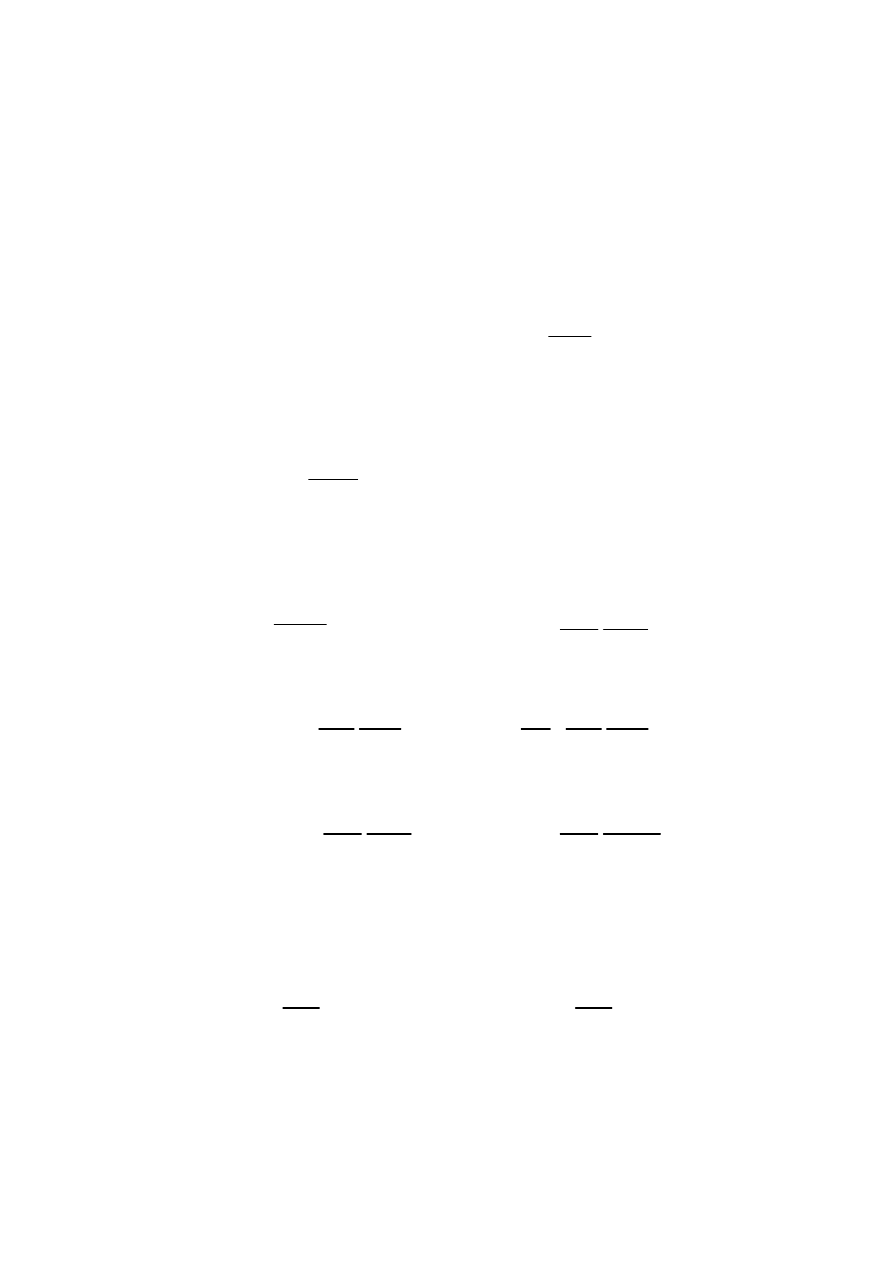
Dla maszyny prądu stałego, wykorzystywanej jako element automatyki,

wyznaczmy wybrane transmitancje. Sygnałem wejściowym może być np.

napięcie twornika (dla maszyny obcowzbudnej) a sygnałem wyjściowym

prędkość obrotowa. Korzystając z równań wyprowadzonych wyżej otrzymamy

równanie obwodu elektrycznego:

dt

di

L

k

i

R

u

t

t

t

t

t

+

+

=

φ

Równanie dynamiki:

t

o

e

i

k

M

M

dt

d

J

φ

ω

=

−

=

Przyjmijmy, że moment obciążenia jest równy M

o

=0, otrzymamy:

t

i

k

dt

d

J

φ

ω

=

dt

d

k

J

i

t

ω

φ

=

)

(

dt

d

k

J

dt

d

L

k

dt

d

k

J

R

u

t

t

t

ω

φ

φ

ω

φ

+

+

=

2

2

dt

d

k

J

L

k

dt

d

k

J

R

u

t

t

t

ω

φ

φω

ω

φ

+

+

=

Dokonując transformaty Laplace'a (przy założeniu zerowych warunków

początkowych) otrzymamy:

)

(

)

(

)

(

2

s

s

k

J

L

s

k

s

s

k

J

R

u

t

t

t

ω

φ

φω

ω

φ

+

+

=

Transmitancję wyznaczamy zatem z zależności:

φ

φ

φ

ω

k

s

k

J

R

s

k

J

L

s

u

s

s

G

t

t

t

+

+

=

=

2

1

)

(

)

(

)

(

φ

φ

φ

ω

k

s

k

J

R

s

k

J

L

s

u

s

s

G

t

t

t

+

+

=

=

2

1

)

(

)

(

)

(

1

1

)

(

)

(

)

(

2

2

2

+

+

=

=

s

k

J

R

s

k

J

L

k

s

u

s

s

G

t

t

t

φ

φ

φ

ω

Oznaczmy:

t

t

e

R

L

T

=

– elektromagnetyczna stała czasowa

2

φ

k

JR

T

t

M

=

elektromechaniczna stała czasowa

φ

k

k

1

=

- wzmocnienie

Otrzymamy:

1

)

(

2

+

+

=

s

T

s

T

T

k

s

G

M

M

e

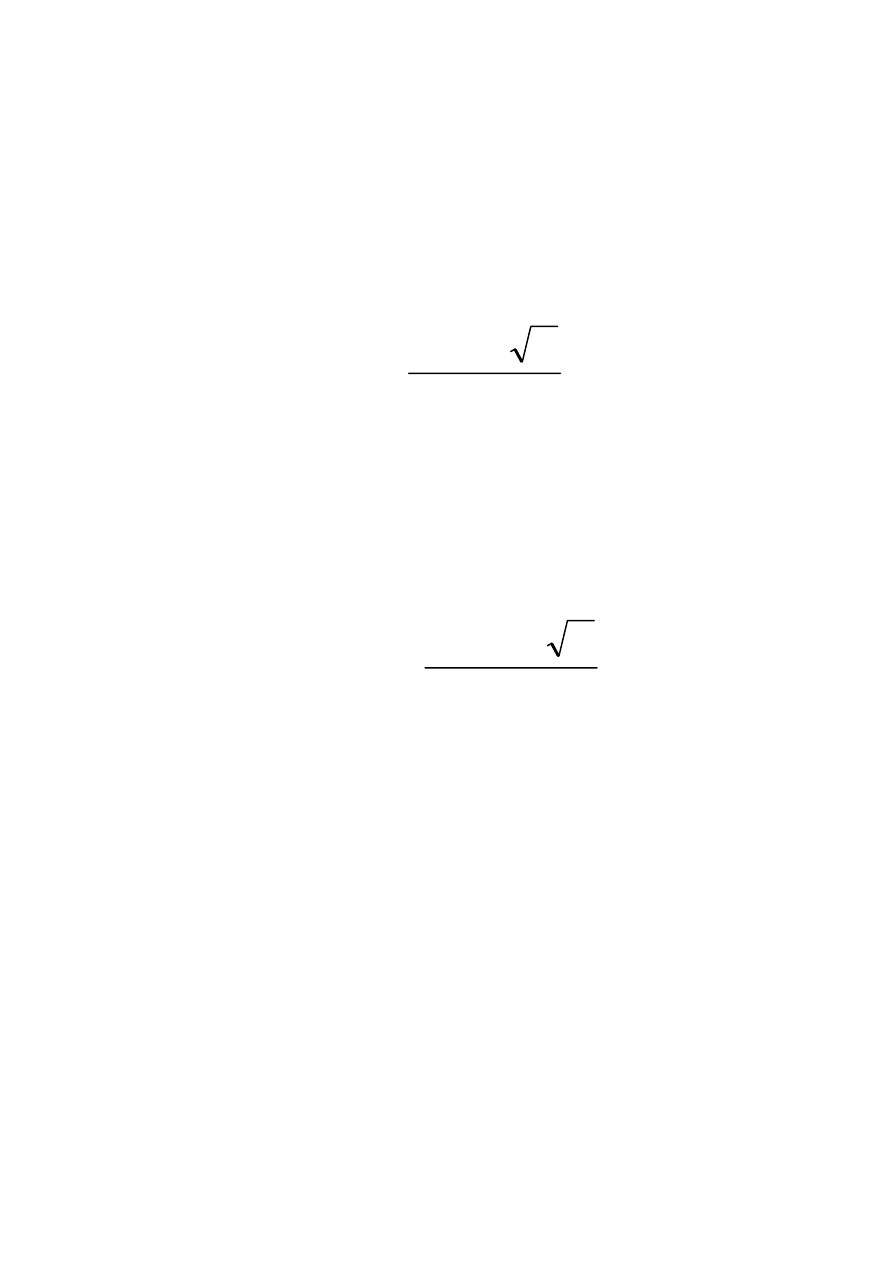
Przebieg wartości prędkości kątowej przy skokowej zmianie napięcia

zależy od biegunów transmitancji. Bieguny transmitancji mają postać zależną od

wartości:

e

M

M

T

T

T

4

2

−

=

∆

Jeśli

∆≥0 bieguny mają tylko część rzeczywistą postaci:

e

M

M

T

T

T

s

2

2

,

1

∆

±

−

=

Przebieg prędkości ma wówczas charakter aperiodyczny, natomiast

w przypadku gdy:

0

4

2

<

−

=

e

M

M

T

T

T

∆

Przebieg ma charakter oscylacyjny tłumiony. Bieguny przyjmują wartość:

e

M

M

T

T

j

T

s

2

2

,

1

∆

±

−

=

Z warunku tego wynika, że oscylacyjna odpowiedź prędkości występuje,

gdy spełniona jest zależność:

e

M

T

T

4

<